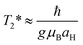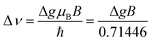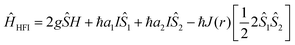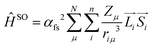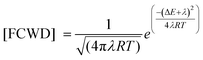Open Access Article
Open Access ArticleMaking triplets from photo-generated charges: observations, mechanisms and theory
Dáire J.
Gibbons
 ab,
Aram
Farawar
a,
Paul
Mazzella
a,
Stéphanie
Leroy-Lhez
ab,
Aram
Farawar
a,
Paul
Mazzella
a,
Stéphanie
Leroy-Lhez
 *b and
René M.
Williams
*b and
René M.
Williams
 *a
*a
aMolecular Photonics Group, Van't Hoff Institute for Molecular Sciences (HIMS), Universiteit van Amsterdam, Science Park 904, 1098 XH Amsterdam, Netherlands. E-mail: r.m.williams@uva.nl
bPEIRENE – EA7500, Faculty of Sciences and Technology – University of Limoges, 123 avenue Albert Thomas, 87060 Limoges, France. E-mail: stephanie.lhez@unilim.fr
First published on 23rd January 2020
Abstract
Triplet formation by charge recombination is a phenomenon that is encountered in many fields of the photo-sciences and can be a detrimental unwanted side effect, but can also be exploited as a useful triplet generation method, for instance in photodynamic therapy. In this Perspective we describe the various aspects that play a role in the decay of charge separated states into local triplet states. The observations and structures of a selection of (pre-2015) molecular electron donor–acceptor systems in which triplet formation by charge recombination occurs are reported. An overview is given of some more recent systems consisting of BODIPY dimers, and BODIPYs attached to various electron-donor units displaying this same triplet formation process. A selection of polymer–fullerene blends in which triplet formation by (non-geminate) charge recombination has been observed, is presented. Furthermore, in-depth information regarding the mechanistic aspects of triplet formation by charge recombination is given on spin dephasing, through hyperfine interactions, as well as on spin–orbit coupling occurring simultaneously with charge recombination. The limits and constraints of these factors and their role in intersystem crossing are discussed. A pictorial view of the two mechanisms is given and this is correlated to aspects of the selection rules for triplet formation, the so-called El-Sayed rules. It is shown that the timescale of triplet formation by charge recombination is indicative for the mechanism that is responsible for the process. The relatively slow rates (CRkT ∼ 1 × 108 s−1 or slower) can be correlated to proton hyperfine interactions (also called the radical pair mechanism), but substantially faster rates (CRkT ∼ 1 × 109 up to 2.5 × 1010 s−1 or faster) have to be correlated to spin–orbit coupling effects. Several examples of molecular systems showing such fast rates are available and their electron donor and acceptor orbitals display an orthogonal relationship with respect to each other. This orientation of (the nodal planes of) the π-orbitals of the donor and acceptor units is correlated to the mechanisms in photodynamic agents and photovoltaic blends.
1. Introduction
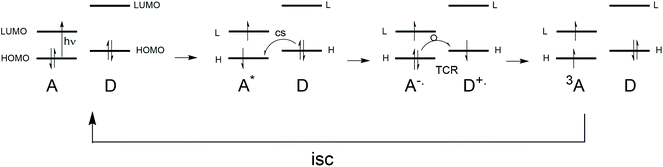
Triplet excited state formation is of great importance for many applications such as photo-initiators for photopolymerization,1 photodynamic (anticancer) therapy,2 photodynamic antimicrobial chemotherapy3 as well as light emitting diodes containing triplet emitters.4 In photovoltaics, making triplets by using singlet fission5 entails the promise of passing the Shockley–Queisser limit6 by creating two free charged pairs from one photon. However, next to creating charges by using triplet excited states, also the reverse process, the formation of triplet states from charges has gained a lot of interest, especially in recent investigations of organic thin film blends that relate to photovoltaic materials.7–9 Various reports on these matters state that there is no clarity regarding the mechanistic aspects of this loss channel in organic photovoltaic materials,10–12 especially when occurring on a sub-nanosecond timescale.Upon local photo-excitation of an electron donor–acceptor system, the excited singlet state is formed, from which charge separation can occur. The process of photoinduced charge separation has been described extensively,13 and will not be dwelled upon here. Most charges that are photogenerated recombine back to a ground state singlet. Sometimes, high lying charge-transfer states can even repopulate the singlet excited state, leading to so-called delayed luminescence.14 However, instead of recombining to the singlet, the charges can also recombine to form a triplet state. This pathway is more exotic, but there are many examples where this triplet formation by charge recombination process, sometimes also called triplet charge recombination, plays a role in the photophysical processes occurring after photoexcitation.
The triplet excited state contains two unpaired electrons with the same spin in separate orbitals. In the absence of a magnetic field, the three triplet levels are degenerate only for a totally symmetric system. However, for an asymmetric environment the so-called zero field splitting (characterized by D and E) orients the spin-vectors along the molecular x–y–z axis giving the Tx, Ty and Tz triplet levels. Applying a magnetic field results in the Zeeman effect and the thus introduced magnetic operator (Hamiltonian) converts the levels into the more often encountered T+, T0 and T− levels represented by their spin orientations relative to the magnetic field.15,16
In this work, examples are given of the experimental observations regarding triplet formation by charge recombination in molecular electron donor–acceptor systems studied in solution as well as in various polymer–fullerene thin film blends. Special attention is given to recent work on BODIPY dyes that are attached to electron donors, as well as BODIPY dimers. Next, the currently known mechanistic aspects for these processes are presented. Both (H-HFI) proton hyperfine interactions (= radical pair mechanism, RPM) as well as spin–orbit coupling are discussed in detail with relation to charge recombination. Focus is on the mechanistic aspects regarding the “electron spin–flip”, implying that this is the rate determining step in these systems (not the energetics). A correlation (as well as a visualization) is made between the spin–orbit charge transfer intersystem crossing (SOCT-ISC) mechanism and the El-Sayed rules, the spin selection rules for triplet state formation (see section 5).
It has to be noted that a third, more exotic (singlet fission) mechanism has also been proven. In a thin film of a TDI (terrylene-3,4:11,12-bis(dicarboximide)) derivative, an excited state dimer with charge-transfer character can split into two triplet states by singlet fission.17 This third mechanism is beyond the scope of this Perspective.
Magnetic field effects in time resolved electron spin/paramagnetic resonance (TR-ESR/TR-EPR) also fall beyond the scope of this perspective. Interestingly these aspects regarding triplet formation by charge recombination have been reviewed very recently.18
This Perspective is partly meant to be set up as a tutorial review. It assumes general knowledge of photoinduced charge separation as well as basic knowledge on triplet states. Indeed, the recombination of charges forming a triplet state as the “product” is our topic. This is an illustrative review, it is not a comprehensive survey, and reports on research published between 1968 and June 2019.
Within the theory of electron transfer, creating charges with light is often well described and understood within the frame-work of the Classical Marcus equation. The recombination of the charges is always more complex, often requiring the Semi-classical Marcus theory. Creating long-lived charges (by controlling the charge recombination) in order to use the energy of the photons to create an (electro)chemical potential or electricity still is an important scientific challenge. We believe that charge recombination to a triplet state is one of the most complex aspects of the electron transfer theory, as the role of spin comes into play and becomes one of the determining factors, next to all the other factors in the electron transfer theory.
Triplet formation by charge recombination is an alternative method to generate triplet states. Other methods are using the heavy atom effect or using triplet sensitization. The heavy atom effect is potentially expensive (for instance with Pd or Pt) and also enhances spin orbit coupling back to the ground state. For triplet sensitization we need other triplet forming systems that can transfer their triplet excited state energy. By simply incorporating an electron donor or acceptor we can change the properties of molecules converting them into systems with high triplet yields by applying the triplet formation by charge recombination mechanism.
2. Fast molecular electron donor–acceptor systems (pre-2015)
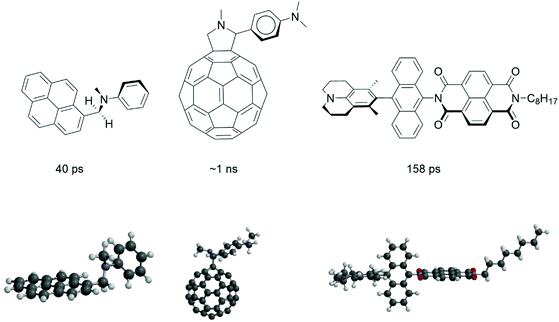
We start with a selection of four molecular electron donor acceptor systems to show that structural factors play an important role in fast charge recombination to the triplet state. It is instructive to look at the some of the old work of Noburu Mataga, one of the most excellent Japanese photochemists of the 20th century. The amount of detail and insight that this work displays is flabbergasting and a more in-depth explanation of some of these insights is part of our current mission.Mataga and co-workers19 observed the formation of locally excited triplet states (with τCR(T) = 40 ps, τCR(T) = decay time of charge-transfer (CT) state correlating to the time of formation of the local triplet state T) from charge-transfer intermediates in 1981. The fastest rate of triplet formation by charge recombination (CRkT = 2.5 × 1010 s−1) was observed for N-methyl-N-phenyl-1-pyrenemethanamine (see Fig. 1) in hexane.
These studies uncovered “the very fast generation of the triplet state localized on the pyrene (acceptor) moiety via the intramolecular charge-transfer state (referred to as hetero-excimer). The intersystem crossing rate depends rather strongly upon the mutual configuration of donor and acceptor groups as well as the solvent polarity.19 The compounds with one CH2 group where the two moieties are close but not parallel have much larger CRkT values compared to compounds with two or three CH2 groups where the formation of a sandwich-type charge-transfer complex is possible”. As reported by Mataga et al.19 “the matrix element of the spin–orbit coupling interaction between the heteroexcimer state and the so-called 3La state of pyrene, will become enhanced in the perpendicular configuration” (the La transitions of pyrene are directed in the long axis of the molecule). This reasoning is the same as in the case of the relatively large spin–orbit coupling matrix element between π–π* and n–π* transitions.19 Mataga and co-workers point to the perpendicular nodal planes of the molecular orbitals of the (aniline)donor and (pyrene)acceptor playing a role in the process (see also section 5).
In 1995 Williams and Verhoeven reported20 that “the relatively high triplet yield (ΦT = 0.8) and the absence of fluorescence (97% quenched) of the bridged C60 (acceptor)–aniline (donor) system (see Fig. 1) indicates that charge recombination to the local fullerene triplet is a major decay pathway of the charge-transfer state in dichloromethane (a solvent with medium polarity)”. Since nanosecond transient absorption spectroscopy was applied, it can be inferred that this charge recombination is occurring on a ∼ns time-scale. The 3D structure (Fig. 1) shows that the aniline donor is virtually orthogonal to the curvature of the fullerene π-system. Just like the molecule studied by Mataga, a ∼90° angle between donor and acceptor is present.
Indeed, Williams et al. encountered triplet formation by charge recombination in 1995 as an exotic event without putting much emphasis on it. This work however has triggered computational studies that give useful insight: computational chemistry has advanced to such a level that excited state charge transfer processes are within reach. It is important to note that for such systems TD-DFT calculations on excited state electron transfer processes are possible. TD-DFT calculations of the electron transfer time (τCS = 27 ps) of this system21 in the strongly polar benzonitrile solvent as well as more exact determination of experimental times22 of charge separation (τCS = 5 ps) and recombination to the ground state (τCR = 32 ps) have been reported. These latter results imply that accurate TD-DFT computations can be obtained for such excited state charge transfer processes and it would be highly interesting and computationally challenging to use TD-DFT to determine the charge-transfer integrals for triplet formation by charge recombination (see section 5).
Wasielewski et al. investigated “intersystem crossing in a series of donor-bridge-acceptor molecules involving photo-generated strongly spin exchange-coupled radical ion pairs” in 2012.23 Their fastest system has a 3,5-dimethyl-4-julolidine (DMJ) donor, which is connected via an anthracene bridge to a naphthalene-1,8:4,5-bis(dicarboximide) (NI) acceptor. “Femtosecond transient absorption spectroscopy shows that photo-driven charge separation produces DMJ+˙-An-NI−˙ quantitatively (τCS ≤ 10 ps), and that charge recombination (with τCR(T) = 158 ps) to the triplet state on An occurs (CRkT = 6.3 × 109 s−1)”. The NI π system is perpendicular to that of An and parallel to that of DMJ. “Clearly, charge recombination in DMJ+˙-An-NI−˙ will formally require two electron and/or hole transfers between mutually perpendicular π systems to produce 3*An and necessitates consideration of the orbital changes of both charge transfers”.
“The triplet sublevels populated by spin–orbit coupling in these molecules depend on the donor–acceptor geometry of the charge-separated state. This is consistent with the fact that the intersystem crossing mechanism requires suitable donor and acceptor orbitals which are nearly perpendicular. Electron transfer results in a large orbital angular momentum change that must be compensated by a fast spin flip to keep the overall angular momentum of the system constant”.23 Spin–orbit charge-transfer intersystem crossing (SOCT-ISC) is the nomenclature for the mechanism of these molecular systems. It relates directly to the mechanistic aspects for the orthogonal systems reported by Mataga and co-workers, as described earlier. In some of the slower molecules reported by Wasielewski, the radical pair mechanism (HFI) and SOCT-ISC operate simultaneously, with similar rates (τCR(T) = 10 ns).
Van Willigen and co-workers observed fast direct conversion of the singlet charge-transfer state into a local triplet state for naphthyl-acridinium compounds with EPR. Their experimental data is consistent with a (charged-shifted singlet state) 1CSH → 3LE (locally excited triplet state) mechanism of triplet-state formation.24 In particular, the 10-methyl-9-(1-naphthalenyl)acridinium hexafluorophosphate dyad (1) (see Fig. 2) was held orthogonal due to steric rotational hindrance of the C–H groups of both electron donor (naphthyl) and acceptor (acridinium) subunits.
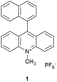 | ||
| Fig. 2 10-Methyl-9-(1-naphthalenyl)acridinium hexafluorophosphate dyad that undergoes triplet formation by charge recombination from a charge-transfer state.24 | ||
These examples of molecular electron donor–acceptor systems indicate that the specific orientation of the π-systems of the donor and acceptor are of great importance for the occurrence of fast triplet formation by charge recombination, and that this process is facilitated by spin–orbit coupling.
Many more examples of molecular systems are available in which the more general, slower triplet formation by charge recombination occurs. Verhoeven et al. reported rates of CRkT ∼ 1 × 108 s−1 for (HFI-limited) co-planar dimethoxynaphthanlene(donor)–dicyanovinyl(acceptor) systems studied with EPR25 and with transient absorption spectroscopy.26 Furthermore, for an artificial photosynthetic reaction center27 a rate of CRkT = 2.2 × 107 s−1 was obtained. Based on these examples it is concluded that relatively slow rates (CRkT ∼ 1 × 108 s−1 or slower) can be correlated to and can be dominated by proton hyperfine interactions (if spin inversion is the rate determining step and not the electron transfer energetics). Substantially faster rates however (CRkT ∼ 1 × 109 up to 2.5 × 1010 s−1 or faster), have to be correlated to spin–orbit coupling effects in orthogonal systems, as also inferred by Mataga et al.19 and Wasielewski et al.23
3. BODIPY-based dimers and dyads
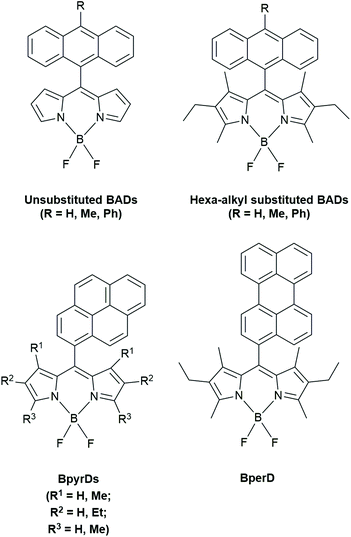
We proceed with an overview of recent work on BODIPY systems. The renewed strong interest in making triplets from charged states has resulted in a great variety of molecular structures, and attempts are made to obtain the ultimate system for this purpose. If we combine these works with the results presented in the previous section we can unify these two parts (see section 5).Over the past two years, there have been a score of investigations into the use of BODIPY-related dyads as a heavy atom-free photosensitizer (PS). The following discussion entails these investigations as well as their outcomes, impact and applications. In general, BODIPY dyes by themselves are strongly fluorescent and are generally characterized by a fluorescence quantum yield close to unity.28 Early 2017, Filatov et al.29 demonstrated that BODIPY(acceptor)–anthracene(donor) dyads (BADs) form triplet states via photoinduced electron transfer (PeT). When excited with light these BADs yield charge separated states (CS or CT state) which, under the right conditions (solvent, donor–acceptor strength, distance) undergo charge recombination (CR) to form the desired triplet state. Using single crystal X-ray crystallography, the authors demonstrated that when irradiated under aerobic conditions, these BADs react with singlet oxygen (1O2) resulting in oxygen addition onto the anthracene moiety. Upon reaction with 1O2, these dyads formed adducts where the 1O2 was covalently bound to the anthracene by breaking the aromaticity. These showed strongly increased fluorescence (because PeT is now impossible) and the authors noted that this property could be used in in vivo imaging in the future.
Zhao has made several contributions in the area of “BODIPY-based dyads that undergo triplet generation by CR”. In 2017, with Wang30 they studied BADs similar to ones of Filatov et al.29 (Fig. 3). Additionally, other BADs were also prepared in order to enhance spin–orbit charge-transfer intersystem crossing (SOCT-ISC), which is related to an orthogonal geometry.
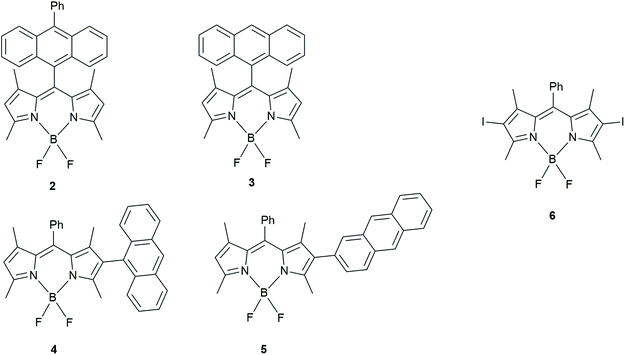 | ||
| Fig. 3 BODIPY-anthracene dyads studied by Wang and Zhao to determine how chromophore orientation influences their application as triplet PSs.30 | ||
Dyads, 4 and 5, were compared with 2 and 3 (also studied by Filatov et al. in 2018, vide infra).31 Using DFT calculations, they showed that 4 had the most restricted orthogonal geometry followed by 2, 3 and 5. The triplet yields however, did not follow that trend in polar solvents. In fact, the electron donor–acceptor structures that were connected via the meso (5 position) of the BODIPY unit had the highest triplet yields (3 = 96% triplet yield in acetonitrile). BADs 4 and 5, whose donor–acceptor moieties were connected via the position 2 of the BODIPY, only had triplet yields of ≤31% measured in dichloromethane, acetonitrile and toluene.
The authors state that orthogonality isn't the only necessity for quantitative triplet yields. They tentatively propose that the parallel/antiparallel (ground state) dipole moment orientation of the donor and acceptor results in more efficient intersystem crossing (ISC), thus creating higher triplet state yields. To our knowledge however, there is no theory that links these two aspects.
As reported19 by Mataga et al., it is the matrix element of the spin–orbit coupling interaction between the charge-transfer state and the triplet state that will become enhanced in the perpendicular configuration and is responsible for the rate of triplet formation by charge recombination (see also section 5: Mechanistic aspects).
Zhao and Wang tested the capability of 2 in triplet–triplet annihilation up-conversion (TTA UC). Using perylene as a triplet acceptor, the quantum yield for up-conversion was 15.8%, which is slightly higher than conventional TTA UC candidates (like the heavy atom containing BODIPY 6, that was also studied).
Zhang et al. synthesized four covalent BODIPY heterodimers in which dihedral angles tune the photosensitizing ability.32 They aimed to understand the mechanism of triplet formation in BODIPY dimers as well as to elucidate “how dihedral angles in a BODIPY dimer affect the triplet state formation and whether it is possible to tune the T1 formation efficiency”. With the use of laser-flash photolysis and Near-Infrared (NIR) luminescence, the authors reported that the dimers in which the two units are perpendicular to each other are better triplet PSs than ones where the BODIPY units are coplanar. Comparing the UV-Vis absorption spectra of the dimers, the authors indicated that the lower dihedral angles between the BODIPY units result in the larger exciton coupling. The BODIPY dimer with a dihedral angle of 62° (d2; Fig. 4) showed the largest triplet yield (94% in toluene), which was corroborated by other models.33
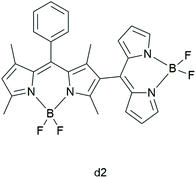 | ||
| Fig. 4 BODIPY dimer d2, studied by Zhang et al.32 | ||
Polar solvents stabilize the CS state and therefore solvent polarity has a substantial effect on the triplet formation and 1O2 production. The steric hindrance induced by the methyl groups in the BODIPY dimers make the two chromophores orthogonal to each other and thus, allow them to be excellent triplet PSs.31 The triplet formation is due to CR from CSS that results from PeT (Fig. 5). The photosensitizing ability of these PSs can be tuned not only by dihedral angles, but also by manipulation of solvent polarity.
 | ||
| Fig. 5 Illustration of triplet formation shown by Zhang et al.32 D is electron donor, A is electron acceptor. | ||
Liu et al. prepared BODIPY dimers to determine the mechanism of triplet formation in these compounds (Fig. 6).34 The rates of triplet formation are given in Table 1. The photophysical properties were studied using time-resolved and steady-state fluorescence spectroscopy. The fluorescence properties were solvent polarity dependent whereas this was not the case for the UV-absorption.
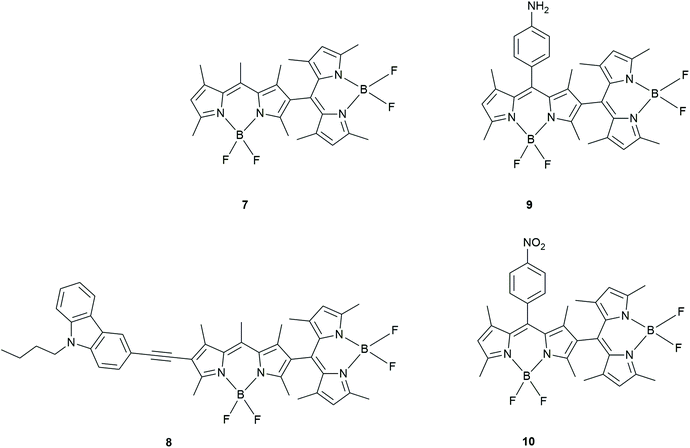 | ||
| Fig. 6 BODIPY dimers prepared by Liu et al.34 | ||
| Cmpds | Solvent | CR k T (s−1) | (ΦF) | Φ Δ |
Φ
Δ/ΦΔR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
Ref. |
|---|---|---|---|---|---|---|
| a Ratio relative to Rose Bengal in MeOH (= ΦΔR). b 1O2 quantum yields (= ΦΔ) determined in EtOH. c Not given in paper. d Not determined. e Too low to be determined.29–31,34,36 The relatively slow rates in DMF of compounds 2 and 3 are remarkable. The fast rate in ACN is from ref. 39. | ||||||
| 2 | TOL | 0.81; 0.79 | 0.10 | 30 and 31 | ||
| 2 | DCM | 0.01; 0.024 | 0.95 | 30 and 31 | ||
| 2 | ACN | 3.5 × 108 | 0.002; 0.007 | 0.84 | 30, 31 and 39 | |
| 2 | DMF | 1.75 × 105 | 0.01 | 0.59b | 31 | |
| 3 | TOL | 0.84; 0.92 | 0.04 | 30 and 31 | ||
| 3 | DCM | 0.14; 0.072 | 0.82 | 30 and 31 | ||
| 3 | ACN | 0.01; 0.006 | 0.86 | 30 and 31 | ||
| 3 | DMF | 1.25 × 105 | 0.011 | 0.53b | 31 | |
| 4 | TOL | 0.39 | 0.20 | 30 | ||
| 4 | DCM | 0.10 | 0.24 | 30 | ||
| 4 | ACN | 0.01/0.02 | 0.11 | 30 | ||
| 5 | TOL | 0.42 | 0.11 | 30 | ||
| 5 | DCM | 0.20 | 0.13 | 30 | ||
| 5 | ACN | 0.04 | 0.05 | 30 | ||
| 7 | TOL | 0.80 | 0.16 | 34 | ||
| 7 | THF | 4.0 × 108 | 0.063 | 0.85 | 34 | |
| 7 | DCM | 7.7 × 108 | 1.41 | 34 | ||
| 7 | ACN | 2.1 × 109 | 0.001 | 0.41 | 34 | |
| 9 | TOL | 0.628 | 0.18 | 34 | ||
| 9 | THF | 0.001 | 34 | |||
| 9 | DCM | 0.85 | 34 | |||
| 9 | ACN | 0.001 | 0.14 | 34 | ||
| 10 | TOL | 0.033 | 0.55 | 34 | ||
| 10 | THF | 0.001 | 34 | |||
| 10 | DCM | 0.25 | 34 | |||
| 10 | ACN | 0.001 | 34 | |||
| 11 | DCM | 1 × 109 | 0.04 | 0.81 | 36 | |
| 12 | DCM | 1 × 109 | 0.07 | 0.65 | 36 | |
A red shifted BODIPY dimer, (8; with a carbazole moiety) as well as BODIPY dimers with donating or withdrawing groups attached to these BODIPY dimers (9 and 10) showed a decrease in the triplet yield. This was determined by comparing the intensity of the ground state bleaching signals and singlet oxygen quantum yields.
A calculation of the Gibbs free energy for PeT in these BODIPY dimers determined that charge separation in 10 is thermodynamically allowed. The authors stated that the triplet state yield is highest in solvents with moderate polarity. They claim that the ISC involved in this CR process is now most efficient (Table 1) as the triplet state is accessible in these moderate polarity solvents.
Even though no long-lived triplet state was observed in 8, it has a cathodic shift of oxidation potential as well as an anodic shift of its reduction potential. Therefore, the authors conclude that the carbazole (donor) moiety facilitates charge separation leading to a unique CSS between one of the BODIPYs and this functional group. These results were not seen in the BODIPY dimers 9 and 10. Using femtosecond TA spectroscopy, the authors found ISC was most efficient in solvents with moderate polarity, especially for the unsubstituted dimer 7. These studies were also supported by TD-DFT calculations showing that the energy of the CSS was high in non-polar solvents and low in polar solvents. This implied CR was a driving force of ISC in solvents with moderate polarity and thus clarified the mechanism of SOCT-ISC in orthogonal BODIPY dimers. The carbazole containing BODIPY dimer (8) exhibits inefficient ISC.
BODIPY dimer 7 has the highest singlet oxygen yield and the nitro-containing BODIPY dimer 10 shows a decrease in the triplet yield in solvents like dichloromethane and THF. In the amino-containing BODIPY dimer 9, however, there appears to be inefficient ISC in THF.
In 2018 Filatov et al. also reported that the solvent dependent fluorescence of BADs and their ISC relied on donor–acceptor couplings.31 The authors compared the triplet state yields (formed either by RP-ISC or SOCT-ISC from the CT state) of their BADs to the values published in their previous paper.29 This comparison showed that especially the unsubstituted BAD displayed high populations of the CT state that was independent of the solvent polarity.
Studying the steady state absorption and emission properties of these BADs, it was found that the emission of the BADs was greatly affected by solvent polarity. Changing the substitution pattern in the BODIPY or anthracene subunits has a strong effect on the spectroscopic properties of these dyads. For example, BADs containing methyl groups on the 1, 3, 5 and 7 positions of the BODIPY indicated very efficient PeT in these dyads. The PeT efficiency of the BADs mainly depends on the electronic coupling between the donor–acceptor subunits and their redox potentials.
1O2 sensitization experiments were conducted with a variety of different BADs in both ethanol and hexane. They differed in extended conjugation, phenylene spacers and alkyl substitutions on the anthracene and BODIPY moieties. The emission quantum yields varied depending on solvent polarity and subunit structure. In hexane, there were higher 1O2 quantum yields obtained for 3,5-dimethyl-substituted BADs. The BADs with unsubstituted BODIPY (see Fig. 7) showed the lowest 1O2 quantum emission yields in ethanol (0.05–0.12) and higher values of 0.43 in hexane. The introduction of a phenylene spacer, thus increasing the distance between the electron donor and acceptor, reduces the PeT efficiency as the electronic coupling is decreased. The authors claimed that the different 1O2 emission quantum yields can be partly due to the larger energy gap between the local excited singlet state of the BODIPY (SBDP) and the CT singlet state (SCT), which is altered by the introduction of alkyl substituents. The authors found that the PeT is largely dependent on the SCT/SBDP energy gap and that increasing the distance between the donor and acceptor (by a phenylene spacer) minimizes ISC and results in poor triplet yields.
 | ||
| Fig. 7 BODIPY dyads studied by Filatov et al.31,35 | ||
Femtosecond and nanosecond TA spectroscopy was carried out on these dyads and they were split into two different sets. The first set was composed of molecules with the same anthracene unit and chemically varied BODIPY components while the second set kept the BODIPY constant and varied the anthracene. TA spectroscopy proved fast energy transfer (EnT) between Anthracene and BODIPY in orthogonal BADs. In lower polarity solvents, like toluene, the generated singlet states of these BADs decayed to the ground state without forming the CT states, indicating poor PeT. The authors were able to prove that in their orthogonal BAD (9-methylanthrancene and 1,3,5,7-tetramethyl BODIPY), the mechanism of triplet state formation was CT state recombination as opposed to direct ISC. With TA spectroscopy the authors show that in their BADs, triplet generation via CR was much less efficient in non-polar solvents even though a small amount of triplet formation occurred.
DFT calculations and X-ray crystallography proved that directly linked BADs had almost orthogonal angles (68–88 °C) clearly showing that all BADs studied were orthogonal with respect to the orientation of the BODIPY and anthracene subunits. This orthogonality would increase ISC. The electronic coupling between the local excited singlet state of the BODIPY (SBDP) and the CT singlet state (SCT) is responsible for PeT efficiency. This orthogonal geometry allows efficient electron transfer, providing high yields of CT resulting in efficient ISC and high triplet yields. Increasing the steric bulk onto already orthogonal BADs, by adding ethyl groups onto the 2 and 6 position of the BODIPY, results in a decreased PeT efficiency which decreases CT yields, ISC efficiency and overall triplet yields. Deviations from orthogonality in their BADs also reduced triplet state yields highlighting the importance of orthogonality in their dyads to produce the desired triplet state.
In summary of the study of Filatov et al.,31 structural factors and media polarity determine the dominant decay pathway. The correct amount of steric bulk, in terms of alkyl substituents, is needed to make PeT feasible for the BADs in polar solvents. Orthogonality reduces the gap between singlet CT state and triplet CT state. The authors also noticed triplet excited state generation in non-polar solvents in hexa-alkylated BADs.
In 2018, Filatov et al. reported on other dyads that can be used as heavy atom-free oxygen photosensitizers.35 In BODIPY-pyrene (BpyrD) and BODIPY-perylene dyads (BperD), BODIPY triplet states were formed following CSS formation.
They found that the BpyrD dyads produced higher triplet yields compared to previously reported BADs by the same group.29,31 The singlet excited states of pyrene(donor) undergo EnT to the BODIPY(acceptor) core in these dyads, following excitation at 355 nm. This is followed by PeT, generating a CSS equivalent to a radical cation of pyrene (Pyr˙+) and a radical anion of BODIPY (BDP˙−). From this point, the CSS state can undergo ISC via two mechanisms: the radical pair ISC (RP-ISC) or spin–orbit charge-transfer ISC (SOCT-ISC). With the use of transient absorption (TA) spectroscopy, the authors confirmed triplet formation via PeT.
1O2 sensitization, of the triplet states formed from the CT states in these dyads, was evaluated by studying the trapping of 1,3-diphenylisobenzofuran (DPBF) in a polar and non-polar solvent (ethanol and hexane, respectively). They found the most efficient sensitization occurred in the unsubstituted BpyrD dyad in ethanol. The authors concluded that in order for PeT to occur, the energy level of the charge-transfer state (SCT) must be energetically close to that of the electron donor–acceptor's excited energy level (D–A*). Using DFT calculations, they explained that the alkyl groups increased the SCT and reduced the electron accepting ability of the BODIPY moiety.
Hou et al.36 synthesized phenothiazine(PTZ)-anthracene(An) dyads (Fig. 8) with the aim of achieving orthogonal geometry thus enhancing SOCT-ISC. The bond between the electron donor and acceptor was ‘varied to systematically tune the geometry constraint’, therefore resulting in different coupling strengths (VDA) and hopefully, increasing triplet yields. VDA values were determined by using the charge-transfer absorption bands as well as the charge-transfer emission properties.
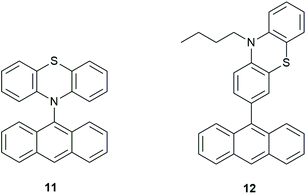 | ||
| Fig. 8 Examples of PTZ-anthracene dyads (11) and (12).36 | ||
They introduced their paper by stating that it had been recently shown that weakly coupled orthogonal multi-chromophore systems exhibit CR induced ISC.37 Hou et al. assume that the more coplanar the donor and acceptor units within the dyad are to each other, the stronger the electronic coupling (higher VDA). The emissive properties of their compounds indicated that the emission was governed by the strength of VDA between the electron donor and acceptor parts of the dyad. The emission of the acceptor appears to be controlled by modulating the conformational restriction.
The authors use time-resolved electron paramagnetic resonance spectroscopy (TR-EPR) to confirm that the overall ISC is not due to the intrinsic ISC of anthracene, but SOCT-ISC must also play a role. The Gibbs free energy values indicated that PeT shows a thermodynamically favoured preference for polar solvents compared to non-polar solvents in their dyads. This corresponds to the fluorescent properties.
Using nanosecond TA spectroscopy, they confirmed that anthracene is a good electron acceptor and show that SOCT-ISC is the main mechanism in their PTZ-An dyads. Using femtosecond TA spectroscopy, they analysed the kinetics of charge transfer and triplet-state formation for their compounds (see also Table 1). TR-EPR can be used to discriminate between different ISC mechanisms (RP-ISC, SOCT-ISC or normal spin–orbit coupling ISC (SO-ISC)).18,38 Each mechanism yields different ESP (electron spin polarization) patterns. The ESP pattern of anthracene was drastically different from that of the PTZ-An dyads. Therefore, the ISC mechanism was largely affected by the attachment of PTZ(donor) to the anthracene.
They reported a novel finding for SOCT-ISC. Not only does the ESP pattern depend on the molecular conformation (orthogonal vs. coplanar), but it is also dependent on the electron donor structure. Using DFT calculations, they verified their approach to be efficient for conformational restriction and thus SOCT-ISC purposes (see also section 5). By introducing a methyl group on a julodine-An dyad that was previously studied by Dance et al.,37 they determined that the conformation was restricted to 69–102° between the electron donor and acceptor.
The authors use electron density difference maps to show that, for compound 11 (chemical structure in Fig. 8), singlet (S1 = 1CT) and triplet (T2 = 3CT) states are characterized by an intramolecular charge-transfer. According to the El-Sayed rules, the rate of ISC is greater if a radiationless transition involves a change of molecular orbital type. Leading on from this, the increasing spin–orbit coupling between the 1CT and T1 states can lead to a higher ISC rate. Computational results of this work are discussed further in section 5.
In 2019, Buck et al. reported that triplet formation in BODIPY-based dyads is controlled by spin-allowed transitions.39 SOCT-ISC has to be faster than competing processes in order to form triplets in ‘non-triplet-forming compounds’ like BODIPY or perylene.
The authors show a generic scheme for triplet formation in donor–acceptor dyads (Fig. 9) that complies to the work of El-Sayed in 1974,40 the work of Van Willigen,24 Wasielewski,23,37,41 and Filatov, Senge29,31,35 and Buck et al.39
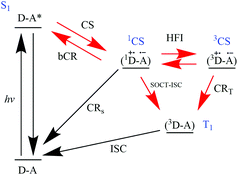 | ||
| Fig. 9 Jablonski-type energy diagram of process involving the photon absorption of a donor–acceptor dyad (D–A) to form a singlet localized on A (S1A*). This singlet can then undergo charge separation to a charge-separated state (1CS). In certain conditions, a triplet (T1) can be formed by recombination of the charges.39 | ||
According to the authors, the recent studies conducted by Filatov et al.,29,31,35 Zhao et al.,30,34,36 lack magnetic field effects (MFE) measurements clearly indicating that SOCT-ISC is the main transition to populate triplet excited states. Buck et al. proceeded to carry out studies to answer one question: in relation to Fig. 9, “how do the processes: CS, CRS and CRT; relate to each other in terms of producing triplets?”
The authors used general orthogonal BODIPY-based D–A dyads to systematically tune the oxidation and reduction potentials therefore investigating the Gibbs energy changes associated with the three processes and how they affect triplet quantum yields. Their study revealed that the spin-allowed processes (CS and CRS) largely control the triplet yield formation, rather than CRT (or SOCT-ISC). They also provided two general guidelines for improving triplet quantum yields in orthogonal D–A motifs, namely the close distance between donor and acceptor (<5 Å) and the adjustment of the CS state energy to suppress CRS pathway. The latter can most likely be done by making the CS energetically close to S1.
In this section, we see that BODIPY moieties in donor–acceptor dyads that form triplet states via charge recombination can act as the electron acceptor or as both donor and acceptor (in the case of BODIPY dimers). BODIPY-based dyads have applications in in vivo imaging as well as in the many other photochemical processes. When these dyads are orthogonal they can undergo SOCT-ISC to form triplet states. In sterically strained BODIPY-anthracene Dyads (BADs), the highest triplet yields are observed in non-polar solvents. An optimal dihedral angle of approximately 62° is repeatedly found between the donor and acceptor moieties of these BADs. The ISC of these PSs can be tuned, not only by the angles between the two electron transfer moieties, but also by manipulation of the solvent polarity. Attaching electron donating and withdrawing groups to BODIPY dimers has reportedly resulted in a decrease in triplet yield. However, it is yet to be investigated whether this statement is true for all BODIPY dimers. The driving force for charge recombination and SOCT-ISC in orthogonal BODIPY dimers is optimal in solvents with moderate polarity. Singlet oxygen quantum yields vary depending on solvent polarity and subunit structure.
In summary, the key is to find the ideal balance between initial charge separation and recombination pathways. It has been shown that promoting SOCT-ISC, by suppressing the spin-allowed transitions using a unique feature of electron-transfer reactions known as the Marcus inverted region, allows triplet formation by charge recombination to occur under favourable conditions but it is not always the preferred route. It is clear that ISC is dependent on solvent polarity and that SOCT-ISC can be the main ISC mechanism in orthogonal dyads. Some of the dyads discussed have shown promising results in vitro. Specifically, derivatives of the BODIPY-Anthracene Dyads and BODIPY-pyrene dyads, that were discussed by Filatov et al., have shown to have in vitro cytotoxicity against human breast cancer cells.42 For more information on recent work on BODIPY molecules and their triplet states we refer to some excellent review papers.43–45
From the great variety of compounds presented above we tentatively select two molecules to discuss a unifying theme in section 5: the BAD compound 2 (see Fig. 3) and the BODIPY dimer d2 (see Fig. 4). Both compounds give singlet oxygen/triplet yields above 90% in the optimal solvent.
4. Polymer–fullerene blends
Within organic photovoltaic research, there are many examples where triplet formation by charge recombination is reported to occur in thin solid films.7 These films consist of electron donating polymers with the (fullerene) electron acceptor incorporated into it. However, in contrast to the molecular electron donor–acceptor and BODIPY systems discussed before, these observations cannot be correlated to structural information regarding donor–acceptor orientation. The most studied combination with respect to this particular triplet formation pathway is PCPDTBT:PC60BM.In 2013, Friend and co-workers7 observed formation of the polymer T1 state due to bimolecular charge recombination (= triplet formation by charge recombination) in a series of polymer–fullerene systems in which the lowest-energy molecular triplet exciton (T1) of the polymer is lower in energy than the charge-transfer (CT) state. They stated that the formation of triplet excitons can be the main loss mechanism in organic photovoltaic cells. Four fullerene derivatives (PC60BM, PC70BM, IC60MA, IC60BA) and two polymers were used (PIDT-PhanQ = (poly(indacenodithiophene-co-phenanthro[9,10-b]quinoxaline) as well as PCPDTBT = (poly([2,6-(4,4-bis-(2-ethylhexyl)-4H-cyclopenta[2,1-b;3,4-b′]-dithiophene)-alt-4,7-(2,1,3-benzothiadiazole)]). Charges are formed within the instrument response time (2 ns) in all blends (see Fig. 10 for the molecular structures).
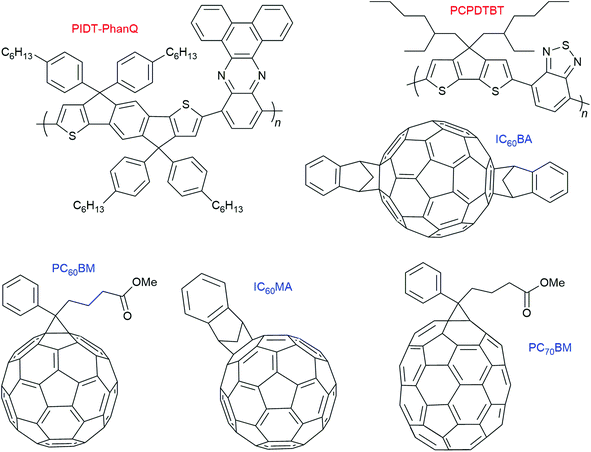 | ||
| Fig. 10 Molecular structures of the polymers and fullerene acceptors used by Friend and co-workers.7 | ||
In the polymer–fullerene blends of PIDT-PhanQ:IC60MA and PIDT-PhanQ:IC60BA, triplet excitons are formed through bimolecular recombination on nanosecond timescales. They report that the values of β (rate constant for triplet-charge annihilation) vary by a factor of two with laser fluence. Triplet-charge annihilation occurs when a triplet state (in the film) interacts with a charge (in the film) and they annihilate each other. At fluence of 2 μJ cm−2 for the PIDT-PhanQ:ICBA blend they obtained a value of 0.58 for α (final triplet fraction) and a value of 2.2 × 10−10 cm3 s−1 for β. This demonstrates that a large fraction of charges underwent bimolecular recombination mediated by 3CT, to form triplet excitons. A characteristic timescale for their observations is 10 ns. By using PCPDTBT as the second polymer the authors generalized the results.
“According to spin statistics, the encounters of spin-uncorrelated electrons and holes generate charge-transfer states with both singlet (1CT) and triplet (3CT) spin character in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. Relaxation of 3CT states to T1 states (energetically favoured), can be strongly suppressed by wave-function delocalization, allowing for the dissociation of 3CT states back to free charges and enhancing the device performance. Decreasing charge recombination is possible due to the interplay between electron spin, energetics and delocalization of charges in these organic semiconductors”.7 This work focuses on proton hyperfine interactions being the mechanism for the interconversion of singlet CT into triplet CT states. Spin–orbit coupling is not considered. At their earliest observation time of t = 2 ns, 50% of the triplet states in PIDT-PhanQ:ICBA are already formed. Interestingly, this could imply that spin–orbit coupling plays a role here.
3 ratio. Relaxation of 3CT states to T1 states (energetically favoured), can be strongly suppressed by wave-function delocalization, allowing for the dissociation of 3CT states back to free charges and enhancing the device performance. Decreasing charge recombination is possible due to the interplay between electron spin, energetics and delocalization of charges in these organic semiconductors”.7 This work focuses on proton hyperfine interactions being the mechanism for the interconversion of singlet CT into triplet CT states. Spin–orbit coupling is not considered. At their earliest observation time of t = 2 ns, 50% of the triplet states in PIDT-PhanQ:ICBA are already formed. Interestingly, this could imply that spin–orbit coupling plays a role here.
The same PCPDTBT polymer was studied in 2015 by Laquai et al.9 who demonstrated that after exciton dissociation and free charge formation, fast sub-nanosecond non-geminate recombination (recombination of charges that were not created together by one photoexcitation) leads to a substantial population of the polymer's triplets state in a PCPDTBT:PC60BM blend. This complements the earlier work of Friend. It seems that in this blend of materials, two rates of triplet formation by charge recombination can occur, a fast sub-ns rate and a slow process on the 10 ns timescale. Laquai et al.9 also reported that PSBTBT:PC60BM blends (with a silicon atom bridgehead) show a higher charge generation efficiency, but less triplet state formation at similar free charge carrier concentrations. The film morphology of the two blends are similar in terms of crystallinity, phase segregation, and interfacial contacts. But silicon substitution has a significant impact on the morphology of the blend (as well as hole mobility) and solid-state morphology. The interfacial structures of PSBTBT:PC60BM blends reduce non-geminate recombination, leading to superior device performance compared to optimized PCPDTBT:PC60BM blends. It is characterized by a decreased π–π stacking distance in conjunction with an increased lamellar stacking distance. For the PSBTBT:PC60BM blend, there is a significant change in the solid-state morphology that is not only related to the 2-ethylhexyl side chain organization, but also to an increase in molecular order and packing/aggregation of the PSBTBT polymer chains. Solid-state NMR studies also indicate a possible folding of the butyric methyl ester functionalities of the fullerene of PCBM to the PCPDTBT.
In 2014, Friend and co-workers revealed that upon addition of ODT (octane-dithiol), triplet generation in PCPDTBT:PC70BM was strongly promoted due to an increased generation of free charges.46 Recent measurements47,48 on PCPDTBT:PC60BM blends revealed a lifetime of these CT states of a few hundred picoseconds, which according to the authors is too short to create a substantial yield of triplets by intersystem crossing (but as we discussed earlier, such observations have been made for molecular systems in solution, see section 2). The population of polymer triplet states occurs if the triplet state is lower in energy than the interfacial triplet CT state. This causes a downhill energy transfer process, which competes with re-dissociation of the CT state. This process adds another loss channel to the efficiency-limiting processes in organic solar cells, and hence likely decreases its efficiency.
Durrant and co-workers observed the generation of polymer triplet excitons in SiIDT–2FBT:PC70BM (but not for SiIDT–DTBT:PC70BM), (Fig. 11). This occurs on a timescale of 1 ns (independent of laser-fluence, but charge generation is influenced by applied electrical bias). Population of singlet CT states is assumed to be followed by intersystem crossing (by HFI) to degenerate triplet CT states. There is no comment on the short time scale of this process. Charge recombination from 3CT then populates the lowest lying polymer triplet state (T1), thus limiting free charge generation in this system. Instead of CT state, the authors used the terminology of bound polaron pair (BPP). In contrast to the work of Friend and co-workers, the authors have inferred geminate charge recombination, implying that the charges that recombined into triplets have not escaped each other's coulomb field. The dynamics of free charge separation competing with recombination to polymer triplet states is studied in two closely related polymer–fullerene blends with differing polymer fluorination, differing linking thiophene groups and different photovoltaic performance by Durrant and co-workers. No quantification of the theoretical timescales relating to HFI or SOCT-ISC were reported.
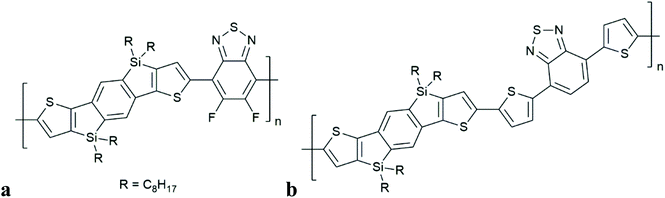 | ||
| Fig. 11 Structures of polymers in which triplet formation by charge recombination has been observed, in combination with fullerene adducts: SiIDT–2FBT (a), SiIDT–DTBT (b), studied by Durrant et al.8 | ||
“For the SiIDT–2FBT:PC70BM blend, electron transfer across the interface creates coulomb-bound BPP states with a spin singlet character, in which the hole resides on the polymer chain, while the electron resides on the fullerene molecule. Motion of the polarons within their coulomb attraction field is likely to reduce their charge-exchange integral thus creating energetically degenerate triplet and singlet bound states that can efficiently interconvert, enabled by hyperfine interactions.49 Once generated, the triplet BPP states serve as precursors for subsequent efficient back electron transfer to the lower lying polymer triplet excitons”.8
Other studies on charge recombination in low band gap polymer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fullerene donor–acceptor blends also show sub-ns triplet state formation from charges for both PDBTTT:PC60BM,50 and diketopyrrolopyrrole (DPP) type polymer blends with fullerene adducts.51,52
fullerene donor–acceptor blends also show sub-ns triplet state formation from charges for both PDBTTT:PC60BM,50 and diketopyrrolopyrrole (DPP) type polymer blends with fullerene adducts.51,52
The formation of triplet states in thin film blends of low band gap polymers and fullerene adducts has been the focus of many studies. The great variety of polymer molecular structures, the different types of morphologies and crystalline regions, different energetics as well as the large influence of laser power applied in optical studies makes triplet formation by charge recombination difficult to pinpoint within this field. Furthermore, interface layers and a potential difference (of 0.5 to 1 V) in real operating devices will induce band bending and change energetics. However, recombination to triplets can proceed faster than charge extraction and can be observed in working devices even under short-circuit conditions. The studies reported here are performed on spin-coated films on quartz.
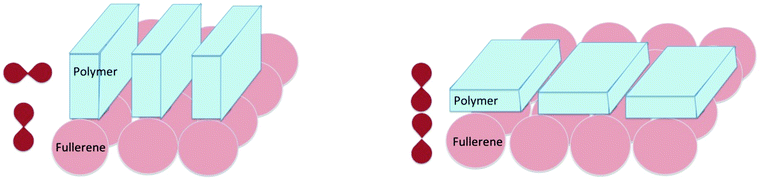
Considering the previous sections on molecular donor–acceptor systems and BODIPY's, there are hints to the following suggestion: the orientation of the π systems of electron donor and acceptor units in the solid state will influence the charge recombination process to the same extent as in well-defined molecular systems in solution. This implies that the specific orientation of the π systems of the polymer, relative to the π system of the fullerene adduct will be an important factor to control (Fig. 12).
The suggestion that we postulate and model in Fig. 12 indicates that for the thin films containing two dyes (perylene red and pyrene), two different conformations/complexes (similar to those in Fig. 12) must be present too. These two conformations are in agreement with the two reported rates of ∼1.04 × 1010 and 7.21 × 107 s−1 for triplet state formation by charge recombination in a mixture of pyrene and perylene red (N,N′-bis(2,6-di-isopropylphenyl)-1,6,7,12-tetraphenoxy-perylene- 3,4:9,10-tetracarboxylic acid bis-imide).53
5. Mechanistic aspects
In the previous sections we have reported various examples of molecules and materials in which triplet formation by charge recombination has been observed, and important factors such as the orientation of donor and acceptor, the nodal planes of orbitals involved, hyperfine interactions and spin–orbit coupling have been indicated. Here we describe some of these mechanisms in more detail and correlate them to representative rates.Proton hyperfine interactions
Next to spin–lattice relaxation (T1) and spin–spin (longitudinal) relaxation (T2), spin de-phasing can also occur due to hyperfine coupling (coupling between nuclear spin and electron spin) and cause intersystem crossing. This process can be approximated by using T2*, the transverse relaxation time (T1 > T2 > T2*) also known as the spin de-coherence or the spin de-phasing (interconversion) timescale, which is given by:It depends on the g-value (mainly ranging between 1.80 up to 2.20), μB, the electronic Bohr magneton (5.78838 × 10−5 (eV T−1)), the hyperfine coupling constant (aH) as well as Planck's constant (6.58212 × 10−16 (eV s)). The magnitude of the hyperfine constant (in Tesla) has a large influence on the spin de-phasing time. If we simplify this and assume g = 2 we get T2* = (5.686 × 10−9/aH), with the aH values expressed here in mT. Through the hyperfine interaction, the spin of the nuclei can interact with the electron spin causing it to change and thereby spin–flip. Hyperfine interactions are named after the hyperfine splitting of the peaks observed in EPR (or ESR) spectra.
For the molecular donor–acceptor system of Mataga and co-workers,19 we can take values for the radical anion of pyrene and the radical cation of dimethylaniline. The three hyperfine coupling constants for the unsubstituted pyrene radical anion have been reported54 to be 0.489, 0.226 and 0.10 mT with the g-value55 being 2.002724. We can then estimate the value of T2* to be between 1.16 × 10−8 s and 5.68 × 10−8 s. The fastest rate would be CRkT = 8.61 × 107 s−1, which is remarkably close to that measured53 in thin films containing pyrene CRkT = 7.21 × 107 s−1. However, clearly the rate in the orthogonal molecular system studied by Mataga et al. in solution is much higher,19 and cannot be explained with the T2*.
For N,N-dimethylaniline, the hyperfine coupling constants for the ortho and meta hydrogen atoms56 are between 0.6 and 0.079 mT from which we can estimate T2* between 7.18 × 10−8 s and 9.48 × 10−9 s (fastest rate of CRkT = 1.05 × 108 s−1) in reasonable agreement with those obtained for pyrene.
In order to estimate the timescale of intersystem crossing, we need to look into EPR data of polymer–fullerene blends. In purely organic photovoltaic materials, the main nuclear spin that is present is related to the protons (H-HFI). The presence of other atoms in the polymer (besides hydrogen, carbon and nitrogen) that have a high relative abundance of isotopes with nuclear spin like fluorine, sulphur or phosphorus can be of importance.
There are various reports57,58 of g-values for polymer–fullerene blends and they all are very close to 2, ranging from ∼1.998 to 2.005. For P3HT/PC61BM and P3HT/PC71BM composites effective, isotropic g-factors of the methanofullerene anion radicals were 1.99983 and 2.00360, respectively.
The hyperfine constants, however, are not so easily obtained, but also indicate a slow process (∼5 to 22 ns timescale relating to aH values of 32.2 and 7.3 MHz [∼(32.2/28) = 1.15 and ∼0.26 mT] reported for thin films with fluorine containing oligomers [e.g. dithienosilole-fluorobenzothiadiazole] and PBCM).59 The hyperfine coupling constant is directly related to the distance between peaks in a spectrum and its magnitude indicates the extent of delocalization of the unpaired electron over the molecule. However, we can also use the Δg values.
A second approach to estimate the rate of triplet formation by charge recombination is related to magnetic field effects.60,61 Using the magnitude of the magnetic field (B) of the Earth, together with the g-values of the radical cationic and radical anionic species, it is possible to estimate a timescale for the process.
Based on the information on H-HFI, we have to conclude that rates of triplet formation by charge recombination (109 s−1 up to 1010 s−1), that are one or two orders of magnitude higher than the rates related to HFI (108 s−1), have to be related to other physical effects and can be not be explained by spin dephasing.
By looking into the quantum chemical background of the H-HFI interactions more insight can be gained into this mechanism. The Hamiltonian given62 by Frankevich et al. describes the hyperfine interactions:
The first term represents the Zeeman interaction which depends on the g factor, with Ŝ the total spin vector, H the magnetic field. The second and third terms represent the interaction between the electron (Ŝ1,2) and nuclear (I) spins while the fourth term represents the exchange interaction J(r) or the quantum mechanical correction to the classical electron–electron repulsion. J(r) is based on the Pauli exclusion principle, which says that no two electrons can have the same four quantum numbers (in other words if two electrons occupy the same orbital, they must have antiparallel spins). This leads to a quantum mechanical correction to the classical electron–electron repulsion. This will usually increase the energy for paired spins or singlets and decrease the energy of unpaired spin states or triplet states because the electrons cannot occupy the same orbital.
These H-HFI effects in a system can be visualized by looking at the interactions between the hydrogen atoms nuclear spin (I) and the spin of the electron (S1) (Fig. 13). The relatively slow process can be viewed as small separate pushes of the nuclear spin momenta resulting in a relatively slow dephasing of the electron spin of the radical cation or radical anion. A vector description of these spin–spin interactions is given in Fig. 13.
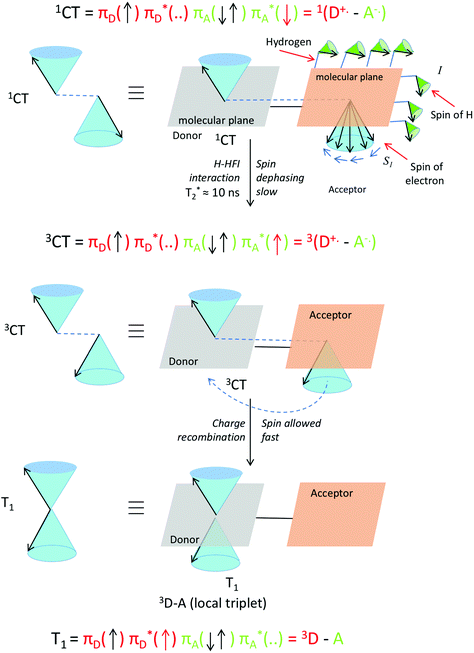 | ||
| Fig. 13 Visualization of proton hyperfine interactions (H-HFI) within a co-planar electron donor–acceptor compound. Within the singlet charge-transfer excited state (top), the interaction between the electron spin (S1) and the nuclear spin of the H atoms (I), leads to slow spin dephasing (T2*). This interconverts the singlet charge-transfer excited state into the triplet charge-transfer excited state (middle). When this is formed, fast spin allowed charge recombination to a local triplet state can occur (bottom). The T0 level is populated specifically (and not the T+ or T−, see also Fig. 15). The red arrow in the three electron configurations depicts the dephasing and transferring electron. A magnetic field is present in the z direction, for the purpose of simple spin representation. | ||
Spin–orbit coupling
Due to the conservation of momentum, a change in (electron) spin magnetic momentum has to be compensated by a change in orbital magnetic momentum. The change of molecular orbitals related to a transition is coupled to the change in electron spin. “In molecules such as acetone and, for example, aromatic ketones, that are known for their high triplet yields, the n–π* transition of the carbonyl group can be viewed as the transfer of charge from the lone pair of the oxygen atom to the π* orbital mainly located on the carbon atom.63 This exemplifies the importance of charge transfer in triplet state formation. The orbital magnetic momentum is changed when the interacting orbitals are located in different areas of the space on the molecule, compensating the change of spin magnetic momentum of the electron (spin–orbit coupling)”. In fullerene C60, the orbitals related to the (very efficient) transition to the triplet state change from “pole” based to “equator” based.64 Thereby, the change in orbital magnetic momentum can be anticipated.Orthogonal donor and acceptor units can easily fulfil the change in orbital magnetic momentum, upon back electron transfer interaction. As discussed earlier, this mechanism has been implied by Mataga and co-workers19 in 1981. It was also inferred in 1996 on the basis of TR-EPR of acridinium systems by van Willigen et al.24
By looking into the quantum chemical background of spin–orbit coupling interactions, we can gain more insight into this mechanism. Spin–orbit coupling is the result of the spin-operator expressed by its Hamiltonian.
We can use the approach given65 by Beljonne and Bredas:
“The spin–orbital Hamiltonian is the interaction between the spin and orbital motions of an electron (spin–orbit coupling) and induces a mixing between singlet and triplet excitations.
This Hamiltonian represents the coupling between the spin and orbital momenta of the nucleus (μ) and the electron (i).
The Golden-rule expression for radiation-less transitions can be used to compute the intersystem crossing rates, kIFISC, between an initial singlet state I and a final triplet state F:
| kIFISC = (2π/ℏ)〈1Ψ10|HSO|3ΨF0〉2 [FCWD] |
The FCWD term (in high-temperature limit) is given by:
Here, ΔE is the energy difference between the initial and final states, (here the singlet–triplet energy splitting), and λ denotes the Marcus reorganization energy”.
So basically, the expressions are very similar to the regular equations for electron transfer, but the main difference is the Hamiltonian. In regular electron transfer processes, this is related to the electronic coupling between the electronic orbitals of two states. Now it relates to the coupling of the spin magnetic momenta and the orbital magnetic momenta of the two states. It is not the electronic coupling (normally called V, or HDA) but the spin–orbit coupling between the initial and final states.
The wavefunctions on which the spin–orbit Hamiltonian operates can be specified in more detail: the orbitals of the radical anion and the orbitals of the radical cation (the charge-transfer state) and the orbitals belonging to the final triplet state should be the ones to consider.
This gives us the so called “spin–orbit coupling matrix element”(= SOCME). Orthogonality of the nodal planes of the interacting orbitals may be an important factor.
| 〈1Ψ10|HSO|3ΨF0〉 = 〈1D˙+–A˙−10|HSO|3D–AF0〉 |
The selection rules for triplet state formation are known from the work of Mostafa El-Sayed (El-Sayed rules).40,66 These rules have been visually correlated to orbitals and electron spin by Turro.67 Turro demonstrated via the use of orbitals in the carbonyl group of acetone how intersystem crossing is the movement of an electron from a Py orbital to a Px orbital (Fig. 14). First, such an example is presented here using a rotating vector description of electron spin, which is then correlated to the spin-vector description and to molecular orbital changes occurring in orthogonal electron donor–acceptor systems (Fig. 15).
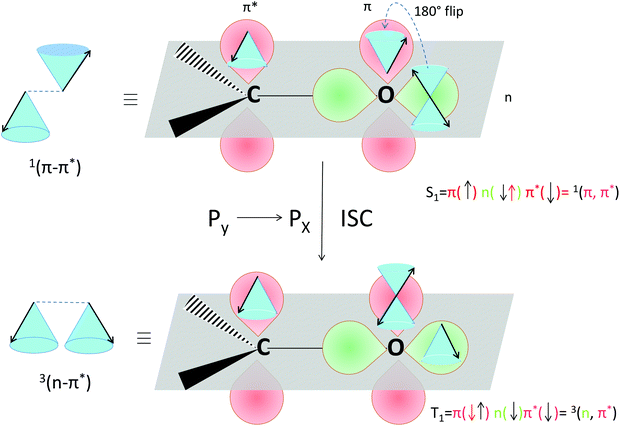 | ||
| Fig. 14 Visualization of the selection rules for spin–orbit coupling for a carbonyl compound. For a 1(π–π*) singlet excited state (top), the transition between the orthogonal doubly occupied n orbital (green) and π orbital (red, single occupation) provides the spin–orbit coupling to enable the electron spin flip and produce the 3(n–π*) triplet excited state (bottom). We use the rotating frame vector representation and the selection rules for triplet state formation of a 1(π–π*) singlet into a 3(n–π*) triplet (adapted from ref. 67). It is a qualitative orbital description of the basis for allowed intersystem crossing. The red arrow in the two electron configurations depicts the flipping electron. A magnetic field is present in the z direction, for the purpose of simple spin representation. | ||
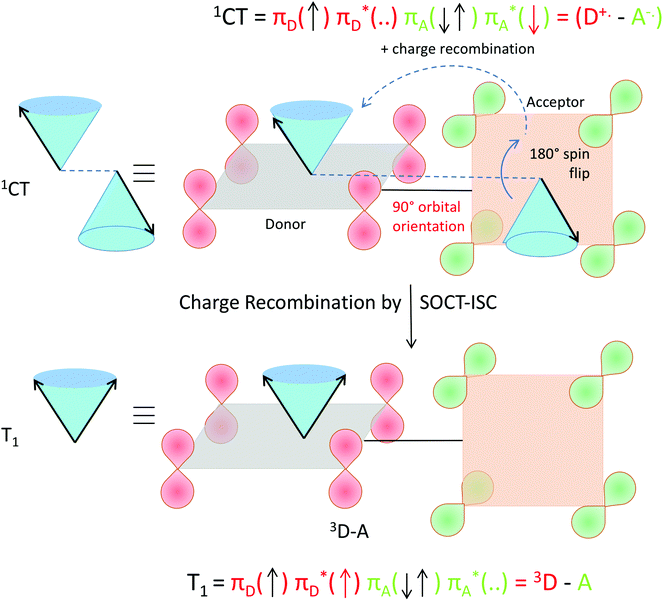 | ||
| Fig. 15 Visualization of spin–orbit charge transfer inter system crossing (SOCT-ISC) within an orthogonal electron donor–acceptor compound. Within the singlet charge-transfer excited state (top), the transition between the singly occupied orthogonal acceptor π*-orbital (green) and donor π-orbital (red, single occupation + empty π*) provides the spin–orbit coupling to enable the simultaneous spin flip and produce the local triplet state excited state 3(π–π*) on the donor (bottom). Upon charge transfer accompanied by an electron spin flip, the orbital magnetic momentum change (of the orthogonal orbitals involved in the transition) compensates for change of electron spin magnetic momentum. The orthogonal orbital (nodal plane) relation in the transition is important. The T+ (or T−) level is populated specifically (and not the T0 level, see also Fig. 13). The red arrow in the two electron configurations depicts the flipping and transferring electron. A magnetic field is present in the z direction, for the purpose of simple spin representation. | ||
Considering that HFI and SOCT-ISC mechanisms can operate in one particular system at the same time, it is important to stress that HFI is a ‘localized’ interaction occurring between electron spin and nearby nuclear spins. As such, the timescale of this process will not depend on the distance (nor orientation) between the donor and acceptor unit. However, in the SOCT-ISC mechanism a coupling term is present, that will show a strong distance (and orientation) dependence.68
Further inspection of Fig. 15 shows two more aspects: without dephasing, the triplet level that is formed specifically by SOCT-ISC is the so-called T+ (or the T−) level. In the T0 level the two electron-spins point in opposite directions and should have the same phase (see e.g.Fig. 13, a result of spin dephasing; see also ref. 16, page 147). Furthermore, the spin–orbit Hamiltonian will operate between the charge-transfer state (consisting of the ‘electronically coupled’ radical cation and radical anion) and a local triplet state that can be localized on the donor or the acceptor.
| 〈1ΨI0|HSO|3ΨF0〉 = 〈1D˙+–A˙−I0|HSO|3D–AF0〉 |
| 〈1ΨI0 |HSO|3ΨF0〉 = 〈1D˙+–A˙−I0 |HSO|D–3AF0〉 |
If the triplet is formed on the donor, the orbital symmetry of the radical anion of the acceptor will play a more important role (next to that of the donor triplet) for the magnitude of the spin–orbit coupling interaction matrix element. If the triplet is formed on the acceptor, the orbital symmetry of the radical cation of the donor (next to that of the acceptor triplet) will play a more dominant role in the transition.
As discussed in section 2, Weber and co-workers have been able to apply computational chemistry to determine important aspects for the triplet formation by charge recombination for compound 11 and 12.36 By using experimental data from charge-transfer absorption and charge-transfer emission properties they determined a rather large VDA value of 0.16 eV (= 1290 cm−1) for 12 (related to the charge separation). By using DFT methods (TD-DFT and the Dalton code) they were able to calculate the magnitude of the spin–orbit coupling interaction matrix element (SOCME) to be 2.37 cm−1 for compound 12, and 0.37 cm−1 for compound 11. These small interaction energies are enough to mediate charge recombination to the triplet (by SOCT-ISC) on a ∼1 ns timescale. So clearly is it possible nowadays to calculate the magnitude of the coupling that mediates TCR. This is also possible with ADF (see section 6).
Although it is most certainly an oversimplification, we can apply a frontier molecular orbital description (FMO) as a starting point to identify the orbitals that mainly play a role in the triplet formation by charge recombination process. Such an approach results in the simplified orbital representation in Fig. 16. By using such an FMO scheme,69–71 we can identify that the TCR process will be an interaction between the HOMO of the acceptor and the HOMO of the donor. We refer here to the orbitals of the neutral system. In fact, the SOMO of the radical cation of the donor and the HOMO (below the SOMO) of the radical anion are the active orbitals, but for simplicity we consider the orbitals of the neutrals. We assume that the symmetry properties of these orbitals are similar.
For the system studied by Mataga as well as for the BAD system 3 and the BODIPY dimer d2 the HOMO of the donor together with the HOMO of the acceptor clearly show a special feature. Double orthogonality of the nodal planes is observed. Not only are the nodal planes related to the two molecular planes of donor and acceptor orthogonal, also the ‘secondary’ nodal planes of the orbitals are orthogonal! This was already stipulated by Mataga in 1981, but here we visualize these requirements for triplet formation by charge recombination (see Fig. 17). Note that for compound 4 these requirements do not hold, and that this compound does not show substantial TCR (as well as for compounds BB5 and BB6 in ref. 34) (Fig. 3).
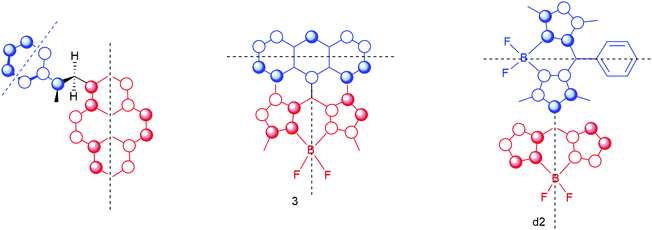 | ||
| Fig. 17 Orbital representation of the HOMO of the electron-donor (in blue) and the HOMO of the electron-acceptor (in red). The black dotted lines represent the secondary orthogonal nodal plane. The first orthogonal nodal planes of the orbitals are the molecular planes of the donor unit and acceptor unit (with a ∼90° angle between the π systems). Double orthogonality of the nodal planes is present. See Fig. 1 for a 3D model of the first molecule. | ||
Note that in d2 there is a ∼90° twist angle between the red part and the blue part. In the first molecule both angles (between the molecular planes and the secondary nodal planes) are approaching 60°. For 3 the angle is estimated to be between 78 and 85° (see ref. 31).
A similar approach can be applied to systems in which the triplet is formed on the donor (like in the polymer fullerene blends discussed in section 4). Here however, the character of the LUMO of the donor and the LUMO of the acceptor will be the most significant (again referring to the orbitals of the neutral systems). This does imply that the energetics has to be such that TCR is possible, leading to triplet formation on the donor.
Hereby we have identified a unifying theme, that connects the early donor acceptor systems (in section 2) with the recent BODIPY work (in section 3): double orthogonality of the nodal planes. The key is not the ground state dipole moment, nor the transition dipole moment of the two separate transitions (CT and triplet), but the specific orbital symmetry properties. This fits the concept that the spin–orbit Hamiltonian operates between the initial and final state and has a maximum output when orbitals are orthogonal.
6. Conclusions and outlook
Triplet formation by charge recombination has been observed in numerous molecular electron donor–acceptor systems.72 However, examples of systems in which this process occurs well below a 10 ns timescale, are scarce. The recent intensive research on BODIPY systems has renewed the interest in triplet formation by charge recombination, as well the work on organic photovoltaic materials. The main viable mechanistic factors that play a role in the formation of triplet states in which the precursor state is not a locally excited singlet state, but a charged state, are proton hyperfine interactions (H-HFI) as well as spin–orbit coupling (SOCT-ISC). These two interactions can be quantified (see section 5). When we look at the various other possible mechanisms we see that they occur on a much longer timescale.Triplet formation can occur by geminate (in molecular systems) or by non-geminate processes (in thin films). In long lived (geminate or non-geminate) charge-transfer states, HFI is inevitable and will lead to formation of triplet CT states through the localized interactions of nuclear spins and electron spin on a ∼10 ns timescale. Electron donor acceptor systems that do not contain nuclear spins are so far unknown (to us). The triplet CT state can recombine fast to a local triplet state without spin-forbiddenness (via spin-allowed transitions), if the energetics allows this. However, in short lived singlet CT states, fast competitive spin–orbit coupling can lead to direct local triplet state formation on a ∼40 ps timescale. The selection rules for triplet state formation become important and imply short distance and orthogonal orbitals, with double orthogonality of the nodal planes. As the origins of these interactions (HFI and SOCT-ISC) have a quantum-chemical basis these effects will ultimately be related to the nature of the Hamiltonian that couples the two states: a trivial assessment with complex consequences. With modern computational methods however, it is possible to calculate the so-called transfer integrals (or SOCME) between CT states and local triplet excited states, (also as a function of a rotating bond between donor and acceptor) for the SOCT-ISC mechanism. From several experimental studies, 60° angles between the nodal planes of the orbitals seems optimal. FMO analysis suggests that double orthogonality of the nodal planes is an important factor.
The physical and quantum chemical effects that play a role in the formation of local (excited) triplet states from charged states can be visualized by using a spin-vector description together with a molecular orbital representation. Thereby we can understand and describe these factors in a better way, expanding on the visualizations provided us by Turro.
We can exploit triplet formation by charge recombination by using it as an ‘alternative’ method to generate triplet states. This paper begs the question: what can the produced triplets be used for? While there will likely be many applications in the photosciences, we have seen their application in PDT already. Can all dyads that undergo triplet charge recombination be used for Photodynamic Therapy? In Vitro tests can be carried out to determine the best candidates. After this, evaluation of their photosensitizer properties will have to be assessed. BODIPY's can also be attached to known photosensitizers to see what their capability as a singlet oxygen photosensitizer is. There is also an ideal situation that many types of dyads can use this triplet formation method that results in the next big photosensitizer that cannot only be used in photodynamic therapy but in many other photo-associated applications as well.
Applying the principles of triplet formation by charge recombination to photodynamic therapy not only implies optimizing the orientation of the donor and acceptor (and the nodal planes of their orbitals), but also the charge generation has to be optimal and the energy difference between the CT state and the triplet state has to be fine-tuned.
If we want to understand, control or predict charge recombination, we need to quantify the 1CT → 3CT interconversion characterized by T2* (and HFI) as well as the 1CT → T1 conversion characterized by the SOCME, the transfer integral for the SOCT-ISC mechanism. Both quantities can be determined experimentally73 or with computational chemistry.36,59,74,75
Abbreviatons
| T+/T0/T− | Triplet excited state energy levels |
| τ | Lifetime (in seconds) |
| τ CR(T) | Time of formation of the triplet state corresponding to the decay time of the charge-transfer state |
| T | Triplet excited state |
| CR k T | Rate of triplet formation by charge recombination |
| DFT | Density functional theory |
| 3 L a | Triplet state with La symmetry using Platt's notation of the symmetry of the excited state of a molecule |
| π | Pi orbital |
| π* | Pi* orbital |
| n | Lone pair molecular orbital |
| C60 | Fullerene |
| ns | Nanosecond |
| BAD | BODIPY-anthracene dyad |
| CSS | Charge separated state |
| CR | Charge recombination |
| CS | Charge separation |
| CT | Charge transfer |
| 1O2 | Singlet oxygen |
| 3D | Three dimensional |
| EnT | Energy transfer |
| Fig. | Figure |
| ISC | Intersystem crossing |
| TD-DFT | Time-dependent density functional theory |
| τ CS | Electron transfer time in a donor–acceptor dyad from the donor to the acceptor to form a charge separated state |
| τ CR | Charge recombination time |
| DMJ | 3,5-Dimethyl-4-julolidine |
| NI | Naphthalene-1,8:4,5-bis(dicarboximide) |
| An | Anthracene |
| DMJ-An-NI | 3,5-Dimethyl-4-julolidine Naphthalene-1,8:4,5-bis(dicarboximide)triad with an anthracene linker |
| DMJ(+˙)-An-NI(−˙) | Charge separated state of DMJ-An-NI |
| ps | Picoseconds (10−12 seconds) |
| s−1 | Unit of rates of physical and chemical processes (per second) |
| SOCT-ISC | Spin–orbit charge-transfer intersystem crossing |
| SOCME | Spin–orbit coupling matrix element |
| RP-ISC | Radical pair intersystem crossing |
| EPR | Electron paramagnetic resonance spectroscopy |
| 1CSH | Charged-shifted singlet state |
| 3LE | Localized-excited triplet state |
| k T | Rates of triplet formation |
| SOMO | Singly occupied molecular orbital |
| HFI | Hyperfine interactions |
| PS | Photosensitizer |
| PeT | Photoinduced electron transfer |
| TOL | Toluene |
| THF | Tetrahydrofuran |
| DCM | Dichloromethane |
| ACN | Acetonitrile |
| TA | Transient absorption |
| BODIPY | Boron-dipyrromethene |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 764837. We thank the Universiteit van Amsterdam for structural support. We thank Caspar Williams for language corrections.References
- W. Rutsch, K. Dietliker, D. Leppard, M. Köhler, L. Misev, U. Kolczak and G. Rist, Recent development in photoinitiators, Prog. Org. Coat., 1996, 27, 227–239, DOI:10.1021/jp001348j.
- L. B. Rocha, F. Schaberle, J. M. Dąbrowski, S. Simões and L. G. Arnaut, Intravenous Single-Dose Toxicity of Redaporfin-Based Photodynamic Therapy in Rodents, Int. J. Mol. Sci., 2015, 16, 29236–29249, DOI:10.3390/ijms161226162.
- M. Wainwright, Photodynamic antimicrobial chemotherapy (PACT), J. Antimicrob. Chemother., 1998, 42, 13–28, DOI:10.1590/S0100-879X2010007500141.
- A. van Dijken, J. J. A. M. Bastiaansen, N. M. M. Kiggen, B. M. W. Langeveld, C. Rothe, A. Monkman, I. Bach, P. Stössel and K. Brunner, Carbazole Compounds as Host Materials for Triplet Emitters in Organic Light-Emitting Diodes: Polymer Hosts for High-Efficiency Light-Emitting Diodes, J. Am. Chem. Soc., 2004, 126, 7718–7727 CrossRef CAS.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, External Quantum efficiency above 100% in a Singlet-Exciton-Fission––Based Organic Photovoltaic Cell, Science, 2013, 340, 334–337 CrossRef CAS.
- W. Shockley and H. J. Queisser, Detailed Balance Limit of Efficiency of p-n Junction Solar Cells, J. Appl. Phys., 1961, 32, 510–519, DOI:10.1063/1.1736034.
- A. Rao, P. C. Y. Chow, S. Gélinas, C. W. Schlenker, C.-Z. Li, H. L. Yip, A. K.-Y. Jen, D. S. Ginger and R. H. Friend, The role of spin in the kinetic control of recombination in organic photovoltaics, Nature, 2013, 500, 435–439, DOI:10.1038/nature12339.
- S. D. Dimitrov, S. Wheeler, D. Niedzialek, B. C. Schroeder, H. Utzat, J. M. Frost, J. Yao, A. Gillett, P. S. Tuladhar, I. McCulloch, J. Nelson and J. R. Durrant, Polaron pair mediated triplet generation in polymer/fullerene blends, Nat. Commun., 2015, 6, 6501–6508, DOI:10.1038/ncomms7501.
- F. Etzold, I. A. Howard, N. Forler, A. Melnyk, D. Andrienko, M. R. Hansen and F. Laquai, Sub-ns triplet state formation by non-geminate recombination in PSBTBT:PC70BM and PCPDTBT:PC60BM organic solar cells, Energy Environ. Sci., 2015, 8, 1511–1522, 10.1039/c4ee03630a.
- I. A. Howard, N. C. Greenham, A. Abrusci, R. H. Friend and S. Westenhoff, Charge Transfer and Charge Separation in Conjugated Polymer Solar Cells, in Nanostructured conductive polymers, ed. A. Eftekhari, Wiley, ch. 13, 2010, pp. 531–561 (see especially page 555) Search PubMed.
- D. W. Gehrig, Unraveling Efficiency-Limiting Processes in Organic Solar Cells by Ultrafast Spectroscopy – Impact of Chemical Structure and Morphology on Photophysics and Efficiency, PhD Dissertation, Johannes Gutenberg-Universität, Mainz, 2015. page 185. http://pubman.mpdl.mpg.de/ Search PubMed.
- X.-K. Chen, T. Wang and J.-L. Brédas, Suppressing Energy Loss due to Triplet Exciton Formation in Organic Solar Cells: The Role of Chemical Structures and Molecular Packing, Adv. Energy Mater., 2017, 7, 1602713–1602721, DOI:10.1002/aenm.201602713.
- See for example: N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, ch. 7, 2009 Search PubMed; R. M. Williams, Introduction to Electron Transfer, 2007, DOI:10.13140/RG.2.2.16547.30244; R. M. Williams, Introduction to Photo-induced Electron Transfer in “Mathematica”-V5. Classical Marcus Equation Calculator, 2019, DOI:10.13140/RG.2.2.20531.89125/2 and references therein.
- M. Lor, J. Thielemans, L. Viaene, M. Cotlet, J. Hofkens, T. Weil, C. Hampel, K. Müllen, J. W. Verhoeven, M. Van der Auweraer and F. C. De Schryver, Photoinduced Electron Transfer in a Rigid First Generation Triphenylamine Core Dendrimer Substituted with a Peryleneimide Acceptor, J. Am. Chem. Soc., 2002, 124, 9918–9925 CrossRef CAS PubMed.
- N. J. Turro, The triplet state, J. Chem. Educ., 1969, 46, 2–6 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, ch. 2 and 3, 2009 Search PubMed.
- E. A. Margulies, J. L. Logsdon, C. E. Miller, L. Ma, E. Simonoff, R. M. Young, G. C. Schatz and M. R. Wasielewski, Direct Observation of a Charge-Transfer State Preceding High-Yield Singlet Fission in Terrylenediimide Thin Films, J. Am. Chem. Soc., 2017, 139, 663–671 CrossRef CAS.
- Y. Hou, X. Zhang, K. Chen, D. Liu, Z. Wang, Q. Liu, J. Zhao and A. Barbon, Charge separation, charge recombination, long-lived charge transfer state formation and intersystem crossing in organic electron donor/acceptor dyads, J. Mater. Chem. C, 2019, 7, 12048–12074, 10.1039/C9TC04285G.
- T. Okada, I. Karaki, E. Matsuzawa, N. Mataga, Y. Sakata and S. Misumi, Ultrafast Intersystem Crossing in Some Intramolecular Heteroexcimers, J. Phys. Chem., 1981, 85, 3957–3960 CrossRef CAS.
- R. M. Williams, J. M. Zwier and J. W. Verhoeven, Photoinduced Intramolecular Electron Transfer in a Bridged C60 (Acceptor)-Aniline (Donor) System; Photophysical Properties of the First “Active” Fullerene Diad, J. Am. Chem. Soc., 1995, 117, 4093–4099 CrossRef CAS.
- M. H. Lee, B. D. Dunietz and E. Geva, Calculation from First Principles of Intramolecular Golden-Rule Rate Constants for Photo-Induced Electron Transfer in Molecular Donor–Acceptor Systems, J. Phys. Chem. C, 2013, 117, 23391–23401 CrossRef CAS.
- P. Hudhomme and R. M. Williams, Energy And Electron Transfer In Photo- And Electro-Active Fullerene Dyads, in Fundamental and Applications of Carbon Nano Materials, World Scientific Publishing Company, 2011 Search PubMed.
- M. T. Colvin, A. B. Ricks, A. M. Scott, D. T. Co and M. R. Wasielewski, Intersystem Crossing Involving Strongly Spin Exchange-Coupled Radical Ion Pairs in Donor–bridge–Acceptor Molecules, J. Phys. Chem. A, 2012, 116, 1923–1930 CrossRef CAS PubMed.
- H. van Willigen, G. Jones and M. S. Farahat, Time-Resolved EPR Study of Photoexcited Triplet-State Formation in Electron-Donor-Substituted Acridinium Ions, J. Phys. Chem., 1996, 100, 3312–3316 CrossRef CAS.
- M. Wegner, H. Fischer, M. Koeberg, J. W. Verhoeven, A. M. Oliver and M. N. Paddon-Row, Time-resolved CIDNP from photochemically generated radical ion pairs in rigid bichromophoric systems, Chem. Phys., 1999, 242, 227–234, DOI:10.1016/S0301-0104(99)00047-6.
- M. R. Roest, A. M. Oliver, M. N. Paddon-Row and J. W. Verhoeven, Distance Dependence of Singlet and Triplet Charge Recombination Pathways in a Series of Rigid Bichromophoric Systems, J. Phys. Chem. A, 1997, 101, 4867–4871, DOI:10.1021/jp970969i.
- H. Imahori, K. Tamaki, D. M. Guldi, C. Luo, M. Fujitsuka, O. Ito, Y. Sakata and S. Fukuzumi, Modulating Charge Separation and Charge Recombination Dynamics in Porphyrin–Fullerene Linked Dyads and Triads: Marcus-Normal versus Inverted Region, J. Am. Chem. Soc., 2001, 123, 2607–2617, DOI:10.1021/ja003346i.
- A. Loudet and K. Burgess, BODIPY Dyes and Their Derivatives: Syntheses and Spectroscopic Properties, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS PubMed.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, H. Savoie, K. J. Flanagan, C. Sy, E. Sitte, M. Telitchko, F. Laquai, R. W. Boyle and M. O. Senge, Generation of Triplet Excited States via Photoinduced Electron Transfer in meso-anthra-BODIPY: Fluorogenic Response toward Singlet Oxygen in Solution and in Vitro, J. Am. Chem. Soc., 2017, 139, 6282–6285 CrossRef CAS PubMed.
- Z. Wang and J. Zhao, BODIPY–Anthracene Dyads as Triplet Photosensitizers: Effect of Chromophore Orientation on Triplet-State Formation Efficiency and Application in Triplet–Triplet Annihilation Upconversion, Org. Lett., 2017, 19, 4492–4495 CrossRef CAS PubMed.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. J. Flanagan, M. Telitchko, T. Wiesner, F. Laquai and M. O. Senge, Control of triplet state generation in heavy atom-free BODIPY–anthracene dyads by media polarity and structural factors, Phys. Chem. Chem. Phys., 2018, 20, 8016–8031 RSC.
- X.-F. Zhang, X. Yang and B. Xu, PET-based bisBODIPY photosensitizers for highly efficient excited triplet state and singlet oxygen generation: tuning photosensitizing ability by dihedral angles, Phys. Chem. Chem. Phys., 2017, 19, 24792–24804 RSC.
- R. M. Williams, Distance and orientation dependence of photoinduced electron transfer through twisted, bent and helical bridges: :A Karplus relation for charge transfer interaction, Photochem. Photobiol. Sci., 2010, 9, 1018–1026 RSC.
- Y. Liu, J. Zhao, A. Iagatti, L. Bussotti, P. Foggi, E. Castellucci, M. Di Donato and K.-L. Han, A Revisit to the Orthogonal BODIPY Dimers: Experimental Evidence for the Symmetry Breaking Charge Transfer-Induced Intersystem Crossing, J. Phys. Chem. C, 2018, 122, 2502–2511 CrossRef CAS.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. J. Flanagan, T. Wiesner, F. Laquai and M. O. Senge, BODIPY-pyrene and perylene dyads as heavy atom-free singlet oxygen sensitizers, ChemPhotoChem, 2018, 20, 8016–8031 CAS.
- Y. Hou, T. Biskup, S. Rein, Z. Wang, L. Bussotti, N. Russo, P. Foggi, J. Zhao, M. Di Donato, G. Mazzone and S. Weber, Spin–Orbit Charge Recombination Intersystem Crossing in Phenothiazine–Anthracene Compact Dyads: Effect of Molecular Conformation on Electronic Coupling, Electronic Transitions, and Electron Spin Polarizations of the Triplet States, J. Phys. Chem. C, 2018, 122, 27850–27865 CrossRef CAS.
- Z. E. X. Dance, S. M. Mickley, T. M. Wilson, A. B. Ricks, A. M. Scott, M. A. Ratner and M. R. Wasielewski, Intersystem Crossing Mediated by Photoinduced Intramolecular Charge Transfer: Julolidine-Anthracene Molecules with Perpendicular pi Systems, J. Phys. Chem. A, 2008, 112, 4194–4201 CrossRef CAS.
- S. Weber, Transient EPR, eMagRes, 2017, 6, 255–270 CAS.
- J. T. Buck, A. M. Boudreau, A. DeCarmine, R. W. Wilson, J. Hampsey and T. Mani, Spin-Allowed Transitions Control the Formation of Triplet Excited States in Orthogonal Donor-Acceptor Dyads, Chem, 2019, 5, 138–155 CAS.
- M. A. El-Sayed, Effect of spin orbit interactions on the dipolar nature of the radiative microwave zero-field transitions in aromatic molecules, J. Chem. Phys., 1974, 60, 4502–4507 CrossRef CAS.
- Z. E. X. Dance, Q. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, Time-Resolved EPR Studies of Photogenerated Radical Ion Pairs Separated by p-Phenylene Oligomers and of Triplet States Resulting from Charge Recombination, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef CAS.
- S. Callaghan, M. A. Filatov, H. Savoie, R. W. Boyle and M. O. Senge, In vitro cytotoxicity of a library of BODIPY-anthracene and -pyrene dyads for application in photodynamic therapy, Photochem. Photobiol. Sci., 2019, 18, 495–504 RSC.
- J. Zhao, K. Chen, Y. Hou, Y. Che, L. Liu and D. Jia, Recent progress in heavy atom-free organic compounds showing unexpected intersystem crossing (ISC) ability, Org. Biomol. Chem., 2018, 16, 3692–3701 RSC.
- J. Zhao, K. Xu, W. Yang, Z. Wang and F. Zhong, The triplet excited state of BODIPY: formation, modulation and application, Chem. Soc. Rev., 2015, 44, 8904–8939 RSC.
- M. A. Filatov, Heavy-atom-free BODIPY photosensitizers with intersystem crossing mediated by intramolecular photoinduced electron transfer, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- P. C. Y. Chow, S. Gélinas, A. Rao and R. H. Friend, Quantitative Bimolecular Recombination in Organic Photovoltaics through Triplet Exciton Formation, J. Am. Chem. Soc., 2014, 136, 3424–3429, DOI:10.1021/ja410092n.
- Y. Tamai, K. Tsuda, H. Ohkita, H. Benten and S. Ito, Charge-carrier generation in organic solar cells using crystalline donor polymers, Phys. Chem. Chem. Phys., 2014, 16, 20338–20346, 10.1039/c4cp01820f.
- M. C. Scharber, C. Lungenschmied, H.-J. Egelhaaf, G. Matt, M. Bednorz, T. Fromherz, J. Gao, D. Jarzab and M. A. Loi, Charge transfer excitons in low band gap polymer based solar cells and the role of processing additives, Energy Environ. Sci., 2011, 4, 5077–5083, 10.1039/c1ee02181h.
- R. Haberkorn, M. E. Michel-Beyerle and R. A. Marcus, On spin-exchange and electron-transfer rates in bacterial photosynthesis, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 4185–4188 CrossRef CAS.
- D. W. Gehrig, I. A. Howard and F. Laquai, Charge Carrier Generation Followed by Triplet State Formation, Annihilation, and Carrier Recreation in PDBTTT-C/PC60BM Photovoltaic BlendsBlends, J. Phys. Chem. C, 2015, 119, 13509–13515, DOI:10.1021/acs.jpcc.5b03467.
- J. R. Ochsmann, D. Chandran, D. W. Gehrig, H. Anwar, P. K. Madathil, K.-S. Lee and F. Laquai, Triplet State Formation in Photovoltaic Blends of DPP-Type Copolymers and PC71BM, Macromol. Rapid Commun., 2015, 36, 1122–1128 CrossRef CAS PubMed.
- R. M. Williams, H.-C. Chen, D. Di Nuzzo, S. C. J. Meskers and R. A. J. Janssen, Ultrafast charge and triplet state formation in Diketopyrrolopyrrole Low Band Gap Polymer/Fullerene blends: influence of Nanoscale Morphology of Organic Photovoltaic Materials on charge recombination to the Triplet State, J. Spectrosc., 2017, 6867507, DOI:10.1155/2017/6867507.
- R. M. Williams, N. Vân Anh and I. H. M. van Stokkum, Triplet Formation by Charge Recombination in Thin Film Blends of Perylene Red and Pyrene: Developing a Target Model for the Photophysics of Organic Photovoltaic Materials, J. Phys. Chem. B, 2013, 117, 11239–11248 CrossRef CAS.
- C. M. Kirk, ESR studies of radical ions, PhD thesis, University of Canterbury, 1975 Search PubMed.
- B. G. Segal, M. Kaplan and G. K. Fraenkel, Measurement of g Values in the Electron Spin Resonance Spectra of Free Radicals, J. Chem. Phys., 1965, 43, 4191–4200 CrossRef CAS.
- B. M. Latta and R. W. Taft, Substituent Effects on the Hyperfine Splitting Constants of N,N- Dimethylaniline Cation Radicals, J. Am. Chem. Soc., 1967, 89, 5172–5178 CrossRef CAS.
- V. I. Krinichnyi and E. I. Yudanova, Light-Induced EPR Study of Charge Transfer in P3HT/PC71BM Bulk Heterojunctions, J. Phys. Chem. C, 2012, 116, 9189–9195 CrossRef CAS.
- V. I. Krinichnyi and E. I. Yudanova, Influence of morphology of low-band-gap PCDTBT:PC71BM composite on photoinduced charge transfer: LEPR spectroscopy study, Synth. Met., 2015, 210, 148–155 CrossRef CAS.
- S. A. J. Thomson, J. Niklas, K. L. Mardis, C. Mallares, I. D. W. Samuel and O. G. Poluektov, Charge Separation and Triplet Exciton Formation Pathways in Small-Molecule Solar Cells as Studied by Time-Resolved EPR Spectroscopy, J. Phys. Chem. C, 2017, 121, 22707–22719 CrossRef CAS.
- J. W. Verhoeven, On the role of spin correlation in the formation, decay, and detection of long-lived, intramolecular charge-transfer states, J. Photochem. Photobiol., C, 2006, 7, 40–60 CrossRef CAS.
- K. Maeda, K. B. Henbest, F. Cintolesi, I. Kuprov, C. T. Rodgers, P. A. Liddell, D. Gust, C. R. Timmel and P. J. Hore, Chemical compass model of avian magnetoreception, Nature, 2008, 453, 387–390 CrossRef CAS.
- E. L. Frankevich, A. A. Lymarev, I. Sokolik, F. E. Karasz, S. Blumstengel, R. H. Baughman and H. H. Hörhold, Polaron-pair generation in poly(phenylene vinylenes), Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 9320–9324, DOI:10.1103/PhysRevB.46.9320.
- D. Veldman, S. M. A. Chopin, S. C. J. Meskers, M. M. Groeneveld, R. M. Williams and R. A. J. Janssen, Triplet Formation Involving a Polar Transition State in a Well-Defined Intramolecular Perylenediimide Dimeric Aggregate, J. Phys. Chem. A, 2008, 112, 5846–5857 CrossRef CAS.
- M. Kállay, K. Németh and P. R. Surján, Triplet State Characteristics of Higher Fullerenes, J. Phys. Chem. A, 1998, 102, 1261–1273 CrossRef.
- D. Beljonne, Z. Shuai, G. Pourtois and J. L. Bredas, Spin−Orbit Coupling and Intersystem Crossing in Conjugated Polymers: A Configuration Interaction Description, J. Phys. Chem. A, 2001, 105, 3899–3907 CrossRef CAS.
- M. A. El-Sayed, Triplet state. Its radiative and nonradiative properties, Acc. Chem. Res., 1968, 1, 8–16 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, ch. 5, 2009, p. 284. Note that the second representation in Fig. 5.9(a) (top line) on page 285 is not correct: a 1(n,π*) is depicted (should be a 1(π,π*)) Search PubMed.
- B. Hu, L. Yan and M. Shao, Magnetic-Field Effects in Organic Semiconducting Materials and Devices, Adv. Mater., 2009, 21, 1500–1516 CrossRef CAS.
- R. M. Williams, M. Koeberg, J. M. Lawson, Y.-Z. An, Y. Rubin, M. N. Paddon-Row and J. W. Verhoeven, Photoinduced Electron Transfer to C60 across Extended 3- and 11-Bond Hydrocarbon Bridges: Creation of a Long-Lived Charge-Separated State, J. Org. Chem., 1996, 61, 5055–5062 CrossRef CAS.
- M. N. Paddon-Row, Electron and Energy Transfer, in Stimulating Concepts in Chemistry, VCH, Weinheim, 2000, pp. 267–291 Search PubMed.
- R. M. Williams, A highly soluble asymmetric perylene-bis(dicarboximide)-acceptor system incorporating a methylene bridged methoxybenzene-donor: solvent dependence of charge transfer interactions, Turk. J. Chem., 2009, 33, 727–737 CAS.
- S. I. van Dijk, P. G. Wiering, C. P. Groen, A. M. Brouwer, J. W. Verhoeven, W. Schuddeboom and J. M. Warman, Solvent-dependent switching between two dipolar excited states in a rigidly extended trichromophoric system, J. Chem. Soc., Faraday Trans., 1995, 91, 2107–2114 RSC.
- D. Veldman, S. M. A. Chopin, S. C. J. Meskers and R. A. J. Janssen, Enhanced Intersystem Crossing via a High Energy Charge Transfer State in a Perylenediimide−Perylenemonoimide Dyad, J. Phys. Chem. A, 2008, 112, 8617–8632 CrossRef CAS.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, Up-Conversion Intersystem Crossing Rates in Organic Emitters for Thermally Activated Delayed Fluorescence: Impact of the Nature of Singlet vs Triplet Excited States, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed.
- P. A. B. Haase, M. Repisky, S. Komorovsky, J. Bendix and S. P. A. Sauer, Relativistic DFT Calculations of Hyperfine Coupling Constants in 5d Hexafluorido Complexes: [ReF6] 2− and [IrF6]2−, Chem. – Eur. J., 2018, 24, 5124–5133 CrossRef CAS.
| This journal is © The Royal Society of Chemistry and Owner Societies 2020 |