Recent progress of electrowetting for droplet manipulation: from wetting to superwetting systems
Peicheng
Teng
ab,
Dongliang
Tian
*c,
Haiyan
Fu
*d and
Shutao
Wang
 ab
ab
aKey Laboratory of Bio-Inspired Materials and Interfacial Science, CAS Center for Excellence in Nanoscience, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, P. R. China
bUniversity of Chinese Academy of Sciences, Beijing, P. R. China
cKey Laboratory of Bio-Inspired Smart Interfacial Science and Technology of Ministry of Education, Beijing Advanced Innovation Center for Biomedical Engineering, School of Chemistry, Beihang University, Beijing, P. R. China. E-mail: tiandl@buaa.edu.cn
dSchool of Information Science and Technology, Hainan Normal University, Haikou, Hainan, P. R. China. E-mail: fuhaiyan@hainnu.edu.cn
First published on 21st October 2019
Abstract
Many engineering and industrial technologies as well as biological processes are closely related to surface wettability. The control of surface wettability attracts much attention due to the prospective applications based on liquid and droplet manipulation. However, the dynamic modification of wetting is still a challenging issue both in theoretical models and practical applications. Electrowetting (EW) is one of the most widely used methods for controlling the wettability of liquids due to its fast responding speed, large switching range and excellent durability. Since Gabriel Lippmann first discovered the electrocapillary (ECP) phenomenon in 1875, which is a precursor of electrowetting, there has been considerable progress in this field, especially accompanied with the development of wettability and interface science. In this paper, we review the developments of EW for droplet manipulation in view of wetting to superwetting systems over the past decades, including theoretical basis, electrodes and fluid systems, droplet manipulation and special phenomena induced by EW. Finally, we discuss several difficult challenges in this field and provide future research directions from our perspective.
1. Introduction
Wetting is a common surface phenomenon in many engineering and technology fields, such as chemicals, materials, and biomedical areas. Over the past 200 years, studies on static wetting have developed worldwide, and innumerable great achievements have been made in this field. As a pioneer, Thomas Young defined surface wettability by proposing the concept of the contact angle (CA). Since then, engineers and scientists from different fields have systematically studied materials with various wettabilities and developed functional surfaces with special capabilities, such as superhydrophilic surfaces (water contact angle (WCA) less than 5°) and superhydrophobic surfaces (WCA > 150°). In addition, static wetting models for explaining the wetting behaviours on these surfaces have been well established. However, the dynamic regulation of the wetting properties on these surfaces is still a challenging issue. Functional surfaces with controllable wettability, which can respond to external stimuli, have attracted enormous interest due to the prospective applications based on liquid and droplet manipulation. To date, various methods have been developed to manipulate droplets, including optical,1,2 magnetic,3,4 surface acoustic wave5,6 and thermal capillary7,8 techniques. Nevertheless, all the methods mentioned above have different defects, which limit their practical applications. For instance, optical methods are associated with relatively low throughput, and the lasers used in some systems may lead to biocompatibility problems. Magnetic actuation of droplets is a comparably convenient method to manipulate droplet movement. However, this approach requires the addition of magnetic nanoparticles to the droplet. Moving droplets with surface acoustic waves can cause a single droplet to orientate along the microchannel path in a non-invasive manner; however, this requires specially designed microchannels with satisfactory acoustic reflectivity. Also, a droplet floating on another immiscible liquid can be manipulated by thermal capillary waves with the help of a low gravity environment.Compared to the above methods, electrowetting (EW) is one of the most widely used ways for controlling the wettability of liquids; this is mainly because of its fast response speed (several milliseconds), large switching range (several tens of degrees), excellent durability (hundreds of thousands of switching cycles) and low energy consumption (10–100 μW). As a consequence, EW is very important in a host of practical applications, such as microfluidics, variable-focus microlenses, and other microelectromechanical systems (MEMS).
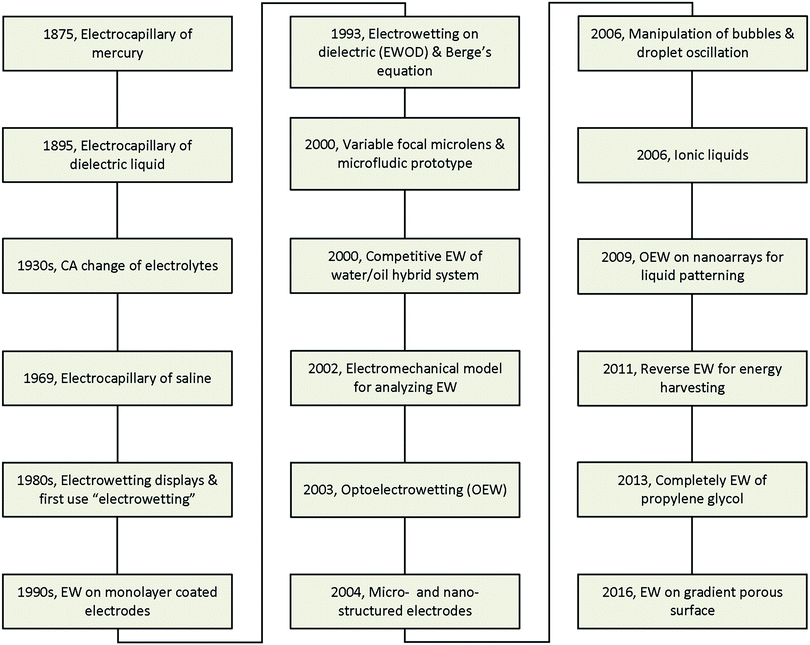
The major developments in EW are summarized in Fig. 1. The earliest reports related to EW can be traced back to 1875. In that year, G. Lippmann published his pioneering research on the electrocapillary effect,9 which is the earliest comprehensive investigation in this field. Briefly, by decreasing the surface charge between mercury and an electrolyte which was initially positive, it was found that the capillary depression of the mercury and hence the interfacial tension firstly increased to the maximum and then decreased. Based on this, Lippmann proposed the formula of electrocapillarity, that is, the famous Lippmann equation:
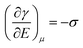 | (1) |
However, all the studies mentioned above remained far from practical application due to the involvement of toxic mercury or the inevitable electrolysis, beyond hundreds of millivolts. Then, in 1993, B. Berge et al.20 proposed the idea of covering dielectric films on plate electrodes to eliminate the problem of electrolysis. In brief, for a polymer film covering a steel disc, the CA decreased to about 30° on PET and 70° on PTFE under applied voltages of 200 V and 1000 V, respectively. This effect is known as electrowetting on insulator coated electrodes (EICE) or electrowetting on a dielectric (EWOD), the latter of which is used more widely. Since then, almost all published papers about EW have utilized this process due to the large amplitude of the CA change, simplicity of fabrication, and low cost of the materials. This process directly contributed to the outbreak of research on EW in the early 2000s and was greatly important in facilitating the development of EW. Two main practical applications of EW emerged in 2000, namely variable focal lenses21 and microfluidic prototypes.22 Meanwhile, C. Oehr et al.23 systemically studied the EW characteristics of water/oil hybrid systems and proposed the competitive EW effect at the interface of two immiscible liquids. However, there was still no recognized mechanism until T. B. Jones24 reported that EW is essentially an electromechanical process. Subsequently, certain functional materials were introduced in EWOD to enhance its performance and enrich its applications. For example, C. Kim et al.25 first proposed optoelectrowetting for optical actuation of liquid droplets. Also, micro- and nano-structured electrodes were first introduced by T. N. Krupenkin et al.26 Other interesting behaviours reported later included bubble manipulation in an aqueous environment27 and droplet oscillation under an AC electric field.28 Ionic liquids, a type of non-aqueous conducting liquid, have also been introduced in EWOD.29 Our group30 proposed photoelectric cooperative wetting (PCW) on nanoarrays for liquid patterning. Additionally, a novel energy harvesting system based on reverse EW was reported.31 Complete EW of propylene glycol, which involves a transition of EW from partial to complete wetting on a common planar electrode, was also reported in 2013.32 Recently, our group33 demonstrated that EW on a gradient porous surface can be used for liquid transport. With the cooperative effects of an electric field and gradient surface energy, this method can continuously transfer oil droplets underwater by directional motion.
With the development of surface wettability and materials science, many new research results on EW have been achieved. In this review, we aim to emphasize recent progress and breakthroughs in EW over the past decades. In Section 2, we give a brief introduction to the theoretical basis because the early theoretical developments were already comprehensively reviewed by F. Mugele and J. Baret.34 In Section 3, the development of fluid systems and electrodes is reviewed to demonstrate the accomplishments and contributions to practical applications. In Section 4, we summarize different modes of droplet manipulation, including transfer, oscillation, capillary bridge, permeation and bouncing. Other special phenomena induced by EW, such as a controllable Cheerios effect, suppression of the coffee stain effect and electrofreezing under an EW field, are also reviewed in Section 5. Finally, we discuss some difficult challenges both in theory and application and provide future research directions from our perspective.
2. Theoretical basis
The theoretical basis of EW was well established in the early 2000s. Lippmann–Young's equation, which associates CA changes with an electric field, is central to all mainstream physical principles in EW. Researchers from different fields have provided different interpretations of this equation. In this section, we will briefly introduce Lippmann–Young's equation from different points of view (Section 2.1). Additionally, the deviation of practical models from ideal models is discussed (Section 2.2).2.1. Lippmann–Young's equation
Based on general Gibbs interfacial thermodynamics, an elegant derivation of eqn (1) can be obtained:35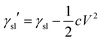 | (2) |
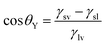 | (3) |
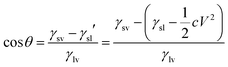 | (4) |
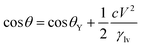 | (5) |
Another approach was published by B. Berge and co-workers.36 Their theoretical model is an ideal capacitor composed of a liquid droplet and planar electrode. In this case, EW is treated as a capacitor charging process. Because charge redistribution between the battery and capacitor decreases the energy of the system, the increased solid–liquid contact area caused by the CA change can increase the capacitance and thus redistribute the charge.
However, T. B. Jones et al. proposed that EW is an electromechanical process in nature,24,37,38 which is gradually being accepted by more researchers. They modified Pellat's experiment to establish and analyse the theoretical model of a charged conductive droplet in an electric field. The net electrical body force on the droplet, named the Maxwell stress, results in the macroscopic EW behaviour. From this point of view, EW is an entirely electromechanical process and is irrespective of the CA, which was verified by F. Mugele and J. Buehrle.39 Based on their results, EW can only affect apparent CA, while the local CA near the three-phase contact line (TCL) is independent of the applied voltage at the scale of dielectric thickness. In other words, the microscopic CA is consistent with Young's CA. T. B. Jones also discussed the relationship between EW and DEP.24 Although they are essentially the same and often occur together, EW is the effect of an electric field upon the CA, while DEP refers to the liquid actuation caused by a net electromechanical force. This perspective provides a physical picture of CA reduction in mechanics and hence provides a theoretical basis for many applications based on liquid actuation.
2.2. Various practical factors
In almost all published papers, the parabolic relation of the applied voltage and the cosine of the measured CA partly deviate from Lippmann–Young's equation.40 The curve is shown to hold at low voltage; however, deviation occurs at high voltage. These deviations originate from the approximation of the ideal capacitor, which ignores various practical effects, including the fringe fields of the capacitor, the tip effect around the TCL, imperfect conduction of the electrolyte and electrification of the dielectric layer. Moreover, a phenomenon named contact angle saturation (CAS) is always found when exceeding the critical voltage. To date, the studies on the physical mechanism of CAS are far from conclusive; this is commonly considered to be one of the most important challenges in this field.From the viewpoint of the electromechanical process, sufficient Maxwell stress can lead to complete spreading of droplets. In other words, according to eqn (5), CA can reach 0° as long as the applied voltage is large enough. However, the effective voltage applied to the droplet is always lower than the voltage applied to the whole system. To determine the reason for this voltage loss, researchers have reported several hypotheses regarding CA saturation. As reported by A. G. Papathanasiou and A. G. Boudouvis, macroscopic electrostatic analysis showed that the electric field generated around TCL was ten times stronger than the surrounding uniform field.41 They hypothesised that charge is injected and trapped in the dielectric film, resulting in local dielectric breakdown near the TCL. The trapped charge in the dielectric film has no effect on EWOD, and the resulting charge shielding effect decreases the Maxwell stress. This trapped charge model was validated by analysing charge migration between the trapped charge states and liquid charge states in EW at lipid bilayers.42 Trapped charges decrease the Maxwell stress and eventually result in CAS. Although this mechanism may apply in some EWOD cases, trapped charge and local dielectric breakdown can be avoided by applying alternating voltages and using high dielectric-strength dielectric films. Another mechanism is electrostatic repulsion. A charged droplet on the electrode substrate usually generates a ring of satellite droplets around the mother droplet.36 The droplet becomes unstable under high voltage, and its CA decrease is prevented as a result of electrostatic repulsion. However, electrostatic repulsion decreases significantly when the conductivity of the droplets is approved.
Because CAS is a universal phenomenon in EWOD devices, a general mechanism that is irrespective of the materials and other experimental conditions is more convincing. The mechanism of ionization of the insulating surroundings was first proposed by B. Berge and co-workers.43 They observed luminescence caused by gas ionization at TCL and analysed the related electrical discharge. Charge leakage induces gas luminescence and thus decreases the driving force in EWOD. Molecular simulations validated that the apparent CA deviates from Lippmann–Young's equation when charges escape from the droplet and leak into its surrounding medium.44 For immiscible liquid surroundings, D. Andelman et al.45 predicted that ions could be injected from the aqueous droplet into the surrounding oil phase, resulting in CAS as well.
Finally, one study that must be mentioned is that by J. Heikenfeld et al.,46 who experimentally validated that CAS was invariant with many factors in EWOD, including dielectric thickness, interfacial tension, pH, ion type and size, solute/solvent interaction, DC vs. AC, oil surface tension and dielectric type. Because the final saturated CA was basically around 60° regardless of the abovementioned conditions, they believed that these experimental data refuted some existing hypotheses, including dielectric charging, surrounding charging and electrostatic repulsion. At least, they demonstrated that the existing hypotheses had many limitations, although this work did not unambiguously establish the cause of CAS. Additionally, these experimental data clearly indicate that saturation is a time-dependent phenomenon, and different physical mechanisms may play leading roles at different time scales during saturation. Therefore, pursuit of a universal theory for CAS continues.
3. Electrodes and fluid systems in EWOD
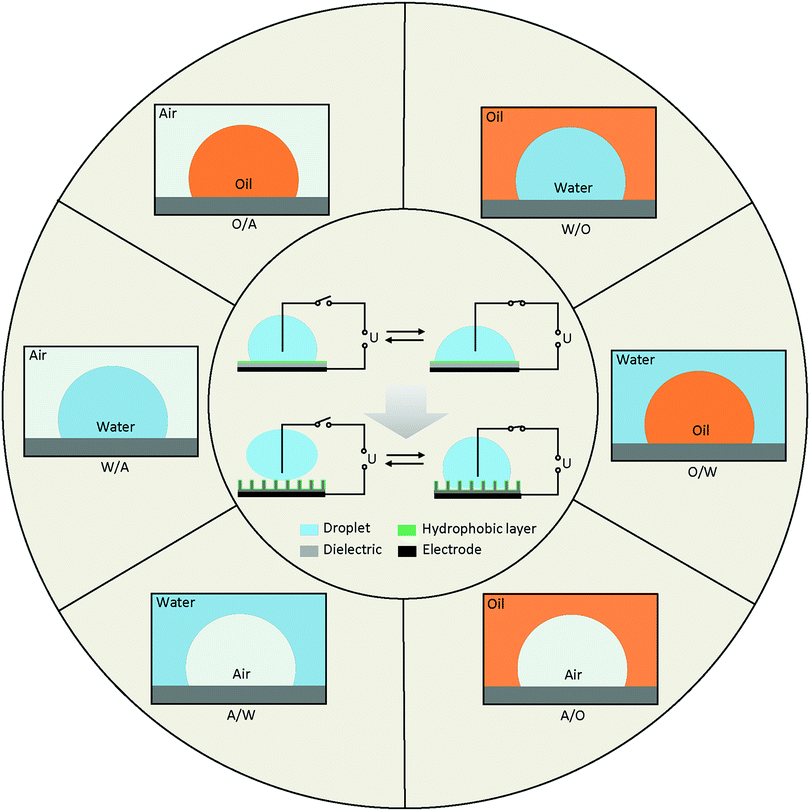
Diagrams of EWOD are shown in Fig. 2 (inside the circle), including a conductive droplet and an electrode covered with dielectric and hydrophobic layers. The CA of the droplet decreases with increasing electric field. In the case of a superhydrophobic system, the initial CA is larger than 150° and decreases to ∼100° under a certain electric field. EWOD with superhydrophobic electrodes shows robust performance, especially in reversibility and weak friction of the solid–liquid interface, both of which are important in droplet manipulation and practical applications (Section 4).The CA change range is affected by various properties of the electrode and fluid system, which is one of the most important characteristics in EWOD. Over the past decades, innumerable materials with different functions were introduced in EWOD to enhance the performance of CA changes on demand. For example, superhydrophobic electrodes with micro- and nanostructured surfaces are used to reduce friction between the droplet and surface electrode. Meanwhile, reduction of the pinning force around TCL was demonstrated to be an excellent strategy for actuation of a large range of CA changes. Furthermore, diversified liquid systems composed of immiscible electrolytic solutions were introduced to achieve more robust EWOD and develop a series of applications. In this section, we will review the electrodes and fluid systems over the past decades to demonstrate their accomplishments and contributions in practical applications. The electrodes with various properties and surface morphologies are discussed in Section 3.1, and the fluid systems with multivariate components and surroundings are presented in Section 3.2.
3.1. Electrodes in EWOD
Typical microstructured electrodes are shown in Fig. 3b, including Si nanopillars,26 SU-8 microposts,50 aligned carbon nanofibres,52 Si nanowires,48 Si nanobricks,53 ZnO nanorods,54 Si nanowires48 on Si micropillars,55 lotus leaf structures56 and polypyrrole nano-protrusions.57 These micro- and nano-structures are of great significance to the research and application of materials with different dimensions. Although the surface morphologies are different, the CA change ranges on these electrodes are quite similar. As a driving electric field of tens of volts is added, the apparent CA will decrease from >150° to ∼100°. As shown in Fig. 3c, two models are used to analyse the wetting states on micro- and nanostructured surfaces, i.e., the Wenzel state and Cassie–Baxter state. For the Cassie–Baxter state, air pockets are trapped between droplet and surface structure, while in the Wenzel state, the droplet permeates into the surface structure. For example, T. N. Krupenkin et al.26 demonstrated that EWOD on micro- and nanostructured surfaces undergo a transition from the Cassie–Baxter model to the Wenzel model. During this transition, the energy dissipation originates from the propagation of liquid implemented in the micro- and nanostructures. As a result, the pinning force around TCL is so enormous that the transition becomes irreversible when the electric field is removed.53,58 From this point of view, two general methods can be used to reverse the wettability transition from the Wenzel state to the Cassie state, thereby providing additional energy to this system and minimizing undesirable energy dissipation.
Introducing additional energy is an effective method to realize the wettability transition from the Wenzel state to the Cassie–Baxter state. N. Krupenkin et al.53 realized reversibility of EWOD by momentarily increasing the temperature of the substrate surface. High temperature is conducive to increase the volume of trapped gas and vapor to reach the Cassie–Baxter state and hence promote the reversibility. Also, C. J. Kim et al.59 reported a method of electrolysis to generate gas from an electrode surface, inducing the Wenzel state to Cassie–Baxter state transition. Another reported method that promotes leaving the sticky Wenzel state is droplet vibration, which is accomplished by direct vertical vibration of the substrate60 and droplet oscillation (see Section 4.2).
Decreasing energy dissipation in the wetting process is another effective way to achieve a reversible wettability transition. During this process, surface engineering of the electrode is a necessary method to obtain a surface with low energy dissipation. The pinning force at this electrode surface can be effectively decreased. Additionally, EWOD of an aqueous droplet in an oil environment has been widely studied. The pinning force is significantly suppressed due to the lubricant effect of the oil film trapped between the electrode surface and droplet, which is further discussed in W/O and O/W systems (Section 3.2.2). It must be emphasized that energy dissipation in EWOD originates from the pinning force at the TCL, which plays a more important role in the reversibility of EWOD, as reviewed by A. G. Papathanasiou.61 For an EWOD system with a given surface chemistry and roughness, the surface tension and pinning force at the TCL are the key driving forces to actuate the droplet movement. From this viewpoint, A. G. Papathanasiou proposed more concrete alternatives to promote reversibility: (i) creating dual scale roughness with dense structures with low solid fractions to realize moderate energy loss from micro-Wenzel (but nano-Cassie) to micro-Cassie (also nano-Cassie),62 and (ii) using thick dielectrics to avoid high liquid profile curvature because decreasing the radius of curvature causes the liquid to substitute the air gaps between the asperities.
The pyroelectric effect has also been introduced in EW. Lithium niobate (LiNbO3) is a colourless solid that is insoluble in water. It can generate a temporary voltage when it is heated or cooled. Based on the pyroelectric effect, P. Ferraro et al.69 designed a liquid micro-lens controlled by a temperature gradient. These results expanded the forms to activate EW instead of the single electric field. From our perspective, other stimuli, such as magnetic and mechanical fields, can also be utilized to activate EW; thus, it is applicable in more fields.
3.2. Fluid systems in EWOD
The fluid system is an important and decisive factor for achieving different EWOD performance. According to actual requirements, there are numerous combinations of fluid systems containing various components of droplet and surroundings. To simplify this, we provide an outline based on the different types of TCLs (Fig. 2), including water in air (W/A), water in oil (W/O), oil in water (O/W), oil in air (O/A), air in water (A/W) and air in oil (A/O).Many of these systems have been studied, and a series of applications has been developed. For example, most digital microfluidics are based on W/A and O/A systems, and variable-focus microlenses always utilize W/O and O/W systems. A/W and A/O systems involve bubble and microcapsule manipulation, which is also a research focus in labs on chips (LOC).
The influence of viscosity should also be considered in the actuation of oil. Existing research indicates that the viscosity only affects the magnitude of actuation and makes no difference in the principles of EW. Y. Fouillet et al.75 reported that viscosity mainly impacts the velocity of droplet actuation. However, the minimum voltage required for actuation is independent of the viscosity. They suggested that the velocity decreases with increasing viscosity mainly because of the friction at the TCL, and no further conclusions were made on this point. S. Lee et al.76 studied the influence of viscosity on oscillation. They demonstrated that the viscosity of the drop only affects the oscillation amplitude and not the resonance frequency. When the drop viscosity is beyond the critical value, drop oscillation is suppressed.
Ionic liquids (ILs) can be considered as another type of oil in O/A systems. The use of ILs as a novel class of electrolyte in EWOD was first reported by J. Ralston and co-workers.29 They demonstrated that imidazolium- and pyrrolidinium-based ILs show small ranges of CA change (∼10 to 20°) on Teflon AF 1600. The relatively small CA change is mainly due to the small initial CA (∼70°). The maximum CA change of ILs under EWOD is about 50°.77 Also, asymmetric responses of positive and negative voltage are common in ILs; this may originate from the asymmetry of the cation and anion in ILs. Later, many EWOD behaviors of different types of ILs and relevant microfluidics devices were successively reported by researchers.77–79
EWOD of two immiscible pure-dielectric liquids (or where at least one is dielectric) is the foundation of electrically controlled variable-focus microlenses and displays. A small droplet of insoluble oil is immersed in a conductive aqueous solution or vice versa. Under an electric field, the wettability of the electrode surface is significantly enhanced, modifying the morphology of the confined droplet and hence the focal length of the liquid lens. This concept is known as competitive electrowetting and was proposed by B. Janocha and co-workers.23
Compared with ambient air, the EWOD of aqueous droplets in an oil environment minimizes both evaporation and CA hysteresis, resulting in enhanced repeatability and reversibility. The CA hysteresis is very small (<2°) because the oil film trapped in the electrode surface plays a role in lubrication.83,84 H. Verheijen and M. Prins85 first reported reversible EW using an aqueous droplet on a Teflon AF 1600 hydrophobic layer, which is of great significance in commercializing EWOD based microlenses and displays.86–88 Additionally, W/O system-based droplet manipulation demonstrates faster velocities and lower actuating voltages compared to air environments.89
A special W/O system, named electrowetting on liquid-infused film (EWOLF), was proposed by Z. Wang and co-workers.90 As a dielectric layer, a liquid-infused film is achieved by locking a liquid lubricant (e.g. silicon oil) in a porous substrate. The pinning force at the contact line of the liquid–liquid interface is negligible; thus, this configuration leads to fast EWOD response with excellent reversibility compared with conventional EWOD on superhydrophobic electrodes. The transient response of EWOLF also demonstrated unexpected excellence, consuming only 45 ms to stabilize droplet oscillation compared with 500 ms of conventional EWOD.90 The suppression of droplet oscillation in the transient response is attributed to the viscous liquid–liquid interface. The is because additional wetting ridges around droplets can anchor contact lines and thus enhance dissipation of viscous oscillation energy. Subsequent research achieved low actuating voltages91 (decrease from 500 V to 5 V) and digital microfluidics with fast droplet transport (85 mm s−1) and stable repeatability (>5000 times),92 showing great performance improvement compared with typical EWOD devices.
For O/W systems, an oil droplet immersed in water weakly adheres to a hydrophobic electrode surface. Based on this, our group realized movement of an oil droplet on a gradient pore polystyrene substrate because the adhesion between the oil droplet and substrate could be efficiently decreased in the O/W system.33,93 Another peculiar phenomenon in O/W systems is detachment of the oil droplet from the electrode surface. A typical O/W system is formed by an oil droplet adhered on a hydrophobic polymer surface with surrounding water. When the electric field is applied, the CA of the oil droplet increases due to the competitive effect of the surrounding water,23 ultimately leading to oil droplet detachment. The critical conditions for detachment depend on the droplet volume, viscosity and applied voltage, as proposed by J. Hong and S. Lee.94 They also demonstrated three-dimensional digital microfluidic (3D-DMF) platforms with the aid of vertical movement of the oil droplet, which is of great importance in cell culture, electronic cooling, and sampling of microparticles.
Bubbles will retract under an electric field due to a decrease of the ambient CA. Consequently, adhesion between the bubbles and substrate decreases as a result of the decreased conformal contact. When the adhesion force is decreased below the buoyancy of the bubbles, detachment can be observed.93,97 Moreover, manipulation of bubbles is significant in heat transfer. By controlling bubble detachment, it is possible to adjust the temperature or steam generation in the process of heat transfer. E. Wang et al.98 reported a switch of heat transfer through in situ manipulation of bubbles. Under the influence of an electric field, bubble nucleation is significantly enhanced; hence, the heat transfer coefficient increases.
4. Droplet manipulation
Droplet manipulation is the foundation of all applications of EWOD. Physical descriptions of droplet movement through asymmetric EWOD actuation can be interpreted from different perspectives, including asymmetric electrostatic energy, surface tension and hydrostatic pressure, as summarized by W. Nelson and C. J. Kim.70 These descriptions are not contradictory. In fact, they enrich the understanding of EWOD-driven droplet movement from different aspects.As an illustration, Fig. 4 shows a cross section of a droplet in a typical EWOD device. The CA in the original state is assumed as 90° to simplify the analysis and focus more on the active region. When the lower right electrode is activated and all other electrodes are grounded, the droplet moves to the right as its CA changes to θV. It should be pointed out in particular that the Young's angle is maintained, as shown in the enlarged figures. Young's angle is a microscopic expression of the distance of χ from an electrode surface, as discussed previously in Section 2.1. It has been proven that EWOD can only affect the apparent CA, whereas the microscopic CA near the TCL is independent of the applied voltage.39 From the perspectives of micro-angle (or Young's angle) and macro-angle (or apparent angle), force analysis can be divided into case (1) and case (2), respectively. As shown in the figure, in case (1), the net force acting on the droplet in the horizontal direction is
| F = F(V) |
F = γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θV θV |
| F = [(P0 − Pr) − (P0 − Pa)]h = (Pa − Pr)h |
F = F(V) = γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θV = (Pa − Pr)h θV = (Pa − Pr)h |
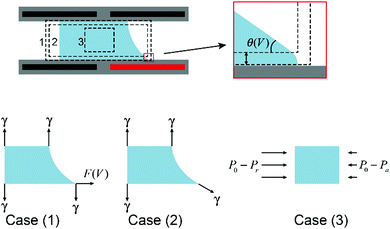 | ||
| Fig. 4 Cross section of a droplet in a typical EWOD device with force analysis from different perspectives. | ||
Based on the movement of droplets under EWOD, we reviewed various modes of droplet manipulation, such as transfer, oscillation, capillary bridge, permeation and bouncing. The basic development overviews and potential applications of each mode are summarized in this section.
4.1. Transfer
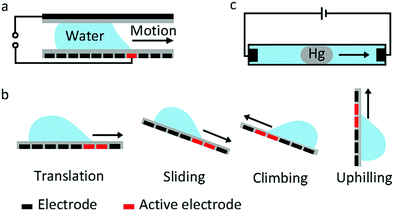
Droplet transfer is the most typical and common manipulation mode in many EWOD devices. The earliest proposal of droplet transfer in EW dates back to 1990. E. Matsumoto et al.100 proposed a model describing liquid flow in a small channel. As their simulation results demonstrated, EW was a viable strategy for microactuation. For a 10 μm radius channel, the pressure generated by EW can reach 0.01 MPa, which is comparable to a micropump. Subsequently, M. Pollack and R. Fair et al.22 reported the transfer of discrete microdroplets based on EW. As shown in Fig. 5a, two planar electrodes were fabricated on glass, where the bottom electrode consisted of a linear array of spaced electrodes. When a voltage of 40 to 80 V was applied, saline droplets could be successively transferred at average velocities of 30 mm s−1. These studies laid the foundation for subsequent microfluidic research. More recently, a new strategy to manipulate underwater oil droplets for unidirectional motion was demonstrated by our group.33 The effects of EW and surface gradient wettability cooperated to realize continuous oil droplet transfer.The aforementioned sandwich structure of electrodes and electrolyte is complex and results in a very large frictional force that restricts droplet transfer. To address these problems, U. Yi and C. Kim101 studied EWOD actuation on coplanar electrodes with no cover plate (Fig. 5b). They demonstrated basic droplet manipulation techniques, including moving, cutting and merging of 0.1 μL droplets on this coplanar electrode. More sensing mechanisms can be introduced in this coplanar EWOD configuration and thus increase its flexibility for various applications.
Other special behaviours of droplet transport are sliding, climbing and uphilling. J. Kim and M. Kaviany102 studied the sliding behaviour of a droplet adhered on an inclined substrate (Fig. 5b). For a sufficiently small droplet volume (Bond number less than 0.8), actuation is difficult because the effect of EW is limited. For a sufficiently large droplet (Bond number greater than 2.5), gravity dominates, and the droplet can slide spontaneously. In the Bond number region between 0.8 and 2.5, the droplet adheres on the inclined surface at the start state and slides down when an appropriate voltage is applied. According to theoretical simulations, EW introduces a radial electrostatic force around the TCL, breaking the balance between surface tension and friction. As a result, the droplet can slide down when an appropriate voltage is applied. Droplet climbing on a inclined substrate and even uphilling on a vertical substrate were studied by A. K. Das and co-workers.103–106 They demonstrated that the driving force caused by EW could overcome gravity; this droplet manipulation can be utilized in integrated microfluidic analysis systems.
J. Lee and C. Kim107 explored a so-called continuous EW phenomenon for MEMS. A mercury droplet immersed in saline electrolyte can move towards a cathode (Fig. 5c) as a result of asymmetric polarization of the mercury droplet. With an applied voltage of only 2.8 V, the transfer speed of a mercury droplet in this system could reach 40 mm s−1. Then, Wan et al.108 studied the fundamental EWOD behaviours of mercury. On a parylene film, a mercury droplet underwent CA changes of 74° (from 141° to 67°) with good reversibility under an electric field of 25 V. Then, researchers focused on Galinstan, a nontoxic liquid-metal alloy. M. Dickey et al.109 demonstrated movement of a Galinstan liquid droplet inside a capillary wall utilizing a continuous EW effect. Recently, many applications based on EWOD of Galinstan have been reported, including a mechanical pump system,110 an integrated liquid cooling system111 and a controlled electrical switch.112
4.2. Oscillation
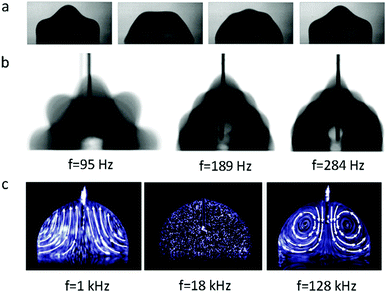
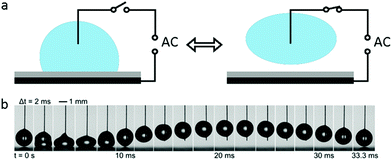
When an AC electric field is applied, the actuation behaviour of the liquid droplet changes. Under low frequency EWOD, the droplet oscillates with variable voltage. Droplet oscillation under an AC electric field was first reported by M. Gunji and M. Washizu.113 They observed a transformation between the elongation and restored states of a saline droplet under an AC electric field. Then, J. D. Sterling et al.28 observed shape oscillations of droplets on a planar solid surface. With electric fields of 60 V and 180 Hz, droplet oscillation was observed (Fig. 6a). Droplet oscillations were studied systematically by K. Kang et al.114 They demonstrated that excitation of droplets into various modes of oscillation depends significantly on the input frequency. As shown in Fig. 6b, the droplets oscillated at a certain input frequency, and the pattern of oscillation varied with different resonance frequencies. This study is significant for EW-based variable-focus microlenses and displays. Further developments should investigate the unstable nature of EW, which is important in EW-based liquid lenses and reflective displays.Meanwhile, for sufficiently high frequency EWOD, circulatory flow inside the droplet was observed by K. H. Kang and co-workers.115 In the frequency range of 10 Hz to 15 kHz, they observed rapid flow. Also, in the frequency range of about 35 to 256 kHz, a distinct type of flow was observed which was also significantly affected by the electrolyte concentration (Fig. 6c). The driving mechanism of these hydrodynamic flows was provided by F. Mugele and co-workers.116 At this high frequency, energy dissipation of the electric field in the bulk liquid cannot be ignored because the Joule heating effect leads to a temperature increase of several degrees. As a result, the temperature increase leads to gradient distributions of conductivity and permittivity; thus, an applied electric field can induce hydrodynamic flow.
4.3. Capillary bridge
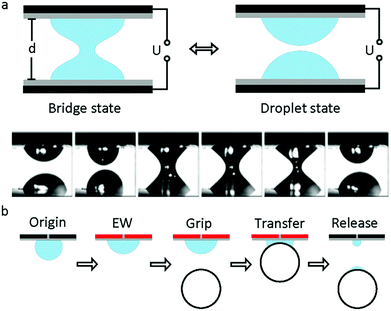
The study of capillary bridges caused by EWOD was first reported by F. Mugele and co-workers.117 As shown in Fig. 7a, two droplets formed a capillary bridge between two parallel electrodes. Under an electric field, both droplets tended to spread on the electrode; thus, the height of each droplet decreased. As a result, the droplet state was formed when it decreased to a critical height. For an appropriate separation distance of the electrode, the system can oscillate periodically between the droplet state and capillary state. Additionally, the relationship among the droplet morphology, electrode separation and applied voltage was analysed.118 For different combinations of control parameters, three different states of the system existed, including stationary capillary bridges, stationary separated droplets and periodic oscillations.This oscillation can promote the mixing performance of droplets on a millimetre scale. Compared to diffusion, the mixing speed of the oscillation system increases by 2 orders of magnitude.119 Moreover, Vasudev et al.120–122 proposed a microgripper based on manipulation of a liquid bridge (Fig. 7b), where the planar electrode was initially hydrophobic (CA around 120°). When an electric field was applied, the electrode became hydrophilic (CA less than 90°) and then approached a glass bead to form a liquid bridge. The bead was lifted up and transferred. When the applied voltage was removed, this microgripper released the glass bead instantaneously. The mechanism of this microgripper is based on the dynamic regulation of surface tension and capillary forces between the planar electrode and the object. Additionally, substitution of ionic liquids for water enabled this microgripper to function in high temperature and vacuum environments.123 Subsequently, Zhao et al.124 reported that adhesion between the droplet and superhydrophobic MnO2 nanotube arrays could be controlled by the polarity of the applied electric field. They demonstrated controllable liquid transportation between the upper and lower electrode plates. These systems have great prospects in the fields of micro-assembly and fabrication.
4.4. Permeation
Recently, an interesting phenomenon in which a droplet permeates into a superhydrophobic electrode triggered by an electric field had aroused wide attention. V. Lifton et al.125 first reported an electrically tunable nanomesh with controllable droplet permeability based on EWOD. In the absence of voltage, the electrolyte formed a Cassie–Baxter state on a superhydrophobic membrane-filter, as shown in Fig. 8a. Upon applied voltage, the nanomesh became hydrophilic; hence, the liquid permeated it and then contacted the hydrophilic collector. Additionally, they proposed the application of a smart microbattery.126 In this smart microbattery, the electrochemical reaction is controlled by a tunable membrane separating the liquid electrolytes and solid electrodes. When this membrane is triggered by an electric field, electrolytes permeate through the electrodes and electricity is generated. The separation of electrolytes and electrodes has importance in prolonging service life because the active components in this battery are kept apart.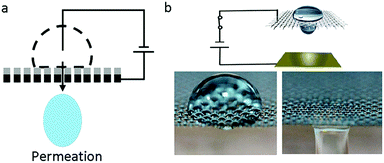 | ||
| Fig. 8 Droplet permeation. (a) A diagram of droplet permeation. (b) Process of droplet permeation on a graphene-coated nickel mesh with an applied electric field. | ||
Our group30,66 reported a liquid printing method based on the electric-triggered permeation of pigment droplets, realizing smart printing with controllable patterns. S. Nugen et al.127 utilized this electric-triggered permeation to control the rate of fluid flow on paper-fluidic sensors. Also, K. Oh et al.128 performed a comprehensive study on the flow control technique. They used graphene-coated nickel mesh as the flow-control membrane (Fig. 8b). The transition between repellency and permeability of the liquid droplet was controlled by an electric-responsive membrane. Furthermore, oil–water mixtures, including oil-in-water and water-in-oil emulsions, can be efficiently (≥99.9%) separated on demand based on the difference of oil and water permeability.129–131 These new strategies of EW-induced oil/water separation would be significant for smart filtration, micro-reaction, microfluidic systems, etc.
4.5. Bouncing
Another interesting behavior of a droplet in EWOD is bouncing on the substrate. Droplet bouncing was first reported by K. Kang and co-workers.114 When observing the oscillation of a droplet under AC electric field, they found that the droplet tended to bounce away from the substrate. Based on this, they performed systematic research on the droplet bouncing, utilizing a superhydrophobic substrate with a needle electrode above it (Fig. 9a).132,133 As shown in Fig. 9b, a saline droplet with a volume of 8 μL bounced on a superhydrophobic substrate with an electric field of 100 Vrms and 30 to 31 Hz. In this configuration, the shape deformation and bouncing of the droplet significantly depend on the AC frequency because droplet bouncing only occurs in very narrow frequency ranges. All these results indicate that droplet bouncing is dominated by resonance. They also studied the detailed bouncing mechanisms with regard to the jumping height and the energy conversion.133 They proposed that the work done by the applied electric field could stretch the droplet to store energy, and bouncing would occur when the electric field was removed. Based on the bouncing behavior, they demonstrated a 3D droplet digital microfluidic system in which a sessile droplet could be transported away from surfaces for further applications. This work provides conditions to study transporting droplets with antigravity and lays the foundation for more methods of droplet manipulation.5. Other special phenomena induced by EW
As an efficient method to regulate solid–liquid interfacial properties, EW induces many special phenomena and interesting devices in some fields related to dynamic controllable wettability. For example, Mugele et al.134 demonstrated regular coalescence of a droplet array condensing onto a flat hydrophobic electrode, which is due to the enhanced coalescence of droplets caused by structured electrodes. Furthermore, Chen et al.135 designed a quadrupedal microrobot that could easily sink and rise to the water surface based on four regulatable EW pads. In this section, we summarize other special phenomena relating to EW that have emerged in recent years in the hope of providing a more comprehensive understanding of EW.5.1. Controllable Cheerios effect
The so-called “Cheerios effect” was first proposed by D. Vella and L. Mahadevan.136 They observed that breakfast cereals floating in milk always clump together or stick to the walls of the breakfast bowl. The Cheerios effect is a common phenomenon in which small floaters are either repelled or attracted by the sidewall of the container, depending on the combined effects of capillary interaction and buoyancy.137–139 Because buoyancy is related to the inherent properties of floaters, the regulation of capillary interaction is vital to control the Cheerios effect. This capillary force is highly dependent on the wettability of the sidewalls and floaters. Thus, repulsion or attraction between the floaters and the sidewall is meditated by CA changes. S. Cho et al.140 implemented EWOD to regulate the CA of a sidewall which was composed of a conductor and dielectric layer. Therefore, the interaction forces between the floaters and sidewall switched easily between repulsion and attraction. Based on this, N. Crane et al.141 reported accurate manipulation of floaters, including position, alignment, assembly and transport, demonstrating an alternative method for positioning and assembly.5.2. Suppressing the coffee stain effect
The coffee stain effect originates from the differential evaporation rates between the edge and the interior of a droplet.142 The influence of EW on the coffee stain effect was studied by F. Mugele et al.143 They found that EW efficiently suppressed coffee stains of both colloidal particles and DNA solutions in an AC electric field. The mechanism of suppression caused by EW is based on the decrease of the pinning force at the TCL and enhancement of the internal mixing speed. The combination of these two effects prevents the accumulation of solutes around the TCL. These results have significance in improving detection sensitivity in the field of microfluidic technology, such as micro-detection and micro-reaction systems.5.3. Electrofreezing under EW
Electrofreezing is the electrically induced freezing of supercooled water. Electrofreezing under EW studies the behavior of ice nucleation in water droplets in the EW configuration. V. Bahadur et al.144 and R. Shaw et al.145 demonstrated that the freezing temperatures of water droplets increased in an applied electric field. Also, the increase of the freezing temperature became saturated at high voltage. These results led to a deeper understanding of the mechanism of electrofreezing, where nucleation is primarily affected by the TCL instead of a previously recognized solid–liquid interface. This is because a hydraulic disturbance in supercooled water caused by EW can enhance crystallization. From our perspective, electrofreezing has potential for rapid advancement in the field of regulating liquid–solid phase changes.6. Conclusion and outlook
In order to give a clear picture of the development of droplet manipulation in EW, recent progress is summarized in this review. We provide an overview of the mainstream physical principles, various electrodes and fluid systems in EWOD, different droplet manipulation techniques and several special phenomena induced by EW. Additionally, the following challenges are worthy of further discussion for future study directions.(1) Currently, the effect of the electric field on surface tension is difficult to measure directly. The alternative method is to characterize changes in the CA to indirectly test the surface tension. This method is not particularly convincing because the apparent CA does not fully represent microscale interfacial tension. Disclosing the mechanism of the effect of the electric field on interfacial tension will provide a deeper understanding of EW and may bring about a technological revolution in this field.
(2) The use of EW to dynamically control wettability can be complemented and perfected by theoretical construction of dynamic wetting.
(3) Developing multidimensional and multifunctional electrodes for new EWOD systems with enhanced reversibility and stability as well as multi-field cooperation will extend the fundamental research and applications of EW.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 21671012 and 61762034) and the Natural Science Foundation of Beijing Municipality (2172033).References
- K. Dholakia and T. Čižmár, Nat. Photonics, 2011, 5, 335–342 CrossRef CAS.
- S.-Y. Park and P.-Y. Chiou, Adv. OptoElectron., 2011, 2011, 909174 Search PubMed.
- J. R. Dorvee, A. M. Derfus, S. N. Bhatia and M. J. Sailor, Nat. Mater., 2004, 3, 896–899 CrossRef CAS PubMed.
- D. Tian, N. Zhang, X. Zheng, G. Hou, Y. Tian, Y. Du, L. Jiang and S. X. Dou, ACS Nano, 2016, 10, 6220–6226 CrossRef CAS.
- T. Franke, A. R. Abate, D. A. Weitz and A. Wixforth, Lab Chip, 2009, 9, 2625–2627 RSC.
- Z. Wang and J. Zhe, Lab Chip, 2011, 11, 1280–1285 RSC.
- J. Z. Chen, S. M. Troian, A. A. Darhuber and S. Wagner, J. Appl. Phys., 2005, 97, 014906 CrossRef.
- E. F. Greco and R. O. Grigoriev, Phys. Fluids, 2009, 21, 042105 CrossRef.
- G. Lippmann, Ann. Chim. Phys., 1875, 5, 494–549 Search PubMed.
- H. Pellat, C. R. Acad. Sci. Paris, 1895, 119, 691–694 Search PubMed.
- A. Frumkin, A. Gorodetskaya, B. Kabanov and N. Nekrasov, Phys. Z. Sowjetunion, 1932, 1, 255–284 CAS.
- A. Frumkin and C. Double, Actual. Sci. Ind., 1936, 373, 5–36 Search PubMed.
- A. Frumkin and A. Gorodetzkaja, Acta Physicochim. URSS, 1938, 9, 327–340 CAS.
- G. Beni and S. Hackwood, Appl. Phys. Lett., 1981, 38, 207–209 CrossRef CAS.
- G. Beni and M. Tenan, J. Appl. Phys., 1981, 52, 6011–6015 CrossRef CAS.
- J. H. Jackel and S. Beni, Appl. Phys. Lett., 1982, 40, 4–5 CrossRef.
- J. L. Jackel, S. Hackwood, J. J. Veselka and G. Beni, Appl. Opt., 1983, 22, 1765–1770 CrossRef CAS PubMed.
- J. A. M. Sondag-Huethorst and L. G. J. Fokkink, J. Electroanal. Chem., 1994, 367, 49–57 CrossRef CAS.
- J. A. M. Sondaghuethorst and L. G. J. Fokkink, Langmuir, 1994, 10, 4380–4387 CrossRef CAS.
- B. Berge, C. R. Acad. Sci. Paris Ser. II, 1993, 317, 157–163 CAS.
- B. Berge and J. Peseux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 159–163 CrossRef CAS.
- M. G. Pollack, R. B. Fair and A. D. Shenderov, Appl. Phys. Lett., 2000, 77, 1725–1726 CrossRef CAS.
- B. Janocha, H. Bauser, C. Oehr, H. Brunner and W. Gopel, Langmuir, 2000, 16, 3349–3354 CrossRef CAS.
- T. B. Jones, Langmuir, 2002, 18, 4437–4443 CrossRef CAS.
- P. Y. Chiou, H. Moon, H. Toshiyoshi, C. J. Kim and M. C. Wu, Sens. Actuators, A, 2003, 104, 222–228 CrossRef CAS.
- T. N. Krupenkin, J. A. Taylor, T. M. Schneider and S. Yang, Langmuir, 2004, 20, 3824–3827 CrossRef CAS.
- Y. Zhao and S. K. Cho, Micro bubble manipulation towards single cell handling tool, IEEE, 2006 Search PubMed.
- R. Miraghaie, J. D. Sterling and A. Nadim, Technical Proceedings of the 2006 NSTI Nanotechnology Conference and Trade Show, 2006, vol. 2, pp. 610–613.
- S. Millefiorini, A. H. Tkaczyk, R. Sedev, J. Efthimiadis and J. Ralston, J. Am. Chem. Soc., 2006, 128, 3098–3101 CrossRef CAS.
- D. Tian, Q. Chen, F.-Q. Nie, J. Xu, Y. Song and L. Jiang, Adv. Mater., 2009, 21, 3744–3749 CrossRef CAS.
- T. Krupenkin and J. A. Taylor, Nat. Commun., 2011, 2, 448 CrossRef.
- G. McHale, C. V. Brown and N. Sampara, Nat. Commun., 2013, 4, 1605 CrossRef CAS.
- D. Tian, L. He, N. Zhang, X. Zheng, Y. Dou, X. Zhang, Z. Guo and L. Jiang, Adv. Funct. Mater., 2016, 26, 7986–7992 CrossRef CAS.
- F. Mugele and J. C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705–R774 CrossRef CAS.
- A. W. Adamson and A. P. Gast, Physical chemistry of surfaces, Interscience, New York, 1967 Search PubMed.
- M. Vallet, B. Berge and L. Vovelle, Polymer, 1996, 37, 2465–2470 CrossRef CAS.
- T. B. Jones, K. L. Wang and D. J. Yao, Langmuir, 2004, 20, 2813–2818 CrossRef CAS.
- T. B. Jones, J. Micromech. Microeng., 2005, 15, 1184–1187 CrossRef.
- F. Mugele and J. Buehrle, J. Phys.: Condens. Matter, 2007, 19, 375112 CrossRef.
- A. I. Drygiannakis, A. G. Papathanasiou and A. G. Boudouvis, Langmuir, 2009, 25, 147–152 CrossRef CAS.
- A. G. Papathanasiou and A. G. Boudouvis, Appl. Phys. Lett., 2005, 86, 164102 CrossRef.
- J. T. Kedzierski, R. Batra, S. Berry, I. Guha and B. Abedian, J. Appl. Phys., 2013, 114, 024901 CrossRef.
- M. Vallet, M. Vallade and B. Berge, Eur. Phys. J. B, 1999, 11, 583–591 CrossRef CAS.
- J. Liu, M. Wang, S. Chen and M. O. Robbins, Phys. Rev. Lett., 2012, 108, 216101 CrossRef.
- T. Yamamoto, M. Doi and D. Andelman, EPL, 2015, 112, 56001 CrossRef.
- S. Chevalliot, S. Kuiper and J. Heikenfeld, J. Adhes. Sci. Technol., 2012, 26, 1909–1930 CAS.
- M. Liu, S. Wang and L. Jiang, Nat. Rev. Mater., 2017, 2, 17036 CrossRef CAS.
- N. Verplanck, E. Galopin, J.-C. Camart, V. Thomy, Y. Coffinier and R. Boukherroub, Nano Lett., 2007, 7, 813–817 CrossRef CAS.
- Z. Wang, Y. Ou, T.-M. Lu and N. Koratkar, J. Phys. Chem. B, 2007, 111, 4296–4299 CrossRef CAS.
- D. L. Herbertson, C. R. Evans, N. J. Shirtcliffe, G. McHale and M. I. Newton, Sens. Actuators, A, 2006, 130, 189–193 CrossRef.
- C. P. Tan and H. G. Craighead, Materials, 2010, 3, 1803–1832 CrossRef CAS.
- L. Zhu, J. Xu, Y. Xiu, Y. Sun, D. W. Hess and C.-P. Wong, J. Phys. Chem. B, 2006, 110, 15945–15950 CrossRef CAS.
- T. N. Krupenkin, J. A. Taylor, E. N. Wang, P. Kolodner, A. Marc Hodes and T. R. Salamon, Langmuir, 2007, 23, 9128–9133 CrossRef CAS.
- J. L. Campbell, M. Breedon, K. Latham and K. Kalantar-Zadeh, Langmuir, 2008, 24, 5091–5098 CrossRef CAS.
- F. Lapierre, P. Brunet, Y. Coffinier, V. Thomy, R. Blossey and R. Boukherroub, Faraday Discuss., 2010, 146, 125–139 RSC.
- J.-T. Feng, F.-C. Wang and Y.-P. Zhao, Biomicrofluidics, 2009, 3, 022406 CrossRef.
- K. S. Teh, Y. Takahashi, Z. Yao and Y.-W. Lu, Sens. Actuators, A, 2009, 155, 113–119 CrossRef CAS.
- F. Lapierre, V. Thomy, Y. Coffinier, R. Blossey and R. Boukherroub, Langmuir, 2009, 25, 6551–6558 CrossRef CAS.
- L. Choongyeop and K. Chang-Jin, Phys. Rev. Lett., 2011, 106, 014502 CrossRef.
- J. B. Boreyko and C.-H. Chen, Phys. Rev. Lett., 2009, 103, 174502 CrossRef.
- A. G. Papathanasiou, Curr. Opin. Colloid Interface Sci., 2018, 36, 70–77 CrossRef CAS.
- T. Verho, J. T. Korhonen, L. Sainiemi, V. Jokinen, C. Bower, K. Franze, S. Franssila, P. Andrew, O. Ikkala and R. H. Ras, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10210–10213 CrossRef CAS.
- P. Y. Chiou, S.-Y. Park and M. C. Wu, Appl. Phys. Lett., 2008, 93, 221110 CrossRef.
- H.-S. Chuang, A. Kumar and S. T. Wereley, Appl. Phys. Lett., 2008, 93, 064104 CrossRef.
- D. Tian, J. Zhai, Y. Song and L. Jiang, Adv. Funct. Mater., 2011, 21, 4519–4526 CrossRef CAS.
- Z. Guo, X. Zhang, X. Zheng, Z. Liu, J. Cai, D. Tian, W. Li, J. Zhai, Y. Song and L. Jiang, J. Mater. Chem. A, 2014, 2, 2498–2503 RSC.
- Z. Guo, X. Zheng, D. Tian, Y. Song, J. Zhai, X. Zhang, W. Li, X. Wang, S. Dou and L. Jiang, Nanoscale, 2014, 6, 12822–12827 RSC.
- D. Tian, Y. Song and L. Jiang, Chem. Soc. Rev., 2013, 42, 5184–5209 RSC.
- P. Ferraro, S. Grilli, L. Miccio and V. Vespini, Appl. Phys. Lett., 2008, 92, 213107 CrossRef.
- W. C. Nelson and C.-J. C. Kim, J. Adhes. Sci. Technol., 2012, 26, 1747–1771 CAS.
- M. G. Pollack, A. D. Shenderov and R. B. Fair, Lab Chip, 2002, 2, 96–101 RSC.
- S. K. Cho, H. J. Moon and C. J. Kim, J. Microelectromech. Syst., 2003, 12, 70–80 CrossRef.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 CrossRef CAS.
- D. Chatterjee, B. Hetayothin, A. R. Wheeler, D. J. King and R. L. Garrell, Lab Chip, 2006, 6, 199–206 RSC.
- R. Baviere, J. Boutet and Y. Fouillet, Microfluid. Nanofluid., 2008, 4, 287–294 CrossRef CAS.
- J. Hong, Y. K. Kim, K. H. Kang, J. Kim and S. J. Lee, Sens. Actuators, B, 2014, 190, 48–54 CrossRef CAS.
- J. Restolho, J. L. Mata and B. Saramago, J. Phys. Chem. C, 2009, 113, 9321–9327 CrossRef CAS.
- Y. S. Nanayakkara, H. Moon, T. Payagala, A. B. Wijeratne, J. A. Crank, P. S. Sharma and D. W. Armstrong, Anal. Chem., 2008, 80, 7690–7698 CrossRef CAS.
- H. Li, M. Paneru, R. Sedev and J. Ralston, Langmuir, 2013, 29, 2631–2639 CrossRef CAS.
- C. W. Monroe, L. I. Daikhin, M. Urbakh and A. A. Kornyshev, J. Phys.: Condens. Matter, 2006, 18, 2837–2869 CrossRef CAS.
- C. W. Monroe, M. Urbakh and A. A. Kornyshev, J. Phys.: Condens. Matter, 2007, 19, 375113 CrossRef.
- H. H. J. Girault and D. J. Schiffrin, J. Electroanal. Chem., 1985, 195, 213–227 CrossRef CAS.
- C. Quilliet and B. Berge, Europhys. Lett., 2002, 60, 99–105 CrossRef CAS.
- A. Staicu and F. Mugele, Phys. Rev. Lett., 2006, 97, 167801 CrossRef.
- H. J. J. Verheijen and M. W. J. Prins, Langmuir, 1999, 15, 6616–6620 CrossRef CAS.
- R. A. Hayes and B. J. Feenstra, Nature, 2003, 425, 383–385 CrossRef CAS.
- M. Hagedon, S. Yang, A. Russell and J. Heikenfeld, Nat. Commun., 2012, 3, 1173 CrossRef CAS.
- J. Heikenfeld, K. Zhou, E. Kreit, B. Raj, S. Yang, B. Sun, A. Milarcik, L. Clapp and R. Schwartz, Nat. Photonics, 2009, 3, 292–296 CrossRef CAS.
- D. Brassard, L. Malic, F. Normandin, M. Tabrizian and T. Veres, Lab Chip, 2008, 8, 1342–1349 RSC.
- C. Hao, Y. Liu, X. Chen, Y. He, Q. Li, K. Y. Li and Z. Wang, Sci. Rep., 2014, 4, 6846 CrossRef CAS.
- X. He, W. Qiang, C. Du, Q. Shao, X. Zhang and Y. Deng, J. Mater. Chem. A, 2017, 5, 19159–19167 RSC.
- J. Cao, Q. An, Z. Liu, M. Jin, Z. Yan, W. Lin, L. Chen, P. Li, X. Wang, G. Zhou and L. Shui, Sens. Actuators, B, 2019, 291, 470–477 CrossRef CAS.
- Y. Yan, Z. Guo, X. Zhang, L. He, Y. Li, K. Liu, J. Cai, D. Tian and L. Jiang, Adv. Funct. Mater., 2018, 28, 1800775 CrossRef.
- J. Hong and S. J. Lee, Lab Chip, 2015, 15, 900–907 RSC.
- S. K. Chung and S. K. Cho, J. Micromech. Microeng., 2008, 18, 125024 CrossRef.
- S. K. Chung, Y. Zhao and S. K. Cho, J. Micromech. Microeng., 2008, 18, 095009 CrossRef.
- S. Wang, H. H. Chen and C. L. Chen, Appl. Phys. Lett., 2016, 108, 181601 CrossRef.
- H. J. Cho, J. P. Mizerak and E. N. Wang, Nat. Commun., 2015, 6, 8599 CrossRef CAS.
- K. H. Kang, Langmuir, 2002, 18, 10318–10322 CrossRef CAS.
- E. Colgate and H. Matsumoto, J. Vac. Sci. Technol., A, 1990, 8, 3625–3633 CrossRef CAS.
- U.-C. Yi and C.-J. Kim, J. Micromech. Microeng., 2006, 16, 2053–2059 CrossRef.
- J. Kim and M. Kaviany, J. Appl. Phys., 2007, 101, 103520 CrossRef.
- S. Datta, M. Sharma and A. K. Das, Ind. Eng. Chem. Res., 2014, 53, 6685–6693 CrossRef CAS.
- S. Datta, A. K. Das and P. K. Das, Langmuir, 2015, 31, 10190–10197 CrossRef CAS.
- S. Datta, A. K. Das and P. K. Das, Ind. Eng. Chem. Res., 2016, 55, 3949–3959 CrossRef CAS.
- S. Datta, A. K. Das and P. K. Das, in Fluid Mechanics and Fluid Power – Contemporary Research, ed. A. K. Saha, D. Das, R. Srivastava, P. K. Panigrahi and K. Muralidhar, 2017, pp. 1305–1313 DOI:10.1007/978-81-322-2743-4_124.
- J. Lee and C. J. Kim, J. Microelectromech. Syst., 2000, 9, 171–180 CAS.
- Z. Wan, H. Zeng and A. Feinerman, J. Fluids Eng., 2007, 129, 388–394 CrossRef CAS.
- M. R. Khan, C. Trlica, J.-H. So, M. Valeri and M. D. Dickey, ACS Appl. Mater. Interfaces, 2014, 6, 22467–22473 CrossRef CAS.
- S.-Y. Tang, K. Khoshmanesh, V. Sivan, P. Petersen, A. P. O'Mullane, D. Abbott, A. Mitchell and K. Kalantar-zadeh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3304–3309 CrossRef CAS.
- J. Y. Zhu, S.-Y. Tang, K. Khoshmanesh and K. Ghorbani, ACS Appl. Mater. Interfaces, 2016, 8, 2173–2180 CrossRef CAS.
- J. Wissman, M. D. Dickey and C. Majidi, Adv. Sci., 2017, 4, 1700169 CrossRef.
- M. Gunji and M. Washizu, J. Phys. D: Appl. Phys., 2005, 38, 2417 CrossRef CAS.
- J. M. Oh, S. H. Ko and K. H. Kang, Langmuir, 2008, 24, 8379–8386 CrossRef CAS.
- S. H. Ko, H. Lee and K. H. Kang, Langmuir, 2008, 24, 1094–1101 CrossRef CAS.
- P. Garcia-Sanchez, A. Ramos and F. Mugele, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 015303 CrossRef.
- A. Klingner, S. Herminghaus and F. Mugele, Appl. Phys. Lett., 2003, 82, 4187–4189 CrossRef CAS.
- J. C. Baret and F. Mugele, Phys. Rev. Lett., 2006, 96, 016106 CrossRef.
- F. Mugele, J. C. Baret and D. Steinhauser, Appl. Phys. Lett., 2006, 88, 204106 CrossRef.
- A. Vasudev and J. Zhe, in 2008 17th Biennial University/Government/Industry Micro-Nano Symposium, Proceedings, IEEE, 2008, pp. 6–10, DOI: 10.1109/ugim.2008.9.
- A. Vasudev and J. Zhe, in 2008 51st Midwest Symposium on Circuits and Systems, IEEE, 2008, vol. 1 and 2, pp. 49–52, DOI: 10.1109/mwscas.2008.4616733.
- A. Vasudev and J. Zhea, Appl. Phys. Lett., 2008, 93, 103503 CrossRef.
- A. Al Amin, A. Jagtiani, A. Vasudev, J. Hu and J. Zhe, J. Micromech. Microeng., 2011, 21, 125025 CrossRef.
- X.-D. Zhao, H.-M. Fan, J. Luo, J. Ding, X.-Y. Liu, B.-S. Zou and Y.-P. Feng, Adv. Funct. Mater., 2011, 21, 184–190 CrossRef CAS.
- V. A. Lifton, J. A. Taylor, B. Vyas, P. Kolodner, R. Cirelli, N. Basavanhally, A. Papazian, R. Frahm, S. Simon and T. Krupenkin, Appl. Phys. Lett., 2008, 93, 043112 CrossRef.
- V. A. Lifton and S. Simon, J. Microelectromech. Syst., 2011, 20, 73–82 CAS.
- C. K. W. Koo, F. He and S. R. Nugen, Analyst, 2013, 138, 4998–5004 RSC.
- R. Tabassian, J.-H. Oh, S. Kim, D. Kim, S. Ryu, S.-M. Cho, N. Koratkar and I.-K. Oh, Nat. Commun., 2016, 7, 13345 CrossRef CAS.
- G. Kwon, A. K. Kota, Y. Li, A. Sohani, J. M. Mabry and A. Tuteja, Adv. Mater., 2012, 24, 3666–3671 CrossRef CAS.
- X. Lin, F. Lu, Y. Chen, N. Liu, Y. Cao, L. Xu, W. Zhang and L. Feng, Chem. Commun., 2015, 51, 16237–16240 RSC.
- X. Zheng, Z. Guo, D. Tian, X. Zhang and L. Jiang, Adv. Mater. Interfaces, 2016, 3, 1600461 CrossRef.
- S. J. Lee, S. Lee and K. H. Kang, J. Visualization, 2011, 14, 259–264 CrossRef CAS.
- S. J. Lee, S. Lee and K. H. Kang, Appl. Phys. Lett., 2012, 100, 081604 CrossRef.
- D. Baratian, R. Dey, H. Hoek, D. van den Ende and F. Mugele, Phys. Rev. Lett., 2018, 120, 214502 CrossRef CAS.
- Y. Chen, N. Doshi, B. Goldberg, H. Wang and R. J. Wood, Nat. Commun., 2018, 9, 2495 CrossRef.
- L. Mahadevan and D. Vella, Am. J. Phys., 2012, 73, 817–825 Search PubMed.
- D. L. Hu and J. W. M. Bush, Nature, 2005, 437, 733–736 CrossRef CAS.
- D. L. Hu, M. Prakash, B. Chan and J. W. M. Bush, Exp. Fluids, 2007, 43, 769–778 CrossRef.
- Y. Yu, M. Guo, X. Li and Q. S. Zheng, Langmuir, 2007, 23, 10546–10550 CrossRef CAS.
- J. Yuan, J. Feng and S. K. Cho, Langmuir, 2015, 31, 8502–8511 CrossRef CAS.
- J. M. Carballo, Q. Ni, J. Vasquez and N. B. Crane, Colloids Surf., A, 2017, 512, 118–128 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. J. N. Witten, Nature, 1997, 389, 827 CrossRef CAS.
- H. B. Eral, D. M. Augustine, M. H. G. Duits and F. Mugele, Soft Matter, 2011, 7, 4954–4958 RSC.
- K. Carpenter and V. Bahadur, Langmuir, 2015, 31, 2243–2248 CrossRef CAS.
- F. Yang, R. A. Shaw, C. W. Gurganus, S. K. Chong and Y. K. Yap, Appl. Phys. Lett., 2015, 107, 264101 CrossRef.
| This journal is © the Partner Organisations 2020 |