Pressure-induced valence transition in the mixed-valence (Sm1/3Ca2/3)2.75C60 fulleride†
Naoya
Yoshikane
 a,
Keisuke
Matsui
a,
Keisuke
Matsui
 a,
Takeshi
Nakagawa
a,
Takeshi
Nakagawa
 b,
Anastasia G. V.
Terzidou
b,
Anastasia G. V.
Terzidou
 c,
Yasuhiro
Takabayashi
c,
Yasuhiro
Takabayashi
 de,
Hitoshi
Yamaoka
de,
Hitoshi
Yamaoka
 f,
Nozomu
Hiraoka
g,
Hirofumi
Ishii
g,
John
Arvanitidis
f,
Nozomu
Hiraoka
g,
Hirofumi
Ishii
g,
John
Arvanitidis
 c and
Kosmas
Prassides
c and
Kosmas
Prassides
 *ad
*ad
aDepartment of Materials Science, Graduate School of Engineering, Osaka Prefecture University, Osaka 599-8531, Japan. E-mail: k.prassides@mtr.osakafu-u.ac.jp; Tel: +81 72 254 6162
bCenter for High-Pressure Science & Technology Advanced Research, 100094 Beijing, P. R. China
cPhysics Department, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
dWPI-Advanced Institute for Materials Research (WPI-AIMR), Tohoku University, Sendai 980-8577, Japan
eDepartment of Physical Science and Engineering, Nagoya Institute of Technology, Nagoya 466-8555, Japan
fRIKEN SPring-8 Center, Sayo, Hyogo 679-5148, Japan
gNational Synchrotron Radiation Research Center, Hsinchu 30076, Taiwan
First published on 17th October 2020
Abstract
(Sm1/3Ca2/3)2.75C60 is a member of the family of non-stoichiometric strongly-correlated rare-earth fullerides, (Sm1−xCax)2.75C60 (0 ≤ x ≤ 1), in which an orthorhombic 2 × 2 × 2 supercell of the face-centred cubic (fcc) unit cell of stoichiometric A3C60 (A = alkali metal) fullerides is stabilized by the long-range ordering of partially-occupied metal sites. At ambient temperature and pressure, it is a mixed valence compound with an average Sm valence of +2.33(2) implying a formal charge of −5.78 for the C60 anions. Here we study its electronic response to the application of pressure in the range 0–9 GPa. Synchrotron X-ray absorption measurements in the high-resolution partial fluorescence yield mode (PFY-XAS) at ambient temperature show the onset of an abrupt strongly hysteretic (width ∼2.5 GPa) first-order reversible phase transition at ∼4 GPa, accompanied by a drastic increase in the bulk Sm valence by ∼20% to +2.71(3). This is coincident with the huge lattice contraction and concomitant insulator-to-metal transition encountered before for Sm2.75C60 in the same pressure range and provides a possible explanation of the physical properties in terms of the strong coupling between the lattice and electronic degrees of freedom. The behaviour is reminiscent of the electronic and lattice response to pressure of highly correlated Kondo insulators like SmS and its ternary derivatives, Sm1−xRxS (R = Ca, Y, etc.). However, a distinguishing feature of the fulleride systems is that the C60 anionic sublattice can act as an electron reservoir due to the availability of a close-lying band derived by the t1g orbitals and can accept excess charge as the 4f-electron occupation number decreases. The observed electronic response as a function of pressure is thus opening new possibilities for accessing metallic fullerides at elevated pressures.
1. Introduction
Rare-earth (RE) metal C60 fullerides constitute an intriguing class of strongly-correlated molecular systems1 as they present the possibility of strong coupling between two electronically active sublattices, the anionic pπ(C60) and cationic 4f,5d(RE) sublattices both of which are dominated by strong electronic correlations.2,3 To date, metal fulleride research has been dominated by work on alkali fullerides, especially those with stoichiometry A3C60 (A = alkali metal). These have emerged as archetypal strongly correlated systems with superconducting transition temperatures, Tc as high as 38 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and upper critical magnetic fields, Hc2 in excess of 90 T.5 Nonetheless the electronic properties are entirely dominated by the narrow band behaviour of the C60 anion sublattice – the supporting cation sublattice is invariably electronically inactive and only plays a charge-balancing role as a structural spacer.6 A comparable but exactly reverse situation is encountered in rare earth compounds which represent one of the most fascinating classes of strongly correlated systems that include Kondo insulators and heavy fermions.7,8 Here the properties are dominated by the extreme narrow-band behaviour of the rare-earth cation f-electron sublattice with the supporting anion sublattice again playing a charge-balancing structural-spacer role. As electronically active anion solids, the rare-earth fullerides can have properties intrinsically distinct from comparable rare-earth compounds with closed shell anions, and the emergence of novel phenomena such as co-existence of Kondo f-electron behaviour with C60-based pπ-electron superconductivity may be anticipated.
4 and upper critical magnetic fields, Hc2 in excess of 90 T.5 Nonetheless the electronic properties are entirely dominated by the narrow band behaviour of the C60 anion sublattice – the supporting cation sublattice is invariably electronically inactive and only plays a charge-balancing role as a structural spacer.6 A comparable but exactly reverse situation is encountered in rare earth compounds which represent one of the most fascinating classes of strongly correlated systems that include Kondo insulators and heavy fermions.7,8 Here the properties are dominated by the extreme narrow-band behaviour of the rare-earth cation f-electron sublattice with the supporting anion sublattice again playing a charge-balancing structural-spacer role. As electronically active anion solids, the rare-earth fullerides can have properties intrinsically distinct from comparable rare-earth compounds with closed shell anions, and the emergence of novel phenomena such as co-existence of Kondo f-electron behaviour with C60-based pπ-electron superconductivity may be anticipated.
Rare-earth fulleride phases are not widely available mainly because of the synthetic difficulties in affording phase-pure materials in a reproducible way. Of interest has been the preparation of Eu6C60 and Eu9C70 fullerides that led to the isolation of molecular ferromagnets, which exhibit conducting and giant magnetoresistive behaviour with significant π(C60)-f,d(Eu) orbital interactions modulating the magnetic exchange.9–11 However, most of the research work on rare-earth fullerides has focused on materials with stoichiometry, RE2.75C60 (RE = Yb, Sm). These non-stoichiometric compounds crystallize with a 2a × 2a × 2a superstructure of the face-centred cubic (fcc) unit cell of A3C60 alkali fullerides arising from the long-rage ordered arrangement of partially occupied tetrahedral interstices (Fig. 1 inset).12,13 The RE2.75C60 unit cell comprises 32 C60 units and 88 RE atoms together with 8 RE partially occupied sites. Although early claims for superconductivity12,14 in this family proved erroneous,13,15,16 it was apparent from the presence of non-stoichiometry and deviation from the ideal “RE3C60” stoichiometry that these materials may be endowed with interesting electronic properties associated with mixed valence states of the RE ions, i.e. that the average RE valence should be greater than +2. Indeed, magnetic susceptibility data clearly indicated deviation of the RE valence from +2.13,15
As a result of these considerations, an important finding was then that both Sm2.75C60 and Yb2.75C60 were discovered to exhibit on cooling isosymmetric phase transitions that are accompanied by giant negative thermal expansion (NTE).13,15 The origin of this isotropic lattice response was ascribed to a temperature-induced valence transition of the RE ions from +(2 + ε) towards +(2 + ε′) with ε′ < ε and this interpretation was supported by synchrotron X-ray absorption measurements.1 This effect is immediately reminiscent of the valence or configuration transitions established in typical RE-based Kondo insulators such as SmS.17,18 The connection becomes even more prominent when the electronic properties are probed by the application of external pressure. For instance, SmS undergoes a pressure-induced abrupt catastrophic transition from a semiconducting black to a metallic gold phase that was rationalised phenomenologically by a valence fluctuation (4fn5d0 ↔ 4fn−15d1) model. In a similar fashion, Sm2.75C60 undergoes a pressure-induced first-order phase transition, which is accompanied by a huge lattice collapse of ∼6% at ∼4 GPa and a change in colour to gold, implying a drastic change in the conducting properties.19 Complementary Raman spectroscopic measurements in the same pressure range confirm the occurrence of the transition and support the emergence of metallic behaviour.20 The analogy with the behaviour of the Sm chalcogenides makes the possibility that Sm2.75C60 undergoes a similar pressure-induced valence transition towards a state with an increased average Sm valence +(2 + ε′′) with ε′′ > ε highly likely.
Isovalent or aliovalent cation substitutions have been extensively used in the past to control the electronic configurations of the rare-earth ions and tune the rare-earth exchange interactions, the Fermi level position and the lattice constant (chemical pressure) in mixed valence Kondo insulators such as SmS.21 The ternary phase fields Sm–R–S (R = Y, Ce, Nd, Ca, etc.) are recently drawing much attention in order to bring the insulator-to-metal transition to ambient pressure and utilize the huge NTE that accompanies the valence transition by tuning its operational temperature range.22–24 In the process, it is of particular importance to clarify the differences on the valence transition between controlling size (chemical or physical pressure) and doping (electronic structure).
In a similar fashion, we have initiated the study of the ternary fulleride phases, (Sm1−xCax)2.75C60 (0 ≤ x ≤ 1) in an attempt to mimic chemically the effect of physical pressure on the valence transition of Sm2.75C60 by taking advantage of the robust divalent character of the smaller valence-precise Ca2+ cations.25 We found that the (Sm1−xCax)2.75C60 (0 ≤ x ≤ 1) family of materials obeys Vegard's law with the Sm and Ca metal ions randomly distributed in the available octahedral and tetrahedral interstitial sites.25 They also adopt the same orthorhombic superstructure (space group Pcab) of the face-centred cubic unit cell of A3C60 (A = alkali metal) fullerides arising from the long-range ordering of tetrahedral partially-occupied vacancies (Fig. 1 inset) consistent with the stoichiometry of the materials.25 Moreover X-ray absorption spectroscopy measurements in the partial fluorescence yield mode (PFY-XAS) at the Sm-L3 edge have authenticated the mixed valence state of Sm across the whole series of (Sm1−xCax)2.75C60 compositions. In particular, it turns out that, at ambient conditions, chemical pressure sensitively tunes the 4f electron occupation number with the average Sm valence, ν increasing quasi-continuously by >10% as x increases from 0 (for Sm2.75C60, ν = +2.07(3)) to 2/3 (for (Sm1/3Ca2/3)2.75C60, ν = +2.33(2)). At the same time, the C60 anion charge remains nearly invariant at ≈−5.78.25
To date, there has been no direct study of the rare-earth electronic states in rare-earth fullerides at elevated pressures. Synchrotron X-ray powder diffraction19 and Raman spectroscopy20 agree on the occurrence of a hysteretic phase transition for Sm2.75C60 in the vicinity of 4 GPa with dramatic changes in both lattice size and electronic/conducting properties. Here, we directly address the issue of the evolution of the Sm electronic states with applied pressure by means of PFY-XAS spectroscopy at the Sm-L3 edge. We chose to investigate the calcium co-doped (Sm1/3Ca2/3)2.75C60 fulleride as this was found to incorporate Sm at the highest average valence, ν known for these systems at ambient pressure at +2.33(2).25 We find that ν initially increases monotonically to ∼4 GPa whereupon an abrupt phase transformation sets in – this is accompanied by a rapid increase in ν to +2.71(3) at ∼6.5 GPa. The electronic changes are reversible upon the release of pressure and are characterized by a large hysteresis, signature of the first-order nature of the transformation. They provide a possible rationalization of the pressure-induced drastic changes in structural and optical properties of rare-earth fullerides that may be coupled with the extreme fragility of the rare-earth valence.
2. Results and discussion
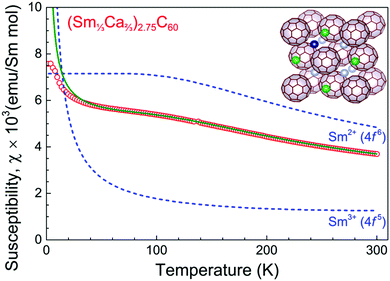
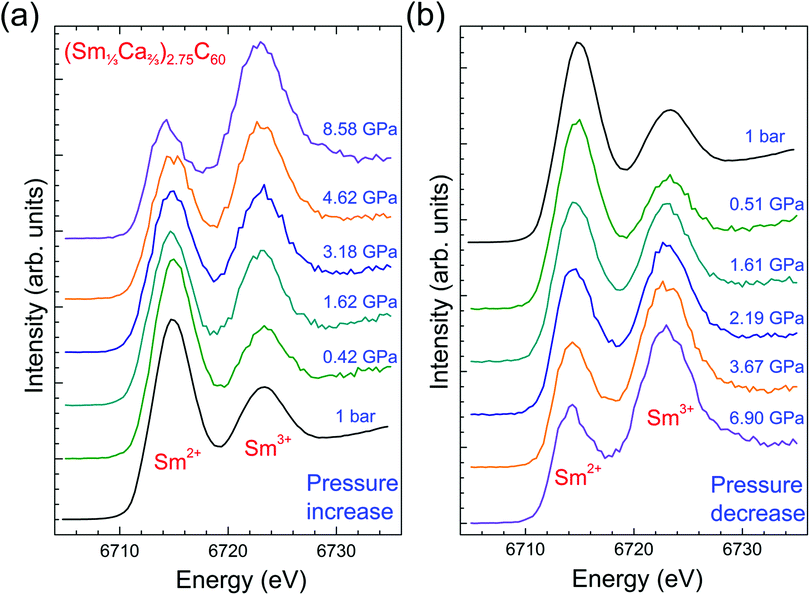
(Sm1/3Ca2/3)2.75C60 is a member of the (Sm1−xCax)2.75C60 (0 ≤ x ≤ 1) family of materials with x = 2/3. Fig. 1 shows the measured magnetic susceptibility, χ vs. temperature data for (Sm1/3Ca2/3)2.75C60, along with those calculated for the free Sm2+ and Sm3+ ions. For Sm2+ (4f6, 7F0), there is only a van Vleck contribution to the magnetic susceptibility, originating from the mixing of the J = 0 ground and the J = 1 excited state. On the other hand, the calculated susceptibility of Sm3+ (4f5, 6H5/2) is derived by summing the corresponding Curie and van Vleck (mixing of the J = 5/2 ground and J = 7/2 excited states) contributions.13 In mixed valence Sm-based compounds, an estimate of the average samarium valence can be derived from the magnetic susceptibility data at sufficiently high temperatures as a linear combination of the contributions of the two distinct Sm2+ and Sm3+ valence states.26 As it can be inferred from Fig. 1, the experimental values of the susceptibility of (Sm1/3Ca2/3)2.75C60 at high temperatures fall between those calculated for the two ionic states, in accord with the mixed valence character of samarium in this material. The experimental data can be reproduced well down to ∼50 K (below which valence transitions are expected)13,15 assuming 0.68 and 0.32 contributions from Sm2+ and Sm3+, respectively (solid line through the data). These values lead to an estimate of the average samarium valence, ν of +2.32 in excellent agreement with that obtained directly by PFY-XAS measurements at ambient conditions (+2.33(2)) for the same composition.25The PFY-XAS spectra of (Sm1/3Ca2/3)2.75C60 at the Sm-L3 edge at various pressures are displayed in Fig. 2 together with that measured under ambient conditions. We note that, since only one quantum transition (an intermediate state belonging to a shallow level) is selected in this X-ray spectroscopic technique, the lifetime broadening of the spectra (mainly originating from the deep core-hole in the final state) is suppressed, leading to a much better resolution than typical XAS measurements.27 Compared to the ambient pressure spectrum in which the sample was contained in a glass capillary,25 the sample chamber of the Be gasket in the present high pressure experiments is significantly more transparent to the synchrotron X-ray beam in the incident photon energy range used. This introduces the danger of causing radiation damage to the soft fulleride solids by X-ray illumination in the course of the measurements. Therefore, in order to avoid the occurrence of sample degradation, the incident X-ray beam power was reduced by a factor of ∼30 compared to that of the ambient pressure experiments by introducing appropriately thick aluminium foil filters. This unavoidably led to a worsening in the signal-to-noise ratio compared to that achieved at ambient pressure (Fig. 2).25 Nonetheless, good data statistics and improved spectral resolution still allow us to follow the pressure evolution of the average samarium valence with sufficient accuracy.
The appearance of two peaks separated by ∼8 eV in the spectra shown in Fig. 2 and corresponding to the 2p → 5d dipolar excitations for divalent (lower energy peak) and trivalent (higher energy peak) samarium, unambiguously evidences the mixed valence character of the samarium ions in (Sm1/3Ca2/3)2.75C60 at both ambient and elevated pressures.28 At ambient and low pressures, the higher intensity of the Sm2+ peak compared to that of the Sm3+ one qualitatively indicates that the average samarium valence, ν is closer to +2 rather than +3. This situation is gradually altered with increasing pressure as the Sm3+ peak gains in intensity at the expense of that of Sm2+, signalling a drastic decrease in the 4f electron occupation of the samarium ions induced by pressure. The reverse valence transition (Sm3+ → Sm2+) occurs upon pressure release. The transformation is reversible as the relative intensity of the two peaks in the spectrum recorded at 0.51 GPa upon depressurization is comparable to that in the spectra measured at ambient pressure and at 0.42 GPa at the start of the present measurements (Fig. 2a and b).
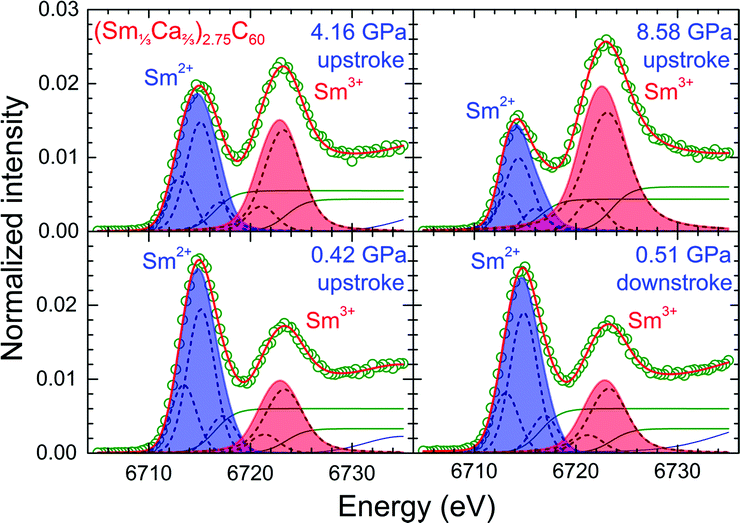
In order to extract quantitative information about the average valence, ν of samarium in (Sm1/3Ca2/3)2.75C60 and its pressure dependence, the data were fitted by appropriate functions to account for the contributions of the Sm2+ and Sm3+ peaks together with that of the background. The fits of the PFY-XAS spectra at selected pressures recorded during the upstroke (P = 0.42, 4.16 and 8.58 GPa) and downstroke (P = 0.51 GPa) cycles are shown in Fig. 3. The spectral contribution attributed to Sm2+ was fitted by the sum of three Voigt functions (one main and two satellites) for the main peak and an arctangent-like function to account for the background originating from the corresponding transitions to the continuum. The need to use more than one Voigt function to satisfactorily reproduce each white peak originates from the crystal-field splitting of the Sm 5d band.24,29 A similar fitting strategy was used for the Sm3+ spectral contribution except that it was found necessary to include only two Voigt functions to describe the corresponding main peak. In the lower pressure range of the experiments, an additional Voigt function was included in order to account for the small spectral uplift above 6730 eV (underlying baseline in Fig. 3). Fig. S1 and S2 (ESI†) collect together the pressure dependence of the energies and intensities of the individual subpeaks of the Sm2+ and Sm3+ components employed in the fits of the experimental PFY-XAS data. The average Sm valence, ν can be derived then from the relative integrated intensities of the divalent, I(+2) and the trivalent, I(+3) Sm PFY-XAS peaks (corresponding shaded areas in Fig. 3) by the expression: ν = 2 + {I(+3)/[I(+2) + I(+3)]}.
The fit of the PFY-XAS spectrum at 0.42 GPa yields a value for the average samarium valence, ν = +2.31(3), similar to that obtained from the corresponding measurements on the same composition at ambient pressure (ν = +2.33(2)).25 Such an agreement clearly demonstrates the reproducibility of our findings and confirms the successful loading of the highly air-/moisture-sensitive sample into the diamond anvil cell (DAC) for the high pressure experiments, completely avoiding any degradation. At the same time, the fit of the spectrum recorded at the highest pressure of our experiments (8.58 GPa), where the trivalent samarium peak clearly dominates, provides a value, ν = +2.71(3) for the average Sm valence – this corresponds to an increase of the Sm valence by 0.4 induced by pressure. Comparable changes associated with the pressure-induced transition from the semiconducting to the metallic phase have been reported for the Sm monochalcogenides, namely ∼0.8 for SmS, ∼0.6 for SmSe and ∼0.5 for SmTe.24
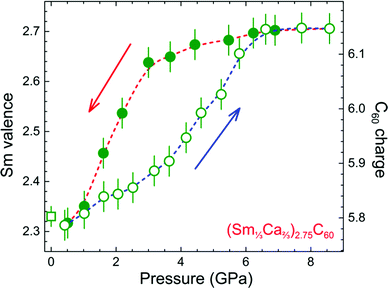
The pressure dependence of ν in (Sm1/3Ca2/3)2.75C60, as obtained from the fits of all the high pressure data recorded during the upstroke and downstroke cycles, is illustrated in Fig. 4. In the beginning, the valence increases slowly and continuously from +2.31(3) to +2.49(3) as the pressure approaches ∼4 GPa. This is followed first by a pressure regime (∼4–6.5 GPa) whereupon the average valence rapidly increases reaching a value of +2.71(3) and then by a plateau where ν remains invariant up to ∼9 GPa, the highest pressure reached in the present measurements. On the other hand, upon pressure release, the average samarium valence is robust over a broad pressure range decreasing only very slightly to a value of +2.64(3) between 9 and 3 GPa. However, this is followed next by a rapid drop to +2.32(3) at 0.51 GPa (the lowest pressure achieved during depressurization), a value essentially identical to that measured at the beginning of the experiment at 0.42 GPa. The data confirm the reversible nature of the pressure-induced electronic changes and exclude any extraneous origin of the phase transformation as well as any sample degradation due to X-ray illumination. The large hysteretic behaviour – pressure width of the hysteresis loop is ∼2.5 GPa – of the reversible Sm2+ ↔ Sm3+ valence change (Fig. 4) is consistent with the transition being first-order in nature analogous to what is established for SmS.30 Noticeably however, when compared with Sm2.75C60, the transition here appears to be more sluggish and the hysteretic loop significantly broader.
In (Sm1/3Ca2/3)2.75C60, the abrupt Sm valence transition occurs over the range of 4 to 6.5 GPa upon pressurization. As both the lattice collapse and the insulator-to-metal transition evidenced for the binary Sm2.75C60 fulleride also occur over a comparable pressure range of 4–5 GPa,19,20 the present results provide direct evidence for the strong coupling between the charge and lattice degrees of freedom – both structural and conductivity changes are driven by changes in the electronic configuration possibly mediated by the C60 anionic sublattice.
The latter has the potential to act as a charge reservoir accepting electrons from the Sm 4f/5d bands in the course of the valence transition. The availability of the t1g-derived C60 band, which can begin to be populated when the Sm valence exceeds values of 2.5–2.6 (Fig. 4) and the t1u-derived C60 band is full, appears to be a crucial ingredient to allowing the valence change to proceed. Such an availability contrasts with the cases in which the anion sublattice comprises closed-shell anions like the chalcogenides.
Finally, given that the valence transition of samarium at elevated pressure is towards the generation of the magnetic Sm3+ ion with a 4f5:6H5/2 configuration also opens up the possibility of coupling to the magnetic degrees of freedom and the emergence of long-range magnetic ordering, in analogy with the Sm monochalcogenides in the high pressure golden phase.31
3. Conclusions
In summary, we have employed synchrotron X-ray spectroscopic (PFY-XAS) measurements to investigate the electronic properties of the mixed valence fulleride, (Sm1/3Ca2/3)2.75C60 at elevated pressures. The observed pressure response of the average Sm valence, ν is similar to that of strongly correlated Kondo insulators such as SmS with a sharp decrease in the 4f-electron occupation number occurring abruptly above ∼4 GPa. The resulting ∼20% increase in ν to +2.71(3) coincides with the occurrence of a concomitant lattice collapse and the appearance of metallic behaviour in the same pressure range in the parent mixed valence fulleride, Sm2.75C60 providing a possible explanation of the observed properties, that may involve the strong coupling between lattice and electronic (valence) degrees of freedom. The availability of the t1g-derived band of C60 appears crucial in being able to accommodate the excess charge generated by the pressure-induced Sm2+ → Sm3+ transition after the t1u-derived band becomes fully occupied at ν ≈ +2.55 and drive the system to the metallic state. Therefore, given that the C60 sublattice can support superconductivity, the possibility emerges that mixed valence rare-earth fullerides can become superconducting at higher C60 doping levels achieved by further increase in the average rare-earth valence at elevated pressures, opening new prospects in this research field. Finally, the valence transition is reversible and of first-order as evidenced by its highly hysteretic behaviour together with the complete recovery of the electronic properties upon pressure release.4. Experimental section
The (Sm1/3Ca2/3)2.75C60 polycrystalline sample used in this work was prepared, chemically analyzed and structurally characterized, as reported elsewhere.25 Due to the extreme sensitivity of the sample to air and moisture, all manipulations were undertaken in argon-filled gloveboxes (H2O/O2 < 0.1 ppm).Ambient-pressure magnetic measurements were performed on a ca. 20 mg sample, sealed in a thin-walled quartz ampoule with a Quantum Design SQUID MPMS5 magnetometer. Temperature dependent magnetic susceptibility data were collected at 2 and 4 T under field-cooled protocols at temperatures between 1.8 and 300 K. The total susceptibilities were obtained after subtracting the diamagnetic core contributions from the difference of the values measured at applied magnetic fields of 4 and 2 T.
PFY-XAS spectra of (Sm1/3Ca2/3)2.75C60 at the Sm-L3 edge were collected at room temperature at the Taiwan BL12XU beamline, SPring-8, Japan, in a 90° geometry. For these experiments, the emitted photon energy was fixed around the maximum of the Lα1 emission line at ∼5636 eV, while the incident photon energy was scanned across the Sm-L3 edge.32 For every individual spectrum, four different scans in the energy range 6735–6705 eV, divided into 90 energy steps with a measurement time of 5 s each, were averaged. The spectral intensity was normalized to the intensity recorded by a monitor situated before the DAC in which the sample was loaded. High pressure was generated by means of a 4-pin type DAC with a culet size of 700 μm, utilizing a 30 μm thick Be gasket with a 250 μm diameter hole at the centre. A pellet fragment of the sample was carefully placed in the sample chamber of the Be gasket, inside an Ar gas atmosphere glovebox in order to avoid sample oxidation. Daphne 7373 oil, which solidifies at 2.2 GPa at room temperature33 was used as the pressure transmitting medium, while the pressure was calibrated by means of the ruby fluorescence method.34
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank SPring-8 for access to synchrotron X-ray facilities and Dr A Machida for the use of the glovebox at the facility. AGVT acknowledges the support by the Hellenic Foundation for Research and Innovation (HFRI) under the HFRI PhD Fellowship grant (Fellowship Number: 707). This work was financially supported by Grants-in-Aid for Scientific Research (JSPS KAKENHI Grant Numbers JP18H04303, JP18K18724, and JP19H04590) by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, by the Murata Foundation and by the KAKENHI Specific Support Operation of Osaka Prefecture University. The experiments at the SPring-8 Taiwan beamline BL12XU were performed under SPring-8 Proposal No. 2017B4268, 2018B4252 and 2019A4264, corresponding to NSRRC Proposal No. 2018-1-058-1, 2018-1-058-3 and 2018-1-058-5, respectively.Notes and references
- K. Prassides, Y. Takabayashi and T. Nakagawa, Mixed valency in rare-earth fullerides, Philos. Trans. R. Soc., A, 2008, 366, 151–161 CrossRef CAS.
- Y. Takabayashi and K. Prassides, Unconventional high-Tc superconductivity in fullerides, Philos. Trans. R. Soc., A, 2016, 374, 20150320 CrossRef.
- P. Wachter, Intermediate valence and heavy fermions, in Handbook on the physics and chemistry of rare earths, ed. K. A. Gschneidner, L. Eyring, G. H. Lander and G. R. Chopin, Elsevier Science B. V., Amsterdam, 1994, vol. 19, pp. 177–388 Search PubMed.
- Y. Takabayashi, A. Y. Ganin, P. Jeglic, D. Arcon, T. Takano, Y. Iwasa, Y. Ohishi, M. Takata, N. Takeshita, K. Prassides and M. J. Rosseinsky, The disorder-free non-BCS superconductor Cs3C60 emerges from an antiferromagnetic insulator parent state, Science, 2009, 323, 1585–1590 CrossRef CAS.
- Y. Kasahara, Y. Takeuchi, R. H. Zadik, Y. Takabayashi, R. H. Colman, R. D. McDonald, M. J. Rosseinsky, K. Prassides and Y. Iwasa, Upper critical field reaches 90
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tesla near the Mott transition in fulleride superconductors, Nat. Commun., 2017, 8, 14467 CrossRef CAS.
tesla near the Mott transition in fulleride superconductors, Nat. Commun., 2017, 8, 14467 CrossRef CAS. - R. H. Zadik, Y. Takabayashi, G. Klupp, R. H. Colman, A. Y. Ganin, A. Potocnik, P. Jeglic, D. Arcon, P. Matus, K. Kamaras, Y. Kasahara, Y. Iwasa, A. N. Fitch, Y. Ohishi, G. Garbarino, K. Kato, M. J. Rosseinsky and K. Prassides, Optimized unconventional superconductivity in a molecular Jahn-Teller metal, Sci. Adv., 2015, 1, e1500059 CrossRef.
- C. M. Varma, Mixed-valence compounds, Rev. Mod. Phys., 1976, 48, 219–238 CrossRef CAS.
- Q. Si and F. Steglich, Heavy fermions and quantum phase transitions, Science, 2010, 329, 1161–1166 CrossRef CAS.
- K. Ishi, A. Fujiwara, H. Suematsu and Y. Kubozono, Ferromagnetism and giant magnetoresistance in the rare-earth fullerides Eu6−xSrxC60, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 134431 CrossRef.
- T. Takenobu, D. H. Chi, S. Margadonna, K. Prassides, Y. Kubozono, A. N. Fitch, K. Kato and Y. Iwasa, Synthesis, structure, and magnetic properties of the fullerene-based ferromagnets Eu3C70 and Eu9C70, J. Am. Chem. Soc., 2003, 125, 1897–1904 CrossRef CAS.
- I. Margiolaki, S. Margadonna, K. Prassides, T. Hansen, K. Ishii and H. Suematsu, Magnetic structure of the europium fulleride ferromagnet Eu6C60, J. Am. Chem. Soc., 2002, 124, 11288–11289 CrossRef CAS; J. Arvanitidis, D. Christofilos, G. A. Kourouklis, A. Paloumpi, K. Papagelis, S. Ves, Y. Iwasa and K. Prassides, Raman spectroscopic study of the rare-earth fullerides Eu6−xSrxC60, Nanoscale, 2011, 3, 2490–2493 RSC.
- E. Özdaş, A. R. Kortan, N. Kopylov, A. P. Ramirez, T. Siegrist, K. M. Rabe, H. E. Bair, S. Schuppler and P. H. Citrin, Superconductivity and cation-vacancy ordering in the rare-earth fulleride Yb2.75C60, Nature, 1995, 375, 126–129 CrossRef.
- J. Arvanitidis, K. Papagelis, S. Margadonna, K. Prassides and A. N. Fitch, Temperature-induced valence transition and associated lattice collapse in samarium fulleride, Nature, 2003, 425, 599–602 CrossRef CAS.
- X. H. Chen and G. Roth, Superconductivity at 8 K in samarium-doped C60, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15534–15536 CrossRef CAS.
- S. Margadonna, J. Arvanitidis, K. Papagelis and K. Prassides, Negative thermal expansion in the mixed valence ytterbium fulleride, Yb2.75C60, Chem. Mater., 2005, 17, 4474–4478 CrossRef CAS.
- M. Akada, T. Hirai, J. Takeuchi, T. Yamamoto, R. Kumashiro and K. Tanigaki, Superconducting phase sequence in RxC60 fullerides (R = Sm and Yb), Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094509 CrossRef.
- A. Jayaraman, V. Narayanamurti, E. Bucher and R. G. Maines, Continuous and discontinuous semiconductor-metal transition in samarium monochalcogenides under pressure, Phys. Rev. Lett., 1970, 25, 1430–1433 CrossRef CAS.
- D. Malterre, M. Grioni and Y. Baer, Recent developments in high-energy spectroscopies of Kondo systems, Adv. Phys., 1996, 45, 299–348 CrossRef CAS.
- J. Arvanitidis, K. Papagelis, S. Margadonna and K. Prassides, Lattice collapse in mixed-valence samarium fulleride Sm2.75C60 at high pressure, Dalton Trans., 2004, 3144–3146 RSC.
- S. M. Souliou, J. Arvanitidis, D. Christofilos, K. Papagelis, S. Ves, G. A. Kourouklis, K. Prassides, Y. Iwasa and K. Syassen, High-pressure Raman study of the Sm2.75C60 fulleride, High-Pressure Res., 2011, 31, 13–17 CrossRef CAS.
- A. Jayaraman, P. Dernier and L. D. Longinotti, Study of the valence transition in SmS induced by alloying, temperature, and pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 11, 2783–2794 CrossRef CAS; A. Jayaraman and R. G. Maines, Study of the valence transition in Eu-, Yb-, and Ca-substituted SmS under high pressure and some comments on other substitutions, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 4154–4161 CrossRef.
- K. Takenaka, Progress of research in negative thermal expansion materials: paradigm shift in the control of thermal expansion, Front. Chem., 2018, 6, 267 CrossRef.
- Y. Yokoyama, H. Hasegawa, Y. Mizuno, D. Asai, Y. Okamoto, H. S. Suzuki, K. Takehana, Y. Imanaka and K. Takenaka, Effects of Y substitution on the electronic structure and charge dynamics of SmS, Phys. Rev. B, 2019, 100, 245143 CrossRef CAS.
- D. G. Mazzone, M. Dzero, AM. M. Abeykoon, H. Yamaoka, H. Ishii, N. Hiraoka, J.-P. Rueff, J. M. Ablett, K. Imura, H. S. Suzuki, J. N. Hancock and I. Jarrige, Kondo-induced giant isotropic negative thermal expansion, Phys. Rev. Lett., 2020, 124, 125701 CrossRef CAS.
- N. Yoshikane, T. Nakagawa, K. Matsui, H. Yamaoka, N. Hiraoka, H. Ishii, J. Arvanitidis and K. Prassides, Chemical tuning of samarium valence in mixed valence (Sm1−xCax)2.75C60 fullerides, J. Phys. Chem. Solids, 2020 Search PubMed , under review.
- M. B. Maple and D. Wohlleben, Nonmagnetic 4f shell in the high-pressure phase of SmS, Phys. Rev. Lett., 1971, 27, 511–515 CrossRef CAS.
- J.-P. Rueff and A. Shukla, Inelastic X-ray scattering by electronic excitations under high pressure, Rev. Mod. Phys., 2010, 82, 847–896 CrossRef CAS; H. Yamaoka, Pressure dependence of the electronic structure of 4f and 3d electron systems studied by X-ray emission spectroscopy, High-Pressure Res., 2016, 36, 262–274 CrossRef.
- G. Materlik, J. E. Muller and J. W. Wilkins, L-edge absorption spectra of the rare earths: assessment of the single-particle picture, Phys. Rev. Lett., 1983, 50, 267–270 CrossRef CAS; E. Beaurepaire, J. P. Kappler and G. Krill, X-ray-absorption near-edge structure study in mixed-valent samarium systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 6768–6776 CrossRef.
- I. Jarrige, H. Yamaoka, J.-P. Rueff, J.-F. Lin, M. Taguchi, N. Hiraoka, H. Ishii, K. D. Tsuei, K. Imura, T. Matsumura, A. Ochiai, H. S. Suzuki and A. Kotani, Unified understanding of the valence transition in the rare-earth monochalcogenides under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115107 CrossRef.
- P. P. Deen, D. Braithwaite, N. Kernavanois, L. Paolasini, S. Raymond, A. Barla, G. Lapertot and J. P. Sanchez, Structural and electronic transitions in the low-temperature, high-pressure phase of SmS, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 245118 CrossRef.
- A. Barla, J. P. Sanchez, Y. Haga, G. Lapertot, B. P. Doyle, O. Leupold, R. Rüffer, M. M. Abd-Elmeguid, R. Lengsdorf and J. Flouquet, Pressure-induced magnetic order in golden SmS, Phys. Rev. Lett., 2004, 92, 066401 CrossRef CAS; A. Barla, J.-P. Sanchez, J. Derr, B. Salce, G. Lapertot, J. Flouquet, B. P. Doyle, O. Leupold, R. Rüffer, M. M. Abd-Elmeguid and R. Lengsdorf, Valence and magnetic instabilities in Sm compounds at high pressures, J. Phys.: Condens. Matter, 2005, 17, S837–S848 CrossRef.
- H. Yamaoka, I. Jarrige, N. Tsujii, M. Imai, J.-F. Lin, M. Matsunami, R. Eguchi, M. Arita, K. Shimada, H. Namatame, M. Taniguchi, M. Taguchi, Y. Senba, H. Ohashi, N. Hiraoka, H. Ishii and K.-D. Tsuei, Electronic structure of YbGa1.15Si0.85 and YbGaxGe2−x probed by resonant X-ray emission and photoelectron spectroscopies, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 104525 CrossRef.
- K. Yokogawa, K. Murata, H. Yoshin and S. Aoyama, Solidification of high-pressure medium Daphne 7373, Jpn. J. Appl. Phys., 2007, 46, 3636–3639 CrossRef CAS.
- H. K. Mao, J. Xu and P. M. Bell, Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions, J. Geophys. Res., 1986, 91, 4673–4676 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Pressure dependence of the energies and intensities of the subpeaks used in the fitting of the experimental PFY-XAS spectra of Sm1/3Ca2/3C60. See DOI: 10.1039/d0qm00707b |
| This journal is © the Partner Organisations 2020 |