Using nickel to fold discrete synthetic macromolecules into single-chain nanoparticles

Abstract

Macromolecules found in Nature display a precise control over the primary as well as higher ordered architectures. To mimic the folding found in Nature, we herein demonstrate the design and characterization of single-chain nanoparticles that are formed by the folding of sequence-defined macromolecules with metal ions. The study showcases the influence of the loop size of such precision macromolecules on their relative hydrodynamic radius. The sequence-defined structures are fabricated using thiolactone chemistry, where two picolyl moieties are installed forming a valuable ligand system for subsequent metal complexation. Next, metal ions such as Ni(II) and Cu(II) ions are introduced to fold the unimers into sequence-defined single-chain nanoparticles (SD-SCNPs). After proving the successful complexation using a trimer, a systematic study is conducted altering the distance between the respective ligands by incorporating variable numbers of non-functionalized spacer units. Finally, the loop size formation of the SD-SCNPs is evidenced by DOSY measurements. The result indicates that the positioning of the ligands plays a crucial role on the compaction process and, more specifically, on the final size of the SD-SCNP. In addition, molecular dynamics (MD) simulations show the effects of the sequence and Ni(II) complexation on the structure and compaction of the SD-SCNPs, and highlight the differences of the nanoparticles’ shape when varying the number of spacer units. Finally, the system is further expanded to a dodecamer and even a heptadecamer with drastically decreased hydrodynamic radii after compaction.

---

Introduction

Nature expresses precision in (macro)molecule design in two fundamental ways: (i) sequence-defined addition of essential building blocks such as amino acids or nucleotides leading to uniformly tailored biomacromolecules and (ii) intra- and inter-molecular assembly to higher ordered architectures.¹ Since a couple of years, polymer chemists mimic Nature's precision by controlling the monomer sequence in synthetic macromolecules.^2–6

Thus, sequence-defined macromolecules, a vastly advancing field in polymer science, have been developed to attain Nature's precision synthetically with the possibility to extend the applicable monomeric library to non-natural compounds. For instance, the preparation of highly defined artificial biomacromolecules was assisted by earlier Nobel-Prize-awarded methodology such as the Merrifield synthesis. By adapting the protocols, sequence-defined synthetic macromolecules can be prepared using solid-phase approaches.^3,7 Furthermore, other routes were developed, such as liquid-phase synthesis^2,8 and single unit monomer insertion (SUMI)^9–12 where diverse chemical platforms allow for efficient monomer installation. These monodisperse and precise macromolecules are used in bioinspired applications such as information storage^13,14 and encryption,^15,16 as well as enzymatic-like catalysis.¹⁷ Recent reviews are highlighting the advances on the field of discrete synthetic macromolecules focusing on their properties and applications.^18–20

Earlier attempts to mimic protein folding were performed using linear polymeric chains with dispersity ranging from approx. 1.1²¹ up to 2.23.²² The introduction of functional moieties along the backbone enables intramolecular compaction upon a stimulus. This subclass of materials referred to as single-chain nanoparticles (SCNPs), emerged in the early 2000s.^23,24 A diverse library of folding chemistries including irreversible covalent linkage formation^25–27 reversible covalent bonds,^28–30 supramolecular interactions,^31,32 and degradable (self-immolative) bonds³³ was described to form SCNPs. Due to their specific characteristics, SCNPs find application in many fields, such as drug delivery,^34–37 catalysis,^25,38,39 imaging,^40–43 sensors⁴⁴ and responsive materials.^45,46 The morphology and dynamics of these nanostructures have been revealed by combining experimental and molecular simulation studies, mainly in solution.^47–49 In particular, it has been reported that the sparse morphology of current SCNPs in solution resembles that of intrinsically disordered proteins.⁴⁹ Consequently, several strategies have been proposed for controlling the SCNP folding^49–51 but the tuning of their internal structure remains an unsolved issue. Nevertheless, the morphology of SCNPs in solution is expected to influence their activity and selectivity, in particular for catalysis applications.^25,51,52

In addition to SCNPs, other monodisperse structures have been studied, more specifically foldamers and bioactive macrocycles. Macrocycles such as cyclic peptides are the first class combining precise primary structure with a higher ordered architecture. Here, loops are formed mainly via head-to-tail cyclization,⁵³ but they can also emerge from side chain-to-side chain,⁵⁴ head-to-side chain or side chain-to-tail.⁵⁵ Cyclic peptides have found broad applications from drug delivery⁵⁶ to nanomaterials.⁵⁷ However, macrocycles are not limited to natural or biological macromolecules but cyclization of linear synthetic sequence-defined macromolecules has also been studied, as highlighted in recent papers by the groups of Alabi⁵⁸ and Meier.⁵⁹

The second important class of monodisperse, synthetic macromolecules to be highlighted in this section is the one of foldamers, which collapse spontaneously into a secondary structure (e.g. helix). Foldamers can be derived from biotic (such as peptoids⁶⁰ or peptide nucleic acids⁶¹) and abiotic (e.g. oligo-phenyl-ethylenes⁶² and aromatic oligoamides⁶³) building blocks. In the work of Zuckermann, the binding affinity of a peptoidic two-helix bundle towards zinc was studied.⁶⁴

In the current work, we will focus on the metallo-induced folding of synthetic sequence-defined structures for which we investigated the impact of the distance between two functional handles on the folding behaviour. The relevance of such a study was outlined in different perspectives. In 2011, Lutz and Sawamoto emphasized the importance of controlling primary and secondary structures.⁶⁵ More recently, Meier and Barner-Kowollik reiterated the influence of spatial precision in macromolecular design.⁶⁶

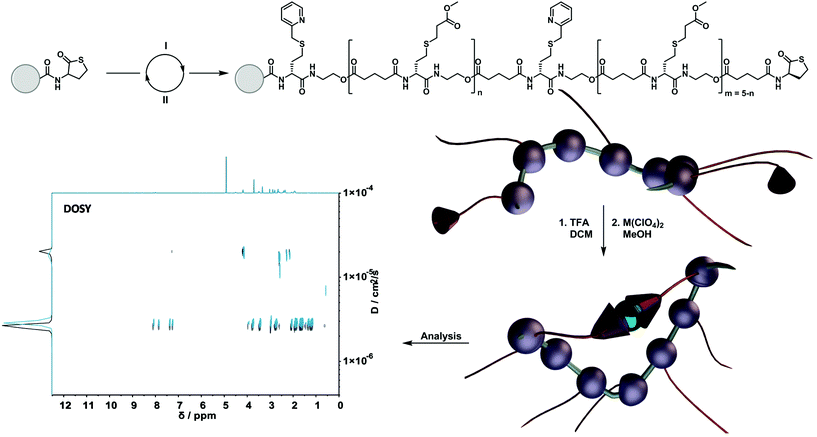
A careful scan of existing synthetic protocols for the design of sequence-defined macromolecules with the option for a precise installation of suitable moieties for subsequent folding resulted in the choice for the well-known thiolactone-based protocol.⁷ Here, picolyl moieties could be easily installed, forming a valuable ligand system for subsequent metal complexation (vide infra). Thus, the obtained precisely designed single-chain nanoparticles allowed us to investigate the influence of different loop sizes – being the distance between two functional cross-linking units in a chain – on the size of the formed nanoparticle. The synthesis is outlined as follows: (i) an iterative two-step solid-phase approach using thiolactone chemistry to synthesize sequence-defined macromolecules; (ii) a selected metal-induced intra-molecular complexation to compact the structures and investigate their behaviour (Scheme 1).

Scheme 1 Preparation of sequence-defined macromolecules using thiolactone chemistry on a solid phase support. (I) Opening of the thiolactone via aminolysis and introduction of the functional group using a thiol-X reaction. (II) Elongation step using TLa-COOH in a DIC-coupling reaction to close the cycle. After the cleavage of the resin, the single-chain folding was induced with M(ClO₄)₂ (M = Cu(II) or Ni(II)). The formation of the SD-SCNP was confirmed using DOSY measurements.

Taking inspiration from the work of Chattopadhyay and co-workers,⁶⁷ a picolyl moiety was chosen to design a N,S-ligand, which can construct stable N₂S₂ donor sets with different metal species (e.g. Cu(II) and Ni(II)⁶⁸ ions). Subsequently, we studied the effect of an increasing loop size on the folding behaviour by incorporating from one up to fifteen spacer units between the functional handles.

Results and discussion

The sequence-defined macromolecules were synthesized via a solid-phase approach. Therefore, a 2-chlorotrityl chloride-functionalized polystyrene-resin was chosen and modified with a (R)-thiolactone (TLa) moiety based on an earlier described protocol.⁴ Upon aminolysis a thiol is released, giving access to the different thiol-X reaction pathways. In order to introduce functionality precisely along the oligomer, two thiol-X reactions were chosen: (i) the highly efficient thiol-Michael addition and (ii) the thiol-halide reaction. To elongate the oligomers, an acid functionalised thiolactone unit ((R)-TLa-COOH, see ESI† for the complete structure and synthesis) was reintroduced via N,N′-diisopropylcarbodiimide (DIC) coupling. The two functionalities that were used in the current work were a picolyl group and a methyl ester as spacer unit. Importantly, the ligand synergy between sulphur and nitrogen can only be established via the thiol-halide reaction, thus explaining the choice of two distinct reaction pathways.

Compaction of sequence-defined oligomers into SCNPs

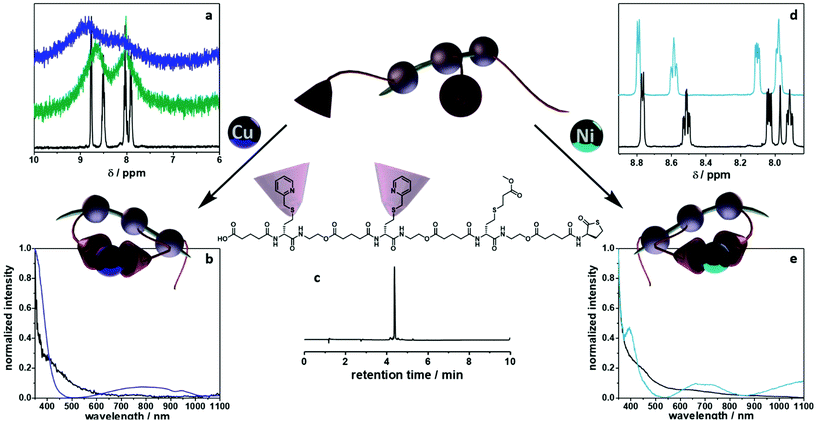
To fully investigate the potential of the N,S ligand towards complexation, a model sequence-defined trimer was first synthesized to establish the previously presented protocol. The trimer entails two adjacent picolyl groups and one methyl ester (see Fig. 1c). The sequential growth was monitored via liquid chromatography coupled to ESI-MS (LC-ESI-MS) (Fig. 1c). Additionally, the purity of the final product was confirmed by ¹H NMR. Afterwards, the sequence was submitted to complexation with two metals: Ni(II) introduced as Ni(ClO₄)₂ salt and Cu(II) introduced as Cu(ClO₄)₂. First, the Cu(II) complex was formed with the trimer in a two-step reaction.⁶⁷ Cu(ClO₄)₂ was added to the oligomer to form a precursor complex, then NaCl was added to exchange the anion and form a stable complex. ¹H NMR spectra were recorded after each step, showcasing a visible shift of resonances in the aromatic region. However, with the complex formation, the resonances broadened due to the paramagnetic character of Cu(II) ions (Fig. 1a). A clear colour shift from blue to green was observed confirming the successful complexation, which was verified via UV–Vis measurements (Fig. 1b). On the other hand, upon reaction with Ni(ClO₄)₂, the visible feedback was less noticeable (Fig. 1e), but a shift of the trimer's aromatic proton resonances indicated the successful complex formation without any broadening (Fig. 1d). Furthermore, the complex with Ni(ClO₄)₂ was detected using high resolution ESI-MS (Fig. S39†). The measurement of the trimer revealed both the complexed form (along with adducts indicated in Table S12†) and the non-complexed form. The opening of the metallo-SD-SCNP was attributed to the short heating when the solution travels through the spray capillary (heated to 320 °C). Finally, a LC-ESI-MS of the complexed trimer was recorded (Fig. S5†). The recorded spectra displayed two peaks at different elution time. It could be due to the interaction with the column and the water used for the measurement that both the complexed and non-complexed species could be observed. Thereby, it was demonstrated that the trimer can be successfully complexed using two different metal ions. After the trimer study, the folding behaviour of longer oligomers was explored, where the loop size (distance between the two pyridinyl moieties) was varied. Therefore, six heptamers were synthesized using a semi-automated protocol. The aminolysis in combination with the introduction of the methyl ester groups and each subsequent elongation using (R)-TLa-COOH were performed using an adapted peptide synthesizer, allowing the fast synthesis of the macromolecules.⁷ The nomenclature of the sequences was chosen according to the position of the picolyl groups on the oligomeric backbone (from S1,2 to S1,7). To confirm the folding of the oligomers and evidence the hydrodynamic radius’ reduction, the fast and robust DOSY technique⁶⁹ was chosen. Critically, the formed oligomeric particles were too small to be precisely measured via DLS.⁷⁰ The nickel ion was selected for the design of the systematic loop size-dependent SCNP formation because of the clearer resonances obtained during NMR measurements (Fig. 1d). After the synthesis of a library of heptamers, Ni(ClO₄)₂ was added to a 0.01–0.02 molar methanol solution of the oligomer. Then, DOSY measurements prior and after collapse were compared (see Fig. 2).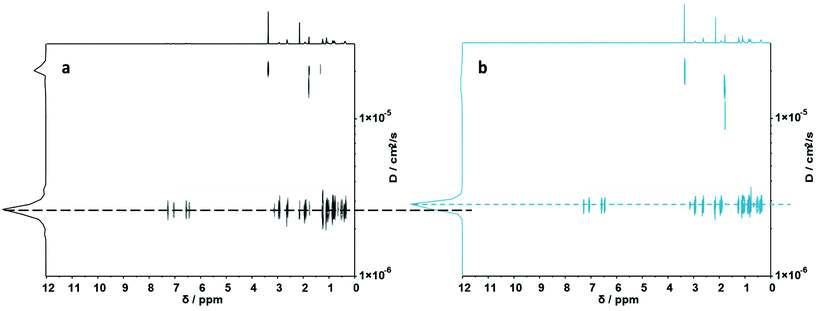

Fig. 1 Model study using a trimer. (a) Zoom of the ¹H NMR spectra in the aromatic region for the folding with Cu(II) species (black – trimer, green – first step of complexation, blue – second step of reaction). (b) UV–Vis traces for the complexation via Cu(II) ions (black – trimer, blue – complexed analogue). (c) Structure and LC-ESI MS trace of the trimer. (d) Zoom of the ¹H NMR spectra in the aromatic region for the folding with Ni(II) species (black – trimer, turquoise – complexed analogue). (e) UV–Vis traces of the trimer (black) and its complexed form (turquoise) using Ni(II) ions.

Fig. 2 (a) DOSY (500 MHz) spectrum of S1,7. (b) DOSY (500 MHz) spectrum of its folded structure. Dashed lines display diffusion coefficients of the corresponding macromolecules.

Fig. 2a showcases the DOSY spectrum of sequence S1,7. All other DOSY measurements (i.e. S1,2–S1,6) can be found in the ESI.† The dashed line highlights the diffusion coefficient of the macromolecule. Here, the Stokes–Einstein relation⁷¹ provides an hydrodynamic radius (R_h) of 1.36 nm. Comparing the diffusion traces’ maxima of Fig. 2a and b, a shift of the diffusion coefficient upon the complex formation was observed. The shift resulted in a decrease of the hydrodynamic radius to 1.30 nm, indicating the intramolecular folding and thereby the formation of a sequence-defined oligomeric single-chain nanoparticle.

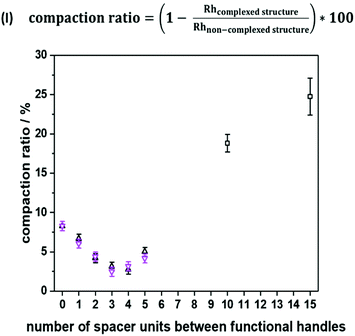
To emphasize folding effects for all sequences, we calculated the compaction ratio, i.e. the ratio between hydrodynamic radii of both folded and non-folded sequences (see Fig. 3, eqn (I)). The hydrodynamic radius’ numerical value of the folded oligomer was divided through the numerical value of its non-complexed analogue to obtain the size decrease as a percentage. It was expected that with an increasing number of spacer units between the picolyl handles, a decrease of the hydrodynamic radius would be observed, as the end-to-end vector would be decreased with an increasing loop size. Experimentally, a minimum value of the compaction ratio was observed for an intermediate number of spacer units (see Fig. 3). Most significantly, the compaction ratio of S1,2 (i.e. both functional moieties in close proximity) was found the highest of all heptamers (8%). Thus, the formed SCNPs were the smallest. Then, the compaction ratio decreased from 8% (for S1,2) to 3% (for S1,4) and increased again to 5% (for S1,7). The experiments were repeated, and the results showed a reproducibility with an error below 1%. An explanation for the minimum was not found.

Fig. 3 Compaction of heptamers (two datasets represented by purple and black triangles), dodecamer and heptadecamer (represented by black squares) based on hydrodynamic radii, as estimated experimentally from diffusion coefficients.

In addition to the set of heptamers with two picolyl functionalities, an oligomer with only one picolyl moiety (S7) was synthesized to underpin that both picolyl moieties are necessary for the intramolecular folding. As previously established, Ni(ClO₄)₂ was added to a 0.01 molar methanol solution of the sequence. The R_h obtained through DOSY measurements increased after the addition of the Ni(II) ions from 1.28 nm to 1.32 nm, indicating the reaction of the ligand functionality with the metal ion but not the formation of SCNPs (see Fig. S36†). Since dimerization could in principle also occur with this oligomer, a reference sequence without any picolyl functionalities was also synthesized with the aim to demonstrate that only those units, and thus no other functionalities along the oligomeric structure, are responsible for the folding. However, this hypothesis could not be confirmed via a similar DOSY experiment as a result of the insolubility of this oligomer in methanol.

Moreover, the SCNP was studied during temperature dependent DOSY measurements (Fig. S37†) revealing that the complexed form unfolds upon heating to 100 °C. For the study, the complex was dissolved in DMF and heated in steps of 20 °C from 25 °C to 100 °C. A DOSY spectrum was recorded at each equilibrated temperature. Afterwards, the system was cooled down in the same intervals, scanning a second spectrum for each of those steps. After the heating cycle was completed, an increase in the size of the SCNP was observed, indicating the expansion of the SCNP and thus the reversion of the complexation. In addition to the DOSY measurements, the successful complexation was confirmed using UV–Vis measurements (Fig. S38†) and ¹H NMR spectra (Fig. S12†) as described for the model study using the trimer. Furthermore, the complexed structure was observed during high resolution ESI-MS measurements (Fig. S40†). Observing the heptamer in HR-ESI MS was more challenging. A small excess of the Ni(II) ions was therefore added to shift the equilibrium towards the complexed form. Consequently, additional salt adduct formation could be observed as indicated in Table S13.† Further, two species were observed in a LC-ESI-MS spectrum, similar to the trimer study (Fig. S6†). Finally, the oligomer length was further increased up to a dodecamer (sequence S1,12) and heptadecamer (sequence S1,17) to showcase the folding for larger structures. The previously described protocol was adapted to ensure full conversions by prolonging the reaction time of the elongation steps. The picolyl functionalities were placed at both ends of the oligomer. The folding, again induced with Ni(ClO₄)₂ resulted in a compaction ratio of 18% for the dodecamer and 24% for the heptadecamer (Fig. 3). The observed ratios indicated that with an increasing length of the oligomers, the value for the compaction ratio increased as well and was comparable to the ones obtained for disperse polymeric single-chain nanoparticles, e.g. 13% observed from Murray and Fulton³⁰ or 22% recorded by Steinkoenig et al.⁷²

Molecular modelling: effect of sequence and complexation

To gain insights into the structure and dynamics of the heptamers as a function of the complexation and the spacer length, molecular dynamics (MD) simulations were performed for three comparable sequences in terms of number of spacer units (i.e. S1,2; S1,4 and S1,7). Fig. 4a shows the modelled structure of S1,7 with the numbering of fragments used for the analysis of MD simulations. MD simulations highlighted the collapse of the oligomer upon complexation, as shown in Fig. 4b (left), corresponding to the last snapshot of the simulations for S1,7 (taken at 750 ns). In Fig. 4b, the compaction of heptamers with the nickel ion has been evaluated by comparing 2D colour-coded distance maps (see Computational details in the ESI† for details) for non-complexed and complexed S1,7 sequences. The 2D distance maps of the non-complexed heptamers showed that, in average, the distance between picolyl moieties is above 25 Å (see yellow regions in Fig. 4b). In contrast, the distances between these moieties of complexed S1,7 decreased below 25 Å, indicating that the complexation with the nickel ion leads to significant conformational changes. To highlight compaction effects along the oligomeric structure, the distance map of the non-complexed heptamer has been subtracted from that of the complexed heptamer (Fig. 4b right). The resulting difference distance map displayed slightly yellow regions corresponding to the complexation of the functional units with the nickel ion. The 2D difference distance map of S1,7 showed regions of higher yellow colour intensity compared to those of S1,2 and S1,4 (Fig. 4c). These results indicated that the conformational changes of the heptamers upon complexation of the nickel ion were more pronounced with increasing spacer length.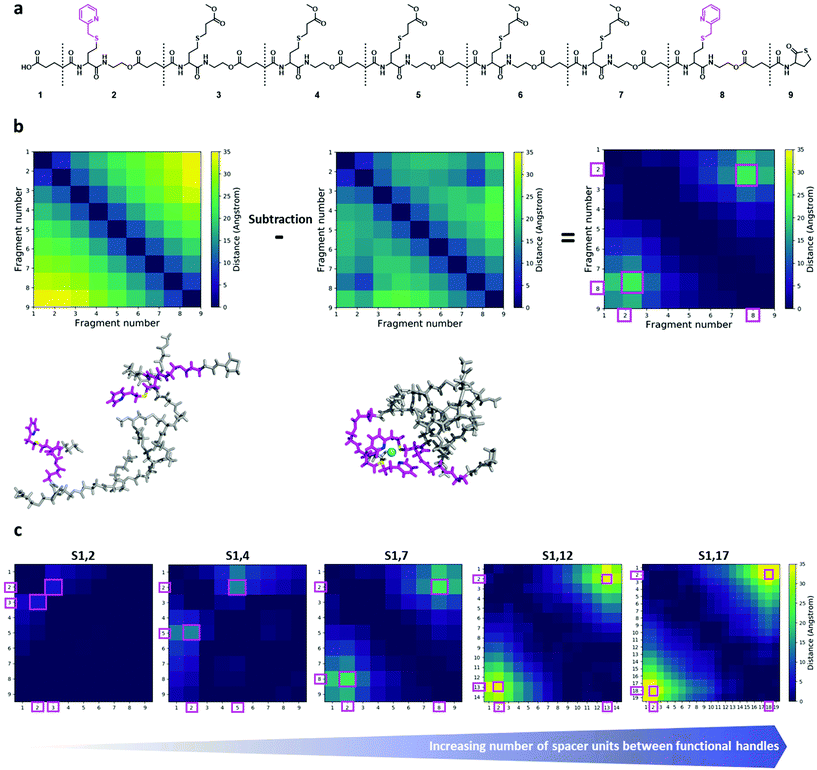

Fig. 4 (a) Chemical structure of the model sequence S1,7. Molecular model of the heptamer is constructed by joining nine fragments. The corresponding fragment numbers are also shown. The functional handles are depicted in magenta. (b) Left: last snapshots of MD simulations of S1,7 for non-complexed (top) and complexed (bottom) structures, in sticks representation. The two functional handles are shown in magenta, with nitrogen and sulphur atoms in blue and yellow, respectively; the nickel ion is depicted as a cyan sphere. (b) Middle: corresponding 2D distance maps (for the fragment number, see Fig. 4a). (b) Right: the 2D difference distance map is obtained by subtracting the 2D distance map of the non-complexed sequence from that of the complexed sequence. The regions with large conformational changes, corresponding to complexation sites, are represented by large distances (yellowish regions) and marked with magenta squares. (c) 2D difference distance maps of the different sequences. From left to right: S1,2/S1,4/S1,7/S1,12/S1,17. The regions with large conformational changes, corresponding to complexation sites, are represented by large distances (yellowish regions) and marked with magenta squares.

Further, the change in conformation upon compaction was supported by the corresponding Root-Mean-Square Fluctuation plots (ESI Fig. S47†), which showed a bell-shaped profile, characteristic of flexible polymeric systems. Therefore, the non-complexed heptamers were highly flexible at the termini and unstructured in the middle of the chain, while the complexation with the nickel ion reduced their conformational freedom, leading to a more structured overall arrangement at the functional picolyl handles.

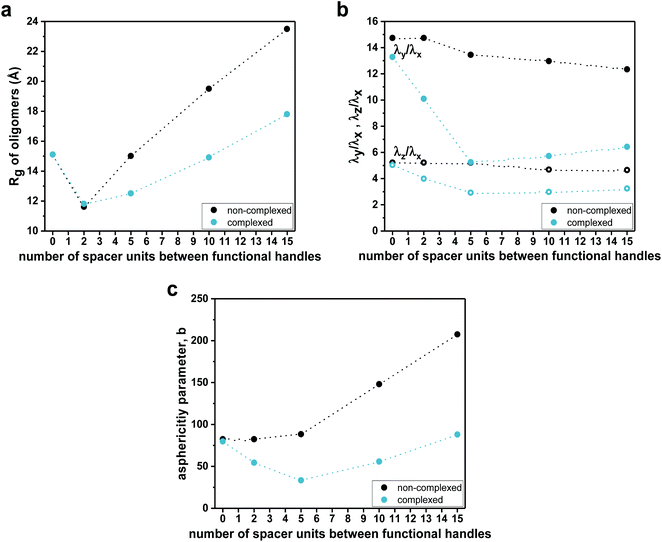
To evaluate the effect of the complexation on the compactness of heptamers, the radii of gyration (R_g) were estimated from MD simulations (Fig. 5a). It is important to note that the hydrodynamic radii (R_h), determined from experimental diffusion coefficients (from DOSY experiments), were based on a model that assumes that SCNPs are hard spheres in solution, giving access to the ‘apparent’ sizes of the SCNPs without information about the absolute size of SCNPs.⁶⁹ In this particular context, radii of gyration and shape descriptors determined from sufficiently long MD simulations gave access to a counterpoint to hydrodynamic radii in terms of sizes and shape of heptamers. For the non-complexed heptamers (black dots), the average value of R_g of the S1,4 sequence was low compared to those found for the S1,2 and S1,7 sequences (see Fig. 5a). However, while the average values of R_g of S1,2 and S1,4 were not influenced much by the complexation, the S1,7 sequence had a lower average value of R_g in its complexed form. Therefore, the simulations suggested that the S1,7 sequence was the most compacted upon complexation. These observations were consistent with the folding effect represented by the 2D distance maps (Fig. 4 for S1,7 and ESI Fig. S43, S44† for S1,2 and S1,4, respectively). However, estimates of R_g were averaged over the entire set of MD conformations (see values and standard deviations in the ESI†). The deviation from the ideal spherical shape was not included in such a measurement. Thus, the main challenge was to characterize the shape of heptamers in non-complexed and complexed forms more precisely.

Fig. 5 (a) Plots of theoretical radii of gyration (R_g) as a function of the number of spacer units for non-complexed (dashed black line) and complexed (solid turquoise line) sequences. (b) Plots of eigenvalues ratios as a function of the number of spacer units for non-complexed (dashed black lines) and complexed (solid turquoise lines) sequences. (c) Plots of asphericity parameter b as a function of the number of spacer units for non-complexed (dashed black line) and complexed (solid turquoise line) sequences.

Consequently, the shape characteristics of the heptamers were analysed.^73–75 They were described by the ratios λ_z/λ_x and λ_y/λ_x of principal moments of the gyration tensor, referred to as shape descriptors (see details in the ESI†). The evolution of shape descriptors with the number of spacer units is shown in Fig. 5b. For non-complexed heptamers, all the ratios of eigenvalues were comparable, regardless of the spacer length, which indicated that the heptamers were elongated in one direction and the number of spacer units did not influence the degree of elongation. On the other hand, for the compacted heptamers, the ratios of the eigenvalues converged to a similar value when increasing the spacer length. Thus, the results suggested that, upon complexation, the heptamers with an increasing number of spacer units tended to a spherical shape, which was consistent with the last snapshots of MD simulations (see for example Fig. 4 left for S1,7 and Fig. S43, Fig. S44† for S1,2 and S1,4, respectively).

The asphericity parameter b has previously been used to describe the shape of both folded and unfolded polymeric systems,⁷⁶ and thus the average values for each sequence were calculated. Since b is a linear combination of the eigenvalues of the gyration tensor (see details in the ESI†), a similar behaviour as in λ_z/λ_x and λ_y/λ_x was observed in the average value of the asphericity parameter b as a function of the spacer length (Fig. 5c). Indeed, for the non-complexed heptamers, the values of the asphericity parameter b were large, indicating that the shapes of heptamers were far from a spherical symmetry. In contrast, for the complexed heptamers, the asphericity b decreased as the spacer length increases, again pointing out that the structures evolved from elongated (for close functional handles) towards more compact conformations when the number of spacer units was increased.

The overall change in the solvent-accessible surface area of heptamers upon complexation was an additional effect of local conformational rearrangements. On an average, the heptamers gained around 1230 Ų of solvent accessibility upon complexation (Table S15†). This could be related to a more structured overall arrangement of the heptamers upon compaction, leading the structures to get more exposed to the surrounding methanol molecules. However, the accessibility of complexed heptamers was not influenced by the spacer length. Although the complexed structures adopted more compact conformations as the spacer length increased, they had similar percentages of their surface areas that were exposed to the surrounding solvent indicating that the most compact structure (i.e. S1,7) had likely a more complex surface roughness compared to those of the more extended structures (i.e. S1,2 and S1,4).

To investigate the effect of the spacer length on their folding behaviour, we further performed MD simulations for the dodecamer (S1,12) and the heptadecamer (S1,17), containing two functional handles separated by 10 and 15 spacer units, respectively. MD simulations show the same qualitative trends as those observed for complexation experiments. Average values of radii of gyration (Fig. 5a) suggested that upon complexation the compaction increases with an increasing number of spacer units in the sequence. Indeed, the 2D distance maps indicated that the conformational changes of oligomers upon complexation are more pronounced when increasing the length of the spacer (see Fig. 4c). As for the heptamers, complexation leads to a more structured overall arrangement at the picolyl functional handles for the longer oligomers (see ESI Fig. S43 and 44†). Furthermore, analysis of the shape descriptors and the asphericity parameter b revealed that the morphologies of SCNPs of S1,12 and S1,17 (Fig. 5b and c) are closer to spherical objects (lower asphericity) than the non-complexed oligomers. This effect is more pronounced as the spacer length increases. However, though some local compact globular shapes are formed in the 3D structure, SCNPs still exhibit extended portions (loop-like structures), which lead to non-spherical morphologies.

Conclusions

In summary, we described the synthesis and nickel-induced folding of sequence-defined oligomers into single-chain nanoparticles. A systematic study showed that different loop sizes influence the folding behaviour of sequence-defined macromolecules. Thiolactone chemistry was utilized to form sequence-defined macromolecules in which picolyl functionalities have been introduced along the oligomeric backbone establishing a N₂S₂ donor set. In a model study, the successful complexation with Ni(II) as well as Cu(II) ions was showcased using a trimer and the results visualized via¹H NMR as well as UV–Vis measurements. In the next step, the folding behaviour dependent on the loop sizes was investigated for six heptamers. Hydrodynamic radii were obtained via DOSY measurements and compaction ratios have been calculated. The latter ranged from 3% to 8% for different loop sizes. Finally, the complexation experiments were performed up to the level of the heptadecamer. Molecular modelling rationalized the effect of complexation on the compaction and flexibility of the oligomers, and showed that the conformational changes upon complexation of Ni(II) are more pronounced as the number of spacer units increases. Importantly, shape descriptors revealed that upon complexation the morphologies of SD-SCNPs from heptamers tend towards a spherical shape with an increasing number of spacer units. However, further increasing the oligomers length up to the heptadecamer (15 spacer units) reduces the sphericity of SCNPs, which show extended loop-like portions. Altogether, the results presented here show that the sequence control enables to attain different degrees of compaction and 3D structures of SCNPs in solution.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The collaboration between the research groups of Ghent and Mons is supported by the Excellence of Science (EOS joint program Research Foundation Flanders (FWO) – Fund for Scientific Research (FNRS) project 30650939. J. S. acknowledges FWO for the Postdoctoral fellowship (12ZH820N). The authors thank C. Barner-Kowollik for the access to the high resolution ESI-MS instrument, D. Buyst, T. J. Van Den Begin, J. Goeman and B. De Meyer for technical assistance. The authors acknowledge J. Winne and N. Badi for fruitful discussions. Computational resources have been provided by the Consortium des équipements de Calcul Intensif (CéCI), funded by the FNRS under Grant 2.5020.11.

Notes and references

1. C.-I. Brändén and J. Tooze, Introduction to protein structure, Garland Pub, New York, 2nd edn, 1999.
2. S. C. Solleder and M. A. R. Meier, Angew. Chem., Int. Ed., 2014, 53, 711–714.
3. T. T. Trinh, C. Laure and J.-F. Lutz, Macromol. Chem. Phys., 2015, 216, 1498–1506.
4. C. Mertens, M. Soete, M. L. Ślęczkowski, A. R. A. Palmans, E. W. Meijer, N. Badi and F. E. Du Prez, Polym. Chem., 2020, 11, 4271–4280.
5. J. Li, M. Leclercq, M. Fossepré, M. Surin, K. Glinel, A. M. Jonas and A. E. Fernandes, Polym. Chem., 2020, 11, 4040–4046.
6. M. L. Ślęczkowski, I. Segers, Y. Liu and A. R. A. Palmans, Polym. Chem., 2020, 11, 7393–7401.
7. S. Martens, J. Van den Begin, A. Madder, F. E. Du Prez and P. Espeel, J. Am. Chem. Soc., 2016, 138, 14182–14185.
8. J. C. Barnes, D. J. C. Ehrlich, A. X. Gao, F. A. Leibfarth, Y. Jiang, E. Zhou, T. F. Jamison and J. A. Johnson, Nat. Chem., 2015, 7, 810–815.
9. D. Oh, M. Sawamoto and M. Ouchi, Polym. Chem., 2019, 10, 1998–2003.
10. Y. Zhou, Z. Zhang, C. M. Reese, D. L. Patton, J. Xu, C. Boyer, A. Postma and G. Moad, Macromol. Rapid Commun., 2020, 41, 1900478.
11. J. Xu, C. Fu, S. Shanmugam, C. J. Hawker, G. Moad and C. Boyer, Angew. Chem., Int. Ed., 2017, 56, 8376–8383.
12. J. Vandenbergh, G. Reekmans, P. Adriaensens and T. Junkers, Chem. Commun., 2013, 49, 10358.
13. A. C. Boukis and M. A. R. Meier, Eur. Polym. J., 2018, 104, 32–38.
14. M. Soete, C. Mertens, R. Aksakal, N. Badi and F. Du Prez, ACS Macro Lett., 2021, 10, 616–622.
15. J.-A. Amalian, G. Cavallo, A. Al Ouahabi, J.-F. Lutz and L. Charles, Anal. Chem., 2019, 91, 7266–7272.
16. J. O. Holloway, F. Van Lijsebetten, N. Badi, H. A. Houck and F. E. Du Prez, Adv. Sci., 2020, 7, 1903698.
17. A. E. Fernandes, O. Riant, K. F. Jensen and A. M. Jonas, Angew. Chem., Int. Ed., 2016, 55, 11044–11048.
18. R. Aksakal, C. Mertens, M. Soete, N. Badi and F. Du Prez, Adv. Sci., 2021, 8, 2004038.
19. B. Genabeek, B. A. G. Lamers, C. J. Hawker, E. W. Meijer, W. R. Gutekunst and B. V. K. J. Schmidt, J. Polym. Sci., 2021, 59, 373–403.
20. C. Yang, K. B. Wu, Y. Deng, J. Yuan and J. Niu, ACS Macro Lett., 2021, 10, 243–257.
21. P. J. M. Stals, M. A. J. Gillissen, R. Nicolaÿ, A. R. A. Palmans and E. W. Meijer, Polym. Chem., 2013, 4, 2584.
22. S. Babaoglu, D. Karaca Balta and G. Temel, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1998–2003.
23. D. Mecerreyes, V. Lee, C. J. Hawker, J. L. Hedrick, A. Wursch, W. Volksen, T. Magbitang, E. Huang and R. D. Miller, Adv. Mater., 2001, 13, 204–208.
24. E. Harth, B. V. Horn, V. Y. Lee, D. S. Germack, C. P. Gonzales, R. D. Miller and C. J. Hawker, J. Am. Chem. Soc., 2002, 124, 8653–8660.
25. A. Sanchez-Sanchez, A. Arbe, J. Colmenero and J. A. Pomposo, ACS Macro Lett., 2014, 3, 439–443.
26. A. E. Cherian, F. C. Sun, S. S. Sheiko and G. W. Coates, J. Am. Chem. Soc., 2007, 129, 11350–11351.
27. A. Sanchez-Sanchez, S. Akbari, A. J. Moreno, F. L. Verso, A. Arbe, J. Colmenero and J. A. Pomposo, Macromol. Rapid Commun., 2013, 34, 1681–1686.
28. B. T. Tuten, D. Chao, C. K. Lyon and E. B. Berda, Polym. Chem., 2012, 3, 3068.
29. O. Shishkan, M. Zamfir, M. A. Gauthier, H. G. Börner and J.-F. Lutz, Chem. Commun., 2014, 50, 1570.
30. B. S. Murray and D. A. Fulton, Macromolecules, 2011, 44, 7242–7252.
31. T. Mes, R. van der Weegen, A. R. A. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2011, 50, 5085–5089.
32. E. J. Foster, E. B. Berda and E. W. Meijer, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 118–126.
33. J. T. Offenloch, J. Willenbacher, P. Tzvetkova, C. Heiler, H. Mutlu and C. Barner-Kowollik, Chem. Commun., 2017, 53, 775–778.
34. A. P. P. Kröger and J. M. J. Paulusse, J. Controlled Release, 2018, 286, 326–347.
35. A. P. P. Kröger, N. M. Hamelmann, A. Juan, S. Lindhoud and J. M. J. Paulusse, ACS Appl. Mater. Interfaces, 2018, 10, 30946–30951.
36. C.-C. Cheng, D.-J. Lee, Z.-S. Liao and J.-J. Huang, Polym. Chem., 2016, 7, 6164–6169.
37. Y. Liu, S. Pujals, P. J. M. Stals, T. Paulöhrl, S. I. Presolski, E. W. Meijer, L. Albertazzi and A. R. A. Palmans, J. Am. Chem. Soc., 2018, 140, 3423–3433.
38. H. Rothfuss, N. D. Knöfel, P. W. Roesky and C. Barner-Kowollik, J. Am. Chem. Soc., 2018, 140, 5875–5881.
39. T. Terashima, T. Mes, T. F. A. De Greef, M. A. J. Gillissen, P. Besenius, A. R. A. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2011, 133, 4742–4745.
40. D. N. F. Bajj, M. V. Tran, H.-Y. Tsai, H. Kim, N. R. Paisley, W. R. Algar and Z. M. Hudson, ACS Appl. Nano Mater., 2019, 2, 898–909.
41. J. Liu, G. Feng, R. Liu, N. Tomczak, L. Ma, G. G. Gurzadyan and B. Liu, Small, 2014, 10, 3110–3118.
42. A. B. Benito, M. K. Aiertza, M. Marradi, L. Gil-Iceta, T. Shekhter Zahavi, B. Szczupak, M. Jiménez-González, T. Reese, E. Scanziani, L. Passoni, M. Matteoli, M. De Maglie, A. Orenstein, M. Oron-Herman, G. Kostenich, L. Buzhansky, E. Gazit, H.-J. Grande, V. Gómez-Vallejo, J. Llop and I. Loinaz, Biomacromolecules, 2016, 17, 3213–3221.
43. C. T. Adkins, J. N. Dobish, S. Brown and E. Harth, ACS Macro Lett., 2013, 2, 710–714.
44. M. A. J. Gillissen, I. K. Voets, E. W. Meijer and A. R. A. Palmans, Polym. Chem., 2012, 3, 3166.
45. A. Sanchez-Sanchez, D. A. Fulton and J. A. Pomposo, Chem. Commun., 2014, 50, 1871–1874.
46. L. Greb, H. Mutlu, C. Barner-Kowollik and J.-M. Lehn, J. Am. Chem. Soc., 2016, 138, 1142–1145.
47. P. A. Klonos, N. Patelis, E. Glynos, G. Sakellariou and A. Kyritsis, Macromolecules, 2019, 52, 9334–9340.
48. A. J. Moreno, F. Lo Verso, A. Sanchez-Sanchez, A. Arbe, J. Colmenero and J. A. Pomposo, Macromolecules, 2013, 46, 9748–9759.
49. J. A. Pomposo, I. Perez-Baena, F. Lo Verso, A. J. Moreno, A. Arbe and J. Colmenero, ACS Macro Lett., 2014, 3, 767–772.
50. F. Lo Verso, J. A. Pomposo, J. Colmenero and A. J. Moreno, Soft Matter, 2015, 11, 1369–1375.
51. S. Basasoro, M. Gonzalez-Burgos, A. J. Moreno, F. Lo Verso, A. Arbe, J. Colmenero and J. A. Pomposo, Macromol. Rapid Commun., 2016, 37, 1060–1065.
52. Y. Bai, X. Feng, H. Xing, Y. Xu, B. K. Kim, N. Baig, T. Zhou, A. A. Gewirth, Y. Lu, E. Oldfield and S. C. Zimmerman, J. Am. Chem. Soc., 2016, 138, 11077–11080.
53. S. A. Kates, N. A. Solé, C. R. Johnson, D. Hudson, G. Barany and F. Albericio, Tetrahedron Lett., 1993, 34, 1549–1552.
54. A. Piserchio, G. D. Salinas, T. Li, J. Marshall, M. R. Spaller and D. F. Mierke, Chem. Biol., 2004, 11, 469–473.
55. D. Van Lysebetten, S. Felissati, E. Antonatou, L. L. G. Carrette, P. Espeel, E. Focquet, F. E. Du Prez and A. Madder, ChemBioChem, 2018, 19, 641–646.
56. A. Nasrolahi Shirazi, D. Mandal, R. K. Tiwari, L. Guo, W. Lu and K. Parang, Mol. Pharm., 2013, 10, 500–511.
57. R. Chapman, K. A. Jolliffe and S. Perrier, Adv. Mater., 2013, 25, 1170–1172.
58. M. Porel, D. N. Thornlow, N. N. Phan and C. A. Alabi, Nat. Chem., 2016, 8, 590–596.
59. K. S. Wetzel and M. A. R. Meier, Polym. Chem., 2019, 10, 2716–2722.
60. R. J. Simon, R. S. Kania, R. N. Zuckermann, V. D. Huebner, D. A. Jewell, S. Banville, S. Ng, L. Wang, S. Rosenberg and C. K. Marlowe, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 9367–9371.
61. P. Nielsen, M. Egholm, R. Berg and O. Buchardt, Science, 1991, 254, 1497–1500.
62. J. C. Nelson, Science, 1997, 277, 1793–1796.
63. D.-W. Zhang, X. Zhao, J.-L. Hou and Z.-T. Li, Chem. Rev., 2012, 112, 5271–5316.
64. B.-C. Lee, T. K. Chu, K. A. Dill and R. N. Zuckermann, J. Am. Chem. Soc., 2008, 130, 8847–8855.
65. M. Ouchi, N. Badi, J.-F. Lutz and M. Sawamoto, Nat. Chem., 2011, 3, 917–924.
66. M. A. R. Meier and C. Barner-Kowollik, Adv. Mater., 2019, 31, 1806027.
67. S. Sarkar, A. Patra, M. G. B. Drew, E. Zangrando and P. Chattopadhyay, Polyhedron, 2009, 28, 1–6.
68. A. Patra, B. Mondal, B. Sen, E. Zangrando and P. Chattopadhyay, J. Chem. Sci., 2015, 127, 1883–1893.
69. E. Blasco, B. T. Tuten, H. Frisch, A. Lederer and C. Barner-Kowollik, Polym. Chem., 2017, 8, 5845–5851.
70. E. Tomaszewska, K. Soliwoda, K. Kadziola, B. Tkacz-Szczesna, G. Celichowski, M. Cichomski, W. Szmaja and J. Grobelny, J. Nanomater., 2013, 2013, 1–10.
71. A. Einstein, Ann. Phys., 1905, 322, 549–560.
72. J. Steinkoenig, T. Nitsche, B. T. Tuten and C. Barner-Kowollik, Macromolecules, 2018, 51, 3967–3974.
73. N. K. Balabaev, M. A. Mazo and E. Yu. Kramarenko, Macromolecules, 2017, 50, 432–445.
74. W. Huang and V. Zaburdaev, Soft Matter, 2019, 15, 1785–1792.
75. H. Arkın and W. Janke, J. Chem. Phys., 2013, 138, 054904.
76. R. I. Dima and D. Thirumalai, J. Phys. Chem. B, 2004, 108, 6564–6570.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1py00229e

---