Auger electron angular distributions following excitation or ionization from the Xe 3d and F 1s levels in xenon difluoride†
Ruaridh
Forbes
 a,
Paul
Hockett
a,
Paul
Hockett
 b,
Ivan
Powis
b,
Ivan
Powis
 c,
John D.
Bozek
c,
John D.
Bozek
 d,
Stephen T.
Pratt
d,
Stephen T.
Pratt
 e and
David M. P.
Holland
e and
David M. P.
Holland
 *f
*f
aPULSE Institute, SLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
bNational Research Council of Canada, 100 Sussex Dr. Ottawa, ON K1A 0R6, Canada
cSchool of Chemistry, University of Nottingham, Nottingham NG7 2RD, UK
dSynchrotron SOLEIL, l'Orme des Merisiers, Saint-Aubin, BP 48, 91192 Gif-sur-Yvette, France
eChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA
fDaresbury Laboratory, Daresbury, Warrington, Cheshire WA4 4AD, UK. E-mail: david.holland@stfc.ac.uk
First published on 24th December 2021
Abstract
Linearly polarized synchrotron radiation has been used to record polarization dependent, non-resonant Auger electron spectra of XeF2, encompassing the bands due to the xenon M45N1N45, M45N23N45, M45N45N45 and M45N45V and fluorine KVV transitions. Resonantly excited Auger spectra have been measured at photon energies coinciding with the Xe 3d5/2 → σ* and the overlapped Xe 3d3/2/F 1s → σ* excitations in XeF2. The non-resonant and resonantly excited spectra have enabled the Auger electron angular distributions, as characterized by the βA parameter, to be determined for the M45N45N45 transitions. In the photon energy range over which the Auger electron angular distributions were measured, theoretical results indicate that transitions into the εf continuum channel dominate the Xe 3d photoionization in XeF2. In this limit, the theoretical value of the atomic alignment parameter (A20) characterizing the core ionized state becomes constant. This theoretical value has been used to obtain the Auger electron intrinsic anisotropy parameters (α2) from the βA parameters extracted from our non-resonant Auger spectra. For a particular Auger transition, the electron kinetic energy measured in the resonantly excited spectrum is higher than that in the directly ionized spectrum, due to the screening provided by the electron promoted into the σ* orbital. The interpretation of the F KVV Auger band in XeF2 has been discussed in relation to previously published one-site populations of the doubly charged ions (XeF22+). The experimental results show that the ionization energies of the doubly charged states predominantly populated in the decay of a vacancy in the F 1s orbital in XeF2 tend to be higher than those populated in the decay of a vacancy in the Xe 4d level in XeF2.
1. Introduction
Recent theoretical studies,1,2 employing methods that allow the inclusion of many-body phenomena, have investigated the single and double ionization spectra associated with the valence and Xe 4d orbitals in the xenon fluorides (XeF2, XeF4, and XeF6). The influence of intra- and interatomic relaxation processes on the decay of a vacancy in the Xe 4d level, through the emission of an Auger electron, was also studied. Subsequent work3 enabled relativistic effects and electron correlation to be considered. Of particular significance to the present work on the Xe 3d and F 1s Auger spectra of XeF2 are the calculated one-site and two-site populations of each dicationic state in the double ionization spectra.2 Such populations have been discussed previously in relation to Auger spectra.4,5 Here, we employ the calculated populations for XeF2 to assess the doubly ionized final states reached in the Auger decay of a vacancy in the F 1s shell and show that they differ from those populated in the Auger decay of a vacancy in the Xe 4d level of XeF2.6Our studies of the Auger processes initiated by the creation of a vacancy in the Xe 3d level of XeF2 are timely as they add to the fundamental spectroscopic information required to interpret recent time-resolved X-ray pump/X-ray probe molecular dynamics experiments on this molecule.7
Several previous experimental investigations6,8–11 have studied the effect of the electronegative fluorine ligands on the central xenon atom in XeF2 by measuring the ionization energies of the Xe 4d, 4p, 4s and 3d levels. A comparison between these values and those of the corresponding levels in the atomic species shows that withdrawal of valence electron density from the xenon atom leads to an increase in the ionization energies. The Xe 4d and 3d shake-up spectra have also been recorded, and assignments have been proposed for some of the satellite states.6,10 Southworth et al.12 have measured the total and partial ion yields of XeF2 associated with the Xe 3d5/2, Xe 3d3/2 and F 1s levels in the photon energy range 660–740 eV. Their results suggest that the molecule with the 3d core hole may dissociate through Coulomb repulsion. The M45N45N45 Auger spectrum of Xe in XeF2 has been recorded by Aksela et al.13 using Mg Kα (1.254 keV) radiation but the electron angular distributions could not be measured.
In the present work, linearly polarized synchrotron radiation has been employed to record polarization dependent electron spectra encompassing all the Auger decay transitions associated with an initial Xe 3d or F 1s vacancy in XeF2. Non-resonant (normal) Auger spectra of the M45N45N45 transition have been measured at several photon energies between 687 and 800 eV, thereby allowing the electron angular distributions, as characterized by the βA parameter, to be determined. In addition, a wide kinetic energy range spectrum, encompassing the structure due to the M45N1N45, M45N23N45, M45N45N45 and M45N45V transitions, has been measured at 705 eV, using two polarization orientations. Resonantly excited Auger spectra, covering a similar kinetic energy range, have been recorded at 669.9 and 682.8 eV, coinciding with the Xe 3d5/2 → σ* and the unresolved Xe 3d3/2 → σ* and F 1s → σ* transitions, respectively.12 These resonant spectra have enabled the shifts in the Auger electron kinetic energy, due to the screening provided by the electron excited into the σ* orbital, to be studied. Finally, the spectrum associated with the F KVV transition has been recorded at a photon energy of 800 eV. The structure observed in this spectrum is discussed in relation to the one-site and two-site populations of the doubly charged final states.2
Our discussion of the Auger electron angular distributions follows those given recently for the iodine M45N45N4514 and N45VV15 transitions in CH3I. The continuum multiple scattering – Xα (CMS–Xα) approach16 has been used to determine the spatial distribution of molecular axes (which depends upon the relative values of the dipole-allowed, symmetry-resolved, photoionization cross sections17,18) following Xe 3d ionization in XeF2, as well as to calculate the partial l-wave contributions to the Xe 3d photoionization cross section. We use these theoretical predictions to help interpret the measured Auger electron angular distributions.
According to our calculations (ESI,† Table S1), the ground state molecular orbital configuration of XeF2 (D∞h symmetry) may be given as
| F1s2Xe3d10Xe4s2Xe4p6Xe4d108σg25σu29σg26σu24πu43πg410σg25πu4 |
2. Experimental apparatus and procedure
The Auger electron spectra were recorded with a VG Scienta R4000 hemispherical electron energy analyser mounted on the soft X-ray undulator-based PLÉIADES beamline at the SOLEIL synchrotron radiation facility. Detailed descriptions of the beamline and station instrumentation have been reported previously14,26,27 so only a summary is given here.The undulator allows the electric vector of the linearly polarized synchrotron radiation to lie either parallel or perpendicular to the acceptance axis of the electron analyser. The beamline employs a modified Petersen type monochromator. The spectra were recorded using a grating having 600 lines per mm together with an exit slit width of 100 μm. This combination results in a theoretical optical resolution of ∼480 meV at a photon energy of 670 eV and 640 meV at 800 eV.
The electron spectrometer was mounted in a fixed position and photoionization occurred within an in-house designed cell6 to minimize the throughput of the sample. The inlet system and the spectrometer were extensively passivated prior to the measurement of spectra to minimize the contribution from atomic xenon. The Auger spectra were recorded with an analyser pass energy of 50 eV and a 0.5 mm curved entrance slit, resulting in a spectrometer resolution of 62.5 meV.
The translational Doppler broadening contributes to the overall line width. For electron kinetic energies of 520 eV, which is appropriate for the Xe M45N45N45 transition in XeF2, and 640 eV, which is appropriate for the F KVV transition, the corresponding Doppler width contributions are ∼22 and 24 meV, respectively.
The Auger electron angular distribution, from excitation of randomly oriented molecules or unpolarized atoms using 100% linearly polarized radiation, is given by28–30
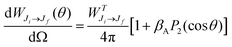 | (1) |
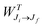 is the total Auger decay rate between initial and final states having total angular momentum Ji and Jf, respectively, θ is the angle between the momentum of the ejected Auger electron and the electric vector of the linearly polarized radiation (the alignment axis), βA is a parameter describing the Auger electron angular distribution for that particular transition, P2(cos
is the total Auger decay rate between initial and final states having total angular momentum Ji and Jf, respectively, θ is the angle between the momentum of the ejected Auger electron and the electric vector of the linearly polarized radiation (the alignment axis), βA is a parameter describing the Auger electron angular distribution for that particular transition, P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the Legendre polynomial of second degree, and dΩ is the differential solid angle element in the direction specified by the polar angle θ. Eqn (1) can be rearranged into the more convenient form26
θ) is the Legendre polynomial of second degree, and dΩ is the differential solid angle element in the direction specified by the polar angle θ. Eqn (1) can be rearranged into the more convenient form26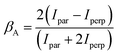 | (2) |
The electron kinetic energy scale was calibrated by recording a spectrum encompassing the Xe M45N45N45 Auger decay in XeF2 and using the value of 530.88 eV for the peak due to the unresolved 1D2 and 1G4 final states in the M4N45N45 transition.13
3. Fitting of the M45N45N45 Auger spectrum
The procedure used to fit the peaks due to the xenon M45N45N45 Auger decay in XeF2 was similar to that already described in detail in relation to the iodine M45N45N45 transitions in CH3I.14 Hence only a brief summary, together with information specific to XeF2, is given here.The two-hole final state configuration 4d−2 gives rise to nine terms13 (Table 1), but not all of these transitions were resolved in our spectra. The three pairs of states that were not resolved correspond to (1D2, 1G4), (3P1, 3P0) and (3F3, 3F2). Thus, six peaks (numbered 1–6, Table 1) were fitted to the structure due to the M5N45N45 transition, and another six peaks (numbered 7–12) were fitted to the M4N45N45 transition. The fitting allows the electron kinetic energy, the angular distribution parameter βA, and the intensity, of each peak to be extracted from the experimental spectra. We consider first the fitting of the non-resonant spectra. Aksela et al.13 recorded spectra, at a photon energy of 1.254 keV, encompassing the M45N45N45 Auger decay in atomic Xe and in XeF2, and found that the width of the sharpest component, due to the 3F4 final state in the M4N45N45 transition, was 0.15–0.2 eV broader in XeF2 than in Xe. Recent measurements of the inherent lifetime widths of the Xe 3d−1 states in atomic xenon32 have determined widths of ∼500 meV for the Xe 3d5/2−1 and 3d3/2−1 states. We adopt a lifetime width of 750 meV for the Xe 3d initial hole state in XeF2. Furthermore, we set the total instrumental broadening (representing the combined spectrometer broadening and the Doppler contribution) to 75 meV. The photon resolution does not affect the fitting of the non-resonant Auger spectra. In our fitting, the initial core–hole lifetime and the total instrumental broadening were held at fixed values of 750 and 75 meV, respectively.
| Transition | Final state | Peak number | Auger electron kinetic energya (eV) | β A (expt.)bc | Experimental | Calculated | |||
|---|---|---|---|---|---|---|---|---|---|
| α 2 (expt)cd | α 2 | α 2 | α 2 | α 2 | |||||
| a This work. Auger electron kinetic energies obtained by fitting the spectrum recorded at a photon energy of 710 eV. b This work. The average βA parameter for the M4 (3d3/2−1) core hole was obtained by averaging the values obtained at four photon energies (701, 705, 710 and 800 eV). c This work. The quoted uncertainty is due only to electron counting statistics and peak fitting, and does not take any systematic errors into account. d This work. The experimental α2 parameters were obtained from the experimental βA parameters using theoretical values A20(D5/2) = −0.21 and A20(D3/2) = −0.20. e Experimental results on atomic xenon obtained at a photon energy of 697.75 eV.40 f Experimental results on atomic xenon using proton impact at an energy of 3.6 MeV.39 g Calculated (Chen56) α2 parameters for the M45N45N45 transitions in atomic xenon. h Calculated (Tulkki et al.57) α2 parameters for the M5N45N45 transitions in atomic xenon. | |||||||||
| M5N45N45 | 1S0 | 1 | 512.97 ± 0.01 | 0.106 ± 0.059 | −0.505 ± 0.281 | −0.71 ± 0.15 | −1.069 | −1.069 | |
| 1D2 | 2 | 518.34 ± 0.01 | 0.086 ± 0.025 | −0.410 ± 0.119 | −0.7 ± 0.3 | −0.17 | −0.131 | −0.124 | |
| 1G4 | −0.719 | −0.710 | |||||||
| 3P1 | 3 | 519.21 ± 0.03 | 0.129 ± 0.042 | −0.614 ± 0.200 | −0.87 | −0.748 | −0.749 | ||
| 3P0 | −1.069 | −1.069 | |||||||
| 3P2 | 4 | 519.91 ± 0.02 | 0.075 ± 0.017 | −0.357 ± 0.081 | −0.2 ± 0.4 | −0.389 | −0.371 | ||
| 3F3 | 5 | 521.44 ± 0.01 | 0.014 ± 0.013 | −0.067 ± 0.062 | −0.25 ± 0.12 | −0.1 | 0.331 | 0.336 | |
| 3F2 | −0.222 | −0.226 | |||||||
| 3F4 | 6 | 523.06 ± 0.01 | −0.065 ± 0.011 | 0.310 ± 0.052 | 0.3 ± 0.2 | 0.378 | 0.386 | ||
| M4N45N45 | 1S0 | 7 | 525.52 ± 0.01 | 0.167 ± 0.028 | −0.835 ± 0.140 | −1.0 | −1.0 | −1.000 | |
| 1D2 | 8 | 530.88 ± 0.01 | 0.052 ± 0.010 | −0.260 ± 0.050 | −0.6 ± 0.4 | −0.33 ± 0.1 | 0.050 | ||
| 1G4 | −0.653 | ||||||||
| 3P1 | 9 | 531.71 ± 0.02 | 0.113 ± 0.023 | −0.565 ± 0.115 | 0.5 ± 0.4 | −0.43 ± 0.1 | −0.799 | ||
| 3P0 | −1.000 | ||||||||
| 3P2 | 10 | 532.63 ± 0.01 | −0.032 ± 0.011 | 0.160 ± 0.055 | 0.39 ± 0.13 | 0.24 ± 0.16 | 0.378 | ||
| 3F3 | 11 | 533.95 ± 0.01 | −0.083 ± 0.016 | 0.415 ± 0.080 | 0.49 ± 0.15 | 0.53 ± 0.22 | 0.432 | ||
| 3F2 | 0.738 | ||||||||
| 3F4 | 12 | 535.65 ± 0.03 | 0.256 ± 0.175 | −1.280 ± 0.875 | −0.9 ± 0.5 | −0.826 | |||
For the resonantly excited Auger spectra, if the photon bandwidth is narrower than the level width of the neutral excited state (Xe 3d5/2−1σ* or Xe 3d3/2−1σ* in our case), then the initial state width can be neglected and replaced by a Gaussian representing the photon bandwidth. Our fitting used fixed Gaussian widths of 485 and 500 meV at photon energies of 669.9 and 682.8 eV, respectively, corresponding to the Xe 3d5/2−1σ* and Xe 3d3/2−1σ* resonances.
4. Calculation of the Xe 3d in XeF2 photoionization partial cross section and the spatial distribution of molecular axes using the CMS–Xα approach
The Xe 3d partial cross section in XeF2 photoionization and the spatial distribution of molecular axes in the Xe 3d−1 ionized state were calculated using methods described previously.15,16Briefly, electric dipole photoionization matrix elements were computed using the static-exchange CMS–Xα method.16,33,34 A model molecular potential, with the Xe–F separation set to be 1.9754 Å as determined by a MP2/def2-QZVP geometry optimisation, was constructed by placing overlapping spherical regions on the atomic centres, all enclosed within an outer spherical region placed at the centre of mass. Bound state eigenvalues and eigenfunctions within this potential were found, utilising an angular basis of spherical harmonic functions (ranging up to lmax = 7, 5 and 3 for respectively the outer-, Xe- and F- regions), and numerical integration to obtain the radial terms. Then, using the Xα exchange potential to relate electron density to potential, the trial model potential was iterated to self-consistency. After adapting the asymptotic potential region to have the correct long range Coulombic interaction appropriate for a separating ion–electron system, continuum electron wavefunctions were generated using multiple scattering equations with an expanded angular basis having lmax = 10, 8, 6 (outer-, Xe-, F-regions respectively). Hence, utilising orthogonal one-electron initial (bound) orbital and continuum functions from this potential, electric dipole photoionization matrix elements were calculated, permitting the Xe 3d photoionization partial cross section and the spatial distribution of molecular axes, I(θion), in the Xe 3d−1 ionized state to be evaluated.
The alignment of molecular axes can be expressed as a distribution having the form15,35
I(θion) = 1 + βionP2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θion) θion) | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θion) is the Legendre polynomial of second order, and θion is the angle between the electric vector of the linearly polarized radiation and the molecular axis. The calculation of βion from the dipole matrix elements was more fully described in connection with our previous investigation of CH3I.15
θion) is the Legendre polynomial of second order, and θion is the angle between the electric vector of the linearly polarized radiation and the molecular axis. The calculation of βion from the dipole matrix elements was more fully described in connection with our previous investigation of CH3I.15
5. Results and discussion
5.1. Overview
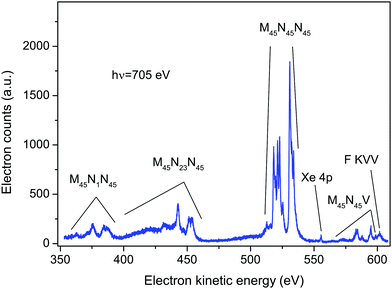
An electron spectrum recorded at a photon energy of 705 eV, using perpendicularly polarized radiation, is plotted in Fig. 1. This spectrum encompasses the structure due to the principal Auger transitions (M45N1N45, M45N23N45, M45N45N45 and M45N45V) associated with the decay of the Xe 3d5/2−1 or 3d3/2−1 hole states in XeF2. Apart from the bands due to the M45N45V transition, these Auger bands strongly resemble the corresponding bands in atomic xenon.36–41 As will be discussed in sections 5.2.4 and 5.2.5, it appears likely that structure arising from the M45N45V transition in XeF2 occurs in the same electron kinetic energy range as that associated with the fluorine KVV transition in XeF2. In particular, our experimental results suggest that the peak observed at a kinetic energy of 601.53 eV (Fig. 1) should be attributed to the F KVV decay.The calculations performed by Partanen et al.41 indicate that, in atomic xenon, satellite Auger transitions originating from the 3d−15p−1 state also contribute in this electron kinetic energy range. Fig. S1 in ESI† shows a spectrum recorded at a photon energy of 705 eV using parallel polarized radiation. In that spectrum an additional peak appears at a binding energy of 216.5 ± 0.2 eV (corresponding to a kinetic energy of 488.5 eV) due to photoionization from the Xe 4s orbital in XeF2. As the photoelectron angular distribution parameter βe for the 4s orbital is ∼2, a peak due to this orbital is not discernible in the spectrum recorded with perpendicularly polarized radiation. Direct photoionization from the Xe 4p orbital in XeF2 gives rise to the weak peak occurring at a kinetic energy of ∼556 eV in Fig. 1. Photoionization from the Xe 4s and Xe 4p orbitals in XeF2 has been a subject of considerable interest9,42 because electron correlation strongly affects the spectrum. However, this topic will not be discussed further in the present work.
Polarization dependent, non-resonant Auger spectra encompassing the M45N45N45 transition were measured at photon energies of 687, 689, 701 705, 710 and 800 eV. In addition, polarization dependent resonantly excited Auger spectra, covering a wide kinetic energy range, were measured at photon energies of 669.9 and 682.8 eV. The lower of these energies coincides with the Xe 3d5/2 → σ* transition.12 The higher energy (682.8 eV) corresponds to the excitation energy of a single peak observed in the ion yield.12 However, that peak was attributed to the unresolved Xe 3d3/2 → σ* and F 1s → σ* transitions, with the calculated oscillator strength of the latter transition being ∼20 times larger than that of the former. Furthermore, the peak is superimposed upon a continuum mainly due to ionization of the Xe 3d5/2 level.
5.2. Auger electron band structure
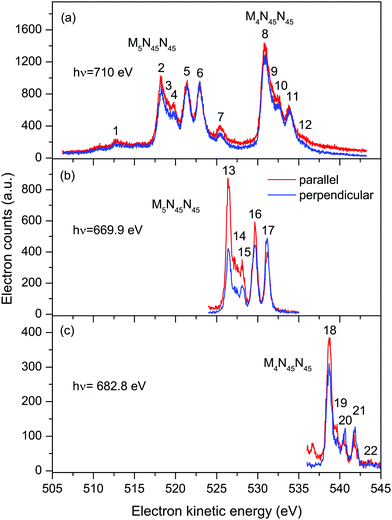 | ||
| Fig. 2 Auger electron bands due to the M45N45N45 transitions in XeF2 recorded with parallel (red) and perpendicularly (blue) polarized radiation. The non-resonant spectrum (a) was measured at a photon energy of 710 eV. The resonantly excited spectra [(b) and (c)] were measured at photon energies of 669.9 eV (3d5/2 → σ* transition) and 682.8 eV (3d3/2 → σ* transition). The kinetic energies of the peaks numbered 1–22 are given in Tables 1 and 2. | ||
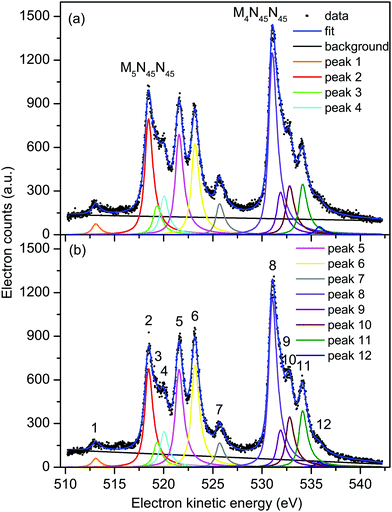 | ||
| Fig. 3 Non-resonant Auger electron bands due to the M45N45N45 transitions in XeF2 recorded with parallel (a) and perpendicularly (b) polarized radiation at a photon energy of 710 eV. The raw and the fitted data are shown (see text for details). The kinetic energies of the peaks numbered 1–12 are given in Table 1. | ||
At these three photon energies, and in the kinetic energy range over which each spectrum is plotted, direct photoionization should not give rise to any structure. However, Partanen et al.41 have calculated that features due to the 3d5/2−15p−1 → 4d−25p−1 transitions in atomic xenon should occur in the kinetic energy range slightly lower than that encompassing the M5N45N45 Auger bands, and presumably similar transitions arising from the 3d3/2−15p−1 initial state would lie at slightly higher kinetic energies. The analogous satellite Auger decays in XeF2 may be responsible for the background underlying the bands due to the M45N45N45 transitions. Our fitted spectrum (Fig. 3) shows that the background contribution is taken into account in a satisfactory manner. The M4N45N45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M5N45N45 intensity branching ratio, obtained from the fits of the non-resonant Auger spectra, is shown in Fig. S2 (ESI†).
M5N45N45 intensity branching ratio, obtained from the fits of the non-resonant Auger spectra, is shown in Fig. S2 (ESI†).
Table 1 contains the results extracted from the fitting of the non-resonant M45N45N45 spectra. The peaks are assigned by analogy with the corresponding peaks in atomic xenon.37 Our analysis yields an electron kinetic energy of 518.34 eV for peak 2, due to the unresolved 1D2 and 1G4 states belonging to the M5N45N45 transition. Using this energy, together with our calibration value of 530.88 eV for the corresponding states in the M4N45N45 transition, results in a M4–M5 spin–orbit splitting of 12.54 eV. Bancroft et al.9 have reported a spin–orbit splitting of 12.68 eV for the Xe 3d5/2−1 and 3d3/2−1 hole states in XeF2.
The Auger electron kinetic energies for the corresponding states extracted from the fitting of the resonantly excited spectra (Figs. S3 and S4) at 669.9 eV (3d5/2 → σ*) and 682.8 eV (3d3/2 → σ*) are listed in Table 2. In these spectra, the final states are singly ionized with an electron promoted into the σ* LUMO. Thus, in Table 2, the states are denoted, for example, as 4d−2(3F4)σ*. If the weak peak associated with the 1S0 state is ignored, the Auger electron kinetic energies, following resonant excitation at 669.9 or 682.8 eV, are shifted, on average, to higher energies by 8.15 and 7.90 eV, respectively, compared to the corresponding values in the non-resonant spectrum (Table 1).
| Transition and final state | Peak number | Auger electron kinetic energy (eV) | β A (expt) a | α 2 (expt) ab |
|---|---|---|---|---|
a The quoted uncertainty is due only to electron counting statistics and peak fitting, and does not take any systematic errors into account.
b The experimental α2 parameters were obtained from the experimental βA parameters using A20 = 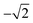 .
c Auger electron kinetic energies and βA parameters obtained by fitting the resonantly excited spectrum recorded at a photon energy of 669.9 eV.
d Auger electron kinetic energies and βA parameters obtained by fitting the resonantly excited spectrum recorded at a photon energy of 682.8 eV. .
c Auger electron kinetic energies and βA parameters obtained by fitting the resonantly excited spectrum recorded at a photon energy of 669.9 eV.
d Auger electron kinetic energies and βA parameters obtained by fitting the resonantly excited spectrum recorded at a photon energy of 682.8 eV.
|
||||
| Xe 3d5/2−1σ* → 4d−2σ* c | ||||
| 4d−2(1D2 + 1G4)σ* | 13 | 526.45 ± 0.01 | 0.498 ± 0.02 | −0.352 ± 0.01 |
| 4d−2(3P0,1)σ* | 14 | 527.32 ± 0.01 | 0.564 ± 0.05 | −0.399 ± 0.04 |
| 4d−2(3P2)σ* | 15 | 528.12 ± 0.01 | 0.355 ± 0.04 | −0.251 ± 0.03 |
| 4d−2(3F2 + 3F3)σ* | 16 | 529.65 ± 0.01 | 0.060 ± 0.02 | −0.042 ± 0.01 |
| 4d−2(3F4)σ* | 17 | 531.17 ± 0.01 | −0.143 ± 0.02 | 0.101 ± 0.01 |
| Xe 3d3/2−1σ* → 4d−2σ* d | ||||
| 4d−2(1D2 + 1G4)σ* | 18 | 538.70 ± 0.01 | 0.132 ± 0.02 | −0.093 ± 0.01 |
| 4d−2(3P0,1)σ* | 19 | 539.59 ± 0.02 | 0.182 ± 0.06 | −0.129 ± 0.04 |
| 4d−2(3P2)σ* | 20 | 540.53 ± 0.01 | −0.373 ± 0.04 | 0.264 ± 0.03 |
| 4d−2(3F2 + 3F3)σ* | 21 | 541.81 ± 0.01 | −0.406 ± 0.04 | 0.287 ± 0.03 |
| 4d−2(3F4)σ* | 22 | 543.69 ± 0.07 | −0.164 ± 0.3 | 0.116 ± 0.21 |
Six intense Auger transitions, together with some weak correlation satellites at lower kinetic energies, are predicted for the M45N1N45 Auger decay.41 For the M5 hole, one of these transitions is associated with peak 23 (Fig. 4(a) and Table 3), and the other two transitions with peak 24. Likewise, for the M4 hole, peaks 27 and 28 are attributed to one and two transitions, respectively. Table 3 lists the kinetic energies of these peaks in XeF2, obtained from the non-resonantly excited spectrum recorded at a photon energy of 705 eV. In the resonantly excited spectrum obtained at a photon energy of 669.9 eV, where only those peaks due to transitions involving an M5 hole will be observed, the two shifted peaks appear at 379.25 eV (peak 25) and 383.78 eV (peak 26). Similarly, in the resonantly excited spectrum obtained at a photon energy of 682.8 eV, where only those peaks due to transitions involving an M4 hole will be observed, the two shifted peaks appear at 391.76 eV (peak 29) and 395.11 eV (peak 30). Thus, in the resonantly excited spectra encompassing the M45N1N45 transition, the peaks are shifted by 8.01 eV towards higher kinetic energy.
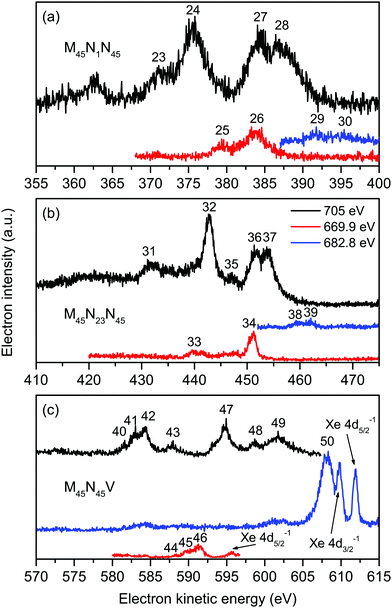 | ||
| Fig. 4 The non-resonant (hν = 705 eV), and resonantly excited (hν = 669.9 and 682.8 eV) Auger electron spectra of XeF2 showing bands due to the Xe M45N1N45 (a), Xe M45N23N45 (b) and Xe M45N45V and F KVV (c) transitions. All of these spectra were measured with perpendicularly polarized radiation. The kinetic energies of the peaks numbered 23–50 are given in Table 3. | ||
| Transition | Peak number | Auger electron kinetic energy (eV) | ||
|---|---|---|---|---|
| hν = 705 eV | hν = 669.9 eV | hν = 682.8 eV | ||
| M5N1N45 | 23 | 371.03 | ||
| 24 | 375.46 | |||
| 25 | 379.25 | |||
| 26 | 383.78 | |||
| M4N1N45 | 27 | 384.23 | ||
| 28 | 387.13 | |||
| 29 | 391.76 | |||
| 30 | 395.11 | |||
| M5N23N45 | 31 | 431.28 | ||
| 32 | 442.83 | |||
| 33 | 439.46 | |||
| 34 | 451.10 | |||
| M4N23N45 | 35 | 446.93 | ||
| 36 | 451.63 | |||
| 37 | 453.73 | |||
| 38 | 459.93 | |||
| 39 | 462.03 | |||
| M5N45V | 40 | 581.53 | ||
| 41 | 582.98 | |||
| 42 | 584.33 | |||
| 43 | 587.93 | |||
| 44 | 588.35 | |||
| 45 | 589.65 | |||
| 46 | 591.30 | |||
| M4N45V | 47 | 594.78 | ||
| 48 | 598.68 | |||
| F KVV | 49 | 601.53 | ||
| 50 | 608.16 | |||
The structure associated with the M45N23N45 Auger decay in XeF2 strongly resembles that observed in the analogous band in atomic xenon although the kinetic energies of the corresponding features are shifted by ∼2 eV to lower energy. We discuss only five of the numerous peaks associated with the M45N23N45 Auger band (Fig. 4(b)). According to Partanen et al.,41 peaks 31 and 32 involve an M5 hole, whereas peaks 35–37 involve an M4 hole (Table 3). The kinetic energies of these peaks obtained in the non-resonantly excited spectrum are listed in Table 3, together with the energies of peaks 33 and 34, and the energies of peaks 38 and 39, obtained from the resonantly excited spectra recorded at photon energies of 669.9 and 682.8 eV, respectively. The kinetic energies of the peaks in the resonantly excited spectra are shifted by ∼8.3 eV to higher energy compared to the corresponding values in the non-resonant spectrum.
In the absence of detailed theoretical guidance, we assume that peaks 40–43 in the Auger spectrum of XeF2 arise from an M5 hole (Fig. 4(c)). The kinetic energies associated with these peaks are given in Table 3. In the resonantly excited spectrum recorded at a photon energy of 669.9 eV, where structure involving an M5 initial hole is expected to appear, we observe peaks 44–46, which seem to correspond to peaks 40–42, shifted by ∼6.8 eV towards higher kinetic energy (Table 3). Thus, a shifted M5N45V Auger band is observed in the resonantly excited spectrum although the shift is smaller than those measured for the M45N1N45, M45N23N45 and M45N45N45 transitions.
The resonantly excited spectrum recorded at a photon energy of 682.8 eV is dominated by a broad and intense peak occurring at a kinetic energy of 608.16 eV. A very weak feature also appears between ∼601–603 eV. The kinetic energy of the intense peak is slightly lower than those due to the Xe 4d5/2,3/2 main-lines in XeF2 which are observed at kinetic energies of ∼612 and ∼610 eV (Fig. 4(c)).
Fig. 5 shows sections of the resonantly excited, polarization dependent spectra plotted as a function of binding energy. In the spectrum recorded at 669.9 eV, the shake-up structure associated with the Xe 4d main-lines in XeF2 resembles that measured and discussed previously.6,10 The broad peak observed in the spectra recorded at 682.8 eV does not appear to be part of the expected shake-up structure. The intensity of this peak in the spectrum measured with parallel polarized radiation is approximately the same as that in the spectrum measured with perpendicularly polarized radiation. Hence, the electron angular distribution is isotropic. Since the broad peak does not seem to result from a transition involving the Xe atom in XeF2, an alternative explanation needs to be sought.
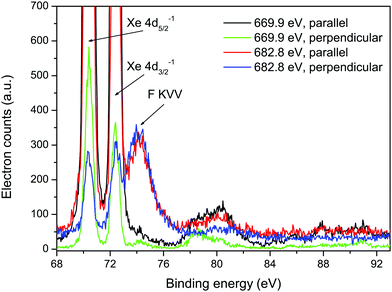 | ||
| Fig. 5 Resonantly excited electron spectra recorded at photon energies of 669.9 and 682.8 eV, using parallel and perpendicularly polarized radiation, plotted as a function of binding energy. The two intense peaks at binding energies of 70.38 and 72.39 eV arise from the Xe 4d5/2−1 and 4d3/2−1 states, and the structure observed between ∼77 and 83 eV is due to the associated shake-up satellites.6 | ||
The F KVV Auger spectrum in HF44 occurs in the electron kinetic energy range 590–650 eV, and the peak having the lowest energy appears at ∼595 eV. Auger electron peaks arising from similar transitions and hence possessing similar energies can be anticipated in XeF2. Two additional sources of information have been used to guide our interpretation of the broad peak. First, as already mentioned, the calculations performed by Southworth et al.12 showed that the single peak observed in the ion yield at 682.8 eV should be attributed to the overlapped and unresolved Xe 3d3/2 → σ* and F 1s → σ* transitions, with the oscillator strength for the latter transition being ∼20 times larger than that of the former. Second, owing to the shielding provided by the electron promoted into the σ* orbital, the Auger electron band resulting from resonant excitation (F 1s → σ*) will be shifted by a few eV to higher energy compared to the corresponding band due to non-resonant (direct) ionization.
If we assume that peak 49 in the non-resonant (hν = 705 eV) Auger spectrum of XeF2, having an electron kinetic energy of 601.53 eV (Table 3) results from a transition originating from the (F 1s)−1 ionic state, and that the broad peak observed at a kinetic energy of 608.16 eV in the resonantly excited spectrum (hν = 682.8 eV) corresponds to the same Auger decay process but with the initial neutral excited state being (F 1s)−1σ*, then the shift in kinetic energy is 6.63 eV. Such a shift to higher kinetic energy is consistent with expectations.
Further support for the assignment of peak 49 to a transition involving the F 1s level is provided by the Auger electron angular distribution. For the broad peak at 608.16 eV, the electron angular distribution is isotropic (Fig. 5) as would be expected for excitation from an atomic 1s orbital, since the excited state cannot be aligned. Our Auger electron angular distribution measurements for processes involving the Xe 3d level in XeF2 show that, although the βA values are not large, they are nonetheless non-zero. This is consistent with the small, but finite, values of atomic alignment predicted for ionization from the Xe 3d level.30
The absence of any intense peaks in the resonantly excited spectrum recorded at a photon energy of 682.8 eV that could be attributed to peaks 47 and 48 shifted to higher kinetic energies suggests that neither of these peaks is associated with an initial state having a vacancy in the F 1s level. Since the calculated oscillator strength for the Xe 3d3/2 → σ* transition is much lower than that for the F 1s → σ* transition,12 an Auger electron peak associated with the M4N45V decay, but shifted to higher energy due to the shielding, would be expected to be of low intensity in the resonantly excited spectrum. Based on the limited evidence available, we tentatively attribute peaks 47 and 48 to the M4N45V Auger transitions. The very weak feature, observed at kinetic energies between 601 and 603 eV in the resonantly excited spectrum, might correspond to peak 47, shifted to slightly higher kinetic energy.
Such considerations allowed satisfactory assignments to be proposed for the F KLL spectrum in SiF4. The theoretical results showed that three separate groups of dicationic states, having 2p−2, 2s−12p−1, and 2s−2 character (where s and p refer to the fluorine atomic orbitals), located on one-site (one fluorine atom) dominate the Auger spectrum. The F KVV in XeF2 Auger spectrum (Fig. 6) can be interpreted in a similar manner. The labelling of the Auger electron peaks in XeF2, shown in Fig. 6, follows that predicted for SiF4.5 A similar interpretation has been given for the structure observed in the Auger electron spectrum of HF.44 As would be expected, the Auger electron spectra resulting from a vacancy in the F 1s level of HF, SiF4 and XeF2 exhibit similar characteristic peaks.
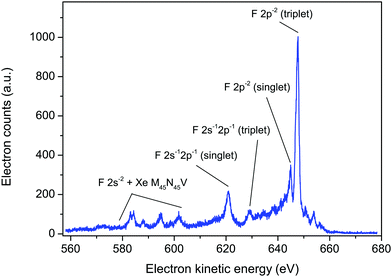 | ||
| Fig. 6 The fluorine KVV and xenon M45N45V Auger electron spectrum in XeF2, recorded at a photon energy of 800 eV, using perpendicularly polarized radiation. The peaks have been labelled as F 2p−2, 2s−12p−1 and 2s−2 (triplet or singlet) in a manner analogous to those predicted for SiF4.5 | ||
Based on the theoretical predictions for SiF4,5 the intense peak at 647.7 eV in XeF2 and the weaker peak at 644.9 eV (Fig. 6) are most likely the triplet and singlet states, respectively, associated with the 2p−2 one-site population. Likewise, the peaks at 629.1 and 620.8 eV may correspond to the theoretically predicted triplet and singlet states, respectively, associated with the 2s−12p−1 one-site populations. In SiF4, the 2s−2 dicationic states were associated with structure observed in the kinetic energy range 590–600 eV. However, in XeF2 the features observed in this energy region appear more complex as a consequence of the additional, overlapping peaks due to the M45N45V transitions.
The F KVV Auger spectrum of XeF2 has not been studied theoretically but Buth et al.2 have calculated the one-site and the two-site populations of the double ionization spectra and we make use of these predictions to discuss our experimental results. Fig. 7 shows the F KVV Auger spectrum plotted as a function of the double ionization energy, where we have used the reported value of 691.23 eV for the F 1s in XeF2 ionization energy.8 Also plotted in Fig. 7 is the Xe 4d in XeF2 Auger spectrum,6 where we have used the Xe 4d5/2 in XeF2 ionization energy of 70.38 eV.6 It is evident that the final doubly ionized states predominantly populated in the decay of a hole in the Xe 4d shell have energies which are lower than those predominantly populated in the decay of a hole in the F 1s orbital. Such a pattern is consistent with our Mulliken atomic populations (Table S1, ESI†) which predict that the HOMO (5πu) has a significant Xe 5p lone-pair character.
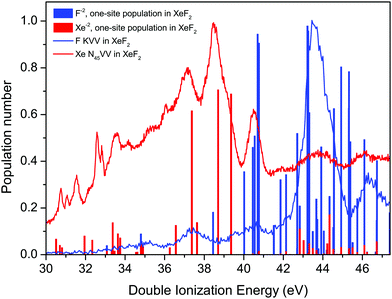 | ||
| Fig. 7 The experimental Auger electron spectra, plotted as a function of the energy of the final doubly ionized state, due to the decay of a vacancy in the F 1s orbital of XeF2, and to the decay of a vacancy in the Xe 4d level in XeF2.6 The calculated one-site populations (F−2 and Xe−2) of the doubly ionized states in XeF2 have been taken from Buth et al.2 Most of the sticks showing the populations typically contain contributions from more than one state. | ||
The calculated one-site populations of the dicationic states of XeF2 are plotted in Fig. 7. These show that the doubly ionized states at energies below ∼40 eV possess a significant Xe−2 population, and hence would be expected to play a key role in the decay of a vacancy in the Xe 4d orbital. Note that we adopt the notations, given by Buth et al.,2 of labelling the one-site states possessing a large dicationic population number on either xenon or a single fluorine as Xe−2 or F−2, respectively. Doubly ionized states possessing a high F−2 one-site population are evident at energies above 40 eV and a dense cluster of such states is predicted between 42 and 46 eV, which coincides with the most prominent peak in the experimental spectrum. The weak structure observed in the F KVV spectrum in the energy range below ∼42 eV may be attributed to states predicted to have a small F−2 character.
As discussed previously in our work on the 4d−1 ionization of XeF2,6 the experimental assignments of the XeF22+ final states with double valence holes in Fig. 7 are not possible at this time. Calculations of the doubly ionized states by Buth et al.2 show a large number of possible states (18 within 5 eV of threshold), and the experimental double ionization threshold differs from the theoretical value by 2.32 eV. The density of states problem becomes even greater at the higher energies of the F2+ states. Finally, although the experimental spectrum appears relatively simple, the broad structure at higher binding energies obscures the fact that multiple states are contributing to each feature.
5.3. Auger electron angular distributions
In discussing the Auger electron angular distributions, we adopt the two-step formulation of the Auger process46 in which the initial core excitation or core ionization is assumed to be independent of the subsequent decay. Within this framework, for processes occurring in an atom, the Auger electron angular distribution parameter, βA, as defined by eqn (1), can be written with βA factored into two components29,30| βA = A20α2 | (4) |
Of particular relevance to the present work are the theoretical studies of photoinduced alignment in core hole states in the rare gases,30 and subsequent work48 covering a wider range of elements. These investigations30 show that, in the non-relativistic limit, the alignment A20(D5/2) and A20(D3/2) resulting from inner shell photoionization of an atomic d orbital, depend upon the ratio
| R23d→εp/R23d→εf | (5) |
Auger electron angular distributions have also been studied in several small linear molecules [ref. 49–51, and references therein]. For the molecular case, where the quantization axis is taken as the molecular symmetry axis, the alignment of the state emitting the Auger electron arises from the anisotropic spatial distribution of the molecular ion axes in the lab frame following photoionization, as expressed in eqn (3). The Auger electron angular distribution parameter, βA, may be factored as15,18,52
| βA = βioncA | (6) |
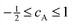 .18
.18
The results from our CMS–Xα calculations (Fig. 8(a)) show that, in the Xe 3d−1 ionized state in XeF2, the molecular axes are not aligned to any significant degree in the photon energy range covered in our measurements of the Auger electron angular distributions. The parameter βion does, however, display weak oscillations around zero with increasing photon energy. Since cA has a fixed value for a given Auger transition, eqn (6) implies that the predicted oscillations in sign of βion should be matched by corresponding changes in sign of βA. Experimentally (Fig. 9) there is no evidence of these anticipated variations. Moreover, since the calculated values of βion, in the photon energy range of interest, are small, the use of eqn (6) to match the experimentally observed βA values requires very large values of cA which lie outside the permitted range. It is concluded that the molecular limit represented by eqn (6) does not provide an adequate description for these XeF2 Auger transitions.
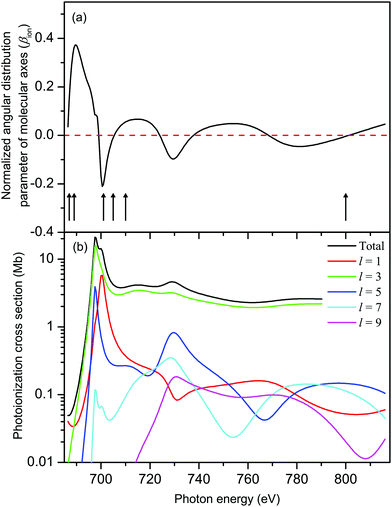 | ||
| Fig. 8 (a) The calculated, normalized, angular distribution parameter (βion) characterizing the spatial distribution of molecular axes in XeF2 in the Xe 3d-1 ionized state. The vertical bars with arrowheads indicate the photon energies at which measurements of the Auger electron angular distributions associated with the M45N45N45 transition were made. The βA parameters derived from these measurements are plotted in Fig. 9. (b) The calculated (CMS–Xα) Xe 3d photoionization cross section of XeF2 decomposed into l–wave components. | ||
An examination of the eigenvectors obtained by quantum chemistry molecular orbital calculations (see Table S1, population analysis in ESI†) confirms, unsurprisingly, that the orbitals we label as 3d are essentially pure atomic Xe 3d in character, sharing no population with the F atoms. Moreover, the 3d eigenvalues (reported as Koopmans ionization energies in Table S1, ESI†) show that symmetry splitting by the molecular field is completely negligible (≤26 meV). Evidently, these deep-lying Xe 3d levels are insensitive to the molecular field. This suggests that the Auger electron angular anisotropy may be more profitably considered as an atomic-like process.
This behaviour parallels our findings concerning the feasibility of using calculated values of βion to interpret the non-resonant Auger electron angular distributions resulting from I 3d ionization in CH3I.14 We can note that the Auger electron bands due to the xenon M45N1N45, M45N23N45 and M45N45N45 transitions in XeF2 closely resemble those due to the analogous transitions in atomic xenon, and hence appear atomic-like. We also note that our experimentally derived βA value for a particular final state associated with the M45N45N45 transition in XeF2 is similar to that for the corresponding state in atomic xenon.40 Hence, we continue by assuming the atomic limit model, represented by eqn (4), for the M45N45N45 Auger electron angular distributions in XeF2.
The calculated total, and l-resolved, Xe 3d in XeF2 photoionization cross sections are plotted in Fig. 8(b). Apart from a small energy range close to threshold, the l = 3 partial wave dominates all the others by 1–2 orders of magnitude. Hence, R23d→εp/R23d→εf → 0. In this limit,30 one obtains the energy-independent alignments:
| A20(D5/2) = −0.21 and A20(D3/2) = −0.20 | (7) |
For photoexcitation by linearly polarized radiation from an atomic ground state having J = 0 to an excited state with J = 1, A20 has an energy independent value of 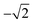 .52,53 We assume this value of the alignment parameter is valid for the resonantly excited Xe 3d → σ* spectra.
.52,53 We assume this value of the alignment parameter is valid for the resonantly excited Xe 3d → σ* spectra.
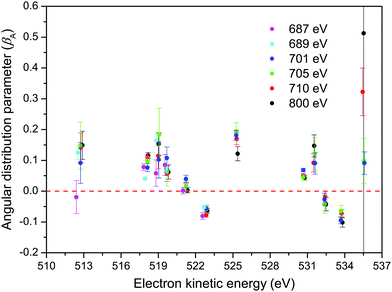
The βA parameters for the M45N45N45 Auger transition, derived from the fits of our non-resonant spectra, are plotted in Fig. 9. For a particular final doubly ionized state, the experimental βA-values exhibit little variation as a function of photon energy, as already noted. This observation is consistent with the essentially constant alignment terms, A20, theoretically predicted across the energy range over which the measurements were made. Our experimental values for the α2 parameters, obtained by averaging the βA parameters for a specific final state over several photon energies, and using the values for A20 given in eqn (7), are listed in Table 1.
Several theoretical methods have been employed to calculate the α2 parameters for the M45N45N45 transitions in atomic xenon.54–58 The theoretical values calculated by Chen56 and Tulkki et al.57 are given in Table 1. Apart from the value associated with the 1S0 state belonging to the M5N45N45 transition, the agreement between experiment and theory appears reasonable, although not all of the final states give rise to resolvable features in the experimental spectrum. The discrepancy in the calculated and measured values for the 1S0 state can probably be attributed to the low intensity of the associated peak in the experimental spectrum.
Although our α2 parameters for the M45N45N45 transition in XeF2 are in fair accord with those derived by Karvonen et al.40 from the non-resonant M45N45N45 spectrum in atomic xenon, obtained through photoionization, some significant discrepancies are apparent. In fact, better agreement is found with the results obtained by Hiltunen et al.39 using proton impact, as seen in Table 1.
The alignment of the intermediate neutral state, following resonant excitation (Xe 3d5/2,3/2 → σ*) is much higher than that of the non-resonant core-ionized state. This higher degree of alignment leads to the Auger electron angular distributions measured in the resonantly excited Auger spectra (Table 2) being more anisotropic than those associated with non-resonant ionization. Unfortunately, no theoretical predictions for these resonantly excited α2 parameters are available for comparison with the current experimental results.
6. Summary
Polarization dependent electron spectra of XeF2, encompassing the bands due to the xenon M45N1N45, M45N23N45, M45N45N45 and M45N45V and fluorine KVV Auger transitions have been recorded using linearly polarized synchrotron radiation. Non-resonantly excited spectra have been measured at several photon energies between 687 and 800 eV, and resonantly excited spectra have been measured at energies coinciding with the Xe 3d5/2 → σ* and the overlapping Xe 3d3/2 → σ* and F 1s → σ* transitions in XeF2. The polarization dependent spectra have allowed the Auger electron angular distributions to be determined. The Auger bands associated with the xenon M45N1N45, M45N23N45 and M45N45N45 transitions in XeF2 are similar to those for the analogous transitions in atomic xenon, thereby allowing assignments to be proposed for some of the observed structure. The Auger electron spectrum due to the M45N45V transition differs from that due to the M45N45O transition in atomic xenon, indicating the involvement of delocalized molecular orbitals. Moreover, our spectra indicate that peaks due to the M4N45V transitions in XeF2 occur in a similar kinetic energy range as those resulting from the F KVV decay in XeF2.The interpretation of the F KVV Auger band in XeF2 has been discussed in relation to results from a theoretical study of the F KLL spectrum in SiF4. The theoretical study showed that the 2 h configurations possessing a high one-site population (both holes in the same fluorine atom) were those associated with the strongest peaks in the Auger spectrum. In a similar manner, doubly ionized states of XeF2 having a high calculated one-site population have been shown to be those predominantly populated in the decay of a F 1s vacancy in XeF2. The experimental spectra show that the ionization energies of the doubly charged states populated in the decay of a hole in the Xe 4d orbital in XeF2 tend to be lower than those populated in the decay of a hole in the F 1s orbital in XeF2. This finding is consistent with the calculated one-site population analysis, which reflects the greater electron density on the F atoms (more screening) and the lower electron density on the Xe atom (less screening). Tentative assignments for some of the peaks observed in the F 1s Auger spectrum in XeF2 have been suggested, based upon predictions for the analogous structure in the F 1s Auger spectrum of SiF4. However, a theoretical study of the Xe 4d and F 1s Auger spectra in XeF2 is needed to confirm these proposed assignments and to identify several additional features.
The Auger electron intrinsic anisotropy parameters for the Xe M45N45N45 transition in XeF2 have been obtained from the measured angular distributions parameters by using a theoretical, limiting value, of the alignment parameter A20, in an atomic approximation. This limiting value should be valid in the photon energy range over which the measurements were taken, where the Xe 3d photoionization cross section is dominated by transitions into the εf continuum channel. The values of the derived α2 parameters for the Xe M45N45N45 transition in XeF2 are similar to those measured and calculated for the analogous transitions in atomic xenon.
Author contributions
The manuscript was written through contributions of all the authors. All the authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank C. Buth and L. Cederbaum for making the digital data from their calculations on the double ionization potentials of XeF2 available to us, and for helping us with their interpretation. D. M. P. H. is grateful to the Science and Technology Facilities Council (United Kingdom) for financial support. S. T. P. is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under contract No. DE-AC02-06CH11357. We are grateful to the SOLEIL staff for running the facility and providing beamtime under Project No. 20190046.References
- C. Buth, R. Santra and L. S. Cederbaum, J. Chem. Phys., 2003, 119, 7763 CrossRef CAS.
- C. Buth, R. Santra and L. S. Cederbaum, J. Chem. Phys., 2003, 119, 10575 CrossRef CAS.
- M. Pernpointner and L. S. Cederbaum, J. Chem. Phys., 2005, 122, 214302 CrossRef PubMed.
- F. Tarantelli, A. Sgamellotti and L. S. Cederbaum, J. Chem. Phys., 1991, 94, 523 CrossRef CAS.
- F. O. Gottfried, L. S. Cederbaum and F. Tarantelli, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 2118 CrossRef CAS PubMed.
- R. Forbes, P. Hockett, I. Powis, J. D. Bozek, D. M. P. Holland and S. T. Pratt, J. Chem. Phys., 2021, 155, 194301 CrossRef CAS PubMed.
- A. Picón, C. S. Lehmann, C. Bostedt, A. Rudenko, A. Marinelli, T. Osipov, D. Rolles, N. Berrah, C. Bomme, M. Bucher, G. Doumy, B. Erk, K. R. Ferguson, T. Gorkhover, P. J. Ho, E. P. Kanter, B. Krässig, J. Krzywinski, A. A. Lutman, A. M. March, D. Moonshiram, D. Ray, L. Young, S. T. Pratt and S. H. Southworth, Nat. Commun., 2016, 7, 11652 CrossRef PubMed.
- T. X. Carroll, R. W. Shaw, T. D. Thomas, C. Kindle and N. Bartlett, J. Am. Chem. Soc., 1974, 96, 1989 CrossRef CAS.
- G. M. Bancroft, P.-Å. Malmquist, S. Svensson, E. Basilier, U. Gelius and K. Siegbahn, Inorg. Chem., 1978, 17, 1595 CrossRef CAS.
- J. S. Tse, D. J. Bristow, G. M. Bancroft and G. Schrobilgen, Inorg. Chem., 1979, 18, 1766 CrossRef CAS.
- J. N. Cutler, G. M. Bancroft, J. D. Bozek, K. H. Tan and G. J. Schrobilgen, J. Am. Chem. Soc., 1991, 113, 9125 CrossRef CAS.
- S. H. Southworth, R. Wehlitz, A. Picón, C. S. Lehmann, L. Cheng and J. F. Stanton, J. Chem. Phys., 2015, 142, 224302 CrossRef PubMed.
- S. Aksela, G. M. Bancroft, D. J. Bristow, H. Aksela and G. J. Schrobilgen, J. Chem. Phys., 1985, 82, 4809 CrossRef CAS.
- R. Forbes, A. De Fanis, C. Bomme, D. Rolles, S. T. Pratt, I. Powis, N. A. Besley, S. Nandi, A. R. Milosavljević, C. Nicolas, J. D. Bozek, J. G. Underwood and D. M. P. Holland, J. Chem. Phys., 2018, 149, 094304 CrossRef PubMed.
- R. Forbes, A. De Fanis, D. Rolles, S. T. Pratt, I. Powis, N. A. Besley, A. R. Milosavljević, C. Nicolas, J. D. Bozek and D. M. P. Holland, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 155101 CrossRef CAS.
- I. Powis, Chem. Phys., 1995, 201, 189 CrossRef CAS.
- J. L. Dehmer and D. Dill, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 18, 164 CrossRef CAS.
- D. Dill, J. R. Swanson, S. Wallace and J. L. Dehmer, Phys. Rev. Lett., 1980, 45, 1393 CrossRef CAS.
- C. R. Brundle, M. B. Robin and G. R. Jones, J. Chem. Phys., 1970, 52, 3383 CrossRef CAS.
- C. R. Brundle, G. R. Jones and H. Basch, J. Chem. Phys., 1971, 55, 1098 CrossRef CAS.
- B. W. Yates, K. H. Tan, G. M. Bancroft, L. L. Coatsworth, J. S. Tse and G. J. Schrobilgen, J. Chem. Phys., 1986, 84, 3603 CrossRef CAS.
- G. M. Bancroft, S. Aksela, H. Aksela, K. Gürtler, K. H. Tan, B. W. Yates and J. S. Tse, J. Phys. B: At. Mol. Phys., 1987, 20, 3057 CrossRef CAS.
- H. Basch, J. W. Moskowitz, C. Hollister and D. Hankin, J. Chem. Phys., 1971, 55, 1922 CrossRef CAS.
- F. J. Comes, R. Haensel, U. Nielsen and W. H. E. Schwarz, J. Chem. Phys., 1973, 58, 516 CrossRef CAS.
- U. Nielsen and W. H. E. Schwarz, Chem. Phys., 1976, 13, 195 CrossRef CAS.
- I. Powis, D. M. P. Holland, E. Antonsson, M. Patanen, C. Nicolas, C. Miron, M. Schneider, D. Y. Soshnikov, A. Dreuw and A. B. Trofimov, J. Chem. Phys., 2015, 143, 144304 CrossRef CAS PubMed.
- R. Forbes, A. De Fanis, C. Bomme, D. Rolles, S. T. Pratt, I. Powis, N. A. Besley, M. Simon, S. Nandi, A. R. Milosavljević, C. Nicolas, J. D. Bozek, J. G. Underwood and D. M. P. Holland, J. Chem. Phys., 2018, 149, 144302 CrossRef PubMed.
- S. Flügge, W. Mehlhorn and V. Schmidt, Phys. Rev. Lett., 1972, 29, 7 CrossRef.
- E. G. Berezhko and N. M. Kabachnik, J. Phys. B: At. Mol. Phys., 1977, 10, 2467 CrossRef CAS.
- E. G. Berezhko, N. M. Kabachnik and V. S. Rostovsky, J. Phys. B: At., Mol. Opt. Phys., 1978, 11, 1749 CrossRef CAS.
- J. Jauhiainen, A. Ausmees, A. Kivimäki, S. J. Osborne, A. Naves de Brito, S. Aksela, S. Svensson and H. Aksela, J. Electron Spectrosc. Relat. Phenom., 1994, 69, 181 CrossRef CAS.
- M. Jurvansuu, A. Kivimäki and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 012502 CrossRef.
- D. Dill and J. L. Dehmer, J. Chem. Phys., 1974, 61, 692 CrossRef CAS.
- J. W. Davenport, PhD thesis, University of Pennsylvania, 1976.
- S. M. Bellm, J. A. Davies, P. T. Whiteside, J. Guo, I. Powis and K. L. Reid, J. Chem. Phys., 2005, 122, 224306 CrossRef PubMed.
- L. O. Werme, T. Bergmark and K. Siegbahn, Phys. Scr., 1972, 6, 141 CrossRef CAS.
- S. Aksela, H. Aksela and T. D. Thomas, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 19, 721 CrossRef CAS.
- H. Pulkkinen, H. Aksela and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 1195 CrossRef CAS PubMed.
- A. Hiltunen, H. Aksela, S. Aksela, G. Víkor, S. Ricz and B. Sulik, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, L793 CrossRef CAS.
- J. Karvonen, A. Kivimäki, H. Aksela, S. Aksela, R. Camilloni, L. Avaldi, M. Coreno, M. de Simone and K. C. Prince, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 315 CrossRef CAS.
- L. Partanen, M. Huttula, S.-M. Huttula, H. Aksela and S. Aksela, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 4515 CrossRef CAS.
- M. Ohno, J. Electron Spectrosc. Relat. Phenom., 2003, 130, 19 CrossRef CAS.
- A. Kivimäki, H. Aksela, J. Jauhiainen, M. Kivilompolo, E. Nõmmiste and S. Aksela, J. Electron Spectrosc. Relat. Phenom., 1998, 93, 89 CrossRef.
- R. W. Shaw and T. D. Thomas, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 1491 CrossRef CAS.
- H. Siegbahn, L. Asplund and P. Kelfve, Chem. Phys. Lett., 1975, 35, 330 CrossRef CAS.
- W. Mehlhorn, in Atomic Inner-Shell Physics, ed. B. Crasemann, Plenum Press, New York, 1985, p.119 Search PubMed.
- H. Aksela, S. Aksela and N. Kabachnik, in VUV and Soft X-Ray Photoionization, ed. U. Becker and D. A. Shirley, Plenum Press, New York, 1996, p. 401 Search PubMed.
- U. Kleiman and B. Lohmann, J. Electron Spectrosc. Relat. Phenom., 2003, 131–132, 29 CrossRef.
- O. Hemmers, F. Heiser, J. Eiben, R. Wehlitz and U. Becker, Phys. Rev. Lett., 1993, 71, 987 CrossRef CAS PubMed.
- R. F. Fink, M. N. Piancastelli, A. N. Grum-Grzhimailo and K. Ueda, J. Chem. Phys., 2009, 130, 014306 CrossRef CAS PubMed.
- E. Antonsson, M. Patanen, C. Nicolas, S. Benkoula, J. J. Neville, V. L. Sukhorukov, J. D. Bozek, P. V. Demekhin and C. Miron, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 042506 CrossRef.
- N. M. Kabachnik, S. Fritzsche, A. N. Grum-Grzhimailo, M. Meyer and K. Ueda, Phys. Rep., 2007, 451, 155 CrossRef CAS.
- U. Hergenhahn, N. M. Kabachnik and B. Lohmann, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 4759 CrossRef CAS.
- N. M. Kabachnik and I. P. Sazhina, J. Phys. B: At., Mol. Opt. Phys., 1988, 21, 267 CrossRef CAS.
- N. M. Kabachnik, I. P. Sazhina, I. S. Lee and O. V. Lee, J. Phys. B: At., Mol. Opt. Phys., 1988, 21, 3695 CrossRef CAS.
- M. H. Chen, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 1684 CrossRef CAS PubMed.
- J. Tulkki, N. M. Kabachnik and H. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 1277 CrossRef CAS PubMed.
- A. Yu. Elizarov and I. I. Tupitsyn, J. Exp. Theor. Phys., 2003, 97, 658 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04797c |
| This journal is © the Owner Societies 2022 |