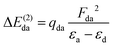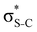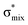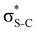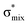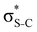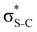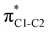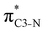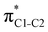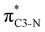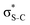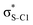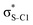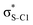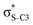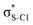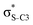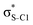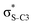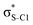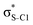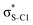Electron delocalisation in conjugated sulfur heterocycles probed by resonant Auger spectroscopy†
Jessica B.
Martins‡
 a,
Carlos E. V.
de Moura
a,
Carlos E. V.
de Moura
 bc,
Gildas
Goldsztejn
bc,
Gildas
Goldsztejn
 d,
Oksana
Travnikova
d,
Oksana
Travnikova
 ae,
Renaud
Guillemin
ae,
Iyas
Ismail
ae,
Loïc
Journel
ae,
Renaud
Guillemin
ae,
Iyas
Ismail
ae,
Loïc
Journel
 ae,
Dimitrios
Koulentianos§
ae,
Dimitrios
Koulentianos§
 af,
Mario
Barbatti
af,
Mario
Barbatti
 cg,
Alexsandre F.
Lago
cg,
Alexsandre F.
Lago
 h,
Denis
Céolin
h,
Denis
Céolin
 e,
Maria Luiza M.
Rocco
e,
Maria Luiza M.
Rocco
 i,
Ralph
Püttner
i,
Ralph
Püttner
 j,
Maria Novella
Piancastelli
j,
Maria Novella
Piancastelli
 ak,
Marc
Simon
ak,
Marc
Simon
 ae and
Tatiana
Marchenko
ae and
Tatiana
Marchenko
 *ae
*ae
aSorbonne Université, CNRS, UMR 7614, Laboratoire de Chimie Physique-Matière et Rayonnement, F-75005 Paris, France. E-mail: tatiana.marchenko@sorbonne-universite.fr
bDepartment of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA
cAix-Marseille University, CNRS, ICR, Marseille, France
dUniversité Paris-Saclay, Institut des Sciences Moléculaires d'Orsay ISMO, UMR CNRS 8214, F-91405 Orsay, France
eSynchrotron SOLEIL, L'Orme des Merisiers, Saint-Aubin, F-91192 Gif-sur-Yvette Cedex, France
fDepartment of Physics, University of Gothenburg, Origovägen 6B, SE-412 96 Gothenburg, Sweden
gInstitut Universitaire de France, 75231 Paris, France
hCentro de Ciências Naturais e Humanas, Universidade Federal do ABC (UFABC), 09210-580, Santo André, São Paulo, Brazil
iInstituto de Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro 21941-909, Brazil
jFachbereich Physik, Freie Universität Berlin, D-14195 Berlin, Germany
kDepartment of Physics and Astronomy, Uppsala University, SE-751 20 Uppsala, Sweden
First published on 15th March 2022
Abstract
We propose a novel approach for an indirect probing of conjugation and hyperconjugation in core-excited molecules using resonant Auger spectroscopy. Our work demonstrates that the changes in the electronic structure of thiophene (C4H4S) and thiazole (C3H3NS), occurring in the process of resonant sulfur K-shell excitation and Auger decay, affect the stabilisation energy resulting from π-conjugation and hyperconjugation. The variations in the stabilisation energy manifest themselves in the resonant S KL2,3L2,3 Auger spectra of thiophene and thiazole. The comparison of the results obtained for the conjugated molecules and for thiolane (C4H8S), the saturated analogue of thiophene, has been performed. The experimental observations are interpreted using high-level quantum-mechanical calculations and the natural bond orbital analysis.
1 Introduction
Conjugation is an important concept in organic chemistry describing electron delocalisation over the molecule through the overlapping molecular orbitals. The interaction between p-orbitals or π-orbitals leads to π-conjugation, whereas the interaction between the orbitals involving at least one σ-bond is commonly referred to as hyperconjugation.1–3 In a broad sense that we adopt in this work, one can distinguish geminal and vicinal hyperconjugation involving interaction of orbitals at the same atom or at the adjacent atoms, respectively3.Although electron delocalisation in conjugated systems cannot be directly observed experimentally, it can be probed indirectly through observable phenomena resulting from the electron delocalisation. For example, thermodynamic stability of aromatic compounds was often interrogated in experimental chemistry to quantify the degree of conjugation relative to the reference compounds.4 Vibrational spectroscopy was shown to be sensitive to hyperconjugation in hydrazides in the gas phase and in solution.5
From the theoretical side, the conjugation phenomenon can be addressed by using the Natural Bond Orbital (NBO) method.6,7 In this approach, localised bonds and lone pairs are the basic units to describe the chemical structure of molecules following the Lewis model. The so-called stabilisation energy can be used to quantitatively estimate the conjugation “strength” describing how much the potential energy of a molecular system with delocalised electron density is lower with respect to a hypothetical reference system with an ideal Lewis structure.
Stability of conjugated systems is generally considered as a characteristic of an electronic ground state. Extension of the conjugation concept to the lowest electronically excited states and its relevance for chemical reactivity has been addressed in ref. 8. Despite the numerous studies on core ionisation of conjugated molecules exposed to X-ray radiation (see for example ref. 9 and 10), to the best of our knowledge, a possible evolution of stabilisation energy in the process of core excitation and consecutive electronic decays has not been addressed so far.
One of the most powerful techniques providing access to the dynamic changes of electronic structure in core-excited molecules is resonant Auger spectroscopy (RAS) (see ref. 11 and references therein). Our work demonstrates a novel application of RAS as a probe of conjugation and hyperconjugation effects in core-excited aromatic molecules. We demonstrate, both experimentally and theoretically, that the changes of electronic structure of thiophene (C4H4S) and thiazole (C3H3NS), occurring in the process of resonant sulfur K-shell excitation and Auger decay, affect the stabilisation energy resulting from π-conjugation and hyperconjugation. The variations in the stabilisation energy manifest themselves in the resonant S KL2,3L2,3 Auger spectra of thiophene and thiazole. The choice of these molecules is motivated by the growing attention to their role as building blocks for promising organic materials used for solar cells, chemical sensors, photovoltaic devices, among other applications.12–17 The results obtained in the conjugated molecules are compared to the resonant Auger spectra of thiolane (C4H8S), the saturated analogue of thiophene. The experimental observations are qualitatively reproduced with high-level quantum-mechanical calculations and are interpreted in terms of conjugation and hyperconjugation effects using the NBO method.
2 Computational details
2.1 Multiconfigurational calculations for core-excited states
In order to estimate the transition energies to the core-excited states, we applied the Inner-Shell Multiconfigurational Self-Consistent Field (IS-MCSCF) procedure.18 In this state-specific method, the active space is split in multiple groups, as in the Restricted Active Space Self-Consistent Field19,20 (RASSCF) formulation: one group containing the inner-shell orbitals (labelled as RAS1), and another group containing the remaining orbitals of interest (labelled as RAS2 and, when necessary, RAS3). Each of these groups has a particular electronic occupancy assigned, according to the target state, and is optimised in different SCF steps, avoiding the variational collapse for the convergence of highly excited states. The procedure is adjustable and can also be generalised to any construction of active spaces.21 Using this procedure we can obtain the individual vertical absorption transitions, the shape of the molecular orbitals and estimate the Auger electron kinetic energies.For the ground state of the thiophene and thiazole molecules, we applied a wave function CASSCF(12e,10o), with 12 electrons in the active space and 10 orbitals including the bonding and antibonding pairs of orbitals related to the σS–C (4 orbitals) and π-bonds (4 orbitals), and the orbitals related to sulfur lone pairs (2 orbitals). An equivalent selection was made for the thiolane molecule, using a wave function CASSCF(8e,6o), including the bonding and antibonding pairs related to the σS–C (4 orbitals) and the orbitals related to sulfur lone pairs (2 orbitals). The same active spaces were applied as the valence active spaces of IS-MCSCF calculations (RAS2) describing the lowest core-excitation transitions.
When calculating the core-excited states using the IS-MCSCF method, we include their corresponding core orbitals in the active space. For the sulfur K-shell excitation, the RAS1 group contains the orbital equivalent to S 1s and its occupancy is constrained to one electron, moving the other 1s electron to the RAS2 valence group. For the final states, resulting from sulfur Auger KLL spectator decay, the RAS1 group contains the three S 2p orbitals and its total occupancy is constrained to four electrons so that one electron is moved to the valence active space and another one, related to the Auger emission, is removed from the system.
The state-specific IS-MCSCF wave functions for the intermediate 1s−1V core-excited states were directly calculated selecting their state symmetry. For the final 2p−2V states, we applied a state-average (SA) multiconfigurational wave function between all the investigated states, amounting to six states for thiophene and thiazole molecules (SA6-IS-MCSCF) and three states for thiolane molecule (SA3-IS-MCSCF).
Additionally, to describe the higher-energy transitions in the S 1s absorption spectra, we extended the IS-MCSCF calculations to core-excited states related to the excitations beyond the active spaces described above. These calculations setup include an additional active space (RAS3) containing four virtual orbitals of a given symmetric irreducible representation. The single-electron excitation from the RAS1 to the RAS3 is described by constraining the electron occupancy of RAS3 to one. The excited states were obtained by SA-IS-MCSCF calculations, in which each RAS group is optimised in a distinct self-consistent step, with the first four states equally weighted (SA4-IS-MCSCF). For each irreducible representation, an individual SA4-IS-MCSCF calculation was performed, in which the RAS3 space was composed by four orbitals assigned to this representation.
Electronic transition energies were obtained as a difference between the ground and excited states energies (ΔMCSCF). Oscillator strengths for S 1s excitations were obtained using the IS-MCSCF molecular orbitals as the basis to the calculation of the transition dipole moments between the ground state and the excited states using the Restricted Active Space Configuration Interaction (RASCI)19 method.
Ground state equilibrium geometries were obtained by the geometry optimisation procedure at the second-order Møller–Plesset perturbation theory (MP2) level (see ESI†).22 Relativistic scalar effects were recovered by 4th Douglas–Kroll–Hess method (DKH).23–25 We applied the core-extended Dunning's correlated consistent polarized basis set, aug-cc-pCVTZ-DK.26–31 A similar approach was previously applied to sulfur core-hole states providing a good agreement with the experiment.32 All calculations were done using MOLPRO 2012 package.33,34
2.2 Natural bond orbitals for core-excited states
The role of conjugation and the related stabilisation energy in the process of resonant Auger decay of core-excited states was evaluated using the NBO method relying on the second-order perturbation theory analysis of the Fock matrix.35–37 The NBO analysis was previously applied in the assignment of XANES (X-ray absorption near-edge spectroscopy) spectra of actinide complexes.38The NBOs are an orthonormal set of localised one-centre or two-centre orbitals describing the electron density distribution on the atoms (lone pairs) and between the atoms (bonds) in a molecule. This set of localised orbitals represents the Lewis structure. For the ideal localised Lewis structure representation, the NBO occupancy q is an integer (q = 2 for filled orbitals and q = 1 for open-shell orbitals). In NBO analysis, the electron delocalisation is described as a deviation from the ideal Lewis structure towards the molecular orbitals picture and is reflected in a variation of the NBO occupancy from an integer.
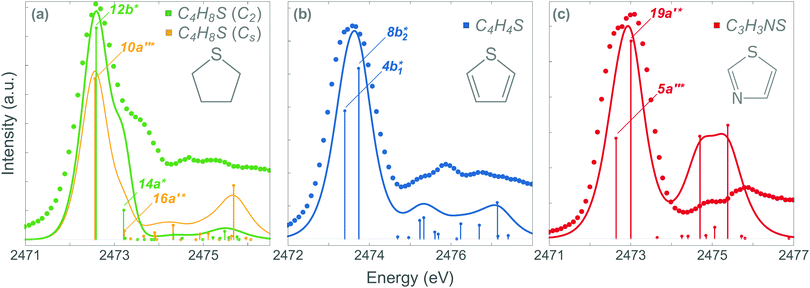
The stabilisation energy (ΔE(2)da) can be used to quantify the strength of the conjugation effect due to electron delocalisation between an occupied donor NBO(d) and a non-occupied acceptor NBO(a), and is calculated as:
As the perturbation theory analysis of the Fock matrix requires a single electronic configuration wave function, we described each 1s−1V and 2p−2V core excited state with a state-specific Restricted open-shell Hartree–Fock (ROHF) method.41 A two-step self-consistent procedure was applied, similar to the approach used in the IS-MCSCF calculations. Ground-state wave functions were obtained by the Restricted Hartree–Fock (RHF) method.42 Then, using the molecular orbitals resulting from these calculations, we obtained the NBO sets for each electronic state involved in our analysis.
3 Experiment
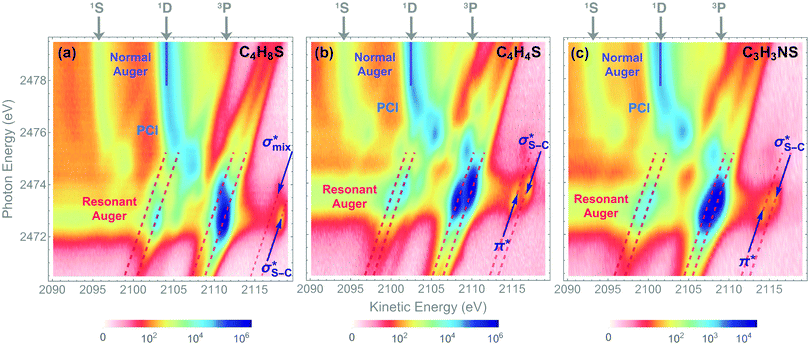
The measurements were performed at the HAXPES end station, based on a hemispherical electron analyser, installed on the GALAXIES beam line at the synchrotron SOLEIL.43,44 The vapour of the studied samples, liquid at room temperature, was transferred to the experimental chamber through a sealed gas inlet system. The pressure inside the chamber was kept constant during the measurements. We recorded the resonant Auger S KL2,3L2,3 spectra for thiophene, thiolane, and thiazole molecules in the gas phase with a total resolution of about 0.3 eV, including the photon bandwidth and the spectrometer resolution. The electron kinetic energy and the photon energy were calibrated using the well-known Argon LMM Auger spectrum and Argon 2p−1 photoelectron spectrum,45 which were measured under the same experimental conditions.The Auger S KL2,3L2,3 spectra were obtained for the photon energies between 2470 eV and 2480 eV tuned in steps of 0.1 eV for thiophene and thiolane, and 0.2 eV for thiazole. This photon energy range stretches from below the S 1s → LUMO (lowest unoccupied molecular orbital) resonant excitation to beyond the S 1s ionisation threshold located around 2478 eV. The fine-tuning of the photon energy allows visualising the Auger spectra as 2D maps showing a continuous evolution of the Auger electron kinetic energy as a function of the photon energy. The X-ray absorption-like partial electron yield (PEY) spectra for sulfur K-edge were obtained by integrating the intensity of the 2D maps signal over electron kinetic energy.
4 Results and discussion
4.1 Absorption spectra
The experimental PEY and the calculated absorption spectra near the sulfur K-edge for thiolane, thiophene, and thiazole molecules are presented in Fig. 1. The calculated spectra were shifted by −3.2 eV for thiazole and −2.7 eV for thiophene and thiolane, respectively, to compare with the experimental spectra. The calculated vertical transitions were broadened with Voigt functions. The Lorentzian part of a Voigt function represents the lifetime broadening of the S 1s hole, 0.52 eV full-width at half-maximum (FWHM).46 The Gaussian part accounts for the experimental resolution and the broadening due to a possible nuclear motion in the core-excited states, which varies for different states.We start the discussion with the thiolane molecule (Fig. 1a). Thiolane can exist in the envelope (CS) and twisted (C2) enantiomeric forms, with the latter being the most stable one in the gas phase.47 The experimental PEY spectrum (green dots) shows an intense peak at the photon energy of 2472.6 eV and a shoulder at ≈2473.5 eV. These features are attributed in the calculated absorption spectrum to the S 1s → 12b* and S 1s → 14a* transitions for the twisted form (solid green line) and S 1s → 10a′′* and S 1s → 16a′* transitions for the envelope enantiomer (solid orange line). The natural orbitals are labelled in symmetry notation (see also Fig. 2). Our calculations show very similar results for transition energies in the two enantiomeric forms (see Table 1). Therefore, we will limit our further discussion to the most stable twisted enantiomer. The results for thiolane in the envelope enantiomeric form can be found in the ESI.†
The thiophene PEY spectrum is presented in Fig. 1b together with theoretical calculations. The experimental spectrum (blue dots) is dominated by a broad, barely resolved peak composed of the transitions from S 1sshell to the first two unoccupied molecular orbitals at the photon energies of 2473.2 eV and 2473.6 eV, which our calculations attribute to 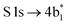 and
and 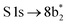 transitions, respectively. A similar unresolved peak composed of two overlapping transitions was earlier reported in thiophene S 1s NEXAFS around the photon energy of 2473.4 eV.48
transitions, respectively. A similar unresolved peak composed of two overlapping transitions was earlier reported in thiophene S 1s NEXAFS around the photon energy of 2473.4 eV.48
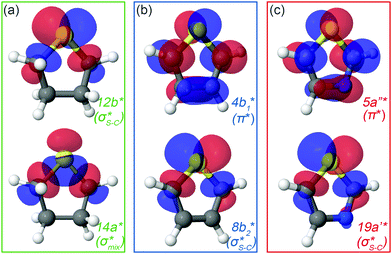 | ||
| Fig. 2 Natural orbitals obtained at the IS-MCSCF level for (a) thiolane in twisted conformation, (b) thiophene and (c) thiazole corresponding to S 1s → LUMO/LUMO+1 excitation. | ||
The dominant peak in the experimental PEY spectrum of thiazole (Fig. 1c) has a clear double-peak structure with the maxima at 2472.6 eV and 2473.2 eV, which we attribute to S 1s → 5a′′* and S 1s → 19a′* transitions, respectively.
Although the calculated absorption spectra agree quite well with the experimental PEY measurements for the two lowest absorption transitions, discrepancies are observed at higher excitation energies due to the limitations of the SA multiconfigurational approach applied to describe their electronic structure. Moreover, the appropriate description of these diffuse states with a mixed valence-Rydberg character requires a larger basis set than the one used in the present study. Here we focused our interest on the lowest absorption transitions as described below.
In the IS-MCSCF method, each core-excited state is described by a wave function which can be represented by a unique set of one-electron natural orbitals.49Fig. 2 shows the natural orbitals corresponding to the S 1s → V excitation in thiolane, thiophene and thiazole molecules, where V stands for LUMO or LUMO+1. Detailed information about the natural orbitals, such as their occupancies and irreducible representations can be found in ESI.†
For thiolane, the shapes of the obtained natural orbitals (Fig. 2a) allow us to assign the 12b* (LUMO) as the 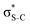 orbital. The 14a* (LUMO+1) in thiolane was previously assigned as
orbital. The 14a* (LUMO+1) in thiolane was previously assigned as 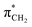 ,48 by an analogy with the transition observed in cyclic50 and non-cyclic51 alkanes. However, analysing the occupancy of the calculated natural orbitals, we can attribute it to an antibonding
,48 by an analogy with the transition observed in cyclic50 and non-cyclic51 alkanes. However, analysing the occupancy of the calculated natural orbitals, we can attribute it to an antibonding 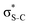 orbital with a mixed Rydberg character of s- and p-atomic orbitals from sulfur and the nearest carbon atoms, which we label as
orbital with a mixed Rydberg character of s- and p-atomic orbitals from sulfur and the nearest carbon atoms, which we label as 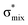 .
.
The same analysis for the 1s−1V excited states is presented in Fig. 2b and c for thiophene and thiazole, respectively. In both molecules, the LUMO and LUMO+1 are attributed to π* and 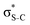 orbitals, respectively. Our assignment regarding thiophene agrees with the previous experimental study48 and is further confirmed by ΔSCF52 and PBE (Perdew–Burke–Ernzerhof) density functional53 calculations.
orbitals, respectively. Our assignment regarding thiophene agrees with the previous experimental study48 and is further confirmed by ΔSCF52 and PBE (Perdew–Burke–Ernzerhof) density functional53 calculations.
4.2 Auger KLL decay
The dominant relaxation mechanism of S* (1s−1V) core-excited states is the so-called KLL spectator Auger decay leading to a singly charged S (2p−2V) final state. Here two 2p electrons participate in the Auger decay, one filling in the S 1s core hole and the other one being ejected to the continuum. The S KLL Auger spectra for the three investigated molecules are presented in Fig. 3 as 2D maps showing Auger electron kinetic energies as a function of the incident photon energy. The intensity is represented by a colour scale. At the top of the 2D maps, above the S 1s ionisation threshold (around 2478 eV), one can observe the onset of normal KLL Auger lines. The kinetic energy of a normal Auger line is generally independent of the photon energy. However, close to the ionisation threshold, normal Auger lines are distorted and shifted to higher kinetic energy due to the presence of the post-collision-interaction (PCI) effect.54–56 The sloped curves below the ionisation threshold highlighted by the dashed lines around the photon energy of 2473 eV correspond to the resonant KLL spectator Auger decay.The S KLL normal Auger spectrum consists of three multiplet lines corresponding to the 1S, 1D, and 3P terms of 2p−2 final-state configuration. The strongest line of the multiplet 1D is highlighted by a solid blue line. Naturally, the multiplets of the normal Auger spectrum observed above the ionisation threshold are reproduced for every 2p−2V final state in the resonant Auger spectrum. However, due to the screening of the core by the spectator electron promoted to the valence molecular orbital V, the whole 2p−2V multiplet structure is shifted to higher kinetic energies by a so-called spectator shift. Generally, the higher the energy of the core-excited state 1s−1V with respect to the ground state, the smaller the spectator shift in the final state 2p−2V. This is illustrated in Fig. 3a for the case of thiolane. The multiplet structure of the resonant Auger spectrum with a spectator electron in a Rydberg state (photon energy ≈ 2475 eV) is only slightly blue-shifted with respect to the normal Auger spectrum, whereas the resonant Auger spectrum with a spectator electron in the 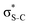 (LUMO) (photon energy = 2472.6 eV) has the largest spectator shift of around 8 eV compared to the normal Auger spectrum.
(LUMO) (photon energy = 2472.6 eV) has the largest spectator shift of around 8 eV compared to the normal Auger spectrum.
The situation is different, however, in thiophene and thiazole (Fig. 3b and c), where the largest spectator shift corresponds to the resonant Auger decay with the spectator electron in the σ*(LUMO+1). In contrast, the resonant Auger decay with the spectator electron in the π*(LUMO) manifests a smaller spectator shift. Such effect indicates that a rearrangement of the electronic structure in the process of resonant excitation and Auger decay in these molecules reverses the order of the first two excited states on the energy scale. For example, in the core-excited state of thiophene E(1s−1π*) < E(1s−1σ*), whereas in the final state E(2p−2π*) > E(2p−2σ*), where E is the energy of the state with respect to the ground state. The same inversion holds for thiazole. Consequently, for the Auger electron kinetic energies Ekin we observe that Ekin(1s−1π* → 2p−2π*) < Ekin(1s−1σ* → 2p−2σ*) in the spectra of both molecules.
The experimentally observed inversion of the excited states is supported by our high-level quantum-mechanical calculations. The IS-MCSCF calculations provide the energy values for the intermediate core-excited S 1s−1V and the final S 2p−2V electronic states that allow obtaining kinetic energy of Auger electrons as E(1s−1V) − E(2p−2V). Table 1 summarises the experimental and calculated energies of the core-excited and final states, the corresponding Auger electron kinetic energies, the electronic configurations, and the assignment of the orbitals involved. For the final 2p−2V states, the main electronic configurations of the states with the lowest energies (2p−2(3P)V) are shown; note that the 2pi−2V configurations with i = x, y, z do not contribute to these states.
The results of our calculations for all the investigated molecules corroborate the experimental observations. Comparing the calculated energy order for the first two core-excited states and for the corresponding final states in each of the molecules, we can observe that the order of these states is preserved in thiolane and reversed in thiophene and thiazole. This inversion is further reflected in the calculated resonant Auger electron kinetic energies, which qualitatively reproduce our experimental observations.
4.3 NBO analysis
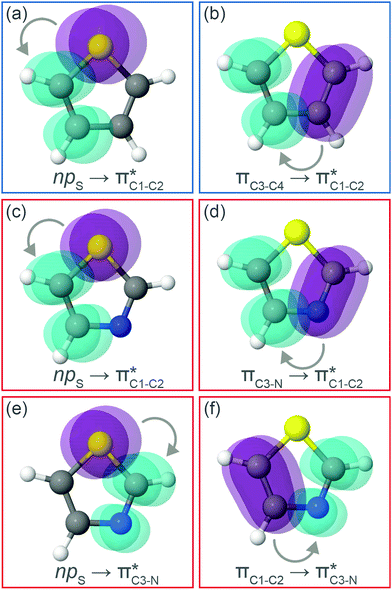
To understand why the energy order of the core-excited and final states reverses in the conjugated thiophene and thiazole molecules, we need to assess the role of π-conjugation and hyperconjugation effects in the electronic structure of these molecules. Such assessment has been done using the NBO method introduced briefly in Section 2. Considering the single-reference wave function required for this analysis, we applied the IS-ROHF approach to obtain the molecular orbitals related to the investigated excited states. The energies of core-excited and final states calculated at this level of theory qualitatively agree with IS-MCSCF results presented in Table 1.Let us first consider π-conjugation in the conjugated molecules, resulting from electron delocalisation over the donor lone pairs or π-NBOs and the acceptor π*-NBOs. Fig. 4 shows the donor–acceptor NBO interactions involved in π-conjugation in thiophene and thiazole in the electronic ground state. The acceptor NBOs (shown in Fig. 4 in cyan) are the antibonding 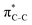 and
and 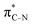 orbitals. Several donor NBOs must be considered. There are two lone pairs at the sulfur atom: one with a hybrid sp2-character oriented in the plane of the molecule and another one with a pure p-character (labelled “npS” in the following), which is oriented out of the plane of the molecule. One can expect, therefore, that only the interaction between the π*-NBO acceptor and the npS lone-pair donor can efficiently contribute to the stabilisation of the Lewis structure (see Fig. 4a, c and e), whereas the interaction with the sp2 lone pair is negligible. Another stabilising interaction occurs between the bonding πC–C and πC–N NBOs and the alternate antibonding π*-NBO (Fig. 4b, d and f).
orbitals. Several donor NBOs must be considered. There are two lone pairs at the sulfur atom: one with a hybrid sp2-character oriented in the plane of the molecule and another one with a pure p-character (labelled “npS” in the following), which is oriented out of the plane of the molecule. One can expect, therefore, that only the interaction between the π*-NBO acceptor and the npS lone-pair donor can efficiently contribute to the stabilisation of the Lewis structure (see Fig. 4a, c and e), whereas the interaction with the sp2 lone pair is negligible. Another stabilising interaction occurs between the bonding πC–C and πC–N NBOs and the alternate antibonding π*-NBO (Fig. 4b, d and f).
The stabilisation energies ΔE(2) obtained for the most relevant NBO interactions contributing to π-conjugation are presented in Table 2 for thiophene and thiazole in the ground, the intermediate S 1s−1π* and the final S 2p−2π* states. We see that the stabilisation energy values decrease between the ground and the intermediate core-excited states. The stabilisation is further reduced upon the relaxation to the final state via KLL spectator Auger decay. Particularly important is the stabilising interaction between the npS lone pair and the π*-NBO. In the ground state, this interaction results in a high stabilisation energy. The situation dramatically changes in the intermediate S 1s−1π* and the final S 2p−2π* states, where ΔE(2) decreases, respectively, by about a factor of five and a factor of ten compared to the ground state.
Our analysis shows that the observed weakening of stabilisation energy is related to the decrease of the off-diagonal NBO Fock matrix element Fda, which describes the overlap between the donor and acceptor NBOs, and the enhancement of the energy difference εa − εd between the donor and acceptor NBOs (see eqn (1)). Core excitation at the S 1s shell followed by KLL Auger decay leads to contraction of the electron density in the npS lone pair NBO and, consequently, to a weaker overlap with the acceptor π*-NBO. Meanwhile, the energy difference εa − εd between the donor and acceptor NBOs increases due to a relatively strong reduction of the localised npS orbital energy εd caused by the increased core charge. This trend indicates a significant reduction of π-conjugation in both thiophene and thiazole upon core excitation and Auger decay. The detailed information on the NBO orbital energy differences εa − εd and off-diagonal NBO Fock Matrix elements Fda for the investigated molecules can be found in the ESI.†
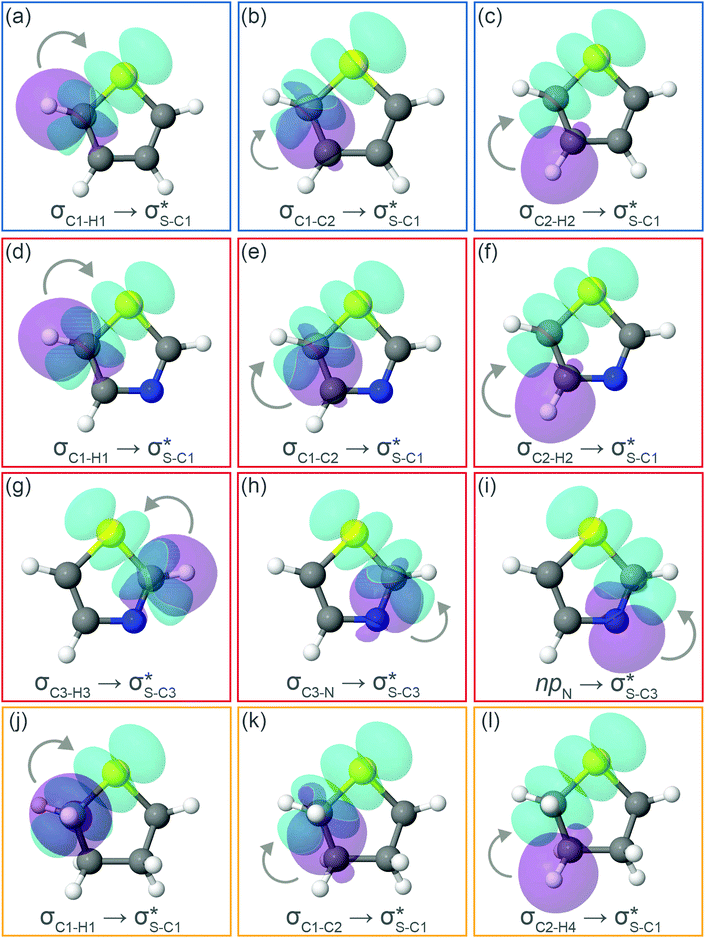
Now let us consider hyperconjugation. In the investigated molecules this effect results from electron delocalisation between the donor lone-pair or σ-NBOs and the acceptor σ*-NBOs. We focus our discussion on the interactions where the antibonding 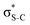 NBOs act as acceptors. The donor σ-NBOs include the geminal σC–C, σC–N and σC–H, as well as the vicinal σC–H. Furthermore, in thiazole, a nitrogen atom lone pair with a hybrid sp2-character (labeled “npN”) acts as a vicinal donor NBO. Fig. 5 shows the donor–acceptor NBO interactions involved in the discussed hyperconjugation interactions in thiophene, thiazole, and thiolane in the electronic ground state. In Fig. 5 the vicinal hyperconjugation interactions are shown in the right column, while the left and middle columns correspond to the cases of geminal hyperconjugation interactions.
NBOs act as acceptors. The donor σ-NBOs include the geminal σC–C, σC–N and σC–H, as well as the vicinal σC–H. Furthermore, in thiazole, a nitrogen atom lone pair with a hybrid sp2-character (labeled “npN”) acts as a vicinal donor NBO. Fig. 5 shows the donor–acceptor NBO interactions involved in the discussed hyperconjugation interactions in thiophene, thiazole, and thiolane in the electronic ground state. In Fig. 5 the vicinal hyperconjugation interactions are shown in the right column, while the left and middle columns correspond to the cases of geminal hyperconjugation interactions.
The stabilisation energies ΔE(2) for the most relevant NBO interactions contributing to hyperconjugation are presented in Table 3 for all the investigated molecules. In the ground state, stabilisation energy values are relatively low for all the considered NBO interactions. Specifically, the stabilisation energy is close to zero for the cases of geminal hyperconjugation where the electron delocalisation leads to weakening of the involved σ-bonds. In contrast, in the vicinal hyperconjugation interactions the non-zero stabilisation energies in the ground state result from the enhancement of the π-character of a bond between two σ-bonded adjacent atoms. Core excitation at the S 1s shell followed by spectator KLL Auger decay leads to a moderate increase in stabilisation energy values for the all the considered cases.
Our analysis shows that the observed enhancement of ΔE(2) is mainly caused by larger Fda values in the core-excited and final states compared to the ground state. Creation of a positive charge at the core of the S atom induces redistribution of electron density in the σS–C towards the S atom and in the donor σC–C and σC–H NBOs to the adjacent C atom. Since polarisation of the acceptor 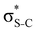 NBO is reversed with respect to the σS–C, its electron density shifts to the C atom. The described electron density redistribution leads to a stronger overlap between the donor σ and acceptor σ* NBOs and, consequently, larger Fda values.
NBO is reversed with respect to the σS–C, its electron density shifts to the C atom. The described electron density redistribution leads to a stronger overlap between the donor σ and acceptor σ* NBOs and, consequently, larger Fda values.
Additionally, a slight reduction of the energy difference εa − εd between the donor and acceptor NBOs, caused by a relative decrease of the acceptor 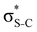 NBO energy εa due to the presence of the charged core of the S atom, further contributes to the observed increase of stabilisation energy. Therefore, we can conclude that the considered hyperconjugation interactions and the related stabilisation of the σ-orbitals are enhanced in the intermediate and the final states. In the conjugated molecules, the enhanced stabilisation leads to the decrease of the S 2p−2σ* final state energy with respect to the 2p−2π* state, thus contributing to the experimentally observed effect.
NBO energy εa due to the presence of the charged core of the S atom, further contributes to the observed increase of stabilisation energy. Therefore, we can conclude that the considered hyperconjugation interactions and the related stabilisation of the σ-orbitals are enhanced in the intermediate and the final states. In the conjugated molecules, the enhanced stabilisation leads to the decrease of the S 2p−2σ* final state energy with respect to the 2p−2π* state, thus contributing to the experimentally observed effect.
The hyperconjugation interactions occuring in the investigated molecules are not limited to the ones involving acceptor 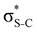 NBOs discussed above. For example, there exist vicinal hyperconjugation interactions between a sulfur-atom lone pair with a hybrid sp2-character (npS(sp2)), acting as a donor NBO, and the acceptor NBOs, such as
NBOs discussed above. For example, there exist vicinal hyperconjugation interactions between a sulfur-atom lone pair with a hybrid sp2-character (npS(sp2)), acting as a donor NBO, and the acceptor NBOs, such as 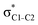 and, specifically for the thiazole molecule,
and, specifically for the thiazole molecule, 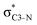 . The stabilisation energy values for these interactions (see ESI†) are relatively low in the ground state and further decrease towards the final state. Therefore, in contrast to the previously discussed cases, these hyperconjugation interactions reduce the stabilisation of the σ-orbital in the final states and do not contribute to the experimentally observed effect.
. The stabilisation energy values for these interactions (see ESI†) are relatively low in the ground state and further decrease towards the final state. Therefore, in contrast to the previously discussed cases, these hyperconjugation interactions reduce the stabilisation of the σ-orbital in the final states and do not contribute to the experimentally observed effect.
To summarise, our NBO analysis shows that in conjugated molecules, relaxation of the intermediate S 1s−1V state via resonant Auger KLL decay to the final S 2p−2V state is accompanied by a significant destabilisation due to reduced π-conjugation. Furthermore, several hyperconjugation interactions contribute to an enhanced stabilisation in the final states. The combination of both effects results in the experimentally observed inversion of the energy order for the core-excited and final states in thiophene and thiazole molecules.
We would like to note that although the stabilisation energy ΔE(2) is a useful notion to quantify the conjugation effects, it cannot be directly related to any physical observable and, therefore, cannot serve for quantitative comparison to the experimental and calculated values of electron transition energies. A systematic analysis of a series of molecules using the NBO method may establish a correlation between the stabilisation energy and an experimental observable of interest, as recently demonstrated in the analysis of electron delocalisation in a series of isolated capped peptides.57
5 Conclusions
We have demonstrated a novel application of resonant Auger spectroscopy as a probe of conjugation effects in core-excited aromatic molecules.High-resolution Auger sulfur KL2,3L2,3 2D maps for thiophene, thiazole, and thiolane molecules were recorded at the HAXPES end-station on the GALAXIES beamline at the synchrotron SOLEIL. Analysis of the experimental data in the conjugated thiophene and thiazole molecules shows that in the process of core excitation and resonant spectator Auger decay, the energy order of the first two core-excited states and the corresponding final states reverses. This effect is absent in thiolane, the saturated analogue of thiophene.
Our IS-MCSCF calculations assign the lowest core-excited states in the conjugated molecules as S 1s−1π* and 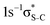 . The calculated electron transition energies reproduce the experimentally observed order inversion: in the intermediate state E(1s−1π*) < E(1s−1σ*), whereas in the final state E(2p−2π*) > E(2p−2σ*).
. The calculated electron transition energies reproduce the experimentally observed order inversion: in the intermediate state E(1s−1π*) < E(1s−1σ*), whereas in the final state E(2p−2π*) > E(2p−2σ*).
We attribute the observed effect to the fact that the stabilisation of the conjugated molecules resulting from π-conjugation and hyperconjugation is affected by the process of core-excitation and Auger decay. The NBO method allowed us to evaluate the stabilisation energy in the ground, the intermediate and the final states. A strong stabilising interaction between the sulfur p-type lone pair and the antibonding π*-NBOs in the ground state is found to be significantly reduced in the intermediate and final states, leading to destabilisation of the π-system. On the other hand, an enhanced stabilisation resulting from hyperconjugation interactions between the antibonding σ*-NBOs and the bonding σ-NBOs was found for the core-excited and final states with respect to the ground state. Therefore, a combination of both trends leads to the observed inversion of the energy order of the core-excited and the final states. We expect this phenomenon to be general and therefore applicable as a probe of conjugation in gas-phase molecules as well as in larger systems such as conjugated polymers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Experiments were performed on the GALAXIES beam line at SOLEIL Synchrotron, France (Proposal No. 99140034 and 99160043). We are grateful to the SOLEIL staff for smoothly running the facility. J. B. M and T. M. acknowledge financial support from the French Agence Nationale de la Recherche (ANR) through the ATTOMEMUCHO project (ANR-16-CE30-0001). C. E. V. M. and M. B. acknowledge funding from the WSPLIT project (ANR-17-CE05-0005-01). D. K. acknowledges support from LabEx MiChem, France, from the Swedish Research Council (VR) and the Knut and Alice Wallenberg foundation, Sweden. A. F. L. thanks the Brazilian funding agencies CAPES and CNPq for the support. M. L. M. R. thanks CNPq for financial support. We are grateful to Dr Valérie Brenner and Dr Nicolas Sisourat for useful discussions of the project.Notes and references
- R. S. Mulliken, C. A. Rieke and W. G. Brown, J. Am. Chem. Soc., 1941, 63, 41–56 CrossRef CAS
.
- I. V. Alabugin, K. M. Gilmore and P. W. Peterson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 109–141 CAS
.
- I. V. Alabugin, G. d. P. Gomes and M. A. Abdo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1389 Search PubMed
.
- S. W. Slayden and J. F. Liebman, Chem. Rev., 2001, 101, 1541–1566 CrossRef CAS PubMed
.
- E. Gloaguen, V. Brenner, M. Alauddin, B. Tardivel, M. Mons, A. Zehnacker-Rentien, V. Declerck and D. J. Aitken, Angew. Chem., Int. Ed., 2014, 53, 13756–13759 CrossRef CAS PubMed
.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS
.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS
.
- M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425 CrossRef CAS PubMed
.
- V. Myrseth, L. Saethre, K. Børve and T. Thomas, J. Org. Chem., 2007, 72, 5715–5723 CrossRef CAS PubMed
.
- O. Travnikova, S. Svensson, D. Céolin, Z. Bao and M. N. Piancastelli, Phys. Chem. Chem. Phys., 2009, 11, 826–833 RSC
.
- M. N. Piancastelli, T. Marchenko, R. Guillemin, L. Journel, O. Travnikova, I. Ismail and M. Simon, Rep. Prog. Phys., 2019, 83, 016401 CrossRef PubMed
.
- J. Luo, B. Hu, C. Debruler and T. L. Liu, Angew. Chem., Int. Ed., 2018, 57, 231–235 CrossRef CAS PubMed
.
- P. Hudhomme, EPJ Photovoltaics, 2013, 4, 40401 CrossRef CAS
.
- M. Eising, C. E. Cava, R. V. Salvatierra, A. J. G. Zarbin and L. S. Roman, Sens. Actuators, B, 2017, 245, 25–33 CrossRef CAS
.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed
.
- D. Bevk, L. Marin, L. Lutsen, D. Vanderzande and W. Maes, RSC Adv., 2013, 3, 11418–11431 RSC
.
- A. Facchetti, Chem. Mater., 2011, 23, 733–758 CrossRef CAS
.
- A. B. Rocha, J. Chem. Phys., 2011, 134, 024107 CrossRef PubMed
.
- J. Olsen, B. O. Roos, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1988, 89, 2185–2192 CrossRef CAS
.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS
.
- C. E. V. de Moura, R. R. Oliveira and A. B. Rocha, J. Mol. Model., 2013, 19, 2027–2033 CrossRef PubMed
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef
.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS
.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 756–763 CrossRef CAS PubMed
.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS PubMed
.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS
.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS
.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS
.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS
.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS
.
- L. R. Varas, L. H. Coutinho, R. B. Bernini, A. M. Betancourt, C. E. V. de Moura, A. B. Rocha and G. G. B. de Souza, RSC Adv., 2017, 7, 36525–36532 RSC
.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS
.
-
H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, http://www.molpro.net Search PubMed
.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS
.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed
.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CAS
.
- D.-C. Sergentu, T. J. Duignan and J. Autschbach, J. Phys. Chem. Lett., 2018, 9, 5583–5591 CrossRef CAS PubMed
.
-
F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, 2005 Search PubMed
.
- T. M. Krygowski and B. T. Stepien, Chem. Rev., 2005, 105, 3482–3512 CrossRef CAS PubMed
.
- C. C. J. Roothaan, Rev. Mod. Phys., 1960, 32, 179–185 CrossRef
.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS
.
- D. Céolin, J. Ablett, D. Prieur, T. Moreno, J.-P. Rueff, T. Marchenko, L. Journel, R. Guillemin, B. Pilette, T. Marin and M. Simon, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 188–192 CrossRef
.
- J.-P. Rueff, J. Ablett, D. Céolin, D. Prieur, T. Moreno, V. Balédent, B. Lassalle-Kaiser, J. Rault, M. Simon and A. Shukla, J. Synchrotron Radiat., 2015, 22, 175–179 CrossRef CAS PubMed
.
- L. Avaldi, G. Dawber, R. Camilloni, G. C. King, M. Roper, M. R. F. Siggel, G. Stefani and M. Zitnik, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 3953–3966 CrossRef CAS
.
- J. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS
.
- A. D. Boese and R. Boese, Cryst. Growth Des., 2015, 15, 1073–1081 CrossRef CAS
.
- A. P. Hitchcock, J. A. Horsley and J. Stöhr, J. Chem. Phys., 1986, 85, 4835–4848 CrossRef CAS
.
- P.-O. Löwdin and H. Shull, Phys. Rev., 1956, 101, 1730–1739 CrossRef
.
- A. P. Hitchcock, D. C. Newbury, I. Ishii, J. Stöhr, J. A. Horsley, R. D. Redwing, A. L. Johnson and F. Sette, J. Chem. Phys., 1986, 85, 4849–4862 CrossRef CAS
.
- A. P. Hitchcock and I. Ishii, J. Electron Spectrosc. Relat. Phenom., 1987, 42, 11–26 CrossRef CAS
.
- S. Behyan, Y. Hu and S. G. Urquhart, J. Chem. Phys., 2013, 138, 214302 CrossRef PubMed
.
- G. N. George, M. J. Hackett, M. Sansone, M. L. Gorbaty, S. R. Kelemen, R. C. Prince, H. H. Harris and I. J. Pickering, J. Phys. Chem. A, 2014, 118, 7796–7802 CrossRef CAS PubMed
.
- M. U. Kuchiev and S. A. Shenerman, Sov. Phys. Usp., 1989, 32, 569–587 CrossRef
.
- V. Schmidt, Rep. Prog. Phys., 1992, 55, 1483–1659 CrossRef CAS
.
- R. Guillemin, S. Sheinerman, R. Püttner, T. Marchenko, G. Goldsztejn, L. Journel, R. K. Kushawaha, D. Céolin, M. N. Piancastelli and M. Simon, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 012503 CrossRef
.
- V. Brenner, E. Gloaguen and M. Mons, Phys. Chem. Chem. Phys., 2019, 21, 24601–24619 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05910f |
| ‡ Present address: Advanced Photon Source, Argonne National Laboratory, 9700 S. Cass Ave, Lemont, IL 60439, USA. E-mail: jbarbosamartins@anl.gov |
| § Present address: Center for Free Electron Laser Science, Deutsches Elektronen-Synchrotron DESY, Notkestrasse 85, 22607 Hamburg, Germany. |
| This journal is © the Owner Societies 2022 |