Open Access Article
Open Access ArticleMagnetic nature and hyperfine interactions of transition metal atoms adsorbed on ultrathin insulating films: a challenge for DFT†
Sergio
Tosoni
 * and
Gianfranco
Pacchioni
* and
Gianfranco
Pacchioni

Dipartimento di Scienza dei Materiali, Università di Milano-Bicocca, Via Roberto Cozzi 55, 20125 Milan, Italy. E-mail: sergio.tosoni@unimib.it
First published on 15th June 2022
Abstract
The magnetic ground state and the hyperfine coupling parameters of some first-row transition metal (TM) atoms (Ti, Cr, Mn, Fe, Co, and Ni) adsorbed on ultrathin insulating oxide films are studied by means of DFT calculations. The results obtained using GGA, screened hybrid, and GGA+U functionals are compared for TMs adsorbed on free-standing MgO(100). Then, the case of adsorption on MgO mono- and bilayers supported on Ag(100) is studied using GGA+U. Along with the problematic aspects inherent to the calculation of hyperfine coupling constants, a critical dependence on the magnetic state and electron configuration of the TM is reported, which implies a real challenge for the state-of-the-art DFT methods. In the cases where all functionals considered provide a coherent magnetic and electron configuration, however, the calculated hyperfine parameters do not depend significantly on the choice of the functional. In this respect, the role of the metal support in the hyperfine coupling constants is highly system-dependent and becomes crucial in all cases where the support modifies the oxidation state of the adatom, induces a change in the bonding site or simply induces a rearrangement of the orbital energy diagram. This has important implications for the modelling of single TM atoms deposited on insulating ultrathin films supported on metals for application in quantum technologies or as memory devices.
1. Introduction
In the last decade great advances have been made in the study of isolated transition metal atoms deposited on the surface of an inert support.1,2 There are various reasons why these species are attracting increasing interest. In catalysis, metal atoms stabilized on a support constitute a new class of single atom catalysts, where the catalytic activity is related to the presence of specific isolated active sites.3–5 The adsorption, diffusion, and nucleation of single metal atoms on inert surfaces are on the basis of the nucleation and growth of supported nanoclusters or nanoparticles,6 and the evolution of these aggregates as a function of temperature. This depends on the spill-over of individual atoms from small metal aggregates to large ones, a diffusion mediated process known as Ostwald ripening.7An area where impressive progress has been made is in the study of supported metal atoms as potential units to store or manipulate information. Engineering and fabrication of single atomic or molecular spins is of key importance for emerging quantum technologies. Combining high-resolution scanning tunneling microscopy (STM) with accurate single site electron paramagnetic resonance (EPR) measurements has opened the way towards the possible realization of quantum devices where the coupling between the magnetic atoms and the support is used to encode information.8–10
To this end, transition metal atoms have been deposited on “inert” supports, usually consisting of an ultrathin layer of an insulating material (MgO, h-BN, and NaCl) grown on a metal single crystal. It is useful to remind why this kind of support is used. First of all, there is the necessity to decouple the electronic wave function of the deposited atoms from that of the support, something that is almost impossible when the support is metallic and that requires an insulating buffer layer. On the other hand, STM can only be used in connection with conductive supports. The idea to grow ultrathin layers of an insulator, usually an oxide, on a metal to study the properties of supported species goes back to the early 1990s when it was introduced to study at the atomistic level the structure of model catalysts consisting of supported metal particles.11–13 We will see below that 30 years of work in this area have shown that the ultrathin films are not entirely decoupling the supported species from the underlying metal surface, and that in specific cases electron exchange via direct tunneling is possible, with consequent changes of the properties of the supported metals.14 In this respect, ultrathin layers represent a new class of materials with properties that may differ significantly from those of the corresponding bulk materials.15
The idea of using isolated TM atoms to encode information is closely connected with their magnetic properties. The development of single-atom EPR has opened the way towards the study of isolated magnetic impurities or adsorbates. This is remarkable as conventional EPR studies on chemical species require spins of the order of 1010 in order to produce a measurable signal.16 Conventional EPR is an extremely sensitive technique in terms of impurity species, but it cannot be used in the context of isolated, single-atom species.
When magnetic metal atoms are deposited on a surface, their hyperfine interactions can change substantially due to the polarization of the (n + 1)s and nd orbitals that follows the formation of a bond to the support. Au atoms deposited on the (100) surface of a MgO single crystal result in a strong decrease of the isotropic component of the hyperfine coupling constant due to s–d hybridization.17 For K atoms deposited on polycrystalline MgO the shift in spin density is so pronounced that in the past the change from the gas-phase to adsorbed K atoms has been interpreted as the result of a net charge transfer to the oxide, with the formation of EPR silent K+ ions. In contrast, combined EPR and theoretical calculations based on density functional theory (DFT) have shown that there is no charge transfer in K/MgO, but only spin polarization with strong reduction of the isotropic part of the hyperfine constant.18 These two examples show that the bonding of a free metal atom to a surface can change, also substantially, its magnetic properties.
When the support consists of ultrathin films 2–3 atomic layers thick, other phenomena can take place related to spontaneous electron tunneling. For instance, in a recent EPR study of single iron phthalocyanine [FePc] molecules deposited on MgO/Ag(100) ultrathin films, it has been found that while this molecule possesses a spin S = 1 in the bulk or on several surfaces, it has a spin S = ½ on this support.19 The molecule becomes negatively charged, [FePc]−, due to the spontaneous transfer of one electron from the “insulating” support, according to a mechanism proposed long ago for the case of Au atoms on MgO/Ag(100) films.17 The mechanisms underlying the electron exchange and ways to control it have been recently discussed by Sterrer and coworkers in the context of a study of pentacene molecules adsorbed on MgO/Ag(100) films.20
There are also more dramatic examples of the interaction of TM atoms with ultrathin insulating layers. Cr or Co atoms deposited by soft-landing on two layers of NaCl supported on Au(111) result in the spontaneous incorporation of TM atoms into the NaCl film resulting in the substitutional doping of the insulating layer.21,22 These examples demonstrate that the interaction of TM atoms with two-dimensional insulating films can result in complex interactions that modify the nature of the adsorbed species or of the support.
Modeling these systems with first principles calculations is important for various reasons.23 First of all, DFT calculations provide reliable information about the interaction of metal atoms with the surface (adsorption sites, stability, charge state, etc.). Then, one can study the nature of the ground state, magnetic or not, and the formal occupation of the s, p, and d states; if this results in hyperfine interactions, these can be compared with experimental measurements now available, thanks to the impressive advances mentioned above. An important caveat concerning the magnetic properties of adatoms calculated using DFT should be mentioned: Kohn–Sham orbitals are not eigenfunctions of the total spin operator, but only of its z-component.24,25 However, the former is an experimental observable, while the latter is not. The other aspect where theory can provide important insight is into the nature of the support, totally inert, partly interacting, or strongly bound to the adsorbed metal species. All these aspects need to be treated at a high-level of theory, as the competition between different electronic configurations for an adsorbed TM atom may depend on the level of theory used, in particular if one is interested in spin properties. Commonly used DFT functionals (based on the Generalized Gradient Approximation, GGA) tend to delocalize unpaired electrons or holes, due to the severe underestimation of the band gap.26 For this reason, the study of trapped charges in semiconductors or insulators requires self-interaction corrected functionals, such as the DFT+U approach or hybrid exchange–correlation functionals. For all these reasons, the study of isolated TM atoms on a support by means of DFT calculations is not only interesting but also challenging.27
This is not the first DFT study of TM atoms on a support and of their magnetic properties. The trends in the hyperfine interactions of a series of adatoms on MgO, NaCl, h-BN, and Cu2N have been recently investigated using GGA by Shehada et al.28 With respect to this study, our work presents two new aspects: (1) the calculations have been performed using self-interaction corrected functionals (both hybrid and DFT+U methods); and (2) the role of the metal support has been explicitly considered by modeling MgO 1–2 layer films on Ag(100) and comparing the results with those obtained on a 3-layers thick MgO slab that properly represents a MgO single crystal. The problem of the magnetic nature of TM atoms on oxide surfaces has been addressed also in other studies. Trends in the bonding of TM to MgO, the preferred adsorption sites (O-top, cation top, and bridge site) and the ground state of the TM adatom have been discussed in the past.29–35
This paper is structured as follows: in Section 2 the adopted computational methodology is described. In Section 3.1, the results obtained using GGA, screened-hybrid, and GGA+U functionals for TM bound to MgO(100) are compared and assessed. In Section 3.2, the case of TM adsorbed on metal-supported mono- and bilayers is discussed. A final discussion is summarized in Section 4.
2. Computational details
Density functional theory (DFT) spin-polarized calculations are carried out with the code VASP 6.36,37 The potentials are adopted according to the Projector Augmented Wave scheme.38,39 The O (2s, 2p), Mg (2p, 3s), and Ag (4d, 5s) states are treated explicitly. For the first-row transition metal adatoms, small-core potentials are adopted, including (3p, 3d, 4s) states. Two different functionals are adopted: the Perdew, Burke and Ernzerhof exchange and correlation functional,40 within the Generalized Gradient Approximation (GGA), and the screened hybrid Heyd, Scuseria and Ernzerhof HSE06 functional.41 Long-range dispersion is included according to the D3 approach from Grimme, applying the Becke–Johnson damping function.42,43 A kinetic energy cutoff of 400 eV is adopted. Convergence criteria of 10−5 eV and 10−2 eV Å−1 are used to truncate the electronic and ionic loops, respectively.The free-standing MgO(100) surface is modelled with a 3√2 × 3√2 supercell of a three-layer slab. The reciprocal space sampling reduces to Γ point. The MgO/Ag interface is built as discussed in previous papers,44 assuming a coincidence between MgO(100) √2 × √2R45° and Ag(100) (1 × 1). Oxygen atoms are put in registry with the underlying Ag atoms, while the Mg atoms occupy hollow positions. The MgO thickness varies from one (monolayer, ML) to two atomic layers (bilayer, BL). The Ag support is modelled with a 4-layer thick slab, where the atoms from the bottom layer are frozen into their bulk positions, while the positions of all other atoms are relaxed. In order to ensure high dilution of the adsorbed adatoms, a 4 × 4 supercell is adopted. The reciprocal space is sampled with a Γ-centred 2 × 2 × 1 mesh of K-points.
The adsorption energy (Eads) is calculated as the energy of the adsorbed adatom with respect to the clean surface and the gas-phase transition metal atom in its magnetic ground state. Two aspects need to be mentioned to the readers in this respect: (i) DFT provides broken-symmetry solutions where the d-orbitals manifold is no longer degenerate, and also the spin symmetry is affected and (ii) a remarkable dependence of the calculated adsorption energy from the specific functional adopted has been previously reported, for instance in the case of Cu atoms on MgO.45
The magnetic properties of gas-phase and adsorbed TMs are described reporting two quantities: the number of unpaired electrons in the atomic orbitals (Nα–Nβ), as derived from the integration of the projected density of states, and the estimated electron configuration.
The main structural and electronic parameters of the MgO/Ag interface, calculated with PBE+D3 and HSE06+D3, are summarized in the ESI,† Table S1. GGA accurately describes the Ag work function, while HSE06 incurs a remarkable underestimation. This may affect the charge transfer phenomena determining the electronic and magnetic properties of any adsorbate on metal-supported oxide films. The difficulties of hybrid functionals in treating metallic systems have been discussed in the past,46 and the screened hybrid functionals, such as HSE06, partly mitigate the problem but, as shown also here, a certain inaccuracy remains. On the other hand, however, the critical failure of GGA in describing electronic and magnetic properties of transition metal oxides has been widely documented in the literature, as discussed in the previous section. A partial solution to this problem consists of the use of the DFT+U approach, where the U correction is applied only to specific sub-sections of the system of interest. Here we adopt the following three-step approach:
1. The magnetic ground state of the adatom on free-standing MgO is determined with HSE06.
2. The converged wave function is used as a starting input for the self-consistent determination of the Hubbard parameter U47–49 to be applied to the 3d orbitals of the adatom.
3. The self-consistently determined U is used as an onsite potential on the adatom adsorbed on metal supported MgO films, where the MgO/Ag interface is treated with bare GGA.
It must be pointed out that the self-consistent determination of U is not a variational process, and therefore one cannot claim that this value is exact. However, it depends only on the electronic structure of the transition metal adatom on MgO calculated with the best method available here, namely HSE06, without any empirical input, which ensures a certain robustness to this approach.
The self-consistently determined Hubbard parameters for all transition metal adatoms are reported in Table 1. A careful assessment of this approach with respect to the hybrid HSE06 is performed for all adatoms adsorbed on MgO 3L in Section 3.1.
We studied the hyperfine interactions of the electron spin with the nuclear spin of the TM. In fact, also the hyperfine parameters of the neighboring 17O nuclides contain some relevant information on how the spin density spills over to the support when the TM atom is adsorbed on MgO. However, for the sake of conciseness, we did not include this information in the paper. The hyperfine spin-Hamiltonian, Hhfc = S·A·I, is given in terms of the hyperfine matrix A which describes the coupling of the electron with the nuclear spin.51 The components of A can be represented as:
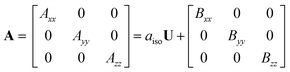 | (1) |
| aiso = (2μo/3)gNβNgeβe〈ρs〉 | (2) |
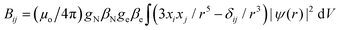 | (3) |
We use the nuclear gyromagnetic factor, gN, experimentally determined,50 as reported in Table 1.
The approach has been preliminarily tested with PBE with respect to previous experimental and computational data for some isolated atoms, Table 2. We start the analysis for a series of light non-metallic elements (H, B–F). For the second row series B–F, post Hartree–Fock calculations of the hyperfine parameters have also been recently published.52 Then, we extend the analysis to the series of alkali metals (Li–Rb), and we finally consider two elements from group 11 (Cu and Au), for which fully relativistic all-electron calculations were previously presented.53 Overall, it appears that the PBE-PAW approach adopted in this paper yields reasonably accurate results for atoms displaying large aiso (e.g. H, Na, Rb, Cu, and Au), in spite of the various approximations implied.54 Notably, F is as well a critical case. However, the method becomes much less reliable if one deals with atoms displaying smaller isotropic hyperfine constants. This is not surprising, if one considers that hyperfine parameters depend on electron–nucleus interactions, where the description of the shielding effect and polarizability of the core electrons play a role. Here, we rely on PAW potentials to describe core electrons within the plane-wave approach, whose strength lies in the possibility to efficiently treat adatoms and insulating films supported on conductive substrates. It must be noticed, however, that a strong dependence on the method and the basis set is reported also in the case of sophisticated post-Hartree–Fock calculations for the (B–F) series.52
| Calculated aisoa (MHz) | Experimental aiso (MHz) | ||
|---|---|---|---|
| a Present work. b Ref. 55. c Ref. 56. d Ref. 57. e Ref. 58. f Ref. 59. g Ref. 60. h Ref. 61. i Ref. 62. j Ref. 63. k Ref. 64. | |||
| Non-metals | H | 1429.8 | 1420.4b |
| B | 45.8 | 11.6,c 18.6d | |
| C | 82.3 | 19.5,e 22.5f | |
| N | 40.3 | 10.5g | |
| O | 117.4 | −34.5h | |
| F | 1034.2 | 301.7h | |
| Alkali metals | Li | 300.5 | 400.8b |
| Na | 885.8 | 885.8b | |
| K | 112.4 | 229.8b | |
| Rb | 900.9 | 1011.7b | |
| Transition metals | Cu | 6452.9 | 5867i |
| Au | 3079.4 | 3053,j 3138k | |
Being aware of this limitation, we focus the discussion on the effect of the substrate on the magnetic and hyperfine properties of the adatoms, rather than on their accurate prediction, which seems to be a task that may require high levels of theory beyond DFT.
To this end, it is important to compare the experimental results and calculations also in the case of a supported single atom, as we do for Au and Au1/MgO(100) system, Table 3. For the free Au atom, we compare our data calculated with PBE and HSE06 functionals to previous computational data calculated with a slightly different GGA functional (PW91),17 also including the spin orbit coupling, as well as to the experimental value.17 Overall, all these computational approaches provide a reasonably good estimate of aiso, with deviations smaller than 10% with respect to the experiment. Experimentally, a small anisotropic component b is also reported (26 MHz), which is not reproduced by any computational result, where the isolated atom has a spherical symmetry. The most relevant change induced by the adsorption on MgO is a large decrease of the isotropic constant, from 3138 to 1405 MHz. The anisotropic component almost vanishes (2.7 MHz). All calculations correctly predict the strong decrease of aiso, with a variable quantitative agreement with the experiment. The data from the present work seem to overperform those presented in ref. 17, with both PBE+D3 and HSE06+D3 within 100 MHz from the experiment. The very small value of b is hard to reproduce for all computational approaches.
| a iso (MHz) | b (MHz) | ||
|---|---|---|---|
| a Ref. 17. b Ref. 64. c Mg21O21 cluster model. d Present work, (3√2/2 × 3√2/2)R45°, 3L slab model. e Single point with HSE06 at the PBE+D3 geometry, present work. f Full relaxation with HSE06+D3, present work. | |||
| Free Au1 | PW91+ SOa | 3015 | — |
| PBE | 3079 | — | |
| HSE06 | 2908 | — | |
| Experimentb | 3138 | 26 | |
| Au1/MgO(100) | PW91+SOac | 1704 | 7.3 |
| PBE+D3d | 1426 | 11.3 | |
| HSE06+D3de | 1494 | 9.8 | |
| HSE06+D3df | 1508 | 10.1 | |
| Experimenta | 1405 | 2.7 | |
3. Results and discussion
3.1 MgO(100)
In this section we discuss the adsorption of Ti, Cr, Mn, Fe, Co, and Ni adatoms on a three-layer MgO(100) slab that well represents the bare MgO surface. For each atom, we compare the results with PBE+D3, HSE06+D3 and PBE+Usc+D3. At first, a scan of several possible adsorption sites has been performed with PBE+D3 and HSE06: oxygen-top (T), bridge (B) and Mg-top (M) (here we denote as bridge the Mg–Mg or O–O bridge site, that in other studies is classified as hollow). In all cases, the most stable adsorption site on MgO 3L is T, for all the considered adatoms. On the supported films, on the contrary, a certain variability is observed (vide infra). For the T adsorption site, the calculations have then been repeated also with PBE+U.In the case of Ti, Table 4, the adsorption energy, Eads, decreases almost by a factor of two passing from PBE+D3 (−2.20 eV) and HSE06+D3 (−1.67 eV) to PBE+Usc + D3 (−1.10 eV). Conversely, the Ti–O and Ti–Mg distances follow the opposite trend. Notably, only in the case of PBE+Usc+D3 a small tilt (2.8°) of the adatom with respect to the O lattice site is found. Conversely, the predicted Ti–O distance is significantly larger compared to the other functionals.
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| a Tilted by 2.8°. | |||||||||
| Free Ti | PBE | — | — | — | — | 2.0 | 4s2 3d2 | 48.4 | — |
| HSE06 | — | — | — | — | 2.0 | 4s2 3d2 | 48.7 | — | |
| PBE+Usc | — | — | — | — | 2.0 | 4s2 3d2 | 52.2 | — | |
| Ti1/MgO(100) | PBE+D3 | T | −2.20 | 1.85 | 3.04 | 2.0 | 4s2 3d2 | 45.9 | 6.3 |
| HSE06+D3 | T | −1.67 | 1.95 | 3.09 | 2.0 | 4s2 3d2 | 45.6 | 25.7 | |
| PBE+Usc+D3 | Ta | −1.10 | 2.14 | 3.17 | 2.0 | 4s2 3d2 | 55.6 | 30.6 | |
The magnetic properties of the Ti atom, both in the gas-phase and adsorbed on MgO(100), are reported in Table 4. For the gas-phase atom, all functionals report a triplet ground state, corresponding to the 4s2 3d2 electron configuration. The Fermi contact term, aiso, is very similar, 48.4 MHz (PBE), 48.7 MHz (HSE06) and 52.2 MHz (PBE+Usc). The situation for Ti1/MgO, Table 4, does not report big changes with respect to the free Ti atom. A triplet ground state (4s2 3d2) is forecasted using all three functionals, similar to what was previously reported.32 The Fermi contact term is also quite similar, varying from 45.9 MHz for PBE, to 45.6 MHz for HSE06 and 55.6 MHz for PBE+U. The anisotropic term, b, is almost negligible for PBE (6.3 MHz) and remarkably larger for HSE06 (25.7 MHz) and PBE+U (30.6 MHz).
In the case of Cr1/MgO, Table 5, the three functionals considered behave similarly to what was observed for Ti, as far as the trends in terms of adsorption energy (PBE > HSE06 > PBE+U) and bond distances (PBE < HSE06 < PBE+U) are concerned.
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| Free Cr | PBE | — | — | — | — | 6.0 | 4s1 3d5 | 149.3 | — |
| HSE06 | — | — | — | — | 6.0 | 4s1 3d5 | 140.4 | — | |
| PBE+Usc | — | — | — | — | 6.0 | 4s1 3d5 | 141.5 | — | |
| Cr1/MgO(100) | PBE+D3 | T | −0.93 | 1.90 | 3.01 | 4.0 | 4s2 3d4 | 33.3 | 2.2 |
| HSE06+D3 | T | −0.63 | 1.94 | 3.02 | 4.0 | 4s2 3d4 | 26.4 | 1.8 | |
| PBE+Usc+ D3 | T | −0.33 | 2.01 | 3.08 | 4.0 | 4s2 3d4 | 30.6 | 2.0 |
For the isolated Cr atom, Table 5, all functionals report the same magnetic ground state (septuplet, 4s1 3d5) and very similar Fermi contact terms: 149.3 MHz (PBE), 140.4 MHz (HSE06) and 141.5 MHz (PBE+U). A quenching of the magnetic state to quintuplet, 4s2 3d4, is predicted by all functionals upon adsorption of Cr on MgO. It is worth noting that Cr maintains a neutral state on the surface, and the change in the magnetic ground state is simply due to the splitting of the 3d manifold as a consequence of the overlap with the orbitals of the substrate. The Fermi contact term depends drastically on the 4s occupation, and sensibly decreases if a 4s2 state is reached, as predicted by all three functionals (Table 5). The anisotropic term, b, is small for all three functionals.
In the case of Mn (Table 6), the adatom is adsorbed with Eads varying between −1.17 eV (PBE+D3), −0.97 (HSE06+D3) and −0.60 eV (PBE+U+D3). The magnetic ground state is always a sextuplet, but a small polarization of the support is reported for HSE06 (the integral of the charge population of the Mn orbitals yields 4.96 electrons) and PBE (4.91), Table 6.
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| Free Mn | PBE | — | — | — | — | 5.0 | 4s2 3d5 | 277.8 | — |
| HSE06 | — | — | — | — | 5.0 | 4s2 3d5 | 270.1 | — | |
| PBE+Usc | — | — | — | — | 5.0 | 4s2 3d5 | 282.0 | — | |
| Mn1/MgO(100) | PBE+D3 | T | −1.17 | 2.01 | 3.08 | 4.9 | 4s2 3d5 | 321.6 | 1.7 |
| HSE06+D3 | T | −0.97 | 2.07 | 3.12 | 5.0 | 4s2 3d5 | 284.8 | 0.5 | |
| PBE+Usc+ D3 | T | −0.60 | 2.24 | 3.23 | 5.0 | 4s2 3d5 | 312.2 | −0.6 |
The analysis of the hyperfine properties for the free Mn atom (Table 6) reveals a substantial agreement between all three functionals (the differences related to the adopted functional are within 12 MHz). No substantial change is reported for the adatom's magnetic ground state upon adsorption on MgO(100) in terms of charge state, spin multiplicity or electron configuration. However, the small spin polarization previously described in the case of PBE induces a larger increase (around 10%) of the calculated aiso compared to the free adatom's case. The anisotropic b term is close to zero, similarly to what was observed for Cr.
Moving to the case of Fe, Table 7, a trend analogous to the previous cases in terms of adsorption energy and bond distances as a function of the adopted functional is observed. It is worth noting, however, that the larger affinity of Fe for oxygen, compared to other metals, translates into larger Eads and smaller adatom–oxygen distances, Table 7. As far as the magnetic properties of Fe are concerned, a quintuplet magnetic state corresponding to a 4s2 3d6 occupation is obtained with HSE06 and PBE+U. PBE, instead, provides a solution where 3d and 4s states are strongly mixed, preserving thus the total spin multiplicity, but at the price of a strong orbital contamination. Notably, the Fermi contact term calculated with PBE (93.7 MHz) is more than twice that calculated with HSE06 (39.5 MHz) and PBE+U (45.9 MHz). Overall, the case of Fe1/MgO looks simpler than the free Fe atom, since all three functionals provide an analogous solution in terms of spin multiplicity and electron configuration, which also implies a substantial agreement for aiso (52.5 MHz with PBE, 44.5 MHz with HSE06 and 45.9 MHz for PBE+U) and b, very small in all cases.
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| Free Fe | PBE | — | — | — | — | 4.0 | 4s1.5 3d6.5 | 93.7 | — |
| HSE06 | — | — | — | — | 4.0 | 4s2 3d6 | 39.5 | — | |
| PBE+Usc | — | — | — | — | 4.0 | 4s2 3d6 | 40.4 | — | |
| Fe1/MgO(100) | PBE+D3 | T | −1.80 | 1.89 | 2.96 | 3.9 | 4s2 3d6 | 52.5 | −3.7 |
| HSE06+D3 | T | −1.35 | 1.92 | 2.98 | 3.9 | 4s2 3d6 | 44.5 | −4.5 | |
| PBE+Usc+D3 | T | −0.94 | 2.01 | 3.06 | 4.0 | 4s2 3d6 | 45.9 | −5.5 |
The case of Co is quite peculiar. As shown in Table 8, the adsorption energy obtained with HSE06+D3 is larger compared to PBE, in spite of larger Co–O and Co–Mg distances. This can also be related to the difficulties of PBE in getting the right magnetic ground state for the Co atom, vide infra. As observed in the other cases, PBE+U yields remarkably smaller Eads, even though the Co–O and Co–Mg distances are comparable.
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| a Excited state by 0.31 eV. | |||||||||
| Free Co | PBE | — | — | — | — | 3.0 | 4s1 3d8 | 1111.0 | — |
| PBEa | — | — | — | — | 3.0 | 4s2 3d7 | 309.4 | — | |
| HSE06 | — | — | — | — | 3.0 | 4s2 3d7 | 302.9 | — | |
| PBE+Usc | — | — | — | — | 3.0 | 4s2 3d7 | 310.0 | — | |
| Co1/MgO(100) | PBE+D3 | T | −1.58 | 1.84 | 2.90 | 2.8 | 4s1 3d8 | 560.0 | −47.5 |
| HSE06+D3 | T | −1.74 | 1.93 | 2.93 | 2.9 | 4s1 3d8 | 489.4 | 34.6 | |
| PBE+Usc+D3 | T | −0.87 | 1.89 | 2.94 | 2.9 | 4s1 3d8 | 620.0 | −47.3 | |
In Table 8 the magnetic properties of free- and MgO-adsorbed Co atoms are reported. It can be seen that, for the free atom, PBE reports a different electron configuration (4s13d8) compared to HSE06 and PBE+U (4s23d7). This reflects in a very large Fermi contact term with PBE (1111.0 MHz) with respect to HSE06 (302.9 MHz) and PBE+U (310.0 MHz). If the calculation of free Co with PBE is forced to the same 4s2 3d7 electron configuration obtained with HSE06 and PBE+U, also aiso becomes relatively close to what was obtained with the other functionals (309.4 MHz), Table 8. Upon adsorption on MgO, all functionals predict a rearrangement to a 4s1 3d8 configuration, with a net magnetization between 2.8 (PBE) and 2.9 (HSE06 and PBE+U), indicating a certain transfer of spin polarization to the O atom bound to the TM atom. The Fermi contact shows a strong increase with respect to the free Co atom in (4s23d7) configuration up to 560.0 MHz (PBE), 489.4 MHz (HSE06) and 620.0 MHz (PBE+U). The anisotropic constant, b, is larger in absolute value compared to the previous cases, and varies between −47 MHz (PBE and PBE+U) and 34.6 MHz (HSE06).
The last case examined is Ni. The adsorption energy is much larger for PBE+D3 (−2.15 eV) compared to HSE06+D3 (−1.33 eV) and PBE+U+D3 (−1.19 eV), Table 9. PBE also gives a shorter Ni–O bond distance (1.79 Å) compared to the other functionals. The discrepancy of PBE compared to HSE06 and PBE+U is even more drastic if one considers the magnetic properties of nickel on MgO, Table 9. While for the free atom a substantially coherent picture is obtained comparing the three functionals (triplet magnetic ground state corresponding to a 4s13d9 electron configuration and very large Fermi contact varying between 996.0 MHz for PBE and 940.2 MHz for HSE06), in the case of Ni/MgO(100) we assist to a severe failure of PBE; this functional, indeed, predicts that the Ni atom maintains a neutral charge state, but rearranges to a closed-shell 4s03d10 electron configuration, implying a diamagnetic character of the TM atom. This prediction is not confirmed by the hybrid HSE06+D3 functional, where the Ni adatom maintains a paramagnetic 4s13d9 open-shell singlet configuration, with a large residual Fermi contact term of 820.9 MHz. The low-spin open shell configuration was already determined as the ground state for hybrid functional calculations on Ni1/MgO.32 The PBE+U functional substantially agrees with the higher-quality hybrid HSE06, yielding an open-shell singlet configuration with an aiso term as large as 872.1 MHz. The anisotropic b term is not negligible (34.3 MHz for HSE06 and 37.5 MHz for PBE+U). The standard GGA approach, thus, fails to identify the magnetic nature of adsorbed Ni atoms, as previously reported.30 The complexity of Ni is related to the specific nature of this atom, where the 4s23d8 (3F) and 4s13d9 (3D) atomic configurations are separated by 25 meV only, while the closed shell 4s03d10 (1S) configuration is 1.82 higher in energy.65
| Method | Site | E ads (eV) | R O (Å) | R Mg (Å) | N α–Nβ | El. Conf. | a iso (MHz) | b (MHz) | |
|---|---|---|---|---|---|---|---|---|---|
| a Open shell singlet. | |||||||||
| Free Ni | PBE | — | — | — | — | 2.0 | 4s13d9 | 996.0 | — |
| HSE06 | — | — | — | — | 2.0 | 4s13d9 | 940.2 | — | |
| PBE+Usc | — | — | — | — | 2.0 | 4s13d9 | 964.9 | — | |
| Ni1/MgO(100) | PBE+D3 | T | −2.15 | 1.79 | 2.81 | 0.0 | 4s03d10 | 0.00 | 0.00 |
| HSE06+D3 | T | −1.33 | 1.91 | 2.86 | 0.0a | 4s13d9 | 820.9 | 34.3 | |
| PBE+Usc+D3 | T | −1.19 | 1.96 | 2.95 | 0.0a | 4s13d9 | 872.1 | 37.5 | |
3.2 Ag-Supported MgO films
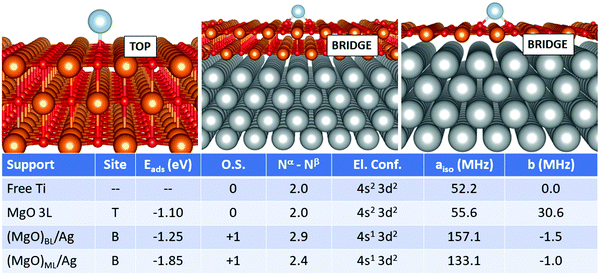
In this section, we examine a further class of supports, consisting of ultrathin films of MgO supported on Ag(100). This is, in fact, the type of support used for single-atom applications in the domains of memory resistors and microelectronics for the reasons mentioned in the introduction. In this work, we considered both MgO monolayers (ML) and bilayers (BL). From a methodological point of view, a compromise is necessary: while GGA functionals combined with PAW potentials fail in some cases to provide the right magnetic ground-state of both free and adsorbed TM atoms (see previous section), the hybrid HSE06 functional ensures a better description of the magnetic properties, but predicts poorly the Ag work function, a key-parameter in determining the final charge state of adsorbates on metal-supported thin films, among others. In this context, PBE+U represents a good compromise, ensuring a reasonable treatment of both the adatom's magnetic properties and the metal support. We thus rely on PBE+U+D3 for all calculations described in this section. We should point out, however, that the reliability of the Hubbard parameters described above has been tested only for the case of magnetic properties of the TM adatoms, which does not imply that they could generally be applied to different systems.We start from the case of Ti, Fig. 1. The effect of the metal support is already evident as soon as one looks at the most favourable adsorption site, which switches from oxygen-top (T) for free-standing MgO to bridge (B) for supported bi- and monolayers. The adsorption energy increases from −1.10 eV (free-standing MgO) to −1.25 eV for (MgO)BL/Ag and −1.85 eV for (MgO)ML/Ag. Most importantly, Ti is adsorbed in a neutral state on free-standing MgO, while it loses an electron to a formal Ti1+ state on Ag-supported films. Conversely, the electron configuration changes from 4s2 3d2 to 4s1 3d2 upon ionization. This has strong implications on the hyperfine properties. The Fermi contact term on MgO 3L is 55.6 MHz (very close to the free atom) and increases to 157.1 MHz on (MgO)BL/Ag, where the total number of unpaired electrons on the adatom is 2.9. In (MgO)ML/Ag, the mixing with the Ag states is stronger, resulting in a partial quenching of magnetization to 2.4 electrons, a partial transfer of the spin density to the O atoms on the surface, and a consequent decrease of the Fermi contact to 133.1 MHz. The anisotropic term is very small in all cases.
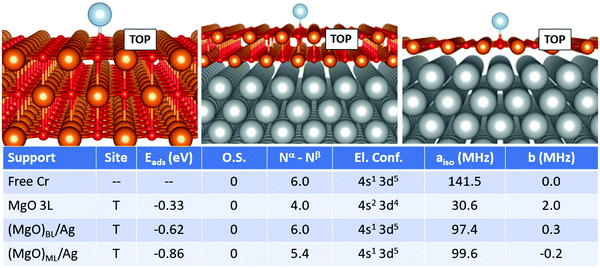
For Cr, Fig. 2, the most favourable adsorption site is always oxygen-top (T) on all supports. At variance from the case of Ti, no ionization of the adatom is reported. The adsorption energy yielded on MgO 3L (−0.33 eV) is remarkably smaller compared to that on (MgO)BL/Ag (−0.62 eV). The total number of unpaired electrons passes from 4.0 to 6.0. Moreover, the presence of the metal support induces a change in the electron configuration, which switches from 4s2 3d4 on MgO 3L to 4s1 3d5 on (MgO)BL/Ag, with a strong impact on the Fermi contact term, which passes from 141.5 MHz for the free atom, also displaying a 4s1 3d5 electron configuration to 30.6 MHz on MgO 3L (4s2 3d4) and further increases to 97.4 MHz on (MgO)BL/Ag (4s1 3d5). On (MgO)ML/Ag, finally, a further increase in Eads is reported (−0.86 eV). As observed also for Ti, the net magnetization quenches to 5.4 electrons. The Fermi contact term is 99.6 MHz, close to what was obtained on (MgO)BL/Ag. The anisotropic term is very small on all supports.
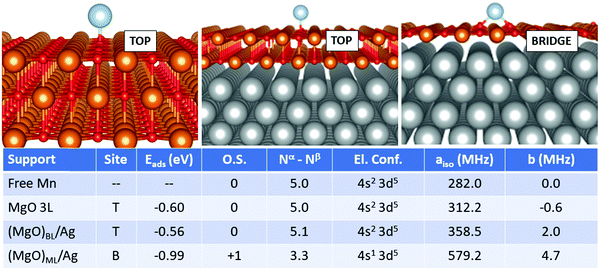
In the case of Mn, Fig. 3, we observe that the adatom is moderately bound in the top position on MgO 3L and (MgO)BL/Ag (Eads is −0.60 eV and −0.56 eV, respectively). On (MgO)ML/Ag there is a strong increase in the adsorption energy (−0.99 eV) and the most favourable adsorption site is now bridge. While Mn is adsorbed in the neutral state on MgO 3L and (MgO)BL/Ag, ionization to Mn1+ takes place on (MgO)ML/Ag. An electron is lost from the 4s orbital, generating a (4s1 3d5) electron configuration, at variance from the (4s2 3d5) configuration observed for the isolated Mn atom and for Mn adsorbed on MgO 3L and (MgO)BL/Ag. The Fermi contact term slightly increases from 282.0 MHz (isolated adatom), to 312.2 MHz (MgO 3L), and 358.5 MHz (supported bilayer). Then, a strong increase is observed on the supported ML (579.2 MHz) due to the presence of an unpaired electron in the 4s orbital. The anisotropic term also follows the same increasing trend.
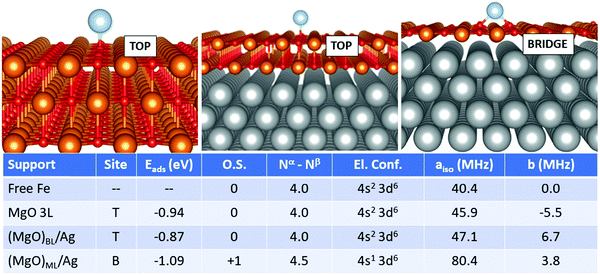
In the case of Fe, Fig. 4, the adsorption on the supported MgO films differs, in particular for the monolayer, from the adsorption on free-standing MgO. The most favourable adsorption site is top on MgO 3L and (MgO)BL/Ag, while it switches to bridge for (MgO)ML/Ag. Once again, the monolayer exhibits a peculiar behaviour. The adsorption energy, at variance to what was reported in the previous cases, does not undergo a very large increase passing from MgO 3L (−0.94 eV), (MgO)BL/Ag (−0.87 eV) to (MgO)ML/Ag (−1.09 eV). The main difference with the cases of Ti, Cr, and Mn, in this respect, lies in the relatively stronger bond of Fe on MgO(100). From the point of view of the magnetic and hyperfine properties, we observe little changes passing from the free atom to Fe1/MgO 3L and Fe1/(MgO)BL/Ag: on these supports, the Fe atom maintains its neutral state and a net magnetization of 4.0 electrons, as well as a (4s2 3d6) electron configuration. The Fermi contact term increases slightly from 40.4 MHz (free adatom) to 45.9 MHz (free-standing MgO) and 47.1 MHz (supported bilayer). The anisotropic term B reaches values close to 11 MHz on MgO 3L and (MgO)BL/Ag. The situation is different on the silver-supported MgO monolayer, where a partial electron transfer occurs from the Fe 4s orbital to the metal support, resulting in a Fe magnetization to 4.5 unpaired electrons. This reflects in an increase by almost a factor of two of aiso (80.4 MHz), while b slightly decreases to 3.8 MHz Fig. 5.
Isolated Fe species on (MgO)BL/Ag have been studied experimentally by means of spin-polarized scanning tunnelling spectroscopy in combination with single-atom electron spin resonance.9 The Fe atom is assumed to occupy only oxygen-top sites, and the large hyperfine constant (231 MHz) is explained in connection with the predominant alignment of the electron spin density along the z-axis (i.e. parallel to the applied magnetic field). Our calculations confirm the top site as the only stable adsorption site (a calculation starting from a bridge configuration spontaneously evolved to the top), but a remarkably smaller hyperfine constant (47 MHz) is calculated. This can be attributed to the fact that the five 3d orbitals of the Fe atoms are no longer degenerate and that different occupations are possible, in particular the 3d(z2) orbital with a component normal to the surface can be doubly or singly occupied, with consequent effect on aiso. Furthermore, one should consider the intrinsic limitations of DFT in predicting the hyperfine coupling constants of some atoms, see Table 2.
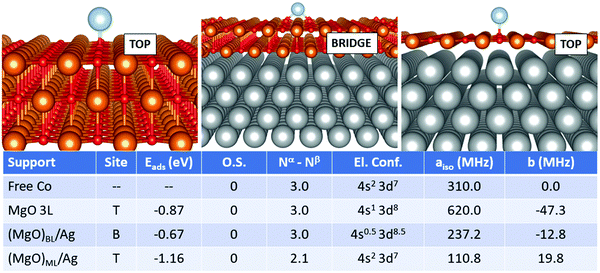
Cobalt is perhaps one of the most complicated cases seen so far. The adsorption geometry switches from top (free-standing MgO) to bridge (supported bilayer) and back to top (supported monolayer). The adsorption strength does not follow a regular trend, being −0.87 eV (free-standing MgO), −0.67 eV (supported bilayer) and −1.16 eV (supported monolayer). This is probably caused by the non-banal mixing of states between the adatom, the MgO film and the silver support. Notably, Co is not ionized on any support, but, as discussed in the previous section, its electron configuration changes from (4s2 3d7) in the free atom to (4s1 3d8) on MgO 3L. On (MgO)BL/Ag, the 4s and 3d states are mixed up envisaging a fractional occupation, even though the net magnetization still consists of 3 unpaired electrons. On (MgO)ML/Ag, on the contrary, the magnetic moment is remarkably quenched and the 4s orbital is again doubly occupied. The Fermi contact term displays strong oscillations and is 310.0 MHz on the free atom, it doubles to 620.0 MHz on the supported bilayer and decreases to 110.8 MHz on the supported ML, as a consequence of the double occupation of the Co(4s) orbital and the quenching of the magnetization on the Co(3d) orbitals, induced by the overlap with the metal support wave function. The dipolar tensor also oscillates from −47.3 MHz (MgO 3L) to −12.8 MHz and 19.8 MHz on the supported films.
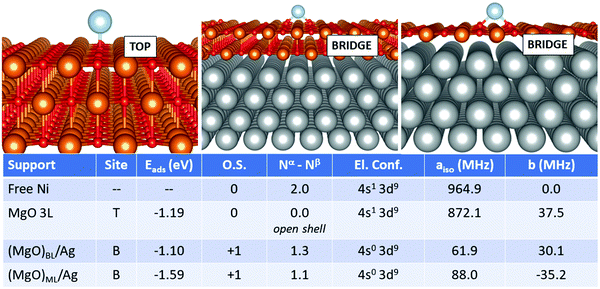
Finally, we move to the case of Ni, Fig. 6. Also in this case, the adsorption on the supported films differs substantially from that of the free-standing case. On MgO 3L, the Ni atom is adsorbed neutrally with an open-shell singlet magnetic ground state and a (4s1 3d9) electron configuration. The adsorption energy is −1.19 eV (top site). On (MgO)BL/Ag, Ni loses one electron and is adsorbed as Ni+ on a bridge site with an Eads of −1.10 eV. The net magnetization decreases to 1.3 electrons, and the loss of a 4s electron implies a dramatic decrease of the Fermi contact term from 872.1 MHz (free-standing MgO) to 61.9 MHz (supported ML). The case of (MgO)ML/Ag is quite similar to the bilayer, but the adsorption energy is larger. The Fermi contact term is 88.0 MHz, close to the bilayer, reflecting a similar magnetic ground state and electron configuration. The dipolar term does not undergo dramatic variations passing from the free-standing support to the metal-supported ones. The preference for the bridge site and the positive character assumed by the Ni adatom on (MgO)ML/Ag is in agreement with previous GGA+U calculations.35
4. Conclusions
We have compared the calculated magnetic and hyperfine properties of a set of first-row transition metal atoms adsorbed on free-standing and silver-supported MgO thin films. The aim of the work is not so much to provide “exact” values of the hyperfine coupling constants that can be used as a guide for experiment, but rather to show the complexity associated with the determination of these properties using electronic structure calculations based on DFT. In fact, there are two important aspects that cannot be underestimated: (1) the method used to determine the spin properties, as the use of different functionals can result in different ordering of the magnetic states and in different ground states; (2) the model adopted to represent the support since the use of ultrathin insulating layers does not prevent from a possible interchange of electrons between adatoms and supporting metals. The results of the calculations on a bulk oxide can differ substantially from those on supported layers.Indeed, the results confirm that the problem under investigation is a real challenge for the state-of-the-art DFT methods. On the one hand, the well-documented drawbacks of GGA in accounting for the magnetic properties and localized states in oxidic matrices are once again revealed. On the other, the screened hybrid functionals, that definitely represent a better choice to treat wide-gap insulators and highly correlated electrons, worsen the description of the metallic support. The approach proposed here consists of determining self-consistently a Hubbard parameter for each adatom, starting from the HSE06 solution for the TM atom adsorbed on free-standing MgO; the adsorption on the metal supported films is then studied with PBE+Usc. This scheme well reproduces the results obtained for TM/MgO for most of the adatoms (Ti is perhaps the most critical case).
The role of the metal support in this type of simulations has been debated in the literature, claiming that it should be small,28 or even that the tendency of DFT to overestimate the mixing between Ag, MgO and TM orbitals may actually worsen the quality of the results.9 The results exposed here seem to suggest a more complex picture, characterized by a pronounced system dependency. In some cases, such as Fe or Mn, we do not report striking differences between TM/MgO and TM/(MgO)BL/Ag (in this respect, the supported ML is a very different substrate). In other cases, Cr, Co, and Ni, the presence of the metal substrate induces a charge transfer or a change in electronic configuration that in turn strongly affects the hyperfine parameters. The predicting power of calculations on free-standing model structures, in a frame of potential applications where the real system is indeed an ultrathin supported film, is thus questionable and requires some care.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Ministero dell’Istruzione, dell’Università e della Ricerca (Grant no. 20179337R7 MULTI-e) through the PRIN national program is acknowledged. The help of our colleague Dr Farahnaz Maleki in discussing and assessing the data presented in this paper is also kindly acknowledged.References
- I. G. Rau, S. Baumann, S. Rusponi, F. Donati, S. Stepanow, L. Gragnaniello, J. Dreiser, C. Piamonteze, F. Nolting, S. Gangopadhyay, O. R. Albertini, R. M. Macfarlane, C. P. Lutz, B. A. Jones, P. Gambardella, A. J. Heinrich and H. Brune, Reaching the magnetic anisotropy limit of a 3d metal atom, Science, 2014, 344, 988–992 CrossRef CAS PubMed
.
- F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Ž. Šljivančanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Magnetic remanence in single atoms, Science, 2016, 352, 318–321 CrossRef CAS PubMed
.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Single-atom catalysis of CO oxidation using Pt1/FeOx, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed
.
- X. F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-atom catalysts: A new frontier in heterogeneous catalysis, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed
.
- L. Liu and A. Corma, Confining isolated atoms and clusters in crystalline porous materials for catalysis, Nat. Rev. Mater., 2021, 6, 244–263 CrossRef CAS
.
- R. P. Galhenage, H. Yan, S. A. Tenney, N. Park, G. Henkelman, P. Albrecht, D. R. Mullins and D. A. Chen, Understanding the Nucleation and Growth of Metals on TiO2: Co Compared to Au, Ni, and Pt, J. Phys. Chem. C, 2013, 117, 7191–7201 CrossRef CAS
.
- C. C. Yec and H. C. Zeng, Synthesis of complex nanomaterials via Ostwald ripening, J. Mater. Chem. A, 2014, 2, 4843–4851 RSC
.
- S. Baumann, W. Paul, T. Choi, C. P. Lutz, A. Ardavan and A. J. Heinrich, Electron paramagnetic resonance of individual atoms on a surface, Science, 2015, 350, 417–420 CrossRef CAS PubMed
.
- P. Willke, Y. Bae, K. Yang, J. L. Lado, A. Ferrón, T. Choi, A. Ardavan, J. Fernández-Rossier, A. J. Heinrich and C. P. Lutz, Hyperfine interaction of individual atoms on a surface, Science, 2018, 362, 336–339 CrossRef CAS PubMed
.
- T. S. Seifert, S. Kovarik, D. M. Juraschek, N. A. Spaldin, P. Gambardella and S. Stepanow, Longitudinal and transverse electron paramagnetic resonance in a scanning tunneling microscope, Sci. Adv., 2020, 6, eabc5511 CrossRef CAS PubMed
.
-
H.-J. Freund, H. Kuhlenbeck and M. Neumann, in Adsorption on Ordered Surfaces of Ionic Solids and Thin Films, Springer, Berlin, 1993, pp. 136–146 Search PubMed
.
- S. C. Street, C. Xu and D. W. Goodman, The physical and chemical properties of ultrathin oxide films, Annu. Rev. Phys. Chem., 1997, 48, 43–68 CrossRef CAS PubMed
.
- M. Bäumer and H. J. Freund, Metal deposits on well-ordered oxide films, Prog. Surf. Sci., 1999, 61, 127–198 CrossRef
.
- G. Pacchioni, L. Giordano and M. Baistrocchi, Charging of metal atoms on ultrathin MgO/Mo(100) films, Phys. Rev. Lett., 2005, 94, 226104 CrossRef PubMed
.
- L. Giordano and G. Pacchioni, Oxide Films at the Nanoscale: New Structures, New Functions, and New Materials, Acc. Chem. Res., 2011, 44, 1244–1252 CrossRef CAS PubMed
.
-
Electron Paramagnetic Resonance, ed. M. Brustolon and E.
Giamello, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2009 Search PubMed
.
- M. Yulikov, M. Sterrer, M. Heyde, H. P. Rust, T. Risse, H. J. Freund, G. Pacchioni and A. Scagnelli, Binding of single gold atoms on thin MgO(001) films, Phys. Rev. Lett., 2006, 96, 146804 CrossRef PubMed
.
- M. Chiesa, E. Giamello, C. Di Valentin, G. Pacchioni, Z. Sojka and S. Van Doorslaer, Nature of the chemical bond between metal atoms and oxide surfaces: New evidences from spin density studies of K atoms on alkaline earth oxides, J. Am. Chem. Soc., 2005, 127, 16935–16944 CrossRef CAS PubMed
.
- X. Zhang, C. Wolf, Y. Wang, H. Aubin, T. Bilgeri, P. Willke, A. J. Heinrich and T. Choi, Electron spin resonance of single iron phthalocyanine molecules and role of their non-localized spins in magnetic interactions, Nat. Chem., 2022, 14, 59–65 CrossRef CAS PubMed
.
- P. Hurdax, M. Hollerer, P. Puschnig, D. Lüftner, L. Egger, M. G. Ramsey and M. Sterrer, Controlling the Charge Transfer across Thin Dielectric Interlayers, Adv. Mater. Interfaces, 2020, 2000592 CrossRef CAS
.
- Z. Li, H.-Y. T. Chen, K. Schouteden, K. Lauwaet, L. Giordano, M. I. Trioni, E. Janssens, V. Iancu, C. Van Haesendonck, P. Lievens and G. Pacchioni, Self-Doping of Ultrathin Insulating Films by Transition Metal Atoms, Phys. Rev. Lett., 2014, 112, 026102 CrossRef CAS PubMed
.
- Z. Li, H. Y. T. Chen, K. Schouteden, E. Janssens, C. Van Haesendonck, P. Lievens and G. Pacchioni, Spontaneous doping of two-dimensional NaCl films with Cr atoms: aggregation and electronic structure, Nanoscale, 2015, 7, 2366–2373 RSC
.
- G. Pacchioni and H. Freund, Chem. Rev., 2013, 113, 4035–4072 CrossRef CAS PubMed
.
- P. S. Bagus and B. I. Bennett, Singlet–triplet splittings as obtained from the Xα-scattered wave method: A theoretical analysis, Int. J. Quantum Chem., 1975, 9, 143–148 CrossRef CAS
.
- F. Illas, I. P. R. Moreira, J. M. Bofill, M. Filatov and F. Illas, Spin Symmetry Requirements in Density Functional Theory: The Proper Way to Predict Magnetic Coupling Constants in Molecules and Solids, Theor. Chem. Acc., 2006, 116, 587–597 Search PubMed
.
- G. Pacchioni, F. Frigoli, D. Ricci and J. A. Weil, Theoretical description of hole localization in a quartz Al center: The importance of exact electron exchange, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 054102 CrossRef
.
- C. Sousa, S. Tosoni and F. Illas, Theoretical Approaches to Excited-State-Related Phenomena in Oxide Surfaces, Chem. Rev., 2013, 113, 4456–4495 CrossRef CAS PubMed
.
- S. Shehada, M. dos Santos Dias, F. S. M. Guimarães, M. Abusaa and S. Lounis, Trends in the hyperfine interactions of magnetic adatoms on thin insulating layers, npj Comput. Mater., 2021, 7, 1–10 CrossRef
.
- I. Yudanov, G. Pacchioni, K. Neyman and N. Rösch, Systematic Density Functional Study of the Adsorption of Transition Metal Atoms on the MgO(001) Surface, J. Phys. Chem. B, 1997, 101, 2786–2792 CrossRef CAS
.
- A. Markovits, M. K. Skalli, C. Minot, G. Pacchioni, N. López and F. Illas, The competition between chemical bonding and magnetism in the adsorption of atomic Ni on MgO(100), J. Chem. Phys., 2001, 115, 8172 CrossRef CAS
.
- N. Lopez, J. C. Paniagua and F. Illas, Controlling the spin of metal atoms adsorbed on oxide surfaces: Ni on regular and defective sites of the MgO(001) surface, J. Chem. Phys., 2002, 117, 9445 CrossRef CAS
.
- N. López, F. Illas, A. Markovits, C. Minot and J. C. Paniagua, Adsorption energy and spin state of first-row transition metals adsorbed on MgO(100), Phys. Rev. B: Condens. Matter Mater.
Phys., 2003, 67, 6 CrossRef
.
- E. Florez, F. Mondragón, P. Fuentealba and F. Illas, Effect of surface site on the spin state of first-row transition metals adsorbed on MgO: Embedded cluster model and hybrid density functional theory calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075426 CrossRef
.
- S. Sicolo, L. Giordano and G. Pacchioni, Adsorption of Late Transition Metal Atoms on MgO/Mo(100) and MgO/Ag(100) Ultrathin Films: A Comparative DFT Study, J. Phys. Chem. C, 2009, 113, 16694–16701 CrossRef CAS
.
- O. R. Albertini, A. Y. Liu and B. A. Jones, Site-dependent magnetism of Ni adatoms on MgO/Ag(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214423 CrossRef
.
- G. Kresse and J. Hafner,
Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 15410 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- J. Pal, M. Smerieri, E. Celasco, L. Savio, L. Vattuone, R. Ferrando, S. Tosoni, L. Giordano, G. Pacchioni and M. Rocca, How Growing Conditions and Interfacial Oxygen Affect the Final Morphology of MgO/Ag(100) Films, J. Phys. Chem. C, 2014, 118, 26091–26102 CrossRef CAS
.
- N. Lopez, F. Illas, N. Rösch and G. Pacchioni, Adhesion energy of Cu atoms on the MgO(001) surface, J. Chem. Phys., 1999, 110, 4873 CrossRef CAS
.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, Screened hybrid density functionals applied to solids, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed
.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed
.
- S. Dudarev and G. Botton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS
.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef
.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Taylor and Francis Group, Boca Raton, FL 33487-2742, 89th edn, 2008 Search PubMed
.
-
J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance. Elementary Theory and Practical Applications, John Wiley and Sons, Hoboken (NJ), 2007 Search PubMed
.
- D. Feller, J. F. Stanton and E. R. Davidson, Atomic isotropic hyperfine properties for first row elements (B–F) revisited, J. Chem. Phys., 2022, 156, 034304 CrossRef CAS PubMed
.
- I. Malkin, O. L. Malkina, V. G. Malkin and M. Kaupp, Scalar relativistic calculations of hyperfine coupling tensors using the Douglas–Kroll–Hess method, Chem. Phys. Lett., 2004, 396, 268–276 CrossRef CAS
.
- O. V. Yazyev, I. Tavernelli, L. Helm and U. Röthlisberger, Core spin-polarization correction in pseudopotential-based electronic structure calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115110 CrossRef
.
-
C. Daul, H. Fischer, F. H. Morton, K. F. Preston and A. von Zalewsky, Atoms, Inorganic Radicals and Radicals in Metal Complexes (Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology - New Series), Springer, Berlin, 1977 Search PubMed
.
- J. S. M. Harvey, L. Evans and H. Lew, Diagonal and Off-Diagonal Hyperfine Structure in the Ground Multiplets of Boron and Aluminum by the Atomic Beam Method; Magnetic Dipole Radial Parameters, Can. J. Phys., 1972, 50, 1719–1727 CrossRef CAS
.
- W. R. M. Graham and W. Weltner, B atoms, B2 and H2BO molecules: ESR and optical spectra at 4° K, J. Chem. Phys., 1976, 65, 1516–1521 CrossRef CAS
.
-
W. Weltner, Magnetic Atoms and Molecules, Van Nostrand-Reinhold Co. Inc., New York, 1983 Search PubMed
.
- G. Wolber, H. Figger, R. A. Haberstroh and S. Penselin, Atomic beam magnetic resonance investigations in the 2p 2 3 P ground multiplet of the stable carbon isotopes12C and13C, Z. Phys. A: Hadrons Nucl., 1970, 236, 337–351 CrossRef CAS
.
- J. M. Hirsch, G. H. Zimmerman, D. J. Larson and N. F. Ramsey, Precision measurement of the hyperfine structure and g factor of atomic nitrogen 14, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 16, 484–487 CrossRef CAS
.
- J. S. M. Harvey, Hyperfine structure in ground multiplets of 17 O and 19 F, Proc. R. Soc. London, Ser. A, 1965, 285, 581–596 Search PubMed
.
- Y. Ting and H. Lew, Hyperfine Structure of Cu63 and Cu65, Phys. Rev., 1957, 105, 581–588 CrossRef CAS
.
- G. Wessel and H. Lew, Hyperfine Structures of Silver and Gold by the Atomic Beam Magnetic Resonance Method, Phys. Rev., 1953, 92, 641–646 CrossRef CAS
.
- D. M. Lindsay and P. H. Kasai, Anisotropic parameters for the valence p orbitals of the group IB elements, J. Magn. Reson., 1985, 64, 278–283 CAS
.
-
C. E. Moore, Atomic energy levels as derived from the analyses of optical spectra, US Department of Commerce, National Bureau of Standards, Washington D.C., 1949, vol. 2 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01224c |
| This journal is © the Owner Societies 2022 |