On the use of vibronic coherence to identify reaction coordinates for ultrafast excited-state dynamics of transition metal-based chromophores
Bryan C.
Paulus
 and
James K.
McCusker
and
James K.
McCusker
 *
*
Department of Chemistry, Michigan State University, 578 South Shaw Lane, East Lansing, MI 48824, USA. E-mail: jkm@chemistry.msu.edu
First published on 6th June 2022
Abstract
The question of whether one can use information from quantum coherence as a means of identifying vibrational degrees of freedom that are active along an excited-state reaction coordinate is discussed. Specifically, we are exploring the notion of whether quantum oscillations observed in single-wavelength kinetics data exhibiting coherence dephasing times that are intermediate between that expected for either pure electronic or pure vibrational dephasing are vibronic in nature and therefore may be coupled to electronic state-to-state evolution. In the case of a previously published Fe(II) polypyridyl complex, coherences observed subsequent to 1A1 → 1MLCT excitation were linked to large-amplitude motion of a portion of the ligand framework; dephasing times on the order of 200–300 fs suggested that these degrees of freedom could be associated with ultrafast (∼100 fs) conversion from the initially formed MLCT excited state to lower-energy, metal-centered ligand-field excited state(s) of the compound. Incorporation of an electronically benign but sterically restrictive Cu(I) ion into the superstructure designed to interfere with this motion yielded a compound exhibiting a ∼25-fold increase in the compound’s MLCT lifetime, a result that was interpreted as confirmation of the initial hypothesis. However, new data acquired on a different chemical system – Cr(acac′)3 (where acac′ represents various derivatives of acetylacetonate) – yielded results that call into question this same hypothesis. Coherences observed subsequent to 4A2 → 4T2 ligand-field excitation on a series of molecules implicated similar vibrational degrees of freedom across the series, but exhibited dephasing times ranging from 340 fs to 2.5 ps without any clear correlation to the dynamics of excited-state evolution in the system. Taken together, the results obtained on both of these chemical platforms suggest that while identification of coherences can indeed point to degrees of freedom that should be considered as candidate modes for defining reaction trajectories, our understanding of the factors that determine the interplay across coherences, dephasing times, and electronic and geometric structure is insufficient at the present time to view this parameter as a robust metric for differentiating active versus spectator modes for ultrafast dynamics.
Introduction
Chemical processes – thermal and photochemical, intra- as well as intermolecular – proceed along complex potential energy surfaces that define pathways from reactants to products. Each step in this process will have an optimal trajectory that competes with alternate, non-productive pathways that serve as mechanisms for energy dissipation. Having a priori control of these trajectories – in effect dictating the reaction pathway along which the system evolves – has been a long-standing goal for chemists. Current theories that provide the conceptual basis for our understanding and chemical intuition about molecular processes generally assume that the kinetic energy of reactants is not stored as the system moves from peaks to valleys but rather is thermalized and therefore dissipated, leading to the exponential nature of barrier crossings for reaction dynamics. If we could alter this paradigm by programming the desired reaction pathway using information about the interplay between the electronic and vibrational degrees of freedom of a system, reactions could be choreographed at the molecular level with much greater precision and efficiency. To achieve this, one needs to exploit processes that involve strong coupling of electronic and nuclear degrees of freedom, which in turn requires the identification of trajectories that involve phase coherent vibrational motions and nonadiabatic mechanisms. By designing molecules with vibrational modes that couple the desired reactant and product states, one could, in theory, optimize the efficiency of a given chemical process by making dissipative reaction pathways less favorable. In effect, such an advance would enable chemists to control chemical dynamics through synthetic design driven by the informed application of quantum information about the system reflected in a phenomenon known as coherence.1,2The concept of coherence is one that we are at once very familiar with and wholly unfamiliar with. Sitting at a stop light, we all notice when our turn signal and the one on the car in front of us is slightly out-of-phase. The specifics of this phase relationship ultimately leads to a beat pattern where, for a brief period of time, the two blinkers are fully synchronized: this is one form of coherence. In quantum mechanics, coherence refers to a correlation between different degrees of freedom in a quantum object such that their properties can only be represented as a superposition. A simple example of this is the idea of resonance.3 Benzene, for instance, has two main resonance structures denoted by ψ1 and ψ2 (Fig. 1); neither of these two Kekulé structures correspond to the true wavefunction of benzene. Furthermore, the molecule is not flickering back and forth between them. The true wavefunction is a superposition, i.e., a linear combination of each Kekulé wavefunction described by aψ1 + bψ2 and is a form of quantum mechanical coherence.
When considering coherence in the context of excited-state dynamics, ultrashort laser pulses with bandwidths that are broad enough to span multiple vibrational levels on an electronic excited state can excite several vibrational levels simultaneously. The resulting wavefunction is represented by a linear combination of each of the constituent wavefunctions as shown in eqn (1),
 | (1) |
 | ||
| Fig. 2 Pictorial representation of a coherent superposition state – more commonly referred to as a wavepacket – resulting from a linear combination of oscillatory wavefunctions as described by eqn (1). | ||
The time-dependent evolution of the wavepacket just described ultimately provides us with the chemical insight we need to take advantage of coherence in terms of synthetic design. Excited-state absorption spectra are no different than ground-state profiles insofar as they reflect a superposition of Franck–Condon overlap factors that arise between the two electronic states involved in the transition. In the case of transient absorption spectroscopy, the two states involved are the excited state that is formed upon photoexcitation and higher-lying excited states that the probe beam samples to yield the excited-state absorption spectrum. The critical difference is that the oscillatory nature of the wavepacket on the excited-state potential surface results in changes in the Franck–Condon factors as the wavepacket evolves in time. This manifests as fine structure superimposed on the kinetics associated with excited-state evolution (Fig. 3), fine structure that contains information on the coupling that exists between the electronic and nuclear degrees of freedom of the molecule and thus contains a blueprint of how a given excited-state process depends on and/or is dictated by the electronic and geometric properties of the system.
Despite the wealth of information these coherence signatures possess, there is a significant problem that arises: how does one differentiate coherences associated with degrees of freedom that are relevant to the excited-state process of interest (e.g., intersystem crossing, electron transfer, energy transfer, etc.) – so-called “active modes” – from coherences that can arise along coordinates having nothing to do with that process (“spectator modes”)? A non-linear molecule has 3N − 6 vibrational degrees of freedom, so in order for vibronic coherence to be of use as a design principle, it’s necessary to figure out which subset of those 3N − 6 degrees of freedom are actually relevant from the perspective of photofunctionality. With this report, we present results on two different chemical systems that we have explored that highlight the nature of this difficulty with the goal of stimulating a dialog on how to transform coherence from an observational phenomenon to one that can (potentially) guide chemical innovation.
Experimental section
General
All reagents were purchased from Sigma-Aldrich or Strem Chemical and used as received unless otherwise indicated. The syntheses of tris(2,4-pentanediono)chromium(III) (Cr(acac)3), tris(3-chloro-2,4-pentanediono)chromium(III) (Cr(3-Cl-acac)3), tris(3-bromo-2,4-pentanediono)chromium(III) (Cr(3-Br-acac)3), tris(3-iodo-2,4-pentanediono)chromium(III) (Cr(3-I-acac)3), and tris(2,2,6,6-tetramethyl-3,5-heptanediono)chromium(III) (Cr(TMHD)3) were prepared as described elsewhere.5Computational methods
All calculations were performed with Gaussian 09 software6 on the Michigan State University High Performance Computing Center servers. Previously optimized geometries for Cr(acac)3 and Cr(TMHD)3 were used as starting geometries for Cr(acac)3 and Cr(TMHD)3 ground state optimizations.7 Optimizations were performed using the unrestricted B3LYP functional, 6-311G** basis set, tight convergence criteria; calculations for Cr(3-I-acac)3 were unique in that the LANL2DZ basis set was used. Choice of solvent used for the polarizable continuum model had little effect on the results in the frequency region of interest, but Cr(acac)3 calculations were performed in acetonitrile, Cr(TMHD)3 in tetrahydrofuran, Cr(3-Cl-acac)3 and Cr(3-I-acac)3 in dichloromethane, and Cr(3-Br-acac)3 in toluene. Mass weighted vector displacement diagrams of each pertinent vibrational mode were created in the Visual Molecular Dynamics program.8Time resolved spectroscopy
The ultrafast time-resolved absorption spectrometer used for these studies has been described in detail previously.9,10 Briefly, a Ti:sapphire oscillator (Coherent: Mantis) provides a ∼400 mW, 80 MHz seed beam centered at ∼800 nm for use in a regenerative amplifier (Coherent: Legend Elite) with a 527 nm Nd:YLF pump (Coherent: Evolution) producing a 1 KHz pulse train of approximately 35 fs 1 mJ pulses at 800 nm. This output is split using a 70/30 beam splitter with the higher energy portion used to pump a two-stage optical parametric amplifier (OPA) (Coherent: OperA Solo) to generate a visible pump beam which is used as the excitation source during the transient absorption experiment. This pump beam is again split with a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 beam splitter with the lower energy portion being used as a probe beam for degenerate pump–probe experiments. The remaining 30% of the 800 nm output from the regenerative amplifier is either used to pump a second OPA (Coherent: Opera Solo) to generate a probe beam for single wavelength nondegenerate pump–probe experiments or used to make a white light continuum by attenuating the power and focusing ∼1 μJ pulses into a 3 mm sapphire window. This white light continuum can again be used for single wavelength nondegenerate pump–probe experiments or a large swath of the continuum can be measured using full spectrum measurements. Group velocity dispersion for each OPA output is corrected using a folded prism compressor. Pump–probe delay is adjusted by routing the pump OPA output into a computer-controlled translation stage (Aerotech). Pump and probe polarizations are set to ∼54.7° relative to each other to eliminate anisotropic contributions to the signal and focused into a 1 mm quartz cuvette containing the sample. The pump pulse energies were set in the range of 3–6 μJ and the signal was checked for linearity by halving the pump power using a variable neutral density filter wheel. Probe pulse energies were set to 1/10th of the pump.
10 beam splitter with the lower energy portion being used as a probe beam for degenerate pump–probe experiments. The remaining 30% of the 800 nm output from the regenerative amplifier is either used to pump a second OPA (Coherent: Opera Solo) to generate a probe beam for single wavelength nondegenerate pump–probe experiments or used to make a white light continuum by attenuating the power and focusing ∼1 μJ pulses into a 3 mm sapphire window. This white light continuum can again be used for single wavelength nondegenerate pump–probe experiments or a large swath of the continuum can be measured using full spectrum measurements. Group velocity dispersion for each OPA output is corrected using a folded prism compressor. Pump–probe delay is adjusted by routing the pump OPA output into a computer-controlled translation stage (Aerotech). Pump and probe polarizations are set to ∼54.7° relative to each other to eliminate anisotropic contributions to the signal and focused into a 1 mm quartz cuvette containing the sample. The pump pulse energies were set in the range of 3–6 μJ and the signal was checked for linearity by halving the pump power using a variable neutral density filter wheel. Probe pulse energies were set to 1/10th of the pump.
Single-wavelength measurements were obtained by passing the pump beam through a 446 Hz mechanical chopper. A monochromator (Jarrell Ash: MonoSpec 18; 1200 grooves per mm grating, blaze 500 nm) was placed after the sample and used to select a 3.8 nm FWHM slice of the probe beam spectrum to be measured on an amplified silicon photodiode (Thor laboratories: PDA55). The center wavelength of this slice of the probe spectrum is specified for each single wavelength TA trace. A reference beam is produced from a reflection of the probe beam off a microscope slide cover slip inserted into the beam path prior to the sample. This reference beam is measured on another amplified silicon photodiode and attenuated with neutral density filters and an iris until its intensity matches that of the signal beam. Both the signal and reference beams are coupled to a lock-in amplifier (Stanford Research: SR810) which is synchronized to the chopper modulating the pump beam. Connection of the lock-in amplifier to a data acquisition card allows the signal to be converted from analogue to digital. Data were acquired and analyzed using a locally written LabView program.
Full spectra were acquired by collimating the white light continuum probe and focusing it into the sample using spherical mirrors. A lens placed after the sample was then used to focus the transmitted continuum probe into a liquid light guide which was coupled to a spectrometer (Spex 270 M) with 1 mm entrance slits. A grating (300 grooves per mm; blaze 600 nm) within the spectrometer dispersed the probe beam onto a diode array detector (Hamamatsu: HC233-0900; C5964 NMOS, 1 × 512 pixel array) affording a roughly 300 nm spectral window. Data were acquired using a locally written LabView program by first collecting “dark counts”, which is effectively a measurement of the pump beam scatter reaching the detector in the absence of the probe beam. Next, a background is collected by measuring the signal with both pump and probe incident on the sample at negative time delay. The dark counts spectrum is then subtracted from this background to provide a baseline (I0) for calculating the change in absorbance as a function of pump–probe delay.
Results and discussion
Transition metal complexes represent an excellent conduit for examining the interplay between electronic and vibrational dynamics due to the nature of their electronic structures. Specifically, the spin-state variability associated with ions of the d-block, the co-existence of both charge-transfer and ligand-field excited states – each of these being defined by distinct differences in intramolecular charge distribution and degree of coupling to the structure of the molecule – as well as chemical tunability allow for the kind of compositional flexibility that is necessary in order to connect excited-state evolution to electronic structure, geometric structure, and molecular functionality.As indicated in the Introduction, one of the difficulties associated with identifying the degrees of freedom relevant for defining excited-state reaction trajectories is the sheer number of vibrational modes that large molecules possess. A variable we have proposed that may serve as a means of differentiating active versus spectator modes is the dephasing time of the coherence.11–13 Upon excitation with a sufficiently short laser pulse, the initial excited state is characterized by a coherent superposition of vibrational states that are all phase-locked; the motion of this wavepacket is what gives rise to the oscillations shown in Fig. 3 and described by eqn (1). This phase relationship will eventually degrade due to any number of reasons, e.g., interactions with solvent, excited-state processes within the chromophore, etc., leading to a damping of the oscillations and eventual loss of the characteristic oscillatory pattern. For a pure vibrational mode, i.e., one that would be observed following direct excitation of a ground-state vibration, dephasing times on the order of 1–10 ps are routinely observed.14 In contrast, electronic coherences dephase much more rapidly, i.e., on the order of a few tens to a hundred femtoseconds.15 We have postulated that modes exhibiting dephasing times between these two extremes may indicate a vibronic nature to that mode, thereby linking it to the coupled evolution of the electronic and vibrational degrees of freedom following photoexcitation. If true, one could potentially use dephasing times as a means of reducing the dimensionality of the problem of identifying active modes from 3N − 6 to a much smaller subset of trajectories. This in turn would provide physical insight into the nuclear motions of the molecule that (potentially) define the reaction coordinate and provide a roadmap for imparting synthetic control over ultrafast excited-state dynamics through targeted chemical design.
As far as we are aware, there is no robust theory to support (or refute) the notion of linking dephasing times of observed coherences to that corresponding vibration’s role in the excited-state process(es) associated with the population dynamics. Herein we will present results on two chemical systems that we have studied – one for which this correlation appears to hold and another where its validity is questionable – with the goal of stimulating discussion around this issue.
Dephasing times as an indicator of reaction coordinate: the photophysics of an Fe(II) polypyridyl complex and manipulation of metal-to-ligand charge transfer-state lifetimes
A recent report from our lab represents a case study in which synthetic redesign targeting vibrational degrees of freedom with coherence dephasing times in the range of 100s of femtoseconds appears to have been successful.16 The chemical platform is based on polypyridyl complexes of Fe(II). Chromophores in this general class are of interest as potential earth-abundant alternatives to compounds based on rare metals such as ruthenium and iridium for applications reliant on photo-induced electron transfer chemistry (e.g., solar energy conversion, photo-redox catalysis, etc.).17 A critical problem with such systems is the sub-100 fs lifetime associated with the MLCT excited states of compounds like [Fe(bpy)3]2+ (where bpy is 2,2′-bipyridine).18 This corresponds to a reduction in lifetime by 6–7 orders of magnitude relative to the corresponding state in a compound such as [Ru(bpy)3]2+ and effectively undercuts the ability to leverage the chemical potential stored in this type of charge-separated excited state. The origin of the problem is tied to the difference in the relative energies of the charge-transfer and ligand-field (i.e., “d–d”) excited-state manifolds between compounds of the first- versus second- and third-row transition series.19 Specifically, the limited radial extension of the 3d orbitals (as compared to 4d and 5d) due to the primogenic effect20 attenuates metal–ligand overlap, thereby reducing the magnitude of ligand field-induced splitting among those orbitals in a given compound. This positions the ligand-field excited states lower in energy than what one finds in corresponding second- and third-row metal complexes to where the lowest energy ligand-field excited states now sit below the MLCT states, in contrast to the situation one finds for their heavier congeners (Fig. 4). This energetic situation, combined with the large difference in equilibrium geometry that characterizes these excited ligand-field states, is the main driver for the ultrafast charge-transfer to ligand field-state conversion seen in these compounds. | ||
| Fig. 4 Qualitative potential energy surface diagrams appropriate for an octahedral d6 metal ion of the second or third transition series (left) and the first-row (right). The inversion in relative energies between the MLCT and ligand-field states contributes to ultrafast non-radiative decay in the case of the latter, which limits the utility of compounds like [Fe(bpy)3]2+ for photo-induced electron transfer chemistry. Adapted from ref. 19. | ||
The most successful approach thus far toward circumventing this problem has been through the use of carbene-based ligands,21 which present significantly stronger ligand fields to a given metal center due to their strongly σ-donating character and has the effect of destabilizing the ligand-field excited states: if pushed sufficiently high in energy, one can realize an electronic structure that more closely resembles that of a second- or third-row transition metal complex. This strategy amounts to manipulation of the y-axis in the potential energy surface drawings in Fig. 4, which raised a question in our minds as to whether one could also tackle the problem through manipulation of the x-axis, i.e., the reaction coordinate. We posited that identification of vibronic coherences could aid in this regard by allowing for the visualization of the structural degrees of freedom that couple to the MLCT-to-LF state conversion, and then use that information as the basis of synthetically tailoring ligands to interfere with evolution along those degrees of freedom. We therefore conceived of the chemical platform shown in Scheme 1, which allows for modifications of the structural integrity of the ligand framework along the metal–ligand bond stretch coordinate as well as torsional motion about the primary coordination sphere; both of these degrees of freedom have been implicated in the dynamics of interconversion between the low-spin (1A1) and high-spin (5T2) forms of Fe(II) complexes.22
 | ||
| Scheme 1 Multidentate ligand (L) synthesized for the study of the use of vibronic coherence for probing the reaction coordinate for ultrafast MLCT-state relaxation in an Fe(II) polypyridyl complex (from ref. 16). | ||
A full report of this work has been published elsewhere,16 so for the purposes of this discussion we will merely summarize the key observations and results. Excitation into the 1A1 → 1MLCT absorption of the mononuclear Fe(II) complex with sub-50 fs pulses revealed an MLCT lifetime of 110 ± 30 fs, a value that is typical for Fe(II) polypyridyl complexes. The bandwidth of the excitation pulse was sufficient to create a wavepacket on the MLCT-state surface, producing quantum oscillations that were superimposed on the single-wavelength kinetic traces (Fig. 5). Analysis of the data indicated the presence of vibrational signatures corresponding to energies of 127 ± 5 cm−1, 156 ± 2 cm−1, 173 ± 3 cm−1, and 215 ± 12 cm−1. All of these modes exhibited dephasing times between the two extremes mentioned above, with the 156 ± 2 cm−1 mode being the most well-defined in terms of error bars at 300 ± 30 fs. This intermediate dephasing time led us to speculate that some (or all) of these modes could be vibronic in nature and therefore coupled to the MLCT-to-LF conversion process that we were seeking to suppress. DFT calculations enabled us to visualize these modes, all of which indicated large amplitude motion associated with the aliphatic portions of the molecule (Fig. 6). We postulated that incorporation of an electronically benign metal ion in the N4 coordination site on both ends of the macrocycle would attenuate this motion and possibly decouple it from the reaction coordinate, leading to an increase in the MLCT-state lifetime. Photophysical data were therefore collected on the [FeCu2(L)]4+ under identical conditions as the iron-only system. The amplitude of the quantum oscillations observed for this compound were attenuated relative to [Fe(L)]2+, and we noted a small but discernible increase in the dephasing times of the relevant modes. While these observations were suggestive that we had achieved the desired result, proof was obtained in the form of transient absorption spectra which clearly showed enhanced persistence of the optical signature associated with the bpy− radical anion in the MLCT excited state (Fig. 7). The measured lifetime of the 3MLCT state of the [FeCu2(L)]4+ complex was 2.6 ± 0.1 ps, corresponding to a ca. 25-fold increase in the lifetime of that state.
 | ||
| Fig. 5 Time-resolved absorption data acquired on [Fe(L)]2+ in CH3CN solution following ca. 40 fs excitation at 600 nm. The plot on the left shows single-wavelength kinetics measurements collected at 658 nm; the red line superimposed on the kinetics data corresponds to a simulation of the data derived from a linear predictive single-valued decomposition analysis based on eqn (1) (right). The mode at 154 cm−1 is pictured in Fig. 6. (Adapted from ref. 16.) | ||
 | ||
| Fig. 6 DFT-based vector displacement diagram of the 154 cm−1 mode identified from the LPSVD analysis of the data plotted in Fig. 5. The large-amplitude motion of the ligand framework evident above and below the Fe(II) coordination site (red) was targeted for chemical modification via binding to Cu(I). | ||
 | ||
| Fig. 7 Full-spectrum time-resolved absorption data acquired on [Fe(L)]2+ (left) and [FeCu2(L)]4+ (right) in CH3CN solution following ca. 40 fs excitation at 600 nm. Positive absorptions to the red of 625 nm are associated with the bpy− species that is only present in the MLCT excited state of the compound. The appearance of this signal in [FeCu2(L)]4+ indicates that this excited state persists for a much longer period of time, indicating that the incorporation of the Cu(I) ions into the structure has caused a ∼25-fold increase in the MLCT-state lifetime relative to [Fe(L)]2+. Adapted from ref. 16. | ||
We viewed the results on this Fe(II)-based system as a successful, albeit empirical demonstration of the idea that one can leverage information contained in coherences as a means of guiding synthetic design. In this case, the goal was identifying vibrational degrees of freedom that served to define the reaction coordinate along which the compound evolves from the MLCT state to lower energy, metal-centered ligand-field states (essentially the x-axis in Fig. 4). This result notwithstanding, data on one molecule is simply not sufficient to argue that intermediate dephasing times constitutes a robust criterion upon which to rely for the identification of active modes along a given reaction coordinate. In order to probe this question in greater detail, we turn to a chemical platform that we had previously explored over a decade ago but can now examine in far greater detail.
The basic photophysics of Cr(acac)3
One of the motivations underpinning the study of Fe(II)-based charge-transfer chromophores is their potential utility for facilitating photo-induced electron transfer chemistry. The strong visible absorption cross-section of these compounds is an important attribute in this regard, but unravelling details concerning excited-state dynamics is challenging due to the complexity of their electronic structures. It is for this reason that we began examining the ultrafast photophysics of Cr(acac)3 (where acac is the mono-deprotonated form of acetylacetone). Chromium(III), possessing a d3 valence configuration, has significantly fewer metal-centered electronic excited states than a low-spin d6 ion like Fe(II). In particular, the isolation of the lowest-energy 4A2 → 4T2 spin-allowed d–d absorption at 560 nm allows for selective excitation into a single electronic state; with only the lower energy 2E state and ground-state energetically accessible, the number of possible relaxation pathways is extremely limited (Fig. 8). Finally, the small size of the ligand framework translates to a reduction in the size of the compound’s vibrational partition function, which in turn will simplify analysis of vibronic coherences that may be created in an ultrafast time-resolved absorption measurement. | ||
| Fig. 8 (Left) Solution-phase absorption (solid line) and 90 K emission (dashed) spectra of Cr(acac)3. The broad absorption centered at 560 nm corresponds to the lowest energy 4A2 → 4T2 ligand-field absorption, whereas the emission at 790 nm arises from the 2E excited state that is formed in <100 fs following excitation. Adapted from ref. 23. (Right) Qualitative potential energy surface diagrams appropriate for Cr(acac)3, with the corresponding ligand-field splitting diagrams depicting the valence d-orbital based electronic structure. The PES for the 2T1g state has been omitted for clarity. | ||
Our initial ultrafast time-resolved absorption measurements23 led to a model whereby initial formation of the 4T2 state was followed by intersystem crossing to the lower-energy 2E state with a time constant that exceeded our temporal resolution at that time (<100 fs). Longer time-scale measurements indicated a ground-state recovery time constant of ∼800 ps: given this, a process with a 1.1 ± 0.2 ps time constant that appeared to correspond to a narrowing and slight shift of a transient absorption profile that was virtually indistinguishable to the known differential absorption spectrum of the 2E state was assigned to vibrational relaxation in the 2E excited state. Subsequent studies by Kunttu and co-workers focused on the use of ultrafast infrared absorption spectroscopy,24,25 which is expected to be much more discriminating for vibrational relaxation dynamics than what can be inferred from electronic absorption spectra.26 Their data were consistent with an initial, sub-100 fs 4T1,2 → 2E intersystem crossing process, but biphasic kinetics associated with bleach recovery of the C–O and C–C stretching modes of the ligand of 15 ps and 760 ps indicated a more complex process than we initially suggested.
A more detailed discussion and analysis of the population dynamics of this system can be found elsewhere,27 but a basic picture of what is most broadly consistent with all of the experimental and computational28 studies on this system of which we are aware is summarized in Fig. 9. This model retains our initial hypothesis of impulsive intersystem crossing to the 2E state immediately following 4A2 → 4T2 excitation. This is followed by (thermally activated) back-intersystem crossing to the 4T2 state that occurs in competition with evolution on the 2E surface, resulting in a bifurcation of the excited-state population density. The back-intersystem crossing process accesses an internal conversion process from the 4T2 state back to the ground state (ca. 1 ps), which then cools (τ ∼ 10–15 ps). The fraction of population that does not undergo back-intersystem crossing cools on the 2E surface with a time constant of ∼7 ps, whereupon it also relaxes back to the ground state but on the much longer time scale of ∼800 ps identified by both our group and that of Kunttu.
 | ||
| Fig. 9 Jablonski diagram for Cr(acac)3, summarizing results from published femtosecond time-resolved absorption studies. | ||
The role of vibronic coherence in this system begins with a study we published in 2010.29 The initial motivation for this work was to take advantage of improved temporal resolution to try and quantify the time constant for the 4T2 → 2E intersystem crossing process that eluded us in the earlier study. While the ISC process could not be definitively identified, what we did observe was the first example of excited-state coherence in a coordination complex. The oscillation was fit to a ca. 164 cm−1 mode and assigned to a torsional motion about the primary coordination sphere of the compound. The nature of this motion coupled with the fact that (1) the coherence appears instantaneously upon excitation and persists through what was known to be the time scale of 4T2 → 2E intersystem crossing, and (2) a dephasing time of ∼70 fs led to the speculation that this mode might define the reaction coordinate along which ISC proceeds. Inspection of the motion associated with the 164 cm−1 coherence reveals large amplitude displacement on the periphery of the acac ligand, so a derivative was synthesized that replaced the terminal CH3 groups with tert-butyl groups (TMHD) in order to increase the steric bulk of this portion of the ligand framework. A time-dependent change in the spectral profile was interpreted as being associated with the 4T2 → 2E intersystem crossing process, suggesting a slowing in these dynamics of over an order of magnitude in response to this steric modification of the ligand. It should be noted that this study was published prior to the work of Kunttu and co-workers, so the interpretation of these data was based on what now must be viewed as an incorrect model for the overall kinetics of this class of compounds. We must therefore revisit this analysis in light of Kunttu’s work and the higher quality data we have been able to obtain on these chromophores since our previous report.
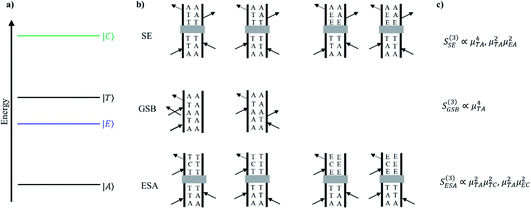
Because there are many mechanisms by which a coherence can be created in a sample during a pump–probe transient absorption experiment, it is important to assess the specific origin of each oscillatory component carefully. As mentioned in the Introduction, one can often exploit the disparity of time scales for dephasing between purely electronic and purely vibrational coherences to identify the type of coherence being monitored, i.e. electronic or vibrational. Electronic coherences typically dephase on sub-100 fs timescales,30,31 whereas vibrational coherences can require several picoseconds to completely dephase.32–35 In the system of interest, oscillations persist from several hundreds of femtoseconds to several picoseconds,7,36 excluding purely electronic coherences as a likely component of the signal. This leaves three possible origins for the oscillatory components in the data: (1) ground state vibrational coherence in the solvent, (2) ground state vibrational coherence in the solute, or (3) vibrational coherence in the excited electronic state of the solute. Solvent contributions can often be identified by performing the pump–probe experiment on neat solvent or performing a frequency domain Raman experiment and are therefore easily accounted for.
Discerning the nature of the solute coherence is in general more difficult. For this, it is helpful to consult a Feynman diagram: one appropriate for the Cr(acac)3 system is shown in Fig. 10. The processes depicted are stimulated emission (SE), ground state bleaching (GSB) and excited state absorption (ESA).37 The magnitude of the signal from each of these processes is a function of the probability of each necessary field interaction occurring, which is proportional to the transition dipole of the transition it induces. In the system of interest, both SE and GSB involve transitions solely between ligand field states, either between the 4A2 and 4T2 states or the 4A2 and 2E states. Due to their Laporte and/or spin forbidden nature, the transition dipoles associated with these features – essentially those coupling to the ground state – are small. In contrast, transitions arising from the 2E and/or 4T2 states will couple to charge-transfer states at higher energy, which are Laporte- and spin-allowed and will therefore possess substantially larger transition dipoles. Based on these considerations, the amplitudes of ESA signals will be much greater than for SE or GSB. Furthermore, we can acquire a rough estimate of the magnitude of this disparity by approximating the squared transition dipole for the 4A2 ↔ 4T2 and the ligand field ↔ charge transfer manifold transitions as the extinction coefficients in the ground state absorption spectra of Cr(acac)3 (∼100 M−1 cm−1)23 and [Fe(bpy)3]2+ (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1),16 respectively. From the third order response functions listed in Fig. 10, these values imply that the ESA signal is approximately 100-fold larger than those for GSB or SE. This is further supported by the observation that the TA spectrum for the systems of interest are positive throughout the visible spectrum.5,36,38 We can therefore conclude that any observed coherences in the time-resolved excited-state spectroscopy of Cr(acac)3 or its derivatives must be associated with an electronic excited state.
000 M−1 cm−1),16 respectively. From the third order response functions listed in Fig. 10, these values imply that the ESA signal is approximately 100-fold larger than those for GSB or SE. This is further supported by the observation that the TA spectrum for the systems of interest are positive throughout the visible spectrum.5,36,38 We can therefore conclude that any observed coherences in the time-resolved excited-state spectroscopy of Cr(acac)3 or its derivatives must be associated with an electronic excited state.
Now that we have established the nature of the signals that will be observed during a transient absorption experiment, it is important to address the mechanisms by which coherences dephase. In the optical Bloch picture, dephasing occurs primarily by population relaxation (T1) and pure dephasing  caused by random environmental fluctuations that cause a loss of phase information. The contributions of these two processes to the observed homogenous dephasing time (T2) are additive as seen in eqn (2),
caused by random environmental fluctuations that cause a loss of phase information. The contributions of these two processes to the observed homogenous dephasing time (T2) are additive as seen in eqn (2),
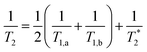 | (2) |
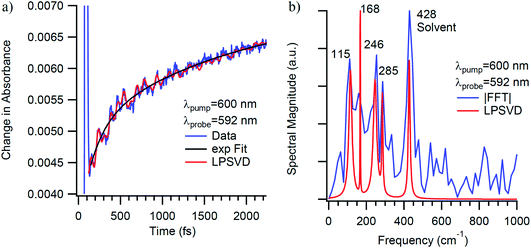
The vibrational coherences of Cr(acac)3 and their corresponding dephasing times following 4A2 → 4T2 excitation were monitored using transient absorption spectroscopy. Studies were conducted in acetonitrile, 1,4-dioxane, and tetrahydrofuran while probing on the red and blue edges of the excited state absorption feature. For the purposes of the present discussion, we will focus only on vibrational modes at 193 cm−1 and 461 cm−1.40 These appear robustly in data acquired in all three solvents and are largely independent of pump wavelength across the 4A2 → 4T2 absorption envelope and probe wavelengths spanning the excited-state absorption spectrum in the visible region and are therefore clearly associated with the electronic excited state(s) of the solute molecule (Fig. 11).
 | ||
| Fig. 11 (a) Single-wavelength kinetics of excited-state evolution in Cr(acac)3 in CH3CN solution at 592 nm following ∼40 fs excitation into the 4A2 → 4T2 absorption at 600 nm. The blue line corresponds to the experimental data, whereas the black and red lines correspond to a fit to a single-exponential decay model and an LPSVD analysis of the oscillatory features. (b) LPSVD (red) and fast Fourier transform (FFT, blue) analyses of the oscillatory components of the data shown in part (a). It should be noted that the data shown here are from a single measurement, whereas those discussed more generally in the text (and in Fig. 12) reflect an average of multiple data sets, hence the slight discrepancy in the vibrational frequencies. | ||
The lower frequency 193 cm−1 mode observed here is likely a more accurate value of the frequency observed previously.29 The dephasing time observed in this study (350 ± 130 fs) is also significantly longer than reported originally (70 fs) but is still substantially shorter than the ∼ps dephasing times typically thought of for vibrational coherences. The 461 cm−1 mode, on the other hand, shows a dephasing time of 1130 ± 500 fs that fits well with traditional values for pure vibrational coherences. Using the vibrational relaxation time constants of 7 ps and 12 ps measured by Kunttu and co-workers for the excited- and ground-electronic states, respectively,25 the ground-state recovery time of ∼1 ns is far too long for this electronic process to contribute to the observed dephasing time. Rather, the time scale for vibrational relaxation implies that the bulk of the dephasing occurs via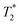 with a time constant of 1.3 ps, in agreement with the standard observation that most dephasing in liquids is due to pure dephasing.33 Based on these and other considerations arising from resonance Raman linewidth analyses, we conclude that the 461 cm−1 mode is most likely a pure vibrational mode evolving on the 2E excited state of the compound and therefore not associated with the reaction coordinate for the 4T2 → 2E intersystem crossing process.
with a time constant of 1.3 ps, in agreement with the standard observation that most dephasing in liquids is due to pure dephasing.33 Based on these and other considerations arising from resonance Raman linewidth analyses, we conclude that the 461 cm−1 mode is most likely a pure vibrational mode evolving on the 2E excited state of the compound and therefore not associated with the reaction coordinate for the 4T2 → 2E intersystem crossing process.
A corresponding analysis of the 193 cm−1 mode was inconclusive due in part to a significantly lower amplitude of the corresponding feature in the experimental Raman spectrum and distortion of the spectral shape from background signals that could not be adequately subtracted from the data. So, the presence of this feature in the coherence signal coupled with its intermediate dephasing time means that a link between dephasing time and the identification of an active mode along the reaction coordinate is still viable. Using density functional theory (DFT) calculations, we can start to acquire a better idea of the nature of each vibrational mode observed in the TA experiments and further define the type of motions active during the ISC process. It is important to reiterate that the vibrational modes in Cr(acac)3 are predominantly sampled from the 2E state which has the same electron configuration as the ground state and as such, is expected to have similar vibrational frequencies. The vibrational modes calculated for the ground electronic state should thus serve as an adequate substitute for vibrational modes in the excited state of Cr(acac)3 and simplify the calculations. On the basis of frequency matching, the 193 cm−1 and 461 cm−1 modes can be assigned to the pair of metal–ligand bond stretching vibrations calculated at 185 cm−1 and 453 cm−1, respectively (Fig. 12). Given the σ-antibonding character of the initially generated 4T2 state and the significant displacement along these types of coordinates on the 4T2 → 2E trajectory, it also makes intuitive sense that these modes involve significant distortion of the metal–ligand bond distance. The lower frequency 193 cm−1 mode is characterized by the entire ligand pushing toward the metal center while the two oxygen atoms splay outwards. The 461 cm−1 mode shows a slightly different motion, where each ligand compresses inward to make a smaller volumetric footprint through a decrease in the bite angle of the ligand. Neither of these vibrational modes involve the oxygen atoms moving in a linear trajectory with respect to the metal–oxygen bond vector, but rather appear more torsional in nature.
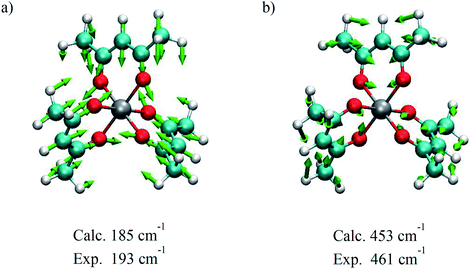 | ||
| Fig. 12 Nuclear displacements associated with the coherent oscillations shown in Fig. 11 at (a) 193 cm−1 and (b) 461 cm−1. The modes were visualized based on DFT calculations that yielded the energies indicated, whereas the experimental numbers reflect averages over multiple data sets. | ||
It seems likely that a twisting motion would be effective in relaxing the Laporte selection rule and thus enhance the efficiency of an interconfigurational process such as the 4T2 → 2E conversion. Indeed, evidence of the importance of torsional motion in transition metal complexes has been observed in several systems. Endicott and co-workers have shown trigonal twisting distortions to facilitate 2E → 4A2 ISC in octahedral Cr(III) complexes.41,42 In the case of Fe(II) complexes, Purcell used an angular overlap-based analysis to propose that Bailar and Ray–Dutt twisting deformations may be involved in the racemization dynamics of [Fe(phen)3]2+ (where phen = 1,10-phenanthroline) by facilitating interconversion between its low-spin (1A1) and high-spin (5T2) configurations,43 a model that was supported theoretically by Vanquickenborne and Pierloot44 and experimentally by McCusker et al., who showed that the kinetics of 5T2 → 1A1 relaxation appeared to depend on synthetic perturbations along torsional degrees of freedom.45 Hörner and co-workers later showed that both trigonal twisting and ligand breathing motions are likely coupled to the 1A1 ↔ 5T2 conversion in constrained Fe(II)-based spin-crossover systems.46 So, it is certainly reasonable that the types of motion identified in the coherence signatures observed for Cr(acac)3 could be coupled with the dynamics of 4T2 → 2E intersystem crossing. The 340 fs dephasing time of the 193 cm−1 mode is certainly something we would have described as the type of intermediate dephasing time that proved successful (at least empirically) for identifying a viable reaction coordinate in the case of the Fe(II) polypyridyl complex. That stated, the 461 cm−1 mode, which has been assigned as a pure vibrational mode in part due to its longer dephasing time, is strikingly similar to the 193 cm−1 mode in terms of its nuclear displacement. It therefore remains to be determined what significance, if any, do we ascribe the different dephasing times associated with these modes as it pertains to the 4T2 → 2E intersystem crossing reaction coordinate (and, more broadly, as a diagnostic tool for synthetic control of ultrafast dynamics)?
Chemical perturbations and their effect on vibronic coherences
In an effort to answer the question just posed, we consider transient absorption data we have acquired on several additional compounds: Cr(3-R-acac)3 (where R = Cl, Br, and I) and Cr(TMHD)3. These compounds represent different chemical perturbations to the basic Cr(acac)3 framework. Incorporating substituents in the 3-position of the acac ligand (i.e., the carbon atom between the two C–O groups) induces changes that are more electronic in nature rather than structural by affecting both the basicity of the oxygen donor atoms as well as the π interactions between the ligand and the t2g-symmetry orbitals of the metal center (the so-called nephelauxetic effect). Modifications at the 1- and 5-positions (e.g., tert-butyl groups replacing CH3 groups in TMHD), on the other hand, primarily affect the sterics of the system.The 4A2 → 4T2 absorption band of Cr(3-Cl-acac)3 (564 nm, 79 M−1 cm−1) is slightly redshifted from the 560 nm maximum in Cr(acac)3, consistent with the increased π-basicity of the chloro-substituted ligand raising the energy of the t2g orbital set and thus marginally decreasing the ligand field strength of the compound by ∼125 cm−1. Based on analogous assignments on Cr(acac)3, the bands centered at 272 and 358 nm can be assigned to intraligand π → π* and n → π* transitions, respectively.
Early time full spectrum TA data on Cr(3-Cl-acac)3 following 600 nm excitation into the red edge of the 4A2 → 4T2 ground state absorption band showed a clear decay in the blue and red edges of the transient absorption band similar to what was observed for the unsubstituted Cr(acac)3 parent molecule. Global fitting of the data to two sequentially decaying kinetic components revealed a 1.07 ps kinetic component responsible for the spectral changes at early times, again similar to what was observed for Cr(acac)3. Given the similar kinetics and observations between the two compounds, the ∼1.1 ps kinetic component of Cr(3-Cl-acac)3 can be assigned in an analogous manner to the parent compound, i.e., a convolution of processes involving 4T2 → 4A2 internal conversion subsequent to impulsive 4T2 → 2E intersystem crossing and back-conversion as the system thermalizes. Single wavelength datasets show an average time constant of 1.24 ± 0.07 ps, in good agreement with the full spectrum fit and quite similar to the time constant observed in the unsubstituted Cr(acac)3 compound.
Coherent oscillations were detected following excitation of Cr(3-Cl-acac)3 similar to that described for Cr(acac)3. The most robustly observed feature was a 149 cm−1 mode which was observed at all pump–probe combinations and confirmed to be associated with the chromophore. The nuclear displacements that characterize this degree of freedom are virtually identical to the 193 cm−1 mode observed for Cr(acac)3, with the reduction in energy likely the result of the increased reduced mass of the vibration due to the incorporation of the chloro group in the ligand framework of Cr(3-Cl-acac)3. Strikingly similar results were obtained for Cr(3-Br-acac)3 and Cr(3-I-acac)3, with coherent oscillations observed at energies of 123 cm−1 and 101 cm−1, respectively. Vector displacement representations of these modes for all three of these new derivatives (as well as the parent Cr(acac)3 complex) are illustrated in Fig. 13.
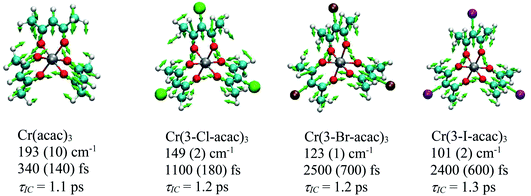 | ||
| Fig. 13 Nuclear displacements associated with the coherent oscillations identified for the Cr(3-R-acac)3 derivatives. Below each compound’s name is listed the DFT calculated frequency associated with the coherence feature, the measured dephasing time, and the time constant corresponding to the observed kinetics for excited-state evolution based on the model shown in Fig. 9. | ||
With these results in hand, we can gain further insights by comparing the results on each compound. First, it is clear by the qualitatively similar spectral evolution across the series that the excited state decay mechanism is likely the same for each member, i.e., following excitation into the 4T2 state, the molecule rapidly undergoes impulsive, ultrafast ISC to the doublet manifold followed by back-intersystem crossing to create a quasi-equilibrium between the 4T2 and 2E states. This provided a pathway whereby a portion of the 4T2 population can relax back to the ground state with a time constant of ∼1 ps while leaving some population to thermalize in the 2E state. Perhaps unsurprisingly given the identical decay mechanisms across the Cr(3-R-acac)3 series, the coherent vibrational mode that is active in each compound is also very similar. What is striking is the wide variation in the dephasing times for this mode, ranging from an “intermediate” value of ca. 350 fs in Cr(acac)3 to ∼2.5 ps for both Cr(3-Br-acac)3 and Cr(3-I-acac)3. From the Feynman diagram shown in Fig. 10, we know that the coherences sampled during the TA experiments must be from an electronic excited state (4T2 or 2E). Given that the internal conversion time constant of ca. 1 ps is significantly smaller than the ca. 2.5 ps dephasing time for the heavier halogen-substituted derivatives (i.e., R = Br and I), it is clearly the case that this vibrational mode is not sampled from the 4T2 state in these systems. That stated, one cannot use this line of reasoning as definitively in the cases of either Cr(3-Cl-acac)3 or Cr(acac)3 since the dephasing times in these compounds are comparable to or shorter than the population dynamics associated with interconversion between the 4T2 and 2E states.
Data acquired on Cr(TMHD)3 provides one final component to this discussion. In the previously published study,29 a pronounced change in the evolution of the spectral profile was attributed to a decrease in the rate of the initial intersystem crossing from the 4T2 state to the lower-lying 2E state relative to what was inferred for Cr(acac)3. This interpretation must be questioned in light of the work published by Kunttu subsequent to the 2010 study,24,25 but the fact that there is an obvious difference in the time-dependent characteristics of the differential absorption profile between Cr(acac)3 and Cr(TMHD)3 indicates that the kinetics of the latter have changed more dramatically than what was observed due to compositional variations across the Cr(3-R-acac)3 series. So, the introduction of steric bulk on the periphery of the ligand framework is clearly altering the excited-state dynamics of the system, but the question now is which process is being affected and does the dephasing time provide an indicator as to whether a given mode is coupled to this process.
Time-resolved absorption data were acquired on Cr(TMHD)3 as a function of pump and probe wavelength in dioxane, benzene, and THF solutions; a representative example is shown in Fig. 14. Modes at 125 ± 10 cm−1, 173 ± 12 cm−1, and 249 ± 6 cm−1 with dephasing times of 680 ± 420 fs, 770 ± 450 fs, and 960 ± 700 fs were identified consistently across all sample conditions. Vector projections of the 173 cm−1 and 249 cm−1 modes bear resemblance to modes identified in the other compounds that have been discussed in this report, and while it appears that the more sterically encumbered Cr(TMHD)3 does exhibit dephasing times that are intermediate between the unsubstituted Cr(acac)3 (340 fs) and the halogenated 3-substituted analogs, the error bars derived from sampling data across all of the various sample conditions makes it difficult to reach any firm conclusions. It does seem to be the case that the Cr(3-R-acac)3 series of compounds gave rise to a reduction in the vibrational frequency of the dominant mode and a concomitant increase in the dephasing time, whereas an opposite effect is evident in response to increased steric bulk on the periphery of the ligand framework. This trend prompts the question of whether there is an inverse relationship between the vibrational frequency (and by extension the vibrational period) and the susceptibility of a vibrational mode to be dephased by various excited-state processes (e.g., vibrational relaxation, intersystem crossing, internal conversion) or if there is a more subtle relationship between the collection of vibrational frequencies of a molecule and these excited-state dynamics at work. At this stage, the data we have in hand (as well as the current state of theoretical treatments of this issue) does not allow us to draw any firm conclusions at this time.
Concluding comments
We have presented an overview of two chemical systems in which excited-state coherences were used in an effort to gain insight into the vibrational degrees of freedom that served to define the reaction coordinate of ultrafast excited-state dynamics. In particular, it was postulated that coherence dephasing times that were intermediate between that expected for pure electronic versus pure vibrational processes were vibronic and therefore could constitute a metric by which certain modes could be singled out as likely candidates for synthetic manipulation. If successful, such an approach would provide a roadmap for how one could use ultrafast spectroscopy to guide synthetic design. In the case of an Fe(II) polypyridyl complex, identification of large-amplitude motions in the experimentally observed excited-state coherences suggested a mechanism for altering the trajectory of MLCT-to-LF state evolution. The incorporation of an electronic benign but sterically impactful metal ion in this portion of the superstructure yielded a compound whose MLCT excited-state lifetime was indeed extended by more than an order of magnitude. We have also presented a counterexample in the form of the electronically and vibrationally much simpler Cr(acac)3 platform. In this system, photoexcitation into the lowest energy 4A2 → 4T2 ligand-field absorption leads to an ultrafast intersystem crossing process to the lower lying 2E state, followed by an excited-state evolution process that bifurcates between back-intersystem crossing to the 4T2 state (with subsequent internal conversion back to the ground state) and vibrational relaxation on the 2E surface. Quantum oscillations superimposed on the observed kinetics suggested common vibrational degrees of freedom across a series of derivatives of the parent Cr(acac)3 complex, but wide variations in dephasing times from 340 fs to over 2 ps did not reveal any clear correlation with evolution along the operative reaction coordinates. So, while the results on the Fe(II) system reveal an instance where this correlation appears to have worked, the Cr(acac)3 results suggest that such a metric is far from robust as a predictive element for synthetic design.We are therefore left with the same question with which we began, i.e., can one use information from quantum coherences to inform on the degrees of freedom that couple to ultrafast excited-state dynamics? From the limited information available on this issue (much of which is contained in the results we have just presented), the only thing that seems clear at this stage is that the answer to this question is not clear. At present, dephasing times can suggest which modes might be of interest, but definitive proof that a given mode is, in fact, relevant to the reaction coordinate must still rely on an approach along the lines of what we demonstrated for the Fe(II) system, i.e., synthetic modification and subsequent experimental measurements on that new compound to determine if the synthetic change has had the desired effect. We believe that resolution of this issue – and an answer to what we believe is a potentially transformative approach to controlling excited-state dynamics a priori – will require a synergistic effort across teams with synthetic, spectroscopic, and theoretical expertise. We would argue that transition metal complexes provide a uniquely suitable platform for such an effort due to the fact that their electronic structures are intrinsically vibronic in nature and possess a degree of compositional flexibility to allow for the type of structure–property correlations that will be required. Efforts along these lines are currently underway.
Conflicts of interest
The authors confirm that there are no conflicts of interest to declare.Acknowledgements
The authors wish to acknowledge contributions from Dr Joel N. Schrauben and Dr Eileen D. Foszcz for their efforts in the initial development of the Cr(acac)3-based project. The research on the Fe(II) polypyridyl complexes was supported through a grant from the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Science, Office of Science, U.S. Department of Energy under Grant No. DE-FG02-01ER15282. The Cr(acac)3 was previously supported by the U.S. National Science Foundation under grant no. CHE-1300096, with continuing work now supported under CHE-2154233.Notes and references
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, R. A. Ratner, F. C. Spano, B. K. Whaley and X. Zhu, Using Coherence to Enhance Function in Chemical and Biological System, Nature, 2017, 543, 647–656 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson III, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and B. K. Whaley, Exploiting chemistry and molecular systems for quantum information science, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS.
- An excellent discussion of how one can link quantum coherence to a range of well-known chemical phenomena can be found in the information boxes contained in ref. 1.
- A. H. Zewail, Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS.
- J. N. Schrauben, Electronic Structure and Excited State Dynamics of Chromium(III) Complexes, PhD thesis, Michigan State University, 2010 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- E. D. Foszcz, Understanding the Interplay Between Geometry and Ultrafast Dynamics in Ligand Field Excited States of Inorganic Chromophores, PhD thesis, Michigan State University, 2015 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- A more complete discussion of the experimental set-up as well as pulse characterization, data analysis procedures, etc. can be found in ref. 5, 7, 10 and 27.
- A. M. Brown, C. E. McCusker, M. C. Carey, A. M. Blanco-Rodríguez, M. Towrie, I. P. Clark, A. Vlček and J. K. McCusker, Vibrational Relaxation and Redistribution Dynamics in Ruthenium(II) Polypyridyl-Based Charge-Transfer Excited State: A Combined Ultrafast Electronic and Infrared Absorption Study, J. Phys. Chem. A, 2018, 122, 7941–7953 CrossRef CAS PubMed.
- L. Wang, M. A. Allodi and G. S. Engel, Quantum coherences reveal excited-state dynamics in biophysical systems, Nat. Rev. Chem., 2019, 3(8), 477–490 CrossRef.
- Y. Nagasawa, Ultrafast photon echo experiments in condensed phase: detection of solvation dynamics, coherent wavepacket motions and static inhomogeneity, J. Photochem. Photobiol., C, 2011, 12(1), 31–45 CrossRef CAS.
- (a) F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Vibronic coherence in oxygenic photosynthesis, Nat. Chem., 2014, 6(8), 706–711 CrossRef CAS PubMed; (b) J. D. Gaynor, J. Sandwisch and M. Khalil, Vibronic coherence evolution in multidimensional ultrafast photochemical processes, Nat. Commun., 2019, 10(1), 5621 CrossRef CAS PubMed; (c) P. Karak, K. Ruud and S. Chakrabarti, Demystifying the Origin of Vibrational Coherence Transfer Between the S1 and T1 States of the Pt-pop Complex, J. Phys. Chem. Lett., 2021, 12(40), 9768–9773 CrossRef CAS PubMed.
- J. C. Dean and G. D. Scholes, Coherence Spectroscopy in the Condensed Phase: Insights into Molecular Structure, Environment, and Interactions, Acc. Chem. Res., 2017, 50(11), 2746–2755 CrossRef CAS PubMed.
- It should be noted that, to our knowledge, there has never been any report describing the observation of an electronic coherence signal for a transition metal-containing complex.
- B. C. Paulus, S. L. Adelman, L. L. Jamula and J. K. McCusker, Leveraging excited-state coherence for synthetic control of ultrafast dynamics, Nature, 2020, 582(7811), 214–218 CrossRef CAS.
- (a) O. S. Wenger, Is Iron the New Ruthenium?, Chem.–Eur. J., 2019, 25(24), 6043–6052 CrossRef CAS PubMed; (b) C. Wegeberg and O. S. Wenger, Luminescent First-Row Transition Metal Complexes, JACS Au, 2021, 1, 1860–1876 CrossRef CAS PubMed.
- K. J. Gaffney, Capturing photochemical and photophysical transformations in iron complexes with ultrafast X-ray spectroscopy and scattering, Chem. Sci., 2021, 12, 8010–8025 RSC , and references therein.
- J. K. McCusker, Electronic structure in the transition metal block and its implications for light harvesting, Science, 2019, 363(6426), 484–488 CrossRef CAS.
- (a) P. Pyykko, Relativistic Effects in Structural Chemistry, Chem. Rev., 1988, 88, 563–594 CrossRef CAS; (b) M. Kaupp, The Role of Radial Nodes of Atomic Orbitals for Chemical Bonding and the Periodic Table, J. Comput. Chem., 2007, 28, 320–325 CrossRef CAS PubMed.
- (a) Y. Liu, T. Harlang, S. E. Canton, P. Chábera, K. Suárez-Alcántara, A. Fleckhaus, D. A. Vithanage, E. Göransson, A. Corani, R. Lomoth, V. Sundström and K. Wärnmark, Towards Longer-Lived Metal-to-Ligand Charge Transfer States of Iron(II) Complexes: An N-Heterocyclic Carbene Approach, Chem. Commun., 2013, 49, 6412 RSC; (b) T. Reuter, A. Kruse, R. Schoch, S. Lochbrunner, M. Bauer and K. Heinze, Higher MLCT Lifetime of Carbene Iron(II) Complexes by Chelate Ring Expansion, Chem. Commun., 2021, 57, 7541–7544 RSC; (c) J. Steube, L. Burkhardt, A. Päpcke, J. Moll, P. Zimmer, R. Schoch, C. Wölper, K. Heinze, S. Lochbrunner and M. Bauer, Excited-State Kinetics of an Air-Stable Cyclometalated Iron(II) Complex, Chem.–Eur. J., 2019, 25, 11826–11830 CrossRef CAS PubMed.
- (a) D. C. Ashley and E. Jakubikova, Ray-Dutt and Bailar Twists in Fe(II)-Tris(2,2′-Bipyridine): Spin States, Sterics, and Fe–N Bond Strengths, Inorg. Chem., 2018, 57, 5585–5596 CrossRef CAS; (b) J. Nance, D. N. Bowman, S. Mukherjee, C. T. Kelley and E. Jakubikova, Insights into the Spin-State Transitions in [Fe(tpy)2]2+: Importance of the Terpyridine Rocking Motion, Inorg. Chem., 2015, 54, 11259–11268 CrossRef CAS PubMed; (c) H.-Y. Kwon, D. C. Ashley and E. Jakubikova, Halogenation Affects Driving Forces, Reorganization Energies and “Rocking” Motions in Strained [Fe(Tpy)2]2+ Complexes, Dalton Trans., 2021, 50, 14566–14575 RSC . See also ref. 43 and 45.
- E. A. Juban and J. K. McCusker, Ultrafast Dynamics of 2E State Formation in Cr(acac)3, J. Am. Chem. Soc., 2005, 127, 6857–6865 CrossRef CAS PubMed.
- E. M. S. Maçôas, R. Kananavicius, P. Myllyperkiö, M. Pettersson and H. Kunttu, Relaxation Dynamics of Cr(acac)3 Probed by Ultrafast Infrared Spectroscopy, J. Am. Chem. Soc., 2007, 129, 8934–8935 CrossRef PubMed.
- E. M. S. Maçôas, S. Mustalahti, P. Myllyperkiö, H. Kunttu and M. Pettersson, Role of Vibrational Dynamics in Electronic Relaxation of Cr(acac)3, J. Phys. Chem. A, 2015, 119, 2727–2734 CrossRef PubMed.
- While time-resolved vibrational studies represent the most direct way for probing vibrational relaxation dynamics, transient absorption spectra do provide some insights along these lines. See ref. 10 for an example.
- B. C. Paulus, Insights into the Photophysical Reaction Coordinate of 1st Row Transition Metal Chromophores from Vibrational Coherences, PhD thesis, Michigan State University, 2020 Search PubMed.
- H. Ando, S. Iuchi and H. Sato, Theoretical Study on Ultrafast Intersystem Crossing of Chromium(III) Acetylacetonate, Chem. Phys. Lett., 2012, 535, 177–181 CrossRef CAS.
- J. N. Schrauben, K. L. Dillman, W. F. Beck and J. K. McCusker, Vibrational Coherence in the Excited State Dynamics of Cr(acac)3: Probing the Reaction Coordinate for Ultrafast Intersystem Crossing, Chem. Sci., 2010, 1, 405–410 RSC.
- S. De Silvestri, G. Cerullo and G. Lanzani, Coherent Vibrational Dynamics, CRC Press, Boca Raton, FL, 2008 Search PubMed.
- P. J. Reid, C. Silva and P. F. Barbara, Electronic Coherence, Vibrational Coherence, and Solvent Degrees of Freedom in the Femtosecond Spectroscopy of Mixed-Valence Metal Dimers in H2O and D2O, J. Phys. Chem., 1995, 99, 2609–2616 CrossRef CAS.
- P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, 2011 Search PubMed.
- R. Monni, G. Auböck, D. Kinschel, K. M. Aziz-Lange, H. B. Gray, A. Vlček and M. Chergui, Conservation of Vibrational Coherence in Ultrafast Electronic Relaxation: The Case of Diplatinum Complexes in Solution, Chem. Phys. Lett., 2017, 683, 112–120 CrossRef CAS.
- Q. Wang, R. W. Schoenlein, L. A. Peteanu, R. A. Mathies and C. V. Shank, Vibrationally Coherent Photochemistry in the Femtosecond Primary Event of Vision, Science, 1994, 266, 422–424 CrossRef CAS PubMed.
- (a) S. Rafiq and G. D. Scholes, Slow Intramolecular Vibrational Relaxation Leads to Long-Lived Excited-State Wavepackets, J. Phys. Chem. A, 2016, 120, 6792–6799 CrossRef CAS PubMed; (b) S. Rafiq and G. D. Scholes, From Fundamental Theories to Quantum Coherences in Electron Transfer, J. Am. Chem. Soc., 2019, 141, 708–722 CrossRef CAS PubMed.
- Additional details can be found in the ESI associated with ref. 29.
- It should be noted that the mechanism by which ground state vibrational coherence in the solute is generated (impulsive stimulated Raman scattering) can be grouped with GSB in terms of the sign of the signal.
- Additional details can be found in ref. 23.
- E. Gershgoren, Z. Wang, S. Ruhman, J. Vala and R. Kosloff, Investigating Pure Vibrational Dephasing of I3− in Solution: Temperature Dependence of T2* for the Fundamental and First Harmonic of ν1, J. Chem. Phys., 2003, 118, 3660–3667 CrossRef CAS.
- There are a number of additional signals that are accounted for through resonance Raman specrtra, bandwidth analyses, etc. Details can be found in ref. 27.
- M. W. Perkovic and J. F. Endicott, Stereochemical Tuning of Chromium(III) Photophysics With N,N′,N′′-tris(alkylamine)-1,4,7-triazacyclononane complexes, J. Phys. Chem., 1990, 94, 1217–1219 CrossRef CAS.
- M. W. Perkovic, M. J. Heeg and J. F. Endicott, Stereochemical Perturbations of the Relaxation Behavior of 2E Chromium(III). Ground-State X-Ray Crystal Structure, Photophysics, and Molecular Mechanics Simulations of the Quasi-Cage Complex [4,4′,4′′-Ethylidynetris(3-Azabutan-1-Amine)]Chromium Tribromide, Inorg. Chem., 1991, 30, 3140–3147 CrossRef CAS.
- K. F. Purcell, Pseudorotational Intersystem Crossing in d6 Complexes, J. Am. Chem. Soc., 1979, 101, 5147–5152 CrossRef CAS.
- L. G. Vanquickenborne and K. Pierloot, Role of Spin Change in the Stereomobile Reactions of Strong-Field d6 Transition-Metal Complexes, Inorg. Chem., 1981, 20, 3673–3677 CrossRef CAS.
- J. K. McCusker, A. L. Rheingold and D. N. Hendrickson, Variable-Temperature Studies of Laser-Initiated 5T2 → 1A1 Intersystem Crossing in Spin-Crossover Complexes: Empirical Correlations between Activation Parameters and Ligand Structure in a Series of Polypyridyl Ferrous Complexes, Inorg. Chem., 1996, 35, 2100–2112 CrossRef CAS.
- P. Stock, E. Deck, S. Hohnstein, J. Korzekwa, K. Meyer, F. W. Heinemann, F. Breher and G. Hörner, Molecular Spin Crossover in Slow Motion: Light-Induced Spin-State Transitions in Trigonal Prismatic Iron(II) Complexes, Inorg. Chem., 2016, 55, 5254–5265 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |