Root-aligned SMILES: a tight representation for chemical reaction prediction

Abstract

Chemical reaction prediction, involving forward synthesis and retrosynthesis prediction, is a fundamental problem in organic synthesis. A popular computational paradigm formulates synthesis prediction as a sequence-to-sequence translation problem, where the typical SMILES is adopted for molecule representations. However, the general-purpose SMILES neglects the characteristics of chemical reactions, where the molecular graph topology is largely unaltered from reactants to products, resulting in the suboptimal performance of SMILES if straightforwardly applied. In this article, we propose the root-aligned SMILES (R-SMILES), which specifies a tightly aligned one-to-one mapping between the product and the reactant SMILES for more efficient synthesis prediction. Due to the strict one-to-one mapping and reduced edit distance, the computational model is largely relieved from learning the complex syntax and dedicated to learning the chemical knowledge for reactions. We compare the proposed R-SMILES with various state-of-the-art baselines and show that it significantly outperforms them all, demonstrating the superiority of the proposed method.

---

1 Introduction

Efficiently designing valid synthetic routes for valuable molecules plays a vital role in drug discovery and material design, which mainly involves forward synthesis prediction and retrosynthesis prediction. The former predicts reaction outcomes (product) with a given set of substrates (reactants and reagents), and the latter predicts reactants for a target compound. They are both challenging as the search space of all possible transformations is huge by nature. In the early days, expert synthetic chemists could design synthesis routes with their familiar reactions. To integrate more chemical knowledge and be more efficient, the first computer-aided synthesis planning program LHASA¹ was formally proposed by Corey et al. and showed great potential. Since then, many rule-based organic synthesis systems have come out, such as SYNLMA,² WODCA,³ and Synthia.⁴ However, with the increase in chemical reaction rules, the cost of manually hard-coding chemical rules into computer systems is getting higher. Alternatively, people have begun to explore fully data-driven approaches, where the current literature can be roughly categorized into two schools: selection-based methods^5–10 and generation-based methods.^11–22 Selection-based methods turn synthesis prediction into a ranking or classification problem, where the goal is to rank the matched reaction templates^5–8 or target molecules^9,10 higher than those unmatched for the input molecule. Despite encouraging results achieved, selection-based methods are unable to predict templates that are not in the training set, which makes it suffer from poor generalization on new target structures and reaction types. Generation-based methods, however, address the synthesis prediction with a generative model (e.g., transformers^11–19 or GNNs^20–22) where target compounds are generated, which significantly alleviates the poor generalization issue of selection-based methods.

Before applying generation-based methods for synthesis prediction, the first and critical step is to select the appropriate representation forms of both the product and the reactants. Two types of molecular representations are most widely used currently, including molecular graphs and string sequences. A molecular graph explicitly describes the topological structure of the molecule, upon which the recently well-developed GNNs^23,24 can be directly leveraged. However, graph-based representations involve a graph generation problem, which is challenging and usually solved by sequential graph edit operation predictions.^20–22 In contrast, another popular paradigm to represent molecules is using strings that are generated following some predefined chemical notation systems, of which the simplified molecular-input line-entry system (SMILES)²⁵ is most widely used currently. With strings as the representations of molecules, synthesis prediction can be formulated as the typical seq2seq translation problem in natural language processing, where plenty of methods or models can be borrowed.

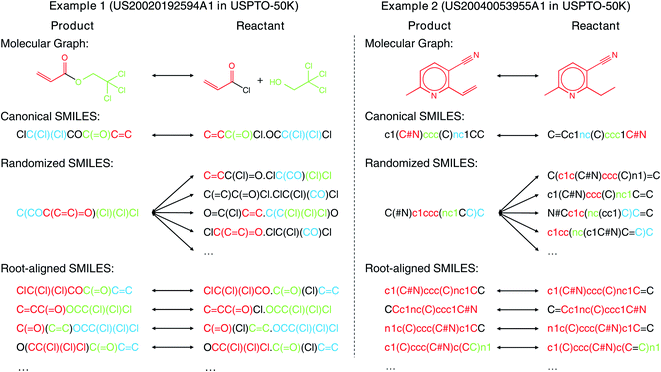
SMILES has been widely used for both forward synthesis prediction^17,26–28 and retrosynthesis prediction^11–19 in the current literature. However, in this work, we argue that the general-purpose SMILES is deficient for the synthesis prediction problem. Since SMILES is generated by a depth-first traversal of the molecular graph, a molecule can have multiple valid SMILES representations, which leads to the existence of multiple correct output SMILES for a given input SMILES. The one-to-many mapping between input SMILES and output SMILES renders synthesis prediction extremely challenging as the computational model should learn not only the chemical rules for chemical reactions but also the SMILES syntax for SMILES string validity. Several canonicalization methods^29,30 can be adopted to generate canonical SMILES that ensures a one-to-one mapping between molecules and SMILES. However, these methods are designed for each individual molecule without considering the relationship between product and reactant molecules, resulting in the large input–output SMILES discrepancy, as shown by the two examples (2,2,2-trichloroethyl prop-2-enoate and 2-ethyl-6-methylpyridine-3-carbonitrile) in Fig. 1. The large input–output SMILES discrepancy leaves the search space of reactants huge, degrading the performance of synthesis prediction models. Moreover, the canonical SMILES is incompatible with some data augmentation techniques where multiple SMILES are needed for one molecule to bypass the data scarcity issue, as the concept of “canonical SMILES” is violated by multiple SMILES for one molecule.

Fig. 1 Comparison of differences between input and output with different molecular representations for retrosynthesis prediction. The root atom of root-aligned SMILES is bold. The common structures that contain at least two atoms of input and output are represented with the same color. The more colored fragments in the output, the more similar they are.

In contrast to the large edit distance between the input and the output SMILES adopted in existing models, the molecular graph topology is in fact largely unaltered from reactants to products as the molecular changes usually occur locally during the chemical reactions.⁸ Therefore, in this article, we propose the root-aligned SMILES (R-SMILES) for more efficient synthesis prediction. As shown in Fig. 1, for each chemical reaction, R-SMILES adopts the same atom as the root (i.e., the starting atom) of the SMILES strings for both the products and the reactants, which makes the input and the output SMILES maintain a one-to-one mapping and highly similar to each other. The high similarity between the input and output makes synthesis prediction with R-SMILES very close to the typical autoencoding problem^31,32 where the goal is to learn an identity mapping between the input and the output, with some bottleneck features summarizing the most important aspects in the data. Motivated by this, we propose a transformer-based autoencoder for synthesis prediction. With the proposed R-SMILES, we first pretrain the proposed autoencoder with the cheaply available unlabeled molecular data for extracting the compact molecular representations and mastering essential SMILES syntax in the decoder. Then the model is finetuned with the reaction data, where the model is largely relieved from learning the complex syntax and can be dedicated to learning the chemical knowledge for reactions. We conducted extensive experiments to validate the proposed method on various synthesis tasks, including product to reactant, product to synthon, synthon to reactant, and reactant to product which all demonstrates the efficiency of the proposed R-SMILES. Compared with other baselines, our product-to-reactant and reactant-to-product variants both yield significantly superior performance on the public benchmark datasets. For a better understanding of the proposed method, we visualize the cross-attention mechanism in transformer with R-SMILES. Furthermore, we provide several multistep retrosynthesis examples successfully predicted by our method, which illustrates its great potential in complicated synthesis planning tasks.

2 Methods

To thoroughly evaluate the performance of the R-SMILES proposed for synthesis prediction, we implement our method on different synthesis tasks, including reactant-to-product, product-to-reactant, product-to-synthon, and synthon-to-reactant. The first two can be classified as the template-free method and the other two as the semi-template method. Template-free methods^{11–14,17–19,22,33} learn a direct mapping between products and reactants. Here for simplicity, the product is abbreviated as P and the reactant as R. The direct transformation between products and reactants is denoted by P2R or R2P. Semi-template methods^15,16,20,21 decompose retrosynthesis into two stages: (1) first identify intermediate molecules called synthons, and then (2) complete synthons into reactants. We use S to represent synthons, and P2S and S2R to represent the two stages, respectively. These four tasks are all formulated as end-to-end seq2seq problems and solved by the same model architecture to make comparisons with state-of-the-art (SOTA) methods. Many existing retrosynthesis work^7,8,20–22 demonstrate their performances with the reaction type known for each product. Since the reaction type is not always available in real-world scenarios, all experiments in this work are carried out without this information.

2.1 Datasets and data preprocessing

Experiments are conducted on USPTO-50K,³⁴ USPTO-MIT³⁵ and USPTO-FULL,⁷ all of which are widely used as public benchmarking datasets for the synthesis prediction task. USPTO-50K is a high-quality dataset containing about 50 000 reactions with accurate atom mappings between products and reactants. USPTO-MIT contains about 400 000 reactions as the training set, 30 000 reactions as the validation set and 40 000 reactions as the test set. USPTO-FULL is a much larger dataset for chemical reactions, consisting of about 1 000 000 reactions. For retrosynthesis prediction, reactions that contain multiple products are duplicated into multiple reactions to ensure that every reaction in data has only one product. Invalid data that contains no products or just a single ion as reactants are removed.

We use the same data split as previous researchers^5,7,35 for all the datasets. During the pretraining stage, depending on whether it is a forward or retrosynthesis prediction, products or reactants in the training set of USPTO-FULL are used for self-supervised training, where molecules in the test set of USPTO-50K and USPTO-MIT are removed.

2.2 Root-aligned SMILES

First of all, we follow Schwaller et al.'s²⁷ regular expression to tokenize SMILES to meaningful tokens. To get R-SMILES, we have to find the common structures of the source and the target, which can be found by atom mapping or substructure matching algorithms.³⁶ In this work, we use atom mapping in the reactions to find the common structures.

The root alignment operation is effortless in the P2R stage, where the input is only a single product. We can select a root atom from the product randomly first, and set it as the root atom to obtain the product SMILES. According to the new order of product tokens, we can find each corresponding root atom for reactants. We remove all atom mapping from the final input and output to avoid any information leak. An example of the root alignment is shown in Table 1. In the S2R stage, we put the product and synthon SMILES together as input, separated by a special token that does not exist in the SMILES syntax. We choose to align reactants to synthons to minimize the difference between the input and the output since there is a one-to-one mapping between synthons and reactants. The product is aligned to the largest synthon (i.e., the synthon with the most atoms). Taking the reaction in Table 1 as the example, first we can get the synthon with atom-mapping that is “[C:1]([CH:2]=[CH2:3])=[O:4]·[O:5][CH2:6][C:7]·([Cl:8])([Cl:9])[Cl:10]”. By selecting [Cl:8] and [C:1] as the roots of the synthons, we can obtain the input as “ClC(Cl)(Cl)COC(=O)C=C〈split〉ClC(Cl)(Cl)CO·C(=O)C=C” and the output as “ClC(Cl)(Cl)CO·C(=O)(Cl)C=C”. In the R2P stage, we align the product SMILES to the largest reactant. After root alignment, the input and output are highly similar to each other, which helps the model to reduce the search space and makes cross-attention stronger.

Table 1 An example (US20020192594A1 in USPTO-50K) of performing root alignment in the P2R stage. The root atoms are bold. (1) Select a reaction from the dataset. (2) Randomly select an atom as the root atom. [Cl:8] is selected here. (3) Obtain the product R-SMILES with specified root atom. (4) Remove the atom mapping to get the final input. (5) From the left to the right of the product SMILES, look for the atom mapping that appears on the reactant SMILES. Once found, the atom is selected as the root of the reactant. [C:1] and [Cl:8] are selected here. (6) Obtain the reactant R-SMILES without atom mapping to get the final output. (7) Tokenize the SMILES

Step			Example(id 66, USPTO-50K dataset): reactants ≫ products
(1)	Original data		Cl[C:1]([CH:2]=[CH2:3])=[O:4]·[OH:5][CH2:6][C:7]([Cl:8])([Cl:9])[Cl:10]
			≫[C:1]([CH:2]=[CH2:3])(=[O:4])[O:5][CH2:6][C:7]([Cl:8])([Cl:9])[Cl:10]
(2)	Randomly select a root atom from product		[C:1]([CH:2]=[CH2:3])(=[O:4])[O:5][CH2:6][C:7]([Cl:8])([Cl:9])[Cl:10]
(3)	Product R-SMILES with root atom mapping		[Cl:8][C:7]([Cl:9])([Cl:10])[C:6][O:5][C:1](=[O:4])[C:2]=[C:3]
(4)	Atom-mapping removal		ClC(Cl)(Cl)COC(=O)C=C
(5)	Select reactant roots according to product		Cl[C:1]([CH:2]=[CH2:3])=[O:4]·[OH:5][CH2:6][C:7]([Cl:8])([Cl:9])[Cl:10]
(6)	Reactant R-SMILES without atom mapping		ClC(Cl)(Cl)CO·C(=O)(Cl)C=C
(7)	Tokenization	Source	ClC(Cl)(Cl)COC(=O)C=C
		Target	ClC(Cl)(Cl)CO·C(=O)(Cl)C=C

---

2.3 Data augmentation with R-SMILES

Following the data augmentation strategy of the previous researchers,^16–18 we apply 20× augmentation at training and test sets of USPT0-50K, and 5× augmentation at training and test sets of USPTO-MIT and USPTO-FULL. When training the model, by enumerating different atoms as the root of SMILES, we can obtain multiple input–output pairs as the training data. In the inference stage, we input several different SMILES representing the same input to obtain multiple sets of outputs. Then we acquire the final prediction result by scoring these outputs uniformly. You can find the detail of how to make model predictions with data augmentation in the ESI.†

To highlight the superiority of R-SMILES, we use the vanilla transformer³⁷ without any modification. The source code is available online at https://github.com/otori-bird/retrosynthesis. The detailed descriptions of the model architecture and training details are available in the ESI.†

3 Results and discussion

3.1 Statistical analysis of the minimum edit distance with R-SMILES

We first provide some statistical analysis of the minimum edit distance between the input and the output for retrosynthesis prediction with or without the proposed R-SMILES in Table 2. The minimum edit distance between two strings is defined as the minimum number of editing operations (including insertion, deletion, and substitution) needed to transform one into the other. Here we adopt it to measure the discrepancy between input and output SMILES. Without R-SMILES, the average minimum edit distance between product and reactant SMILES is 17.9 on USPTO-50K, 17.0 on USPTO-MIT, and 19.8 on USPTO-FULL. However, with the proposed R-SMILES, the minimum edit distances become 14.1, 13.5, and 16.6, decreasing by 21%, 21%, and 16%, respectively. Moreover, to alleviate the overfitting problem, data augmentation with randomized SMILES is critical and widely used in existing methods,^16–18,28 but it would inevitably lead to a significant increase in the edit distance. For example, with 5× augmentation, the minimum edit distance is increased to 28.4 on USPTO-50K, which is more than two times of that of the proposed R-SMILES (14.1), where the minimum edit distance of R-SMILES keeps unchanged with data augmentation. The larger discrepancy and one-to-many mapping of randomized SMILES make the learning problem more difficult, hindering the performance of synthesis prediction.

Table 2 Edit distance with/without root alignment. Except for the data size, all figures are shown on average. Dataset^×m: m times data augmentation. Pro.: product SMILES. Rea.: reactant SMILES

Dataset	Data size	Length		Edit distance
		Pro.	Rea.	w/o	w/
USPTO-50K^×1	50 016	43.4	47.4	17.9	14.1 (−21%)
USPTO-50K^×5	250 060	45.1	49.6	28.3	14.1 (−50%)
USPTO-50K^×10	500 160	45.3	49.9	30.0	14.1 (−53%)
USPTO50K^×20	1 000 240	45.4	50.0	30.2	14.1 (−53%)
USPTO-MIT^×1	482 132	40.6	46.1	17.0	13.5 (−21%)
USPTO-MIT^×5	2 410 660	41.6	47.0	26.7	13.5 (−49%)
USPTO-FULL^×1	960 198	41.4	48.1	19.8	16.6 (−16%)
USPTO-FULL^×5	4 800 990	43.1	50.4	29.2	16.6 (−43%)

---

3.2 Comparisons with SOTA methods

We make comparisons between the proposed method and existing SOTA competitors for all four tasks. Top-K exact match accuracy, which represents the percentage of predicted reactants that are identical to the ground truth, is adopted as the metric to evaluate the performance. We additionally adopt the maximal fragment accuracy¹⁷ to evaluate the performance of P2R. The maximal fragment accuracy (MaxFrag), inspired by classical retrosynthesis, requires the exact match of only the largest reactant. The top-K exact match accuracy is used as the main metric to report the performance, and the maximal fragment accuracy is adopted in some cases for a more comprehensive comparison. Experiments are conducted on USPTO-50K, USPTO-MIT, and USPTO-FULL datasets.

Results of forward synthesis prediction are shown in Table 3. Similar to Schwaller et al.,²⁸ we conduct experiments in two settings: “separated” and “mixed”. The latter is a more challenging task as the model has to recognize the reactants correctly. Except that MEGAN²² is a graph-based method, others are all transformer-based. It is clear that our method outperforms others in most cases. Although Chemformer³⁸ uses much more model parameters and data than ours for pretraining, our method still obtains better results with the exception of top-1 accuracy. In different settings, the top-5 accuracy of our method is equal to or even higher than the top-20 accuracy of MEGAN, which fully illustrates the high efficiency of our method.

Table 3 Top-K accuracy of forward synthesis on the USPTO-MIT dataset. “Separated” and “mixed” denote whether reagents are separated from reactants or not

USPTO-MIT top-K accuracy (%)
Setting	Model	K = 1	2	5	10	20
Separated	MT^22,28	90.5	93.7	95.3	96.0	96.5
	MEGAN^22	89.3	92.7	95.6	96.7	97.5
	AT^17	91.9	95.4	97.0	—	—
	Chemformer^38	92.8	—	94.9	95.0	—
	Ours	92.3	95.8	97.5	98.0	98.6
Mixed	MT^22,28	88.7	92.1	94.2	94.9	95.4
	MEGAN^22	86.3	90.3	94.0	95.4	96.6
	AT^17	90.4	94.6	96.5	—	—
	Chemformer^38	91.3	—	93.7	94.0	—
	Ours	91.0	95.0	96.8	97.0	97.3

---

Results of retrosynthesis prediction are shown in Tables 4 and 5, from which we make the following three main conclusions: (1) generally speaking, the proposed P2R variant consistently outperforms SOTA competitors by a large margin. On the USPTO-50K dataset, it outperforms the current best template-free method by absolute 2.8%, 4.9% and 2.5% in top-1, top-10 and top-50 exact match accuracy, respectively. On the USPTO-MIT dataset, it also outperforms the concurrent work RetroTRAE⁴⁰ that only reports the top-1 accuracy, and yields better performance at other top-K accuracies than any other method. On the more challenging USPTO-FULL dataset, the accuracy improvement is still very substantial, by 2.3% in top-1, 3.1% in top-10, and 9.0% in top-50. Similarly, our P2S and S2R variants also achieve the best results except for the top-1 accuracy on the USPTO-50K dataset. The top-10 accuracies of them even reach 99.1% and 97.4%, respectively. We also combine these two phases together to get our product-to-synthon-to-reactant method that outperforms the current best semi-template method by absolute 1.8% and 6.1% in top-5 and top-10 accuracy, respectively. These impressing and consistent results demonstrate the superiority of the proposed method over SOTA methods. (2) Although Levenshtein augmentation³⁹ ensures the high similarity between the input and output SMILES as we do, it cannot guarantee the one-to-one mapping between them, which largely inhibits its performance. By specifying the root atom of input and output SMILES, our method can effectively guarantee the one-to-one mapping between them. (3) Our P2R variant achieves superior or at least comparable performance to the current SOTA template-based method LocalRetro⁸ on the USPTO-50K dataset. However, as template-based approaches are well known to be poor at generalizing to new reaction templates and coping with the huge number of reaction templates, the performances of LocalRetro on two large datasets USPTO-MIT and USPTO-FULL are substantially worse than ours, which strongly demonstrates the limitations of template-based methods. All these results verify the effectiveness and the superiority of our proposed method.

Table 4 Top-K accuracy in P2S and S2R stages on the USPTO-50K dataset

USPTO-50K top-K accuracy(%)
Stage	Model	K = 1	3	5	10
P2S	G2Gs^20	75.8	83.9	85.3	85.6
	GraphRetro^21	70.8	92.2	93.7	94.5
	RetroPrime^16	65.6	87.7	92.0	—
	Ours	75.2	94.4	97.9	99.1
S2R	G2Gs^20	61.1	81.5	86.7	90.0
	GraphRetro^21	75.6	87.7	92.9	96.3
	RetroPrime^16	73.4	87.9	89.8	90.4
	Ours	73.9	91.9	95.2	97.4

---

Table 5 Top-K single-step retrosynthesis results on USPTO-50K (top), USPTO-MIT (middle), and USPTO-FULL (bottom) datasets

Category	Model	K = 1	3	5	10	20	50
a Our product-to-synthon-to-reactant variant. b Our product-to-reactant variant. c Denotes that the result is implemented by the open-source code with well-tuned hyperparameters.
USPTO-50K top-K accuracy (%)
Template-based	Retrosim^5	37.3	54.7	63.3	74.1	82.0	85.3
	Neuralsym^6	44.4	6.3	72.4	78.9	82.2	83.1
	GLN^7	52.5	69.0	75.6	83.7	89.0	92.4
	LocalRetro^8	53.4	77.5	85.9	92.4	—	97.7
Semi-template	G2Gs^20	48.9	67.6	72.5	75.5	—	—
	GraphRetro^21	53.7	68.3	72.2	75.5	—	—
	RetroXpert^15	50.4	61.1	62.3	63.4	63.9	64.0
	RetroPrime^16	51.4	70.8	74.0	76.1	—	—
	Ours^a	49.1 ± 0.42	68.4 ± 0.53	75.8 ± 0.62	82.2 ± 0.72	85.1 ± 0.81	88.7 ± 0.88
Template-free	Liu's Seq2seq^11	37.4	52.4	57.0	61.7	65.9	70.7
	Levenshtein^39	41.5	48.1	50.0	51.4	—	—
	GTA^18	51.1 ± 0.29	67.6 ± 0.22	74.8 ± 0.36	81.6 ± 0.22	—	—
	Dual-TF^33	53.3	69.7	73.0	75.0	—	—
	MEGAN^22	48.1	70.7	78.4	86.1	90.3	93.2
	Tied transformer^19	47.1	67.2	73.5	78.5	—	—
	AT^17	53.5	—	81.0	85.7	—	—
	Ours^b	56.3 ± 0.15	79.2 ± 0.28	86.2 ± 0.34	91.0 ± 0.46	93.1 ± 0.48	94.6 ± 0.56
	MEGAN^22 (MaxFrag)	54.2	75.7	83.1	89.2	92.7	95.1
	Tied transformer^19 (MaxFrag)	51.8	72.5	78.2	82.4	—	—
	AT^17 (MaxFrag)	58.5	—	85.4	90.0	—	—
	Ours^b (MaxFrag)	61.0 ± 0.14	82.5 ± 0.26	88.5 ± 0.30	92.8 ± 0.35	94.6 ± 0.45	95.7 ± 0.53
USPTO-MIT top-K accuracy (%)
Template-based	Neuralsym^6	47.8	67.6	74.1	80.2	—	—
	LocalRetro^8	54.1	73.7	79.4	84.4	—	90.4
Template-free	Liu's Seq2seq^11	46.9	61.6	66.3	70.8	—	—
	AutoSynRoute^14	54.1	71.8	76.9	81.8	—	—
	RetroTRAE^40	58.3	—	—	—	—	—
	Ours^b	60.3 ± 0.22	78.2 ± 0.28	83.2 ± 0.36	87.3 ± 0.38	89.7 ± 0.35	91.6 ± 0.44
USPTO-FULL top-K accuracy (%)
Template-based	Retrosim^5	32.8	—	—	56.1	—	—
	Neuralsym^6	35.8	—	—	60.8	—	—
	GLN^7	39.3	—	—	63.7	—	—
	LocalRetro^8^c	39.1	53.3	58.4	63.7	67.5	70.7
Semi-template	RetroPrime^16	44.1	—	—	68.5	—	—
Template-free	MEGAN^22	33.6	—	—	63.9	—	74.1
	GTA^18	46.6 ± 0.20	—	—	70.4 ± 0.15	—	—
	AT^17	46.2	—	—	73.3	—	—
	Ours^b	48.9 ± 0.18	66.6 ± 0.24	72.0 ± 0.34	76.4 ± 0.40	80.4 ± 0.45	83.1 ± 0.52

---

3.3 Superiority of the proposed R-SMILES with data augmentation

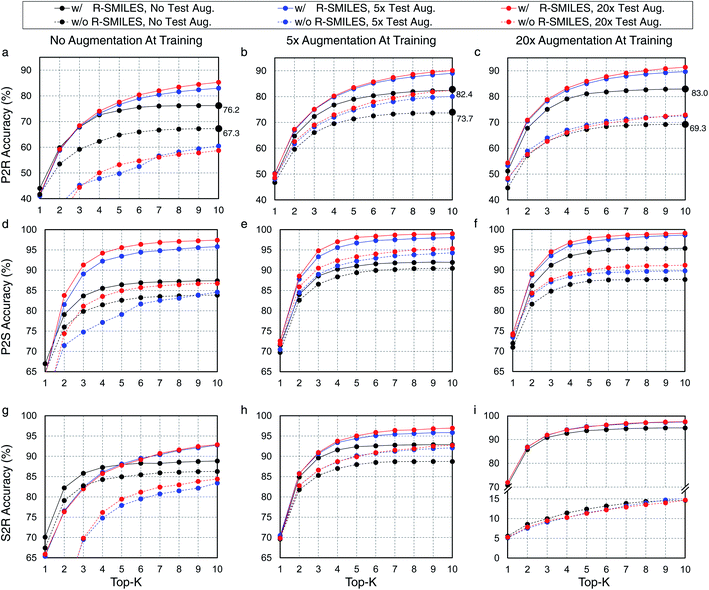
Here we evaluate the superiority of the proposed R-SMILES when data augmentation is applied in retrosynthesis tasks. We adopt the vanilla transformer,³⁷ a popular language translation model, as the retrosynthesis model. In retrosynthesis prediction, data augmentation can be applied to both the training and the test data,¹⁷ or only one of them. To test the performance of R-SMILES with data augmentation, different times of augmentation are conducted on training and test data. Here we take the widely used canonical SMILES as the baseline for comparisons. Experiments are conducted on the USPTO-50K dataset, with P2R, P2S, and S2R variants. Results are shown in Fig. 2. In each subplot, the solid and dashed lines represent the performance with and without R-SMILES, and different colors represent times of data augmentation. First of all, it is evident that the solid lines are consistently above the dashed lines with the same color in each subplot, which reveals that the performance with R-SMILES is consistently superior to the widely used canonical SMILES in the same data augmentation scenario. An interesting observation is that if no training data augmentation is applied (Fig. 2a, d and g), doing augmentation on the test data usually lowers the performance with the canonical SMILES. However, with the proposed R-SMILES, the accuracy is improved as expected, which indicates that the proposed method is more compatible with test data augmentation even though augmentation is not applied at the training time. Finally, by making plot-level comparisons, we can find that with more training data augmentation, the proposed R-SMILES yield higher accuracy. For example, if no data augmentation is applied at test time, 5× and 20× data augmentation of the training set increase the top-10 accuracy from 76.2% to 82.4% and 83.0%, respectively. However, without R-SMILES, the model may yield inferior performance if too much training data augmentation is applied. In the same case as the example above, 5× data augmentation increases top-10 accuracy from 67.3% to 73.7%, but 20× augmentation decreases it to only 69.3%. The underlying reason is that if too much training data augmentation is applied without R-SMILES, the retrosynthesis task becomes a one-to-many problem mentioned in Fig. 1, which is extremely difficult for the model to learn useful chemical knowledge for retrosynthesis. However, if no training data augmentation is used, the model may easily suffer from the overfitting problem, which leaves a trade-off issue regarding the data augmentation. From the experimental results in Fig. 2, it can be clearly seen that our proposed R-SMILES perfectly solves this issue and can reliably enjoy the higher performance with more data augmentation until reaching saturation.

Fig. 2 Top-K accuracy (%) with/without R-SMILES on USPTO-50K for P2R (a)–(c), P2S (d)–(f), and S2R (g)–(i). The solid lines (w/ R-SMILES) and dashed lines (w/o R-SMILES) represent the performance with or without R-SMILES, respectively. The lines with different colors represent the performance in different test set augmentation scenarios.

3.4 Visualization of cross-attention mechanism in transformer with R-SMILES

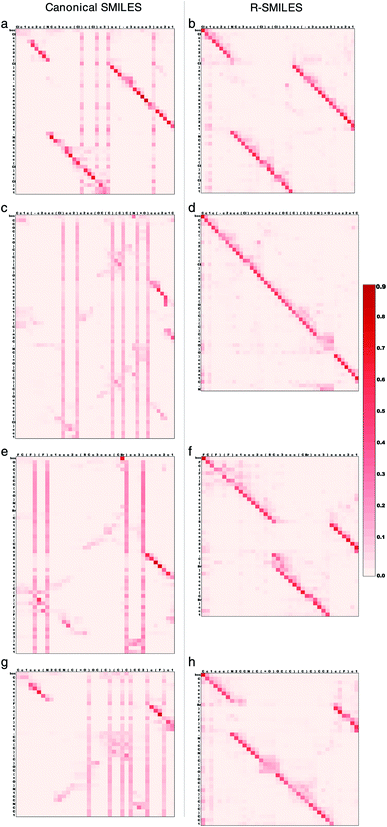
To further illustrate how the transformer works with R-SMILES, we randomly selected four reactions and display the visualization of the cross-attention maps in the retrosynthesis prediction in Fig. 3. The adopted transformer is an autoregressive model, where the last predicted token is taken as input for predicting the next token. The cross-attention represents the correlation between reactant tokens and product tokens. By feeding the same canonical SMILES to the models trained with R-SMILES or canonical SMILES and averaging the attention of each attention head in the last layer of the Transformer Decoder, we can get these attention maps to make a direct comparison. In Fig. 3a where the canonical SMILES of the product and the target reactant is highly similar to each other, it can be seen that the model could capture the aligned tokens and made the correct predictions. However, the attention of output tokens tended to pay much attention to some input tokens related to the SMILES syntax like ‘)’, and this problem exists in all maps obtained by the model trained with canonical SMILES. In contrast, with the proposed R-SMILES, the model gave the attention in Fig. 3b that is paid more on corresponding tokens and also succeeded. In Fig. 3c, although the canonical SMILES of the product and the target reactant is also highly similar, the model gave a disordered attention map and failed, which indicates that its ability to capture alignment information is insufficient. However, the model trained with R-SMILES not only obtained a well-aligned attention map in Fig. 3d, but also correctly predicted the target R-SMILES, where the target R-SMILES is also the canonical SMILES. In Fig. 3e and g where the canonical SMILES of the product and the target reactant is quite different, the model trained with canonical SMILES was unable to find alignment and had to focus on the global information, which ultimately led to the disordered attention maps and the failure of the predictions. However, thanks to the small discrepancy of R-SMILES pairs, in Fig. 3f and h the model trained with R-SMILES gave ordered attention maps and succeeded to predict the target R-SMILES. These results all demonstrate that our proposed R-SMILES effectively allows the model to focus on learning chemical knowledge for reactions and thus improves the accuracy of the model prediction. The attention maps of the forward reaction prediction and other layers can be found Fig. S3 and S4,† from which the same conclusion can be drawn.

Fig. 3 Visualization of the cross-attention obtained by the canonical SMILES (left) and the proposed R-SMILES (right) in the retrosynthesis prediction. (a), (c), (e) and (g) The attention maps obtained by the model trained with canonical SMILES. (b), (d), (f) and (h) The attention maps obtained by the model trained with R-SMILES. The input tokens are along the x axis, and the output tokens are along the y axis. Each row in the attention map represents the attention over the input tokens for predicting the next output token. Each column represents the attention between an input token with each output token. The “bos” token is the beginning of output tokens and will be removed after the decoding process completes.

3.5 Evaluating R-SMILES in more aspects of retrosynthesis

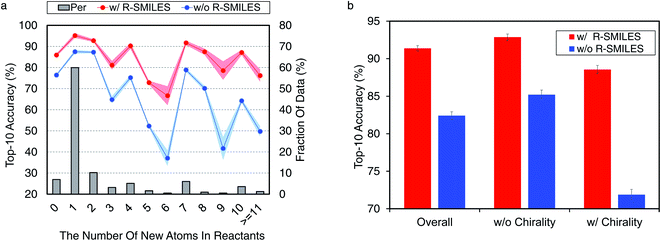
Here we conduct further studies to shed more light on the proposed R-SMILES when applied to retrosynthesis. Specifically, we investigate the performance of R-SMILES with some more complex reactions in the USPTO-50K, including reactions involving many new atoms in the reactants and chirality.

3.5.1 The number of new atoms in reactants. According to the number of new atoms (hydrogen atoms do not count) in reactants, we illustrate top-10 accuracy with or without R-SMILES and the amount of data in Fig. 4a. Similar to the previous results, the red line is always above the blue line, illustrating that the performance with R-SMILES surpasses the other by a large margin. In addition, the more new atoms in reactants, the larger improvement, especially for the situations with small amounts of data. For the reactions whose numbers of new atoms are 9, the improvement is impressively 39.3%, demonstrating that R-SMILES remains robust even with small amounts of data. This is because with R-SMILES that reduces the differences between the input and the output SMILES, the model can pay attention to the new fragments in the output SMILES.

Fig. 4 Accuracies for complex reactions. (a) Top-10 accuracy according to the number of new atoms in reactants. The red and blue lines represent the performance with/without R-SMILES. The gray bar means the percentage of this kind of reaction in the test set. (b) Top-10 accuracy for reactions involving with/without chirality. The red and blue bars represent the performance with or without R-SMILES.

3.5.2 Chirality. Chirality is a property of asymmetry and is important in drug discovery and stereochemistry. It can be represented by ‘@’ or ‘@@’ in SMILES sequences. We count 935 reactions with chirality in our test set of USPTO-50K and exhibit the top-10 accuracy with or without chirality and overall accuracy in Fig. 4b. When chirality exists in the reaction, the accuracy without R-SMILES drops 13.3%. In comparison, ours drops only 4.3%, proving that even in the presence of chirality, R-SMILES can still help the model focus on the more meaningful differences between the input and output SMILES. To be more specific, we believe that R-SMILES helps the chiral reaction mainly in two ways: (1) as shown in Table S1,† the reduction of editing distance of the chiral reaction is more significant than the overall one. (2) For USPTO datasets, the chiral signatures of the input and output tend to be identical after alignment, which makes the model usually only need to maintain the chiral consistency.

For other top-K accuracies, results for both indicators are similar and can be found in Fig. S5.† These results all demonstrate the effectiveness and robustness of R-SMILES.

3.6 Multistep retrosynthesis prediction by our method

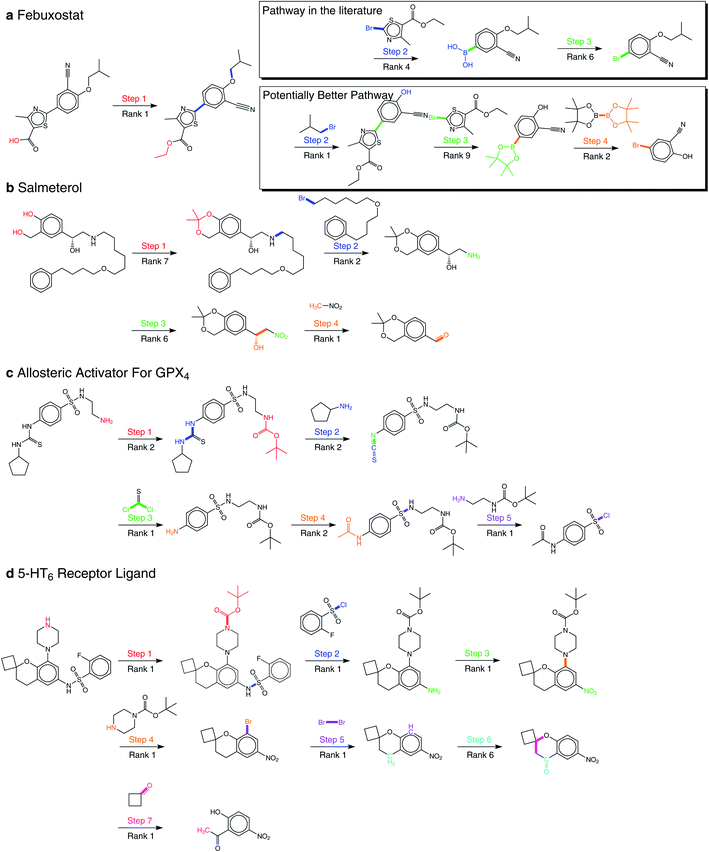
By applying our product-reactant variant recursively, we verify our method with several multistep retrosynthesis examples reported in the literature, including febuxostat,⁴¹ salmeterol,⁴² an allosteric activator for GPX₄,¹⁴ and a 5-HT₆ receptor ligand.⁴³ As shown in Fig. 5, our method successfully predicts the complete synthetic pathway for these examples.

Fig. 5 Multistep retrosynthesis predictions by our method. (a) Febuxostat. (b) Salmeterol. (c) An allosteric activator for GPX₄. (d) A 5-HT₆ receptor ligand. The reaction centers and transformations from products to reactants are highlighted in different colors at different reaction steps. In addition to the reaction pathway in the literature, we report a potentially better reaction pathway for febuxostat.

Febuxostat (Fig. 5a) is a novel anti-gout drug as the non-purine selective inhibitor of xanthine oxidase. Cao et al.⁴¹ reported a new reaction pathway for it based on the Suzuki cross-coupling reaction in 2016. Our predicted first step is hydrolysis of the ester, which is exactly the same as reported. For the remaining reaction steps, our method provides two different synthetic routes. The first one is the same as reported, where 3-cyano-4-isobutoxyphenyl boronic acid and ethyl 2-bromo-4-methylthiazole-5-carboxylate are taken as the reactants of the Suzuki cross-coupling reaction. However, the second one reports nucleophilic substitution to get aryl boronic esters for the Suzuki cross-coupling reaction. The final steps of them both involve borylation, where the second one is reported by Ishiyama et al.⁴⁴ We can make a detailed comparison between these two pathways in terms of yield and price: (1) there are two main findings for us in Urawa et al.'s study:⁴⁵ (a) boronic acid is thermally less stable than the corresponding boronic ester. Thus, boronic ester is more likely to be better for avoiding possible thermal decomposition. (b) The introduction of pinacol boronate can effectively reduce the generation of side reactions, i.e., reductive dehalogenation reactions, which helps to afford the desired product quantitatively. The second synthetic pathway is consistent with these findings, which shows that the second is likely to have higher yields. (2) From the Reaxys database, it can be found that the building block of the second pathway is much cheaper compared to the first path. Therefore, we believe that our method suggests a potentially better synthetic pathway for febuxostat.

Salmeterol (Fig. 5b) is a potent, long-acting, β2-adrenoreceptor agonist. Guo et al.⁴² proposed a reaction pathway for it based on the asymmetric Henry reaction. Although the first three steps provided by our method do not exist in the literature, they are all explainable. The first step reports the hydrolysis of cyclic acetal, where cyclic acetal has been proved to be stable. Considering the high activity of the phenolic hydroxyl group and the hydroxyl group connected to the benzyl group, the formation of cyclic acetal can effectively prevent the occurrence of side reactions, which illustrates the model has distinguished the properties of protection groups and preserved them to the starting compound. The second step involves the amination of halohydrocarbon, and the third step involves the reduction of the nitro group. The final step, which is the core reaction, is the asymmetric Henry reaction, where our method has successfully reproduced the generation of new chiral centers at the rank-1 prediction. This result also matches our conclusion of the great performance involving chirality as mentioned above.

The synthetic pathway of the GPX₄ activator compound (Fig. 5c) is reported by Lin et al.,¹⁴ who predicted the synthetic pathway with a template-free model by enumerating different reaction types. However, even without the reaction type, our method succeeds for all five reaction steps within the top-2 predictions, which directly demonstrates the superiority of our method. Among these five reaction steps, the Hinsberg reaction of the final step is the core reaction of the whole synthetic pathway. Our method succeeds in finding it at the rank-1 prediction.

Nirogi et al.⁴³ proposed a benzopyran sulfonamide derivative as an antagonist of 5-HT₆ receptor (Fig. 5d) in 2015. Although the synthetic pathway consists of seven reaction steps, our method succeeds at the rank-1 prediction for all steps except the sixth one predicted at rank-6. The second and fourth steps have attracted our attention, which are the Hinsberg reaction and nucleophilic aromatic substitution reaction (SNAr). In the Hinsberg reaction, primary amines are able to react with benzenesulfonyl chloride. In SNAr, the meta-nitro group reduces the density of electron cloud, which is conducive to the occurrence of reaction. The success of key steps in the long synthetic pathway further demonstrates the robustness of our method.

For all 22 reactions in these four examples, our method succeeds at the top-10 predictions, and mostly at the top-2 predictions. In addition, our method proposes a novel synthetic pathway for febuxostat that is more consistent with experimental experience. These exciting results all demonstrate the great potential of our method for multistep retrosynthesis.

3.7 Limitations

Even though our method currently achieves SOTA results on the USPTO datasets, the proposed R-SMILES has its own limitations. We calculated the accuracy of retrosynthesis for ring-opening and forming reactions in different datasets. Results are shown in Table 6. It can be seen that the accuracy of R-SMILES is not so high as that of other reactions. To make it clearer, we also calculated the edit distance between the input and the output SMILES for these reactions, as shown in Table 6. Compared with that of non-ring reaction R-SMILES, the edit distance of ring reactions is significantly larger. These results again verify our main motivation in this work that large distance between input and output strings will degrade the reaction prediction performance. You can check the results of other datasets in Table S3.†

Table 6 The edit distance and top-K accuracy of single-step retrosynthesis for ring and non-ring reactions on the USPTO-50K dataset

Reaction type	Edit distance	K = 1	3	5	10
a Without root alignment. b With root alignment.
Overall^a	30.2	49.9	68.5	75.0	80.2
Non-ring reaction^a	29.7	53.0	71.5	78.0	83.3
Ring-opening reaction^a	37.8	23.3	42.0	49.7	54.6
Ring-forming reaction^a	27.6	26.4	37.1	40.0	45.0
Overall^b	14.1 (−53%)	56.3	79.1	86.0	91.0
Non-ring reaction^b	13.3 (−55%)	58.8	81.5	88.5	93.1
Ring-opening reaction^b	23.4 (−38%)	30.7	56.3	61.9	65.9
Ring-forming reaction^b	17.5 (−37%)	38.0	57.9	63.6	71.9

---

The atom mapping annotations in the dataset may also be a limitation of the proposed method. Fortunately, in practice several fully automated atomic mapping tools have been developed, such as Indigo and RXNMapper,⁴⁶ which could be utilized for automatically generating the atom-mapping information. Albeit not perfectly accurate, these tools make the proposed method feasible on datasets without atom-mapping annotations. In fact, for the reported results on the USPTO-FULL dataset in our manuscript, all the R-SMILES are generated with the Indigo toolkit. The proposed method, as shown in Table 5, outperforms other competitors at any top-K accuracy. We believe these results give us a glimpse at the effectiveness of the proposed method on datasets without any atom-mapping annotations.

4 Conclusions

In this article, we propose R-SMILES for chemical reaction prediction. Unlike canonical SMILES that is widely adopted in the current literature, R-SMILES specifies a tightly aligned one-to-one mapping between the input and output SMILES, which decreases the edit distance significantly. With R-SMILES, the synthesis prediction model is largely relaxed from learning the complex syntax and can be dedicated to learning the chemical knowledge for reactions. We implement different variants to validate the proposed R-SMILES, both yielding superior performance to state-of-the-art methods. To better understand the proposed method, we further provide several interesting discussions, e.g. the visualization of the cross-attention between input and output tokens. Finally, the synthetic pathways of some organic compounds are successfully predicted to showcase the effectiveness of the proposed method.

Albeit striking performance achieved in retrosynthesis, we believe that the potential of R-SMILES is not fully explored in this work. From the perspective of methods, since R-SMILES maintains the high similarity of the input and the output, retrosynthesis can be formulated as a grammatical error correction problem rather than a translation from scratch. To address the limitations mentioned above, in the future we will also try to align multiple atoms to obtain more similar input–output pairs, as well as to combine our method with the latest automatic atom mapping method for the datasets without atom mapping annotations.

Data availability

The data and code used in the study are publicly available from our github repository: https://github.com/otori-bird/retrosynthesis.

Author contributions

Zipeng Zhong: conceptualization, investigation, methodology, validation, visualization and writing – original draft. Jie Song: investigation, methodology, validation and writing – review & editing. Zunlei Feng: investigation, methodology, validation and writing – review & editing. Tiantao Liu: validation, visualization and writing – review & editing. Lingxiang Jia: investigation and validation. Shaolun Yao: investigation and validation. Min Wu: supervision. Tingjun Hou: supervision and project administration. Mingli Song: supervision and project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by Zhejiang Provincial Science and Technology Project for Public Welfare (LGG22F020007), Key Research and Development Program of Zhejiang Province (2020C01024), the Starry Night Science Fund of Zhejiang University Shanghai Institute for Advanced Study (Grant No. SN-ZJU-SIAS-001), the Fundamental Research Funds for the Central Universities (2021FZZX001-23), and Zhejiang Lab (No.2019KD0AD01/014).

Notes and references

1. D. A. Pensak and E. J. Corey, ACS Symp. Ser., 1977, 61, 1–32.
2. P. Johnson, I. Bernstein, J. Crary, M. Evans, T. Wang and H. P. BA Holme, ACS Symp. Ser., 1989, 408, 102–123.
3. J. Gasteiger, M. Pförtner, M. Sitzmann, R. Höllering, O. Sacher, T. Kostka and N. Karg, Perspect. Drug Discovery Des., 2000, 20, 245–264.
4. S. Szymkuć, E. P. Gajewska, T. Klucznik, K. Molga, P. Dittwald, M. Startek, M. Bajczyk and B. A. Grzybowski, Angew. Chem., Int. Ed., 2016, 55, 5904–5937.
5. C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 1237–1245.
6. M. H. Segler and M. P. Waller, Chem.–Eur. J., 2017, 23, 5966–5971.
7. H. Dai, C. Li, C. Coley, B. Dai and L. Song, Advances in Neural Information Processing Systems, 2019.
8. S. Chen and Y. Jung, JACS Au, 2021, 1, 1612–1620.
9. Z. Guo, S. Wu, M. Ohno and R. Yoshida, J. Chem. Inf. Model., 2020, 60, 4474–4486.
10. H. Lee, S. Ahn, S.-W. Seo, Y. Y. Song, E. Yang, S. J. Hwang and J. Shin, Proceedings of the 31th International Joint Conference on Artificial Intelligence, 2021, pp. 2673–2679.
11. B. Liu, B. Ramsundar, P. Kawthekar, J. Shi, J. Gomes, Q. Luu Nguyen, S. Ho, J. Sloane, P. Wender and V. Pande, ACS Cent. Sci., 2017, 3, 1103–1113.
12. P. Karpov, G. Godin and I. V. Tetko, Artificial Neural Networks and Machine Learning – ICANN: Workshop and Special Sessions, 2019, pp. 817–830.
13. S. Zheng, J. Rao, Z. Zhang, J. Xu and Y. Yang, J. Chem. Inf. Model., 2019, 60, 47–55.
14. K. Lin, Y. Xu, J. Pei and L. Lai, Chem. Sci., 2020, 11, 3355–3364.
15. C. Yan, Q. Ding, P. Zhao, S. Zheng, J. Yang, Y. Yu and J. Huang, Advances in Neural Information Processing Systems, 2020, pp. 11248–11258.
16. X. Wang, Y. Li, J. Qiu, G. Chen, H. Liu, B. Liao, C.-Y. Hsieh and X. Yao, Chem. Eng. J., 2021, 420, 129845.
17. I. V. Tetko, P. Karpov, R. Van Deursen and G. Godin, Nat. Commun., 2020, 11, 1–11.
18. S.-W. Seo, Y. Y. Song, J. Y. Yang, S. Bae, H. Lee, J. Shin, S. J. Hwang and E. Yang, Proceedings of the AAAI Conference on Artificial Intelligence, 2021, pp. 531–539.
19. E. Kim, D. Lee, Y. Kwon, M. S. Park and Y.-S. Choi, J. Chem. Inf. Model., 2021, 61, 123–133.
20. C. Shi, M. Xu, H. Guo, M. Zhang and J. Tang, Proceedings of the 37th International Conference on Machine Learning, 2020, pp. 8818–8827.
21. V. R. Somnath, C. Bunne, C. Coley, A. Krause and R. Barzilay, Advances in Neural Information Processing Systems, 2021, pp. 9405–9415.
22. M. Sacha, M. Błaz, P. Byrski, P. Dabrowski-Tumanski, M. Chrominski, R. Loska, P. Włodarczyk-Pruszynski and S. Jastrzebski, J. Chem. Inf. Model., 2021, 61, 3273–3284.
23. M. Schlichtkrull, T. N. Kipf, P. Bloem, R. Van Den Berg, I. Titov and M. Welling, The Semantic Web, 2018, pp. 593–607.
24. P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, 2017, arXiv,  DOI:10.48550/arXiv.1710.10903.
25. D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
26. J. Nam and J. Kim, 2016, arXiv,  DOI:10.48550/arXiv.1612.09529.
27. P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098.
28. P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583.
29. N. M. O'Boyle, J. Cheminf., 2012, 4, 1–14.
30. N. Schneider, R. A. Sayle and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2111–2120.
31. Y. Pu, Z. Gan, R. Henao, X. Yuan, C. Li, A. Stevens and L. Carin, Advances in Neural Information Processing Systems, 2016.
32. K. He, X. Chen, S. Xie, Y. Li, P. Dollár and R. Girshick, 2021, arXiv,  DOI:10.48550/arXiv.2111.06377.
33. R. Sun, H. Dai, L. Li, S. Kearnes and B. Dai, Advances in Neural Information Processing Systems, 2021, pp. 10186–10194.
34. N. Schneider, N. Stiefl and G. A. Landrum, J. Chem. Inf. Model., 2016, 56, 2336–2346.
35. W. Jin, C. Coley, R. Barzilay and T. Jaakkola, Advances in Neural Information Processing Systems, 2017.
36. P. Englert and P. Kovács, J. Chem. Inf. Model., 2015, 55, 941–955.
37. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. u. Kaiser and I. Polosukhin, Advances in Neural Information Processing Systems, 2017.
38. R. Irwin, S. Dimitriadis, J. He and E. J. Bjerrum, Machine Learning: Science and Technology, 2022, 3, 015022.
39. D. Sumner, J. He, A. Thakkar, O. Engkvist and E. J. Bjerrum, ChemRxiv, 2020 DOI:10.26434/chemrxiv.12562121.v2.
40. U. V. Ucak, I. Ashyrmamatov, J. Ko and J. Lee, Nat. Commun., 2022, 13, 1–10.
41. Q. M. Cao, X. L. Ma, J. M. Xiong, P. Guo and J. P. Chao, Chin. J. New Drugs, 2016, 25, 1057–1060.
42. Z.-L. Guo, Y.-Q. Deng, S. Zhong and G. Lu, Tetrahedron: Asymmetry, 2011, 22, 1395–1399.
43. R. V. Nirogi, R. Badange, V. Reballi and M. Khagga, Asian J. Chem., 2015, 27, 2117.
44. T. Ishiyama, M. Murata and N. Miyaura, J. Org. Chem., 1995, 60, 7508–7510.
45. Y. Urawa, H. Naka, M. Miyazawa, S. Souda and K. Ogura, J. Organomet. Chem., 2002, 653, 269–278.
46. P. Schwaller, B. Hoover, J.-L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2021, 7, eabe4166.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02763a

---