Open Access Article
Open Access ArticleEu2+ emission from thermally coupled levels – new frontiers for ultrasensitive luminescence thermometry†
Małgorzata
Sójka
 a,
Marcin
Runowski
a,
Marcin
Runowski
 *b,
Teng
Zheng
b,
Andrii
Shyichuk
*b,
Teng
Zheng
b,
Andrii
Shyichuk
 a,
Dagmara
Kulesza
a,
Dagmara
Kulesza
 a,
Eugeniusz
Zych
a,
Eugeniusz
Zych
 *a and
Stefan
Lis
*a and
Stefan
Lis
 b
b
aUniversity of Wroclaw, Faculty of Chemistry 14. F. Joliot-Curie Street, Wroclaw 50-383, Poland. E-mail: eugeniusz.zych@chem.uni.wroc.pl
bAdam Mickiewicz University, Faculty of Chemistry Uniwersytetu Poznańskiego 8, Poznań 61-614, Poland. E-mail: runowski@amu.edu.pl
First published on 24th December 2021
Abstract
Designing luminescent thermometers operating in a broad T-range, spanning hundreds of degrees, presenting high thermal sensitivity and good resolution is one of the greatest challenges in the field. In this paper, we present SrB4O7:Eu2+, a novel luminescent thermometer, operating in the T-range of 11–600 K and presenting unprecedentedly high relative thermal sensitivity, i.e., up to ≈10.5%/K and ≈22.6%/K, using either Eu2+ luminescence decay time or intensity ratio as thermometric parameters, respectively. Such good performance classifies the SrB4O7:Eu2+ phosphor as the most sensitive inorganic luminescent thermometer ever reported. The temperature dependences of both luminescence intensity ratios and the emission decay time result from the same physical effect, i.e., thermal coupling of the lowest 5d1 excited level of Eu2+ and the 6P7/2 excited level of the 4f7 configuration of the dopant. The latter one is located ≈130 cm−1 below the 5d1. Such a strong coupling changes the contribution of the emission from the two levels, in response to the temperature change, but without any significant luminescence thermal quenching. This beneficial situation allows measuring spectra with a high signal-to-noise ratio, which lowers the uncertainty of the temperature measurement (improves resolution) in the whole operating T-range. The SrB4O7:Eu2+ material offers a broad operating T-range, as well as unprecedentedly high relative thermal sensitivity and low uncertainty of the temperature measurement.
1. Introduction
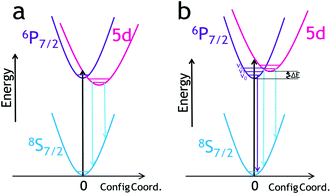
Developing highly sensitive luminescent thermometers is a challenging task. When the required/expected temperature range to be detected exceeds several hundred degrees, the design of such thermometers becomes even more demanding.1,2 As noted in ref. 3 a wide measuring range and high sensitivity of luminescent thermometers are slightly opposite requirements. Hence, one cannot expect that the high relative thermal sensitivity may be retained over the range of hundreds of degrees. However, it is conceivable a luminescent thermometer can operate over such a wide T-range, offering simultaneously high thermal sensitivity in the whole T-range, due to the use of a multi-parameter (multi-mode) sensing strategy.4–6 Such characteristics of a luminescent thermometer may be useful in various practical applications.Luminescence of Eu2+ typically consists of broadband emission resulting from its 5d → 4f transition. Fig. 1a presents the situation when the 5d level has lower energy than the 6P7/2 one and then only the 5d → 4f emission may occur. This situation is not attractive from the point of view of luminescence thermometry. Yet, Eu2+ may also generate photons as a consequence of the 4f → 4f transition, when the 6P7/2 excited manifold of the 4f7 configuration is located below the lowest-energy 5d1 level of the ion (see Fig. 1b). While generally uncommon, in some hosts such 4f → 4f emission of Eu2+ occurs, presenting the characteristic narrow lines, associated with the intra-configurational 6P7/2 → 8S7/2 transition.7,8 For the reasons discussed below, it may occur at rather low temperature values (cryogenic T-range). If the 6P7/2 level is located below the 5d1 one, both levels may be thermally-coupled. Since the lifetime of the 6P7/2 level is typically much longer (forbidden f–f transitions) than the lifetime of the 5d level (parity-allowed d–f transitions), once the coupling occurs, the 5d → 4f transition contributes to the emission effectively. The luminescence character may then change upon the increase of temperature, from the entirely intra-configurational 4f → 4f transition (narrow lines) to the inter-configurational 5d → 4f one (broadband).8
In such a situation, with increasing temperature, not only does the luminescence spectrum change significantly but also the emission decay time shortens, as the contribution of the parity-allowed 5d → 4f transition increases.10 Consequently, both the shape of the luminescence spectrum and the decay time of the emission may be potentially useful for thermometric applications. We shall present in this paper that such characteristics of Eu2+ luminescence may lead to unprecedentedly high relative thermal sensitivity of an optical thermometer, combined with a very broad operating T-range. Importantly, we consider the harmonization of both effects within a single inorganic compound is a significant achievement with the prospect of searching for other phosphors showing similar effects, and possibly offering even better thermometric performance.
The SrB4O7 host lattice is an excellent candidate for activation with Ln2+ ions. It has been shown that the tetrahedral structure of the BO4 groups stabilizes such dopants effectively, even in an oxidizing atmosphere and at high temperatures.11,12 The reducing capability of the host has been already demonstrated for Sm2+,13,14 Yb2+,15 Tm2+,16 Nd2+,17 and even Bi2+18,19 ions, despite their lower reduction potential, compared to Eu3+. The stability of Eu2+ in the SrB4O7 host was proven many years ago.8
Recently, we have presented the benefits of applying the 5d → 4f emissions of Pr3+ and Tm2+ in luminescence thermometry, showing that the use of their inter-configurational transitions greatly enhances the relative thermal sensitivity of such thermometers.20–24 Now, we turn our attention to the Eu2+ luminescence and its possible utility in the optical determination of temperature. The emission intensity of this ion is often strong, due to the broadband parity-allowed 4f → 5d excitation transition, that can be easily realized using standard light sources, which also widens the variety of potential applications.
Until now, a few strategies to exploit Eu2+ luminescence as an optical thermometer were employed. These involved the ratio of the Eu2+/Eu3+ emission intensities,25,26 the ratio of emission bands from Eu2+ occupying different sites of the host lattice,27,28 the rate of energy transfer between Eu2+ and other d- or f-block elements.29 Yet, to the best of our knowledge, there are no reports on the use of the Eu2+ 5d → 4f and 4f → 4f transition intensity ratio as a thermometric parameter. Detailed analysis of the fundamental research results on SrB4O7:Eu2+8 led us to the conclusion that this phosphor may offer particularly interesting thermometric properties. In this paper, we explore the idea focusing both on the SrB4O7:Eu2+ luminescence spectra and the emission kinetics. We show that SrB4O7:Eu2+ may work as a dual-mode ratiometric luminescent thermometer, using the luminescence intensity ratio (LIR) of its emission features and decay time of its luminescence. Moreover, we prove that it can operate in a broad T-range and show unprecedentedly high relative thermal sensitivity in cryo-range, whichever of the two modes is exploited.
2. Experimental
2.1. Synthesis
A powder SrB4O7:Eu2+ (3 mol%) was synthesized via a conventional solid-state (ceramic) method. SrCO3 (Sigma-Aldrich, 99.9%), H3BO3 (Chempur, p.a.), Eu2O3 (Stanford Materials, 99.99%) were the starting materials. The stoichiometric mixture of the reagents (with 5 mol% excess of H3BO3) was thoughtfully ground in an agate mortar with some acetone as a wetting medium. After natural drying, the mixture was transferred into a porcelain crucible covered with a lid and was heated in a furnace for 5 h at 700 °C in air. After cooling down, the powder was ground again and heat-treated for 5 h at 850 °C twice, with an intermediate grinding. It was crucial to cover the crucible with a lid to preclude the evaporation of B2O3 from the reacting mixture and limit the oxygen flow.2.2. Characterization
Powder X-ray diffraction pattern (XRD) was recorded using a Bruker D8 Advance diffractometer. The measurement was performed in the 2θ range of 10–60°, using Cu Ka1 radiation (λ = 1.5406 Å) with the counting time 0.2 s and the step 0.008°. The reference pattern was taken from Inorganic Crystal Structure Database (ICSD, #14383). The morphology of the sample was analyzed using a Hitachi S-3400N scanning electron microscope (SEM). Photoluminescence (PL), PL excitation spectra (PLE), and luminescence decay (DEC) traces were recorded in the 11–600 K temperature range, with FLS1000 Fluorescence Spectrometer from Edinburgh Instruments Ltd. For PL and PLE measurements a 450 W continuous xenon arc lamp was used as the excitation source, while for DEC traces a 60 W Xe pulse lamp was employed. The sample was mounted on a copper holder in a closed-cycle helium cryostat from Lake Shore Cryotronics, using Silver Adhesive 503 glue from Electron Microscopy Sciences. TMS302-X double grating excitation and emission monochromators of 325 mm focal lengths were used, and the luminescence signal was recorded with a Hamamatsu R928P high-gain photomultiplier detector, thermoelectrically cooled to −22 °C. The excitation spectra were corrected for the incident light intensity and the emission spectra were corrected for the spectral sensitivity of the recording system.3. Results
3.1. Structural and morphological properties.
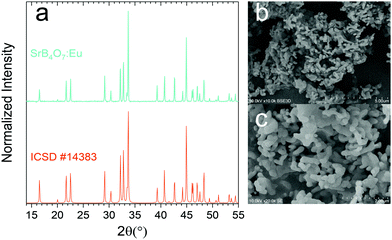
Fig. 2a–c presents the results of the structural and morphological characterization of the obtained powder phosphor. The measured XRD diffractogram matches perfectly with the ICSD #14383 reference pattern of SrB4O7, proving the expected orthorhombic structure (P21nm) of the synthesized phosphor material. In SrB4O7 there is only one Sr2+ cationic site with Cs point symmetry, and Eu2+ obviously enters this position. Representative SEM images of the synthesized phosphor material are presented in Fig. 2b and c. The grains have a narrow size distribution and show an elongated shape with about 1 μm length and about 100–150 nm thickness.3.2. Photoluminescence properties
Fig. 3a presents the PLE spectra of Eu2+ luminescence monitored at 367.2 nm and recorded at 11 and 300 K. Fig. 3b shows the PL spectra recorded at the same temperature values, under 300 nm excitation. A detailed analysis of the luminescence spectroscopy of the SrB4O7:Eu2+ system, including assignment of the observed lines, has already been presented by Meijerink et al.8 Here, we only discuss the temperature-dependent properties, important for the thermometric analysis presented below. The PLE spectra (Fig. 3a) consist of two broad overlapping bands covering roughly 240–280 nm and 280–360 nm ranges. Both bands are assigned to the inter-configurational 4f7 → 4f65d1 transitions. In the spectrum recorded at 11 K, numerous vibronic features can be observed at the low-energy part of the spectrum. The PL spectrum at low-temperature (Fig. 3b) reveals a strong sharp line of the 6P7/2 → 8S7/2 (4f → 4f) transition and a well-resolved vibrational structure at its longer wavelengths/lower energy side. The PL spectrum changes significantly when the temperature increases. A broad PL band is observed at 300 K. It originates from the inter-configurational 4f65d1 → 4f7(8S7/2) transition. Similarly, a significant change of the PL spectrum with temperature was observed in SrAl12O19:Eu2+.30 The onset of the broadband is blue-shifted in respect to the main 6P7/2 → 8S7/2 line, indicating that the energetically lowest (emitting) 5d1 level is located above the 6P7/2 excited level of the 4f7 configuration of Eu2+, as discussed in the Introduction part and presented in Fig. 1b. The reason for such location of energy levels in the SrB4O7:Eu2+ material is the high coordination number (CN = 9) of the Eu2+/Sr2+, which makes the crystal field splitting of the 5d configuration fairly low.7,9 Additionally, the low covalency of the bonds shifts the 4f65d1 configuration to a higher energy region. Solarz et al. proved a weak crystal field splitting for Sm2+ in the SrB4O7 host lattice, as well.31 The position of the 5d → 4f luminescence band of Eu2+ depends greatly on the host lattice properties. It may vary from 367 nm in SrB4O7:Eu2+ (Fig. 3b), up to even 850 nm in Ca3Sc2Si3O12:Eu2+.32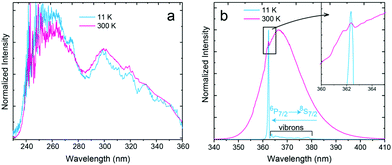 | ||
| Fig. 3 (a) PLE and PL spectra of SrB4O7:Eu2+ microparticles. The PLE spectrum was monitored at 367.2 nm and recorded at 11 and 300 K. (b) PL spectra recorded at 11 K and 300 K excited at 300 nm. In-depth analysis of the ZPL lines and vibronic transitions was presented in ref. 8. | ||
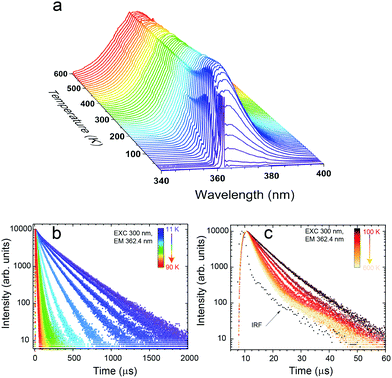
For thermometric purposes, we measured the temperature dependence of the PL spectra (Fig. 4a) and decay traces of Eu2+ luminescence (Fig. 4b and c) in the T-range of 11–600 K. With the increasing temperature, three narrow lines, blue-shifted in respect to the 6P7/2 → 8S7/2 transition emerge (see Fig. 4a and Fig. S1 in ESI†). These three higher-energy components result from the thermally populated Stark sub-levels of the 6P7/2 manifold,8i.e., from the 6P7/2 → 8S7/2 intra-configurational transition of Eu2+. Their spectral positions are in good agreement with the theoretically calculated splitting of the 6P7/2 state into four Stark sub-levels, for the Cs symmetry.33 With increasing temperature, the 4f65d1 → 4f7 broadband component suddenly appears and dominates the spectrum above 60 K. This obviously reflects the thermal population of the 5d1 level, as discussed in the Introduction. Despite the increasing intensity of the inter-configurational emission, the 6P7/2 → 8S7/2 luminescence is clearly visible even up to ≈600 K, being potentially useful for luminescence thermometry applications.
Apart from the PL spectrum, the decay kinetics of Eu2+ emission also reveal a significant temperature dependence. Fig. 4b and c present decay traces of Eu2+ luminescence, recorded in the 11–600 K range. As the temperature increases, the decay time drastically shortens. Such characteristics of the luminescence kinetics are also in accordance with the energy scheme of Eu2+ presented in Fig. 1b. At the lowest temperature (11 K), the spin- and parity-forbidden 6P7/2 → 8S7/2 emission dominates, and this implicates the longest decay time. With increasing temperature, the contribution from the 5d → 4f parity-allowed (but spin-forbidden) transition systematically increases, shortening the decay time. Meijerink et al.8 have shown that the lowest level of the 4f65d1 excited configuration lies ∼130 cm−1 above the lowest excited Stark sub-level of 6P7/2 of Eu2+. Due to the mentioned small energy difference, efficient thermal coupling of the 4f65d1 and the 4f7 (6P7/2) states can occur even at low temperatures. Note that both the intra-configurational 6P7/2 → 8S7/2 and the inter-configurational 4f65d1 → 8S7/2 emission bands have the same terminal (ground) level, and the corresponding transitions start from the thermally coupled states.7,34 In such a system, with the ΔE representing the energy difference between the involved levels, the rates of transitions from the levels being p2→1 (the 4f → 4f in the discussed system) and p3→1 (5d → 4f), the luminescence decay time (τ), at temperature T is well described by eqn (1):34–37
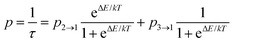 | (1) |
The luminescence decay curves recorded at higher temperature values presented in Fig. 4c (having a dominant contribution of the 5d → 4f emission), exhibit nearly a single exponential behavior, although the perfect fits required the use of a two-exponential function, eqn (2):38
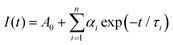 | (2) |
Thus, for temperature sensing applications, the average decay time, ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) calculated according to eqn (3):38
calculated according to eqn (3):38
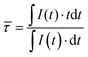 | (3) |
The most potent changes of the luminescence decay time occur between ≈10 and 100 K, when it decreases from ∼300 μs to ∼14 μs, see Fig. 5a. At higher temperature values, the decay time further shortens monotonically, proving the growing contribution of the allowed 5d → 4f transition to the total emission of Eu2+.
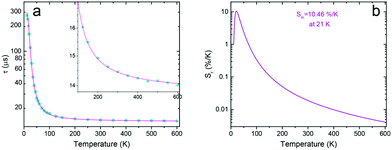 | ||
Fig. 5 (a) Average decay time ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) (eqn (3)) of SrB4O7:Eu2+ under 300 nm excitation and monitored at 362.4 nm. (b) Calculated relative thermal sensitivity of the investigated phosphor. (eqn (3)) of SrB4O7:Eu2+ under 300 nm excitation and monitored at 362.4 nm. (b) Calculated relative thermal sensitivity of the investigated phosphor. | ||
3.3. Luminescence decay time as a thermometric parameter
One of the most important parameters for characterizing and comparing the performance of a luminescence thermometer with other thermometers is its relative thermal sensitivity (Sr). Using the luminescence decay time as a thermometric parameter, Sr was calculated according to eqn (4):39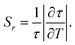 | (4) |
Applying the luminescence decay time mode, the SrB4O7:Eu thermometer shows the maximal relative thermal sensitivity, Sm = 10.46%/K at 21 K. This is one of the highest relative thermal sensitivities reported, using the luminescence decay time as a thermometric parameter. At higher temperature values, the relative sensitivity decreases rapidly and monotonously. Yet, up to 600 K, the decay time may serve as a reliable thermometric parameter, which makes the operating range as broad as 11–600 K.
3.4. Luminescence intensity ratio as a thermometric parameter
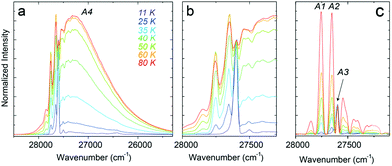
The temperature-induced changes in the luminescence spectra are evidently attractive for luminescence thermometry, as well (see Fig. 4a). To determine the thermometric parameters, we chose four different spectral areas denoted as A1, A2, A3 (4f → 4f narrow emission lines), and A4 (5d → 4f broad emission band) presented in Fig. 6. It should be noted that the two emissions discussed above, i.e., 5d → 4f and the 6P7/2 → 8S7/2 (4f → 4f) superimpose strongly, which poses the question about the possibility of separating the corresponding, spectrally overlapping bands. Moreover, with increasing temperature, the number of narrow lines clearly contributes to the total luminescence changes, as the number of vibronic features and those related to the transitions from the thermally-populated Stark sub-levels change in the PL spectrum. This can be seen in Fig. 6a.To calculate the intensities of the individual PL constituents, we separated the broad feature (band), corresponding to the 5d → 4f transition (A4, Fig. 6b), in order to extract the narrow-line components from the PL spectrum (A1–A3, Fig. 6c). For clarity and reproducibility, the applied procedure is depicted in Fig. S2a–c (ESI†), for representative temperature values. All the calculated values of the integrated areas are presented in Fig. S3 (ESI†). Consequently, the thermometric parameters Δ, were calculated for 5 different luminescence intensity ratios. Three of them (Δ1, Δ2, and Δ3) involved the ratio between the broadband and one of the narrow lines. The next two fractions (Δ4 and Δ5) represent the intensity ratios between the narrow lines. Thus, the Δ parameters were calculated according to eqn (5):
 | (5) |
The thermal evolution of the Δ1−5 parameters is presented in Fig. 7a. The errors in the determination Δ1−5 were calculated using eqn (6):40
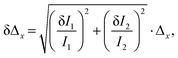 | (6) |
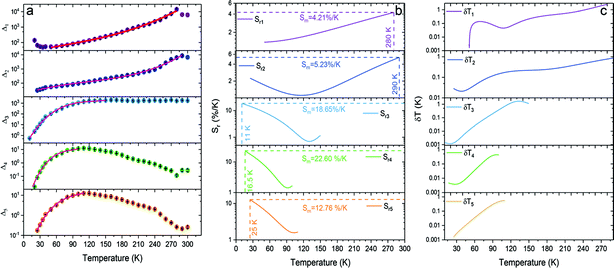 | ||
| Fig. 7 (a) Thermal evolution of Δ parameters for the SrB4O7:Eu2+ phosphor, (b) its relative thermal sensitivities, and (c) corresponding temperature uncertainties. | ||
The temperature dependence of the thermometric parameters Δ1–5 was successfully fitted using empirical functions, i.e., 3th-order polynomials because the Boltzmann function did not give good fits. We will return to this observation in the Discussion section. Table S1 (ESI†) presents the fitting parameters for each of the Δ1–5 thermometric parameters. The relative thermal sensitivities were calculated using eqn (3), where τ is replaced by Δ. Fig. 7b presents the calculated Sr values for each investigated Δ parameter. For Sr4, an unprecedentedly high value of the maximal relative sensitivity, Sm4 = 22.60% K−1 at 16.5 K, was obtained. To the best of our knowledge, this is the best-reported value so far for inorganic materials doped with lanthanide ions. It should also be noted that for each thermometric parameter used, the calculated relative sensitivity is virtually always greater than 1% K−1, within the entire operating T-range. Importantly, also for the other Δ parameters, the obtained Sm values are very high within the cryogenic T-range, (see Fig. 7b). It is worth noting that for Δ1 and Δ2 parameters the Sr values increase with temperature elevation, whereas for the Δ3–Δ5 ones the Sr values decrease, as clearly shown in Fig. 7b. Hence, utilizing the developed optical thermometer, the temperature of the system can be monitored in a very broad range, with high thermal sensitivities, better than 1% K−1 over the entire operating T-range.
The high values of relative thermal sensitivities are accompanied with high thermal resolutions (reaching even 10−3 K in the cryogenic T-range), i.e., small uncertainty values (δT, Fig. 7c) calculated using eqn (7):40
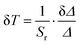 | (7) |
4. Discussion
It is notable that the maximal values of the relative thermal sensitivities (Sm) are very high both for the luminescence lifetimes (Sm ≈ 10.5% K−1) and for the band intensity ratios (Sm ≈ 22.6% K−1). The highest Sr values can be achieved in the T-range of 11–50 K. However, the operating range of the developed temperature sensor material – SrB4O7:Eu2+ – spans the 11–600 K range, using different sensing modes – lifetimes and intensity ratios. This makes the luminescent thermometer both a wide-range and extraordinarily sensitive tool. Its capability to work in different modes and to operate with multi-parameters makes it a universal sensor for thermometric purposes.Table 1 compares the most important optical thermometry figure of merits, of the developed sensor SrB4O7:Eu2+ with other high-performance inorganic, luminescent thermometers reported in the literature. Recently, Marciniak et al.41 presented an original strategy to develop luminescence thermometers based on a reversible phase transition and achieved Sm = 11.8% K−1 at 295 K (that is, around room temperature). In turn, the inorganic optical thermometer developed in this work is currently the leader in terms of thermal sensitivity in the cryogenic T-range.
| Material | Measured parameter | S m (% K−1) | T m (K) | T-range (K) | Equation type for Δ or τ-fitting | Ref. |
|---|---|---|---|---|---|---|
| a Eestimated based on figures in given references. | ||||||
| SrB4O7:Eu2+ | τ | 10.47 | 21 | 11–600 | Three-level system equation36 | This work |
| Δ 1 | 4.21 | 280 | 50–280 | Polynomial equation | ||
| Δ 2 | 5.23 | 290 | 25–290 | |||
| Δ 3 | 18.65 | 11 | 11–150 | |||
| Δ 4 | 22.60 | 16.5 | 16.5–100 | |||
| Δ 5 | 12.76 | 25 | 25–110 | |||
| LiYO2:Eu3+ | Δ | 11.80 | 295 | 263–376a | From experimental data | 41 |
| Sr2Ge0.75Si0.25O4:Pr3+ | Δ | 9.20 | 65 | 18–600 | Mott–Seitz equation | 21 |
| Sr2GeO4:Pr3+ | Δ | 9.00 | 22 | 17–600 | Mott–Seitz equation | 20 |
| YVO4:Nd3+ | Δ | 9.00 | 123 | 123–873 | Boltzmann equation | 46 |
| LaF3:Er3+,Yb3+ | Δ | 6.61 | 15 | 15–105 | Mott–Seitz equation | 47 |
| Bi2MoO6: Er3+,Tm3+,Yb3+ | Δ | 5.50 | 293 | 293–623 | Polynomial equation | 48 |
| Y2Ti2O7:Pr3+ | Δ | 5.25 | 289 | 289–573 | Semi-empirical equation | 49 |
| SrTiO3:Lu3+ | Δ | 4.60 | 200 | 120–290a | From experimental data | 50 |
| ZnGa2O4:Cr3+ | Δ | 2.80 | 310 | 77–450 | Boltzmann equation | 51 |
| Bi2SiO5:Yb3+,Tm3+@SiO2 | Δ | 2.60 | 280 | 400–800 | Boltzmann equation | 52 |
| TiO2:Sm3+ | Δτ | 10.54 | 330 | 298–383a | Not reported | 53 |
| 10.15 | 339 | |||||
| Al2O3:Sm2+ | Δτ | 4.80 | 298 | 298–648 | Boltzmann equation | 54 |
| 1.20 | 531 | 100–620 | ||||
| SrTiO3:Tb3+ | τ | 8.83 | 180 | 10–230 | From experimental data | 50 |
| SrB4O7:Sm2+ | τ | 3.36 | 550 | 300–673 | Boltzmann equation | 55 |
| Y2SiO5:Pr3+ | τ | 2.67 | 417 | 11–500 | Double-barrier equation | 56 |
| GAG:Mn3+,Mn4+ | τ | 2.08 | 249 | 123–350a | Mott–Seitz equation | 57 |
As we mentioned in the Introduction part, achieving a broad operating T-range combined with high relative sensitivity is a great challenge in the field of luminescence thermometry. In this paper, we showed that the Eu2+ luminescence in the strontium borate host matrix may fulfill the most important requirements of such thermometers. Thermal coupling of the excited states, the 6P7/2 level of the 4f7 configuration, and the lowest level of the 4f65d1 configuration may offer both spectacular sensitivity and a wide operating range, spanning from cryogenic to at least 600 K. Since the energy of the 6P7/2 level is basically fixed and independent of the host, the only way to design such thermometers is to maintain the energy of the 4f65d1 excited state slightly above the 6P7/2 emitting level.
The energy of the lowest state of the 4f65d1 excited configuration is defined by the crystal-field splitting of this configuration, as well as by the ionicity of the chemical bonding of Eu2+. These bonds should be strongly ionic to shift the entire 4f65d1 configuration to higher energies. Then, the crystal-field splitting of the configuration should be as low as possible, to avoid shifting the lowest-energy 4f65d1 level too much downward. These requirements are in some sense contradictory since the ionic bonds exert a fairly high crystal-field strength. Yet, what may help is the introduction of the Eu2+ ion into a large site with a high coordination number of ligands that readily form ionic bonds. Apparently, these basic requirements are quite well-fulfilled in the SrB4O7:Eu phosphor. In order to shift the maximal relative sensitivity of the sensor to a higher temperature region, the gap between the lowest 4f65d1 level and the 6P7/2 level below it should be greater than 130 cm−1 in SrB4O7:Eu2+.
We would like to emphasize, yet, the difference (from the luminescence thermometry point of view) between the Eu2+ emission used here and the previously published properties of Pr3+ emission.20–22 In thermometers using the latter dopant, emissions from the non-thermally-coupled levels were exploited and thermal quenching of such emissions was inherently utilized to get a high-performance sensor. This necessarily degraded the emission intensity deteriorating their thermal resolution (by decreasing the signal-to-noise ratio). On the contrary, in the case of the SrB4O7:Eu2+ sensor material, the emission of Eu2+ is not thermally quenched in the classical sense – the energy gained by the ion is not lost non-radiatively but is split between the two emitting levels of the dopant, instead. This is an important advantage, as the overall emission intensity is hardly dependent on temperature, with a respective reduction in the uncertainty of the measured temperature.
At first, it is surprising that the thermometric parameters based on luminescence intensity ratio (Fig. 7a) could not be effectively fitted using the Boltzmann function, despite the 6P7/2 and the 4f65d1 emitting levels are obviously thermally coupled. In the earlier literature, one may find examples of similar divergence from anticipations.42,43 Such a problem is typically encountered when luminescence intensity ratio in a wide range of temperature is analyzed or complex relaxation processes between (or from) the thermally coupled levels take place.42,44 Such circumstances seem to exist in the SrB4O7:Eu2+ phosphor. The decay time of the 5d → 4f luminescence presents measurable (and useful for temperature sensing) changes from 11 to 600 K, while the 5d → 4f/4f → 4f luminescence intensity ratio appeared useful as thermometric parameter merely up to about 280 K. Detailed understanding of all aspects of the reasons of the non-Boltzmann dependence of the ratio of the emissions would require much more comprehensive examination of the phosphor. Possibly, more thorough computational exploration of deconvolution of the experimental spectra into the numerous components would be needed.
Finally, we note that the Eu2+ the characteristics of the luminescence of the SrB4O7:Eu2+ phosphor presents some similarity with emission of Cr3+ in some hosts. The latter ion shows interesting thermometric properties when its thermally coupled 4T2 and 2E excited states are employed.43,45 And also in this case this is the crystal field which plays an important role. When it is strong enough to lift the 4T2 level above the 2E one, the Boltzmann distribution between them defines the thermometric performance of the selected phosphor. Yet, also for Cr3+, the Boltzmann law is obeyed over a limited range of temperature and in wide ranges it is not,43 exactly as for Eu2+. Thus, the physics defining the SrB4O7:Eu2+ phosphor thermometric performance and standing behind the Cr3+ activated luminescence thermometers are fairly similar.
5. Conclusions
Here, we have shown that the selection of an appropriate host matrix (in our case SrB4O7) embedded with the desired, optically active divalent lanthanide ions (in this case Eu2+) is essential for the development of highly sensitive optical thermometers. The decisive role in designing such temperature sensors is an interplay between the inter- and intra-configurations transitions within the activator ion, where the relative energy difference of the corresponding excited states is crucial to achieving unprecedentedly high thermal sensitivity and great resolution of the final luminescent thermometer. In this work, it was found that the luminescence properties of the investigated SrB4O7:Eu2+ phosphor are very promising for thermometric purposes. Its emission spectra, as well as the decay kinetics, are strongly temperature-dependent. In the cryogenic temperature range, below ≈20 K, the emission results mainly from the intra-configurational 6P7/2 → 8S7/2 transition, while with increasing temperature, the broadband luminescence resulting from the inter-configurational 5d → 4f transition begins to appear, and increasingly contributes to the overall emission intensity. This results from the thermal coupling of the two emitting levels separated only by about 130 cm−1. Another consequence of this thermal coupling between the excited 6P7/2 and the lowest 4f65d1 levels is the strong temperature dependence of the luminescence decay time, which significantly shortens with increasing temperature. Altogether, the SrB4O7:Eu2+ phosphor presents very attractive properties for thermometric purposes. Its broad operating range in ratiometric mode spans the 11–280 K range, and its maximal relative sensitivities vary from ≈4 to above 22% K−1 (depending on the Δ parameter used). Using the luminescence decay time as a thermometric parameter the operating range is even broader, namely 11–600 K, and the maximal relative thermal sensitivity was found to reach 10.46% K−1, which is one of the highest values ever reported for relative sensitivity based on a luminescence decay time. Importantly, the high sensitivity values are in line with great thermal resolutions, which reach even 10−3 K in the cryogenic T-range. This paper proves that Eu2+ luminescence may offer much more for thermometry than previously thought.Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Polish National Science Centre (NCN) under grant #UMO 2018/29/B/ST5/00420. Publication partially financed by the program “Excellence Initiative – Research University”.References
- M. D. Dramićanin, J. Appl. Phys., 2020, 128, 040902 CrossRef.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- Y. Gao, Y. Cheng, T. Hu, Z. Ji, H. Lin, J. Xu and Y. Wang, J. Mater. Chem. C, 2018, 6, 11178–11183 RSC.
- M. Runowski, P. Woźny, S. Lis, V. Lavín and I. R. Martín, Adv. Mater. Technol., 2020, 1901091 CrossRef CAS.
- M. A. Hernández-Rodríguez, K. Kamada, A. Yoshikawa, J. E. Muñoz-Santiuste, A. Casasnovas-Melián, I. R. Martín, U. R. Rodríguez-Mendoza and V. Lavín, J. Alloys Compd., 2021, 161188 CrossRef.
- L. Marciniak, K. Elzbieciak-Piecka, K. Kniec and A. Bednarkiewicz, Chem. Eng. J., 2020, 388, 124347 CrossRef CAS.
- G. Blasse and B. Grabbmaier, Luminescent Materials, Springer-Verlag, Berlin Heidelberg, 1994 Search PubMed.
- A. Meijerink, J. Nuyten and G. Blasse, J. Lumin., 1989, 44, 19–31 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2013, 135, 93–104 CrossRef CAS.
- J. G. Bunzli and S. V. Eliseeva, Springer Ser. Fluoresc., 2011, 1–45 CAS.
- M. Suta and C. Wickleder, J. Lumin., 2019, 210, 210–238 CrossRef CAS.
- M. Suta, F. Lavoie-Cardinal and C. Wickleder, Angew. Chem., Int. Ed., 2020, 59, 10949–10954 CrossRef CAS PubMed.
- F. Datchi, R. LeToullec and P. Loubeyre, J. Appl. Phys., 1997, 81, 3333–3339 CrossRef CAS.
- T. Zheng, M. Runowski, P. Woźny, S. Lis and V. Lavín, J. Mater. Chem. C, 2020, 8, 4810–4817 RSC.
- G. Blasse, G. J. Dirksen and A. Meijerink, Chem. Phys. Lett., 1990, 167, 41–44 CrossRef CAS.
- P. Solarz, J. Komar, M. Głowacki, M. Berkowski and W. Ryba-Romanowski, RSC Adv., 2017, 7, 21085–21092 RSC.
- W. Xu and J. R. Peterson, J. Alloys Compd., 1997, 249, 213–216 CrossRef CAS.
- M. De Jong, A. Meijerink, R. A. Gordon, Z. Barandiarán and L. Seijo, J. Phys. Chem. C, 2014, 118, 9696–9705 CrossRef CAS.
- M. De Jong, A. Meijerink, Z. Barandiarán and L. Seijo, J. Phys. Chem. C, 2014, 118, 17932–17939 CrossRef CAS.
- C. D. S. Brites, K. Fiaczyk, J. F. C. B. Ramalho, M. Sójka, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2018, 1701318 CrossRef.
- M. Sójka, J. F. C. B. Ramalho, C. D. S. Brites, K. Fiaczyk, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2019, 7, 1901102 CrossRef.
- M. Sójka, C. D. S. Brites, L. D. Carlos and E. Zych, J. Mater. Chem. C, 2020, 8, 10086–10097 RSC.
- P. Bolek, J. Zeler, C. D. S. Brites, J. Trojan-Piegza, L. D. Carlos and E. Zych, Chem. Eng. J., 2021, 421, 129764 CrossRef CAS.
- T. Zheng, M. Sójka, M. Runowski, P. Woźny, S. Lis and E. Zych, Adv. Opt. Mater., 2021, 9, 2101507 CrossRef CAS.
- Y. Pan, X. Xie, Q. Huang, C. Gao, Y. Wang, L. Wang, B. Yang, H. Su, L. Huang and W. Huang, Adv. Mater., 2018, 30, 3–8 Search PubMed.
- L. Zhou, P. Du and L. Li, Sci. Rep., 2020, 10, 1–11 CrossRef PubMed.
- D. Stefańska, M. Stefanski and P. J. Dereń, J. Alloys Compd., 2021, 863, 1–7 CrossRef.
- R. Zhou, C. Liu, L. Lin, Y. Huang and H. Liang, Chem. Eng. J., 2019, 369, 376–385 CrossRef CAS.
- R. Zhou, L. Lin, H. Zhao, T. Deng and J. Li, Mater. Chem. Front., 2021, 5, 6071–6081 RSC.
- D. Dutczak, T. Jüstel, C. Ronda and A. Meijerink, Phys. Chem. Chem. Phys., 2015, 17, 15236–15249 RSC.
- P. Solarz, M. Karbowiak, M. Głowacki, M. Berkowski, R. Diduszko and W. Ryba-Romanowski, J. Alloys Compd., 2016, 661, 419–427 CrossRef CAS.
- I. V. Berezovskaya, V. P. Dotsenko, A. S. Voloshinovskii and S. S. Smola, Chem. Phys. Lett., 2013, 585, 11–14 CrossRef CAS.
- J. G. Bunzli and S. V. Eliseeva, Springer Ser. Fluoresc., 2011, 1–45 CAS.
- K. Fiaczyk, A. J. Wojtowicz and E. Zych, J. Phys. Chem. C, 2015, 119, 5026–5032 CrossRef CAS.
- B. Di Bartolo and R. Summitt, Phys. Today, 1970, 23, 105–107 CrossRef.
- G. A. M. Dalhoeven and G. Blasse, J. Solid State Chem., 1981, 39, 35–38 CrossRef CAS.
- P. Kisliuk and C. A. Moore, Phys. Rev., 1967, 160, 307–312 CrossRef CAS.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, US, Boston, MA, 2006, pp. 1–26 Search PubMed.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799 RSC.
- C. D. S. Brites, A. Millán and L. D. Carlos, Handbook on the Physics and Chemistry of Rare Earths, 2016, vol. 49, pp. 339–427 Search PubMed.
- L. Marciniak, W. Piotrowski, M. Szalkowski, V. Kinzhybalo, M. Drozd, M. Dramicanin and A. Bednarkiewicz, Chem. Eng. J., 2022, 427, 131941 CrossRef CAS.
- R. G. Geitenbeek, H. W. De Wijn and A. Meijerink, Phys. Rev. Appl., 2018, 10, 1 RSC.
- M. Back, J. Ueda, M. G. Brik and S. Tanabe, ACS Appl. Mater. Interfaces, 2020, 12, 38325–38332 CrossRef CAS PubMed.
- M. Suta and A. Meijerink, Adv. Theory Simul., 2020, 3, 1–32 Search PubMed.
- M. Back, J. Ueda, H. Nambu, M. Fujita, A. Yamamoto, H. Yoshida, H. Tanaka, M. G. Brik and S. Tanabe, Adv. Opt. Mater., 2021, 9, 1–11 Search PubMed.
- A. A. Kalinichev, M. A. Kurochkin, E. V. Golyeva, A. V. Kurochkin, E. Lähderanta, M. D. Mikhailov and I. E. Kolesnikov, J. Lumin., 2018, 195, 61–66 CrossRef CAS.
- A. M. Kaczmarek, M. K. Kaczmarek and R. Van Deun, Nanoscale, 2019, 11, 833–837 RSC.
- T. Zheng, M. Runowski, N. Stopikowska, M. Skwierczyńska, S. Lis, P. Du and L. Luo, J. Alloys Compd., 2021, 890, 161830 CrossRef.
- R. Lei, X. Luo, Z. Yuan, H. Wang, F. Huang, D. Deng and S. Xu, J. Lumin., 2019, 205, 440–445 CrossRef CAS.
- W. Piotrowski, M. Kuchowicz, M. Dramićanin and L. Marciniak, Chem. Eng. J., 2022, 428, 131165 CrossRef CAS.
- J. Ueda, M. Back, M. G. Brik, Y. Zhuang, M. Grinberg and S. Tanabe, Opt. Mater., 2018, 85, 510–516 CrossRef CAS.
- E. Casagrande, M. Back, D. Cristofori, D. Cristofori, J. Ueda, S. Tanabe, S. Palazzolo, F. Rizzolio, F. Rizzolio, V. Canzonieri, V. Canzonieri, E. Trave and P. Riello, J. Mater. Chem. C, 2020, 8, 7828–7836 RSC.
- M. D. Dramićanin, Ž. Antić, S. Ćulubrk, S. P. Ahrenkiel and J. M. Nedeljković, Nanotechnology, 2014, 25, 485501 CrossRef PubMed.
- A. Ćirić, S. Stojadinović, Z. Ristić, I. Zeković, S. Kuzman, Ž. Antić and M. D. Dramićanin, Adv. Mater. Technol., 2021, 6, 1–10 Search PubMed.
- Z. Cao, X. Wei, L. Zhao, Y. Chen and M. Yin, ACS Appl. Mater. Interfaces, 2016, 8, 34546–34551 CrossRef CAS PubMed.
- M. Sójka, M. Runowski, P. Woźny, L. D. Carlos, E. Zych and S. Lis, J. Mater. Chem. C, 2021, 9, 13818–13831 RSC.
- L. Marciniak and K. Trejgis, J. Mater. Chem. C, 2018, 6, 7092–7100 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05022b |
| This journal is © The Royal Society of Chemistry 2022 |