High-order harmonic generation by aligned homonuclear diatomic cations
Received
27th May 2023
, Accepted 6th October 2023
First published on 6th October 2023
Abstract
We introduce the theory of high-order harmonic generation by aligned homonuclear diatomic cations using a strong-field approximation. The target cation is represented as a system which consists of two atomic (ionic) centres and one active electron, while the driving field is either a monochromatic or bichromatic field. For a linearly polarised driving field, we investigate the differences between the harmonic spectra obtained with a neutral molecule and the corresponding molecular cation. Due to the larger ionisation potential, the molecular cations can withstand much higher laser-field intensity than the corresponding neutral molecule before the saturation effects become significant. This allows one to produce high-order harmonics with energy in the water-window interval or beyond. Also, the harmonic spectrum provides information about the structure of the highest-occupied molecular orbital. In order to obtain elliptically polarised harmonics, we suggest that an orthogonally polarised two-colour field is employed as a driving field. In this case, we analyse the harmonic ellipticity as a function of the relative orientation of the cation in the laser field. We show that the regions with large harmonic ellipticity in the harmonic energy-orientation angle plane are the broadest for cations whose molecular orbital does not have a nodal plane. Finally, we show that the molecular cations exposed to an orthogonally polarised two-colour field represent an excellent setup for the production of elliptically polarised attosecond pulses with a duration shorter than 100 as.
1 Introduction
Powerful X-ray sources are needed for various experimental investigations. Typical examples of these sources include large synchrotrons and X-ray free-electron laser facilities.1,2 However, tabletop schemes for the generation of X-rays with the desired characteristics are particularly useful. One such scheme is based on the laser-induced process called high-order harmonic generation (HHG).2–6 In this process, the atom or molecule is first ionised by a strong laser field. Then the freed electron propagates with its dynamics governed by the applied field, and finally, due to the oscillatory character of this field, the electron can return to the vicinity of the parent atom or molecule which may lead to recombination accompanied by high-energy-photon emission. The energy of this photon is equal to the sum of the ionisation potential and the energy gained in the laser field, while its frequency can be expressed as an integer multiple of the frequency of the applied field. The emitted harmonic photon can be linearly polarised or elliptically polarised depending on the type of the applied field and the employed target. The harmonic ellipticity and the harmonic emission rate can be controlled using the laser-field parameters as control knobs. Only a limited number of these parameters are available for a monochromatic field, while for the so-called tailored laser fields, the number of these parameters is much larger. High-order harmonics can be produced using either gaseous or solid targets. In the present paper we are interested in the former case, while useful information about the emission of high-order harmonics from solid materials can be found in the recently-written review papers.7,8
Particularly important are the high-order harmonics with energy higher than 100 eV and lower than 1000 eV. This region includes a “water-window” interval (282–533 eV) for which water does not interact with the electromagnetic radiation. The photons with energy from the water-window interval were produced by exposing helium and neon atoms to the near-infrared linearly polarised field.4,5,9,10 The region 100–1000 eV also includes the L-edges of many atoms, i.e., the absorption peaks caused by the electron excitation from the occupied 2p to the unfilled d orbital. For example, the L-edge of manganese appears at 640 eV, while for copper, it appears at 930 eV. Apart from the high energy, for many applications it is also beneficial that the high-order harmonics are elliptically polarised with a controllable ellipticity. Specifically, the elliptically polarised light has found its application in the research of chiral molecules11–15 and magnetic materials.16–19 For the atomic targets, the emitted harmonics can be linearly or elliptically polarised depending on the type of driving field, while the harmonics generated by the molecular targets are elliptically polarised regardless of the type of the applied field.20,21 For example, when the HHG process is induced by exposing atoms to a linearly polarised field, the obtained harmonics are linearly polarised, while for the ω–3ω orthogonally polarised two-colour (OTC) driving field the emitted harmonics are elliptically polarised.22 An OTC laser field consists of two linearly polarised components with orthogonal polarisations and frequencies which are integer multiples of the fundamental frequency. The ellipticity of the harmonics generated by exposing molecules to a linearly polarised field is usually small. On the other hand, for a tailored driving field, the ellipticity of the emitted harmonics can become large, particularly for heteronuclear molecules.21,23,24
The selection rules determine which harmonics appear in the harmonic spectrum and which are suppressed. These rules depend on the symmetry properties of the system which consists of the target atom or molecule and the applied field.25 The selection rules can be derived using group theory and taking into account the full symmetry of the laser-matter system26 or by investigating the dynamical symmetry of the driving field and the target system.27 For example, the atoms exposed to a linearly polarised field emit only odd harmonics, while for the ω–2ω OTC field, both odd and even harmonics are present in the spectrum.28
In this paper, we investigate HHG using homonuclear diatomic molecular cations exposed to the one- and two-component laser fields. The molecular cations play a fundamental role in interstellar chemistry because the reactions between the neutral molecules are strongly suppressed due to the low temperature.29,30 To date, many of the confirmed interstellar species are cations,31 the last one discovered being HC3S+ and CH3CO+.32,33 Moreover, due to the fact that their ionisation potential is much higher, the molecular cations can be exposed to a much higher laser-field intensity than the neutral molecules, before the saturation effects become significant. Consequently, harmonics with a high energy can be generated. Another way to produce high-energy harmonics relies on mid-IR lasers.4,34,35 However, this method comes with significant experimental challenges due to the fact that the conversion efficiency decreases with increasing driving-field wavelength.36 The main goal of the present paper is to establish the theory of HHG using molecular cations and to investigate the similarities and differences between the results obtained using this theory and the analogous theory for HHG using neutral molecules.
The most accurate way to calculate the harmonic emission rate is by using the full, three-dimensional ab initio methods.37–41 These methods are based on the solution of the time-dependent Schrödinger equation. The method based on the R-matrix theory39,40 can be used for an arbitrary multielectron atoms, ions and molecules exposed to the laser field with an arbitrary polarisation. However, this method, as well as the other ab initio methods, is time-consuming particularly for molecular targets. Consequently, the molecular calculations are usually carried out in reduced dimensions,42–46 while the full three-dimensional calculations are only applied to the simple molecular species such as the H2+ ion and neutral H2 molecule. For example, three-dimensional calculations are conducted to calculate the HHG spectrum47,48 and the above-threshold ionisation yield,49–51 and to investigate the lateral photoelectron momentum distribution52 and photoelectron holography.53 Another ab initio approach is based on time-dependent density-functional theory which relies on the Kohn–Sham equations for atomic orbitals.54–57 This approach includes the interaction of electrons with the laser field and residual ion as well as the electron–electron exchange–correlation interaction, and allows one to simulate, for example, the HHG in argon56 and xenon.57 The high accuracy of the xenon calculations was confirmed by comparing with experimental results.57
In order to avoid long calculations, we introduce the semi-analytical theory based on the strong-field approximation (SFA) which neglects the interaction of the liberated electron with the parent ion upon eventual recombination. This approximation is suitable for near-infrared laser fields because in this case the liberated electron is significantly displaced from the region where its parent ion is located and the Coulomb interaction can be neglected during the propagation. A similar theory was introduced previously for neutral molecules.58–63 For the hydrogen atom, good agreement between the HHG spectra obtained using the SFA-based theory and the TDSE-based theory was reported for a linearly polarised driving field.38 More recently, the harmonic spectra of a neon atom obtained using the R-matrix theory,40 which takes into account the contributions of all electrons, were compared with the results obtained using the single-active electron approach.64 Good qualitative agreement was reported, indicating that the multielectron effects only slightly affect the conversion efficiency. This leads us to the conclusion that our SFA-based theory can be employed to investigate the HHG process at least qualitatively, while a more advanced theory is probably necessary for the more-detailed quantitative investigation. The paper is organised as follows. In Section 2 we introduce our SFA theory of the HHG by homonuclear diatomic cations and compare the obtained expressions with those of the homonuclear diatomic molecules. The results computed by the numerical integration and the saddle-point method are presented and discussed in Section 3 for various homonuclear diatomic cations. Finally, Section 4 summarises the main ideas and conclusions of the paper. The atomic units are used throughout the paper.
2 Theoretical background
We consider the molecular cation as a system of two atomic (ionic) centres A and B and an electron. Introducing the Jacobi coordinates,65 the total Hamiltonian of the system can be written in the form which allows the centre-of-mass motion to be analysed independently of the relative motion. The solution of the equation which governs the centre-of-mass motion is the Volkov state, while the relative motion is determined by the Hamiltonian58| | 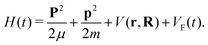 | (1) |
Here, r and R are the Jacobi coordinates, p and P are the corresponding conjugate momenta, V(r,R) is the potential energy of the system in the absence of the laser field, while VF(t) = −(err + eRR)·E(t) is the interaction with the applied field E(t). Also, the reduced electron and nuclear masses are m = meMAB/M and μ = mAmB/MAB, respectively, with MAB = mA + mB, M = me + MAB, where mA, mB and me are the masses of the atomic centres A and B and of the electron, respectively. The relative charges er and eR are
| er = [MABe−me(eA + eB)]/M, |
where eA, eB and e = −1 are the charges of the atomic centres A and B and of the electron, respectively.
2.1 Time-dependent dipole
The rate of emission of the harmonic photon with frequency ωK = nω, wave vector K and unit polarisation vector êK is given by61,66,67| | 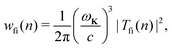 | (3) |
where the T-matrix element is| | 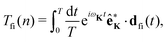 | (4) |
with the time-dependent dipole| | 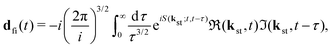 | (5) |
| | 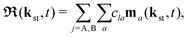 | (6) |
| | 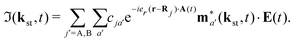 | (7) |
Here, ℜ(kst,t) and ℑ(kst,t) are the recombination and ionisation matrix elements, respectively. The summations over j and j′ are the summations over the atomic centres, while the remaining sums refer to the atomic orbitals. The matrix element is given by| | | ma(kst,t) = 〈ψ(0)a| − (err + eRR)|kst + erA(t)〉, | (8) |
where ψ(0)a is the Slater-type orbital| | 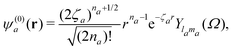 | (9) |
with the expansion coefficients and ζa tabulated in ref. 68, A(t) is the vector potential of the field E(t), 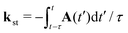 is the stationary momentum where t is the recombination time and τ is the so-called travel time. Finally, the action can be written as
is the stationary momentum where t is the recombination time and τ is the so-called travel time. Finally, the action can be written as 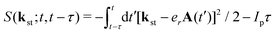 where Ip is the ionisation potential.
where Ip is the ionisation potential.
The above expressions were obtained using the Born–Oppenheimer approximation and the electronic energy and wave function are evaluated at the equilibrium nuclear position.69 These expressions are valid regardless of the values of the relative charges. For homonuclear diatomic cations, eA + eB = 2 so that the relative charges are eR = 1 − eA and er ≈ e = −1. If the electron is liberated from the atomic centre A, eA = 1 and eRA = 0, while for the ionisation from the atomic centre B we have eB = 1 and eRB = 0. This is different in comparison with the case of neutral homonuclear diatomic molecules (see Section IIC in ref. 61). The recombination and ionisation matrix elements, given by (6) and (7), become
| | 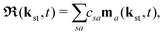 | (10) |
| | 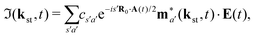 | (11) |
with
ma(
kst,
t) = 〈
ψ(0)a|
r|
kst +
A(
t)〉 and
R0 the equilibrium internuclear distance. The summations over the atomic centres A and B are replaced by the summations over
s = ±1 and
s′ = ±1 where the value +1 (−1) corresponds to the atomic centre A (B). Let us now compare these expressions with those corresponding to the neutral molecules [eqn (5) and (6) in ref.
21]. Clearly, both ionisation and recombination parts of the time-dependent dipole are changed. More precisely, in the recombination part, the exponential term exp{−
is[
kst +
A(
t)]·
R0/2}, present for neutral molecules, is now absent, while in the ionisation part, the exponential term exp(
is′
kst·
R0/2) is replaced by exp[
is′
A(
t −
τ)·
R0/2]. The change in the recombination part of the time-dependent dipole has two major consequences. For the neutral molecules, the summation over
s = ±1 in the recombination matrix element
ℜ(
kst,
t) led to the analytical conditions for the interference minima. This was possible because the coefficients
csa are related by the relationship
c−1a =
σaλc1a, where
σaλ = (−1)
la−ma+mλ for gerade symmetry and
σaλ = (−1)
la−ma+mλ+1 for ungerade symmetry and
mλ is the projection of the orbital angular momentum on the internuclear axis.
70 The atomic orbitals with
σaλ = +1 (
σaλ = −1) are sometimes called even (odd) atomic orbitals. The exponential term which led to the interference-minima conditions is absent for the molecular cations thus implying that the interference minima should not be observed for this type of the target. Besides this, it is also clear that the odd orbitals do not contribute to the recombination matrix element
ℜ(
kst,
t).
The train of the in-phase-mode-locked harmonics can produce the attosecond pulse train. The quantitative measure of the phase locking of the train of the N subsequent harmonics starting with the harmonic n0 is given by the ratio of the coherent over the incoherent sum of the harmonic intensities71,72
| | 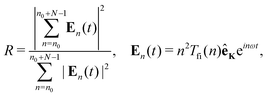 | (12) |
where
En(
t) is the field of the
nth harmonic and
t is the harmonic emission time. The ideal phase-locking corresponds to the value
R =
N, while
R = 1 describes the randomly oscillating modes.
2.2 Saddle-point method
The behaviour of the T-matrix element (4) is mainly determined by the factors which appear in the exponent and the integrals can be analysed by applying the saddle-point method. The ionisation and recombination times, for which the contribution to the T-matrix element is significant can be determined as the solutions of the system of saddle-point equations ∂S(kst;t,t0)/∂t0 = 0, ∂S(kst;t,t0)/∂t = 0, which for the HHG lead to| | 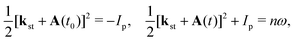 | (13) |
where t0 and t are the ionisation and recombination times, respectively. These equations are derived for the atomic targets but the ionisation potential corresponds to the molecular cations. Then, the T-matrix element can be written in the form| | 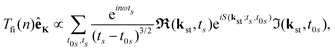 | (14) |
where the summation is over the solutions of the saddle-point eqn (13). These solutions, which contribute to the medium- and high-energy parts of the spectrum appear in pairs and can be classified using the multiindex (α,β,m).73,74 In particular, for the recombination time t restricted to 0 ≤ t < T there are infinitely many pairs of solutions for the ionisation time t0 ordered by the index m in such a way that −(m + 1/2)T ≤ t0 < −(m − 1/2)T where m = 0,1,2,… This means that the electron travel time is longer for a larger m value. For a given value m there are two pairs of solutions: the one with a longer travel time is denoted by β = −1, while the one with a shorter travel time is denoted by β = +1. Finally, the solutions which correspond to one particular pair and have slightly different travel times are distinguished by the index α. After the cutoff, one solution of the pair diverges and it should be discarded for an energy higher than the cutoff energy.
2.3 Driving field
In our paper, the driving field is| | E(t) = E1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(rωt)êzL + E2 sin(rωt)êzL + E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(sωt + φ)êxL, sin(sωt + φ)êxL, | (15) |
where Ej, j = 1,2, are the electric-field amplitudes, ω is the fundamental frequency, r and s are integers, φ is the relative phase between the laser-field components and the polarisation plane is defined by the unit vectors êzL and êxL. This field becomes linearly polarised for E2 = 0. We assume that the molecular cation is restricted to the polarisation plane and define the orientation angle θL as the angle between the internuclear axis and the axis defined by the unit vector êzL. The components of the T-matrix element Tfi(n) = Tfi(n)êK along the unit vectors êzL and êxL can be calculated numerically, which allows one to determine the degree of circular polarisation of the emitted harmonics| | 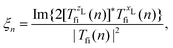 | (16) |
and consequently, the harmonic ellipticity20| | 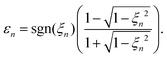 | (17) |
3 Numerical results
In the present paper we illustrate our findings using the N2+, O2+, C2+ and Li2+ cations as examples. We assume that an active electron is liberated from the highest-occupied molecular orbital (HOMO) and neglect the contribution of other molecular orbitals. The molecular orbital is modelled by a linear combination of the atomic orbitals which are represented by the Slater-type orbitals. For the N2+ and O2+ cations, we compare the obtained results with those of the neutral N2 and O2 molecules. The parameters of the HOMO of these molecules and molecular cations are given in Table 1,68,75 while the coordinate space wave functions are shown in Fig. 1. The saturation intensity is calculated using the barrier-suppression ionisation model,76 and the axis along the molecular axis is denoted as the z axis.
Table 1 Equilibrium internuclear distance, ionisation potential, saturation intensity, magnetic quantum number and the atomic orbitals used to model the HOMO of the molecular cations and neutral molecules analysed in this paper
| Molecular species |
HOMO |
R
0 (a.u.) |
I
p (eV) |
I
BSI (1014 W cm−2) |
m
a
|
Atomic orbitals |
| N2+ |
3σg |
2.113 |
28.56 |
26.6 |
0 |
1s,1s′,2s,2s′,3s,2p,2p′,2p′′,3d,3d′,3d′′,4f |
| O2+ |
1πg |
2.122 |
26.22 |
18.9 |
1 |
2p,2p′,2p′′,3d,4f |
| C2+ |
1πu |
2.348 |
22.17 |
9.7 |
1 |
2p,2p′,2p′′,2p′′′,3d,3d′,4f |
| Li2+ |
2σg |
5.051 |
11.22 |
0.6 |
0 |
1s,1s′,2s,3s,3s′,3s′′,2p,2p′,2p′′,2p′′′,3d |
| N2 |
3σg |
2.068 |
15.58 |
2.4 |
0 |
1s,1s′,2s,2s′,3s,2p,2p′,2p′′,3d,3d′,3d′′,4f |
| O2 |
1πg |
2.282 |
12.30 |
0.9 |
1 |
2p,2p′,2p′′,3d,4f |
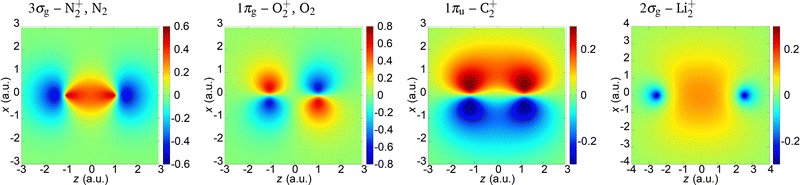 |
| | Fig. 1 Wave functions of the HOMO (indicated above the panels) for the molecules and molecular cations analysed in the paper. | |
The 3σg (which corresponds to the N2+ and N2) and 2σg (which corresponds to the Li2+) orbitals are qualitatively similar. They do not have nodal planes. The 1πg molecular orbital which is HOMO of O2+ and O2 has two nodal planes (xy and zy; y being the axis orthogonal to the polarisation plane), while the 1πu molecular orbital which is HOMO of C2+ has one nodal plane (zy).
3.1 Linearly polarised field
In this subsection, we investigate the case in which HHG is induced by a linearly polarised field. We start by comparing the harmonic emission rate for the neutral molecule and the corresponding molecular cation.
3.1.1 N2 molecule and N2+ cation.
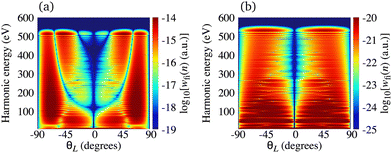
In Fig. 2(a) we present the logarithm of the harmonic emission rate as a function of the harmonic energy (black solid line), together with the partial contributions of different atomic orbitals (dashed-dotted, dashed, dotted and dashed-double-dotted lines) for the N2 molecule exposed to the linearly polarised field with intensity I = E12 = 1015 W cm−2 and the wavelength of 1300 nm. The orientation angle is θL = 0°. For these values of the driving-field parameters, the dipole approximation is still accurate.77–80 The harmonic emission rate is predominantly determined by the p orbitals, while the s and d orbitals contribute significantly only in the narrow energy regions. The contribution of the f orbitals is negligible for all harmonics. Fig. 2(b) displays analogous results obtained using the N2+ cation and the same driving field as in Fig. 2(a). The corresponding harmonic emission rate is roughly two to three orders of magnitude lower than the harmonic emission rate of the N2 molecule. This is because the ionisation potential of the N2+ cation is much higher. Moreover, the saturation effects for the neutral molecules exposed to the laser field with an intensity I = 1015 W cm−2 are significant. (According to the barrier-suppression ionisation model [IBSI(109 W cm−2) = 4I4p(eV)] the saturation intensity for the N2 molecule is 2.4 × 1014 W cm−2.76) We presented the results for this unrealistically high intensity only for a qualitative comparison with the results for the N2+ cation. The molecular cation has a much higher ionisation potential so that it can withstand the applied field of this intensity without immediate ionisation. Furthermore, there are two additional differences between the N2+ yield and the yield which corresponds to the neutral N2 molecule. First, the p and f orbitals do not contribute to the cation spectrum at all. This happens because, for the 3σg HOMO symmetry, the factor 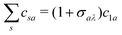 , where σaλ = −1 for p and f atomic orbitals, leads to the zero value of the recombination matrix element ℜ(kst,t). Secondly, the total harmonic emission rate of the N2+ cation exhibits a clear minimum for the harmonic energy around 325 eV. In this region, the contributions of the s and d orbitals are higher than the total spectrum, thus leading to the conclusion that this minimum appears due to the destructive interference of the contributions of different atomic orbitals. In order to investigate how this minimum depends on the molecular orientation, in Fig. 3 we present the logarithm of the harmonic emission rate of the N2+ cation, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. The minimum, which appears due to the destructive interference of the contributions of different atomic orbitals, is present for all values of the orientation angle. For −30° < θL < 30° the minimum appears at roughly the same energy (around 320 eV), while for the orientation angle closer to θL = ±90° this minimum appears for lower energy (around 200 eV). This implies that, in order for this minimum to be experimentally verified, the molecular cations in the sample do not have to be ideally oriented. Interestingly, as the driving-field intensity decreases, the position of the minimum and the harmonic emission rate do not change significantly. Only the position of the cutoff moves towards the lower energy. For example, for the orientation angle θL = 0° and the driving-field intensity I = 6 × 1014 W cm−2 the cutoff appears at 335 eV, just after the discussed minimum which is still around 325 eV, thus making it less pronounced. For larger values of the laser-field intensity, the position of the minimum barely changes at all.
, where σaλ = −1 for p and f atomic orbitals, leads to the zero value of the recombination matrix element ℜ(kst,t). Secondly, the total harmonic emission rate of the N2+ cation exhibits a clear minimum for the harmonic energy around 325 eV. In this region, the contributions of the s and d orbitals are higher than the total spectrum, thus leading to the conclusion that this minimum appears due to the destructive interference of the contributions of different atomic orbitals. In order to investigate how this minimum depends on the molecular orientation, in Fig. 3 we present the logarithm of the harmonic emission rate of the N2+ cation, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. The minimum, which appears due to the destructive interference of the contributions of different atomic orbitals, is present for all values of the orientation angle. For −30° < θL < 30° the minimum appears at roughly the same energy (around 320 eV), while for the orientation angle closer to θL = ±90° this minimum appears for lower energy (around 200 eV). This implies that, in order for this minimum to be experimentally verified, the molecular cations in the sample do not have to be ideally oriented. Interestingly, as the driving-field intensity decreases, the position of the minimum and the harmonic emission rate do not change significantly. Only the position of the cutoff moves towards the lower energy. For example, for the orientation angle θL = 0° and the driving-field intensity I = 6 × 1014 W cm−2 the cutoff appears at 335 eV, just after the discussed minimum which is still around 325 eV, thus making it less pronounced. For larger values of the laser-field intensity, the position of the minimum barely changes at all.
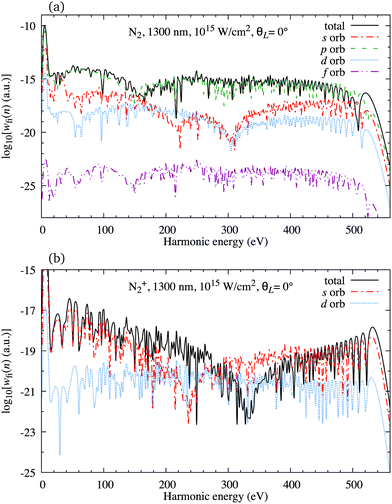 |
| | Fig. 2 Logarithm of the harmonic emission rate as a function of the harmonic energy (black solid line), together with the partial contributions of different atomic orbitals (as indicated in the legend) for the N2 molecule [panel (a)] and N2+ molecular cation [panel (b)] exposed to the linearly polarised field with intensity I = E12 = 1015 W cm−2 and a wavelength of 1300 nm. The orientation angle is θL = 0°. | |
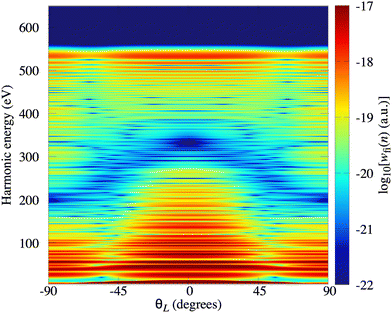 |
| | Fig. 3 Logarithm of the harmonic emission rate of the N2+ cation, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. | |
The minimum which appears due to the destructive interference of the contributions of different atomic orbitals can also be discussed using the saddle-point method. The solutions of the saddle-point eqn (13), which contribute to the medium- and high-energy parts of the spectrum, can be classified using the multiindex (α,β,m)73,74 as discussed in Section 2.2. In Fig. 4(a) we present the real part of the ionisation (left part of the panel) and recombination (right part of the panel) times which are obtained as the solutions of the saddle-point eqn (13) as functions of the harmonic energy, for the same configuration of the molecular cation and the driving field as in Fig. 2(b). The presented solutions have a travel time τ < 2.5T and the values of α, β and m are indicated in the panel. The solutions whose contributions should be discarded after the cutoff are plotted by the dashed lines. Clearly, there is one pair of solutions with m = 0 [green lines in Fig. 4(a)]. These solutions have the shortest travel time. Then, there are two pairs of solutions with m = 1, the one with shorter travel time has β = 1 [blue lines in Fig. 4(a)], and the one with longer travel time with β = −1 [red lines in Fig. 4(a)]. One pair of solutions with m = 2 is also presented in Fig. 4(a) [black lines in Fig. 4(a)]. The two solutions of one pair approach each other near the cutoff which helps one to determine which solutions lead to the significant contribution to the harmonic emission rate in a discussed part of the spectrum. For example, the solutions (β,m) = (−1,0) approach each other for the energy above 500 eV, while the solutions (β,m) = (1,1) approach each other for the energy lower than 300 eV. The minimum which we discussed earlier appears for the harmonic energy around 325 eV. In this region, the solutions (α,β,m) = (±1, −1,0) and (α,β,m) = (±1, −1,1) lead to the nonnegligible contributions to the T-matrix element. In Fig. 4(b) we display the partial contributions of the saddle-point solutions to the time-dependent dipole, which enters the expression for the T-matrix element, and consequently the harmonic emission rate. The solutions (α,β,m) = (±1, −1,0) and (α,β,m) = (±1, −1,1) exhibit clear minima for the harmonic energy around 325 eV. This shows us that the observed minimum does not appear due to the destructive interference of different saddle-point contributions, but it stems from the destructive interference of the contributions of different atomic orbitals, i.e., it is caused by the geometry of the cation's HOMO. Further analysis can be performed by calculating the partial contributions of the saddle-point solutions to the time-dependent dipole by modelling the HOMO using only the s atomic orbitals. In this case the minimum appears for the energy around 225 eV [this is in agreement with the results presented by the red dash-dotted line in Fig. 2(b)] and it is caused by the destructive interference of different s orbitals used to construct the HOMO. Similarly, the partial contributions calculated with HOMO modelled using only d orbitals does not exhibit any significant minima [which is in agreement with the results presented by the blue dotted line in Fig. 2(b)]. Taking into account the source of the discussed minimum, we must say that our findings may depend on the way how the molecular HOMO is modelled, i.e., if the Slater-type orbitals are replaced by more advanced Dyson-type orbitals.
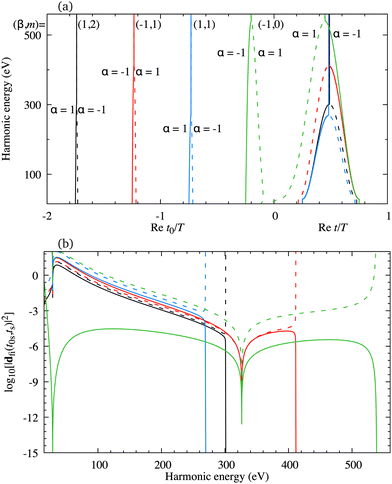 |
| | Fig. 4 The real part of the ionisation [left part of the panel (a)] and recombination [right part of the panel (a)] times as functions of the harmonic energy for four pairs of solutions of the saddle-point equations, together with the partial contributions of these solutions to the time-dependent dipole dfi [panel (b)]. The driving field and the target cation configuration are the same as in Fig. 2(b). | |
3.1.2 O2 molecule and O2+ cation.
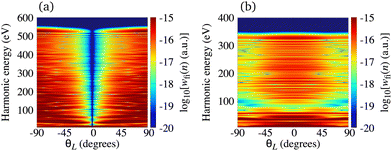
The situation is different for the O2+ cation whose HOMO is 1πg. In Fig. 5 we present the logarithm of the harmonic emission rate of the O2 molecule [(panel (a)] and O2+ cation [(panel (b)], exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. Similarly, as in the case of the N2 and its corresponding cation, the interference minima only appear when the neutral molecule is used as a target. Furthermore, for the orientation angle θL = 0° and θL = ±90° the harmonic emission rate is zero because of the two nodal planes of the 1πg HOMO (see Fig. 1). The minimum caused by the destructive interference of the contributions of different atomic orbitals does not appear for the O2+ cation. To explain the absence of this minimum we recall that the HOMO of the O2+ cation is modelled by the p, d and f atomic orbitals (see Table 1). For the 1πg symmetry, it is σaλ = +1 for d orbitals and σaλ = −1 for p and f orbitals, which means that only d orbitals contribute to the recombination matrix element ℜ(kst,t). The fact that only one type of the atomic orbitals contribute to the recombination matrix element explains the absence of the destructive interference minimum. Finally, comparing the black solid lines in Fig. 2(a) and (b) and comparing Fig. 5(a) and (b) we conclude that, for the O2 and O2+ pair, the difference between the harmonic emission rate is much more pronounced than for the N2 and N2+ pair. More precisely, for the N2+ cation, the harmonic emission rate is two to three orders of magnitude lower than the harmonic emission rate of the N2 molecule. On the other hand, the harmonic emission rate of the O2+ cation is more than five orders of magnitude lower than the corresponding rate of the O2 molecule. This happens because for the O2+ cation only one d orbital contributes to the recombination matrix element, while for the N2+ cation five s and three d orbitals contribute to the recombination matrix element. In addition, the difference between the ionisation potentials of the O2+ cation and O2 molecule is larger than that for the N2+ cation and N2 molecule (see Table 1).
 |
| | Fig. 5 Logarithm of the harmonic emission rate of the O2 molecule [(panel (a)] and the O2+ cation [(panel (b)], exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. | |
3.1.3 C2+ and Li2+ cations.
In the above example, only one type of the atomic orbitals (d orbital of the O2+ cation) contributed to the recombination matrix element, which caused the absence of the destructive interference minimum. A similar situation occurs if the contribution of one atomic orbital is dominant.
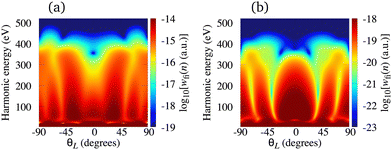
A typical example of this situation is the C2+ cation, with HOMO constructed from the p, d and f atomic orbitals, and the Li2+ cation, with HOMO constructed from the s, p and d atomic orbitals. In the former (later) case, the HOMO is 1πg (2σg) so that only p (s) and f (d) orbitals contribute to the recombination matrix element. In Fig. 6, we present the logarithm of the harmonic emission rate of the C2+ [panel (a)] and Li2+ [panel (b)] cations as a function of the harmonic energy and the orientation angle θL. The results for the C2+ cation are obtained using the laser field with the same parameters as in Fig. 2, while the results for the Li2+ cation correspond to a linearly polarised field with intensity I = E12 = 6 × 1013 W cm−2 and the wavelength of 2800 nm. For the Li2+ cation, the lower laser-field intensity is necessary due to a low saturation intensity (the ionisation potential of this cation is only 11.22 eV). As for the O2+ cation, the minimum caused by the destructive interference of the contributions of different atomic orbitals is absent. In the present case, this happens due to the contribution of one type of the atomic orbitals being dominant, while the contribution of the other type can be neglected. More specifically, the contribution of f orbitals in the C2+ HOMO, as well as the contribution of d orbitals in the Li2+ HOMO, are negligible and the destructive interference does not occur. This remains valid for all values of the orientation angle θL.
 |
| | Fig. 6 Logarithm of the harmonic emission rate of the C2+ [(panel (a)] and Li2+ [(panel (b)] cations, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL. The results for the C2+ cation are obtained using the laser field with the same parameters as in Fig. 2, while the results for the Li2+ cation correspond to a linearly polarised field with the intensity I = E12 = 6 × 1013 W cm−2 and the wavelength of 2800 nm. | |
Finally, we conclude this section by emphasising the most important findings. Contrary to the case of the neutral diatomic molecules, the interference minima caused by a destructive interference of the contributions which correspond to the different atomic centres of the same molecule do not appear if the molecular cation is employed as a target. On the other hand, the structural minima, caused by the geometry characteristics of the HOMO, may appear as a complete suppression of the HHG for some molecular orientations [examples being shown in Fig. 5(b) and 6(a)]. Furthermore, due to the fact that the molecular orbital is modelled as a linear combination of the atomic orbitals, these minima may also appear due to the destructive interference of the contributions of different atomic orbitals (the example is shown in Fig. 3). The structural minima may be present for both neutral molecules and molecular cations. However, for the molecular species examined in this paper, we have found that the minima caused by a destructive interference of the contributions of different atomic orbital are present only for the N2+ cation.
3.2 Orthogonally polarised two-colour field
After analysing the linearly polarised diving field, we now turn our attention to the case of an OTC field. This section has two goals. The first one is to investigate the possibility of using this field to induce elliptically polarised light, particularly in the high-energy region. The second goal is to investigate whether the scheme based on the HHG by molecular cations can be used to produce isolated attosecond pulses.
3.2.1 Generation of elliptically polarised light.
As we have mentioned previously, the harmonics generated using the molecular targets are elliptically polarised regardless of the type of the applied field. However, for a linearly polarised driving field, the ellipticity of the emitted harmonics is usually small for all values of the orientation angle θL and all values of the harmonic-photon energy. This is usually not the case if the tailored laser field is employed as a driving field. In the present contribution we use the rω–sω OTC field as an example of a tailored laser field. For homonuclear molecular cations exposed to the ω–2ω OTC field, both odd and even harmonics are emitted, while for the ω–3ω OTC field, only odd harmonics can be expected in the spectrum. In both cases, the emitted harmonics are elliptically polarised with ellipticity which depends on the relative phase φ and the orientation angle θL.
The N2+ cation exposed to the ω–2ω OTC field represents a particularly useful combination for production of the elliptically polarised harmonics in the water-window region with a significant harmonic emission rate. In Fig. 7 we present the logarithm of the harmonic emission rate and the harmonic ellipticity of the N2+ cation for odd [panel (a) and (b)] and even [panel (c) and (d)] harmonics, obtained using the ω–2ω OTC field with the relative phase φ = 0°, as a function of the harmonic energy and the orientation angle θL. The intensity of both field components is I = E12 = E22 = 1015 W cm−2, while the fundamental wavelength is 1300 nm. For the N2+ cation, this intensity still does not require the saturation effects to be taken into consideration. The harmonic emission rate does not depend much on the orientation angle θL [see panels (a) and (c)] and it is suppressed only for narrow regions around θL = 0°, particularly for even harmonics. This is a consequence of the fact that the N2+ HOMO does not possess any nodal planes. The harmonic ellipticity is large for various values of the orientation angle and the harmonic energy. For the orientations ±θL, the harmonic ellipticity is opposite. The regions with a significant ellipticity are much more sharply defined than for the neutral molecules [cf. the Fig. 7(b) and (d) with Fig. 7 in ref. 21]. In addition, the harmonic ellipticity does not change erratically as a function of the harmonic energy (including the low-energy region), which was the case when neutral molecules were employed as targets.21 Furthermore, a particularly interesting situation happens for the harmonic energy slightly below 300 eV where the harmonic ellipticity remains large for a broad range of values of the orientation angle, thus implying that the harmonics with large ellipticity can be produced even if the molecules in the sample are not ideally oriented. This region is moved towards the lower energy (slightly below 200 eV) for the intensity of the field components I = 5 × 1014 W cm−2, and towards the higher energy for I > 1015 W cm−2.
 |
| | Fig. 7 Logarithm of the harmonic emission rate and the harmonic ellipticity of the N2+ cation for odd [panel (a) and (b)] and even [panel (c) and (d)] harmonics, obtained using the ω–2ω OTC field with the relative phase φ = 0°, as a function of the harmonic energy and the orientation angle θL. The intensity of both field components is the same I = E12 = E22 = 1015 W cm−2, while the fundamental wavelength is 1300 nm. | |
Contrary to the case of the N2+ cation, the harmonic emission rate for cations whose HOMOs possess a nodal plane (e.g. C2+) depends to a significant extent on the orientation angle θL. This becomes much more pronounced for the cations whose HOMOs possess two nodal planes (e.g. O2+). In these cases, the minima, analogous to those shown in Fig. 5(b) and 6(a), i.e., caused by the geometry of the molecular orbital, are present in the spectra. However, for an ω–2ω OTC driving field these minima do not appear for the fixed values of the orientation angle θL. They appear as the curves in the harmonic energy-orientation angle plane. In order to illustrate this behaviour, in Fig. 8 we present the logarithm of the harmonic emission rate of the C2+ [panel (a)] and O2+ [panel (b)] cations as a function of the harmonic energy and the orientation angle θL. Even harmonics are taken as an example. In both cases, there are regions in the harmonic energy-orientation angle plane where the harmonic emission rate is suppressed. This is particularly pronounced for the O2+ cation because its HOMO has two nodal planes. In this case, the regions with the suppressed harmonic emission rate appear for θL around ±35° and ±70°. Due to the more pronounced dependence of the harmonic emission rate on the orientation angle, the harmonic ellipticity changes more rapidly as a function of this parameter for a given harmonic-photon energy. Consequently, if a relatively good alignment of the sample in use is not possible, the molecular cations whose HOMO does not possess the nodal planes remain the favourable option for production of the elliptically polarised harmonics.
 |
| | Fig. 8 Logarithm of the harmonic emission rate of the C2+ [panel (a)] and O2+ [panel (b)] cations, for even harmonics obtained using the ω–2ω OTC field, as a function of the harmonic energy and the orientation angle θL. The field parameters are the same as in Fig. 7. | |
The elliptically polarised light with high frequency can also be generated using the ω–3ω OTC field and molecular cations. This combination supports only odd harmonics. Using our theory we have investigated the N2+, O2+, C2+ and Li2+ cations, and we have concluded that the main drawback of the HHG by molecular cations exposed to the ω–3ω OTC field is that the harmonic ellipticity almost erratically oscillates as a function of the harmonic energy regardless of the type of the HOMO. The only exceptions appear in the low-energy region of the spectrum well below the lower boundary of the water-window interval. As examples, in Fig. 9 we present the harmonic ellipticity for the C2+ [panel (a)] and O2+ [panel (b)] cations, exposed to the ω–3ω OTC field, as a function of the harmonic energy and the orientation angle θL. In both cases the harmonic ellipticity is a rapidly oscillating function of the harmonic energy for all values of the orientation angle. The corresponding harmonic emission rate is significant and it does not depend much on the orientation angle θL. These conclusions remain similar for the N2+ and Li2+ cations.
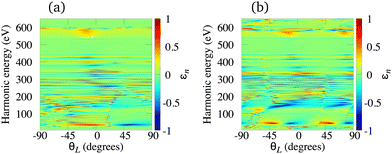 |
| | Fig. 9 Harmonic ellipticity for the C2+ [panel (a)] and O2+ [panel (b)] cations, exposed to the ω–3ω OTC field, as a function of the harmonic energy and the orientation angle θL. Other field parameters are the same as in Fig. 7. | |
The discussed characteristics of the generated harmonics also significantly depend on the relative phase φ between the laser-field components. For a bicircular field, this parameter was not useful because its change only leads to the rotation of the applied field around the axis perpendicular to the polarisation plane.81 However, this parameter is of particular importance for an OTC field.22
3.2.2 Generation of the isolated attosecond pulses.
By changing the relative phase the harmonic emission rate and the harmonic ellipticity can be successfully controlled. Typically, for the ω–2ω OTC field, the harmonic emission rate is a smooth function of the harmonic energy for some values of the relative phase, while for the other values it exhibits rapid oscillations. Finally, some intervals of the values of the relative phase lead to strong suppression of the harmonic emission for all except low-energy harmonics.20–23 This was explained in ref. 22 using a simple man's model which is based on the solution of the Newton equation for the electron in the laser field. In short, in order for the harmonic photon to be emitted, the liberated electron has to be driven back in the vicinity of the parent atom or molecule. Classically, this happens only for certain values of the relative phase between the laser-field components, while for other values, the electron does not return to the parent ion. However, the electron is a quantum-mechanical object and the spread of its wavepacket will lead to some overlap with the bound state even for those values of the relative phase for which, classically, the electron does not return to the parent ion. As a consequence, for these values of the relative phase, the harmonic emission will be strongly, but not completely suppressed.
As a rule, for the ω–2ω OTC field with the relative phase φ ∈ [0°,45°] the harmonic spectrum is very different from the one obtained using a linearly polarised field (for such OTC field, the oscillations of the harmonic emission rate of the subsequent odd or even harmonics are absent). However, the harmonic emission rate is usually quite different for the odd and even harmonics. This means that the odd harmonics alone or the even harmonics alone form a phase-locked train which can be used to generate an attosecond pulse. In Fig. 10(a) we present the logarithm of the harmonic emission rate for odd (black and blue solid lines) and even (red and green dashed lines) harmonics as a function of the harmonic energy for the neutral N2 and O2 molecules exposed to the ω–2ω OTC field with the same parameters as in Fig. 7. The orientation angle is indicated in the panel. The peaks which appear for the harmonic energy equal to the integer multiple of the energy of the driving-field photon are connected by a continuous curve. The harmonic emission rate of the subsequent odd or even harmonics is a smooth function of the harmonic energy but the rates of the odd and next or previous even harmonic are generally different. This is particularly pronounced for the O2 molecule due to the presence of the nodal planes in its HOMO. As a result, these configurations are not quite favourable for attosecond pulse generation.
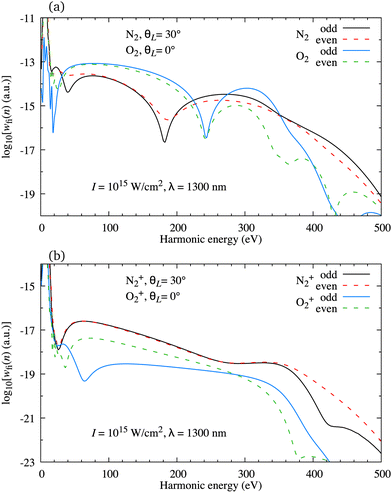 |
| | Fig. 10 Logarithm of the harmonic emission rate for odd (black and blue solid lines) and even (red and green dashed lines) harmonics as a function of the harmonic energy for the neutral N2 and O2 molecules [panel (a)] and the N2+ and O2+ molecular cations [panel (b)], exposed to the ω–2ω OTC field with the same parameters as in Fig. 7. The orientation angle is indicated in the panels. | |
We have found previously that attosecond pulses with a full width at half maximum less than 100 as can be generated using the atomic targets and the ω–3ω OTC field,82 while slightly longer pulses can be produced with the CO2 molecule exposed to the ω–2ω OTC field.24 Now we investigate if the molecular cations can be used to produce the isolated attosecond pulse. In Fig. 10(b) we present the same results as in Fig. 10(a) but for the N2+ and O2+ molecular cations. As for the neutral O2 molecule, the subsequent harmonics obtained using the O2+ cation as a target are emitted with a significantly different harmonic emission rate. However, this is not the case for the N2+ cation which generates odd and even harmonics with almost exactly the same harmonic emission rate. This remains true for most harmonics with an energy lower than the cutoff energy. In addition, the change of the relative phase in the interval φ ∈ [0°,45°] modulo π does not much affect this conclusion. This promotes the configuration that assumes the use of the molecular cations with the HOMO without nodal planes and the ω–2ω OTC driving field as particularly promising for the production of the attosecond pulses.
In order to illustrate the possibility of production of the attosecond pulse train using the earlier mentioned configuration, in Fig. 11 we present the ratio R, eqn (12), as a function of time for N = 22 [panel (a)] and N = 46 [panel (b)] harmonics, starting from n0 = 304. The harmonics are obtained by exposing the N2+ cation to the ω–2ω OTC field with the same parameters as in Fig. 7. The value of the ratio R is relatively close to its optimal value R = N and the duration of the attosecond pulse can be lower than 100 as. The number of attosecond pulses per optical cycle depends on the dynamical symmetry of the applied field. For example, the rω–sω bicircular field follows Cr+s rotational symmetry, while the rω–sω OTC field has C2 (C1) rotational symmetry for r + s even (odd). In general, the Cn rotational symmetry means that the applied field is invariant with respect to the rotation by the angle 2π/n around the axis perpendicular to the polarisation plane. Our ω–2ω OTC field only possesses the trivial C1 symmetry, which means that only one attosecond pulse is emitted per optical cycle. This is the advantage with respect to the ω–3ω OTC field. The obtained attosecond pulse has elliptical polarisation due to the fact that the subsequent harmonics are elliptically polarised.
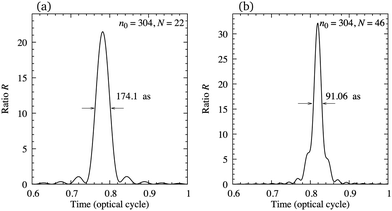 |
| | Fig. 11 Ratio R as a function of time for N = 22 [panel (a)] and N = 46 [panel (b)] harmonics, starting from n0 = 304, generated by exposing the N2+ cation to the ω–2ω OTC field with the same parameters as in Fig. 7. | |
Apart from the ω–2ω OTC field, the ω–3ω combination has also attracted a lot of attention.20,21 In this case, and for molecular cations as targets, the dependence of both the harmonic emission rate and the harmonic ellipticity on the relative phase φ is much less pronounced than for the ω–2ω OTC field. Additionally, the energy regions with in-phase-mode-locked harmonics are rare so this field configuration is not suitable for attosecond pulse generation. Also, the C2 rotational symmetry of this field would lead to the generation of two attosecond pulses per optical cycle.
In conclusion, the molecular cations exposed to an OTC laser field can successfully be used for the generation of attosecond pulses. A particularly promising configuration includes the ω–2ω OTC field and the molecular cations with HOMO which does not have the nodal planes. The relative phase between the laser-field components can be employed as a control knob which allows fine-tuning of the harmonic emission rate and the harmonic ellipticity.
4 Conclusions
By representing a diatomic molecular cation as a system which consists of two atomic (ionic) centres and one electron, we have formulated a theory of high-order harmonic generation based on the strong-field approximation. The ionisation potential of the molecular cation is much higher than the ionisation potential of the corresponding neutral molecule so that, in the former case, a much stronger laser field can be employed to induce the HHG process, without being worried about the saturation effects. The harmonic emission rate has been calculated by the numerical integration or by using the saddle-point method which allows one to better understand the underlying physics of the process.
First, we have investigated the HHG induced by a linearly polarised field with intensity in the order of 1015 W cm−2 and wavelength of 1300 nm. For these values of the laser-field parameters, the strong-field approximation is justified due to the large electron excursion in the driving field. Also, these parameters allow the generation of high-order harmonics with energy in the water-window interval and beyond. The dependence of the harmonic emission rate on the orientation angle is different for different symmetries of the HOMO. More specifically, the presence of the nodal planes in HOMO leads to the suppression of the harmonic emission for particular values of the molecular orientation angle. Moreover, since the molecular orbital is constructed from different atomic orbitals, it is possible that the contributions of the two types of atomic orbitals are comparable. In this case, these contributions may interfere and their destructive interference leads to a minimum in the harmonic spectrum. This minimum has been investigated using the saddle-point method which confirmed that it is caused by a destructive interference of the contributions of different atomic orbitals, and not by a destructive interference of the contributions of different saddle-point solutions. Furthermore, we have found that the position of this minimum slowly changes as a function of the orientation angle so that it should be possible to confirm its existence even with the sample in which molecular cations are not perfectly aligned. The suppression of the harmonic emission rate induced by the presence of the nodal planes should not depend on the particular set of atomic orbitals used to model HOMO. However, this might not be the case for the minimum caused by the interference of the partial contributions of different atomic orbitals.
Even though the emitted harmonics are elliptically polarised for a linearly polarised driving field, their ellipticity is usually small, except for some isolated values of harmonic energy and the orientation angle. Using tailored laser fields provides a much better basis for the production of the high-order harmonics with a significant ellipticity. A particularly interesting example of these fields provides an OTC field, for which the harmonic emission rate and the harmonic ellipticity can easily be tuned using the relative phase between the laser-field components as a control parameter. For the ω–2ω OTC field, both odd and even harmonics are emitted. We have found that the best candidate for production of the high-energy elliptically polarised light is the N2+ cation. In this case, the harmonic emission rate only slightly depends on the orientation angle and the emitted harmonics can have a large ellipticity for broad and well-defined regions in the harmonic energy-orientation angle plane. This is not the case for the O2+ and C2+ cations for which the harmonic emission rate depends significantly on the orientation angle. This happens due to the presence of the nodal planes in the HOMO of these cations. For the ω–3ω OTC field, only odd harmonics are present in the spectrum. In this case, the harmonic ellipticity may become significant, but it almost erratically changes as a function of the harmonic energy.
In the final part of the paper, we have analysed the possibility of using the molecular cations for production of the attosecond pulse train. In order to obtain an attosecond pulse with short duration, it is necessary to have a comb of subsequent harmonics with almost exactly the same harmonic emission rate. For neutral molecules exposed to the ω–2ω OTC driving field, the harmonic emission rate of subsequent odd or even harmonics is almost the same, but there is a significant difference between the harmonic emission rate for an odd and next or previous even harmonic. This is particularly pronounced for the molecules whose HOMO has nodal planes. When the N2+ molecular cation is used as a target, the harmonic emission rate of the subsequent odd and even harmonics is almost exactly the same, which represents an ideal condition for the generation of attosecond pulses. Moreover, due to the dynamical symmetry of the ω–2ω OTC field, only one attosecond pulse is emitted per optical cycle.
We believe that high-order harmonic generation by molecular cations represents an additional tool for exploration of the structure of the molecular orbital. Also, high-order elliptically polarised harmonics, with the energy of several hundreds of electronvolts, can successfully be produced if an OTC field is employed to induce the process. Finally, the configuration with a molecular cation employed as a target and an OTC field employed as a driving field allows one to produce the elliptically polarised attosecond pulse with a duration of less than hundred attoseconds. We hope that our paper will stimulate further analysis of the molecular cations particularly using more advanced ab initio theories.
Author contributions
All authors contributed equally to the paper.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We gratefully acknowledge support by the Ministry for Science, Higher Education and Youth, Canton Sarajevo, Bosnia and Herzegovina.
Notes and references
- N. Smith, Phys. Today, 2001, 54, 29 CrossRef CAS
 .
.
- R. Schoenlein, T. Elsaesser, K. Holldack, Z. Huang, H. Kapteyn, M. Murnane and M. Woerner, Philos. Trans. R. Soc., A, 2019, 377, 20180384 CrossRef CAS
 .
.
- T. Popmintchev, M. C. Chen, D. Popmintchev, P. Arpin, S. Brown, S. Ališauskas, G. Andriukaitis, T. Balčiunas, O. D. Mücke, A. Pugzlys, A. Baltuška, B. Shim, S. E. Schrauth, A. Gaeta, C. Hernández-García, L. Plaja, A. Becker, A. Jaron-Becker, M. M. Murnane and H. C. Kapteyn, Science, 2012, 336, 1287 CrossRef CAS
 .
.
- S. M. Teichmann, F. Silva, S. L. Cousin, M. Hemmer and J. Biegert, Nat. Commun., 2016, 7, 11493 CrossRef CAS
 .
.
- A. S. Johnson, D. R. Austin, D. A. Wood, C. Brahms, A. Gregory, K. B. Holzner, S. Jarosch, E. W. Larsen, S. Parker, C. S. Strüber, P. Ye, J. W. G. Tisch and J. P. Marangos, Sci. Adv., 2018, 4, eaar3761 CrossRef PubMed
 .
.
- S. L. Cousin, N. Di Palo, B. Buades, S. M. Teichmann, M. Reduzzi, M. Devetta, A. Kheifets, G. Sansone and J. Biegert, Phys. Rev. X, 2017, 7, 041030 Search PubMed
 .
.
- C. Yu, S. Jiang and R. Lu, Adv. Phys. X, 2019, 4, 1562982 CAS
 .
.
- E. Goulielmakis and T. Brabec, Nat. Photonics, 2022, 16, 411 CrossRef CAS
 .
.
- G. J. Stein, P. D. Keathley, P. Krogen, H. Liang, J. P. Siqueira, C.-L. Chang, C.-J. Lai, K.-H. Hong, G. M. Laurent and F. X. Kärtner, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 155601 CrossRef
 .
.
- S. L. Cousin, F. Silva, S. Teichmann, M. Hemmer, B. Buades and J. Biegert, Opt. Lett., 2014, 39, 5383 CrossRef CAS PubMed
 .
.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187 CrossRef PubMed
 .
.
- U. Hergenhahn, E. E. Rennie, O. Kugeler, S. Marburger, T. Lischke, I. Powis and G. Garcia, J. Chem. Phys., 2004, 120, 4553 CrossRef CAS PubMed
 .
.
- A. Ferré, C. Handschin, M. Dumergue, F. Burgy, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, L. Merceron, E. Mével, L. Nahon, S. Petit, B. Pons, D. Staedter, S. Weber, T. Ruchon, V. Blanchet and Y. Mairesse, Nat. Photonics, 2014, 9, 93 CrossRef
 .
.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Géneaux and I. Powis, Phys. Chem. Chem. Phys., 2016, 18, 12696 RSC
 .
.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed
 .
.
- S. Eisebitt, J. Lüning, W. F. Schlotter, M. Lörgen, O. Hellwig, W. Eberhardt and J. Stöhr, Nature, 2004, 432, 885 CrossRef CAS PubMed
 .
.
- C. Boeglin, E. Beaurepaire, V. Halte, V. Lopez-Flores, C. Stamm, N. Pontius, H. A. Durr and J. Y. Bigot, Nature, 2010, 465, 458 CrossRef CAS
 .
.
- O. Kfir, S. Zayko, C. Nolte, M. Sivis, M. Möller, B. Hebler, S. S. P. K. Arekapudi, D. Steil, S. Schäfer, M. Albrecht, O. Cohen, S. Mathias and C. Ropers, Sci. Adv., 2017, 3, eaao4641 CrossRef PubMed
 .
.
- J. L. Ellis, K. M. Dorney, D. D. Hickstein, N. J. Brooks, C. Gentry, C. Hernández-García, D. Zusin, J. M. Shaw, Q. L. Nguyen, C. A. Mancuso, G. S. M. Jansen, S. Witte, H. C. Kapteyn and M. M. Murnane, Optica, 2018, 5, 479 CrossRef CAS
 .
.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2020, 102, 023107 CrossRef
 .
.
- D. Habibović and D. B. Milošević, Photonics, 2020, 7, 110 CrossRef
 .
.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2019, 100, 031401(R) CrossRef
 .
.
- D. Habibović, W. Becker and D. B. Milošević, Eur. Phys. J. D, 2021, 75, 122 CrossRef
 .
.
- D. Habibović, W. Becker and D. B. Milošević, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 134004 CrossRef
 .
.
- X. Liu, X. Zhu, L. Li, Y. Li, Q. Zhang, P. Lan and P. Lu, Phys. Rev. A, 2016, 94, 033410 CrossRef
 .
.
- O. Neufeld, D. Podolsky and O. Cohen, Nat. Commun., 2019, 10, 405 CrossRef
 .
.
- D. Habibović, W. Becker and D. B. Milošević, Symmetry, 2021, 13, 1566 CrossRef
 .
.
- H. Eichmann, A. Egbert, S. Nolte, C. Momma, B. Wellegehausen, W. Becker, S. Long and J. K. McIver, Phys. Rev. A, 1995, 51, R3414 CrossRef CAS PubMed
 .
.
- W. D. Watson, Astrophys. J., 1973, 183, L17 CrossRef CAS
 .
.
- E. Herbst and W. Klemperer, Astrophys. J., 1973, 185, 505 CrossRef CAS
 .
.
-
https://cdms.astro.uni-koeln.de/classic/molecules
.
- J. Cernicharo, C. Cabezas, Y. Endo, N. Marcelino, M. Agúndez, B. Tercero, J. D. Gallego and P. de Vicente, Astron. Astrophys., 2021, 646, L3 CrossRef
 .
.
- J. Cernicharo, C. Cabezas, S. Bailleux, L. Margulès, R. Motiyenko, L. Zou, Y. Endo, C. Bermúdez, M. Agúndez, N. Marcelino, B. Lefloch, B. Tercero and P. de Vicente, Astron. Astrophys., 2021, 646, L7 CrossRef CAS PubMed
 .
.
- J. Li, X. Ren, Y. Yin, K. Zhao, A. Chew, Y. Cheng, E. Cunningham, Y. Wang, S. Hu and Y. Wu,
et al.
, Nat. Commun., 2017, 8, 186 CrossRef PubMed
 .
.
- N. Ishii, K. Kaneshima, K. Kitano, T. Kanai, S. Watanabe and J. Itatani, Nat. Commun., 2014, 5, 3331 CrossRef PubMed
 .
.
- A. D. Shiner, C. Trallero-Herrero, N. Kajumba, H.-C. Bandulet, D. Comtois, F. Légaré, M. Giguére, J.-C. Kieffer, P. B. Corkum and D. M. Villeneuve, Phys. Rev. Lett., 2009, 103, 073902 CrossRef CAS PubMed
 .
.
- B. Fetić, K. Kalajdžić and D. B. Milošević, Ann. Phys., 2013, 525, 107–117 CrossRef
 .
.
- B. Fetić and D. B. Milošević, J. Mod. Opt., 2013, 60, 1466–1474 CrossRef
 .
.
- D. D. A. Clarke, H. W. van der Hart and A. C. Brown, Phys. Rev. A, 2018, 97, 023413 CrossRef
 .
.
- A. C. Brown, G. S. J. Armstrong, J. Benda, D. D. A. Clarke, J. Wragg, K. R. Hamilton, Z. Mašín, J. D. Gorfinkiel and H. W. van der Hart, Comput. Phys. Commun., 2020, 250, 107062 CrossRef CAS
 .
.
- V. A. Tulsky and D. Bauer, Phys. Rev. Res., 2020, 2, 043083 CrossRef CAS
 .
.
- K. J. Yuan and A. D. Bandrauk, Phys. Rev. A, 2011, 84, 013426 CrossRef
 .
.
- M. Peters, T. T. Nguyen-Dang, E. Charron, A. Keller and O. Atabek, Phys. Rev. A, 2012, 85, 053417 CrossRef
 .
.
- Y. Li, Y. Zhou, M. He, M. Li, P. Lan and P. Lu, Phys. Rev. A, 2016, 94, 013422 CrossRef
 .
.
- S. Brennecke and M. Lein, Phys. Rev. A, 2018, 98, 063414 CrossRef CAS
 .
.
- M. He, Y. Li, Y. Zhou, M. Li, W. Cao and P. Lu, Phys. Rev. Lett., 2018, 120, 133204 CrossRef CAS PubMed
 .
.
- G. Lagmago Kamta and A. D. Bandrauk, Phys. Rev. A, 2004, 70, 011404(R) CrossRef
 .
.
- J. Heslar, D. A. Telnov and S.-I. Chu, Phys. Rev. A, 2018, 97, 043419 CrossRef CAS
 .
.
- M. Awasthi, Y. V. Vanne and A. Saenz, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 3973–3985 CrossRef CAS
 .
.
- J. Fernández and L. B. Madsen, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 085602 CrossRef
 .
.
- M. Murakami and S.-I. Chu, Phys. Rev. A, 2016, 94, 043425 CrossRef
 .
.
- L. Xin, H. C. Qin, W. Y. Wu and F. He, Phys. Rev. A, 2015, 92, 063803 CrossRef
 .
.
- X. B. Bian and A. D. Bandrauk, Phys. Rev. Lett., 2012, 108, 263003 CrossRef PubMed
 .
.
-
M. A. L. Marques and E. K. Gross, Time-Dependent Density Functional Theory, Springer, Berlin, 2003 Search PubMed
 .
.
-
C. A. Ullrich, Time-dependent Density-Functional Theory: Concepts and Applications Reprinted, with Corrections, Oxford University Press, Oxford, 2012 Search PubMed
 .
.
- A. A. Romanov, A. A. Silaev, M. V. Frolov and N. V. Vvedenskii, Phys. Rev. A, 2020, 101, 013435 CrossRef CAS
 .
.
- A. A. Romanov, A. A. Silaev, T. S. Sarantseva, M. V. Frolov and N. V. Vvedenskii, New J. Phys., 2021, 23, 043014 CrossRef CAS
 .
.
- D. B. Milošević, Phys. Rev. A, 2006, 74, 063404 CrossRef
 .
.
- C. B. Madsen and L. B. Madsen, Phys. Rev. A, 2006, 74, 023403 CrossRef
 .
.
- C. Figueira de Morisson Faria, Phys. Rev. A, 2007, 76, 043407 CrossRef
 .
.
- S. Odžak and D. B. Milošević, Phys. Rev. A, 2009, 79, 023414 CrossRef
 .
.
- C. Figueira de Morisson Faria and B. B. Augstein, Phys. Rev. A, 2010, 81, 043409 CrossRef
 .
.
- A. Etches and L. B. Madsen, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 155602 CrossRef
 .
.
- K. Finger, D. Atri-Schuller, N. Douguet, K. Bartschat and K. R. Hamilton, Phys. Rev. A, 2022, 106, 063113 CrossRef CAS
 .
.
-
A. Messiah, Quantum Mechanics, North-Holland, Amsterdam, 1999 Search PubMed
 .
.
-
D. B. Milošević, in Super-Intense Laser-Atom Physics, ed. B. Piraux and K. Rz
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) ewski, Kluwer, Dordrecht, 2001, pp. 229–238 Search PubMed
ewski, Kluwer, Dordrecht, 2001, pp. 229–238 Search PubMed  .
.
- D. B. Milošević and F. Ehlotzky, Adv. At., Mol., Opt. Phys., 2003, 49, 373–532 Search PubMed
 .
.
- P. E. Cade and A. C. Wahl, At. Data Nucl. Data Tables, 1974, 13, 339–389 CrossRef CAS
 .
.
-
P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, Oxford, 2001 Search PubMed
 .
.
- A. C. Wahl, J. Chem. Phys., 1964, 41, 2600 CrossRef CAS
 .
.
- D. B. Milošević and W. Becker, J. Mod. Opt., 2005, 52, 233–241 CrossRef
 .
.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2000, 62, 011403 CrossRef
 .
.
- S. P. Popruzhenko, Ph. A. Korneev, S. P. Goreslavski and W. Becker, Phys. Rev. Lett., 2002, 89, 023001 CrossRef CAS PubMed
 .
.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2002, 66, 063417 CrossRef
 .
.
-
https://cccbdb.nist.gov/homo1.asp
.
- S. Augst, D. D. Meyerhofer, D. Strickland and S. L. Chin, J. Opt. Soc. Am. B, 1991, 8, 858–867 CrossRef CAS
 .
.
- J. Maurer and U. Keller, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 094001 CrossRef CAS
 .
.
- R. Kahvedžić and S. Gräfe, Phys. Rev. A, 2022, 105, 063102 CrossRef
 .
.
- D. Habibović and D. B. Milošević, Phys. Rev. A, 2022, 106, 033101 CrossRef
 .
.
- R. Kahvedžić, D. Habibović, W. Becker, S. Gräfe and D. B. Milošević, Ann. Phys., 2023, 535, 2200616 CrossRef
 .
.
- D. B. Milošević and W. Becker, Phys. Rev. A, 2016, 93, 063418 CrossRef
 .
.
- D. Habibović, W. Becker and D. B. Milošević, J. Opt. Soc. Am. B, 2021, 38, 3367 CrossRef
 .
.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab and
Dino
Habibović
*ab and
Dino
Habibović
 a
a
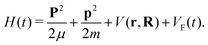
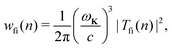
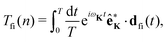
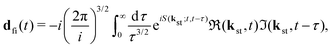
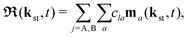
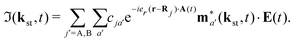
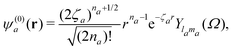
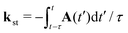 is the stationary momentum where t is the recombination time and τ is the so-called travel time. Finally, the action can be written as
is the stationary momentum where t is the recombination time and τ is the so-called travel time. Finally, the action can be written as 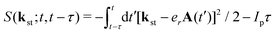 where Ip is the ionisation potential.
where Ip is the ionisation potential.
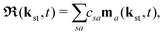
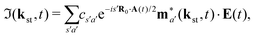
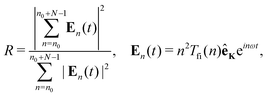
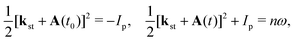
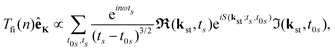
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(rωt)êzL + E2
sin(rωt)êzL + E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(sωt + φ)êxL,
sin(sωt + φ)êxL,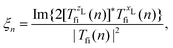
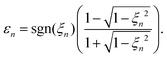

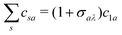 , where σaλ = −1 for p and f atomic orbitals, leads to the zero value of the recombination matrix element ℜ(kst,t). Secondly, the total harmonic emission rate of the N2+ cation exhibits a clear minimum for the harmonic energy around 325 eV. In this region, the contributions of the s and d orbitals are higher than the total spectrum, thus leading to the conclusion that this minimum appears due to the destructive interference of the contributions of different atomic orbitals. In order to investigate how this minimum depends on the molecular orientation, in Fig. 3 we present the logarithm of the harmonic emission rate of the N2+ cation, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. The minimum, which appears due to the destructive interference of the contributions of different atomic orbitals, is present for all values of the orientation angle. For −30° < θL < 30° the minimum appears at roughly the same energy (around 320 eV), while for the orientation angle closer to θL = ±90° this minimum appears for lower energy (around 200 eV). This implies that, in order for this minimum to be experimentally verified, the molecular cations in the sample do not have to be ideally oriented. Interestingly, as the driving-field intensity decreases, the position of the minimum and the harmonic emission rate do not change significantly. Only the position of the cutoff moves towards the lower energy. For example, for the orientation angle θL = 0° and the driving-field intensity I = 6 × 1014 W cm−2 the cutoff appears at 335 eV, just after the discussed minimum which is still around 325 eV, thus making it less pronounced. For larger values of the laser-field intensity, the position of the minimum barely changes at all.
, where σaλ = −1 for p and f atomic orbitals, leads to the zero value of the recombination matrix element ℜ(kst,t). Secondly, the total harmonic emission rate of the N2+ cation exhibits a clear minimum for the harmonic energy around 325 eV. In this region, the contributions of the s and d orbitals are higher than the total spectrum, thus leading to the conclusion that this minimum appears due to the destructive interference of the contributions of different atomic orbitals. In order to investigate how this minimum depends on the molecular orientation, in Fig. 3 we present the logarithm of the harmonic emission rate of the N2+ cation, exposed to a linearly polarised field, as a function of the harmonic energy and the orientation angle θL, for the same field parameters as in Fig. 2. The minimum, which appears due to the destructive interference of the contributions of different atomic orbitals, is present for all values of the orientation angle. For −30° < θL < 30° the minimum appears at roughly the same energy (around 320 eV), while for the orientation angle closer to θL = ±90° this minimum appears for lower energy (around 200 eV). This implies that, in order for this minimum to be experimentally verified, the molecular cations in the sample do not have to be ideally oriented. Interestingly, as the driving-field intensity decreases, the position of the minimum and the harmonic emission rate do not change significantly. Only the position of the cutoff moves towards the lower energy. For example, for the orientation angle θL = 0° and the driving-field intensity I = 6 × 1014 W cm−2 the cutoff appears at 335 eV, just after the discussed minimum which is still around 325 eV, thus making it less pronounced. For larger values of the laser-field intensity, the position of the minimum barely changes at all.








.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) ewski, Kluwer, Dordrecht, 2001, pp. 229–238 Search PubMed
ewski, Kluwer, Dordrecht, 2001, pp. 229–238 Search PubMed .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


