DOI:
10.1039/D3FD00030C
(Paper)
Faraday Discuss., 2023,
246, 179-197
Pulsed electrolysis – explained†
Received
6th February 2023
, Accepted 9th March 2023
First published on 10th March 2023
Abstract
Lately, there has been high interest in electrolysis under dynamic conditions, the so-called pulsed electrolysis. Different studies have shown that in pulsed electrolysis, selectivity towards certain products can be improved compared to steady-state operation. Many groups also demonstrated that the selectivity can be tuned by selection of pulsing profile, potential limits, as well as frequency of the change. To explain the origin of this improvement, some modeling studies have been performed. However, it seems that a theoretical framework to study this effect is still missing. In the present contribution, we suggest a theoretical framework of nonlinear frequency response analysis for the evaluation of the process improvement under pulsed electrolysis conditions. Of special interest is the DC component, which determines how much the mean output value under dynamic conditions will be different from the value under steady-state conditions. Therefore, the DC component can be considered as a measure of process improvement under dynamic conditions compared to the steady-state operation. We show that the DC component is directly dependent on nonlinearities of the electrochemical process and demonstrate how this DC component can be calculated theoretically as well as how it can be obtained from measurements.
Traditionally, electrochemical processes take place under steady-state conditions, galvanostatically at constant current or potentiostatically at constant cell potential. This way of operation is also preferred. However, the dynamic and volatile nature of renewable energies puts new requirements on electrochemical processes. Therefore, the dynamic mode of operation appears attractive in order to address the challenges of the energy transition. If electrochemical processes are operated dynamically this is usually termed pulsed electrolysis. The historical developments and summary of pulsed electrolysis are described in some recent review papers.1–3 The major examples of interest were water electrolysis, but also CO2 reduction. In water electrolysis, the scientific question is if the process efficiency can be improved in pulsed operation compared to the steady state. With this respect, influences of dynamic current or cell potential inputs on the performance have been studied. In the case of CO2 reduction, the scientific question was if selectivity of a certain product can be improved by operation under dynamic conditions. Here, mainly change in the potential as an input was studied and the product distribution (in terms of faradaic efficiency) was determined under steady-state and dynamic conditions. In the case of water electrolysis, there is no consensus if dynamic conditions are enhancing or deteriorating the performance of the water electrolyzer.2,3 In the case of CO2 reduction, it seems that the pulsed electrolysis increases selectivity towards certain products. This was confirmed independently with several research groups and different catalysts (e.g. copper and silver). The origin of improvement in CO2 reduction product selectivity is attributed to various reasons in the literature. Some authors assign the improvement under dynamic operation to the change in the catalyst surface. For example, Engelbrecht et al.4 could evidence changes in the copper catalyst surface, with the help of scanning electron microscopy micrographs upon changing cathode potential in a broad range from −1.8 V vs. RHE to +0.42 V vs. RHE. However, it was also observed that the improvement takes place even without changes in the catalyst surface. Kim et al.5 to avoid changes in the catalyst morphology, set the potential change between −0.8 V vs. RHE and −1.15 V vs. RHE and still observed increase in faradaic efficiency towards C2+ products. They attributed this effect to an increase in CO adsorbed coverage to H adsorbed coverage under dynamic conditions, as well as the change in local CO2 concentration. In an another study,6 a time dependent continuum model of pulsed electrolysis on copper was developed and was able to represent experimentally observed effects of pulsed electrolysis. Based on this study, pulsing results in dynamic changes in the pH and CO2 concentration near the copper surface, which finally led to enhancement of C2+ product selectivity.
Casebolt et al.1 in their review paper state that the pulsing mechanism is quite complex and influenced by several processes occurring at the same time like (i) change in local concentration of reactants, products, intermediates, and spectators in the electrochemical double layer, (ii) restructuring of facets including oxide formation, and (iii) dynamic changes in interfacial chemistry, in particular of surface adsorbates. The authors further point out that the extent to which these processes dominate is based on the applied pulsed program and they suggest using modeling and machine learning to determine the optimal pulse profile for optimal performance. These authors named a further challenge, namely the definition of improvement in the pulsed operation and question what the optimal way to represent selectivity, activity, and energy efficiency is. Also, based on previous studies it is not clear how to extract the faradaic current contributions from pulse profiles with double layer charging current contributions. It seems that the theoretical framework to discuss this topic is missing.
In general, in pulsed electrolysis, the electrochemical system is perturbed by an electrical input (potential or current) of high amplitude and certain frequency. The procedure is similar to a well-known and broadly applied technique in electrochemistry, electrochemical impedance spectroscopy (EIS). However, in EIS small input amplitudes are used, therefore the system response is always linear. If higher input amplitudes are used the system response is termed a nonlinear frequency response (NFR). As we discussed in our previous publications,7,8 for a weakly nonlinear system NFR is:
| | | yqs(t) = yss + yDC + hI(t) + hII(t) + hIII(t) + … | (1) |
where
yqs is the system output (current or cell potential) after a periodic quasi-steady state has been established,
yss is the steady-state value of the output,
yDC is the non-periodic part of the NFR (DC component) and
hi,
i = 1 − ∞ are the first and higher-order harmonics of the NFR.
Eqn (1) is obtained when the system input (cell potential or current) is perturbed cosinusoidally around an established steady state. In the case of a linear system (small input amplitude), the DC component and higher-order harmonics are equal to zero. The DC component is caused by nonlinearities of the process. It determines how much the mean output value under dynamic conditions,
ymean, will be different from the value under steady-state conditions,
yss. This effect is well discussed in the chemical engineering community (and references therein).
9,10 It was recognized that (i) depending on the process this effect can be either positive or negative, therefore both process improvement or process deterioration can be observed under dynamic conditions; (ii) the effect will be larger for highly nonlinear systems; (iii) since most chemical processes are nonlinear in nature, there is an opportunity to improve the time-averaged performance such as selectivity, yield, and production rates of chemical reactors under dynamic conditions; (iv) there are different ways to operate the system dynamically, for example, to modulate one or more input variables with different forcing parameters,
i.e. frequency, wave shape, amplitudes, and phase differences; (v) due to the richness of different forcing strategies it is always possible to find at least one mode that will achieve the chosen objectives (for reactor systems: increased conversion, improved selectivity, increased catalyst activity,
etc.); (vi) this very richness presents a challenge of how to decide which forcing strategy to use and how to find it efficiently.
This effect was also recognized in electrochemistry as a so-called faradaic rectification (FR).11 FR was especially studied with respect to AC corrosion, but it was also used for determination of kinetic parameters of electrochemical reactions.12 In our recent publications we discussed how the DC component can be obtained experimentally and have introduced a theoretical framework to study the DC component.8 It is based on a concept of higher-order frequency response functions (FRFs). Petkovska et al. initially introduced this concept for different applications in chemical engineering (adsorption, membrane, and chemical reaction systems).13–16 The NFR method is based on the Volterra series, and the Fourier transform. For a cosinusoidal input modulation, the output can be expressed in the form of a Volterra series:
| | | yqs(t) = yss + y1(t) + y2(t) + y3(t) +… | (2) |
where
| | 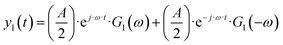 | (3) |
| | 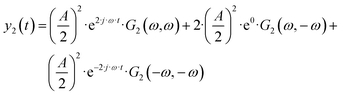 | (4) |
etc., with
G1(
ω) being the 1
st-order FRF (EIS admittance/impedance), and
G2(
ω,
ω) and
G2(
ω,−
ω) the symmetrical and asymmetrical 2
nd-order FRF, respectively. The FRFs are not input dependent and for potential as an input have units of A m
−2 V
−n, where
n is the order of the FRF (1 for the 1
st-order FRF, 2 for the 2
nd-order FRF,
etc.). In
eqn (4), there is one aperiodic term. This term is the main part of the DC component in accordance with:
| | 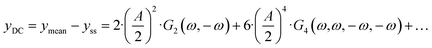 | (5) |
Depending on the input signal amplitude, higher-order terms (like
G4(
ω,
ω,−
ω,−
ω)) will contribute to the DC component. All FRFs are inherently related to the mechanism and parameters of the investigated system. While the linear part of the response (
G1(
ω)) is well known and broadly studied in electrochemistry (EIS), the 2
nd-order symmetrical FRF,
G2(
ω,
ω), is significantly less studied
7 and the asymmetrical 2
nd-order FRF,
G2(
ω,−
ω), is a largely overlooked part of the NFR.
7,12 However, the
G2(
ω,−
ω), and eventually higher-order asymmetrical FRFs are of interest for the quantification of process improvement under forced periodic operation.
8 In the present contribution we show how
G2(
ω,−
ω) can be used for the understanding of selectivity improvement under forced periodic operation (pulsed electrolysis). We show that the improvement compared to steady state is caused by nonlinearities of electrochemical reactions. We also give suggestions on how to determine figures of merit under forced periodic (pulsed) conditions. We consider here an example of recent interest: CO
2 reduction.
Results and discussion
Theoretical considerations of improved selectivity towards one product in pulsed electrolysis
To demonstrate the origin of selectivity improvement under dynamic operation, a simple example of two electrochemical reactions taking place in parallel has been selected. Let us assume further that one reaction is the hydrogen evolution reaction (HER) and the second one is the carbon dioxide reduction reaction (CO2RR):| | | CO2 + H2O + 2e− ⇄ CO + 2OH− | (7) |
The kinetics of both reactions can be described by Tafel formalisms:| | if,H2(t) = −i0,H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αH2fE(t)) exp(−αH2fE(t)) | (8) |
| | if,CO(t) = −i0,CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αCOfE(t)) exp(−αCOfE(t)) | (9) |
where i0,i, αi, i = H2, CO are exchange current densities (A cm−2) and charge transfer coefficients of two parallel reactions, E(t) is potential (V) and 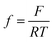 , with F being Faraday's constant (C mol−1), R universal gas constant (J mol−1 K−1), and T temperature (K). Similar formulations were already reported by Weng et al.17 The parameter values used later on in simulations (see List of Symbols) are also adopted from Weng et al.17 Since the original manuscript’s kinetics were expressed with respect to overpotentials (and not potentials (E(V)) as in the present case, exchange current densities are recalculated taking into account the values of equilibrium potentials. Both partial currents are defined as negative assuming a convention with cathodic currents being negative. In eqn (6), formally, protons are considered as the hydrogen source. The concentration of protons under near neutral conditions based on Marcandalli et al.18 is negligible. These authors discussed different proton donors in bicarbonate buffers like H2CO3, HCO3− or water and assumed different proton donors in different potential regions. This increases the complexity of HER but has no further impact for current analysis, assuming both HER and CO2RR taking place at relatively low overpotentials.
, with F being Faraday's constant (C mol−1), R universal gas constant (J mol−1 K−1), and T temperature (K). Similar formulations were already reported by Weng et al.17 The parameter values used later on in simulations (see List of Symbols) are also adopted from Weng et al.17 Since the original manuscript’s kinetics were expressed with respect to overpotentials (and not potentials (E(V)) as in the present case, exchange current densities are recalculated taking into account the values of equilibrium potentials. Both partial currents are defined as negative assuming a convention with cathodic currents being negative. In eqn (6), formally, protons are considered as the hydrogen source. The concentration of protons under near neutral conditions based on Marcandalli et al.18 is negligible. These authors discussed different proton donors in bicarbonate buffers like H2CO3, HCO3− or water and assumed different proton donors in different potential regions. This increases the complexity of HER but has no further impact for current analysis, assuming both HER and CO2RR taking place at relatively low overpotentials.
Further model equation describes charge transfer dynamics at the electrode interface in accordance with:
| | 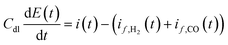 | (10) |
where
Cdl is the double layer capacity (F m
−2) and
i(
t) is the cell current density (A m
−2) containing contributions from both faradaic and double layer currents.
To derive an expression for the asymmetrical 2nd-order frequency response function (G2(ω,−ω)), a periodic input has to be defined. We consider two cases: (i) potential as a periodic input and (ii) current as a periodic input.
Case (i): potential as a periodic input
For simplicity, we assume that potential is a cosinusoidal input which is defined as:| | 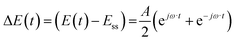 | (11) |
where A is the input amplitude (V) and Ess is the steady-state potential (V) value.
The output signal is the cell current density:
| | 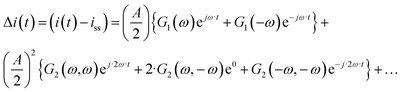 | (12) |
As can be seen, the output contains contributions from the linear part of the response (
G1(
ω)), and nonlinear contributions (
G2(
ω,
ω),
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G2
G2(
ω,−
ω),…) (only nonlinear contributions related to nonlinearity at frequency of 2
ω, where
ω is the fundamental frequency (input frequency) are shown). If the input amplitude is very large,
eqn (12) has to be complemented with contributions of higher-order frequency response functions at frequencies 3
ω, 4
ω and so on. The nonlinear contribution contains both periodic and aperiodic terms. The aperiodic term is represented by
G2(
ω,−
ω) FRF and is a main part of the DC component. This DC component characterizes dynamic processes only if the processes are nonlinear. It indicates if the process can be improved under dynamic operation or not. The theoretical expression for
G2(
ω,−
ω) has been derived as described in ESI (S1).
† Additionally,
G2(
ω,−
ω) can also be determined experimentally.
8 For the nonlinear dynamic model as introduced before it follows:
| | 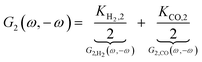 | (13) |
where
Ki,2 = −
i0,iαi2f2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
αifEss),
i = H
2, CO. The asymmetrical 2
nd-order FRF is influenced by kinetic parameters of both reactions. In the present example these contributions (
G2,
H2(
ω,−
ω),
G2,CO(
ω,−
ω)) add up. The negative sign of
G2(
ω,−
ω) is due to a sign convention, where cathode currents are considered negative. Since the mean current value under periodic operation (see
eqn (1)) is expressed as:
| | 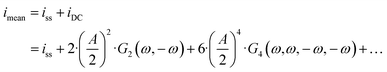 | (14) |
and both the steady-state current (
iss) as well as
G2(
ω,−
ω) terms are negative, the mean current value under dynamic operation will be higher (absolute value) than under steady-state conditions.
Eqn (14) shows that with an increase in input amplitude, mean current value will also increase if the signs of higher-order terms are also negative (for the present example it can easily be shown that the
G4(
ω,
ω,−
ω,−
ω) contribution will be negative).
However, we see that this effect is caused by kinetics of both reactions. To demonstrate how the selectivity of one reaction is influenced by dynamic operating conditions, we define an expression for the faradaic efficiency (FE) under dynamic conditions as a ratio of mean partial current density, if,i,mean, and mean total current density during periodic operation, imean:
| | 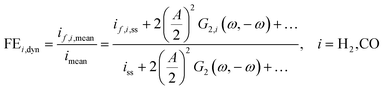 | (15) |
This expression is similar to the expression for FE under steady-state conditions, stating that the FE of one component is a ratio of a partial current density of one component divided by the total current density. Under dynamic conditions, both partial currents, as well as the total current, will contain DC contributions. Assuming nonlinearities up to the second harmonics, DC contributions will be expressed as
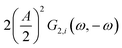
and
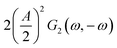
terms for partial and total current densities respectively. It should be noted that for very large input amplitudes additional terms should be considered. It follows also that the FE under dynamic operation depends on the input signal amplitude. However, FRFs, like
G2(
ω,−
ω), are not amplitude dependent. As a consequence, the same model (derived here for a cosine input signal) can be used for calculation of FE for different input signals.
19
One can also define other figures of merit under dynamic conditions, like specific energy consumption. For steady state, specific energy consumption (electrical energy needed to produce a unit mass of product) is defined as:
| | 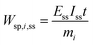 | (16) |
where
t is time (h),
Iss steady-state current (A), and
mi mass of product
i (kg). Under dynamic conditions one can show that:
| | 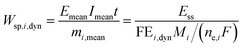 | (17) |
where
Mi is molecular weight of product
i (kg mol
−1). Since for potential as an input
Emean =
Ess, the specific energy consumption under dynamic conditions will decrease if the FE under dynamic conditions is improved compared to steady-state conditions.
In the present example, the asymmetrical FRFs are not dependent on frequency. This is due to the assumption that the input potential does not depend on the ohmic resistance, and also the disregard of the effects of mass transport and adsorbed intermediates. In classical electrochemical experiments, the potential at the electrode interface will be influenced by the ohmic drop, but also other effects might be contributing. In our previous publication,7 the expression for asymmetrical 2nd-order FRF assuming ohmic drop contributions has been shown. In such a case, asymmetrical 2nd-order FRF depends not only on kinetic parameters but also on double layer resistance and ohmic resistance. At low frequencies, the contributions of these terms become negligible and the asymmetrical 2nd-order FRF shows dependence only on kinetic parameters. Therefore, FE, as well as specific energy consumption under dynamic operating conditions, will also be frequency dependent. Furthermore, the present example doesn't consider mass transport effects. Mass transport in general has smaller time constant than the electrochemical reaction, meaning it is expected to have an influence on the asymmetrical 2nd-order FRF at low frequencies.8
Case (ii): current as a periodic input
For simplicity we assume that current density is a cosinusoidal input which is defined as:| | 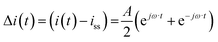 | (18) |
where A is the input amplitude and iss is steady-state current density value. The output signal is the potential:| | 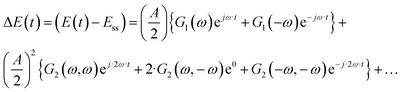 | (19) |
By following the same procedure as described previously and in our previous publications, one can derive the asymmetrical 2nd-order FRF with current as an input:| | 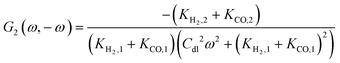 | (20) |
where Ki,1 = i0,iαif![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αifEss) and i = H2, CO.
exp(−αifEss) and i = H2, CO.
Unlike the expression for potential input (eqn (13)), the asymmetrical 2nd-order FRF for current input is not just kinetic parameter dependent, but it also depends on double layer capacity and, therefore, it is also frequency dependent.
Additionally, when total current density is the modulated input during periodic operation, its mean value, imean, will be equal to the steady-state current density, iss. However, mean partial current densities, if,i,mean, can be different from their values in the steady state:
| | 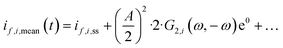 | (21) |
where
i = CO,H
2.
Thus, one can define FE under dynamic conditions for current as an input. For CO FE, it will follow:
| | 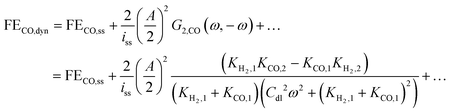 | (22) |
where
G2,CO(
ω,−
ω) is the asymmetrical 2
nd-order FRF for partial current of CO.
Eqn (22) shows that, unlike dynamic FE with potential as an input, dynamic FE with current as an input is double layer capacitance and frequency dependent. Also, the mean partial current depends not only on the kinetic parameters of one reaction, but also on the kinetic parameters of the other reaction. Furthermore, the improvement or the deterioration of CO FE under dynamic conditions compared to the steady-state conditions is dependent only on the values of the charge transfer coefficients of the two parallel reactions. The CO FE will be improved only if the charge transfer coefficient of CO2RR is greater than the one of HER. More details regarding this can be found in ESI S2.†
We can further define specific energy consumption under dynamic conditions with current as an input as:
| | 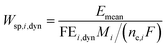 | (23) |
As one can see, dynamic operation with current as an input influences specific energy consumption through both mean output potential and dynamic operation FE values.
In Fig. 1a, simulated 2nd-order asymmetrical FRFs for input potential and input current at the steady-state potential value of −0.7 V and the corresponding steady-state current value of −13.11 mA cm−2 are shown, while Fig. 1b shows simulated mean partial CO current densities for potential or current as an input. For both cases the same steady-state operating point was considered (−0.7 V, −13.11 mA cm−2) with an amplitude for input potential of 0.1 V and for input current of 50% of the steady-state current value. In both cases, there is an improvement compared to the steady state.
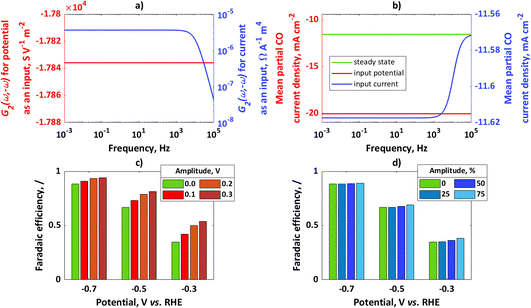 |
| | Fig. 1 (a) Asymmetrical 2nd-order frequency response functions for potential or current as an input, (b) mean partial CO current densities for potential or current as an input; for comparison, steady-state current value has been shown; conditions: input potential amplitude 0.1 V, input current amplitude 50% iss, (c) faradaic efficiencies for potential as an input at different steady states and different amplitudes, (d) faradaic efficiencies for current as an input at different steady states (same steady-state points as in (c) and different amplitudes (amplitudes are expressed as percentages of iss). | |
In absolute numbers, it seems that the improvement for potential as an input is higher than for current as an input. A reason for this observation is that partial currents under dynamic conditions depend on input signal amplitude. The amplitude of potential of 0.1 V causes a different change than the change caused by an amplitude of current of 50% iss (for example, a Tafel slope of 100 mV dec−1 means that a potential change of 100 mV causes a current value change of 10 times that; therefore, the chosen current amplitude value will cause a smaller change than the chosen potential amplitude). In Fig. 1c, the influence of the input potential amplitude on CO FE at different steady-state values of potential at frequency ω = 10 mHz has been shown. Similarly, in Fig. 1d the influence of input current amplitude on CO FE at frequency ω = 10 mHz and different steady-state values has been shown. For the chosen kinetic parameters, CO FE is always higher under dynamic operation than under steady-state conditions and increases with an increase in amplitude of the input modulation. The main kinetic parameter which causes higher CO FE compared to H2 FE is a charge transfer coefficient. Since the charge transfer coefficient of CO is larger than that of H2, change of electrical inputs (current, potential) always causes improvement compared to the steady-state operation. This effect will be more expressed at lower overpotentials, while at higher overpotentials the improvement due to dynamic operation will not be significant.
In the next part, we show an experimental validation of this effect.
Experimental validation
To validate theoretical findings, dynamic experiments have been performed with bulk silver electrodes. In previous literature on pulsed electrolysis on silver, very large potential steps were applied, with a difference between the cathodic and anodic potential of more than 2 V.20 Under such conditions, not only faradaic efficiencies for CO and H2 were affected, but there were also completely new products not typical for silver, like CH4, that were detected. To explain such changes, a more complex kinetic model would have to be considered, and the changes in the catalyst itself could not be neglected. Such analysis is beyond the scope of this study. Therefore, our dynamic experiments were limited to the potential region where only two products (H2 and CO) are expected and the amplitudes of change are relatively low (in comparison to previous literature), but still significant enough to cause nonlinear effects in the response. Two different set-ups were tested (flow reactor and a rotating disk electrode). In both set-ups bulk silver electrodes were tested, but the surface areas were different (6.25 cm2 and 0.196 cm2 for flow and rotating disk electrode set-ups respectively). At first, the CO2 reduction in the flow cell was studied under steady-state conditions at two different flow rates. The potentiostatic experiments at different potential values during 50 min were conducted and current values have been recorded. At the same time, product distribution was measured by using a GC. Usually, steady-state conditions could be established after 40 min. The GC data was used for determination of partial current densities. Based on the literature, CO and hydrogen are the main products of CO2RR in the range of potentials studied in this publication. According to Hatsukade et al.,21 further products like CH4, C2H5OH, and CH3OH form at potentials more negative than −1.2 V vs. RHE. Additionally, formic acid is present at very small quantities in the whole potential range, but it becomes more significant (more than 1% FE) only at potentials more negative than ca. −1.05 V vs. RHE. Therefore, in the present study we concentrate only on products in the gas phase. In Fig. 2a, CO and H2 partial current densities have been shown at two different flow rates. For comparison, literature data by Hatsukade et al.21 has been shown. Their literature set-up was termed “batch” in the present publication, since the liquid was not circulated (only CO2 was purged through the cell). As one can see, there is an excellent agreement between literature results and our experimental observations, in the potential region up to −1.1 V vs. RHE. At more negative potentials, the limiting current behavior is observed for the CO2 reaction. Our flow cell shows lower mass transport limitations and, therefore, limiting current values are a bit higher than in the “batch” case. The dependence of the limiting current on flow conditions indicates diffusion limitation. In our measurement, the gas chromatography (GC) set up did not have enough sensitivity for H2 determination at low current density. Therefore, measured values are shown only at higher current densities. The H2 literature data are a bit scattered at lower currents. In general, H2 partial currents show limiting current behavior in the potential range from −0.8 to −1.1 V vs. RHE, while currents are increasing again at potentials more negative than −1.1 V vs. RHE. The dependence of partial currents on potential is further reflected in the typically observed bell-shaped curve for FECO, with the maximum FECO at a potential of ca −1.05 V vs. RHE and a maximum CO partial current at ca. −1.2 V vs. RHE. There are different interpretations of this behavior in the literature. Zhu et al.22 concluded that the decrease in the CO current density at high overpotentials is caused not only by the decrease in CO2 concentration due to mass transport, surface charge effects, and pH increase but also by lateral interactions between adsorbed species. Other authors assumed that the change in the H2 partial current density slope in the semi-log plot is caused by a change from one proton donor to another donor, and interplay between mass transport and electrolyte composition.18 In the present case we should just note that the apparent charge transfer coefficient of the hydrogen reaction is “low” in the potential range from −0.8 to −1.1 V vs. RHE, while it is “high” at potentials more negative than −1.1 V vs. RHE. We should also note that the apparent charge transfer coefficients for CO partial currents behave exactly opposite to the H2 case. Based on the theoretical considerations, the partial reaction showing higher apparent charge transfer coefficients will hypothetically show improved selectivity under dynamic conditions. To validate this we performed dynamic and steady-state experiments at two input potentials (−0.84 V vs. RHE and −1.2 V vs. RHE). Please note that both values are not ohmic drop corrected. The iR corrected mean potentials are −0.83 V vs. RHE and −1.05 V vs. RHE. The mean values for the input potential under dynamic conditions and the steady-state potential values coincide with each other (Fig. 2b). The input potential values (U) also contain contributions from the ohmic drop between the working and reference electrode in accordance to:| | | U(t) = E(t) + RΩ·i(t) | (24) |
As can be seen, the ohmic drop corrected potential (E) is dependent on current density value, and therefore it will have different values for steady-state and dynamic operation. If the absolute mean current values under dynamic operation are higher than under steady-state conditions, the ohmic drop free potential (E) under dynamic operation will be more positive compared to steady-state operation. The input signal in the flow cell was a triangular wave, with an amplitude of 250 mV for the mean potential of −0.84 V vs. RHE, and 400 mV for the mean potential of −1.2 V vs. RHE. A triangular wave can be represented as a combination of a sinusoidal wave at a fundamental frequency and additional harmonics at odd frequencies (3ω, 5ω, 7ω…). Consequently, not only nonlinear contributions at the fundamental frequency (ω) but also nonlinear contributions related to higher harmonics will have to be considered in the theoretical description of FE under dynamic conditions. However, in a previous study using a square wave input it was shown that the theoretical prediction of the DC component improves by considering higher order FRFs, but even consideration of a sinusoidal input at the fundamental frequency was giving a satisfactory agreement.19 Therefore, bearing in mind that for the triangular wave the most prominent frequency is still the base frequency, we assume that the dynamic effect on faradaic efficiency in the output signal will be influenced mainly by the base frequency, comparable to a single sinusoidal input.
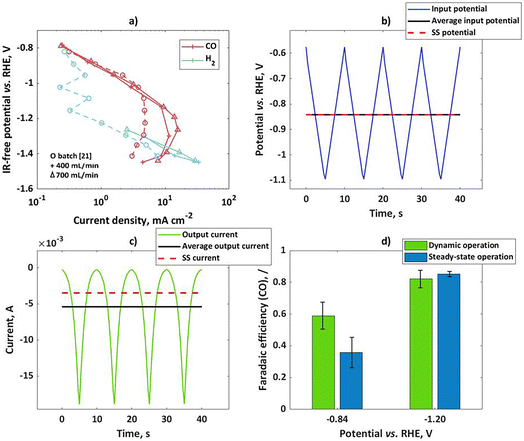 |
| | Fig. 2 (a) Influence of the flow rate on experimental steady-state CO and H2 partial current densities on bulk silver electrode in the flow cell; for comparison literature data from ref. 21 (circles) have been shown, (b) input potential in the flow cell in form of a triangular wave, with an amplitude of 250 mV for mean as well as steady-state potential of −0.84 V vs. RHE, (c) output current response in the time domain upon input potential perturbation (b) with mean current and steady-state current values, (d) faradaic efficiencies for potential as an input at two steady states (not iR-corrected) and amplitudes of 250 and 400 mV at −0.84 and −1.2 V vs. RHE respectively; other conditions: 0.1 M KHCO3, CO2 saturated at 25 °C and pH = 6.8. | |
The output signal was a current, expressed as a current density in Fig. 2c. The mean values of the current outputs were calculated and shown also in Fig. 2c. Additionally, steady-state current density values have been shown. As one can see, there is a shift between mean current under dynamic operation and a steady-state current value. This shift is the DC component, which was discussed before. In the present case the shift shows the positive impact of dynamic operation, the system performance improves under forced periodic operation compared to steady-state operation. Since the total current is influenced by contributions of both reactions, it is interesting to see how this improvement reflects in terms of the H2 and CO formation reactions. In the present set-up determination of product distribution for both steady-state and dynamic operation was performed with the help of a GC. The GC is better suited for the steady-state operation, while for dynamic operation it would be better to obtain a time resolved signal, which could be used for the determination of the mean values. In the present set-up, this was not possible. Therefore, mean values of CO faradaic efficiency are based on GC analysis after 40 min of forced periodic operation. The dynamic and steady-state CO faradaic efficiencies at two different potentials are shown in Fig. 2d. As can be seen, the dynamic operation shows advantages over the steady state at potential of −0.84 V vs. RHE, while there is no improvement at −1.2 V vs. RHE. This agrees quite well with our expectations since the first potential value is in the region of a higher apparent CO charge transfer coefficient than H2, while the second one is in the region of a low CO apparent charge transfer coefficient.
We performed further experiments with the rotating disc electrode set-up. One advantage of using this set-up is that there are well-defined hydrodynamics and therefore well-defined mass transfer conditions which can be easily implemented in the model. Additionally, noise caused by gas evolution at higher currents was less pronounced when using a rotating disc electrode. Therefore, with a rotating disc electrode we could perform experiments with more concentrated buffer solutions (e.g. 1.5 M). In these experiments, we have chosen a potential value of −0.93 V vs. RHE and studied the influence of input amplitude and frequency range. The input signal was a sinusoidal wave in all these experiments. In Fig. 3a, we show the input potential signal in the time domain at a mean potential of −0.93 V vs. RHE and an amplitude of 0.2 V RMS at a frequency of 0.1 Hz. The mean value under dynamic conditions coincides with the steady-state potential value. In Fig. 3b the output signal, expressed in terms of current densities, is also shown. For the sake of comparison, the steady-state current value under the same conditions has been shown. As in the case of the flow cell, the absolute value of the mean current is higher than the value of the steady-state current, meaning that the periodic operation under these conditions has a positive impact. The CO faradaic efficiencies have been calculated for the dynamic and steady-state conditions at the input potential value of −0.93 V vs. RHE as a function of input signals amplitudes at different frequencies (Fig. 3c). Additionally, specific energy consumptions for the CO products have been calculated (Table 1).
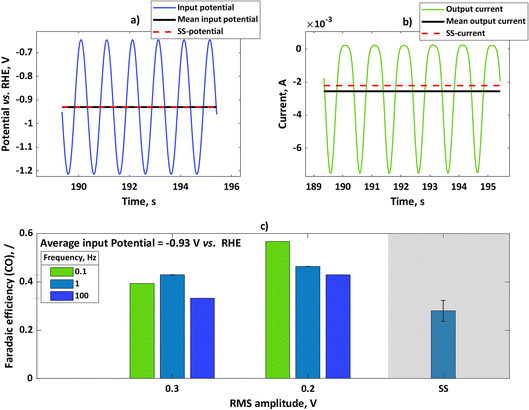 |
| | Fig. 3 (a) Input potential in the time domain for experiments with rotating silver disc electrode with an amplitude of 0.2 V RMS for mean as well as steady-state potential of −0.93 V vs. RHE, (b) output current response in the time domain upon input potential perturbation (a) with mean current and steady-state current values, (c) influence of input signal amplitude on faradaic efficiencies for potential as an input at a steady-state value of −0.93 V vs. RHE (not iR-corrected) at different frequencies. Other conditions: 1.5 M KHCO3, CO2 saturated at 25 °C and pH = 7.8. | |
Table 1 Specific energy consumptions at −0.93 V vs. RHE as a function of input amplitude at different frequencies
| RMS amplitude, V |
Frequency, Hz |
Specific energy consumption, kW h kg−1 |
| 0.3 |
0.1 |
3.82 |
| 1 |
3.58 |
| 100 |
4.53 |
| 0.2 |
0.1 |
2.65 |
| 1 |
3.24 |
| 100 |
3.50 |
| SS |
— |
5.87
|
As depicted, at all studied frequencies and input amplitudes the dynamic operation has an advantage over steady-state operation. However, there is an effect of the frequency and amplitude on the faradaic efficiency under dynamic conditions. It seems that lower frequencies are more favored for dynamic operation at both studied amplitudes. This can be explained by theoretical considerations which were shown before, where linear effects (like double layer, or ohmic resistance (not shown here)) dominate at higher frequencies, leading to no improvement under dynamic conditions (please see also ref. 8). The influence of amplitude is more complex. The simple model indicates that the faradaic efficiency is always increasing with an increase in amplitude. The experiment does not show this effect and smaller faradaic efficiencies are obtained with an increase in input signal amplitude. The simple model which was discussed before considers only kinetics, and oversimplifies CO2RR and HER. To describe these influences, a more complex model is required that considers the effects of adsorbed species, mass transport, and buffer kinetics, which is the subject of our future work. The specific energy consumption is directly related to faradaic efficiency under dynamic conditions. As Table 1 shows, the specific energy consumption can be significantly reduced under forced periodic conditions in comparison to the steady-state value. There is a great potential to influence this value by fine tuning amplitude, frequency, and operating potential.
Conclusions
In the present contribution, we suggest a theoretical framework of nonlinear frequency response analysis for the evaluation of process improvement under pulsed electrolysis conditions. Of special interest is the DC component, which determines how much the mean output value under dynamic conditions will differ from the value under steady-state conditions. Therefore, the DC component can be considered as a measure of process improvement under dynamic conditions compared to steady-state operation. We show that the DC component is directly dependent on nonlinearities of electrochemical processes and demonstrate how the DC component can be calculated theoretically as well as how it can be obtained from measurements. The DC component depends on the amplitude of the input as well as the frequency. It is a periodic term appearing in the main output (e.g. current), as well as in the auxiliary outputs (e.g. partial faradaic currents). We show that the faradaic efficiency under dynamic conditions will depend on the DC component in the main output as well as in auxiliary outputs. Other figures of merit like specific energy consumption, will depend only on the faradaic efficiency under dynamic conditions when using potential as an input. When using current as an input, they will also depend on the mean value of potential output. For a simple example of two kinetically controlled parallel reactions, the main kinetic parameter influencing faradaic efficiency under dynamic conditions is the charge transfer coefficient. Reactions having higher charge transfer coefficient values will always be improved under forced periodic conditions compared to steady-state conditions. This improvement should be obtained independent of input (potential or current). To validate these theoretical findings, dynamic experiments on bulk silver have been performed. In general, the experiments confirmed the main observations. However, the experimental effect of amplitude change seems to be more complex. Therefore, in future studies, more complex kinetic schemes should be considered, and mass transfer effects should be also taken into account.
Experimental section
Flow cell
A two-compartment electrochemical flow cell was made in-house by machining from poly(methyl methacrylate) (PMMA). The compartments were separated by a porous diaphragm (Zirfon™ Perl UTP 500). Anolyte and catholyte were recirculated through two separate electrolyte reservoirs containing 300 mL of 0.1 M KHCO3 (Sigma-Aldrich®, ≥99.95%) by membrane pumps (Liquiport® NF 1.100 RC, KNF Group) with a flow rate of 730 mL min−1. 10 mL of 2 mM EDTA was added to each electrolyte reservoir to avoid any influences from impurities in the electrolyte. Both reservoirs were temperature controlled at 25 °C and continuously purged with CO2 gas (100 mL min−1, >99.5 vol%), the saturated solution having a pH of 6.8.
A planar silver foil (30 × 30 × 1 mm, >99.99%, Sigma-Aldrich®), polished with diamond suspensions (1, 0.25, 0.05 μm MetaDI™ Buehler Ltd.), and planar glassy carbon plate (30 × 30 × 5 mm, Sigradur™G, HTW GmbH) were used as the working and counter electrode respectively. The exposed geometric electrode area for both electrodes was 6.25 cm2. The Ag/AgCl reference electrode (3 M NaCl, RE-1BP, ALS Co. Ltd) was connected via a closed Luggin capillary to the WE compartment. However, all potentials in the manuscript are recalculated vs. RHE by using the following equation:
Uvs.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RHE = Uvs. RHE = Uvs.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ag/AgCl + 0.059pH + 0.196 V. Ag/AgCl + 0.059pH + 0.196 V. |
For this calculation, the bulk pH value has been considered (pH = 6.8 for the CO
2 saturated solution) and the influence of the pH change at the electrode surface was not considered. The potential-pulse polarization was realized with a potentiostat (Parstat® 3000A DX, Ametek Inc.). The experimental protocol consisted of application of steady-state potentials (−0.84 V and −1.20 V
vs. RHE) and consecutive potentiostatic cycling with the same mean potentials as the steady-state values, with an amplitude of 250 mV and 400 mV within upper and lower potential limits (−1.20…−1.70 V and −1.40 V…−2.20 V
vs. RHE), and frequency of 0.1 Hz for 40 min each. The mentioned potential values of the protocol are not
iR-corrected. The mean total current was calculated as a time-weighted average of the recorded data points.
The output gas stream of the gas head space from the closed catholyte reservoir was supplied to a GC (Agilent® microGC 3000) in bypass operation and sampled every 10 min, detecting the CO concentration. After 40 min the stabilized CO concentration was used for CO partial current and faradaic efficiency calculation.
| | | if,CO,mean = ṄtotalxCOne,COF | (25) |
where
Ṅtotal is the total molar flux from the gas outlet mol s
−1,
xCO the detected molar fraction of CO,
ne,CO = 2 is the number of exchanged electrons per CO formed.
| | 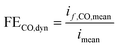 | (26) |
All experimental trials were repeated twice to confirm the reproducibility and error bars show the standard deviation of experimental values.
Rotating disk electrode
All rotating disk electrode experiments were performed in a three-electrode cell assembly with a working volume of 150 mL (RRPG310, Pine Research Instrumentation, Inc.). A silver disk shroud (0.196 cm2, E6R2 series, Pine Research Instrumentation, Inc.) was used as the working electrode. The electrode was polished with diamond suspensions (1, 0.25, 0.05 μm MetaDI™ Buehler Ltd.) and sonicated in distilled water. A platinum mesh enclosed inside a cathode compartment was used as the counter electrode and an Ag/AgCl (3 M NaCl, RE-1BP, ALS Co. Ltd) electrode placed inside a Luggin capillary was used as the reference electrode. Later, the potentials measured were converted to the RHE scale as shown before. Like the flow cell experiments, only the bulk pH was considered. 1.5 M KHCO3 (≥99.95%, Sigma-Aldrich®) solution was used as the electrolyte. 13 mL of 2 mM EDTA was added to the electrolyte to avoid influences from impurities. The electrolyte was saturated by purging with CO2 (40 mL min−1, >99.5 vol%) before the experiment until a stable pH of 7.8 was reached. The electrolyte was also continuously purged with CO2 during the experiment. The temperature of the cell was maintained at 25 °C with the help of a cooling jacket controlled by a thermostat (Windaus-Labortechnik). A rotor (MSR series, Pine Research Instrumentation, Inc.) was used to control the rotation rate at 2500 rpm. All measurements were performed using a potentiostat (ModuLab® XM ECS, Solartron Analytical). Steady-state measurements were performed at −0.93 V vs. RHE, where a constant potential was applied for a total time of 25 min. Following a 10 min saturation period of the head space, 3 consecutive samples were collected at 5 min intervals each by a GC (Agilent® microGC 3000) which was connected to the headspace of the cell. In the case of dynamic operation, experiments were performed at the same steady-state potential (−0.93 V) at three different frequencies (0.1, 1 and 100 Hz) and two different RMS amplitudes (0.3 V and 0.2 V). The mean potential and current were calculated by averaging the points collected during the experiment. The experiments were performed for the same duration as steady-state experiments and the product gas in the head space was analyzed similarly. In both steady-state and dynamic experiments, the measured CO concentration averaged from the collected samples was used to calculate the CO partial currents and the FE using eqn (25) & (26).
List of symbols
|
A
| Amplitude of input modulation |
|
C
dl
| Double layer capacitance, 0.2 F m−2 |
|
E
| Electrode potential, iR-free potential, V |
|
F
| Faraday's constant, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.33 C mol−1 485.33 C mol−1 |
| FE | Faradaic efficiency, / |
|
G
| Frequency response function |
|
G
1(ω) | 1st-order frequency response function |
|
G
2(ω,ω) | Symmetrical 2nd-order frequency response function |
|
G
2(ω,−ω) | Asymmetrical 2nd-order frequency response function |
|
h
i
,i = 1 − ∞ |
i
th-order harmonic |
|
i
| Current density, A cm−2 |
|
I
| Current, A |
|
i
f
| Partial (faradaic) current density, A cm−2 |
|
i
0,H2, i0,CO | Anodic and cathodic exchange current densities, 9.80 × 10−4 A cm−2 and 7.15 × 10−5 A cm−2, respectively |
|
K
| Coefficients in expressions for frequency response functions |
|
m
| Weight, kg |
|
M
| Molar mass, kg mol−1 |
|
n
e
| Number of electrons, / |
|
Ṅ
total
| Total molar flux from the gas outlet, mol s−1 |
|
R
| Universal gas constant, 8.314 J mol−1 K−1 |
|
R
Ω
| Ohmic resistance, Ω cm2 |
|
t
| Time, h |
|
T
| Temperature, 298 K |
|
U
| Total potential, V |
|
W
sp
| Specific energy consumption, W h kg−1 |
|
y
| Output signal |
|
y
DC
| DC component |
|
x
CO
| Molar fraction of CO, / |
|
α
H2, αCO | Anodic and cathodic charge transfer coefficients, 0.27 and 0.44, respectively |
|
j
| Imaginary unit, / |
|
ω
| Radial frequency, rad s−1 |
Subscripts
| dyn | Dynamic operation |
| DC | DC component value |
|
i = H2, CO | Faradaic reaction products |
| mean | Mean value |
| ss | Steady-state value |
Data availability
The raw data of this study are available in Edmond at https://doi.org/10.17617/3.CCHCNR.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors greatly acknowledge German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) support in the framework of DFG Research Unit, FOR2397 Multiscale analysis of complex three-phase systems: Oxygen and Carbon dioxide reduction, project number VI845/1-2. TM is affiliated with the International Max Planck Research School (IMPRS) for Advanced Methods in Process and Systems Engineering, Magdeburg, Germany. The authors kindly acknowledge Grant Louis Fiedler, Purdue University – West Lafayette, currently an exchange student at Otto-von-Guericke University Magdeburg, for a careful grammar check. Open Access funding provided by the Max Planck Society.
References
- R. Casebolt,
et al., Pulse check: potential opportunities in pulsed electrochemical CO2 reduction, Joule, 2021, 5(8), 1987–2026 CrossRef CAS.
- N. Monk and S. Watson, Review of pulsed power for efficient hydrogen production, Int. J. Hydrogen Energy, 2016, 41(19), 7782–7791 CrossRef CAS.
- T. Liu,
et al., A review of pulse electrolysis for efficient energy conversion and chemical production, J. Energy Chem., 2021, 59, 69–82 CrossRef CAS.
- A. Engelbrecht,
et al., On the Electrochemical CO2 Reduction at Copper Sheet Electrodes with Enhanced Long-Term Stability by Pulsed Electrolysis, J. Electrochem. Soc., 2018, 165(15), J3059 CrossRef CAS.
- C. Kim, L.-C. Weng and A. T. Bell, Impact of Pulsed Electrochemical Reduction of CO2 on the Formation of C2+ Products over Cu, ACS Catal., 2020, 10(21), 12403–12413 CrossRef CAS.
- J. C. Bui,
et al., Dynamic Boundary Layer Simulation of Pulsed CO2 Electrolysis on a Copper Catalyst, ACS Energy Lett., 2021, 6(4), 1181–1188 CrossRef CAS.
- T. Vidaković-Koch,
et al., Nonlinear Frequency Response Analysis: A Recent Review and Perspectives, Curr. Opin. Electrochem., 2021, 30, 100851 CrossRef.
- L. A. Živković,
et al., Evaluation of Electrochemical Process Improvement Using the Computer-Aided Nonlinear Frequency Response Method: Oxygen Reduction Reaction in Alkaline Media, Front. Chem., 2020, 8 DOI:10.3389/fchem.2020.579869.
- A. Marković, A.-S. Morgenstern and M. Petkovska, Evaluation of the potential of periodically operated reactors based on the second order frequency response function, Chem. Eng. Res. Des., 2008, 86(7), 682–691 CrossRef.
- D. Nikolic Paunic and M. Petkovska, Evaluation of periodic processes with two modulated inputs based on nonlinear frequency response analysis. Case study: CSTR with modulation of the inlet concentration and flow-rate, Chem. Eng. Sci., 2013, 104, 208–219 CrossRef CAS.
- K. B. Oldham, Faradaic rectification: theory and application to the Hg22+/Hg electrode, Trans. Faraday Soc., 1957, 53, 80–90 RSC.
- A. S. Baranski and P. M. Diakowski, High frequency faradaic rectification voltammetry at microelectrodes, J. Phys. Chem. B, 2006, 110(13), 6776–6784 CrossRef CAS PubMed.
- M. Petkovska and D. D. Do, Use of Higher-Order Frequency Response Functions for Identification of Nonlinear Adsorption Kinetics: Single Mechanisms under Isothermal Conditions, Nonlinear Dyn., 2000, 21(4), 353–376 CrossRef.
- M. Petkovska, Application of Nonlinear Frequency Response to Adsorption Systems with Complex Kinetic Mechanisms, Adsorption, 2005, 11(1), 497–502 CrossRef.
- M. Petkovska,
et al., Investigation of gas transport through porous membranes based on nonlinear frequency response analysis, Adsorption, 2011, 17(1), 75–91 CrossRef CAS.
- M. Petkovska, D. Nikolić and A. Seidel-Morgenstern, Nonlinear Frequency Response Method for Evaluating Forced Periodic Operations of Chemical Reactors, Isr. J. Chem., 2018, 58(6–7), 663–681 CrossRef CAS.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Modeling gas-diffusion electrodes for CO2 reduction, Phys. Chem. Chem. Phys., 2018, 20, 16973–16984 RSC.
- G. Marcandalli, A. Goyal and M. T. M. Koper, Electrolyte Effects on the Faradaic Efficiency of CO2 Reduction to CO on a Gold Electrode, ACS Catal., 2021, 11(9), 4936–4945 CrossRef CAS PubMed.
- D. Nikolić and M. Petkovska, Evaluation of Performance of Periodically Operated Reactors for Single Input Modulations of General Waveforms, Chem. Ing. Tech., 2016, 88(11), 1715–1722 CrossRef.
- R. Shiratsuchi and G. Nogami, Pulsed Electroreduction of CO2 on Silver Electrodes, J. Electrochem. Soc., 1996, 143(2), 582 CrossRef CAS.
- T. Hatsukade,
et al., Insights into the electrocatalytic reduction of CO2 on metallic silver surfaces, Phys. Chem. Chem. Phys., 2014, 16, 13814–13819 RSC.
- X. Zhu, J. Huang and M. Eikerling, Electrochemical CO2 Reduction at Silver from a Local Perspective, ACS Catal., 2021, 11(23), 14521–14532 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
M.
Sivasankaran‡
a,
M.
Sivasankaran‡
 a,
C.
Blümner‡
ab,
A.
Sorrentino
a and
T.
Vidaković-Koch
a,
C.
Blümner‡
ab,
A.
Sorrentino
a and
T.
Vidaković-Koch
 *a
*a
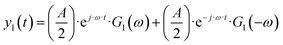
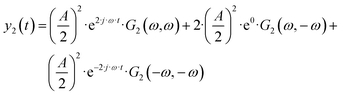
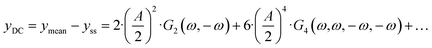
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αH2fE(t))
exp(−αH2fE(t))![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αCOfE(t))
exp(−αCOfE(t))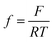 , with F being Faraday's constant (C mol−1), R universal gas constant (J mol−1 K−1), and T temperature (K). Similar formulations were already reported by Weng et al.17 The parameter values used later on in simulations (see List of Symbols) are also adopted from Weng et al.17 Since the original manuscript’s kinetics were expressed with respect to overpotentials (and not potentials (E(V)) as in the present case, exchange current densities are recalculated taking into account the values of equilibrium potentials. Both partial currents are defined as negative assuming a convention with cathodic currents being negative. In eqn (6), formally, protons are considered as the hydrogen source. The concentration of protons under near neutral conditions based on Marcandalli et al.18 is negligible. These authors discussed different proton donors in bicarbonate buffers like H2CO3, HCO3− or water and assumed different proton donors in different potential regions. This increases the complexity of HER but has no further impact for current analysis, assuming both HER and CO2RR taking place at relatively low overpotentials.
, with F being Faraday's constant (C mol−1), R universal gas constant (J mol−1 K−1), and T temperature (K). Similar formulations were already reported by Weng et al.17 The parameter values used later on in simulations (see List of Symbols) are also adopted from Weng et al.17 Since the original manuscript’s kinetics were expressed with respect to overpotentials (and not potentials (E(V)) as in the present case, exchange current densities are recalculated taking into account the values of equilibrium potentials. Both partial currents are defined as negative assuming a convention with cathodic currents being negative. In eqn (6), formally, protons are considered as the hydrogen source. The concentration of protons under near neutral conditions based on Marcandalli et al.18 is negligible. These authors discussed different proton donors in bicarbonate buffers like H2CO3, HCO3− or water and assumed different proton donors in different potential regions. This increases the complexity of HER but has no further impact for current analysis, assuming both HER and CO2RR taking place at relatively low overpotentials.
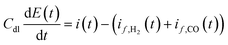
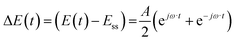
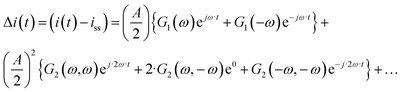
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G2(ω,−ω),…) (only nonlinear contributions related to nonlinearity at frequency of 2ω, where ω is the fundamental frequency (input frequency) are shown). If the input amplitude is very large, eqn (12) has to be complemented with contributions of higher-order frequency response functions at frequencies 3ω, 4ω and so on. The nonlinear contribution contains both periodic and aperiodic terms. The aperiodic term is represented by G2(ω,−ω) FRF and is a main part of the DC component. This DC component characterizes dynamic processes only if the processes are nonlinear. It indicates if the process can be improved under dynamic operation or not. The theoretical expression for G2(ω,−ω) has been derived as described in ESI (S1).† Additionally, G2(ω,−ω) can also be determined experimentally.8 For the nonlinear dynamic model as introduced before it follows:
G2(ω,−ω),…) (only nonlinear contributions related to nonlinearity at frequency of 2ω, where ω is the fundamental frequency (input frequency) are shown). If the input amplitude is very large, eqn (12) has to be complemented with contributions of higher-order frequency response functions at frequencies 3ω, 4ω and so on. The nonlinear contribution contains both periodic and aperiodic terms. The aperiodic term is represented by G2(ω,−ω) FRF and is a main part of the DC component. This DC component characterizes dynamic processes only if the processes are nonlinear. It indicates if the process can be improved under dynamic operation or not. The theoretical expression for G2(ω,−ω) has been derived as described in ESI (S1).† Additionally, G2(ω,−ω) can also be determined experimentally.8 For the nonlinear dynamic model as introduced before it follows: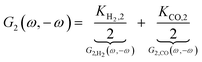
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αifEss), i = H2, CO. The asymmetrical 2nd-order FRF is influenced by kinetic parameters of both reactions. In the present example these contributions (G2,H2(ω,−ω), G2,CO(ω,−ω)) add up. The negative sign of G2(ω,−ω) is due to a sign convention, where cathode currents are considered negative. Since the mean current value under periodic operation (see eqn (1)) is expressed as:
exp(−αifEss), i = H2, CO. The asymmetrical 2nd-order FRF is influenced by kinetic parameters of both reactions. In the present example these contributions (G2,H2(ω,−ω), G2,CO(ω,−ω)) add up. The negative sign of G2(ω,−ω) is due to a sign convention, where cathode currents are considered negative. Since the mean current value under periodic operation (see eqn (1)) is expressed as: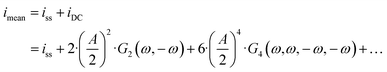
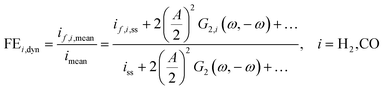
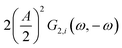 and
and 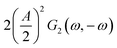 terms for partial and total current densities respectively. It should be noted that for very large input amplitudes additional terms should be considered. It follows also that the FE under dynamic operation depends on the input signal amplitude. However, FRFs, like G2(ω,−ω), are not amplitude dependent. As a consequence, the same model (derived here for a cosine input signal) can be used for calculation of FE for different input signals.19
terms for partial and total current densities respectively. It should be noted that for very large input amplitudes additional terms should be considered. It follows also that the FE under dynamic operation depends on the input signal amplitude. However, FRFs, like G2(ω,−ω), are not amplitude dependent. As a consequence, the same model (derived here for a cosine input signal) can be used for calculation of FE for different input signals.19
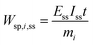
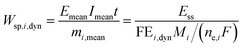
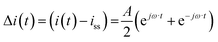
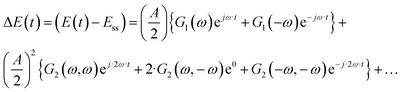
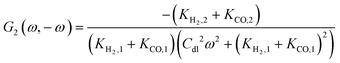
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−αifEss) and i = H2, CO.
exp(−αifEss) and i = H2, CO.
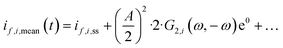
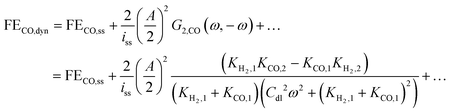
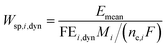

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RHE = Uvs.
RHE = Uvs.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ag/AgCl + 0.059pH + 0.196 V.
Ag/AgCl + 0.059pH + 0.196 V.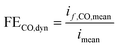
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485.33 C mol−1
485.33 C mol−1

