Open Access Article
Open Access ArticleAn experimental and theoretical investigation of the N(2D) + C6H6 (benzene) reaction with implications for the photochemical models of Titan†
Nadia
Balucani
 *a,
Adriana
Caracciolo‡
a,
Gianmarco
Vanuzzo
*a,
Adriana
Caracciolo‡
a,
Gianmarco
Vanuzzo
 a,
Dimitrios
Skouteris
a,
Dimitrios
Skouteris
 b,
Marzio
Rosi
b,
Marzio
Rosi
 c,
Leonardo
Pacifici
a,
Piergiorgio
Casavecchia
c,
Leonardo
Pacifici
a,
Piergiorgio
Casavecchia
 a,
Kevin M.
Hickson
a,
Kevin M.
Hickson
 *d,
Jean-Christophe
Loison
*d,
Jean-Christophe
Loison
 d and
Michel
Dobrijevic
e
d and
Michel
Dobrijevic
e
aDipartimento di Chimica, Biologia e Biotecnologie, Università degli Studi di Perugia, 06123 Perugia, Italy. E-mail: nadia.balucani@unipg.it
bMaster-Tec SrL, Via Sicilia, 41, 06128 Perugia, Italy
cDipartimento di Ingegneria Civile e Ambientale, Università degli Studi di Perugia, 06100, Perugia, Italy
dUniv. Bordeaux, CNRS, Bordeaux INP, ISM, UMR 5255, F-33400 Talence, France
eUniv. Bordeaux, CNRS, LAB, UMR 5804, F-33600 Pessac, France
First published on 21st April 2023
Abstract
We report on a combined experimental and theoretical investigation of the N(2D) + C6H6 (benzene) reaction, which is of relevance in the aromatic chemistry of the atmosphere of Titan. Experimentally, the reaction was studied (i) under single-collision conditions by the crossed molecular beams (CMB) scattering method with mass spectrometric detection and time-of-flight analysis at the collision energy (Ec) of 31.8 kJ mol−1 to determine the primary products, their branching fractions (BFs), and the reaction micromechanism, and (ii) in a continuous supersonic flow reactor to determine the rate constant as a function of temperature from 50 K to 296 K. Theoretically, electronic structure calculations of the doublet C6H6N potential energy surface (PES) were performed to assist the interpretation of the experimental results and characterize the overall reaction mechanism. The reaction is found to proceed via barrierless addition of N(2D) to the aromatic ring of C6H6, followed by formation of several cyclic (five-, six-, and seven-membered ring) and linear isomeric C6H6N intermediates that can undergo unimolecular decomposition to bimolecular products. Statistical estimates of product BFs on the theoretical PES were carried out under the conditions of the CMB experiments and at the temperatures relevant for Titan’s atmosphere. In all conditions the ring-contraction channel leading to C5H5 (cyclopentadienyl) + HCN is dominant, while minor contributions come from the channels leading to o-C6H5N (o-N-cycloheptatriene radical) + H, C4H4N (pyrrolyl) + C2H2 (acetylene), C5H5CN (cyano-cyclopentadiene) + H, and p-C6H5N + H. Rate constants (which are close to the gas kinetic limit at all temperatures, with the recommended value of 2.19 ± 0.30 × 10−10 cm3 s−1 over the 50–296 K range) and BFs have been used in a photochemical model of Titan’s atmosphere to simulate the effect of the title reaction on the species abundances as a function of the altitude.
1. Introduction
The study of the atmospheric chemistry of the planets of the Solar System can help us to understand the evolution of our own atmosphere and its primordial composition before the emergence of life drastically altered it.1 Among the others, the case of Titan (a massive moon of Saturn with a dense N2-dominated atmosphere) is particularly interesting because of the rich organic chemistry occurring in its upper atmosphere.1–4 After several space missions and ground-based observations, involving also ALMA in recent years,5 our knowledge of the atmosphere of Titan has reached an unprecedented level2,3 and new measurements from the James Webb Space Telescope promise to enrich further the list of organic molecules that have been identified so far.6 In addition to nitrogen (accounting for ca. 95–98% of the composition depending on the altitude considered), the second most abundant component is methane (varying from ca. 2% in the upper atmosphere up to ca. 5% close to the surface). The chemistry initiated by the activation of N2 and CH4 by UV photons or energetic particles leads to the formation of trace components including higher hydrocarbons, nitriles and other N-containing organic molecules.7–9 Since the first missions, we learnt that Titan is covered by organic haze made up of aerosols. After early laboratory experiments trying to simulate the conditions of the atmosphere of Titan,10 polycyclic aromatic hydrocarbons (PAHs) were proposed as the main component of that aerosol. The presence of PAHs would imply that aromatic rings are formed starting from the main components of Titan and the subsequent detection of benzene, the simplest aromatic hydrocarbon (with a first tentative detection by the Infrared Space Observatory,11 later confirmed by the Composite Infrared Spectrometer (CIRS) onboard Cassini12 in the stratosphere and by the analysis of the data recorded by the Ion Neutral Mass Spectrometer onboard Cassini13 in the thermosphere), supported this interpretation. We now know that benzene is quite diffuse in Titan as it has been identified in the upper atmosphere (peak around 1000 km),13 in the mesosphere,14 and in the stratosphere of Titan,12 and even on the surface as seen upon the impact of the Huygens probe.15 Furthermore, benzene ice clouds have been detected in the stratosphere.16 Various formation routes of benzene have been considered. In the photochemical model we will use in this work, benzene is formed by both ionic production pathways in the ionosphere (mainly by the reaction C4H3+ + C2H4 and to a lesser extent by C3H5+ + C2H2 and C4H2+ + C2H) and neutral pathways (C2H3 + C4H3 and C3H3 + C3H3) with a similar global efficiency.17The detection of N-containing aromatic compounds is also of interest to the present work. The presence of the N-heterocyclic molecules pyridine and pyrimidine was considered after the analysis of Cassini mass spectra where ions at m/z 80 and 81 (associated with C5H5NH+ and C4H4N2H+, and possibly corresponding to protonated pyridine and pyrimidine) were detected,18 but remote spectroscopy could not confirm this suggestion and only upper limits were derived.19 However, the analysis of the strong unidentified emission near 3.28 μm in the upper daytime atmosphere reported by Dinelli et al.20 (extending from 600 km up to 1250 km) led to the suggestion that, in addition to PAHs, several N-containing PAHs (such as N-heterocyclic compounds like phenanthridine or aromatic amines like 2-naphthylamine) are the carrier of this band which cannot be explained with non-aromatic species.21 Likewise, the analysis of the data recorded by the Cassini Plasma Spectrometer Ion Beam Spectrometer strongly suggests that PAHs and N-containing PAHs are responsible for the heavy positive ions signal (170–310 Da).22
Therefore, the incorporation of nitrogen in aromatic compounds needs to be explained. Molecular nitrogen is not a reactive species, but it can be activated either by dissociation or ionization induced by EUV photons, cosmic rays and solar winds as well as other energetic particles like electrons from the magnetosphere of Saturn.7–9 Interestingly, photodissociation, dissociative photoionization, cosmic ray induced dissociation, electron impact as well as N2+ dissociative recombination can produce atomic nitrogen in the first electronically excited 2D state in similar amounts to the ground 4S state.7–9,23 N(4S) exhibits very low reactivity with closed shell molecules,23–25 while N(2D) is reactive with the typical molecules identified in the atmosphere of Titan, including CH4 and H2.26–28 N(2D) is metastable but has a radiative lifetime long enough (6.1 × 104 s and 1.4 × 105 s for the 2D3/2 and 2D5/2 fine structure states, respectively)29 to react in binary collisions with other constituents of the upper atmosphere of Titan.7–9
In the Perugia laboratory, featuring a crossed molecular beam (CMB) apparatus with mass spectrometric detection, some of the present authors have investigated numerous reactions between N(2D) and molecular species of interest in the atmospheric chemistry of Titan.26–28,30–40 Interestingly, in all the investigated N(2D) reactions with C-containing molecules the formation of products containing a novel C–N bond has been observed.26,31–40 Dedicated electronic structure calculations of the reactive potential energy surface (PES) have also been performed for those reactions.
In the Bordeaux laboratory, featuring a continuous supersonic flow apparatus, the kinetics of several reactions involving N(2D) and hydrocarbons36,41–43 have been determined in a range of temperatures, T, from 50 K to 296 K, encompassing those of relevance for Titan and the results have been incorporated in a photochemical model developed in-house.8 These studies have shown that most reactions of N(2D) are faster than what was believed, approaching the gas kinetic limit down to very low T. In some cases, a significant effect in the photochemical model outcomes was observed.36,41–43
In the case of the reaction N(2D) + allene, we have already combined the Perugia and Bordeaux expertise to derive the rate coefficients and the product branching fractions (BFs) as a function of the temperature. The results have been included in the photochemical model and the effects analysed.36 This approach is pivotal to improve current photochemical models of Titan’s atmosphere because many relevant elementary reactions have never been investigated in laboratory experiments and are included in chemical networks of the models with estimated values of rate constants and product BFs.
In the present work, we use the same combined approach to study the reaction N(2D) + C6H6 with the aim to understand the chemistry of N(2D) with aromatic species after that with aliphatic molecules. In particular, we wish to explore whether (1) the reaction of N(2D) with the simplest aromatic is fast as in the case of aliphatic unsaturated hydrocarbons, also at the very low T typical of Titan (94–200 K); (2) the aromatic ring is preserved upon the chemical attack by the very reactive species N(2D) or the reaction causes a ring contraction and/or the loss of aromaticity (both cases have been previously observed in reactions involving benzene and other atomic/radical species44–49); (3) the N atom can be incorporated in the ring possibly forming pyridine in a N/CH exchange channel (preliminary calculations performed ad hoc have indicated that this reaction path is exothermic and correlates with the reactants50,51); (4) other N-containing cyclic organic molecules can be formed (the same preliminary calculations have already indicated that there are other open reactive channels;50,51 the PES derived by another research group that also performed statistical estimates of the product branching fractions confirmed that52). If confirmed that N is incorporated into the aromatic ring or in other cyclic non-aromatic compounds, this reaction could be added to the list of processes generating the precursors of the N-containing PAHs observed in Titan, together with other routes characterized by the CMB method in the group of Kaiser53–57 or inferred by plasma studies in air.58,59 Finally, the rate constant and product BFs as a function of temperature derived in this study are used in a photochemical model of Titan’s atmosphere to simulate the effect of the title reaction on the species abundances (including new products formed) as a function of the altitude.
The Perugia group has already investigated the related reactions between benzene and atomic oxygen48,49 and the reaction between N(2D) and pyridine.40 In both cases, ring-contraction mechanisms have been found to be important. Similarities and differences will be noted in the paper.
According to the present theoretical calculations the N(2D) + benzene reaction exhibits numerous energetically open channels, with the most relevant ones being the following (the reported enthalpies of reaction are those calculated in the present work at the CCSD(T)-CBS level, see Section 3.1):
| N(2D) + C6H6 → C5H5 + HCN ΔH00 = −397 kJ mol−1 | (1) |
| N(2D) + C6H6 → C5H5 + HNC ΔH00 = −337 kJ mol−1 | (2) |
| N(2D) + C6H6 → C5H5CN + H ΔH00 = −311 kJ mol−1 | (3) |
| N(2D) + C6H6 → C4H4N + C2H2ΔH00 = −269 kJ mol−1 | (4) |
| N(2D) + C6H6 → C5H6 + CN ΔH00 = −198 kJ mol−1 | (5) |
| N(2D) + C6H6 → C4H4NCCH + HΔH00 = −172 kJ mol−1 | (6) |
| N(2D) + C6H6 → C6H5N + H ΔH00 = −157 kJ mol−1 | (7) |
| N(2D) + C6H6 → o-C6H5N + HΔH00 = −132 kJ mol−1 | (8) |
| N(2D) + C6H6 → p-C6H5N + H ΔH00 = −110 kJ mol−1 | (9) |
| N(2D) + C6H6 → C5H5N + CH ΔH00 = −45 kJ mol−1 | (10) |
The paper is organized as follows. In Sections 2 and 3 we describe the experimental techniques and the theoretical methods, respectively, adopted to investigate the title reaction. In Section 4 we report the experimental results. In Section 5 we describe the PES used to interpret the experimental results and the predictions of statistical simulations of product BFs. A general discussion of the results is given in Section 6, and the effects of the title reaction in a photochemical model of Titan’s atmosphere is then examined in Section 7, before the conclusions.
2. Experimental methods
2.1 The crossed molecular beam experiments
The scattering experiments were carried out by using a CMB apparatus that has been described in detail elsewhere.60,61 Briefly, two well-collimated, in angle and velocity, continuous supersonic beams of the reactants are crossed at 90° in a large scattering chamber with a background pressure of 2 × 10−6 mbar in operating conditions, which assures single-collision conditions. The detection system consists of an electron impact ionizer, a quadrupole mass filter and a Daly-type detector. The ionizer is located in the innermost region of a triply differentially pumped ultra-high-vacuum chamber, which is maintained in the 10−11 mbar pressure range in operating conditions by extensive turbo- and cryo-pumping. The whole detector unit can be rotated in the collision plane around an axis passing through the collision center and product/reactant velocity distributions can be derived from time-of-flight (TOF) measurements. Beam conditions and other details of the experimental conditions are given in the ESI.† The resulting collision energy, Ec, was 31.8 kJ mol−1.The laboratory (LAB) angular distribution, N(Θ), was measured with respect to the nitrogen beam direction. The secondary target beam (benzene beam) was modulated at 160 Hz with a tuning fork chopper for background subtraction. Velocity distributions of the products were obtained at selected LAB angles by measuring time-of-flight, N(Θ, t) distributions using the cross-correlation TOF technique with four 127 bit pseudorandom sequences.60 High-time resolution was achieved by spinning the TOF disk, located at the entrance of the detector, at 328 Hz corresponding to a dwell time of 6 μs per channel. TOF counting times varied from 60 to 180 min depending upon signal intensity. The analysis of raw data has been performed by the usual forward convolution approach where trial CM product angular, T(θ), and translational energy,  , distributions are assumed, averaged, and transformed to the LAB frame for comparison with the experimental data until the best-fit of the LAB distributions is achieved.60,61
, distributions are assumed, averaged, and transformed to the LAB frame for comparison with the experimental data until the best-fit of the LAB distributions is achieved.60,61
2.2 Kinetic experiments
The kinetic experiments described here were performed using an existing continuous supersonic flow or Laval nozzle apparatus. The principal attributes of this system have been presented in earlier work,62 while the main modifications that have been made to allow us to follow the kinetics of atomic radical reactions are described in later work.63–66 Three different Laval nozzles based on the carrier gases Ar or N2 were employed during this investigation to access four different low temperature flows between 50 and 177 K (one nozzle was used with both Ar and N2 to generate flows with characteristic temperatures of 127 and 177 K, respectively). The nozzle properties are summarized in Table 1 of Nuñez-Reyes et al.43 Room temperature measurements (296 K) were conducted with Ar as the carrier gas in the absence of a Laval nozzle and by reducing the flow velocity to avoid pressure gradients in the reactor. N(2D) atoms are only slowly quenched by N2 and Ar67 so the use of these carrier gases did not adversely affect the excited state populations. Details of the methods used for the generation and detection of N(2D) atoms, as well as for the introduction of the benzene co-reagent are provided in the ESI.†3. Theoretical methods
3.1 Electronic structure calculations of potential energy surface (PES)
The theoretical investigation of the reaction between N(2D) and C6H6 was performed adopting a well-established computational strategy previously used for the investigation of many other bimolecular reactions.26,31,34–39,68–70 The PES of the N(2D) + C6H6 system was first characterized by locating the lowest stationary points (minima and transition states) at the B3LYP level of theory in conjunction with the 6-311+G** basis set.71,72 The optimization of all the stationary points was then refined by the use of the same hybrid density functional with a larger basis set, i.e. the Dunning correlation consistent valence polarized aug-cc-pVTZ basis set.73–75 At the same level of theory we have computed the harmonic vibrational frequencies in order to check the nature of the stationary points, i.e. minimum if all the frequencies are real, saddle point if there is one, and only one, imaginary frequency. The assignment of the saddle points was performed using intrinsic reaction coordinate (IRC) calculations.76,77 The energy of all the stationary points was computed then at the CCSD(T) level78–80 using the same basis set aug-cc-pVTZ.73–75 Both the B3LYP and the CCSD(T) energies were corrected to 0 K by adding the zero point energy (ZPE) correction computed using the scaled harmonic vibrational frequencies evaluated at the B3LYP level. The energy of N(2D) was estimated by adding the experimental81 separation N(4S)–N(2D) of 230 kJ mol−1 to the energy of N(4S) at all levels of calculation. Preliminary reports on a portion of the PES have been already given,50,51 but the full PES and statistical calculations based on the Rice–Ramsperger–Kassel–Marcus (RRKM) method are presented here. Furthermore, for selected stationary points, which were demonstrated to be relevant for the main reactive channels from RRKM calculations using the CCSD(T) PES, more accurate calculations were performed at the CCSD(T) level corrected with a Density Fitted (DF) MP2 extrapolation to the complete basis set (CBS) and with corrections for core electrons excitations. In particular, we compute the energies as:| ECBS = E(CCSD(T)/aug-cc-pVTZ) + [E(CCSD(T,core)/cc-pVTZ) − E(CCSD(T)/cc-pVTZ)] + [E(DF-MP2/CBS) − E(DF-MP2/aug-cc-pVTZ)] | (11) |
| E(DF-MP2/CBS) = E[(DF-MP2)/aug-cc-pVQZ] + 0.5772 × [E(DF-MP2/aug-cc-pVQZ) − E(DF-MP2/aug-cc-pVTZ)] | (12) |
The E(DF-MP2/CBS) extrapolation was performed using Martin’s two parameter scheme82 and the related energies were used for the kinetic (statistical) investigation described below. These energies will be denoted as CBS although they include also the core–valence correlation correction. The accuracy of these very accurate calculations should be within ±5 kJ mol−1.
The DFT and CCSD(T) calculations were done using Gaussian 09 (ref. 83) while the CBS calculations were done with MOLPRO.84,85 The analysis of the vibrational frequencies was performed using Molekel.86
3.2 Statistical estimates of the product branching fractions
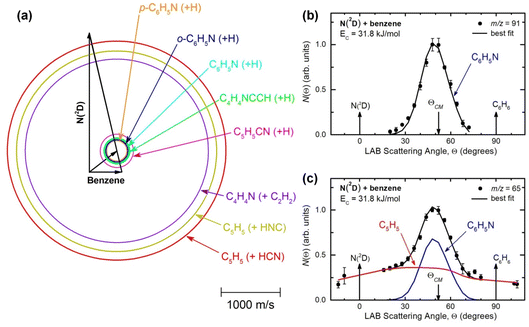
RRKM calculations for the N(2D) + C6H6 reaction were performed using a code implemented in our group for this purpose.26,31,68–70 The microcanonical rate constant k(E) for a specific reaction at a specific total energy is given by the expression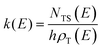 where N(E) represents the sum of states at the transition state at energy E, ρ(E) is the density of states of the reactant, and h is Planck’s constant. N(E) is obtained by integrating the relevant density of states up to energy E, and the rigid rotor/harmonic oscillator model is assumed. Since many reaction channels are H-displacement processes, tunnelling (as well as quantum reflection) was included in the RRKM calculations by using the corresponding imaginary frequency of the transition state and calculating the tunneling probability for the corresponding Eckart barrier.
where N(E) represents the sum of states at the transition state at energy E, ρ(E) is the density of states of the reactant, and h is Planck’s constant. N(E) is obtained by integrating the relevant density of states up to energy E, and the rigid rotor/harmonic oscillator model is assumed. Since many reaction channels are H-displacement processes, tunnelling (as well as quantum reflection) was included in the RRKM calculations by using the corresponding imaginary frequency of the transition state and calculating the tunneling probability for the corresponding Eckart barrier.
For the cases in which we were not able to locate a clear transition state in the exit channel, the corresponding microcanonical rate constant was obtained through a variational approach: k(E) was evaluated at various points along the reaction coordinate and the point which minimizes the rate constant was chosen, in accordance with the variational theory.87 For dissociation steps in which, due to difficulties in the electronic structure calculations, no intermediates points are available, the products at infinite separation were taken into account as a possible “transition state”. After the calculation of all microcanonical rate constants, a Markov (stochastic) matrix was set up for all intermediates and final channels to derive the product branching fractions for the overall reaction. k(E) is subsequently Boltzmann averaged for each temperature of interest to yield k(T).
4. Experimental results
4.1 CMB experiments
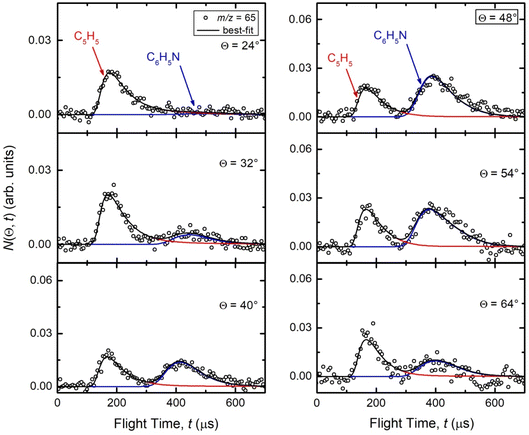
Reactive scattering signals were observed at m/z = 91 (C6H5N+), m/z = 90 (C6H4N+), m/z = 66 (C5H6+), and m/z = 65 (C5H5+) (with relative intensities of 1.00, 0.17, 0.09, and 0.78 at Θ = 48° using an energy of the ionizing electrons of 70 eV). Full sets of angular and TOF distributions were determined only at m/z = 91, 90, and 65. The signal at m/z = 66 was too weak to perform scattering measurements while angular and TOF distributions at m/z = 79 (corresponding to pyridine mass from channel (10)) could not be achieved because of the strong interfering signal due to the elastic scattering of benzene with one 13C (the m/z of 13CC5H6+ is 79).Fig. 1a depicts the velocity vector (so called “Newton”) diagram of the experiment, while Fig. 1b and c show the LAB angular distributions measured at m/z = 91 and m/z = 65, respectively. The circles in the Newton diagram delimit the maximum speed of the indicated heavy products with gross formula C6H5N formed in the H-displacement channels (3) and (6–9) (with five possible structures: 2-cyano-cyclopentadiene, 1-ethynyl-pyrrole, phenylnitrene, and ortho-/para-N-cycloheptatriene radicals), C5H5 formed in the HCN/HNC elimination channels (1) and (2), and C4H4N (pyrrolyl) formed in the C2H2 elimination channel (4). The maximum CM speed was obtained by assuming that all the available energy, ETOT (= Ec − ΔH00), for the corresponding channel is released into product translational energy.
 | ||
| Fig. 1 (a) Velocity vector diagram (“Newton” diagram) for the N(2D) + C6H6 (benzene) reaction at Ec = 31.8 kJ mol−1 with superimposed color-coded circles that delimit the speed in the CM frame of the indicated primary products. Product LAB angular distributions at (b) m/z = 91 and (c) m/z = 65. The black solid curves superimposed on the experimental data (dots) are LAB angular distributions calculated by using the best-fit CM functions shown in Fig. 3. Partial contributions, as resulted from the best-fit procedure and originating from H-displacement (blue) and ring-contraction (red) channels, are also shown in the m/z = 65 angular distribution (see text). | ||
The solid dots in Fig. 1b and c represent the average of five angular scans with counting times of 100 s at each angle per scan (the error bars represent the standard deviation). On the basis of energy and linear momentum conservation laws, the reactive signal recorded at m/z = 91 corresponds unambiguously to the heavy co-product(s) of the H-displacement channel(s). Because of the limited experimental resolution and the similarity in the energetics and dynamics of these channels, we were not able to disentangle them based only on the analysis of the experimental data and the data could be fit using a single set of best-fit T(θ) and 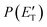 .
.
The m/z = 90 angular distribution (not shown) was identical to that at m/z = 91 indicating that the reactive signal at m/z = 90 originates from dissociative ionization of the C6H5N product(s) from the H-displacement channels. Therefore, no H2 elimination was seen to occur.
During the data analysis of the m/z = 65 LAB distributions, it was necessary to consider two contributions. According to that analysis, the angular distribution measured at m/z = 65 is the result of one component peaking around ΘCM (similar in all respects to the angular distribution recorded at m/z = 91 and, therefore, originating from the products of the H-displacement channels via dissociative ionization) while two wings of comparable intensity originate from other product channels. The presence of two different contributions is more clearly visible in the TOF spectra (see Fig. 2) collected at six different LAB angles (24°, 32°, 40°, 48°, 54°, and 64°). A fast and a slow peak are easily visible from 40° to 54° with the relative importance varying with the angle. Considering the kinematics of the various possible channels, this additional contribution can be ascribed to the occurrence of either channel (1) and/or channel (2). Possibly, also channels (4), associated with C2H2 formation, and (5), associated with CN elimination, could contribute to the m/z = 65 distributions via the −1 daughter ions of C4H4N (pyrrolyl) and C5H6 (cyclopentadiene) products, respectively. In the TOF distributions, the fast peak is associated to channels (1), (2), (4) and (5) while the slower peak is associated to the H-displacement channels and has exactly the same characteristics of the analogous peak measured at m/z = 91 (see Fig. S1 in the ESI†). In the TOF distributions at angles outside the scattering angular range of C6H5N (Θ = 24° and, to some extent, 32° and 64°), only the contribution originating from channel (1) – or (2), (4) and (5) – is visible. During the analysis, the two contributions were disentangled and the CM total flux 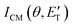 was derived by considering the relation
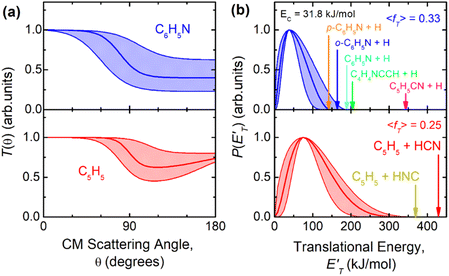
was derived by considering the relation 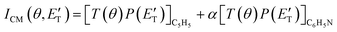 , where α weighs the contribution of the H-displacement channel(s) to the signal recorded at m/z = 65 and is a best-fit parameter.60,61 The best-fit value of α(C6H5N) was minor being only 0.032. However, as can be expected on the basis of energy and momentum conservation and of the relation between the CM and LAB reactive fluxes,60,61 the signal intensity of the C6H5N co-products of the indicated five H-displacement channels appears to be strongly enhanced in the LAB system because of the small Newton circles compared to those associated to the C5H5 scattered by the relatively heavy HCN (or HNC) co-product. If we refer to the total available energy for the o-C6H6CN + H channel, the resulting average fraction of the total available energy channeled into product translation, 〈fT〉, is 0.33.
, where α weighs the contribution of the H-displacement channel(s) to the signal recorded at m/z = 65 and is a best-fit parameter.60,61 The best-fit value of α(C6H5N) was minor being only 0.032. However, as can be expected on the basis of energy and momentum conservation and of the relation between the CM and LAB reactive fluxes,60,61 the signal intensity of the C6H5N co-products of the indicated five H-displacement channels appears to be strongly enhanced in the LAB system because of the small Newton circles compared to those associated to the C5H5 scattered by the relatively heavy HCN (or HNC) co-product. If we refer to the total available energy for the o-C6H6CN + H channel, the resulting average fraction of the total available energy channeled into product translation, 〈fT〉, is 0.33.
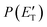 , are displayed for the H-displacement (top panel) and C5H5-forming (bottom panel) channels. The best-fit T(θ) function for the C6H5N product(s) is strongly forward peaked. It indicates that the H-displacement channels proceed via an osculating complex mechanism.88 The
, are displayed for the H-displacement (top panel) and C5H5-forming (bottom panel) channels. The best-fit T(θ) function for the C6H5N product(s) is strongly forward peaked. It indicates that the H-displacement channels proceed via an osculating complex mechanism.88 The 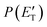 function for the H-displacement channel(s) peaks at about 35 kJ mol−1 and dies off at about 135 kJ mol−1. Within the error bars, this cut-off energy is consistent with the total available energy for the formation of the two isomers o-C6H5N and p-C6H5N, while it is substantially lower than the maximum total available energy for the C5H5CN + H channel and slightly lower than those for the C4H4NCCH + H channel and C6H5N + H channel.
function for the H-displacement channel(s) peaks at about 35 kJ mol−1 and dies off at about 135 kJ mol−1. Within the error bars, this cut-off energy is consistent with the total available energy for the formation of the two isomers o-C6H5N and p-C6H5N, while it is substantially lower than the maximum total available energy for the C5H5CN + H channel and slightly lower than those for the C4H4NCCH + H channel and C6H5N + H channel.
4.2 Kinetic results
Excess concentrations of both co-reagents NO and C6H6 (with respect to the minor reagents C(3P) and N(2D)) were used during these experiments, allowing the pseudo-first-order approximation to be applied. As a result, the N(2D) fluorescence emission signal, IN(2D) (assumed to be proportional to [N(2D)]), obeys a biexponential rate law with the following form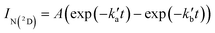 | (13) |
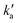 and
and 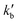 are the pseudo-first-order rate constants for N(2D) loss and formation, respectively, and t is the reaction time corresponding to the delay between photolysis and probe lasers. Nevertheless, as the first few microseconds of N(2D) formation could not be exploited due to PMT saturation issues, a single exponential rate law of the type
are the pseudo-first-order rate constants for N(2D) loss and formation, respectively, and t is the reaction time corresponding to the delay between photolysis and probe lasers. Nevertheless, as the first few microseconds of N(2D) formation could not be exploited due to PMT saturation issues, a single exponential rate law of the type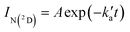 | (14) |
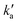 is actually made up of several different contributions, namely N(2D) loss by reaction with C6H6, kN(2D)+C6H6[C6H6], N(2D) loss by reaction with NO, kN(2D)+NO[NO] and N(2D) loss by other processes including reactions with impurities and loss by diffusion. The first two terms dominate here, with the third term negligible in comparison. As [NO] is fixed for any single series of experiments, the difference in decay time between the traces in Fig. S2† is entirely due to the change in C6H6 concentration.
is actually made up of several different contributions, namely N(2D) loss by reaction with C6H6, kN(2D)+C6H6[C6H6], N(2D) loss by reaction with NO, kN(2D)+NO[NO] and N(2D) loss by other processes including reactions with impurities and loss by diffusion. The first two terms dominate here, with the third term negligible in comparison. As [NO] is fixed for any single series of experiments, the difference in decay time between the traces in Fig. S2† is entirely due to the change in C6H6 concentration.
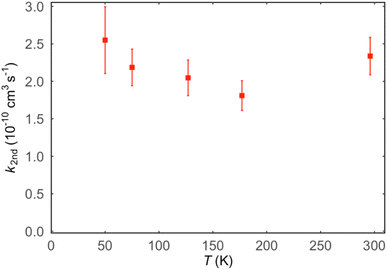
Values of the second-order rate constant for the N(2D) + C6H6 reaction at a given temperature kN(2D)+C6H6(T) were obtained by recording several decay curves similar to those shown in Fig. S2† at various C6H6 concentrations while keeping the NO concentration constant. The results of these experiments are displayed in Fig. 4, where 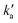 is plotted as a function of [benzene] for five temperatures from 50 K to 296 K. The solid lines represent weighted fits to the individual datasets. The gradients of these lines yield the values for kN(2D)+C6H6 with the intercept corresponding essentially to kN(2D)+NO[NO]. The derived second-order rate constants are plotted as a function of temperature in Fig. 5 and are summarized in Table 1 along with other relevant information. To the best of our knowledge, there are no earlier experimental studies of the kinetics of the N(2D) + C6H6 reaction. As the reaction rate does not display a large temperature dependence, we recommend the use of a temperature independent rate constant in photochemical models with a value of (21.9 ± 3.0) × 10−11 cm3 s−1 over the 50–296 K range.
is plotted as a function of [benzene] for five temperatures from 50 K to 296 K. The solid lines represent weighted fits to the individual datasets. The gradients of these lines yield the values for kN(2D)+C6H6 with the intercept corresponding essentially to kN(2D)+NO[NO]. The derived second-order rate constants are plotted as a function of temperature in Fig. 5 and are summarized in Table 1 along with other relevant information. To the best of our knowledge, there are no earlier experimental studies of the kinetics of the N(2D) + C6H6 reaction. As the reaction rate does not display a large temperature dependence, we recommend the use of a temperature independent rate constant in photochemical models with a value of (21.9 ± 3.0) × 10−11 cm3 s−1 over the 50–296 K range.
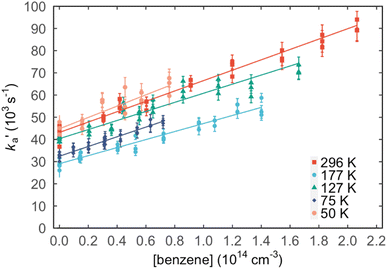 | ||
Fig. 4 Plots of the pseudo-first-order rate constant, 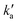 , versus [C6H6] for a range of temperatures: (red squares) 296 K; (light blue circles) 177 K; (green triangles) 127 K; (dark blue diamonds) 75 K; (pink circles) 50 K. The solid lines are weighted linear least-squares fits to the individual datasets. The error bars on individual data points are derived from exponential fits to traces such as those displayed in Fig. S2† and are shown at the level of a single standard deviation. , versus [C6H6] for a range of temperatures: (red squares) 296 K; (light blue circles) 177 K; (green triangles) 127 K; (dark blue diamonds) 75 K; (pink circles) 50 K. The solid lines are weighted linear least-squares fits to the individual datasets. The error bars on individual data points are derived from exponential fits to traces such as those displayed in Fig. S2† and are shown at the level of a single standard deviation. | ||
| T/K | N | [C6H6]/1014 cm−3 | [NO]/1014 cm−3 | k N(2D)+C6H6/10−11 cm3 s−1 |
|---|---|---|---|---|
| a Uncertainties on the temperatures represent the statistical (1σ) errors obtained from Pitot tube measurements of the impact pressure. b Number of individual measurements. c Uncertainties on the measured rate constants represent the combined statistical (1σ) and estimated systematic (10%) errors. | ||||
| 296 | 30 | 0–2.1 | 6.4 | (23.4 ± 2.5)c |
| 177 ± 2a | 33 | 0–1.4 | 4.1 | (18.1 ± 2.0) |
| 127 ± 2 | 33 | 0–1.7 | 4.6 | (20.5 ± 2.4) |
| 75 ± 2 | 30 | 0–0.7 | 3.0 | (21.9 ± 2.4) |
| 50 ± 1 | 18 | 0–0.8 | 4.2 | (25.5 ± 4.5) |
5. Theoretical results
5.1 The potential energy surface
The theoretical characterization of the PES of the system N(2D) + benzene leads to the identification of 18 minima, 25 transition states and 10 exit channels. A simplified scheme of the PES is shown in Fig. 6 while the complete PES is reported in Fig. S3–S6 of the ESI.† The structures of the most relevant minima and transition states, as well as those of several unusual products, are also shown in the ESI (Fig. S7–S9).† The numbering of the minima, the transition states and the products channels is the same as that adopted in the previous work of Chin et al.52 to make the comparison easier. All the pathways considered in the work of Chin et al. are present in our calculations, but additional paths have also been identified.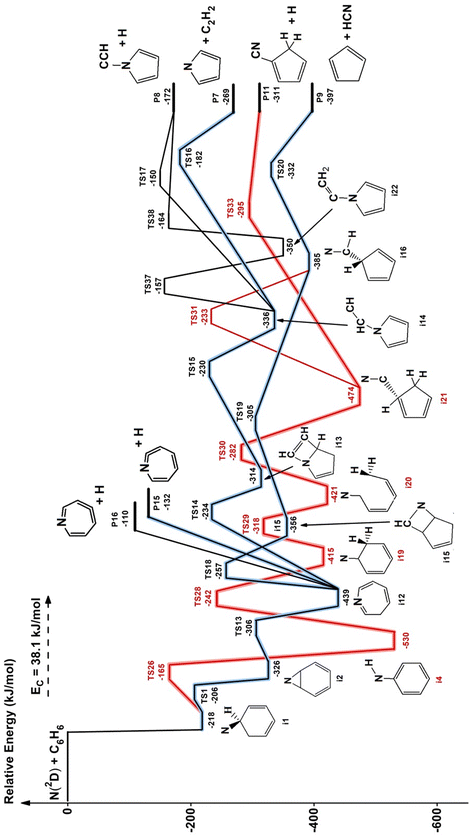 | ||
| Fig. 6 Potential energy surface for the reaction N(2D) + C6H6. Relative energies computed at CBS level with inclusion of core–valence correlation and ZPE correction. The product channels P11, P15, and P16 were not present in the work of Chin et al.52 due to the overlooking of some pathways (see text). For the sake of simplicity, a few pathways have been neglected; only the channels predicted statistically to be relevant at Ec = 31.8 kJ mol−1 are shown (for more details, see ESI†). | ||
We performed preliminary statistical calculations, including all the computed reactive channels at the CC level, to evaluate the BFs of all the channels. In this way, we selected only the exit channels for which a non-negligible BF was obtained. Then the energy of these channels was recalculated at the very accurate CBS level (these are the values reported in Fig. 6).
In the calculations at the B3LYP level, the interaction of nitrogen in its excited 2D state with C6H6 leads to a van der Waals complex with a very long (longer than 3 Å) N–C distance. The stability of this complex is strongly overestimated because of the very poor description of nitrogen in its excited 2D state. Since the presence of this initial complex has no influence on the reactive channels, we have not considered it in the higher-level calculations. As shown in Fig. 6, the interaction of N(2D) with benzene leads to the formation of the i1 intermediate (more stable than the reactants by 218 kJ mol−1) in which one of the carbon atoms has changed hybridization from sp2 to sp3 making a new bond with the nitrogen atom. The i1 intermediate, overcoming a small barrier of only 12 kJ mol−1, can isomerize to i2 which, following the path TS13 → i12 → TS18 → i15 → TS19 → i16 → TS20, finally leads to the products cyclopentadienyl radical and hydrogen cyanide (P9) (channel (1)). RRKM calculations suggest it to be the main reaction channel (see below). Once intermediate i12 is formed, however, it can also lose an H-atom without any barrier from C1, C2 or C3 giving rise to three different products, the most stable of which is the one associated with the H-loss from C1 (P15), the second from C3 (P16) while the loss of H from C2 is the least favored.
The two last exit channels P15 and P16, which are originating in a barrier-less fashion from the 7-member ring intermediate i12, were not considered in the work of Chin et al.52 i12 can also isomerize to intermediate i13, overcoming a barrier of 205 kJ mol−1, which, following the path TS15 → i14 → TS16, gives rise to the products C4H4N (pyrrolyl) and acetylene (P7) (channel 4). i14 can also give rise to the products C4H4NCCH + H (P8) (channel 6) through TS17 or following the path TS37 → i22 → TS38. This last pathway was not considered by Chin et al.52 Finally, i1, by overcoming a barrier of 53 kJ mol−1, can isomerize also to the very stable intermediate i4 which, following the path TS28 → i19 → TS29 → i20 → TS30 → i21 → TS33, gives rise to the products C5H5CN + H (P11) (channel 3). i21 can also give rise to the products C5H5 + HCN (P9) (channel 1) through the pathway TS31 → i16 → TS20. These last two reactive channels, originating from i4, were not considered in the work of Chin et al.52
Comparing the energies reported in Fig. 6 with those reported in Fig. 1 and 2 of the article by Chin et al.52 we can notice an almost constant difference of about 20 kJ mol−1, the energies of Chin et al. being systematically lower than ours. However, this difference is due almost entirely to the error that Chin et al.52 made in computing the energy of N(2D). They computed the energy of N(2D) at the same level of the other points reported in the PES, while we estimated this energy by adding the experimental excitation energy to the computed energy of N(4S). We evaluated an energy difference of 25 kJ mol−1 at the CBS level between the experimental excitation energy of N(2D) and that calculated. This is the most important contribution to the difference between the energies reported by Chin et al.52 and those calculated in this work. The rest of the difference is due to the fact that we included in our calculations also the core–valence correlation contribution. We believe therefore that our results are more accurate than those reported by Chin et al.52 and the error is within ±5 kJ mol−1.
5.2 RRKM estimates of the product branching fractions
RRKM estimates of product branching fractions were performed considering the collision energy of the CMB experiment (31.8 kJ mol−1) and for three different temperatures corresponding to the surface temperature of Titan (94 K), its stratospheric temperature (175 K) and the temperature at 1000 km of altitude where benzene has its abundance peak (200 K). The calculated BFs are referring to the limit of zero pressure which is a good approximation for CMB experiments and the stratosphere and thermosphere of Titan. All the possible elementary processes, including back-dissociation for the first intermediate i1 and back-isomerization of all intermediates, have been considered in the RRKM calculations to obtain the branching fractions, reported in Table 2. The results reported here have been obtained by using the CBS values of energy. Preparatory RRKM calculations on the CC PES, however, provided very similar results. Under all the considered conditions, the dominant channel is the one leading to C5H5 + HCN (1) with a BF varying from 0.860 at 94 K to 0.745 under the conditions of the CMB experiment. The other most important channels are channel (4) leading to C4H4N + C2H2 (BF varying from 0.051 at 94 K to 0.056 at the experimental Ec) and channel (8) leading to o-C6H5N + H, which has the strongest energy/temperature dependence (BF varying from 0.048 at 94 K to 0.135 at the experimental Ec) as already seen in the case of other H-displacement channels.37,38,48,49 This can be rationalized by considering that this channel originates from the dissociation of the i12 intermediate which is readily formed by a two-step isomerization of the initial intermediate i1. The competition affects almost only channel (1) which is, indeed, the lowest energy pathway originating from the same intermediate i12. The yield of channel (9), also originating from i12, increases with the available energy, even though it remains marginal under all the conditions considered. All the other contributions show little dependence on the energy available to the system.| Channel number and products | CMB Expt, Ec = 31.8 kJ mol−1 | RRKM, Ec = 31.8 kJ mol−1 | RRKMa, Ec = 41.8–0 kJ mol−1 | RRKM, 94 K | RRKM, 175 K | RRKM, 200 K |
|---|---|---|---|---|---|---|
| a Ref. 52. | ||||||
| (3) C5H5CN + H | 0.08 ± 0.04 | 0.053 | 0.030–0.023 | 0.039 | 0.040 | 0.040 |
| (6) C4H4NCCH + H | Negligible | 0.006–0.004 | Negligible | Negligible | Negligible | |
| (7) C6H5N + H | Negligible | Negligible | Negligible | Negligible | Negligible | |
| (8) o-C6H5N + H | 0.135 | nd | 0.048 | 0.053 | 0.058 | |
| (9) p-C6H5N + H | 0.011 | nd | 0.003 | 0.003 | 0.003 | |
| (1) C5H5 + HCN | 0.92 ± 0.04 | 0.745 | 0.889–0.915 | 0.860 | 0.852 | 0.849 |
| (2) C5H5 + HNC | Negligible | Negligible | Negligible | Negligible | Negligible | |
| (4) C4H4N + C2H2 | 0.056 | 0.075–0.058 | 0.051 | 0.051 | 0.052 | |
| (5) C5H6 + CN | Negligible | Negligible | Negligible | Negligible | Negligible | |
| (10) C5H5N + CH | nd | Negligible | Negligible | Negligible | Negligible | Negligible |
The BFs derived from the present RRKM calculations are reported for all ten exothermic reactive channels in Table 2, where they are also compared with both the experimental BFs and theoretical BFs from a previous theoretical study.52 There is a substantial agreement with those results,52 if one considers that channels (8) and (9) were not considered in that study. As already commented, it is the presence of these alternative dissociation channels (in particular channel (8)) that reduces the yield of C5H5 + HCN and this nicely explains the difference in the BF for channel (1) in the two cases.
6. Discussion
The rate coefficients determined in this work vary between 1.8 and 2.6 × 10−10 cm3 s−1 with no obvious trend with the temperature. Therefore, the title reaction is fast in the entire range of temperature investigated and close to the gas kinetic limit. According to the PES derived in this work, as well as that derived by Chin et al.52 the title reaction is characterized by the absence of an energy barrier in the entrance channel with no other major barriers leading to exothermically accessible products. This is perfectly in line with the experimental results. If we compare the rate constant of this reaction with those already investigated by us with the same experimental method and concerning the reactions of N(2D) with hydrocarbons relevant for Titan, we note that the rate constants of the title reaction have values comparable to those of the N(2D) reactions with unsaturated hydrocarbons (C2H2, C2H4 and allene)36,42,43 and the same behavior with the temperature, while they are significantly larger than those determined for the N(2D) reactions with saturated hydrocarbons (CH4, C2H6, and C3H8)41 which are smaller and characterized by a significant decrease as the temperature falls. This comparison sustains again what is seen by the theoretical calculations, that is, the N(2D) reactions are barrierless when they involve unsaturated hydrocarbons and proceed with an addition mechanism guided by the electron density of multiple C–C bonds, while they are characterized by a small entrance barrier when they involve hydrocarbons with only sigma bonds and the insertion mechanism is the only option.The analysis of the CMB results points to the occurrence of two groups of mechanisms: (1) the H-displacement channels, which can be accompanied by the formation of five different isomeric molecular products, and (2) the ring contraction channels with the elimination of a molecular moiety, which actually correspond to four possible routes leading to the cyclopentadienyl radical and HCN (1) or HNC (2), pyrrolyl radical and C2H2, (4) and cyclopentadiene and CN (5). The yield of the H-displacement channels is minor (overall BF = 0.08 ± 0.04) (see Table 2), while the dominant reaction channel is the one leading to the destruction of the aromatic ring via a ring-contraction process (overall BF = 0.92 ± 0.04). According to the theoretical calculations, the BF of HNC is negligible, while it is 0.745 for HCN production under the conditions of the CM experiments (Ec = 31.8 kJ mol−1) (see Table 2). The much more favorable formation of HCN with respect to HNC mainly originates from the very unfavorable competition of the isomerization of the initial addition intermediate i1 (located at −218 kJ mol−1) to i4 (the precursor leading to HNC formation via TS4 → i5 → TS5 → i6 → TS11 (see Fig. S4 in the ESI†)) with respect to the isomerization of i1 to i2 (the precursor leading to HCN formation) via TS1. TS1 is located much lower in energy (at −206 kJ mol−1, see Fig. 6) with respect to TS4 (see Fig. 6) (−182 kJ mol−1 at the CC level, see Fig. S5 in ESI†). Theory predicts that after the facile isomerization of the initial benzazirine intermediate (i2) to the seven-member ring N-cycloheptatriene intermediate (i12), the latter can evolve to bimolecular products via three main competitive pathways: (i) the main one leading to C5H5 + HCN (channel (1)) (BF = 0.745) via a series of four isomerizations (see Fig. 6); (ii) the second one leading, in a barrier-less fashion, dominantly (BF = 0.135) to o-C6H5N (ortho-N-cycloheptatriene radical) + H, and in minor part (BF = 0.011) to p-C6H5N (para-N-cycloheptatriene radical) + H; (iii) the third one leading to C4H4N (pyrrolyl radical) + C2H2 (acetylene) (BF = 0.056). Therefore, the theory predicts that a small contribution to the reactive scattering comes from channel (4). Indeed, we have some experimental evidence that the pyrrolyl radical (m/z = 66) is formed, because we observed at the CM angle a small signal intensity at m/z = 66, larger than that due to the 13C natural isotopic abundance of C5H5 (cyclopentadienyl) (m/z = 65). Considering the theoretical BFs, the yield of HCN channel (1) is more than 13 times larger than that of the C2H2 channel (4) (see Table 2) and, therefore, it is not surprising that the signal at m/z = 66 is about nine times smaller than the one at m/z = 65. The small signal at m/z = 66 could also be associated to the C5H6 (cyclopentadiene) + CN formation channel (5), but for this channel the theory predicts a negligible BF.
Regarding the H-displacement channels, according to our electronic structure calculations five isomers with gross formula C6H5N can be formed (see Section 5 and Fig. 6). A satisfactory fit of the LAB angular and TOF distributions was achieved by using a single set of CM functions for the H-displacement channel(s), which implies that our data are not sensitive enough to allow disentangling of the possible different contributions to the signal at the same m/z, because the enthalpies of reaction of these channels are not very different and the reaction mechanism is the same. Among the possible H-displacement channels (3) and (6)–(9), those predicted by RRKM as more significant are o-C6H5N + H (8) (BF = 0.135) and C5H5CN (2-cyano-cyclopentadiene) + H (3) (BF = 0.053), with p-C6H5N + H (9) being minor (BF = 0.011). The other two H-displacement channels, (6) and (7), have a negligible BF (this is due to the high isomerization barriers along the corresponding reaction pathways). The reason why channel (8) is predicted to be more abundant than channel (3) is because the former arises from the initial intermediate i2 without an exit barrier and the latter from the initial intermediate i4, which is formed from i1 with much less probability than i2, as already discussed.
It is interesting to examine the variation of the product BFs with energy (temperature). As Table 2 shows, the BF of the dominant C5H5 + HCN channel (1) is predicted to increase substantially with the lowering of the temperature (energy), while the BFs for the H-forming channels, especially the main channel (8), decrease substantially. Our predicted trend is in agreement with that predicted by Chin et al.52 (see Table 2). However, we emphasize that the main H-displacement channel (8) was not revealed by the study of Chin et al., who overall underestimate substantially (by a factor larger than five at Ec = 31.8 kJ mol−1) the H-forming channels with respect to our findings, and therefore overestimate somewhat the C5H5 + HCN channel. Notably, however, the present and Chin et al. studies predict a similar BF for the pyrrolyl + acetylene channel (4) (see Table 2).
A final comment is in order concerning the channel leading to C5H5N (pyridine) + CH. We could not investigate it experimentally because of elastic interference from the secondary beam. However, the theoretical BF resulted to be negligible because of the presence of very high isomerization barriers (especially TS9) to its precursor i9 (see Fig. S5 in the ESI†). Therefore, the title reaction cannot be considered a formation route of this species.
In the Perugia laboratory we have recently investigated two related reactions, that is the N(2D) reaction with another small aromatic (pyridine)40 and the reaction of both ground and electronically excited atomic oxygen with benzene.48,49 The experimental BFs for the reaction with pyridine are quite different with respect to the BFs of the title reaction. In that case, indeed, the H-displacement channels (that could be associated with four distinct isomeric co-products) are dominant with a BF of ca. 0.65 at a comparable collision energy (33.5 kJ mol−1) while the BF of the analogous ring-contraction channel (associated with the formation of C4H4N (pyrrolyl radical) and HCN) is only 0.35. The PES of N(2D) + pyridine has not been characterized to date and, therefore, we cannot provide a reason for such a different behavior. Interestingly, the best fit CM angular distributions were found to be symmetric for both the H-displacement channels and the ring-contraction channels, while in the present case they both show some forward bias. Despite the expected similarities, the detailed reaction mechanism is different in the two cases. The comparison with the O(3P,1D) + C6H6 reactions (investigated at Ec = 34.3 kJ mol−1) is also interesting. In that case, for the reaction of O(3P) the experimental BFs are 0.66 for the H-displacement channel and 0.32 for the ring-contraction channel (leading to C6H5 + CO after intersystem crossing to the underlying singlet PES). But if we focus on the reaction of O(1D), then the BFs are very similar to those obtained here, with a BF for the H-displacement channel of only 0.04 and a BF for the ring-contraction channel (leading to C5H6 + CO and to C5H5 + CO + H) of 0.96. In conclusion, the detailed shape of the underlying PESs and the reaction mechanism with its variation with the total available energy are essential in determining the product BFs and also the extent of the aromatic ring preservation mechanism.
7. Implications for the modeling of the atmosphere of Titan
To examine the effects of the present experimental determinations on the chemistry of Titan’s atmosphere, we included the N(2D) + benzene reaction in the 1D-photochemical model described in Dobrijevic et al.,92 which treats the chemistry of neutrals and cations (anions are not considered in this study as they have only a minor influence on the overall chemistry), and the coupling between them from the lower atmosphere to the ionosphere. Details of the recent updates of the chemical scheme are presented in Benne et al.,93 with a subsequent update in Vanuzzo et al.36 Two different simulations were performed during this investigation. The first simulation represents the nominal model where the N(2D) + benzene reaction is neglected. For the second one, we included the N(2D) + benzene reaction using the rate constants and simplified BFs determined in this study, as we have assumed that the reaction leads to the production of o-C6H5N + H with a yield of 9% and of C5H5 + HCN with a yield of 91%. In addition, we completed the chemical network for o-C6H5N, the main fate of which is the reaction with H atoms giving mainly C5H5 + HCN considering the PES of the C6H6N system presented in Fig. 6.Overall, we verify that the inclusion of the N(2D) + benzene reaction has a minor effect on the chemistry of Titan’s atmosphere. Firstly, even if the flux of the N(2D) + benzene reaction is not negligible, it corresponds to only 5% of the destruction pathways of benzene and therefore has little effect on its abundance. Secondly, in the thermosphere there are other sources of C5H5, which is mainly produced by the photodissociation of C5H6 which is, in turn, mostly produced by the ion–molecule reaction C3H5+ + C2H4 → c-C5H7+ + H2 followed by the electronic dissociative recombination of C5H7+ (1-cyclopentene-2-ylium). The N(2D) + benzene reaction produces new species however, here identified with o-C6H5N for simplicity, that reach an abundance relative to N2 of 4 × 10−10 around 1150 km. At that altitude, the main fate of o-C6H5N will be to react with H to produce C5H5 + HCN and, therefore, is not expected to form new potentially detectable molecules or to be a significant source of the N-containing aromatic species identified in the thermosphere.21,22 However, even though the main sink of o-C6H5N is the reaction with H, the reaction of o-C6H5N with CH3 can give an important contribution. In the current model, the products of this reaction are not explicitly described. Instead, these are included in a generic aromatic compound encompassing all the unknown aromatics of the model (a minor generic compound compared to benzene). It will be important in the future to study this reaction which could potentially lead to aromatic nitrogen heterocycles and, in particular, to the ethenyl-pyridine molecule.
Furthermore, roughly 4% of the reactive flux is actually leading to 1-cyano-1,3-cyclopentadiene, even though we have not explicitly included channel (3) in our model for simplicity (all the H-displacement flux was associated to the formation of o-C6H5N). 1-Cyano-1,3-cyclopentadiene has just been detected (together with its less stable 1-cyano-2,4-cyclopentadiene isomer) in the interstellar medium towards the Taurus Molecular Cloud.94,95 Having a very strong dipole moment and considering that its reaction with H should not be efficient under the conditions of Titan,96 this species might be a target for remote detection. In this respect, we note that the James Webb Space Telescope has been recently directed towards the atmosphere of Titan searching for new species.6
8. Conclusions
The reaction N(2D) + C6H6 was investigated in a combined experimental and theoretical approach. Experimental rate constants and product BFs are in line with the prediction based on a novel PES. The kinetic experiments provided us with the rate constant as a function of temperature from 50 K to 296 K, a range that includes the values relevant to the atmosphere of Titan (the recommended value in the 50–296 K range is 2.19 ± 0.30 × 10−10 cm3 s−1). These values, in the gas-kinetic limit, confirm the barrierless nature of the reaction, as indicated by the electronic structure calculations of the PES. The CMB experiments, complemented by statistical (RRKM/ME) calculations of the product BFs on the high-level ab initio PES, have identified the main reaction channels. The ring-contraction mechanism was found to be dominant in the CMB experiments (with a BF of 0.92) in good agreement with RRKM predictions according to which the channel leading to cyclopentadienyl + HCN (BF = 0.745) dominates and some contribution from the channel leading to pyrrolyl + C2H2 (BF = 0.056) is also possible. H-Displacement channels give a small contribution in the CMB experiments as well as in the RRKM estimates that predict o-N-cycloheptatriene as the main molecular product. Pyridine is not formed through an N/CH exchange channel. The effect of the energy available to the system on BFs is such that can only be seen in the competition between the cyclopentadienyl + HCN channel and the H-displacement channel leading to o-C6H5N. Under the conditions relevant for Titan, the yield of C5H5 increases up to ca. 0.85 while that of o-C6H5N becomes ca. 0.05–0.06. The BFs of the other channels are not so sensitive to the temperature.The recommended value of the rate constant and the derived product BFs have been used in a 1-D photochemical model of Titan’s atmosphere to simulate the effect of the title reaction on the species abundances (including any new products formed) as a function of the altitude. It is found that the inclusion of the N(2D) + benzene reaction has only a minor effect on the amount of benzene but new N-bearing species could be formed and accumulate. Remote detection of 1-cyano-1,3-cyclopentadiene may be feasible due to its large dipole moment.
A more general conclusion is that aromatic rings are not so resistant to the chemical attack as commonly believed, at least not in the case of very energetic reactants like electronically excited species. This is the fourth case we have investigated where ring contraction of small aromatics (benzene or pyridine) is a significant (if not the dominant) reaction pathway, after O(3P,1D) + benzene (significant in the case of the 3P reaction, dominant in the case of the 1D reaction),48,49 O(3P,1D) + pyridine (largely dominant in both cases)91 and N(2D) + pyridine (significant).40 It will be interesting to verify whether a similar mechanism is present also in the case of polycyclic aromatic hydrocarbons which are supposed to accumulate in various environments because of their chemical stability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Italian Space Agency (ASI, DC-VUM-2017-034, Grant no. 2019-3 U.0 Life in Space). The authors acknowledge support from also the Italian MUR, University of Perugia within the program “Department of Excellence-2018-2022-Project AMIS” and the “Dipartimento di Ingegneria Civile e Ambientale” of the University of Perugia within the project “Dipartimenti di Eccellenza 2018–2022” and the Herla Project http://www.hpc.unipg.it/hosting/vherla/vherla.html Università degli Studi di Perugia for allocated computing time. K. M. H. acknowledges support from the French program “Physique et Chimie du Milieu Interstellaire” (PCMI) of the CNRS/INSU with the INC/INP co-funded by the CEA and CNES as well as funding from the “Program National de Planétologie” (PNP) of the CNRS/INSU.References
- N. Balucani and D. Skouteris, Gas-phase Prebiotic Chemistry Driven by Ultraviolet Photolysis of Simple Molecules, in Prebiotic Photochemistry: from Urey–Miller-like Experiments to Recent Findings, ed. F. Saija and G. Cassone, Comprehensive Series in Photochemical and Photobiological Science No. 20, Royal Society of Chemistry, Cambridge, ch. 3, 2021, pp. 37–59 Search PubMed.
- Titan: Surface, Atmosphere and Magnetosphere, ed. I. Mueller-Wodarg, C. Griffith, E. Lellouch and T. Cravens, Cambridge University Press, 2014 Search PubMed.
- Titan from Cassini-Huygens, ed. R. Brown, J. P. Lebreton and J. Waite, Springer, Heidelberg, 2010 Search PubMed.
- N. Balucani, Chem. Soc. Rev., 2012, 41, 5473–5483 RSC.
- A. E. Thelen, C. A. Nixon, R. G. Cosentino, M. A. Cordiner, N. A. Teanby, C. E. Newman, P. G. J. Irwin and S. B. Charnley, Planet. Sci. J., 2022, 3, 146 CrossRef.
- C. A. Nixon, et al. , Publ. Astron. Soc. Pac., 2016, 128, 018007 CrossRef.
- V. Vuitton, R. V. Yelle, S. J. Klippenstein, S. M. Hörst and P. Lavvas, Icarus, 2019, 324, 120–197 CrossRef CAS.
- J. C. Loison, E. Hébrard, M. Dobrijevic, K. M. Hickson, F. Caralp, V. Hue, G. Gronoff, O. Venot and Y. Bénilan, Icarus, 2015, 247, 218–247 CrossRef CAS.
- K. Willacy, S. Chen, D. J. Adams and Y. L. Yung, Astrophys. J., 2022, 933, 230 CrossRef.
- C. Sagan, B. N. Khare, W. R. Thompson, G. D. McDonald, M. R. Wing, J. L. Bada, T. Vo-Dinh and E. T. Arakawa, Astrophys. J., 1993, 414, 399–405 CrossRef CAS PubMed.
- A. Coustenis, A. Salama, B. Schulz, S. Ott, E. Lellouch, Th. Encrenaz, D. Gautier and H. Feuchtgruberc, Icarus, 2003, 161, 383–403 CrossRef CAS.
- A. Coustenis, et al. , Icarus, 2007, 189, 35–62 CrossRef CAS.
- J. H. Waite Jr, et al. , Science, 2007, 316, 870–875 CrossRef CAS PubMed.
- T. T. Koskinen, R. V. Yelle, D. S. Snowden, P. Lavvas, B. R. Sandel, F. J. Capalbo, Y. Benilan and R. A. West, Icarus, 2011, 216, 507–534 CrossRef CAS.
- H. B. Niemann, et al. , Nature, 2005, 438, 779–784 CrossRef CAS PubMed.
- S. Vinatier, B. Schmitt, B. Bézard, P. Rannou, C. Dauphin, R. de Kok, D. E. Jennings and F. M. Flasar, Icarus, 2018, 310, 89–104 CrossRef CAS.
- J. C. Loison, M. Dobrijevic and K. M. Hickson, Icarus, 2019, 329, 55–71 CrossRef CAS.
- V. Vuitton, R. V. Yelle and M. J. McEwan, Icarus, 2007, 191, 722–742 CrossRef.
- C. A. Nixon, A. E. Thelen, M. A. Cordiner, Z. Kisiel, S. B. Charnley, E. M. Molter, J. Serigano, P. G. J. Irwin, N. A. Teanby and Y.-J. Kuan, Astrophys. J., 2020, 160, 205 CAS.
- B. M. Dinelli, M. López-Puertas, A. Adriani, M. L. Moriconi, B. Funke, M. García-Comas and E. D’Aversa, Geophys. Res. Lett., 2013, 40, 1489–1493 CrossRef CAS.
- M. López-Puertas, B. M. Dinelli, A. Adriani, B. Funke, M. García-Comas, M. L. Moriconi, E. D’Aversa, C. Boersma and L. J. Allamandola, Astrophys. J., 2013, 770, 132 CrossRef.
- R. P. Haythornthwaite, A. J. Coates, G. H. Jones, A. Wellbrock, J. H. Waite, V. Vuitton and P. Lavvas, Planet. Sci. J., 2021, 2, 26 CrossRef.
- O. Dutuit, et al. , Astrophys. J. Suppl. Ser., 2013, 204, 20 CrossRef.
- K. Sato, K. Misawa, Y. Kobayashi, M. Matsui, S. Tsunashima, Y. Kurosaki and T. Takayanagi, J. Phys. Chem. A, 1999, 103, 8650–8656 CrossRef CAS.
- T. Suzuki, Y. Shihira, T. Sato, H. Umemoto and S. Tsunashima, J. Chem. Soc., Faraday Trans., 1993, 89, 995–999 RSC.
- N. Balucani, A. Bergeat, L. Cartechini, G. G. Volpi, P. Casavecchia, D. Skouteris and M. Rosi, J. Phys. Chem. A, 2009, 113, 11138–11152 CrossRef CAS PubMed.
- N. Balucani, P. Casavecchia, L. Bañares, F. J. Aoiz, T. Gonzales-Lezana, P. Honvault and J. M. Launay, J. Phys. Chem. A, 2006, 110, 817–829 CrossRef CAS PubMed.
- N. Balucani, M. Alagia, L. Cartechini, P. Casavecchia, G. G. Volpi, L. A. Pederson and G. C. Schatz, J. Phys. Chem. A, 2001, 105, 2414–2422 CrossRef CAS.
- Y. Ralchenko, A. E. Kramida and J. Reader, NIST Atomic Spectra Database (Ver. 4.0.1), National Institute of Standards and Technology, Gaithersburg, MD, 2006 Search PubMed.
- Z. Homayoon, J. M. Bowman, N. Balucani and P. Casavecchia, J. Phys. Chem. Lett., 2014, 5, 3508–3513 CrossRef CAS PubMed.
- N. Balucani, F. Leonori, R. Petrucci, M. Stazi, D. Skouteris, M. Rosi and P. Casavecchia, Faraday Discuss., 2010, 147, 189–216 RSC.
- N. Balucani, M. Alagia, L. Cartechini, P. Casavecchia, G. G. Volpi, K. Sato, T. Takayanagi and Y. Kurosaki, J. Am. Chem. Soc., 2000, 122, 4443–4450 CrossRef CAS.
- N. Balucani, L. Cartechini, M. Alagia, P. Casavecchia and G. G. Volpi, J. Phys. Chem. A, 2000, 104, 5655–5659 CrossRef CAS.
- N. Balucani, D. Skouteris, F. Leonori, R. Petrucci, M. Hamberg, W. D. Geppert, P. Casavecchia and M. Rosi, J. Phys. Chem. A, 2012, 116, 10467–10479 CrossRef CAS PubMed.
- L. Mancini, G. Vanuzzo, D. Marchione, G. Pannacci, P. Liang, P. Recio, M. Rosi, D. Skouteris, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2021, 125, 8846–8859 CrossRef CAS PubMed.
- G. Vanuzzo, L. Mancini, G. Pannacci, P. Liang, D. Marchione, P. Recio, Y. Tan, M. Rosi, D. Skouteris, P. Casavecchia, N. Balucani, K. M. Hickson, J.-C. Loison and M. Dobrijevic, ACS Earth Space Chem., 2022, 6, 2305–2321 CrossRef CAS PubMed.
- P. Liang, L. Mancini, D. Marchione, G. Vanuzzo, F. Ferlin, P. Recio, Y. Tan, G. Pannacci, L. Vaccaro, M. Rosi, P. Casavecchia and N. Balucani, Mol. Phys., 2022, 120, e1948126 CrossRef.
- G. Vanuzzo, D. Marchione, L. Mancini, P. Liang, G. Pannacci, P. Recio, Y. Tan, M. Rosi, D. Skouteris, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2022, 126, 6110–6123 CrossRef CAS PubMed.
- M. Rosi, S. Falcinelli, P. Casavecchia, N. Balucani, P. Recio, A. Caracciolo, G. Vanuzzo, D. Skouteris and C. Cavallotti, in Computational Science and its Applications – ICCSA 2021, ed. O. Gervasi, B. Murgante, S. Misra, C. Garau, I. Blečić, D. Taniar, B. O. Apduhan, A. M. A. C. Rocha, E. Tarantino, C. M. Torre, Springer International Publishing, Cham, 2021, pp. 620–631 Search PubMed.
- P. Recio, D. Marchione, A. Caracciolo, V. J. Murray, L. Mancini, M. Rosi, P. Casavecchia and N. Balucani, Chem. Phys. Lett., 2021, 779, 138852 CrossRef CAS.
- D. Nuñez-Reyes, J.-C. Loison, K. M. Hickson and M. Dobrijevic, Phys. Chem. Chem. Phys., 2019, 21, 6574–6581 RSC.
- K. M. Hickson, C. Bray, J.-C. Loison and M. Dobrijevic, Phys. Chem. Chem. Phys., 2020, 22, 14026–14035 RSC.
- D. Nuñez-Reyes, J.-C. Loison, K. M. Hickson and M. Dobrijevic, Phys. Chem. Chem. Phys., 2019, 21, 22230–22237 RSC.
- N. Balucani, O. Asvany, A. H. H. Chang, S. H. Lin, Y. T. Lee, R. I. Kaiser, H. F. Bettinger, P. V. R. Schleyer and H. F. Schaefer III, J. Chem. Phys., 1999, 111, 7457–7471 CrossRef CAS.
- F. Zhang, Y. Guo, X. Gu and R. I. Kaiser, Chem. Phys. Lett., 2007, 440, 56–63 CrossRef CAS.
- D. S. N. Parker, B. B. Dangi, N. Balucani, D. Stranges, A. M. Mebel and R. I. Kaiser, J. Org. Chem., 2013, 78, 11896–11900 CrossRef CAS PubMed.
- H. F. Bettinger, P. V. R. Schleyer, H. F. Schaefer III, P. R. Schreiner, R. I. Kaiser and Y. T. Lee, J. Chem. Phys., 2000, 113, 4250–4264 CrossRef CAS.
- C. Cavallotti, C. De Falco, L. Pratali Maffei, A. Caracciolo, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. Lett., 2020, 11, 9621–9628 CrossRef CAS PubMed.
- G. Vanuzzo, A. Caracciolo, T. K. Minton, N. Balucani, P. Casavecchia, C. de Falco, A. Baggioli and C. Cavallotti, J. Phys. Chem. A, 2021, 125, 8434–8453 CrossRef CAS PubMed.
- N. Balucani, L. Pacifici, D. Skouteris, A. Caracciolo, P. Casavecchia and M. Rosi, in Computational Science and its Applications – ICCSA 2018, ed. O. Gervasi, B. Murgante, S. Misra, E. Stankova, C. M. Torre, A. M. A. C. Rocha, D. Taniar, B. O. Apduhan, E. Tarantino and Y. Ryu, Springer International Publishing, Cham, , pp. 763–772 Search PubMed.
- N. Balucani, L. Pacifici, D. Skouteris, A. Caracciolo, P. Casavecchia, S. Falcinelli and M. Rosi, in Computational Science and its Applications – ICCSA 2019, ed. S. Misra, O. Gervasi, B. Murgante, E.Stankova, V. Korkhov, C. Torre, A. M. A. C. Rocha, D. Taniar, B. O. Apduhan and E. Tarantino, Springer International Publishing, Cham, 2019, pp. 316–324 Search PubMed.
- C.-H. Chin, T. Zhu and J. Z. H. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 12408–12420 RSC.
- D. S. N. Parker, R. I. Kaiser, O. Kostko, T. P. Troy, M. Ahmed, A. M. Mebel and A. G. G. M. Tielens, Astrophys. J., 2015, 803, 53 CrossRef.
- L. Zhao, et al. , Phys. Chem. Chem. Phys., 2021, 23, 18495–18505 RSC.
- D. S. N. Parker, T. Yang, B. B. Dangi, R. I. Kaiser, P. P. Bera and T. J. Lee, Astrophys. J., 2015, 815, 115 CrossRef.
- B. J. Sun, C. H. Huang, S. Y. Chen, S. H. Chen, R. I. Kaiser and A. H. H. Chang, J. Phys. Chem. A, 2014, 118, 7715–7724 CrossRef CAS PubMed.
- D. S. N. Parker, R. I. Kaiser, O. Kostko, T. P. Troy, M. Ahmed, B.-J. Sun, S.-H. Chen and A. H. H. Chang, Phys. Chem. Chem. Phys., 2015, 17, 32000–32008 RSC.
- A. I. Begley, N. S. Shuman, B. A. Long, R. Kämpf, L. Gyr, A. A. Viggiano and R. Zenobi, J. Phys. Chem. A, 2022, 126, 1743–1754 CrossRef CAS PubMed.
- Z. Zhang, X. Gong, S. Zhang, H. Yang, Y. Shi, C. Yang, X. Zhang, X. Xiong, X. Fang and Z. Ouyang, Sci. Rep., 2013, 3, 3481 CrossRef PubMed.
- P. Casavecchia, F. Leonori, N. Balucani, R. Petrucci, G. Capozza and E. Segoloni, Phys. Chem. Chem. Phys., 2009, 11, 46–65 RSC.
- P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204 Search PubMed.
- N. Daugey, P. Caubet, B. Retail, M. Costes, A. Bergeat and G. Dorthe, Phys. Chem. Chem. Phys., 2005, 7, 2921–2927 RSC.
- K. M. Hickson, J.-C. Loison, P. Larregaray, L. Bonnet and V. Wakelam, J. Phys. Chem. A, 2022, 126, 940–950 CrossRef CAS PubMed.
- Y. Wu, J. Cao, H. Ma, C. Zhang, W. Bian, D. Nuñez-Reyes and K. M. Hickson, Sci. Adv., 2019, 5, eaaw0446 CrossRef CAS PubMed.
- D. Nuñez-Reyes and K. M. Hickson, Phys. Chem. Chem. Phys., 2018, 20, 17442–17447 RSC.
- K. M. Hickson and J.-C. Loison, J. Phys. Chem. A, 2022, 126, 3903–3913 CrossRef CAS PubMed.
- C. L. Lin and F. Kaufman, J. Chem. Phys., 1971, 55, 3760–3770 CrossRef CAS.
- D. Marchione, L. Mancini, P. Liang, G. Vanuzzo, F. Pirani, D. Skouteris, M. Rosi, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2022, 126, 3569–3582 CrossRef CAS PubMed.
- D. Skouteris, N. Balucani, C. Ceccarelli, N. Faginas Lago, C. Codella, S. Falcinelli and M. Rosi, Mon. Not. R. Astron. Soc., 2019, 482, 3567–3575 CrossRef CAS.
- D. Skouteris, N. Balucani, N. Faginas-Lago, S. Falcinelli and M. Rosi, Astron. Astrophys., 2015, 584, A76 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359–401 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. Olsen, P. Jørgensen, H. Koch, A. Balkova and R. J. Bartlett, J. Chem. Phys., 1996, 104, 8007–8015 CrossRef CAS.
- C. E. Moore, Atomic Energy Levels, Natl. Bur. Stand. (U.S.) Circ. N. 467, U.S., GPO, Washington, DC, 1949 Search PubMed.
- J. M. L. Martin, Chem. Phys. Lett., 1996, 259, 669–678 CrossRef CAS.
- M. Frisch, et al., Gaussian 09, Revision D.01, 2009 Search PubMed.
- H.-J. Werner, et al., MOLPRO, Version 2021.2, a Package of Ab Initio Programs, 2010, see: https://www.molpro.net Search PubMed.
- H.-J. Werner, et al. , J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- P. Flükiger, H. P. Lüthi, S. Portmann and J. Weber, MOLEKEL 4.3, Swiss Center for Scientific Computing, Manno, Switzerland, 2000–2002 Search PubMed.
- S. J. Klippenstein, J. Chem. Phys., 1992, 96, 367–371 CrossRef.
- G. A. Fisk, J. D. McDonald and D. R. Herschbach, General discussion, Discuss. Faraday Soc., 1967, 44, 228–230 Search PubMed.
- A. M. Schmoltner, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1989, 91, 5365–5373 CrossRef CAS.
- A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, S. Tanteri, C. Cavallotti and P. Casavecchia, Chin. J. Chem. Phys., 2019, 32, 113–122 CrossRef CAS.
- P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405 CrossRef CAS PubMed.
- M. Dobrijevic, J. Loison, K. Hickson and G. Gronoff, Icarus, 2016, 268, 313–339 CrossRef CAS.
- B. Benne, M. Dobrijevic, T. Cavalié, J.-C. Loison and K. M. Hickson, Astron. Astrophys., 2022, 667, A169 CrossRef CAS.
- M. C. McCarthy, et al. , Nat. Astron., 2021, 5, 176–180 CrossRef.
- K. L. K. Lee, P. B. Changala, R. A. Loomis, A. M. Burkhardt, C. Xue, M. A. Cordiner, S. B. Charnley, M. C. McCarthy and B. A. McGuire, Astrophys. J. Lett., 2021, 910, L2 CrossRef CAS.
- Q. Mao, L. Cai and H. Pitsch, Combust. Flame, 2020, 222, 423–433 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S9; Tables S1 and S2. See DOI: https://doi.org/10.1039/d3fd00057e |
| ‡ Present address: Institute of Chemistry and Chemical Engineering, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland. |
| This journal is © The Royal Society of Chemistry 2023 |