On the mechanistic complexity of oxygen evolution: potential-dependent switching of the mechanism at the volcano apex

Abstract

The anodic four-electron oxygen evolution reaction (OER) corresponds to the limiting process in acidic or alkaline electrolyzers to produce gaseous hydrogen at the cathode of the device. In the last decade, tremendous efforts have been dedicated to the identification of active OER materials by electronic structure calculations in the density functional theory approximation. Most of these works rely on the assumption that the mononuclear mechanism, comprising the *OH, *O, and *OOH intermediates, is operative under OER conditions, and that a single elementary reaction step (most likely *OOH formation) governs the kinetics. In the present manuscript, six different OER mechanisms are analyzed, and potential-dependent volcano curves are constructed to comprehend the electrocatalytic activity of these pathways in the approximation of the descriptor G_max(U), a potential-dependent activity measure based on the notion of the free-energy span model. While the mononuclear description mainly describes the legs of the volcano plot, corresponding to electrocatalysts with low intrinsic activity, it is demonstrated that the preferred pathway at the volcano apex is a strong function of the applied electrode potential. The observed mechanistic complexity including a switch of the favored pathway with increasing overpotential sets previous investigations aiming at the identification of reaction mechanisms and limiting steps into question since the entire breadth of OER pathways was not accounted for. A prerequisite for future atomic-scale studies on highly active OER catalysts refers to the evaluation of several mechanistic pathways so that neither important mechanistic features are overlooked nor limiting steps are incorrectly determined.

---

New concepts

The present manuscript addresses the oxygen evolution reaction (OER), a four-electron process of high relevance due to its application in electrolyzers or metal–air batteries for energy conversion and storage, respectively. While the conventional approach to identify promising materials for the OER relies on the application of electronic structure theory, it is a common procedure to suppose a single reaction mechanism, based on which limiting reaction steps are identified. Knowledge of the limiting step is believed to spur the design of advanced materials for this kinetically sluggish process. Herein, it is demonstrated that, particularly for highly active OER catalysts, several reaction mechanisms are operative in dependence of the applied electrode potential, comprising a switch of the favored pathway with increasing overpotential. The reported findings may accelerate the discovery of high-performance OER materials by theoretical considerations, providing guidelines of how to describe the mechanistic processes to determine limiting reaction steps. Noteworthy, the presented volcano approach is not restricted to the OER, but rather is of universal nature and can be exerted to any electrocatalytic process to quantify the mechanistic complexity of coupled proton–electron transfer steps at electrified solid/liquid interfaces.

1 Introduction

Oxygen evolution (OER) represents the bottleneck in proton exchange membrane (PEM) electrolyzers, ideally fueled by renewable electricity, to harvest the energy vector gaseous hydrogen (H₂).^1–3 The reason for the slow OER kinetics is related to the consecutive transfer of four proton–electron pairs to produce a single molecule of gaseous oxygen at the anode:

2H₂O → O₂ + 4H⁺ + 4e⁻, U⁰_OER = 1.23 V vs. reversible hydrogen electrode (RHE) (1)

Despite tremendous efforts to design active electrode coatings for the kinetically sluggish OER, yet electrode potentials of at least 1.50 V vs. RHE or even higher are needed to reach current densities in the order of 10 mA cm⁻² or several kA m⁻² for solar-cell devices or industrial applications, respectively.⁴ These harsh anodic conditions cause an additional challenge relating to electrocatalyst stability, and particularly in acidic electrolytes electrode materials are prone to degrade under operational conditions.^5,6

Since more than a decade, electronic structure calculations in the density functional theory (DFT) approximation have been largely used to steer the design of OER catalysts with enhanced electrocatalytic activity.^7–10 This field of research has been driven by the pioneering works of Nørskov and coworkers, who invented a simple approach to derive the free-energy changes, ΔG_j (j = 1, 2, 3, 4), relating to the elementary steps in the OER mechanism.¹¹ Knowledge of the ΔG_j values enables the approximation of electrocatalytic activity by connecting the largest free-energy change under equilibrium conditions to the electrocatalytic rate via Brønsted–Evans–Polanyi (BEP) relation in the framework of thermodynamic overpotential, η_TD.¹² Determination of η_TD has been used to comprehend the trends of materials in a homologous series with respect to OER activity by constructing volcano plot, a popular concept in electrocatalysis which, however, relies on the common presumption of a single reaction mechanism.^13–15

Based on the early works of Rossmeisl and coworkers on the OER over transition-metal oxides,^16,17 the OER is assumed to follow the so-called mononuclear description, consisting of the *OH, *O, and *OOH adsorbates:

M + H₂O → M–OH + H⁺ + e⁻ ΔG₁ (2)

M–OH → M–O + H⁺ + e⁻ ΔG₂ (3)

M–O + H₂O → M–OOH + H⁺ + e⁻ ΔG₃ (4)

M–OOH → M + O_2(g) + H⁺ + e⁻ ΔG₄ (5)

In eqn (2)–(5), M denotes the catalytically active surface site (e.g., an undercoordinated metal atom), and the four OER free-energy changes meet the criterion of eqn (6):

ΔG₁ + ΔG₂ + ΔG₃ + ΔG₄ = +4.92 eV @U = 0 V vs. RHE (6)

In 2011, Koper related the slow kinetics of the OER to a scaling relation of the intermediate states in the OER mechanism in that the binding energies of the *OH and *OOH intermediates are intrinsically coupled.¹⁸ The sum of the free-energy changes ΔG₂ and ΔG₃ amounts to about 3.20 eV at U = 0 V vs. RHE, thus exceeding the predicted theoretical optimum of 2e × 1.23 V = 2.46 eV.¹⁹ Given the fact that Rossmeisl and coworkers demonstrated by means of DFT calculations that the theory of Koper holds true for a plethora of planar metal oxide surfaces,²⁰ the mononuclear description of eqn (2)–(5) has been tacitly assumed as a universal OER mechanism for any material class.²¹ This finding was substantiated by the predicted thermodynamic overpotential based on the scaling relation (η_TD = (3.20–2.46 eV)/2e = 0.37 V) which is in the same order of magnitude as the experimental overpotential of highly active OER catalysts to reach 10 mA cm⁻² (around η_OER = U − U⁰_OER = 0.30 V) about a decade ago.²²

Nowadays, even experimentalists use the framework of the ΔG_j values to discuss their experimental results and to identify limiting reaction steps, thus often implying the need of severe approximations to translate kinetic Tafel plots to the thermodynamic picture of adsorption free energies.^23–26 One approximation, though, has been largely adopted from theoretical studies in the DFT approximation since it has been well-accepted to define a single elementary reaction, based on a single mechanistic description, as the rate-determining step (RDS), and it is additionally presumed that the RDS is not altered with increasing overpotential.²⁹ This notion appears simplistic considering the dynamic nature of heterogeneous catalysts, which may comprise mechanistic implications relating to the elementary steps in dependence of the driving force.³⁰ Also, even for a single mechanistic description, the RDS may change upon increasing overpotential since this is the common rationalization of a change in the Tafel slope with enhanced driving force.³¹

The present study aims to convey a different way of thinking in that the OER over a certain electrode material is not assumed to follow a single pathway when the driving force is enhanced, but rather the opportunity of several OER mechanisms is studied by volcano analyses. Volcano plots have been established as a powerful tool in electrocatalysis research to comprehend the trends of catalysts in a homologous series of materials, particularly if they factor overpotential and kinetic effects into the evaluation of binding energies.^32–35 For the OER, though, the common approach refers to the construction of volcano curves based on the mononuclear mechanism (cf.eqn (2)–(5)) under equilibrium conditions (η_OER = 0 V), and the volcano analysis based on the descriptor η_TD indicates that either the formation of the *OOH or the *O adsorbate refers to the potential-dependent step (PDS) at the left and right volcano legs, respectively (cf.Fig. 1).²⁰ Please note that the PDS may differ from the RDS, as discussed in recent works.^36,37 Herein, we exert a different strategy in that potential-dependent volcano plots are derived not only for the mononuclear description, but rather six different OER pathways from the literature are incorporated into the analysis.^{16,17,29,38–43} This approach would not be feasible without the activity descriptor G_max(U),⁴⁴ a potential-dependent activity measure for the electrocatalytic activity based on the idea of the free-energy span model,⁴⁵ which, in contrast to the descriptor η_TD, can be linked to the RDS in a potential-dependent fashion.⁴⁶ While the methodology to apply the notion of G_max(U) is described in detail in the Methods section, the different OER mechanisms considered in the analysis are introduced in the following.

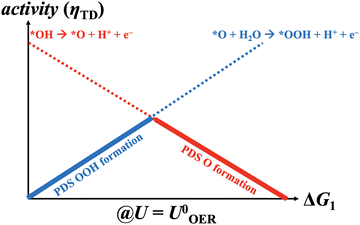Fig. 1 Generalized volcano plot for the oxygen evolution reaction based on the mononuclear mechanism under equilibrium conditions (U = 1.23 V vs. RHE). *OOH and *O formations are reconciled with the potential-dependent steps (PDS) at the left and right volcano legs, respectively.

2 Reaction mechanisms

Six different reaction mechanisms are considered in the present study. Please note that all these reaction mechanisms are written down for acidic conditions. For alkaline conditions, the main difference refers to the fact that hydroxide anions rather than water serve as the reactant, as evident from previous studies.⁴⁷ Given that the free energy of hydroxide anions is related to water as a reference when using canonical or grand canonical approaches to derive the adsorption-free energies of the elementary steps,⁴⁸ the mechanistic pathways can be easily translated to alkaline conditions. Please note that the electrocatalytic activity of electrode materials can change upon pH alteration, and the modeling of pH effects requires the application of grand canonical formalisms rather than canonical approaches such as the computational hydrogen electrode approach.^49–51

(i) Mononuclear mechanism (cf.eqn (2)–(5))

(ii) Bifunctional mechanism I (cf.eqn (7)–(10))

Rossmeisl and coworkers proposed that two adjacent sites can be operative in the OER in that a surface oxygen atom, *O_A, next to the catalytically active site serves as a proton acceptor for the splitting of a water molecule on the oxygen-covered surface:³⁸

M + *O_A + H₂O → M–OH + *O_A + H⁺ + e⁻ ΔG_a (7)

M–OH+ *O_A→ M–O + *O_A + H⁺ + e⁻ ΔG_b (8)

M–O + *O_A + H₂O → M–OO + *OH_A + H⁺ + e⁻ ΔG_c (9)

M–OO + *OH_A → M + *O_A + O_2(g) + H⁺ + e⁻ ΔG_d (10)

(iii) Bifunctional mechanism II (cf.eqn (11)–(15))

Like the bifunctional mechanism I, a surface atom next to the catalytically active site serves as a proton acceptor, but the splitting of the second water molecule under formation of the *OOH adsorbate refers to a chemical (rather than an electrochemical) step:^29,38,39

M + *O_A + H₂O → M–OH + *O_A + H⁺ + e⁻ ΔG_e (11)

M–OH + *O_A → M–O + *O_A + H⁺ + e⁻ ΔG_f (12)

M–O + *O_A + H₂O → M–OOH + *OH_A ΔG_g (13)

*OH_A → *O_A + H⁺ + e⁻ ΔG_h  (14)

M–OOH → M + O_2(g) + H⁺ + e⁻ ΔG_i (15)

(iv) Binuclear mechanism (cf.eqn (16)–(20))

About a decade ago, Busch and coworkers suggested a binuclear mechanism, in which two neighboring oxygen species recombine in a chemical step under the formation of gaseous oxygen:^41,42

M + M + H₂O → M–OH + M + H⁺ + e⁻ ΔG_j (16)

M–OH + M + H₂O → M–OH + M–OH + H⁺ + e⁻ ΔG_k (17)

M–OH + M–OH → M–O + M–OH + H⁺ + e⁻ ΔG_l (18)

M–O + M–OH → M–O + M–O + H⁺ + e⁻ ΔG_m (19)

M–O + M–O → M + M + O_2(g) ΔG_n (20)

(v) Oxide mechanism (also denoted as *OO⋯*OO recombination mechanism, cf.eqn (21)–(25))

Recently, Binninger and Doublet reported another OER pathway for IrO₂(110) where the catalytic cycle commences from a fully *O-covered surface and contains the formation of gaseous oxygen via the chemical recombination of two adjacent *OO *OO groups.⁴³ This pathway may have been triggered by the fact that the *OO intermediate was spectroscopically identified and computationally predicted by Rao, Kolb, and others for the case of RuO₂,^52,53 and the presence of the *OO adsorbate for transition-metal oxides is consistent with experimental results from operando X-ray spectroscopy or cyclic voltammetry for IrO_x:^54,55

M–O M–O + H₂O → M–OOH M–O + H⁺ + e⁻ ΔG_o (21)

M–OOH M–O + H₂O → M–OOH M–OOH + H⁺ + e⁻ ΔG_p (22)

M–OOH M–OOH → M–OOH M–OO + H⁺ + e⁻ ΔG_q (23)

M–OOH M–OO → M–OO M–OO + H⁺ + e⁻ ΔG_r (24)

M–OO M–OO → M–O M–O + O_2(g) ΔG_s (25)

(vi) Two-electron water oxidation (cf.eqn (26)–(28))

For applied electrode potentials exceeding 1.76 V vs. RHE, the formation of hydrogen peroxide via a two-electron process is a competing side reaction under OER conditions:⁵⁶

2 e⁻ water oxidation: 2 H₂O → H₂O₂ + 2 H⁺ + 2 e⁻ U⁰ = 1.76 V vs. RHE (26)

M + H₂O → M–OH + H⁺ + e⁻ ΔG_t (27)

M–OH + H₂O → M + H₂O₂ + H⁺ + e⁻ ΔG_u (28)

The free-energy changes ΔG_α (α = a,…,u) of the various mechanistic pathways are related by a rigorous thermodynamic treatment to the free energies of the reaction intermediates, thereby making use of the scaling relations between the *OH and *O as well as the *OH and *OOH adsorbates,^8,20 to determine the activity measure G_max(U) (cf. Methods section). The free-energy change ΔG₁, referring to the formation of *OH, is used as descriptor in the OER volcano plot. Given that Rossmeisl and coworkers reported that basically all relevant materials to the oxygen electrocatalysis are within ΔG₁ = [−0.50, 2.50] eV,⁵⁷ this free-energy regime with a step size of 0.01 eV is used as a basis set to compile volcano curves at four different applied electrode potentials, U = 1.23 V, 1.40 V, 1.60 V, and 1.80 V vs. RHE. All further information relating to the modeling approach is provided in the Methods section.

3 Results

Fig. 2 depicts volcano curves for the OER at U = 1.23 and 1.40 V vs. RHE. The resulting volcano lines are obtained by analyzing the five four-electron OER mechanisms, and the energetically favored pathways are extracted in dependence of the descriptor ΔG₁. This procedure can be retraced by Figure S1 in the supplemental where volcano curves of all mechanisms, corresponding to the raw data of Fig. 2(a), are shown at U = 1.23 V vs. RHE.

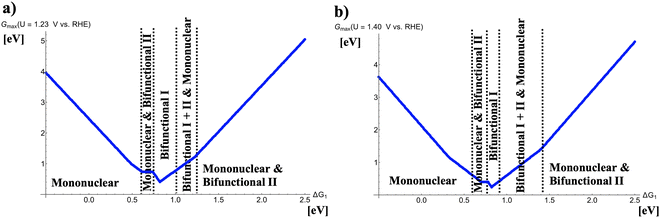Fig. 2 Potential-dependent volcano plots for various pathways of the oxygen evolution reaction at (a) U = 1.23 V vs. RHE and (b) U = 1.40 V vs. RHE. The energetically favored mechanisms in the approximation of G_max(U) as a potential-dependent activity measure are indicated in dependence of the adsorption free energy of the *OH intermediate, ΔG₁. To derive the volcano curves, the following scaling relations are taken into account: ΔG₂ + ΔG₃ = 3.20 eV and ΔG₂ = 2 × ΔG₁.

Fig. 2(a) indicates that different mechanistic descriptions are energetically preferred in dependence of the descriptor ΔG₁. While for ΔG₁ < 0.60 eV the mononuclear mechanism governs the OER volcano, competition between the mononuclear and bifunctional I pathways is observed for 0.60 eV < ΔG₁ < 0.73 eV. Interestingly, at the volcano apex corresponding to the catalysts with the highest OER activity, the bifunctional I mechanism is operative (0.73 eV < ΔG₁ < 1.00 eV). For weaker bonding of the *OH intermediate, 1.00 eV < ΔG₁ < 1.25 eV, the mononuclear, bifunctional I, and bifunctional II descriptions compete with identical values of G_max(U) whereas for ΔG₁ > 1.25 eV, the mononuclear and bifunctional II mechanisms determine the volcano slope.

While U = 1.23 V vs. RHE refers to the electrochemical equilibrium, catalytic turnover can only be obtained if a finite overpotential is applied to make the overall reaction exergonic. The situation in Fig. 2(b) can be seen as a low overpotential regime of oxygen evolution, and it turns out that the OER volcano at U = 1.40 V vs. RHE remains the same qualitative characteristics as under equilibrium conditions. Quantitively, the width of certain mechanistic windows in the volcano is altered. Particularly, the apex (0.78 eV < ΔG₁ < 0.91 eV) comprises a smaller free-energy regime consisting of the bifunctional I mechanism whereas the free-energy range of the mononuclear, bifunctional I, and bifunctional II descriptions on the right side next to the volcano top is enlarged (0.91 eV < ΔG₁ < 1.40 eV).

In Fig. 3, the respective volcano curves for U = 1.60 and 1.80 V vs. RHE are compiled. Fig. 3(a) indicates that at the volcano apex (ΔG₁ = 0.80 eV), competition between four different OER mechanisms with identical values of G_max(U = 1.60 V vs. RHE) is observed. For even larger OER overpotentials (cf.Fig. 3(b)), the oxide mechanism prevails for 0.71 eV < ΔG₁ < 0.81 eV whereas all five OER mechanisms (mononuclear, oxide, bifunctional I, bifunctional II, and binuclear) compete in the free-energy regime of 0.81 eV < ΔG₁ < 0.90 eV. In Fig. 3(b), also the two-electron water oxidation culminating into the formation of hydrogen peroxide is factored into the analysis. This mechanistic pathway, however, does not conflict with the formation of gaseous oxygen in the case of highly active OER catalysts at the volcano apex; rather, a succinct volcano top at weak bonding of the *OH intermediate is observed, indicating that the free-energy regime of ΔG₁ > 1.50 eV may result in the electrochemical synthesis of H₂O₂ with high selectivity since the opposing four-electron OER is efficiently suppressed.

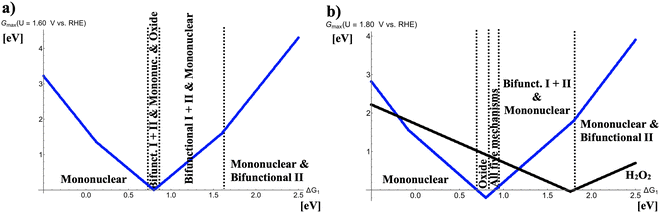Fig. 3 Potential-dependent volcano plots for various pathways of the oxygen evolution reaction at (a) U = 1.60 V vs. RHE and (b) U = 1.80 V vs. RHE. The energetically favored mechanisms in the approximation of G_max(U) as a potential-dependent activity measure are indicated in dependence of the adsorption free energy of the *OH intermediate, ΔG₁. The black volcano curve in panel b) refers to the two-electron water oxidation with H₂O₂ as the main product. To derive the volcano curves, the following scaling relations are taken into account: ΔG₂ + ΔG₃ = 3.20 eV and ΔG₂ = 2 × ΔG₁.

In contrast to the mechanistic changes at the volcano apex upon increasing driving force, the legs of the OER volcano remain largely unaffected in that the volcano slope is governed by the mononuclear mechanism, or mononuclear, bifunctional I, and bifunctional II descriptions, or the mononuclear and bifunctional II mechanisms for strong bonding of *OH, slightly weak bonding of *OH, and weak bonding of *OH, respectively (cf.Fig. 2 and 3).

4 Discussion

The main result of the presented modeling approach refers to the identification of a potential-dependent switching of the preferred mechanism at the volcano apex. More precisely, the volcano curves suggest that for a highly active OER catalyst, the bifunctional I description is operative for small overpotentials (U = 1.40 V vs. RHE) whereas also the mononuclear, oxide, or bifunctional II mechanisms may play a role in the potential regime of about U = 1.60 V vs. RHE. For even larger overpotentials (U = 1.80 V vs. RHE), the oxide pathway is favored at the volcano top while the two-electron water oxidation with hydrogen peroxide as main product reveals an independent volcano curve. Recalling the fact that, commonly, only a single mechanism is assumed to govern the performance of an OER electrocatalyst independent of the applied overpotential, the observed finding can be interpreted as a paradigm change. It therefore appears of importance to factor several mechanistic pathways into the atomic-scale analysis of electrode materials for oxygen evolution, independent whether electronic structure calculations in the DFT approximation are applied or experimental Tafel plots are translated into the framework of adsorption free energies.^23–29 Only the dedicated evaluation of several competing pathways (cf. Section 2) may allow comprehending the electrocatalytic activity of OER catalysts with reasonable accuracy and may enable determination of the RDS without biased approximations.

Based on the suggested mechanistic pathways in Section 2, it may seem that the presented analysis of the mechanistic pathways is restricted to metal oxides. While the OER over IrO₂ is discussed as a prototypical example in Section 4.1, I would like to emphasize that the derived volcano plots may even go beyond the application of metal oxides. This finding is underpinned by the fact that for materials with a single active center, e.g., single-atom catalysts (SAC), ligands in axial position or located on the nitrogen or carbon backbone can serve as a second adjacent active site, such as discussed in the literature.^58–60 Therefore, the importance of considering various reaction mechanisms for the design of OER catalysts may be of universal nature and may not only hold true for metal oxides.

4.1 OER over IrO₂

One prototypical example for a dispute on the RDS in the literature refers to the OER over IrO₂, which due to its application as anode material in PEM electrolyzers is among the most studied systems in the field. Initial thermodynamic considerations by Rossmeisl and coworkers suggested that the formation of the *OOH intermediate within the mononuclear mechanism (cf.eqn (4)) refers to the PDS,¹⁷ and this step was also assumed to be kinetically limiting using the tacit assumption of PDS = RDS. Ping and Goddard investigated the OER over IrO₂(110) by calculating selected transition states of the elementary steps.⁴⁰ These authors concluded that *OOH formation is rate determining, however, by a chemical reaction step in the realm of the bifunctional II mechanism (cf.eqn (13)). It should be considered that for the grand canonical framework in the DFT calculations, only chemical steps but no electrochemical processes were considered for the transition-state calculations. Exner and Over applied the free-energy diagram approach to the OER over IrO₂(110) by combining DFT calculations and single-crystalline Tafel plot experiments for the thermodynamics and kinetics, respectively.⁶¹ These authors demonstrated that *OOH decomposition within the mononuclear mechanism (cf.eqn (5)) refers to the RDS, thereby additionally outlining the opportunity of decoupled proton–electron transfer in that *OO⁻ is formed as a precursor species for product formation. Ha and Larsen reported in a theoretical work that, besides *OOH formation within the mononuclear mechanism (cf.eqn (4)), also the recombination of two adjacent *O groups within the binuclear mechanism contributes to the high electrocatalytic activity of IrO₂ (cf.eqn (20)).⁶² On the contrary, Jones and coworkers suggested that the OER over IrO₂(110) is governed by the *OOH formation in the realm of the bifunctional II mechanism (cf.eqn (13)),²⁹ thereby reproducing the initial result by Ping and Goddard. Recently, Binninger and Doublet put forth that the oxide mechanism with the *OO⋯*OO recombination step (cf.eqn (25)) corresponds to the RDS for IrO₂(110) due to a smaller free-activation energy compared to *OOH formation under typical OER conditions.⁴³

Besides the above theoretical works, also experimental studies are emerging that relate the measured kinetic current density by microkinetic considerations to the kinetically limiting reaction step. Takanabe and coworkers combined microkinetic considerations by analyzing Tafel plots and the reaction order in terms of pH to comprehend the limiting step of the OER over IrO_x, illustrating that *OOH formation within the mononuclear mechanism (cf.eqn (4)) is rate determining.²⁴ On the contrary, Krewer and coworkers applied a dynamic microkinetic model approach by analyzing cyclic voltammograms between 0.1 V and 1.6 V vs. RHE.⁵¹ The authors that reported that up two three steps, namely, *OO formation (cf.eqn (23)), *OOH formation by a chemical step (cf.eqn (13)), and O₂ detachment by a chemical step (either eqn (25) or *OO → * + O₂) are kinetically limiting for IrO₂ nanoparticles.⁶³

Mapping the above literature summary to the potential dependent OER volcano plots (cf.Fig. 2 and 3), it can be concluded that none of these studies is fully conclusive. It can be fairly assumed that IrO₂ or IrO_x is located at the top or close to the apex of the volcano where the potential-dependent switching of the reaction mechanism is observed, and thus, selectivity is in favor of oxygen rather than of peroxide formation (cf.Fig. 3(b)). All the above-listed works rely on the analysis of a single mechanism, or a maximum of two to three different mechanistic descriptions whereas the entire breadth of the mechanistic OER complexity is not considered in the analysis. Therefore, the present article may serve as an appeal to the community in that future studies on highly active OER catalysts require the evaluation of several mechanistic pathways in order not to overlook important mechanistic features and to omit erroneous conclusions on limiting steps in the framework of the RDS. Machine learning could play an important role in this regard, as recently demonstrated for IrO₂-based materials, among others.^64–66

4.2 Subtleties of the volcano approach

In the following, the most common assumption of the mononuclear description as operative pathway in the OER is further discussed. The volcano curves of Fig. 2 and 3 indicate that the mononuclear mechanism is a proper choice for the volcano legs, corresponding to materials with low intrinsic activity. As such, it is yet a valid strategy to apply the common modeling approach of assuming the mononuclear mechanism for the description of OER to rule out inactive catalysts with unfavorable binding energies.⁶⁷ However, the mononuclear mechanism alone can never entirely identify highly active catalysts, particularly not with respect to the kinetically limiting reaction steps when considering the mechanistic competition of the various pathways at the volcano apex (cf.Fig. 2 and 3).

While the potential-dependent volcano curves in Fig. 2 and 3 are universal in that they are not related to a specific material class, they are based on certain approximations (cf. Methods section). While the scaling relation between the *OH and *OOH intermediates is well accepted, also smaller scaling-relation intercepts than the conventional value of 3.20 eV have been reported in the literature, for instance relating to the consideration or neglection of the aqueous solvent in the DFT calculations.^68–70 Therefore, the same mechanistic analysis is conducted for a scaling-relation intercept of 3.00 eV, and the corresponding volcano curves are depicted in the ESI,† Fig. S2 and S3. It is evident that, besides some minor changes relating to the preferred mechanism in dependence of ΔG₁, the main conclusion of this article in terms of the potential-dependent switching of the OER mechanism at the volcano apex is not altered.

A promising strategy for materials design in the OER refers to the notion of breaking scaling relation in that the free-energy difference between the *OH and *OOH intermediates is reduced.⁷¹ In this context, it should be noted that Calle–Vallejo and coworkers have already pointed out the limited applicability of this approach to exploring better OER materials by thermodynamic analysis.⁷² This can be explained by incorporating the reaction kinetics into the OER volcano plot, indicating that the breaking of the OER scaling relation can be even accompanied by decreased electrocatalytic activity, which was also statistically proven.^73,74 Most electrode materials reveal a scaling relation between the *OH and *OOH intermediates in the order of 3.00 eV and 3.20 eV,⁵⁷ and this is the reason why this data range is studied in the present contribution by the construction of volcano plots. Reducing the intercept of the *OH vs. *OOH scaling relation, though, does not guarantee improved catalytic performance in the OER.^72–74

An even more critical limitation of the presented volcano curves refers to the assumption of a scaling relation between the *OH and *O adsorbates. This scaling relation, also denoted as ΔG₂ = 2 × ΔG₁, is much less pronounced than the *OH vs. *OOH scaling relation. Therefore, a sensitivity analysis of the *OH vs. *O scaling relation is provided in the ESI,† Fig. S4–S7. It is indicated that the main results of this study are not prone to change when the energetics of the *O and *OH intermediates are altered to a reasonable extent.

Finally, it would like to emphasize that the present descriptor-based volcano study on the OER mechanisms discusses the electrocatalytic activity in the approximation of G_max(U) while catalyst decomposition or structural reorganizations are not explicitly accounted for in the assessment of the mechanistic pathways. DFT-based studies on catalyst decomposition under anodic conditions are starting to appear in the literature,^75–77 and it is of high relevance to comprehend activity–stability trends for OER catalysts.⁷⁸ Contemplation of electrocatalyst stability, though, is beyond the scope of the present modeling study, thereby emphasizing that free-energy estimates of how to correlate decomposition pathways to OER activity are still missing. Therefore, the present work focuses solely on the electrocatalytic activity by a volcano-based trend study, and the obtained result in terms of the mechanistic complexity at the OER apex may motivate that, besides the breadth of OER pathways, also a variety of degradation mechanisms are included in future DFT-based studies of model materials. This may enable expanding activity–selectivity investigations of electrocatalytic processes to more refined activity–selectivity–stability studies.⁷⁹

5 Conclusions

The theoretical description of electrified solid/liquid interfaces can be broadly classified into three categories: (a) first-principles or continuum model studies of the electric double layer at the interface, (b) method development to move from a constant-charge description to a constant-potential formalism, and (c) computational electrocatalysis by focusing on the energetics of the elementary reaction steps, thereby applying heuristic tools to quantify electrocatalytic activity. The present manuscript addresses the last category, aiming to convey a new way of thinking in that a plethora of different mechanistic pathways are factored into the volcano plot for the industrially relevant oxygen evolution reaction (OER). This is achieved by assessing the electrocatalytic activity by the descriptor G_max(U) in dependence of the adsorption free energy of the *OH intermediate, ΔG₁, for which a basis set corresponding to the material space of available OER catalysts is defined. While the volcano legs of the OER volcano are mainly governed by the mononuclear OER mechanism, it is noteworthy that a potential-dependent switching of the preferred mechanism at the volcano apex is observed in that bifunctional, binuclear, mononuclear, or oxide pathways govern the electrocatalytic activity in dependence of the applied overpotential. While commonly, the OER kinetics is discussed by referring to a change in the rate-determining step (RDS) for a single mechanism with increasing overpotential, the present analysis puts forth that not only the RDS but even the reaction mechanism may change upon alteration of the driving force. This result limits the meaningfulness of previous theoretical or experimental studies aiming at the identification of limiting steps in the framework of the RDS since it is a common practice to assume that a single mechanism or even a single RDS governs the OER performance, independent of the applied driving force. It is therefore inevitable that future studies on highly active OER catalysts require the evaluation of several mechanistic pathways to omit erroneous conclusions on the RDS and not to overlook important mechanistic features.

6 Methods

The presented modeling approach relies on an in-house methodology that connects the adsorption free energies of the intermediate species in the electrocatalytic processes of eqn (1)–(28) to electrocatalytic activity by the descriptor G_max(U) to compile volcano curves for oxygen evolution. In the following, this procedure is illustrated on the example of the mononuclear mechanism (cf.eqn (2)–(6)). The free energies of the reaction intermediates *OH, *O, and *OOH in dependence of the applied electrode potential are given by eqn (29)–(33):

G_M(U) = 0 (29)

G_M–OH(U) = ΔG₁ −1 × e × U (30)

G_M–O(U) = ΔG₁ + ΔG₂ −2 × e × U (31)

G_M–OOH(U) = ΔG₁ + ΔG₂ + ΔG₃ −3 × e × U (32)

G_M+O2(U) = +4.92 eV −4 × e × U (33)

By considering the scaling relations of eqn (34) and (35),

ΔG₂ + ΔG₃ = SRI (34)

ΔG₂ = 2 × ΔG₁ (35)

The energetics of the intermediate states are:

G_M(U) = 0 (36)

G_M–OH(U) = ΔG₁ −1 × e × U (37)

G_M–O(U) = 3 × ΔG₁ −2 × e × U (38)

G_M–OOH(U) =ΔG₁ + SRI −3 × e × U (39)

G_M+O2(U) = +4.92 eV −4 × e × U (40)

For the scaling-relation intercept (SRI), we adopt values of SRI = 3.20 eV (cf.Fig. 2 and 3) as well as SRI = 3.00 eV (cf. ESI,† Fig. S2 and S3), corresponding to the recent literature.^68–70 For the scaling relation between the *OH and *O adsorbates (cf.eqn (35)), a sensitivity analysis is provided in the ESI† (cf. Fig. S4–S7), indicating that the main results of this study are not altered upon reasonable modification of this free-energy relation. The free-energy change ΔG₁ serves as the descriptor in the volcano analysis, and it is varied within the free-energy regime of ΔG₁ = [−0.50, 2.50] eV with a step size of 0.01 eV.

Based on the energetics of the intermediate states, the descriptor G_max(U) is evaluated by considering all possible free-energy spans between the reaction intermediates:^44,79

G_max(U) = max{G_M–OH(U) − G_M(U); G_M–O(U) − G_M(U); G_M–OOH(U) − G_M(U); G_M–O(U) − G_M–OH(U); G_M–OOH(U) − G_M–OH(U); G_M+O2(U) − G_M–OH(U); G_M–OOH(U) − G_M–O(U); G_M+O2(U) − G_M–O(U); G_M+O2(U) − G_M–OOH(U)} (41)

Volcano curves arise by plotting G_max(U) as a function of ΔG₁ for a constant applied electrode potential, U. This analysis is not only performed for the mononuclear mechanism in a potential-dependent fashion (cf.Fig. 2 and 3), but also for the other mechanistic descriptions (cf.eqn (7)–(28)). Here, we summarize the energetics of the intermediate states for each mechanism. For a detailed derivation of how to correlate the adsorption free energies to the descriptors ΔG₁ and SRI, we refer to a recent work on the four-electron and two-electron oxygen reduction reactions where these correlations for the reverse reaction are described in detail.⁸⁰

6.1 Bifunctional mechanism I

G _M(U) = 0 (42)

G _M–OH(U) = ΔG₁ −1 × e × U (43)

G _M–O(U) = 3 × ΔG₁ −2 × e × U (44)

G _M–OO+*OH(U) = 4 × ΔG₁ −3 × e × U (45)

G _M+O2(U) = +4.92 eV −4 × e × U (46)

6.2 Bifunctional mechanism II

G _M(U) = 0 (47)

G _M–OH(U) = ΔG₁ −1 × e × U (48)

G _M–O(U) = 3 × ΔG₁ −2 × e × U (49)

G _M–OOH+*OH(U) = −ΔG₁ + SRI −2 × e × U (50)

G _M–OOH(U) = ΔG₁ + SRI −3 × e × U (51)

G _M+O2(U) = +4.92 eV −4 × e × U (52)

6.3 Binuclear mechanism

G _M+M(U) = 0 (53)

G _M–OH+M(U) = ΔG₁ −1 × e × U (54)

G _{M–OH+M–OH}(U) = 2 × ΔG₁ −2 × e × U (55)

G _M–O+M–OH(U) = 4 × ΔG₁ 13 × e × U (56)

G _M–O+M–O(U) = 6 × ΔG₁ −4 × e × U (57)

G _M+O2(U) = +4.92 eV −4 × e × U (58)

6.4 Oxide mechanism (*OO⋯*OO recombination mechanism)

G _M–O+M–O(U) = 0 (59)

G _{M–OOH+M–O}(U) = −2 × ΔG₁ + SRI −1 × e × U (60)

G _{M–OOH+M–OOH}(U) = −4 × ΔG₁ + 2 × SRI −2 × e × U (61)

G _{M–OOH+M–OO}(U) = −2 × ΔG₁ + 2 × SRI −3 × e × U (62)

G _{M–OO+M–OO}(U) = +2 × SRI −4 × e × U (63)

G _{M–O+M–O+O2}(U) = +4.92 eV −4 × e × U (64)

6.5 Two-electron water oxidation

G _M+H2O(U) = 0 (65)

G _M–OH(U) = ΔG₁ −1 × e × U (66)

G _M+H2O2(U) = +3.52 eV −2 × e × U (67)

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

KSE acknowledges funding by the Ministry of Culture and Science of the Federal State of North Rhine-Westphalia (NRW Return Grant). KSE is associated with the CRC/TRR247: “Heterogeneous Oxidation Catalysis in the Liquid Phase” (Project number 388390466-TRR 247), the RESOLV Cluster of Excellence, funded by the Deutsche Forschungsgemeinschaft under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV, and the Center for Nanointegration (CENIDE). This article is based upon the work from COST Action 18234, supported by COST (European Cooperation in Science and Technology).

References

1. G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, The hydrogen economy, Phys. Today, 2004, 57, 39–44.
2. M. Carmo, D. L. Fritz, J. Merge and D. Stolten, A Comprehensive Review on PEM Water Electrolysis, Int. J. Hydrogen Energy, 2013, 38, 4901–4934.
3. M. F. Lagadec and A. Grimaud, Water electrolysers with closed and open electrochemical systems, Nat. Mater., 2020, 19, 1140–1150.
4. J. Kibsgaard and I. Chorkendorff, Considerations for the scaling-up of water splitting catalysts, Nat. Energy, 2019, 4, 430–433.
5. S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, The Stability Number as a Metric for Electrocatalyst Stability Benchmarking, Nat. Catal., 2018, 1, 508–515.
6. H. Over, Fundamental Studies of Planar Single-Crystalline Oxide Model Electrodes (RuO₂, IrO₂) for Acidic Water Splitting, ACS Catal., 2021, 11, 8848–8871.
7. Z. W. Seh, J. Kibsgaard, C. H. Dickens, I. B. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining Theory and Experiment in Electrocatalysis: Insights Into Materials Design, Science, 2017, 355, eaad4998.
8. M. Busch, N. B. Halck, U. U. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Beyond the top of the volcano? – A unified approach to electrocatalytic oxygen reduction and oxygen evolution, Nano Energy, 2016, 29, 126–135.
9. S. Back, K. Tran and Z. W. Ulissi, Toward a design of active oxygen evolution catalysts: insights from automated density functional theory calculations and machine learning, ACS Catal., 2019, 9, 7651–7659.
10. M. J. Kolb and F. Calle-Vallejo, The bifunctional volcano plot: Thermodynamic limits for single-atom catalysts for oxygen reduction and evolution, J. Mater. Chem. A, 2022, 10, 5937–5941.
11. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. J. Jonsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
12. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1, 37–46.
13. O. Kasian, J.-P. Grote, S. Geiger, S. Cherevko and K. J. J. Mayrhofer, The Common Intermediates of Oxygen Evolution and Dissolution Reactions during Water Electrolysis on Iridium, Angew. Chem., Int. Ed., 2018, 57, 2488–2491.
14. H. Cui, H.-X. Liao, Z.-L. Wang, J.-P. Xie, P.-F. Tan, D.-W. Chu and P. Jun, Synergistic electronic interaction between ruthenium and nickel-iron hydroxide for enhanced oxygen evolution reaction, Rare Metals, 2022, 41, 2606–2615.
15. F. Gao, J. He, H. Wang, J. Lin, R. Chen, K. Yi, F. Huang, Z. Lin and M. Wang, Te- mediated electro-driven oxygen evolution reaction, Nano Res. Energy, 2022, 1, e9120029.
16. J. Rossmeisl, A. Logadottir and J. K. Nørskov, Electrolysis of Water on (Oxidized) Metal Surfaces, Chem. Phys., 2005, 319, 178–184.
17. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of Water on Oxide Surfaces, J. Electroanal. Chem., 2007, 607, 83–89.
18. M. T. M. Koper, Thermodynamic Theory of Multi-Electron Transfer Reactions: Implications for Electrocatalysis, J. Electroanal. Chem., 2011, 660, 254–260.
19. M. T. M. Koper, Theory of Multiple Proton-Electron Transfer Reactions and its Implications for Electrocatalysis, Chem. Sci., 2013, 4, 2710–2723.
20. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165.
21. J. Zhang, H. B. Yang, D. Zhou and B. Liu, Adsorption Energy in Oxygen Electrocatalysis, Chem. Rev., 2022, 122, 17028–17072.
22. C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135, 16977–16987.
23. H. B. Tao, J. Zhang, J. Chen, L. Zhang, Y. Xu, J. G. Chen and B. Liu, Revealing Energetics of Surface Oxygen Redox from Kinetic Fingerprint in Oxygen Electrocatalysis, J. Am. Chem. Soc., 2019, 141, 13803–13811.
24. T. Nishimoto, T. Shinagawa, T. Naito and K. Takanabe, Microkinetic assessment of electrocatalytic oxygen evolution reaction over iridium oxide in unbuffered conditions, J. Catal., 2020, 391, 435–445.
25. J. T. Mefford, Z. Zhao, M. Bajdich and W. C. Chueh, Interpreting Tafel Behaviour of Consecutive Electrochemical Reactions Through Combined Thermodynamics and Steady State Microkinetic Approaches, Energy Environ. Sci., 2020, 13, 622–634.
26. H. Ooka, M. E. Wintzer and R. Nakamura, Non-Zero Binding Enhances Kinetics of Catalysis: Machine Learning Analysis on the Experimental Hydrogen Binding Energy of Platinum, ACS Catal., 2021, 11, 6298–6303.
27. J. Geppert, F. Kubannek, P. Röse and U. Krewer, Identifying the oxygen evolution mechanism by microkinetic modelling of cyclic voltammograms, Electrochim. Acta, 2021, 380, 137902.
28. S. B. Scott, R. R. Rao, C. Moon, J. E. Sørensen, J. Kibsgaard, Y. Shao-Horn and I. Chorkendorff, The low overpotential regime of acidic water oxidation part I: the importance of O₂ detection, Energy Environ. Sci., 2022, 15, 1977–1987.
29. H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. N. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Perez- Ramirez, B. Roldan Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Key role of chemistry versus bias in electrocatalytic oxygen evolution, Nature, 2020, 587, 408–413.
30. C. Luan, M. Corva, U. Hagemann, H. Wang, M. Heidelmann, K. Tschulik and T. Li, Atomic-Scale Insights into Morphological, Structural, and Compositional Evolution of CoOOH during Oxygen Evolution Reaction, ACS Catal., 2023, 13, 1400–1411.
31. J. O. 'M. Bockris and A. K. N. Reddy, in Modern Electrochemistry 2, ed. A. Plenum/Rosetta, New York, 1973.
32. K. S. Exner, Does a Thermoneutral Electrocatalyst Correspond to the Apex of a Volcano Plot for a Simple Two-Electron Process?, Angew. Chem., Int. Ed., 2020, 59, 10236–10240.
33. H. Ooka and R. Nakamura, Shift of the optimum binding energy at higher rates of catalysis, J. Phys. Chem. Lett., 2019, 10, 6706–6713.
34. Y. Zhang, J. Zhang and J. Huang, Potential-dependent volcano plot for oxygen reduction: mathematical origin and implications for catalyst design, J. Phys. Chem. Lett., 2019, 10, 7037–7043.
35. E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, On the shifting peak of volcano plots for oxygen reduction and evolution, Electrochim. Acta, 2022, 426, 140799.
36. M. T. M. Koper, Analysis of electrocatalytic reaction schemes: Distinction between rate- determining and potential-determining steps, J. Solid State Electrochem., 2013, 17, 339–344.
37. K. S. Exner, Is Thermodynamics a Good Descriptor for the Activity? Re-Investigation of Sabatier's Principle by the Free Energy Diagram in Electrocatalysis, ACS Catal., 2019, 9, 5320–5329.
38. N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Beyond the Volcano Limitations in Electrocatalysis – Oxygen Evolution Reaction, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688.
39. Y. H. Fang and Z. P. Liu, Mechanism and Tafel Lines of Electro-Oxidation of Water to Oxygen on RuO₂(110), J. Am. Chem. Soc., 2010, 132, 18214–18222.
40. Y. Ping, R. J. Nielsen and W. A. Goddard, The Reaction Mechanism with Free Energy Barriers at Constant Potentials for the Oxygen Evolution Reaction at the IrO₂(110) Surface, J. Am. Chem. Soc., 2017, 139, 149–155.
41. M. Busch, E. Ahlberg and I. Panas, Electrocatalytic oxygen evolution from water on a Mn(III–V) dimer model catalyst—A DFT perspective, Phys. Chem. Chem. Phys., 2011, 13, 15069–15076.
42. M. Busch, Water oxidation: From mechanisms to limitations, Curr. Opin. Electrochem., 2018, 9, 278–284.
43. T. Binninger and M. L. Doublet, The Ir–OOOO–Ir transition state and the mechanism of the oxygen evolution reaction on IrO₂(110), Energy Environ. Sci., 2022, 15, 2519–2528.
44. K. S. Exner, A Universal Descriptor for the Screening of Electrode Materials for Multiple-Electron Processes: Beyond the Thermodynamic Overpotential, ACS Catal., 2020, 10, 12607–12617.
45. S. Kozuch and S. Shaik, How to conceptualize catalytic cycles? The Energetic Span Model, Acc. Chem. Res., 2011, 44, 101–110.
46. K. S. Exner, Why approximating electrocatalytic activity by a single free-energy change is insufficient, Electrochim. Acta, 2021, 375, 137975.
47. Q. Liang, G. Brocks and A. Bieberle-Hütter, Oxygen evolution reaction (OER) mechanism under alkaline and acidic conditions, J. Phys. Energy, 2021, 3, 0260015.
48. A. Groß, Reversible vs. Standard Hydrogen Electrode Scale in Interfacial Electrochemistry from a Theoretician's Atomistic Point of View, J. Phys. Chem. C, 2022, 126, 11439–11446.
49. X. Hu, S. Chen, L. Chen, Y. Tian, S. Yao, Z. Lu, X. Zhang and Z. Zhou, What is the Real Origin of the Activity of Fe–N–C Electrocatalysts in the O₂ Reduction Reaction? Critical Roles of Coordinating Pyrrolic N and Axially Adsorbing Species, J. Am. Chem. Soc., 2022, 144, 18144–18152.
50. H. Yu, S. E. Weitzner, J. B. Varley, B. C. Wood and S. A. Akhade, Surface Engineering of Copper Catalyst through CO* Adsorbate, J. Phys. Chem. C, 2023, 127, 1789–1797.
51. N. Abidi, K. R. G. Lim, Z. W. Seh and S. N. Steinmann, Atomistic modeling of electrocatalysis: Are we there yet?, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1499.
52. R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, L. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Towards Identifying the Active Sites on RuO₂(110) in Catalyzing Oxygen Evolution, Energy Environ. Sci., 2017, 10, 2626–2637.
53. R. R. Rao, M. J. Kolb, L. Gordana, A. F. Pederson, Y. Katayama, J. Hwang, A. Mehta, H. You, J. R. Lunger, H. Zhou, N. B. Halck, T. Vegge, L. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Operando identification of site-dependent water oxidation activity on ruthenium dioxide single-crystal surfaces, Nat. Catal., 2020, 3, 516–525.
54. D.-Y. Kuo, J. K. Kawasaki, J. N. Nelson, J. Kloppenburg, G. Hautier, K. M. Shen, D. G. Schlom and J. Suntivich, Influence of Surface Adsorption on the Oxygen Evolution Reaction on IrO₂(110), J. Am. Chem. Soc., 2017, 139, 3473–3479.
55. V. Saveleva, L. Wang, D. Teschner, T. Jones, A. Gago, K. A. Friedrich, S. Zafeiratos, R. Schlögl and E. R. Savinova, Operando Evidence for a Universal Oxygen Evolution Mechanism on Thermal and Electrochemical Iridium Oxides, J. Phys. Chem. Lett., 2018, 9, 3154–3160.
56. S. Siahrostami, G.-L. Li, V. Viswanathan and J. K. Nørskov, One- or Two-Electron Water Oxidation, Hydroxyl Radical, or H₂O₂ Evolution, J. Phys. Chem. Lett., 2017, 8, 1157–1160.
57. S. Divanis, T. Kutlusoy, I. M. I. Boye, I. C. Man and J. Rossmeisl, Oxygen evolution reaction: a perspective on a decade of atomic scale simulations, Chem. Sci., 2020, 11, 2943–2950.
58. J. H. Montoya, L. C. Seitz, P. Chakthranont, A. Vojvodic, T. F. Jaramillo and J. K. Nørskov, Materials for solar fuels and chemicals, Nat. Mater., 2017, 16, 70–81.
59. X. Chen, L. Yu, S. Wang, D. Deng and X. Bao, Highly active and stable single iron site confined in graphene nanosheets for oxygen reduction reaction, Nano Energy, 2017, 32, 353–358.
60. C. Zhang, J. Sha, H. Fei, M. Liu, S. Yazdi, J. Zhang, Q. Zhong, X. Zou, N. Zhao, H. Yu, Z. Jiang, E. Ringe, B. I. Yakobson, J. Dong, D. Chen and J. M. Tour, Single-Atomic Ruthenium Catalytic Sites on Nitrogen-Doped Graphene for Oxygen Reduction Reaction in Acidic Medium, ACS Nano, 2017, 11, 6930–6941.
61. K. S. Exner and H. Over, Beyond the Rate-Determining Step in the Oxygen Evolution Reaction over a Single-Crystalline IrO₂(110) Model Electrode: Kinetic Scaling Relations, ACS Catal., 2019, 9, 6755–6765.
62. M.-A. Ha and R. E. Larsen, Multiple Reaction Pathways for the Oxygen Evolution Reaction May Contribute to IrO₂ (110)'s High Activity, J. Electrochem. Soc., 2021, 168, 024506.
63. J. Geppert, P. Röse, S. Czioska, D. Escalera-López, A. Boubnov, E. Saraçi, S. Cherevko, J.-D. Grunwaldt and U. Krewer, Microkinetic Analysis of the Oxygen Evolution Performance at Different Stages of Iridium Oxide Degradation, J. Amer. Chem. Soc., 2022, 144, 13205–13217.
64. J. Timmermann, F. Kraushofer, N. Resch, P. Li, Y. Wang, Z. Mao, M. Riva, Y. Lee, C. Staacke, M. Schmid, C. Scheurer, G. S. Parkinson, U. Diebold and K. Reuter, IrO₂ Surface Complexions Identified through Machine Learning and Surface Investigations, Phys. Rev. Lett., 2020, 125, 206101.
65. X. Mao, L. Wang and Y. Li, Machine-Learning-Assisted Discovery of High-Efficient Oxygen Evolution Electrocatalysts, J. Phys. Chem. Lett., 2023, 14, 170–177.
66. S. N. Steinmann, Q. Wang and Z. W. Seh, How machine learning can accelerate electrocatalysis discovery and optimization, Mater. Horiz., 2023, 10, 393–406.
67. M. C. Groenenboom, R. M. Anderson, D. J. Horton, Y. Basdogan, D. F. Roeper, S. A. Policastro and J. A. Keith, Doped amorphous Ti oxides to deoptimize oxygen reduction reaction catalysis, J. Phys. Chem. C, 2017, 121, 16825–16830.
68. V. Viswanathan and H. A. Hansen, Unifying solution and surface electrochemistry: limitations and opportunities in surface electrocatalysis, Top. Catal., 2014, 57, 215–221.
69. F. Calle-Vallejo, A. Krabbe and J. M. Garcia-Lastra, How Covalence Breaks Adsorption-Energy Scaling Relations and Solvation Restores Them, Chem. Sci., 2017, 8, 124–130.
70. K. S. Exner, Design Criteria for Oxygen Evolution Electrocatalysts from First Principles: Introduction of a Unifying Material-Screening Approach, ACS Appl. Energy Mater, 2019, 2, 7991–8001.
71. J. Perez-Ramirez and N. Lopez, Strategies to break linear scaling relationships, Nat. Catal., 2019, 2, 971–976.
72. O. Pique, F. Illas and F. Calle-Vallejo, Designing water splitting catalysts using rules of thumb: Advantages, dangers and alternatives, Phys. Chem. Chem. Phys., 2020, 22, 6797–6803.
73. K. S. Exner, Why the breaking of the OOH versus OH scaling relation might cause decreased electrocatalytic activity, Chem Catal, 2021, 1, 258–271.
74. S. Razzaq and K. S. Exner, Statistical analysis of breaking scaling relation in the oxygen evolution reaction, Electrochim. Acta, 2022, 412, 140125.
75. N. Karmodak, L. Bursi and O. Andreussi, Oxygen evolution and reduction on two-dimensional transition metal dichalcogenides, J. Phys. Chem. Lett., 2022, 13, 58–65.
76. A. S. Raman and A. Vojvodic, Providing atomistic insights into the dissolution of rutile oxides in electrocatalytic water splitting, J. Phys. Chem. C, 2022, 126, 922–932.
77. A. Zagalskaya and V. Alexandrov, Role of defects in the interplay between adsorbate evolving and lattice oxygen mechanisms of the oxygen evolution reaction in RuO₂ and IrO₂, ACS Catal., 2020, 10, 3650–3657.
78. M. Wohlgemuth, M. L. Weber, L. Heymann, C. Baeumer and F. Gunkel, Activity-Stability Relationships in Oxide Electrocatalysts for Water Electrolysis, Front. Chem., 2022, 10, 913429.
79. S. Razzaq and K. S. Exner, Materials Screening by the Descriptor G_max(η): The Free-Energy Span Model in Electrocatalysis, ACS Catal., 2023, 13, 1740–1758.
80. K. S. Exner, Steering Selectivity in the Four-Electron and Two-Electron Oxygen-Reduction Reactions: On the Importance of the Volcano Slope, ACS Phys. Chem. Au, 2023 DOI:10.1021/acsphyschemau.2c00054.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00047h

---