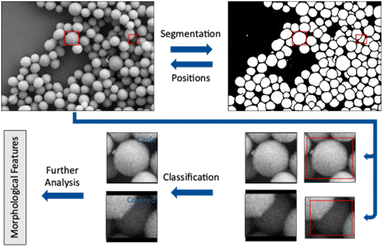
Open Access Article
Open Access ArticleDeep learning for automated size and shape analysis of nanoparticles in scanning electron microscopy
Jonas Bals and
Matthias Epple *
*
Inorganic Chemistry, Centre for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen, 45117 Essen, Germany. E-mail: matthias.epple@uni-due.de
First published on 19th January 2023
Abstract
The automated analysis of nanoparticles, imaged by scanning electron microscopy, was implemented by a deep-learning (artificial intelligence) procedure based on convolutional neural networks (CNNs). It is possible to extract quantitative information on particle size distributions and particle shapes from pseudo-three-dimensional secondary electron micrographs (SE) as well as from two-dimensional scanning transmission electron micrographs (STEM). After separation of particles from the background (segmentation), the particles were cut out from the image to be classified by their shape (e.g. sphere or cube). The segmentation ability of STEM images was considerably enhanced by introducing distance- and intensity-based pixel weight loss maps. This forced the neural network to put emphasis on areas which separate adjacent particles. Partially covered particles were recognized by training and excluded from the analysis. The separation of overlapping particles, quality control procedures to exclude agglomerates, and the computation of quantitative particle size distribution data (equivalent particle diameter, Feret diameter, circularity) were included into the routine.
Introduction
Many products contain micro- or nanoscale powder materials. Such materials must be analysed with high precision for any application with respect to particle size and particle shape distribution. A common method for the analysis of particles is scanning electron microscopy (SEM).1 SEM can be operated in different modes, i.e. secondary electron detection mode (SE) and scanning transmission electron mode (STEM). SE images have a high field of depth and are especially well suited to show surface details, including the surface topography in a pseudo-three-dimensional representation. STEM images have a higher spatial resolution and give a two-dimensional representation of particles. The images generated by these two modes are fundamentally different in terms of their pixel intensity distribution and overall appearance. Therefore, an automated image analysis needs different approaches to deal with SE and STEM images, respectively.Usually, SEM images are analysed by experienced human reviewers to count and measure the depicted particles, e.g. to determine the particle size distribution of a given sample.2 Another particle property which is generally of interest is the particle shape. If images show an assembly of particles with different shapes, their classification into different categories (e.g. sphere, cube, rod, or triangle) is usually done manually. This is a time-consuming process which may be biased by a human reviewer.3 To accomplish a fast and objective analysis, there is a strong need for non-biased, rapid methods to analyse SEM images.4
Machine learning has been applied to detect and identify objects of high variability in SEM images.5,6 In principle, this permits a more objective and usually much faster analysis than a human assessment.7–12 Semantic segmentation of images into coherent areas of the same class (e.g. foreground and background) is possible by convolutional autoencoders (CNNs) like the UNet architecture.13 UNet and its various developments were highly successful in biomedical image processing, and several attempts were made to apply it to nanoparticle analysis as well.14 Further efforts to classify particles according to their shape were carried out by dedicated classification networks.15,16
The workflow presented here includes two steps performed by convolutional neural networks (CNN) to accomplish a full analysis of SEM images of nanoparticles. The first step is to label each pixel as either foreground or background (segmentation). Coherent areas of foreground pixels (“particles”) are then cut out and processed by a second neural network to determine the shape of the individual particle (classification). In this step, partially covered particles are identified and removed from the classification. A subsequent analysis of particle size, diameter, and circularity of all particles shown in an image is finally performed.
Results and discussion
Training a neural network leads to a model which is adapted to a given dataset after training on a representative set of features from this dataset. This model, in our case a convolutional neural network, recognizes features within the dataset and learns to correlate these features with an associated class. The associated class is denoted as label. In the segmentation, these labels are given for each pixel and can be either foreground or background. In the shape classification, a case label describes the shape of a given particle (e.g. cube or sphere). In each training step an image shown to the network generates an output which is a probability distribution over all possible cases. A segmentation network will calculate the probability for each pixel to be either foreground or background. A classification network will calculate a probability for each particle to belong to a shape class of the training dataset. This probability distribution is then compared with the true output, i.e. the ground truth.5,14,17,18The loss function measures the difference between prediction and true label. A small difference between prediction and true label leads to a small loss and a better performance of the network. Each presentation of all images of a given training dataset to the network is called an epoch. The network parameters are changed several times during one epoch. The adaptation is performed after a mini-batch (a part) of images has been shown to the network. An optimizer algorithm uses the loss function to gradually adjust the parameters of the network. A high loss results in a strong adaptation of the network parameters. Training ends when the network is no longer improving its adaption to the training data, i.e. the loss function does not further decrease. This can require several hundred training epochs.19
Two different workflows were generated here, one for SE images and one for STEM images. This was necessary because the image types represented by SE and STEM images are strongly different. Both workflows shared the UNET++ architecture for segmentation.20
Training procedure for segmentation
SEM images usually show two-dimensional representations of particles having a three-dimensional shape. Of course, geometric information is lost by such a projection. This is often tacitly ignored, e.g. circular particles are assumed to be spherical, quadratic particles are assumed to be cubic, etc. In fact, a circular particle may also be disc-like because particles are usually settling on their largest face during sample preparation for SEM. This will lead to images where most discs are sitting on their circular face instead of their edge. This is a fundamental problem which can only be addressed by recording SEM data taken from different angles.The segmentation training dataset consisted of 30 SE and 12 STEM images, respectively. We also used 32 SE images published by Ruehle et al.21 Validation datasets contained 16 SE images and 3 STEM images, respectively. These images had typical sizes of 2000 × 1600 pixels. The particles in both image types were typically separated by 1 to 3 pixels, i.e. the particle density was high (as common in scanning electron microscopy).
Because the input of UNet++ was fixed to 512 × 512 pixels, we randomly cut out patches of the training images. For data augmentation, we artificially altered each image by random rotation, flipping, intensity variation, shearing, and zooming (up to 15% each) before cutting out image patches. The number of patches per image depended on the image size. Bigger images resulted in more patches. Approximately 450 patches were cut out of the 30 SE images. Approximately 180 patches were cut out of the 12 STEM images. The random extraction of patches from each image was performed in each epoch. An epoch was finished after each patch of each image was processed once by the CNN. Fig. 1 illustrates this step.
 | ||
| Fig. 1 Representative SEM image from the training dataset for segmentation containing ZnO nanorods (2048 × 1886 pixels; SE mode). Orange boxes show typical cut-out patches used for training. | ||
Segmentation of SEM images by UNet++
Since its introduction by Ronneberger et al. in 2015, UNET has demonstrated its usefulness for the segmentation of medical images.13 We applied the improvement of UNet, i.e. UNet++,20,22 to a wide range of different SEM images. The major difference between UNET and UNET++ is the link between encoder and decoder via nested dense convolutional layers which enhances semantic segmentation.23 The network weights were changed after each patch.Several problems emerge when training a neural network with SE and STEM images of nanoparticles.
First, in STEM images, the particles can touch or overlap and even form continuous aggregates (agglomerates) with no separating background between them. These aggregates cannot be separated into individual particles. For a precise size analysis, agglomerates must therefore be excluded.3 We achieved this by explicitly training the classification network to identify agglomerates.
Second, in SE images, the particles can also overlap but borders of particles are usually well distinguishable. The particles are separated by a thin line, sometimes as narrow as one pixel.
Third, particles in SE images can be present in different intensities ranging from dark (overshadowed particles) to bright (particles close to the electron detector; see Fig. 1). The neural network must adapt to these differences.
The problem extends to overlapping particles. Humans tend to impose an expected geometry to a partially covered particle, e.g. by assuming that a particle of which 80% are seen as sphere is implicitly considered as a sphere. However, if there is no information on the missing 20%, this assumption is based on subjective expectations and not on experimental data. Of course, no method can supplement pixels which are not visible because they are behind another particle in the front. In that case, the true particle shape (ground truth) is unknown.
The preparation of samples is therefore decisive to obtain good segmentation and classification results. A low particle density on the sample holder usually leads to well separated particles. Nevertheless, the assessment of a large number of particles (>1000) is necessary to ensure a reliable statistical representation of a given sample. Unfortunately, images showing many overlapping particles (often by solvent evaporation during sample preparation) are most common when particles are depicted by SEM (see Fig. 1).
Ronneberger et al. introduced weight loss maps to overcome the problem of a narrow separation of objects.13 Weight loss maps are matrices of the same size as the image that give each pixel an individual weight. In our case, the weight of each background pixel is given by its distance to the next particle edge (distance-based weight loss maps). These pixels are particularly important to separate adjacent particles. By giving these separating background pixels a higher weight, we forced the neural network to focus on the immediate background around each particle (Fig. 2). Weight loss maps were computed for ground truth annotation masks which were manually prepared before the network was trained. Due to the higher weights for separating background pixels between particles, the network predominantly learned to segment those areas. Thus, in the application of networks to any new image, no weights were needed because the network was already sensibilized (i.e. trained) to those areas. Notably, calculating weight maps requires considerable computing time.
 | ||
| Fig. 2 SE image depicting SiO2 microspheres (A1) with corresponding segmentation map (B1), and distance-based weight loss map calculated by eqn (1) (C1). STEM image of Au nanoparticles (A2) with segmentation map (B2) and intensity-based weight loss map (C2). Each background pixel (black) of the segmentation map was assigned with an individual weight loss depending on the distance to the edges of the two nearest particles. These weights varied between 1 and 11 for SE images and 1 and 13 for STEM images. The general weight of foreground pixels (white) was 1. | ||
In STEM images, background pixels between two touching particles can be very bright (see Fig. 2-A2). The model erroneously merges such particles because it cannot identify a separating border between them. To train the model to distinguish between bright background and particles we included the image intensity into the training process. The combination of distance-based weight loss maps and the pixel brightness led to a model which successfully separated touching particles. We denote this approach intensity-based weight loss maps in the following. Eqn (1) shows the modified version of Ronneberger et al.13 for the weight of each pixel w(x)
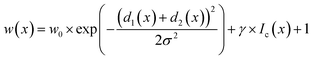 | (1) |
Segmentation results
Segmentation results of the validation dataset are shown in Table 1. As reference we used the default UNet architecture trained on the same data. Experiments for both types of weight loss maps were carried out for SE and STEM images. We used intensity-based weight loss maps for STEM images and distance-based weight loss maps for SE images, respectively. We validated each model with different metrics. Abbreviations used in eqn (2)–(7) refer to the following: TP – True Positive, FP – False Positive, TN – True Negative, FN – False Negative. These metrics can be used in segmentation and classification. In terms of segmentation each pixel is counted, while in terms of classification each image of a particle is counted.
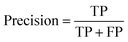 | (2) |
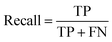 | (3) |
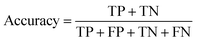 | (4) |
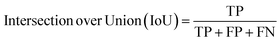 | (5) |
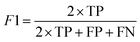 | (6) |
| Pixel error = 100 − accuracy | (7) |
| CNN | Type | Precision | Recall | Accuracy | IoU | F1 | Pixel error | Rand error |
|---|---|---|---|---|---|---|---|---|
| Unet | SE (distance-based weight loss maps) | 97 ± 1% | 97 ± 2% | 97 ± 2% | 94 ± 2% | 97 ± 1% | 3 ± 2% | 2 ± 1% |
| STEM (intensity-based weight loss maps) | 96 ± 4% | 93 ± 5% | 99.5 ± 0.5% | 90 ± 6% | 94 ± 3% | 0.5 ± 0.5% | 1.0 ± 0.9% | |
| Unet++ | SE (distance-based weight loss maps) | 97 ± 1% | 96 ± 5% | 97 ± 7% | 93 ± 2% | 96 ± 5% | 3 ± 3% | 2 ± 2% |
| SE (intensity-based weight loss maps) | 98 ± 2% | 93 ± 3% | 96 ± 2% | 91 ± 3% | 95 ± 1% | 4 ± 12% | 3 ± 16% | |
| SE (particles only) | 98 ± 2% | 95 ± 3% | 94 ± 2% | 93 ± 3% | 96 ± 1% | 13 ± 12% | 18 ± 16% | |
| STEM (distance-based weight loss maps) | 96 ± 4% | 91 ± 7% | 99 ± 1% | 88 ± 1% | 93 ± 7% | 1 ± 4% | 1.1 ± 0.6% | |
| STEM (intensity-based weight loss maps) | 96 ± 6% | 96 ± 4% | 99.7 ± 0.4% | 92 ± 7% | 96 ± 4% | 0.3 ± 0.4% | 1 ± 1% | |
| STEM (particles only) | 99 ± 1% | 96 ± 4% | 96 ± 3% | 94 ± 4% | 97 ± 2% | 13 ± 28% | 8 ± 12% |
In addition, we calculated the Rand error.24 The Rand error measures the degree in which two segmentations (the true label and the model prediction) disagree whether a given pixel belongs to the same object in both segmentations. Therefore, the Rand error measures how well particles are separated, with 0% indicating a good separation and 100% an unsuccessful separation.
The introduction of intensity-based weight loss maps significantly improved the segmentation performance of UNet++ for STEM images. However, SE images did not benefit from the application of intensity-based weight loss maps. SE images usually have a wide distribution of grayscales. In SE images, background and particles share the same range of pixel intensity, whereas in STEM images background and particles are strongly different (two distinct peaks of pixel intensities). The background between touching particles in STEM can reach the same intensity as the particles. This is not the case for SE images where particles often surrounded by a darker rim due to lower electron excitation. The models UNet and UNet++ performed almost equally on both types of images. UNet++ uses only 7.7 million parameters compared to 31 million parameters of UNet.25 Thus, it is much faster than UNet without compromising the segmentation ability. Overall, the segmentation procedure was very efficient. The introduction of intensity-based weight maps led to a significant improvement in the IoU by 4% for STEM images. This is due to the better separation of touching particles by segmentation of background pixels.
Shape classification
Segmentation of images is only the first step of analysis. Next, parameters that describe particle size and shape are of interest.The classification of single particles was performed by two different CNNs: Alexnet for STEM images and ResNet34 for SE images. We initialized both networks according to He et al.26 As optimizing algorithm, we used ADAM27 with the default settings of Tensorflow.28 As loss function, we used the cross-entropy loss function introduced by Fisher.29 Both networks were tested against their validation dataset.
After segmentation of raw particles from the background, the particle bounding boxes were slightly enlarged and cut out from the SEM image. For each particle, the cut-out area was larger than the close-fitting bounding box to provide surrounding information for the following classification network (Fig. 3). As classification networks, we used AlexNet for STEM images because of the limited data (<1000 images per class).19 Larger networks require a more variable dataset which was not available for STEM images. A variation in terms of particle orientation and colour distribution is not given in STEM images which are just 2D representations with a very limited distribution of either very dark (background) or very bright (particle) grayscales. For SE images, the larger ResNet34 was the preferred option due to its performance in the ILSVRC 2015.30 For the even deeper variants like ResNet50, we observed a lack of data variation. We were not able to train ResNet50 to the same extent as it was possible with ResNet34.
Shape classification of particles from STEM images by AlexNet
For the shape classification of single particles from STEM images, a modified AlexNet architecture was used. This network was developed by Zeiler and Fergus31 and modified by us by reducing the number of channels in the fully connected layers by a factor of two. In total, 3000 manually classified single images of gold and silver nanoparticles in the classes circle, rod, triangle, square, pentagon, hexagon, agglomerate, and covered were used for training (ground truth). The class “covered” consisted of manually identified particles that were partially covered by other particles in the foreground. The network was specifically trained to recognize these by suitable training images of partially covered particles. Similarly, the class “agglomerate” created and trained with suitable images. Images of single particles were resized to 224 × 224 pixels, while preserving the aspect ratio as depicted in Fig. 3. Data augmentation similar to the segmentation training was applied by random cropping, rotation, and flipping to increase the training dataset. Gaussian noise was also applied for data augmentation by adding a matrix of random values to the image. Class weighing was applied to take different numbers of images in the individual classes into account, using standard procedures.Shape classification of particles from SE images by ResNet34
The analysis of single particles from SE images was performed by ResNet34.16 Altogether, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 images of manually classified SiO2, ZnO, Ag, Au, and TiO2 nanoparticles in the classes sphere, sphere-like, cube, rod, and covered particles were used (80% for training, 20% for validation; ground truth). Two different classes for spherical objects were introduced. The class “sphere” comprised round, ball-shaped objects, whereas the class “sphere-like” comprised a range of deformed, elongated, and indented particles. Data augmentation and class weighing was performed as with AlexNet (see above).
000 images of manually classified SiO2, ZnO, Ag, Au, and TiO2 nanoparticles in the classes sphere, sphere-like, cube, rod, and covered particles were used (80% for training, 20% for validation; ground truth). Two different classes for spherical objects were introduced. The class “sphere” comprised round, ball-shaped objects, whereas the class “sphere-like” comprised a range of deformed, elongated, and indented particles. Data augmentation and class weighing was performed as with AlexNet (see above).
Results of shape classification
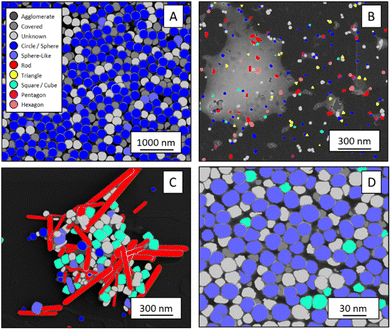
The shape classification results are shown in Table 2 and Fig. 4. We have labelled the categories corresponding to 3D shapes (SE) or their corresponding 2D projections (STEM) according to Munoz-Marmol et al.32 The mean accuracy (eqn (4)) of the validation dataset for particles imaged by SE and classified by ResNet34 was 93%, and for particles imaged by STEM and classified by AlexNet 95%.| Accuracy per class | Covered | Circle/sphere | Sphere-like | Rod | Triangle | Square/cube | Pentagon | Hexagon | Agglomerate | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| STEM (2D) | 97% | 96% | — | 95% | 97% | 94% | 91% | 95% | 91% | 95% |
| SE (3D) | 93% | 86% | 89% | 99% | — | 96% | — | — | — | 93% |
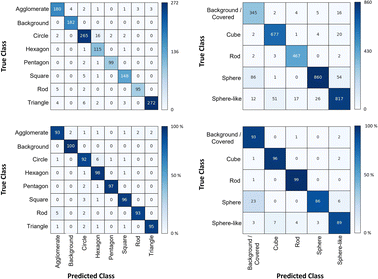 | ||
| Fig. 4 Confusion matrix for the shape classification of nanoparticles. Left: results for STEM images; right: results for SE images. | ||
The classification networks were then applied to images which were neither used in training nor in validation. Fig. 5 shows representative results. Because both training datasets contained partially covered particles, both networks were trained to identify and exclude partially covered particles. This procedure assured that particles within one class were similar. The shape classification by CNNs gave an overall high accuracy. The application of the validated networks led to an unexpected behaviour when classifying particles whose appearance differed from the trained morphologies. Images of particles with shapes unknown from the training like stars or octahedra showed similar probabilities for many classes, i.e. the probability distribution was almost evenly spread among a number of classes. In that case, the classification would have been made by the network based on small differences between the class probabilities (e.g. 34% vs. 30% vs. 28%), i.e. decided by a few percent of probability or less. Therefore, as an additional quality control we introduced a confidence limit of 75%. If the probability was below the confidence limit, the particle would be classified as “unknown”. As confidence limit we used the typical human certainty when classifying a given particle of about 75%.3 Note that the classes for particles identified as “covered” and “agglomerate” (STEM only) were defined as individual classes during training. This assignment was not perfect which is not surprising because there are many different shapes for partially covered or agglomerated particles. The incorporation of partially covered particles into the classification and the subsequent numerical particle analysis would have strongly compromised the resulting data. As typical case, a partially covered circle could appear as sickle-like object, leading to a classification as rod and wrong numerical input data.
In general, SEM images without any covered particles are difficult to acquire as most real images contain covered particles. Thus, some degree of covered particles must be tolerated by any practically applicable classification model. The average false classification rate was 5% for STEM images and 7% for SE images (see Table 2). Thus, covered particles classified by the segmentation model as foreground were classified by a 95% chance for STEM and 93% for SE as background particles/covered particles by the classification model. We consider this as an acceptable error. Furthermore, we did not find deviations in the particle diameter size distributions by including minimally covered particles.
Numerical data for particle sets
Particle dimensions can be expressed by several methods. Typically, minimum and maximum Feret diameters are used to define particle dimensions. The maximum (or minimum) Feret diameter is the maximum (or minimum) length of a straight line from one end of the particle to another regardless of the orientation. The classification of each particle into a specific shape class and the exclusion of covered particles made it possible to calculate particle edge lengths/radii directly from their segmented area. We used standard equations to correlate edge length and area for each geometric shape, e.g. by using the area of a spherical particle to compute its diameter and its perimeter. Rod lengths can be expressed by the maximum Feret diameter. Together with the area of a rod, the average rod thickness and the aspect ratio can be computed, assuming a rectangular particle shape. Edge lengths for non-spherical objects are useful, e.g., for nanoparticles with distinct aspect ratio. We found a good agreement between human evaluators and the segmentation/classification routine. Table 3 illustrates this for spheres shown in Fig. 5A.| Perimeter/nm | Area/nm2 | Convex hull area/nm2 | Circularity/— | Minimum Feret diameter/nm | Equivalent circle diameter/nm | Circle diameter by human evaluator/nm | |
|---|---|---|---|---|---|---|---|
| Average | 625 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 489 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625 |
0.97 | 204 | 213 | 230 |
| Std. dev. | 160 | 4955 | 4630 | 0.03 | 19 | 14 | 17 |
| Number of analysed particles | 1480 | 1480 | 1480 | 1480 | 1480 | 1360 | 100 |
The approach presented here compares well with other methods for image segmentation and classification.11 We have shown previously that a more classical approach of machine learning using random forest classifier is not capable of nanoparticle segmentation in STEM images.3 Furthermore, a classification of shapes by principle component analysis of morphological features is not sufficient to distinguish between particles.33 In general, deep neural networks are superior to shallow classification and regression algorithms like watershed segmentation34 or custom-made feature detectors35 for image segmentation or classification as summarized in ref. 36.
Experimental
Scanning electron microscopy
SEM micrographs were recorded with two scanning electron microscopes, i.e. an Apreo S LoVac (Thermo Fisher Scientific) instrument with a segmented STEM (transmission mode) detector, and a FEI Quanta 400F instrument with a secondary electron (SE) detector. Particle were drop-cast onto carbon-coated copper grids and dried in air. Electrically insulating materials were sputter-coated with AuPd (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) before SEM analysis.
20) before SEM analysis.
Computational hardware and software
Neural network training was performed with an NVIDIA GeForce GTX 1660 on a Lenovo IdeaCetre T540 – 15ICK G Workstation. Images used in final validation were not used in any training. Anaconda 4.10.3 with Python 3.9.7 and Tensorflow/Keras 2.8.0 were used to implement the neural networks. OpenCV Version 4.5.3 was used to calculate particle properties.Conclusions
The capability of an automated analysis to classify STEM and SE images of nanoparticles was demonstrated. The workflow used the CNN UNet++ for segmentation and the CNNs AlexNet and ResNet34 for shape classification. The segmentation of SEM images of nanoparticles into coherent foreground areas (particles) and background is possible with high efficiency, and even overlapping or touching particles were often separable. Weight-loss maps based on the distance of background pixels to the particle borders together with the image intensity considerably improved the segmentation of STEM images but did not improve the segmentation of SE images. The intensity variations occurring in an SEM image are usually unavoidable but may be improved by a good sample preparation, i.e. a low particle density with few overlapping particles. The performance of UNet++ was comparable to UNet. However, UNet++ was faster due to fewer parameters than in UNet, requiring less computing time. The subsequent classification of individual particles into different shapes gave reliable results. Each coherent foreground area of the segmentation map was assigned to one of the previously defined shape categories. The introduction of a class of partially covered particles into the training procedure considerably improved the classification results. In conclusion, CNNs can be used to obtain statistical information about particles of defined shapes. Tacitly, it is assumed that particles which are excluded from the classification have the same size and shape distribution as those particles included in the analysis. This, however, it is a reasonable assumption.Author contributions
Conceptualization: both authors; methodology: both authors; investigation: both authors; programming: J. B.; visualization: J. B.; validation: both authors; writing—original draft preparation: both authors; writing—review: both authors. both authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Mrs Qianmin Chen, Mr Rui Guo, Dr Jens Helmlinger, Mrs Aikaterini Karatzia, Dr Mateusz Olejnik, and Dr Kevin Pappert for the synthesis of samples and provision of their images and data. For SEM operation and sample preparation, we are grateful to Tobias Bochmann, Ursula Giebel and Dr Kateryna Loza.Notes and references
- H. Fissan, S. Ristig, H. Kaminski, C. Asbach and M. Epple, Anal. Methods, 2014, 6, 7324–7334 RSC
.
- M. M. Modena, B. Ruehle, T. P. Burg and S. Wuttke, Adv. Mater., 2019, 31, 1901556 CrossRef PubMed
.
- J. Bals, K. Loza, P. Epple, T. Kircher and M. Epple, Materialwiss. Werkstofftech., 2022, 53, 270–283 CrossRef CAS
.
- M. H. Modarres, R. Aversa, S. Cozzini, R. Ciancio, A. Leto and G. P. Brandino, Sci. Rep., 2017, 7, 13282 CrossRef PubMed
.
- E. A. Holm, R. Cohn, N. Gao, A. R. Kitahara, T. P. Matson, B. Lei and S. R. Yarasi, Metall. Mater. Trans. A, 2020, 51, 5985–5999 CrossRef CAS
.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83 CrossRef
.
- J. Timoshenko, C. J. Wrasman, M. Luneau, T. Shirman, M. Cargnello, S. R. Bare, J. Aizenberg, C. M. Friend and A. I. Frenkel, Nano Lett., 2018, 19, 520–529 CrossRef PubMed
.
- A. B. Oktay and A. Gurses, Micron, 2019, 120, 113–119 CrossRef CAS PubMed
.
- J. M. Ede and R. Beanland, Sci. Rep., 2020, 10, 8332 CrossRef CAS
.
- M. Ilett, J. Wills, P. Rees, S. Sharma, S. Micklethwaite, A. Brown, R. Brydson and N. Hondow, J. Microsc., 2020, 279, 177–184 CrossRef CAS PubMed
.
- H. Kim, J. Y. Han and T. Y. J. Han, Nanoscale, 2020, 12, 19461–19469 RSC
.
- B. Lee, S. Yoon, J. W. Lee, Y. Kim, J. Chang, J. Yun, J. C. Ro, J. S. Lee and J. H. Lee, ACS Nano, 2020, 14, 17125–17133 CrossRef CAS PubMed
.
- O. Ronneberger, P. Fischer and T. Brox, arXiv, preprint, arXiv:1505.04597, DOI:10.1007/978-3-319-24574-4_28.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal, S. J. L. Billinge, E. Holm, S. P. Ong and C. Wolverton, npj Comput. Mater., 2022, 8, 59 CrossRef
.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Presented in part at the Proceedings of the 25th International Conference on Neural Information Processing Systems – Volume 1, Lake Tahoe, Nevada, 2012 Search PubMed
.
- K. He, X. Zhang, S. Ren and J. Sun, Presented in part at the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 27–30 June 2016, 2016 Search PubMed
.
- R. Jacobs, Comput. Mater. Sci., 2022, 211, 111527 CrossRef CAS
.
- K. P. Treder, C. Huang, J. S. Kim and A. I. Kirkland, Microscopy, 2022, 71, i100–i115 CrossRef CAS PubMed
.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed
.
- Z. Zhou, M. M. Rahman Siddiquee, N. Tajbakhsh and J. Liang, in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Springer, 2018, pp. 3–11, DOI:10.1007/978-3-030-00889-5_1
.
- B. Ruehle, J. F. Krumrey and V. D. Hodoroaba, Sci. Rep., 2021, 11, 4942 CrossRef CAS PubMed
.
- Z. Zhou, M. M. R. Siddiquee, N. Tajbakhsh and J. Liang, IEEE Trans. Med. Imag., 2020, 39, 1856–1867 Search PubMed
.
- G. Huang, Z. Liu, L. van der Maaten and K. Q. Weinberger, Presented in part at the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 21–26 Search PubMed
.
- R. Unnikrishnan, C. Pantofaru and M. Hebert, IEEE Trans. Pattern Anal. Mach. Intell., 2007, 29, 929–944 Search PubMed
.
- K. M. Saaim, S. K. Afridi, M. Nisar and S. Islam, Ultramicroscopy, 2022, 233, 113437 CrossRef CAS PubMed
.
- K. He, X. Zhang, S. Ren and J. Sun, arXiv, 2015, preprint, arXiv:1512.03385, DOI:10.48550/arXiv.1512.03385.
- D. P. Kingma and J. Ba, arXiv, 2015, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu and X. Zheng, Presented in Part at the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2016 Search PubMed
.
- J. Aldrich, Stat. Sci., 1997, 12, 162–176 Search PubMed
.
- K. He, X. Zhang, S. Ren and J. Sun, arXiv, 2015, preprint, arXiv:1502.01852, DOI:10.48550/arXiv.1502.01852.
- M. D. Zeiler and R. Fergus, Presented in Part at the Computer Vision – ECCV 2014, Cham, 2014 Search PubMed
.
- M. Munoz-Marmol, J. Crespo, M. J. Fritts and V. Maojo, Nanomedicine, 2015, 11, 457–465 CrossRef CAS PubMed
.
- A. Hughes, Z. Liu, M. Raftari and M. E. Reeves, PeerJ, 2015, 2, e671v671 Search PubMed
.
- R. Baiyasi, M. J. Gallagher, L. A. McCarthy, E. K. Searles, Q. Zhang, S. Link and C. F. Landes, J. Phys. Chem. A, 2020, 124, 5262–5270 CrossRef CAS PubMed
.
- A. F. De Siqueira, F. C. Cabrera, A. Pagamisse and A. E. Job, Microsc. Res. Tech., 2014, 77, 71–78 CrossRef PubMed
.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |