Open Access Article
Open Access ArticleFirst-principles mode-specific reaction dynamics
Gábor
Czakó
 *,
Balázs
Gruber
,
Dóra
Papp
*,
Balázs
Gruber
,
Dóra
Papp
 ,
Viktor
Tajti
,
Viktor
Tajti
 ,
Domonkos A.
Tasi
,
Domonkos A.
Tasi
 and
Cangtao
Yin
and
Cangtao
Yin

MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: gczako@chem.u-szeged.hu
First published on 5th April 2024
Abstract
Controlling the outcome of chemical reactions by exciting specific vibrational and/or rotational modes of the reactants is one of the major goals of modern reaction dynamics studies. In the present Perspective, we focus on first-principles vibrational and rotational mode-specific dynamics computations on reactions of neutral and anionic systems beyond six atoms such as X + C2H6 [X = F, Cl, OH], HX + C2H5 [X = Br, I], OH− + CH3I, and F− + CH3CH2Cl. The dynamics simulations utilize high-level ab initio analytical potential energy surfaces and the quasi-classical trajectory method. Besides initial state specificity and the validity of the Polanyi rules, mode-specific vibrational-state assignment for polyatomic product species using normal-mode analysis and Gaussian binning is also discussed and compared with experiment.
I. Introduction
Energy efficiency is a fundamental question at many fields of basic and applied sciences. Physical chemists aim to understand this question at the deepest atomic and molecular level. One can invest energy into chemical reactions via translational, vibrational, and rotational excitations of the reactants and the reactive system can utilize the different forms of energy with different efficiency. The so-called Polanyi rules1 say that translational energy activates early-barrier, reactant-like transition-state-controlled reactions more efficiently than vibrational excitation, whereas the reverse is true in the case of late-barrier processes, which have product-like transition states. However, Polanyi uncovered these rules for simple reactions of atoms with diatomic molecules, where the reactants have only one vibrational degree of freedom.1 Polyatomic molecules have different vibrational modes corresponding to various stretching and bending motions, which may have specific effects on the reactivity. Vibrational mode specificity was first revealed in 1984 by quasi-classical trajectory (QCT) computations for the H + HOD reaction.2 The simulations showed that excitation of the OH stretching mode of the reactant significantly enhances the H2 + OD channel.2 This theoretical finding was later confirmed by the experiments of the Crim3,4 and Zare5 groups in the early 1990s, which was a nice demonstration of the predictive power of theoretical reaction dynamics studies. The first fully quantum simulation of a polyatomic chemical reaction was performed by Zhang and Light in 1997 underpinning the mode specificity of the H + HOD reaction.6The next important step in the mode-specific chemistry was the investigation of the reactions of H, F, and Cl atoms with methane (CH4, CHD3, etc.).7–20 From the theoretical part, Espinosa-García and co-workers8 pioneered with their semi-empirical potential energy surface (PES)-based QCT simulations and Bowman and co-workers with their reduced-dimensional quantum computations,9 as well as with QCT studies on fully ab initio permutationally-invariant PESs.12 From the experimental side we should mention again Crim11 and Zare7 and their co-workers. Furthermore, in 2003 the Liu group21 set a new state-of-the-art for crossed-beam velocity-map-imaging of chemical reactions by measuring correlated product vibrational distributions for the F + CD4 → DF + CD3 reaction. This experimental technique was later used for the Cl + CHD3 and F + CHD3 reactions revealing departures from the Polanyi rules14 and unexpected CH stretching effects hindering CH bond cleavage,16 respectively. Following a few earlier theoretical studies on atom + methane systems,8–10,12,13,15 the first author of the present article started to investigate the mode-specific dynamics of the F/Cl/O + CHD3 reactions as a postdoc in the Bowman group about 15 years ago.17–20 We developed analytical PESs by fitting high-level ab initio energy points, allowing efficient QCT simulations.20 Our PESs and simulations18,22 provided new insights into the Liu experiments14,16 and led to several collaborative theoretical-experimental studies with Liu and co-workers23–26 as well as QCT-quantum studies with the groups of Zhang,19 Guo,26,27 and Yang.26,27
By the 2010s vibrational mode specificity had been thoroughly studied, however, much less was known about the effect of the initial rotation on the reactivity, especially in the case of a polyatomic reactant. The rotational motion of a polyatomic molecule can be characterized by the quantum number J corresponding to the total rotational angular momentum and its projection(s) to various principal axes resulting in Ka and Kc quantum numbers for asymmetric and K for symmetric tops. Different K values correspond to different types of rotation, for example, K = 0 and K = J mean tumbling and spinning motion, respectively. Following our previous collaborative experimental-theoretical work on Cl + CHD3(JK), we call these rotational states as rotational modes.26 Thus, similarly to the above-discussed vibrational mode-specific studies, we can investigate the initial rotational mode specificity of polyatomic chemical reactions. Such studies were performed for H2O+ + H2/D2,28,29 H/F/Cl + H2O,30–32 H/Cl/O + CHD3,26,33–35 and the F− + CH3F/CH3Cl/CH3I36,37 considering systems up to six atoms.
Besides the investigation of the initial state dependence of the reactivity, one is also interested in following the energy transfer from reactants to products. Most of the theoretical and experimental studies can only determine the translational and internal energy, or in some cases the total vibrational and rotational energy, of the products, however, little is known about the mode-specific energy distributions in the case of a polyatomic product. Experimentally, Liu and co-workers could probe specific vibrational states of the methyl (CH3, CD3, CHD2, etc.) products of the atom + methane reactions.14,16,21 Theoretically, Corchado and Espinosa-García38 as well as Czakó and Bowman17 developed mode-specific product vibrational analysis methods using a projection of the final coordinates and velocities of quasi-classical trajectories onto the normal coordinate space. However, classically the molecular vibrations are not quantized and rounding the classical actions to integer numbers may result in unphysical vibrational states. Bonnet and Rayez39,40 proposed the so-called Gaussian binning (GB) method, which assigns a weight for each reactive trajectory, thereby incorporating some quantum effect into the QCT product analysis. The computational cost of GB, however, scales exponentially with the number of the vibrational modes, thus the original GB algorithm was found impractical for polyatomic products. To solve this problem, in 2009 Czakó and Bowman17 proposed the one-dimensional GB (1GB) method,17,41 which is efficient even for large product molecules. 1GB was first employed for the F + CHD3 (v1 = 0, 1) → HF/DF + CD3/CHD2 reactions17 and later many applications by different groups showed its usefulness.42–56
The early mode-specific studies focused on neutral systems and theoretically usually six or less atoms could be treated. Following some early work of Hennig and Schmatz57–59 on the X− + CH3Y systems, where X and Y are halogens, our group started to investigate the mode-specific dynamics of bimolecular nucleophilic substitution (SN2) reactions.60 In 2016 Szabó and Czakó in collaboration with the Guo and Yang groups reported vibrational mode-specific wave packet dynamics computations for the F− + CH3Cl SN2 reaction using a 6-dimensional model and a high-level ab initio PES.60 In 2018 an experimental-theoretical collaboration between the Wester, Guo, and Czakó groups found that CH stretching excitation is a spectator in the F− + CH3I SN2 reaction, whereas enhances the proton-transfer channel.61 Our analytical PESs were also utilized in mode-specific quantum dynamics computations for SN2 reactions by Wang and co-workers.62,63
Moving beyond six-atom systems applying first-principles theory is challenging because of the high-dimensionality of the PES.64 Nevertheless, several post-six-atom reactions were studied recently by analytical PES-based or direct dynamics approaches, and for some of them even mode-specific computations were also performed.65–102 Espinosa-García and co-workers77,78 and/or our group90,91,93 investigated the mode-specificity in the reactions of ethane (C2H6) with H, F, Cl, and OH, while Lu and Li82 studied the F + CH3OH reaction. We also reported mode-specific computations for HBr/HI + C2H5,96–98 CH2OO + NH399 and post-six-atomic ion–molecule reactions, such as OH− + CH3I102 and F− + CH3CH2Cl.54
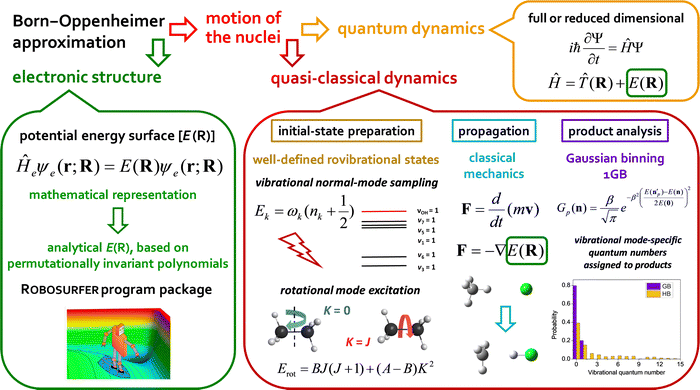
In the present Perspective article, we focus on our most recent first-principles mode-specific dynamics studies of the F/Cl/OH + C2H6,90,91,93 HBr/HI + C2H5,96–98 OH− + CH3I,102 and F− + CH3CH2Cl54 reactions, covering both neutral and ionic systems with 7–10 atoms. Our theoretical approach is based on (1) automated ab initio analytical PES development utilizing our Robosurfer program system103 interfaced with the Molpro electronic structure package104,105 and the permutationally-invariant polynomial fitting codes,106,107 as well as (2) QCT simulations using the new PESs. A graphical overview of the first-principles mode-specific reaction dynamics approach is presented in Fig. 1. In the next sections we describe how initial vibrational and rotational excitations affect the reactivity and the product energy release, while we also show how to perform mode-specific product analysis and demonstrate the utility of the 1GB approach. The review of these recent applications may set new directions for future mode-specific investigations for complex chemical systems.
II. Vibrational mode specificity
For 4–6-atomic reactions initial-vibrational-state-specific reactivity can be studied using full- or reduced-dimensional quantum dynamics methods (see Fig. 1) as many examples on X + H2O/NH3/CH4, [X = H, F, Cl] etc. show in the literature.6,9,10,19,33,108,109 For larger systems the QCT approach provides an efficient tool to study mode-specific reactivity (see also Fig. 1), where the N-atomic non-linear (linear) reactants can be prepared in any vibrational state characterized by quantum numbers (n1, n2,…, n3N–6(5)) by selecting normal coordinates (Qk) and momenta (Pk) as110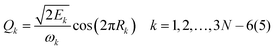 | (1) |
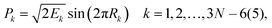 | (2) |
Fig. 2 shows the potential energy profiles of the valence-isoelectronic X + C2H6 → HX + C2H5 [X = F, Cl, OH] reactions.83,84,92 In the case of X = F, the reaction is highly exothermic with a slightly submerged very reactant-like transition state (TS). For X = OH the exothermicity is about half of that of the X = F reaction, and a classical (adiabatic) barrier with 4.0 (2.1) kcal mol−1 height and a reactant-like TS structure emerge. The vibrationally-adiabatic reaction pathway of Cl + C2H6 is exothermic (−3.1 kcal mol−1) and has a submerged slightly-late barrier (−2.1 kcal mol−1), whereas classically the reaction becomes slightly endothermic (2.0 kcal mol−1) with a positive barrier height (2.2 kcal mol−1). We investigated the mode-specific reactivity of these X + C2H6 reactions90,91,93 considering singly-excited initial vibrational modes as indicated in Fig. 2.
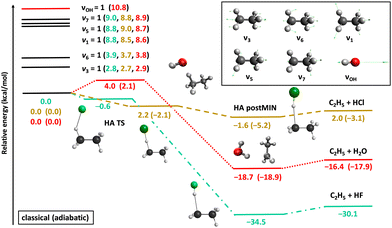 | ||
| Fig. 2 Schematic potential energy surfaces of the X + C2H6 [X = F, Cl, OH] hydrogen-abstraction reactions showing the stationary-point structures and their classical (adiabatic) relative energies corresponding to the analytical PESs,83,84,92 as well as selected normal modes and singly-excited vibrational levels of the reactants.90,91,93 | ||
One of the main concerns in mode-specific reaction dynamics is the intramolecular vibrational-energy redistribution (IVR) prior to collision, which may undermine the mode-specific effects. We examined IVR in ethane by computing the time evolution of its mode-specific energies90 using the normal mode analysis technique48 developed for product analysis (see details in Section IV). Fig. 3 shows the mode energies of the ground-state (v = 0), CH3-deformation-excited (v6 = 1), and symmetric-CH-stretching-excited (v1 = 1) C2H6 as a function of time prior to collision. For v = 0 quantum mechanically no IVR can occur, however, classically the energy may flow from the high-frequency modes to the low-frequency ones. As Fig. 3 shows this classical “IVR” occurs within a few hundred femtoseconds, nevertheless, some mode-specific character of the energy distribution remains until the reactants collide, which usually happens in the 150–650 fs time range in our simulations. If the reactant is excited, IVR can occur even quantum mechanically/experimentally. The v6 = 1 state is a good example, where IVR is not significant, whereas the v1 = 1 state loses its CH stretching-excited character as the reactants approach each other. Here QCT may overestimate the speed of IVR, because the effect may come from both the artifacts of classical mechanics and the real IVR, which is a fundamental process in vibrationally excited molecules. Nevertheless, the reactant retains some CH stretching-excited character in the entrance channel, suggesting mode specificity in the X + C2H6 reactions.
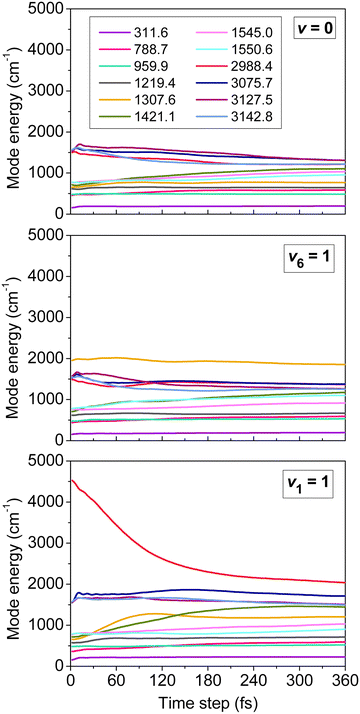 | ||
| Fig. 3 Mode-specific vibrational energies of a non-interacting C2H6 molecule as a function of time corresponding to the ground (v = 0), CH3 deformation-excited (v6 = 1), and symmetric CH stretching-excited (v1 = 1) states.90 The modes are labeled by their harmonic frequencies (in cm−1). | ||
Initial-vibrational-state-specific cross sections of the X + C2H6 [F, Cl, OH] reactions as a function of collision and total energy are shown in Fig. 4. The cross sections increase with collision energy and the shape of the excitation functions (cross sections vs. collision energy) is similar for X = F and OH. The higher reactivity of F + C2H6 is expected because of its lower (negative) barrier and higher exothermicty as well as the spherical character of one of the reactants (F), while the reaction of OH requires a special orientation. For both X = F and OH the excitations of the CH stretching modes enhance the reactivity the most efficiently, as expected as a CH bond breaks during the hydrogen-abstraction processes. The other modes either do not have significant effect on the reactivity or slightly inhibit the reaction, like CC stretching (v3). Considering the total energy (collision energy and vibrational energy) dependence of the reactivity, in the case of the F + C2H6 reaction one can clearly see that at a given total energy the ground-state reaction has the highest reactivity, which means that it is advantageous to invest the energy into translational motion, in accord with the Polanyi rules in the case of an early-barrier reaction. However, for the also early-barrier OH + C2H6 reaction the picture is less obvious: except v3 and vOH excitations, many modes promote the reaction similarly or more efficiently than translational energy, in contradiction with the Polanyi rules. This finding is not completely surprising, because, as we mentioned earlier, the Polanyi rules were formulated for atom + diatom reactions and there is no guarantee that these rules always remain valid for polyatomic processes. In fact, violations of the Polanyi rules have been found for several systems such as, for example, F + H2O,111 OH + H2S,112 and Cl + CHD3.14,18 The cross sections of the Cl + C2H6 reaction decrease with increasing collision energy, because the adiabatic reaction pathway is clearly submerged. Similarly to the X = F and OH cases, CH stretching excitations promote the reactivity the most efficiently, whereas the v6 mode has only a minor enhancement and v3 excitation has negligible effect or causes a slight inhibition at the lowest collision energies. Since translational energy does not activate the reaction, at a given total energy the vibrationally-excited reactions have higher reactivity, in accord with the Polanyi rules in the case of a late-barrier reaction.
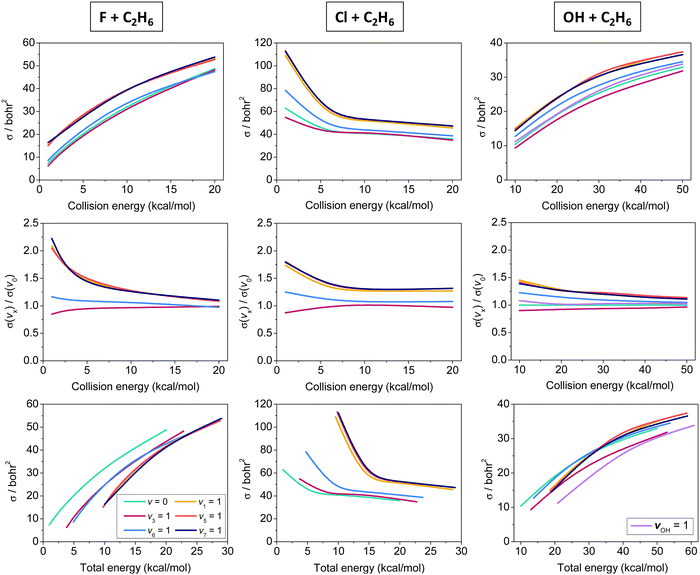 | ||
| Fig. 4 Vibrational mode-specific cross sections and their ratios as a function of collision energy and cross sections as a function of total energy for the X + C2H6 [X = F, Cl, OH] hydrogen-abstraction reactions.90,91,93 | ||
In 2013 Jiang and Guo113 proposed a sudden vector projection (SVP) method as a generalization of the Polanyi rules. The SVP approach calculates the overlap between the normal modes of the reactant with the imaginary mode of the TS. SVP has been proven useful in many applications,90,114,115 though it has limitations: it (1) works well only for direct processes, (2) cannot account for IVR, (3) cannot describe inhibition, and (4) does not consider collision energy dependence. We applied SVP for the Cl + C2H6 reaction and found good overall agreement with the QCT results, for example, the largest SVP values were obtained for the CH stretching modes.90
In Fig. 5 we show initial-state-dependent product internal and relative translational energy distributions for the X + C2H6 → HX + C2H5 [X = F, Cl, OH] reactions. For all three reactions the translational energy distributions show virtually no initial vibrational state dependence, suggesting that the reactants’ vibrational excitation energy transfers into the internal degrees of freedom of the products. For X = F and Cl, the internal energy distributions of the C2H5 products blue-shift approximately with the amount of the initial vibrational excitation energy, showing that the major part of the excess vibrational energy remains in the polyatomic product. For X = OH mode-specific effects are also seen in the product internal energy distributions. CH stretching excitation energy mainly remains in the C2H5 product, whereas OH stretching becomes a spectator mode, exciting the H2O product as the extents of the blue-shifts show in Fig. 5. It is also evident that the H2O products are formed vibrationally excitedly, in accord with the early-barrier nature of the OH + C2H6 reaction.
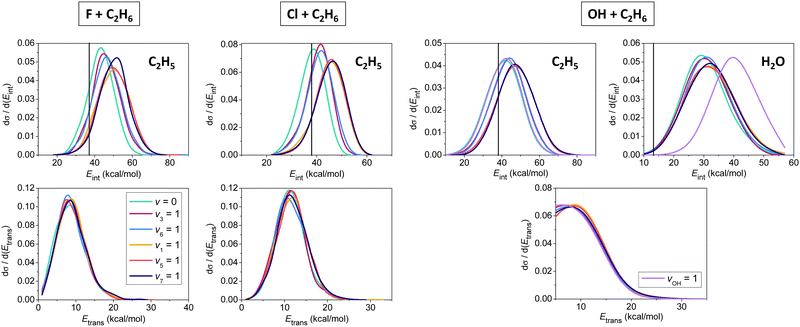 | ||
| Fig. 5 Normalized vibrational mode-specific product internal (upper panels) and relative translational (lower panels) energy distributions for the X + C2H6 [X = F, Cl, OH] hydrogen-abstraction reactions at a collision energy of 10 kcal mol−1.90,91,93 Vertical lines show the zero-point energies of the products. | ||
We also investigated the mode specificity in the HX + C2H5 [X = Br, I] reactions,96–98 whose schematic potentials are shown in Fig. 6. In both cases the main reaction pathway is hydrogen abstraction, which goes through submerged pre-reaction complexes and TSs leading to the X + C2H6 products. For both X = Br and I hydrogen abstraction is exothermic, and the exothermicity is about twice as larger in the case of X = I due to the lower dissociation energy of HI relative to HBr. Besides hydrogen abstraction, halogen abstraction can also occur via endothermic pathways resulting in H + C2H5X products, as also shown in Fig. 6. Here the energetics for X = Br and I are similar, because the HBr vs. HI and C–Br vs. C–I bond-energy differences are close to each other.
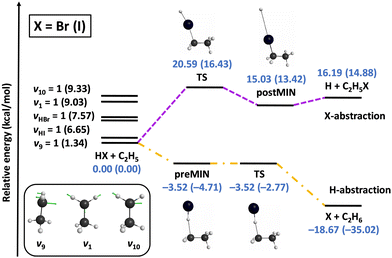 | ||
| Fig. 6 Schematic potential energy surfaces of the HX + C2H5 [X = Br, I] reactions showing the stationary-point structures and their classical relative energies corresponding to the analytical PESs, as well as selected normal modes and singly-excited vibrational levels of the reactants.98 | ||
The mode-specific cross sections of the HX + C2H5 [X = Br, I] H- and X-abstraction reactions as a function of collision energy are shown in Fig. 7. At low collision energies H abstraction dominates, but around 30–40 kcal mol−1 the X-abstraction channel opens, and at higher collision energies the two channels become competitive. HX vibrational excitation enhances both abstraction channels, but the promotion effect is much more substantial for X abstraction. As a HX bond breaks in both abstraction processes, we may not expect significant impact on reactivity upon C2H5 excitations. This is true for the X-abstraction channel, but for H abstraction clear inhibition effects are found, especially in the case of the excitation of the CH2 wagging (v9) mode inducing steric hindrance.
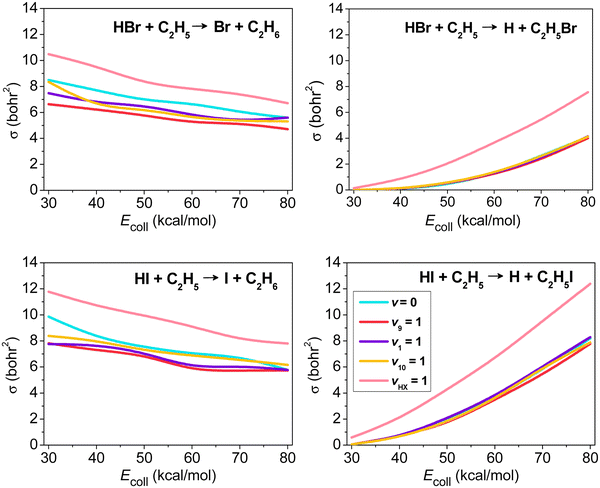 | ||
| Fig. 7 Vibrational mode-specific cross sections as a function of collision energy for the hydrogen- and halogen-abstraction channels of the HX + C2H5 [X = Br, I] reactions.98 | ||
Besides the neutral systems, we have also performed mode-specific investigations for ion–molecule reactions.54,60,61,102 Here we highlight our most recent results on the OH− + CH3I system.102 Its main reaction channel is the SN2, which is highly exothermic and may proceed via the submerged back-side attack Walden-inversion, the also slightly submerged double-inversion or the high-barrier front-side attack pathway, as shown in Fig. 8. In addition to the SN2 channel, there is a less exothermic proton-abstraction channel, which leads to the H2O + CH2I− products via an also submerged reaction path. It is interesting to see how the excitation of selected vibrational modes, CI stretching (v3), umbrella (v2), symmetric CH stretching (v1), and OH stretching (see Fig. 8), affects the reactivity of this barrier-less reaction.
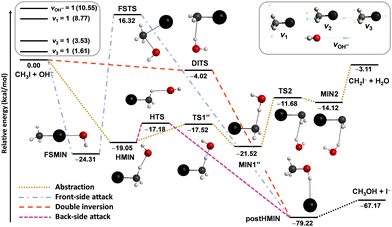 | ||
| Fig. 8 Simplified schematic potential energy surface of the OH− + CH3I reaction showing the stationary-point structures and their classical relative energies corresponding to the analytical PES87 along the different reaction pathways, as well as selected normal modes and singly-excited vibrational levels of the reactants.102 | ||
The mode-specific cross sections for the SN2 and proton-abstraction channels of the OH− + CH3I reaction are shown in Fig. 9. As expected in the case of barrier-less exothermic reactions, the reactivity decreases with increasing collision energy for both channels. However, it is somewhat surprising that the thermodynamically favored SN2 channel has significantly lower reactivity than proton abstraction. This may be explained by the dominance of H-bonded complex and TS formation in the entrance channel (see Fig. 8), which favors proton abstraction over the deep product well of the substitution pathway. The SN2 channel is clearly enhanced by the excitation of the CI stretching and umbrella modes, as expected, because the CI bond breaks and the CH3 group inverts via an umbrella motion during Walden inversion, which is the dominant SN2 pathway. The CH and OH stretchings have less effect on the SN2 reactivity, they mostly behave as spectators in the substitution process. In the case of proton abstraction, the CH stretching excitation promotes the reaction the most efficiently, as expected, since a CH bond breaks in the abstraction process. The umbrella motion also helps the proton transfer, whereas the CI and OH stretching excitations have negligible effects on the abstraction reactivity. The total energy dependence of the mode-specific reactivity is tricky, because extra collision energy significantly decreases the reactivity, therefore, at a given total energy it is the most advantageous if a major part of the energy is in vibration and a minor part is in translation. Thus, the highest-energy vibrational modes (CH and OH stretchings) show the most substantial enhancement effects, however, in some cases, due to an indirect reason, i.e., less energy remains for translation, which results in higher reactivity. The CH stretching effects were also studied experimentally by Wester and co-workers116,117 for the iso-electronic F− + CH3I reaction, and their main observations are in agreement with the present theoretical results for the OH− + CH3I system. For the OH− + CH3I reaction reduced-dimensional quantum dynamics computations were also carried out by Rao and Wang63 using our PES.87 The promotion effect of the CI stretching excitation was found in the quantum study as well, however, in the reduced-dimensional model the umbrella excitation unexpectedly hindered the SN2 reactivity. This inhibition effect may be an artifact of the model of Rao and Wang as the Palma-Clary-type 6-dimensional quantum computations found promotion effects upon umbrella excitation in the case of the F− + CH3Cl reaction.60 These findings may motivate future experiments for umbrella-excited SN2 reactions.
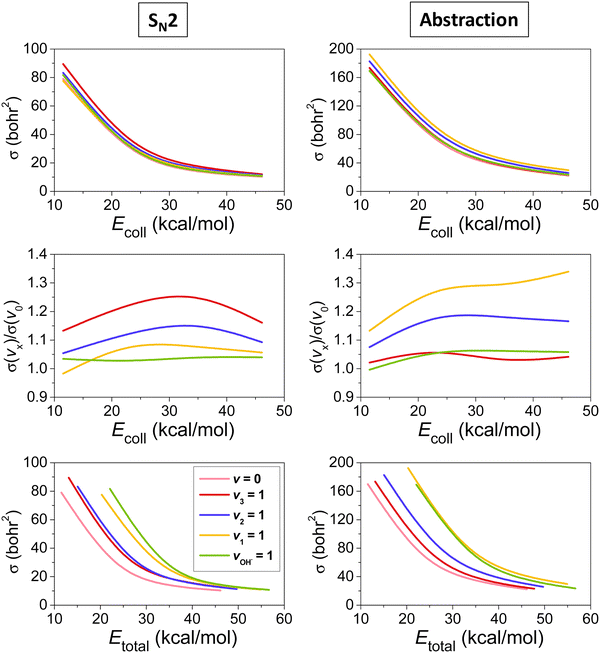 | ||
| Fig. 9 Vibrational mode-specific cross sections and their ratios as a function of collision energy and cross sections as a function of total energy for the SN2 and proton-abstraction channels of the OH− + CH3I reaction.102 | ||
III. Rotational mode specificity
In QCT simulations one can also prepare the reactants in a specific rotational state (see Fig. 1). In the case of a symmetric top molecule the initial rotational angular momentum vector, jPAS = (jPASx, jPASy, jPASz), corresponding to quantum numbers J and K can be obtained via the following expressions in the principal axis system (PAS):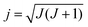 | (3) |
| jPASz = K | (4) |
jPASx = (j2 − K2)1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2πR 2πR | (5) |
jPASy = (j2 − K2)1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2πR 2πR | (6) |
We studied the rotational-mode-specific reactivity of several symmetric top molecules such as CHD3,26,35 CH3X [X = F, Cl, I],36,37 and C2H6.118 Here we focus on our most recent results on the Cl + C2H6(v = 0, JK) reaction.118 In Fig. 10 we show the JK-specific cross sections as a function of collision energy for the Cl + C2H6 reaction considering two limiting cases, which correspond to tumbling (K = 0) and spinning (K = J) rotation. As seen, rotational excitation usually enhances the reactivity and the effects of the spinning excitations are clearly more significant than the corresponding tumbling enhancements. This finding can be explained by the facts that the K = 0 states have much smaller energies than the corresponding K = J states (see Fig. 10), and the centrifugal force caused by the spinning excitation elongates the CH bonds thereby promoting their cleavage. We found similar spinning rotational effect in the proton-abstraction channel of the F− + CH3I reaction.37
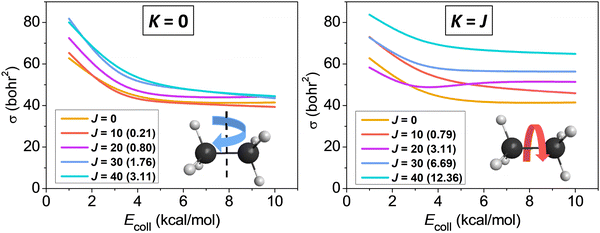 | ||
| Fig. 10 Rotational-state-specific cross sections as a function of collision energy for the Cl + C2H6(v = 0, JK) reaction.118 The rotational energies are given in parentheses in kcal mol−1. | ||
IV. Mode-specific product vibrational distributions
Following the early work of Corchado and Espinosa-García,38 we developed a normal mode analysis method to compute mode-specific product vibrational distributions from QCT simulations (see Fig. 1).17,48 The key steps of the normal mode analysis approach are summarized below:(1) We perform a normal mode analysis at the equilibrium structure of the product in the center of mass frame.
(2) We find the best overlap between the actual geometry of the product and its equilibrium structure by an exact Eckart transformation.48,119
(3) We project the Cartesian coordinates and velocities of the product to the normal mode space.
(4) We compute the energy for each normal mode using the quadratic harmonic expression for the potential.
(5) The mode-specific non-integer vibrational quantum numbers are determined from the mode energies using the quantum mechanical energy formula of a harmonic oscillator. Then the integer quantum numbers are obtained by rounding the real values to the nearest integer.
The above analysis may provide unphysical vibrational states due to the rounding issue (rounding up may result in energetically not available states) and the breakdown of the normal mode analysis at highly distorted structures. To handle these issues, we proposed the 1GB method,17,48 which assigns a weight for each product (p) as
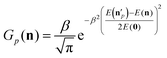 | (7) |
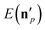 is the actual vibrational energy of the pth product, which should be computed using the velocities in the Cartesian space and the PES used in the QCT simulation. With these definitions 1GB solves both the rounding and normal mode analysis breakdown issues mentioned above. 1GB has been employed by several research groups for various systems with great success,42–56 below we highlight our most recent results.
is the actual vibrational energy of the pth product, which should be computed using the velocities in the Cartesian space and the PES used in the QCT simulation. With these definitions 1GB solves both the rounding and normal mode analysis breakdown issues mentioned above. 1GB has been employed by several research groups for various systems with great success,42–56 below we highlight our most recent results.
We computed the mode-specific vibrational distributions for the H2O product of the OH + C2H6(v = 0) reaction93 and we show the populations of the bending mode in Fig. 11. The computed mode-specific distributions allow comparison with the infrared chemiluminescence data measured by Butkovskaya and Setser.120 As Fig. 11 shows, the agreement between theory93 and experiment120 is excellent. Both the computed and measured data show that H2O is mainly formed in the ground bending state (∼70%), the one-quantum excitation has about 20–25% probability, and the populations of the overtones are small and decrease with increasing vibrational quanta. Here we did not use 1GB, because H2O does not have low-frequency torsional modes, which would compromise the normal mode analysis, and there are several open vibrational states, which makes the rounding issue less problematic. Note, that when we studied the dissociation dynamics of the water dimer, the use of 1GB was essential, because the H2O fragments could be formed in only two vibrational states.42 In the case of OH + C2H6 Rangel et al.86 also computed the mode-specific distributions for the H2O product using their PES-2020 and found similar populations as described above. They applied 1GB as well, and obtained qualitatively the same results as with standard binning.
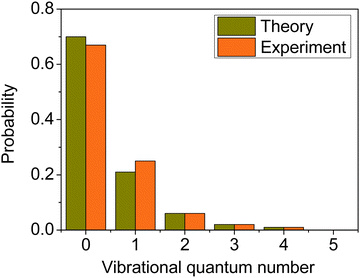 | ||
| Fig. 11 Comparison of the computed93 (collision energy of 10 kcal mol−1) and measured120 bending mode specific vibrational distributions for the H2O product of the OH + C2H6(v = 0) hydrogen-abstraction reaction. | ||
Mode-specific vibrational distributions for selected modes of the CH3CH2F product of the F− + CH3CH2Cl(v = 0) SN2 reaction54 are shown in Fig. 12. In the case of symmetric CH3 stretching the standard histogram binning shows the dominance of the ground stretching state as expected, however, gives small populations up to and beyond 15 quanta, which is clearly unphysical. The reason behind this issue is the breakdown of the normal mode analysis due to the large amplitude torsional motion of the CH3 group. The 1GB method solves this problem and provides non-zero populations for the ground (80%) and first-excited (20%) stretching states only, i.e., the unphysical small populations completely vanish. In the case of the CF-stretching and CH2-wagging modes 1GB also shows that the ground state is the most populated (∼60%), but excitations with one quantum (∼20%) and two quanta (∼20%) are also significant and small populations up to 5–6 quanta are found as well. This finding is in agreement with our chemical intuition as these two modes play an active role in the Walden inversion process.
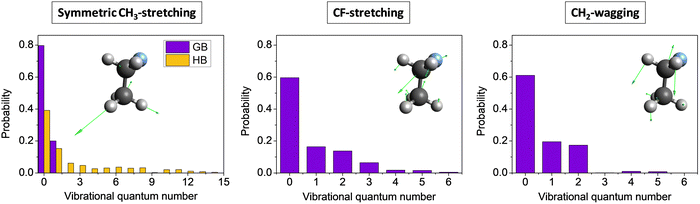 | ||
| Fig. 12 Symmetric CH3-stretching, CF-stretching, and CH2-wagging mode-specific vibrational distributions for the CH3CH2F product of the F− + CH3CH2Cl(v = 0) SN2 reaction obtained by histogram binning (HB, left panel) and Gaussian binning (GB, all panels) at a collision energy of 26.5 kcal mol−1.54 | ||
V. Summary and conclusions
We have reviewed the field of mode-specific reaction dynamics from our perspective, focusing on recent results for several neutral and ionic reactive systems beyond six atoms. The main general conclusions can be summarized as follows:(1) IVR prior to collision can be monitored using the mode-specific product analysis method. Even if some IVR occurs, mode-specific dynamics can be obtained. Here we should mention that the timescale of an experiment may be longer than that of a QCT simulation. Furthermore, it is unclear which portion of IVR found in QCT simulations comes from a real effect and from the classical nature of the trajectories.
(2) Mode-specific effects can be obtained for barrier-less reactions, where the submerged TS can serve as a bottleneck for reactivity.
(3) The violation of the Polanyi rules is not unexpected in polyatomic processes.
(4) Rotational mode-specificity is a highly unexplored area of this field. Our computations show that specific types of rotations have different effects on the reactivity.
(5) In the case of multi-channel reactions different initial vibrational excitations may promote different channels, allowing the control of chemical processes.
(6) Excess vibrational energy usually shows up in product vibration, whereas the product translational energy is not affected.
(7) QCT simulations allow to compute mode-specific product vibrational distributions. To include some quantum spirit, the 1GB method was proposed, which is essential if only few quantum states are available and/or the normal mode analysis fails due to high distortions of the product.
On one hand, the present perspective article shows that a lot of valuable knowledge accumulated in the field of mode-specific reaction dynamics thanks to the interplay of theory and experiment. On the other hand, there is a lot more to do, for example, it would be beneficial to have more experimental and/or quantum dynamics results for mode-specific product distributions, which could be compared with the QCT results. Hopefully the present subjective review will motivate us to move this field forward.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the National Research, Development and Innovation Office-NKFIH, K-146759, project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme, the Momentum (Lendület) Program of the Hungarian Academy of Sciences, and the National Young Talent Scholarship (grant no. NTP-NFTÖ-22-B-0050 for D. A. T.) for financial support. We acknowledge KIFÜ for awarding us access to computational resource based in Hungary at Debrecen.References
- J. C. Polanyi, Science, 1987, 236, 680 CrossRef CAS PubMed.
- G. C. Schatz, M. C. Colton and J. L. Grant, J. Phys. Chem., 1984, 88, 2971 CrossRef CAS.
- A. Sinha, M. C. Hsiao and F. F. Crim, J. Chem. Phys., 1990, 92, 6333 CrossRef CAS.
- R. B. Metz, J. D. Thoemke, J. M. Pfeiffer and F. F. Crim, J. Chem. Phys., 1993, 99, 1744 CrossRef CAS.
- M. J. Bronikowski, W. R. Simpson, B. Girard and R. N. Zare, J. Chem. Phys., 1991, 95, 8647 CrossRef CAS.
- D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691 RSC.
- W. R. Simpson, T. P. Rakitzis, S. A. Kandel, T. Lev-On and R. N. Zare, J. Phys. Chem., 1996, 100, 7938 CrossRef CAS.
- J. C. Corchado, D. G. Truhlar and J. Espinosa-García, J. Chem. Phys., 2000, 112, 9375 CrossRef CAS.
- D. Y. Wang and J. M. Bowman, J. Chem. Phys., 2001, 115, 2055 CrossRef CAS.
- M. Yang, D. H. Zhang and S.-Y. Lee, J. Chem. Phys., 2002, 117, 9539 CrossRef CAS.
- S. Yoon, S. Henton, A. N. Zivkovic and F. F. Crim, J. Chem. Phys., 2002, 116, 10744 CrossRef CAS.
- Z. Xie, J. M. Bowman and X. Zhang, J. Chem. Phys., 2006, 125, 133120 CrossRef PubMed.
- J. Sansón, J. C. Corchado, C. Rangel and J. Espinosa-García, J. Phys. Chem. A, 2006, 110, 9568 CrossRef PubMed.
- S. Yan, Y.-T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723 CrossRef CAS PubMed.
- J. Espinosa-García, J. Chem. Phys., 2009, 130, 054305 CrossRef PubMed.
- W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Chem. Phys., 2009, 131, 244302 CrossRef PubMed.
- G. Czakó and J. M. Bowman, Science, 2011, 334, 343 CrossRef PubMed.
- Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839 CrossRef PubMed.
- J. J. Lin, J. Zhou, W. Shiu and K. Liu, Science, 2003, 300, 966 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Am. Chem. Soc., 2009, 131, 17534 CrossRef PubMed.
- G. Czakó, Q. Shuai, K. Liu and J. M. Bowman, J. Chem. Phys., 2010, 133, 131101 CrossRef PubMed.
- B. Zhang, K. Liu and G. Czakó, J. Phys. Chem. A, 2015, 119, 7190 CrossRef CAS PubMed.
- H. Pan, F. Wang, G. Czakó and K. Liu, Nat. Chem., 2017, 9, 1175 CrossRef CAS PubMed.
- R. Liu, F. Wang, B. Jiang, G. Czakó, M. Yang, K. Liu and H. Guo, J. Chem. Phys., 2014, 141, 074310 CrossRef PubMed.
- R. Liu, M. Yang, G. Czakó, J. M. Bowman, J. Li and H. Guo, J. Phys. Chem. Lett., 2012, 3, 3776 CrossRef CAS PubMed.
- Y. Xu, B. Xiong, Y.-C. Chang and C. Y. Ng, J. Chem. Phys., 2012, 137, 241101 CrossRef PubMed.
- A. Li, Y. Li, H. Guo, K.-C. Lau, Y. Xu, B. Xiong, Y.-C. Chang and C. Y. Ng, J. Chem. Phys., 2014, 140, 011102 CrossRef PubMed.
- B. Jiang, D. Xie and H. Guo, J. Chem. Phys., 2011, 135, 084112 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, J. Chem. Phys., 2014, 140, 034112 CrossRef PubMed.
- H. Song and H. Guo, J. Phys. Chem. A, 2015, 119, 6188 CrossRef CAS PubMed.
- Z. Zhang and D. H. Zhang, J. Chem. Phys., 2014, 141, 144309 CrossRef PubMed.
- F. Wang, H. Pan and K. Liu, J. Phys. Chem. A, 2015, 119, 11983 CrossRef CAS PubMed.
- G. Czakó, J. Phys. Chem. A, 2014, 118, 11683 CrossRef PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 12231 CrossRef PubMed.
- P. Papp and G. Czakó, J. Phys. Chem. A, 2020, 124, 8943 CrossRef CAS PubMed.
- J. C. Corchado and J. Espinosa-García, Phys. Chem. Chem. Phys., 2009, 11, 10157 RSC.
- L. Bonnet and J. C. Rayez, Chem. Phys. Lett., 1997, 277, 183 CrossRef CAS.
- L. Bonnet and J. C. Rayez, Chem. Phys. Lett., 2004, 397, 106 CrossRef CAS.
- L. Bonnet and J. Espinosa-García, J. Chem. Phys., 2010, 133, 164108 CrossRef CAS PubMed.
- G. Czakó, Y. Wang and J. M. Bowman, J. Chem. Phys., 2011, 135, 151102 CrossRef PubMed.
- J. D. Sierra, L. Bonnet and M. González, J. Phys. Chem. A, 2011, 115, 7413 CrossRef CAS PubMed.
- L. Bonnet, J. Espinosa-García, J. C. Corchado, S. Liu and D. H. Zhang, Chem. Phys. Lett., 2011, 516, 137 CrossRef CAS.
- E. García, J. C. Corchado and J. Espinosa-García, J. Comput. Theor. Chem., 2012, 990, 47 CrossRef.
- G. Czakó and J. M. Bowman, J. Chem. Phys., 2012, 136, 044307 CrossRef PubMed.
- G. Czakó and J. M. Bowman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7997 CrossRef PubMed.
- G. Czakó, J. Phys. Chem. A, 2012, 116, 7467 CrossRef PubMed.
- R. Conte, B. Fu, E. Kamarchik and J. M. Bowman, J. Chem. Phys., 2013, 139, 044104 CrossRef PubMed.
- L. Bonnet and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2017, 19, 20267 RSC.
- Y. Zhu, L. Tian, H. Song and M. Yang, J. Phys. Chem. A, 2020, 124, 6794 CrossRef CAS PubMed.
- L. Zhang, J. Chen and B. Jiang, J. Phys. Chem. C, 2021, 125, 4995 CrossRef CAS.
- M. Braunstein, L. Bonnet and O. Roncero, Phys. Chem. Chem. Phys., 2022, 24, 5489 RSC.
- V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 8166 RSC.
- Q. Yu and J. M. Bowman, Nat. Commun., 2023, 14, 3527 CrossRef CAS PubMed.
- J. Li, Z. Tu, H. Xiang, Y. Li and H. Song, Phys. Chem. Chem. Phys., 2023, 25, 20997 RSC.
- C. Hennig and S. Schmatz, J. Chem. Phys., 2004, 121, 220 CrossRef CAS PubMed.
- C. Hennig and S. Schmatz, J. Chem. Phys., 2005, 122, 234307 CrossRef PubMed.
- C. Hennig and S. Schmatz, Chem. Phys. Lett., 2007, 446, 250 CrossRef CAS.
- Y. Wang, H. Song, I. Szabó, G. Czakó, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322 CrossRef CAS PubMed.
- M. Stei, E. Carrascosa, A. Dörfler, J. Meyer, B. Olasz, G. Czakó, A. Li, H. Guo and R. Wester, Sci. Adv., 2018, 4, eaas9544 CrossRef PubMed.
- Y. Li, Y. Wang and D. Wang, J. Phys. Chem. A, 2017, 121, 2773 CrossRef CAS PubMed.
- S. Rao and D. Wang, Chin. J. Chem. Phys., 2023, 36, 169 CrossRef CAS.
- G. Czakó, T. Győri, D. Papp, V. Tajti and D. A. Tasi, J. Phys. Chem. A, 2021, 125, 2385 CrossRef PubMed.
- B. Fu, Y.-C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9733 CrossRef CAS PubMed.
- X. Shan and D. C. Clary, Phys. Chem. Chem. Phys., 2013, 15, 1222 RSC.
- J. Li and H. Guo, J. Chem. Phys., 2015, 143, 221103 CrossRef PubMed.
- B. Hornung, T. J. Preston, S. Pandit, J. N. Harvey and A. J. Orr-Ewing, J. Phys. Chem. A, 2015, 119, 9452 CrossRef CAS PubMed.
- J. Zhang, L. Yang, J. Xie and W. L. Hase, J. Phys. Chem. Lett., 2016, 7, 660 CrossRef CAS PubMed.
- B. Fu, X. Shan, D. H. Zhang and D. C. Clary, Chem. Soc. Rev., 2017, 46, 7625 RSC.
- M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950 CrossRef CAS PubMed.
- E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25 CrossRef PubMed.
- S. Pandit, B. Hornung, G. T. Dunning, T. J. Preston, K. Brazener and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2017, 19, 1614 RSC.
- O. Roncero, A. Zanchet and A. Aguado, Phys. Chem. Chem. Phys., 2018, 20, 25951 RSC.
- C. Rangel and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2018, 20, 3925 RSC.
- J. Espinosa-Garcia and M. G. Chamorro, Phys. Chem. Chem. Phys., 2018, 20, 26634 RSC.
- J. Espinosa-Garcia, J. Calle-Cancho and J. C. Corchado, Theor. Chem. Acc., 2019, 138, 116 Search PubMed.
- J. C. Corchado, M. G. Chamorro, C. Rangel and J. Espinosa-Garcia, Theor. Chem. Acc., 2019, 138, 26 Search PubMed.
- D. Troya, J. Phys. Chem. A, 2019, 123, 6911 CrossRef CAS PubMed.
- D. Lu, J. Behler and J. Li, J. Phys. Chem. A, 2020, 124, 5737 CrossRef CAS PubMed.
- D. Lu, J. Li and H. Guo, CCS Chem., 2020, 2, 882 CrossRef CAS.
- D. Lu and J. Li, Theor. Chem. Acc., 2020, 139, 157 Search PubMed.
- D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762 Search PubMed.
- D. Papp and G. Czakó, J. Chem. Phys., 2020, 153, 064305 CrossRef CAS PubMed.
- J. Espinosa-Garcia, C. Rangel, J. C. Corchado and M. Garcia-Chamorro, Phys. Chem. Chem. Phys., 2020, 22, 22591 RSC.
- C. Rangel, M. Garcia-Chamorro, J. C. Corchado and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2020, 22, 14796 RSC.
- D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775 RSC.
- B. Bastian, T. Michaelsen, L. Li, M. Ončák, J. Meyer, D. H. Zhang and R. Wester, J. Phys. Chem. A, 2020, 124, 1929 CrossRef CAS PubMed.
- J. Meyer, V. Tajti, E. Carrascosa, T. Győri, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977 CrossRef CAS PubMed.
- D. Papp, J. Li, H. Guo and G. Czakó, J. Chem. Phys., 2021, 155, 114303 CrossRef CAS PubMed.
- D. Papp and G. Czakó, J. Chem. Phys., 2021, 155, 154302 CrossRef CAS PubMed.
- B. Gruber, V. Tajti and G. Czakó, J. Chem. Phys., 2022, 157, 074307 CrossRef CAS PubMed.
- B. Gruber, V. Tajti and G. Czakó, J. Phys. Chem. A, 2023, 127, 7364 CrossRef CAS PubMed.
- C. Yin, V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 24784 RSC.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 29084 RSC.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 3083 RSC.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 9944 RSC.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 20241 RSC.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 26917 RSC.
- X. Lu, C. Shang, L. Li, R. Chen, B. Fu, X. Xu and D. H. Zhang, Nat. Commun., 2022, 13, 4427 CrossRef CAS PubMed.
- X. Lu, L. Li, X. Zhang, B. Fu, X. Xu and D. H. Zhang, J. Phys. Chem. Lett., 2022, 13, 5253 CrossRef CAS PubMed.
- D. A. Tasi and G. Czakó, J. Chem. Phys., 2024, 160, 044305 CrossRef CAS PubMed.
- T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, et al., Molpro, version 2023.2, a package of ab initio programs,see https://www.molpro.net Search PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577 Search PubMed.
- Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26 CrossRef CAS PubMed.
- H. Song, W. Xie, C. Zhang and M. Yang, J. Phys. Chem. A, 2022, 126, 663 CrossRef CAS PubMed.
- R. Welsch and U. Manthe, J. Chem. Phys., 2015, 142, 064309 CrossRef PubMed.
- W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp.399–407 Search PubMed.
- J. Li, B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 982 CrossRef CAS PubMed.
- H. Xiang, Y. Lu, H. Song and M. Yang, Chin. J. Chem. Phys., 2022, 35, 200 CrossRef CAS.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104 CrossRef PubMed.
- H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679 CrossRef CAS PubMed.
- H. Song, J. Li, M. Yang, Y. Lu and H. Guo, Phys. Chem. Chem. Phys., 2014, 16, 17770 RSC.
- T. Michaelsen, B. Bastian, P. Strübin, J. Meyer and R. Wester, Phys. Chem. Chem. Phys., 2020, 22, 12382 RSC.
- T. Michaelsen, B. Bastian, A. Ayasli, P. Strübin, J. Meyer and R. Wester, J. Phys. Chem. Lett., 2020, 11, 4331 CrossRef CAS PubMed.
- D. Papp and G. Czakó, J. Phys. Chem. A, 2022, 126, 2551 CrossRef CAS PubMed.
- A. Y. Dymarsky and K. N. Kudin, J. Chem. Phys., 2005, 122, 124103 CrossRef PubMed.
- N. I. Butkovskaya and D. W. Setser, Int. Rev. Phys. Chem., 2003, 22, 1 Search PubMed.
| This journal is © the Owner Societies 2024 |