Theoretical insights into dopamine photochemistry adsorbed on graphene-type nanostructures

Abstract

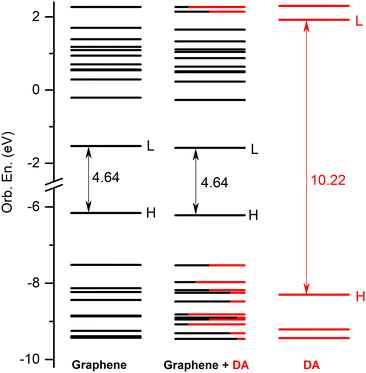
The equilibrium geometry structures and light absorption properties of the dopamine (DA) and dopamine-o-quinone (DAQ) adsorbed on the graphene surface have been investigated using the ground state and linear-response time-dependent density functional theories. Two types of graphene systems were considered, a rectangular form of hexagonal lattice with optimized C–C bond length as the model system for graphene nanoparticles (GrNP) and a similar system but with fixed C–C bond length (1.42 Å) as the model system for graphene 2D sheet (GrS). The analysis of the vertical excitations showed that three types of electronic transitions are possible, namely, localized on graphene, localized on the DA or DAQ, and charge transfer (CT). In the case of the graphene–DA complex, the charge transfer excitations were characterized by the molecule-to-surface (MSCT) character, whereas the graphene–DAQ was characterized by the reverse, i.e. surface-to-molecule (SMCT). The difference between the two cases is given by the presence of an energetically low-lying unoccupied orbital (LUMO+1) that allows charge transfer from the surface to the molecule in the case of DAQ. However, it was also shown that the fingerprints of excited electronic states associated with the adsorbed molecules cannot be seen in the spectrum, as they are mostly suppressed by the characteristic spectral shape of graphene.

---

1 Introduction

The photochemical behaviour of an organic molecule can change fundamentally when it is adsorbed on a metal or semiconductor surface.^1–4 Not only do the photochemical properties of the adsorbed molecule change, but new, more complex photo-processes may also appear, such as, electron or energy transfer to metal surfaces,^5,6 substrate–adsorbate photocoupling,⁷ surface driven photooxidation^8,9 or more complex photocatalytic processes.¹⁰ Moreover, the wide range of these properties can offer several research and industrial applications, such as, development of high-performance dye-sensitized solar cells,¹¹ building new, functionalized materials for electrode material for fuel cells and batteries,^12,13 materials for 3D printing¹⁴ or creating micropatterns with desired biofunctional properties.¹⁵

Inspired by the composition of adhesive proteins in mussels, Lee and co-workers^16,17 have shown that dopamine (DA) through the self-polymerization process can form thin, surface-adherent polydopamine films (PDA)^18,19 onto a wide range of inorganic and organic materials, including noble metals, oxides, polymers, semiconductors, and ceramics.^20–26

On the other hand, carbon-based nanomaterials are one of the most widely discussed, researched and applied synthetic nanomaterials, due to their diverse capabilities, such as excellent electronic, magnetic and optical properties. At the same time, their chemical versatility allows them to be easily manipulated in laboratory and industrial environments, to be biocompatible and to be considered as a chemically robust platform.^27–32

Taking into account the properties of the individual systems presented in the previous two paragraphs, further interesting behaviour can be observed in the case of the dopamine–graphene complex. First of all, one should mention the use of graphene as a DA sensor^33–37 or that of PDA for the reduction of graphene oxide,³⁸ but their complex was also used for making polymer filters,³⁹ to improve electrochemical performances of supercapacitors⁴⁰ or Li–S batteries,⁴¹ to use as high-performance material for biosensing^42,43 or as an efficient electrocatalysts^44–46 as well as to apply it in cancer therapy.⁴⁷ But what makes it particularly more interesting is the photochemical application of the graphene–dopamine complex,^48–52 especial as photothermal therapy for cancer.⁵³

Although DA is a relatively small molecule, its photochemical behaviour strongly dependents on its the concentration and tautomer forms as well as on the pH of the solvent environment,^54,55 and it is therefore much more difficult to unambiguously identify the fingerprints of different tautomers in the experimental UV-Vis spectrum. Similarly to DA, graphene exhibits complex photochemical behaviour, as the shape of the spectrum is highly dependent on the atomic configuration and size of the graphene structure.^56–62

Accurate theoretical reproduction of experimental UV-Vis spectra is a challenge in itself, even for intermediate molecules,⁶³ especially with respect to the accurate description of the electron correlation and the response function. This is particularly true for complex, multi-component supramolecular systems.^64–68 At the same time, graphene nanostructures have been successfully applied to the detection of e.g. catechol,⁶⁹ where also the UV-Vis spectroscopy technique was considered for the structure recognition. In such a case, the question arises whether it is possible to identify the individual components on the basis of the resulting adsorption spectrum, or whether this resulting spectrum has any characteristic feature that suggests that the two components form a well-defined joint complex.

The aim of our study is to give a detailed description for the photochemistry behavior, and in particular, for nature of the electronic transitions induced by an electromagnetic radiation in the cases of graphene – dopamine and graphene – dopamine-o-quinone complexes using the framework of the time-dependent density functional theory, with the aim of investigating whether graphene as a tool helps to facilitate the identification of adsorbed molecules on it surface.

2 Computational details

The equilibrium geometries and normal mode vibrational frequencies of individual molecules, the graphene sheet and different molecule–graphene binary complexes were computed in the framework of density functional theory (DFT) considering the ωB97X-D3BJ exchange–correlation (XC) functional⁷⁰ by including the Grimme's empirical dispersion correction scheme^71,72 and using the def2-TZVPP triple-ζ basis set of the Karlsruhe group⁷³ as implemented in the Orca program suite.^74,75 The electronically excited state calculations and equilibrium geometry optimizations were computed using the time-dependent version of the same DFT framework considering the Tamm–Dancoff approximation (TDA) approximation.⁷⁶ The RIJCOSX approximation⁷⁷ designed to accelerate Hartree–Fock and hybrid DFT calculations were considered together with the Def2/J⁷⁸ auxiliary basis set for Coulomb fitting and the def2-TZVPP/C⁷⁹ auxiliary basis set for correlation fitting in the case of TD-DFT calculations. During the geometry optimization of the molecule–graphene binary complex the graphene part was kept frozen and the Partial Hessian Vibrational Analysis (PHVA) method⁸⁰ has been used for obtaining the normal mode vibrational frequencies of the unconstrained part of the binary complex. The theoretical prediction of the fluorescence rate was made based on the path integral approach to the dynamics by solving Fermis Golden Rule-like equation including vibronic coupling in forbidden transitions (the so-called Herzberg–Teller effect (HT)) and Duschinsky rotations between modes of different states.^81–83 The amount of transferred charge between the complex constituents was obtained based on the analysis of the charge population (Löwdin atomic charges) of a given electronically excited state density computed in the TDDFT framework. The molecular geometries were built, analyzed and further manipulated using Multiwfn⁸⁴ Gabedit⁸⁵ and Avogadro⁸⁶ programs, while the molecular graphics were created using the GaussView⁸⁷ software.

3 Results and discussion

3.1 Geometry structures

As a first step, a two-dimensional (three zig-zag and seven armchair edges) rectangular graphene nano-sheet with fully aromatic hexagonal rings (see Fig. 1) was considered in two geometrical configurations. In the first case its structure has been fully optimized in order to mimic the graphene-type nanoparticle (GrNP), while in the second case all C–C bond lengths were kept as 1.42 Å for reproducing the 2D infinite dimensional graphene sheet (GrS) geometry.⁸⁸ The geometry optimization leads to an irregular honeycomb lattice, where the C–C bond length varies between 1.38–1.47 Å.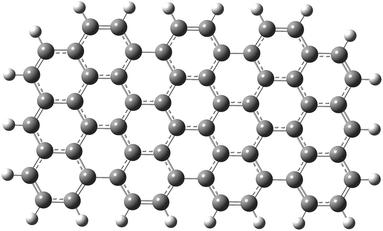

Fig. 1 The molecular graphics of the graphene nanoparticle with three zig-zag and seven armchair edges.

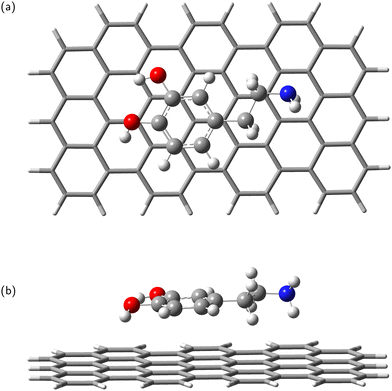
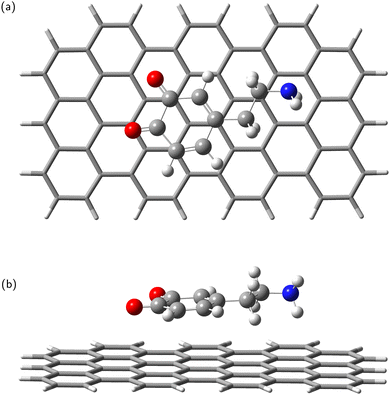
In the next step, the dopamine (DA) and dopamine-o-quinone (DAQ) molecules were deposited on the GrNP-type graphene sheet and the geometry of the molecules as well as their relative position to the graphene sheet were optimized, while the geometry of the graphene sheet was was kept fixed. In the equilibrium geometry configuration, the DA molecule is slightly tilted with respect to the graphene sheet, with the O atoms of the hydroxyl group at 3.2 and 3.26 Å from the graphene plane, respectively, and the N atom of the amine group at 3.51 Å (see Fig. 2). A similar arrangement can be observed for DAQ, where the O atoms of the hydroxyl groups are 3.14 Å and 3.19 Å away, while the N atom of the amine group is 3.52 Å from the graphene plane (see Fig. 3). Adsorption energy of DA on the GrNP surface is −20.24 kcal mol⁻¹, while that of DQ is −20.11 kcal mol⁻¹, of which the deformation energy is only 0.41 kcal mol⁻¹ and 0.13 kcal mol⁻¹, respectively. As for the ground state charge distribution, there is a charge transfer of 0.068 e from the DA to the surface (called as molecule-to-surface charge transfer or MSCT), while for DAQ the charge transfer to the graphene is only 0.031 e.

Fig. 2 Dopamine adsorbed on graphene surface: top-view (a) and side-view (b).

Fig. 3 Dopamine adsorbed on graphene surface: top-view (a) and side-view (b).

3.2 Electronic excited states and UV absorption spectra

In order to gain more insight into the nature of the initial (vertical) and relaxed excited states, the first 30 electronic excited states were computed separately for each molecule and graphene sheet, and for different molecule–graphene binary complexes.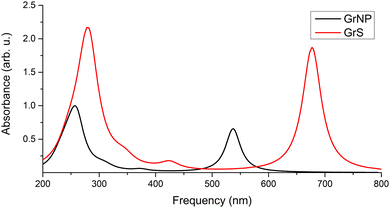

DA. Given that the results for dopamine have already been reported,^54,55 only the excited states of the graphene sheet and binary complexes will be discussed in more detail. Briefly, DA presents spectral characteristics with peak maxima at 280 nm and 218 nm (see Fig. 1 in ref. 54). However, as for the equilibrium geometry of the first excited state (S₁), the C–O bonds of the DA's hydroxyl groups are shortened (from 1.377 Å and 1.362 Å to 1.360 Å and 1.348 Å) and the C–C bonds of the benzene ring are stretched, with all six bonds being longer than 1.4 Å (the bond values are 1.425, 1.403, 1.421, 1.407, 1.416 and 1.412, respectively in Å).

DAQ. Oxidation of DA using different oxidation agents can easily lead to the quinone form,⁸⁹ which induces an additional spectral peak around 390 nm in the UV absorption spectra. TDDFT calculations have shown that this additional peak comes from the contribution of the S₀ → S₃ electronic excitation, while the S₁ and S₂ excitations have nearly zero oscillator strength and do not result in any noticeable effect on the spectrum. For the electronic excited state energy values, oscillator strengths and the most intense orbital transition see Table S1 (ESI†), as well as for the UV absorption spectra see Fig. S1 from the ESI† file. The geometry optimization of the S₁ electronic excited state leads mainly to the stretching of the C–C bond, to which carbon atoms are the carboxyl groups attached (from 1.553 Å to 1.625 Å).

Graphene. Graphene is a 2D solid that has interesting physics due to its unusual electronic band structure,⁸⁸ and consequently also has unusual optical properties through a wide absorption spectral region given by intraband transitions (π → π*) at low photon energies (0.0–5.0 eV in the far-infrared spectral range) and by interband transitions (π → σ*) at higher energies (over 5.0 eV from mid-infrared to ultraviolet).^90,91 However, state-of-the-art theoretical calculations have shown that in order to reproduce the experimental spectrum accurately, it is necessary to take electron correlation into account.^92,93 On the other hand, graphene-like materials with lower dimension (1D wires), such as graphene nanoribbons, substantially different electronic band structure and optical properties than graphene.^94,95 Although with significant differences, a similar spectral profile in the UV-Vis absorption spectrum can be found for graphene nanocrystals of finite dimensions (0D structures), 10–50 nm.^96,97 That is, the peak around 4.5 eV and the long decay shoulder towards lower energy values, which in turn can vary depending on the shape and size of the particle. The experimental UV absorption spectra of graphene nanoparticles^60,98 showed an intense spectral peak centred at 269 nm and a very long shoulder that is over-expanded up to 700 nm (see Fig. 1 in ref. 60). At the same time, theoretical calculations based on TDDFT showed that for a 0D graphene particle with a dimension of a few nanometres, additional peaks of lower intensity can appear in the 350–700 nm interval, which is clearly influenced by the dimension of the graphene model system.^61,62,99 Theoretical UV absorption spectra were computed considering the graphene nanostructure shown in Fig. 1 both in the optimized (GrNP) and fixed (GrS) geometry forms, by applying the TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory. Their spectral shapes are presented in Fig. 4, while their detailed spectral features (spectral shape, wavelength lines and intensities) is shown in Fig. S2 and Table S2 in the ESI† file. Theoretical results show an intense peak around the 260–280 nm as it can be observed in the experimental spectra,^60,98 but in the present analysis there are also additional peaks associated mainly with the first excited states (537 nm for GrNP and 677 nm for GrS) that are likely to depend on the dimension of the chosen graphene model system. Furthermore, it is clear that the peak observed in the experimental spectrum around 270 nm is given by the higher states in the excitation spectrum (S₁₈ and S₂₁ for GrNP and S₁₇ and S₁₉ for GrS) and the longer shoulder of 350–700 nm region comes from the lower but weakly intense excited states. By analyzing the so-called natural difference orbitals (NDO) for electronic transitions between the ground state and the different excited states, it is observed that the S₀ → S₁ transition is a π → π* type excitation along two consecutive C–C aromatic bonds, thus forming a zig-zag chain along the longer dimension both for the GrNP- and GrN-type graphene structures (see Table S3 in the ESI† file).

Fig. 4 Theoretical UV absorption spectra of the model graphene lattice both in the optimized (GrNP) and fixed (GrS) geometry forms, computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.

It is important to note that in the case of graphene, only a simplified model has been considered, where the 2D solid state character and the band structure have been discarded. Instead, a finite dimensional hydrocarbon structure has been adopted which results in discrete electronic states. Compared to the experimental UV spectrum of graphene, this simple model is already able reproduce the most important features of the UV spectrum. Of course, in order to accurately follow the changes in the electron structure of graphene induced by the adsorbed molecules, the simplified model described here is no longer suitable, it needs for solid-state model.

DA–graphene. First, the GrNS form was used on graphene models. The energetic scheme of highest occupied and lowest unoccupied molecular orbitals (MO) in the energy range of [−10.0 eV to 2.5 eV] computed for the individual fragments (GrNP or DA) as well as for the joined graphene–DA binary complex is shown in Fig. 5. As can be observed from the figure, the energies of the molecular orbitals of the binary complex follow the topology of graphene much more closely than that of DA. In this sense, the binary complex is not a classical donor–acceptor system,¹⁰⁰ since the HOMO orbital of DA is energetically much lower, and the LUMO orbital is much higher than that of graphene. Although, for occupied MOs, the DA contribution is observed starting with the HOMO−1, for unoccupied orbitals the DA contribution is only seen from the LUMO+11 upwards. For details see Fig. 5, while the frontier orbitals of DA are shown in Table S4 in the ESI† file. As the next step, the first thirty electronic excited state energies of the graphene–DA binary complex has been computed using the theoretical framework described in Section 2. Accordingly, their energy values and oscillator strengths are collected in Table 1, while the theoretical UV absorption spectra is shown in Fig. 6. In terms of light absorption intensity, the S₁, S₂, S₁₀, S₁₁, S₁₆, S₂₀ and S₂₃ excited states are worth highlighting. In the UV absorption spectrum the S₁ excited state gives the peak at 540 nm, S₂ the hump at 377 nm, S₁₀ and S₁₁ the spectral shoulder at 310 nm, while S₁₆, S₂₀ and S₂₃ together give the high peak at 260 nm. These electronic transitions are partly related to pure GrNP (S₁, S₂, S₁₀ and S₁₁), pure charge transfer (S₁₆) and partly to mixed GrNP and charge-transfer (S₂₀ and S₂₃) electronic states, while DA alone has no significant contribution. Yet, as far as the role of DA is concerned, it is manifested by the appearance of a DA to GrNP (molecule-to-surface charge transfer or MSCT) transition (for ex. S₁₆) alongside the pure GrNP-type transitions that diminishes the intensity of the absorption or slightly shifts the absorption peaks (e.g. from 537 nm to 540 nm in the case of S₁). Of the thirty excited states, seventeen are purely GrNP-localized excitations, six have a charge-transfer character, six show a mixed form of the two types, while only one state is observed to have a typical DA excitation (S₂₉). The detailed data on the thirty excited states mentioned above, such as the most significant molecular orbital excitations and the NDOs (or natural density orbitals) are given in Table S5 in the ESI† file. As far as the electron charge distribution after excitation is concerned, the so-called charge transfer (or CT) excitations are the most interesting electronic states. The theoretical description of these electronic excitations is not so straightforward, due to the large electron–hole separation along the molecular system.^101–104 It has been shown¹⁰⁵ that the wB97X-D exchange–correlation functional can efficiently describe not only the valence, but also the charge transfer and Rydberg electronic excitations. It is known that, CT excitations are not specific to any of the isolated molecular fragments, and during the excitation there is a large charge transfer from one fragment to another, in this particular case from DA to graphene. Accordingly, the maximum amount of charge transferred from DA to graphene is 0.798 e which is found for the S₂₆ state. The other such states are S₆, S₇, S₉, S₁₆ and S₂₈, to which charge transfers of 0.117 e, 0.397 e, 0.317 e, 0.398 e and 0.130 e have been occurred. It can be observed that a feature of the CT states, especially when accompanied by a high charge transfer, is that the coefficients of the one-electron excitations from deeper filled MO orbitals to the LUMO orbital are high compared to the other one-electron excitations (e.g., for S₂₆ the coefficient of the HOMO−10 → LUMO excitation is 0.60). There is also a charge transfer effect in the mixed “GrNP + CT” states, but its magnitude is generally smaller than in the pure CT states, i.e. less than 0.1 e (the only exception is S₂₃ where it is 0.114 e). The typical DA-like S₂₉ state does not appear to be a purely DA-localized excitation either, but there is also a MSCT component in this case with a charge transfer of 0.149 e, which means that part of the DA excitation is transferred to the graphene surface. However, the high order of the DA-related electronic excitation level (29th) is not surprising, since the wavelength of the first electronic excited state calculated in the isolated state is 266 nm,⁵⁴ which is close to the wavelength of the S₂₉ excited state (240 nm). As for the UV absorption compiled spectra of the individual components and the binary system, it can be observed that graphene-like electronic transitions are the dominant components in the higher wavelength range of the spectrum (300–700 nm), while in the fingerprint of the DA appears in the lower spectral range (200–300 nm), but its intensity looks very low compared to that of graphene. From the point of view of light absorption, the CT states can be considered active, although not all of them have been assigned a large oscillator strength. The role of S₉ and S₁₆ electronic excited states should be highlighted, which could not be completely suppressed by the strong peak of graphene centred at 261 nm (S₂₀), so that a weaker shoulder of the spectrum at 300 nm could be observed (see Fig. 6).

Fig. 5 The molecular orbital energy scheme (in eV) of the individual, graphene and DA components and of the mixed graphene–DA binary complex (H = HOMO, L = LUMO) based on the fragment orbital contribution analysis.

Table 1 The first thirty electronic excited state energies (in nm), their oscillator strengths, transferred charges and electronic transition types (either located on the GrNP and on DA fragments or charge transfer states between the fragments) of the GrNP–DA binary complex, computed at TDDFT/ωB97X-V/def2-TZVPP level of theory

Si	1	2	3	4	5	6	7	8	9	10
CT = Charge transfer character
λ (nm)	540	377	374	364	357	342	331	323	321	312
Osc. Str.	1.6763	0.0807	0.0008	0.0006	0.0001	0.0026	0.0068	0.0085	0.0212	0.0725
Charge tr. (e)	0.001	0.026	0.003	0.004	0.014	0.117	0.397	0.006	0.317	0.043
Type	GrNP	GrNP	GrNP	GrNP	GrNP	CT	CT	GrNP	CT	GrNP + CT

---

Si	11	12	13	14	15	16	17	18	19	20
λ (nm)	304	303	295	285	283	271	267	267	262	261
Osc. Str.	0.0838	0.0358	0.0348	0.0012	0.0155	0.2183	0.1371	0.0751	0.1166	0.7479
Charge tr. (e)	0.004	0.003	0.025	0.040	0.084	0.398	0.080	0.028	0.012	0.084
Type	GrNP	GrNP	GrNP	GrNP	GrNP + CT	CT	GrNP + CT	GrNP	GrNP	GrNP + CT

---

Si	21	22	23	24	25	26	27	28	29	30
λ (nm)	259	257	255	253	250	248	245	244	240	239
Osc. Str.	0.0067	0.0309	0.7957	0.0243	0.0613	0.0171	0.0153	0.3103	0.0449	0.0053
Charge tr. (e)	0.027	0.031	0.114	0.032	0.102	0.798	0.106	0.130	0.149	0.041
Type	GrNP	GrNP	GrNP + CT	GrNP	GrNP + CT	CT	GrNP + CT	CT	DA + CT	GrNP

---

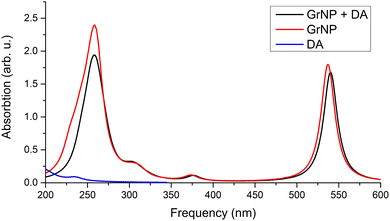Fig. 6 Theoretical UV absorption spectra of the graphene–DA binary complex computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.

When the GrS type was used as the graphene surface, the first forty excited states were analysed rather than the first thirty. This was necessary because in the first thirty states there wasn’t any excitation that could be associated with the DA. When this interval was increased to forty, it was possible to identify the DA-related excited state as S₃₄, which also has a mixed state coming from the locally excited DA- and MSCT-type transitions, and the amount of transferred charge is 0.272 e. In addition, three, pure CT states were also identified, S₉, S₁₇ and S₂₅, with charge transferred from DA to GrS (MSCT) amounts of 0.816 e, 0.456 e and 0.603 e, respectively. Twelve of the thirty-six remaining excited states are pure GrS, while twenty-four are of mixed “GrS + CT” type.

DAQ–graphene. The energetic scheme of highest occupied and lowest unoccupied MOs in the energy range of [−10.0 eV to 2.5 eV] computed for the individual fragments (GrNP or DAQ) as well as for the joined graphene–DAQ binary complex is shown in Fig. 7, while the frontier orbitals of DAQ are shown in Table S6 in the ESI† file. In almost the same way as in the previous case, especially as far as the occupied orbitals are concerned, the energies of the molecular orbitals of the binary complex follow the topology of graphene much better than those of DAQ. As for the unoccupied orbitals, the situation changes in that the DAQ also has a low virtual orbitals (LUMO, see third column of energy levels at Fig. 7) which in turn can affect the nature of the electronic excitation. Similarly as in the previous case, the first 30 excited states were calculated for the DAQ–graphene binary complex. Accordingly, their energy values and oscillator strengths are collected in Table 2, while the theoretical UV absorption spectra is shown in Fig. 8. The two large peaks in the spectrum are given by S₁, S₂₄ and S₂₅ excited states. The other two smaller peaks are defined by the S₃ and S₄ states, while the second larger peak is defined by the S₁₄ and S₁₅ states. As regards the nature of the excited states, unlike the graphene–DA system, in the present case the first three excited states are of a different nature than those seen in the previous case. There, all three were of pure graphene type, whereas here the first is of mixed “GrNP + CT” type, the second is of DAQ type and the third is of pure CT type. What is also very surprising is that not only MSCT-type charge transfer can be observed, but also charge transfer in the opposite direction, i.e. surface-to-molecule charge transfer (or SMCT). This reverse direction is manifested in the fact that the value of the transferred charge is negative. If one considers that in the ground state 0.031 e charge migrated from DAQ to graphene, and for the S₁ excited state it is −0.034 e, then it can be concluded that in fact 0.065 e charge was transferred from graphene to DAQ during the excitation. Overall, eighteen of the first thirty excited states were found to be related to pure GrNP, four to mixed “GrNP + CT”, five to pure CT and the remaining three to DAQ fragment excitation. Considering, in general, the charge transfer value obtained for the ground state (i.e. 0.031 e), only the S₂₂ and S₂₄ states are the ones where very little additional charge amount is transferred from the DAQ to the graphene surface, 0.004 e and 0.022 e respectively, the other twenty-eight cases show SMCT type charge transfer effects. Furthermore, the five CT electronic states are S₃, S₁₆, S₁₈, S₂₁ and S₃₀, with charges of −0.836 e, −0.698 e, −0.756 e, −0.799 e and −0.749 e migrating from the graphene surface to the DAQ molecule.

Fig. 7 The molecular orbital energy scheme (in eV) of the individual, graphene and DAQ components and of the mixed graphene–DAQ binary complex (H = HOMO, L = LUMO) based on the fragment orbital contribution analysis.

Table 2 The first thirty electronic excited state energies (in nm), their oscillator strengths, transferred charges and electronic transition types (either located on the GrNP and on DAQ fragments or charge transfer states between the fragments) of the GrNP–DAQ binary complex, computed at TDDFT/ωB97X-V/def2-TZVPP level of theory

Si	1	2	3	4	5	6	7	8	9	10
CT = Charge transfer character.
λ (nm)	547	518	472	376	374	364	357	340	332	326
Osc. Str.	1.5631	0.0010	0.1244	0.0691	0.0054	0.0053	0.0014	0.0044	0.0068	0.0026
Charge tr. (e)	−0.034	0.050	−0.836	0.023	0.022	0.025	0.028	0.021	−0.024	0.000
Type	GrNP + CT	DAQ	CT	GrNP	GrNP	GrNP	GrNP	GrNP	DAQ	GrNP

---

Si	11	12	13	14	15	16	17	18	19	20
λ (nm)	325	323	314	304	304	297	294	288	285	281
Osc. Str.	0.0000	0.0146	0.0980	0.0488	0.0472	0.0202	0.0209	0.0081	0.0159	0.0056
Charge tr. (e)	0.050	0.021	0.000	0.000	0.014	−0.698	−0.084	−0.756	−0.048	0.018
Type	DAQ	GrNP	GrNP	GrNP	GrNP	CT	GrNP + CT	CT	GrNP + CT	GrNP

---

Si	21	22	23	24	25	26	27	28	29	30
λ (nm)	277	268	265	263	263	259	258	256	253	250
Osc. Str.	0.0270	0.0957	0.0026	0.7773	0.5549	0.1103	0.0246	0.1413	0.1526	0.0598
Charge tr. (e)	−0.799	0.035	−0.015	0.053	0.014	0.014	0.020	0.029	0.015	−0.749
Type	CT	GrNP	GrNP + CT	GrNP	GrNP	GrNP	GrNP	GrNP	GrNP	CT

---

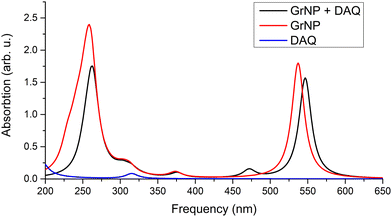Fig. 8 Theoretical UV absorption spectra of the graphene–DAQ binary complex computed at TDDFT/ωB97X-D3BJ/def2-TZVPP level of theory.

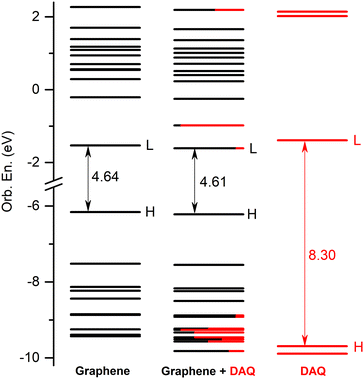
When the excitations between the canonical MO orbitals are analyzed for these CT excitations, it can be seen that there is always a transition with a large weight in the individual MO excitation scheme from certain occupied orbital to the same LUMO+1 orbital. Namely, for S₃ is H → L+1 (93%), for S₁₆ is H−1 → L+1 (64%), for S₁₈ is H−4 → L+1 (61%), for S₂₁ is H−2 → L+1 (77%) and for S₃₀ is H−5 → L+1 (50%) excitation, respectively. A similar excitation scheme is true for DAQ-like excitations, with the difference that the excitation starts from even lower MO orbitals and goes to L+1. Namely, for S₂ is H−9 → L+1 (54%), for S₉ is H−8 → L+1 (26%) and for S₁₁ is H−19 → L+1 (63%) excitation, respectively.

The detailed data on the thirty excited states mentioned above, such as the most significant molecular orbital excitations and the NDOs are given in Table S7 in the ESI† file. Concerning the UV-Vis absorption spectrum in particular, it can be observed that the spectrum of the graphene–DAQ complex is very similar to that of graphene. Difference is made by the peak obtained for the S₃ CT-type excited state (around 472 nm), which cannot be seen in the graphene spectrum (see Fig. 8). As for the DAQ, some contribution from S₉ (332 nm) can be observed in the UV spectrum, however, the absorption intensity associated with this electronic transition is quite small.

No significant change in the nature of the excited states was observed when instead of the GrNP form the GrS-type graphene structure was considered. For example, the nature of the S₁, S₂ and S₃ excited states remains the same, except that the excitation wavelengths are shifted to higher (lower energy) values. That is, instead of 547 nm, 518 nm and 472 nm, values of 686 nm, 530 nm and 516 nm were obtained.

3.3 Excited state relaxation dynamics

The relaxation dynamics of electronic excited states on metal or semiconductor 2D surface looks a very complex phenomena.^106–109 Since excited states can be localize on one or the other constituent of the molecule–surface complex, or charges can easily migrate from the molecule to the surface or vice versa, relaxation processes can also occur either on the components separately or even inside the binary system. Accordingly, it was already shown, that non-radiative relaxation can occur either on the graphene surface¹¹⁰ itself or in the binary complex,^111–118 but at the same time, excited states in the case of slightly modified GrNP can also decay via fluorescence phenomena.^119,120 Given that the relatively moderate size of the chosen graphene model (62 carbon and 22 hydrogen atoms) does not require the use of, e.g., a solid-state based physical model, in the present case the binary molecule–graphene complex will be considered as a macromolecular system with two interacting constituents and treated with the ordinary DFT and TDDFT methods suitable for molecular systems. Second, non-radiative phenomena were also not considered, as they require a very complex theoretical framework and huge computation resources to describe them. Third, as a further approximation, the dynamics of the surface (geometry deformation) has been neglected, because we are more interested in the dynamics of the adsorbed molecule. This was achieved by keeping the atoms of the surface fixed during the normal mode vibration and excited state geometry optimization calculations. In order to follow the relaxation of the higher excited states without considering the internal conversion phenomena between adjacent electronic states, the “root following” condition was imposed during the geometry relaxation.

DA–graphene. Since, different constraints for the geometries were applied, only the pure CT and DA-related excited states were investigated, except for S₁. (i) S₁ – during the geometry optimization, the geometrical parameters of the DA molecule did not change, only the relative orientation of the molecule with respect to the graphene plane. However, this change is also very minimal, e.g. the inter-planar distance between the DA and graphene will be only 0.002 Å shorter. The absorption wavelength of S₁ remains unchanged after the geometric optimization, at 540 nm. Furthermore, the amount of charge transfer induced initially by the vertical excitation comes back after optimization to the ground state value of 0.069 e. It is well known that an important moment in the relaxation of excited states is when the system reaches its first excited state. From there it can reach the S₀ ground state through different relaxation channels (radiative or even non-radiative). From this point of view, it would be interesting to investigate the role of DA in a possible fluorescence deactivation mechanism. To this end, both the ground and the first excited state normal mode vibrations have been computed by considering only the vibrations of the DA. For this purpose, the Partial Hessian Vibrational Analysis (PHVA) method⁸⁰ was applied. In this way, the role of the DA on the fluorescence rate of the DA–graphene complex through the vibronic coupling can be estimated. The fluorescence rate has been computed using the both the Frank–Condon (FC) and Hertzberg–Teller (HT) approximations, but for vibrations, the effects of intermolecular modes have been considered separately. It was observed that without the contribution of the intermolecular modes the fluorescence rate was 8.48 × 10⁸ s⁻¹ (i.e. lifetime 1.18 ns) and the whole rate is given by the FC approximation, while when the intermolecular modes were included the rate was an order of magnitude higher (i.e. the rate was 6.54 × 10⁹ s⁻¹ and the lifetime 0.15 ns) and for the fluorescence rate a contribution of 10% comes from the HT effects. This may indicate that adsorbed DA molecules can accelerate the deactivation process through the vibronic coupling with the graphene surface; (ii) S₇ – this is an MSCT state whose geometric optimization brings the OH fragments of the DA closer to the graphene surface, with one O at 3.11 Å (Δ = −0.08 Å) and the other at 3.23 Å (Δ = −0.03 Å) from the surface. In addition, each C–O bond becomes 0.01 Å shorter and the aromatic character of the benzene ring is slightly distorted by two C–C bonds becoming 0.01 Å longer and the other four with 0.005 Å shorter. In this way the value of the charge transferred is reduced from 0.397 e to 0.250 e, but the order of the excited state remains 7th; (iii) S₉ – in this case no significant change in the geometry of the DA was found, only the relative position of the DA changed slightly where the DA moving away from the graphene by 0.12 Å. Similar to S₁ state, the amount of charge transfer induced initially by the vertical excitation comes back after optimization to the ground state value of 0.064 e, the order of the excited state becomes 3th; (iv) S₁₆ – in this case, is observed that the DA is tilted so that one of the OH and NH₂ groups comes a little closer to the surface (Δ (O⋯GrNP) = −0.06 Å and Δ (N⋯GrNP) = −0.04 Å), but the DA does not suffer internal geometry changes. On the other hand, there is a significant change in the magnitude of the transferred charge, since it was initially only 0.398 e, but increases to 0.624 e during relaxation, and the order of the excited state changes from 16 to 5; (v) S₂₆ – as in the S₁₆ case, there is only a slight tilt, the DA's own geometry remains unchanged. What is different from the previous case, however, is the decrease in charge transfer from 0.798 e to 0.291 e. The order of the excited state decreases to 19; (vi) S₂₉ – this excited state is interesting from the point of view of whether the geometric changes of the DA during relaxation are similar to the geometric changes obtained for the S₁ state of the isolated DA. Analyzing the lengths of the C–O and aromatic C–C bonds, it is found that they do not differ substantially, one of the C–O bonds being shorter by only 0.01 Å but most importantly, the length of the aromatic C–C bonds does not exceed 1.4 Å which should be between 1.4 and 1.42 for the S₁ state equilibrium geometry of the isolated DA (see bond distance values of S₁ equilibrium geometry given in Section 3.2). Accordingly, it can be said that, the relaxation of the DA lying on the graphene surface, after the characteristic DA-type vertical excitation, does not follow the geometric deformation observed for its S₁ state in its isolated case, but rather, it is more similar to the bond values found for S₀ ground state geometry. During the geometric relaxation, DA comes closer to the surface through its OH fragments (on average by 0.08 Å), while the NH₂ fragment moves away (by 0.09 Å). The charge transfer effects increase from 0.149 e to 0.217 e and the final order of the excited state is 26th.

DAQ–graphene. Similar to DA, only the relaxations of S₁, locally excited DAQ and CT-type excited states were investigated. (i) S₁ – in contrast to the case of DA, where no geometry changes were observed in the DA molecule itself during the excitation at S₁ state, significant changes were observed for DAQ. The most significant changes are seen for the C=O bonds, where they change from 1.206 Å and 1.208 Å in the ground state to 1.242 Å and 1.244 Å in the S₁ state. These changes also affect the hexagonal ring configuration, in particular the C–C bond to which the carbonyl groups are attached. Namely, from 1.553 Å the bond length is shorten to 1.505 Å. The relative position of DAQ with respect to the plane of graphene also changes, with the O atoms of the carbonyl groups approaching the graphene from 3.14 Å and 3.15 Å to 2.84 Å and 2.85 Å while the distance of NH₂ from the plane of graphene remains almost unchanged (3.51 Å). After geometric optimization, the absorption wavelength of S₁ also changes significantly to 651 nm. The charge transfer value obtained during vertical excitation also jumps enormously, from −0.034 e to −0.736 e, clearly suggesting that during geometry relaxation the localized excitation character on the GrNP diminishes and the CT-type excitation character increases. Since the geometry deformation for DAQ in the S₁ excited state is significant compared to the ground state geometry, the method used for DA to determine the fluorescence rate in the framework of the harmonic oscillator approach is no longer valid. Therefore, in this case, neither the fluorescence rate nor the lifetime was computed; (ii) S₂ – S₂ is considered mostly locally excited state on DAQ, where an additional slight charge transfer occurs from the DAQ to the graphene surface. Geometry optimization with the root following constrain leads to a slight detachment of carbonyl groups, from 3.14 Å and 3.19 Å to 3.19 Å and 3.26 Å, respectively. The equilibrium geometry will also be S₁ as the final state order, but this S₁ state is only a local minimum compared to the geometry obtained in the previous S₁ state optimization, with a conformational energy difference of 1.404 kcal mol⁻¹. Also, the geometry changes observed in the DAQ are more typical to the S₁ equilibrium geometry of the isolated DAQ, i.e. the length of the C–C bond from the six-membered ring, which includes the carbonyl groups, is not shortened but stretched, from 1.553 Å to 1.616 Å. The amount of transferred charge remains unchanged, namely +0.050 e transferred from DAQ to the graphene surface. (iii) S₃ – considering the root following condition, the geometry optimization of the S₃ state leads to the same equilibrium geometry as found for S₁. For geometry relaxation and charge transfer effects, see the results presented for the S₁ case; (iv) S₁₆ – for this case, it was found that the carbonyl groups move closer (Δ (O⋯GrNP) = −0.14 Å to the graphene surface relative to their ground state geometry, while the amine group moves away (Δ (N⋯GrNP) = +0.07 Å)), so that the relative position of the DAQ becomes more tilted. The internal geometry of the DAQ also changes slightly, e.g. the C=O bonds slightly increase (≈0.02 Å) and the C–C bond from the hexagonal ring containing these carbonyl groups decreases by the same difference. Furthermore, the amount of transferred charge decreases from −0.698 e to −0.324 e and the final order of the excited state is the 14th; (v) S₁₈ – the equilibrium geometry is identical to that found for S₁₆, the value of the transferred charge is similarly reduced from −0.756 e to −0.315 e, and the final order of the excited state is also the 14th; (vi) S₂₁ – the only change compared to the previous two cases is that, like the carbonyl groups, the amine group is come closer to the surface, but the trend is similar. Namely, the transferred charge decreases from −0.799 e to −0.473 e, and the final order of the state becomes the 18th.

4 Conclusions

In the present work, the equilibrium geometry structures and light absorption properties of the dopamine (DA) and dopamine-o-quinone (DAQ) adsorbed on the graphene surface has been investigated using the ground state and linear-response time-dependent density functional theories. Two types of graphene nanostructures were considered, one of them with optimized C–C bond length as the model system for graphene nanoparticles (GrNP), while the second being a similar system but with fixed C–C bond length (1.42 Å) as the model system for graphene 2D sheet (GrS). For both the GrNP and GrS model systems, the theoretical UV-Vis spectra show a more intense peak around 270 nm, which is consistent with the experimental results and is due to higher electronic transitions. It has been shown that the simplified graphene model consists in a finite-dimensional aromatic hydrocarbon system with discrete electronic states, can reproduce the main features of the experimental UV spectrum of graphene and, as a surface model, can act as a proper environment in interaction with the adsorbed molecules. Analyzing the natural difference orbital profiles characteristic for the vertical electronic excitation three types of electronic transitions were observed in the cases of graphene–DA and graphene–DAQ binary complexes. Namely, locally excited on graphene, locally excited on the molecule and charge transfer (CT) states characteristic for the charge migration induced by the excitation. For CT states, two different types of states have been identified, one when the charge is transferred from the molecule to the surface, called molecule-to-surface CT (or MSCT), and the other when the transfer occurs from the surface to the molecule, called surface-to-molecule CT (or SMCT). MSCT is characteristic of DA, while SMCT is characteristic of DAQ, and the difference between the two cases are given by the presence of an energetically low-lying unoccupied orbital (LUMO+1) that allows charge transfer from the surface to the molecule in the case of DAQ. Analyzing the spectral profiles of the UV-Vis absorption spectra, it was found that, the fingerprints of excited electronic states associated with the adsorbed molecules on the graphene surface cannot be seen in the spectrum, as they are mostly suppressed by the characteristically broad spectral shape of graphene, which is given by the lower-lying (typically the first ten) electronically excited states. As far as the relaxation dynamics of the excited states are concerned, two different scenarios were obtained for the two molecules, DA and DAQ. In the case of DA, it is observed that the molecule itself does not suffer any geometric change after the electronic excitation, only its relative position with respect to the surface changes and, of course, the quality of the CT states. The opposite effect is true for DAQ, that is, the ground-state geometry of DAQ changes substantially during the geometry relaxation of locally-DAQ and CT-type excited states. This different behavior is possible because the hydroxyl groups in the dopamine molecule have been replaced by carbonyls.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the UEFISCDI public institution under the Romanian Ministry of Education, project code: PN-III-P4-ID-PCE-2020-0770. We are also grateful for the financial support from Romanian Ministry of Research, Innovation and Digitization through Programme 1 – Development of the National Research and Development System, Subprogram 1.2 – Institutional Performance – Funding Projects for Excellence in RDI, contract no. 37PFE/30.12.2021. The authors thank INCDTIM, Cluj-Napoca Data Center, for providing computer facilities.

Notes and references

1. J. T. Yates and H. Petek, Chem. Rev., 2006, 106, 4113–4115.
2. Y. Matsumoto, Bull. Chem. Soc. Jpn., 2007, 80, 842–855.
3. C. Sousa, S. Tosoni and F. Illas, Chem. Rev., 2013, 113, 4456–4495.
4. J. Zhao, M. Feng, D. B. Dougherty, H. Sun and H. Petek, ACS Nano, 2014, 8, 10988–10997.
5. J. L. Gray, The Physics of the Solar Cell, John Wiley & Sons, Ltd, 2010, pp. 82–129.
6. S. M. Brülls, V. Cantatore, Z. Wang, P. L. Tam, P. Malmberg, J. Stubbe, B. Sarkar, I. Panas, J. Mårtensson and S. Eigler, Chem. – Eur. J., 2020, 26, 6694–6702.
7. C. Frischkorn and M. Wolf, Chem. Rev., 2006, 106, 4207–4233.
8. T. L. Thompson and J. T. Yates, Chem. Rev., 2006, 106, 4428–4453.
9. Á. Morales-García, F. Viñes, C. Sousa and F. Illas, J. Phys. Chem. Lett., 2023, 14, 3712–3720.
10. Q. Guo, C. Zhou, Z. Ma, Z. Ren, H. Fan and X. Yang, Ann. Rev. Phys. Chem., 2018, 69, 451–472.
11. K. Sharma, V. Sharma and S. S. Sharma, Nanoscale Res. Lett., 2018, 13, 381.
12. J. Kramer, S. Soukiazian, S. Mahoney and J. Hicks-Garner, J. Power Sources, 2012, 210, 122–128.
13. N. N. Sakhadeo and T. U. Patro, Ind. Eng. Chem. Res., 2022, 61, 5366–5387.
14. A. Bandyopadhyay, K. D. Traxel and S. Bose, Mater. Sci. Eng., R, 2021, 145, 100609.
15. Y. Wang, G. Zheng, N. Jiang, G. Ying, Y. Li, X. Cai, J. Meng, L. Mai, M. Guo, Y. S. Zhang and X. Zhang, Nat. Rev. Methods Primers, 2023, 3, 68.
16. H. Lee, S. M. Dellatore, W. M. Miller and P. B. Messersmith, Science, 2007, 318, 426–430.
17. J. H. Ryu, P. B. Messersmith and H. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 7523–7540.
18. J. Liebscher, R. Mrówczyński, H. A. Scheidt, C. Filip, N. D. Hădade, R. Turcu, A. Bende and S. Beck, Langmuir, 2013, 29, 10539–10548.
19. Q. Lyu, N. Hsueh and C. L. L. Chai, Polym. Chem., 2019, 10, 5771–5777.
20. Y. Ding, L.-T. Weng, M. Yang, Z. Yang, X. Lu, N. Huang and Y. Leng, Langmuir, 2014, 30, 12258–12269.
21. V. Ball, Front. Bioeng. Biotechnol., 2018, 6, 109.
22. H. A. Lee, E. Park and H. Lee, Adv. Mater., 2020, 1907505.
23. K. Lee, M. Park, K. G. Malollari, J. Shin, S. M. Winkler, Y. Zheng, J. H. Park, C. P. Grigoropoulos and P. B. Messersmith, Nat. Commun., 2020, 11, 4848.
24. D. Aguilar-Ferrer, J. Szewczyk and E. Coy, Catal. Today, 2022, 397–399, 316–349.
25. Z. Qin, D. Li, Y. Ou, S. Du, Q. Jiao, J. Peng and P. Liu, Crystals, 2023, 13, 976.
26. M. L. Alfieri, L. Panzella and A. Napolitano, Eur. J. Org. Chem., 2024, e202301002.
27. M. L. Mueller, X. Yan, J. A. McGuire and L. S. Li, Nano Lett., 2010, 10, 2679–2682.
28. S. Kaniyankandy, S. N. Achary, S. Rawalekar and H. N. Ghosh, J. Phys. Chem. C, 2011, 115, 19110–19116.
29. F. R. Baptista, S. A. Belhout, S. Giordani and S. J. Quinn, Chem. Soc. Rev., 2015, 44, 4433–4453.
30. V. Strauss, R. A. S. er, F. Hauke, A. Hirsch and D. M. Guldi, J. Am. Chem. Soc., 2015, 137, 13079–13086.
31. S. Zhu, Y. Song, J. Wang, H. Wan, Y. Zhang, Y. Ning and B. Yang, Nano Today, 2017, 13, 10–14.
32. X.-M. Huang, L.-Z. Liu, S. Zhou and J.-J. Zhao, Front. Phys., 2020, 15, 33301.
33. A. Pandikumar, G. T. S. How, T. P. See, F. S. Omar, S. Jayabal, K. Z. Kamali, N. Yusoff, A. Jamil, R. Ramaraj, S. A. John, H. N. Lim and N. M. Huang, RSC Adv., 2014, 4, 63296–63323.
34. Y. Luo, L. Ma, X. Zhang, A. Liang and Z. Jiang, Nanoscale Res. Lett., 2015, 10, 230.
35. Z. Hsine, R. Mlika, N. Jaffrezic-Renault and H. Korri-Youssoufi, Chemosensors, 2022, 10, 249.
36. M. Abrantes, D. Rodrigues, T. Domingues, S. S. Nemala, P. Monteiro, J. Borme, P. Alpuim and L. Jacinto, J. Nanobiotechnol., 2022, 20, 495.
37. M. Chatterjee, P. Nath, S. Kadian, A. Kumar, V. Kumar, P. Roy, G. Manik and S. Satapathi, Sci. Rep., 2022, 12, 9061.
38. C. Silva, F. Simon, P. Friedel, P. Pötschke and C. Zimmerer, Nanomaterials, 2019, 9, 902.
39. P. S. Kasbe, H. Gade, S. Liu, G. G. Chase and W. Xu, ACS Appl. Bio Mater., 2021, 4, 5180–5188.
40. W. Li, W. Yang, M. Wu, M. Zhao and X. Lu, Electrochim. Acta, 2022, 426, 140776.
41. L. Zhou, Y. Zong, Z. Liu and A. Yu, Renewable Energy, 2016, 96, 333–340.
42. A. Jedrzak, T. Rebiś, M. Nowicki, K. Synoradzki, R. Mrówczyński and T. Jesionowski, Appl. Surf. Sci., 2018, 455, 455–464.
43. F. Vulcano, A. Kovtun, C. Bettini, Z. Xia, A. Liscio, F. Terzi, A. Heras, A. Colina, B. Zanfrognini, M. Melucci, V. Palermo and C. Zanardi, 2D Mater., 2020, 7, 024007.
44. R. Mrówczyński, A. Bunge and J. Liebscher, Chem. – Eur. J., 2014, 20, 1–8.
45. D.-D. Wang, X. Gao, L. Zhao, J. Zhou, S. Zhuo, Z. Yan and W. Xing, RSC Adv., 2018, 8, 16044–16051.
46. D. Damberga, V. Fedorenko, K. Grundšteins, S. Altundal, A. Šutka, A. Ramanavićius, E. Coy, R. Mrówczyński, I. Iatsunskyi and R. Viter, Nanomaterials, 2020, 10, 2438.
47. R. Mrówczyński, ACS Appl. Mater. Interfaces, 2018, 10, 7541–7561.
48. X. Xie, C. Mao, X. Liu, L. Tan, Z. Cui, X. Yang, S. Zhu, Z. Li, X. Yuan, Y. Zheng, K. W. K. Yeung, P. K. Chu and S. Wu, ACS Cent. Sci., 2018, 4, 724–738.
49. C. Wu, X. Guan, J. Xu, Y. Zhang, Q. Liu, Y. Tian, S. Li, X. Qin, H. Yang and Y. Liu, Biomaterials, 2019, 205, 106–119.
50. S. Mei, X. Xu, R. D. Priestley and Y. Lu, Chem. Sci., 2020, 11, 12269–12281.
51. I. Zmerli, J.-P. Michel and A. Makky, Multifunct. Mater., 2021, 4, 022001.
52. R. Chen, B. Lin and R. Luo, Heliyon, 2022, 8, e12105.
53. M. Wang, B. Li, Y. Du, H. Bu, Y. Tang and Q. Huang, RSC Adv., 2021, 11, 8420–8429.
54. A. Falamas, A. Petran, A.-M. Hada and A. Bende, Int. J. Mol. Sci., 2022, 23, 5483.
55. K. Hirata, K.-I. Kasai, K. Yoshizawa, G. Grégoire, S.-I. Ishiuchi and M. Fujii, Phys. Chem. Chem. Phys., 2022, 24, 10737–10744.
56. S. Chopra and L. Maidich, RSC Adv., 2014, 4, 50606–50613.
57. H. Vovusha and B. Sanyal, RSC Adv., 2015, 5, 4599–4608.
58. E. Gruber, R. A. Wilhelm, R. Pétuya, V. Smejkal, R. Kozubek, A. Hierzenberger, B. C. Bayer, I. Aldazabal, A. K. Kazansky, F. Libisch, A. V. Krasheninnikov, M. Schleberger, S. Facsko, A. G. Borisov, A. Arnau and F. Aumayr, Nat. Commun., 2016, 7, 13948.
59. Y. Miyamoto and A. Rubio, J. Phys. Soc. Jpn., 2018, 87, 041016.
60. M. Cayambe, C. Zambrano, T. Tene, M. Guevara, G. T. Usca, H. Brito, R. Molina, D. Coello-Fiallos, L. S. Caputi and C. V. Gomez, Mater. Today: Proc., 2021, 37, 4027–4030.
61. M. A. Jabed, J. Zhao, D. Kilin and T. Yu, J. Phys. Chem. C, 2021, 125, 14979–14990.
62. S. Özönder, C. Ünlü, C. Güleryüz and L. Trabzon, ACS Omega, 2023, 8, 2112–2118.
63. P. P. Fehér, Á. Madarász and A. Stirling, Chem. Methods, 2023, 3, e202200069.
64. N. A. Besley, Chem. Phys. Lett., 2004, 390, 124–129.
65. N. A. Besley and A. J. Blundy, J. Phys. Chem. B, 2006, 110, 1701–1710.
66. A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356.
67. J. M. Herbert, X. Zhang, A. F. Morrison and J. Liu, Acc. Chem. Res., 2016, 49, 931–941.
68. N. S. Hill and M. L. Coote, in Annu. Rep. Comput. Chem., ed. D. A. Dixon, Elsevier, 2019, vol. 15, pp. 203–285.
69. M. Coros, F. Pogăcean, L. Măgerusan, M.-C. Roşu, A. S. Porav, C. Socaci, A. Bende, R.-I. Stefan-van Staden and S. Pruneanu, Sens. Actuators, B, 2018, 256, 665–673.
70. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
71. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
72. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
73. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
74. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
75. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
76. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
77. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
78. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
79. A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597.
80. H. Li and J. H. Jensen, Theor. Chem. Acc., 2002, 107, 211–219.
81. B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2018, 148, 034104.
82. Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Chem. Phys., 2007, 126, 114302.
83. R. R. Valiev, V. Cherepanov, R. Nasibullin, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500.
84. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
85. A.-R. Allouche, J. Comput. Chem., 2011, 32, 174–182.
86. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
87. R. Dennington, T. Keith and J. Millam, Gaussview 6.1.1, Semichem Inc., Shawnee Mission, KS, 2009.
88. A. H. Castro-Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
89. L. Khalafi, M. Rafiee and S. Fathi, Spectrochim. Acta, Part A, 2014, 118, 695–701.
90. K. F. Mak, M. Y. Sfeir, Y. Wu, C. H. Lui, J. A. Misewich and T. F. Heinz, Phys. Rev. Lett., 2008, 101, 196405.
91. K. F. Mak, L. Ju, F. Wang and T. F. Heinz, Solid State Commun., 2012, 152, 1341–1349.
92. L. Yang, J. Deslippe, C.-H. Park, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2009, 103, 186802.
93. P. E. Trevisanutto, M. Holzmann, M. Côté and V. Olevano, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 121405.
94. R. Denk, M. Hohage, P. Zeppenfeld, J. Cai, C. A. Pignedoli, H. Söde, R. Fasel, X. Feng, K. Müllen, S. Wang, D. Prezzi, A. Ferretti, A. Ruini, E. Molinari and P. Ruffieux, Nat. Commun., 2014, 5, 4253.
95. Y. Ge and T. S. Fisher, Front. Nanotechnol., 2022, 4, 999292.
96. S. Kim, S. W. Hwang, M.-K. Kim, D. Y. Shin, D. H. Shin, C. O. Kim, S. B. Yang, J. H. Park, E. Hwang, S.-H. Choi, G. Ko, S. Sim, C. Sone, H. J. Choi, S. Bae and B. H. Hong, ACS Nano, 2012, 6, 8203–8208.
97. Z. Jin, P. Owour, S. Lei and L. Ge, Curr. Opin. Colloid Interface Sci., 2015, 20, 439–453.
98. X. E. Zhao, C. H. Lei, Y. H. Wang, F. Qu, S. Y. Zhu, H. Wang and J. M. You, RSC Adv., 2016, 6, 72670–72675.
99. D. K. Rai and A. Shukla, Sci. Rep., 2019, 9, 7958.
100. T. Tasnim, M. J. Ayodele and S. P. Pitre, J. Org. Chem., 2022, 87, 10555–10563.
101. S. Kümmel, Adv. Energy Mater., 2017, 7, 1700440.
102. N. T. Maitra, Annu. Rev. Phys. Chem., 2022, 73, 117–140.
103. D. Mester and M. Kállay, J. Chem. Theory Comput., 2022, 18, 1646–1662.
104. J. M. Herbert, Phys. Chem. Chem. Phys., 2024, 26, 3755–3794.
105. J. Liang, X. Feng, D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2022, 18, 3460–3473.
106. P. Avouris and B. N. J. Persson, J. Phys. Chem., 1984, 88, 837–848.
107. H. Petek, J. Chem. Phys., 2012, 137, 091704.
108. G. Floß, G. Granucci and P. Saalfrank, J. Chem. Phys., 2012, 137, 234701.
109. H.-T. Chen, J. Chen, D. V. Cofer-Shabica, Z. Zhou, V. Athavale, G. Medders, M. F. S. J. Menger, J. E. Subotnik and Z. Jin, J. Chem. Theory Comput., 2022, 18, 3296–3307.
110. S. Chen, N. Ullah, Y. Zhao and R. Zhang, ChemPhysChem, 2019, 20, 1–6.
111. W. Ouyang, W. Dou and J. E. Subotnik, J. Chem. Phys., 2015, 142, 084109.
112. W. Dou, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2015, 142, 084110.
113. W. Dou, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2015, 142, 234106.
114. W. Dou, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2015, 143, 189902.
115. J. Chen, Z. Jin, W. Dou and J. Subotnik, J. Phys. Chem. C, 2021, 125, 2884–2899.
116. Z. Jin and J. E. Subotnik, J. Chem. Theory Comput., 2021, 17, 614–626.
117. A. Bende, A.-A. Farcas, A. Falamas and A. Petran, Phys. Chem. Chem. Phys., 2022, 24, 29165–29175.
118. A. Bende and A.-A. Farcas, Int. J. Mol. Sci., 2023, 24, 2906.
119. C. H. Lui, K. F. Mak, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 127404.
120. J. Wang, S. Cao, Y. Ding, F. Ma, W. Lu and M. Sun, Sci. Rep., 2016, 6, 24850.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00432a

---