Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Time-resolved surface reaction kinetics in the pressure gap
Tzu-En
Chien
 ,
Lea
Hohmann
,
Lea
Hohmann
 and
Dan J.
Harding
and
Dan J.
Harding
 *
*
Department of Chemical Engineering, KTH Royal Institute of Technology, Stockholm 100 44, Sweden. E-mail: djha@kth.se
First published on 30th January 2024
Abstract
We extend the use of our recently developed Near-Ambient Pressure Velocity Map Imaging (NAP-VMI) technique to study the kinetics and dynamics of catalytic reactions in the pressure gap. As an example, we show that NAP-VMI combined with molecular beam surface scattering allows the direct measurement of time- and velocity-resolved kinetics of the scattering and oxidation of CO on the Pd(110) surface with oxygen pressures at the surface up to 1 × 10−5 mbar, where different metastable surface structures form. Our results show that the c(2 × 4) oxide structure formed at low O2 pressure is highly active for CO oxidation. The velocity distribution of the CO2 products shows the presence of two reaction channels, which we attribute to reactions starting from two distinct but rapidly interconverting CO binding sites. The effective CO oxidation reaction activation energy is Er = (1.0 ± 0.13) eV. The CO2 production is suppressed at higher O2 pressure due to the number of antiphase domain boundaries increasing, and the missing row sites are filled by O-atoms at O2 pressures approaching 1 × 10−6 mbar. Filling of these sites by O-atoms reduces the CO surface lifetime, meaning the surface oxide is inactive for CO oxidation. We briefly outline further developments planned for the NAP-VMI and its application to other types of experiments.
1 Introduction
CO oxidation on palladium is one of the most studied catalytic processes. It is important for emission control in automobiles and in industries. It is also a simple system which has been used to study the details of catalytic reaction mechanisms. Systematic studies of CO oxidation on palladium can be traced back to Ertl et al. from 1969.1–5 Recent studies have focused on reactions under high pressure, where different surface structures can form, using in situ/operando techniques.6–12 These studies of CO oxidation essentially mirror the developments in experimental techniques to study surface reactions, from Temperature Programmed Desorption (TPD) and Low Energy Electron Diffraction (LEED) in the early days up to recent Surface X-ray Diffraction (SXRD) and Ambient Pressure X-ray Photoelectron Spectroscopy (AP-XPS). Despite this work, questions remain regarding the active phase of the catalyst during the reaction and the possible reaction mechanisms.13–18 The desire to better understand surface reactions, to close the “pressure gap” between surface science and catalyst applications, and to answer these open questions is still driving the development of new experimental techniques to study surface reactions. One of the current frontiers is the development of experiments that combine (near-) ambient pressure with high time resolution, allowing the direct measurement of reaction kinetics on metastable surfaces. The time-resolved AP-XPS techniques recently developed in Lund can probe both the surface and the gas composition during reactions with sub-ms resolution.19,20 AP-XPS probes the product density above the surface rather than the reactive flux. While this distinction probably does not deteriorate the experimental time resolution, due to the small distance at which the gas ionization occurs above the surface, some information about the products is lost. In contrast, the near-ambient pressure velocity map imaging (NAP-VMI) technique we apply here cannot directly probe the surface but allows the time-dependence and the speed distribution of the reaction products to be measured. This dynamic information, such as the product speed distributions, can be extremely valuable. It enables the separation of multiple reaction channels, which is not possible with most other techniques, and provides information about the reaction mechanism(s).Among the low Miller index palladium surfaces, CO oxidation on Pd(110) is the least explored, probably due to the surface reconstructions that occur during adsorption. Despite this, research on the Pd(110) surface has been conducted in a pressure range from ultra-high vacuum (UHV) up to several bars using different techniques. Interactions of Pd(110) and oxygen have been studied with low energy electron diffraction (LEED),1,21–23 thermal desorption spectroscopy (TDS),21,23–25 scanning tunneling microscopy (STM),26–28 X-ray photoelectron spectroscopy (XPS),22,23,29,30 surface X-ray diffraction (SXRD)22 and DFT.22,28 Oxygen adsorbs dissociatively on Pd(110) above 160 K and several structures were observed, p(1 × 3), p(1 × 2), (2 × 3)-1D, c(2 × 4), c(2 × 6) and complex structures at different surface temperatures and oxygen exposures.21 The oxygen-induced reconstructions of Pd(110) are complicated and the c(2 × 4) structure is by far the most investigated. The c(2 × 4) structure consists of a Pd(110) (1 × 2)-missing row structure and oxygen atoms adsorbed on the ridge rows in a zigzag pattern.22 The O/Pd(110) surface forms the c(2 × 4) structure at 10−8 mbar which remains up to oxygen pressures of 10−7 mbar. On further increase of the oxygen pressure, the anti-phase domain boundaries fill up the Pd(110) missing row structure until, at oxygen pressure 5 × 10−6 mbar, all missing row structure disappears. Higher oxygen pressures lead to complex (7 × 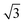 ) and (9 ×
) and (9 × 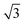 ) surface oxide structure.22
) surface oxide structure.22
CO adsorbs molecularly on Pd(110) at room temperature and can also cause a (1 × 2)-missing row reconstruction.30–34 At low CO coverage (θCO < 0.3), CO randomly adsorbs on (1 × 1)-pristine surface; at high CO coverage (0.3 < θCO < 0.75), Pd(110) reconstructs into (1 × 2)-missing row structure and forms a c(4 × 2)–CO structure in which CO molecules are able to adsorb both on the ridges and in the troughs.31,33 This interpretation of the adsorption sites is suggested by IR spectra and XPS; however, it has been questioned by Zhang et al.34 They suggested that CO adsorbs on first-layer Pd short-bridge sites and second-layer Pd bridge sites using the extended London–Eyring–Polyani–Sato (LEPS) method. CO oxidation on Pd(110) has been studied in conventional UHV setups with LEED,3,35 RAIRS35 and XPS;36,37 or in operando setups with PM-IRAS,15,16 AP-XPS6,30,38 and Planar Laser Induced Fluorescence (PLIF).10,38 Many of these studies come to conflicting conclusions, presumably due to differences in measurement methods and reactor design. Kondoh et al. used AP-XPS to study the Pd(110) surface structure during CO oxidation at 200 mTorr.6 They observed the increase in CO2 production, which coincided with the formation of the complex (7 ×  ) and (9 ×
) and (9 ×  ) surface oxides and concluded that these surface oxides are the active phases. On the other hand, Gao et al. showed a transient high CO2 turnover frequency (TOF) just after “light-off” and reached a lower plateau due to mass transfer limitation (MTL).15,18 In the MTL region, only ∼0.01% of active sites are required to sustain this level of reaction. From this observation, they concluded that the surface oxide is not the most active phase. Instead, they asserted that the reduced metal is the most active phase at both low- and high-pressure conditions.
) surface oxides and concluded that these surface oxides are the active phases. On the other hand, Gao et al. showed a transient high CO2 turnover frequency (TOF) just after “light-off” and reached a lower plateau due to mass transfer limitation (MTL).15,18 In the MTL region, only ∼0.01% of active sites are required to sustain this level of reaction. From this observation, they concluded that the surface oxide is not the most active phase. Instead, they asserted that the reduced metal is the most active phase at both low- and high-pressure conditions.
In this work, we demonstrate the extension of NAP-VMI to directly study the time-resolved kinetics and dynamics of CO oxidation reactions on Pd(110) in the “pressure gap”. To obtain a full understanding of the scattering/reaction processes, both CO and CO2 are probed. Time-resolved kinetics and speed distributions of the CO2 products are presented. The results show that while CO2 production first increases with oxygen pressure, it is highly suppressed at O2 pressures above 1 × 10−7 mbar. CO surface lifetimes measured under the same conditions are shown to be much shorter than those on clean surfaces. The CO2 speed distribution shows evidence for two reaction channels, which we attribute to CO approaching O-atoms from different binding sites.
2 Methods
2.1 Near-ambient pressure velocity map imaging
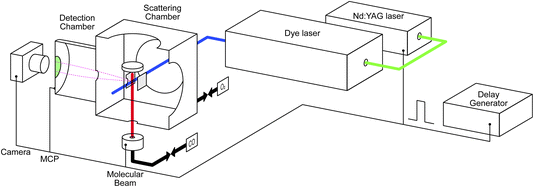
The study was conducted with our recently developed near-ambient pressure velocity map imaging instrument. The details can be found elsewhere;39 a brief description is provided below. Fig. 1 illustrates the experimental setup. It consists of a scattering chamber, detection chamber, preparation chamber (not shown), molecular beam source chamber (not shown), laser system, and delay generator. A Pd(110) single crystal with a dimension of 10 mm in radius and 2 mm in thickness is mounted on a homemade manipulator. This allows the sample to move between the preparation and scattering chambers. It can be heated up to 1000 K, and a chromel-alumel (K-type) thermocouple is attached to the edge of the crystal for temperature measurement and control. The sample is first cleaned in the preparation chamber by argon ion sputtering for 10 minutes and is then annealed at 1000 K for 5 minutes, followed by cooling the sample below 400 K by turning off the heating element. Several cleaning cycles are repeated before moving the sample to the scattering chamber. The ion optics for velocity mapping are located in the center of the scattering chamber, with the sample surface positioned 16 mm above the ionization center. We used the conventional three-electrode setup (repeller, extractor, and ground) for the velocity mapping. The voltages are set at R = 1000 V, and E1 = 720 V, with the rest of the electrodes grounded.Tunable UV laser pulses (210–216 nm) are generated by tripling the fundamental output (630–648 nm) of a dye laser (DCM in ethanol) pumped by the second harmonic output of a pulsed Nd:YAG laser (532 nm). CO molecules are ionized using a 2+1 REMPI process via the E1Π ← X1Σ+ transition.40 We use the S(10) transition for detection of scattered molecules as the J = 10 state is barely populated in the incident beam but is one of the most populated in the scattered distribution. CO2 is detected using laser ionization around 212 nm. We expect this to be a 2+1 REMPI process, presumably via 1-photon-forbidden 1Σ+g and/or 1Πg Rydberg states.41–46 Work is ongoing in our lab to try to determine these details. Typical laser power is around 0.7 mJ per pulse before the laser enters the scattering chamber. Using resonant ionization schemes opens the possibility to make product-state-resolved scattering measurements for CO and, with more work, CO2; however, we do not do that in the current study.
Ions are velocity-mapped and projected onto a Z-stack microchannel plate (MCP) detector (Photek), which is located in the detector chamber. This is separated by a 3 mm aperture from the scattering chamber. A short gate pulse applied to the MCP allows us to select the targeted ions and reduce background noise. A phosphor screen mounted after the MCP converts the electron pulses into light pulses, which are captured by a CCD camera. Imaging detection offers the possibility to measure scattering angular distributions quickly and with high resolution. However, one of the compromises we made in designing the NAP-VMI was the small size of the VMI volume and the corresponding small acceptance angle for particles scattered from the surface. In our previous report,39 we determined a maximum angular acceptance of ±25° for surface scattering. In practice, the angular acceptance is smaller (<±15° in the x–y plane) due to combination of the molecular beam radius, laser ionization volume, and the VMI region, which prevents us from measuring angular distributions for CO2 reaction products. Further developments of the ion optics will attempt to increase the angular acceptance.
We extend the NAP-VMI to obtain kinetic measurements by taking advantage of using a pulsed laser and a pulsed molecular beam. Controlling the delay between the two allows for time-dependent measurements. A delay generator is used to control the delay times for several components: the laser pulse, the molecular beam pulse, the MCP gating, and the camera shutter. The laser has a repetition rate of 10 Hz. The pulsed valve (Amsterdam Piezo Valve) operates at a 10 Hz repetition rate with a valve opening time of 50 μs.47 A gas pressure of 1–3 bar is maintained behind the pulsed valve; we use either pure gas or a mixture of 10% to 40% of the gas with helium. With a 10% beam, we estimate that around 1012 molecules reach the scattering chamber per pulse, which means that less than 0.002 ML of CO is introduced to the surface per molecular beam pulse. In the CO oxidation experiment, the second gas is introduced to the scattering chamber using a leak valve, maintaining a constant pressure of up to 10−3 mbar as measured by a cold cathode gauge. Dosing in this way has several advantages: we can achieve higher pressures, which the NAP-VMI is designed for. Our method is a simple alternative to using a second molecular beam, including an easier method for estimating the flux to the surface. Additionally, the system's chemical potential is better defined than with pulsed molecular beams. Compared to earlier titration experiments, where the surface was first dosed with oxygen and then the reaction with CO was studied, we are able to maintain the surface at different oxygen coverages for extended periods.
2.2 Data treatment
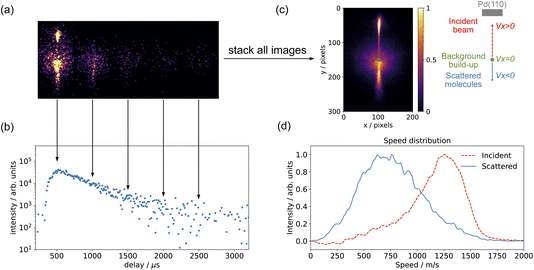
The methods we use to determine the time-dependent kinetics of surface reactions are based on the Velocity Resolved Kinetics (VRK) method developed in Alec Wodtke's group in Göttingen.48,49 Velocity resolved detection allows the time-dependent flux of desorbing molecules to be determined by physically deconvoluting the surface residence time from the spread in flight time from the surface to the ionization region.Fig. 2 shows the basic data treatment workflow from a single image to the full speed distribution. In principle, a single laser shot at a fixed molecular beam delay provides an image of the scattering velocity distribution. In practice, due to the limited signals in each image, we combine several tens or hundreds of laser shots to acquire a complete velocity map image. For time-resolved measurements, we recorded images while varying the delay between the pulsed molecular beam and the pulsed laser. Fig. 2(a) shows the individual images of CO scattering on Pd(110) across a series of molecular-beam delays; while Fig. 2(c) shows the images combined over all delay scans, which represents the whole scattering event. Three distinct features are visible in the images: (1) the background build-up at the center of the image, these are molecules which have undergone multiple scattering events with the surface and with the ion optics and are centered at zero velocity in the lab frame; (2) the upper part represents the incident molecular beam; and (3) the lower part represents the scattered molecules. Velocity calibration was determined from the known velocities of N2 fragments from N2O photodissociation.39 For CO (m/z = 28), one pixel is equivalent to 12 m s−1. Fig. 2(b) shows the time-resolved measurement of CO scattering, with each data point collected from an individual molecular-beam delay image, as shown in Fig. 2(a). For the CO scattering signals, we selected a region spanning 40–60 pixels and a 20-degree sector below the center. Fig. 2(d) shows the speed distribution of both the CO incident beam (a 20-degree sector above the center) and the scattered molecules (a 20-degree sector below the center); the contribution of background build-up is removed by averaging the build-up signal outside the surface normal direction. The flux of CO is calculated by multiplying the CO signal by its velocity. The same method was used for measuring CO2. However, the pixel to velocity calibration was different. For CO2 (m/z = 44), one pixel is equivalent to 10 m s−1.
3 Results and discussion
3.1 CO scattering on clean Pd(110)
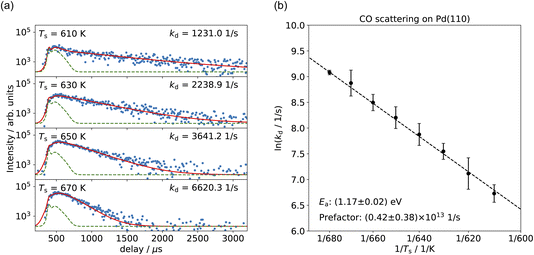
Fig. 3(a) shows the time-resolved measurement of CO scattering on Pd(110) at various temperatures. The residence time of CO molecules decreases as surface temperature increases. The kinetic trace does not have the bi-exponential features observed in ref. 48, therefore the kinetic model of the CO scattering flux can be described with eqn (1).48,49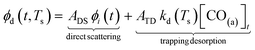 | (1) |
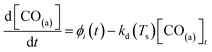 | (2) |
We fit this kinetic model to the experimental kinetic traces to determine the desorption rate coefficients of CO on Pd(110) for the known surface temperatures. The red curves in Fig. 3(a) show typical fits. Fig. 3(b) shows the Arrhenius plot of the rate coefficients determined in this way for CO trapping desorption. From this, we determine a desorption activation energy of (1.17 ± 0.02) eV and a pre-factor of (0.42 ± 0.38) × 1013 s−1. Jones et al. report a desorption activation energy of 1.27 eV to 1.37 eV,37 depending on coverage determined from a Redhead analysis50 of TPD spectra with an assumed pre-factor of 5 × 1013 s−1. The discrepancy between our activation energy and that of Jones et al.37 appears to be due to the large value of the pre-factor they used, leading to a larger activation energy.
Transition state theory (TST)51 allows us to derive the CO binding energy on Pd(110) and compare it with other studies. The sticking probability is a key parameter in TST. Several studies have reported varying values for the initial sticking probability of CO on Pd(110), ranging from 0.4 to 1.37,52–54 We determine binding energies from a 2D TST calculation48,55 and obtain D2D0 = (1.46–1.52) eV, depending on the value of the sticking probability that we use, which is consistent with previous findings. Conrad et al. used TPD to determine the isosteric energy of adsorption of 1.17 eV to 1.73 eV.56 Raval et al. reported the heats of adsorption of 1.38 eV to 1.9 eV.32 The reasons for the broad spread of the heats of adsorption in their reported adsorption energy are unclear but might be due to the relative ease with which surface reconstructions can be induced on Pd(110), leading to different surface structures and various adsorption sites, that are beyond the scope of this study.
3.2 CO oxidation on Pd(110)
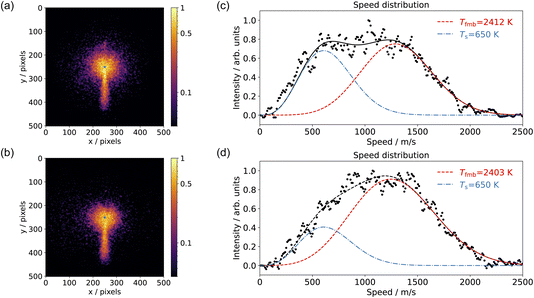
Fig. 4 shows examples of CO2 velocity map images along with their speed distributions normal to the surface. We selected the area below the center within a 20-degree sector. Fig. 4(a) shows the CO2 production from CO oxidation on Pd(110) at pO2 = 7.5 × 10−8 mbar in the scattering chamber, using a pure CO beam at surface temperature Ts = 650 K; Fig. 4(b) used a 10% O2 in He beam at surface temperature Ts = 650 K and pCO = 5 × 10−6 mbar in the scattering chamber; Fig. 4(c) and (d) show the corresponding speed distributions for Fig. 4(a) and (b), respectively. The CO2 speed distribution is very broad and has a significant intensity at both low (thermal) and high (hyperthermal) speeds. This suggests two reaction channels: one producing slow CO2 and one fast CO2. It is not the first time that two CO oxidation channels have been observed on a metal surface. Neugebohren et al. observed the two channels for CO oxidation on Pt(111) surface.57 They attributed the thermal channel to reactions through step sites and the hyperthermal channel to reactions occurring on terrace sites. Moula et al. observed the two channels for CO oxidation on Pd(110) surface,58,59 with the slow component having a wider angular distribution. They associated the fast component with reactions on the flat surface and the slow component with reactions on surface structural defects. We adopted the same fitting methods for our speed distribution: the slow component has the Maxwell–Boltzmann distribution of the surface temperature, and the fast component is described by a flowing Maxwell–Boltzmann distribution.60,61 The energy of the fast component was expressed in the temperature unit as Tfmb = 〈E〉/2k, where 〈E〉 is the mean energy and k is the Boltzmann constant. Our CO2 speed distributions are in agreement with their findings, although we did not observe the difference in angular distribution due to the limitation of the VMI angular acceptance in the current setup.Several reaction mechanisms have been proposed for CO oxidation on metal surfaces, especially when modeling CO oxidation oscillations.2 These include reactions involving subsurface oxygen and reactions occurring on different active sites (step, terrace, atop, bridge, hole, …).57,62,63 To investigate the potential role of subsurface oxygen atoms in CO oxidation, we conducted the experiment using an O2 beam with leaked CO molecules in the scattering chamber, shown in Fig. 4(b) and (d). Under these experimental conditions, we assume we can rule out the involvement of subsurface oxygen. The results from the CO2 speed distribution still indicate two reaction channels, suggesting that subsurface oxygen atoms are not essential for producing these two channels. It does not imply that subsurface oxygen atoms do not exist; rather, it emphasizes that they are unimportant in the context of the active surface O-atoms. Therefore, we will only consider surface oxygen atoms in subsequent discussions.
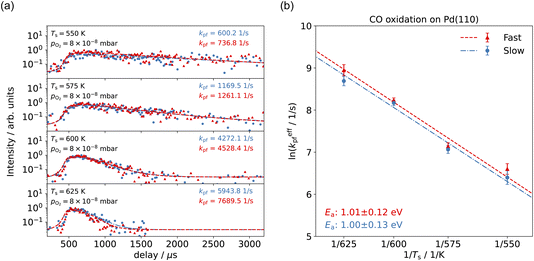
With VMI detection, we can independently measure the kinetics of the reactions producing thermal and hyperthermal CO2 based on the different product velocity distributions. Fig. 5(a) shows the kinetic traces of CO2 production for surface temperature Ts = 550–625 K at pO2 = 8 × 10−8 mbar in the scattering chamber, with a CO pure beam. The blue dots, representing the slow component, are integrated from the 20–50 pixel range within a 20-degree sector below the center; the red dots, which represent the fast component, are integrated from the 120–180 pixel range within a 20-degree sector below the center. Unlike the Pt(111) case,57 where the different speed components had different kinetics, the time-resolved kinetic traces of CO2 production for the slow and the fast component are almost identical. Under these reaction conditions, we expect to have pseudo-first order kinetics where the time-dependence of the reaction rate depends only on the CO coverage. The fact that we observe the same time dependence for both speed components suggests that the CO molecules are able to move freely on the surface on a faster (sub μs) time-scale than our experiment can probe. Another possibility is the existence of two types of surface oxygen atoms leading to two reaction channels. Based on previous studies, there is only one type of O-atom on the O/Pd(110) surface at this oxygen pressure22 though we cannot currently rule out the influence of steps or other defects.
We have developed a simple kinetic model to describe the reaction using a modified Langmuir–Hinshelwood (L–H) mechanism based on fast diffusion and interchange of CO between two distinct binding sites, from where the reaction can start, with one oxygen adsorption site. We assume there is no oxygen atom desorption and that CO2 immediately desorbs from the surface after reaction:
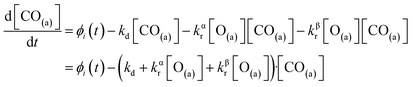 | (3) |
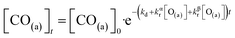 | (4) |
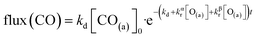 | (5) |
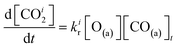 | (6) |
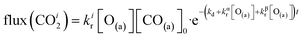 | (7) |
The reaction rate coefficient is k(Ts) = kd + (kαr + kβr)·[O(a)]. Since the oxygen flux to the surface is much larger than the CO flux; therefore, we assumed the number of O-atoms on the surface, [O(a)] remained constant throughout the reaction, giving a pseudo first-order kinetics rate coefficient. By fitting eqn (7) to the kinetic traces we obtain an effective pseudo-first order rate coefficient kpf(Ts) = kd + (kαpf + kβpf). At low O-coverage, we can use the CO desorption rate coefficients (kd) obtained from CO scattering on clean Pd(110) to extract an effective pseudo-first order rate for the oxidation reaction, keffpf(Ts) = kαpf + kβpf. Fig. 5(b) shows the Arrhenius plot of the effective CO oxidation rate coefficients obtained from each channel. In both cases, an activation energy of (1.0 ± 0.13) eV is determined. The fact that we observe two reaction channels with the same time-dependence, and therefore rates, leads us to the conclusion that we are still measuring an effective rate, as the CO interchange is too fast for us to resolve. Determining the individual activation energies will require either better time-resolution to separate the two channels and/or accurate measurement of the branching fractions between the two channels. This interpretation is consistent with the observations31,32 that two binding modes are populated for CO on reconstructed Pd(110) and the insensitivity to steps and other defects compared to CO on Pt. The two sites are close (in space and energy) which makes it more likely that they remain in equilibrium during the reaction.
There are multiple values of activation energy reported for CO oxidation on Pd(110) between 0.47 eV and 1.49 eV.64–67 The broad range of activation energy in previous reports might be due to differences in experimental conditions and methods. Berlowitz et al. reported values of 1.13 eV and 1.44 eV for low surface temperatures (<460 K) and higher temperatures (475 K to 625 K), respectively.66 Ehsasi et al. obtained a low value of 0.47 eV under CO oscillation conditions.64 Nakao et al. report a high value of 1.49 eV when using a mixed CO/O2 molecular beam.65,67
Fig. 6 shows the changes in the effective CO oxidation rate coefficient, keffpf = kαpf + kβpf and total CO2 production as a function of oxygen pressure, ranging from 2.5 × 10−8 to 1 × 10−6 mbar at 650 K. The apparent rate coefficient for CO2 from both thermal and hyperthermal channel, k(Ts), increases with oxygen pressure and reaches a maximum at pO2 = 5 × 10−7 mbar. Under these conditions, the reactions are so fast that we are limited by the time resolution of the molecular beam. The total CO2 production initially increases with oxygen pressure and reaches its maximum at pO2 = 5 × 10−8 mbar. Further increases in oxygen pressure suppress the CO2 production. In an effort to understand the changes that are occurring in the reaction mechanism at higher oxygen pressure we have performed kinetic measurements probing the CO under the same conditions. Fig. 7 shows the CO scattering kinetics at Ts = 600 K with no oxygen and pO2 = 5 × 10−6 mbar in the scattering chamber. On the clean Pd(110) surface (no oxygen in the chamber), only a few CO molecules directly scatter, and most of the CO molecules have a longer residence time. At high O2 pressures, the CO scattering signal becomes stronger than that from the clean metal surface and the lifetime becomes much shorter, implying that CO molecules do not adsorb/stick as strongly on O/Pd(110) as on the clean surface. This can be due to a reduction in the CO sticking probability, leading to direct scattering, or due to a reduction in the CO binding energy, leading to faster desorption at a given temperature. We tried to derive the adsorption activation energy from the temperature-dependent desorption rates, but they are too fast even at room temperatures and we are currently unable to measure them. This very fast desorption reduces the probability of CO oxidation and suppresses the CO2 production. Westerström et al. reported a phase diagram for Pd(110) under various oxygen pressures.22 A missing row-Pd(110) with a c(2 × 4)–O structure forms at low O2 pressure (10−8 mbar to 10−7 mbar). As O2 pressure increases, the number of anti-phase domain boundaries increases, causing the missing row structure to disappear at pO2 = 1 × 10−6 mbar. The surface eventually forms a (2 × 1)–2O structure and later transforms into complex surface oxide structures. Our results directly demonstrate that the c(2 × 4)–O structure, which forms at low oxygen pressure, is highly active. In contrast, the complex surface oxide structures formed at high oxygen pressure are less reactive because CO desorbs very quickly at the relevant temperature.
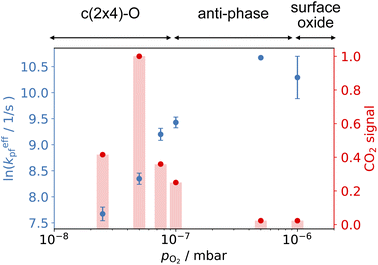 | ||
| Fig. 6 Comparison of the CO oxidation apparent rate coefficients (left) and normalized total CO2 production (right) at 650 K and various O2 pressure in the scattering chamber. CO2 signal is normalized to pO2 = 5 × 10−8 mbar. (Top) shows the corresponding structure in ref. 22. | ||
3.3 Two reaction channels
Understanding how energy transfer processes are controlled by the local geometry can provide information about how reaction pathways and transition states change in the presence of different active sites.68 Ladas et al. conducted a CO oxidation titration experiment on a highly oxygen-covered Pd(110) surface by LEED.3 Their results showed that in the beginning of the reaction, the surface exhibited a c(2 × 6)–O structure. Fukui et al. used RAIRS to identify the CO adsorption site on a Pd(110)–c(2 × 4)–O surface.35 At the beginning of their thermal desorption reaction spectroscopy (316 K), CO molecules had adsorption peaks at 1910 and 1960 cm−1. These peaks align with the findings from Raval et al. on CO/Pd(110), that they assign these peaks to CO molecules adsorbed on the ridges and in the troughs on the Pd(110)–(1 × 2) missing row structure.31 On the other hand, Zhang and co-workers did not agree with the CO adsorption sites proposed by Raval et al.; they suggest that CO adsorbs on first layer Pd short-bridge sites and second layer Pd bridge sites.34Based on the results presented in Fig. 4–7, we propose the following reaction pathway. CO molecules on the c(2 × 4)–O surface can approach the O-atoms from the two CO adsorption sites described in previous reports31,34 and result in two reaction channels, observed in our experiment. If the CO species interconvert quickly, this can lead to two channels with the same time dependence. As the O2 pressure increases, the anti-phase domain boundaries fill up the missing row structure. This could give the appearance of a Pd(110)–c(2 × 6)–O structure when observed by LEED.3 Consequently, this complex surface oxide structure prevents the adsorption of CO molecules to the surface. Fig. 8 shows the speed distribution of CO2 at pO2 = 5 × 10−6 mbar, where the CO2 reaction is significantly suppressed. Due to the low intensity in CO2 signal, the image was acquired at a single molecular beam delay (where the most CO2 was detected) and integrated over 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots. The results show that the slow channel is highly suppressed at both low (400 K) and high temperature (650 K); and the fast component exhibits a faster speed distribution (higher average kinetic energy) at low surface temperatures. The suppression of the slow component can be attributed to the disappearance of one of the CO adsorption sites. At pO2 > 1 × 10−6 mbar, the O/Pd(110) shows a Pd(110)–c(2 × 1)–2O surface oxide structure, and the Pd(110)-missing row structure is filled.22 The filling of the missing row suggests the elimination of the trough structures. Thus, we attribute the slow channel to the CO adsorption in the troughs of the Pd(110)–(1 × 2) missing row structure, supporting the findings of Raval et al.31 The fast channel can result from CO adsorption on the ridges of the Pd(110)–(1 × 2) missing row structure or the defect sites on the Pd(110)–c(2 × 1)–2O surface oxide (both on the top layer of O/Pd(110)). Yamanaka reported the increases of CO2 vibrational and rotational temperatures (which correspond to reductions in translational kinetic energies) on the Pd(110)–(1 × 2) missing row structure compared to the pristine Pd(110) surface.63 This observation supports our assumptions that the slow channel is associated with the Pd(110)–(1 × 2) missing row structure, where the CO can react from the troughs. The reason why a lower surface temperature results in CO2 molecules with higher average kinetic energy is currently unclear. It could be due to the rigidity of the surface.69
000 laser shots. The results show that the slow channel is highly suppressed at both low (400 K) and high temperature (650 K); and the fast component exhibits a faster speed distribution (higher average kinetic energy) at low surface temperatures. The suppression of the slow component can be attributed to the disappearance of one of the CO adsorption sites. At pO2 > 1 × 10−6 mbar, the O/Pd(110) shows a Pd(110)–c(2 × 1)–2O surface oxide structure, and the Pd(110)-missing row structure is filled.22 The filling of the missing row suggests the elimination of the trough structures. Thus, we attribute the slow channel to the CO adsorption in the troughs of the Pd(110)–(1 × 2) missing row structure, supporting the findings of Raval et al.31 The fast channel can result from CO adsorption on the ridges of the Pd(110)–(1 × 2) missing row structure or the defect sites on the Pd(110)–c(2 × 1)–2O surface oxide (both on the top layer of O/Pd(110)). Yamanaka reported the increases of CO2 vibrational and rotational temperatures (which correspond to reductions in translational kinetic energies) on the Pd(110)–(1 × 2) missing row structure compared to the pristine Pd(110) surface.63 This observation supports our assumptions that the slow channel is associated with the Pd(110)–(1 × 2) missing row structure, where the CO can react from the troughs. The reason why a lower surface temperature results in CO2 molecules with higher average kinetic energy is currently unclear. It could be due to the rigidity of the surface.69
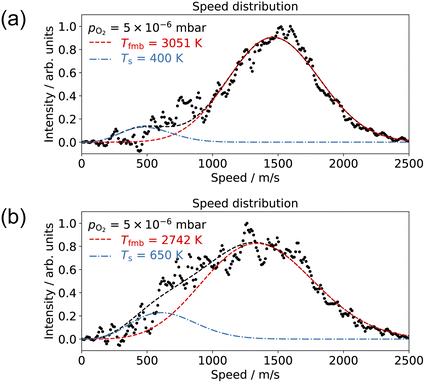 | ||
| Fig. 8 Comparison of the CO2 speed distribution for CO oxidation with 10% CO/He molecular beam and pO2 = 5 × 10−6 mbar in the scattering chamber at surface temperatures of (a) 400 K and (b) 650 K. | ||
The reaction scenario we present, involving two interchangeable CO adsorption sites and one oxygen adsorption site, is consistent with our experimental data, kinetic modeling, and previous reports. However, there are still unresolved aspects in understanding the complete reaction mechanisms, such as the CO adsorption site on the metastable Pd(110) surface structures and dynamics of CO2 products. Further experimental developments to improve the time resolution and angular acceptance of the NAP-VMI may help, as will the support of high-level theory.
4 Conclusion and outlook
Time- and velocity-resolved kinetics of the scattering and oxidation of CO on Pd(110) surface with oxygen pressures at the surface up to 1 × 10−5 mbar were studied using NAP-VMI combined with molecular beam surface scattering techniques. For CO scattering, we determined the CO desorption activation energy to be Ed = (1.17 ± 0.03) eV. For CO oxidation, we identified two reaction channels from the speed distribution. The apparent CO reaction activation energy was Er = (1.0 ± 0.13) eV. The reaction scenario we propose, which involves two types of interchangeable CO adsorption sites that react with a single type of oxygen adatom, is consistent with previous reports, our experimental data, and kinetic modeling. Furthermore, we attribute the fast component to CO adsorption on the top layer of O/Pd(110) structures and the slow component to CO adsorption on the troughs of the Pd(110)–(1 × 2) missing row structure. Under different oxygen pressures, various metastable surface structures can be formed. CO2 production is suppressed at high oxygen pressure (>1 × 10−7 mbar), where the anti-phase and complex surface oxide structures are formed. Therefore, the Pd(110) surface oxide is less active than the clean Pd(110) for CO oxidation reaction. Finally, the reactive molecular beam scattering from different metastable surfaces, made possible with NAP-VMI, can provide new insight into surface reactions and reaction mechanisms. The combination of kinetic and dynamic information about reaction products complements more surface sensitive methods such as AP-XPS, RAIRS, or LEED. The NAP-VMI technique should be applicable to a range of other gas-condensed phase interfaces where high pressures are scientifically interesting, e.g. combined with LID-VRK,70 or unavoidable, such as scattering from liquid microjets. Further developments to the instrument are possible to allow operation at higher pressures and to move towards ambient pressure VMI.Author contributions
Tzu-En Chien: data curation; formal analysis; investigation; methodology; visualization; writing – original draft. Lea Hohmann: data curation; formal analysis; investigation; software; methodology; writing – review & editing. Dan J. Harding: project administration; supervision; funding acquisition; investigation; conceptualization; methodology; writing – review & editing.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
We acknowledge the financial support of the Swedish Foundation for Strategic Research (SSF; Grant No. ITM17-0236). We thank Henrik Öström for the loan of the Pd(110) crystal, as well as Alice Schmidt-May and Franziska Dahlmann for carefully reading of the manuscript.References
- G. Ertl and P. Rau, Surf. Sci., 1969, 15, 443–465 CrossRef CAS.
- S. Ladas, R. Imbihl and G. Ertl, Surf. Sci., 1989, 219, 88–106 CrossRef CAS.
- S. Ladas, R. Imbihl and G. Ertl, Surf. Sci., 1993, 280, 14–22 CrossRef CAS.
- T. Engel and G. Ertl, J. Chem. Phys., 1978, 69, 1267–1281 CrossRef CAS.
- G. Ertl, Surf. Sci., 1994, 299–300, 742–754 CrossRef CAS.
- H. Kondoh, R. Toyoshima, Y. Monya, M. Yoshida, K. Mase, K. Amemiya and B. S. Mun, Catal. Today, 2016, 260, 14–20 CrossRef CAS.
- M. A. Van Spronsen, J. W. Frenken and I. M. Groot, Chem. Soc. Rev., 2017, 46, 4347–4374 RSC.
- S. M. McClure and D. W. Goodman, Chem. Phys. Lett., 2009, 469, 1–13 CrossRef CAS.
- S. Blomberg, U. Hejral, M. Shipilin, S. Albertin, H. Karlsson, C. Hulteberg, P. Lömker, C. Goodwin, D. Degerman and J. Gustafson, et al. , ACS Catal., 2021, 11, 9128–9135 CrossRef CAS PubMed.
- S. Blomberg, C. Brackmann, J. Gustafson, M. Aldeén, E. Lundgren and J. Zetterberg, ACS Catal., 2015, 5, 2028–2034 CrossRef CAS PubMed.
- J. Zhou, S. Blomberg, J. Gustafson, E. Lundgren and J. Zetterberg, J. Phys. Chem. C, 2017, 121, 23511–23519 CrossRef CAS.
- L. Rämisch, S. M. Gericke, S. Pfaff, E. Lundgren and J. Zetterberg, Appl. Surf. Sci., 2022, 578, 152048 CrossRef.
- B. Hendriksen, S. Bobaru and J. Frenken, Surf. Sci., 2004, 552, 229–242 CrossRef CAS.
- R. Van Rijn, O. Balmes, A. Resta, D. Wermeille, R. Westerström, J. Gustafson, R. Felici, E. Lundgren and J. Frenken, Phys. Chem. Chem. Phys., 2011, 13, 13167–13171 RSC.
- F. Gao, Y. Wang, Y. Cai and D. Goodman, J. Phys. Chem. C, 2009, 113, 174–181 CrossRef CAS.
- F. Gao, S. M. McClure, Y. Cai, K. K. Gath, Y. Wang, M. Chen, Q. Guo and D. W. Goodman, Surf. Sci., 2009, 603, 65–70 CrossRef CAS.
- R. Van Rijn, O. Balmes, R. Felici, J. Gustafson, D. Wermeille, R. Westerström, E. Lundgren and J. W. M. Frenken, J. Phys. Chem. C, 2010, 114, 6875–6876 CrossRef CAS.
- F. Gao, Y. Wang and D. W. Goodman, J. Phys. Chem. C, 2010, 114, 6874 CrossRef CAS.
- A. Shavorskiy, G. D'Acunto, V. Boix De La Cruz, M. Scardamaglia, S. Zhu, R. H. Temperton, J. Schnadt and J. Knudsen, ACS Appl. Mater. Interfaces, 2021, 13, 47629–47641 CrossRef CAS PubMed.
- A. Shavorskiy, E. Kokkonen, E. Redekop, G. D'Acunto, J. Schnadt and J. Knudsen, Synchrotron Radiat. News, 2022, 35, 4–10 CrossRef.
- J. Goschnick, M. Wolf, M. Grunze, W. Unertl, J. Block and J. Loboda-Cackovic, Surf. Sci., 1986, 178, 831–841 CrossRef CAS.
- R. Westerström, C. Weststrate, J. Gustafson, A. Mikkelsen, J. Schnadt, J. N. Andersen, E. Lundgren, N. Seriani, F. Mittendorfer and G. Kresse, et al. , Phys. Rev. B, 2009, 80, 125431 CrossRef.
- A. Titkov, A. Salanov, S. Koscheev and A. Boronin, Surf. Sci., 2006, 600, 4119–4125 CrossRef CAS.
- J.-W. He and P. Norton, Surf. Sci., 1988, 204, 26–34 CrossRef CAS.
- J.-W. He, U. Memmert and P. R. Norton, J. Chem. Phys., 1989, 90, 5088–5093 CrossRef CAS.
- H. Tanaka, J. Yoshinobu and M. Kawai, Surf. Sci., 1995, 327, L505–L509 CrossRef CAS.
- H. Niehus and C. Achete, Surf. Sci., 1996, 369, 9–22 CrossRef.
- M. Kralj, T. Pertram, N. Seriani, F. Mittendorfer, A. Krupski, C. Becker and K. Wandelt, Surf. Sci., 2008, 602, 3706–3713 CrossRef CAS.
- D. Zemlyanov, B. Klötzer, H. Gabasch, A. Smeltz, F. H. Ribeiro, S. Zafeiratos, D. Teschner, P. Schnörch, E. Vass and M. Hävecker, et al. , Top. Catal., 2013, 56, 885–895 CrossRef CAS.
- R. Toyoshima, M. Yoshida, Y. Monya, K. Suzuki, K. Amemiya, K. Mase, B. S. Mun and H. Kondoh, J. Phys. Chem. C, 2013, 117, 20617–20624 CrossRef CAS.
- R. Raval, S. Haq, G. Blyholder and D. A. King, J. Electron Spectrosc. Relat. Phenom., 1990, 54–55, 629–638 CrossRef CAS.
- R. Raval, S. Haq, M. A. Harrison, G. Blyholder and D. A. King, Chem. Phys. Lett., 1990, 167, 391–398 CrossRef CAS.
- M. Ramsey, F. Leisenberger, F. Netzer, A. Roberts and R. Raval, Surf. Sci., 1997, 385, 207–215 CrossRef CAS.
- J. Zhang, Z. Wang and Z. X. Wang, Surf. Interface Anal., 2011, 43, 1038–1045 CrossRef CAS.
- K.-I. Fukui, H. Miyauchi and Y. Iwasawa, J. Phys. Chem., 1996, 100, 18795–18801 CrossRef CAS.
- M. Bowker, I. Z. Jones, R. A. Bennett, F. Esch, A. Baraldi, S. Lizzit and G. Comelli, Catal. Lett., 1998, 51, 187–190 CrossRef CAS.
- I. Z. Jones, R. A. Bennett and M. Bowker, Surf. Sci., 1999, 439, 235–248 CrossRef CAS.
- S. Blomberg, J. Zetterberg, J. Gustafson, J. Zhou, C. Brackmann and E. Lundgren, Top. Catal., 2016, 59, 478–486 CrossRef CAS.
- T.-E. Chien, L. Hohmann and D. J. Harding, J. Chem. Phys., 2022, 157, 034201 CrossRef CAS PubMed.
- M. A. Hines, H. A. Michelsen and R. N. Zare, J. Chem. Phys., 1990, 93, 8557–8564 CrossRef CAS.
- M. Wu, D. P. Taylor and P. M. Johnson, J. Chem. Phys., 1991, 94, 7596–7601 CrossRef CAS.
- E. C. Inn, K. Watanabe and M. Zelikoff, J. Chem. Phys., 1953, 21, 1648–1650 CrossRef CAS.
- W. Chan, G. Cooper and C. Brion, Chem. Phys., 1993, 178, 401–413 CrossRef CAS.
- S. P. McGlynn, J. W. Rabalais, J. R. McDonald and V. Scherr, Chem. Rev., 1971, 71, 73–108 CrossRef CAS.
- M.-J. Hubin-Franskin, J. Delwiche, B. Leclerc and D. Roy, J. Phys. B: At., Mol. Opt. Phys., 1988, 21, 3211 CrossRef CAS.
- G. Stark, K. Yoshino, P. Smith and K. Ito, J. Quant. Spectrosc. Radiat. Transfer, 2007, 103, 67–73 CrossRef CAS.
- D. Irimia, D. Dobrikov, R. Kortekaas, H. Voet, D. A. van den Ende, W. A. Groen and M. H. Janssen, Rev. Sci. Instrum., 2009, 80, 113303 CrossRef PubMed.
- K. Golibrzuch, P. R. Shirhatti, J. Geweke, J. Werdecker, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Am. Chem. Soc., 2015, 137, 1465–1475 CrossRef CAS PubMed.
- D. J. Harding, J. Neugebohren, H. Hahn, D. J. Auerbach, T. Kitsopoulos and A. M. Wodtke, J. Chem. Phys., 2017, 147, 013939 CrossRef PubMed.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- J. C. Tully, Surf. Sci., 1994, 299–300, 667–677 CrossRef CAS.
- M. Hirsimäki and M. Valden, J. Chem. Phys., 2001, 114, 2345–2354 CrossRef.
- J. Goschnick, M. Grunze, J. Loboda-Cackovic and J. Block, Surf. Sci., 1987, 189–190, 137–146 CrossRef CAS.
- K. Yagi-Watanabe and H. Fukutani, J. Chem. Phys., 2000, 112, 7652–7659 CrossRef CAS.
- H. Kato, J. Yoshinobu and M. Kawai, Surf. Sci., 1999, 427–428, 69–73 CrossRef CAS.
- H. Conrad, G. Ertl, J. Koch and E. Latta, Surf. Sci., 1974, 43, 462–480 CrossRef CAS.
- J. Neugebohren, D. Borodin, H. W. Hahn, J. Altschäffel, A. Kandratsenka, D. J. Auerbach, C. T. Campbell, D. Schwarzer, D. J. Harding and A. M. Wodtke, et al. , Nature, 2018, 558, 280–283 CrossRef CAS PubMed.
- M. G. Moula, S. Wako, G. Cao, I. Kobal, Y. Ohno and T. Matsushima, Appl. Surf. Sci., 2001, 169–170, 268–272 CrossRef CAS.
- S. Wako, M. G. Moula, G. Cao, K. Kimura, I. Kobal, Y. Ohno and T. Matsushima, Langmuir, 2000, 16, 2689–2696 CrossRef CAS.
- J. Hurst, C. Becker, J. Cowin, K. Janda, L. Wharton and D. Auerbach, Phys. Rev. Lett., 1979, 43, 1175 CrossRef CAS.
- K. C. Janda, J. E. Hurst, C. A. Becker, J. P. Cowin, D. J. Auerbach and L. Wharton, J. Chem. Phys., 1980, 72, 2403–2410 CrossRef CAS.
- M. Bassett and R. Imbihl, J. Chem. Phys., 1990, 93, 811–821 CrossRef CAS.
- T. Yamanaka, Phys. Chem. Chem. Phys., 2008, 10, 5429–5435 RSC.
- M. Ehsasi, C. Seidel, H. Ruppender, W. Drachsel, J. Block and K. Christmann, Surf. Sci. Lett., 1989, 210, L198–L208 CrossRef CAS.
- K. Nakao, S.-I. Ito, K. Tomishige and K. Kunimori, Catal. Today, 2006, 111, 316–321 CrossRef CAS.
- P. J. Berlowitz, C. H. Peden and D. W. Goodman, J. Phys. Chem., 1988, 92, 5213–5221 CrossRef CAS.
- K. Nakao, S.-i. Ito, K. Tomishige and K. Kunimori, J. Phys. Chem. B, 2005, 109, 17553–17559 CrossRef CAS PubMed.
- L. Zhou, A. Kandratsenka, C. T. Campbell, A. M. Wodtke and H. Guo, Angew. Chem., Int. Ed., 2019, 58, 6916–6920 CrossRef CAS PubMed.
- R. Gerber, Chem. Rev., 1987, 87, 29–79 CrossRef CAS.
- K. Papendorf, K. Golibrzuch, T. Zhong, S. Schwabe, T. N. Kitsopoulos and A. M. Wodtke, Chem.: Methods, 2022, 2, e202200017 CAS.
| This journal is © The Royal Society of Chemistry 2024 |