Inelastic scattering of NO(A²Σ⁺) + CO₂: rotation–rotation pair-correlated differential cross sections

Abstract

A crossed beam velocity-map ion-imaging apparatus has been used to determine differential cross sections (DCSs) for the rotationally inelastic scattering of NO(A²Σ⁺, v = 0, j = 0.5) with CO₂, as a function of both NO(A, v = 0, N′) final state and the coincident final rotational energy of the CO₂. The DCSs are dominated by forward-peaked scattering for all N′, with significant rotational excitation of CO₂, and a small backward scattered peak is also observed for all final N′. However, no rotational rainbow scattering is observed and there is no evidence for significant product rotational angular momentum polarization. New ab initio potential energy surface calculations at the PNO-CCSD(T)-F12b level of theory report strong attractive forces at long ranges with significant anisotropy relative to both NO and CO₂. The absence of rotational rainbow scattering is consistent with removal of low-impact-parameter collisions via electronic quenching, in agreement with the literature quenching rates of NO(A) by CO₂ and recent electronic structure calculations. We propose that high-impact-parameter collisions, that do not lead to quenching, experience strong anisotropic attractive forces that lead to significant rotational excitation in both NO and CO₂, depolarizing product angular momentum while leading to forward and backward glory scattering.

---

Introduction

Experimental and theoretical studies of rotationally inelastic molecular collisions have a long history, underpinned by the importance of these collisions in atmospheric, combustion and astrochemical environments. The interaction of experiment and theory has led to repeated improvements in the level of dynamical detail that may be measured in experiments, and in the accuracy of the potential energy surfaces (PESs) that determine those dynamics. Small molecule-atom scattering may now be predicted with effectively quantitative accuracy, supported by powerful insights into the roles of both classical and quantum effects. The NO(X²Π) + rare gas (Rg) systems have been the backbone of this effort, with crossed-molecular-beam velocity-map ion imaging (CMB-VMI) the primary experimental methodology.^1–12

Molecule–molecule scattering provides new challenges to both experiment and theory. For theory, the additional dimensions and electrons make high-level electronic structure calculations significantly more challenging and expensive, and similarly scattering calculations, particularly quantum scattering (QS), rapidly become prohibitively large. In experiments, the additional rotational energy levels present in the molecular collider provide a challenge in both state preparation, and in unravelling the scattering dynamics. Individual rotational energy levels in the unobserved product result in nested spheres of scattering in velocity space, crushed or sliced into rings in a velocity-map image. Interpretation of such images in terms of rotationally correlated differential cross sections (DCSs) is difficult if initial state selection is purely from molecular beam rotational cooling. Therefore, ‘conventional’ CMB-VMI studies of molecule–molecule scattering have been largely confined to collisions with H₂ and its isotopologues.^13–15

The addition of quantum-state selection to one of the partners significantly helps the analysis and interpretation of the images. Brouard and co-workers have shown that for NO(X) + O₂ scattering, the DCSs as a function of rotational energy in the unobserved partner can be extracted from CMB-VMI experiments when the NO(X) was initially state-selected using the Stark effect.¹⁶ We have shown that optical state selection can be similarly used to simplify molecule–molecule scattering in measurements of NO(A) + N₂, CO and O₂ scattering.^17,18 Clearly, decreasing the collision-energy spread relative to typical rotational energy spacings provides the opportunity to dramatically enhance the experimental resolution. Stark deceleration provides both initial state selection and high-resolution collision energy control, and has been used in studies by van de Meerakker and co-workers to determine correlated DCSs for collisions of NO(X) with O₂, CO, and D₂.^19–22 Most recently, they have introduced Stark-effect state selection to the collider beam as well, providing full initial state selection of both colliders with high collision-energy resolution, for NO(X) + ND₃ scattering.²³

In this paper, we extend our NO(A) optical-state-selection experiments to a new collision partner, CO₂. As well as presenting a new challenge through its closely spaced rotational levels, it is also an interesting collision partner because it rapidly quenches NO(A). Measurements of the quenching cross section (σ_Q) as a function of temperature show negative-activation-energy behaviour, with σ_Q = 68 Ų at 294 K, decreasing to 51 Ų at 765 K.²⁴ Experiments probing the products of quenching show that both NO(X) and CO₂ are produced vibrationally excited, and suggest that a reactive channel leading to NO(X), CO and O(³P) may also be important.^25,26 Recent electronic structure calculations by Petit and co-workers predict strong forces on the NO(A)–CO₂ potential energy surface (PES) that will steer the system towards a suspected quenching pathway that involves CO₂ bending, broadly consistent with the experimental observations.²⁷ Our own NO(A)–CO₂ van der Waals PES calculations show that strong long-range attractive forces are present.²⁸ NO(A) + CO₂ therefore appears to be an interesting collision system to compare to our previous experimental and theoretical work on NO(A) + N₂, CO and O₂.^18,29,30

In this paper we present new experimental CMB-VMI measurements of NO(A) + CO₂ rotationally inelastic scattering, from which we extract DCSs as a function of energy transferred to CO₂ for specific NO(A, N′) final states. We also present additional PES calculations for NO(A) + CO₂, which address the question of whether the basis set superposition error (BSSE) corrections in our previous work overestimated the attractive well depth.²⁸ These results are then discussed in the context of both our own and Petit and co-workers’ ab initio PESs, our previous measurements of NO(A) + N₂, CO and O₂ scattering, and general models of molecule–molecule scattering from the recent literature.

Experimental

The experimental apparatus has been described in detail previously.^{17,18,31–35} In brief, a pair of pulsed molecular beams were crossed at right angles within a set of velocity-map ion optics. One beam contained NO (BOC, 99.998%) seeded (10%) in Ne (BOC, 99.999%), produced from a backing pressure of 3 bar. The other beam was of pure CO₂ (BOC, 99.999%) produced from a backing pressure of 5 bar. The NO beam had a Gaussian speed distribution with a mean of 797 m s⁻¹ and a full width at half maximum (FWHM) of 57 m s⁻¹. The CO₂ beam, as measured by VMI of a trace concentration of NO, had a mean of 722 m s⁻¹, and a FWHM of 52 ms⁻¹. The resulting collision energy, E_coll, had a Gaussian distribution with a mean of 863 cm⁻¹ and a FWHM of 88 cm⁻¹.

NO(A²Σ⁺, v = 0, N = 0, j = 0.5) was prepared in the crossing region of the molecular beams by an approximately 5 ns pulse of ≈226 nm laser light via the Q₁(0.5) line of the NO(A²Σ⁺–X²Π) (0,0) transition. The preparation laser pulse was linearly polarized perpendicular to the plane of the molecular beams; note that this initial state cannot be rotationally aligned. After a delay of 370 ns, the NO(A²Σ⁺, v = 0, N′) products of rotational energy transfer (RET) were probed via a (1 + 1′) REMPI scheme, consisting of a probe pulse resonant with specific R-branch lines of the NO(E²Σ⁺–A²Σ⁺) (0,0) transition around 600 nm, and an ionisation pulse at 532 nm. The spectroscopy of the NO(E–A) transition results in the simultaneous and equal probing of both j = N + ½ and j = N − ½ spin-rotation levels for each N′. The NO⁺ ions were then velocity-mapped onto a microchannel plate detector with a phosphor screen, and the resulting images were recorded with a CCD camera.

Images were recorded for final rotational states N′ = 5–10 inclusive. In each case multiple independent experiments were performed, recording images in which the polarization of the probe laser was alternated between in the image plane (H) and perpendicular to the image plane (V), together with background images in which the CO₂ molecular beam was delayed by 1 ms relative to the NO molecular beam. Each experiment consisted of 16 000 shots across each of the H, V signals and associated background images, i.e. 64 000 in total. The background images enable subtraction of signals arising from non-resonant 2-photon 532 nm ionisation of un-scattered NO(A), which forms a beam spot at the NO beam velocity.³⁵ The probe laser wavelength was scanned across the complete Doppler width of the probe transition 5 times during each experiment. Background images (V and H) were then subtracted from their appropriate signal images to generate the scattering images that have been fitted. The total number of independent experiments varied from 10 to 18, depending on the observed signal-to-noise for each state.

Image analysis

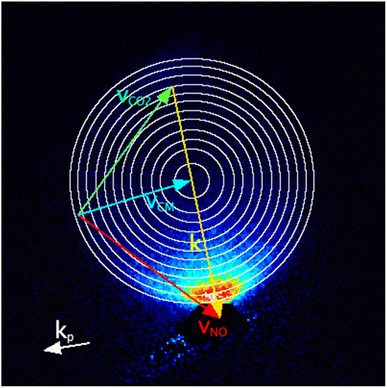
The images were analysed to extract the DCSs as a function of the internal energy transferred to the collision partner, ΔE_CO2. Image inversion methods used in photodissociation, such as the Abel transform, are not suitable for analysis of crossed beam scattering images that do not possess cylindrical symmetry. We have therefore used the forward simulation ‘peeling’ methodology we have recently described and applied to collisions of NO(A) + N₂, O₂ and CO.¹⁸ In brief, in this method the data images are sequentially fitted to extract the DCS for different discrete user-specified energy transfers to the internal (here, rotational) modes of the unobserved collision partner, i.e. CO₂. First, basis images for the chosen DCS angular basis functions are Monte-Carlo simulated, including all known experimental parameters (e.g. molecular beam velocity distributions, ion-imaging resolution), for collisions in which zero energy has been transferred to CO₂ rotation. If desired, the basis images can include the effects of product angular momentum polarization as predicted by independent models, e.g. scattering calculations or kinematic apse conservation. The basis images are least-squares fitted to the experimental images, only considering an outermost region of pixels that includes those contributing to this initial (zero) energy transfer, but excludes the inner filled region of the image where a significant contribution would also be expected from the next, non-zero, discrete energy transfer to the CO₂. This fit determines the DCS for zero energy transfer to CO₂. This DCS is then used in a simulation of the whole area of the image, generating a best-fit representation of the contribution this energy transfer makes to the data image. This is then subtracted from the data image, removing the contribution of this energy transfer to the data; this is the ‘peeling’ step. The process is then repeated for the rest of the user-defined energy transfers, sequentially determining the DCS for a particular energy transfer and ‘peeling’ it from the data, until the final set of basis images is fitted to the entire remaining image.

In total, 12 discrete values of ΔE_CO2 were chosen, spanning the range 0 to 630 cm⁻¹. The spacing of the CO₂ rotational levels is small (the rotational constant, B_CO2 = 0.41 cm⁻¹) compared to the experimental collision energy resolution. The spread of speeds of the CO₂ molecular beam indicates good internal cooling of the CO₂, but even at rotational temperatures of 5–10 K typical of a pulsed molecular beam, significant population is expected in several initial (i.e. j = 0, 2, 4, 6) rotational levels. It was therefore not reasonable to attempt to assign specific CO₂ Δj transitions to the ΔE_CO2. Instead, the ΔE_CO2 were initially spaced by 80 cm⁻¹, with the spacings subsequently decreasing to keep the NO(A) product velocity spacing approximately constant, resulting in ΔE_CO2 = 0, 80, 160, 240, 310, 370, 430, 480, 530, 570, 600 and 630 cm⁻¹. The Newton diagram for NO final state N′ = 10, including circles representing the in-plane final speeds arising from these 12 energy transfers to CO₂, is shown in Fig. 1, overlaid on the summed experimental data for this state.

Fig. 1 Newton diagram superimposed on an experimental image for final state N′ = 10. Labels indicate the average laboratory frame velocities of NO (v_NO), CO₂ (v_CO2), relative collision velocity (k) and the velocity of the centre of mass (v_CM). The rings indicate the in-plane scattered final speeds for the 12 values of ΔE_CO2. Also indicated is the propagation direction of the probe laser, k_p. NO beamspot-subtraction artefacts have been masked.

The DCS basis functions for each ΔE_CO2 slice of the overall image were represented by triangles, which we have shown are better suited for fitting strongly forward-scattered images than Legendre functions.^18,31 The first, ΔE_CO2 = 0 cm⁻¹, slice was fitted to 25 basis functions, providing a θ = 7.5° scattering-angle spacing. The peeling procedure necessarily results in slices of decreasing signal level with increasing ΔE_CO2, and the number of DCS basis functions was accordingly decreased, depending on the overall signal-to-noise of the images for a particular N′, such that the 12th slice was fitted with either 3 or 5 DCS basis functions.

In our previously published fitting of images from NO(A) + N₂, O₂ and CO scattering strong product angular momentum polarization was observed.¹⁸ This was included in the fitting through forward simulation by assuming that angular momentum was conserved within the frame of the kinematic apse (KA). This assumption has been widely applied in NO(X) inelastic scattering, and commonly holds in rigid-shell collisions. However, in these measurements of NO(A) + CO₂ scattering only relatively weak angular momentum polarization effects were observed, which were not consistent with application of the KA model. For most final N′ at most scattering angles there was no observable difference between the H and V polarization images. The largest observed difference was for N′ = 8 at θ ≈ 20°, where the V–H difference signal was ≈8% of the V + H sum signal. In the absence of a suitable model for forward simulation, and because the observed effects were relatively small and therefore would only result in small changes to measured DCSs, the images were fitted with the assumption of zero product angular momentum polarization. In practice, this is equivalent to fitting both H and V images simultaneously to the same basis function images.

Theory methods

The electronic structure calculations followed the approach described in our recent paper:²⁸ pair natural orbital single-reference unrestricted coupled cluster with singles, doubles, with perturbative triples (PNO-CCSD(T)), here extended with the F12 ansatz, hence PNO-CCSD(T)-F12b. For all of the calculations, the t-aug-cc-pVTZ basis set has been used,^36,37 with the respective even-tempered augmented auxiliary basis set for the resolution of identity in the F12-methods. All calculations were performed with the MOLPRO 2023.2 program package.^38–40 Calculations were performed for three cuts through the PES, connecting four of the distinct intermolecular relative orientations described by Soulié and Paterson,^29,30 which displayed the deepest attractive wells in our previous NO(A) + CO₂ calculations.²⁸

Results

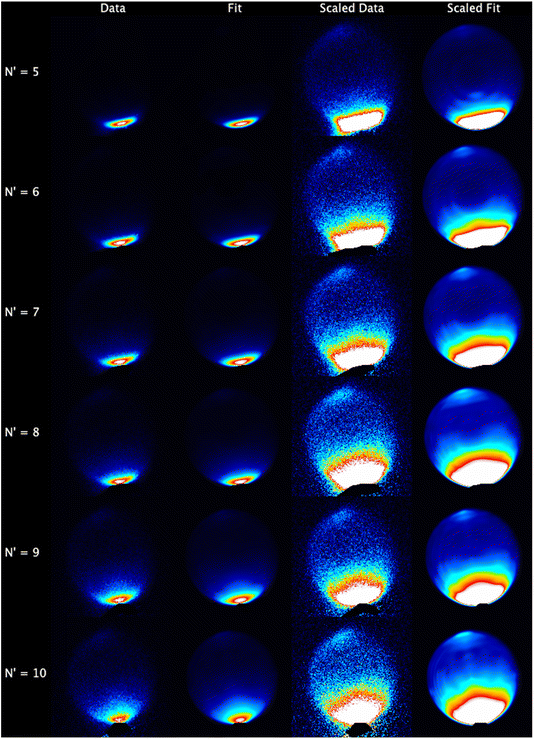
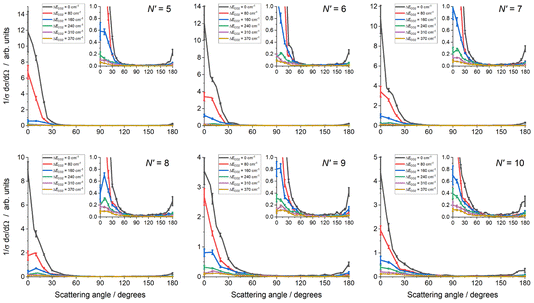
The experimental data images and fits resulting from the analysis procedure are presented in Fig. 2, where the individual images for each N′ final state for both probe polarizations have been summed. For all N′ the images display strong forward scattering, and, to better show the full range of scattering, Fig. 2 also shows rescaled images with the maximum intensity set to respectively 1/15th (N′ = 5, 6), 1/10th (N′ = 7, 8) and 1/5th (N′ = 9, 10) of the data peak signal for that N′. The rescaled images clearly show that a much weaker backward scattered peak is also present for all N′. While there is a general trend towards a wider range of scattering angles with increasing N′, very little sideways scattered signal is observed, with the peak intensity for all N′ occurring at a scattering angle of θ = 0°. In addition, the forward scattered peaks extend towards the centre of the images. This is clear evidence of forward-scattered NO formed in coincidence with rotationally excited CO₂. The fits are generally in very good agreement with the data, reproducing all the observed features.

Fig. 2 Experimental data and fits. (Left to right) Summed V + H data; summed V + H fit; scaled summed V + H data; scaled summed V + H fit. (Top to bottom) Final states N′ = 5 to 10. The individual experimental measurements for each N′ have been fitted independently as described in the text, and the relevant images summed for presentation here. For example, the N′ = 10 images are the result of fitting to 10 V and H polarization pairs of images, and the data and fit images presented are therefore each the sum of 20 images. The rescaled images have their maximum intensity set to 1/15th (N′ = 5 and 6), 1/10th (N′ = 7 and 8) and 1/5th (N′ = 9 and 10) of the data image maximum, respectively. NO beamspot subtraction artefacts have been masked.

The mean DCSs determined from the fits to the individual measurements are shown in Fig. 3 for all NO(A, N′) as a function of ΔE_CO2. Only the first 6 values of ΔE_CO2 are presented for visual clarity; these represent ≥ 90% of the total scattering cross section for all N′. For each N′ the total cross section has been normalized to unity, removing variations in experimental signal levels and allowing direct comparison of the scattering into different ΔE_CO2 for different N′. As expected from inspection of the images, the DCSs for all N′ are strongly forward scattered, peaking in all cases at θ = 0°. For all N′, the largest scattering contribution comes from the elastic ΔE_CO2 = 0 cm⁻¹ energy transfer slice, but substantial forward-scattered contributions to the total cross section are also made by higher ΔE_CO2 slices. As N′ increases the scattering spreads to wider angles, and the contribution of higher ΔE_CO2 slices increases. However, there is little or no scattering in the range 45° < θ < 135°, which we broadly define as ‘sideways’, regardless of N′ or ΔE_CO2. In contrast, there is a clear backwards-scattered component to the DCSs for all final-N′, peaking at 180°, consistent with the raw data. For all N′, this backwards peak is also largest for the elastic ΔE_CO2 = 0 cm⁻¹ channel, and its magnitude relative to the forward-scattered peak increases with increasing-N′.

Fig. 3 Differential cross sections (DCSs) as a function of energy transfer to CO₂, ΔE_CO2, for final NO rotational states N′ = 5 to 10, averaged over the independent fits to individual experimental measurements. The total integral cross section for each final state has been normalised to unity. For clarity, only the DCSs for the first 6 ΔE_CO2 values are displayed. The insets show the same angular range (0 to 180°) as the main graphs with a reduced vertical range to show the backward scattered peak and enable comparison of the higher ΔE_CO2 DCSs. In each case the error bars represent 1 standard error of the mean.

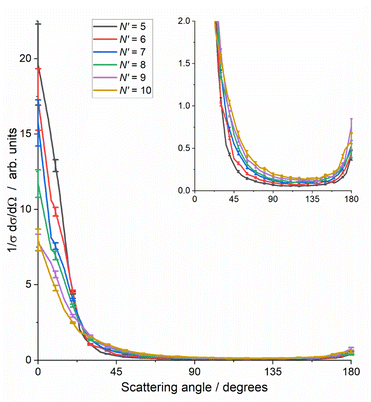
Fig. 4 reinforces these trends with the final-N′, showing the total DCS, summed over all ΔE_CO2, including the higher ΔE_CO2 slices not shown in Fig. 3. As noted for Fig. 3, the total cross section for each N′ has been normalised to unity to allow comparison, i.e. these DCSs have been integrated over sin θ dθ dφ. These total DCSs are of course also dominated by forward scattering, with very little sideways scattering and a small backward peak. This backward peak ranges in size from ≈2% of the forward peak for N′ = 5, to ≈10% for N′ = 9, 10. The range of the forward-scattered peak also steadily extends as N′ increases.

Fig. 4 Total differential cross sections, summed over all CO₂ internal energies, as a function of NO final rotational state, N′ = 5 to 10. The inset covers a reduced vertical range to enable comparison of the sideways and backwards scattering. For each N′ the integral cross section is separately normalized to unity, and the error bars represent 1 standard error.

Integrating the DCSs for individual ΔE_CO2 slices for each N′ yields relative integral cross sections, which are shown in the main panel of Fig. 5. The sum of the cross sections is normalized to unity, as noted in the discussion of Fig. 3. These reinforce the steady increase in energy transfer to the CO₂ that is observed with increasing N′, and also shows the small, but clearly non-negligible contribution of higher ΔE_CO2 slices above 350 cm⁻¹. Finally, the inset to Fig. 5 shows the average energy transfer to CO₂ as a function of N′, derived from the information in the main panel. This clearly increases steadily with increasing N′, with no indication of a plateau at the highest-N′. Also shown for the purposes of comparison in this panel are the equivalent average energy transfers for N₂, CO and O₂ from our recent work.¹⁸

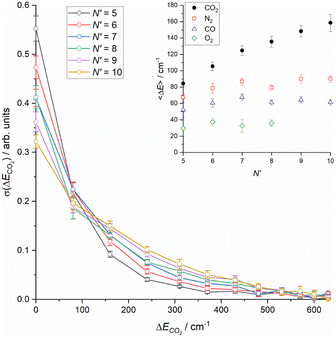Fig. 5 (Main panel) Sum-normalised integral scattering cross sections as a function of energy transfer to CO₂ for all final NO rotational states, N′. (Inset) Average energy transfer to collision partner as a function of final NO rotational state, N′, for CO₂ (this work) and N₂, CO and O₂ (Luxford et al.¹⁸). Errors in both main panel and inset are 2σ.

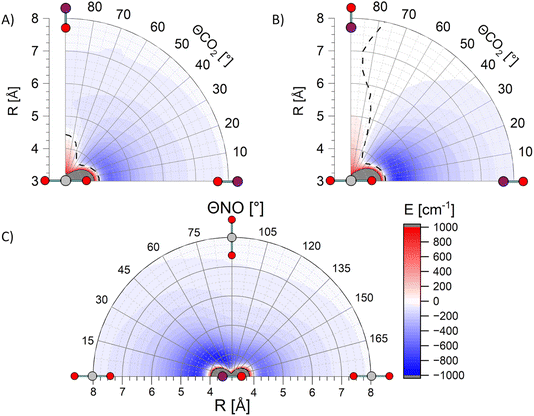
Fig. 6 shows three exemplary cuts through the PES calculated at the PNO-CCSD(T)-F12b level of theory.^41,42 In contrast to our previously published surfaces,²⁸ these are not corrected for basis set superposition error (BSSE) via counterpoise correction, as the usage of the F12b formalism reduces this phenomenon significantly due to the much faster convergence to the basis set limit. This is demonstrated with a comparison of global minima for all three cuts through the surface, with and without counterpoise BSSE-correction, in Table 1.

Fig. 6 Cuts through the NO(A) + CO₂ potential energy surface calculated at the PNO-CCSD(T)-F12b level of theory. (A) Linear (LinO) to T-shaped (TO) geometries for NO rotating around CO₂ with O-atom pointing at CO₂. (B) Linear (LinN) to T-shaped (TN) geometries for NO-rotating about CO₂ with N-atom pointing at CO₂. (C) CO₂ rotating around NO, from linear pointing at N-atom (LinN), through T-shaped (H), to linear pointing at O-atom (LinO). The dashed lines in panels (A) and (B) indicate the 0 cm⁻¹ contour, separating attractive and repulsive regions of the PES.

Table 1 Well depth, V_min, relative to separated NO(A) and CO₂ for the specified cuts through the NO(A) + CO₂ surface shown in Fig. 6, for PNO-CCSD(T)²⁸ and PNO-CCSD(T)-F12b with and without BSSE correction. LinO and TO are linear and T-shaped geometries, respectively, with the O-atom of NO pointing at CO₂. LinN and TN are linear and T-shaped geometries, respectively, with the N-atom of NO pointing at CO₂. H is a T-shaped geometry with O of CO₂ pointing at the side of NO

Cut through surface	PNO-CCSD(T) Vmin/cm^−1		PNO-CCSD(T)-F12b Vmin/cm^−1
	Non-BSSE-corrected	BSSE-corrected	Non-BSSE-corrected	BSSE-corrected
LinO to TO	−738	−508	−558	−534
LinN to TN	−921	−730	−769	−742
LinN to H to LinO	−1008	−823	−876	−854

---

Discussion

It is helpful to first summarise for comparison, the fundamental principles of RET dynamics observed in the many literature studies of diatom + atom scattering, including our own NO(A) + Rg experiments, at collision energies significantly greater than the attractive well depth.^31–35 All possible values of the impact parameter, b, are necessarily sampled in collisions in a crossed-beam experiment. High impact-parameter collisions predominately sample attractive forces, and lead to small Δj transitions dominated by forward scattering. This forward peak may be the result of glory scattering, requiring an attractive well, or alternatively can arise from diffraction around the repulsive core.^7,31 Lower-impact parameter collisions predominately sample the repulsive wall of the PES and lead to a peak in the DCS that moves from the forward hemisphere progressively sideways and backwards as Δj increases, so-called ‘rotational rainbow’ scattering.^4,34 These fundamental trends have also been observed in diatom-molecule scattering, for example in collisions of NO(X) with H₂, CH₄, and O₂.^16,43,44

However, when additional dynamical channels are present, and processes other than RET can occur, then this conventional picture starts to break down, as we have shown in our recent work on RET of NO(A) in collisions with N₂, O₂ or CO.¹⁸ For NO(A) + O₂, no sideways or backwards scattering was observed, with essentially only forward-scattered NO(A, N′) formed in coincidence with low-rotation O₂. In contrast, in the dynamics of NO(A) + N₂ and CO, moderate sideways and backwards scattering with significant N₂ and CO rotation was detected. Our interpretation, supported by PES calculations and consistent with the NO(A) + O₂ quenching cross section,^{24,29,30,45,46} was that with O₂ the low-impact-parameter collisions which would otherwise lead to sideways or backwards scattering with substantial rotational excitation, instead result in quenching. Hence, the only NO(A, N′) products are the result of high-impact-parameter collisions. Calculation of the van der Waals NO(A)–O₂ PES showed that the long-range attractive forces that would be sampled in such high-impact-parameter collisions were not very anisotropic, particularly with respect to rotation of O₂.³⁰ Such collisions would be expected to lead to forward scattering with low O₂ rotational excitation. In contrast, in collisions with N₂ and CO these quenching pathways either do not exist, or are behind substantial energetic barriers, and the NO(A, N′) products observed have sampled the full range of impact parameters, giving rise to sideways and backwards scattering and significant rotational excitation of both products.

Does a similar picture underlay the NO(A) + CO₂ results presented here? Very rapid quenching is present in NO(A) + CO₂, with σ_Q ≈ 50 Ų at the collision energy of the experiment, corresponding (assuming 100% efficiency within this range) to a maximum impact parameter of b_Q ≈ 4 Å.²⁴ Recent theory from Bridgers et al. has provided insight into the quenching pathway.²⁷ In particular, they found strongly attractive interactions as the N-end of NO approached an O-atom of CO₂. At interatomic distances of R_N–O ≤ 2.8 Å this resulted in the onset of transfer of electron density to CO₂ with associated CO₂ bending, with a simultaneous rise in the energy of NO(X) + CO₂. They accordingly assign this as a pathway to a conical intersection leading to quenching. These interatomic distances are largely consistent (converting to centre-of-mass separation, R) with b_Q = 4 Å. Interactions resulting from the O-end of NO approaching an O-atom of CO₂ were also attractive, but consistently weaker than from the N-end, and although similar pathways to quenching are possible, the N-approach probably dominates quenching. Bridgers et al. also predicted longer-range attractive forces, in broad agreement with the experimentally observed negative temperature dependence of σ_Q.

We hence propose that the absence of significant sideways or backwards scattering in our experimental results (ignoring for now the isolated peak centred at θ = 180°), i.e. the absence of rotational rainbow scattering, is consistent with the removal of low-impact-parameter collisions by quenching, as we have previously proposed for NO(A) + O₂.¹⁸ The remaining scattering is therefore, under this assumption, once again the result of large-impact-parameter scattering, i.e. b > 4 Å. However, in contrast to our previous experiments on NO(A) + O₂ we see substantial energy transfer to CO₂ for this forward scattering. This implies that the long-range NO(A)–CO₂ PES has substantial anisotropy, including with respect to rotation of the CO₂ relative to NO, required to generate torques on the CO₂.

The absence of any significant product angular momentum polarization also provides further evidence for strong rotational torques that are not the result of hard-shell repulsive scattering. The largest normalised differences (V–H/V + H) observed in our NO(A) + CO₂ data are ≈5%, compared to the ≈25% observed for NO(A) + N₂. Strong angular momentum polarization has also recently been reported in CO(X) + CO and CO(X) + N₂, for collisions which have primarily sampled the repulsive wall of the PES, i.e. for high-j′ sideways and backward scattered product states.⁴⁷ The KA model, which described the observed polarization effects in NO(A) + N₂, predicts maximum normalised differences of ≈25% for NO(A) + CO₂. While KA scattering is well known in diatom + atom scattering, it is only expected to hold in ‘hard’ repulsive-wall collisions, and deviations have been observed before in systems with stronger attractive forces, for example NO(X) + Kr and NO(A) + Kr.^31,48 It therefore seems reasonable to assume that the lack of strong polarization effects in NO(A) + CO₂ is a consequence of collisions dominated by strong attractive forces, especially those providing torques out of the plane of collision.

Corroboration for this assertion can be provided by theory. We have recently published an ab initio PES for NO(A)–CO₂, based on single reference calculations at the PNO-CCSD(T) level of theory.²⁸ The BSSE in those calculations was a substantial percentage of the well-depth. The F12 formalism used in the new calculations presented here provides approximately an order of magnitude reduction in the BSSE. There is nevertheless excellent agreement between the new calculations and the published PES. This gives us confidence in the overall accuracy of the BSSE-corrected PNO-CCSD(T) PES, and we conclude that we can therefore use it reliably in our interpretation of the scattering dynamics.

Diagnostic tests of the previously-published PES show significant multireference character at intermolecular separations R < 4 Å, similar to the electronic structure diagnostics seen in our NO + O₂ calculations, and consistent once again with access to quenching channels at short range.^28,29 At the longer ranges for which the PNO-CCSD(T) calculations are reliable, the PES displays deep attractive wells for both the linear NO–CO₂ and ON–CO₂ geometries, also shown on the PNO-CCSD(T)-F12b PES in Fig. 6, with a global minimum relative to the separated NO(A) and CO₂, V_min = −730 cm⁻¹, for ON–CO₂ at R = 4.5 Å. No repulsive interactions occur for these linear–linear geometries at R > 4 Å. In contrast geometries in which the end of one molecule interacts with the side of the other, or in which side–side interactions occur, are generally significantly less attractive, and in some cases are repulsive at R > 4 Å. The substantial variation of the potential as a function of the intermolecular angles θ_NO and θ_CO2 implies strong rotational torques on both NO and CO₂, even for these relatively long-range (R > 4 Å) ‘glancing’ collisions which would generally be expected to result in forward scattering. The additional substantial variation in the PESs for in-plane/out-of-plane interactions (i.e. as a function of azimuthal angle φ) are consistent with torques that could depolarize product angular momentum.

We therefore believe that a mechanism based on anisotropic long-range attractive forces provides a coherent explanation for the observation of strongly forward-scattered, rotationally excited but depolarized products in NO(A) + CO₂ collisions. We can compare this with alternative mechanisms proposed to explain other recent literature examples of molecule–molecule collisions leading to forward scattering with substantial rotational excitation of both molecules. In CO–CO scattering, Sun et al. reported forward scattering with symmetric excitation (FSSE), for example a channel where both CO products were formed in j′ = 15. However, in the kinematically similar CO–N₂ system this channel was absent.^47,49 QCT calculations on ab initio PESs demonstrated that the forward scattered high-j–high-j products observed in the CO–CO system arise from collisions in which an initial repulsive wall interaction generated the high rotational excitation, and the resulting sideways scattering is subsequently redirected forwards by the relatively strongly attractive dipole–dipole forces present. Although the dipole–dipole and dipole–quadrupole forces are obviously absent in CO–N₂, QCT calculations show that it is actually the relative weakness of the repulsive forces which is responsible for the absence of FSSE, as such trajectories cannot generate symmetrically-excited j′ = 15 products at all.^47,49

While the CO–CO system shows a specific mechanism for symmetric excitation, forward scattering with simultaneous rotational excitation in both molecules has been observed in other systems that lack this symmetry, specifically NO(X) + CO, O₂ and HD.^19,21,22,50 Van de Meerakker and co-workers have introduced the hard-collision glory scattering (HCGS) model as a general explanation of this phenomenon. The HCGS model predicts that in low-impact-parameter ‘hard’ collisions, in which a significant fraction of the available energy is transferred to product rotation, the then relatively slowly recoiling products can undergo glory scattering though redirection of the trajectory by even weak attractive forces. The conditions under which HCGS is significant depend on the ratios of the PES well depth to collision energy (V_min/E_coll) and the energy transfer to collision energy (ΔE/E_coll). Hence it will only be important under specific PES and kinematic constraints.

Assigning our NO(A) + CO₂ scattering to the HCGS model is, however, problematic. The most obvious flaw is that under our assumptions about the quenching pathways the regions of the PES that are leading to rotationally inelastic scattering are almost entirely attractive. Strong HCGS is observed in systems where the ratio V_min/E_coll is low, but the ratio ΔE/E_coll is high, i.e. much of the collision energy is transferred to rotation, and the attractive forces are strong enough to redirect the scattering forwards. At our collision energy, V_min/E_coll = 0.85, and from van de Meerakker and co-workers, a significant contribution from HCGS would only be expected for ΔE/E_coll > 0.6, i.e. ΔE > 520 cm⁻¹.⁵⁰ Hence, even if we assume that rotational energy transfer arising from purely attractive interactions plays the same role in providing slowly recoiling products, even for N′ = 10 with 220 cm⁻¹ of NO rotational energy, only the ΔE_CO2 > 310 cm⁻¹ slices fall into the HCGS regime. We therefore suggest that conventional glory scattering is responsible for the strong forward scattering with significant ΔE_CO2 for the majority of the NO final states, driven by the deep well that is comparable to our collision energy. We are not aware of any pair-correlated DCS measurements on PESs of similar well-depth, but we can compare to the significantly less attractive NO(X)–ND₃ system (isotropic well depth ≈ −100 cm⁻¹) at a lower collision energy, e.g. 158 cm⁻¹.²³ For the highest NO(X) rotational state probed, j = 6.5 with rotational energy E_rot ≈ 80 cm⁻¹, scattering peaks at θ = 0° and significant (up to 30 cm⁻¹) coincident ND₃ rotational excitation is observed. This suggests that forward-scattered rotation–rotation excitation is possible without invoking the HCGS, at appropriate V_min/E_coll ratios.

Finally, we turn to the backward scattered peak observed in NO(A)–CO₂. The NO(X)–ND₃ system also provides a possible explanation for its presence. A similar backward peak was observed for NO(X)–ND₃ collisions when E_coll < V_min.²³ Van de Meerakker and co-workers²³ assign this scattering to soft collision backward glories (SCBG), which were also previously observed in Li + HF inelastic scattering.⁵¹ They based this assignment on both a structureless-particle classical collision model, and partial-wave analysis of their quantum scattering calculations. The SCBG model shows that when E_coll < V_min, for a narrow range of impact parameters there will be collisions that lead to a half-orbit, resulting in sharply focussed backward scattering. Such backward glories are predicted to be much weaker than forward glories but are a general feature of inelastic scattering. Although our collision energy is slightly higher than V_min of the van der Waals PES, we believe that the appearance of the sharp backward scattering for all NO product states is most likely the result of these backward glories.

Conclusions

We have measured the rotational-state-correlated DCSs for inelastic scattering of NO(A, j = 0.5) with CO₂. The DCSs for all NO(N′) product states are strongly forward scattered, with significant coincident rotational excitation of the CO₂. A small backward-scattered peak is also observed in the DCS for all final states. The strong and anisotropic long-range attractive forces found in our ab initio van der Waals PESs provide a mechanism for both the strong forward ‘conventional’ glory scattering observed, and the backward peak, assigned as a soft collision backward glory. We believe that the absence of rotational rainbow scattering is the result of low-impact-parameter collisions primarily leading to electronic quenching of NO(A).

These interpretations would of course be improved by comparison to scattering calculations, but these are substantially complicated by the presence of the quenching channel. In principle, multi-reference calculations of the PESs involved and the conical intersections that connect them are possible, similar to our recently published NO(X/A) + O₂ PESs.^29,30 Trajectory calculations including surface-hopping could then, also in principle, be performed.⁵² Conventional coupled-channel time-independent QS calculations on a system such as NO(A) + CO₂ at the experimental collision energy are prohibitively expensive owing to the very large number of open channels involved. Hence new approaches, such as mixed quantum/classical theory, will be needed as molecule–molecule scattering moves to more complicated systems such as this.⁵³

Author contributions

JGL: investigation (experiment); TRS: investigation (experiment); MF: writing – reviewing and editing; KGM: writing – reviewing and editing; LC: investigation (theory), writing – reviewing and editing; MJP: conceptualization (theory), supervision (theory), writing – reviewing and editing; MLC: conceptualization (experiment), supervision (experiment), analysis (experiment), writing – original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the U.K. Engineering and Physical Sciences Research Council for funding through grants EP/J017973/1, EP/P001459/1 and EP/T021675/1.

References

1. C. G. Heid, V. Walpole, M. Brouard, P. G. Jambrina and F. J. Aoiz, Nat. Chem., 2019, 11, 662–668.
2. B. Nichols, H. Chadwick, S. D. S. Gordon, C. J. Eyles, B. Hornung, M. Brouard, M. H. Alexander, F. J. Aoiz, A. Gijsbertsen and S. Stolte, Chem. Sci., 2015, 6, 2202.
3. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina and S. Stolte, J. Chem. Phys., 2013, 138, 104310.
4. C. J. Eyles, M. Brouard, C. H. Yang, J. Klos, F. J. Aoiz, A. Gijsbertsen, A. E. Wiskerke and S. Stolte, Nat. Chem., 2011, 3, 597–602.
5. T. de Jongh, Q. Shuai, G. L. Abma, S. Kuijpers, M. Besemer, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2022, 14, 538–544.
6. T. de Jongh, M. Besemer, Q. Shuai, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2020, 368, 626–630.
7. J. Onvlee, S. D. S. Gordon, S. N. Vogels, T. Auth, T. Karman, B. Nichols, A. van der Avoird, G. C. Groenenboom, M. Brouard and S. Y. T. van de Meerakker, Nat. Chem., 2017, 9, 226–233.
8. S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790.
9. A. von Zastrow, J. Onvlee, S. N. Vogels, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, Nat. Chem., 2014, 6, 216–221.
10. C. Amarasinghe, H. W. Li, C. A. Perera, M. Besemer, J. X. Zuo, C. J. Xie, A. van der Avoird, G. C. Groenenboom, H. Guo, J. Klos and A. G. Suits, Nat. Chem., 2020, 12, 528–535.
11. A. Gijsbertsen, H. Linnartz, G. Rus, A. E. Wiskerke, S. Stolte, D. W. Chandler and J. Klos, J. Chem. Phys., 2005, 123, 224305.
12. K. T. Lorenz, D. W. Chandler, J. W. Barr, W. W. Chen, G. L. Barnes and J. I. Cline, Science, 2001, 293, 2063–2066.
13. O. Tkac, A. K. Saha, J. Loreau, Q. L. Ma, P. J. Dagdigian, D. H. Parker, A. van der Avoird and A. J. Orr-Ewing, Mol. Phys., 2015, 113, 3925–3933.
14. O. Tkac, Q. L. Ma, C. A. Rusher, S. J. Greaves, A. J. Orr-Ewing and P. J. Dagdigian, J. Chem. Phys., 2014, 140, 204318.
15. C. K. Bishwakarma, G. van Oevelen, R. Scheidsbach, D. H. Parker, Y. Kalugina and F. Lique, J. Chem. Phys., 2018, 149, 121101.
16. M. Brouard, S. D. S. Gordon, B. Nichols, E. Squires, V. Walpole, F. J. Aoiz and S. Stolte, J. Chem. Phys., 2017, 146, 204304.
17. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2017, 147, 013912.
18. T. F. M. Luxford, T. R. Sharples, M. Fournier, C. Soulie, M. J. Paterson, K. G. McKendrick and M. L. Costen, J. Phys. Chem. A, 2023, 127, 6251–6266.
19. G. Q. Tang, M. Besemer, J. Onvlee, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, J. Chem. Phys., 2022, 156, 214304.
20. G. Tang, M. Besemer, T. de Jongh, Q. Shuai, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, J. Chem. Phys., 2020, 153, 064301.
21. Z. Gao, T. Karman, S. N. Vogels, M. Besemer, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2018, 10, 469–473.
22. Z. Gao, T. Karman, G. Tang, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Phys. Chem. Chem. Phys., 2018, 20, 12444–12453.
23. G. Tang, M. Besemer, S. Kuijpers, G. C. Groenenboom, A. van der Avoird, T. Karman and S. Y. T. van de Meerakker, Science, 2023, 379, 1031–1036.
24. T. B. Settersten, B. D. Patterson and J. A. Gray, J. Chem. Phys., 2006, 124, 234308.
25. M. A. B. Paci, J. Few, S. Gowrie and G. Hancock, Phys. Chem. Chem. Phys., 2013, 15, 2554–2564.
26. T. B. Settersten, B. D. Patterson, H. Kronemayer, V. Sick, C. Schulz and J. W. Daily, Phys. Chem. Chem. Phys., 2006, 8, 5328–5338.
27. A. N. Bridgers, J. A. Urquilla, J. Im and A. S. Petit, J. Phys. Chem. A, 2023, 127, 7228–7240.
28. L. Craciunescu, E. M. Liane, A. Kirrander and M. J. Paterson, J. Chem. Phys., 2023, 159, 124303.
29. C. Soulié and M. J. Paterson, J. Chem. Phys., 2022, 157, 164304.
30. C. Soulié and M. J. Paterson, Phys. Chem. Chem. Phys., 2022, 24, 7983–7993.
31. J. G. Leng, T. R. Sharples, K. G. McKendrick and M. L. Costen, Phys. Chem. Chem. Phys., 2022, 24, 6525–6534.
32. T. R. Sharples, J. G. Leng, T. F. M. Luxford, K. G. McKendrick, P. G. Jambrina, F. J. Aoiz, D. W. Chandler and M. L. Costen, Nat. Chem., 2018, 10, 1148–1153.
33. T. F. M. Luxford, T. R. Sharples, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 084312.
34. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 174304.
35. T. R. Sharples, T. F. M. Luxford, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2015, 143, 204301.
36. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
37. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988.
38. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. K. Kats, T. R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, Version 2023.2, a Package of Ab Initio Programs, https://www.molpro.net.
39. H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. L. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
40. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 242–253.
41. Q. L. Ma, M. Schwilk, C. Köppl and H. J. Werner, J. Chem. Theory Comput., 2017, 13, 4871–4896.
42. Q. L. Ma and H. J. Werner, J. Chem. Theory Comput., 2019, 15, 1044–1052.
43. Z. Gao, S. N. Vogels, M. Besemer, T. Karman, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, J. Phys. Chem. A, 2017, 121, 7446–7454.
44. X. D. Wang, P. A. Robertson, F. J. J. Cascarini, M. S. Quinn, J. W. McManus and A. J. Orr-Ewing, J. Phys. Chem. A, 2019, 123, 7758–7767.
45. J. L. Guardado, D. J. Hood, K. Luong, N. M. Kidwell and A. S. Petit, J. Phys. Chem. A, 2021, 125, 8803–8815.
46. K. J. Blackshaw, N. K. Quartey, R. T. Korb, D. J. Hood, C. D. Hettwer and N. M. Kidwell, J. Chem. Phys., 2019, 151, 104304.
47. Z. F. Sun, R. J. A. Scheidsbach, M. C. van Hemert, A. van der Avoird, A. G. Suits and D. H. Parker, Phys. Chem. Chem. Phys., 2023, 25, 17828–17839.
48. M. Brouard, H. Chadwick, S. D. S. Gordon, B. Hornung, B. Nichols, J. Klos, F. J. Aoiz and S. Stolte, J. Chem. Phys., 2014, 141, 164306.
49. Z. F. Sun, M. C. van Hemert, J. Loreau, A. van der Avoird, A. G. Suits and D. H. Parker, Science, 2020, 369, 307–309.
50. M. Besemer, G. Q. Tang, Z. Gao, A. van der Avoird, G. C. Groenenboom, S. Y. T. van de Meerakker and T. Karman, Nat. Chem., 2022, 14, 664–669.
51. H. J. Loesch and F. Stienkemeier, J. Chem. Phys., 1993, 99, 9598–9602.
52. C. Robertson and M. J. Paterson, Chem. Commun., 2022, 58, 9092–9095.
53. D. Babikov and A. Semenov, J. Phys. Chem. A, 2016, 120, 319–331.

---