Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heterogeneous Li coordination in solvent-in-salt electrolytes enables high Li transference numbers†
Anne
Hockmann
ab,
Florian
Ackermann‡
a,
Diddo
Diddens
 ac,
Isidora
Cekic-Laskovic
ac,
Isidora
Cekic-Laskovic
 c and
Monika
Schönhoff
c and
Monika
Schönhoff
 *a
*a
aInstitute of Physical Chemistry, University of Münster, Corrensstraße 28/30, 48149 Münster, Germany. E-mail: schoenho@uni-muenster.de
bInternational Graduate School Battery Chemistry, Characterization, Analysis, Recycling, and Application (BACCARA), University of Münster, Corrensstraße 40, 48149 Münster, Germany
cHelmholtz Institute Münster, IEK-12, Forschungszentrum Jülich GmbH, Corrensstraße 48, 48149 Münster, Germany
First published on 5th March 2024
Abstract
The transport properties and the underlying coordination structure of a ternary electrolyte consisting of lithium bis(trifluoromethanesulfonyl)imide (LiTFSI), 1,2-dimethoxyethane (DME), and 1,3-dioxolane (DOL) is studied over a wide concentration range, up to that of a Solvent-in-Salt (SiS) electrolyte. Among other advantages for next-generation battery applications, SiS electrolytes offer a high lithium transference number (tLi) of 0.73. We analyze the transport mechanism by electrophoretic NMR (eNMR), providing the mobilities (μi) of all species. Intriguingly, in the SiS region, the mobility of the neutral species DME exceeds the cation mobility (μDME > μLi), suggesting a heterogeneous transport mechanism, where the Li+ mobility is averaged over different species. Based on Raman spectroscopy, NMR spectroscopy and MD simulations, we derive a model for a concentration-dependent Li+ coordination environment with a heterogeneous Li+ coordination in the SiS region, where the 1st coordination shell either consists of TFSI− and DOL only, or of DME, TFSI−, and DOL. Lithium ions partially coordinated by DME migrate faster in an electric field, in contrast to lithium ions solely coordinated by anions and DOL molecules, explaining the peculiarity of the rapidly migrating neutral DME molecules. Further, DME is identified as an exclusively bidentate ligand, while TFSI− and DOL act as bridging ligands coordinating different Li+ ions. Thus, Li+ coordination heterogeneity is the basis for Li+ transport heterogeneity and for achieving very high Li+ transference numbers. In addition, an effective dynamic decoupling of Li+ and anions occurs with an Onsager coefficient σ+− ≈ 0. These results provide a deeper understanding of the very efficient lithium-ion transport in SiS electrolytes, with the potential to bring further improvements for battery applications.
Introduction
The pursuit of next generation batteries beyond the established Li-ion technology is driven by the need for high energy densities in mobile applications, but also for safer and more environmentally friendly battery cell chemistries. The aim is to increase the overall performance of batteries while enabling a more sustainable product life cycle, e.g. by using abundant transition metals in the electrode materials, and focusing on energy-efficient cell production.1–5 The introduction of alternative active materials, however, imposes a range of new requirements for the whole battery cell chemistry. The liquid electrolyte, as the only component physically interfacing with every other battery cell component, governs the overall performance and safety of the resulting chemistry by simultaneously coping with issues arising from the active materials, e.g. dendrite growth, exfoliation, or active-material loss. In the case of lithium–sulfur (LiS) batteries, highly concentrated liquid electrolytes are considered as promising candidates to overcome these drawbacks. Due to the high conducting salt concentration, they contain no non-coordinating solvents and exhibit an anion-rich lithium solvation shell, leading to several advantages like broader thermal and electrochemical stability, a robust inorganic SEI, the suppression of lithium dendrite growth and dissolution of polysulfides. Moreover, this unique solvation structure results in a high rate capacity, improved galvanostatic cycling, a high coulombic efficiency, and a high level of safety. In addition, high lithium transference numbers (tLi) of up to 0.7 were reported for different high-concentration electrolytes, which is notably higher than the values ranging from 0.2 to 0.4 observed for common dilute and moderately concentrated electrolytes.6–11On the other hand, high-concentration electrolytes suffer from a high viscosity and low ionic conductivity.6,12–17 Though conductivity is a vital bulk property of each battery electrolyte, it is not decisive for the overall electrochemical performance, as indicated by the relevant key performance indicators. The latter include parameters such as high specific capacity, capacity retention, coulombic efficiency and suppressed lithium dendrite formation, which can be achieved in high-concentration electrolytes, and make them interesting candidates for application.18,19
The reported particularly high lithium transference numbers in high-concentration electrolytes are generally attributed to a change in the lithium transport mechanism due to ionic aggregates. However, distinct differences regarding the dominant transport mechanism are reported, dependent on the used conducting salts and solvents. On the one hand, Borodin et al. showed a nano-heterogeneity in an aqueous electrolyte, with relatively immobile anion-rich domains and aqueous Li+-conducting percolating channels.8 On the other hand, Dokko et al. and Nakanishi et al. reported an enhanced tLi for sulfolane-based electrolytes, postulating an ion-hopping mechanism supported by a chain-like lithium ion coordination of the anions and sulfolane molecules.9,20 A similar mechanism was proposed by Kondou et al. for two keto-ester-based systems, which are also able to act as bridging ligands similar to sulfolane. However, when methyl levulinate (ML) was used as the solvent, this transport mechanism was not observed, but rather a less effective vehicular transport, since ML coordinates lithium bidentate, in contrast to sulfolane.21 Finally, Self et al. studied a propylene carbonate-based electrolyte containing two different lithium salts. They found that ion hopping and ligand exchange take place in the system, too. However, vehicular transport still exists and is strongly dependent on the conducting salt used. Therefore, the vehicular transport mostly accounts for the efficiency of the ion transport.22 Overall, these examples show that the ion transport mechanism strongly depends on the coordination properties of the used conducting salt and solvent molecules.
In 2013, Suo et al. published an article in which, in contrast to the systems discussed above, an electrolyte comprising two different ethereal solvents, namely 1,2-dimethoxyethane (DME) and 1,3-dioxolane (DOL), is used.10 As the conducting salt, they used lithium bis(trifluoromethanesulfonyl)imide (LiTFSI). Additionally, they defined Solvent-in-Salt (SiS) electrolytes as a class of concentrated salt solutions, in which the salt-to-solvent ratio by volume and/or mass exceeds unity.10,15 In this region, they also reported surprisingly high tLi up to 0.73. Raman studies showed strong lithium-anion clustering, which led to the suggestion that the observed high lithium transference number is caused by “Li-ion exchange between aggregated ion pairs and solvent molecules”, assuming a Li transport similar to the mechanism in poly(ethylene oxide) (PEO).23 However, the role of the two different solvent molecules, and consequently the exact transport mechanism, is not yet fully understood. Since the above discussed articles clearly show that the lithium transport mechanism in highly concentrated liquid electrolytes strongly depends on the coordination properties of the used components, it is crucial to investigate the bi-solvent electrolyte formulation reported by Suo et al.10 in more detail.
In this work, a concentration series of LiTFSI dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (vol
1 (vol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vol) mixture of DME and DOL at molal concentrations ranging from 1–7 M, according to Suo et al.,23 is investigated. The aim is to gain a deeper understanding of the mechanisms causing the reported highly efficient lithium transport. Therefore, electrophoretic NMR (eNMR) is applied, which is a versatile technique for the direct determination of a molecule's drift velocity in an electric field.24,25 The species-selective transport behavior of all molecular components is analyzed based on the Li+ coordination environment, as characterized by various spectroscopic methods. Additionally, molecular dynamics (MD) simulations are performed and compared to the experimental results. From the obtained results, a model description of the average first coordination shell of lithium, dependent on the conducting salt concentration, is derived. In particular, the mobilities obtained from eNMR exhibit a positive mobility of the neutral species DME in the SiS domain, which exceeds the mobility of Li+. Combined with the observed exclusive bidentate coordination of DME in contrast to the bridging ligands DOL and TFSI−, this suggests a heterogeneous lithium coordination, with consequences for transport: lithium cations containing DME in their coordination exhibit larger drift velocities as compared to cations coordinated only by anions and DOL, since the latter are more strongly coordinated to neighboring cations at high salt concentrations. Therefore, these results serve as an explanation for the reported high tLi values.
vol) mixture of DME and DOL at molal concentrations ranging from 1–7 M, according to Suo et al.,23 is investigated. The aim is to gain a deeper understanding of the mechanisms causing the reported highly efficient lithium transport. Therefore, electrophoretic NMR (eNMR) is applied, which is a versatile technique for the direct determination of a molecule's drift velocity in an electric field.24,25 The species-selective transport behavior of all molecular components is analyzed based on the Li+ coordination environment, as characterized by various spectroscopic methods. Additionally, molecular dynamics (MD) simulations are performed and compared to the experimental results. From the obtained results, a model description of the average first coordination shell of lithium, dependent on the conducting salt concentration, is derived. In particular, the mobilities obtained from eNMR exhibit a positive mobility of the neutral species DME in the SiS domain, which exceeds the mobility of Li+. Combined with the observed exclusive bidentate coordination of DME in contrast to the bridging ligands DOL and TFSI−, this suggests a heterogeneous lithium coordination, with consequences for transport: lithium cations containing DME in their coordination exhibit larger drift velocities as compared to cations coordinated only by anions and DOL, since the latter are more strongly coordinated to neighboring cations at high salt concentrations. Therefore, these results serve as an explanation for the reported high tLi values.
Experimental
Materials and sample preparation
The conducting salt lithium bis(trifluoromethanesulfonyl)imide (LiTFSI, Sigma-Aldrich, 99%, dried at 100 °C under high vacuum overnight) was dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture, by volume, of the solvents 1,3-dioxolane (DOL, Sigma-Aldrich, 99.8%, anhydrous, with ∼75 ppm BHT as an inhibitor, used as received) and 1,2-dimethoxyethane (DME, Sigma-Aldrich, >99.5%, anhydrous, used as received). Samples with molal conducting salt concentrations (see eqn (S1)†) between 1 and 7 mol L−1 were prepared and handled in a glove box under an argon atmosphere. The corresponding molar LiTFSI concentrations and oxygen-to-lithium ratios were determined via density measurements (Rudolph Research Analytical DDM 2910) at 26.5 °C and are given in Table S1 in the ESI.†
1 mixture, by volume, of the solvents 1,3-dioxolane (DOL, Sigma-Aldrich, 99.8%, anhydrous, with ∼75 ppm BHT as an inhibitor, used as received) and 1,2-dimethoxyethane (DME, Sigma-Aldrich, >99.5%, anhydrous, used as received). Samples with molal conducting salt concentrations (see eqn (S1)†) between 1 and 7 mol L−1 were prepared and handled in a glove box under an argon atmosphere. The corresponding molar LiTFSI concentrations and oxygen-to-lithium ratios were determined via density measurements (Rudolph Research Analytical DDM 2910) at 26.5 °C and are given in Table S1 in the ESI.†
NMR experiments
All NMR experiments for the nuclei 1H, 7Li, and 19F, except electrophoretic mobility measurements and some diffusion measurements taken at 30 °C, were conducted at 26.5 °C on a Magritek Spinsolve spectrometer operating at 60 MHz 1H frequency and providing magnetic field gradients up to 0.16 T m−1.Spin relaxation
The longitudinal spin relaxation time T1 was obtained by performing inversion recovery experiments.26 Employing the Carr–Purcell–Meiboom–Gill (CPMG) experiment, the transversal relaxation time T2 was determined, using a delay τ between 180° pulses of 1 ms.27,28 The maximal delay was adjusted to the respective nucleus and sample (1H: 1 to 3 s; 19F: 2 to 5 s; 7Li: 2 to 25 s).PFG-NMR diffusion
The self-diffusion coefficients D were determined via pulsed field gradient (PFG) NMR using the pulsed gradient stimulated echo sequence.29 For each sample and investigated nucleus, the pulse duration and maximal gradient strength were adjusted and the observation time Δ was set to 100 ms. Additionally, the measurements were reproduced using a shorter Δ of 50 ms to exclude convection artefacts. Diffusion experiments were conducted at 26.5 °C at 60 MHz and at 30 °C at 400 MHz in combination with the electrophoretic experiments; see below.Electrophoretic NMR (eNMR)
Electrophoretic mobilities μ were determined by employing eNMR, using a 400 MHz Bruker Avance III HD spectrometer and a sample holder with electrodes, as described previously.24 A double stimulated echo pulse sequence was employed for convection compensation,30 where the electric field is inverted in between the second and third magnetic field gradient pulse.31 A recycle delay of 60 s between scans allows for dissipation of heat generated by Joule heating. The observation time was 100 ms, the gradient pulse durations were 1 ms (1H and 19F) and 3 ms (7Li), and the temperature was T = 30 °C. The gradient strength was kept constant during the experiment at a value chosen appropriately for each sample and nucleus, in order to achieve a high phase shift while maintaining a reasonable signal-to-noise ratio. In each experiment, the applied voltage was incremented from low to high values with an alternating sign of the first pulse. The resulting eNMR spectra were evaluated via an approximation by phase-sensitive Lorentzian profiles, as described previously.32 In the fitting procedure, the phases of 1H resonances corresponding to the same molecule were set to equal values. The voltage-dependent phase shift ϕ − ϕ0 was determined as the difference between the determined phase angle at a given voltage and the phase angle at 0 V. The phase shift is linearly dependent on the gyromagnetic ratio γ, the magnetic field gradient strength G and duration δ, the observation time between the encoding and decoding gradient pulses Δ, the electrophoretic mobility μ, and the applied electric field E, which is given by the applied voltage divided by the electrode distance d. In contrast to battery cell experiments, polarization effects can be neglected due to the short electric field pulses, and the full potential applies to the sample; see also the consistency with impedance data in the ESI, Fig. S1.†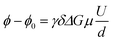 | (1) |
The electrophoretic mobility was determined from a linear approximation according to eqn (1). Three independent measurements on different samples are performed for each sample and nucleus and the resulting mobilities averaged.
Impedance spectroscopy
All impedance spectroscopy (IS) measurements were conducted at 30 °C using a frequency analyzer (Novocontrol Alpha, Montabaur, Germany), and an in-house-built symmetrical sample cell made of white copper with gold-coated electrodes. Each experiment was conducted with a voltage amplitude of 10 mV. The conductivity of each respective electrolyte was determined from the dc plateau under the assumption of a sample cell behavior described by the Randles circuit in the absence of faradaic reactions.33Raman spectroscopy
Raman spectra were taken on a MultiRAM FT-Raman spectrometer (Bruker, Ettlingen). The laser had a wavelength of 1064 nm and a power of 263 mW. The samples were measured in an NMR tube with a resolution of 1 cm−1 in the range of 30–3600 cm−1. Raman bands for vibrations of TFSI− (∼445 cm−1), DME (∼840 cm−1), and DOL (∼940 cm−1) were baseline-corrected and deconvoluted using the software OPUS 8.5 (Bruker). Deconvolution yields two, three, or three peaks, respectively, each a combination of 40% Gauss and 60% Lorenz line shapes. The peaks were assigned to resonances for uncoordinated and coordinated TFSI−, DME and DOL, respectively. Their respective integrals, Acoord and Afree, were employed to calculate the coordinated fraction, fcoord, according to a procedure described earlier, which assumes equal Raman scattering coefficients of the free and coordinated species.34,35 | (2) |
MD simulations
The MD simulations were run using the software package GROMACS (version 2019.3)36 with the OPLS-AA force field37 for the solvents and the CL&P force field38,39 for the ions. The evaluation was performed using routines written in Python 3.7.2 based on the MDAnalysis package.40,41 Initially, a cubic simulation box with about 1000 molecules was generated by means of PACKMOL (version 20.010).42 After this initialization, a relaxation run was produced at 426.85 °C for 10 ns. The equilibration was performed at the target temperature 26.5 °C for 100 ns. The simulation time of the final production run was 1 μs. The simulations were run for four compositions with molal concentrations of 1 M, 3 M, 5 M, and 7 M. To implicitly include polarization effects, the partial charges of the ions were scaled by a factor of 0.8, as reported elsewhere for similar systems.43,44Results and discussion
Li salt/DOL/DME electrolyte formulations are investigated over a wide range of concentrations, spanning the transition from Salt-in-Solvent to Solvent-in-Salt. First of all, transport measurements highlight the specific features of ion transport in Solvent-in-Salt electrolytes. To assess the transport of all constituent species, we performed species-selective NMR transport measurements. To distinguish between the different NMR-active nuclei of the electrolyte systems, they are labelled as illustrated in Scheme 1.Diffusion and spin relaxation
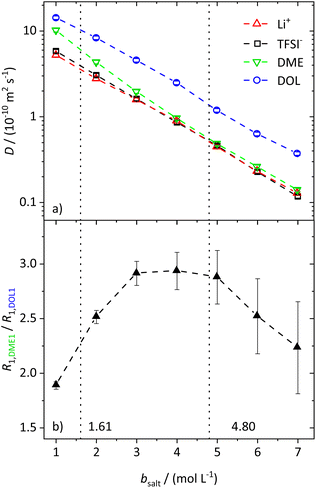
In the range from 1 to 7 mol L−1, the self-diffusion coefficients D for the cations, anions, and solvent molecules are obtained via PFG-NMR (Fig. 1a). For all species, D decreases with increasing conducting salt concentration. This can be mainly interpreted as an overall decrease in system dynamics, which is very common for electrolytes.45,46 Moreover, over the whole concentration range, one observes equal diffusion coefficients of Li+ and TFSI−. Whether this equality is a coincidence, or whether it suggests correlated diffusion of Li+ and TFSI− in the form of ion pairs, can be judged by calculating the ionicity. The ionicity, or inverse Haven ratio HR−1, is obtained from eqn (3), where σ corresponds to the ionic conductivity measured via IS, and σNE is the ionic conductivity estimated from the self-diffusion coefficients using the Nernst–Einstein equation (eqn (4)) with the charge number zi, the concentration ci, and the self-diffusion coefficient Di of the ionic species, as well as the temperature T, the Faraday constant F and the gas constant R.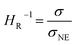 | (3) |
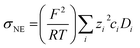 | (4) |
The conductivity data from IS are shown in the ESI, Fig. S1a,† and largely agree with earlier data from Suo et al.10 The values for σNE are substantially larger (see comparison in Fig. S1a†), and consequently the ionicities are low, in the range of 0.2 to 0.3 (see ESI, Fig. S1b†). These low values highlight the non-ideality of the electrolyte, exhibiting a low dissociation degree and strong ion correlations.
While the self-diffusion coefficients of both ions are almost identical, distinct differences can be noticed in the diffusion of the solvent molecules. Fig. 1a shows that DDME is more strongly affected by an increasing amount of salt than DDOL and approaches the values of the ions at high conducting salt concentrations. This is not the case for DOL, where DDOL exceeds DLi by the same factor, irrespective of salt concentration. Therefore, DME seems to coordinate to Li+ rather than DOL, leading to a smaller fraction of free DME molecules, and a higher similarity in the diffusion coefficients of DME and the ions.
The assumption of a preferred coordination of Li+ cations by DME molecules is evaluated by analyzing the spin–lattice relaxation rates R1 of the protons of the two solvent molecules. First of all, the spin–lattice and spin–spin relaxation rates, R1 and R2, of all species in the electrolyte system increase with an increasing salt concentration due to the generally slowed down dynamics. These trends are shown and explained in more detail in the ESI (see Fig. S2†). However, by investigating the ratio of the relaxation rates R1 of the protons of the two different solvent species (see Fig. 1b for the protons DME1 and DOL1 according to Scheme 1), the influence of the general effect of slowed down dynamics is eliminated, such that variations in the local coordination environment of the solvent molecules can be identified.
With values from 1.6 to 3.0, the ratio does not vary strongly over the whole conducting salt concentration range, while the relaxation rates vary by an order of magnitude. This confirms that concentration-dependent variations in the overall system dynamics are largely compensated by forming the ratio. Nevertheless, a maximum around bsalt = 4 mol L−1 is detected, which can be attributed to changes in the local dynamics of the individual solvent species with salt addition. We note that the system is in motional narrowing (see the identity of the R1 and R2 values of the same protons in Fig. S2b,† where an increase in R1 indicates reduced local dynamics). Thus, at moderate conducting salt concentrations, the DME local dynamics is more strongly reduced compared to that of DOL, while at conducting salt concentrations higher than 4.8 M, the dynamics of DOL is more affected. The considered electrolyte formulations with conducting salt concentrations exceeding 4.8 M fulfill the definition of a SiS electrolyte; therefore this concentration represents the starting point of the SiS region. Thus, again these trends indicate that at moderate conducting salt concentrations, DME coordinates Li+ rather than DOL, while DOL starts to participate in the coordination shell of the cation in the SiS region, leading to a stronger increase in its relaxation rate R1,DOL1. This coordination preference will be the basis of a later introduced stochiometric model; see below.
Electrophoretic mobilities
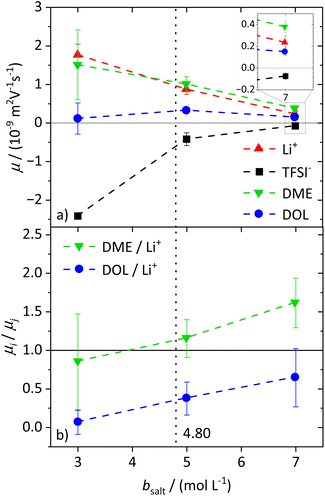
To characterize the migration of each of the molecular species in an electric field, eNMR is applied. In the case of 1H eNMR, a deconvolution of the partially overlapping DOL and DME resonances with their respective phase shifts is required, which is performed according to a previously established procedure.32 Representative spectra are given in the ESI, Fig. S3.† The electrophoretic mobilities μ obtained from 1H, 7Li and 19F eNMR according to eqn (1) are shown in Fig. 2a. Conducting salt concentrations lower than 3 M are not measurable due to DOL polymerization in the electric field. The mobilities of the anion are negative over the whole conducting salt concentration range, which corresponds to a drift towards the positive electrode, while the opposite sign applies for the cation. This is in line with expectations, as well as the decrease in the absolute values of the mobility with increasing conducting salt concentration, similar to the self-diffusion coefficients in Fig. 1a.Regarding the solvents DME and DOL, a mobility of zero is measured for DOL at the lowest salt concentration of bsalt = 3 mol L−1, as expected for a neutral species. However, for DME we observed a positive mobility, which is regarded as identical to μLi within the observed error, leading to the assumption that DME not only coordinates the lithium cations, but even forms cationic clusters, so-called dynamic clusters, which form the cationic species migrating in the electric field. A migration of neutral species in an electric field was previously observed for solvate ionic liquids, where glyme–Li+ complexes are sufficiently long-lived to constitute the migrating species.47 A similar migration of DME with Li+ can be concluded here. For higher conducting salt concentrations, μDOL also turns positive, implying that some of the DOL molecules coordinate and migrate with the cations. This is the case from b = 5 mol L−1 onwards and confirms the onset of DOL coordination to Li+ in the SiS domain.
Interestingly for conducting salt concentrations in the SiS region, the mobility of DME is even higher than the mobility of lithium; see inset in Fig. 2a. This observation is unexpected, and implies that the neutral species DME migrates on average faster in the electric field than the lithium cation. The solvent-to-lithium mobility ratios increasing with conducting salt concentration, depicted in Fig. 2b, illustrate this clearly, with a transition of μDME/μLi values smaller than one to values larger than one in the SiS concentration region. Furthermore, Fig. 2b shows that with increasing conducting salt concentration, not only the DME but also the DOL mobility increases in relation to that of lithium. However, it does not exceed one and thus, it is likely that there is still a fraction of free and not migrating DOL molecules reducing the average mobility of this species compared to the cation.
Transference numbers
The lithium transference numbers determined by eNMR and obtained from eqn (5), teNMR, and the transport number tapp obtained from diffusion NMR and calculated using eqn (6) are shown in Fig. 3.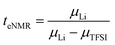 | (5) |
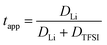 | (6) |
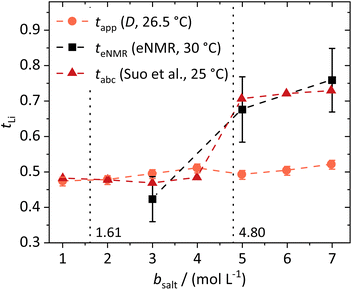 | ||
| Fig. 3 Lithium transference numbers dependent on the molal conducting salt concentration bsalt determined via diffusion NMR, eNMR, and potentiostatic current measurements by Suo et al.10 The dashed lines serve as a guide to the eye, and the vertical dotted lines result from a model-based interpretation marking different regimes of the lithium coordination shell. | ||
They are compared to tabc, the transference number obtained by Suo et al.10via potentiostatic measurements under anion blocking conditions. It is important to note that the three different transport coefficients describe different phenomena and properties of the electrolyte formulation. While teNMR describes the fraction of charge transport associated with species containing the 7Li nucleus in relation to the total conductivity of the solution, the transport number tapp is an approximation of the transference number, assuming fully dissociated electrolytes and neglecting ion correlations. For moderate conducting salt concentrations, between 1 and 4 M, the transference number teNMR equals the transport number tapp of 0.5. However, a steep increase is observed for both transference numbers for electrolytes in the SiS region. This mismatch signifies the relevance of dynamic correlations for highly concentrated electrolytes in the SiS domain.
On the other hand, the potentiostatic transference number tabc describes the lithium current under anion blocking conditions in relation to the total current in the electrolyte, which is in good agreement with teNMR. We note that an agreement of tabc and teNMR is not a general feature, as in concentrated electrolytes both quantities may differ largely, since they are affected by ion correlations in a different manner.48
This difference is given by the dependence of tabc and teNMR on the Onsager coefficients σ++, σ+−, and σ−−, where the latter describe the dynamic correlations between the charged species:49
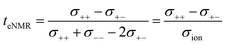 | (7) |
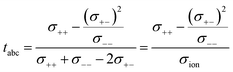 | (8) |
Therefore, an agreement of these transference numbers (tabc = teNMR), as observed here, implies:
| σ−− = σ+− or σ+− = 0 | (9) |
We calculate the Onsager coefficients from the MD simulation results, which are discussed further below and used to elucidate the Li+ coordination environment. Since we realized that there are deviations of the absolute values of dynamic quantities from experimental ones, especially at ultra-high conducting salt concentrations, we analyze the relative magnitude σij normalized to σion; see description in the ESI and Fig. S4.†
We indeed find σ+−/σion ≈ 0 over the whole concentration range (see Fig. S4†), explaining the peculiar agreement of tabc and teNMR. The vanishing dynamic correlation of Li+ and the anion implies an effective dynamic decoupling of the Li+ transport from anion transport. The combination with a strong increase in σ++/σion with concentration (see Fig. S4†), evidencing a structural Li+ transport, yields a strong increase in the Li+ transference number.
From these dynamic findings, first conclusions on the concentration-dependent Li+ coordination environment can be drawn. With a reduction in the oxygen-to-lithium ratio, the ion coordination and consequently the ion transport changes to a mechanism favoring lithium. In dilute and moderately concentrated electrolytes, Li+ is migrating jointly with its first coordination shell consisting of DME molecules, as discussed above, via a vehicular mechanism. This vehicle is of a similar size to the anion, which might lead to similar drift velocities and to a transference number of 0.5. With increasing conducting salt concentration, the DME concentration becomes insufficient to provide a full coordination of the lithium cations; thus the coordination environment of Li+ becomes heterogeneous, influencing the ion transport. The high lithium transference number of approximately 0.7 in the SiS region suggests that the mechanism of lithium transport is drastically changed, which we will analyze in detail by studying the coordination environment in the following sections. Interestingly, this change is accompanied by a transition of the DME/Li mobility ratio from <1 to >1; see Fig. 2b.
Raman spectra
In order to interpret the concentration-dependent lithium transport mechanisms based on a stochiometric model for the Li+ coordination shell, we first analyze the local coordination environment of Li+via Raman spectroscopy, chemical shifts in the NMR spectra of the different molecules, and MD simulations. The vibrational Raman bands of the anion and of the two solvent molecules are shown in Fig. 4. The shown spectra are normalized to the molar fraction of salt. In the case of the anion, depicted in Fig. 4a, the band at around 742 cm−1 is assigned to free or only loosely coordinating anions, while the increasing band at 747 cm−1 corresponds to coordinated or even aggregated anions.23,34,35,50,51 Regarding Fig. 4b, the three bands around 850 cm−1 arise from DME, with the two bands on the left assigned to free molecules, and the one on the right-hand side to an increasing amount of coordinated DME molecules.50–52 Vibrational bands of DOL are observed around 960 cm−1, consistent with the grey line for pure DOL in Fig. 4b. The two intense bands correspond to free DOL molecules. In addition, we observe a small band at around 910 cm−1, which is increasing with salt concentration. To the best of our knowledge, this band was not reported earlier and we interpret it here as the vibration of coordinated DOL molecules. This is reasonable, as on the one hand a similar band arises for a concentrated electrolyte based on tetrahydrofuran53 and on the other hand this band is increasing with the conducting salt concentration, while the other bands assigned to DOL decrease. Exemplary fits of the vibrational bands of the three coordinating molecular species are presented in the ESI (see Fig. S5†). In the following section, the fractions of coordinating molecules fcoord,Raman are calculated according to eqn (2) from the deconvoluted spectra.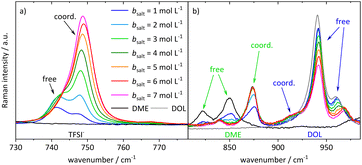 | ||
| Fig. 4 Stack plot of the Raman spectra of the electrolyte system at different conducting salt concentrations. Vibration band (a) of the anion and (b) of the two solvent molecules. | ||
Average first coordination shell of lithium
In the following, we discuss the first coordination shell of the Li+ ions dependent on the conducting salt concentration, based on the Raman bands, chemical shifts and coordination numbers obtained from MD simulation results. As all methods suggest a coordination preference in the order DME > TFSI− > DOL, we assume a model for the average lithium coordination shell dependent on the conducting salt concentration shown in Fig. 5a, where for dilute and moderately concentrated electrolytes, Li+ is only coordinated by DME molecules. Here, three DME molecules, i.e. 6 oxygens, coordinate one lithium cation, resulting in a lithium coordination number Nc = 6. A total coordination number of almost six over the whole concentration range is indicated by MD simulations; see Fig. 5b. This is in accordance with literature on different electrolytes, generally reporting a coordination number of 4–6 oxygens around lithium cations.54–59 In the high-concentration region, above a 1.61 M salt concentration, the concentration of DME is too low to provide an Nc of six. Thus, the anions participate in the lithium coordination. When reaching the ultra-high-concentration SiS region, the stoichiometry of the electrolyte requires a further change in the average lithium coordination shell, since above bsalt = 4.80 mol L−1 the number of DME and TFSI− oxygens becomes insufficient to fully coordinate Li+. Here, DOL also has to coordinate to some extent to still achieve Nc = 6. Interestingly, this stoichiometric definition of the SiS region agrees well with the volumetric definition (Vsalt/Vsolvent > 1), and with the onset of the high-transference-number regime; see Fig. 3.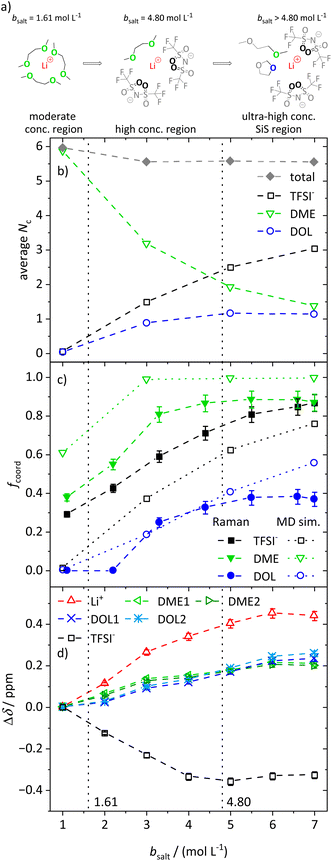 | ||
| Fig. 5 (a) Illustration of the average lithium coordination shell for the introduced model based on two discussed conditions. (b) Average lithium coordination number Nc of the anion and solvent oxygens (open symbols) as well as the total coordination number (gray diamonds) from MD simulations. (c) Fraction of coordinating molecules fcoord for the different species (TFSI− black squares, DME green triangles, DOL blue circles) from the Raman bands (filled symbols) as well as from MD simulations (open symbols) as a function of the conducting salt concentration. (d) Chemical shift difference Δδ referenced to the chemical shift of the 1 M electrolyte for each investigated NMR signal. Solvent signals are as explained in Scheme 1. The dashed lines in all graphs serve as a guide to the eye, and the vertical dotted lines result from the model-based interpretation seen in (a) marking different regimes of the lithium coordination shell. | ||
As described, the two limiting concentrations, 1.61 and 4.80 M, divide the concentration range into three sections, namely moderate, high and ultra-high concentration (SiS) regions, which are marked in Fig. 5b–d and previous graphs to ensure a direct comparison to the introduced model.
As already mentioned, Fig. 5b shows the coordination number Nc of oxygens in the proximity of Li+, calculated from the radial distribution function (RDF) obtained from the MD simulations. Next to the total coordination number, the coordination numbers of the oxygens of the different ligands Nc,i are also shown. They directly translate to the introduced model and are in very good agreement: both introduced conditions, namely Nc = 6 and the coordination preference of DME > TFSI− > DOL, are reflected. Fig. 5b shows an average coordination of Li+ by six ODME in the moderately concentrated region, and for ultra-high conducting salt concentrations of 7 M in the SiS region, DME and DOL coordinate on average with one oxygen atom each and TFSI− with more than three oxygens, just as the model in Fig. 5a predicts.
However, in contrast to the model in Fig. 5a, DOL already starts to coordinate lithium at concentrations below the second limiting concentration of 4.80 M. In addition, Fig. 5b reveals a slightly reduced total Nc from 6 to 5.8 with increasing conducting salt concentration. There might be sterical hindrances in the high-concentration electrolytes, preventing a local packing with an optimized Li+ coordination. In addition, entropic contributions, overcoming small energy differences of Li–oxygen interactions, may significantly broaden transitions between the regimes. Nevertheless, in spite of the simplistic nature of the model, especially concerning the high-concentration region, it is still providing a suitable guideline for the changes in the average lithium coordination shell with increasing conducting salt concentration.
Using the just discussed Nc,i values, we calculated the coordinating fractions of the different coordination sites fcoord,MD from the MD simulations results using eqn (10). Here, nLi describes the total number of lithium cations and Otot,i the total number of oxygens of the particular species in the simulation box of a certain electrolyte formulation.
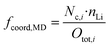 | (10) |
The obtained values are shown in Fig. 5c and compared to fcoord,Raman, calculated according to eqn (2) and based on the Raman spectra shown in the previous section.
The experimental results support the introduced model. Of the three Li+-coordinating molecules, it is DME for which the highest fraction is coordinated, followed by TFSI− and then DOL. At high conducting salt concentration, it is again DME that reaches a plateau, where all DME molecules are coordinating, again followed by TFSI− and finally DOL, which both only reach lower maximum fractions of coordination. The transitions from a homogeneous DME-coordination (see moderately concentrated region, Fig. 5a) to a mixed DME–TFSI− coordination in the high-concentration region, and further to a mixed coordination involving DOL in the ultra-high-concentration SiS region, are not very sharp transitions. TFSI− already starts to coordinate in the moderately concentrated region and DOL starts to coordinate Li+ before the second limiting concentration is reached, as already discussed.
Moreover, Fig. 5c also shows a qualitatively very good agreement between two of the used methods, namely Raman measurements and MD simulations, proving that the MD simulations are a reliable addition to experimental studies. The deviations between these two techniques can be traced to their respective uncertainties. While the deconvolution of the Raman bands may contain slight systematic deviations, the force fields used for the MD simulations describe polarization effects due to the ions only approximately, leading to deviations from the real system, especially at ultra-high conducting salt concentrations where polarization effects play an important role. The same applies for the comparison of the self-diffusion coefficients calculated from the MD simulations and measured by PFG-NMR, shown in Fig. S6.† Despite deviations of the absolute values in the SiS region, the MD simulations reproduce the experimentally observed trend quite well, which, in combination with the structural quantities in Fig. 5, demonstrates that the utilized force field adequately captures the most important trends of the conducting salt concentration dependence.
Finally, the coordination behavior of the different species can be analyzed experimentally by evaluating the chemical shift dependent on the conducting salt concentration, shown in Fig. 5d. Since the chemical shift is dependent on the electronic environment of a nucleus, changes in this shift, Δδ, reflect changes in the coordination environment. Here, we reference the changes Δδ to the shift in a molal concentration of 1 M. It has to be noted that lithium and hydrogen nuclei are dominated by diamagnetic shielding, while fluorine is mostly influenced by paramagnetic shielding, leading to an opposite shift direction.60 Further, it has to be considered that chemical shifts of different nuclei, namely 1H, 19F, and 7Li, are compared. Therefore, the magnitude of the change in δ can only be compared for the two solvent molecules, since both are measured via1H NMR spectroscopy. Exemplary stack plots of the NMR spectra for all species are shown in Fig. S7.†
The changes in the chemical shift Δδ shown in Fig. 5d also match the proposed model. Generally, we observed that the addition of conducting salt causes a deshielding for all investigated species due to ionic clustering. However, there are distinct differences for the different coordinating species: at lower salt concentrations, the chemical shift of DME is more strongly affected by an increasing salt concentration compared to the chemical shift of DOL. Therefore, the condition that DME coordinates Li+ rather than DOL is confirmed. The most drastic changes in the chemical shifts should occur in the high-concentration region, since, according to the model, TFSI− starts to participate in the coordination of Li+, which has a major impact on the local electronic environment of Li+ and all coordinating species. This is indeed apparent in the highest slope of Δδ observed for Li+, TFSI− and DME in this region. However, ΔδDOL also changes before the second limiting concentration is reached, in agreement with the MD simulations. Therefore, the evaluation of the chemical shift reproduces this slight deviation from the proposed model as discussed for Fig. 5b and c. Nevertheless, ΔδDOL keeps changing above the second limiting salt concentration 4.80 M, while the Δδ values of the other species reach plateau values, which is again in agreement with the proposed model. The local electronic environment of these species and thus their chemical shift does not change significantly if one coordinating oxygen of DME is on average exchanged with an oxygen of DOL, as shown in Fig. 5a.
We note, however, that Fig. 5a displays an average coordination environment. A monomodal coordination of only one oxygen of DME to Li+ seems unlikely and leads to the expectation that the coordination of DME to Li+ is occurring with both oxygens. This is supported by the distribution of molecular coordination numbers, Nm,i, shown in Fig. S8,† where the average number of coordinating DME molecules, Nm,DME, is approximately half as large as the respective oxygen coordination numbers, Nc,DME, in Fig. 5b. Fig. S8† also demonstrates a certain heterogeneity of the coordination environment, as the actual molecular coordination numbers partly differ from the average. This increasing heterogeneity with increasing conducting salt concentration is also shown in snapshots of the MD simulation boxes; see Fig. S9.†
In order to support the assumption of this heterogeneity and its consequences for transport properties, we evaluated the MD simulations in more detail, as presented in the next section.
Heterogeneity in Li+ coordination and its impact on ion transport
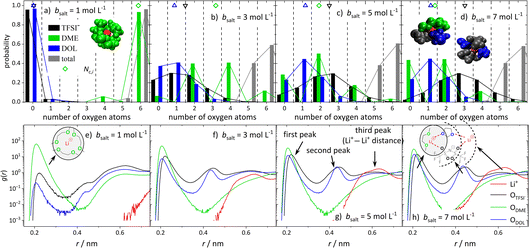
In order to obtain insights into the actual 1st coordination shell of lithium and the deviation from the proposed average model, we evaluated the distribution of coordination numbers of the oxygen atoms of the different ligands, ODME, ODOL, and OTFSI, over the concentration range. The results are shown in Fig. 6a–d for four conducting salt concentrations. For the anions, the histograms resemble a normal distribution. Moreover, the histograms show that from a 3 M salt concentration upwards, about 40% of the lithium cations are no longer coordinated by six oxygens, but by five.Interestingly, for DME, in contrast to DOL and TFSI−, only even coordination numbers are found. Due to its molecular structure, DME is a bidentate ligand and forms energetically favored chelate complexes with the lithium cation, leading to the observed even coordination numbers. Even though TFSI− is a bidentate ligand too, monodentate coordination is also observed in Fig. 6 for this ligand. Apparently, sterical hindrance can reduce the energy gain of a bidentate coordination. Additionally, the histograms in Fig. 6 exhibit, as expected, that the coordination structure of Li+ in the (ultra-)high-concentration electrolytes is rather heterogeneous and not separated into cations still coordinated only by DME molecules and cations coordinated by anions and DOL. Similar results are obtained by analyzing the molecular coordinating number for the different species, Nm,i, shown in Fig. S8.†
Since the structural properties in Fig. 5 show a good agreement between MD simulations and experiments, the radial distribution function (RDF) can be used to gain information on the global electrolyte structure in addition to the already discussed first coordination shell of the cations. Fig. 6e–h show the RDFs dependent on the distance r to a lithium cation for the oxygen atoms of the anion and solvent molecules, as well as the distance to other Li+ cations. The first peak around 0.22 nm refers to the first coordination shell of Li+, which was already discussed above. However, the RDFs for the (ultra-)high-concentration electrolytes exhibit second peaks around 0.44 nm, which are growing with an increasing amount of conducting salt. Interestingly, a second peak is only observed for DOL and the anion and not for DME. This confirms that DME coordinates as a bidentate ligand, such that both oxygens are part of the first peak in the RDF. In contrast, DOL can only coordinate monodentate due to its ring structure and similarly, the bulky TFSI− anion cannot bind with all four oxygens to the same Li+. Thus, these oxygens occur at a larger distance from the Li+ cation and form the second peak at 0.44 nm, which is rising with increasing conducting salt concentration due to the increasing amount of TFSI− and DOL coordinating Li+.
Analyzing the probability of certain Li+–Li+ distances (red lines in Fig. 6e–h), it can be noticed that a peak arises at 0.6 nm, which grows with an increasing amount of conducting salt. This illustrates that for the ultra-high-concentration system, in which the oxygen-to-Li ratio is decreasing, the TFSI− and DOL molecules in the first coordination shell of a lithium cation directly coordinate a second Li+ with their free oxygen atoms. Thus, these molecules bridge between different cations, leading to aggregation. However, this bridging behavior is impossible for DME when coordinating in a bidentate fashion. In conclusion, two different coordination environments for lithium are possible and according to Fig. 6d most frequently observed in the SiS domain. On the one hand, there is a coordination including one DME molecule (i.e. two ODME) next to anions and DOL, and on the other hand a coordination only by anions and DOL without the oxygens of DME. Regarding Fig. 6d, the distribution between these two coordination environments in the 7 M electrolyte is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, since the probability of counting either zero or two ODME in the first coordination shell of lithium is 50%, respectively.
1, since the probability of counting either zero or two ODME in the first coordination shell of lithium is 50%, respectively.
Impact of heterogeneous Li+ coordination on Li+ transport
With this information about the Li+ coordination in mind, conclusions about the lithium transport mechanisms become feasible. Firstly, all the initially discussed dynamic properties, namely diffusion, relaxation, and migration, show changes in the concentration behavior according to the limiting concentrations/concentration regions based on the introduced model for the average 1st lithium coordination shell, leading to the assumption that this coordination behavior is also influencing the lithium transport mechanism. In particular, the experimental results showed that SiS electrolytes exhibit a high Li+ transference number (see Fig. 3); thus the cation is more mobile than the anion. Additionally, in this SiS concentration region, it turned out that DME exhibits a faster migration in the electric field than the cation (see Fig. 2). Considering the apparent exclusive bidentate coordination behavior of DME in contrast to the bridging properties of DOL and TFSI−, the experimental results are rather conclusive. A Li+ ion with a coordination shell that contains next to TFSI− and DOL also a DME molecule, contains the whole DME molecule and thus is less affected by bridging to the next coordination shell, i.e. a second Li+. Therefore, Li+ cations in a DME-rich coordination environment can move more freely, dragging along the DME molecule. In contrast, Li+ ions in coordination shells only consisting of DOL and TFSI− are more subject to bridging and aggregation. This explains why the cation mobility is in general higher than the anion mobility, resulting in the observed high lithium transference number. Clear evidence for the impact of the heterogeneous lithium coordination on transport is given by the fact that the mobility of the uncharged DME molecule is higher than that of Li+ in the SiS region. In view of the heterogeneous coordination, this peculiar finding can now be explained. At ultra-high conducting salt concentration, DME is exclusively coordinated to the faster-migrating Li+ species; it thus has a high electrophoretic mobility. The signal of Li+, however, is averaged over DME-coordinated Li+ with a high mobility, and Li+ in a TFSI−/DOL coordination environment with a lower mobility, leading to μLi < μDME.However, all the described effects only exist in the ultra-high-concentration SiS electrolytes with bsalt > 4.8 mol L−1. Here, the oxygen-to-cation ratio is so small that the bridging properties of DOL and TFSI− dominate, which is observed via the growing Li+–Li+ peak in Fig. 6e–h. This peak is observed at conducting salt concentrations higher than 4.8 M, indicating an aggregated system with the discussed transport behavior.
Conclusion
To conclude, a broad experimental investigation of the coordination structure in a bi-solvent electrolyte dependent on the conducting salt concentration, from moderate to ultra-high concentration, Solvent-in-Salt electrolyte formulations, is performed and supported by MD simulations. The investigation yielded a basic model for the average first coordination shell of the lithium cation, leading to limiting concentrations where the coordination environment changes. These limits are also reflected in the experimental results. Therefore, changes in the dynamic properties of the electrolyte, for example the mobility, are explained by changes in the lithium coordination and thus, lithium transport mechanism.More precisely, it is found that the preferred coordination number of six oxygens around Li+ is almost reached over the whole concentration region and that DME coordinates Li+ rather than TFSI− and TFSI− rather than DOL. In addition to that, the MD simulations revealed that the TFSI− and DOL molecules act as bridging ligands and coordinate more than one lithium cation at once in the ultra-high-concentration electrolyte due to the low oxygen to Li+ ratio. In contrast, DME is a bidentate, not bridging, ligand. Thus, this difference in the coordinating properties of the ligands in combination with the limited availability of DME molecules separates the lithium coordination environment into two frequent coordination shells: a coordination shell including one DME molecule and a coordination without any DME. This explains the finding of a faster and a slower migrating Li+ species. The first one is partly coordinated to DME, which also explains the unexpected high mobility of DME, and the second one is only coordinated by TFSI− and DOL and therefore part of a larger aggregate.
In summary, all these investigations show that merging the properties of two solvents of different lithium coordination strengths with an ultra-high conducting salt concentration creates interesting transport phenomena. In particular, the heterogeneous coordination environment of Li+ ions, as highlighted here, is responsible for the high lithium transference number, since it enhances the structural Li+ transport in combination with an effective dynamic decoupling of Li+ and anion transport with σ+−/σion ≈ 0. In conclusion, electrolytes with ultra-high conducting salt concentrations not only offer high performance concerning key performance indicators, but also a high tLi, making them, in spite of their low ionic conductivity, promising candidates for next generation battery applications.
Author contributions
A. H.: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. F. A.: investigation, methodology, validation, visualization, writing – original draft. D. D.: resources, software, writing – review and editing. I. C.-L: writing – review and editing. M. S.: data curation, funding acquisition, project administration, resources, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Martin Lorenz for assistance with the repetition of an eNMR measurement. A. H. is supported by the Ministry of Culture and Science of the State North Rhine Westphalia in course of the International Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA). The MD simulations for this work were performed on the computer cluster PALMA II of the University of Münster.References
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- M. Greenwood, J. M. Wrogemann, R. Schmuch, H. Jang, M. Winter and J. Leker, J. Power Sources Adv., 2022, 14, 100089 CrossRef.
- L. G. Lu, X. B. Han, J. Q. Li, J. F. Hua and M. G. Ouyang, J. Power Sources, 2013, 226, 272–288 CrossRef CAS.
- A. Manthiram, ACS Cent. Sci., 2017, 3, 1063–1069 CrossRef CAS PubMed.
- M. Winter, B. Barnett and K. Xu, Chem. Rev., 2018, 118, 11433–11456 CrossRef CAS PubMed.
- Y. Ugata and N. Yabuuchi, Trends Chem., 2023, 5, 672–683 CrossRef CAS.
- J. Alvarado, M. A. Schroeder, M. Zhang, O. Borodin, E. Gobrogge, M. Olguin, M. S. Ding, M. Gobet, S. Greenbaum, Y. S. Meng and K. Xu, Mater. Today, 2018, 21, 341–353 CrossRef CAS.
- O. Borodin, L. Suo, M. Gobet, X. Ren, F. Wang, A. Faraone, J. Peng, M. Olguin, M. Schroeder, M. S. Ding, E. Gobrogge, A. von Wald Cresce, S. Munoz, J. A. Dura, S. Greenbaum, C. Wang and K. Xu, ACS Nano, 2017, 11, 10462–10471 CrossRef CAS PubMed.
- K. Dokko, D. Watanabe, Y. Ugata, M. L. Thomas, S. Tsuzuki, W. Shinoda, K. Hashimoto, K. Ueno, Y. Umebayashi and M. Watanabe, J. Phys. Chem. B, 2018, 122, 10736–10745 CrossRef CAS PubMed.
- L. Suo, Y. S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed.
- P. Zhou, X. Zhang, Y. Xiang and K. Liu, Nano Res., 2023, 16, 8055–8071 CrossRef CAS.
- Y. Ishino, K. Takahashi, W. Murata, Y. Umebayashi, S. Tsuzuki, M. Watanabe, M. Kamaya and S. Seki, Energy Technol., 2019, 7, 1900197, DOI:10.1002/ente.201900197.
- H.-J. Peng, J.-Q. Huang, X.-B. Cheng and Q. Zhang, Adv. Energy Mater., 2017, 7, 1700260 CrossRef.
- S. Zhang, K. Ueno, K. Dokko and M. Watanabe, Adv. Energy Mater., 2015, 5, 1500117 CrossRef.
- V. A. Azov, K. S. Egorova, M. M. Seitkalieva, A. S. Kashin and V. P. Ananikov, Chem. Soc. Rev., 2018, 47, 1250–1284 RSC.
- Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Nat. Energy, 2019, 4, 269–280 CrossRef CAS.
- Y. Yamada and A. Yamada, J. Electrochem. Soc., 2015, 162, A2406–A2423 CrossRef CAS.
- M. Armand, P. Axmann, D. Bresser, M. Copley, K. Edström, C. Ekberg, D. Guyomard, B. Lestriez, P. Novák, M. Petranikova, W. Porcher, S. Trabesinger, M. Wohlfahrt-Mehrens and H. Zhang, J. Power Sources, 2020, 479, 228708 CrossRef CAS.
- G. A. Giffin, Nat. Commun., 2022, 13, 5250 CrossRef CAS PubMed.
- A. Nakanishi, K. Ueno, D. Watanabe, Y. Ugata, Y. Matsumae, J. Liu, M. L. Thomas, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2019, 123, 14229–14238 CrossRef CAS.
- S. Kondou, M. L. Thomas, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2019, 21, 5097–5105 RSC.
- J. Self, K. D. Fong and K. A. Persson, ACS Energy Lett., 2019, 4, 2843–2849 CrossRef CAS.
- L. Suo, F. Zheng, Y.-S. Hu and L. Chen, Chin. Phys. B, 2016, 25, 016101 CrossRef.
- M. Gouverneur, J. Kopp, L. van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680–30686 RSC.
- M. Holz, Chem. Soc. Rev., 1994, 23, 165 RSC.
- R. L. Vold, J. S. Waugh, M. P. Klein and D. E. Phelps, J. Chem. Phys., 1968, 48, 3831–3832 CrossRef CAS.
- H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630–638 CrossRef CAS.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- E. L. Hahn, Phys. Rev., 1950, 80, 580–594 CrossRef.
- E. Pettersson, I. Furó and P. Stilbs, Concepts Magn. Reson., 2004, 22A, 61–68 CrossRef CAS.
- Q. H. He and Z. H. Wei, J. Magn. Reson., 2001, 150, 126–131 CrossRef CAS PubMed.
- F. Schmidt, A. Pugliese, C. C. Santini, F. Castiglione and M. Schönhoff, Magn. Reson. Chem., 2020, 58, 271–279 CrossRef CAS PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2001 Search PubMed.
- P. Nürnberg, E. I. Lozinskaya, A. S. Shaplov and M. Schönhoff, J. Phys. Chem. B, 2020, 124, 861–870 CrossRef PubMed.
- Q. Zhou, P. D. Boyle, L. Malpezzi, A. Mele, J.-H. Shin, S. Passerini and W. A. Henderson, Chem. Mater., 2011, 23, 4331–4337 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- J. N. Canongia Lopes and A. A. H. Pádua, Theor. Chem. Acc., 2012, 131, 1129 Search PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, D. L. Dotson, J. B. Domanski, S. Buchoux, I. M. Kenney and O. Beckstein, Proc. Python Sci. Conf., 2016, 98–105, DOI:10.25080/Majora-629e541a-00e.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- N. Molinari, J. P. Mailoa and B. Kozinsky, Chem. Mater., 2018, 30, 6298–6306 CrossRef CAS.
- A. Thum, A. Heuer, K. Shimizu and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2020, 22, 525–535 RSC.
- R. Raccichini, J. W. Dibden, A. Brew, J. R. Owen and N. García-Aráez, J. Phys. Chem. B, 2018, 122, 267–274 CrossRef CAS PubMed.
- K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2011, 115, 18384–18394 CrossRef CAS.
- F. Schmidt and M. Schönhoff, J. Phys. Chem. B, 2020, 124, 1245–1252 CrossRef CAS PubMed.
- S. Pfeifer, F. Ackermann, F. Sälzer, M. Schönhoff and B. Roling, Phys. Chem. Chem. Phys., 2021, 23, 628–640 RSC.
- N. M. Vargas-Barbosa and B. Roling, ChemElectroChem, 2020, 7, 367–385 CrossRef CAS.
- Y. Yamada, M. Yaegashi, T. Abe and A. Yamada, Chem. Commun., 2013, 49, 11194–11196 RSC.
- P. Zeng, Y. Han, X. Duan, G. Jia, L. Huang and Y. Chen, Mater. Res. Bull., 2017, 95, 61–70 CrossRef CAS.
- H. Yoshida and H. Matsuura, J. Phys. Chem. A, 1998, 102, 2691–2699 CrossRef CAS.
- K. Qian, S. Seifert, R. E. Winans and T. Li, Energy Fuels, 2021, 35, 19849–19855 CrossRef CAS.
- M. Bochenska, V. C. Kravtsov and V. E. Zavodnik, J. Inclusion Phenom. Mol. Recognit. Chem., 1997, 28, 125–140 CrossRef CAS.
- X. Bogle, R. Vazquez, S. Greenbaum, A. Cresce and K. Xu, J. Phys. Chem. Lett., 2013, 4, 1664–1668 CrossRef CAS PubMed.
- W. A. Henderson, N. R. Brooks, W. W. Brennessel and V. G. Young, Chem. Mater., 2003, 15, 4679–4684 CrossRef CAS.
- G. Mao, M.-L. Saboungi, D. L. Price, M. B. Armand and W. S. Howells, Phys. Rev. Lett., 2000, 84, 5536–5539 CrossRef CAS PubMed.
- U. Olsher, R. M. Izatt, J. S. Bradshaw and N. K. Dalley, Chem. Rev., 1991, 91, 137–164 CrossRef CAS.
- K. Yuan, H. Bian, Y. Shen, B. Jiang, J. Li, Y. Zhang, H. Chen and J. Zheng, J. Phys. Chem. B, 2014, 118, 3689–3695 CrossRef CAS PubMed.
- J. N. Dahanayake, C. Kasireddy, J. P. Karnes, R. Verma, R. M. Steinert, D. Hildebrandt, O. A. Hull, J. M. Ellis and K. R. Mitchell-Koch, in Annu. Rep. NMR Spectro., ed. G. A. Webb, Academic Press, 2018, pp. 281–365 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: PDF file containing densities, ionic conductivities, relaxation rates for all species, eNMR phase shifts, deconvolution of Raman spectra, diffusion data, NMR spectra, histograms of the molecular coordination numbers, and snapshots of the MD simulation box. See DOI: https://doi.org/10.1039/d4fd00012a |
| ‡ Current address: BASF SE, Carl-Bosch-Straße 38, 67056 Ludwigshafen/Rhein, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |