Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gaussian processes for finite size extrapolation of many-body simulations†
Edgar Josué Landinez Borda*a,
Kenneth O. Berarda,
Annette Lopezb and
Brenda Rubenstein *a
*a
aDepartment of Chemistry, Brown University, Providence, Rhode Island 02912, USA. E-mail: edgar_landinez_borda@brown.edu; brenda_rubenstein@brown.edu
bDepartment of Physics, Brown University, Providence, Rhode Island 02912, USA
First published on 25th March 2024
Abstract
Key to being able to accurately model the properties of realistic materials is being able to predict their properties in the thermodynamic limit. Nevertheless, because most many-body electronic structure methods scale as a high-order polynomial, or even exponentially, with system size, directly simulating large systems in their thermodynamic limit rapidly becomes computationally intractable. As a result, researchers typically estimate the properties of large systems that approach the thermodynamic limit by extrapolating the properties of smaller, computationally-accessible systems based on relatively simple scaling expressions. In this work, we employ Gaussian processes to more accurately and efficiently extrapolate many-body simulations to their thermodynamic limit. We train our Gaussian processes on Smooth Overlap of Atomic Positions (SOAP) descriptors to extrapolate the energies of one-dimensional hydrogen chains obtained using two high-accuracy many-body methods: coupled cluster theory and Auxiliary Field Quantum Monte Carlo (AFQMC). In so doing, we show that Gaussian processes trained on relatively short 10–30-atom chains can predict the energies of both homogeneous and inhomogeneous hydrogen chains in their thermodynamic limit with sub-milliHartree accuracy. Unlike standard scaling expressions, our GPR-based approach is highly generalizable given representative training data and is not dependent on systems’ geometries or dimensionality. This work highlights the potential for machine learning to correct for the finite size effects that routinely complicate the interpretation of finite size many-body simulations.
1. Introduction
Over the past few decades, ab initio electronic structure methods have transformed our ability to design materials by enabling researchers to predict the macroscopic and emergent behavior of solids from a basic knowledge of their constituent atoms. Researchers can now routinely model the electronic and geometric properties of systems ranging from quantum materials to heterogeneous catalysts with – or very near – chemical accuracy. However, the accuracy that accompanies many-body electronic structure methods such as Coupled Cluster (CC) theory, Quantum Monte Carlo (QMC), and many-body perturbation theories often comes at a steep cost: these methods typically scale as a high degree polynomial with system size. For example, Coupled Cluster Singles, Doubles, and Perturbative Triples [CCSD(T)] conventionally scales as O(N3M4), where N is the number of electrons and M is the size of the basis set, while Auxiliary Field Quantum Monte Carlo (AFQMC) typically scales as O(N2M2 + M2N).1 In contrast, mean field methods such as Density Functional Theory (DFT) scale as O(N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)2,3 or O(N),4 when locality is a good approximation, but are only predictive when the degree of electron correlation is mild. Historically, the comparatively steep scaling of many-body methods has thwarted their direct application to solids with large unit and/or supercells, limiting their use to systems with just tens to, potentially, hundreds of atoms. However, such smaller, more computationally-accessible systems cannot manifest the same long-range correlations as are present in larger, more realistic solids, and can exhibit spurious boundary effects that confound their interpretation. Indeed, given the remarkable accuracy of many modern electronic structure methods, these finite size errors are often the largest sources of error in many calculations of solids.5,6 This leads to a long-standing conundrum: if many-body methods may only be directly applied to smaller, finite systems, how can they be leveraged to predict the properties of larger, more realistic solids?
N)2,3 or O(N),4 when locality is a good approximation, but are only predictive when the degree of electron correlation is mild. Historically, the comparatively steep scaling of many-body methods has thwarted their direct application to solids with large unit and/or supercells, limiting their use to systems with just tens to, potentially, hundreds of atoms. However, such smaller, more computationally-accessible systems cannot manifest the same long-range correlations as are present in larger, more realistic solids, and can exhibit spurious boundary effects that confound their interpretation. Indeed, given the remarkable accuracy of many modern electronic structure methods, these finite size errors are often the largest sources of error in many calculations of solids.5,6 This leads to a long-standing conundrum: if many-body methods may only be directly applied to smaller, finite systems, how can they be leveraged to predict the properties of larger, more realistic solids?
To increase the feasibility of many-body methods for the prediction of the properties of solids in their infinite-size, “thermodynamic limit” researchers have developed approaches that correct results for smaller systems to predict the properties of larger systems. Such so-called finite size corrections consist of two main contributions: one-body and two-body corrections, which ameliorate the one- and two-body contributions to the total energy, respectively. One-body finite size errors typically stem from shell-filling effects that lead to a mis-estimation of the kinetic energy6,7 and can therefore be corrected by a judicious averaging over k-points.8 For example, in mean field theories, integrating over many points in the first Brillouin zone can be circumvented by instead approximating quantities using mean-value points known as Baldereschi points.9 While many-body methods such as QMC methods need to integrate over the full simulation supercell, not just one point, twist averaging10 provides a means of averaging over a set of angles (offset vectors) on the Brillouin zone of the supercell that results in a rapid convergence of the one-body effects.6,10 In contrast, two-body finite size effects stem from errors in the Coulomb and exchange–correlation interactions and are more challenging to correct. These effects can be alleviated by introducing modified versions of these interactions, such as model periodic Coulomb corrections.6,7 An alternative approach for correcting both one- and two-body finite size effects is to determine finite size corrections using methods that scale more gracefully with system size, such as Density Functional Theory (DFT).6,7,11 Such methods are used to estimate the differences in energies between smaller and larger systems, and then these differences are added to the smaller-sized many-body calculations. One such DFT-based approach is the Kwee, Zhang, Krakauer correction (KZK).12 While such corrections are now widely applied to materials, they inherently lack the accuracy that would be possible if many-body corrections that take strong correlation into account were applied.
Even though these one- and two-body corrections markedly reduce finite-size errors, extrapolations to the thermodynamic limit are often still made to reduce any remaining errors. The simplest approach for performing these extrapolations is to fit many-body results obtained at smaller system sizes (e.g., 2 × 2 or 3 × 3 supercells) to functional forms that enable extrapolation to larger system sizes.7,11 Nevertheless, it is often unclear which functional form should be employed since it can vary with the geometry, dimensionality, and electronic phase of the material.5,8 This is especially true for systems with atypical geometries and boundary conditions. It is also of particular importance for calculations involving excited states, including gap and exciton binding energy calculations, because excited states can be more difficult to converge to their thermodynamic limit.13–15 When a system’s correlation energy converges slowly, the number of points necessary for accurate fitting can exceed computational constraints, limiting the overall utility of such extrapolations and the results they yield.8,16
One potentially promising approach for estimating many-body corrections that can reduce this computational expense is machine learning. Machine learning methods surrogate more complex models with regressions that have lower computational complexity, thereby accelerating prediction.17–19 In the context of condensed matter physics, machine learning has been employed to accelerate the prediction and discovery of new materials based upon the properties of known materials20 as well as to learn the presence of certain phases based upon their known signatures.21,22 Machine learning techniques have moreover recently been harnessed to accelerate and improve the accuracy of quantum Monte Carlo methods (see a more detailed discussion in Section 2).8,18,23–28 To approach the problem of determining accurate, many-body finite size corrections, one can analogously imagine using data from smaller system sizes to train machine learning algorithms to predict the properties of systems of larger sizes. An early such work used energies and densities from the density matrix renormalization group to learn the DFT kinetic energy functional of hydrogen chains in the thermodynamic limit.29 More recently, while this work was being prepared, Gaussian process regression techniques were shown to be able to successfully learn corrections to coupled cluster calculations in k-space. More specifically, Mihm et al.8,30 employed the transfer structure factor to quantify the finite size effects present in coupled cluster theories’ correlation energy. They then innovatively bypassed directly computing the structure factor for G values approaching zero (i.e., in the thermodynamic limit) by flexibly representing the structure factor using Gaussian Process Regression.
In this work, we leverage Gaussian Process Regression (GPR)31 to learn finite size corrections in real-space to homogeneous (one-dimensional) and inhomogeneous (two-dimensional) hydrogen chains modeled using the first-principles, many-body methods Coupled Cluster (CC) Theory and Auxiliary Field Quantum Monte Carlo (AFQMC). Kernel methods like Gaussian processes31 are advantageous because they are not parametric and make use of Bayesian inference that can come at a lower O(Nt3) (where Nt is the size of the training set) cost than more complicated parametric methods such as neural networks that scale with the number of layers employed.17 Gaussian processes have also been shown to make equally, if not more, accurate predictions than neural networks when less training data is available, which is an important consideration when training is to be performed on data generated using relatively expensive electronic structure calculations.32 We use Gaussian processes to first predict the energies of one-dimensional, homogeneous hydrogen chains of varying lengths using atomic environment descriptors that enable us to incorporate information regarding the geometry and electronic density of each atom and its neighbors. Importantly, even though machine learning methods are most accurate for interpolation, we demonstrate that training our models on the energies of one-dimensional hydrogen chains containing 10–30 atoms enables us to predict (extrapolate) the energies of chains of more than 100 atoms, nearing the thermodynamic limit, with sub-milliHartree accuracy. To contextualize the accuracy of our methods, we compare the accuracy of our predictions to that of polynomial fits to larger-sized systems, the so-called “subtraction trick”,33 and other alternative regression methods. Finally, to demonstrate the generalizability and robustness of our approach, we show that our technique can readily be adapted to also extrapolate the energies of heterogeneous chains of hydrogen dimers, which possess more free parameters, to their thermodynamic limit. This work thus illustrates that machine learning is a relatively cheap, yet accurate means of correcting for finite size effects in many-body simulations that can potentially address many of the challenges the many-body modeling community faces predicting the properties of solids in the thermodynamic limit.
In the spirit of a Faraday Discussion, in Section 2, we begin with a discussion of the emerging synergies between machine learning techniques and stochastic electronic structure methods. We then describe the machine learning methods, descriptors, and electronic structure techniques we employ in our finite-size extrapolation research in Section 3. We next present our primary results demonstrating our technique’s ability to accurately correct for finite size errors in Section 4. We conclude by discussing the relative merits and potential applications of our algorithm in Sections 5 and 6.
2. Machine learning in stochastic electronic structure
Over the past decade, an increasing amount of research has shown that stochastic electronic structure and machine learning methods can form a very fruitful partnership that both accelerates and extends the capabilities of stochastic methods. Because stochastic electronic structure methods are often more expensive than other common electronic structure methods such as Density Functional Theory, machine learning techniques hold the promise of making stochastic electronic structure techniques less costly. At the same time, the high accuracy of most stochastic electronic structure techniques like Diffusion,34,35 Full Configuration Interaction,36 and Auxiliary Field37,38 Quantum Monte Carlo methods can provide ML techniques with high-quality data that can be used to correct less accurate predictions.One triumph of the union of these techniques has been the generation of machine learned force fields from QMC energies and gradients.27,39–41 QMC energies and forces calculated for representative configurations are used to train a variety of different neural networks, e.g., Behler–Parrinello Neural Networks,42 or other architectures, which are in turn used to predict the energies and forces for other configurations, accelerating geometry relaxation and/or ab initio molecular dynamics simulations.43,44 For instance, in recent work, Diffusion Monte Carlo energies and forces were used to generate a force field using a hierarchical Δ-machine learning scheme based upon the Deep Potential Molecular Dynamics (DPMD) framework45 that was able to successfully uncover a new phase of hydrogen.27 Since QMC has historically met challenges calculating forces,46 recent work has also exploited machine learning architectures to learn force fields from energy data alone.39 Other ways to further reduce the cost of QMC data generation for training itself employ either Δ-ML47 or transfer learning.48 These techniques first learn potentials and forces, using data from less accurate, but less costly theories and then correct those force fields by either adding a machine learned correction or updating the less accurate force field with select higher accuracy information. Both methods capitalize on the fact that less accurate theories can often reproduce much of the correct physical behavior of a system, meaning that high accuracy methods are effectively only needed to correct specific phenomena or regions of the potential energy surface. Further opportunities lie in better harnessing the statistical nature of stochastic methods to more efficiently train such force fields.49 Overall, QMC-quality force fields open up the grand possibilities of studying dynamics in large molecular or solid state systems with relatively little overhead, making QMC dynamics a practical reality.
Stochastic methods and machine learning techniques have also been fruitfully paired to develop new neural network-based variational ansatze. The Variational Principle, which states that the ground state wave function of a system can best be approximated by varying the parameters and forms of trial wave functions to minimize the energy of the system, has long been used to produce wave function ansatze in computational quantum chemistry and physics. Often, such ansatze have been optimized using QMC (i.e., Variational Monte Carlo methods) and used either on their own or as starting points for projection-based QMC techniques.6,50 Historically, the forms of these variational ansatze have been specified based upon knowledge of the chemistry/physics they ultimately aim to describe (e.g., Gutzwiller51 or pairing52 wave functions) or confidence that their form is generalizable and expressive enough to describe the phenomenon under study (e.g., backflow wave functions).53 Specifying the forms of trial wave functions based upon the physics expected can potentially lead to circular logic in which the physics that is expected to be seen is incorporated into a variational wave function form that then recovers that physics.
Recently, machine learning has been employed to overcome this limitation by providing a means of creating highly expressive variational wave functions. One of the most popular means of achieving this has been to use deep neural networks to specify a given variational wave function and then to optimize that neural network using the energy and/or variance as a loss function.54 Examples of such variational neural networks include DeepQMC,55 FermiNet,23 and PauliNet,24 all of which have shown promise determining the ground states of challenging chemical systems. PauliNet and FermiNet, for example, use deep neural networks to learn a parameterized form of the Jastrow factor and backflow functions and maintain antisymmetry using Slater determinants. Unlike traditional methods that use single-particle orbitals, FermiNet employs functions invariant under two-electron permutations and incorporates back-flow-like transformations for enhanced accuracy.56
An alternative approach to combining the expression and optimization of wave functions with machine learning has been neural network quantum states.57 One promising form of neural network quantum states established by Carleo and Troyer are Restricted Boltzmann Machines, which implement a representation of the wave function through hidden and visible layers.57 The Boltzmann distribution models the probabilities associated with different configurations of visible and hidden nodes based on the energy; lower energies are favored to accommodate the variational principle which guides the optimization of wave function parameters. These wave functions can then be extrapolated to larger systems by reusing the learned features of the wave function to initialize a machine learning model applied to a similar, but larger system.58,59 This process of transferring the learning done for one type of problem to a related, but different problem makes seemingly out-of-reach problems, such as the thermodynamic limit, computationally feasible. Success with the transverse-field Ising model,57 Heisenberg model,57 and molecules60 has been demonstrated. Akin to the use of GPR in this work, Gaussian Processes have also been used to specify wave functions called Gaussian Process States.61 These wave functions are expressed as the exponential of a GP estimator and thus, as Gaussian processes more generally, are highly generalizable and can provide critical information about uncertainties. Such machine learning-based wave functions offer a potential means of achieving unprecedented levels of accuracy without the need for typically more expensive projection techniques.
Given these successes combining stochastic methods with machine learning approaches – and the many more we have not been able to discuss due to space constraints – here, we focus on the possibility of using machine learning methods to extend QMC’s capabilities in a different way: by facilitating the extrapolation of QMC results to the thermodynamic limit.
3. Methods
3.1 Gaussian Approximation Potentials (GAP)
In this work, we employ Gaussian Process Regression (GPR) to predict finite size corrections for discrete hydrogen chains. We have focused on GPR62 because it has previously been shown to yield high accuracy results with less training data than comparable methods.32 This is an especially desirable property when one is interested in performing regressions on data obtained from comparatively costly many-body simulations, since computational expense practically limits how much reference data can reasonably be collected. The Bayesian nature of GPR also makes it possible to compute the variance of its predictions, which greatly facilitates the interpretation of its results.63 For these reasons, we employ a GPR-based approach which is very similar in flavor to the Gaussian Approximation Potential (GAP) approach.64 We first summarize our approach at a high level and then provide more details in subsequent subsections.A GPR is a random process which takes input vectors xi and maps them to random variables y = f(x) with a multivariate, normal joint distribution with covariance (K)31,63
| p(f(x)) ∼ N(μ,K). | (1) |
| K(xi,xj) = ϕ(xi)·ϕ(xj). | (2) |
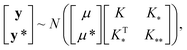 | (3) |
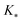 , and
, and 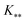 represent the covariances among the training data, training and unobserved data, and unobserved data, respectively. Based upon Bayes’ rule, the posterior distribution is Gaussian since the joint distribution is Gaussian. The posterior distribution can be expressed as
represent the covariances among the training data, training and unobserved data, and unobserved data, respectively. Based upon Bayes’ rule, the posterior distribution is Gaussian since the joint distribution is Gaussian. The posterior distribution can be expressed as
P(y*|y) ∼ N(ŷ,![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) ), ),
| (4) |
| y* = ŷ = K−1yK(X,X*) | (5) |
| σ* = K(X*,X*) − K(X,X*)TK(X,X)−1K(X,X*). | (6) |
| y* = ŷ = (K + σ2)−1yK(X,X*). | (7) |
| α = (K + σ2I)−1y. | (8) |
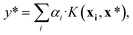 | (9) |
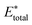 , using the equation
, using the equation
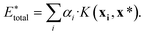 | (10) |
3.2 Atomic environment descriptors and regression model
In contrast with physics-based approaches for describing a system, machine learning models are often more expressive, meaning that a single model has the potential to describe many different systems. One way to constrain the predictions of a machine learning model is to include prior physical information in the surrogate model. This can be achieved by making the model invariant to symmetries, including translational, rotational, or permutation symmetries, or constraints, in order to suppress spurious correlations. These symmetries or constraints are usually incorporated into the model in two ways: explicitly integrating these symmetries into the regression algorithm or designing features that are invariant to the symmetry transformations.Here, we incorporate symmetries via the latter approach using Smooth Overlap of Atomic Positions (SOAP) descriptors that are invariant to rotation and translation. These atomic environment descriptors represent the electron density at some point r by the superposition of the Gaussian densities of atoms with the same atomic number Z in the neighborhood of that point
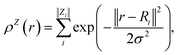 | (11) |
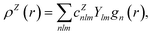 | (12) |
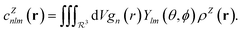 | (13) |
In this work, we use the Dscribe library67 to obtain the descriptors. This library implements SOAP descriptors using a partial power spectrum that only includes real spherical harmonics. Because the density depends on the square of the distances between points, it is already invariant to translation. A descriptor vector, p, is formed from elements of the power spectrum
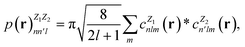 | (14) |
The original SOAP descriptors compare the local atomic environments using a kernel that is the dot product of the normalized power spectra between different configurations
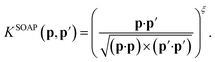 | (15) |
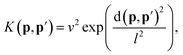 | (16) |
3.3 Comparing environments with global descriptors
The descriptor vector, p, of an atomic structure depends on the number of atoms of each species and is created by concatenating the different combinations of atomic species, each with n radial basis functions and a maximum angular number lmax.65 As a result, structures with different numbers of atoms, M, N, have different numbers of descriptors. One way to deal with descriptor vectors of differing lengths is to pad the feature vectors with zeros such that their dimensions match those of the descriptor vectors with the largest number of features in the samples. A similar approach involves padding the dummy (missing) features with values selected to decrease the biases the missing features would otherwise introduce.68An alternative that can reduce bias is the use of global descriptors. These descriptors characterize the whole structure, i.e., the features depend on all of the atoms, rendering the number of features independent of the number of atoms in the structure. However, such an approach may diminish the quality of the kernel, since the descriptors may not have enough resolution to distinguish subtle differences between structures because of their global nature. A very simple and intuitive method to make the kernel global is to construct an “average kernel:”69
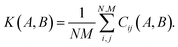 | (17) |
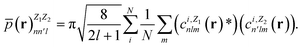 | (18) |
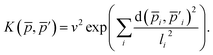 | (19) |
4. Results
4.1 One-dimensional, homogeneous hydrogen chains
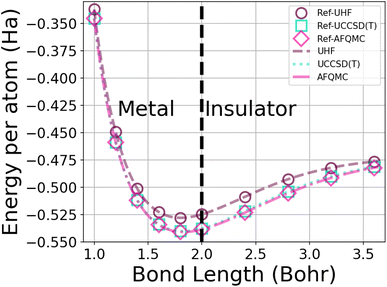 | ||
| Fig. 1 Energy per atom vs. bond length for a 50-atom hydrogen chain using the UHF, UCCSD(T), and AFQMC methods in the STO-6G basis. The symbols depict the energies from calculations from ref. 1, while the dotted lines interpolate among 250 of our database energies. AFQMC error bars are too small to see. | ||
This system furthermore exhibits a metal-to-insulator transition when stretched homogeneously, which occurs at 1.8 Bohr.1 This transition is of second order, meaning that it is continuous with respect to the energy, but can be characterized by the polarization or spin correlation functions.70 Dimerization of pairs of hydrogen atoms in the chains can be observed by looking at the electron density profile along the chains, as in Fig. 2. The maxima correspond to the nuclear positions, while the deep minima indicative of dimerization may be observed between pairs of atoms at all of the chain lengths depicted. Methods capable of predicting the energies as a function of bond length must implicitly be able to predict energies across these transitions.
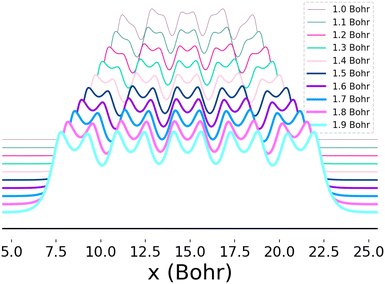 | ||
| Fig. 2 Electron density as a function of atomic position (x) for 10-atom hydrogen chains. Each curve depicts the electron density profile when the chain is stretched homogeneously at the bond lengths indicated in the legend. The change in the distance between and depth of adjacent local minima as the bond distance is increased reflects the onset of dimerization. The densities depicted here were computed using Full-Configuration Interaction74 and the y-axis was shifted so that the profiles for all bond lengths could be clearly seen. | ||
In order to generate enough data for training, we created a database of the energies of hydrogen chains at varying bond lengths using UHF and two many-body methods – UCCSD(T)74 and AFQMC75 – in the minimal STO-6G basis. UCCSD(T) has long been considered the gold standard for accuracy for quantum chemistry calculations,74,76 and is seeing an increasing number of applications to solids.77,78 AFQMC75 is a second-quantized QMC method that, despite its typical use of the phaseless approximation,79 has been shown to achieve chemical accuracy in systems ranging from small molecules,80–82 to complexes,82,83 to strongly correlated solids.84,85 As a check on our databases, we produced and extended the benchmarks of Motta et al.1 with sub-milliHartree accuracy (see Fig. 1).
To perform our UHF and UCCSD(T) calculations, we use the open source software PySCF.86 For the AFQMC calculations, we use the high-performance implementation of AFQMC in QMCPACK.87 Within QMCPACK, we employ UHF wave functions produced by PySCF as trial wave functions and perform calculations with a time step of 0.005, 1000 walkers, a Cholesky decomposition threshold of 10−8, and 104 steps in the phaseless approximation.75 Energies are computed with the hybrid estimator. Using all of these methods, we compute 250 points for each 10–60-atom chain with bond lengths ranging from 1 to 3.65 Bohr. For chains of 70 to 100 atoms, we compute 40 points within the same range of bond lengths in order to conserve computational resources. The 10–30 atom data was used for training, while chains with larger numbers of atoms were used for benchmarking and analysis.
The descriptors are first generated for all of the atoms of each chain in the database. A global descriptor is then obtained by averaging each descriptor over the atoms within each chain. Finally, feature selection is carried out by obtaining leverage scores from a CUR decomposition.88 The leverage scores are ordered in descending order and features are taken until 97% of the leverage score is accounted for. To perform the CUR decomposition, a Singular Value Decomposition (SVD)88 is conducted given a singular value threshold that defines the rank of the decomposition. For this purpose, we used optimal hard thresholding,89 which makes an optimal choice based on the dimensions and the estimated noise in the features or global descriptors matrix. We don’t orthogonalize the features or use covariate principal coordinate analysis to improve our current feature selection, as further discussed in Section 5.90
A Gaussian kernel with multiple length scales allows more sensitivity to global descriptors without greatly increasing the complexity of the model. We used the maximum likelihood31 method to optimize the kernel hyper-parameters. We employed up to 500 configurations for training and 250 for validation.
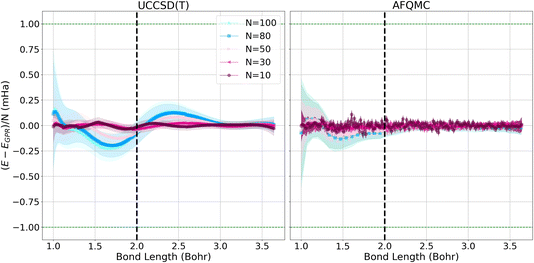
Fig. 3 depicts the differences between the energies computed with the UCCSD(T) (left) and AFQMC (right) methods, and their respective GPR predictions. In both cases, the differences between the predictions and the calculated energies are less than 1 mHa. It is reassuring to note that the short chain length predictions are most accurate throughout the prediction interval, which is a consequence of training the Gaussian processes on short chains. Prediction errors grow with the lengths of the chains because the generalization error increases with system size. This is reflected in the larger confidence intervals that accompany the larger chain length predictions. Hydrogen chains have previously been observed to exhibit slower convergence at short bond lengths because their total chain lengths are not yet long enough to converge finite size effects that stem from long-range Coulomb interactions. This comparatively slow convergence is likely responsible for the larger error bars we observe at short bond lengths.1 At bond lengths longer than 3 Bohr where dissociation begins to occur, the error is significantly smaller and expected to converge faster because chains with longer total lengths will more rapidly converge the long-range Coulomb interaction.
The quality and characteristics of the AFQMC-based GPR predictions are similar to that of the UCCSD(T)-based predictions. Higher accuracies are again observed for shorter chains and at larger bond lengths. The AFQMC-GPR differences are, however, noisier than the UCCSD(T) differences, which reflects the stochastic character of AFQMC. The AFQMC-GPR differences are, in general, smaller than the UCCSD(T)-GPR predictions, especially at intermediate bond lengths. Overall, the AFQMC predictions are slightly more accurate and homogeneous at all of the bond lengths studied, likely due to a larger consistency within the AFQMC data.
Fig. 4 displays the convergence of the energy per atom to the thermodynamic limit for four representative bond lengths. The circles denote the UCCSD(T) calculations while the squares represent the GPR predictions at each size. As before, the shadows delineate 95% confidence intervals on the GPR calculations. The green dashed line denotes the polynomial regression at the given bond length and the red triangle represents the energy in the thermodynamic limit taken from ref. 1. The GPR prediction of the energy in the thermodynamic limit is made using a chain of 5000 hydrogen atoms. As an illustration of the speed of our regression technique, producing the descriptors for the 5000-atom chain took about 2 minutes on an Intel Core i7-8550U (Turbo 4.0 GHz, 4 Cores, 8 Threads) laptop. We note that the differences between the thermodynamic limit predictions made by the reference regression1 and the polynomial regression performed on our dataset simply reflect the small differences between the two different databases. The GPR predictions are in good agreement with the reference and polynomial regressions, deviating most for bond lengths near the equilibrium bond length (around 1.8 Bohr) where the convergence is less linear. Note that the energies converge one to two orders of magnitude more rapidly at larger bond lengths because the long-range Coulomb interaction is weaker at larger bond lengths, as described earlier.
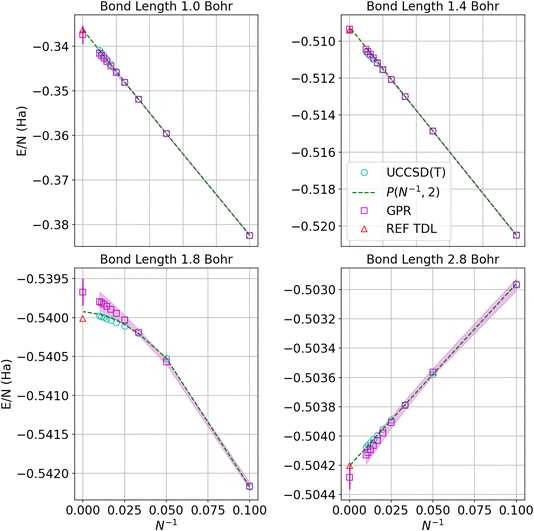 | ||
| Fig. 4 Predictions of the energy per atom in the thermodynamic limit vs. N−1 based on UCCSD(T) results for hydrogen chains with bond lengths of 1.0, 1.4, 1.8, and 2.8 Bohr. Cyan circles denote UCCSD(T) calculations, while maroon squares denote the GPR predictions. The shadow depicts 95% confidence intervals, and the dashed lines depict the polynomial regression of second order at each bond length. The triangle represents the energy in the thermodynamic limit computed in ref. 1. The gap between points at small values of N−1 corresponds to chains between 100 and 5000 atoms, which are prohibitive to model even using less expensive theories. | ||
Fig. 5 similarly exhibits the convergence to the thermodynamic limit for the AFQMC database and its respective GPR predictions. One of the most noticeable differences relative to the UCCSD(T) calculations is that the AFQMC predictions seem more linear close to the equilibrium bond length. This means that the AFQMC calculations can more accurately resolve small, sub-milliHartree differences in the energies as a function of system size and therefore so can the AFQMC-based GPR.
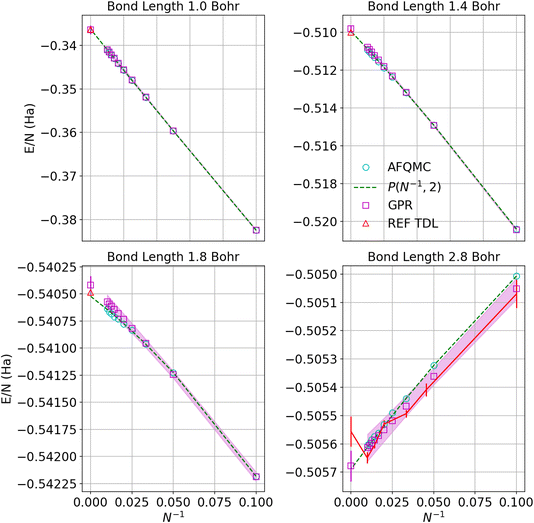 | ||
| Fig. 5 Predictions of the energy per atom in the thermodynamic limit vs. N−1 based on AFQMC results for hydrogen chains with bond lengths of 1.0, 1.4, 1.8, and 2.8 Bohr. Cyan circles denote direct AFQMC calculations, while the maroon squares denote the GPR predictions. The shadow depicts 95% confidence intervals, and the dashed lines depict the polynomial regression of second order at each bond length. The triangle represents the energy in the thermodynamic limit computed in ref. 1. The gap between points at small values of N−1 corresponds to chains between 100 and 5000 atoms, which are too prohibitive to compute using even less expensive theories. Note that the TDL of ref. 1 (REF TDL) for the bond length of 2.8 Bohr was replaced by our TDL extrapolation using a polynomial regression because the reference value seemed to be in disagreement with the rest of the reference’s data at that bond length. | ||
The left panel of Fig. 6 presents the energy of the hydrogen chains as a function of bond length directly calculated using UHF and UCCSD(T) for 100-atom chains, as well as the ref. 1 and GPR predictions in the thermodynamic limit. The energy differences between the N = 100 UCCSD(T), reference, and GPR predictions are hardly perceptible. The right panel of Fig. 6 likewise presents the energy as a function of bond length for the largest, N = 100-atom AFQMC calculations we were able to perform, in addition to the reference and GPR thermodynamic limit predictions. As in the UCCSD(T) case, the discrepancies are too small to discern at this scale.
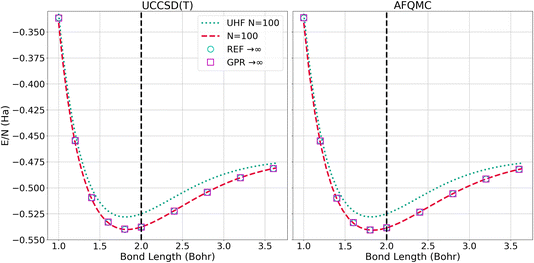 | ||
| Fig. 6 Energy per atom computed for N = 100 chains and predicted for N = ∞ chains using the UCCSD(T) (left) and AFQMC (right) methods. The “REF → ∞” is the TDL extrapolation taken from ref. 1. We plot this reference’s extrapolation so that it can be contrasted with our GPR’s prediction using 5000 atoms. | ||
To more closely examine how the GPR predictions converge with the number of atoms in the chains, in Fig. 7, we plot the difference between the thermodynamic limit predictions of ref. 1 and our UCCSD(T) (left) and AFQMC-based (right) GPR predictions on the milliHartree scale. For both methods, we take N = 5000 hydrogen chain GPR predictions to be representative of the thermodynamic limit. In the left-hand panel, we also plot UCCSD(T) results for N = 200 hydrogen chains, the largest we could directly simulate, to contrast N = 200 with N → ∞ results. We see that, at smaller bond lengths, discrepancies still remain between the N = 200 and N → ∞ results, signifying that finite size effects still influence the energies of even N = 200-length chains.
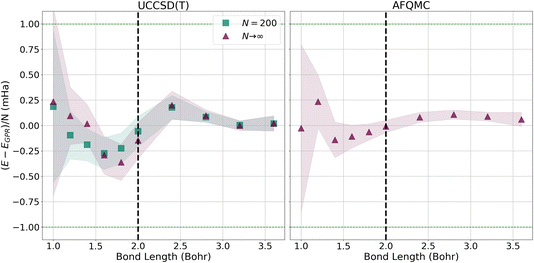 | ||
| Fig. 7 Differences between the energies predicted by ref. 1 and the UCCSD(T) (left) and AFQMC (right) GPR-predicted energies in the thermodynamic limit (red triangles). For both the UCCSD(T) and AFQMC plots, we assume that the GPR prediction using 5000 atoms is representative of the GPR prediction in the thermodynamic limit. On the left, we also plot the UCCSD(T) energies for N = 200 hydrogen chains, the largest we could directly simulate. The shadows depict 95% confidence intervals for the GPR predictions. | ||
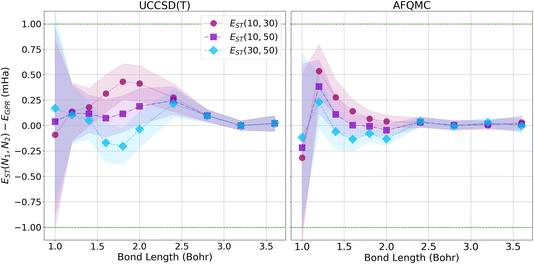
These discrepancies are also manifested in the larger confidence intervals that accompany the GPR predictions. Even so, GPR predictions at all bond lengths studied possess sub-milliHartree accuracy, and the discrepancies between the different chain length predictions disappear at the longest bond lengths studied. In contrast, the right panel of Fig. 7 demonstrates that the AFQMC-based GPR predictions are in much better agreement with ref. 1’s thermodynamic limit predictions, even at shorter bond lengths. This is in line with the results presented earlier in Fig. 3.
Since our calculations were performed with open boundary conditions (OBC), it is also worthwhile to compare our predictions to those produced using the “subtraction trick”,33 in which the energies of systems of different sizes are subtracted to eliminate surface effects from bulk energies. Fig. 8 presents the differences in energy between our GPR predictions of the energies in the thermodynamic limit and those produced using the subtraction trick based on chains of different lengths. The differences in the energies predicted by these approaches is sub-milliHartree at all bond lengths studied, further demonstrating that our GPR predictions are highly accurate relative to a widely-employed benchmark, while also illustrating the surprising accuracy of the subtraction trick. As the subtraction trick eliminates edge effects from energy predictions, this comparison especially highlights the GPR method’s ability to correct for edge effects. It is satisfying to see that the energies predicted by the subtraction trick performed on chains of lengths 30 and 50, which should yield the most accurate predictions of the subtraction trick calculations, are in the greatest agreement with our GPR predictions, especially at intermediate bond lengths. As before, we see that our GPR predictions are in the greatest agreement with the subtraction trick results at longer bond lengths. Indeed, our GPR predictions almost perfectly agree with all three of the subtraction trick predictions at the longest bond lengths studied. Moreover, our AFQMC-based GPR predictions again converge more rapidly and reliably to the thermodynamic limit with increasing bond length. Overall, Fig. 7 and 8 possess very similar features: the GPR predictions overestimate the energies at the shortest bond lengths and then oscillate between under- and overestimating the energies at intermediate bond lengths before coming to agreement at the longest bond lengths. This points to the overwhelming agreement between the polynomial regression and subtraction trick energies. These comparisons also demonstrate that the GPR predictions are not uniformly biased toward over- or underestimating energies.
A more quantitative comparison of the predictions generated by all of these methods can be found in the ESI.†
4.2 Two-dimensional, inhomogeneous hydrogen chains
Given the success of GPR at predicting the energies of homogeneously-stretched hydrogen chains in the thermodynamic limit, we next examine the capacity for the same GPR techniques to predict the energies of inherently heterogeneous chains of hydrogen dimers. As depicted in Fig. 9, these chains of hydrogen dimers are described by two key distances: the intra-dimer bond distance, a, and the inter-dimer bond distance, b. In the following, we generally fix the intradimer distance, a, between 1.0 and 3.5 Bohr, and vary the interdimer distance between 1.0 and a Bohr, maintaining open boundary conditions. While these chains of dimers enable us to retain the same periodicity present in our earlier homogeneous chains, they also enable us to purposefully and controllably introduce heterogeneity into our systems that complicates our prediction problem. Indeed, these chains of dimers manifest several levels of correlation when stretched, typically necessitating the use of advanced quantum chemistry methods to make high-accuracy energy predictions.91 | ||
| Fig. 9 Illustration of the linear chains of hydrogen dimers studied in this work with intradimer distance, a, and interdimer distance, b. | ||
To study the performance of our GPR algorithm on these chains, we generate a database of dimer chain energies starting from UHF calculations with single Slater determinants that we again input into either CCSD(T) or AFQMC calculations. We model our hydrogen atoms using the minimal STO-6G basis set given the steep computational cost of the system with increasing system size. Chains of 5, 10, and 15 dimers for a total of 176 configurations were employed for training. The remaining 315 configurations of chains consisting of 20 to 50 dimers were subsequently used for testing and validation. The same atomic environment descriptors previously employed for the homogeneous chains were also employed here.
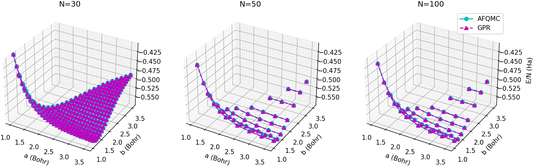
The energy surfaces for chains consisting of N = 30, 50, and 100 atoms are depicted in Fig. 10. It can be seen that the GPR predictions are in qualitative agreement with the AFQMC database values, both for short chains (N = 10) and long chains approaching the thermodynamic limit (N = 100). In particular, GPR is able to well describe both the energy minimum around a = 1.5 Bohr, b = 3.25 Bohr, and highly stretched chains with both a and b greater than 3 Bohr. More detailed slices of the potential energy surface for several values of a are depicted in Fig. 11.
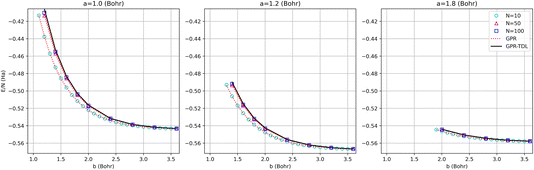 | ||
| Fig. 11 Comparison of GPR and AFQMC predictions for different intra-dimer bond lengths as a function of inter-dimer distances. The N = 10, 50, and 100-atom data are all provided by AFQMC. | ||
As is apparent from these plots, the approach to large inter-dimer separations is highly dependent upon the intra-dimer separation: for small a, the approach is steeper than for large a. This behavior is a sign of correlation between the a and b values and is non-trivial, given the seeming simplicity of the model. This makes the model a useful testbed for multidimensional extrapolations, as further discussed in the ESI.†
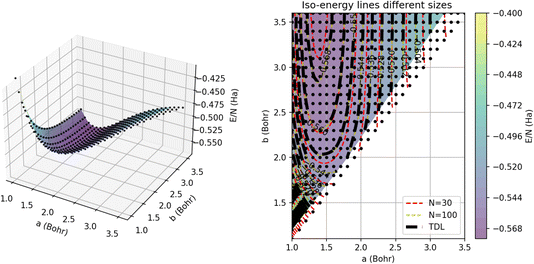
To visualize the energy surface, as shown in Fig. 12, we use triangulation over the sample points and then Delaunay smoothing. The thermodynamic limit was estimated using GPR regression on N = 5000 atoms. On the left, we present the 3D energy surface for a chain of 15 dimers; the black dots denote the energies estimated by GPR in the thermodynamic limit. On the right, we provide a heat map corresponding to the plot on the left annotated with iso-energy contour lines predicted using GPR for systems of different sizes. In particular, the red and yellow dashed lines denote the energies for chains comprised of 15 and 50 dimers, respectively. The errors on these energies are all less than 1 mHa, which is within chemical accuracy.
This plot underscores how the contours change or shift with system size. We can see that the largest differences between the contours occur near the minimum of the plot around an intra-dimer distance of 1.5 Bohr and an inter-dimer distance of 3 Bohr. In this region of the surface, the N = 30 contours differ significantly from the N = 100 contours, which nearly align with the thermodynamic limit contours, suggesting that 100 atoms are nearly enough to converge simulations of this system to their TDL. Away from this minimum, the contours for all three system sizes concur, demonstrating that the system experiences weaker finite size effects for these parameters. GPR’s success extrapolating the energies of this non-trivial, multidimensional model suggests that it is likely to have similar success on the more complex models and solids of interest to the wider scientific community.
5. Discussion of results
Although we employed Gaussian Process Regression in this work, a wide range of other machine learning approaches, including artificial neural networks, could also be used to perform these extrapolations. We opted to employ kernel methods like Gaussian processes because they are non-parametric and make use of Bayesian inference at a comparatively low, O(Nt3) cost, where Nt is the size of the training set.17 It has been proposed92 as a rule of thumb to use Nt = 10 × d, where d is the dimension of the feature space, to train a GPR. In contrast, neural network-based approaches involve matrix-vector multiplications that scale with the number of neurons in the network, Nn, and the dimension of the input vector, d, as O(Nnd). If the number of neurons in the network is small, this implies that neural networks are less expensive to employ than GPR. However, neural networks typically necessitate the use of non-linear activation functions that may increase their overall cost. More importantly, neural networks often suffer from overfitting if care is not taken to reoptimize their number of nodes or structures. Overfitting is much less of a concern for GPR since GPR with the same kernel but more training points is guaranteed to be more accurate. In practice, NNs use at least 2 to 3 orders of magnitude more training data than GPR.17,32 When training data is scarce – as it usually is when many-body electronic structure calculations are involved – GPR-based techniques hence become the method of choice.32 One may also ask whether using GPR on these low-dimensional data sets is more sophisticated than necessary and if other, less sophisticated regression techniques based on a small number of parameters could instead be employed. As demonstrated in the ESI,† we have compared the performance of our GPR approach to that of Bayesian Multivariate Adaptive Regression Splines, a spline-based technique, and found that our GPR approach can extrapolate with significantly greater accuracy. We moreover show that, while one can extrapolate using a few simple parameters, this extrapolation is not readily generalizable to more complex situations in which the parameters to use are less obvious. Lastly, as illustrated throughout this manuscript, GPR inherently quantifies uncertainties, which are critical for being able to determine its accuracy relative to that of other methods.Our studies of low-dimensional hydrogen chains naturally beg the question of how well our techniques can be generalized to more realistic multidimensional solids that are accompanied by an even more rapid growth in computational expense. Much like other GAP methods, our approach should be readily generalizable to higher dimensional systems, given sufficient data and high-quality features. Indeed, here, we took the first step toward demonstrating this by applying our model to both a one-dimensional and a nontrivial two-dimensional system, and in a previous preprint, we demonstrated how a similar GPR-based approach could be leveraged to predict the energies of 3D alloys.93 The key challenge associated with higher-dimensional predictions is the curse of dimensionality: the higher the dimensionality of the space, the more data that is needed for training to learn the larger space with sufficient accuracy to make effective comparisons between different atomic environments. The resulting increase in cost can be slowed through a more judicious selection of features and design of kernels. CUR88 decompositions and Kernelized Principal Covariates Regression90 are excellent alternatives for identifying the most relevant features, which can significantly reduce the dimension of the descriptors of a given data set. More effective kernels may also be constructed through approaches that recursively evaluate the differences between structures.69 For example, De et al. proposed kernels based on regularized structure matching to optimize the comparisons between the atomic environments of different structures.69 Thus, with further technical developments, we believe that the techniques presented here should be readily generalizable to the even larger, more complicated solids that they would most benefit.
6. Conclusions
In summary, in this work, we have presented a Gaussian Process Regression-based approach for predicting the many-body energies of hydrogen chains, the simplest examples of ab initio solids, in the thermodynamic limit. We have shown that, by training on databases of the energies of short (10–30-atom) homogeneous and inhomogeneous hydrogen chains with varying intra- and inter-dimer distances, we can predict the energies of these chains in the thermodynamic limit with sub-milliHartree accuracy relative to predictions made by alternative extrapolation techniques. These alternative techniques, including polynomial regressions and the “subtraction trick”, typically necessitate computing the energies of chains much longer than the chains employed in our training sets. As such, our approach enables the highly accurate prediction of the energies of solids in the thermodynamic limit based upon relatively small systems, and hence, much less expensive calculations. Unlike many finite size extrapolation techniques which apply to systems with only certain geometries, densities, and/or dimensionality, as demonstrated by the easy generalizability of our method to both homogeneous and inhomogeneous chains, our approach is largely agnostic to the physical characteristics of the system studied; as long as there is sufficient and representative training data, our approach can be applied, making it particularly useful for some of the more complex systems of modern interest, such as those at interfaces or having irregular geometries.Data availability
The data that support the findings of this study are openly available online at https://github.com/josuelandinez/LHC_Database.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. J. L. B. would like to thank Amit Samanta for insightful discussions and Qiming Sun for his kind assistance with performing calculations in PySCF. E. J. L. B. (concept, modeling, analysis, manuscript preparation), A. L. (manuscript preparation), and B. R. (concept, mentoring, manuscript preparation) graciously acknowledge support from U.S. Department of Energy, Office of Science, Basic Energy Sciences Award #DE-FOA-0001912. B. R. (concept) also received support from U.S. National Science Foundation grant OIA-1921199 and the Research Corporation of America (concept). This research was conducted using computational resources and services at the Center for Computation and Visualization, Brown University.References
- M. Motta, D. M. Ceperley, G. K.-L. Chan, J. A. Gomez, E. Gull, S. Guo, C. A. Jiménez-Hoyos, T. N. Lan, J. Li, F. Ma, A. J. Millis, N. V. Prokof’ev, U. Ray, G. E. Scuseria, S. Sorella, E. M. Stoudenmire, Q. Sun, I. S. Tupitsyn, S. R. White, D. Zgid and S. Zhang, Phys. Rev. X, 2017, 7, 031059, DOI:10.1103/PhysRevX.7.031059.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- S. Goedecker, Linear scaling electronic structure methods, Rev. Mod. Phys., 1999, 71, 1085–1123, DOI:10.1103/RevModPhys.71.1085.
- S. Mohr, L. E. Ratcliff, L. Genovese, D. Caliste, P. Boulanger, S. Goedecker and T. Deutsch, Accurate and efficient linear scaling DFT calculations with universal applicability, Phys. Chem. Chem. Phys., 2015, 17, 31360–31370, 10.1039/C5CP00437C.
- M. Holzmann, R. C. Clay, M. A. Morales, N. M. Tubman, D. M. Ceperley and C. Pierleoni, Theory of finite size effects for electronic quantum Monte Carlo calculations of liquids and solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 035126, DOI:10.1103/PhysRevB.94.035126.
- N. D. Drummond, R. J. Needs, A. Sorouri and W. M. C. Foulkes, Finite-size errors in continuum quantum Monte Carlo calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125106, DOI:10.1103/PhysRevB.78.125106.
- S. Azadi and W. M. C. Foulkes, Systematic study of finite-size effects in quantum Monte Carlo calculations of real metallic systems, J. Chem. Phys., 2015, 143(10), 102807 CrossRef.
- T. N. Mihm, B. Yang and J. J. Shepherd, Power laws used to extrapolate the coupled cluster correlation energy to the thermodynamic limit, J. Chem. Theory Comput., 2021, 17(5), 2752–2758 CrossRef CAS.
- A. Baldereschi, Mean-value point in the Brillouin zone, Phys. Rev. B: Solid State, 1973, 7, 5212–5215, DOI:10.1103/PhysRevB.7.5212.
- C. Lin, F. H. Zong and D. M. Ceperley, Twist-averaged boundary conditions in continuum quantum Monte Carlo algorithms, Phys. Rev. E, 2001, 64, 016702, DOI:10.1103/PhysRevE.64.016702.
- W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Quantum Monte Carlo simulations of solids, Rev. Mod. Phys., 2001, 73, 33–83, DOI:10.1103/RevModPhys.73.33.
- H. Kwee, S. Zhang and H. Krakauer, Finite-size correction in many-body electronic structure calculations, Phys. Rev. Lett., 2008, 100, 126404, DOI:10.1103/PhysRevLett.100.126404.
- V. Gorelov, Y. Yang, M. Ruggeri, D. M. Ceperley, C. Pierleoni and M. Holzmann, Neutral band gap of carbon by quantum Monte Carlo methods, Condens. Matter Phys., 2023, 26(3), 33701, DOI:10.5488/cmp.26.33701.
- V. Gorelov, M. Holzmann, D. M. Ceperley and C. Pierleoni, Electronic excitation spectra of molecular hydrogen in phase I from quantum Monte Carlo and many-body perturbation methods, arXiv, 2023, preprint, arXiv:2311.08506 [cond-mat.mtrl-sci], DOI:10.48550/arXiv.2311.08506.
- M. Colomé-Tatché, S. I. Matveenko and G. V. Shlyapnikov, Finite-size effects for the gap in the excitation spectrum of the one-dimensional Hubbard model, Phys. Rev. A, 2010, 81, 013611, DOI:10.1103/PhysRevA.81.013611.
- K. Liao and A. Grüneis, Communication: Finite size correction in periodic coupled cluster theory calculations of solids, J. Chem. Phys., 2016, 145(14), 141102 CrossRef.
- P. Mehta, M. Bukov, C.-H. Wang, A. G. R. Day, C. Richardson, C. K. Fisher and D. J. Schwab, A high-bias, low-variance introduction to machine learning for physicists, Phys. Rep., 2019, 810, 1–124, DOI:10.1016/j.physrep.2019.03.001.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborová, Machine learning and the physical sciences, Rev. Mod. Phys., 2019, 91, 045002, DOI:10.1103/RevModPhys.91.045002.
- C. Nyshadham, M. Rupp, B. Bekker, A. V. Shapeev, T. Mueller, C. W. Rosenbrock, G. Csányi, D. W. Wingate and G. L. W. Hart, Machine-learned multi-system surrogate models for materials prediction, npj Comput. Mater., 2019, 5(1), 51, DOI:10.1038/s41524-019-0189-9.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, Recent advances and applications of machine learning in solid-state materials science, npj Comput. Mater., 2019, 5(1), 83, DOI:10.1038/s41524-019-0221-0.
- A. B. Georgescu, P. Ren, A. R. Toland, S. Zhang, K. D. Miller, D. W. Apley, E. A. Olivetti, N. Wagner and J. M. Rondinelli, Database, features, and machine learning model to identify thermally driven metal–insulator transition compounds, Chem. Mater., 2021, 33(14), 5591–5605, DOI:10.1021/acs.chemmater.1c00905.
- J. Carrasquilla, Machine learning for quantum matter, Adv. Phys.: X, 2020, 5(1), 1797528, DOI:10.1080/23746149.2020.1797528.
- D. Pfau, J. S. Spencer, A. G. D. G. Matthews and W. M. C. Foulkes, Ab initio solution of the many-electron Schrödinger equation with deep neural networks, Phys. Rev. Res., 2020, 2, 033429, DOI:10.1103/PhysRevResearch.2.033429.
- J. Hermann, Z. Schätzle and F. Noé, Deep-neural-network solution of the electronic Schrödinger equation, Nat. Chem., 2020, 12(10), 891–897, DOI:10.1038/s41557-020-0544-y.
- A. Glielmo, Y. Rath, G. Csányi, A. De Vita and G. H. Booth, Gaussian process states: A data-driven representation of quantum many-body physics, Phys. Rev. X, 2020, 10, 041026, DOI:10.1103/PhysRevX.10.041026.
- Y. Rath, A. Glielmo and G. H. Booth, A Bayesian inference framework for compression and prediction of quantum states, J. Chem. Phys., 2020, 153(12), 124108, DOI:10.1063/5.0024570.
- H. Niu, Y. Yang, S. Jensen, M. Holzmann, C. Pierleoni and D. M. Ceperley, Stable solid molecular hydrogen above 900 K from a machine-learned potential trained with diffusion quantum Monte Carlo, Phys. Rev. Lett., 2023, 130, 076102, DOI:10.1103/PhysRevLett.130.076102.
- D. Wu, R. Rossi, F. Vicentini and G. Carleo, From tensor-network quantum states to tensorial recurrent neural networks, Phys. Rev. Res., 2023, 5, L032001, DOI:10.1103/PhysRevResearch.5.L032001.
- Li Li, T. E. Baker, S. R. White and K. Burke, Pure density functional for strong correlation and the thermodynamic limit from machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 245129, DOI:10.1103/PhysRevB.94.245129.
- L. Weiler, T. N. Mihm and J. J. Shepherd, Machine learning for a finite size correction in periodic coupled cluster theory calculations, J. Chem. Phys., 2022, 156(20), 204109, DOI:10.1063/5.0086580.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning. Adaptative computation and machine learning series, University Press Group Limited, 2006, ISBN 9780262182539, https://books.google.com.co/books?id=vWtwQgAACAAJ Search PubMed.
- A. Kamath, R. A. Vargas-Hernández, V. K. Roman, T. Carrington and S. Manzhos, Neural networks vs. Gaussian process regression for representing potential energy surfaces: A comparative study of fit quality and vibrational spectrum accuracy, J. Chem. Phys., 2018, 148(24), 241702 CrossRef PubMed.
- E. M. Stoudenmire and S. R. White, Studying two-dimensional systems with the density matrix renormalization group, Annu. Rev. Condens. Matter Phys., 2012, 3(1), 111–128, DOI:10.1146/annurev-conmatphys-020911-125018.
- P. J. Reynolds, J. Tobochnik and H. Gould, Diffusion Quantum Monte Carlo, Comput. Phys., 1990, 4(6), 662–668, DOI:10.1063/1.4822960.
- T. Pang, Diffusion Monte Carlo: A powerful tool for studying quantum many-body systems, Am. J. Phys., 2014, 82(10), 980–988, DOI:10.1119/1.4890824.
- J. C. Greer, Estimating full configuration interaction limits from a Monte Carlo selection of the expansion space, J. Chem. Phys., 1995, 103(5), 1821–1828, DOI:10.1063/1.469756.
- S. Zhang and H. Krakauer, Quantum Monte Carlo method using phase-free random walks with Slater determinants, Phys. Rev. Lett., 2003, 90, 136401, DOI:10.1103/PhysRevLett.90.136401.
- J. Lee, H. Q. Pham and D. R. Reichman, Twenty years of auxiliary-field quantum Monte Carlo in quantum chemistry: An overview and assessment on main group chemistry and bond-breaking, J. Chem. Theory Comput., 2022, 18(12), 7024–7042, DOI:10.1021/acs.jctc.2c00802.
- C. Huang and B. M. Rubenstein, Machine learning diffusion Monte Carlo forces, J. Phys. Chem. A, 2023, 127(1), 339–355, DOI:10.1021/acs.jpca.2c05904.
- J. Tiihonen, R. C. Clay, III and J. T. Krogel, Toward quantum Monte Carlo forces on heavier ions: Scaling properties, J. Chem. Phys., 2021, 154(20), 204111, DOI:10.1063/5.0052266.
- K. Ryczko, J. T. Krogel and I. Tamblyn, Machine Learning Diffusion Monte Carlo Energies, J. Chem. Theory Comput., 2022, 18(12), 7695–7701, DOI:10.1021/acs.jctc.2c00483.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401, DOI:10.1103/PhysRevLett.98.146401.
- W. Ren, W. Fu, X. Wu and J. Chen, Towards the ground state of molecules via diffusion Monte Carlo on neural networks, Nat. Commun., 2023, 14(1), 1860, DOI:10.1038/s41467-023-37609-3.
- M. Scherbela, R. Reisenhofer, L. Gerard, P. Marquetand and P. Grohs, Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks, Nat. Comput. Sci., 2022, 2(5), 331–341, DOI:10.1038/s43588-022-00228-x.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics, Phys. Rev. Lett., 2018, 120, 143001, DOI:10.1103/PhysRevLett.120.143001.
- Note 1. Without corrections, QMC methods typically possess an infinite statistical variance,94 and even with corrections, can scale quite steeply (as Zeff6.5 or greater, where Zeff is the effective nuclear charge).
- B. Huang, O. Anatole von Lilienfeld, J. T. Krogel and A. Benali, Toward DMC accuracy across chemical space with scalable Δ-QML, J. Chem. Theory Comput., 2023, 19(6), 1711–1721, DOI:10.1021/acs.jctc.2c01058.
- P. Broecker, J. Carrasquilla, R. G. Melko and S. Trebst, Machine learning quantum phases of matter beyond the fermion sign problem, Sci. Rep., 2017, 7(1), 8823, DOI:10.1038/s41598-017-09098-0.
- D. M. Ceperley, S. Jensen, Y. Yang, H. Niu, C. Pierleoni, and M. Holzmann, Training models using forces computed by stochastic electronic structure methods, arXiv, 2023, preprint, arXiv:2310.15994, DOI:10.48550/arXiv.2310.15994.
- J. Toulouse, R. Assaraf, and C. J. Umrigar, Chapter Fifteen - Introduction to the Variational and Diffusion Monte Carlo Methods, in, Electron Correlation in Molecules – Ab Initio beyond Gaussian Quantum Chemistry, P. E. Hoggan and T. Ozdogan, Advances in Quantum Chemistry, Academic Press, 2016, vol. 73, pp. 285–314, ISSN: 0065-3276, DOI:10.1016/bs.aiq.2015.07.003.
- J. Kanamori, Electron Correlation and Ferromagnetism of Transition Metals, Prog. Theor. Phys., 1963, 30(3), 275–289, DOI:10.1143/PTP.30.275.
- M. Bajdich, L. Mitas, G. Drobný, L. K. Wagner and K. E. Schmidt, Pfaffian pairing wave functions in electronic-structure quantum Monte Carlo simulations, Phys. Rev. Lett., 2006, 96, 130201, DOI:10.1103/PhysRevLett.96.130201.
- D. Luo and B. K. Clark, Backflow transformations via neural networks for quantum many-body wave functions, Phys. Rev. Lett., 2019, 122, 226401, DOI:10.1103/PhysRevLett.122.226401.
- J. Hermann, J. Spencer, K. Choo, A. Mezzacapo, W. M. C. Foulkes, D. Pfau, G. Carleo and F. Noé, Ab initio quantum chemistry with neural-network wavefunctions, Nat. Rev. Chem., 2023, 7(10), 692–709, DOI:10.1038/s41570-023-00516-8.
- Z. Schätzle, P. B. Szabó, M. Mezera, J. Hermann and F. Noé, DeepQMC: An open-source software suite for variational optimization of deep-learning molecular wave functions, J. Chem. Phys., 2023, 159(9), 094108, DOI:10.1063/5.0157512.
- H. Ye, R. Li, Y. Gu, Y. Lu, D. He and L. Wang, Õ(N2) Representation of General Continuous Anti-symmetric Function, arXiv, 2024, preprint, arXiv:2402.15167 [quant-ph], DOI:10.48550/arXiv.2402.15167.
- G. Carleo and M. Troyer, Solving the quantum many-body problem with artificial neural networks, Science, 2017, 355(6325), 602–606, DOI:10.1126/science.aag2302.
- G. Pescia, J. Nys, J. Kim, A. Lovato and G. Carleo, Message-Passing Neural Quantum States for the Homogeneous Electron Gas, arXiv, 2023, preprint, arXiv:2305.07240 [quant-ph], DOI:10.48550/arXiv.2305.07240.
- R. Zen, L. My, R. Tan, F. Hébert, M. Gattobigio, C. Miniatura, D. Poletti and S. Bressan, Transfer learning for scalability of neural-network quantum states, Phys. Rev. E, 2020, 101, 053301, DOI:10.1103/PhysRevE.101.053301.
- K. Choo, A. Mezzacapo and G. Carleo, Fermionic neural-network states for ab-initio electronic structure, Nat. Commun., 2020, 11, 2368, DOI:10.1038/s41467-020-15724-9.
- Y. Rath and G. H. Booth, Quantum Gaussian process state: A kernel-inspired state with quantum support data, Phys. Rev. Res., 2022, 4, 023126, DOI:10.1103/PhysRevResearch.4.023126.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian process regression for materials and molecules, Chem. Rev., 2021, 121(16), 10073–10141, DOI:10.1021/acs.chemrev.1c00022.
- D. J. C. MacKay, Information Theory, Inference & Learning Algorithms, Cambridge University Press, New York, NY, USA, 2002, ISBN 0521642981 Search PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115(16), 1051–1057, DOI:10.1002/qua.24927.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115, DOI:10.1103/PhysRevB.87.184115.
- M. Rupp, Machine learning for quantum mechanics in a nutshell, Int. J. Quantum Chem., 2015, 115(16), 1058–1073, DOI:10.1002/qua.24954.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949, DOI:10.1016/j.cpc.2019.106949.
- S. J. Davie, N. Di Pasquale and P. L. A. Popelier, Kriging atomic properties with a variable number of inputs, J. Chem. Phys., 2016, 145(10), 104104, DOI:10.1063/1.4962197.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769, 10.1039/C6CP00415F.
- M. Motta, C. Genovese, F. Ma, Z.-H. Cui, R. Sawaya, G. Kin-Lic Chan, N. Chepiga, P. Helms, C. Jiménez-Hoyos, A. J. Millis, U. Ray, E. Ronca, H. Shi, S. Sorella, E. M. Stoudenmire, S. R. White and S. Zhang, Phys. Rev. X, 2020, 10, 031058, DOI:10.1103/PhysRevX.10.031058.
- A. V. Sinitskiy, L. Greenman and D. A. Mazziotti, Strong correlation in hydrogen chains and lattices using the variational two-electron reduced density matrix method, J. Chem. Phys., 2010, 133(1), 014104 CrossRef PubMed.
- L. Stella, C. Attaccalite, S. Sorella and A. Rubio, Strong electronic correlation in the hydrogen chain: A variational Monte Carlo study, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245117, DOI:10.1103/PhysRevB.84.245117.
- J. Hachmann, W. Cardoen and G. K.-L. Chan, Multireference correlation in long molecules with the quadratic scaling density matrix renormalization group, J. Chem. Phys., 2006, 125(14), 144101 CrossRef.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Books on Chemistry, Dover Publications, 2012, ISBN 9780486134598, URL https://books.google.com/books?id=KQ3DAgAAQBAJ Search PubMed.
- H. Shi and S. Zhang, Some recent developments in auxiliary-field quantum Monte Carlo for real materials, J. Chem. Phys., 2021, 154(2), 024107, DOI:10.1063/5.0031024.
- I. Shavitt and R. J. Bartlett, Many-body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge Molecular Science, Cambridge University Press, 2009, DOI:10.1017/CBO9780511596834.
- J. McClain, Q. Sun, G. K.-L. Chan and T. C. Berkelbach, Gaussian-based coupled-cluster theory for the ground-state and band structure of solids, J. Chem. Theory Comput., 2017, 13(3), 1209–1218 CrossRef CAS PubMed.
- X. Wang and T. C. Berkelbach, Excitons in solids from periodic equation-of-motion coupled-cluster theory, J. Chem. Theory Comput., 2020, 16(5), 3095–3103 CrossRef CAS PubMed.
- S. Zhang and H. Krakauer, Quantum Monte Carlo method using phase-free random walks with Slater determinants, Phys. Rev. Lett., 2003, 90, 136401, DOI:10.1103/PhysRevLett.90.136401.
- W. Purwanto, S. Zhang and H. Krakauer, An auxiliary-field quantum Monte Carlo study of the chromium dimer, J. Chem. Phys., 2015, 142(6), 064302 CrossRef.
- W. A. Al-Saidi, S. Zhang and H. Krakauer, Bond breaking with auxiliary-field quantum Monte Carlo, J. Chem. Phys., 2007, 127(14), 144101 CrossRef CAS PubMed.
- J. Shee, B. Rudshteyn, E. J. Arthur, S. Zhang, D. R. Reichman and R. A. Friesner, On achieving high accuracy in quantum chemical calculations of 3d transition metal-containing systems: A comparison of auxiliary-field quantum Monte Carlo with coupled cluster, density functional theory, and experiment for diatomic molecules, J. Chem. Theory Comput., 2019, 15(4), 2346–2358 CrossRef CAS PubMed.
- J. Lee, F. D. Malone and M. A. Morales, Utilizing essential symmetry breaking in auxiliary-field quantum Monte Carlo: Application to the spin gaps of the C36 fullerene and an iron porphyrin model complex, J. Chem. Theory Comput., 2020, 16(5), 3019–3027 CrossRef CAS.
- F. Ma, W. Purwanto, S. Zhang and H. Krakauer, Quantum Monte Carlo calculations in solids with downfolded Hamiltonians, Phys. Rev. Lett., 2015, 114, 226401 Search PubMed.
- F. D. Malone, A. Benali, M. A. Morales, M. Caffarel, P. R. C. Kent and L. Shulenburger, Systematic comparison and cross-validation of fixed-node diffusion Monte Carlo and phaseless auxiliary-field quantum Monte Carlo in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 161104, DOI:10.1103/PhysRevB.102.161104.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip.Rev. Comput. Mol. Sci., 2018, 8(1), e1340, DOI:10.1002/wcms.1340.
- J. Kim, A. D. Baczewski, T. D. Beaudet, A. Benali, M. C. Bennett, M. A. Berrill, N. S. Blunt, E. J. Landinez Borda, M. Casula, D. M. Ceperley, S. Chiesa, B. K. Clark, R. C. Clay, K. T. Delaney, M. Dewing, K. P. Esler, H. Hao, O. Heinonen, P. R. C. Kent, J. T. Krogel, I. Kylänpää, Y. W. Li, M. G. Lopez, Y. Luo, F. D. Malone, R. M. Martin, A. Mathuriya, J. McMinis, C. A. Melton, L. Mitas, M. A. Morales, E. Neuscamman, W. D. Parker, S. D. Pineda Flores, N. A. Romero, B. M. Rubenstein, J. A. R. Shea, H. Shin, L. Shulenburger, A. F. Tillack, J. P. Townsend, N. M. Tubman, B. Van Der Goetz, J. E. Vincent, D. C. Yang, Y. Yang, S. Zhang and L. Zhao, QMCPACK: an open source ab initio quantum Monte Carlo package for the electronic structure of atoms, molecules and solids, J. Phys.: Condens. Matter, 2018, 30(19), 195901, DOI:10.1088/1361-648x/aab9c3.
- G. Imbalzano, A. Anelli, D. Giofré, S. Klees, J. Behler and M. Ceriotti, J. Chem. Phys., 2018, 148(24), 241730, DOI:10.1063/1.5024611.
- M. Gavish and D. L. Donoho, The optimal hard threshold for singular values is 4/√3, IEEE Trans. Inf. Theory, 2014, 60(8), 5040–5053, DOI:10.1109/TIT.2014.2323359.
- R. K. Cersonsky, B. A. Helfrecht, E. A. Engel, S. Kliavinek and M. Ceriotti, Improving sample and feature selection with principal covariates regression, Mach. Learn.: Sci. Technol., 2021, 2(3), 035038, DOI:10.1088/2632-2153/abfe7c.
- W. A. Al-Saidi, S. Zhang and H. Krakauer, Bond breaking with auxiliary-field quantum Monte Carlo, J. Chem. Phys., 2007, 127(14), 144101, DOI:10.1063/1.2770707.
- J. Cui and R. V. Krems, Efficient non-parametric fitting of potential energy surfaces for polyatomic molecules with Gaussian processes, J. Phys. B: At., Mol. Opt. Phys., 2016, 49(22), 224001, DOI:10.1088/0953-4075/49/22/224001.
- C. Nataraj, E. J. Landinez Borda, A. Walle and A. Samanta, A systematic analysis of phase stability in refractory high entropy alloys utilizing linear and non-linear cluster expansion models, Acta Mater., 2021, 220, 117269, DOI:10.1016/j.actamat.2021.117269.
- H. Shi and S. Zhang, Infinite variance in fermion quantum Monte Carlo calculations, Phys. Rev. E, 2016, 93, 033303, DOI:10.1103/PhysRevE.93.033303.
Footnote |
| † Electronic supplementary information (ESI) available: Comparisons of the accuracy of our GPR methods to those of other regression techniques and tables of the energies predicted by the different approaches described here that underlie many of the plots provided in the main text. See DOI: https://doi.org/10.1039/d4fd00051j |
| This journal is © The Royal Society of Chemistry 2024 |