 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-throughput viscoelastic characterization of cells in hyperbolic microchannels†
Felix
Reichel
 abc,
Ruchi
Goswami
abc,
Ruchi
Goswami
 ab,
Salvatore
Girardo
ab,
Salvatore
Girardo
 ab and
Jochen
Guck
ab and
Jochen
Guck
 *abc
*abc
aMax Planck Institute for the Science of Light, Erlangen, Germany. E-mail: jochen.guck@mpl.mpg.de
bMax-Planck-Zentrum für Physik und Medizin, Erlangen, Germany
cDepartment of Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany
First published on 3rd April 2024
Abstract
Extensive research has demonstrated the potential of cell viscoelastic properties as intrinsic indicators of cell state, functionality, and disease. For this, several microfluidic techniques have been developed to measure cell viscoelasticity with high-throughput. However, current microchannel designs introduce complex stress distributions on cells, leading to inaccuracies in determining the stress–strain relationship and, consequently, the viscoelastic properties. Here, we introduce a novel approach using hyperbolic microchannels that enable precise measurements under a constant extensional stress and offer a straightforward stress–strain relationship, while operating at a measurement rate of up to 100 cells per second. We quantified the stresses acting in the channels using mechanical calibration particles made from polyacrylamide (PAAm) and found that the measurement buffer, a solution of methyl cellulose and phosphate buffered saline, shows strain-thickening following a power law up to 200 s−1. By measuring oil droplets with varying viscosities, we successfully detected changes in the relaxation times of the droplets and our approach could be used to get the interfacial tension and viscosity of liquid–liquid droplet systems from the same measurement. We further applied this methodology to PAAm microgel beads, demonstrating the accurate recovery of Young's moduli and the near-ideal elastic behavior of the beads. To explore the influence of altered cell viscoelasticity, we treated HL60 human leukemia cells with latrunculin B and nocodazole, resulting in clear changes in cell stiffness while relaxation times were only minimally affected. In conclusion, our approach offers a streamlined and time-efficient solution for assessing the viscoelastic properties of large cell populations and other microscale soft particles.
Introduction
Cellular viscoelasticity has emerged as a central indicator of cell state and function, playing an increasingly significant role in disease characterization.1–6 Established techniques such as micro-pipette aspiration,1,7 atomic force microscopy,8–10 or the optical stretcher,11–14 while effective in revealing changes in cell deformability and relaxation times, operate on timescales of seconds with throughputs limited to a few hundred cells per hour max. This limitation makes them unsuitable for swift diagnostic applications.To address the need for faster measurements, microfluidic techniques have gained prominence.3,5,15–17 Operating at timescales ranging from below 1 to 100 milliseconds, these platforms offer measurement rates of over 1000 cells per second. However, the quantification of stresses and cell strain in the microchannels remains challenging due to the complex three-dimensional stress distribution on the cell surface.18,19
Viscoelastic analysis typically necessitates a one-dimensional stress–strain relationship to derive mechanistic properties such as elastic moduli, relaxation times, or storage and loss moduli.5,10,20,21 Moreover, in cell mechanics measurements, polymeric crowding agents are often employed to enhance the viscosity of the cell carrier solution.5,16,22,23 This augmentation leads to non-Newtonian behavior, including shear-thinning, the occurrence of normal stress differences, or strain-thickening.24–26 Notably, this behavior is frequently characterized solely in shear, neglecting the qualitatively different behavior in extension.5,22,23
In this study, we address these challenges by introducing hyperbolic microchannels as a novel approach for accurate cell viscoelastic measurements under well-defined tensile stresses and strains. The flow pattern within the hyperbolic channel geometry creates a region of constant stress, simplifying the analysis of experiments. While hyperbolic channels have been used before for cell mechanical measurements, the focus has predominantly been on measuring cell deformability, with little attention given to correlating stresses to strains within the hyperbolic region to quantify cell viscoelastic properties.22,27,28
Our study aims to fill this gap by simultaneously examining both cell deformability and associated stresses within hyperbolic microchannels. Additionally, our methodology extends to the determination of normal stresses in polymeric solutions at varying extension rates.
To underscore the method's capability in measuring changes in relaxation times, we conducted experiments using silicone oil droplets of varying viscosities. Our results not only showcase the ability to detect changes in timescales but also highlight the method's utility in retrieving interfacial tension and droplet viscosity from a single experiment.
Employing a Kelvin–Voigt model, we analyzed the stress–strain relationship to extract the Young's modulus and relaxation times of cells. Validation of our approach involved measurements on polyacrylamide (PAAm) microgel beads,29 demonstrating the recovery of expected Young's moduli and indicating near-elastic behavior based on relaxation times.
Finally, we used the hyperbolic microchannels to investigate changes in HL60 cell viscoelasticity under treatment with the actin polymerization inhibiting drug latrunculin B (LatB) and microtubule depolymerizing reagent nocodazole. Our findings reveal a concentration-dependent decrease in the cells' Young's modulus, while relaxation times show a slight increase.
In conclusion, our results underscore the utility of hyperbolic microchannels for accurate measurements of cell viscoelastic properties in extension at up to 100 cells per second with potential applications in cell research and diagnostics.
Theoretical background
Stresses and deformations in extensional flow
During flow through a converging channel in x-direction with a constant flow rate, Q, the fluid velocity, v, will increase as a function of x. The rate of this velocity increase is called the extension rate,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) :
: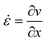 | (1) |
vx = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) x, vy = − x, vy = −![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) y, vz = 0 y, vz = 0 | (2) |
| N1 = σx − σy. | (3) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . For non-Newtonian liquids, N1 usually cannot be derived from η and the behavior in extension has to be characterized independently. Generally, the relation between N1 and the extension rate is described by the extensional viscosity ηE: N1 = ηE
. For non-Newtonian liquids, N1 usually cannot be derived from η and the behavior in extension has to be characterized independently. Generally, the relation between N1 and the extension rate is described by the extensional viscosity ηE: N1 = ηE![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) and ηE will often be dependent on
and ηE will often be dependent on ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) .25,26
.25,26
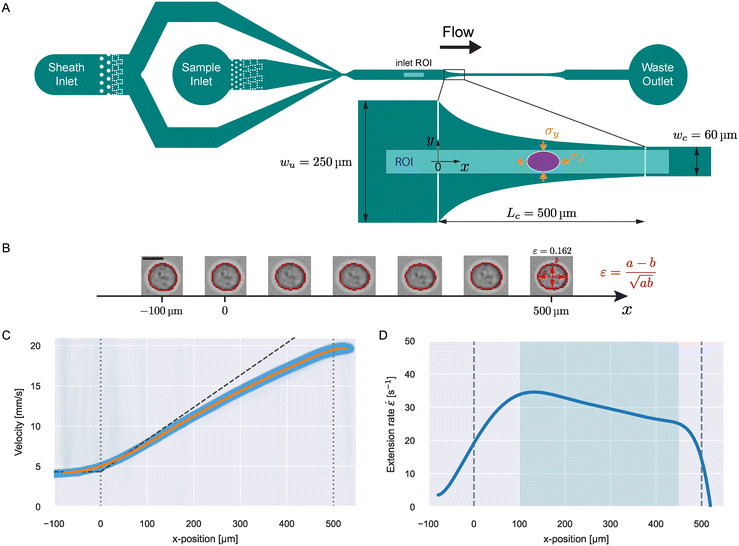 | ||
| Fig. 1 Microfluidic channel design and measurement principle. A) Full design of the microfluidic channel with magnified illustration of the hyperbolic region. The ellipse represents a deformed particle and the stresses in x and y are depicted. The shaded region indicates the ROI for a viscoelasticity measurement in the hyperbolic region. The inlet ROI shown in the full design indicates the region for inlet measurements to correct for optical distortions (see ESI†). B) Trajectory of an exemplary HL60 cell flowing through the hyperbolic region. The detected contours are shown in red. Scale bar represents 10 μm. At the contour of the right-most cell, the strain calculation is explained. C) Velocity trajectories as function of x for single 370 Pa PAAm beads (blue lines) at 0.02 μL s−1 flow rate. The orange line shows a polynomial fit to the data. The dashed, dark-gray line illustrates the theoretical velocity curve predicted by eqn (14). D) Extension rate of the fitted velocity curve in C as function of x. The shaded region highlights the zone of stable extension rate. | ||
For this stress definition, we can define a corresponding net strain as:
| ε = εx − εy. | (4) |
We define the strain in x and y by the deviation of the contour from the initial sphere radius R0:
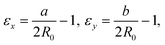 | (5) |
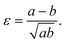 | (6) |
Deformation of liquid droplets in extensional flow
The deformation of a liquid droplet flowing in an extensional field with interfacial tension, γ, droplet viscosity, ηdrop, and viscosity of the carrier solution, η0, is well described in the literature.32,33,36 Here, we use the derivations from Cabral and Hudson to compute γ and ηdrop from the droplet deformation and extension rate.36The droplet deformation is defined by the Taylor deformation:32
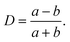 | (7) |
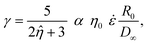 | (8) |
![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) = ηdrop/η0, and the effective viscosity αη0 with:
= ηdrop/η0, and the effective viscosity αη0 with: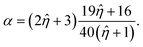 | (9) |
| D(t) = D0e−t/τ, | (10) |
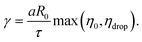 | (11) |
Kelvin–Voigt model analysis
We characterized the viscoelasticity of microgel beads and cells using the Kelvin–Voigt material model: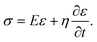 | (12) |
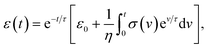 | (13) |
Materials and methods
Microfluidic chip design
The entire chip geometry is shown in Fig. 1A. Flow is introduced via FEP-tubing into the sheath and sample inlet. The sample particles are only delivered to the channel through the sample inlet and the sheath only contains the carrier solution. At the point where sheath and sample flow meet, the sample particles get focused into the channel center before the measurement region (shown as zoomed-in inset). The dotted structures after the inlets show filter pillars that prevent large particles or particle aggregates from clogging or contaminating the measurement region.After sheath focusing, the channel continues straight for 2.4 mm. This was introduced to give particles enough time (several seconds depending on flow rate) to relax from the deformation that is induced by the sheath focusing before reaching the measurement region. The channel height of all chips used for this study was 30 μm. This height was chosen to ensure cells with an approximate diameter of 15 μm will be focused at the flow centerline. For higher channels, cells would take up a lateral equilibrium position off the centerline.37,38
The measurement region, also called hyperbolic region, was designed to ensure a linear increase of the centerline velocity along the x-axis. The centerline velocity, u0, was computed with the following equation:39
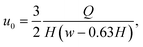 | (14) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , w(x) must be constructed such that ∂u0/∂x =
, w(x) must be constructed such that ∂u0/∂x = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = const. This leads to the following equation for the channel width in the hyperbolic region:
= const. This leads to the following equation for the channel width in the hyperbolic region: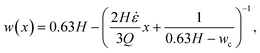 | (15) |
A channel geometry is fully defined by the upper contraction width, wu, lower contraction width, wc, and contraction length, Lc The measures relate to the flow parameters with the following relation (see ESI† text):
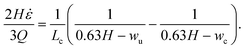 | (16) |
The extension rates for the sample was computed from the fitted velocity curve and is shown in Fig. 1D.
After the hyperbolic contraction, the channel continues straight for about 2 mm to observe the relaxation from the previous stress. Before the waste outlet, an expansion region mirroring the hyperbolic contraction was added to observe objects in expansion. We provide the mask for our chip design in the ESI.†
Device fabrication
Microfluidic chips were produced using standard soft lithography methods with polydimethylsiloxane (PDMS). To produce the master mold, a 30 μm-thick layer of AZ® 15nXT (450 CPS) photoresist (MicroChemicals GmbH, Germany) was spin-coated onto a 4-inch silicon wafer (2000 rpm, 5000 rpm s−1, for 2.8 s) using a spin coater (WS-650Mz-23NPP, Laurell, USA) and soft-baked at 110 °C for 3 minutes. The chip design, depicted on a chromium photomask, was transferred on the coated substrate via UV exposure at 600 mJ cm−2 (MA6 Gen4, Suess MicroTec GmbH, Germany), followed by a post-baking at 120 °C for 1 minute and development in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 dilute solution of AZ® 400 K developer (MicroChemicals GmbH, Germany) in deionized water for 150 seconds. The final master mold received a hydrophobic coating through vapor deposition of 1H,1H,2H,2H-perfluorooctyl-trichlorosilane (Sigma-Aldrich 448931, CAS 78560-45-9) in a vacuum desiccator for 1 day, facilitating the easy peel-off of replicas during replica molding. PDMS (base to curing agent ratio of 10
3 dilute solution of AZ® 400 K developer (MicroChemicals GmbH, Germany) in deionized water for 150 seconds. The final master mold received a hydrophobic coating through vapor deposition of 1H,1H,2H,2H-perfluorooctyl-trichlorosilane (Sigma-Aldrich 448931, CAS 78560-45-9) in a vacuum desiccator for 1 day, facilitating the easy peel-off of replicas during replica molding. PDMS (base to curing agent ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w; VWR 634165S, SYLGARD 184) was poured over the master, degassed, and cured at 78 °C for 1 hour and 15 minutes. Following the cutting of the chips and the creation of 1.5 mm inlet and outlet holes, the PDMS replica was bonded to a glass cover slip (40 × 24 mm2, thickness 2, Hecht, Germany) through an air plasma treatment (Plasma system Atto, Diener Electronic, Germany) at 75 W for 2 min, 20 sccm air flow and 0.4 mbar pressure.
1 w/w; VWR 634165S, SYLGARD 184) was poured over the master, degassed, and cured at 78 °C for 1 hour and 15 minutes. Following the cutting of the chips and the creation of 1.5 mm inlet and outlet holes, the PDMS replica was bonded to a glass cover slip (40 × 24 mm2, thickness 2, Hecht, Germany) through an air plasma treatment (Plasma system Atto, Diener Electronic, Germany) at 75 W for 2 min, 20 sccm air flow and 0.4 mbar pressure.
Production of carrier media
Measurements on oil droplets were performed by dispersing the concentrated droplet solution into a mixture of 83.8 v/v% glycerol (Sigma-Aldrich G5516, CAS 56-81-5) with water. This concentration of glycerol corresponds to a dynamic viscosity of 100 mPa s at 25 °C.41,42Before measurements, cells and beads were suspended into a 0.6 w/w% solution of methyl cellulose (MC) (4000 cPs, Alfa Aesar 036718.22, CAS 9004-67-5) dissolved in phosphate buffered saline (PBS) (Gibco Dulbecco 14190144) following the protocol of Büyükurgancı et al.16,24 The osmolality of PBS was adjusted to values between 280–290 mOsm kg−1 before the addition of MC (VAPRO Vapor Pressure Osmometer 5600, Wescor, USA). To prepare MC–PBS solutions for 1 L of PBS (1010 g), 6.00 g MC powder were utilized, resulting in a 0.594 w/w% MC concentration in the final solution. Following the addition of the powder, the mixtures were maintained at 4 °C under continuous rotation for two days to allow for the dissolution of MC. This process involved placing a rotating mixer (RS-TR05, Phoenix Instrument) in a high-performance pharmacy refrigerator (TSX Series, Thermo Fisher Scientific), with the bottles containing the MC–PBS solution rotating inside. Subsequently, the pH value was adjusted to 7.4 (Orion Star A211 benchtop pH meter, Thermo Scientific) by the addition of NaOH. In the next step, the solutions were sterile-filtered using membrane filters (Merck Millipore Steritop-GP polyethersulfone (PES) membrane, 0.22 μm pore size). The buffer solutions were then stored at 4 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times the desired concentration, ensuring an equivalent DMSO concentration in all treatments (0.01 v/v%). Subsequently, LatB was diluted by a factor of 10
000 times the desired concentration, ensuring an equivalent DMSO concentration in all treatments (0.01 v/v%). Subsequently, LatB was diluted by a factor of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in a 0.6 w% MC–PBS buffer, resulting in final LatB concentrations of 0.1, 1, 5, 10, 25, 50, 100, and 250 nM. The same approach was used for nocodazole (Sigma-Aldrich SML1665, CAS 31430-18-9) to get a final concentration of 1 μM.
000 in a 0.6 w% MC–PBS buffer, resulting in final LatB concentrations of 0.1, 1, 5, 10, 25, 50, 100, and 250 nM. The same approach was used for nocodazole (Sigma-Aldrich SML1665, CAS 31430-18-9) to get a final concentration of 1 μM.
Production of PAAm-microgel beads
PAAm beads were produced according to the protocol introduced by Girardo et al.29 Briefly, a PDMS-based flow-focusing microfluidic chip was used to produce polyacrylamide pre-gel droplets in fluorinated oil (3 M™ Novec™ 7500, Iolitec Ionic Liquids Technologies GmbH, Germany). The fluorinated oil contained ammonium Krytox® surfactant (2.4 w/v%) as the emulsion stabilizer and 0.4 v/v% N,N,N′,N′-tetramethylethylenediamine (TEMED) (Sigma-Aldrich T9281, CAS 110-18-9) as the catalyst. The pre-gel mixture contained acrylamide (40 w/v%) (Sigma-Aldrich A8887) as the monomer, bis-acrylamide (2 w/v%) (Sigma-Aldrich 146072) as the crosslinker, and ammonium persulphate (0.05 w/v%) (Cytiva GE17-1311-01) as the free radical initiator, diluted in 10 mM Tris buffer (pH = 7.48). The total monomer concentration, %cT, in the pre-gel mixture together with the droplet diameter was fine-tuned to obtain beads with precise diameter and elasticity within the desired range. After in-drop polymerization at 65 °C, the beads were washed and resuspended in 1 × PBS (pH = 7.4, Gibco), and ultimately stored at 4 °C.A list of the PAAm beads used in this study is reported with both their total monomer concentration (%cT), mean diameter, and Young's modulus in Table S1.† The Young's modulus of the beads was measured with real-time deformability cytometry (RT-DC, see ESI† text).16,19,24
Production of silicone oil droplets
The same chip design and setup employed in the PAAm bead production was also used for generating silicone oil droplets. This process involved a PDMS-based chip with a channel height of 14 μm and channel width of 15 μm at the cross junction. Before starting the droplet production, the microfluidic chips underwent a treatment by an air plasma (Plasma system Atto, Diener Electronic, Germany) at 75 W for 4 min, 20 sccm air flow and 0.4 mbar pressure. This treatment rendered the surface of the PDMS channel walls hydrophilic, a crucial step to enable on-chip production of an oil-in-water microemulsion.43Two distinct types of droplets were generated using two silicone oils with kinematic viscosities of 500 and 1000 cSt (Sigma-Aldrich 378380 & 378399, CAS 63148-62-9) as the dispersed phase. The continuous phase was a aqueous solution of 2 v/v% poly(ethylene glycol)monooleate (Sigma-Aldrich 460176, CAS 9004-96-0) used as a emulsifier.
Droplets with a kinematic viscosity of 500 cSt were produced under a set pressure of 480 mbar for the continuous phase and 310 mbar for the dispersed phase, resulting in droplets with an average diameter of 16 μm at a production rate of 13.5 Hz. In the case of 1000 cSt droplets, both the continuous and dispersed phases were pressurized at 400 mbar, resulting in droplets with an average diameter of 15.5 μm at a rate of 27 Hz. Droplets were collected inside a 15 mL Falcon tube.
Cell culture
The HL60/S4 cell subline (ATCC Cat# CRL-3306, RRID:CV-CL_II77) was cultured in RPMI 1640 medium with 2 mM L-glutamine (Thermo Fisher #A1049101) with 1% penicillin and streptomycin (Gibco) and 10% heat-inactivated fetal bovine serum (Sigma Aldrich F4135, lot no. 13C519). Cells were grown at 37 °C, with 5% CO2, at densities between 105–106 cells per mL with subculturing every 48–72 hours. Cells used for experiments originated all from the same frozen batch after thawing and were measured in 14–26 passages after initial seeding.Experimental protocol
Measurements were performed using an AcCellerator device with temperature control (Zellmechanik Dresden GmbH, Germany). This device offers high-speed imaging with online contour analysis through the software ShapeIn 2 (Zellmechanik Dresden). All measurements were performed at a chamber temperature of 25 ± 0.5 °C.For a measurement, the microfluidic chip was placed on the stage of an inverted microscope (Axio Observer Z1, Zeiss, Germany) and flow was introduced using syringe pumps (neMESyS 290 N, Cetoni GmbH, Germany) connected to the chip with FEP tubing (0.0625′′ OD, 0.03′′ ID; no. 1520XL, Postnova Analytics). The sheath to sample flow rate ratio was 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for oil droplet experiments and 3
1 for oil droplet experiments and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for all other measurements.
1 for all other measurements.
Imaging was done with a pulsed, high power, blue LED (Zellmechanik Dresden) that was synchronized to a CMOS camera (EoSens CL, MC1362, Mikrotron GmbH, Germany). Experiments for the viscoelasticity of PAAm beads, oil droplets and HL60 cells were imaged through a 20× objective (Plan-Apochromat, ×20/0.8; no. 420650-9902, Zeiss). To measure the stresses acting in the channel based on PAAm bead deformation (see Fig. 2), we used a 40× objective (EC-Plan-Neofluar, ×40/0.75; no. 420360-9900, Zeiss).
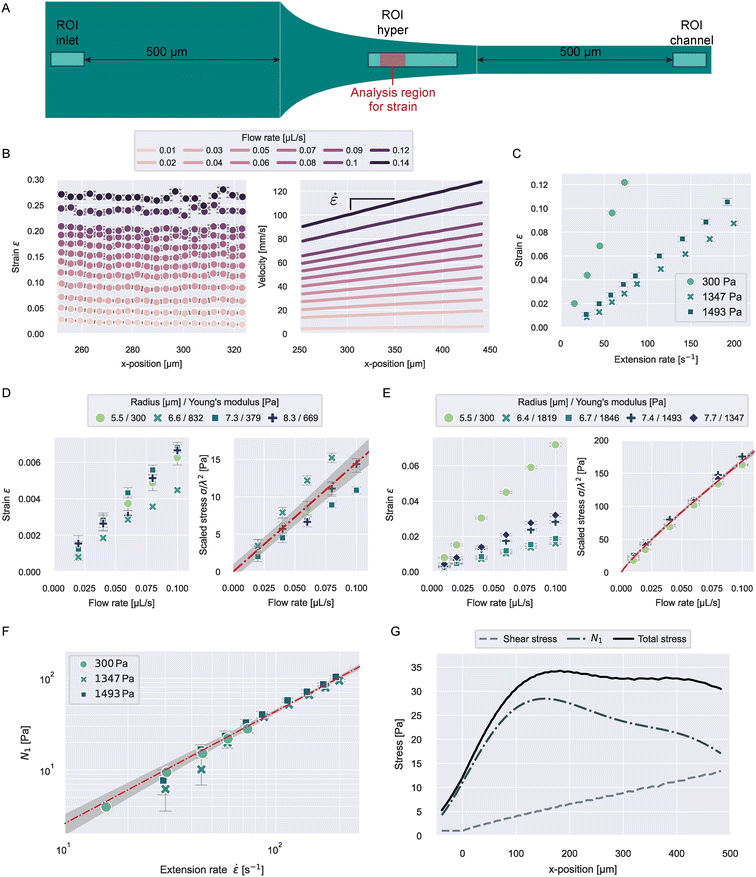 | ||
Fig. 2 Stress characterization of 0.6 w% MC–PBS in the hyperbolic region. A) ROIs for the different stress measurements. The red region in ROI hyper represents the analysis window for the strain data shown in B. B) Strain and velocities of 300 Pa PAAm beads in ROI hyper at different flow rates. Data points represent the median values of all beads in the measurement at the respective x-position. Error bars in all panels indicate standard error of the mean (SEM) C) median strain of PAAm beads with varying stiffness as function of extension rate in the strain analysis region. D) Median strain and apparent shear stress scaled by bead size for different beads in ROI inlet. The line in the scaled stress plot shows a linear fit to the data with 2-σ error band (eqn (23)). E) Median strain and apparent shear stress scaled by bead size for different beads in ROI channel. The line in the scaled stress plot shows a power law fit to the data with 2-σ error band (eqn (24)). F) First normal stress difference N1 (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) for different beads measured in ROI hyper. The line shows a linear fit to the data with 2-σ error band (eqn (27)). G) Shear stress, first normal stress difference, and total stress, calculated from the median extension rate curves with eqn (25), (27), and (28), for 832 Pa PAAm beads flowing through the hyperbolic region (see Fig. 1A) at a flow rate of 0.04 μL s−1. ) for different beads measured in ROI hyper. The line shows a linear fit to the data with 2-σ error band (eqn (27)). G) Shear stress, first normal stress difference, and total stress, calculated from the median extension rate curves with eqn (25), (27), and (28), for 832 Pa PAAm beads flowing through the hyperbolic region (see Fig. 1A) at a flow rate of 0.04 μL s−1. | ||
Tubings for sheath and sample were filled with the respective carrier solution at 0.1 μL s−1 before connecting to the chip and then chips were filled through the sheath inlet using the syringe pump until liquid was pushed out of the sample inlet. Sample suspensions were loaded into the tubing by placing the tubing inside the suspension and setting a negative flow rate of −2 μL s−1 for the sample. The filled chip was then connected to the filled sample tubing to avoid the introduction of air bubbles into the chip. The samples were pushed into the chip at a flow rate of 0.1 μL s−1 before setting the measurement flow rate.
Data acquisition
Data was recorded using the program ShapeIn 2 (Zellmechanik Dresden). The program analyses the images in real-time by finding a contour based on background subtraction and thresholding.16 A number of contour and brightness features are extracted from the image and saved to an hdf5 file.For a viscoelasticity experiment in the hyperbolic region, objects were recorded in a 680 × 54 μm region of interest (ROI, see Fig. 1A), imaged through the 20× objective. The border of the ROI was placed 50 μm after the end of the hyperbolic region (x = Lc + 50 μm). The frame rate was adjusted according to the flow rate to capture about 50 events per object flowing through the ROI.
PAAm beads and silicone oil droplets showed optical distortions dependent on the position in the ROI. To correct for these effects, we measured each sample 500 μm before the hyperbolic region with an ROI of 680 × 102 μm at a flow rate of 0.01 μL s−1 (see inlet ROI in Fig. 1A). In this region, no extensional field is present and at this flow rate, the influence of shear stresses is negligible. The measured deviations in the deformation can be attributed to optical distortions in the setup. The correction curves are shown in Fig. S4–S6.†
Data analysis
The full analysis pipeline is documented at https://gitlab.gwdg.de/cell-viscoelasticity-in-hyperbolic-channels.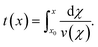 | (17) |
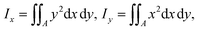 | (18) |
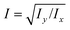 is readily available as a feature in the measurement hdf5 files and known as the inertia ratio. For a perfect ellipse or rectangle, I is equal to the aspect ratio of the contour. The strain definition in eqn (6) can then be rewritten using the inertia ratio:
is readily available as a feature in the measurement hdf5 files and known as the inertia ratio. For a perfect ellipse or rectangle, I is equal to the aspect ratio of the contour. The strain definition in eqn (6) can then be rewritten using the inertia ratio: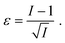 | (19) |
Results and discussion
Characterizing stresses in the hyperbolic region
The first normal stress differences of 0.6 w% MC–PBS in extensional flow were not reported before. We measured the stresses acting in the hyperbolic region using PAAm microgel beads. The Young's modulus, E, of the beads was measured using RT-DC (see ESI† text and Fig. S1). The stress was then deducted from the strain measured in the hyperbolic region:| σ = Eε. | (20) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , beads were measured at different flow rates and the ROI was placed 225 μm after the start of the hyperbolic region (see “ROI hyper” in Fig. 2A). The ROI was chosen to ensure beads were measured at a constant extension rate and had enough time to comply to the acting stress. The relaxation time of the beads was reported before at around 0.1 ms,29 allowing them to fully deform during the several milliseconds they spend in the ROI.
, beads were measured at different flow rates and the ROI was placed 225 μm after the start of the hyperbolic region (see “ROI hyper” in Fig. 2A). The ROI was chosen to ensure beads were measured at a constant extension rate and had enough time to comply to the acting stress. The relaxation time of the beads was reported before at around 0.1 ms,29 allowing them to fully deform during the several milliseconds they spend in the ROI.
Fig. 2B shows the median strain and velocity curves of beads with E = 300 Pa. Medians were computed from all beads at a respective x-position for all flow rates and each curve represents 400–2400 beads (more beads at higher flow rates). We report the number of beads included at every flow condition in Tables S2 and S3.†
As discussed below, the velocity gradient between top and bottom wall causes shear stresses on the beads. The influence of these shear stresses on bead deformation increases with velocity and during flow through the hyperbolic region. To keep the influence of shear stresses on the bead deformation as small as possible when getting closer to x = Lc, the analysis region was restricted to 250 < x < 325 μm. It can be seen that the strain is constant over x in the chosen analysis region for all flow rates, indicating the stress in the chosen ROI can be considered constant.
The velocity curves were analyzed from the full ROI width of 230 μm. In Fig. 2B we show the median velocities for 250 μm < x. The extension rates were computed from the slope of a linear fit to the velocity data.
The resulting median strains and extension rates for three bead types of different stiffness are shown in Fig. 2C. The further analysis was restricted to small strains with ε < 0.125 to stay within the linear elastic regime. For larger strains we observed deviations from linearity for the beads with E = 300 Pa (see Fig. S2E†). The strain values were corrected for influences of optical distortions from the instrument (see Fig. S2A and B†).
Typical object diameters for our experiments were in the range of 10–20 μm. At a channel height of 30 μm, the influence of shear stresses on the deformation cannot be neglected. To quantify this influence, we measured the deformation of the beads 500 μm before entering and after leaving the hyperbolic region (see “ROI inlet” and “ROI channel” in Fig. 2A). The resulting strains are shown in Fig. 2D and E and S2C and D.† The apparent shear stress, σs, can then be calculated similarly to eqn (20).
The shear stress on an object inside the channel is size-dependent because shear stresses increase closer to the channel walls. We found empirically that scaling the apparent stresses quadratically by size resulted in the datapoints collapsing on one line (see Fig. 2D and E). We performed the scaling with the confinement λ defined by:
 | (21) |
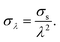 | (22) |
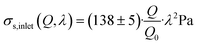 | (23) |
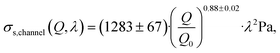 | (24) |
We assumed that the power law exponent presented in eqn (24) can be used to describe the relation of shear stresses and object velocity inside the hyperbolic region. Since the velocity increases approximately linear as a function of x, the apparent shear stress at any point x in the contraction can then be calculated with:
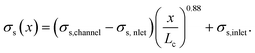 | (25) |
| N1 = Eε − σs. | (26) |
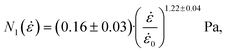 | (27) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0 = 1 s−1. A power law index greater than 1 describes strain-thickening behavior and is commonly observed for polymer solutions.26,31 It is noticeable that the extensional viscosity of the solution (see Fig. S3†) is much higher than the zero-shear viscosity, which is reported at 30 mPa s, highlighting the need for distinct measurements in extension to accurately determine the stresses exerted by MC-solutions, or polymer solutions in general.
0 = 1 s−1. A power law index greater than 1 describes strain-thickening behavior and is commonly observed for polymer solutions.26,31 It is noticeable that the extensional viscosity of the solution (see Fig. S3†) is much higher than the zero-shear viscosity, which is reported at 30 mPa s, highlighting the need for distinct measurements in extension to accurately determine the stresses exerted by MC-solutions, or polymer solutions in general.
Finally, the total stress on an object at any position x inside the hyperbolic region can be calculated from the extension rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) (x), the flow rate, and the confinement:
(x), the flow rate, and the confinement:
σtotal(x, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , Q, λ) = N1( , Q, λ) = N1(![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) + σs(x, Q, λ). ) + σs(x, Q, λ). | (28) |
Mechanics of silicone oil droplets
To verify that our approach is sensitive to detect different relaxation times, we measured silicone oil droplets with different viscosities. The lower viscosity droplets had a dynamic viscosity of 485 mPa s and the higher viscosity sample 970 mPa s, according to the manufacturer.Droplets were analyzed by the Taylor deformation as introduced in eqn (7). The full deformation and extension rate curves as function of x are shown in Fig. S4.† A stable extension rate was achieved after x0 = 110 μm. The droplet deformation was analyzed in the range 110 μm < x < 390 μm. The upper limit for x was chosen to avoid strong effects of the shear stress influencing the deformation. The resulting Taylor deformations as a function of time, where t(x0) = 0, are shown in Fig. 3.
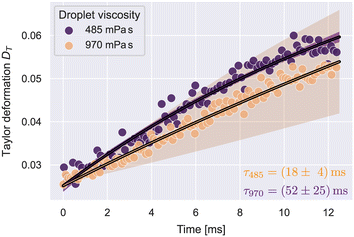 | ||
| Fig. 3 Taylor deformation vs. time for silicone oil droplets at the stable extension rate. The solid lines illustrate fit curves of eqn (29) to the datapoints. Shaded regions show the 2-σ error band of the fit data. The number of droplets N per condition was: N485 = 90, N970 = 421. | ||
According to eqn (10), the data follows an exponential and will equilibrate at D∞. At t = 0, the data shows a pre-deformation D0 caused by stresses acting on the droplets before reaching x0. With these, the deformation curve will have the form:
| DT(t) = D∞(1 − e−t/τ) + D0e−t/τ. | (29) |
Utilizing the analysis in eqn (8)–(11), we determined the interfacial tensions and viscosities of the droplet systems. For this, the extension rate was taken as a constant average, calculated from all datapoints in the analysis region. For the 485 mPa s droplets, we got an interfacial tension of γ = 1.0 ± 0.1 mN m−1 and the viscosity ηdrop = 552 ± 73 mPa s, which resulted in the expected viscosity of the silicone oil, within error margins. For 970 mPa s droplets we got γ = 0.6 ± 0.2 mN m−1 and ηdrop = 711 ± 212 mPa s. The deviation of the resulting viscosity from the expected value can be explained by the large uncertainty of the relaxation time.
Both emulsified droplet systems showed a small interfacial tension of around 1 mN m−1. Similar values for such interfaces have been reported before.45
Viscoelasticity of PAAm-microgel beads
The strain curves of PAAm-microgel beads with Young's moduli of 379, 669, and 832 Pa were measured at flow rates from 0.04–0.10 μL s−1 and analyzed for their viscoelastic behavior with the Kelvin–Voigt model explained in eqn (13). Object times were calculated in reference to x0 = −40 μm. The analysis was restricted to values for −40 μm < x < 490 μm. Strain curves were corrected for optical distortions as shown in Fig. S5A.† An example stress and strain curve as function of time with Kelvin–Voigt fit for 669 Pa beads at 0.04 μL s−1 is shown in Fig. 4A. The data for all conditions are shown in Fig. S5B.†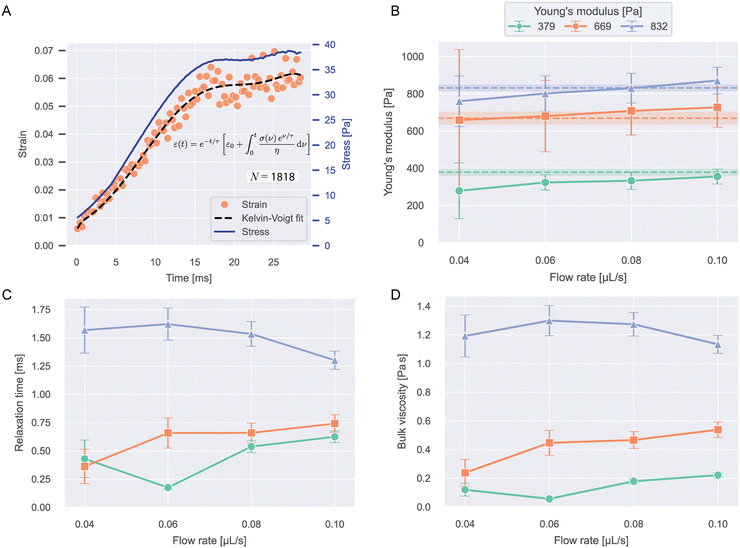 | ||
| Fig. 4 Viscoelasticity of PAAm microgel beads. A) Median strains over time and stress curve for 669 Pa beads at 0.04 μL s−1 flow rate. The dashed line shows the Kelvin–Voigt fit to the datapoints (eqn (13)). N indicates the number of beads included in the plot. B) Young's moduli resulting from the Kelvin–Voigt fit for different flow rates and bead types. Values show fit result ± standard error of the fit. The dashed lines and shaded regions correspond to the respective mean ± SEM Young's modulus measured with RT-DC (see Fig. S1†). C) Relaxation times and D) bulk viscosities of the beads resulting from the fit. | ||
Fig. 4B–D shows the Young's moduli, relaxation times and bulk viscosities resulting from the fit. The error bars indicate standard errors of the fit.
Young's moduli showed a slight increase with flow rate for all bead types and within error margins, the expected values for all conditions could be recaptured, showing that our approach is able to accurately measure object stiffness. Relaxation times were longer for stiffer beads and showed no clear trend with flow rate. The bulk viscosities followed the same trend as the relaxation times.
With relaxation times on the scale of milliseconds, the beads deform almost instantaneously, which can be seen when comparing the strain and stress curves. This implies near-elastic behavior, which is expected for microgels at these timescales.10,29
Viscoelasticity of HL60 cells after LatB and nocodazole treatment
To investigate how actin is contributing to the viscoelastic properties of HL60 cells, we treated the cells with latrunculin B (LatB) at concentrations between 0–250 nM dissolved in the 0.6 w% MC–PBS solution. LatB is known to induce cell softening by inhibiting the polymerization of F-actin.15,46,47Object times were calculated in reference to x0 = −50 μm. The analysis was restricted to values for −50 μm < x < 480 μm. Cells were measured at flow rates 0.01, 0.02, and 0.04 μL s−1 and biological triplicates from different culturing passages were measured for every concentration.
In contrast to beads and oil droplets, the cells showed no position-dependent deformation in the inlet but constant strain offsets, that could not be explained solely by the influence of the shear stress (see Fig. S6†). To account for this offset, we modified eqn (13) by addition of a constant strain offset, εoffset:
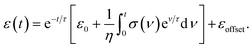 | (30) |
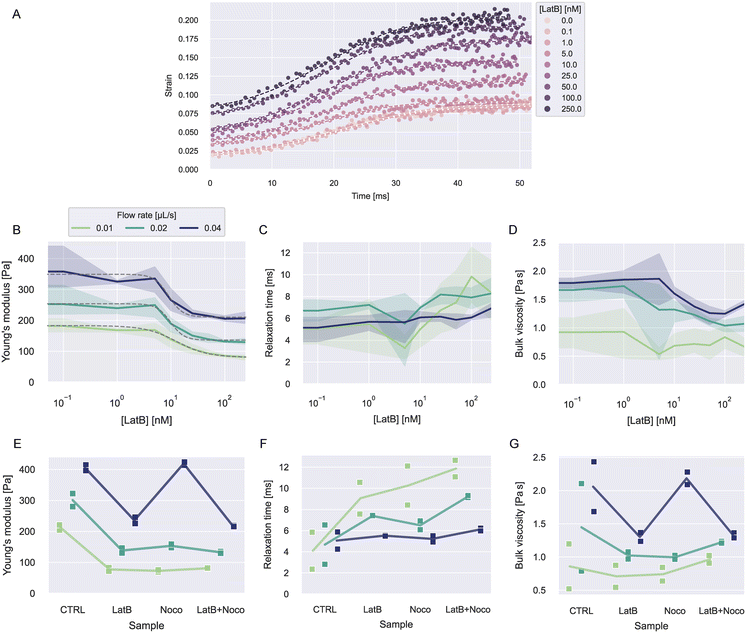 | ||
| Fig. 5 Viscoelasticity of HL60 cells treated with LatB and nocodazole. A) Exemplary strain curves over time and fit curves at different LatB concentration for one experiment date at flow rate 0.02 μL s−1. B–D) Young's moduli, relaxation times, and viscosities dependent on LatB concentration at different flow rates. The solid lines represent the mean value at each concentration and the error bands represent the full range of datapoints. The dashed gray lines in B show fits of a log-logistic growth function to the data (see ESI† text). E–G) Young's moduli, relaxation times, and viscosities for LatB, nocodazole or combined LatB + nocodazole treatment. The solid lines represent the mean of the measurements at each condition. | ||
Fig. 5B–C shows the resulting viscoelastic parameters. The Young's moduli at all flow rates showed a decrease with increasing LatB concentration that followed a log-logistic growth function (see ESI† text and Table S4). This behavior has been described before for latrunculin-treated cells.3,15 Young's moduli increased with increasing flow rate for all concentrations. The apparent increase of elastic moduli of other cell types when measured at faster time scales is widely described in the literature.3,21,23
Relaxation times showed a slight increase with LatB concentration. The relaxation times vary in a range of about 2–12 ms. Similar values have been reported using other microfluidic techniques.5,23 The resulting bulk viscosities showed similar behavior to the Young's modulus, because the relaxation times only show small changes in comparison.
To investigate how microtubuli contribute to the viscoelastic properties, we treated the cells with nocodazole to disrupt the microtubuli polymerization. We used a concentration of 1 μM nocodazole dissolved in 0.6 w% MC–PBS. Additionally, we treated cells at 250 nM LatB and a combination of both treatments. We performed measurements on biological duplicates from different passages for these treatments.
The resulting strain, stress, and fit curves are shown in Fig. S8† and the viscoelastic parameters are shown Fig. 5E–G. Information on the number of cells analyzed for every condition is reported in Tables S5 and S6.† We would like to point out that the LatB data in these results comes from different experiments than the data shown in Fig. 5B–D. It can be seen that nocodazole in addition to LatB had nearly no further influence on the cells' Young's modulus. Treatment with nocodazole alone had a similar effect as LatB when measured at 0.01 and 0.02 μL s−1 but at a flow rate of 0.04 μL s−1, the cells even showed a slight increase of the Young's modulus.
The treatment effect on the relaxation times was flow rate-dependent. At 0.01 μL s−1, the three treatments showed a similar increase in the relaxation time compared to the control condition. The combined treatment with LatB and nocodazole led to the largest increase of relaxation times. At 0.02 μL s−1, this effect was less pronounced and at 0.04 μL s−1 the treatment had nearly no influence on the relaxation times.
The bulk viscosities showed no clear trend with the treatments. For 0.01 and 0.02 μL s−1, the treatments led to a reduction of the mean viscosity but the spread in the data was too large to make definite statements. At 0.04 μL s−1, the viscosity followed the behavior of the Young's modulus, as the relaxation time was hardly affected by the treatments.
Discussion
Our platform was well-suited for accurately measuring the stresses applied by 0.6 w% MC–PBS in extensional flow. We observed strain-thickening following a power law up to an extension rate of 200 s−1. Notably, the extensional viscosities measured were more than 10 times larger than shear viscosities at comparable shear rates. This emphasizes the necessity to independently assess the stresses exerted by polymer solutions in extensional flow, separate from shear stresses.25,26Measurements on silicone oil droplets showcased the platform's sensitivity to changes in relaxation times, allowing for the determination of interfacial tension and droplet viscosities. Challenges were encountered in accurately determining viscosity for droplets with high viscosity due to observation time limitations. This emphasizes the importance of carefully choosing flow rates to guarantee enough time for deformation.
In experiments on PAAm beads, our platform effectively recaptured expected Young's moduli. The rapid adaptation of strain to stress curves in beads suggested near-elastic behavior. We observed that stiffer beads had longer relaxation times. This behavior was rather unexpected for deformable particles, where higher stiffness often leads to faster relaxation.21 A possible explanation for this effect could be the poroelastic nature of the PAAm microgel.10,29,48 Stiffer beads are made of a more densely connected polymer network, leading to smaller pores. Smaller pores cause a smaller permeability of the material for fluid flow. This increased resistance for fluids to move through the microgels could lead to longer relaxation times.10
A viscoelastic response of the microgel can also be influenced by rearrangements of polymers chains or cross-links in the network. This would normally not be expected for PAAm hydrogels but defects in the bead production can lead to such rearrangements when stress is applied.29
We observed a slightly increasing Young's modulus with flow rate of the PAAm beads. A possible explanation could be that the strains induced were outside the linear-elastic regime, which in turn leads to an apparent stiffening at higher strains/flow rates.
Examining HL60 cell behavior under LatB treatment revealed a decrease of the Young's modulus with increasing LatB concentration, consistent with prior studies.3,15,46,47 Intriguingly, at higher flow rates, cells exhibited increased stiffness irrespective of LatB concentration, suggesting an actin-independent effect. Similar stiffening effects were observed with additional nocodazole treatment.
Higher elastic moduli in measurements at shorter time scales or under greater stresses have been reported previously.3,21,49 Another possible explanation for our observation is that cells do not behave as linear elastic materials but rather follow a hyperelastic model.19,50 This can lead to an overestimation of the stiffness at larger deformations for our analysis.
Nocodazole treatment led to a decrease in Young's modulus at slower flow rates and a slight increase at the highest flow rate. The literature is not clear on the effect of nocodazole on cell stiffness: Golfier et al. reported on reduced cell deformability with nocodazole treatment, while Liu et al. reported an increase.47,51 Besides inducing microtubuli disassembly, nocodazole is known to increase cell contractility by releasing GEF-H1 from microtubuli, which consequently leads to RhoA and Rock activation and the formation of actin stress fibers.52 This can lead to stiffening of cells besides the depletion of microtubuli. Our results suggest that this interplay of microtubule disassembly and increased cell contractility might have time scale dependent effects on cell stiffness.
The effect of LatB and/or nocodazole treatment on relaxation times was most pronounced at slower flow rates. Cells are known to exhibit more fluid-like behavior when deformed over a longer time scale.4,21,49,53 At slower flow rates, the cells have more time to adapt to the stress in the channel. The viscous properties only become apparent when cells get stretched over a longer period. This highlights that flow rates need to be chosen carefully to reveal the viscous properties of cells.
Furthermore, the observed relaxation times were close to the values of PAAm beads, highlighting a close to elastic behavior of the cells when measured at millisecond time scales in the hyperbolic channels.
Conclusions
Our microfluidic platform, tailored for high-throughput viscoelastic characterization at up to 100 cells per second, has provided profound insights into the behaviors of complex fluid systems and soft deformable particles.Experiments on droplets, PAAm microgel beads and HL60 cells showed that our platform is sensitive to changes in material stiffness and relaxation times. To investigate the influence of filamentous actin and microtubuli on cell viscoelastic properties, we treated HL60 cells with latrunculin B, nocodazole, or both. Our results highlight that the measurement time scales affect the viscoelastic response to the treatments.
Our current analysis requires a cautious estimation of shear and tensile stresses acting in the microchannel. The influence of shear stresses, mainly resulting from the velocity profile between bottom and top wall in the channel, could be minimized by increasing the height of the channels. This would require an additional focusing step to focus the cells in the center of the channel height.54
Furthermore, the channel profile could be improved to have a better-defined development of the extension rate and a true constant extension rate in the hyperbolic region.55 This would help to get simpler stress estimates in the hyperbolic region and would lead to more straight-forward approaches for analyzing the stress–strain relationship.
Our results illustrate the great potential of hyperbolic microchannel systems for high-throughput measurements of single cell viscoelasticity with a wide range of applications in cell research or diagnostics.
Data availability
Data and analysis scripts to recreate the results presented here can be found at gitlab: https://gitlab.gwdg.de/cell-viscoelasticity-in-hyperbolic-channels. (Persistent identifier (PID): 21.11101/0000-0007-FC23-6; see https://www.pidconsortium.net).Author contributions
Conceptualization: FR, JG; data curation: FR; formal analysis: FR; investigation: FR, methodology: FR, RG, SG; project administration: JG; resources: RG, SG, JG; software: FR; supervision: SG, JG; validation: FR; visualization: FR; funding acquisition: SG, JG; writing – original draft: FR; writing – editing and review: all authors.Conflicts of interest
SG and JG are co-founders of the company Rivercyte GmbH, which offers commercial products and consumables related to deformability cytometry. The other authors declare no conflicts of interest.Acknowledgements
We want to thank Benedikt Hartmann, Shada Abuhattum, and Sebastian Bohle for helpful discussion regarding this study. Additional thanks to Benedikt Hartmann and Eoghan O'Connel for help with dctrack. Special regards to Cornelia Liebers, Manuela Hauke and Christine Schweitzer for taking care of cell culture. Further thanks to Cornelia Liebers for help with production of the MC–PBS solutions. We want to thank Parth Patel, who produced the microfluidic chips for this work. We would like to acknowledge the assistance of ChatGPT3.5, a language model developed by OpenAI, in refining the language of this article. The authors acknowledge the financial support through the base funding of the Max Planck Society to JG. RG and SG receive funding from the European Unions Horizon 2020 research and innovation programs No. 953121 (project FLAMIN-GO). Open Access funding provided by the Max Planck Society.Notes and references
- A. Zak, S. V. Merino-Cortés, A. Sadoun, F. Mustapha, A. Babataheri, S. Dogniaux, S. Dupré-Crochet, E. Hudik, H.-T. He, A. I. Barakat, Y. R. Carrasco, Y. Hamon, P.-H. Puech, C. Hivroz, O. Nüsse and J. Husson, Biophys. J., 2021, 120, 1692–1704 CrossRef CAS PubMed.
- Y. Abidine, A. Giannetti, J. Revilloud, V. M. Laurent and C. Verdier, Cell, 2021, 10, 1704 CrossRef CAS PubMed.
- R. Gerum, E. Mirzahossein, M. Eroles, J. Elsterer, A. Mainka, A. Bauer, S. Sonntag, A. Winterl, J. Bartl, L. Fischer, S. Abuhattum, R. Goswami, S. Girardo, J. Guck, S. Schrüfer, N. Ströhlein, M. Nosratlo, H. Herrmann, D. Schultheis, F. Rico, S. J. Müller, S. Gekle and B. Fabry, eLife, 2022, 11, e78823 CrossRef CAS PubMed.
- J. Dupire, P.-H. Puech, E. Helfer and A. Viallat, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14798–14804 CrossRef CAS PubMed.
- B. Fregin, F. Czerwinski, D. Biedenweg, S. Girardo, S. Gross, K. Aurich and O. Otto, Nat. Commun., 2019, 10, 415 CrossRef CAS PubMed.
- S. Abuhattum, P. Kotzbeck, R. Schlüßler, A. Harger, A. Ariza de Schellenberger, K. Kim, J.-C. Escolano, T. Müller, J. Braun, M. Wabitsch, M. Tschöp, I. Sack, M. Brankatschk, J. Guck, K. Stemmer and A. V. Taubenberger, Sci. Rep., 2022, 12, 10325 CrossRef CAS PubMed.
- R. M. Hochmuth, J. Biomech., 2000, 33, 15–22 CrossRef CAS PubMed.
- Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81 RSC.
- J. R. Staunton, B. L. Doss, S. Lindsay and R. Ros, Sci. Rep., 2016, 6, 19686 CrossRef CAS PubMed.
- S. Abuhattum, D. Mokbel, P. Müller, D. Soteriou, J. Guck and S. Aland, iScience, 2022, 25, 104016 CrossRef CAS PubMed.
- J. Guck, R. Ananthakrishnan, H. Mahmood, T. J. Moon, C. C. Cunningham and J. Käs, Biophys. J., 2001, 81, 767–784 CrossRef CAS PubMed.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan, D. Mitchell, J. Käs, S. Ulvick and C. Bilby, Biophys. J., 2005, 88, 3689–3698 CrossRef CAS PubMed.
- T. Fuhs, F. Wetzel, A. W. Fritsch, X. Li, R. Stange, S. Pawlizak, T. R. Kießling, E. Morawetz, S. Grosser, F. Sauer, J. Lippoldt, F. Renner, S. Friebe, M. Zink, K. Bendrat, J. Braun, M. H. Oktay, J. Condeelis, S. Briest, B. Wolf, L.-C. Horn, M. Höckel, B. Aktas, M. C. Marchetti, M. L. Manning, A. Niendorf, D. Bi and J. A. Käs, Nat. Phys., 2022, 18, 1510–1519 Search PubMed.
- C. Huster, D. Rekhade, A. Hausch, S. Ahmed, N. Hauck, J. Thiele, J. Guck, K. Kroy and G. Cojoc, New J. Phys., 2020, 22, 085003 CrossRef CAS.
- M. Urbanska, H. E. Muñoz, J. Shaw Bagnall, O. Otto, S. R. Manalis, D. Di Carlo and J. Guck, Nat. Methods, 2020, 17, 587–593 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Töpfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- D. R. Gossett, H. T. K. Tse, S. A. Lee, Y. Ying, A. G. Lindgren, O. O. Yang, J. Rao, A. T. Clark and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7630–7635 CrossRef CAS PubMed.
- L. D. Wittwer, F. Reichel and S. Aland, in Modeling of Mass Transport Processes in Biological Media, Elsevier, 2022, pp. 33–56 Search PubMed.
- L. D. Wittwer, F. Reichel, P. Müller, J. Guck and S. Aland, Soft Matter, 2023, 19, 2064–2073 RSC.
- S. Abuhattum, H.-S. Kuan, P. Müller, J. Guck and V. Zaburdaev, Biophys. Rep., 2022, 2, 100054 Search PubMed.
- P. Kollmannsberger and B. Fabry, Annu. Rev. Mater. Res., 2011, 41, 75–97 CrossRef CAS.
- M. Piergiovanni, V. Galli, G. Holzner, S. Stavrakis, A. DeMello and G. Dubini, Lab Chip, 2020, 20, 2539–2548 RSC.
- F. J. Armistead, J. Gala De Pablo, H. Gadêlha, S. A. Peyman and S. D. Evans, Biophys. J., 2019, 116, 1127–1135 CrossRef CAS PubMed.
- B. Büyükurgancı, S. K. Basu, M. Neuner, J. Guck, A. Wierschem and F. Reichel, Soft Matter, 2023, 19, 1739–1748 RSC.
- B. L. Micklavzina, A. E. Metaxas and C. S. Dutcher, Soft Matter, 2020, 16, 5273–5281 RSC.
- S. G. Kim, C. M. Ok and H. S. Lee, J. Rheol., 2018, 62, 1261–1270 CrossRef CAS.
- S. S. Lee, Y. Yim, K. H. Ahn and S. J. Lee, Biomed. Microdevices, 2009, 11, 1021–1027 CrossRef PubMed.
- V. Faustino, R. O. Rodrigues, D. Pinho, E. Costa, A. Santos-Silva, V. Miranda, J. S. Amaral and R. Lima, Micromachines, 2019, 10, 645 CrossRef PubMed.
- S. Girardo, N. Träber, K. Wagner, G. Cojoc, C. Herold, R. Goswami, R. Schlüßler, S. Abuhattum, A. Taubenberger, F. Reichel, D. Mokbel, M. Herbig, M. Schürmann, P. Müller, T. Heida, A. Jacobi, E. Ulbricht, J. Thiele, C. Werner and J. Guck, J. Mater. Chem. B, 2018, 6, 6245–6261 RSC.
- T. J. Ober, S. J. Haward, C. J. Pipe, J. Soulages and G. H. McKinley, Rheol. Acta, 2013, 52, 529–546 CrossRef CAS.
- C. W. Macosko, Rheology: Principles, Measurements, and Applications, Wiley-VCH Verlag, 1994 Search PubMed.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1934, 146, 501–523 CAS.
- J. M. Rallison, Annu. Rev. Fluid Mech., 1984, 16, 45–66 CrossRef.
- M. M. Villone, J. K. Nunes, Y. Li, H. A. Stone and P. L. Maffettone, Soft Matter, 2019, 15, 880–889 RSC.
- R. Roscoe, J. Fluid Mech., 1967, 28, 273–293 CrossRef.
- J. T. Cabral and S. D. Hudson, Lab Chip, 2006, 6, 427–436 RSC.
- Y.-S. Choi, K.-W. Seo and S.-J. Lee, Lab Chip, 2011, 11, 460–465 RSC.
- D. Di Carlo, J. F. Edd, K. J. Humphry, H. A. Stone and M. Toner, Phys. Rev. Lett., 2009, 102, 094503 CrossRef PubMed.
- H. Bruus, in Microscale Acoustofluidics, The Royal Society of Chemistry, 2014, pp. 1–28 Search PubMed.
- A. Mietke, O. Otto, S. Girardo, P. Rosendahl, A. Taubenberger, S. Golfier, E. Ulbricht, S. Aland, J. Guck and E. Fischer-Friedrich, Biophys. J., 2015, 109, 2023–2036 CrossRef CAS PubMed.
- N.-S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288 CrossRef CAS.
- A. Volk and C. J. Kähler, Exp. Fluids, 2018, 59, 75 CrossRef.
- S. C. Kim, D. J. Sukovich and A. R. Abate, Lab Chip, 2015, 15, 3163–3169 RSC.
- M. Herbig, M. Kräter, K. Plak, P. Müller, J. Guck and O. Otto, in Methods in Molecular Biology, Humana Press, New York, NY, 2018, vol. 1678, pp. 347–369 Search PubMed.
- P. Posocco, A. Perazzo, V. Preziosi, E. Laurini, S. Pricl and S. Guido, RSC Adv., 2016, 6, 4723–4729 RSC.
- T. Wakatsuki, B. Schwab, N. C. Thompson and E. L. Elson, J. Cell Sci., 2001, 114, 1025–1036 CrossRef CAS PubMed.
- S. Golfier, P. Rosendahl, A. Mietke, M. Herbig, J. Guck and O. Otto, Cytoskeleton, 2017, 74, 283–296 CrossRef CAS PubMed.
- Z. I. Kalcioglu, R. Mahmoodian, Y. Hu, Z. Suo and K. J. Van Vliet, Soft Matter, 2012, 8, 3393–3398 RSC.
- B. Fabry, G. N. Maksym, J. P. Butler, M. Glogauer, D. Navajas and J. J. Fredberg, Phys. Rev. Lett., 2001, 87, 148102 CrossRef CAS PubMed.
- S. J. Müller, F. Weigl, C. Bezold, C. Bächer, K. Albrecht and S. Gekle, Biomech. Model. Mechanobiol., 2021, 20, 509–520 CrossRef PubMed.
- Y. Liu, K. Mollaeian, M. H. Shamim and J. Ren, Int. J. Mol. Sci., 2020, 21, 392 CrossRef CAS PubMed.
- Y.-C. Chang, P. Nalbant, J. Birkenfeld, Z.-F. Chang and G. M. Bokoch, Mol. Biol. Cell, 2008, 19, 2147–2153 CrossRef CAS PubMed.
- X. Trepat, L. Deng, S. S. An, D. Navajas, D. J. Tschumperlin, W. T. Gerthoffer, J. P. Butler and J. J. Fredberg, Nature, 2007, 447, 592–595 CrossRef CAS PubMed.
- Y. Zhao, Q. Li and X. Hu, Anal. Methods, 2018, 10, 3489–3497 RSC.
- K. Zografos, F. Pimenta, M. A. Alves and M. S. N. Oliveira, Biomicrofluidics, 2016, 10, 043508 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc01061a |
| This journal is © The Royal Society of Chemistry 2024 |
