Heterogeneous reservoir computing in second-order Ta2O5/HfO2 memristors†
Nestor
Ghenzi‡
 ab,
Tae Won
Park‡
a,
Seung Soo
Kim
a,
Hae Jin
Kim
c,
Yoon Ho
Jang
a,
Kyung Seok
Woo
ab,
Tae Won
Park‡
a,
Seung Soo
Kim
a,
Hae Jin
Kim
c,
Yoon Ho
Jang
a,
Kyung Seok
Woo
 *a and
Cheol Seong
Hwang
*a and
Cheol Seong
Hwang
 *a
*a
aDepartment of Materials Science and Engineering and Inter-University Semiconductor Research Center, Seoul National University Gwanak-ro 1, Gwanak-gu, Seoul 08826, Republic of Korea. E-mail: kevinwoo@snu.ac.kr; cheolsh@snu.ac.kr
bUniversidad de Avellaneda UNDAV and Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina
cDepartment of Materials Science and Engineering, Myongji University, Yongin 17058, Korea
First published on 7th December 2023
Abstract
Multiple switching modes in a Ta2O5/HfO2 memristor are studied experimentally and numerically through a reservoir computing (RC) simulation to reveal the importance of nonlinearity and heterogeneity in the RC framework. Unlike most studies, where homogeneous reservoirs are used, heterogeneity is introduced by combining different behaviors of the memristor units. The chosen memristor for the reservoir units is based on a Ta2O5/HfO2 bilayer, in which the conductances of the Ta2O5 and HfO2 layers are controlled by the oxygen vacancies and deep/shallow traps, respectively, providing both volatile and non-volatile resistive switching modes. These several control parameters make the second-order Ta2O5/HfO2 memristor system present different behaviors in agreement with its history-dependent conductance and allow the fine-tuning of the behavior of each reservoir unit. The heterogeneity in the reservoir units improves the pattern recognition performance in the heterogeneous memristor RC system with a similar physical structure.
New conceptsThis study is based on multiple switching modes in a Pt/Ta2O5/HfO2/TiN memristor, which are studied experimentally and numerically through an RC simulation to reveal the importance of nonlinearity and heterogeneity in the RC framework. Unlike most studies, where homogeneous reservoirs are used, heterogeneity is introduced by combining different behaviors of the memristor units. We found that the performance of the Pt/Ta2O5/HfO2/TiN memristors can be controlled to self-rectifying mode with lower noise or leaky mode with higher noise. When the RC system was configured with the self-rectifying mode memristors, its recognition performance was higher than the case with the leaky mode devices, which is understandable from the lower noise of the former. Interestingly, combining the two reservoir units to comprise the heterogeneous RC system improves the recognition factor for pattern recognition even with a similar physical network structure. This finding has not been reported to the community, so we examined such a peculiar effect in detail in this work. |
Introduction
Reservoir computing (RC) is a machine-learning algorithm for processing time-series signals generated by complex dynamical systems, emulating the human brain's highly nonlinear and recursively interconnected architectures.1,2 It is a type of recurrent neural network that employs a “reservoir” as a dynamic feature extractor to process sequential or time series data. The reservoir layer is a vital component of the RC system, extracting features from the temporal input data. The main advantage of the RC is the minimal training data sets and an easy training process through a compact structure of the reservoir layer and a readout layer. Nonetheless, the conventional RC system has been primarily software-based, assuming its operation in the complementary metal oxide semiconductor devices (CMOS) circuits. Such RC systems undermine their crucial merits due to extensive data use, which is the critical hurdle of the current von Neumann computing system, even with the most advanced graphic processing unit.Recently, considerable effort has been devoted to developing memristive devices capable of overcoming the limitations of conventional RC systems.3–6 The previous reports explored the short-term dynamics of a full range of different physical mechanisms, ranging from the usual relaxation of filamentary resistive switching7 to more complex mechanisms, such as ferroelectricity relaxation in ferroelectric field effect transistors,8,9 data loss in ferroelectric tunneling junctions,10,11 short-term memory in interfacial resistive random-access memory,12 optical properties, and quantum effects.13–15 In all these devices, the fading (or volatile) memory with the nonlinear current–voltage (I–V) property of memristors is suitable as the reservoir for hardware-based RC systems. Furthermore, non-fading (or non-volatile) memristors can also be adopted as temporal kernels when combined with capacitors and resistors.16
However, the full potential of memristor-based RC systems has not been explored yet. There could be plenty of room for further performance improvement when more functionality of the memristors is adopted, as shown in this work. Most of the previous memristor-based RC systems adopted a first-order memristor. In those cases, the resistance of the first-order memristor is only determined by a single state variable, s1, which is varied by the input voltage V.17 In the second (or higher) order memristor, on the other hand, its resistance additionally depends on a second (or more) variable, s2 (…sN), allowing more complex dynamics and multifunctional behavior with volatile and non-volatile responses.18 This set of state variables can be linked to internal parameters, such as oxygen vacancy distribution, conductive filament size, local temperature, and trap density.19,20 The Pt/Ta2O5/HfO2/TiN (PTHT) memristors in this work possess several of the mentioned characteristics of second-order memristors,21–24 as shown later.
When the second-order PTHT memristors are adopted, a heterogeneous reservoir can be constructed, different from most previous studies with homogeneous memristor units in the reservoir layer.25–27 In contrast, heterogeneous memristive reservoir units must have different dynamic properties for the given input signal streams, which may further enhance the RC performance.28,29 However, it requires complicated fabrication steps when the memristor-base crossbar arrays (CBA) adopt the first-order memristors. Instead, exploiting the second-order memristors will not require additional memristor fabrication steps; only particular electrical operations will make the heterogeneous reservoir attained.
Zhong et al.26 demonstrated a dynamic memristor approach by applying a controllable mask process to the input data. Nevertheless, the accuracy improvement is mainly based on a complex 3-mask reservoir structure, which resembles a data augmentation technique in the software RC system, rendering the readout layer to obtain more information about the image dataset used.
This work proposes a heterogeneous RC system composed of second-order PTHT memristors, which differs from the previous works. This work focuses on different dynamic behaviors when short pulses are applied to the device. The soft breakdown of the Ta2O5 layer can further modulate the dynamics of the bi-layer film. The PTHT memristor has a self-rectifying fading memory property, characterized by generally low current and low operation variability. This type of performance is primarily ascribed to the charge trap and detrap-based switching mechanism, where the Pt/Ta2O5 and HfO2/TiN interfaces provided the Schottky and quasi-Ohmic contacts, respectively.30–32 This type of operation can be guaranteed as long as the Schottky contact property of the Pt/Ta2O5 interface is retained by limiting the compliance current (Icc) during the switching to a sufficiently low value. However, it changes to the leaky mode when the Icc value increases sufficiently high, adversely interfering with the Schottky contact property. While this type of performance degradation is undesired in usual memory operation with the CBA configuration, it can be used to construct the heterogeneous RC system, as shown in this work.
Therefore, this work first describes how the mode change in the PTHT device is achieved. Then, the different nonlinear dynamics of the self-rectifying and leaky mode PTHT devices are combined to compose the heterogeneous RC system. Finally, the MNIST benchmark accuracy tests evaluate the system performances when the degree of heterogeneity is varied.
Results and discussion
A. Mode change in the second-order PTHT memristors
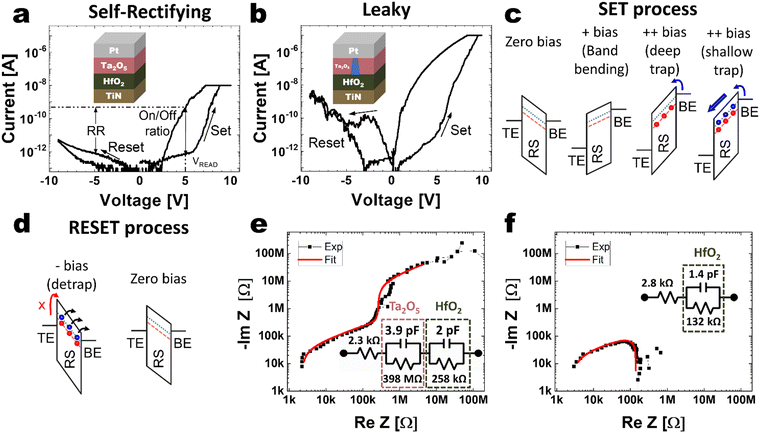
Fig. 1(a) shows the self-rectifying I–V curve of the PTHT device (inset figure) with an Icc value of 10 nA during the set switching, which has already been reported elsewhere.30–33 The device shows an ON/OFF ratio of ∼5 orders of magnitude with a rectifying ratio of ∼4 orders of magnitude. These characteristics are beneficial for passive CBAs. The device shows a typical bipolar switching behavior with an initial high resistance state (HRS). When a DC voltage of +6 V was reached, the device switched to the low resistance state (LRS), indicating a SET operation. After changing the biasing polarity, the device switched back to its HRS for a voltage value exceeding −3 V, indicating a RESET or OFF transition. The electrical response presents two highly nonlinear resistance states with a gradual SET transition. The charge trapping effect in the SET and RESET process is schematically depicted in Fig. 1(c) and (d), where the effect of the deep and shallow traps are depicted.The PTHT memristor can have non-volatile and volatile memory properties due to two distinct trap levels: a deep trap level at 1.0 eV and a shallow trap level at 0.6 eV.30–32 When the PTHT memristor is in the HRS, applying a voltage to the Pt top electrode (TE) results in electron injection from the TiN bottom electrode (BE) to the HfO2 switching layer, transitioning the device to the LRS. Under relatively low (<6 V) and long (ca. DC condition) voltage applications, only the deep traps are filled with electrons, resulting in the non-volatile LRS. In contrast, under the higher voltage stress conditions, the shallow traps also become filled with electrons once all the deep traps are filled. When the voltage level decreases or even terminates, some of the electrons at the shallow traps detrap by thermal disturbance, increasing the device's resistance again. This behavior coincides with the volatile memory. Such a volatile switching property of the HfO2 layer has been confirmed by the emergence of threshold switching in the Pt/HfO2/TiN device (lacking the Ta2O5 layer in the PTHT device).34
The ON/OFF ratio and the rectification ratio can be tuned between 10 and 105 when the Icc value varies between 0.05 nA and 100 nA, as shown in Fig. S2 (ESI†). The linear area dependence of the leakage current in the HRS agrees with the uniform charge-trapping mechanism across the electrode area.
Notably, if the Icc value increases to 1 μA or higher, the Ta2O5 layer becomes too leaky, and the self-rectifying characteristics are lost, as shown in Fig. 1(b). This behavior is named leaky mode. The SET and RESET voltage values are similar to the values in the self-rectifying mode, but the HRS current values are much higher, continuously degrading the ON/OFF ratio. This degradation process is shown in Fig. S3 (ESI†). Fifty cycles of I–V response without the Icc are measured to understand the leaky characteristics better. After the first cycle, the current in the negative polarity increases and becomes a noisy signal, in conjunction with a monotonous increase of the leakage current in the HRS with the positive bias. The evolution of the current measured at 4 V is shown in Fig. S3 (ESI†) inset. An increase in the current value of the HRS can be seen for the first 20 cycles. This increase in the HRS current degrades the on/off ratio from ∼4 to ∼2 orders of magnitude.
The impedance-phase angle was measured at a DC bias of 6 V at compliance currents of 10 nA (self-rectifying device) and 1 μA (leaky device), to analyze the electrical states of the bi-layer film in the PTHT devices. The Nyquist plot shows that the impedance of the leaky device is quite different from the self-rectifying device. To analyze this more closely, electrochemical impedance spectroscopy is used to fit the resistance and capacitance of each film.35
The self-rectifying mode can be modeled electrically as a voltage divider composed of two parallel nonlinear resistor–capacitor elements, as shown in Fig. 1(e). When the Ta2O5 layer is stressed to induce the soft dielectric breakdown, one of the two parallel resistor–capacitor elements is converted to a resistor, mainly by the oxygen vacancy-mediated filament formation inside the Ta2O5 layer (inset of Fig. 1(b) and (f)). The HfO2 resistor and capacitance values for the self-rectifying and leaky mode have slightly different values due to the simplified model which does not consider the possibly different interfaces in each mode.
The charge-trapping-based device exhibits diverse electrical behaviors with different relaxation characteristics by inserting the Ta2O5 layer between the HfO2 dielectric and the Pt electrode. The possibility of generating different dynamics in each device that makes up the reservoir through the volatile or non-volatile response improves the dimensionality of the reservoir, enhancing the distinction between different features that will be imposed on the readout layer. This performance is possible due to the rich dynamics of the Ta2O5/HfO2 bilayer device, whose resistance switching is based on deep and shallow traps.30 The different types of traps grant different relaxation times that give a tuneable nonlinearity.31 The soft breakdown of the Ta2O5 layer in the leaky mode can further modulate the dynamics of the bi-layer film.
The long- (non-volatile) and short-time (volatile) resistance relaxation behaviors are shown in Fig. S4 (ESI†). The PTHT devices are switched to LRS in the self-rectifying and leaky modes by applying a DC sweep up to 9 V with the Icc value of 10 nA and 10 μA, respectively. The LRS resistance values measured at 3 V remained stable up to 500 s due to the stable filling of the deep and shallow traps with electrons in the self-rectifying mode and additional conducting filament involvement in leaky mode (Fig. S4(a), ESI†). This stability allows for exploring its dynamic properties by applying different short pulses without degradation. Subsequently, short pulses with 12 V amplitude and 10 μs length were applied to the LRS devices, and the current decay after the pulse termination was monitored, as shown in Fig. S4(b) (ESI†). As discussed later in detail, the current responses show opposite current flow directions, but both modes have a similar decay time of ∼50 μs.
Other TE materials, such as (In,Sn)2O3 (work function = 4.7 eV) and W (work function = 4.5 eV), are also tested to compare the performance with the Pt TE (work function = 5.3 eV). The detailed DC and AC test results are included in Fig. S5 (ESI†). It was found that the device with the Pt TE showed the most desirable properties due to its high internal field, induced by the highest work function difference with the TiN BE. Therefore, the PTHT devices with the self-rectifying or leaky mode are adopted to compose the heterogeneous RC system, as discussed in the following section.
B. Heterogenous RC with the second-order PTHT memristors
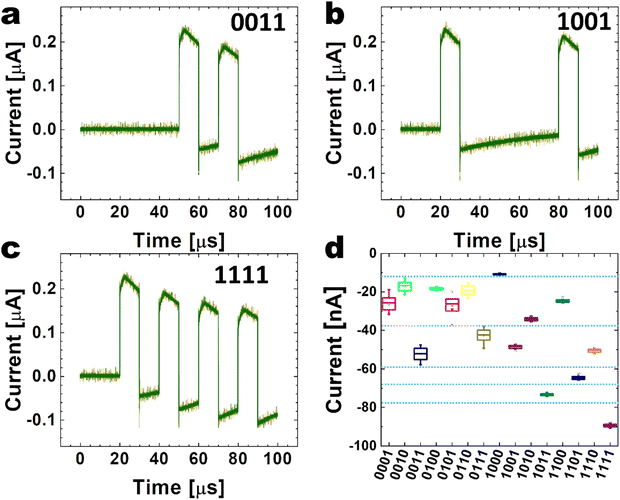
One of the most crucial performances of a memristive reservoir is to separate or identify the diverse input signal streams into the different conductance levels of the given memristor. Therefore, input signals were applied as 4-bit voltage pulse patterns, as shown in Fig. 2(a)–(c) for patterns ca. 0011, 1001, and 1111, to test the separability of the adopted PTHT memristor (reservoir) when it is in the self-rectifying mode.Memristor responses to other 15 non-null 4-bit patterns are shown in Fig. S6 (ESI†). This pulse application will allow the extraction of the dynamic pulse responses of each reservoir unit.
The device current is then measured to observe the current response during the application of the pulses, including the relaxation times when the voltage becomes zero. Before the pulse-type measurement, the device was set to LRS in the self-rectifying mode by the I–V sweep up to 9 V with an Icc of 10 nA. Then, the device current is measured when the voltage pulses with 12 V/10 μs for signal “1” and 0 V/10 μs for signal “0” are applied. No Icc is settled for the pulse measurements. For the given 4-digit input patterns, the same experiments are repeated 50 times to achieve statistical accuracy. Fig. 2(a)–(c) show the current responses for the 0011, 1001, and 1111 inputs. There are several notable findings. First, when the 12 V/10 μs pulse is applied, the current increases for the initial ∼4 μs, which is consistent with the additional SET switching of the device due to additional carrier trapping in the HfO2 layer. However, the current decreases during the subsequent ∼6 μs, incompatible with the SET switching behavior. Second, when the voltage pulse is terminated, a negative current peak occurs, corresponding to the capacitive discharge. Third, a generally negative current flows during the “0” signal, i.e., 0 V/10 μs pulse, is applied after the “1” signal, whose absolute value decays with time. (See Fig. S4(b) for more detailed current–time behavior, ESI†). Such a trend is strengthened as the “1” signal number increases, and finally, a negative current is detected after the 4-digit patterns are passed. The absolute value of the finally detected current depends on the number of “1” signals and their distribution with “0” signals, enabling the reservoir performance. Fig. 2(d) shows the distribution plot of the current estimated between 92.5 and 97.5 μs for the 15 pulse patterns applied to the device, whose current–time data are included in Fig. S6 (ESI†). A minimum overlap between the final states for each pattern is observed, with a low dispersion of the measured current values in each one of these states. The reservoir states can be divided into six regions, indicated by the horizontal dashed lines. This finding indicates that the nonlinear behavior of the self-rectifying mode feasibly separates the input, making the recognition of each digit affordable for the readout layer.
Such a peculiar current–time behavior can be understood in the following way. When the 12 V/10 μs pulse is applied, the traps in the HfO2 are further filled with the injected electrons from the TiN BE during the first ∼4 μs, eventually filling all the traps. With further electron injection, they are trapped at the HfO2/Ta2O5 interface, as the insulating Ta2O5 does not allow the electrons to pass through. Under this circumstance, a local “reverse” electric field can be settled, decreasing the current during the subsequent ∼6 μs. When the voltage pulse is terminated, the charges accumulated in the electrode discharge abruptly, resulting in a negative current pulse. However, the dissipation of the trapped electrons at the HfO2/Ta2O5 interface requires time, so the reverse field presents for a while, resulting in the decaying negative current (with a time constant of ∼50 μs, Fig. S4(b), ESI†) during the subsequent “0” signal period. When such a negative local field remains, the subsequently applied “1” signal cannot induce the positive current as much as the previous “1” signal. Therefore, the finally detected “negative” current depends on the distribution as well as the number of “1” signals, enabling the reservoir performance. These electrical performances are quite repeatable, resulting in the narrow distribution in Fig. 2(d).
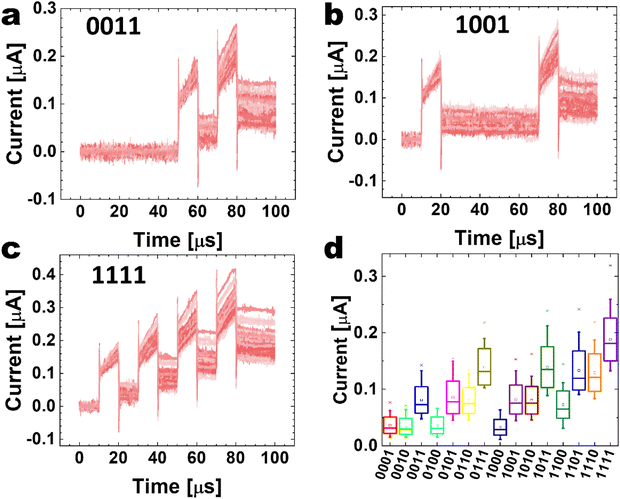
Similarly, the leaky mode device's responses to the 4-bit patterns are shown in Fig. 3 for patterns 0011, 1001, and 1111 and the 15 non-null 4-bit patterns in Fig. S7 (ESI†). The patterns have been applied 50 times each. For these leaky mode tests, the device was set to the LRS by the DC I–V sweep up to 9 V with an Icc of 10 μA, which rendered the Ta2O5 layer leaky.
The dynamic pulse response in the leaky mode shows a different behavior when compared to the self-rectifying mode. The current response during the pulse shows an instantaneous capacitive charging peak followed by a monotonous increase during the 12 V/10 μs pulse application. This behavior can be ascribed to the additional electron trapping in the HfO2 layer and the lost insulating property of the Ta2O5 layer.
When the voltage pulse is terminated, and 0 V/10 μs pulse follows, the capacitive discharging peak is observed, followed by a positive current, which also decays with time. It is noted that these effects accumulate, resulting in the overall higher positive current with the increasing number of “1” pulses, as shown in Fig. 3(d). However, the distribution of the “1” and “0” signals also affects the estimated final current, rendering the leaky mode useful for the reservoir with quite discernible properties from the self-rectifying mode. Also, the final current values for the given input patterns are irregular, making the final signal quite noisy, as shown in Fig. 3(d). Such behavior of residual current of the leaky mode indicates that the HfO2 layer is heavily trapped with electrons during the 12 V/10 μs pulse application, forming a local “forward” field across the dielectric layer. This local “forward” field induces a residual positive current (with a time constant of ∼50 μs, Fig. S4(b), ESI†) even when the 0 V/10 μs pulse is applied.
The variance in each state (considering the 50 times each pattern is applied) is comparable to the current value during the pulse, increasing with more pulses appearing in a defined pattern. This variance is random, as shown in Fig. S7 (ESI†), and unrelated to the potentiation effect observed in the non-volatile synaptic devices. The leaky mode shows a higher variance than the self-rectifying mode. This variance (or noise) produces degraded separability for the different applied patterns. So, the performance of the leaky mode in the reservoir is expected to be lower than the corresponding one in the self-rectifying mode. In the distribution plot of Fig. 3(d), tracing a line to define different regions is unclear, indicating a lower performance. However, the noise observed in the leaky mode can be taken as an additive effect of the reservoir output and the input of the readout layer. This addition typically leads to a regularization effect while training the readout layer and thus is expected to improve recognition performance. Therefore, this noise addition can be taken as an expansion of the training dataset size. Each time a training sample is exposed to the model, some random noise is added to the input variables, making them different every time it is exposed to the model. In this way, adding noise to input samples is a simple form of “data augmentation”. Thus, the noise addition will make the reservoir and the readout layer more efficiently suppress the sample memorizing effect, resulting in a higher dimensional mapping function.36
Overall, the current output in the leaky mode is 2–3 times higher than that in the self-rectifying mode. As it was mentioned earlier, the dynamic AC response was measured in the corresponding LRS. The device in the LRS state corresponds to all deep traps filled with carriers and all shallow traps empty. Therefore, the fading effect dynamics in both modes are related to the shallow traps. Besides, the two types of behavior exhibit different nonlinear characteristics of the current response, improving the separability behavior of pulse patterns for time series processing when combined to compose a heterogeneous RC system, as shown next.
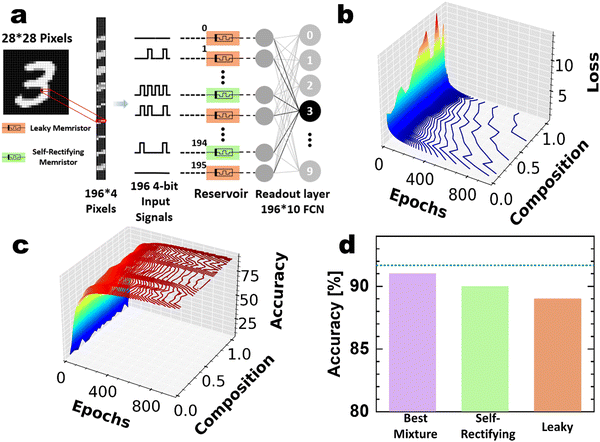
A benchmark numerical test of hand-written digit recognition is carried out using the MNIST37 datasets to evaluate the performance of the PTHT-memristor RC system on image classification. The experimental results previously shown in Fig. 2 and 3 were used for the tests. The critical point of this study is to change the composition of the reservoir with different behaviors in its units. In most studies, the reservoir is composed of identical units, which may degrade the system performance when considering the nonlinear transformation of the input into a valuable representation for learning the input information at the readout layer. In this study, the RC simulation is performed using the self-rectifying and leaky characteristics of the device. A heterogeneous RC node with both types of units and a readout layer is designed to classify the different MNIST digits, as shown in Fig. 4(a). This RC network structure is similar to the previous work by Jang et al.,16 but a single-type memristor, i.e., homogeneous reservoirs, was adopted in the previous work.
The images used for training consist of the 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MNIST digits that are reshaped in a matrix with dimensions 196 × 4 for each digit. The 10
000 MNIST digits that are reshaped in a matrix with dimensions 196 × 4 for each digit. The 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MNIST digits for the testing were reshaped in the same way to be used as input to the 196 units in the reservoir, as schematically depicted in Fig. 4(a). The resulting 4-bit pattern in each row of the 196 × 4 matrix was applied to different devices, and thus, the 196 devices generated the reservoir. Each unit reads the experimental response to 4-bit patterns. The reservoir was structured like a single linear layer, and each unit's output was connected to one neuron of the readout layer. The self-rectifying or leaky mode PTHT device is presented at each reservoir unit location, defining the composition of the heterogeneous reservoir. The effects of mode selection of each unit are shown in more detail below. For each composition, 50 different runs were conducted, and the mean with the variance values of the accuracy was calculated and defined as the percentage of correctly identified digits. The readout layer was trained with the gradient descent method during 1000 epochs.
000 MNIST digits for the testing were reshaped in the same way to be used as input to the 196 units in the reservoir, as schematically depicted in Fig. 4(a). The resulting 4-bit pattern in each row of the 196 × 4 matrix was applied to different devices, and thus, the 196 devices generated the reservoir. Each unit reads the experimental response to 4-bit patterns. The reservoir was structured like a single linear layer, and each unit's output was connected to one neuron of the readout layer. The self-rectifying or leaky mode PTHT device is presented at each reservoir unit location, defining the composition of the heterogeneous reservoir. The effects of mode selection of each unit are shown in more detail below. For each composition, 50 different runs were conducted, and the mean with the variance values of the accuracy was calculated and defined as the percentage of correctly identified digits. The readout layer was trained with the gradient descent method during 1000 epochs.
Fig. 4(b) and (c) show the loss and the recognition performances as a function of the epoch number for the composition of the self-rectifying and leaky mode devices. The saturated recognition rates for the RC system composed of only self-rectifying and leaky devices are 90% and 89%, respectively, consistent with the expectation that the higher separability of the self-rectifying devices will produce higher performance. Interestingly, the highest recognition rate of 91% could be achieved with a composition of 0.3 self-rectifying and 0.7 leaky PTHT devices in the reservoir, as shown in Fig. 4(d). The generally low accuracy values in this figure are attributed to the simple 196 × 10 readout layer structure without involving any hidden neurons.
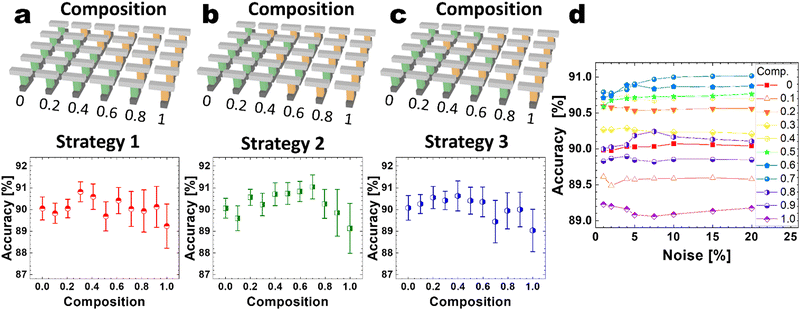
Several further simulations were performed with different strategies to populate the reservoir for a defined composition to understand each unit's relevance in the reservoir structure. All possible combinations are beyond the available computation resources, so three different strategies were considered, as shown in Fig. 5(a)–(c). 196 units were used in the simulations, but only five units are schematically depicted to avoid clutter. Compositions between 0 and 1 are shown with a step of 0.2. When increasing composition is considered, Strategy 1 consists of changing the units from the self-rectifying to the leaky mode in increasing order to satisfy a given composition ratio. Strategy 2 changes the odd units, while Strategy 3 changes the even units. In these two strategies, once the corresponding units are all changed from the self-rectifying mode to the leaky mode, the other units continue changing from the self-rectifying mode to the leaky one. The homogeneous cases of pure self-rectifying and leaky units in the three cases show similar results of 90% and 89%, as expected. When both units are combined, the accuracy improves to 91% in the three cases.
Of the three strategies, Strategy 2 is the one with the highest value. Strategies 1 and 3 present the highest accuracy in a composition value of ∼0.3–0.4 leaky PTHT, while Strategy 2 does at ∼0.7 leaky PTHT device. As Tanaka28 predicted numerically, the noise introduced by the leaky memristor improves the recognition factor due to the increased separability in the reservoir. Besides, the random noise of memristor devices in recognition benchmark tasks can be beneficial as it imposes a regularization in the weights of the readout layer, increasing the accuracy.
Additional analyses were performed to compare the influence of the noise in the leaky mode. The noise influence in the results was considered with Strategy 2, the strategy with the highest accuracy in the benchmark test. Fig. 5(d) shows the performance evaluation when the incorporated noise varied between 2% and 20%. From Fig. 5(d), the mixture of both behaviors (self-rectifying and leaky device) increases the recognition accuracy, with an optimal composition of 0.7 of leaky memristors units for most of the explored noise amplitudes. A maximum accuracy of 91% was obtained, comparable to similar hardware-based reservoir computing systems (Table 1).
| Reference | Accuracy (%) | Speed | Network size | Training size | Power |
|---|---|---|---|---|---|
| Software (ANN) | 91.7 | — | 784 × 10 | 60 k | — |
| This study | 91 | 10 μs | 196 × 10 | 60 k | 2.4 μW |
| Nat. Comm. 12, 5727 (2021)16 | 90 | 1 μs | 196 × 10 | 50 k | 200 μW |
| Nat. Comm. 8, 2204 (2017)25 | 85.8 | 10 ms | 88 × 10 | 20 k | 0.2 μW |
| Adv. Intell. Syst. 1, 1900084 (2019)27 | 83 | 1 ms | 220 × 10 | 60 k | 60 μW |
Five 2 × 2 μm2 PTHT devices are prepared and switched to the low resistance state in the self-rectifying or leaky modes to examine the device-to-device variation effects. They are pulsed with ‘11111’, ‘01010’, ‘10001’, ‘00100’, ‘00111’, ‘01001’, ‘11101’, ‘00001’, ‘11010’, ‘01110’ and ‘10000’ patterns with 12 V/10 μs voltage pulses, which are repeated 50 times. Fig. S8 and S9 (ESI†) show the averaged current responses of the five PTHT devices under the self-rectifying and leaky mode, respectively. Although there are notable variations between the five devices in their current responses in each mode, their general features, i.e., slightly decaying and more notably increasing current in the former and latter cases, remain for all the devices. Therefore, the device-to-device variation do not significantly alter the main conclusion of this work.
The improvement in accuracy when mixing leaky and SR devices may originate from two factors; the first one is related to the different nonlinearities of each device, creating different separability in the reservoir. Secondly, the noise in leaky devices can be regarded as adding noise to the input of the corresponding neuron in the readout layer. The different separability and noise contributed to the accuracy improvement by 0.75% and 0.25%, respectively, as seen in Fig. 5(d). Notably, the readout layer of a neural network determines the accuracy. However, neural networks can memorize the training dataset, known as overfitting, degrading the accuracy. The noise in leaky devices can be seen as a way of regularizing the neural network, overcoming the overfitting issue. Also, the different nonlinearities of leaky and SR devices, which transform the input data differently, provide data augmentation. Data augmentation, which artificially generates more information from the available data, helps increase the accuracy when only an insufficient training dataset is available.
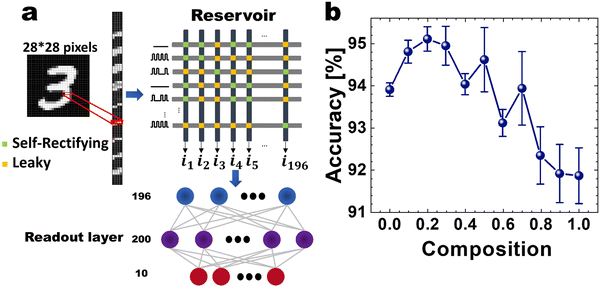
The effects of heterogeneity of the RC system were further examined when the PTHT memristors were arranged in the MxN crossbar array (CBA). Fig. 6(a) shows the schematic diagram showing the RC system for the MNIST data classification with the 196 × 196 CBA. Differently from Fig. 5(a), the chopped 4-bit pixel voltages are input to the rows of the 196 × 196 CBA, and the output currents at the columns are taken and converted to inputs of the readout layer, composed of 196 input, 200 hidden, and 10 output neurons with the corresponding synapses. In this case, the PTHT device's self-rectifying performance, which does not entirely disappear even at the leaky mode, and parallel voltage inputs to the rows mitigate the severe sneak current issue in a passive CBA. The PTHT devices are assumed to be all in self-rectifying mode (composition = 0 in Fig. 6(b)), in leaky mode (composition = 1 in Fig. 6(b)), or having intermediate compositions, where the leaky devices are randomly distributed among the 196 × 196 crosspoints. The simulation results, performed 10 times, are summarized in Fig. 6(b). Due to the higher number of parameters in the readout layer, the accuracy generally increased compared to the results in Fig. 5. In this CBA structure, the cases with only self-rectifying or leaky devices produced the accuracy values of ∼94 and 92%, respectively. However, it shows a value of ∼95% at the composition of 0.2, comparable to the software-based accuracy from a similar network size with a fully connected structure was ∼96%. Therefore, the heterogeneous RC components also improve the identification accuracy compared with the homogeneous case, even with the recurrently connected CBA configuration of the PTHT memristors.
Conclusions
This work systematically investigated the resistive switching behavior and the dynamic response characteristics of Pt/Ta2O5/HfO2/TiN devices for their use as heterogeneous reservoirs in reservoir computing. Two switching modes were acquired according to the compliance current to induce different current responses and their relaxation times for the given voltage pulse inputs. The self-rectifying mode, achieved by limiting the Icc to values <∼10 nA during the DC I–V sweep, showed a “reverse” local field with a longer relaxation time when the voltage pulse was terminated. This mode is also accompanied by high repeatability and low power consumption. In contrast, the leaky mode, achieved by a higher Icc during the DC I–V sweep, showed a “forward” local field with a shorter relaxation time when the voltage pulse was terminated. It is accompanied by higher cycle-to-cycle variation and higher current flow. These two modes present different rectifying properties, fade-out times, and power consumption. Different behaviors in the current evolution were further explored with 4-bit MNIST data patterns. Starting from the fact that the reservoir is the essential part of a reservoir computing system, the concept of heterogeneity in the reservoir was explored. The pattern recognition performance was evaluated from the RC system with the different compositions of the two switching modes. The mixture of the memristors with two modes in the linear reservoir increased the separability in the high dimensional state injected in the readout layer. Mixing the self-rectifying and leaky mode memristors with a ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ratio increased the MNIST data set identification accuracy by ∼2% compared with the RC system with the single-type memristors. Nonetheless, understanding the reason why adding a higher portion (70%) of units with lower separability (leaky device) than the units with higher separability (SR device) results in a better performance requires more study.
7 ratio increased the MNIST data set identification accuracy by ∼2% compared with the RC system with the single-type memristors. Nonetheless, understanding the reason why adding a higher portion (70%) of units with lower separability (leaky device) than the units with higher separability (SR device) results in a better performance requires more study.
It was shown that a heterogeneous reservoir provides a more extensive and diverse set of features for the readout layer so that the system can distinguish between different patterns. This performance is due to the high degree of nonlinearity of the nanofabricated devices with their complex structure of two oxides. Furthermore, the heterogeneous reservoir presents high robustness to noise in patterns not seen during system training. The proposed approach can help increase the capacity of image recognition and time series prediction in ultra-low power edge computing devices.
Methods
Device fabrication
The PTHT device was fabricated in a cross-point configuration on a SiO2/Si substrate. Fig. S1 of online (ESI†) describes the device structure and fabrication steps. A 50 nm-thick TiN was deposited through sputtering (Applied Materials, ENDURA, ENDURA 5500) as a bottom electrode (BE). A switching layer of 10 nm-thick HfO2 film was deposited through thermal atomic layer deposition (CN-1, Atomic Premium) at a 280 °C substrate temperature using tetrakis (dimethyl-amido) hafnium (TDMAHf, Hf(N(CH3)2)4) as a precursor and ozone (O3) as an oxygen source. Subsequently, a 10 nm-thick Ta2O5 thin film was deposited using plasma-enhanced atomic layer deposition (CN1, Atomic Premium plus 200) at a 200 °C substrate temperature with tris (diethyl amido) (tert-butyl-imido) tantalum(V) ((CH3)3CNTa(N(C2H5)2)3) and plasma-activated H2O as Ta precursor and oxygen source, respectively. Finally, a 50 nm-thick Pt film was deposited using an electron-beam evaporator (SORONA, SRN-200i) as a top electrode (TE), following the lift-off process. The electrode area was 64 μm2. Details about the morphological characteristics of the thin films can be found elsewhere.30–32Electrical measurements
The DC current–voltage (I–V) curves were measured using a semiconductor parameter analyzer HP4155A. The AC measurements were performed with a function generator (Agilent AFG 3011C) and an oscilloscope (Wave Surfer 104MXs-B Teledyne LeCroy). The system allows switching connections between DC and AC equipment through a triaxial switching matrix (Keithley 707a). The Pt TE was biased, while the TiN BE was grounded for both DC I–V sweep and AC pulse tests. The impedance-phase angle was measured using an impedance analyzer (Hewlett-Packard 4194A) in the frequency ranging from 100 Hz to 10 MHz.Reservoir computing simulation
The images used for training and testing consist of the 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 + 10
000 + 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MNIST digits. The weight matrix (W) was built by selecting an experimental random 4-bit pattern. In the simulations for the 196 memristors based-linear and the crossbar reservoir, the mean current value between 92.5 and 97.5 μs was used to fill each element of W. For the hardware implementation of the 5-memristor-based linear reservoir, the experimental values were considered during 2 μs in the middle of each one of the applied pulses. Softmax was used as the activation function for the weighted sum to yield the prediction output. The cross-entropy loss was used for the loss function. To minimize the loss function, a gradient-descent-based Adam optimizer was identically used for the readout layer and the different sizes of the FCN. Full-batch-type learning of the readout layer and 784 × 10 FCN was performed in the Python package Sklearn.
000 MNIST digits. The weight matrix (W) was built by selecting an experimental random 4-bit pattern. In the simulations for the 196 memristors based-linear and the crossbar reservoir, the mean current value between 92.5 and 97.5 μs was used to fill each element of W. For the hardware implementation of the 5-memristor-based linear reservoir, the experimental values were considered during 2 μs in the middle of each one of the applied pulses. Softmax was used as the activation function for the weighted sum to yield the prediction output. The cross-entropy loss was used for the loss function. To minimize the loss function, a gradient-descent-based Adam optimizer was identically used for the readout layer and the different sizes of the FCN. Full-batch-type learning of the readout layer and 784 × 10 FCN was performed in the Python package Sklearn.
Author contributions
Nestor Ghenzi and Tae Won Park designed and conducted the experiments, wrote the main manuscript text. Nestor Ghenzi performed the simulations of the reservoir computing framework. Seung Soo Kim and Hae Jin Kim fabricated and characterized morphologically the devices. Yoon Ho Jang and Kyung Seok Woo provided software and methodology supporting. All authors reviewed the manuscript. Cheol Seong Hwang provided the funding support and conceptualization of the work and led the writing review and editing process.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (Grant No. 2020R1A3B2079882).Notes and references
- W. Maass, T. Natschläger and H. Markram, Neural Comput., 2002, 14, 2531–2560 CrossRef PubMed.
- H. Jaeger, Bonn, Germany: German National Research Center for Information Technology GMD Technical Report, 2001, 148, 13.
- M. Lanza, A. Sebastian, W. D. Lu, M. Le Gallo, M. F. Chang, D. Akinwande, F. M. Puglisi, H. N. Alshareef, M. Liu and J. B. Roldan, Science, 2022, 376, 1066 CrossRef PubMed.
- R. Waser, R. Dittmann, C. Staikov and K. Szot, Adv. Mater., 2009, 21, 2632 CrossRef CAS PubMed.
- K. J. Yoon, Y. Kim and C. S. Hwang, Adv. Electron. Mater., 2019, 5, 1800914 CrossRef.
- P. Mannocci, M. Farronato, N. Lepri, L. Cattaneo, A. Glukhov, Z. Sun and D. Ielmini, APL Mach. Learn, 2023, 1, 010902 CrossRef.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef.
- M. Tang, J. Mei, X. Zhan, C. Wang, J. Chai, H. Xu, X. Wang, J. Wu and J. Chen, IEEE Trans. Electron Devices, 2023, 70, 3372 CAS.
- K. Toprasertpong, E. Nako, Z. Wang, R. Nakane, M. Takenaka and S. Takagi, Commun. Eng., 2022, 1, 21 CrossRef.
- D. Kim, J. Kim, S. Yun, J. Lee, F. Seo and S. Kim, Nanoscale, 2023, 15, 8366 RSC.
- Z. Chen, W. Li, Z. Fan, S. Dong, S. Chen, M. Qin, M. Zeng, X. Lu, G. Zhou, X. Gao and J. M. Liu, Nat. Commun., 2023, 14, 3585 CrossRef CAS PubMed.
- J. Park, T. H. Kim, O. Kwon, M. Ismail, C. Mahata, Y. Kim, S. Kim and S. Kim, Nano Energy, 2022, 104, 107886 CrossRef CAS.
- Y. Sun, T. Lin, N. Lei, X. Chen, W. Kang, Z. Zhao, D. Wei, C. Chen, S. Pang, L. Hu, L. Yang, E. Dong, L. Zhao, L. Liu, Z. Yuan, A. Ullrich, C. H. Back, J. Zhang, D. Pan, J. Zhao, M. Feng, A. Fert and W. Zhao, Nat. Commun., 2023, 14, 3434 CrossRef CAS PubMed.
- J. Dudas, B. Carles, E. Plouet, F. J. Grollier and D. Marković, npj Quantum Inf., 2023, 9, 64 CrossRef.
- L. Domingo, G. Carlo and F. Borondo, Sci. Rep., 2023, 13, 8790 CrossRef CAS PubMed.
- Y. H. Jang, W. Kim, J. Kim, K. S. Woo, H. J. Lee, J. W. Jeon, S. K. Shim, J. Han and C. S. Hwang, Nat. Commun., 2021, 12, 5727 CrossRef CAS PubMed.
- F. Corinto, M. Forti and L. O. Chua, Nonlinear Circuits and Systems with Memristors, Springer International Publishing, 2021 Search PubMed.
- G. D. Zhou, Z. R. Wang, B. Sun, F. C. Zhou, L. F. Sun, H. B. Zhao, X. Hu, X. Peng, J. Yan, H. Wang, W. Wang, J. Li, B. Yan, D. Kuang, Y. Wang, L. Wang and S. K. Duan, Adv. Electron. Mater., 2022, 0, 2101127 CrossRef CAS.
- K. S. Woo, J. Kim, J. Han, W. Kim, Y. H. Jang and C. S. Hwang, Nat. Commun., 2022, 13, 5762 CrossRef CAS PubMed.
- Q. Tian, X. Chen, X. Zhao, Z. Wang, Y. Lin, Y. Tao, H. Xu and Y. Liu, Appl. Phys. Lett., 2023, 122, 153502 CrossRef CAS.
- Y. Jiang, D. Wang, N. Lin, S. Shi, Y. Zhang, S. Wang, X. Chen, H. Chen, Y. Lin, K. C. Loong, J. Chen, Y. Li, R. Fang, D. Shang, Q. Wang, H. Yu and Z. Wang, Adv. Sci., 2023, 10, 2301323 CrossRef CAS PubMed.
- A. Khanas, C. Hebert, L. Becerra, X. Portier and N. Jedrecy, Adv. Electron. Mater., 2022, 8, 2200421 CrossRef CAS.
- S. Kim, C. Du, P. Sheridan, W. Ma, S. Choi and W. D. Lu, Nano Lett., 2015, 15, 2203 CrossRef CAS PubMed.
- M. A. Zidan, Y. J. Jeong and W. D. Lu, IEEE Trans. Nanotechnol., 2017, 16, 721 CAS.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 2204 CrossRef PubMed.
- Y. Zhong, J. Tang, X. Li, B. Gao, H. Qian and H. Wu, Nat. Commun., 2021, 12, 408 CrossRef CAS PubMed.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef.
- G. Tanaka, R. Nakane, T. Yamane, D. Nakano, S. Takeda, S. Nakagawa and A. Hirose. Neural Information Processing. ICONIP 2016. Lecture Notes in Computer Science 2016, 9947, 187.
- J. Dong, R. Ohana, M. Rafayelyan and F. Krzakala, Adv. Neural Inf. Process., 2020, 33, 16785 Search PubMed.
- J. H. Yoon, S. J. Song, I. H. Yoo, J. Y. Seok, K. J. Yoon, D. E. Kwon, T. H. Park and C. S. Hwang, Adv. Funct. Mater., 2014, 24, 5086 CrossRef CAS.
- J. H. Yoon, K. M. Kim, S. J. Song, J. Y. Seok, K. J. Yoon, D. E. Kwon, T. H. Park, Y. J. Kwon, X. Shao and C. S. Hwang, Adv. Mater., 2015, 27, 3811–3816 CrossRef CAS PubMed.
- S. S. Kim, S. K. Yong, J. Kim, J. M. Choi, T. W. Park, H. Y. Kim, H. J. Kim and C. S. Hwang, Adv. Electron. Mater., 2022, 9, 22000998 Search PubMed.
- T. Park, S. S. Kim, B. J. Lee, T. W. Park, H. J. Kim and C. S. Hwang, Nanoscale, 2023, 15, 6387 RSC.
- K. S. Woo, Y. Wang, J. Kim, Y. Kim, Y. J. Kwon, J. H. Yoon, W. Kim and C. S. Hwang, Adv. Electron. Mater., 2019, 5, 1800543 CrossRef.
- A. R. C. Bredar, A. L. Chown, A. R. Burton and B. H. Farnum, ACS Appl. Energy Mater., 2020, 3, 66 CrossRef CAS.
- H. Jang, D. McCormack and F. Tong, PLoS Biol., 2021, 19(12), e3001418 CrossRef CAS PubMed.
- Y. LeCun, C. Cortes and C. J. C. Burges 1998. The MNIST Database of Handwritten Digits. New York, USA. https://yann.lecun.com/exdb/mnist/.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00493g |
| ‡ N. Ghenzi and T.W. Park contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |