Open Access Article
Open Access ArticleUltrahigh-power-density BNT ferroelectric multilayer ceramic capacitors for pulse power energy conversion components†
Canyu
Che
 ab,
Yizheng
Bao
ab,
Yizheng
Bao
 b,
Zimeng
Hu
b,
Qiu
Feng
c,
Meng
Xie
b,
Zimeng
Hu
b,
Qiu
Feng
c,
Meng
Xie
 b,
Bin
Zhou
b,
Jia
Yang
d,
Hengchang
Nie
*ab,
Zhipeng
Gao
b,
Bin
Zhou
b,
Jia
Yang
d,
Hengchang
Nie
*ab,
Zhipeng
Gao
 *cd and
Genshui
Wang
*ab
*cd and
Genshui
Wang
*ab
aSchool of Chemistry and Materials Science, Hangzhou Institute for Advanced Study, University of Chinese Academy of Sciences, Hangzhou 310024, China. E-mail: sestonenhc@mail.sic.ac.cn; genshuiwang@mail.sic.ac.cn
bKey Laboratory of Inorganic Functional Materials and Devices, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200050, China
cJoint Laboratory for Extreme Conditions Matter Properties, Southwest University of Science and Technology, Mianyang 621002, China. E-mail: z.p.gao@foxmail.com
dInstitute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China
First published on 18th September 2024
Abstract
Ferroelectric (FE) materials are promising for applications in advanced high-power density systems/energy storage and conversion devices. However, the power density of ceramic components is limited by the electrode area and breakdown strength of bulk ceramic, while the multilayer structure is effective in enhancing the breakdown strength and realizing miniaturization. In this work, Bi0.5Na0.5TiO3–BiAlO3–NaNbO3 multilayer ceramic capacitors (BNT–BA–NN MLCCs) were prepared as pulse power energy conversion components. The electrical properties of MLCCs with different layer thicknesses under temperature and pressure fields were investigated. The relaxor phase was observed in thin layer MLCCs, which was beneficial for pressure depolarization but led to a reduction in remnant polarization (Pr) and temperature stability. Therefore, MLCCs with an appropriate layer thickness are needed to satisfy energy conversion application. Results reveal that Pr is up to 39 μC cm−2 and Eb increased to more than 26 kV mm−1 in BNT–BA–NN MLCCs. On this basis, an ultrahigh output power density up to 2.2 × 109 W kg−1 (GW kg−1) with an output voltage up to 9.8 kV mm−1 is achieved in shock wave measurements, which is superior to that of the reported materials applied in high power pulse sources. The design of MLCCs provides an effective method to satisfy miniaturization and integration requirements for high-power applications.
Introduction
The growing global demand for energy has led to a booming development in the field of energy conversion encompassing electrochemical capacitors, electrochemical batteries, thermal cells and other devices.1 However, electrochemical batteries and capacitors do not meet the specific requirements for long storage duration and high current or voltage power supply in pulse power energy conversion. Pulse power energy conversion is an important technology that plays a significant role in renewable energy, mining and medical industries, such as remote power supplies; mineral, gas and oil explorations and geology-prospecting systems.2,3 Ferroelectric (FE) materials are critical in the field of pulse power energy conversion owing to their rapid response to external stimulus. Among this, shock wave compression drives poled FE materials to release bound electric charges within a rapid period of time (∼μs), generating sharp current/voltage in the megawatt (MW) range.4,5 The energy density is calculated as follows:| e = Pr × Eb | (1) |
Lead-based material Pb0.99(Zr0.95Ti0.05)0.98Nb0.02O3(PZT 95/5) has been considered the most suitable material for ultrahigh-power sources owing to its pressure-driven ferroelectric-antiferroelectric (AFE) phase transition properties under low pressure with high Pr (∼32 μC cm−2) and excellent breakdown strength.6 Bi0.5Na0.5TiO3,7 AgNbO3,8 (K,Na)NbO3,9 BiFeO310 and other materials based on pressure-driven phase transition have been thoroughly explored in response to the demand for ecologically friendly materials. Meanwhile, researchers have sought other alternative materials through various ways, such as chemical modification doping,11 microgeometry effects12 and thin films.13 However, the majority of studies focus on ceramics. The output current/voltage of ceramic components is limited by the electrode area of ceramic components, and the likelihood of a breakdown is further increased by defects and microcracks in bulk ceramic.
Multilayer ceramic capacitors (MLCCs) play an important role in many applications.14,15 Moreover, because breakdown strength (Eb) is correlated with strains and declines exponentially with grain size or sample thickness, MLCCs can be produced to increase Eb.16–18 At present, this structure is used in studies on multilayer piezoactuators and dielectric energy storage,19,20 and it is also an effective method to realize a modular assembly with higher energy level range.21 The bulk ceramic series stacking structure is used for greater power in order to produce more charge, which causes large size and weight in many high-power pulse applications. One efficient way to store additional surface shielding charge is to increase the electrode area. This strategy could make it possible to miniaturize energy storage devices. For example, Shkuratov et al. found that the multilayer structure based on PZT95/5 achieved four orders of magnitude higher performance than that of other types of energy storage devices with an energy density of 3 J cm−3 and power density approximately of 2.4 × 108 W kg−1. Because the number of layers can be adjusted to accommodate different current and voltage levels, this device can meet the requirements for integration and miniaturization for emerging pulse power applications.22
With its distinct oxygen octahedral torsion and cationic displacement superlattice perovskite structure, BNT exhibits a wide range of remarkable electrical properties. Generally, excellent remanent polarization can be obtained in BNT-based materials via appropriate element doping or solid solution formation. For example, the Pr of pure BNT ceramics is ∼38 μC cm−2, while a much higher Pr of 52 μC cm−2 is achieved by forming a solid solution with bismuth aluminate. The BiAlO3 added in small amounts can amplify rhombohedral distortion. The reduction of leakage current and improved sintering behavior can be achieved by appropriately substituting Mn ions into the B site.23 Moreover, owing to the low bulk density being only 66% that of PZT95/5 and the unique relaxor properties, the lead-free BNT-based material is superior as a pulse power source. The ferroelectric-relaxor (FE-RE) phase transition accompanied by a decline in Pr is widely observed in BNT-based materials by modifying the composition or increasing the temperature. Peng et al. found that the introduction of NaNbO3 optimized the phase-transition temperature and pressure in BNT–BA systems. The Bi0.5Na0.5TiO3–BiAlO3–NaNbO3 system (BNT–BA–NN) exhibits enhanced ferroelectric properties.24 A high charge density J (∼38 μC cm−2) was released in a short-circuit under 8.2 GPa and output voltage of ∼25 A (16 mm × 9 mm × 2 mm).7 Thus, BNT–BA–NN is a very potential pulse power source material, and further application of lead-free materials remains to be developed.
Therefore, in this work, as shown in Fig. 1, multi-composition solid solution 0.99((Bi0.5Na0.5)(Ti0.995Mn0.005)O3–0.01BiAlO3)–0.01NaNbO3 (BNT–BA–NN) MLCCs with different layer thicknesses were prepared by the tape-casting method. Various investigations concerning the electrical properties under various temperatures and electric fields were carried out. The change of the property caused by the phase structure in MLCCs with different thicknesses was further characterized. In particular, the depolarization under hydrostatic pressure and shock compression was investigated. A well-developed electrical square current curve was obtained in a dynamic discharging process within 0.3 μs. The output voltage was significantly improved to 9.8 kV mm−1, and a power density of 2.2 × 109 W kg−1 was achieved for the MLCC with a thickness of 35 μm, indicating that the BNT-based multilayer capacitors have great potential for the application of the ultrahigh power density power source for power-electric conversion.
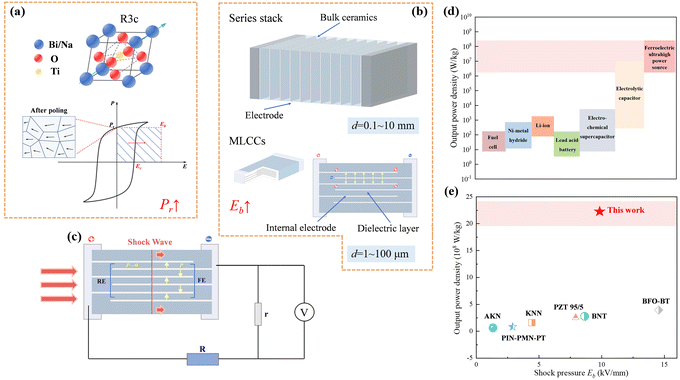 | ||
| Fig. 1 (a) Structure diagram of the BNT and the illustration of energy density in depolarized energy-conversion process; (b) schematics of bulk ceramics and multilayer structure; (c) schematic of the experimental shock-wave loading; (d) plot of specific power for various electrical energy storage devices1,24–26 and comparison of actual output power density and Eb in shock pressure experiments.8–10,22,27,28 | ||
Materials and methods
Solid solutions of 0.99((Bi0.5Na0.5)(Ti0.995Mn0.005)O3–0.01BiAlO3)–0.01NaNbO3 (BNT–BA–NN) were fabricated by the conventional solid-state reaction method. The initial powders of Bi2O3 (99.9%), NaHCO3 (99.5%), TiO2 (99.38%), Al2O3 (99.0%), Nb2O5 (99.5%), and MnCO3 (99.9%) were weighted according to the required composition, then mixed and ball-milled in a planetary ball mill for 4 h. After drying, all the powders were calcined at 650 °C for 2 h in air. Calcined powders were ball-milled twice with the decreasing size of balls for refining the grain size.The BNT–BA–NN multilayer ceramic capacitors were fabricated by the tape-casting method. The ceramic powders of BNT–BA–NN after secondary ball-milling were used for the slurry to make layers. The quantity of ceramic powder (44 wt%), 3.8 wt% PVB (polyvinyl butyral), 1.7 wt% DOP (butyl octyl phthalate), and 0.5 wt% of a dispersant agent were added with ethyl alcohol and ethyl acetate (50 wt%) solvent, and the mixture was ball-milled for 4 h. The resulting slurry was further utilized to form cast films via tape-casting, screen printed to produce the Ag/Pd inner electrode with the total area before sintering of about 1.8 mm2, then stacked and laminated (65 MPa at 65 °C). The organic compound was burned out at 330 °C for 5 h. Thereafter, the multilayer ceramics were co-fired with Ag/Pd internal electrodes at 1080 °C for 2 h in air in the pre-fired powder with the same ingredients. The thickness of the layer after sintering was about 28–88 μm, and these samples were abbreviated herein as BNT-28 μm, BNT-35 μm, BNT-78 μm, and BNT-88 μm.
The crystal structure of ceramics was studied by X-ray diffraction (XRD, D/MAX-2550V, Rigaku, Tokyo, Japan). GSAS software was used to fine-fit the full spectrum to obtain specific cell parameters and phase content results. The microstructure was observed using a TM3000 Tabletop Microscope (Hitachi, Tokyo, Japan). The samples were poled with a DC field of 10 kV mm−1 at 22 °C for 10 min. The dielectric properties were tested by a Hewlett Packard LCR meter. The pyroelectric coefficient p was calculated from the current measured using a Keithley 6517A electrometer/high resistance meter. The thermally-stimulated discharge current test (TSDC) was implemented by a broadband dielectric impedance Alpha spectrometer (Novocontrol Technologies, Montabaur, Germany). The chemical bonds and structural changes of BNT MLCCs were analysed by a LabRAM HR 800 UV micro-Raman spectrometer. The selected area electron diffraction and domain morphology observation were performed using a JEM-2100F field-emission transmission electron microscope (FE-TEM, JEOL, Japan). The specimens for TEM were prepared by an FIB-SEM (Thermo Fisher Scios2, America). The pressure-dependent polarization–electric field (P–E) loops and current–electric field (I–E) curves were measured with an aixACCT TF2000 Analyzer (aixACCT Co., Aachen, Germany). The shock compression experiment was conducted in a normal mode with the polarization direction perpendicular to the shock wave achieved using the one-stage gas gun technique. The voltage signals were recorded using an oscilloscope with a current viewing resistor (r) of 0.8 Ω.
Results and discussion
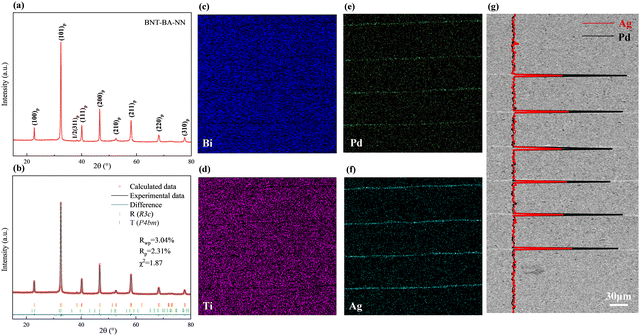
The room-temperature XRD pattern of the BNT–BA–NN ceramic powder is shown in Fig. 2(a), demonstrating a pure perovskite structure. Two adjacent octahedral [TiO6] with antiphase twisting as (a−a−a−) along the [111]p direction leads to a corresponding 1/2(311)p superlattice peak near 38.5° in BNT-based materials.29 The (111)p characteristic peak near 40° split into two peaks, (300)p and (021)p, while the (200)p peak near 45° is a single peak. In order to identify the phase structure for sample in detail, Rietveld refinement using the GSAS software was carried out. The BNT-based sample was refined by a rhombohedral state with the space group of R3c and P4bm. The perfect fitting curve and low reliability factor indicated that the B-site elements diffuse into the BNT lattice and then form a unified solid solution.Fig. 2 shows the micromorphology of the multilayer structure. Fig. 2(c) and (d) display the energy-dispersive spectra (EDS). The section's major-element distribution analysis further reveals that while Ag and Pd primarily gathered in the electrode layer, important elements like Bi and Ti elements are uniformly distributed in the dielectric layer. As shown in Fig. 2(e) and (f), the SEM images of the multilayer section illustrates that the internal electrodes of the multilayer ceramics are complete and uninterrupted. In addition, EDS line scan analysis of the Ag/Pd element based on a high-magnification SEM image further indicates that although bismuth-based materials may react with palladium, which promotes the formation of secondary phases at the interfaces,30 Ag and Pd are only detected at the corresponding site of the inner electrode layers with the ratio of Ag/Pd being essentially 70/30. However, the ionic radius of Ag+ is close to the average ionic size of the A-site cations; thus, a trace of solid solution may be present.31 Accordingly, negligible migration may cause the slightly lower ratio.
Fig. 3 shows the SEM images and the grain size distribution of ceramics. The ceramics exhibit dense microstructures with uniformly distributed grains and clear grain boundaries, indicating excellent crystallinity. The low sintering temperature of 1080 °C is beneficial for the reduction of grain size and the volatilization of ions compared to the high temperature over 1130 °C for solid-state ceramic sintering. Combined with the grain size distribution in Fig. 3(a)–(h), the influence of the particle size of the ceramic powder is explored. The MLCC prepared from the powder without further grinding had an average grain size of 2.29 μm. This is related to the process of grain growth. When the powder with poor uniformity is sintered, the larger grain grows first and absorbs the surrounding small grains. After the reduction of size and thickness, the average grain size of MLCCs further decreased to 0.74 μm. Also, the relatively small grain size is beneficial for the improvement of Eb.
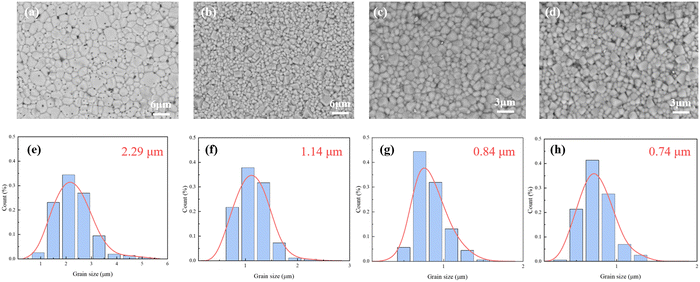 | ||
| Fig. 3 SEM images and grain size distribution of the BNT–BA–NN MLCCs: (a) and (e) BNT-88 μm; (b) and (f) BNT-78 μm; (c) and (g) BNT-35 μm; (d) and (h) BNT-28 μm. | ||
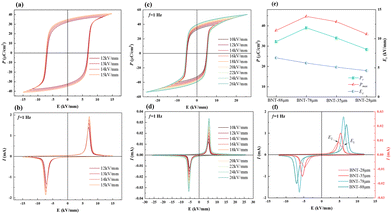
Fig. 4 depicts the polarization–electric field hysteresis loops (P–E) and current–electric field curves (I–E) of the BNT MLCCs measured at room temperature. It can be seen that the BNT sample has typical ferroelectric characteristics with square-typed P–E loops, in which the Pr and Pmax gradually becomes larger with the increase in the electric field. Due to the influence of material thickness on the scattering of conductive filaments during the breakdown process, the breakdown strength of dielectrics is found to increase with decreasing ceramic thickness.32 It supports that the Eb of BNT-88 μm MLCC is over 15 kV mm−1, while the Eb of bulk ceramics is always under 10 kV mm−1 and Pr is up to 38 μC cm−2. Moreover, the Eb of BNT-35 μm MLCC is significantly increased to 26 kV mm−1, which is better than that of bulk ceramics and large-size samples with thick layers. The Pr can reach 39 μC cm−2 under an electric field of 26 kV mm−1.
In contrast to the double current peaks in thicker layer MLCCs, the BNT-28 μm shows four current peaks and the first and third quadrants of the I–E loop with decreased coercive field (Ec) in the P–E loop (Fig. 4, S1). The observation of four current peaks in the I–E loops of BNT-based materials has previously been associated with a field-induced phase transition between a weak tetragonal polar phase and a strong polar rhombohedral phase. The phase transition induced by polarization can be described as R3c/P4bm → R3c/P4mm → R3c.33 The BNT has a polar structure at the maximum applied field, and the polar structure remains upon unloading. With the reversal of the applied field, the polar phase transforms back to the weakly polar phase corresponding to current peak E2. With the increase in negative applied field, the weakly polar phase changes again to the polar structure corresponding to current peak E1. It is found that Ec is directly proportional to the layer thickness, which is also directly proportional to the grain size. Since the size of the domain is related to the grain size, the domain can switch easily due to the refinement of grain and the pressure from internal stress. In addition, the Pmax of MLCCs decrease with decreasing thickness. It is suggested that the domain switching in the MLCC becomes difficult due to the clamping effect on volume change, leading to decreasing polarization.34,35 The BNT-88 μm MLCC prepared from powder without further grinding has an average grain, and it is significantly larger than that of other MLCCs. Since the size of the domain is related to the grain size, BNT-88 μm MLCCs have larger domains than the other samples. The formation of microdomains and macrodomains are driven by oriented ferroelectric nanodomains, and a fast response of the domains under the action of an electric field can be achieved with more nanodomains.36 The Ec of BNT-88 μm increases to 7 kV mm−1, which is significantly higher than that of other MLCCs (∼5 kV mm−1). The electric field is more than double the Ec of other MLCCs when it further increases to 12 kV mm−1. The application of a large electric-field forcibly merges nanodomains into the surrounding lattice, resulting in greater polarization intensity under the same electric field in the other MLCCs and smaller polarization intensity in BNT-88 μm MLCCs.
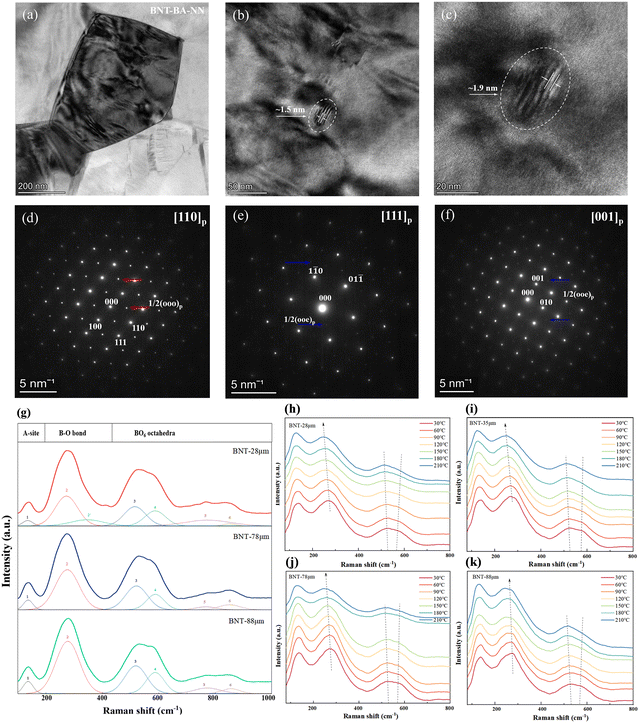
To further explore the intrinsic relationship between the macroscopic properties and microstructure of ceramics, bright-field TEM micrographs and selected-area electron diffractions (SAED) patterns of the BNT–BA–NN ceramic between the electrodes are shown in Fig. 5. As seen in Fig. 5(a), BNT-MLCC displays small grain size and clear grain boundary. Small nanodomains with dimensions of about 1–2 nm are observed in Fig. 5(b) and (c). It should be noted that the SAED images along the [110]p, [111]p and [001]p zone axis show clear 1/2(ooo)p and weak 1/2(ooe)p (hereafter, “o” and “e” refer to odd and even hkl indexes) superlattice reflection (see the blue and red arrow), respectively.37 The 1/2(ooo)p spots indicate the presence of the polar R3c symmetry with anti-phase a+−a−a− oxygen octahedron tilt, which contributes to the induction of high polarization upon applied electric fields.33,38 Besides, the 1/2(ooe)p reflection spots indicate the in-phase a0a0c+ oxygen octahedral tilting.39 This phenomenon implies the coexistence of the R3c (rhombohedral, R) and P4bm (tetragonal, T) phase in the crystal structure and is different to the XRD pattern of the same component ceramic with R3c. The relaxor behavior can also be proved by the four current peaks. The existence of the P4bm phase means the enhancement of relaxation characteristics by the preparation method and specifications of capacitors.
The room-temperature Raman spectra of the dielectric layer of the BNT MLCCs samples in the range of 100–1000 cm−1 are shown in Fig. 5(c). The six major vibration modes shown in the spectra are in agreement with the reported results.40,41 Corresponding to the A1(TO1) mode, the Raman modes ranging from 100 cm−1 to 180 cm−1 are related to the A-site vibration in the perovskite with the general formula ABO3.42,43 Peaks between 200 cm−1 and 400 cm−1 are ascribed to the vibrational modes of the B–O bond, which is associated with short-range Ti–O bond vibrations. The vibrational mode of the BO6 octahedron is indicated by the modes at 400–700 cm−1, which is the bending and stretching of the oxygen octahedra.44 Finally, the last two modes between 700 cm−1 and 900 cm−1 can be correlated to the presence of oxygen vacancies.45,46 The local structure of the samples with decreasing layer thickness transitions from rhombohedral to mixed phases of rhombohedral–tetragonal, as indicated by the splitting of B–O bonds at 250–350 cm−1 and the diffusion and broadening of the oxygen octahedral vibrational mode at 450–650 cm−1.40,47 It demonstrates that the relaxor phase is enhanced by the refinement of grain and thinning layer thickness of the device structure, which is consistent with the SAED result.
Fig. 5(b) and (e) shows the temperature-dependent Raman spectra of BNT MLCCs ceramics in the range of 30–210 °C. The changes in the peaks intensity and Raman shifts are observed during the heating period, indicating structural phase transformation. In all the samples, the peaks at 200–400 cm−1 associated with the short-range Ti–O bond move to lower wave number, supporting that spontaneous polarization decreases with increasing temperature. For the (TO3) mode at 400–700 cm−1, it can be linked to the mixture of the rhombohedral R3c and tetragonal P4bm crystal structure, which is related to the FE-RE phase transition.48 The intensity of peak 3 gradually increases while the intensity of peak 4 decreases, and the two peaks move towards high wavenumber and low wavenumber, respectively. With the increase in the layer thickness, the right peak decreases more slowly (Fig. 5(b)–(d)), which also corresponds to the temperature-induced phase transition in the P–E loop and temperature-dependent dielectric permittivity εr.
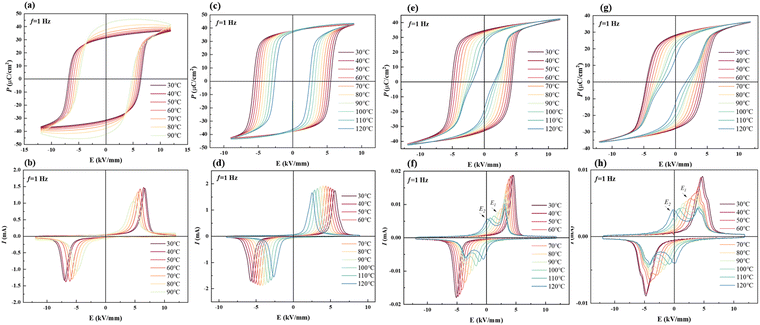
The temperature-dependent electrical properties are usually used to analyse the temperature stability of materials. Fig. 6 shows temperature-dependent P–E loops in all the samples. The decreasing Ec with increasing temperature indicates that the temperature decreases the barrier of domain switching. Fig. 6(a) and (b) show that the P–E loop of BNT-88 μm MLCC is abnormal when it exceeds 80 °C. In Fig. S2(a) (ESI†), high temperature loss indicates the influence of leakage current and εr and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ rise abnormally before reaching 100 °C. Nevertheless, BNT-78 μm MLCC prepared by grinding for further grain refinement shows more stable electrical property in Fig. 6(c) and (d). Pr basically does not vary with temperature, indicating that the depolarization temperature is above 120 °C. Due to the defects in larger grains, it is more likely to generate leakage current, leading to unstable electrical performance. With the refinement of grain, the increase in the grain boundary leads to a reduction in the leakage current. In Fig. S2(c) (ESI†), the sharp change in the dielectric permittivity εr and loss tan
δ rise abnormally before reaching 100 °C. Nevertheless, BNT-78 μm MLCC prepared by grinding for further grain refinement shows more stable electrical property in Fig. 6(c) and (d). Pr basically does not vary with temperature, indicating that the depolarization temperature is above 120 °C. Due to the defects in larger grains, it is more likely to generate leakage current, leading to unstable electrical performance. With the refinement of grain, the increase in the grain boundary leads to a reduction in the leakage current. In Fig. S2(c) (ESI†), the sharp change in the dielectric permittivity εr and loss tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curves at about 98 °C correspond to FE-RE phase transition. The temperature related to phase transition is considered as the depolarization temperature (Td), which is consistent with the peak in the temperature-dependent pyroelectric performance in Fig. S3 (ESI†). Fig. 6(e)–(f) shows that with the increase in temperature, the slightly pinched P–E loops and four-peak I–E curves indicate that this solid solution tends to depolarize at a temperature near Td.49 The temperature of BNT-28 μm as the four current peaks appear is lower than that of the thick layer samples. When the temperature is increasing, the activity of the polar regions increases and becomes more unstable, and the sample exhibits relaxor characteristics at high temperature. Pr decreases obviously, the reverse electric field E2 becomes lower and the distance between the four current peaks is increased.44,50 This result suggests that the leakage current can be reduced with the refinement of grains but the depolarization temperature can be decreased with the increase in the relaxor phase by thinning the layer thickness and reducing the grain size.
δ curves at about 98 °C correspond to FE-RE phase transition. The temperature related to phase transition is considered as the depolarization temperature (Td), which is consistent with the peak in the temperature-dependent pyroelectric performance in Fig. S3 (ESI†). Fig. 6(e)–(f) shows that with the increase in temperature, the slightly pinched P–E loops and four-peak I–E curves indicate that this solid solution tends to depolarize at a temperature near Td.49 The temperature of BNT-28 μm as the four current peaks appear is lower than that of the thick layer samples. When the temperature is increasing, the activity of the polar regions increases and becomes more unstable, and the sample exhibits relaxor characteristics at high temperature. Pr decreases obviously, the reverse electric field E2 becomes lower and the distance between the four current peaks is increased.44,50 This result suggests that the leakage current can be reduced with the refinement of grains but the depolarization temperature can be decreased with the increase in the relaxor phase by thinning the layer thickness and reducing the grain size.
The force-electric energy conversion of ferroelectric materials can be reflected by the electrical properties under hydrostatic pressure. The P–E and I–E loops of BNT MLCCs under pressure are shown in Fig. 7. It can be observed that the Ec of the two samples decrease with the increase in pressure, which proves that the barrier of domain switching decreases with the increase in pressure. As noted in some studies on relaxor ferroelectrics, pressure tends to cause a reduction in the correlation length or radius between clusters as well as in the size of the polar domains.51 For this reason, the P–E loops bundle with the increase in pressure, and the I–E curve shows four current peaks, corresponding to the pressure-driven FE-RE transition.52,53 The separation between the current peak E1 representing ferroelectric domain flipping and the current peak E2 representing FE-RE transition gradually increase with pressure loading, indicating that the FE-RE phase transition is easier and the relaxor phase region becomes larger. The pressure is conducive to breaking the long-range ordered ferroelectric structure and the formation of short-range ordered polar nanoscale PNRs. In addition, the Pmax of the two samples decrease with the pressure applied. The energy barrier for the formation of FE domains in relaxors increases with the external pressure applied.54,55 It proves that the relaxor phase is exhibited in BNT-28 μm at room temperature and Pmax decreases with the increase in clamping stress in samples with the same composition but reduced active thickness in Fig. 4. Compared with BNT-35 μm, BNT-28 μm obviously showed narrower P–E loops under the same pressure with lower Pr, and the I–E curve with the four current peaks appeared under lower pressure. Hence, with the influence of MLCCs thickness design, the sample is more prone to the FE-RE transition when the internal stress increases, and the MLCCs with moderate thickness and clamping stress are more favorable to meet the requirements of residual polarization intensity.
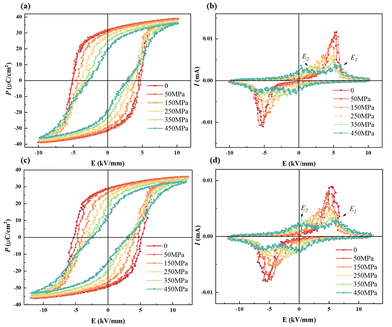 | ||
| Fig. 7 Pressure-dependent P–E and I–E loops of BNT MLCCs: (a) and (b) BNT-35 μm and (c) and (d) BNT-28 μm. | ||
For the high Pr of 39 μC cm−2and the Eb of 26 kV mm−1, the BNT-35 μm MLCC was chosen to conduct the depolarization measurement. From the viewpoint of application, the depolarization process of poled MLCCs under in situ hydrostatic pressure and shock wave compression is used to evaluate force-electric conversion capacity, as shown in Fig. 8(a). Unlike PZT-based materials, no obvious depolarization step or critical pressure point appeared. Compared to other BNT-based ferroelectric materials, the BNT MLCC is more prone to FE–RE phase transition and releases 33% of the remnant polarization at 400 MPa, consistent with the variation of Pr under hydrostatic pressure, which exhibits positive force-electric conversion ability. BNT-35 μm MLCC released 37 μC cm−2 of the remnant polarization in 0.3 μs (Fig. 8(b)) with an energy density of 2.13 J cm−3, which is comparable to that of PZT95/5 ceramics.56 The output voltage is up to 9.8 kV mm−1 (with 200 Ω resistor) at 6.3 GPa shock wave compression. Due to the presence of the inactive microregion in the front of the multilayer capacitor, the increasing bound charges caused by piezoelectric effects result in the appearance of a negative current at the front end of the current signal. The output power density (Poutput) formula of ferroelectric materials,9
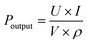 | (2) |
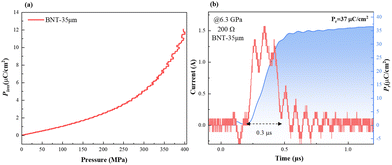 | ||
| Fig. 8 (a) Depolarization under in situ hydrostatic pressure of poled BNT-35 μm; (b) dynamic response behavior of BNT-35 μm with a 200 Ω resistor under 6.3 GPa shock pressure. | ||
Conclusions
In summary, lead-free BNT-based MLCCs were successfully constructed via the tape-casting method. High Pr was obtained by BNT–BA–NN MLCCs. Significantly, the Eb increased to more than 26 kV mm−1 and the output voltage was up to 9.8 kV mm−1 with load resistor in shock wave compression, indicating that the thin layering of the ceramic dielectric can improve the Eb. A high output power density up to 2.2 × 109 W kg−1 was achieved in BNT MLCCs. In addition, the ferroelectric properties and in situ depolarization properties under hydrostatic pressure confirmed the pressure-driven FE-RE phase transitions in the BNT MLCC dielectric layer, and the relaxor phase increased with decreasing layer thickness. This work has revealed the great charm and potential of BNT MLCCs as excellent ultrahigh power density sources for energy storage.Data availability
The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. U2002217) and Student Training Program for Innovation and Entrepreneurship of Hangzhou Institute for Advanced Study, UCAS(CXCY20230305).Notes and references
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- R. E. Setchell, in AIP Conference Proceedings, AIP, Atlanta, Georgia (USA), 2002, vol. 620, pp. 191–196 Search PubMed.
- L. L. Altgilbers, Acta Phys. Pol. A, 2009, 115, 1040–1043 CrossRef CAS.
- S. I. Shkuratov and C. S. Lynch, J. Materiom., 2022, 8, 739–752 CrossRef.
- M. Xie, H. Nie, Z. Liu, T. Lu, Y. Liu and G. Wang, J. Am. Ceram. Soc., 2023, 106, 4678–4698 CrossRef CAS.
- R. E. Setchell, J. Appl. Phys., 2005, 97, 013507 CrossRef.
- P. Peng, H. Nie, G. Wang, Z. Liu, F. Cao and X. Dong, Appl. Phys. Lett., 2018, 113, 082901 CrossRef.
- Z. Liu, T. Lu, F. Xue, H. Nie, R. Withers, A. Studer, F. Kremer, N. Narayanan, X. Dong, D. Yu, L. Chen, Y. Liu and G. Wang, Sci. Adv., 2020, 6, eaba0367 CrossRef CAS PubMed.
- Z. Zhou, L. Fang, Z. Xiong, Y. Zhang, Y. Liu, G. Liu, Y. Liu, R. He, T. Han, J. Li, K. Wang and Z. Gao, Appl. Phys. Lett., 2023, 123, 012904 CrossRef CAS.
- Z. Zhou, Z. Gao, Z. Xiong, G. Liu, T. Zheng, Y. Shi, M. Xiao, J. Wu, L. Fang, T. Han, H. Liang and H. He, Appl. Phys. Lett., 2022, 121, 113903 CrossRef CAS.
- M. Xie, H. Nie, B. Han, Y. Bao, F. Cao and G. Wang, ACS Appl. Mater. Interfaces, 2024, acsami.3c16741 Search PubMed.
- J. Jia, H. Nie, X. He, C. Feng, M. Zhu, C. Wu, G. Wang and X. Dong, J. Am. Ceram. Soc., 2022, 105, 412–418 CrossRef CAS.
- S. I. Shkuratov, J. Baird, V. G. Antipov, C. S. Lynch, S. Zhang, J. B. Chase and H. R. Jo, J. Mater. Chem. A, 2021, 9, 12307–12319 RSC.
- K. Hong, T. H. Lee, J. M. Suh, S.-H. Yoon and H. W. Jang, J. Mater. Chem. C, 2019, 7, 9782–9802 RSC.
- Z. Yao, Z. Song, H. Hao, Z. Yu, M. Cao, S. Zhang, M. T. Lanagan and H. Liu, Adv. Mater., 2017, 29, 1601727 CrossRef PubMed.
- J. Li, Z. Shen, X. Chen, S. Yang, W. Zhou, M. Wang, L. Wang, Q. Kou, Y. Liu, Q. Li, Z. Xu, Y. Chang, S. Zhang and F. Li, Nat. Mater., 2020, 19, 999–1005 CrossRef CAS PubMed.
- H. Palneedi, M. Peddigari, G. Hwang, D. Jeong and J. Ryu, Adv. Funct. Mater., 2018, 28, 1803665 CrossRef.
- M. Feng, Y. Feng, T. Zhang, J. Li, Q. Chen, Q. Chi and Q. Lei, Adv. Sci., 2021, 8, 2102221 CrossRef CAS PubMed.
- C.-H. Hong, H.-P. Kim, B.-Y. Choi, H.-S. Han, J. S. Son, C. W. Ahn and W. Jo, J. Materiom., 2016, 2, 1–24 CrossRef.
- P. Zhao, Z. Cai, L. Wu, C. Zhu, L. Li and X. Wang, J. Adv. Ceram., 2021, 10, 1153–1193 CrossRef CAS.
- P. Lheritier, A. Torelló, T. Usui, Y. Nouchokgwe, A. Aravindhan, J. Li, U. Prah, V. Kovacova, O. Bouton, S. Hirose and E. Defay, Nature, 2022, 609, 718–721 CrossRef CAS PubMed.
- S. I. Shkuratov, J. Baird, V. G. Antipov, S. Zhang and J. B. Chase, Adv. Mater., 2019, 31, 1904819 CrossRef CAS PubMed.
- P. Peng, H. Nie, Z. Liu, W. Ren, F. Cao, G. Wang and X. Dong, J. Am. Ceram. Soc., 2017, 100, 1030–1036 CrossRef CAS.
- Z. Xiong, G. Liu, H. Nie, Y. Liu, Z. Gao, Q. Liu, X. Chen, J. Li, L. Fang, Q. Yang, X. Zhang, J. Tang, G. Wang and X. Dong, J. Am. Ceram. Soc., 2021, 104, 1169–1177 CrossRef CAS.
- N. Jha, P. Ramesh, E. Bekyarova, M. E. Itkis and R. C. Haddon, Adv. Energy Mater., 2012, 2, 438–444 CrossRef CAS.
- H. D. Abruña, Y. Kiya and J. C. Henderson, Phys. Today, 2008, 61, 43–47 CrossRef.
- A. A. Kebede, T. Kalogiannis, J. Van Mierlo and M. Berecibar, Renewable Sustainable Energy Rev., 2022, 159, 112213 CrossRef CAS.
- Z. Gao, W. Peng, B. Chen, S. A. T. Redfern, K. Wang, B. Chu, Q. He, Y. Sun, X. Chen, H. Nie, W. Deng, L. Zhang, H. He, G. Wang and X. Dong, Phys. Rev. Mater., 2019, 3, 035401 CrossRef CAS.
- S. I. Shkuratov, J. Baird, V. G. Antipov, E. F. Talantsev, J. B. Chase, W. Hackenberger, J. Luo, H. R. Jo and C. S. Lynch, Sci. Rep., 2017, 7, 46758 CrossRef PubMed.
- B. N. Rao, A. N. Fitch and R. Ranjan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 060102 CrossRef.
- D. Schuetz, W. Krauss, J. Albering, C. Kurta and K. Reichmann, J. Am. Ceram. Soc., 2010, 93, 1142–1147 CrossRef CAS.
- C. Neusel, H. Jelitto, D. Schmidt, R. Janssen, F. Felten and G. A. Schneider, J. Eur. Ceram. Soc., 2015, 35, 113–123 CrossRef CAS.
- C. Ma, H. Guo, S. P. Beckman and X. Tan, Phys. Rev. Lett., 2012, 109, 107602 CrossRef PubMed.
- L.-F. Zhu, L. Zhao, Y. Yan, H. Leng, X. Li, L.-Q. Cheng, X. Xiong and S. Priya, J. Mater. Chem. A, 2021, 9, 9655–9664 RSC.
- X. Wu, X. Lu, Y. Kan, F. Huang, J. Ma and J. Zhu, Appl. Phys. Lett., 2006, 89, 122910 CrossRef.
- S. Li, T. Hu, H. Nie, Z. Fu, C. Xu, F. Xu, G. Wang and X. Dong, Energy Storage Mater., 2021, 34, 417–426 CrossRef.
- D. Li, Y. Lin, M. Zhang and H. Yang, Chem. Eng. J., 2020, 392, 123729 CrossRef CAS.
- I. Levin and I. M. Reaney, Adv. Funct. Mater., 2012, 22, 3445–3452 CrossRef CAS.
- P. Shi, X. Zhu, X. Lou, B. Yang, X. Guo, L. He, Q. Liu, S. Yang and X. Zhang, Composites, Part B, 2021, 215, 108815 CrossRef CAS.
- A. Prado-Espinosa, J. Camargo, A. Del Campo, F. Rubio-Marcos, M. Castro and L. Ramajo, J. Alloys Compd., 2018, 739, 799–805 CrossRef CAS.
- I. G. Siny, E. Husson, J. M. Beny, S. G. Lushnikov, E. A. Rogacheva and P. P. Syrnikov, Ferroelectrics, 2000, 248, 57–78 CrossRef CAS.
- R. Kang, Z. Wang, W. Liu, L. He, X. Zhu, P. Shi, X. Zhang, L. Zhang and X. Lou, ACS Appl. Mater. Interfaces, 2021, 13, 25143–25152 CrossRef CAS PubMed.
- Z. Wang, R. Kang, L. Zhang, P. Mao, Q. Sun, F. Kang and J. Wang, J. Eur. Ceram. Soc., 2021, 41, 1917–1924 CrossRef CAS.
- D. Schütz, M. Deluca, W. Krauss, A. Feteira, T. Jackson and K. Reichmann, Adv. Funct. Mater., 2012, 22, 2285–2294 CrossRef.
- M. Zannen, A. Lahmar, M. Dietze, H. Khemakhem, A. Kabadou and M. Es-Souni, Mater. Chem. Phys., 2012, 134, 829–833 CrossRef CAS.
- R. Selvamani, G. Singh, V. Sathe, V. S. Tiwari and P. K. Gupta, J. Phys.: Condens. Matter, 2011, 23, 055901 CrossRef PubMed.
- Y. Ding, J. Liu, C. Li, W. Bai, S. Wu, P. Zheng, J. Zhang and J. Zhai, Chem. Eng. J., 2021, 426, 130811 CrossRef CAS.
- X. Liu, J. Zhai and B. Shen, J. Am. Ceram. Soc., 2018, 101, 5604–5614 CrossRef CAS.
- J. Zhang, Z. Pan, F.-F. Guo, W.-C. Liu, H. Ning, Y. B. Chen, M.-H. Lu, B. Yang, J. Chen, S.-T. Zhang, X. Xing, J. Rödel, W. Cao and Y.-F. Chen, Nat. Commun., 2015, 6, 6615 CrossRef CAS PubMed.
- H. Zhang, M. Krynski, A. D. Fortes, T. G. Saunders, M. Palma, Y. Hao, F. Krok, H. Yan and I. Abrahams, J. Am. Chem. Soc., 2024, 146, 5569–5579 CrossRef CAS PubMed.
- G. A. Samara, Phys. Rev. Lett., 1996, 77, 314–317 CrossRef CAS PubMed.
- Z. Liu, W. Ren, H. Nie, P. Peng, Y. Liu, X. Dong, F. Cao and G. Wang, Appl. Phys. Lett., 2017, 110, 212901 CrossRef.
- P. Peng, H. Nie, G. Cheng, Z. Liu, G. Wang and X. Dong, J. Appl. Phys., 2018, 123, 114102 CrossRef.
- Z. Zhao, Y. Cao and R. E. García, J. Eur. Ceram. Soc., 2017, 37, 573–581 CrossRef CAS.
- Y. Lin, H. Nie, M. Xie, F. Cao, P. Peng and G. Wang, Appl. Phys. Lett., 2023, 123, 083903 CrossRef CAS.
- S. I. Shkuratov, J. Baird, V. G. Antipov, E. F. Talantsev, H. R. Jo, J. C. Valadez and C. S. Lynch, Appl. Phys. Lett., 2014, 104, 212901 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03279a |
| This journal is © The Royal Society of Chemistry 2024 |