 Open Access Article
Open Access ArticleTuning the phase separation of cellulose nanocrystals with hydrolysis times: influence of effective dimensions†
Shiyao Hong a,
Ashley Beanb,
Yuan Fangc,
Nathalie Lavoine
a,
Ashley Beanb,
Yuan Fangc,
Nathalie Lavoine *a and
Lucian Lucia
*a and
Lucian Lucia *ab
*ab
aDepartment of Forest Biomaterials, College of Natural Resources, North Carolina State University, Raleigh, NC 27695, USA. E-mail: nmlavoin@ncsu.edu; lalucia@ncsu.edu
bDepartment of Chemistry, College of Sciences, North Carolina State University, Raleigh, NC 27695, USA
cPepsiCo, Valhalla, NY 10595, USA
First published on 28th April 2025
Abstract
This study attempts to quantify a relatively unexplored and very important subject: cellulose nanocrystal (CNC) bundles and their effective dimensions on phase separation and subsequent chiral resolution in CNC suspensions. Currently, there is little data discussing how effective bundle dimensions affect the onset of chiral nematic phase formation despite the fact that theory and experimental data indicate they are important factors. The effect of the extent of hydrolysis on the phase behavior of CNC suspensions was analyzed by correlating it with the critical weight concentration (w0), which is the CNC weight corresponding to the onset of the chiral nematic phase. From Onsager theory and its extension, w0 is primarily a function of CNC size while surface charge exerts a non-negligible effect. CNCs were produced from never-dried bleached softwood pulp under varying acid hydrolysis times to systematically alter sizes and surface charges. Concentration-dependent phase diagrams were mapped to ascertain the w0 of the produced suspensions. The data revealed a clear decrease in w0 when the hydrolysis time increased from 25 to 90 minutes, despite similar individual CNC size and increasing surface charges. This latter discovery following shape and size distribution indicated an increased area-equivalent (AE) diameter from extended hydrolysis, suggesting particle aggregation/bundling. This result was corroborated by elevated particle surface charges from enhanced lateral adherence between CNCs. In contrast to our findings that higher surface charge reduces the effective diameter, the observed decrease in w0 suggests that an earlier onset of the anisotropic phase is driven by CNC bundles, which were more prevalent in samples with elevated surface charge. These observations indicate that CNC bundles play a significant role in promoting the anisotropic phase, counteracting the effect of surface charge on w0. This work therefore provides invaluable insights into the complex interplay of CNC surface charge, shape, and size by shedding light on the importance of hydrolysis time on particle aggregation and phase behavior in CNC suspensions.
Introduction
Liquid crystals (LCs) are substances that exist in a mesomorphic state characterized by a degree of molecular order intermediate between the highly ordered, three-dimensional positional and orientational arrangement of solid crystals and the disordered structure of isotropic liquids.1 This mesomorphic state, specifically known as the liquid crystal (LC) state, possesses long-range orientational order and either partial positional order or complete positional disorder. Consequently, liquid crystals exhibit anisotropic physical properties typical of crystalline solids while maintaining fluid-like behaviours, such as the ability to flow and form droplets. This dual characteristic enables LCs to adopt organized phases and display direction-dependent interactions with light, facilitating the formation of structurally tuneable colours.2Cellulose nanocrystals (CNCs) have garnered particular attention due to their renewable nature and inherent capacity to form liquid-crystalline mesophases composed of rigid, rod-like nanoparticles.3 Although CNCs are usually referred to as lyotropic LCs, this classification is not entirely precise. Unlike typical lyotropic mesophases that form through solvent-induced aggregation or micellization, CNC-based liquid crystals form due to their inherently rigid rod-like molecular structure, characterized by a persistence length comparable to their contour length and significantly greater than their diameter.4 Thus, the formation of CNC mesophases arises from direct interactions between rod-like molecular groups rather than solvent-induced aggregation, distinguishing CNC liquid crystals from conventional lyotropic systems.1
Remarkably, this liquid crystalline arrangement is maintained after water evaporation, allowing for the formation of iridescent films.4 These films exhibit unique optical properties, paving the way for applications ranging from biobased pigments to advanced smart devices like sensors and covert encryption.4,5 To further enhance and diversify the functionality of cellulose-based nanomaterials, a comprehensive understanding of the fundamental physico-chemical principles governing their phase behaviour is essential. Such deeper insight will enable more precise tailoring of their unique liquid crystalline properties, expanding their potential applications across various fields.
Sulphuric acid hydrolysis has been widely adopted as the primary and most common approach for CNC preparation due to its operational ease, efficiency, and induction of chiral properties.6 During hydrolysis, negatively charged sulphate half-ester groups are grafted onto the CNC surface on the oxygen of C6 of the cellulose polymer's topologic glucose monomers (Fig. 1).7 These anionic groups encourage colloidal stability in aqueous suspensions, but also increase CNCs' hydrophilicity, which can cause aggregation in high-ionic-strength environments.8,9
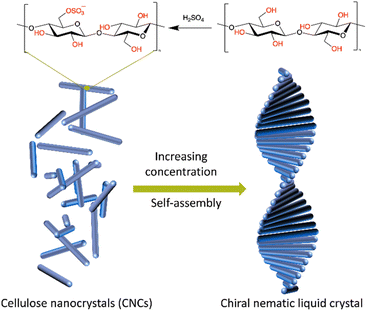 | ||
| Fig. 1 Illustration of the formation of chiral nematic structures of CNCs prepared from sulphuric acid hydrolysis. | ||
A physical property which is of great weight in the self-assembly process is CNC length. The length depends on both cellulosic source and hydrolysis conditions.10 Adjusting hydrolysis parameters—such as sulphuric acid concentration, reaction time, acid-to-pulp ratio, and temperature—offers the distinct opportunity to finely resolve CNC morphology. This precise tunability enhances scalability and functional adaptability, thus making CNCs highly versatile and attractive for various targeted applications.10,11
A previous study has indicated that harsher hydrolysis conditions (higher acid concentration, temperature, and prolonged reaction times) generally produce smaller CNCs with higher surface charges.8 The yield and crystallinity, however, display a parabolic relationship with hydrolysis harshness, i.e., they reach a maximum and subsequently rapidly diminish.8,12 Moreover, insufficiently intense hydrolysis fails to remove disordered regions, resulting in a lower yield of CNCs, while overly harsh conditions degrade crystalline regions reducing both yield and crystallinity.13
The specific influence of individual hydrolysis parameters on CNC characteristics remains challenging to quantify, and their relative importance may vary depending on reaction specifics. Among these parameters, hydrolysis time windows determines the extent of swelling in paracrystalline regions – areas that exhibit partial structural order, possessing characteristics intermediate between fully crystalline (highly ordered) and amorphous (disordered) phases.14 Longer hydrolysis times allows more cellulose chains to swell and undergo attack by sulphuric acid. The impact of hydrolysis time on CNC properties can also correlate with other hydrolysis conditions; for example, hydrolysis times significantly exert a noticeable impact on CNC length at moderately low acid concentrations (60–61%) and a mild temperature of 40 °C, while they significantly impact CNC diameter at higher temperatures (50–55 °C) across the full range of acid concentration.15 Moreover, pre-treatment such as kraft-pulping, bleaching, and drying methods tend to alter results from the reaction condition analysis.16
At low concentrations in water, negatively charged CNCs attain a isotropic colloidal dispersion due to interparticle electrostatic repulsions.4 However, as the concentration of CNC suspension increases, the CNCs adopt a nematic order in order to accommodate increased translational degrees of freedom, which in a non-intuitive way, allows the system to gain entropy.17 This transition is succinctly described by Onsager's theory,18 which identifies the two critical volume fractions determining phase stability: the isotropic phase becomes unstable at a specific volume fraction (Φ0), transitioning fully into the nematic phase at a higher volume fraction (Φ1). These critical volume fractions are defined theoretically by the following eqn (1) and (2) equations:18
 | (1) |
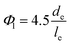 | (2) |
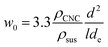 | (3) |
 | (4) |
Despite CNCs having a relatively low aspect ratio (generally < 100), Onsager's theory still provides useful qualitative insights into their phase behaviour. According to Onsager and eqn (1), the critical concentration of CNCs is inversely proportional to their individual crystal aspect ratio, a = l/d for neutral particles. Honorato-Rios et al.20 substantiated Onsager's theory by demonstrating as aspect ratio increases, critical weight concentration decreased, promoting chiral nematics and formation of an anisotropic phase. Further support was garnered by Zhang et al.21 who observed that CNCs with high aspect ratios required lower concentrations to form ordered matrices, in which longer CNCs achieved larger chiral pitches. A similar result was reported by Korolovych et al.,22 illustrating that CNCs with high aspect ratio tend to twist and aggregate, enhancing the helical organization and chiral nematic structure.
Additionally, accurate characterization of CNC dimensions is essential to provide a more complete understanding of phase formation. Conventional size measurements typically consider idealized individual, isolated CNC particles. However, in aqueous suspensions, CNC crystallites frequently adhere laterally, forming aggregates. In a recent unconventional departure from common practice, Parton et al.23 introduced an advanced characterization method considering rectangularity (R) and area-equivalent (AE) diameter, categorizing CNC particles into distorted crystallites, crystallites, bundles, and aggregations (see ESI, Fig. S3†). This comprehensive classification approach provides a more accurate global profile of CNC dimensions and their relationship to phase behaviour. Parton et al. successfully demonstrated that CNC bundles function as colloidal chiral dopants, driving molecular organization and formation of helical mesophases, which explains the observed increase in pitch upon sonication.23,24 Chiral dopants have been identified as crucial components in various systems beyond CNC suspensions. For instance, they play a significant role in colour information technologies, where they control and modify the alignment and helical twisting of liquid crystals, thereby modulating reflected light.25 Following up on Parton's23 research, a bottom-up approach using well-defined cellulose oligomers to investigate a chirality transition from the single oligomer to supramolecular assemblies was carried out by Fittolani et al.26 who also observed a similar role of bundles in chirality translation of CNCs.
Surface charge also significantly influences effective dimensions and subsequent phase behavior of CNCs. Abitbol et al.27 explored how variations in surface charge density (ranging from 0.116 to 0.337 e nm−2) affect phase separation in CNC suspensions with comparable particle sizes. Notably, their particle size analysis relied solely on individual CNCs measured by transmission electron microscopy (TEM), despite reporting substantial particle aggregation (50–60%). They observed that increasing the surface charge density, achieved by adjusting the acid-to-pulp ratio during hydrolysis, elevated the ionic strength within the system. Consequently, higher surface charges correlated with phase separation at increased CNC concentrations, yielding denser helical nematic phases accompanied by reduced suspension viscosity. This behavior arose from increased ionic strength reducing the Debye length, subsequently diminishing CNC effective diameter and thus delaying the onset of the nematic phase. The thinner electrostatic double layer provides CNC particles with more free volume for movement, potentially decreasing their tendency for early phase separation.27–29
In contrast, studies by Shafeiei-Sabet et al.30 and Beck et al.31 reported opposing results. These investigations observed a decrease in the critical concentration for anisotropic phase formation (w0) with increased surface charge density. However, both studies determined CNC particle size by measuring the hydrodynamic size rather than directly assessing aspect ratios. The omission of precise aspect ratio measurements introduced uncertainty, as differences in aspect ratio could significantly influence anisotropic phase formation, complicating direct comparisons and interpretations.
Given the existing divergences in findings, we further investigated the effect of CNC surface charge and effective dimension, which, in a complex interplay, influence each other, and consequently the formation of the anisotropic phase. Typically, the impact of dimensions and ionic strength are probed by altering the external environment of the CNC-water system by, for example, adding electrolytes and fractionating CNC suspensions.20,32 However, the surface charge is controlled during CNC synthesis, whereas changes in hydrolysis conditions can simultaneously alter multiple properties, leading to a complex change in CNC phase behaviour. Therefore, determining the impact of hydrolysis conditions on the phase separation requires a comprehensive determination of the combined effects of the surface charge and effective dimensions of all CNC particles in the system.
Thus, to address gaps on how hydrolysis conditions precisely affect phase formation of CNCs, we investigated hydrolysis time ranging from 25 to 90 minutes, focusing on the onset of the anisotropic phase. The surface charge of CNCs, determined by conductometric titration, increased with extended hydrolysis durations. Furthermore, critical concentrations correlating to the onset of nematic phase were determined from phase diagrams. The results were analysed in terms of CNC size with and without aggregations, as well as surface charge. Finally, the Debye length and effective diameter were calculated to more properly elaborate the factors controlling chiral organization of CNCs.
Experimental
Materials
Never-dried bleached Kraft softwood pulp was provided by WestRock (Covington, VA). Sulphuric acid (H2SO4) (70 wt%) for hydrolysis, Dowex Marathon C hydrogen form strong acid cation exchange resin (SAC) (mixture of styrene/divinylbenzene gel) for ion exchange, sodium hydroxide (NaOH), sodium chloride (NaCl), potassium hydrogen phthalate (C8H5KO4) for conductometric titration, and uranyl acetate (C4H6O6U) (UA) were all purchased from Fisher Scientific (Waltham, MA, US).Preparation of CNCs
The never-dried bleached softwood pulp was freeze-dried and ground into 2 mm powder using a Wiley mill (Thomas Scientific, Swedesboro, NJ, US). A sulphuric acid solution was prepared at 60 wt% and heated to 45 °C using a water bath. This temperature was maintained constantly across all hydrolysis experiments. For each batch of CNCs prepared, 10 g of dry pulp powder was mixed with the sulphuric acid to attain an acid-to-pulp ratio of 24. Different hydrolysis times, namely 25, 45, 60, and 90 min, were employed. The resultant samples were identified as W25, W45, W60, W90, respectively. Continuous stirring was applied during hydrolysis, which was terminated by quenching the reaction with addition of 10-fold deionized (DI) water followed by a 45 min ice bath. The suspension was centrifuged at 10K rpm for 10 min to achieve phase separation. The CNCs sedimented at the bottom of centrifuge bottles and were collected for further dialysis against deionized (DI) water until pH ∼ 5.Phase separation
Phase separation was performed according to Honorato-Rios et al.20 to determine the critical concentration at which phase separation occurs and map out the phase diagram of prepared CNC suspensions. A series of CNC suspensions of different solids content (1, 2, 3, 4, 5, 6 wt%) were prepared and placed in similar, closed volumetric glassware for phase separation observation through two crossed polarized films under ambient temperature.Size characterization
The morphology and size distribution of the CNCs were analysed by transmission electron microscopy (TEM) using a Bio-TEM (HT7800, Hitachi) at 120 kV. The TEM Formvar/carbon grids were cleaned using an ion beam etching system prior to receiving a drop of a 0.05 wt% CNC suspension. Negative staining of the particles was done by addition of uranyl acetate to the suspension over a 15 s reaction time. Image analysis was done on 200–300 particles per batch using ImageJ and MATLAB® for size distribution assessment.Surface charge measurement
Ion exchange was performed on the CNC suspensions using a strong acid cation exchange resin (SAC) prior to surface charge density measurement as reported by Abitbol et al.33 SAC was washed with Milli-Q (Millipore) water and poured into glass columns with fritted glass disks. The columns were tapped as necessary to remove air bubbles and settle the resin. The excess of Milli-Q water (>20 bed volumes) was drained slowly from the top of the resin column. CNC suspensions were diluted to 1 wt% and fed from the top through the column. The initial 2 bed volumes of eluate were discarded to avoid excessive sample dilution. A resin-to-CNCs ratio (g g−1) of 20.8 was used.Conductometric titration of the acid-form CNC suspensions was performed according to the CSA Z5100-14 standard.34 In brief, 10 mL of 1 wt% acid-form CNC suspension was diluted to 198 mL in Milli-Q water and sonicated to achieve a homogeneous suspension. 2 mL of 100 mM NaCl solution was added to increase conductivity to a measurable range (>100 µS cm−1). Under constant stirring, the suspension was titrated using sequential 100 µL aliquots of a 10 mM NaOH solution. The conductivity was measured at each interval in triplicate using a conductivity meter (Orion Versa Star Pro, Thermo Scientific).
Results and discussion
The effect of hydrolysis time on the onset of anisotropic phase
During hydrolysis, we observed a significant colour change (from white to brown) after 90 min of hydrolysis for our starting wood pulp material suggesting sugar oxidation occured. Therefore, the maximum hydrolysis time was determined to be less than 90 min to avoid saccharification. The critical concentration (w0) of our CNC suspensions exhibited a decreasing trend with increasing hydrolysis time (Fig. 2). We noticed a small amount of white precipitant at the bottom of the vials in W60 even at 1 wt%, which was further confirmed at all concentrations from 0.1 to 8 wt%. This indicates that rather than phase separation, large particles sedimented at low concentrations. The phase diagram experiments were replicated, yielding consistent results (Fig. S1†). Specifically, the critical concentration decreased from approximately 5–6 wt% to 2–3 wt% over extended hydrolysis durations. Similar sedimentation was also noted in W45 samples at very low concentrations, likely due to incomplete hydrolysis. In contrast, sedimentation observed in W60 samples was attributed primarily to particle aggregation as supported by subsequent shape analysis. | ||
| Fig. 2 Phase separation of CNC suspensions prepared from different hydrolysis times at different weight concentrations. Red circles indicate the observed aggregation appeared at low concentrations. | ||
Moreover, the white line observed in W90 is likely due to the formation of anisotropic phase of lighter density.35 This phenomenon may be linked to species of wood used and the freeze-drying of the wood pulp prior to the acid hydrolysis. Supporting this possibility, Rosa et al.35 previously reported the formation of similar low-density LC resulting from freeze–thaw cycles applied to CNC suspensions post-dialysis. In their case, the lower density phase emerged due to air initially dissolved in water becoming trapped within the CNC structure when the water froze into ice.
As shown in Fig. 3a, slight augmentation in the sulphur content on the surface of CNCs was observed with prolonged hydrolysis, aligning with findings from previous studies.16 Prior to titration, CNCs were subjected to complete protonation using a SAC resin.33 In line with findings reported by Abitbol et al.,33 the sulphur content of CNCs without SAC treatment closely resembled that observed after SAC treatment (Fig. S2†).33 Hence, we deduced that the as-treated sulphonated CNCs were fully protonated. However, due to changes in size of CNCs, the surface charge density remained similar for W25 and W45, while that of W60 and W90 increased to 0.42 and 0.62 e nm−2, respectively.
The critical concentration (w0) plotted in Fig. 3b as a function of the CNC sulphur content, established a good correspondence with the Debye length (13.81–49.89 nm) (see ESI†), which both decreased with increase in sulphur content. Our results agree with the work of Shafeiei-Sabet et al.30 and Beck et al.,31 where higher surface charge delayed the onset of anisotropic phase formation. In contrast, conflicting results reported by Abitbol et al.27 – who observed the opposite trend – highlighted the necessity for a more critical and comprehensive analysis to reconcile these apparent differences. Driven by this discrepancy, as well as the theoretical prediction based on Onsager's18 theory and our experimental data, we further analysed the shape and size of CNCs, which was followed by analysis of effective dimensions combined with surface charge.
Shape and size distribution of CNCs
The conventional size measurement of CNCs primarily considers individual isolated CNC particles. However, single crystallites are very likely to adhere laterally to each other and aggregate. Therefore, in any singular study, aspect ratio may be overestimated, and surface charge density may be underestimated due to reduced specific surface area of CNCs in such occurrences. As a result, predicting critical concentration of CNC suspensions becomes quite daunting.We therefore included and compared conventional measurements and the approach of Parton et al.23 to analyse the morphology of our CNCs (see ESI†). The area, length, and diameter of all CNC particles were measured manually using ImageJ from TEM images (Fig. S3†). In a typical conventional measurement, we denote the actual length and diameter of individual CNC as li, di, respectively. The aspect ratio ai is derived by li/di. While in the approach of Parton et al.,23 the boundary length and diameter of the CNCs of all types are denoted as lt, dt, respectively. The diameter derived from area is dAE, which was used to calculate the corresponding aspect ratio aAE = lt/dAE. Meanwhile, the rectangularity is given by R = dAE/dt. Lower rectangularity values indicate a more irregular shape, suggestive of aggregates and distorted crystallites. A larger AE diameter suggests a higher likelihood of composite particles.23
For individual CNC, no significant trend of length relative to hydrolysis time was observed (Table 1). Similar results were found for bleached hardwood pulp36 at moderate acid concentration ranges of 58–62 wt%, i.e., the weighted average length of CNCs exhibited minimal variation across different reaction times. Despite prolonged hydrolysis times, there was limited effectiveness in reducing average lengths, likely due to diminishing rates in the latter part of the hydrolysis.37 Relatively shorter CNC nanorods, approaching the LODP limit (140–200 nm for bleached wood pulp), are possibly linked to our freeze-dry conditions, which we applied to wood pulp.38 The average diameter of the CNCs ranged from 3.69 to 4.33 nm, which was relatively smaller than the average diameter (5–10 nm) reported from TEM in previous studies.39 Nonetheless, a smaller standard deviation of the diameter, approximately 1 nm, was observed. Additionally, the wood pulp was subjected to freeze drying to accurately control the acid-to-pulp ratio during the hydrolysis, after which the CNC size possibly reduced slightly.40 As a result, the average aspect ratios of the CNCs were 25 to 40 (Table 1).
| CNC | li (nm) [std] | di (nm) [std] | aia [std] | lt (nm) [std] | dAEa (nm) [std] | dt (nm) [std] | aAEa [std] | Sulphur content (%) [std] | Surface charge density (e nm−2) [std] | Percentage of bundles (%) | dea (nm) | w0 (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Calculated properties. | ||||||||||||
| W25 | 122.33 [41.85] | 4.00 [1.26] | 33.88 [16.56] | 239.90 [110.48] | 8.35 [3.94] | 16.50 [9.82] | 33.29 [18.36] | 0.34 [0.007] | 0.26 [0.04] | 0 | 495.28 | 6 |
| W45 | 104.69 [44.83] | 4.33 [1.07] | 25.47 [13.06] | 148.85 [73.39] | 8.59 [4.21] | 12.92 [7.37] | 19.64 [10.84] | 0.46 [0.027] | 0.29 [0.02] | 0.82 | 245.67 | 4 |
| W60 | 142.93 [61.33] | 3.83 [1.10] | 40.23 [20.77] | 271.91 [148.25] | 12.70 [5.71] | 22.49 [19.46] | 22.70 [10.78] | 0.45 [0.024] | 0.42 [0.02] | 3.08 | 304.18 | 4 |
| W90 | 120.16 [50.34] | 3.69 [1.14] | 35.03 [16.91] | 244.93 [116.04] | 16.28 [8.76] | 27.39 [19.64] | 16.72 [7.18] | 0.53 [0.036] | 0.62 [0.04] | 13.58 | 165.45 | 3 |
In the approach by Parton et al.,23 the distribution of the rectangularity, R, and dAE for each CNC suspension is illustrated in Fig. 4a. Among the different CNC suspensions, W25 displayed the lowest mean rectangularity value, indicating a notable presence of aggregates or distorted crystallites, while the other three suspensions exhibited fewer particles with lessened rectangularity. Given that aggregates and distorted crystallites do not effectively contribute to the formation of anisotropic phase while their impact remains inconclusive, as suggested by Parton et al.,23 only single crystallites and bundles with a rectangularity above 0.5 were selected for subsequent calculations based on the distribution of rectangularity.
 | ||
| Fig. 4 Distributions (a) and respective coloured maps (b) with the colour bar representing the probability of the area equivalent (AE) diameter and rectangularity of the CNCs (as defined by Parton et al.24 and determined by image analysis of TEM micrographs of the CNC suspensions). Relative percentage of four categories of CNC particles (c) according to Parton et al.'s24 method with boundaries at a rectangularity of 0.4 and an AE diameter of 23 nm for CNCs prepared for 25 (W25), 45 (W45), 60 (W60), and 90 (W90) min. | ||
As shown in Fig. 4c, W90 and W60 contained a relatively high percentage of bundles (∼13% and 3%, respectively), while W25 and W45 showed minimal inclusion of bundles. The increased concentration of bundles may be ascribed to the elevated surface charge as indicated by the higher ionic strength (Fig. 3) of the system.
When comparing the dimensions of the individual CNC (li, di) to that of the total CNCs (lt, dt), the lt, dt of W25, W60 are twice the li, di, indicating both lateral and head-to-tail adherence between single particles, while more lateral attachment exists in W45 and W90. Moreover, the length of W45 for both individual and total types of CNCs remained similar, suggesting a reduced number of head-to-tail adherence of single CNCs. Overall, prolonged hydrolysis time and increased surface charge led to elevated ionic strength within the CNC suspensions. This higher ionic strength effectively reduced electrostatic repulsive forces between CNC particles by decreasing the Debye length (Table S2†), thus diminishing their electrostatic double-layer interactions. Consequently, CNC particles experienced reduced repulsion and enhanced lateral attraction, promoting significant lateral adhesion. This process promoted the formation of larger aggregates or bundles stabilized primarily through attractive interactions, which could subsequently be disrupted by sonication according to Parton's observations.23 Although CNC bundles are commonly observed in suspensions,15,39,41 the exact origin of these bundles – whether they arise from the cellulose source or the preparation process – remains elusive.41
Parton et al.23 suggested that the bundles in CNC suspension act as colloidal chiral dopants, facilitating the complete formation of anisotropic phase (w1), although no clear evidence has been found to suggest a similar effect on the onset of the anisotropic phase (w0). We hypothesize, based on our data (Table 1), that CNC bundles promote premature onset of a formal anisotropic phase. To further test our hypothesis, we prepared a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of samples W45 and W90. The resulting phase diagram (Fig. S6†) demonstrated an earlier onset of the anisotropic phase at approximately 2 wt%, which was even lower than the value observed for W90. This effect is likely attributable to changes in ionic strength introduced by incorporating W45.
1 mixture of samples W45 and W90. The resulting phase diagram (Fig. S6†) demonstrated an earlier onset of the anisotropic phase at approximately 2 wt%, which was even lower than the value observed for W90. This effect is likely attributable to changes in ionic strength introduced by incorporating W45.
Effective diameter
To further understand the effect of surface charge, size, and the percentage of bundles on the onset of anisotropic phase, we calculated the effective diameter and qualitatively predicted the critical weight concentration (w0) according to Onsager's theory (eqn (3)). The critical weight concentration displays a more complex relationship with the actual and effective dimension. The effective diameter, de, is determined by both the surface charge and the size of the CNCs. de decreased significantly from 495 to 165 nm as the surface charge increased from 0.34 to 0.53%, along with a decrease in Debye length (50 to 14 nm) (Table 1). These calculated results align with the accepted understanding that an increased CNC surface charge enhances ionic strength, leading to shrinkage of the electrostatic double layer. The critical weight concentration was thus predicted to increase with higher surface charge, as observed by Abitbol et al.27Yet, we observed a decrease in critical weight concentration with extended hydrolysis time (Fig. 3b), suggesting that surface charge and size are not dominant factors. Therefore, the observed trend may have resulted from the increase of CNC bundles, as shown in Fig. 4. The presence of a higher ratio of CNC bundles in the suspension are likely the reason why we observed a decrease in the critical weight concentration (w0) with extended hydrolysis times, implying that the CNC bundles facilitate the onset of the anisotropic phase, as predicted by theory.
Conclusion
This study attempted to more precisely deconvolute the impacts of hydrolysis time on the onset of anisotropic phase formation in CNC suspensions. Our primary focus was to understand how varying hydrolysis times influence the critical concentration at which CNCs transition from an isotropic to an anisotropic phase. By manipulating the hydrolysis time across 25 to 90 minutes, the phase diagram of the CNCs was mapped out to determine the critical weight concentration. The concentration required for anisotropic phase formation increased with longer hydrolysis times. This result deviated from the current understanding of the importance of an increase in surface charge and thus prompted further analysis of CNC shape and size distribution. We observed that prolonged hydrolysis times first led to increased surface charge, which induced more lateral adherence of CNCs. As the time exceeded 45 minutes, both the area-equivalent (AE) diameter and the length of CNCs increased, suggesting the significant presence of CNC aggregates and bundles. The observed increase in CNC bundles, which were reported to act as colloidal chiral dopants, appeared to also facilitate the onset of the anisotropic phase despite higher surface charges which are known to typically retard phase transition. Our findings suggest that while hydrolysis time directly influences CNC dimensions and surface charge, it also plays a much more pronounced role in the formation of CNC bundles than previously suspected. Indeed, theoretical calculations arising from Onsager's model supported our experimental observations, showing that effective dimensions and surface charge are intricately linked to the onset of the anisotropic phase in an opposing way.In conclusion, the phase behaviour of CNC suspensions is a complex interplay of size, shape, and surface charge, all influenced by hydrolysis conditions. Understanding these relationships is crucial for optimizing CNC production for specific applications, as control over hydrolysis conditions can fine-tune physical and chemical properties to achieve desired phase behaviour. Further research is needed to explore the detailed mechanisms behind bundle formation and its impact on CNC phase transitions, which may be important for improved industrial processes and expanded applications for CNC materials.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
SH conceived and designed the experiments. SH, AB synthesized cellulose nanocrystals under the guidance of YF, NL, LL. SH performed characterization under the supervision of YF, NL, LL. All authors contributed to the writing of the manuscript.Conflicts of interest
The views expressed in this manuscript are those of the authors and do not necessarily reflect the position or policy of PepsiCo Inc.Acknowledgements
The authors acknowledge generous financial support from YF and PepsiCo, Inc., and thank Dr Tiffany Abitbol, École Polytechnique Fédérale de Lausanne (EPFL), for the fruitful discussion and exchange. This research was performed in part at the Analytical Instrumentation Facility (AIF) at North Carolina State University, which is supported by the State of North Carolina and the National Science Foundation (award ECCS-2025064). The AIF is a member of the North Carolina Research Triangle Nanotechnology Network (RTNN), a site in the National Nanotechnology Coordinated Infrastructure (NNCI).References
- M. Barón, Pure Appl. Chem., 2001, 73, 845–895 Search PubMed.
- K. J. De France, Can. J. Chem. Eng., 2024, 102, 2695–2713 CrossRef CAS.
- Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500 CrossRef CAS PubMed.
- C. Schütz, J. R. Bruckner, C. Honorato-Rios, Z. Tosheva, M. Anyfantakis and J. P. F. Lagerwall, Crystals, 2020, 10, 199 CrossRef.
- Y. P. Zhang, J. Nanophotonics, 2012, 6, 063516 Search PubMed.
- A. Etale, A. J. Onyianta, S. R. Turner and S. J. Eichhorn, Chem. Rev., 2023, 123, 2016–2048 CrossRef CAS PubMed.
- B. G. Rånby, Discuss. Faraday Soc., 1951, 11, 158–164 RSC.
- O. M. Vanderfleet and E. D. Cranston, Nat. Rev. Mater., 2020, 6, 124–144 CrossRef.
- A. Babaei-Ghazvini, B. Vafakish, R. Patel, K. J. Falua, M. J. Dunlop and B. Acharya, Int. J. Biol. Macromol., 2024, 258, 128834 CrossRef CAS PubMed.
- S. Elazzouzi-Hafraoui, Y. Nishiyama, J.-L. Putaux, L. Heux, F. Dubreuil and C. Rochas, Biomacromolecules, 2008, 9, 57–65 Search PubMed.
- P. Mali and A. P. Sherje, Carbohydr. Polym., 2022, 275, 118668 CrossRef CAS PubMed.
- M. G. Aguayo, A. Fernández-Pérez, C. Oviedo, G. Reyes and P. Reyes-Contreras, Nanomaterials, 2020, 10, 1775 Search PubMed.
- K.-H. Lin, T. Enomae and F.-C. Chang, Molecules, 2019, 24, 3724 CrossRef CAS PubMed.
- Y. Qi, S. Wang, A. A. Liza, J. Li, G. Yang, W. Zhu, J. Song, H. Xiao, H. Li and J. Guo, Carbohydr. Polym., 2023, 319, 121146 CrossRef CAS PubMed.
- S. L. Leong, S. I. X. Tiong, S. P. Siva, F. Ahamed, C.-H. Chan, C. L. Lee, I. M. L. Chew and Y. K. Ho, J. Environ. Chem. Eng., 2022, 10, 108145 CrossRef CAS.
- L. Chen, Q. Wang, K. Hirth, C. Baez, U. P. Agarwal and J. Y. Zhu, Cellulose, 2015, 22, 1753–1762 CrossRef CAS.
- S. Dong, M. J. Bortner and M. Roman, Ind. Crops Prod., 2016, 93, 76–87 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- X. M. Dong, T. Kimura, J.-F. Revol and D. G. Gray, Langmuir, 1996, 12, 2076–2082 CrossRef CAS.
- C. Honorato-Rios, C. Lehr, C. Schütz, R. Sanctuary, M. A. Osipov, J. Baller and J. P. F. Lagerwall, NPG Asia Mater., 2018, 10, 455–465 CrossRef CAS.
- Y. Zhang, Q. Cheng, C. Chang and L. Zhang, J. Appl. Polym. Sci., 2018, 135, 45702 CrossRef.
- V. F. Korolovych, V. Cherpak, D. Nepal, A. Ng, N. R. Shaikh, A. Grant, R. Xiong, T. J. Bunning and V. V. Tsukruk, Polymer, 2018, 145, 334–347 CrossRef CAS.
- T. G. Parton, R. M. Parker, G. T. Van De Kerkhof, A. Narkevicius, J. S. Haataja, B. Frka-Petesic and S. Vignolini, Nat. Commun., 2022, 13, 2657 CrossRef CAS PubMed.
- V. A. Burmistrov, V. V. Aleksandriiskii, I. V. Novikov and O. I. Koifman, Liq. Cryst. Their Appl., 2020, 20, 6–26 CrossRef CAS.
- S. Pieraccini, S. Masiero, A. Ferrarini and G. Piero Spada, Chem. Soc. Rev., 2011, 40, 258–271 Search PubMed.
- G. Fittolani, D. Vargová, P. H. Seeberger, Y. Ogawa and M. Delbianco, J. Am. Chem. Soc., 2022, 144, 12469–12475 Search PubMed.
- T. Abitbol, D. Kam, Y. Levi-Kalisman, D. G. Gray and O. Shoseyov, Langmuir, 2018, 34, 3925–3933 CrossRef CAS PubMed.
- V. S. Raghuwanshi, C. Browne, W. Batchelor and G. Garnier, J. Colloid Interface Sci., 2023, 630, 249–259 CrossRef CAS PubMed.
- Y. Hu and N. Abidi, Langmuir, 2016, 32, 9863–9872 CrossRef CAS PubMed.
- S. Shafeiei-Sabet, W. Y. Hamad and S. G. Hatzikiriakos, Rheol. Acta, 2013, 52, 741–751 CrossRef CAS.
- S. Beck and J. Bouchard, Tappi J., 2016, 15, 363–372 CAS.
- D. Bukharina, M. Kim, M. J. Han and V. V. Tsukruk, Langmuir, 2022, 38, 6363–6375 CrossRef CAS PubMed.
- T. Abitbol, E. Kloser and D. G. Gray, Cellulose, 2013, 20, 785–794 CrossRef CAS.
- E. J. Foster, R. J. Moon, U. P. Agarwal, M. J. Bortner, J. Bras, S. Camarero-Espinosa, K. J. Chan, M. J. D. Clift, E. D. Cranston, S. J. Eichhorn, D. M. Fox, W. Y. Hamad, L. Heux, B. Jean, M. Korey, W. Nieh, K. J. Ong, M. S. Reid, S. Renneckar, R. Roberts, J. A. Shatkin, J. Simonsen, K. Stinson-Bagby, N. Wanasekara and J. Youngblood, Chem. Soc. Rev., 2018, 47, 2609–2679 RSC.
- M. F. Rosa, E. S. Medeiros, J. A. Malmonge, K. S. Gregorski, D. F. Wood, L. H. C. Mattoso, G. Glenn, W. J. Orts and S. H. Imam, Carbohydr. Polym., 2010, 81, 83–92 CrossRef CAS.
- S. Beck-Candanedo, M. Roman and D. G. Gray, Biomacromolecules, 2005, 6, 1048–1054 CrossRef CAS PubMed.
- R. F. Nickerson and J. A. Habrle, Ind. Eng. Chem., 1947, 39, 1507–1512 CrossRef CAS.
- O. A. Battista, S. Coppick, J. A. Howsmon, F. F. Morehead and W. A. Sisson, Ind. Eng. Chem., 1956, 48, 333–335 Search PubMed.
- Z. J. Jakubek, M. Chen, M. Couillard, T. Leng, L. Liu, S. Zou, U. Baxa, J. D. Clogston, W. Y. Hamad and L. J. Johnston, J. Nanopart. Res., 2018, 20, 98 Search PubMed.
- E. Kontturi and T. Vuorinen, Cellulose, 2009, 16, 65–74 CrossRef CAS.
- B. Frka-Petesic, T. G. Parton, C. Honorato-Rios, A. Narkevicius, K. Ballu, Q. Shen, Z. Lu, Y. Ogawa, J. S. Haataja, B. E. Droguet, R. M. Parker and S. Vignolini, Chem. Rev., 2023, 123, 12595–12756 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5na00069f |
| This journal is © The Royal Society of Chemistry 2025 |

