Insight into the role of tunable nitrogen vacancies in transition metal nitrides for ammonia synthesis

Abstract

The thermally catalyzed nitrogen reduction reaction (NRR) is significant in the fertilizer industry and basic catalytic science. This study employs density-functional theory (DFT) calculations to explore the performance of 12 metal nitrides in thermocatalytic NRR by focusing on them. The surface incompleteness in the catalytic environment is simulated by constructing nitrogen vacancies on the metal nitride surfaces. Then the catalytic activity of these surfaces is evaluated in the thermally catalyzed ammonia synthesis process under specific experimental conditions (temperatures of 573, 673, and 773 K, and a pressure of 1 bar), as well as the effect on the activation of N₂ and H₂ molecules. It was found that the NRR performance can be optimized by considering the relationship between the N coordination structure on the catalyst surface and the NRR activity, thus identifying LaN(110)–V(N) and NbN(110) as two highly promising catalysts with notable stability and kinetic activity. It is also found that for metal nitride catalysts, a surface with lattice nitrogen as tetra-coordinated exhibits better NRR activity with lower reaction energy, and the distal pathway is more favorable for all catalyst surfaces studied. The present results provide new ideas for developing efficient metal nitride catalysts for ammonia synthesis and enrich the basic knowledge of metal nitride-catalyzed NRR.

---

Introduction

Ammonia is considered a potential green energy carrier and an essential foundation for chemicals and fertilizer products.^1–3 The most critical and rate-limiting step in the ammonia synthesis process is the dissociation of N₂, which requires significant energy input to overcome the inert triple bond.⁴ To reduce energy consumption, efficient ammonia synthesis under mild conditions is an urgent target of current scientific research.^5,6 At present, electrochemical and photocatalytic methods receive more attention in investigating ammonia synthesis under mild conditions, but their ammonia production efficiency and scale are far from meeting industrial requirements.⁷ Although the Haber–Bosch method needs high temperature and pressure to achieve the desired ammonia yield, the traditional process dominates industrial ammonia synthesis.^8,9 Therefore, large-scale industrial production of NH₃ still relies on traditional thermocatalytic processes.^10,11

In recent years, researchers have been searching for more efficient and environmentally friendly methods for NH₃ synthesis under harsh conditions, and some novel catalysts have been developed.^12–14 Compared to traditional Fe-based catalysts, supported Ru-based catalysts exhibit good NH₃ synthesis performance under mild reaction conditions, and their performance improves further when alkali metals and alkaline earth metals are used as promoters, making the NH₃ synthesis process more efficient.^15–17 In addition, Co-based catalysts also exhibit remarkable catalytic activity under mild conditions.^1,18 For example, a Ba–Co/C catalyst achieved an NH₃ production rate of 88 235 μmol g⁻¹ h⁻¹ at 400 °C and 9 MPa, in which Ba, as a promoter, significantly enhanced the catalytic activity by suppressing the undesirable methane formation on the carbon matrix, even at low loadings.^11,15,19,20

Some ternary nitrides have also attracted increasing attention for their NH₃ synthesis performance.²¹ For instance, a study of Co₃Mo₃N surfaces explored whether nitrogen vacancies could adsorb and activate N₂.²² It was found that within the temperature range for NH₃ synthesis, the (111) surface with nitrogen vacancies, surrounded by a triple hollow structure, exhibited an unexpectedly high concentration of nitrogen vacancies (1.6 × 10¹⁶ to 3.7 × 10¹⁶ cm⁻²), which could effectively adsorb and activate N₂.²³ The Co₃Mo₃N catalyst promoted by Cs exhibited high activity (900 μmol g⁻¹ h⁻¹) at 400 °C and 0.1 MPa, comparable to that of Fe-based and Co-based catalysts under the same conditions.²⁴ Other nitrides such as Co₃ZnN, Ni₃ZnN, Co₃InN, and Ni₃InN have also been found to be ineffective as catalysts, though they decomposed to produce ammonia, indicating their potential in chemical cycles.²⁵ Furthermore, NH₃ production through the reduction of nitrides, including Cu₃N, Ni₃N, Re₃N, Zn₃N₂ and Ta₃N₅, has been reported, but the regeneration of nitrogen gas for chemical looping applications has yet to be realized.^26,27

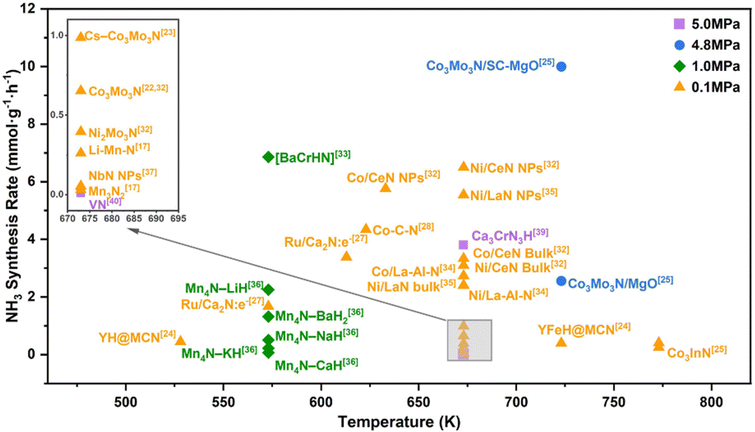
Some metal nitrides have attracted increasing attention due to their high activity in ammonia synthesis reactions.^28,29 Metal nitrides can provide abundant lattice nitrogen for NH₃ formation and abundant nitrogen vacancies to activate N₂.^30–32 The reaction conditions and catalytic rates of various nitride-based catalysts have been reported and are summarized in Fig. 1. In 2018, a systematic study of manganese nitride materials in NH₃ synthesis was conducted, and the reactivity of lattice nitrogen was assessed. For Mn₃N₂, limited reactivity was observed, with only 3.1% of the available lattice nitrogen reacting with hydrogen to form NH₃, while most lattice nitrogen was lost as N₂. In contrast, the addition of a co-metal to manganese nitride altered the pathway of lattice nitrogen reactivity, and it was found that when lithium was used as a co-metal, the nitrogen transfer properties were significantly enhanced, yielding 1306 ± 44 μmol g⁻¹ NH₃ during the first 5 h of the reaction and a total of 1571 ± 53 μmol g⁻¹ NH₃ after 15 h.³³ The amount of NH₃ yielded at the end of the reaction corresponded to 18% of the total usable lattice nitrogen for the reaction. The higher reactivity of Li–Mn–N may be attributed to the dihydrogen activation of lithium, in which case Li–Mn–N behaves more as a nitrogen-transferring reagent than a catalyst.^34,35

Fig. 1 Experimental activities for ammonia synthesis. Overview of the most recent and promising metal nitride catalysts reported for ammonia synthesis. The data points (filled symbols) are extracted from original references based on the following condition: H₂/N₂ = 3.

In addition, nitrogen vacancies are generated during the reduction process, and Li doping also greatly enhances the formation of nitrogen vacancies and reduces the energy demand of N removal.³⁶ Fe and Ni doping in the Mn₄N lattice facilitated the diffusion of N, and Ni doping also reduces the overall flexibility, leading to good H adsorption. Ye et al. have compared the NH₃ synthesis from rare-earth metal nitrides such as CeN, NbN, and LaN.^35,37 For CeN, the catalytic activities of CeN NPs at 0.1 and 0.9 MPa (673 K) were 250 and 1450 μmol g⁻¹ h⁻¹, respectively.³² They also investigated the associative and dissociative synergistic mechanisms for ammonia synthesis on Ni/CeN catalysts. In the Ni/CeN catalytic system, the activation of H₂ and N₂ occurred on Ni and surface nitrogen vacancies, where N₂ molecules were adsorbed and activated on the nitrogen vacancies, continuously reacting with H* to achieve a stable catalytic cycle.³⁸ In contrast, for pure CeN, V_N sites can activate both H₂ and N₂ simultaneously for stable ammonia production. The formation of nitrogen vacancies in Co/CeN leads to a lower figure of merit due to the strong electron-donating capacity of CeN, which facilitates efficient N₂ cleavage on Co. The strong nitrogen affinity of the nitrogen vacancies on the CeN surface leads to promotion of N₂ adsorption and activation at these sites. Due to this unique mechanism, the catalytic activity of Co/CeN is much higher than that of other reported Co-based and Ni-based catalysts, even surpassing that of the traditional Ru-based catalysts. For the Ni/LaN system, the surface nitrogen vacancy formation energy is only 1.6 eV, and the nitrogen vacancy sites on the surface weaken the N≡N bonding, an effect enhanced by the dissociation of H on Ni metal supported on the substrate.³⁹ This effect is enhanced by the dissociation of H on the Ni metal loaded on the carrier. Researchers have also proposed a new high-chemical-stability lanthanide-based catalyst: Ni- and Co-loaded La–Al–N. In NH₃ synthesis, the La₃AlN anti-perovskite structure transformed into the distorted rock salt structure of La–Al–N, with Al atoms doping into the LaN lattice.⁴⁰ Even in this structure, the original functionality of LaN was retained, and the La–Al bonding protected the catalyst from oxidation. After Al doping and H₂O adsorption, OH dissociation was hindered, providing the surface with better chemical stability, significant stability, and catalytic activity. The use of non-precious metals such as Ni and Co made TM/La–Al–N stand out as a promising catalyst in various NH₃ synthesis processes.³⁴

In future catalyst development for NH₃ synthesis, evaluating stable and effective catalysts based on nitrogen vacancy formation energy is a promising approach. Building on this premise, twelve metal nitrides—CeN, Co₃Mo₃N, CrN, Fe₃Mo₃N, La₃AlN, LaN, Mn₄N, MoN, NbN, ScN, TiN, and YN—are investigated as potential catalysts. Their three low-index surfaces are selected as candidate active sites, and the catalytic mechanism of the nitrogen reduction reaction (NRR) is explored by introducing surface defects, with a particular focus on the role of surface nitrogen vacancies in enhancing NH₃ synthesis activity. LaN(110) and NbN(110) are promising candidates, with the LaN(110)–V(N) model showing excellent stability and activity. This study proposes a rational design principle for NRR catalysts based on four-coordinate lattice nitrogen to enhance catalytic performance through surface engineering.

Computational methods

All structural optimization and electronic structure analyses were conducted using the Vienna Ab Initio Simulation Package (6.3.2 VASP) through density functional theory (DFT). In the DFT computational flow, we applied the revised Perdew–Burke–Ernzerhof (RPBE) generalization under the generalized gradient approximation (GGA), and the description of the core electrons was accurately treated with the help of the projected augmented wave (PAW) method.^41,42 In this work, a 500 eV energy cutoff was used to create a plane-wave basis set, and the Brillouin zone was sampled at 3 × 3 × 1 k-points using a Monkhorst–Pack scheme grid, with geometrical optimization until the force becomes less than −0.02 eV m⁻² and the energy difference was less than 10⁻⁵ eV.^43,44 The calculation structures hold 50–60 atoms and two periodic layers. Then three low-index surfaces were selected for the calculations based on the experimentally and theoretically derived X-ray diffraction patterns of the selected metal nitrides. A vacuum space of more than 18 Å was used to avoid interactions between the two periodic cells. In the structural optimization, the bottom three layers of atoms of the surface model were kept fixed to maintain the characteristics of the real surface, while the first layer of atoms of the unit cell was allowed to be fully relaxed during the geometrical optimization for further V_N formation and thermal and zero-point-energy (ZPE) correction calculations.⁴⁵ The geometries of the transition states were determined using the creeping image nudging elastic band (CI-NEB) method. The vibrational frequencies of all species were calculated to analyze the thermodynamic contribution to the free energy.⁴⁶ For each step, the Gibbs free energy change is calculated by the following equation:

ΔG = ΔE + ΔZPE − ΔTS

where ΔE is the reaction energy change obtained directly from the DFT calculation, ΔZPE and ΔS are the ZPE difference and entropy difference, respectively, and T is the temperature.

The nitrogen vacancy formation energy (E_NV) at the surface is defined as

E_NV = E_(VN/slab) − E_(slab) + 1/2E_(N2)

where E_(VN/slab) is the total energy of the optimized surface nitrogen atom desorption configuration on different surfaces, E_(slab) is the total energy of the surface model, and E_(N2) is the total energy of one N₂ molecule.

The proton-coupled electron transfer steps involved in the NRR can be carefully divided into two main pathways: the distant pathway and the alternating pathway.

Results and discussion

Exploration of potentially active surfaces

In this study, we aim to explore and identify the most suitable metal nitride catalysts for the NRR. To this end, 12 structures were chosen as initial candidates, including single-transition-metal nitrides and double-transition-metal nitrides. To better understand the mechanistic details behind the unique catalytic properties of metal nitrides, DFT calculations were employed.

Based on the XRD patterns of the metal nitrides (Fig. S1†), three low-index surfaces were selected from the original unit cell to explore the catalytic active surfaces. To investigate the effect of surface defects on catalytic performance, nitrogen vacancies (denoted as V(N_x)) were introduced into the original metal surfaces, systematically constructing a series of potential defective surfaces. Several typical surface structures and vacancy positions are shown in Fig. 2a and Fig. S2.† The introduction of nitrogen vacancies aims to simulate surface imperfections in real catalytic environments, and subsequently to evaluate their potential impact on catalytic activity. After constructing the defected surfaces with nitrogen vacancies, we further evaluated the thermodynamic stability of these surfaces in the catalytic ammonia synthesis process (Haber–Bosch process). Specifically, we calculated the free formation energies at three key reaction temperatures (T = 573 K, 673 K, 773 K) and at standard pressure (P = 1 bar), as shown in Fig. 2b and Fig. S3–S5.† It was easy to find that double-metal nitrides Co₃Mo₃N((100), (110), (211)), Fe₃Mo₃N((100), (110), (211)), and La₃AlN((100), (110), (111)) have positive Gibbs free energies of V(N) and V(N₂) indicating their poor stability. Any vacancy formation on these surfaces requires significant energy. For the single-metal nitrides CrN((100), (110)), Mn₄N((100), (110)), NbN((100), (110)), LaN((100), (110)), and TiN(111), the surfaces are thermodynamically neutral or favorable for vacancy formation. Therefore, these relatively stable surfaces were further studied for their effect on the activation of N₂ and H₂ molecules.

Fig. 2 (a) Top view of the optimized pristine (100), (110), and (111) surfaces. (b) Relative formation free energies of N vacancies on the above three pristine surfaces at experimental temperature (from 298 K to 773 K) and at 1 bar. The exact locations of the N vacancies created on these three potential surfaces are marked by the numbers in (a).

NRR activity of metal nitrides

The optimized configurations of N₂ adsorption on selected CrN((100), (110)), Mn₄N((100), (110)), NbN((100), (110)), LaN((100), (110)) and TiN(111) pristine and defective surfaces are shown in Fig. S6 and S7.† The activation degree of N₂ was analyzed through adsorption energy and N–N bond length. For the CrN(100) surface, it can be seen that N₂ molecules cannot be adsorbed on the pristine and V(N) surfaces, which is manifested by positive adsorption energy. On the V(N₂) surface, N₂ is adsorbed in an end-on mode with an adsorption energy of −0.66 eV, suggesting that nitrogen vacancy formation on the surface favors N₂ adsorption. For the CrN(110) surface, both the pristine and defective surfaces adsorb N₂ efficiently, and the adsorption energy decreases sequentially with the increase of nitrogen vacancies, indicating that the adsorption of N₂ becomes easier and easier. For Mn₄N, N₂ could not be adsorbed on the intact (100) surface, while it was adsorbed more strongly on the V(N) surface with increased N–N bond lengths and reduced adsorption energies, and the activation of N₂ on the defective surface is not significantly enhanced compared to the pristine surface for the (110) surface. For the NbN(100) surface, for which N₂ is adsorbed in an end-on mode on the pristine surface, the activation of N₂ is gradually enhanced with the increase of nitrogen vacancy concentration, which is manifested by the growth of N–N and the increase of Bader charge of the N₂ adsorbed state. As for the (110) surface, the defective surface is more effective than the pristine surface for N₂ activation. N₂ cannot be effectively activated on either pristine or defective surfaces of LaN(100) and (110). For surfaces with small adsorption energy but difficult N₂ dissociation, H-mediated activation of N₂ is considered.

In summary, for surfaces with positive N₂ adsorption energy on the intact surface, the adsorption energy becomes more and more negative with the increase of surface nitrogen vacancies. For surfaces with negative N₂ adsorption energy on the intact surface, the increase of surface nitrogen vacancies did not have a significant promotion effect on N₂ adsorption. Previous studies have shown that the formation energy of oxygen vacancies on metal oxides is a reliable descriptor for evaluating their catalytic performance. Here, we tested the descriptor of N_vac formation energy with the aim of expressing the energetic intermediate information of the NRR on different metal nitrides. It is noteworthy that a larger E_vac is favorable for N₂ adsorption at the metal site. Quantitatively, the adsorption energy (E_ads) on the defect surface becomes more negative when the nitrogen vacancy formation energy (E_vac) exceeds 1.2 eV, which implies that the nitrogen vacancies (N_vac) have stronger nitrogen (N₂) adsorption and activation capabilities for metal nitrides possessing higher E_vac. Therefore, an increase in E_vac not only contributes to the activation and hydrogenation of N₂ but also weakens the hydrogen binding at the surface N_lat sites; thus E_vac is an effective performance descriptor. A lower vacancy formation energy (E_vac) indicates that vacancies are more easily formed on the catalyst surface. Nitrogen vacancies, as active sites, can lower the reaction energy barrier (ΔG) by stabilizing the reaction intermediates or lowering the transition state energy, which is consistent with the expectation that the presence of nitrogen vacancies can improve the catalytic activity. The adsorption energy of nitrogen (E_ads) reflects the reactant adsorption strength, and its weak correlation with E_vac indicates that the adsorption process is not fully coupled with the vacancy formation mechanism. Vacancies in the system may indirectly affect the local electronic structure of the adsorption sites, but are not directly involved in the adsorption process.

For the NRR, a catalyst surface with E_ads < 0.5 eV of N₂ was selected for the next catalytic hydrogenation reaction. Two reaction mechanism pathways for the NRR have been discussed in the literature: (I) dissociation mechanism, in which the N≡N triple bond is completely dissociated prior to hydrogenation, and (II) association mechanism, in which N₂ is hydrogenated to produce N₂H_xvia a distal or alternating pathway prior to N≡N bond breakage. The relevant data for DFT calculations for all surfaces are listed in Table S1.† Considering both the N–N bond length and adsorption energy, we studied the 15 potential surfaces mentioned above, including CrN(110), CrN(110)–V(N), CrN(110)–V(N₂), Mn₄N(100)–V(N), Mn₄N(100)–V(N₂), NbN(100)–V(N), NbN(100)–V(N₂), NbN(100)–V(N₃), NbN(110), NbN(110)–V(N), LaN (110), LaN(110)–V(N), TiN(110), TiN(111)–V(N₃), and TiN(111)–V(N₄) surfaces. To further analyze the NRR activity of the selected nitride structures, the NRR paths under experimental conditions (T = 573, 673, 773 K, P = 1 bar) were calculated by DFT (Fig. S8–S27†). The complete free energy diagrams of the surface distal and alternate reaction paths were plotted, along with the optimized intermediate structures.

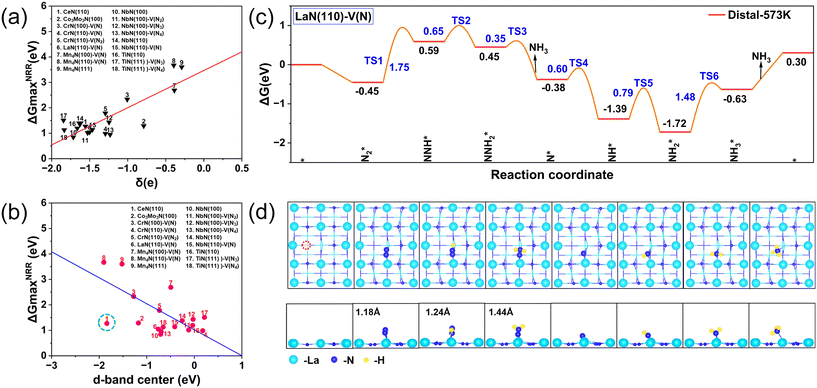
The complete distal pathway free energy diagram of the better-performing LaN(110)–V(N) surface and the optimized intermediate structure are shown in Fig. 3c and d. The distal pathway has the lowest thermodynamic energy span (0.59 eV) on the better-performing LaN(110)–V(N) surface, which is significantly lower than that of the other surfaces and the alternating pathway (e.g., the alternating pathway has an energy span of 1.57 eV on the same surface). The alternating pathway was not selected as the primary pathway because it had a higher energy span and did not show a clear advantage. The distal pathway is able to achieve efficient electron and proton transfer through the active centers on the LaN(110)–V(N) surface. The distal N atoms are preferentially hydrogenated to form NH₃ and released, and the remaining N atoms continue to hydrogenate to form a second NH₃. The transition state energy barriers of this pathway (e.g., TS_3–4 and TS_5–6) are much milder in the experimental temperature range (573 K). The alternating pathway, on the other hand, leads to overall poorer kinetics due to the strong adsorption of intermediates (e.g., N_xH_y) and higher energy barriers. For another surface with better properties (NbN(110)), the step diagram shows that the process N₂* → NNH* requires overcoming a large thermodynamic barrier, and therefore the step of N₂ hydrogenation to produce NNH also determines the rate of this reaction. The N–N bond length in the NNH* intermediate on its defective surface is 1.36 Å, which is significantly longer than that on the intact surface, which is 1.33 Å. The significant extension of the bond length suggests that the modulation of the electronic structure induced by the surface defects weakened the bond strength of the N–N bond, which proves the optimization of the kinetics of the NRR by the surface defects. To investigate the correlation between electron transfer and NRR activity of nitride catalysts, Fig. 3a shows ΔG^max_NRR as a function of Bader charge. Bader charge analysis shows that the NRR performance (red line) increases as the transferred Bader charge increases. The d-band center and ΔG^NRR_max show an overall negative correlation, ΔG^NRR_max gradually decreasing as the d-band center becomes larger (blue line in Fig. 3b). For CeN, since Ce is a rare earth metal, its NRR catalytic performance may be related to the f orbital, and the d-band center is not suitable for use as a descriptor. In Fig. 3c, N₂ is first spontaneously adsorbed at the catalytic center (ΔG = −0.45 eV) with N≡N distance of 1.18 Å. Comparing the difference in the performance of the two NRR catalysts LaN and NbN, DFT calculations show that the N–N bond length in the N₂ molecule adsorbed on the surface of NbN is 1.20 Å, which is significantly longer than that of 1.18 Å in the LaN system. The Bader charge analysis shows that N₂ acquires 1.50|e|, suggesting that N₂ is activated by chemisorption. Second, NNH₂* and NHNH* are produced upward in the subsequent protonation step at energies of −0.14 and 0.15 eV, respectively, suggesting that the distal mechanism is the energetically favorable pathway. Thus, the complete energy profiles of the six calculated transition states (TS) in the distal mechanism are shown in Fig. 3c. Bader charge analysis further reveals the electronic structure differences between NbN and LaN in the N₂ activation mechanism. For the adsorbed-state N₂ molecule, the net charge transfer of N₂ in the NbN system is 0.81|e|, which is slightly higher than that of 0.65|e| in the LaN system, suggesting that the nitrogen vacancies on the NbN surface inject more electrons into the N₂ antibonding orbitals (π*), which leads to an increased degree of polarization of the N≡N bond.

Fig. 3 (a) Relation between ΔG^NRR_max and Bader charge (δ, in units of e). (b) Relation between ΔG^NRR_max and d-band center. (c) Free energy diagram of the distal reaction pathway on the V(N) surface of LaN(110) at 573 K. (d) Structural diagram of the intermediates of the NRR process on the V(N) surface of LaN(110).

Reaction mechanism and electronic structure

To further understand the intrinsic electronic properties of the intermediate-activated La atoms, the bonding properties involved in species were investigated. The densities of states (PDOS) of N₂* and NNH* on the LaN(110)–V(N) and NbN(110) surfaces are illustrated in Fig. 4a and b. The PDOS of N₂* exhibits significant variations, especially near the Fermi energy level. The d-orbital of La overlaps significantly with the p-orbital state of N₂* near the Fermi energy level. This orbital hybridization is attributed to the involvement of the antibonding π* orbital of the N₂ molecule, suggesting that the catalyst partially fills the π* orbitals by electron transfer, thereby weakening the triple bond within the N₂ molecule and promoting N₂ activation.

Fig. 4 The projected density of states (PDOS) of the N₂* and NNH* intermediate states on the (a) LaN(110)–V(N) and (b) NbN(110) surfaces. (c) The –COHP analysis of LaN(110) and LaN(110)–V(N) surface N₂*. (d) Fluctuation of temperature and energy versus time (10 ps) in AIMD simulation.

For the NNH* adsorbed state, the orbital interactions are further enhanced. The d orbital density of states of La exhibits a more pronounced distribution near the Fermi energy level and strongly couples to the p orbitals of NNH*. The broad density of state peaks near the Fermi energy level indicates that the catalyst injects more electrons into the antibonding orbitals of the NNH* molecule (including π* and part of σ*). This electron rearrangement weakens the N≡N bond and enhances N–H bond formation, suggesting that the La atom further activates the adsorbed species. Therefore, the d orbitals of La play a dominant role in the N₂ chemisorption. COHP is a visual indicator of bonding to investigate the chemical bonding and antibonding of atomic pairs. Therefore, COHP analysis was performed for N₂* as shown in Fig. 4c. Compared with the LaN(110) intact surface, the antibonding orbitals of N–N bonds are stronger on the surface with N defects, and the ICOHP result, −8.37 (>−10.96), quantitatively explains the degree of activation of the catalyst for N₂. In addition to high activity and selectivity, AIMD simulations and phonon spectroscopy (see Fig. 4d) further confirmed that the LaN(110)–V(N) catalyst is well stabilized. The slight distortion of the geometrical image shows that the catalyst has significant thermodynamic stability at 773 K. AIMD simulations were performed to analyze the temperature and energy of the structure over 10 ps which indicated that the vibrations in both results are close to the equilibrium state.

Conclusions

Through DFT calculations, 12 different metal nitride catalysts were proposed for the catalytic conversion of N₂ to NH₃ under experimental conditions (T = 573, 673, and 773 K, 1 bar). By analyzing the reaction selectivity and activity, LaN(110) and NbN(110) were identified as promising catalysts. By considering the relationship between the catalyst surface nitrogen coordination structure and NRR activity, this study proposes a rational design principle for NRR catalysts based on the coordination number of lattice nitrogen. The four-coordinate lattice nitrogen is more favorable for NRR activity, with lower reaction energies in the distal pathway. These predictions and findings enrich the fundamental understanding of metal nitrides in NRR catalysis, suggesting that surface engineering with fine local structures of lattice nitrogen on metal nitrides can improve catalytic performance and provide new insights for the rational design and improvement of metal nitride NH₃ synthesis catalysts. In addition, this study breaks through and reveals the unique bifunctional mechanism of metal-free NbN catalysts in the ammonia synthesis reaction. Based on the efficient activation ability of Nb sites for H₂ and the selective adsorption property of nitrogen vacancies for N₂ in precursor materials, NbN exhibits the spatial synergistic effect of multiphase-like catalysis in the homogeneous catalytic system, which provides promising ideas for the design of a new type of nonprecious-metal catalytic system for ammonia synthesis.

Data availability

The data supporting this article have been included as part of the ESI.† All conventional cells are from Materials Project: https://next-gen.materialsproject.org/.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

C. L. greatly appreciates financial support provided by the National Natural Science Foundation of China (grant no. 22473108) and the Foundation of National Key Research and Development Program of China (grant no. 2023YFB3810601).

References

1. A. Cao, V. J. Bukas, V. Shadravan, Z. Wang, H. Li, J. Kibsgaard, I. Chorkendorff and J. K. Nørskov, Nat. Commun., 2022, 13, 2382.
2. F. Chang, Y. Guan, X. Chang, J. Guo, P. Wang, W. Gao, G. Wu, J. Zheng, X. Li and P. Chen, J. Am. Chem. Soc., 2018, 140, 14799–14806.
3. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
4. C. Liu, Q. Li, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Mater. Chem. A, 2019, 7, 4771–4776.
5. Z. Zeng, X. Shen, R. Cheng, O. Perez, N. Ouyang, Z. Fan, P. Lemoine, B. Raveau, E. Guilmeau and Y. Chen, Nat. Commun., 2024, 15, 3007.
6. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
7. X. Peng, M. Zhang, T. Zhang, Y. Zhou, J. Ni, X. Wang and L. Jiang, Chem. Sci., 2024, 15, 5897–5915.
8. A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310.
9. B. A. MacKay and M. D. Fryzuk, Chem. Rev., 2004, 104, 385–402.
10. Y. Guan, C. Liu, Q. Wang, W. Gao, H. A. Hansen, J. Guo, T. Vegge and P. Chen, Angew. Chem., Int. Ed., 2022, 61, e202205805.
11. Q. Wang, J. Pan, J. Guo, H. A. Hansen, H. Xie, L. Jiang, L. Hua, H. Li, Y. Guan, P. Wang, W. Gao, L. Liu, H. Cao, Z. Xiong, T. Vegge and P. Chen, Nat. Catal., 2021, 4, 959–967.
12. C. Liu, H. Zheng, T. Wang, Z. Guo, F. Zhu, H. Xie, G. Qin, H. Li and S. Li, J. Mater. Sci. Technol., 2023, 159, 244–250.
13. T. Wang, Z. Guo, H. Oka, A. Kumatani, C. Liu and H. Li, J. Mater. Chem. A, 2024, 12, 8438–8446.
14. E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245.
15. C. Liu, Q. Wang, J. Guo, T. Vegge, P. Chen and H. A. Hansen, ACS Catal., 2022, 12, 4194–4202.
16. S. Liu, Y. Wang, S. Wang, M. You, S. Hong, T.-S. Wu, Y.-L. Soo, Z. Zhao, G. Jiang, Q. Jieshan, B. Wang and Z. Sun, ACS Sustainable Chem. Eng., 2019, 7, 6813–6820.
17. S. Laassiri, C. D. Zeinalipour-Yazdi, C. R. A. Catlow and J. S. J. Hargreaves, Appl. Catal., B, 2018, 223, 60–66.
18. K. Zhang, A. Cao, L. H. Wandall, J. Vernieres, J. Kibsgaard, J. K. Nørskov and I. Chorkendorff, Science, 2024, 383, 1357–1363.
19. N. Morlanés, S. Sayas, G. Shterk, S. P. Katikaneni, A. Harale, B. Solami and J. Gascon, Catal. Sci. Technol., 2021, 11, 3014–3024.
20. K. Sato, S.-i. Miyahara, K. Tsujimaru, Y. Wada, T. Toriyama, T. Yamamoto, S. Matsumura, K. Inazu, H. Mohri, T. Iwasa, T. Taketsugu and K. Nagaoka, ACS Catal., 2021, 11, 13050–13061.
21. S. Laassiri, C. D. Zeinalipour-Yazdi, N. Bion, C. R. A. Catlow and J. S. J. Hargreaves, Faraday Discuss., 2021, 229, 281–296.
22. C. D. Zeinalipour-Yazdi, J. S. J. Hargreaves and C. R. A. Catlow, J. Phys. Chem. C, 2018, 122, 6078–6082.
23. J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360, eaar6611.
24. P. K. Roy and S. Kumar, Int. J. Hydrogen Energy, 2024, 64, 497–506.
25. R. K. Rai, R. Maligal-Ganesh, W. A. Maksoud, S.-J. Kim, Y. Vaishnav, C. T. Yavuz and Y. Kobayashi, ChemCatChem, 2024, 16, e202301579.
26. A. M. Alexander, J. S. J. Hargreaves and C. Mitchell, Top. Catal., 2012, 55, 1046–1053.
27. M. Kitano, Y. Inoue, H. Ishikawa, K. Yamagata, T. Nakao, T. Tada, S. Matsuishi, T. Yokoyama, M. Hara and H. Hosono, Chem. Sci., 2016, 7, 4036–4043.
28. X. Wang, X. Peng, W. Chen, G. Liu, A. Zheng, L. Zheng, J. Ni, C.-t. Au and L. Jiang, Nat. Commun., 2020, 11, 653.
29. L. Ye, Chem, 2021, 7, 3198–3199.
30. W. Gao, Y. Wang, Q. Wang, Z. Sun, J. Guo and P. Chen, EES Catal., 2024, 2, 780–788.
31. J. O. Conway and T. J. Prior, J. Alloys Compd., 2019, 774, 69–74.
32. T.-N. Ye, S.-W. Park, Y. Lu, J. Li, M. Sasase, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2020, 142, 14374–14383.
33. Y. Guan, W. Zhang, Q. Wang, C. Weidenthaler, A. Wu, W. Gao, Q. Pei, H. Yan, J. Cui, H. Wu, S. Feng, R. Wang, H. Cao, X. Ju, L. Liu, T. He, J. Guo and P. Chen, Chem. Catal., 2021, 1, 1042–1054.
34. Y. Lu, T.-N. Ye, J. Li, Z. Li, H. Guan, M. Sasase, Y. Niwa, H. Abe, Q. Li, F. Pan, M. Kitano and H. Hosono, Angew. Chem., Int. Ed., 2022, 61, e202211759.
35. T.-N. Ye, S.-W. Park, Y. Lu, J. Li, M. Sasase, M. Kitano, T. Tada and H. Hosono, Nature, 2020, 583, 391–395.
36. P. Wang, F. Chang, W. Gao, J. Guo, G. Wu, T. He and P. Chen, Nat. Chem., 2017, 9, 64–70.
37. H. Kumagai, K. Takanabe, J. Kubota and K. Domen, Bull. Chem. Soc. Jpn., 2015, 88, 584–590.
38. Q. Li, C. Liu, S. Qiu, F. Zhou, L. He, X. Zhang and C. Sun, J. Mater. Chem. A, 2019, 7, 21507–21513.
39. Y. Cao, M. A. Kirsanova, M. Ochi, W. Al Maksoud, T. Zhu, R. Rai, S. Gao, T. Tsumori, S. Kobayashi, S. Kawaguchi, E. Abou-Hamad, K. Kuroki, C. Tassel, A. M. Abakumov, Y. Kobayashi and H. Kageyama, Angew. Chem., Int. Ed., 2022, 61, e202209187.
40. Y. Cao, A. Saito, Y. Kobayashi, H. Ubukata, Y. Tang and H. Kageyama, ChemCatChem, 2021, 13, 191–195.
41. C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Am. Chem. Soc., 2019, 141, 2884–2888.
42. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
43. N. Ouyang, C. Wang and Y. Chen, Int. J. Heat Mass Transfer, 2022, 192, 122859.
44. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
45. N. Ouyang, C. Wang, Z. Zeng and Y. Chen, Appl. Phys. Lett., 2021, 119, 061902.
46. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00282f

---