Exploring nickel-catalyzed organochalcogen synthesis via cross-coupling of benzonitrile and alkyl chalcogenols with computational tools

Abstract

The preparation of organochalcogens has increased in recent times due to their promising biological activity properties. This work studies the reaction mechanism of a nickel(0)-catalyzed cross-coupling between benzonitrile and propanethiol to produce new C–S bonds by computational means. The proposed mechanism follows the classical oxidative addition/transmetalation/reductive elimination cross-coupling sequence, involving an unusual oxidative addition of a Ph–CN bond onto the active species. The computed catalytic cycle for thioether synthesis has been examined to determine whether the same protocol could be employed to build the analogous C–Se and C–Te bonds. The proposed mechanism for C–S coupling is validated by microkinetic modeling and shows a very good agreement with available experimental data. The extension of the proposed mechanism to C–Se and C–Te couplings indicates that these new reactions should be operative, although their reaction rates appear to be significantly slower.

---

Introduction

Over the past few decades, the preparation of organochalcogen (Ch = S, Se, Te) compounds has garnered significant interest in synthetic chemistry, largely due to their prevalence in numerous compounds with potential biological interest.¹ The importance of sulfur in biologically active compounds is undisputed and is present in many drugs across different functional groups, e.g. sulfonamides, β-lactams, and thioethers, among others.² Currently, more than 250 sulfur-containing small molecule drugs, showing multiple medicinal applications, have been approved by US FDA.³ It is worth noting that, until recent times, the efficient and selective construction of C–S bonds in transition-metal-catalyzed transformations remained relatively scarce compared to methods developed for other carbon-heteroatom bonds. This was mainly due to catalyst poisoning by sulfur species, particularly thiols and disulfides,⁴ which has been overcome in the last decades with the development of more sophisticated catalytic platforms. Currently, C–S bond formation is completely established as a distinct field and has become an invaluable toolbox for organic synthesis. Furthermore, it seems likely that there will be an even greater demand for sulfur compounds across several different areas, including biochemistry, drug design and natural products. This will undoubtedly continue to drive the discovery of novel catalytic systems that could have an impact on health sciences.⁵

The physiological chemistry of selenium in living organisms is almost exclusively that of selenocysteine, which is found in a few types of selenoproteins.⁶ This residue appears in functional proteins with oxidoreductase activity that are typically involved in the regulation of Ca²⁺ levels,⁷ oxidative stress,⁸ protein folding⁹ and inflammatory processes.¹⁰ Many other selenium-containing compounds, including selenoesters,¹¹ selenocyanates,¹² and ring motifs,¹³ can be employed as anticancer agents.¹⁴ The interest in producing organic compounds bearing selenium has increased over the years and a vast range of synthetic protocols have been developed,^1a,b,15 these include e.g. coupling and hydroselenation processes¹⁶ from a great number of selenium sources such as selenides, diselenides, selenols, selenoesters, elemental selenium, etc. Organotellurium compounds are scarcer than their sulfur and selenium analogs; however, recent advances have shown promising experimental recipes to prepare them through alkyne hydrotelluration,¹⁷ copper-catalyzed aryl iodide reactions with elemental Te,¹⁸ and coupling arylboronic acids with ditelluride reagents in the presence of copper¹⁹ or palladium²⁰ catalysts. Special mention should be made of a synthetic protocol allowing the C–H chalcogenation of Cp rings of ferroceneamides using ditellurides and copper(II) acetate as catalyst.²¹ The biological activity of tellurium, often considered a toxic metalloid possibly due to its affinity to Se,²² has been also studied.²³ Most active Te species have been reported as antioxidants,²⁴ anti-inflammatory,²⁵ and anticancer²⁶ drug candidates.

The current methods employed to build organochalcogen compounds include metal-free,²⁷ photocatalyzed,²⁸ electrochemical²⁹ and organocatalytic³⁰ procedures. Nevertheless, transition metal-catalyzed coupling processes seem to be the best suited candidates to promote these processes due to their availability, functional group tolerance and versatility. At first, palladium was the transition metal of choice to carry out these transformations³¹ but in recent years, there has been a notable increase in the use of first-row transition metal compounds as catalysts, for instance manganese,³² iron,³³ cobalt,³⁴ copper³⁵ and nickel³⁶ systems have provided successful C-chalcogen synthetic platforms. In 2021, Delcaillau and Morandi³⁷ reported a new procedure to prepare functionalized aryl thioethers from aryl nitriles and thiols in the presence of a nickel(0) catalyst (Scheme 1). The usage of the 1,2-bis(dicyclohexylphosphino)ethane (dcype) ligand and potassium tert-butoxide (tBuOK) as the base provided a catalytic platform to achieve this transformation. The process involves both the C–C activation of the aryl nitrile, a relatively unusual electrophilic substrate in cross-coupling, and the formation of the final C–S bond while maintaining a very good functional group tolerance and allowing for the late-stage functionalization of compounds with biological interest.

Scheme 1 Ni-catalyzed C–S coupling between benzonitriles and alkyl thiols as described in ref. 37.

Although the reaction was developed only for coupling aryl nitriles with organic thiolates, the same protocol can be envisaged to promote the same type of reaction with other chalcogenides to construct new C–Ch (Ch = Se and Te) bonds. In this work, the above-described nickel-catalyzed coupling between benzonitrile (PhCN) and various alkyl chalcogenols is investigated by computational means to assess its potential viability to generate C–Se and C–Te bonds. In practice, the coupling between PhCN and propanethiol (HSCH₂CH₂CH₃, HSPr from here on), which has been used as a model system for the long chain alkyl thiols used experimentally, will be studied to find a plausible reaction mechanism for this chemical transformation. Subsequently, the proposed catalytic cycle will be evaluated to predict the feasibility of preparing new C–Ch bonds with the same experimental setup, for which the potential coupling of benzonitrile with propaneselenol (HSePr) and propanetellurol (HTePr) will be explored. In all cases, microkinetic analysis of the reaction outcome will accompany the DFT modeling of the catalytic cycle in order to improve the understanding of the underlying coupling mechanism.

Results and discussion

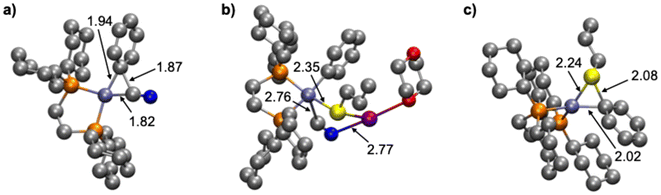
The first stage of this study consists of exploring the reaction mechanism of the process depicted in Scheme 1 to propose a plausible catalytic cycle for the Ni-catalyzed coupling between benzonitrile and propanethiol. Different reaction pathways have been explored for identifying a plausible reaction mechanism; the mechanism that presents the lowest energy requirements is shown in Scheme 2 and the associated relative Gibbs energy profile is represented in Scheme 3. A tridimensional representation of all the species involved in the computed catalytic cycle can be found in Fig. S1 (ESI†).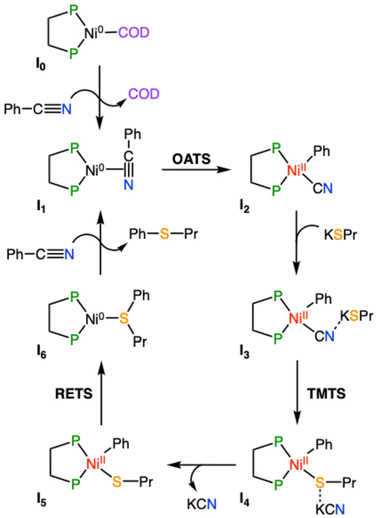

Scheme 2 Plausible reaction mechanism for the Ni-catalyzed coupling between benzonitrile and propanethiol.

Scheme 3 Relative Gibbs energy profile for the Ni-catalyzed coupling between benzonitrile and propanethiol.

The reaction starts from the [Ni(COD)(dcype)] complex (I₀), which is assumed to be formed from the equimolar initial mixture of [Ni(COD)₂] and the diphosphine ligand. The next stage of the reaction consists of an off-cycle replacement to the remaining COD ligand in I₀ by an incoming benzonitrile to produce the [Ni(dcype)(PhCN)] intermediate (I₁). In this compound, benzonitrile is bound onto the nickel ion through the triple C≡N bond, which elongates from 1.15 Å in free benzonitrile to 1.23 Å in I₁, indicating a certain degree of electronic transfer from the ligand to the metal. This replacement process is exergonic by 4.3 kcal mol⁻¹. The reaction proceeds by the oxidative addition of the Ph–CN bond onto the nickel species to form the nickel(II) intermediate [Ni(CN)(dcype)Ph] (I₂). This C–C activation stage is controlled by the associated transition state (OATS), which is located 17.3 kcal mol⁻¹ higher than the previous intermediate. This transition state corresponds to a 3-membered concerted cyclic structure, in which the breaking C–C bond elongates to 1.87 Å, while the Ni–CN and the Ni–Ph distances are 1.82 and 1.94 Å, respectively (Fig. 1a). After this transition state, intermediate I₂ is obtained; this complex adopts the expected square planar geometry and is located 3.2 kcal mol⁻¹ below I₁ (at a relative Gibbs energy of −7.5 kcal mol⁻¹). Propanethiol then enters the catalytic cycle, but it does so in the form of the corresponding potassium salt (KSPr), which is obtained after the direct deprotonation of the thiol with potassium tert-butoxide. This deprotonation process should be considered barrierless because its transition state has a Gibbs energy value lower than the sum of the energies of the separated reactants. The deprotonation process is exergonic by 8.5 kcal mol⁻¹, this amount of energy is added to all the following species. Attempts were made to identify reaction intermediates prior to deprotonation where both reactants would interact favorably; however, all efforts resulted in encounter compounds with higher energies than the transition state or in the fortuitous deprotonation of the thiol. Thus, the formation of KSPr from propanethiol and tBuOK is considered to be complete in a very short time and, consequently, this is the species that will be employed for the computational modeling. The addition of KSPr onto I₂ leads to the formation of a new intermediate (I₃) where the potassium cation interacts with the terminal N of the cyanide, at 2.96 Å. Although this distance seems quite long, it falls well within the sum of the van der Waals radii of both atoms and in the range of distances found for similar species in the Cambridge Structural Database, where this distance spreads between 2.6 and 3.5 Å. This interaction, along with other dispersion contributions between the potassium and the dcype ligand stabilize I₃, causing this species to exhibit a relative Gibbs energy of −29.0 kcal mol⁻¹. Since the terminal nitrogen of the cyano group is not sterically hindered, no transition state was considered to govern this addition stage. The transmetalation step takes then place to exchange the cyanide onto the nickel for the incoming thiolate group. This stage of the reaction is controlled by the corresponding transmetalation transition state (TMTS), which was found by performing a relaxed potential surface energy scan of the Ni–S distance. This process entails the partial reoptimization of I₃ with 0.1 Å decrements from the starting Ni–S distance (4.93 Å) to a much shorter bond distance (2.23 Å), in which the metal has already been bound by the thiolate. While the Ni–S distance decreases, the cyano group was found to migrate from nickel to potassium. The highest energy point found during this procedure should be close to the real transmetalation transition state and was subsequently optimized to finally produce TMTS. In this species, the Ni–S and Ni–C distances are 2.35 and 2.76 Å (Fig. 1b), respectively, whereas the geometrical arrangement of ligands agrees with a distorted trigonal bipyramid, as would be expected for a ligand substitution in a square planar Ni(II) compound. The transmetalation process requires an energy investment of 15.5 kcal mol⁻¹ to take place and produces intermediate I₄. This complex is 3.7 kcal mol⁻¹ higher in energy than I₃, and displays a number of non-covalent interactions between potassium cyanide and the [Ni(dcype)Ph(SPr)] fragment. The release of the coordinated KCN into the reaction mixture gives rise to the obtention of the square planar [Ni(dcype)Ph(SPr)] intermediate (I₅). This species is a bit more stable than the preceding intermediate (0.4 kcal mol⁻¹ lower in energy). The final thioether product, (propylthio)benzene, can be generated by reductive elimination from intermediate I₅; the transition state governing this process (RETS) requires 27.5 kcal mol⁻¹. This concerted trigonal cyclic transition state shows C–S, Ni–C and Ni–S distances of 2.08, 2.02 and 2.24 Å, respectively, and adopts a distorted geometry in which both SPr and Ph group have slightly abandoned their square planar original positions (Fig. 1c). After RETS, the [Ni(dcype)(PhSPr)] intermediate (I₆) is formed. In this compound, the newly formed product remains attached to the nickel(0) center through the sulfur atom of the thioether; the alternative complex in which PhSPr is coordinated to the metal through a η²–(π) interaction of the phenyl ring is 2.7 kcal mol⁻¹ higher in energy. Although I₆ is higher in energy than all the previous nickel compounds (its relative Gibbs energy is −9.4 kcal mol⁻¹) is still viable as a transient species where the product can be released by trapping a new benzonitrile substrate, which would take the reaction back to the initial in-cycle active species (I₁) with a moderate overall energy release (ΔG_R) of 14.4 kcal mol⁻¹.

Fig. 1 Transition states found for the Ni-catalyzed thiolation of benzonitrile, (a) oxidative addition (OATS); (b) transmetalation (TMTS); (c) reductive elimination (RETS). Color code: Ni, iceblue, C, gray; N, blue; O, red; P, orange; S, yellow; K, purple. For clarity H atoms have been omitted. Numeric values correspond to bond distances in Å.

The analysis of the whole catalytic cycle allows several conclusions to be drawn. First, the individual oxidative addition (17.3 kcal mol⁻¹) and reductive elimination (27.5 kcal mol⁻¹) barriers align with the usual behavior of Ni(0)/Ni(II) catalytic cycles, in which the former is lower due to the stabilization of the higher oxidation state, typical from first-row transition metals. Second, the overall barrier of the process (ΔG^‡), formulated within the Energetic Span Model,³⁸ is 30.8 kcal mol⁻¹; this value is obtained as the Gibbs energy difference between the reductive elimination transition state (RETS) and intermediate I₃ (i.e. ΔG^‡ = 1.8 − (−29.0) = 30.8 kcal mol⁻¹). Although it may be qualitatively helpful, it is difficult to judge whether a complex reaction can occur from the value of the activation barrier alone, and 30.8 kcal mol⁻¹ seems to be a relatively high energy requirement for a process working at 110 °C. Today, microkinetic modeling can provide a more quantitative rationalization of the combined ensemble of individual steps of catalytic reactions, leading to the formation of intermediates and products over time. In this case, the microkinetic modeling analysis of the reaction, including the steps shown in Scheme 2, suggests that the computed Gibbs energies are in the appropriate range. Experimentally, the reaction between dodecylthiol and benzonitrile affords a 94% yield in a 16-hour catalytic run, although the product generation rate is unknown. The microkinetic model, which includes the complete experimental setup regarding initial concentrations, reaction time, etc., produces an estimated yield of 85%. However, in the simulation the reaction stops before completion at ca. 12 hours (Scheme 4, dotted line). This behavior can be attributed to the intrinsic formulation of the proposed catalytic cycle, which employs benzonitrile both as an off-cycle activator (to generate I₁) and as a reactant for the subsequent reaction turnovers after the formation of I₆.

Scheme 4 Time evolution of nickel-catalyzed C–S (dotted line: initial mechanism shown in Scheme 2, solid line: modified mechanism including the steps in Scheme 5), C–Se and C–Te theoretical yields produced by microkinetic modeling of the catalytic cycles.

These two roles entail that, as the reaction proceeds, the amount of PhCN decreases up to the point where it can no longer promote the product release from I₆. This causes the reaction to stop at 85% of its course because the remaining 15% of benzonitrile remains trapped mostly as intermediate I₃. This issue can be solved by adding additional stages to the computed reaction mechanism, which provide an alternative pathway to regenerate the active species without using benzonitrile (Scheme 5). The expansion of the catalytic cycle requires the calculation of a new species [Ni(dcype)(KSPr)] (I₇) that may be formed by the replacement of the product in I₆ by KSPr. This modification allows the liberation of the final product without relying on the availability of free benzonitrile. The formation of complex I₇ releases 18.0 kcal mol⁻¹; hence, this intermediate is located −27.4 kcal mol⁻¹ lower than the starting materials. After its formation, I₇ can generate the catalytic active species I₁ by direct exchange between PhCN and KSPr; this process is practically thermoneutral. The inclusion of these two additional reaction stages has a clear effect on the microkinetic model. Initially, when the amount of benzonitrile is significant, the reaction can proceed according to the reaction sequence described in Scheme 2. Along time, as benzonitrile is consumed, the alternative pathway (Scheme 5, bottom) becomes more important for promoting the product release and the regeneration of I₁. The modified microkinetic model affords a theoretical yield of 95% in a 16-hour run (Scheme 4, solid line), practically the same value that was observed experimentally. An additional KSPr/COD exchange at intermediate I₇ was included into the microkinetic model to check whether the initial species active could be sequestered by the thiolate; however, the impact of this stage is insignificant on the final performance of the model and could be discarded. In the end, the relatively close agreement between the experimental and computed reaction outcomes should validate the methodology employed and the proposed catalytic cycle, which can be used as a basis for the prospective study of similar coupling reactions that may promote the formation of C–Se and C–Te bonds.

Scheme 5 Initially proposed (top) and alternative (bottom) stages to regenerate the active species I₁ and to release the final product.

The reaction mechanism has been explored to ascertain whether the studied catalytic system can promote the preparation of the analogous C–Se and C–Te compounds. For this purpose, the starting propanethiol has been replaced by propaneselenol (HSePr) and propanetellurol (HTePr), respectively, and the catalytic cycle has been recomputed. The relative Gibbs energies for these new systems can be found in Table 1.

Table 1 Computed relative Gibbs energies (in kcal mol⁻¹) for all the species involved in the catalytic cycles for C–S, C–Se and C–Te couplings. Bold energies indicate the species determining the Gibbs energy activation barrier

Species	R-SH	R-SeH	R-TeH
I0	0.0	0.0	0.0
I1	−4.3	−4.3	−4.3
OATS	13.0	13.0	13.0
I2	−7.5	−7.5	−7.5
I3	−29.0	−35.2	−40.4
TMTS	−13.4	−19.3	−21.1
I4	−25.3	−30.6	−33.0
I5	−25.7	−30.9	−33.9
RETS	1.8	−2.3	−8.1
I6	−9.4	−9.6	−11.5
I7	−27.4	−34.1	−38.0
I1	−18.7	−18.2	−19.0
Overall ΔGR	−14.4	−13.9	−14.7
Barrier (ΔG^‡)	30.8	32.9	32.3

---

The usage of propaneselenol as substrate presents parallel results to those found for propanethiol. As may be observed, the Gibbs energy profile shows the same features as those found for HSPr, with slightly higher relative energies. The individual transmetalation and reductive elimination barriers require 15.9 and 28.6 kcal mol⁻¹, respectively, indicating that these stages are very similar to those found for propanethiol. The overall barrier of the reaction, computed within the Energetic Span Model as the energy difference between RETS and I₃, is 32.9 kcal mol⁻¹. This barrier is slightly higher than that computed for the C–S coupling, and therefore a slower C–Se coupling should be expected. Indeed, the obtained yield through microkinetic modeling is 24% (Scheme 4), as should be expected for a reaction displaying an energy barrier over 32 kcal mol⁻¹ at 110 °C. In any case, the computed data suggest that the C–Se coupling between selenols and benzonitriles may be viable with the original nickel catalyst, although longer reaction times would be needed.

Propanetellurol shows a similar behavior to the other propyl chalcogenols studied albeit some small differences may be identified. In this case, the transmetalation stage shows an increased activation energy: 15.5, 15.9 and 19.2 kcal mol⁻¹ for HSPr, HSePr and HTePr, respectively, which may be attributed to the larger size of tellurium. For instance, the TMTS for selenium and tellurium, show that while the breaking Ni–CN distance remains in a small range: 2.78 vs. 2.85 Å, the Ni–Se and Ni–Te distances are quite different: 2.34 vs. 2.68 Å, respectively. Hence, it seems that the weaker stabilization of the metal center due to the chalcogen coordination increases the transmetalation barrier. The reductive elimination from intermediate I₅ in the C–Te coupling requires 25.8 kcal mol⁻¹, showing the highest energy requirement along the reaction coordinate. This value is significantly lower than those found for the lighter analogous chalcogens. This reduced energy requirement could be also attributed to the larger size of Te, which should produce a weaker, and thus more easily cleaved, Ni–Te bond that would speed up the reductive elimination. As in the previous cases the overall barrier of the reaction can be calculated as the energy difference between OATS and I₃, which equals to 32.3 kcal mol⁻¹. The microkinetic model of this reaction produces a 34% yield (Scheme 4) in agreement with its relatively large energy requirements; however, the full ensemble of elementary steps shows an overall activity in between to that observed for the previous catalytic systems, suggesting that the nickel(0) catalyst should be able to promote the proposed C–Te coupling at longer reaction times than the analogous C–S process.

It should be noted that the transition from sulfur to the larger chalcogens may open alternative reaction pathways; for example, radical species could be formed either by outer-sphere electron transfer processes or by homolytic cleavage of Ni–Ch bonds of the in-cycle catalytic species. Some of these possibilities, since it would not be plausible to cover all of them, have been calculated to ensure that the catalytic cycle described above remains the preferred pathway when using selenols and tellurols as starting materials. First, the outer-sphere single electron transfer (SET) between the stating nickel(0) intermediate (I₀) and the initial alkyl chalcogenol, to produce the corresponding Ni(I) cationic species and the radical chalcogen anions, has been computed to require more than 60 kcal mol⁻¹ for all the HChPr reactants, indicating that this SET process is highly unlikely to occur during the reaction. The homolytic cleavage of the Ni–Ch bond in intermediate I₅, which would produce the [Ni(dcype)Ph] intermediate and the corresponding ChPr radical, has been found to require more than 36 kcal mol⁻¹ for the three chalcogens. These values suggest that this pathway, although showing relatively close energy requirements to the reductive elimination, could also be ruled out. In fact, it has been reported elsewhere that the formation of chalcogen-centered radicals requires harsh conditions to occur.³⁹ Finally, the formation of dialkyl dichalcogenides from the starting chalcogenols, accompanied by the release of molecular hydrogen has been studied. In this case, the thermodynamics of the processes indicate that this could only be favored for tellurides (ca. −10 kcal mol⁻¹). The transition states for these processes have not been sought but, typically, the formation of dihydrogen requires the presence of a metal support, which is not present in the studied system. In the end, other operative radical processes cannot be ruled out, and only an experimental study of the described selenol and tellurol couplings could claim that the reactions proposed here may be achieved, but this is beyond the scope of this work.

Conclusions

A plausible mechanism has been proposed for the nickel-catalyzed cross-coupling between benzonitrile and propyl chalcogenols (HChPr, Ch = S, Se, Te). The reaction seems to follow the typical oxidative addition/transmetalation/reductive elimination sequence for a nickel(0)-promoted process showing relatively small variations among the studied organochalcogenide compounds.

The calculated overall reaction barriers for coupling benzonitrile with propanethiol, propaneselenol and propanetellurol are 30.8, 32.9 and 32.3 kcal mol⁻¹, respectively. In all cases, the reductive elimination of the final product presents the highest energy requirements, which is usually observed for Ni(II) compounds.

The microkinetic modeling, built from the computed relative Gibbs energies, allows the simulation of the reaction course and serves to positively assess the employed computational methodology. The good agreement between the theoretical and experimental yields of the C–S coupling validate the proposed catalytic cycle, which can be subsequently used to analyze the potential usage of the same catalytic platform to construct C–Se and C–Te bonds. These two processes, which would allow the production of drug-like compounds, appear to be feasible, although the results obtained suggest that the reaction rate would be slower, so that longer reaction times would be required.

Computational details

All the structures have been optimized in solution with the Gaussian16 package⁴⁰ and the B3LYP functional.⁴¹ In the optimization process the Ahlrichs triple-zeta basis set TZVP⁴² has been used for all atoms except for Te, which has been described with the SDD⁴³ basis set and its corresponding ECP. Tight convergence criteria along with ultrafine integration grids have been used ensure satisfactory convergence. In all cases, the solvation energies have been computed in 1,4-dioxane with the SMD⁴⁴ version of the IEFPCM⁴⁵ continuum dielectric solvation model. The dispersion correction terms have been included in all the calculations by using the D3 method of Grimme.⁴⁶ These computational settings are referred to as BS1 scheme. Frequency calculations were carried out for all the stationary points computed with BS1 to ensure the nature of local minima and transition states, which have zero and one imaginary frequencies, respectively. Additional single-point calculations, including solvation and dispersion corrections, were employed to obtain improved Gibbs energy values with larger basis sets on the optimized geometries. The def2-QZVP⁴⁷ basis set was used to describe all the atoms. These computational settings are referred as BS2 scheme. The computed Gibbs energies have been corrected to use a standard state corresponding to species in solution with a concentration of 1 M.

Unless otherwise stated, all the Gibbs energy values in the text correspond to those computed with the larger basis sets BS2 including SMD/PCM solvation and the D3 dispersion terms; the entropic corrections to the Gibbs energy are extracted from the BS1 scheme at 110 °C. The detailed procedure for obtaining the final Gibbs energy values is described in the ESI.† Similar computational settings have been previously employed in other metal-catalyzed reactions, including nickel, and have been shown to produce accurate results.⁴⁸ During the review process, one reviewer asked whether the choice of functional (B3LYP) was appropriate for modeling the studied reaction. To check for this potential issue, the overall reaction barrier of the coupling between propanethiol and benzonitrile was calculated with different density functionals, namely BP86,⁴⁹ PBE,⁵⁰ M06L,⁵¹ MN12SX,⁵² PBE0⁵³ and wB979XD.⁵⁴ This process requires fully recalculating the I₀, KCN and RETS species for each functional. The calculated barriers are: 25.9, 23.1, 25.3, 28.1, 28.2, 31.3 kcal mol⁻¹, for BP86, PBE, M06L, MN12SX, PBE0 and ωB979XD, respectively. The energy barriers found for the pure functionals are excessively low and they should therefore be discarded. In general, the hybrid functionals show higher energy requirements; the only functional showing a barrier close to that found for B3LYP (30.8 kcal mol⁻¹) is ωB979XD (31.3 kcal mol⁻¹), indicating that the latter would produce – broadly speaking – a similar outcome, although its slightly higher barrier would end up producing a slower overall reaction. In any case, the B3LYP microkinetic model is in such good agreement with the available experimental data that any other functional would probably give worse results.

To slightly reduce the computational cost and the conformational noise of the alkylic thiol chain, the original dodecylthiol substrate has been replaced by its shorter analogs propanethiol (HSPr). The same approach has been considered for the selenium and tellurium analogs, therefore propaneselenol (HSePr) and propanetellurol (HTePr) have been used as prospective substrates for the C–Se and C–Te coupling reactions, respectively.

The deprotonation stage of each starting propyl chalcogenol (HChPr) with tBuOK has been computed. These calculations show, in all cases, that the transition state governing this process is lower in energy than the corresponding separated reactants, indicating that the proton transfer should be barrierless under the reaction conditions. An intensive search for stable encounter complexes between HChPr and tBuOK prior to deprotonation has been carried. However, the intermediates found are either more energetic than the initial reactants or undergo spontaneous deprotonation of HChPr.

Special care has been taken when modeling the organometallic species involved in the computed catalytic cycles; in this case, one of the potential important issues is the change in the coordination number of the metal centers along the computed pathways, typically by the binding of substrate or explicit solvent molecules. The calculations indicate that nickel complexes do not tend to expand their coordination sphere by binding additional solvent molecules. On the other hand, potassium seems to prefer adding one coordinated solvent molecule; therefore, one explicit O-bound 1,4-dioxane molecule has been added to all the potassium atoms within the calculations. Thus, in all the schemes included in this report; the coordination number around the nickel centers always corresponds to the number of bound ligands while potassium always bears one attached solvent molecule, which is not displayed for clarity.

The simulation of the reaction kinetics has been performed with the COPASI⁵⁵ software. The rate constants of all the forward and backward steps in the catalytic cycles have been computed from the DFT energy differences using the methodology described in the ESI.† The derived rate constants have been fed into microkinetic models to generate the transient concentrations of all the species along the reaction course. Similar kinetics simulations have been successfully employed to assess and support computed reaction mechanism proposals.⁵⁶

Author contributions

FAGM participated in the investigation, data curation and writing – review of this manuscript. GA was involved in the writing – review & editing procedure. JJ oversaw the conceptualization, formal analysis, visualization, and writing the original and revised version of this work.

Data availability

The computed energy terms to generate the Gibbs energy profiles and the microkinetic modelling data, along with the methodology employed, can be found in the ESI file.†

Computed data for this article are available at ioChem-BD⁵⁷ database and can be retrieved at https://doi.org/10.19061/iochem-bd-6-433.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Spanish Structures of Excellence María de Maeztu program (CEX2021-001202-M) and Generalitat de Catalunya (2021-SGR-00286) is gratefully acknowledged. FAGM thanks the MICINN and the FSE program for the predoctoral grant PRE2019-091164.

References

1. (a) I. P. Beletskaya and V. P. Ananikov, Chem. Rev., 2011, 111, 1596–1636; (b) I. P. Beletskaya and V. P. Ananikov, Chem. Rev., 2022, 122, 16110–16293; (c) C.-S. Wang, Y. Xu, S.-P. Wang, C.-L. Zheng, G. Wang and Q. Sun, Org. Biomol. Chem., 2024, 22, 645–681.
2. (a) E. A. Ilardi, E. Vitaku and J. T. Njardarson, J. Med. Chem., 2014, 57, 2832–2842; (b) K. Laxmikeshav, P. Kumari and N. Shankaraiah, Med. Res. Rev., 2022, 42, 513–575.
3. (a) K. A. Scott and J. T. Njardarson, Top. Curr. Chem., 2018, 376, 5; (b) P. Ertl, E. Altmann and J. M. McKenna, J. Med. Chem., 2020, 63, 8408–8418.
4. L. L. Hegedus and R. W. McCabe, Catalyst Poisoning, M. Dekker, New York, 1984.
5. (a) R. J. Young, S. L. Flitsch, M. Grigalunas, P. D. Leeson, R. J. Quinn, N. J. Turner and H. Waldmann, JACS Au, 2022, 2, 2400–2416; (b) R. A. Shenvi, ACS Cent. Sci., 2024, 10, 519–528.
6. C. W. Nogueira, N. V. Barbosa and J. B. T. Rocha, Arch. Toxicol., 2021, 95, 1179–1226.
7. M. W. Pitts and P. R. Hoffmann, Cell Calcium, 2018, 70, 76–86.
8. (a) A. B. Addinsall, C. R. Wright, S. Andrikopoulos, C. van der Poel and N. Stupka, Biochem. J., 2018, 475, 1037–1057; (b) M. P. Jedrychowski, G. Z. Lu, J. Szpyt, M. Mariotti, R. Garrity, J. A. Paulo, D. K. Schweppe, D. Laznik-Bogoslavski, L. Kazak, M. P. Murphy, V. N. Gladyshev, S. P. Gygi, E. T. Chouchani and B. M. Spiegelman, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10789–10796.
9. V. A. Shchedrina, Y. Zhang, V. M. Labunskyy, D. L. Hatfield and V. N. Gladyshev, Antioxid. Redox Signaling, 2010, 12, 839–849.
10. H. Pothion, C. Jehan, H. Tostivint, D. Cartier, C. Bucharles, A. Falluel-Morel, L. Boukhzar, Y. Anouar and I. Lihrmann, Antioxid. Redox Signaling, 2020, 33, 1257–1275.
11. (a) E. Domínguez-Álvarez, D. Plano, M. Font, A. Calvo, C. Prior, C. Jacob, J. A. Palop and C. Sanmartín, Eur. J. Med. Chem., 2014, 73, 153–166; (b) E. Domínguez-Álvarez, M. Gajdács, G. Spengler, J. A. Palop, M. A. Marć, K. Kieć-Kononowicz, L. Amaral, J. Molnár, C. Jacob, J. Handzlik and C. Sanmartín, Bioorg. Med. Chem. Lett., 2016, 26, 2821–2824; (c) M. Gajdács, G. Spengler, C. Sanmartín, M. A. Marć, J. Handzlik and E. Domínguez-Álvarez, Bioorg. Med. Chem. Lett., 2017, 27, 797–802.
12. (a) N. D. Facompre, I. Sinha, K. El-Bayoumy, J. T. Pinto and R. Sinha, Int. J. Cancer, 2012, 131, 2134–2142; (b) C. Pramita, R. S. Singha and B. Sudin, Anti-Cancer Agents Med. Chem., 2015, 15, 501–510.
13. (a) M. Koketsu, H. O. Yang, Y. M. Kim, M. Ichihashi and H. Ishihara, Org. Lett., 2001, 3, 1705–1707; (b) C. Shi, L. Yu, F. Yang, J. Yan and H. Zeng, Biochem. Biophys. Res. Commun., 2003, 309, 578–583; (c) F. Zhao, J. Yan, S. Deng, L. Lan, F. He, B. Kuang and H. Zeng, Cancer Lett., 2006, 236, 46–53; (d) L. Zhang, L. Zhou, J. Du, M. Li, C. Qian, Y. Cheng, Y. Peng, J. Xie and D. Wang, BioMed Res. Int., 2014, 2014, 696107; (e) P. D. Hanavan, C. R. Borges, B. A. Katchman, D. O. Faigel, T. H. Ho, C.-T. Ma, E. A. Sergienko, N. Meurice, J. L. Petit and D. F. Lake, OncoTargets, 2015, 6(21), 18418–18428; (f) I. Domracheva, I. Kanepe-Lapsa, L. Jackevica, J. Vasiljeva and P. Arsenyan, Life Sci., 2017, 186, 92–101.
14. V. Gandin, P. Khalkar, J. Braude and A. P. Fernandes, Free Radical Biol. Med., 2018, 127, 80–97.
15. (a) P. N. Makhal, A. Nandi and V. R. Kaki, ChemistrySelect, 2021, 6, 663–679; (b) A. I. Doig, K. N. Sands, B. Boongaling, W. Zhou and T. G. Back, Org. Biomol. Chem., 2024, 22, 8881–8897.
16. (a) J.-B. Han, T. Dong, D. A. Vicic and C.-P. Zhang, Org. Lett., 2017, 19, 3919–3922; (b) N. V. Cornelissen, F. Michailidou, F. Muttach, K. Rau and A. Rentmeister, Chem. Commun., 2020, 56, 2115–2118; (c) M. He, L. Gu, Y. Tan, Y. Wang, Y. Wang, C. Zhang and W. Ma, Adv. Synth. Catal., 2020, 362, 5708–5715; (d) M.-Q. Huang, T.-J. Li, J.-Q. Liu, A. Shatskiy, M. D. Kärkäs and X.-S. Wang, Org. Lett., 2020, 22, 3454–3459; (e) A. Capperucci, A. Petrucci, C. Faggi and D. Tanini, Adv. Synth. Catal., 2021, 363, 4256–4263; (f) G. Badshah, C. M. B. Gomes, S. Ali, E. Q. Luz, G. L. Silvério, F. S. Santana, D. Seckler, D. B. Paixão, P. H. Schneider and D. S. Rampon, J. Org. Chem., 2023, 88, 14033–14047; (g) Z. Cao, Q. Wang, H. Neumann and M. Beller, Angew. Chem., Int. Ed., 2024, 63, e202313714; (h) A. Karnat, E. Fouquet and P. Y. Toullec, J. Org. Chem., 2024, 89, 10462–10466.
17. G. Zeni, H. B. Formiga and J. V. Comasseto, Tetrahedron Lett., 2000, 41, 1311–1313.
18. N. Taniguchi, Tetrahedron, 2012, 68, 10510–10515.
19. (a) N. Taniguchi, J. Org. Chem., 2007, 72, 1241–1245; (b) D. Alves, C. G. Santos, M. W. Paixão, L. C. Soares, D. D. Souza, O. E. D. Rodrigues and A. L. Braga, Tetrahedron Lett., 2009, 50, 6635–6638; (c) V. G. Ricordi, C. S. Freitas, G. Perin, E. J. Lenardão, R. G. Jacob, L. Savegnago and D. Alves, Green Chem., 2012, 14, 1030–1034.
20. N. Taniguchi, Tetrahedron, 2016, 72, 5818–5823.
21. M. Sattar, M. Shareef, K. Patidar and S. Kumar, J. Org. Chem., 2018, 83, 8241–8249.
22. L. A. Ba, M. Döring, V. Jamier and C. Jacob, Org. Biomol. Chem., 2010, 8, 4203–4216.
23. (a) E. Domínguez-Álvarez, B. Rácz, M. A. Marć, M. J. Nasim, N. Szemerédi, J. Viktorová, C. Jacob and G. Spengler, Drug Resistance Updates, 2022, 63, 100844; (b) L. Chiaverini, D. Cirri, I. Tolbatov, F. Corsi, I. Piano, A. Marrone, A. Pratesi, T. Marzo and D. La Mendola, Int. J. Mol. Sci., 2022, 23, 7505.
24. (a) L. Engman, J. Persson, K. Vessman, M. Ekström, M. Berglund and C.-M. Andersson, Free Radical Biol. Med., 1995, 19, 441–452; (b) E. Wieslander, L. Engman, E. Svensjö, M. Erlansson, U. Johansson, M. Linden, C.-M. Andersson and R. Brattsand, Biochem. Pharmacol., 1998, 55, 573–584; (c) D. Tanini, A. Grechi, L. Ricci, S. Dei, E. Teodori and A. Capperucci, New J. Chem., 2018, 42, 6077–6083.
25. M. Brodsky, G. Halpert, M. Albeck and B. Sredni, J. Inflammation, 2010, 7, 3.
26. (a) A. Layani-Bazar, I. Skornick, A. Berrebi, M. H. Pauker, E. Noy, A. Silberman, M. Albeck, D. L. Longo, Y. Kalechman and B. Sredni, Cancer Res., 2014, 74, 3092–3103; (b) E. Zigman-Hoffman, B. Sredni, B. Meilik, E. Naparstek and B. Tartakovsky, Leuk. Lymphoma, 2021, 62, 1146–1156; (c) A. Tripathi, A. Khan and R. Srivastava, Amino Acids, 2023, 55, 1361–1370; (d) A. Chaouat, Y. Kalechman, O. Hay, J. E. Manoim, T. Lantner, E. Niderberg, H. Hauschner, D. K. Sredni, T. Cohen, A. Schlesinger, R. Nadler, M. Barda-Saad, E. Noy, M. Albeck, D. L. Longo and B. Sredni, Int. J. Biol. Sci., 2024, 20, 4407–4423.
27. (a) H. Zhang, H. Wang, Y. Jiang, F. Cao, W. Gao, L. Zhu, Y. Yang, X. Wang, Y. Wang, J. Chen, Y. Feng, X. Deng, Y. Lu, X. Hu, X. Li, J. Zhang, T. Shi and Z. Wang, Chem. – Eur. J., 2020, 26, 17289–17317; (b) D. Kundu, RSC Adv., 2021, 11, 6682–6698; (c) D. I. Bugaenko, A. A. Volkov, V. V. Andreychev and A. V. Karchava, Org. Lett., 2023, 25, 272–276.
28. (a) J. Feng, Y. Zhang, X. Wang, J. Liu, V. Benazzi, K. Lu, X. Zhao and S. Protti, Adv. Synth. Catal., 2023, 365, 3413–3431; (b) D. Singla, V. Luxami and K. Paul, Org. Chem. Front., 2023, 10, 237–266.
29. (a) C. Song, K. Liu, X. Dong, C.-W. Chiang and A. Lei, Synlett, 2019, 1149–1163; (b) K. S. Bhati, R. Nagar, B. K. Malviya, M. Shukla, A. K. Jassal, V. P. Verma, D. K. Yadav, N. Kumari and S. Sharma, J. Org. Chem., 2022, 87, 13845–13855; (c) A. Chouhan, K. Ucheniya, L. Yadav, P. K. Jat, A. Gurjar and S. S. Badsara, Org. Biomol. Chem., 2023, 21, 7643–7653; (d) Z.-X. Yang, L.-C. Ding, G.-H. Yang, D. Wang, L. Shi, Y. Li and D. Liang, J. Org. Chem., 2024, 89, 10660–10677.
30. (a) J. Lv, Z. Jin, H. Wang and Y. R. Chi, ACS Sustainable Chem. Eng., 2022, 10, 13901–13916; (b) N. Nowrouzi, M. Abbasi and Z. Zellifard, RSC Adv., 2023, 13, 9242–9246.
31. (a) M. Kosugi, T. Shimizu and T. Migita, Chem. Lett., 1978, 7, 13–14; (b) V. P. Ananikov, N. V. Orlov, S. S. Zalesskiy, I. P. Beletskaya, V. N. Khrustalev, K. Morokuma and D. G. Musaev, J. Am. Chem. Soc., 2012, 134, 6637–6649; (c) J. Xu, R. Y. Liu, C. S. Yeung and S. L. Buchwald, ACS Catal., 2019, 9, 6461–6466; (d) R. Bag and N. K. Sharma, Org. Chem. Front., 2023, 10, 1252–1262; (e) R. S. K. Lalji, N. Monika, M. Gupta, S. Kumar, R. J. Butcher and B. K. Singh, Org. Biomol. Chem., 2024, 22, 5809–5815.
32. (a) M. Bandaru, N. M. Sabbavarpu, R. Katla and V. D. N. Yadavalli, Chem. Lett., 2010, 39, 1149–1151; (b) T.-J. Liu, C.-L. Yi, C.-C. Chan and C.-F. Lee, Chem. – Asian J., 2013, 8, 1029–1034; (c) J. Sun, Y. Wang and Y. Pan, Org. Biomol. Chem., 2015, 13, 3878–3881.
33. (a) A. Correa, M. Carril and C. Bolm, Angew. Chem., Int. Ed., 2008, 47, 2880–2883; (b) S. Guan, Y. Chen, H. Wu and R. Xu, RSC Adv., 2020, 10, 27058–27063; (c) B. Paul, S. Ghosh, S. Das and I. Chatterjee, Org. Biomol. Chem., 2024, 22, 8133–8137.
34. (a) T. Gensch, F. J. R. Klauck and F. Glorius, Angew. Chem., Int. Ed., 2016, 55, 11287–11291; (b) X. Huang, Y. Chen, S. Zhen, L. Song, M. Gao, P. Zhang, H. Li, B. Yuan and G. Yang, J. Org. Chem., 2018, 83, 7331–7340; (c) T. Wang, J. Chen, J. Wang, S. Xu, A. Lin, H. Yao, S. Jiang and J. Xu, Org. Biomol. Chem., 2018, 16, 3721–3725.
35. (a) M. Font, T. Parella, M. Costas and X. Ribas, Organometallics, 2012, 31, 7976–7982; (b) E. Haldón, E. Álvarez, M. C. Nicasio and P. J. Pérez, Inorg. Chem., 2012, 51, 8298–8306; (c) T. Guo, X.-N. Wei, H.-Y. Wang, Y.-L. Zhu, Y.-H. Zhao and Y.-C. Ma, Org. Biomol. Chem., 2017, 15, 9455–9464; (d) Y. Wang, J. Deng, J. Chen, F. Cao, Y. Hou, Y. Yang, X. Deng, J. Yang, L. Wu, X. Shao, T. Shi and Z. Wang, ACS Catal., 2020, 10, 2707–2712; (e) Y. Ru-Jian, Z. Chun-Yan, Z. Xiang, Y.-S. Xiong and X.-M. Duan, Org. Biomol. Chem., 2021, 19, 2901–2906.
36. (a) N. P. N. Wellala and H. Guan, Org. Biomol. Chem., 2015, 13, 10802–10807; (b) M. Iwasaki, N. Miki, Y. Tsuchiya, K. Nakajima and Y. Nishihara, Org. Lett., 2017, 19, 1092–1095; (c) N. W. J. Ang and L. Ackermann, Chem. – Eur. J., 2021, 27, 4883–4887.
37. T. Delcaillau and B. Morandi, Chem. – Eur. J., 2021, 27, 11823–11826.
38. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
39. (a) Q. Sun, Z. Li, X. Zeng, W. Wang, Z. Sun, M. Ge, D. Wang, D. K. W. Mok and F.-T. Chau, ChemPhysChem, 2005, 6, 2032–2035; (b) A. G. Vandeputte, M.-F. Reyniers and G. B. Marin, J. Phys. Chem. A, 2010, 114, 10531–10549.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
41. (a) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627; (d) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
42. (a) A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577; (b) A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
43. (a) T. H. Dunning and P. J. Hay, in Methods of Electronic Structure Theory, ed. H. F. Schaefer, Springer, Boston, US, 1977, pp. 1–27; (b) A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441; (c) J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420.
44. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
45. (a) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094; (b) G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
46. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
47. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
48. (a) J. Jover, Organometallics, 2018, 37, 327–336; (b) J. Jover, Catal. Sci. Technol., 2019, 9, 5962–5970; (c) J. Echeverría and J. Jover, Eur. J. Org. Chem., 2022, 26–31; (d) F. A. Gómez-Mudarra, G. Aullón and J. Jover, Catal. Sci. Technol., 2023, 13, 1381–1394.
49. (a) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824; (b) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
50. (a) J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
51. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
52. R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191.
53. (a) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170; (b) M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
54. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
55. S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074.
56. (a) J. Jover, Phys. Chem. Chem. Phys., 2017, 19, 29344–29353; (b) M. Besora and F. Maseras, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1372; (c) A. H. Motagamwala and J. A. Dumesic, Chem. Rev., 2021, 121, 1049–1076; (d) G. Sciortino and F. Maseras, Theor. Chem. Acc., 2023, 142, 99.
57. M. Álvarez-Moreno, C. de Graaf, N. Lopez, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ob01865f

---