Undemanding synthesis of N,P co-doped carbon nanosheets for the hydrogen evolution reaction: combining experimental quantitative analysis and DFT calculation corroboration

Abstract

Developing a cost-effective catalyst for the hydrogen evolution reaction (HER) is of foremost importance for a new energy layout and has broad development prospects. Metal-free heteroatom-doped carbon materials have emerged as a focal point of research due to their low price, superior electrical conductivity, and exceptional corrosion resistance. However, there is a paucity of detailed examinations into the distinct mechanisms of HER activity enhancement of different forms of heteroatomic species on HER activity. To maximize the potential of metal-free heteroatom-doped carbon materials for the HER, the respective doping effect on the catalytic activity should be elucidated. Herein, we developed a one-step pyrolysis to synthesize N and P co-doped carbon nanosheets. Chain-structured amino acids are cross-linked with phytic acid to form a huge nanocarbon network that lies flat in two dimensions. The prepared catalyst exhibits an active surface area of 93.5 mF cm⁻² and the thickness of the nanoplates was less than 10 nm. The ultra-large active surface area provides the basis for an efficient HER. By changing the feeding ratios of precursors, the proportions of different fractions of N species and P species showed certain trends. By constructing different double-doping models, the changes in the electron cloud density at the double-doped sites within the local π bonds were related to the changing trends of hydrogen adsorption free energy. Experimental and theoretical analyses indicate that under the electronic perturbation of graphitic N and C₃PO, the surrounding carbon atoms undergo charge polarization, and their ΔG_H* is optimized after electron rearrangement, which promotes the HER process.

---

Introduction

Hydrogen stands as a promising energy carrier for supplanting fossil fuels in the future.^1–5 It is differentiated into gray, blue, and green hydrogen, depending on its production methods. Of these varieties, use of green hydrogen, produced via water electrolysis, is acknowledged as the most effective method for reaching carbon neutrality in the future. Nonetheless, this process encounters a considerable challenge due to the high energy barrier associated with the hydrogen evolution reaction (HER), which significantly hinders progress. Therefore, the development of efficient and cost-effective HER catalysts is urgently needed.^6–9 At present, the leading HER catalysts are categorized into noble metal and transition metal-based catalysts.^10–13 Noble metal catalysts are known for their minimal overpotential yet are limited by their rarity and high cost, rendering them impractical for an economy-driven approach.^14–16 In contrast, transition metal based catalysts are economy-friendly, but their application for the HER is hindered by their low conductivity and tendency to aggregate at elevated temperatures, which compromises their suitability for HER tasks.^17,18 In the realm of hydrogen evolution reaction (HER) catalysts, carbon-based materials have emerged as a focal point of research due to their distinctive advantages. The carbon-based materials are known for their adjustable pore structures, which amplify the exposure of catalytic active sites and expedite the transfer of reactant species.^19–24 Additionally, their superior electrical conductivity facilitates rapid electron transfer, while their exceptional corrosion resistance ensures durability in both acidic and alkaline electrolytic environments over prolonged periods. However, a notable challenge with carbon materials is their suboptimal hydrogen adsorption free energy (ΔG_H*), which can impede the efficient adsorption of hydrogen atoms at the active sites.^25–29 Recent advancements suggest that doping carbon materials with heteroatoms can significantly alter the electron cloud density around carbon atoms, thereby potentially optimizing the ΔG_H* towards more favorable conditions.^30–35 Pioneering work by Qu et al.³⁶ has shown that co-doping carbon materials with heteroatoms not only multiplies the active sites on their surface but also promotes a “cooperative coupling” effect. This synergistic interaction markedly boosts the electrochemical activity of the carbon-based catalysts. Similarly, Sergio et al.³⁷ utilized P-rich biomass precursor systems to develop P-doped carbon-based catalysts for the HER. Their research proposes that the P–C bonds, formed at high carbonization temperatures, could serve as the primary active species facilitating the HER. Furthering this line of inquiry, Li et al.³⁸ crafted N-doped vertical graphene (N-VG) arrays through plasma-enhanced chemical vapor deposition, showing exceptional HER performance. Through a combination of experimental observations and theoretical calculations, they identified that all three forms of N doping (graphitic, pyridinium, and pyrrole) contribute positively to the catalyst's HER activity. This series of studies demonstrates the potential of carbon-based materials to serve as highly efficient and durable HER catalysts.

Despite the potential of carbon materials as robust contenders for HER catalysts, the literature predominantly features transition metal-based catalysts, with non-metallic alternatives being vastly underrepresented. Moreover, among the studies on heteroatom-doped non-metallic catalysts, there is a paucity of detailed examinations into the distinct mechanisms of HER activity enhancement of various heteroatomic species, as well as the collaborative effects of dual-heteroatom co-doping. N doping serves as a case, graphitic N, pyridinic N, and pyrrolic N doped in carbon exhibit varied influences on the electron cloud density around neighboring carbon atoms. Such differences necessitate an insight into their density of states, orbital energy level and electron cloud densities to elucidate their doping effect. Apart from that, in the research of P atom doping graphene, most scholars constructed the graphitic P (C₃–P) doping model. However, although the P atoms in graphitic P have high chemical activity, they have high formation energy and are easily oxidized in air. This implies that the preparation conditions of the C₃P structure are harsh and unfavorable for long-term preservation.³⁹ In contrast, C₃PO has a lower binding energy, and is more stable compared to C₃P, indicating that C₃PO is more likely to exist in P-doped graphene. Since the P atoms in C₃PO and C₃P have completely different chemical states, the effect produced by their doping is different. This means that we must include a discussion on C₃PO.

Herein, we developed N, P co-doped carbon-based catalysts by a facile one-step pyrolysis process (Scheme 1). Phytic acid, an environmentally friendly and inexpensive biomass raw material with strong chelating ability, was chosen as a P and C source. Glycine was used as a N source because it is economically friendly, dissolves in water easily, and could crosslink with phytic acid to form a stable N, P co-doped carbon network. The synergistic effects of doping with different heteroatoms were thoroughly investigated by combining experimental results with density functional theory (DFT) calculations. To better understand the effect of N and P species on the HER, the catalysts were thus carbonized at different temperatures to modulate the chemical state of N and P in the resultant carbon materials. This approach identified the optimal active components within the catalyst system. Combining X-ray photoelectron spectroscopy (XPS) results and DFT calculations, we found that the C₃PO structure and graphitic N are the key active species in this catalyst. In particular, C₃PO has the most suitable hydrogen adsorption free energy (ΔG_H* = 0.13) when it is interstitially doped with graphitic N.

Scheme 1 Schematic representation of the synthetic method for CNP.

Experimental

Materials

Glycine and 50% phytic acid were purchased from Wako Pure Chemical Industries Ltd (Osaka, Japan). Pt/C catalyst (20 wt%), isopropanol and Nafion (5 wt%) were purchased from Sigma-Aldrich (Saint Louis, USA). N₂ gas (purity 99.99%) was purchased from Iwatani Fine Gas Co., Ltd. All reagents were used as received without purification.

Synthesis of CNP

Typically, 0.2 g of glycine and 0.16 g of 50% phytic acid were dissolved in 1 mL of deionized water. The mixture was then dried at 90 °C for 2 h to form the C/N/P solid precursor. Other samples with different amounts of N and P were also synthesized using the same procedure. The other detailed proportions of raw materials are listed in Table S1.† The as-made precursor was placed in a tube furnace and heated to 900 °C with a ramp of 5 °C min⁻¹ and kept for 3 h under a N₂ flow (60 mL min⁻¹). The product is denoted as “CNP0.4”, where 0.4 represents the added ratio of phytic acid to glycine. We also prepared CNP0.4 at different carbonation temperatures to investigate the structural changes in heteroatom-doped carbon layers during carbonization processes.

Characterization

The morphology was studied by transmission electron microscopy (TEM, Hitachi H800). Atomic force microscopy (AFM) was used to check the thickness of the nanosheets. The mass ratio of carbon and P was investigated using energy-dispersive X-ray spectroscopy (EDX). The N content was measured using elemental analysis (CHN, PerkinElmer 2400IICHNS/O). Powder X-ray diffraction (XRD, RINT2200 with Cu Kα radiation) was used to determine the structure of the carbon layers. The elemental doping and valence states were evaluated using XPS (JEOL JPS-9000MX) with Mg Kα as the energy source. Raman spectra of the samples were recorded using a confocal Raman microscope (LabRAM HR-800, Horiba, Ltd, Kyoto, Japan).

Electrochemical measurements

To evaluate the hydrogen evolution reaction (HER) activity of the samples, we employed an ALS 2325 bi-potentiostat equipped with a standard three-electrode system. Hg/Hg₂Cl₂ served as the reference electrode for the 0.5 M H₂SO₄ electrolyte, while a graphite rod functioned as the counter electrode. To prepare the working electrode, the following procedure was followed: 8 mg of catalyst powder was dispersed in a solution containing 1 mL of isopropanol, 5 wt% Nafion, and deionized water (V_isopropanol : V_Nafion : V_{Deionized water} = 1 : 1 : 8). The mixture was ultrasonicated to obtain homogeneous catalyst ink. Subsequently, a suspension (4 μg) of the catalyst ink was evenly coated onto a carbon cloth (with an area of 0.1256 cm²) of a rotating ring-disk electrode, forming a thin and uniform carbon layer. The working electrode was thoroughly dried under ambient conditions for 30 min to complete its preparation. The measurement potentials were referenced to the reversible hydrogen electrode (RHE) as determined by the following equation:

E_RHE = E_Hg/Hg2Cl2 + 0.244 (0.5 M H₂SO₄)

To assess the HER activity of the samples, linear sweep voltammetry (LSV) was conducted at a sweep rate of 5 mV s⁻¹ and a rotation speed of 1600 rpm under a N₂ flow at 80 mL min⁻¹. The electrochemical impedance spectroscopy (EIS) measurements were recorded in the frequency range from 200 000 to 10 Hz.

DFT calculation

The density functional theory (DFT) calculations were performed using Gaussian 16W. The B3LYP hybrid density functional in combination with the 6–31g(d,p) and the dispersion correction (keywords: em = gd3bj) were used. The basis set was used in the calculations because it has been shown to be a reliable approach for this type of organic chemical reaction.

Results and discussion

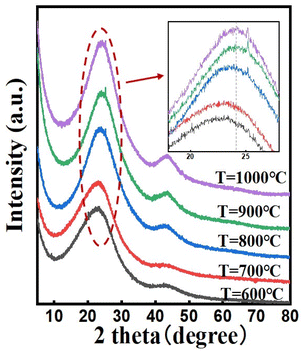
The XRD patterns of the N, P co-doped carbon materials synthesized at different temperatures are shown in Fig. 1. All samples exhibit an XRD pattern with a broad (002) diffraction peak centered at around 2θ = 23° (amorphous carbon peak) and a (101) diffraction broad peak appears centered at around 2θ = 43°, which relates to the formation of graphitic domains in the carbon structure. The enhancement of the signals at the two peaks is attributed to the increased graphitization of the carbon material, which leads to a more orderly arrangement of carbon atoms. Additionally, we observed that with the increase in temperature, both diffraction peaks shift towards higher angles, indicating a contraction in the carbon lattice volume. We believe this may be influenced by two factors. Firstly, as the heat treatment temperature increases, the degree of graphitization of the carbon material increases, leading to changes in the binding structure and a decrease in the interlayer spacing of the carbon lattice. Secondly, with the rise in temperature, the total doping amount of N and P atoms decreases, resulting in a reduction in the volume of the carbon lattice. Furthermore, when the carbonized temperature is over 800 °C, small but sharp diffraction peaks were detected at around 2θ = 25°, which is related to the sp² hybridized carbon, suggesting an increasing number of C=C bonds.⁴⁰ To obtain more penetrating insight into the variation of the interlayer spacing within carbon materials, we have executed a quantitative analysis of the lattice constant for samples prepared at disparate carbonization temperatures. According to Table S2,† as the temperature ascends, the interlayer spacing of carbon materials manifests a descending tendency, thereby confirming that the graphitization degree of the catalyst escalates synchronously with the increasing temperature. It is noteworthy that there is a marginal difference in the interlayer spacing between sample T = 900 °C and T = 1000 °C, which might be imputed to the insertion of oxygen atoms under high temperature conditions.

Fig. 1 XRD patterns of the various samples.

Table 1 lists the changes in N content in the products at different temperatures and raw material mixing ratios. According to the CHN analysis results, the N content in the products decreases with an increase in temperature. This could be due to the competitive reaction between the formation of C=C bonds and C–N bonds. Pyrolysis at high temperatures induces structural changes in carbon materials, where an increase in temperature leads to the transformation of defective carbon structures into sp² hybridized carbon atoms, forming regular hexagonal ring graphite structures. Therefore, at high temperatures, the formation of C=C bonds is favored, and the inner N atoms are gradually eliminated leading to a decrease in the overall N content of the material. Additionally, in conjunction with the XRD patterns, when the heat treatment temperature is between 600 and 900 °C, the interlayer spacing of the carbon lattice becomes narrower with increasing temperature. Notably, when the amount of phytic acid added increases, the doping level of N elements in the product actually increases.

Table 1 The CHN results of the various samples (mass ratio)

Temperature	C[%]	N [%]	N/C
T = 600 °C	45.07	16.85	0.37
T = 700 °C	45.26	17.14	0.38
T = 800 °C	52.19	6.75	0.13
T = 900 °C	59.6	3.33	0.56
T = 1000 °C	68.33	2.26	0.033
Ratio	C[%]	N[%]	N/C
CNP0.2	66.53	2.73	0.041
CNP0.4	59.6	3.33	0.056
CNP0.6	55.46	3.4	0.063

---

Fig. 2 displays the morphology of CNP0.4. According to Fig. 2(a), the homogeneous carbon nanosheets were successfully synthesized. The SEM images were obtained and Fig. 2(b) shows a side view of the carbon block, which reveals that the sample consists of stacked layers of nano-meter-sized sheets in the undispersed state. From the top view of the carbon block (Fig. 2(c)), channels with diameters ranging from 1 μm to 5 μm were observed. Additionally, some surface cracks were found, indicating the presence of tensile stress within the carbon layers.

Fig. 2 (a) The TEM image of sample CNP0.4. (b) The SEM image of sample CNP0.4 from the side view. (c) The SEM image of sample CNP0.4 from the top view. (d) AFM image of CNP0.4 at the micrometer scale and (e) the corresponding 3D height distribution. (f) AFM image of CNP0.4 at the nanometer scale and (g) the corresponding 3D height distribution. (h) The heights of lines i–iii in AFM images.

The numerous channels formed on the surface of the carbon block are due to the decomposition of phytic acid at high temperatures. Phosphoric acid is generated, which has a certain activating effect on the carbon materials. To verify this, the sample with different added phytic acid amounts and various heating temperatures were tested using SEM. According to Fig. S1,† it was observed that as the added amount of phytic acid increased, the number and size of the surface pores on the carbon block also increased. Moreover, no pores were present on the sample surface at 700 °C. As the temperature increased, no significant changes in the surface pores were observed. Combined with the result of CHN analysis, the increasing amount of added phytic acid will enhance the activation effect of phosphoric acid and make the carbon atom content decrease. The ultra-thin carbon layer ensures adequate exposure of active sites, allowing rapid transfer of electrons and species, enhancing the HER activity of the catalyst (Table 2).

Table 2 Height distributions of CNP0.4 at the nanometer scale

Area	Average height (nm)	Maximum height (nm)	Surface area (nm^2)
Polygon 1	1.9	2	20300
Polygon 2	1.3	1.6	8568
Polygon 3	0.8	1.2	21400
Polygon 4	1.8	2	17860
Polygon 5	2.4	2.6	30104

---

The AFM images (Fig. 2(d and f)) and corresponding 3D graphics (Fig. 2(e and g)) were checked to investigate the thickness of the carbon layer. The heights of nanosheets are recorded in Fig. 2(h) and Table 2. We found that the thickness of all nanoplates in Fig. 2(d, f) and Table 2 is no more than 2 nm, and the aspect ratios (area-to-thickness) are more than 4000 : 1, confirming the formation of nanosheets. To verify the uniformity of nanosheet thickness distribution in CNP0.4, we plotted the cumulative distribution frequency curve of thickness. In samples with a diameter of less than 800 nm, 90% of the nanosheets had a thickness below 2.4 nm, and 50% had a thickness below 1.9 nm. Additionally, we constructed box plots for the thickness of samples with diameters less than 800 nm and those within the range of 0.8–15 μm. As depicted in Fig. S4,† the box plot for the thickness distribution of nanosheets with diameters less than 800 nm is wide and flat, indicating a relatively concentrated thickness distribution. Conversely, the box plot for nanosheets with diameters between 0.8 and 1.5 μm is narrow and tall, suggesting a broader thickness distribution range. This phenomenon can be attributed to the higher surface energy of larger nanosheets, which are more likely to adsorb other nanosheets to reduce their surface energy.

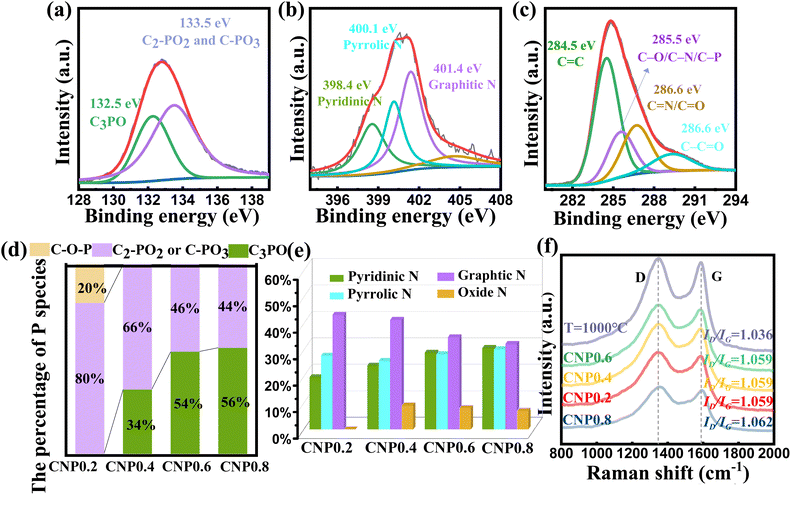
Fig. 3(a) shows the P 2p spectrum of CNP0.4, which could be separated into two subpeaks (132.5 eV for C₃-PO and 133.5 eV for C-PO₃ or C₂PO₂).^41–44 It is worth noting that the peak at 132.5 eV for C₃PO reveals that P atoms were successfully doped into the carbon skeleton and replaced some carbon atoms. The peak at 133.5 eV for C-PO₃ or C₂PO₂ represents the bonding of P atoms with the edge carbon. To investigate the effect of different added phytic acid amounts on the chemical state of doped P, we compared the changes in the C₃PO content of the product at different raw material ratios. As shown in Fig. 3(d), the percentage of C₃PO in the product increased when the amount of phytic acid increased. In contrast, the percentages of C₂-PO₂ and C-PO₃ decrease at high phytic acid concentrations, suggesting the promoted conversion of C–O–P, C₂-PO₂ and C-PO₃ bonds to C₃PO bonds at high phosphate molecule concentrations. Furthermore, the percentages of different P species in the samples were also investigated. C₂PO₂ and C-PO₃ were the main P species present when the heating temperature was 700 °C. The C₃PO structure appeared at 800 °C and its content increased with increasing temperature. When the heating temperature exceeds 1000 °C, C₂PO₂ and C-PO₃ are converted to highly valent oxides (Fig. S6†). The N 1s spectrum can be decomposed into three types of N atoms, as shown in Fig. 3(b), graphitic N (401.4 eV), pyrrolic N (400.1 eV), and pyridinic N (398.4 eV).⁴⁵ This result confirmed that almost all N species were incorporated into the carbon skeletons. To investigate the effect of different added phytic acid amounts on the chemical state of doped N, we compared the change of N species content in the products at different raw material ratios. As shown in Fig. 3(e), the percentage of pyridinic N in the product increases when the addition of phytic acid increases, which may imply that the activation of phytic acid led to the appearance of more edge sites in the carbon material, resulting in the transformation of graphitic N into pyridinic N. Moreover, the variations in the contents of N species during different carbonization temperature processes were documented to determine their high temperature stability. The relevant results are presented in Fig. S7.† We found that the pyridinic N and pyrrolic N contents decrease at high temperature while the graphitic N content increases. This result reveals that pyridinic N and pyrrolic N display suboptimal stability at high temperatures. They are inclined to migrate towards the interior of the carbon layers and will convert into graphitic N. When the temperature reaches 900 °C, NO_x species start to emerge. When the temperature reaches 1000 °C, the pyrrolic N is predominantly converted into NO_x species.⁴⁶ In conjunction with XRD results, the carbon materials exhibit a certain degree of oxidation at 1000 °C, accompanied by an increase in the lattice spacing. In addition, the P 2p spectra, N 1s spectra and Raman spectra of CNP0.4 after the HER were investigated to verify the stability of various species. According to Fig. S8,† the content of each species remained stable before and after the HER test, which could demonstrate the stability of C, N and P species in CNP0.4.

Fig. 3 (a) P 2p spectrum of CNP0.4. (b) N 1s spectrum of CNP0.4. (c) C 1s spectrum of CNP0.4. (d) P species percentage of CNP0.2, CNP0.4, CNP0.6 and CNP0.8. (e) N species percentage of CNP0.2, CNP0.4, CNP0.6, CNP0.8 and (f) Raman spectra of various samples.

To investigate the carbon crystallinity of the catalyst using different phytic acid/glycine ratios, we have carried out Raman spectra for various samples. According to Fig. 3(f), all samples contain typical D and G bands at 1347 and 1589 cm⁻¹ (ref. 47). The I_D/I_G ratios of various samples were calculated to figure out the carbonization degree of the products. For the samples carbonized at 900 °C, their I_D/I_G ratios are all close to 1.06. This suggests similar graphitization levels of the samples carbonized at 900 °C, excluding any influence of different graphitization levels in these samples. However, the catalyst carbonized at 1000 °C exhibit a higher I_D/I_G ratio than the samples carbonized at 900 °C, suggesting its higher graphitization degree. The activity of the hydrogen evolution reaction (HER) was measured using a typical three electrode system consisting of a 0.5 M H₂SO₄ solution. The results are summarized in Fig. 4 and Table S5.† To compare, 20 wt% Pt/C electrode was also tested. In order to figure out the catalytic mechanism, we examined the fatal species that contribute to the performance of the catalyst. According to Fig. 4(a) and Table S5,† the P-doped carbon as well as the N-doped carbon did not exhibit HER catalytic activity, implying that the HER activity of the catalyst is derived from the synergistic promotion of N, P atoms. Furthermore, we investigated the HER activity of the samples heated at different temperatures. As shown in Fig. 4(b), the performance of the catalyst increases first and then decreases with the increasing carbonization temperature. When the carbonization temperature is 900 °C, the catalyst exhibits the best activity, with an overpotential (η) of 306 mV to drive a current density of 10 mA cm⁻², which is much closer to the activity of commercial Pt/C catalyst than other catalysts.

Fig. 4 (a and b) LSV curves of the various samples. (c and d) The corresponding tafel slopes. (e) CV curves of CNP0.4 in 0.5M H₂SO₄ with the sweep rate changed from 10 mV s⁻¹ to 50 mV s⁻¹. (f) ESCA of samples CNP0.2, CNP0.4, CNP0.6 and CNP0.8. (g) ESCA of sample T = 800 °C, 900 °C, 1000 °C, PC and NC. (h) The normalized current density of sample T = 800 °C, 900 °C, 1000 °C, PC and NC. (i) The normalized current density of CNP0.2, CNP0.4, CNP0.6 and CNP0.8.

The increase in catalyst performance up to 900 °C could be attributed to the increasing graphitization degree of the carbon materials and the increasing percentage of C₃PO. When the temperature is higher than 900 °C, the HER performance decreases despite the higher graphitization degree at the elevated temperature. This is probably due to the aggregation of carbon nanosheets at high temperature. In addition, we noticed that samples with carbonation temperatures below 800 °C are not catalytically active. Combined with XPS, we found that C₃PO is generated at 800 °C, which suggests that C₃PO may be the key species providing HER activity. To verify the changing trend of HER performance of samples at different carbonization temperatures, we carbonized samples with other glycine/phytic acid ratios at different temperatures, and the HER results are recorded in Fig. S9.† By comparison, we found that regardless of the ratio of the starting materials, the correlation between the HER performance and the carbonization temperature is similar. In addition, we investigated the effect of the added amount of phytic acid on catalyst performance. We found that the performance of the catalyst increased and then decreased with the increasing amount of phytic acid. Combined with CHN results, we found that the total concentration of both N and P atoms increased with the increase of phytic acid incorporation. Although samples CNP0.6 and CNP0.8 have greater N, P content, their HER activities are still lower than that of sample CNP0.4. This result implies that the total N, P elemental content is not a decisive factor for HER activity. Combined with XPS, we suggest that the determining factor is the percentage of different N and P species. According to Fig. 4(a) and Table S5,† the P-doped carbon, as well as the N-doped carbon did not exhibit HER catalytic activity, implying that the HER activity of the catalyst is derived from the synergistic promotion of N and P atoms. This result implies that the total N, P elemental content is not a decisive factor for HER activity. Combined with XPS, we suggest that the determining factor is the percentage of different N species (graphitic N, pyridinic N and pyrrolic N) and different P species (C–O–P, C₂PO₂, C₃PO and C-PO_x). According to Fig. 3(a), we found that as the phytic acid concentration increased, the percentage of graphitic N, pyridinic N, C₃PO and C₂PO₂ showed a monotonically increasing or monotonically decreasing trend while the performance of the catalysts is not monotonically increasing or decreasing. We believe that there are at least two active species. Since samples CNP0.4, CNP0.6 and CNP0.8 had similar percentages of nitrogen oxide, we excluded the possibility of nitrogen oxide. The content of pyrrolic N and C₂PO₂ is highest in CNP0.2, but they do not exhibit good HER activity, which means that pyrrolic N and C₂PO₂ do not have a good synergistic effect. In addition, in samples CNP0.4, CNP0.6, and CNP0.8, the content of pyrrolic N and C₃PO increased monotonically. However, the HER activity of these three samples monotonically decreases, so we believe that these two structures do not exhibit a good catalytic synergy effect, either. In addition, we found no C–O–P bond in samples CNP0.4, CNP0.6 and CNP0.8, which implies that C–O–P is also not a key active component. In summary, we believe that there are two possibilities for an optimal synergistic system: (1) graphite N and C₃PO, (2) pyridinic N and C₂PO₂.

To better understand the catalytic mechanism, we investigated the Tafel slopes of various samples. Based on Fig. 4(c), the Tafel slope of CNP0.4 is 121 mV dec⁻¹, approaching the theoretical value of the Heyrovsky step, indicating that the HER process follows the Volmer–Heyrovsky mechanism. The changing trend of Tafel slope of the as-made catalysts is consistent with the changing trend of HER activity (Fig. 4(c and d)), which again proves our conclusions. It is noteworthy that although sample CNP0.6 and sample CNP0.8 have similar overpotentials, sample CNP0.6 exhibits a lower tafel slope, which implies that CNP0.6 has superior catalytic activity compared with CNP0.8.

To investigate the intrinsic activities of the catalysts, the electrochemically active surface area (ECSA) of each catalyst was inferred from their double-layer capacitance (C_dl), determinable through cyclic voltammetry (CV). According to Fig. 4(e and f), the Cdl value of CNP0.4 is 93.5 mF cm⁻², much better than that of other catalysts, suggesting the largest exposed active area. The large active surface area provides a terrific basis for promoting the HER. The excellent HER performance of this sample can be clearly proved by comparison with other reported carbon materials (Table S6†). However, when the heat treatment temperature is 1000 °C, the active surface area is reduced, which might be caused by the agglomeration at high temperatures or the decreases in the content of the active species within the catalyst. Furthermore, P-doped carbon materials have a larger active surface area than N-doped carbon materials, which are 16.5 mF cm⁻² and 5 mF cm⁻² respectively (Fig. 4(g)). The error bars of ESCA over 3 separately prepared samples were also tested to reflect the variability in the measurements. According to Fig. S11,† the revised ESCA of CNP 0.2, CNP0.4, CNP0.6, CNP0.8, T = 1000 °C, PC and NC are 34.4 mF cm⁻², 95.3 mF cm⁻², 35.5 mF cm⁻², 33.2 mF cm⁻², 33.5 mF cm⁻², 13.1 mF cm⁻² and 4.2 mF cm⁻², respectively. Upon comparison with other literature reports, we found that the catalysts prepared by this economical and convenient synthesis method exhibited outstanding active surface area compared to other carbon materials with special structures (CNTs, nanosheets and plasma-etched graphene), which was 3 times larger than the best sample in Table S7.†

To eliminate the influence of the exposed active surface area of the catalyst on the sample performance, we confirmed the intrinsic activity by normalizing the current density to ECSA. The trend in intrinsic activity for the samples CNP0.2, CNP0.4, CNP0.6, and CNP0.8 correlates with the trend in their exhibited HER performance (Fig. 4(h and i)). This validates the rationality of the previous conclusions. Combined with Raman spectroscopy, these samples exhibit similar levels of graphitization, suggesting that the crystallinity of the carbon material is not the primary cause of this difference. Furthermore, CNP0.4 demonstrates higher intrinsic activity than the sample T = 800 °C, which can be attributed to the higher degree of graphitization in CNP0.4, facilitating rapid electron transfer. Notably, although the overall activity of the sample T = 1000 °C is lower than that of CNP0.4, its intrinsic activity exceeds that of CNP0.4. Combining XPS and Raman spectra, we propose two possible reasons for this phenomenon. (1) sample T = 1000 °C has a higher degree of graphitization, implying that it contains more ordered conjugated structures. According to Fig. S12,† the conductivity of the catalyst increases when it has a higher graphitization degree. This result indicates that the sp² conjugated structures can promote rapid charge transfer, thereby increasing the intrinsic activity of the catalyst. (2) Compared to T = 900 °C, sample T = 1000 °C contains more graphitic N structures, suggesting that C₃PO and graphitic N may be one of the key factors influencing the intrinsic activity of the catalyst.

To investigate the N, P co-doping effect on active sites, we studied the Turnover frequency (TOF) of CNP0.4. As a comparison, the TOF of PC and NC were also calculated and the results are recorded in Fig. S13.† We found that N and P co-doping can effectively change the ΔG_H* of the active sites. According to Fig. S13,† the N, P co-doped samples exhibited far more catalytic activity than PC and NC. When the overpotential was 250 mV, its TOF was 9 times higher than that of PC and 64 times higher than that of NC. In comparison, PC has a larger active surface area and better intrinsic activity than NC. This implies that the P atoms adjust the electronic structure of the carbon material more efficiently.

The stability of CNP0.4 was evaluated by repeated cyclic voltammogram (CV) sweeps. The CV potential was set from −0.1 V to −0.4 V vs. RHE, with a scanning rate of 50 mV s⁻¹. According to Fig. S14,† a similar LSV curve was obtained after 2000 cycles, suggesting the excellent stability of CNP0.4.

The DFT model was used to explore the role of each component of the N, P co-doped carbon material in the modulation of the graphene electron cloud as well as to analyze the role of different potential sites that may be present on the surface of doped graphene in the HER. The spatial structure as well as the electronic structure of doped graphene was investigated using a clustering model. The examined graphene surface was constructed with 23 benzene rings including 64 carbon and 20 hydrogen atoms. The 84 atoms of graphene ensure that the dimensions of the model are adequate to avoid excessive edge effects that can cause the results to deviate significantly from the actual values. The terminal H atoms were fixed to avoid interactions like those that may occur in a periodic model of plane-wave coding and focus on the chemical interaction and electron transfer at the active site ensemble. All atoms are set to allow relaxation in order to optimize the structure.

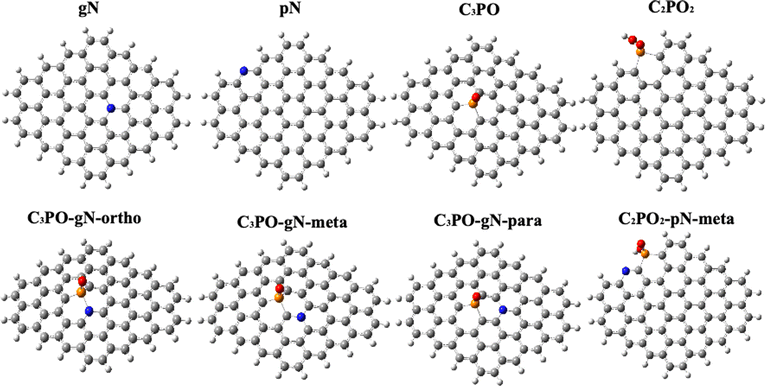
Combining the results of XPS and LSV, we believe that the enhancement effect of N, P co-doped graphene should be due to the synergistic effect of C₃PO & graphitic N or C₂PO₂ & pyridinic N. Therefore, we focus on these two co-doping models. In order to better deconstruct the contribution of each component to the overall catalytic active species we also constructed four single atom doping models, GN (graphitic N doped graphene), PN (pyridinic N doped graphene), C₃PO-G and C₂PO₂-G, respectively. For the possible doping sites and geometry of heteroatom-doped graphene, we calculated the formation energies of the C₃PO structure at the edges of graphene and the C₃PO structure inside graphene to confirm the main doping site of P (Fig. 6(e)). By comparison, we found that two energies are very close to each other, which means that both structures can exist stably. Since we used the in situ doping method and the prepared samples are 2D structures, we think it is more general to explore the C₃PO structure inside graphene, so we set the C₃PO structure inside graphene.⁴⁸ The C₂PO₂ structure has a large spatial structure, which makes it difficult to exist stably inside the carbon lattice, so we focused on the C₂PO₂ structure at the edges of graphene. It should be noted that the P–N bond was not detected in XPS, thus the C₃PO-gN-ortho structure may not exist in the catalyst. However, we have included this configuration for the purpose of discussing the synergistic effect of the N and P atoms. Fig. 5 shows the eight models which are mainly discussed in this paper. Fig. 6(a) and (b) display the optimized configuration of doped graphitic N and pyridinic N. The C–N bond length between graphitic N and surrounding carbon atoms is 1.41 Å, very close to the sp² C=C bond length (1.42 Å) in graphene. Furthermore, the C–N bond angle is 120.1°, almost identical to the sp² C=C bond angle (120.7°) in pure graphene, indicating that graphitic N doping has minimally altered the spatial configuration of the original graphene. Fig. 6(c) illustrates the optimized configuration of C₃PO-doped graphene. The P atom exhibits sp³ hybridization with a bond angle of 100.8°. The three C–P bonds are all 1.76 Å in length, forming an overall triangular pyramid structure. Due to the significant difference in radius between P and C atoms, the doped graphene undergoes noticeable deformation. The C–P bond length is 23.9% longer than the sp² C=C double bond in pure graphene, causing the carbon network to protrude 1.28 Å in the Z direction. This implies a significant expansion of the interlayer spacing of carbon layers. This result is beneficial for preventing carbon layer stacking in 3D space, reducing graphene agglomeration, and offering possibilities for preparing 2D carbon materials. The optimized configuration of the C₂PO₂ structure is shown in Fig. 6(d). The average bond length between P atoms and surrounding carbon atoms is 1.79 Å, with a bond angle of 98°. Unlike the C₃PO structure, the tensile stress of P atoms on graphene forms an angle with the Z direction, resulting in the graphene plane protruding only 0.4 Å along the Z-axis.

Fig. 5 8 optimized models for the heteroatom doped graphene.

Fig. 6 (a) Optimized models for graphitic N doped graphene. (b) Optimized models for pyridinic N doped graphene. (c) Optimized models for C₃PO doped graphene. (d) Optimized models for C₂PO₂ doped graphene. (e) The formation energy of the various structures. * represents the generation energy of the structure in the presence of C₃PO.

It has been proved that the Gibbs free-energy (ΔG_H*) for the surface adsorption of H atoms is a crucial indicator of the acidic HER activity.^49,50 Therefore, we calculated the ΔG_H* (Fig. 7) for the possible active sites in 9 models. According to Sabatier's principle, the interaction force between the HER active site and the H atom should not be too weak or too strong.

Fig. 7 ΔG_H* of (a) graphene(G), (b) graphitic N (NG), (c) pyridinic N (PN), (d) graphene doped with C₃PO, (e) graphene doped with C₂PO₂, (f) graphene doped with C₃PO and graphitic N in the ortho site (C₃PO-gN-ortho), (g) graphene doped with C₃PO and graphitic N in the meta site (C₃PO-gN-meta), (h) graphene doped with C₃PO and graphitic N in the para site (C₃PO-gN-para), (i) graphene doped with C₂PO₂ and graphitic N (C₂PO-pN).

Therefore, when the ΔG_H* value of the catalyst is close to 0, the catalyst is considered to have superior catalytic activity. According to Fig. 7, the ΔG_H* of pure graphene is 1.37 eV (Fig. 7(a)). In the N atom singly doped system, the ΔG_H* of the C carbon atom adjacent to the pyridine N is 1.67 eV (Fig. 7(c)), which is more positive than that of the ΔG_H* of pure graphene, exhibiting inertness to the HER. The neighboring C atom of graphitic N has a ΔG_H* of 0.71 eV (Fig. 7(b)), showing high catalytic activity for the HER than pure graphene. This result proves that pyridine N and graphitic N have different modulation effects on the electronic structure of graphene. For the P single-doped system, the two neighboring C of C₃PO exhibit different ΔG_H*. The ΔG_H* of site 1 is 0.29 eV and that of site 2 is −0.21 eV. It can be seen that the electronic structure of site 2 is greatly adjusted for HER, involving strong interaction with hydrogen atoms, to exhibit a good HER catalytic activity (Fig. 7(d)). The electronic structure of graphene has a greater effect on the ΔG_H* of sites 1 and 2. The difference of ΔG_H* of 1 and 2 site implies that the charge transfer from P sites to site 1and 2 is different. In contrast, although the C₂PO₂ structure (Fig. 7(e)) also promotes HER activity, the neighboring carbons have a more positive ΔG_H*(0.79) compared to C₃PO. In addition, we have investigated the ΔG_H* of the possible active sites when C₃PO is co-doped with graphitic N (neighboring, meta and para). When the graphitic N is in the meta position of the P atom, the ΔG_H* of the 1-site is 0.37 eV (Fig. 7(f)), which shows an enhancement of 0.58 eV compared with that of the ΔG_H* before doping with N atoms. These results indicate that the addition of graphitic N in the neighboring position of the P atom has a synergetic effect on the HER of 2-site. When the graphitic N is located in the interstitial position of the P atom, the ΔG_H* of the 1-site is 0.13 eV (Fig. 7(g)), which is 0.16 eV lower than that before graphitic N doping, much closer to 0 than other active sites. This result indicates that when graphitic N is located in the interstitial site of the C₃PO structure, they have a good synergistic effect, resulting in an optimal HER catalytic activity of the intermediate C. In Fig. 7(h), the ΔG_H* of the 1-site is 0.9 eV, which is 0.61 eV higher than that before doping, which implies that the para-doped graphitic N is able to weaken the interaction of the 1-site with H atoms. From the above results, we get an interesting conclusion that when graphitic N is present in the neighborhood of a C atom around C₃PO, the interaction of the C atom with H will be enhanced. In contrast, when graphitic N is present in its meta site, the interaction of C with the H atoms will be weakened. Furthermore, the synergistic doping effect of C₂PO₂ with pyridine N has also been considered. The carbon atom located between C₂PO₂ and the pyridinic N has a ΔG_H* of 0.79 eV (Fig. 7(i)). The addition of pyridine N makes the interaction between the hydrogen atom and the surrounding carbon atoms weaker than in the C₂PO₂ doped system.

The analysis of the electronic structure is crucial for understanding the mechanism of a co-doping system. The enhancement mechanism of N, P co-doped graphene was first analyzed using electrostatic potential (ESP) energy spectra. The atomic charges and electrostatic potential map of the optimized pristine graphene model are presented in Fig. S15.† It is observed that the atomic charges in graphene alternate between positive and negative values, with the outermost carbon atoms displaying a slight negative charge due to hydrogen passivation. In graphene, the p orbitals of each carbon atom overlap with the p orbitals of the three adjacent carbon atoms, forming a large π-bond conjugated structure. Therefore, the ESP distribution on the surface of pristine graphene is remarkably uniform, indicating that all delocalized electrons in the π system are inert. Due to the higher electronegativity of N (3.06) compared to carbon (2.5), the introduction of N creates an electron-withdrawing inductive effect, causing polarization of the C–N bond and shifting the electron density towards the N atom. According to the results in Fig. S16,† the atomic charge of graphitic N is −0.8, while the atomic charges of the adjacent carbon atoms are 0.362, 0.367, and 0.392, respectively. In contrast, the atomic charge of pyridinic N is −0.382, with the atomic charges of its two neighboring carbon atoms being 0.129 and 0.109, respectively, confirming the presence of the electron-withdrawing inductive effect. Compared to pyridinic N, graphite N exhibits a greater difference in electronegativity with the surrounding carbon atoms, resulting in a stronger polarity of the C–N bond and increased chemical activity. In addition to the electron-withdrawing inductive effect, graphitic N also exhibits electron-donating conjugation effects. This is because the lone pair of electrons on the graphitic N is parallel to the p-orbitals of the surrounding carbon atoms and can be delocalized into the adjacent π-bonds, leading to an increase in the electron density of graphene. Notably, the electrostatic potential around the N is positive in the ESP (electrostatic potential) map of graphitic N, indicating a decrease in electron density around the N atom. Thus, in the graphene model doped with graphitic N, the electron-donating conjugation effect of the graphitic N prevails over the electron-withdrawing inductive effect. This results in an enhancement of electron density on the neighboring and para-position carbon atoms, which subsequently favors hydrogen adsorption. Pyridinic N, being sp² hybridized, has its lone pair of electrons perpendicular to the π-bonds and thus does not participate in conjugation but resides in the sp² hybridized orbital. Consequently, pyridinic N only exhibits an electron-withdrawing inductive effect, leading to a decrease in the electron density of the graphene plane. This is reflected in the ESP diagram of the pyridinic N, where the electrostatic potential above the pyridinic N is negative, which hinders hydrogen adsorption on the adjacent carbon atoms. The electronegativity of the oxygen atom in the C₃PO structure (3.5) is significantly greater than that of the P atom (2.19), resulting in a high polarity of the P=O bond with an electron-withdrawing inductive effect. As observed in Fig. S16† the atomic charge of the central P atom is 1.183, while the atomic charges of the surrounding carbon atoms are −0.45, −0.391, and −0.45, respectively. Combined with the ESP the influence of the oxygen atom causes the atomic charge of the P atom to become more positive. Additionally, the difference in electronegativity between P and C becomes more pronounced, which enhances the polarity of the P–C bonds. Consequently, the electron density shifts towards the neighboring carbon atoms. Combined with the calculations of ΔG_H, we find that the interaction strength between carbon atoms and H atoms does not depend on the magnitude of the charge of its central atom, but on the electron cloud density of the orbitals around the C atom. To summarize, the conjugation effect and the induced effect need to be considered together. When dopant atoms exhibit the overall effect of electron-donation, their neighboring and opposite sites are favorable for hydrogen adsorption, while their interstitial sites are relatively unfavorable for hydrogen adsorption. When the overall effect of dopant atoms is an electron-withdrawing effect, the neighboring and opposite sites are unfavorable for hydrogen adsorption, while the interstitial sites are relatively suitable for hydrogen adsorption. In the C₃PO structure, the electron-withdrawing effect of the O atom is dominant, and the interstitial carbon shows better HER activity. For the co-doped system, when graphitic N is located in the neighboring position, the electron cloud density of its neighboring P atoms increases, and the electron cloud density on the interstitial C atom (site 2) decreases compared to that before N atom doping, and thus provides a fast electron channel for the HER. The opposite is true when the graphitic N is in the para position. In this case, the C atom is located in the interstitial position of graphitic N, and has a lower interaction with the hydrogen atom. The P atom is located in the para-position of graphitic N, and the charge of the atom will become more negative. So, the C–P polarity is weakened, and the electron density that was originally shifted towards the neighboring C position is weakened, which is not conducive to the adsorption of H atoms. It is worth noting that, because the graphitic N is an electron-donating group and P=O is an electron-withdrawing group, the electrons would be transferred from graphitic N to the P atom of P=O via neighboring C. The presence of electron push power from graphitic N and electron pull power from C₃PO leads to regional polarization, which accelerates the transfer of electrons and favors the adsorption towards H atoms. When the graphite is located in an intermediate site, its neighboring C atom electron cloud density increases, enhancing its interaction with H atoms.

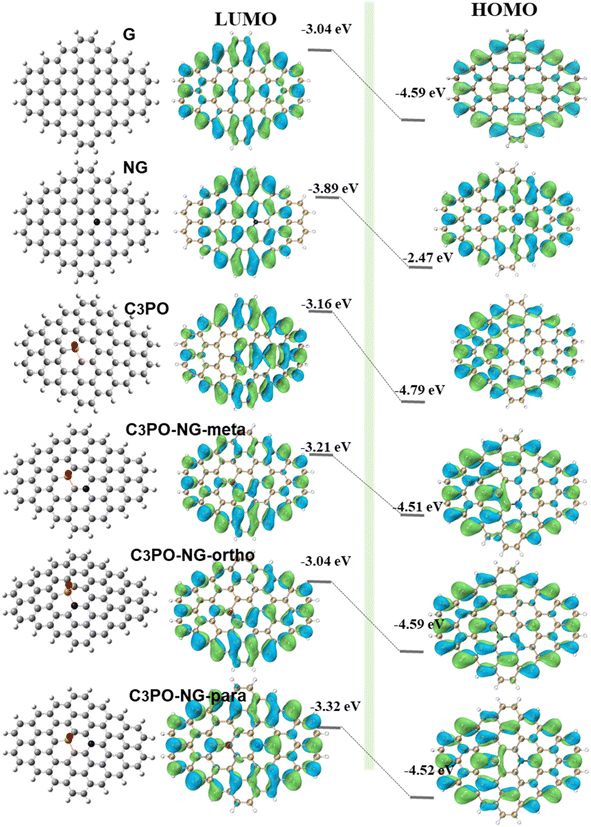
Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) together constitute the frontier orbitals of a molecule. The electrons in these orbitals play a crucial role in chemical reactions. The value of E (LUMO) minus E (HOMO) represents the HOMO–LUMO orbital energy gap, which is an important indicator of the stability, chemical reactivity, conductivity, and electrophilic/nucleophilic capabilities of reactive molecules. Therefore, we analyzed the HOMO and LUMO orbital structures of various doped graphene types.

According to Fig. 8, the LUMO and HOMO values of pure graphene are −3.05 eV and −4.6 eV respectively, with a HOMO–LUMO energy gap of 1.545 eV. Heteroatom doping significantly altered the LUMO and HOMO values of pure graphene. Among the four models containing only one type of dopant, only graphitic N injected electrons into the HOMO orbital of pure graphene, increasing its energy value by 15%. The E (HOMO) values for pyridinic N, C₃PO, and C₂PO₂ are −4.76, −4.78 and −4.73, respectively, reducing the HOMO orbital energy by 3%, 4%, and 2%. This result demonstrates that graphitic N has an electron-donating conjugation effect, enhancing the electron cloud density of graphene and making it more nucleophilic. The other three structures are electron-withdrawing groups, reducing the overall electron cloud density of graphene. The differences in E (LUMO)–E (HOMO) are recorded in the figure. The energy gaps for NG, PN, C₃PO, and C₂PO₂ structures are 1.416, 1.55, 1.635, and 1.71, respectively. Compared to pure graphene, these gaps decreased by 8%, and increased by 0.3%, 5%, and 10%, respectively. This observation indicates that graphitic N doping is beneficial for reducing the energy gap of graphene, resulting in faster electron transfer on the graphene surface and improved conductivity. For NG and C₃PO co-doped graphene, graphitic N can inject electrons into the HOMO orbital, while the P=O group can effectively lower the E (LUMO) of graphene. The synergistic effect of these two leads to a further reduction in graphene's energy gap, accelerating electron transfer on the graphene surface and facilitating adsorption reactions. According to the figure, we found that the energy gaps of ortho-, meta-, and para-position co-doped graphene are 1.31, 1.33, and 1.19, respectively, which are 18%, 14%, and 23% smaller than that of pure graphene.

Fig. 8 The HOMO and LUMO orbitals of the various models.

Conclusions

In summary, the chain-like amino acid structure intersected and liaised with the six-membered ring of phytic acid to produce a carbon network. An ultrathin nanocarbon layer was prepared by one-step pyrolysis, which ensured the full exposure of the active sites. The effect of phytic acid addition on the content of different N, P species in the product was investigated by adjusting the ratio of input materials. Combining experiments and calculations, the interaction strength between C atoms and H atoms is mainly affected by the electron density distribution on the surface of graphene. In particular, both the induced effect and conjugation effect of the dopant atoms should be considered. The ortho and para sites of the electron-donating groups have a milder ΔG_H* compared to the meta site. In contrast, the meta sites of the electron-absorbing atoms have more appropriate ΔG_H* than the ortho site and para site. As a result, when the graphitic N was co-doped at the meta site of C₃PO, they have a synergistic effect and optimal hydrogen adsorption free energy (ΔG_H* = 0.13). In addition, the graphitic N can inject the lone electron into the large π bond, so that the HOMO orbital energy of graphene is enhanced and the HOMO–LUMO spacing is reduced, which accelerates the charge transfer rate and facilitates the adsorption reaction. The best catalyst exhibited outstanding HER activity, with an extraordinarily low overpotential of 306 mV at 10 mA cm⁻².

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Xinran Yang: conceptualization, investigation, visualization, writing – original draft. Ryuji Takada: conceptualization, investigation, visualization, methodology, writing – review & editing. Xinyu Li: conceptualization, investigation, visualization, writing – review & editing. Kotaro Narimatsu: investigation, writing – review & editing. Koji Miyake: conceptualization, supervision, visualization, methodology, writing – review & editing. Yoshiaki Uchida: writing – review & editing. Norikazu Nishiyama: supervision, resources, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The study was partially conducted using a facility at the Research Center for Ultra-High Voltage Electron Microscopy, Osaka University, Suita, Japan. Raman spectra measurements were supported by Prof. Hiroshi Umakoshi, and Assistant Prof. Nozomi Morishita Watanabe.

Notes and references

1. F. Safizadeh, E. Ghali and G. Houlachi, Int. J. Hydrogen Energy, 2015, 40, 256–274.
2. N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181.
3. A. Lasia, in Handbook of Fuel Cells, ed. W. Vielstich, A. Lamm, H. A. Gasteiger and H. Yokokawa, Wiley, 1st edn, 2010.
4. M. Zeng and Y. Li, J. Mater. Chem. A, 2015, 3, 14942–14962.
5. Y. Zheng, Y. Jiao, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2015, 54, 52–65.
6. H. Wang, W. Fu, X. Yang, Z. Huang, J. Li, H. Zhang and Y. Wang, J. Mater. Chem. A, 2020, 8, 6926–6956.
7. J. M. Olivares-Ramírez, M. L. Campos-Cornelio, J. Uribe Godínez, E. Borja-Arco and R. H. Castellanos, Int. J. Hydrogen Energy, 2007, 32, 3170–3173.
8. J. T. Bender, A. S. Petersen, F. C. Østergaard, M. A. Wood, S. M. J. Heffernan, D. J. Milliron, J. Rossmeisl and J. Resasco, ACS Energy Lett., 2023, 8, 657–665.
9. Y. Li, H. Wang, L. Xie, Y. Liang, G. Hong and H. Dai, J. Am. Chem. Soc., 2011, 133, 7296–7299.
10. J. Wei, M. Zhou, A. Long, Y. Xue, H. Liao, C. Wei and Z. J. Xu, Nano-Micro Lett., 2018, 10, 75.
11. X. Cao, Y. Han, C. Gao, Y. Xu, X. Huang, M. Willander and N. Wang, Nano Energy, 2014, 9, 301–308.
12. W. Sheng, M. Myint, J. G. Chen and Y. Yan, Energy Environ. Sci., 2013, 6, 1509.
13. Y. Shi and B. Zhang, Chem. Soc. Rev., 2016, 45, 1529–1541.
14. M. Ďurovič, J. Hnát and K. Bouzek, J. Power Sources, 2021, 493, 229708.
15. P. C. K. Vesborg, B. Seger and I. Chorkendorff, J. Phys. Chem. Lett., 2015, 6, 951–957.
16. F. Sun, Q. Tang and D. Jiang, ACS Catal., 2022, 12, 8404–8433.
17. H. Sun, Z. Yan, F. Liu, W. Xu, F. Cheng and J. Chen, Adv. Mater., 2020, 32, 1806326.
18. J. Kibsgaard, C. Tsai, K. Chan, J. D. Benck, J. K. Nørskov, F. Abild-Pedersen and T. F. Jaramillo, Energy Environ. Sci., 2015, 8, 3022–3029.
19. R. Saini, F. Naaz, A. H. Bashal, A. H. Pandit and U. Farooq, Green Chem., 2024, 26, 57–102.
20. S. Li, Z. Yu, Y. Yang, Y. Liu, H. Zou, H. Yang, J. Jin and J. Ma, J. Mater. Chem. A, 2017, 5, 6405–6410.
21. V. Fung, G. Hu, Z. Wu and D. Jiang, J. Phys. Chem. C, 2020, 124, 19571–19578.
22. S. Ye, F. Luo, T. Xu, P. Zhang, H. Shi, S. Qin, J. Wu, C. He, X. Ouyang, Q. Zhang, J. Liu and X. Sun, Nano Energy, 2020, 68, 104301.
23. Y. Tian, Y. Ye, X. Wang, S. Peng, Z. Wei, X. Zhang and W. Liu, Appl. Catal., A, 2017, 529, 127–133.
24. S. Zhou, X. Yang, W. Pei, N. Liu and J. Zhao, Nanoscale, 2018, 10, 10876–10883.
25. V. Thirumal, R. Yuvakkumar, P. S. Kumar, G. Ravi, M. Shobana, B. Saravanakumar and D. Velauthapillai, Int. J. Hydrogen Energy, 2022, 47, 41461–41467.
26. B. Deng, D. Wang, Z. Jiang, J. Zhang, S. Shi, Z.-J. Jiang and M. Liu, Carbon, 2018, 138, 169–178.
27. Y. Qu, Y. Ke, Y. Shao, W. Chen, C. T. Kwok, X. Shi and H. Pan, J. Phys. Chem. C, 2018, 122, 25331–25338.
28. J. Zhang and L. Dai, Angew. Chem., 2016, 128, 13490–13494.
29. J. Duan, S. Chen, M. Jaroniec and S. Z. Qiao, ACS Catal., 2015, 5, 5207–5234.
30. Y. Ito, W. Cong, T. Fujita, Z. Tang and M. Chen, Angew. Chem., Int. Ed., 2015, 54, 2131–2136.
31. J. Zhou, F. Qi, Y. Chen, Z. Wang, B. Zheng and X. Wang, J. Mater. Sci., 2018, 53, 7767–7777.
32. X. Zhang, Y. Wang, K. Wang, Y. Huang, D. Lyu, F. Yu, S. Wang, Z. Q. Tian, P. K. Shen and S. P. Jiang, Chem. Eng. J., 2021, 416, 129096.
33. X. Li, X. Duan, C. Han, X. Fan, Y. Li, F. Zhang, G. Zhang, W. Peng and S. Wang, Carbon, 2019, 148, 540–549.
34. J. Zhao, Y. Liu, X. Quan, S. Chen, H. Zhao and H. Yu, Electrochim. Acta, 2016, 204, 169–175.
35. S. J. Lee, J. Theerthagiri, P. Nithyadharseni, P. Arunachalam, D. Balaji, A. Madan Kumar, J. Madhavan, V. Mittal and M. Y. Choi, Renewable Sustainable Energy Rev., 2021, 143, 110849.
36. K. Qu, Y. Zheng, X. Zhang, K. Davey, S. Dai and S. Z. Qiao, ACS Nano, 2017, 11, 7293–7300.
37. S. García-Dalí, J. Quílez-Bermejo, J. Castro-Gutiérrez, N. Baccile, M. T. Izquierdo, A. Celzard and V. Fierro, Carbon, 2023, 212, 118154.
38. Y. Li, C. Ai, S. Deng, Y. Wang, X. Tong, X. Wang, X. Xia and J. Tu, Mater. Res. Bull., 2021, 134, 111094.
39. Z. Bi, L. Huo, Q. Kong, F. Li, J. Chen, A. Ahmad, X. Wei, L. Xie and C.-M. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 11421–11430.
40. T. Béguerie, E. Weiss-Hortala and A. Nzihou, Sci. Rep., 2022, 12, 21492.
41. Z. Long, L. Sun, W. Zhu, G. Chen, X. Wang and W. Sun, Chem. Commun., 2018, 54, 8991–8994.
42. Z. Yin, X. Liu, F. Wu, B. Lu, B. Huang, Y. Chen and G. Lin, ACS Sustain. Chem. Eng., 2022, 10, 911–922.
43. J. M. Rosas, R. Ruiz-Rosas, J. Rodríguez-Mirasol and T. Cordero, Carbon, 2012, 50, 1523–1537.
44. L. Jiao, C. Wang, Y. Wu, H. Meng and P. Ji, Catal. Sci. Technol., 2024, 14, 4997–5008.
45. J. R. Pels, F. Kapteijn, J. A. Moulijn, Q. Zhu and K. M. Thomas, Carbon, 1995, 33, 1641–1653.
46. B. Xiao, J. P. Boudou and K. M. Thomas, Langmuir, 2005, 21, 3400–3409.
47. H. Wang, J. Mater. Chem., 2011, 21, 5430.
48. (a) D. Armando, Phys. Chem. Chem. Phys., 2023, 25, 2546F; (b) Ullah, K. Ayub and T. Mahmood, Int. J. Hydrogen Energy, 2021, 46, 37814–37823.
49. A. Yu, N. Joshi, W. Zhang and Y. Yang, Adv. Sens. Energy Mater., 2023, 2, 100061.
50. D. Wang, Z.-P. Liu and W.-M. Yang, ACS Catal., 2018, 8, 7270–7278.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06226d

---