Proton-coupled electron transfer kinetics for the hydrogen evolution reaction of hangman porphyrins†‡
Manolis M.
Roubelakis
,
D. Kwabena
Bediako
,
Dilek K.
Dogutan
and
Daniel G.
Nocera
*
Department of Chemistry, Massachusetts Institute of Technology, 6-335, 77 Massachusetts Avenue, Cambridge, MA 02139-4307, USA. E-mail: nocera@mit.edu; Fax: + 1 617 253 7670; Tel: + 1 617 253 5537
First published on 14th February 2012
Abstract
Cobalt hangman porphyrins catalyze the hydrogen evolution reaction (HER). The hangman group is observed to facilitate HER by mediating a proton-coupled electron transfer (PCET) reaction. The details of the PCET pathway have been determined by comparing rate constants associated with the ET and PT processes of the hangman system to those of the corresponding values measured for porphyrins that lack an internal proton relay. A rapid intramolecular proton transfer from the carboxylic acid hanging group to the reduced cobalt centre of 8.5 × 106 s−1 provides a facile pathway for the formation of Co(II)H, which leads directly to H2 generation.
Broader contextSolar-driven hydrogen production requires the efficient catalysis of the hydrogen evolution reaction (HER). The availability of proton-coupled electron transfer (PCET) pathways is unavoidably central to the proper management of this multi-electron, multi-proton reaction. Thus, in the construction of an HER catalyst, design elements that facilitate this coupling are highly desired. It has been shown that the presence of proton relays in the second coordination sphere of a metal-based catalyst leads to enhanced catalytic HER efficiency. More specific, cobalt hangman porphyrins with a pendant carboxylic acid group positioned above the redox-active macrocycle were found to be better electrocatalysts than the corresponding non-hangman complexes. We report kinetic studies with both hangman and non-hangman systems to reveal the precise PCET pathway involved in the formation of a key CoIIH intermediate, which leads to electrocatalytic hydrogen generation and probe the ability of an internal proton relay in providing a facile proton transfer from the hanging group to the metal centre. Furthermore, we report the associated standard electron transfer and proton transfer rate constants for a PCET controlled HER process. Our studies highlight the utility of proton relay groups in PCET reactions that are central to energy conversion processes, especially the HER. |
The hydrogen evolution reaction (HER) is requisite for solar-to-fuels production.1–4 To avoid energy-wasting reaction barriers, the electron and proton must be coupled throughout the reaction profile of the HER transformation.5,6 To enable this coupling, proton-accepting or proton-donating groups in the second coordination sphere of redox centres has been shown to be particularly useful for enhanced catalytic efficiency of the HER7–15 as well as other energy conversion processes including the oxygen reduction reaction16 and its reverse, the oxygen evolution reaction.17 We have found that the hangman motif is especially attractive for promoting proton-coupled electron transfer (PCET) conversions of small molecule substrates.18,19 The hangman moiety positions an acid/base group above a redox-active metal platform. The hanging group serves as a proton shuttle to deliver protons to or accept protons from substrates bound to the metal centre and in doing so, hangman constructs enable precise control over the nature of the acid/base environment directly adjacent to the redox site. The hangman motif has been particularly attractive for the HER. Cobalt hangman porphyrin 1 (Scheme 1) serves as a HER electrocatalyst as evidenced by enhanced HER efficiency and a shift of the catalytic wave to lower overpotentials compared to analogous non-hangman systems.20 For this conversion, the Co(II)H species is the key intermediate for promoting HER turnover. We now report kinetic studies that investigate the details of the PCET pathway involved in the formation of the Co(II)H species and describe the kinetic parameters that govern the formation of this intermediate.
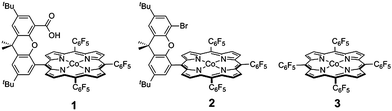 | ||
| Scheme 1 Cobalt hangman porphyrin 1, and non-hangman porphyrins 2 and 3. | ||
Rate constants associated with the electron transfer (ET) and proton transfer (PT) processes of hangman compound 1, were determined and compared with the corresponding values measured for 2 and 3 (Scheme 1), which lack an internal proton relay. Porphyrins 1–3 were synthesized in short synthesis times and in good yields according to already published procedures.16,20,21Fig. 1a shows the voltammetric waves of the formal Co2+/+ couple of 3 acquired from cyclic voltammetry (CV) over a range of scan rates. For simplicity, the formal metal oxidation state will be used herein though we note that the metal orbitals are mixed with the porphyrin ring and hence the formal reduction of the metal invariably involves delocalization of the reducing equivalent onto the porphyrin ring. As the scan rate is increased, the onset of electrochemical irreversibility is observed as the peak separation between anodic and cathodic waves increases.22,23 Under these conditions, the chemical reaction is influenced by the kinetics of the electron transfer process, as opposed to operating under the conditions of diffusion control (indicated by a 60 mV separation at 25 °C).24,25 The “trumpet plot” for the Co2+/+ couple (Fig. 1b and S1b†) of 3 shows the difference between the anodic or cathodic peak potential and midpoint potential (Ep–E°) as a function of the logarithm of scan rate (log ν).24,25 Simulation of CVs (see Supporting Information†) to replicate the shape of the trumpet plot furnishes a value of 0.011 cm s−1 for the standard heterogeneous electron transfer rate constant, ks, of the Co2+/+ couple. The trumpet plot for the Co+/0 couple of 3 is also shown in Fig. 1b (and in Fig. S1d† as well). The ks extracted from the trumpet plot for the Co+/0 couple of 3 is at least an order of magnitude higher than that of the Co2+/+ couple, on the order of 0.2 cm s−1. The ks of 0.012 cm s−1 for the Co2+/+ couple of 1 is the same as that of 3 (Fig. S2†). As previously reported,20 the presence of the carboxylic acid hanging group in 1 results in irreversibility of the Co+/0 redox wave owing to an irreversible reaction between the reduced metal centre and the internal acid group. The Co(0) is observed to be protonated to produce a Co(II)---H species, which in the presence of excess acid reacts in an ensuing step to produce H2. The presence of the hanging group results in a lower onset overpotential for H2 production by ∼200 mV compared to non-hangman systems such as 2.
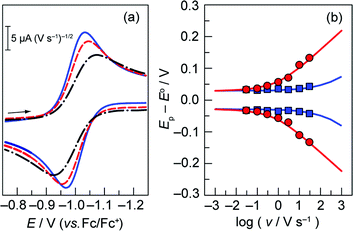 | ||
Fig. 1 (a) Overlay of representative normalized (inorm = i/v1/2) (i is current, v is scan rate) CVs taken of a 0.3 mM solution of cobalt porphyrin 3 in acetonitrile with 0.03 ( ), 0.3 ( ), 0.3 ( ), and 3 ( ), and 3 ( ) V s−1 scan rates, using a glassy carbon electrode. (b) Difference between anodic or cathodic peak potential and midpoint potential (Ep − E°) vs. log of scan rate (E° = −1.00 V for the Co2+/+ couple ( ) V s−1 scan rates, using a glassy carbon electrode. (b) Difference between anodic or cathodic peak potential and midpoint potential (Ep − E°) vs. log of scan rate (E° = −1.00 V for the Co2+/+ couple ( ), and −1.98 V for the Co+/0 couple ( ), and −1.98 V for the Co+/0 couple ( )). Simulated curves are plotted for ks = 0.011 cm s−1 ( )). Simulated curves are plotted for ks = 0.011 cm s−1 ( ) and ks = 0.2 cm s−1 ( ) and ks = 0.2 cm s−1 ( ). The diffusion coefficient (D) of 3 was determined to be 8 × 10−6 cm2 s−1 from the peak current, i, in the reversible limit: i = 0.446FAC°D½(Fν/RT)½ (F is the faraday constant, A is the area of the electrode and C° is the bulk porphyrin concentration). ). The diffusion coefficient (D) of 3 was determined to be 8 × 10−6 cm2 s−1 from the peak current, i, in the reversible limit: i = 0.446FAC°D½(Fν/RT)½ (F is the faraday constant, A is the area of the electrode and C° is the bulk porphyrin concentration). | ||
The similarity in Co2+/+ midpoint potential between 1 and 220 suggests that the position of the reversible Co+/0 wave of 2 (E° at −2.14 V vs. Fc/Fc+) is a good estimate of the Co+/0 midpoint potential of 1 as well. The position of the irreversible Co+/0 peak to more positive potentials than the expected reversible potential is indicative of what is classically considered an EC mechanism, where a heterogeneous electron transfer reaction is followed by a homogeneous chemical reaction.22 In hangman-promoted HER, the “C” step logically involves an intramolecular proton transfer from the hanging group to the metal centre to furnish the hydridic Co(II)H species. This EC mechanism for a hangman platform is as follows,
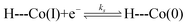 | (1) |
 | (2) |
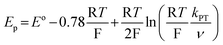 | (3) |
Fig. S3† establishes that the peak potential of the Co+/0 couple of 1 is indeed independent of the concentration of 1 over a range of scan rates. To determine the rate constant associated with the intramolecular proton transfer between the hanging group and the metal centre, CVs were acquired by varying the scan rate between 0.03 and 30 V s−1 (Fig. 2a) at a fixed metalloporphyrin concentration of 0.2 mM. Eqn (3) predicts a linear correlation between the dimensionless parameter (Ep − E°)F/RT and ln v with a slope of −0.5 (Fig. S4b†).22 The experimental data, however, display a distinct curvature that becomes more pronounced at higher scan rates (Fig. 2b). These observations are consistent with kinetic competition between the heterogeneous ET step (eqn (1)) and the irreversible homogeneous PT (eqn (2)).22 As the scan rate is increased, we observe effects attendant to passage into a regime where the ET (along with diffusion) limits the electrochemical response. Although this complication precludes the straightforward determination of kPT from eqn (3), the presence of this mixed control permits determination of the kinetic parameters governing ET and PT steps from a simulation of the dependence of peak potential on scan rate. The peak potential of the slow scan (30 mV s−1) voltammogram was substituted into eqn (3) to obtain an initial estimate of the intramolecular PT rate constant of 3 × 106 s−1. In addition, the ks = 0.2 cm s−1 associated with the Co+/0 couple of 3 (Fig. 1b) was used as an initial approximation for that of the hangman system. These parameters were optimized by CV simulation iteratively until the simulated peak potentials over the range of scan rates agreed with the experimental data, resulting in the fit displayed in Fig. 2b. The results of this fit (see also Fig. S5†) yielded a heterogeneous ET rate constant of 0.24 cm s−1 for eqn (1) and kPT = 8.5 × 106 s−1 for the formation of the Co(II)H species viaeqn (2).
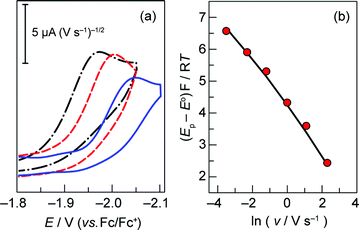 | ||
Fig. 2 (a) Overlay of representative CVs taken of a 0.2 mM solution of 1 in acetonitrile with 0.03 ( ), 0.3 ( ), 0.3 ( ), and 3 ( ), and 3 ( ) V s−1 scan rates, using a glassy carbon electrode. (b) Plot of (Ep − E°)F/RT vs. ln of scan rate (E° = −2.14 V, taken from system 2). Experimental data ( ) V s−1 scan rates, using a glassy carbon electrode. (b) Plot of (Ep − E°)F/RT vs. ln of scan rate (E° = −2.14 V, taken from system 2). Experimental data ( ), simulated curve ( ), simulated curve ( ) plotted for ks = 0.24 cm s−1 and kPT = 8.5 × 106 s−1. ) plotted for ks = 0.24 cm s−1 and kPT = 8.5 × 106 s−1. | ||
In order to compare the kinetics of the intramolecular PT for 1, to an intermolecular PT from an external acid source, CVs of 3 were recorded in the presence of varying amounts of benzoic acid (Fig. 3a and S6†). The Co+/0 redox wave becomes completely irreversible in the presence of excess benzoic acid and a catalytic wave is observed in the CV. In this case, catalytic H2 production is observed upon reduction to Co(0), and thus, a second protonation step must be taken into consideration. Kinetic resolution of the system requires knowledge of which of the two following protonation steps is rate-limiting in the overall catalytic reaction:
 | (4) |
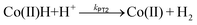 | (5) |
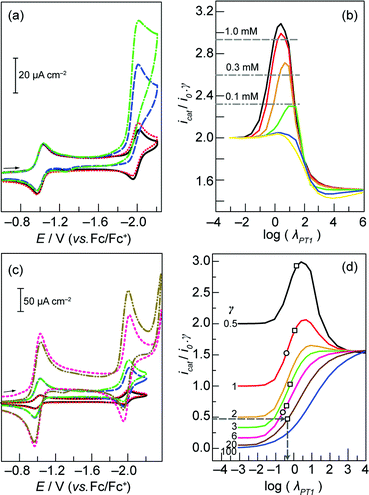 | ||
Fig. 3 (a) CVs of a 0.1 mM solution of 3 in the absence of benzoic acid ( ) and in the presence of 0.05 ( ) and in the presence of 0.05 ( ), 0.3 ( ), 0.3 ( ), and 0.6 ( ), and 0.6 ( ) mM benzoic acid. Scan rate, 30 mV s−1; 0.2 M TBAPF6 in acetonitrile. Glassy carbon working electrode, Ag/AgNO3 reference electrode, and Pt wire counter electrode. (b) Working curves generated by simulating CVs with γ = 0.5 and ρ = 100 ( ) mM benzoic acid. Scan rate, 30 mV s−1; 0.2 M TBAPF6 in acetonitrile. Glassy carbon working electrode, Ag/AgNO3 reference electrode, and Pt wire counter electrode. (b) Working curves generated by simulating CVs with γ = 0.5 and ρ = 100 ( ), 10 ( ), 10 ( ), 1 ( ), 1 ( ), 0.1 ( ), 0.1 ( ), 0.01 ( ), 0.01 ( ), and 0.001 ( ), and 0.001 ( ). Horizontal lines indicate normalized current values (icat/i0γ) obtained at the designated porphyrin concentrations, with half an equivalent of benzoic acid. (c) CVs of 0.1 ( ). Horizontal lines indicate normalized current values (icat/i0γ) obtained at the designated porphyrin concentrations, with half an equivalent of benzoic acid. (c) CVs of 0.1 ( ), 0.3 ( ), 0.3 ( ), and 1 mM ( ), and 1 mM ( ) solutions of 3 in the absence of benzoic acid and in the presence of 0.05 ( ) solutions of 3 in the absence of benzoic acid and in the presence of 0.05 ( ), 0.15 ( ), 0.15 ( ), and 0.5 ( ), and 0.5 ( ) mM benzoic acid, respectively. Scan rate, 30 mV s−1; 0.2 M TBAPF6 in acetonitrile. Glassy carbon working electrode, Ag/AgNO3 reference electrode, and Pt wire counter electrode. (d) Working curves generated by simulating CVs with ρ = 10. Experimental data points for 3 (□) and 2 (○) acquired at scan rates of 30 and 100 mV s−1 respectively. ) mM benzoic acid, respectively. Scan rate, 30 mV s−1; 0.2 M TBAPF6 in acetonitrile. Glassy carbon working electrode, Ag/AgNO3 reference electrode, and Pt wire counter electrode. (d) Working curves generated by simulating CVs with ρ = 10. Experimental data points for 3 (□) and 2 (○) acquired at scan rates of 30 and 100 mV s−1 respectively. | ||
There are three parameters that govern the rate of H2 evolution catalysis, and therefore the magnitude of the peak catalytic current (icat):22
(i) the ratio of substrate (acid) to catalyst (porphyrin) concentration, i.e. the excess factor (γ):
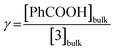 | (6) |
(ii) the dimensionless parameter λPT1 which defines the kinetics of eqn (4):
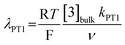 | (7) |
(iii) the competition between eqn (4) and (5), given by ρ where:
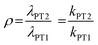 | (8) |
In general, eqn (4) is rate-limiting for ρ > 10 and eqn (5) is rate-limiting for ρ < 0.1. Because the waves for catalysis and for the catalyst in the absence of acid occur at similar potentials, the peak in the CV is due to both substrate and catalyst consumption. The confluence of these two processes precludes an analytical solution to the problem at hand, and mandates the use of CV simulation to generate working curves that relate measurable quantities (i.e. peak current values) to kinetic parameters.22,27 In order to determine which step is rate-limiting, working curves were generated as follows. A CV was simulated for the case of a catalyst at a specified concentration in the absence of substrate (PhCOOH). The peak current associated with the Co+/0 couple was recorded as i0. Next, a CV was simulated for the same catalyst concentration, but with substrate added at an excess factor, γ, of 0.5 for a reaction scheme in which kPT2 is 100 times a specified value of kPT1 (ρ = 100). The peak current associated with this voltammogram was recorded as icat. The normalized current value icat/i0γ was calculated. Varying kPT1 (and thus log λPT1) while maintaining γ = 0.5 and ρ = 100, and determining the corresponding icat (and therefore icat/i0γ) values, furnished the black curve in Fig. 3b. This was repeated for ρ = 10, 1, 0.1, 0.01, and 0.001 to generate the remaining plots in Fig. 3b. The maxima in these working curves define the maximum normalized current values attainable, for a specific ρ.
To determine the value of ρ that is operative during H2 production mediated by 3, and therefore the identity of the rate-limiting step, CVs of solutions containing 0.1, 0.3, and 1 mM 3 were recorded (Fig. 3c), and the Co+/0 peak currents (i0) were determined in each case. CVs were also acquired for solutions with identical concentrations of 3, but containing 0.5 equivalents of benzoic acid (i.e. γ = 0.5) (Fig. 3c), permitting measurement of the corresponding catalytic peak currents (icat). The resultant normalized current ratios (icat/i0γ), that were generated (designated by horizontal lines in Fig. 3b) are only consistent with eqn (4) as the rate-limiting step (ρ ≥ 10), since in the case of 1 mM catalyst concentration, icat/i0γ = 2.9 (Fig. 3b). In contrast, the maximum value for the cases where ρ ≤ 1 is 2.7. Notably, since eqn (4) is rate-limiting, the precise value of ρ cannot be determined; the working curves associated with ρ = 100 and ρ = 10 are almost identical, and the discrepancy between ρ = 1000 and ρ = 100 can be shown to be even less. For that matter, whereas kPT1 may be determined, kPT2 cannot.
To estimate the value of kPT1, we again generated working curves of icat/i0γ vs. log λPT1 based on the icat and i0 values extracted from simulated CVs. In this case, we fixed ρ = 10 for all simulations (since this furnishes the upper limit for kPT1 compared to all other ρ > 10) and varied λPT1 for different values of the excess factor, γ (Fig. 3d). Therefore, one value of γ is associated with each curve in Fig. 3d. Experimental icat and i0 values were then obtained from CVs of a 1.0 mM solution of 3 with increasing concentrations of benzoic acid between 0 (affording i0) and 20 mM (Fig. S6†). Normalized current ratios (icat/i0γ) from these CVs give five distinct points on the vertical axis of the icat/i0γ vs. log λPT1 plots in Fig. 3d. Each one of these values corresponds to a point on the specific working curve associated with the benzoic acid concentration (γ value) of that CV. For each point on the working curves, a log λPT1 value may be determined (grey arrows, Fig. 3d). Each dimensionless parameter, λPT1, thus obtained permitted the calculation of a discrete value of kPT1 (eqn (7)). The calculated rate constants ranged between ∼400 to 1600 M−1 s−1. We thus determined that the intermolecular (2nd order) PT rate constant between benzoic acid and 3 in its reduced Co(0) state is on the order of 1000 M−1 s−1. Previous experimental CV data (i0 and icat values) from the titration of 2 with benzoic acid,20 was evaluated in an identical manner to yield a similar intermolecular PT rate constant of ∼2500 M−1 s−1 for the reaction between the Co(0) centre in 2 and benzoic acid. In comparison to these intermolecular rate constants, the measured intramolecular PT rate constant of 8.5 × 106 s−1 for 1 indicates that the presence of a pendant proton relay proximate to the metal centre gives rise to a rate enhancement that is equivalent to an effective benzoic acid concentration >3000 M.
Conclusions
We have examined the PCET kinetics attendant to the HER activity of cobalt hangman porphyrins. A comparison between the PCET kinetics of 1 and non-hangman systems 2 and 3 forms the basis for establishing the hangman effect. The rate constant for transfer of a proton from the carboxylic acid hanging group to the reduced cobalt centre is 8.5 × 106 s−1. The rapid intramolecular proton transfer provides a facile pathway for the formation of Co(II)H, which reacts with protons to lead directly to H2 generation. The presence of the hanging carboxylic acid group in 1 thus is the basis of the enhanced H2 electrocatalysis and is direct evidence for the “hangman effect” in promoting HER.Acknowledgements
We are indebted to Prof. Cyrille Costentin (Université Paris Diderot) for invaluable discussions. D.K.B. gratefully acknowledges the MIT Energy Initiative for a predoctoral fellowship. This research was supported by DOE grant DE-FG02-05ER15745.References
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS
.
- D. G. Nocera, Inorg. Chem., 2009, 48, 10001–10017 CrossRef CAS
.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS
.
- A. J. Esswein and D. G. Nocera, Chem. Rev., 2007, 107, 4022–4047 CrossRef CAS
.
- R. I. Cukier and D. G. Nocera, Annu. Rev. Phys. Chem., 1998, 49, 337–369 CrossRef CAS
.
- S. Hammes-Schiffer, Acc. Chem. Res., 2009, 42, 1881–1889 CrossRef CAS
.
- B. E. Barton, M. T. Olsen and T. B. Rauchfuss, J. Am. Chem. Soc., 2008, 130, 16834–16835 CrossRef CAS
.
- M. Rakowski DuBois and D. L. DuBois, Chem. Soc. Rev., 2009, 38, 62–72 RSC
.
- A. D. Wilson, R. H. Newell, M. J. McNevin, J. T. Muckerman, M. Rakowski DuBois and D. L. DuBois, J. Am. Chem. Soc., 2006, 128, 358–366 CrossRef CAS
.
- U. J. Kilgore, J. A. S. Roberts, D. H. Pool, A. M. Appel, M. P. Stewart, M. Rakowski DuBois, W. G. Dougherty, W. S. Kassel, R. M. Bullock and D. L. DuBois, J. Am. Chem. Soc., 2011, 133, 5861–5872 CrossRef CAS
.
- M. L. Helm, M. P. Stewart, R. M. Bullock, M. Rakowski DuBois and D. L. DuBois, Science, 2011, 333, 863–866 CrossRef CAS
.
- G. M. Jacobsen, J. Y. Yang, B. Twamley, A. D. Wilson, R. M. Bullock, M. Rakowski DuBois and D. L. DuBois, Energy Environ. Sci., 2008, 1, 167–174 CAS
.
- E. S. Wiedner, J. Y. Yang, W. G. Dougherty, W. S. Kassel, R. M. Bullock, M. Rakowski DuBois and D. L. DuBois, Organometallics, 2010, 29, 5390–5401 CrossRef CAS
.
- C. J. Curtis, A. Miedaner, R. F. Ciancanelli, W. W. Ellis, B. C. Noll, M. Rakowski DuBois and D. L. DuBois, Inorg. Chem., 2003, 42, 216–227 CrossRef CAS
.
- R. M. Henry, R. K. Shoemaker, D. L. DuBois and M. Rakowski DuBois, J. Am. Chem. Soc., 2006, 128, 3002–3010 CrossRef CAS
.
- R. McGuire Jr., D. K. Dogutan, T. S. Teets, J. Suntivich, Y. Shao-Horn and D. G. Nocera, Chem. Sci., 2010, 1, 411–414 RSC
.
- D. K. Dogutan, R. McGuire Jr. and D. G. Nocera, J. Am. Chem. Soc., 2011, 133, 9178–9180 CrossRef CAS
.
- J. Rosenthal and D. G. Nocera, Acc. Chem. Res., 2007, 40, 543–553 CrossRef CAS
.
- J. Rosenthal and D. G. Nocera, Prog. Inorg. Chem., 2007, 55, 483–544 CrossRef CAS
.
- C. H. Lee, D. K. Dogutan and D. G. Nocera, J. Am. Chem. Soc., 2011, 133, 8775–8777 CrossRef CAS
.
- D. K. Dogutan, D. K. Bediako, T. S. Teets, M. Schwalbe and D. G. Nocera, Org. Lett., 2010, 12, 1036–1039 CrossRef CAS
.
-
Elements of Molecular and Biomolecular Electrochemistry, Jean-Michel Savéant, John Wiley & Sons, 2006 Search PubMed
.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed. John Wiley & Sons, 2001 Search PubMed
.
- C. Costentin, M. Robert and J.-M. Savéant, J. Electroanal. Chem., 2006, 588, 197–206 CrossRef CAS
.
- C. Costentin, M. Robert, J.-M. Savéant and A.-L. Teillout, Proc. Natl. Acad. Sci. USA, 2009, 106, 11829–11836 CrossRef CAS
.
- R. S. Nicholson and I. Shain, Anal. Chem., 1964, 36, 706–723 CrossRef CAS
.
- C. P. Andrieux, C. Blocman, J. M. Dumas-Bouchiat, F. M'Halla and J. M. Savéant, J. Electroanal. Chem., 1980, 113, 19–40 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, CV simulation and working curves generation details, additional CVs and the corresponding trumpet plots for compounds 1 and 3, Epvs. [1] plot from the concentration dependence studies with 1, simulated plots of (Ep − E°)F/RT vs. ln of scan rate for 1, benzoic acid titration CVs of a 1.0 mM solution of 3. See DOI: 10.1039/c2ee21123h |
| ‡ This article was submitted following the PCET conference in October 2011. |
| This journal is © The Royal Society of Chemistry 2012 |
