Characterising local environments in high energy density Li-ion battery cathodes: a combined NMR and first principles study of LiFe_xCo_1−xPO₄

Abstract

Olivine-type LiCoPO₄ (LCP) is a high energy density lithium ion battery cathode material due to the high voltage of the Co²⁺/Co³⁺ redox reaction. However, it displays a significantly poorer electrochemical performance than its more widely investigated isostructural analogue LiFePO₄ (LFP). The co-substituted LiFe_xCo_1−xPO₄ olivines combine many of the positive attributes of each end member compound and are promising next-generation cathode materials. Here, the fully lithiated x = 0, 0.25, 0.5, 0.75 and 1 samples are extensively studied using ³¹P solid-state nuclear magnetic resonance (NMR). Practical approaches to broadband excitation and for the resolution of the isotropic resonances are described. First principles hybrid density functional calculations are performed on the Fermi contact shift (FCS) contributions of individual M–O–P pathways in the end members LFP and LCP and compared with the fitted values extracted from the LiFe_xCo_1−xPO₄ experimental data. Combining both data sets, the FCS for the range of local P environments expected in LiFe_xCo_1−xPO₄ have been calculated and used to assign the NMR spectra. Due to the additional unpaired electron in d⁶ Fe²⁺ as compared with d⁷ Co²⁺ (both high spin), LFP is expected to have larger Fermi contact shifts than LCP. However, two of the Co–O–P pathways in LCP give rise to noticeably larger shifts and the unexpected appearance of peaks outside the range delimited by the pure LFP and LCP ³¹P shifts. This behaviour contrasts with that observed previously in LiFe_xMn_1−xPO₄, where all ³¹P shifts lay within the LiMnPO₄–LFP range. Although there are 24 distinct local P environments in LiFe_xCo_1−xPO₄, these group into seven resonances in the NMR spectra, due to significant overlap of the isotropic shifts. The local environments that give rise to the largest contributions to the spectral intensity are identified and used to simplify the assignment. This provides a tool for future studies of the electrochemically-cycled samples, which would otherwise be challenging to interpret.

---

1. Introduction

The widespread goal to reduce greenhouse gas emissions, specifically CO₂, has engaged the scientific community in efforts to develop lithium ion batteries (LIBs) for use in all-electric, hybrid and plug-in hybrid electric vehicles and in grid storage.¹ The layered oxide cathode material Li_xCoO₂ (ref. 2) is in widespread use in the portable communications industry; however, it is unstable towards O₂ loss for x > 0.5 (ref. 3) and is deemed unsuitable for the electrification of automobiles. Padhi et al.⁴ studied olivine-type LiFePO₄ (LFP) in 1997, leading to widespread interest owing to its high stability, long cycle life, fast charge rates in nano-particulate form, high reversible theoretical capacity (170 mA h g⁻¹ as compared with 140 mA h g⁻¹ in LiCoO₂) and safe operating voltage (3.45 V vs. Li⁺/Li). However, the low operating voltage also constitutes its main disadvantage, leading to a low energy density (580 W h kg⁻¹).

The LiMPO₄ (M = Mn, Co or Ni) phases all adopt the olivine structure and have higher operating voltages compared to LFP, at 4.1 V, 4.8 V and 5.0 V vs. Li⁺/Li,^4–8 respectively, and thus have been explored as a method to increase the energy density. However, they have more sluggish kinetics and are more difficult to charge and discharge fully. An alternative strategy is to substitute the Fe²⁺ ions in LFP with one or more of these transition metals (TMs) to form a solid solution on the M site.^4,9 This paper focuses on the binary olivine LiFe_xCo_1−xPO₄ as a potential next generation cathode material, combining the high theoretical energy density of LiCoPO₄ (LCP) at 800 W h kg⁻¹ with the superior electrochemical performance of the Fe phase.¹⁰ Upon charging, the lower oxidation potential of Fe²⁺ implies that Fe²⁺ oxidises to Fe³⁺ first, followed by oxidation of the Co²⁺ sites. Kim et al.¹¹ have proposed that the potential associated with the higher voltage Co²⁺/Co³⁺ couple is sensitive to the nature of the nearby TM ions, where Co²⁺ neighbouring Fe³⁺ sites are thought to react preferentially over Co²⁺ adjoining other Co²⁺ sites. In order to test this hypothesis and understand the basis for the improved electrochemical performance in this class of high energy density materials, the local structure must be probed across the range of electrochemical conditions encountered in battery operation. Here we address the first step of this process, seeking to fully characterise the local structure in the as-synthesized (i.e. fully lithiated) materials.

X-ray diffraction is an important characterisation technique, providing information on long-range structural order and particle size and strain. In contrast, nuclear magnetic resonance (NMR) spectroscopy gives direct insight into the local coordination environment of the nucleus under observation and is particularly suited to study disordered materials. LiFe_xCo_1−xPO₄, like many cathode materials, is paramagnetic at room temperature, containing the high spin 3d⁶ (t⁴_2ge²_g) Fe²⁺ and 3d⁷ (t⁵_2ge²_g) Co²⁺. The nuclear spins (here, the ³¹P sites) interact with the time-averaged magnetic moments of the paramagnetic ions, which are of the order 10³ times greater than the nuclear magnetic moments, resulting in hyperfine interactions that dominate the NMR response. These occur via through-space (dipolar) and through-bond (Fermi contact) interactions, and their magnitudes scale linearly with the field strength for magnetic moments below their saturation values. The dipolar interactions typically result in large spinning sideband manifolds under magic angle spinning (MAS), which, when originating from multiple local environments, can result in a series of overlapping peaks. Meanwhile, the Fermi contact shift (FCS) dominates the ³¹P NMR spectra of LiMPO₄ compounds.¹² The FCS arises out of the transfer of unpaired electron spin density from the M²⁺ sites through an intervening bond network into an s-orbital of the NMR observed nucleus. If the magnetic susceptibility of the material is anisotropic, the dipolar interaction also contributes an additional pseudocontact shift (PCS); however, in the present study, the FCS is significantly larger and the PCS is assumed to be negligible.¹³ The interaction of the nuclei with the anisotropic moment can result in inhomogeneous line broadening which is significant in this system. Despite the inherent challenges these phenomena lead to, the use of paramagnetic solid-state NMR has led to a detailed understanding of the local structures arising in LIB materials.^14–16

³¹P is the most useful nucleus for studying the local structure in LiFe_xCo_1−xPO₄ on account of its high natural abundance (100%), a nuclear spin quantum number I = 1/2 ruling out quadrupolar interactions, and isotropic shifts exhibiting greater spectral dispersion than in ^6,7Li spectra.¹⁷ However, it is challenging to obtain high-resolution ³¹P NMR spectra, due to the high ³¹P gyromagnetic ratio and the strong covalency of the P–O bonds, resulting in large hyperfine shifts. Spectra can be collected in low fields, so as to reduce the size of the broadening (in frequency units), which, in combination with fast MAS speeds, moves the sidebands outside the region of interest. However, this must be balanced against the desire to use higher fields to increase the sensitivity. At higher fields, however, the spinning sideband separation decreases on the ppm scale and pulse sequences that separate the sidebands from the isotropic peaks and permit for large excitation bandwidths may be required. Two commonly used experiments are the magic angle turning (MAT)^18,19 and the phase adjusted sideband separation (PASS)^20–22 sequences. In order to excite the entire region of interest, short high-power adiabatic pulses (SHAPs)²³ or very short radio frequency (RF) pulses must be employed. The adiabatic MAT (aMAT) sequence was first applied in the paramagnetic LiFe_xMn_1−xPO₄ system and uses a series of SHAPs in a modified MAT-type experiment, successfully isolating the isotropic shifts.²⁴ The MATPASS sequence uses short RF pulses and benefits from the fewer increments in the PASS experiment and has shown promising results in other paramagnetic cathode materials.²⁵ We use both methods in the following.

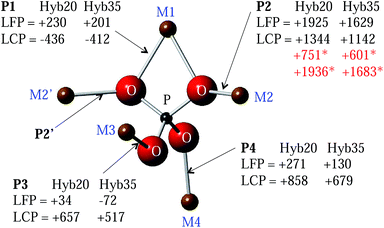
Transfer of spin density via the Fermi contact interaction depends strongly on the geometry of the bond network linking the paramagnetic species with the observed nucleus, reflecting the overlap of orbitals on the paramagnetic ion, oxygen and phosphorus sites. Fig. 1 shows the local structure of a P atom in LiMPO₄ compounds. One crystallographically distinct P site is present, each with 5 neighbouring M cations bridged by O. Two of these M sites are equivalent (M2), resulting in four distinct M–O–P pathways. M1 is linked to P by two P1 pathways, each with equal bond angles of 94.3° and 93.9° in LFP and LCP, respectively, whereas pathways P2, P3 and P4 have bond angles in the range 120–130° (128.1°, 120.0° and 123.7°, respectively in LFP and 127.5°, 122.9° and 126.2°, respectively in LCP), as shown in the ESI.† Here, the bond angles and distances are obtained from the first principles structural optimizations of LFP and LCP performed by Middlemiss et al.²⁶ While the net spin transfer through M–O–P pathways at angles 90° and 180° may be reasonably well rationalised within the Goodenough–Kanamori model,^27,28 intermediate angles present a formidable problem, necessitating the use of electronic structure calculations of varying degrees of sophistication.^14,29

Fig. 1 The P environment in LiMPO₄ (M = Fe, Co) compounds. The first coordination shell of transition metals contains five M sites, leading to four distinct M–O–P pathways. The calculated FCS (ppm) are shown separately for LFP and LCP from ab initio hybrid DFT calculations using the Hyb20 (B3LYP) and Hyb35 exchange–correlation functionals. * first principles calculations on LCP at 0 K reveal a low energy ground state, which lifts the degeneracy of the P2 and P2′ pathways. An average of the two pathway contributions is assumed in this room temperature study.

The assignment of solid-state NMR spectra can be very challenging. Pioneering work by Mauri et al.³⁰ made possible the calculation of shielding tensors for solid-state diamagnetic systems within a linear response formalism. Carlier et al. calculated the spin densities in paramagnetic systems within the density functional theory (DFT) + U approach, applying the results to the interpretation of experimental spectra in an indirect fashion via the use of integrated atomic magnetic moments³¹ and more recently directly via the use of the full-potential LAPW method within the WIEN2k package.^32,33 Other methods by Mali et al. using DFT/Projector Augmented-Wave approaches have also been employed to calculate contact shifts in the Li₂FeSiO₄.³⁴

Kim et al. calculated hyperfine shifts in a variety of Fe(III)-phosphates using periodic hybrid DFT methods.²⁹ Two hybrid exchange–correlations were used: the B3LYP functional, containing 20% Hartree–Fock (HF) exchange (Hyb20) and a 35% HF hybrid (Hyb35). The experimental NMR shifts were found to fall within the range of values bounded by the Hyb20 and Hyb35 results. More recently, Middlemiss et al. used Hyb20 and Hyb35 functionals to calculate P hyperfine shifts in LiMPO₄ and MPO₄ (M = Fe, Mn and Co) compounds.²⁶ In this work, the spin at one of the M sites in the first coordination shell of P is flipped, and the FCS contribution of the inverted M–O–P spin density transfer pathway is obtained as half of the difference between the P hyperfine shift in the flipped and the initial fully aligned spin configurations. Here, we extend this ‘spin-flipping’ approach, previously applied to the LiFe_1−xMn_xPO₄ solid solution,²⁴ making use of the FCS contributions already obtained for the M–O–P pathways in LFP and LCP as shown in Fig. 1 for both the Hyb20 and Hyb35 functionals. As discussed previously, Fe and Co ions are randomly distributed on the 5 M sites around P, giving rise to 32 local P environments (24 of which are distinct, due to the mirror plane located on the P group (resulting in M2 = M2′) reducing the number of inequivalent environments). The hyperfine shifts of all of these environments are calculated using the LFP and LCP end member pathways and used to fit and then assign the experimental NMR spectra. We also explore the effectiveness of different NMR methods to acquire ³¹P spectra in strongly paramagnetic phases.

2. Experimental section

2.1. Synthesis and characterisation

The carbon-coated LiFe_xCo_1−xPO₄ (x = 1, 0.75, 0.5, 0.25, 0) series were synthesized via the solid-state method using iron oxalate, cobalt oxalate, lithium carbonate, ammonium dihydrogen phosphate and carbon precursors in stoichiometric mixtures. After high-energy ball milling for 20 minutes, the reaction mixture was pelletized and heated to 600 °C under flowing argon. The LFP precursors were heated for 6 h.³⁵ For LiFe_0.75Co_0.25PO₄, they were heated for 6 h, then cooled and reheated for a further 11 h. For LiFe_xCo_1−xPO₄ (x = 0.5, 0.25, 0), the precursors were heated for 6 h, cooled and reheated for 11 h twice, before a final 24 h heating step. The additional heating and cooling steps were employed to remove trace impurities.

The X-ray diffraction (XRD) patterns were obtained using a PANalytical Empyrean X-ray diffractometer with a Cu Kα source. The data for LiFe_xCo_1−xPO₄ (x = 1, 0.5, 0.25 and 0) were collected for a total scan time of 9 h and 52 minutes using a step size of 0.017° over a 2θ range of 5–140°. The data for LiFe_0.75Co_0.25PO₄ was collected for a total scan time of 1 h and 41 minutes using a step size of 0.017° over a 2θ range of 5–120°. Rietveld refinements were performed within the TOPAS software.³⁶

2.2. Nuclear magnetic resonance

The ³¹P Hahn echo NMR experiments performed on a 2.35 T Oxford Spectrospin spectrometer (100 MHz for ¹H) at a Larmor frequency of approximately 40.5 MHz were carried out using a 1.3 mm MAS Samoson probe. The Hahn echo pulse sequence was synchronized to two rotor periods, at a spinning speed of 55 kHz, to prevent ringing. A 90° pulse width of 1.1 μs and a recycle delay of 0.02 s were used.

Corresponding ³¹P MATPASS spectra were collected on a Bruker 200 Avance III spectrometer (4.7 T) at a Larmor frequency of 81 MHz, using a 1.8 mm MAS Samoson probe. A series of five 90° pulses with a pulse width of 1.6 μs were employed, and rotor synchronised to a spinning frequency of 40 kHz.²⁴ The recycle delay was 0.015 s. The decay time constant of the Hahn echo/MAT sequence, T^′₂, was obtained at 4.7 T for LFP and LCP using a series of Hahn echoes where τ, the delay separating the centres of the 90° and 180° pulses, was varied between 50 μs and 10 ms in 8 increments. The signal decay was then fitted with an exponential function. The T^′₂ values obtained for LFP and LCP were 367 and 1199 μs, respectively.

Additional ³¹P aMAT data were acquired on a Bruker 500 Avance III spectrometer at a Larmor frequency of 202 MHz, using a 1.3 mm HX Bruker probe. The data were collected using tanh/tan SHAPs,^23,37 sweeping through 5 MHz in 50 μs with a RF amplitude of 417 kHz. The evolution time was set to seven rotor periods (116.67 μs), excluding the lengths of the SHAPs. The recycle delay was set to 100 ms. The spectra of the pure LCP and LFP phases were acquired with a spectral width in the indirect dimension of 147.7 kHz and 32 complex increments, with 9216 scans per increment. The spectra of the co-substituted phases were acquired with a spectral width in the indirect dimension of 1177 kHz and 256 complex increments. The number of scans per increment was 1568, 4224 and 4096, for LiFe_xCo_1−xPO₄x = 0.25, 0.5 and 0.75, respectively. The complex increments were acquired and processed using the echo/anti-echo scheme. All experiments were carried out at a sample temperature estimated at 320 K (elevated from room temperature due to MAS-induced frictional heating).

Testing of the excitation efficiency and separation of the sidebands was carried out on a Bruker 700 Avance III spectrometer (16.45 T) at a Larmor frequency of 283.5 MHz, using a 1.3 mm Bruker probe. The 90° pulse width was 1.42 μs, the recycle delay was 0.015 s and the spinning speed was 60 kHz. Both the SHAP echo and the aMAT data were collected using tanh/tan SHAPs, sweeping through 5 MHz in 50 μs with a RF amplitude of 175.5 kHz. The evolution time in the aMAT sequence was set to seven rotor periods, excluding the length of the SHAPs. 256 complex increments were acquired and processed using the echo/antiecho scheme.

At all fields the ³¹P data were referenced to an 85 wt% H₃PO₄ solution at 0 ppm.

2.3. Hybrid density functional theory

The Fermi contact contributions for the Fe–O–P and Co–O–P pathways in LFP and LCP, respectively, were taken from the values calculated by Middlemiss et al.²⁶ For the ‘distortion’ analysis, in which Fe was placed in the previously optimised LCP structure, and Co, in the previously optimised LFP structure, the Fermi contact contributions were obtained using the same bulk magnetic parameters as for Fe and Co in their native LFP and LCP structures, respectively,^24,26 and neglecting further geometry changes in response to the substitutions, so that the distortions might be regarded as limiting cases. In brief, the first principles solid-state DFT calculations were performed within the CRYSTAL09 linear combinations of atomic orbitals code.³⁸ Two hybrid functionals were used: the B3LYP functional with 20% Hartree–Fock (HF) exchange (Hyb20)³⁹ and a related 35% HF Becke-LYP hybrid (Hyb35).^40–42 The Fermi contact contribution to the hyperfine shift was computed directly from the spin density at the ³¹P nuclear position in the ferromagnetic state and subsequently scaled to a value consistent with the paramagnetic state, as described previously by Middlemiss et al. and Clément et al.^24,26 The bulk magnetic parameters defining the temperature dependent paramagnetic susceptibilities of LFP and LCP were as in the previous study.²⁶ M–O–P bond pathway decompositions of total ³¹P hyperfine shifts were performed by flipping selected M spins in Li₈M₈(PO₄)₈ supercells, where the variations in ³¹P contact shifts due to the flip directly yield the symmetry distinct pathway contributions.²⁶

3. Results and discussion

3.1. X-ray diffraction

LiFe_xCo_1−xPO₄ (x = 1, 0.75, 0.5, 0.25 and 0) were characterised and confirmed as phase pure using XRD. Rietveld refinements of the XRD patterns and analysis of the cell parameters (ESI†) show a linear decrease in the cell volume as the Co content increases, which is consistent with the smaller ionic radius of Co²⁺ in comparison with that of Fe²⁺ (88.5 and 92 pm,⁴³ respectively for the high spin six-fold co-ordinated crystal radii). The linear relationship of the cell parameters with Co content is consistent with Vegard-type behaviour (Fig. 2 and ESI†) and is indicative of a solid solution of Fe and Co on the M site. This is in agreement with the conclusions of the neutron diffraction study of Nytén et al.⁴⁴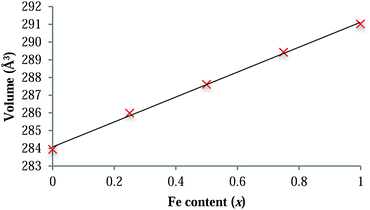

Fig. 2 Plot showing the dependence of the unit cell volume on Fe content across the LiFe_xCo_1−xPO₄ series. The linear correlation (R² = 0.9983) follows Vegard's law.

3.2. Nuclear magnetic resonance

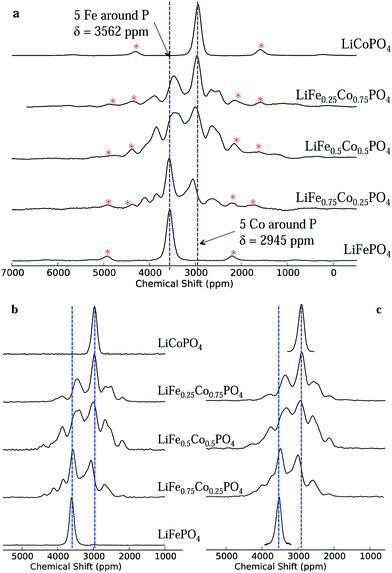
The one-dimensional NMR spectra of LiFe_xCo_1−xPO₄ (x = 1, 0.75, 0.5, 0.25 and 0) acquired at a low magnetic field strength of 2.35 T and a fast spinning frequency of 55 kHz are shown in Fig. 3a. The isotropic shift (δ_iso) of LFP is higher than that of LCP (3562 and 2954 ppm, respectively), but the linewidths are similar, with a full width at half maximum (FWHM) of 6.3 kHz/170 ppm. The NMR spectra of the co-substituted olivines contain two resonances near those of the two end members compounds, but they also contain resonances lying outside the bounds of these two shifts. This is surprising, as it is intuitive to expect the resonances for the intermediate LiFe_xCo_1−xPO₄ (0 < x < 1) stoichiometries to lie between the all-Fe and all-Co shifts, as was the case in our prior study of the LiFe_1−xMn_xPO₄ solid solutions.²⁴

Fig. 3 The ³¹P MAS NMR spectra of LiFe_xCo_1−xPO₄ (where x = 1, 0.75, 0.5, 0.25, 0). In (a), the spectra were acquired using a MAS frequency, ν_r, of 55 kHz and a 100 MHz magnetic field strength. Spinning sidebands are marked with asterisks. Most peaks in the mixed phases lie beyond those assigned to the all-Fe and all-Co P environments (i.e., outside the region contained within the two blue dashed lines). The 1D ³¹P MAS NMR spectra of the isotropic resonances in LiFe_xCo_1−xPO₄ (x = 1, 0.75, 0.5, 0.25, 0) acquired at (b) ν_r = 40 kHz extracted from the 2D MATPASS pulse sequence at a 200 MHz magnetic field and at (c) ν_r = 60 kHz extracted from the 2D aMAT pulse sequence acquired at a 500 MHz magnetic field. The slight additional broadening in (c) is attributed to a temperature distribution in the rotor.

The short pulse widths and low magnetic field strength enable us to excite the whole region of interest in the NMR spectra (additional experiments showing this are presented in the ESI†) while the fast MAS frequencies successfully remove the spinning sidebands of the two most intense peaks in all the spectra (shown by a red asterisk) from the region of the isotropic resonances. Spectra recorded at a lower spinning frequency (40 kHz) and at twice the magnetic field strength (4.7 T; presented in ESI†) show strong peak overlap due to the greater number of sidebands, rendering it virtually impossible to distinguish the different ³¹P isotropic resonances from their sidebands.

The isotropic 1D spectra extracted from the 2D MATPASS and aMAT pulse sequences, recorded at 200 and 500 MHz (4.7 and 11.75 T), respectively, are shown in Fig. 3b and (c). They show good agreement with each other, and with the low magnetic field 1D data, in respect of peak positions and relative intensities, proving that the excitation bandwidth is sufficiently broad at all three fields strengths. Additionally the removal of the sidebands in the aMAT and MATPASS spectra confirms the assignment of the isotropic resonances in the 1D data. The most notable difference in the spectra arises in the slightly larger linewidth and consequent poorer resolution of the peaks in the 500 MHz data. This is ascribed to a larger temperature gradient and broader distribution in shifts (due to the strong temperature dependence of the hyperfine shift). A series of further experiments (presented in the ESI†) confirm that this broadening is unrelated to the magnetic field strength and the pulse sequence.

Additional experiments were carried out to explore the efficiencies of excitation of the aMAT and MATPASS pulse sequences using a physical mixture of LiFePO₄, LiCoPO₄ and LiNiPO₄ (the ³¹P site in LiNiPO₄ resonating at 1800 ppm). The experiments were carried out at a high magnetic field strength (700 MHz/16.45 T), where the isotropic peaks and their spinning sideband manifolds span an extremely large frequency range, of more than 1 MHz in width. In order to test the excitation window of the two pulse sequences, a 1D stimulated echo (consisting of 90° pulses) was compared with a 1D SHAP echo, which employs adiabatic pulses, 90° and adiabatic pulses being employed in the MATPASS and aMAT experiments, respectively, to obtain the broadband excitation. The spectra were compared with a ‘model spectrum’ (representative of perfect excitation), constructed by summing the three Hahn echo spectra,⁴⁵ acquired with carrier frequencies centred at 1500, 2500 and 3500 ppm (presented in the ESI†). When the carrier frequency was placed in the middle of the spectra, both pulse sequences successfully excited the entire range. However, the SHAP echo proved to have a larger excitation window: when the carrier was moved off centre by 0.28 MHz the bandwidths for the stimulated echo and the SHAP echo were 1 MHz and 1.3 MHz, respectively. Both the aMAT and MATPASS experiments successfully separated the sidebands from the isotropic peaks, resulting in spectra with peaks arising only from the unique ³¹P local environments. Since the aMAT pulse sequence is longer than the MATPASS (the former is synchronised to seven rotor periods, the latter to one), it is more susceptible to T^′₂ dephasing effects, i.e., a loss of intensity due to signal decay prior to acquisition. However, the intensities seen here seem to agree well between the aMAT and the MATPASS spectra, and we assume the effect is negligible in this system.

In summary, the results of all three NMR experiments show good agreement, confirming that they are robust techniques for the study of paramagnetic materials. The further spectral analysis detailed below will be performed with the 200 MHz MATPASS data, given poorer peak resolution in the 500 MHz spectra, while, in the 100 MHz data, although the sidebands of the most intense peaks are moved beyond the region of interest, this is not the case for some of the sidebands associated with the weaker peaks.

3.3. Density functional theory calculations

The FCS contributions, δ_P, for each of the M–O–P pathways (P) in LFP and LCP acquired from spin-flipping calculations²⁶ within the Hyb20 and Hyb35 functionals are shown in Fig. 1. Since the FCS contributions are additive to a good approximation,²⁶ the overall ³¹P hyperfine shifts in LiFe_xCo_1−xPO₄ (0 < x < 1) were calculated by placing Fe and Co on the five M sites (resulting in 32 configurations) and by summing over the FCS contributions for the five relevant M–O–P pathways. Further calculations have shown that we only need to consider the first coordination shell of M around P, because the more distant M shells have less than a 2% contribution to the FCS (ESI†).

Since the bond pathway shift contributions were calculated within the LFP and LCP end member structures, there has been no consideration of the local and longer-range distortions induced by Fe and Co co-substitution into the olivine lattice. For example, we know that the cell parameters vary smoothly across the entire stoichiometric range, which might reasonably be expected to be associated with changes in local structure. We explored this effect by calculating the bond pathway contributions when Co and Fe cations were substituted into the fixed LFP and LCP structures, respectively (denoted as Co@LFP and Fe@LCP), Table 1.

Table 1 The bond pathway contributions in the ‘distorted’ structures, i.e. placing Fe and Co in the fixed LCP and LFP structures, respectively (denoted Fe@LCP and Co@LFP), as compared with the original Fe@LFP and Co@LCP data from Middlemiss et al. shown in Fig. 1.²⁶ The calculations were performed by the complete substitution of Fe for Co in the LCP structure, and Co for Fe in the LFP structure, all in eight formula unit supercells

	Fe@LFP, ppm		Fe@LCP, ppm		Co@LCP, ppm		Co@LFP, ppm
	Hyb20	Hyb35	Hyb20	Hyb35	Hyb20	Hyb35	Hyb20	Hyb35
δ P1	230	201	666	577	−436	−412	−436	−394
δ P2	1925	1629	1944	1640	1344	1142	1287	1108
δ P3	34	−72	404	245	657	517	211	127
δ P4	271	130	828	627	858	679	585	442

---

The differences in pathway contributions, Δδ_P, are examined, where, for example, Δδ_P1 is the difference δ_P1(Fe–O–P) − δ_P1(Co–O–P). A reasonable bounding range for the effects of local distortions in the co-substituted olivine may be derived by comparing the differences in bond pathway contributions obtained for TM species in their native environments (Fe@LFP & Co@LCP) versus those obtained from the cross-substituted case (Fe@LCP & Co@LFP), and the two intermediate cases (Fe@LFP & Co@LFP; and Fe@LCP & Co@LCP). We have calculated the averages, ranges and standard deviations for the Δδ_P values obtained in these four cases (Table 2); and take this as representative of the shifts in LiFe_xCo_1−xPO₄. The range of Δδ_P2 is less than 80 ppm, which may be neglected given that the FWHM of the peaks is 170 ppm. However the distortion-induced ranges of Δδ_P3 and Δδ_P4 are significant, at greater than 700 ppm. The findings are consistent with the fact that the P2 bond angles are similar in the LFP and LCP structure (differing by 0.6°), while the P3 and P4 bond angles differ by more than 2.5° in the two structures.

Table 2 The distortion-induced variations in the pathway differences [Δδ_P = δ_P(Fe–O–P) − δ_P(Co–O–P)]: the averages, standard deviations and ranges (maximum Δδ_P–minimum Δδ_P) have been calculated to quantify how much the FCS is likely to vary when Fe and Co are co-substituted into the olivine lattice

Differences in pathway contributions δP(Fe–O–P) − δP(Co–O–P), ppm
	Average		Standard deviation		Range
	Hyb20	Hyb35	Hyb20	Hyb35	Hyb20	Hyb35
ΔδP1	898	792	252	217	463	394
ΔδP2	620	510	35	21	76	46
ΔδP3	−215	−236	335	290	816	707
ΔδP4	−172	−182	358	318	830	734

---

It is easier to rationalise the transfer of electron density for the 90° (P1) pathway, than for the 120° (P2–P4) pathway, as discussed by Grey et al.¹⁴ Using the same model for the P1 pathway (∼90°) in LFP as described for lithium manganates, the doubly occupied O 2p_z orbital can transfer some “down” spin density into a singly occupied Fe²⁺ t_2g orbital and some “up” spin density into the P 4s orbital (as shown in the ESI†). This results in the P having a positive shift, as is seen for the P1 pathway in Fe@LFP.

A simplistic analysis might suggest that Co²⁺ should induce a smaller FCS than Fe²⁺, purely on the basis that the Fe²⁺ has one more unpaired electron than Co²⁺. A corresponding trend is observed in the LiFe_xMn_1−xPO₄ materials, where Fe²⁺ induces a smaller FCS than Mn²⁺ (3d⁵).²⁴ However, it is challenging to rationalise the large negative shift for Co in the P1 pathway. As this large shift is present for Co²⁺ in both the LCP and LFP structures we infer that the electron transfer mechanism is more sensitive to the TM species involved than to the pathway geometry. The results of our earlier study show that there is also a negative FCS for the P1 pathway in the MnPO₄, FePO₄ and CoPO₄ materials.²⁶ As the TM ion decreases in size, the δ_P1 becomes progressively more negative. A linear relationship between the δ_P1 and the M radii (ESI†) is observed, and when the size of the ion is <90 pm the δ_P1 becomes negative. Thus, there is clearly a competing mechanism that result in negative shifts, this mechanism dominating for shorter (more covalent) M–O bonds. The results in Table 1 suggest that for P3 and P4 the transfer of spin density is dominated by pathway geometries, rather than by the number of unpaired electrons in the system, as δ_P3 and δ_P4 are both significantly larger when Co or Fe is in the LCP structure. Tentatively, this is ascribed to the better orbital overlap along the M–O–P P3 and P4 pathways in the LCP structure, owing to shorter bond lengths compared with the LFP structure (3.647 and 3.633 Å, for P3 and P4, respectively, in LCP and 3.72, 3.652 Å, for P3 and P4, respectively, in LFP).

It is clear that the causes of the shifts are complex with multiple competing mechanisms, the orientation of the singly occupied orbitals at each TM site being sensitive to the details of the local anion coordination; the bond pathway contributions are then sensitive to both this orbital orientation and to the geometry of the M–O–P bond network. The results of the distortion analysis suggest that a deviation of the experimentally measured FCS in the LiFe_xCo_1−xPO₄ series from the ideal pathway contributions calculated for Fe@LFP and Co@LCP might reasonably be expected, especially for the P3 and P4 pathways. We therefore proceed by applying a fitting routine to the isotropic NMR spectra to extract the Δδ_P values providing the best fit with the experimental data, as described by Clément et al.²⁴ From the XRD analysis, there is evidence of a solid solution of Fe and Co on the olivine M sublattice,⁴⁴ and so the relative probabilities of the 32 configurations occurring in LiFe_xCo_1−xPO₄ (x = 0.25, 0.5 and 0.75) are calculated using a random model determined by the ratio of Fe to Co in the lattice:

probability = f^a × c^b

where f and c are the fractions of Fe and Co, respectively, in the compound (f + c = 1) and a and b are the number of Fe and Co ions, respectively, in the first coordination shell. The probability of a particular configuration being present in the material determines its contribution to the overall spectral intensity. The effect of the spin–spin relaxation on the spectral intensity also needs to be accounted for. Since the MATPASS pulse sequence is synchronised to 1 rotor period, the signal will decrease in intensity by a factor exp(−τ/T^′₂), where τ is the time delay prior to signal acquisition in the MATPASS sequence (1/spinning speed) and T^′₂ is found by averaging the T^′₂ contributions from Fe and Co around P in the end members, (where the measured Fe (LFP) and Co (LCP) T^′₂ values are 367 μs and 1199 μs, respectively), giving Fe-T^′₂ × f + Co-T^′₂ × c (T^′₂ values listed in ESI†). The relaxation-weighted intensities are then multiplied by the configuration probabilities in order to calculate the intensities of the different resonances anticipated in the NMR spectra and a Gaussian lineshape, 170 ppm in width, is added for each configuration. A minimisation routine is then performed on the spectra of all five materials simultaneously and the pathway differences (and therefore the isotropic shift for each configuration) are fixed across all the spectra. The χ² of the fit was calculated and used as a measure for when a minima was found.

The results from the fit taking the Hyb35 data as initial Δδ_P values are shown in Fig. 4 (the numbering of the 32 local P environments is shown in the ESI†). The fitted spectra show good agreement with the experimental data. The minor changes in the geometry of the P environments between the materials, is likely to be one source of the slight discrepancies between the experimental and the fitted data; any differences in the T^′₂ values for the different environments from those calculated using our simple model are also likely to be important. When the Hyb20 data was used as the initial values for the fit, there was poor agreement with the NMR spectra (ESI†) suggesting that the Hyb35 starting values are a better model for the LiFe_xCo_1−xPO₄ materials. The outputs of the Δδ_P obtained in the fits with the Hyb35 initial values are shown in Table 3. The Δδ_P2 resulted in a small change from the starting values (65 ppm), whereas the Δδ_P3 and Δδ_P4 changed by 110 and 255 ppm, respectively, which is in good agreement with the distortion analysis (Table 2).

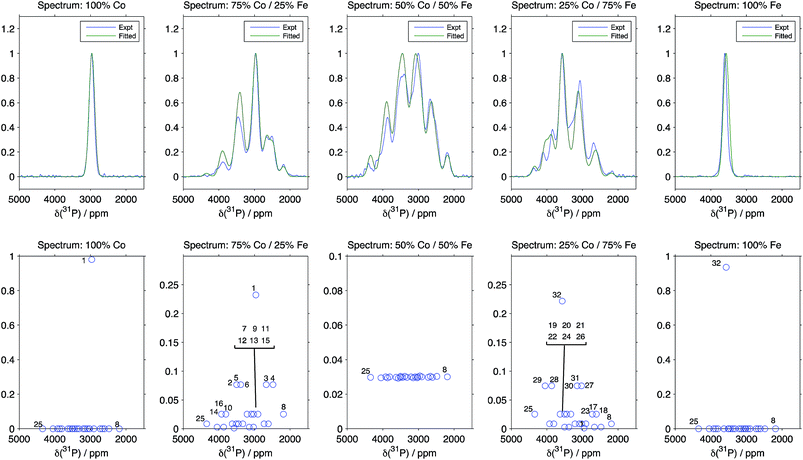Fig. 4 Comparison between the experimental spectra, and the results of fitting the pathway contribution differences using the Hyb35 calculations as starting values and fixing the isotropic shifts of the 32 possible Fe/Co configurations around P (the numbering of the 32 local P environments is shown in the ESI†). R² is 0.9822, 0.9396, 0.9524, 0.9411 and 0.8320 for LiFe_xCo_1−xPO₄ for x = 1, 0.75, 0.5, 0.25 and 0, respectively.

Table 3 The Δδ_P values from the fit compared with the input values

ΔδP, ppm	Fitted output (Fitted)	Initial value: Fe@LFP–Co@LCP Hyb35 calculations
ΔδP1	539	613
ΔδP2	422	487
ΔδP3	−479	−589
ΔδP4	−294	−549

---

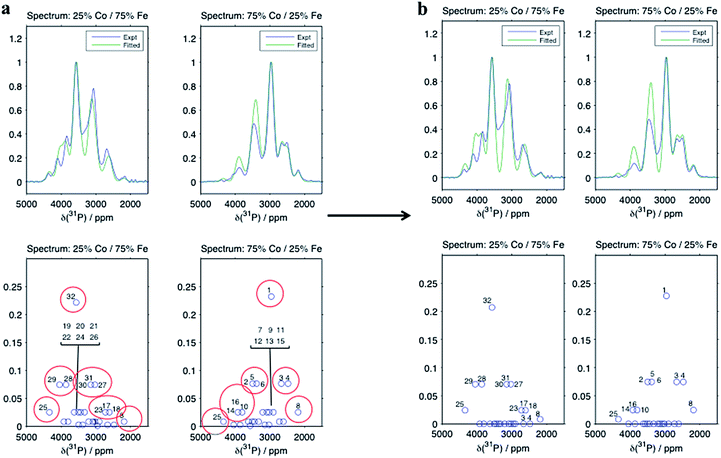
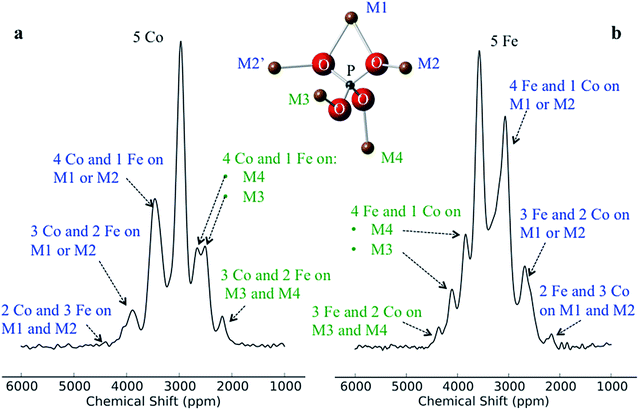
Despite there being 32 P environments (24 of which are distinct because M2 = M2′), there are at most seven distinguishable peaks in the spectra of the co-substituted materials. Examining the intensities of the configurations that fall within each of these peaks for LiFe_0.25Co_0.75PO₄ and LiFe_0.75Co_0.25PO₄, dominant configurations with a significant contribution to the intensity are always clearly evident (circled in Fig. 5a). The output from the Hyb35 fits was re-plotted including only the main contributions to each of the resonances (Fig. 5b). The fitted data still capture the main features of the spectra and result in a good fit (R² = 0.8684 and 0.8712 for LiFe_0.75Co_0.25PO₄ and LiFe_0.25Co_0.75PO₄, respectively, compared with R² = 0.9396 and 0.9411 for LiFe_0.75Co_0.25PO₄ and LiFe_0.25Co_0.75PO₄, respectively, when all of the contributions are included). The most notable differences appear to be around the “all-Fe” and “all-Co” peaks, configurations 32 and 1 respectively, indicating that the lower intensity peaks are most significant in this region. Using the results in Fig. 5 we are able to assign the peaks that are observable in the NMR spectra to a set of dominant configurations (Fig. 6). Importantly, we can make a definitive assignment concerning the number of Fe and Co ions in the local coordination shell. This is what is important for understanding the electrochemistry of these systems in subsequent studies.

Fig. 5 Hyb35 results for the spectra collected at a magnetic field of 200 MHz using (a) all the configurations and (b) including only the highest probability configurations. When only the dominant configurations are included the fitting is still good (R² = 0.9396 and 0.9411 and 0.8684 and 0.8712 including all and only the main contributions, respectively), with only a marked decrease in intensity around the central peak.

Fig. 6 Assignment of the peaks for (a) LiFe_0.25Co_0.75PO₄ and (b) LiFe_0.75Co_0.25PO₄, using only the main contributions from the fittings. When Co is on M1 and/or M2, it results in lower shifts and placing a Co on M3 and/or M4 results in higher shifts. This is true for both materials.

In the LiFe_0.25Co_0.75PO₄ and LiFe_0.75Co_0.25PO₄ spectra, we observe that when the majority TM is exchanged on the M3 or M4 site by the minority TM, the shift for that P environment moves beyond the isotropic shift of the pure majority metal phase (i.e. to above 3600 ppm for LFP and to below 3000 ppm for LCP). This is due to δ_P3 and δ_P4 being larger in LCP as compared with LFP. Thus, Co on the M1 and/or M2 sites results in a lower shift for that environment, while Co on the M3 and/or M4 sites leads to higher shifts. Therefore we have been able to rationalise the appearance of peaks outside the range of the all-Fe and all-Co P environments by the calculation and use of individual M–O–P bond pathway shift contributions. If, as might initially be thought, Fe should always display a larger FCS contribution than Co due its additional unpaired electron, the P shifts in the mixed TM systems would all appear within the bounds of the LFP and LCP peaks, as observed for the LiFe_xMn_1−xPO₄ system.²⁴

4. Conclusions

We have carried out a comprehensive study using solid-state NMR and hybrid DFT calculations of the high energy density LiFe_xCo_1−xPO₄ paramagnetic cathode materials for 0 ≤ x ≤ 1, arriving at a detailed understanding of the NMR spectra. Three different experimental NMR methods for broadband excitation and sideband separation have been employed, allowing for the collection of spectra containing only the isotropic peaks. The adiabatic pulses employed in the aMAT sequence resulted in the largest bandwidth (of greater than 1 MHz). The data acquired at a low magnetic field strength and with fast spinning did not require a 2D pulse sequence, and represents the most trivial of the NMR techniques, however there may be a small overlap between the sidebands of the lower intensity peaks and some of the isotropic peaks. This issue is avoided in the 2D experiments.

First principles hybrid DFT calculations on LFP and LCP have provided us with a tool to calculate the ³¹P hyperfine shifts in LiFe_xCo_1−xPO₄. Using a minimisation fitting routine we assigned the 32 P environments in the co-substituted olivine. Lacking the DFT calculations, it would have proved impossible to rationalise the assignment of the spectra because the majority of the peaks fall beyond the all-Co and all-Fe ³¹P shifts. The origin of this phenomenon comes from the differences in the FCS in two M–O–P pathways (δ_P3 and δ_P4) being greater in LCP than LFP. This contradicts the admittedly simple notion that Fe²⁺ should transfer more electron density onto P than Co²⁺, owing to its greater number of unpaired electrons, and instead suggests that more subtle effects such as the variation of bond lengths and angles in the local shells around the two ions are the source of the effect. In order to render our findings more immediately applicable to future NMR studies of the electrochemical cycling of such materials, we have identified the local configurations that give rise to the dominant experimental peaks, and provide definitive assignments of the resonances in terms of the numbers of Fe and Co ions in the local coordination shell, clearly distinguishing two groups of resonances depending on whether the ions are connected to the phosphate ions via M1/M2–O–P or the M3/M4–O–P pathways.

Acknowledgements

We thank Ben Zhu for his help with the NMR and thoughtful discussions. We also thank the UK EPSRC for a DTA award (FCS) the US DOE for support via NECCES, an Energy Frontier Research Center (DE-SC0001294) (CPG) and the EU ERC for financial support and a Marie Curie intra-European fellowship (ML). AJP, GP and LE were supported by the LABEX iMUST (ANR-10-LABX-0064) of the Université de Lyon, within the program “Investissements d'Avenir” (ANR-11- IDEX-0007) operated by the Agence Nationale de la Recherche (ANR). JVH thanks the EPSRC and the University of Warwick for partial funding of the solid-state NMR infrastructure at Warwick, and acknowledges additional support for this infrastructure obtained through Birmingham Science City: Innovative Uses for Advanced Materials in the Modern World (West Midlands Centre for Advanced Materials Projects 1 and 2), with support from Advantage West Midlands (AWM) and partial funding by the European Regional Development Fund (ERDF).

Notes and references

1. J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
2. K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789.
3. J. N. Reimers and J. R. Dahn, J. Electrochem. Soc., 1992, 139, 2091–2097.
4. A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194.
5. K. Amine, H. Yasuda and M. Yamachi, Electrochem. Solid-State Lett., 2000, 3, 178–179.
6. F. Zhou, M. Cococcioni, K. Kang and G. Ceder, Electrochem. Commun., 2004, 6, 1144–1148.
7. S. Okada, S. Sawa, M. Egashire, J.-I. Yamaki, M. Tabuchi, H. Kageyama, T. Konishi and A. Yoshino, J. Power Sources, 2001, 97-98, 430–432.
8. J. Yang and J. J. Xu, J. Electrochem. Soc., 2006, 153, A716.
9. J. Wolfenstine and J. Allen, J. Power Sources, 2004, 136, 150–153.
10. D.-W. Han, Y.-M. Kang, R.-Z. Yin, M.-S. Song and H.-S. Kwon, Electrochem. Commun., 2009, 11, 137–140.
11. J. Kim, D.-H. Seo, S.-W. Kim, Y.-U. Park and K. Kang, Chem. Commun., 2010, 46, 1305.
12. J. Cabana, J. Shirakawa, G. Chen, T. J. Richardson and C. P. Grey, Chem. Mater., 2010, 22, 1249–1262.
13. T. Pennanen and J. Vaara, Phys. Rev. Lett., 2008, 100, 133002.
14. C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512.
15. L. J. M. Davis, I. Heinmaa, B. L. Ellis, L. F. Nazar and G. R. Goward, Phys. Chem. Chem. Phys., 2011, 13, 5171.
16. L. Zhou, M. Leskes, A. J. Ilott, N. M. Trease and C. P. Grey, J. Magn. Reson., 2013, 234, 44–57.
17. M. C. Tucker, M. M. Doeff, T. J. Richardson, R. Fiñones, E. J. Cairns and J. A. Reimer, J. Am. Chem. Soc., 2002, 124, 3832–3833.
18. S. L. Gann, J. H. Baltisberger and A. Pines, Chem. Phys. Lett., 1993, 210, 405–410.
19. J. Z. Hu, D. W. Alderman, C. Ye, R. J. Pugmire and D. M. Grant, J. Magn. Reson., 1993, 105, 82–87.
20. W. T. Dixon, J. Magn. Reson., 1981, 44, 220–223.
21. W. T. Dixon, J. Chem. Phys., 1982, 77, 1800.
22. O. N. Antzutkin, S. C. Shekar and M. H. Levitt, J. Magn. Reson., 1995, 115, 7–15.
23. G. Kervern, G. Pintacuda and L. Emsley, Chem. Phys. Lett., 2007, 435, 157–162.
24. R. J. Clément, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, J. Am. Chem. Soc., 2012, 134, 17178–17185.
25. I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, J. Am. Chem. Soc., 2012, 134, 1898–1901.
26. D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Chem. Mater., 2013, 25, 1723–1734.
27. J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297.
28. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
29. J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, J. Am. Chem. Soc., 2010, 132, 16825–16840.
30. J. Yates, C. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
31. A. Castets, D. Carlier, Y. Zhang, F. Boucher and M. Ménétrier, J. Phys. Chem. C, 2012, 116, 18002–18014.
32. Y. Zhang, A. Castets, D. Carlier, M. Ménétrier and F. Boucher, J. Phys. Chem. C, 2012, 116, 17393–17402.
33. A. Castets, D. Carlier, Y. Zhang, F. Boucher, N. Marx, R. Gautier, E. Le Fur, L. Le Pollès, L. Croguennec and M. Ménétrier, Solid State Nucl. Magn. Reson., 2012, 42, 42–50.
34. G. Mali, C. Sirisopanaporn, C. Masquelier, D. Hanzel and R. Dominko, Chem. Mater., 2011, 23, 2735–2744.
35. G. Kobayashi, S.-I. Nishimura, M.-S. Park, R. Kanno, M. Yashima, T. Ida and A. Yamada, Adv. Funct. Mater., 2009, 19, 395–403.
36. A. A. Coelho, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 400–406.
37. T.-L. Hwang, P. C. M. van Zijil and M. Garwood, J. Magn. Reson., 1998, 133, 200–203.
38. R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Ziovich-Wilson, Z. Kristallogr., 2005, 571–573.
39. J. Muscat, A. Wander and N. M. Harrison, Chem. Phys. Lett., 2001, 342, 397–401.
40. X. Feng and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 092402.
41. D. S. Middlemiss, L. M. Lawton and C. C. Wilson, J. Phys.: Condens. Matter, 2008, 20, 335231.
42. I. de P. R. Moreira, F. Illas and R. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102.
43. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767.
44. A. Nytén and J. O. Thomas, Solid State Ionics, 2006, 177, 1327–1330.
45. A. J. Pell, R. J. Clément, C. P. Grey, L. Emsley and G. Pintacuda, J. Chem. Phys., 2013, 138, 114201.

---

Footnotes

† Electronic supplementary information (ESI) available: LFP and LCP M–O–P pathway bond lengths and angles, XRD patterns and refinements, experiment to test the excitation window at a magnetic field strength of 100 MHz, comparison of the Hahn echo and the MATPASS pulse sequence at a magnetic field strength of 200 MHz, the Hahn echo, stimulated echo, SHAP echo, aMAT and MATPASS pulse sequences, the LiNiPO₄ synthesis, spectra of a mixture of LiNiPO₄, LFP and LCP at a magnetic field strength of 700 MHz comparing the excitation width for the 90° and adiabatic pulses, the FCS contributions of the second co-ordination shell in LFP and LCP for the Hyb20 and Hyb35 calculations, an electron transfer process in a 90° M–O–P pathway, the δ_P1 plotted as a function of the size of the transition metal for LiMnPO₄, LFP, LCP, MnPO₄, FePO₄ and CoPO₄, the T^′₂ values used for different Fe/Co ratios around P, the labelling of the 32 configurations of Fe and Co around P in the olivine structure and the results from the fitting using the Hyb20 results as input values. See DOI: 10.1039/c4ta00934g

‡ Current address: Department of Chemistry, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK.

§ Current address: Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1 EW, UK.

¶ Current address: Université Lille Nord de France, CNRS, UMR 8181 UCCS, ENSCL, Université de Lille 1, 59652 Villeneuve d'Ascq, France.

---