 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stagnation point flows in analytical chemistry and life sciences
Ayoola T. Brimmo ab and
Mohammad A. Qasaimeh
ab and
Mohammad A. Qasaimeh *ab
*ab
aDivision of Engineering, New York University Abu Dhabi, Saadiyat Island, 129188, Abu Dhabi, UAE. E-mail: maq4@nyu.edu
bTandon School of Engineering, New York University, 6 MetroTech Center, Brooklyn, New York, USA
First published on 3rd November 2017
Abstract
Isolated microfluidic stagnation point flows – stagnation point flows formed within microfluidic interfaces – have come a long way as a tool for characterizing materials, trapping/manipulating micro particles, and generating confined flows and localized chemistries. Early applications of these fluidic stagnation flows focused on characterizing emulsions and polymers. However, in recent times, these flows have taken microfluidic forms to expand the range of applications to single-cell analysis, substrate patterning, and chip-integrated devices, amongst others. This article focuses on reviewing the microfluidics literature to highlight the concept behind isolated microfluidic stagnation point flows, underline different approaches of experimentally resolving them, and then look into their applications in chemistry and life sciences; with a specific focus on micro-total-analysis systems. The literature on this topic is approached historically; from the isolated fluidic stagnation point flow generated by the early four-roll mill to the currently predominating microfluidic stagnation point flows of the cross-slot device. Finally, isolated microfluidic stagnation flows produced by the relatively recent open space microfluidics – opposed jets, microfluidic probes and micropipettes – are critically analyzed and their applications are discussed. Ultimately, the goal of this article is to inform the scientific community on the constructive aspect of microfluidic stagnation flows by demonstrating their past, present, and future applicability in analytical chemistry and life sciences.
1. Introduction
Microfluidic stagnation is a topic that merges the field of microfluidics and hydrodynamic stagnations with a goal of developing and controlling a zero-velocity (stagnation) region within fluid interfaces. In as much as both fields are already fast evolving due to their evident advantages for analytical chemistry and biological research, their merger proposes a more telling advancement opportunity. While microfluidic devices offers an interesting avenue to develop integrated lab-on-chip devices for micro scale reagent volumes, hydrodynamic stagnations increases the resolution of this field to single micro-particles within the reagents. Such capability facilitates single cell resolutions in biological and life science studies, and this could hold the key to currently unresolved medical problems. Isolated microfluidic stagnation flow takes this concept further by generating the stagnation points away from walls/boundaries, and by using only hydrodynamic forces to manipulate them. The main advantage of this approach lay with its ability to isolate the response of trapped molecules/particles to a relatively less invasive environment – several techniques has been used for isolating target particles (e.g. optical, acoustic, and magnetic tweezers), but they require the introduction of secondary fields that could modify the chemistry of trapped particles and hence interfere with the characterization process. For instance, optical tweezers could lead to secondary heating and magnetic tweezers require pre-labeling; which could both affect cell viability. Other advantages of microfluidic stagnations include: localization of chemical reactions, increased maneuverability of trapped particles, increased viability of analyzed bio-particles, and its “open-flow” nature that can accommodate the isolation of larger particle sizes.The development of microfluidic stagnation flows is as rich in its history as it is in its physical applications. As such, this article attempts to critically review its advancement from a historical perspective – important applications are analyzed in a chronological progression in order to also highlight the concept's evolution with time. However, before we go into an in-depth analysis, the following sections present an evolution sketch of the overarching stagnation and microfluidic concepts, theoretical formulations of microfluidic stagnation point flows, and a broad perspective of applications covered in this article.
1.1 Stagnations and microfluidics
Fluidic stagnation is a phenomenon whereby a body of fluid is immobile within a certain region i.e. local velocity is zero. In certain type of flows, this region is limited to a dimensionless point and hence often referred to as a stagnation point.1 D' Alembert first introduced the fluidic stagnation point notion, in 1752, while working on the principle of flow drag on solid boundaries.2,3 At the time, fluidic stagnation was limited to liquid–solid interfaces and labeled as a “disturbance” that can be circumvented by airfoil designs of relatively sharp leading edges.2,3 Two centuries later, Prandtl proposed the boundary layer theory (in 1904), which theorized frictional forces as the cause of the sticking of a very thin fluidic layer (stagnation point) to a rigid boundary (see Fig. 1a).4 Since then, the concept of fluidic stagnation has evolved from theoretical notions in aerodynamics (see Fig. 1b)5,6 and heat transfer,7,8 to a practical tool used today for trapping and manipulating multiple micro-particles.9 This advancement was buoyed by G. I. Taylor in 1934 – when he demonstrated the scientific significance of trapping objects with fluidic stagnation point flows10 (see Fig. 1c), and this subsequently opened up a new field of study aimed at harnessing stagnation point flows for characterizing emulsions and polymers.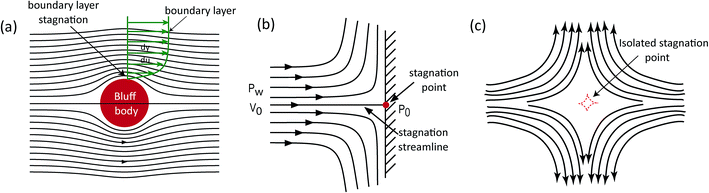 | ||
| Fig. 1 Stagnation flow schematics. (a) Boundary layer stagnation. (b) T-Junction stagnation point flow. (c) Microfluidic isolated stagnation point flow. | ||
Experimental explorations of this phenomenon were classically established in macro scale fluids. However, microfluidics – the study of fluids in channels with dimensions in tens of micrometers11,12 – evolved the physical configuration of stagnation point flows to the micro scale.13 Asides the obvious disparity in scale, another difference between microfluidics and macrofluidics is that, in microfluidics, the effect of surface tension, energy dissipation, and fluidic resistance becomes more dominant than potential flow.11,12,14,15
In addition to these, reduction of sample size, decrease in assay time, and minimization of reagent volume are all advantages of performing analyses in the micro scale, particularly in biology.14 Although studies on microfluidics as a subset of fluid mechanics are relatively new,16 its advancements have propagated swiftly to a wide range of scientific applications.17–20 Of these, a particularly promising outlook is its substitution of conventional biotechnology laboratory methods21 – microfluidics offers the opportunity to achieve comprehensive laboratory protocols on a single chip.15,22 Coupling microfluidics and stagnation techniques, with rapid advances in fluorescence-based molecular imaging and genomic, transcriptomic, and proteomic profiling techniques, incited a revolution in biological analysis of single cells.23 In recent times, this coupling has started to gain traction for applications in accurately controlling and manipulating single cells in lab-on-a-chip devices.24
1.2 Theoretical formulation
The theoretical formulation of the microfluidic stagnation point flows used for trapping micro-particles can be adequately described as a two-dimensional incompressible flow characterized by a velocity vector, which is a linear function of position.25 The proportionality constant of this relation is the distinguishing factor between the flow types; pure extensional, pure rotational and simple shear flows.26 Pure extensional flows constitute adjacent layers of flow towards or away from each other;27 with the rate of extension assumed to be constant throughout the flow.28 A concentric field with a non-zero rotational magnitude generates rotational flows while adjacent flows with opposing magnitudes give rise to the shear flows.This classification also constitutes a convenient way of formulating the different types of microfluidic stagnation point flows. From a mathematical perspective, these flows can be described in 2-D as:29
| ui = aixi | (1) |
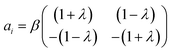 | (2) |
From eqn (1) and (2), the velocity components of the flow is given by:25
| u1 = β(x1(1 + λ) + x2(1 − λ)) | (3) |
| u2 = −β(x1(1 − λ) − x2(1 + λ)) | (4) |
This gives rise to the family of streamlines described by:
| Z = (x1 + x2)2 − λ(x1 − x2)2 | (5) |
Plotting the streamlines for the different types of flows results in the images in Fig. 2a–c. Similarly, Fig. 2d–f shows experimentally captured images of these stagnation point flow fields, specified by eqn (5).
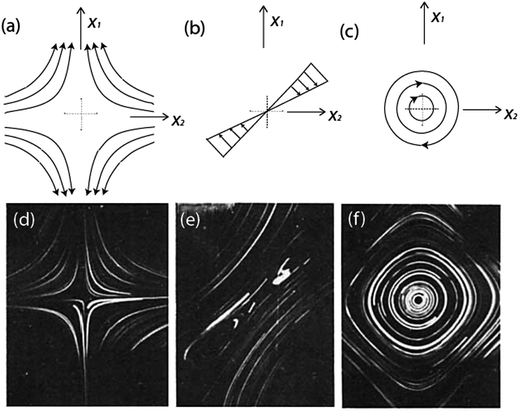 | ||
| Fig. 2 Streamline schematics of stagnation point flow fields. (a) Extensional flow (λ = 1). (b) Shear flow (λ = 0). (c) Rotational flow (λ = −1). Experimental captured photographs for stagnation point flow field. (d) λ = 1. (e) λ = 0. (f) λ = −1. Type parameter varies from pure extensional flow to pure rotational flow. Reprinted with permission. Copyright© 1981 John Wiley & Sons, Inc.31 | ||
Evidently, eqn (5) constitutes the fundamental formulation of these types of flow, and presents a mean of observing them in their theoretical forms. Applications of the stagnation point inherent in their structures are the focus of this review. The following sections highlight developments in the field, classified according to the stagnation point flow generation devices.
1.3 Broad perspectives
The primary function of isolated microfluidic stagnations is to trap particles in a fluid region engineered to have zero velocity gradient. Depending on the mechanism used to generate the stagnation point flow, the trapped object can be further manipulated for a wide range of practical applications in material characterization, localized chemistries, and applications of Micro-Total-Analysis Systems (μTAS) such as: droplet deformation and break up,10,32–35 droplet coalescing,36–39 birefringence of polymers,31,40,41 manipulation of biological particles in vitro,42,43 and single cell analysis,44 among others. These applications of microfluidic stagnation point flows can be traced back to 1934, where it was used by Taylor to investigate the dynamics of stirring multi-phase fluids.10 However, amidst its long history and wide range of theoretical and experimental considerations, there still is no review that cut across the full range of isolated microfluidic stagnation point flows. Consequently, this article reviews the concept behind isolated microfluidic stagnations, the different approaches of experimentally resolving the stagnation point flow under steady and transient conditions, and then look into their applications in chemistry, material characterization and life science. In Section 2, we look into the four-roll mill as the pioneering stagnation point flow-generating device. Although, the four-roll mill cannot be categorically classified as a microfluidic device based on the aforementioned definition, advances in the design of the four-roll mill have greatly contributed to the technological development of microfluidic stagnation point flows; hence our consideration of this device is also of scientific relevance. In Section 3, we delve into the literature of the most predominantly used microfluidic device for generating stagnation point flow – the cross-slot device. Section 4 summarizes the state-of-the-art of stagnation point flows generated by modern open space microfluidic systems.45 Finally, Section 5 presents our view on the future prospects of microfluidic stagnations and our recommendations for the field's critical success factors.2. Four roll mill
The four-roll mill is a device that consists of four cylindrical rollers with centers positioned at the edge of a hypothetical square, rotating either in opposing or concurrent pairs. Developed originally as mills for crushing materials in the 19th century,46 the device has since evolved into fluidic applications. The fluidic four-roll mill (see Fig. 3a) produces a two-dimensional laminar flow field, and depending on the roller speed and configuration, can be used to produce the full range of stagnation point flows described in the previous section. These flows are typically visualized by mounting the setup on top of a microscope. The use of the four-roll mill to generate flow fields can be traced back to 1934 when Taylor used a “four roller” to create an extensional flow (stagnation point flow) in order to study the deformation and burst of drops in an emulsion.10 The diameter of each of his rolls was 2.39 cm and he studied drops ranging from about 800–2000 micrometers in size. As such, this specific four-roll mill cannot be categorically labeled a microfluidic technology. However, since this device evolved into miniaturized version and eventually led to the development of microfluidic stagnation point flow devices, its inclusion in this review holds important historical and technical relevance. The following sections summarize application of four-roll mill generated stagnation point flows for drop dynamics and polymer birefringence studies.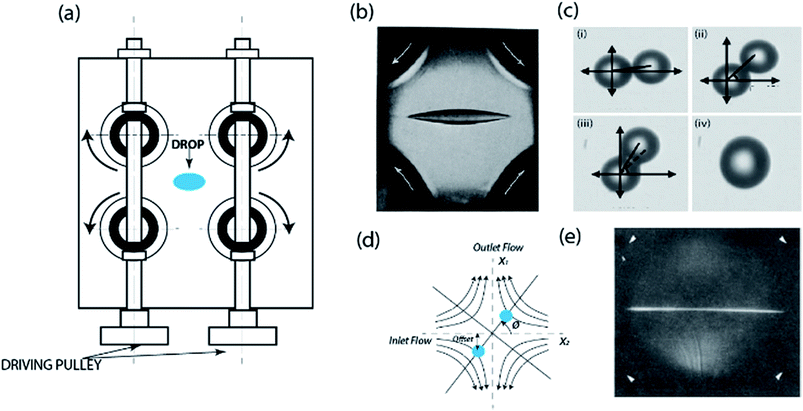 | ||
| Fig. 3 The pioneering application of the stagnation point flows. (a) Schematic of the original four-roll mill for fluidic applications. The diameter of each of rolls is 2.39 cm and the gaps between the rollers are 1 cm. (b) Experimental drop elongation study when trapped within the stagnation point of an extensional flow (stagnation point flow). Sizes of the studied drops ranged from about 800–2000 μm.10 Reprinted with permission. Copyright© 1934, The Royal Society. (c) Experimental visualization of drops coalescence. Reprinted with permission. Copyright© AIP Publishing LLC. (i) contact of the two drops, (ii) thinning of film separating drops, (iii) coalescence, and (iv) daughter droplet formation of the coalescence process.39 (d) Schematic of the four-roll mill generated flow field with the drop position offset.39 Reprinted with permission. Copyright© AIP Publishing LLC. (e) Localized flow birefringence in the four-roll mill. Photographs showing flow birefringence for a 1.5% polyethylene oxide/water solution and velocity gradient of 6 s−1. Arrow indicates orientation of rotation.40 Reprinted with permission. Copyright© 1976 John Wiley & Sons, Inc. | ||
2.1 Drop deformation and break-up
The problem of establishing the break up mechanism of a single drop of fluid, and in particular, the number of different drops a given dimension of droplet would break into, was classically highlighted and theorized by Rayleigh and others.47,48 Experimentally, these works were based on monitoring the breakup of drops, introduced into a pressurized bulk fluid through a hole. This technique neglects the effect of the surrounding fluid's disruptive viscous drag on the bursting of drops, and hence reveals very little about the stirring dynamics of these fluids.49,50 As the principal objective of mixing devices are to increase the surface area at the interface of both phases – for increased mass and heat transfer—these studies did not produce key information intended for designing blenders, and emulsifiers.33,35,51 In order to circumvent these drawbacks, Taylor adapted the four-roll mill generated stagnation point flow (see Fig. 3a and b) to control the bulk fluid's viscosity and rate of deformation through viscous drag, and monitor the corresponding interfacial surface tension.10 In Taylor's work, a drop of fluid immiscible in water was trapped in the stagnation point of a water-based extensional flow and extended by varying the rollers' speed until the drop eventually bursts. When the droplet is introduced into the low speed extensional flow, it takes a spherical shape, in which its surface tension exceeds the viscous and dynamic stresses of the bulk extensional flow. However, as the speed of the rollers increases, the flow's viscous force surpasses the cohesive forces of the drop making it to extend and eventually burst.52 The four-roll mill allows for the variability of the bulk flow's properties and viscous drag and, hence presented a relevant approach for studying the mixing dynamics of multi-phase fluids. Several studies have utilized the technique for analyzing the deformation and burst of viscous droplets.53,54Taylor further used the four roll apparatus to develop a correlation between drop size, roller speed, and dispersed to continuous-phase viscosity ratio. However, his experiments considered only small deformations and results agreed with theoretical estimates for only a limited range of low roller speeds.10 A number of experimental studies were later reported to validate Taylor's theory, such as Torza et al. coquette flow apparatus study,55 and the work of Rumscheidt and Manson, in 1961, that adapted a four-roll device equipped with a magnetic amplifier control, vibration free mounts, and additional reduction gears in order to improve the control and stability of Taylor's device.32 The adjustments made by Rumscheidt and Manson enabled them to demonstrate drop burst as a result of either shear flow or the upper limit of elongation.32 In addition, the effects of added emulsifier, and of electrostatic fields, were investigated as an extension of the apparatus' application in studying coalescence of colliding drops. In 1982, Grace extended the viscosity ratio range experimented on using the four-roll mill and presented correlations for single drop deformation and breakup for a viscosity ratio range of 10−9 – 950, using both rotational and extensional flows.33 The application of these correlations for designing static mixers was also presented in their report.33
By the early 1980's, theories and correlations on drop deformation and break-up, using a variety of flow types, had been reported. A review of these studies, up until the mid-eighties, can be found in the literature.52,53 A common issue experienced in these experiments is the instability of the stagnation points. Based on the governing equations for arbitrarily spatially periodic initial disturbances, it was found that the unbounded flows (0 < λ ≤ 1) are unconditionally unstable, while the shear flow (λ = 0) is stable to all infinitesimal spatially periodic disturbances,25 and even more stable when the number of rolls are increased.56 The growth of initial disturbances is accompanied by a growth of vorticity oriented along the principal axis of extensional strain when λ = 1. Eliminating these disturbances was the motivation of Bentley and Leal's 1986 design and operation of a computer controlled four-roll mill (2.54 cm gap between rolls) for investigations of the dynamics of single viscous drops in another immiscible fluid.34 The computer control device was based on the use of a camera to track the disturbance of the trapped particle, which is transferred to a feedback system to counter these instabilities by adjusting the speed of the rolls independently. When the drop drifts away from the stagnation point due to these disruptions, the adjustment of the roller's speed should be such that new speed acts to pull the drop back to the stagnation point. This scheme proved to be much more advanced than the original four-roll mill in accommodating larger shear rates and flow-type parameter. But, at the same time, the device had not reached its optimal state as it was limited by the 1980s state of the art in imaging and computation technologies.
In a separate study, Bentley and Leal35 used their computerized four-roll mill to validate the small-deformation theory of Barthes–Biesel & Acrivos,57 the large-deformation theory of Hinch & Acrivos,58 and numerical results of Rallison.59 Stone and Leal also used this device to investigate the response of drop dynamics to transient effects – sudden change in flow condition or flow type.60 In their study, the boundary-integral numerical method was used to compliment experiments by investigating the effect of step changes in the shear rate of extensional flows on the interface evolution and velocity fields of the flows, and ultimately on the break-up mechanism.60
Further studies in this line built on Bentley and Leal's automation of the four-roll mill to extend studies on drop dynamics.34 Recent advances include: the use of shear rates higher than the critical value of continuous drop stretching,51 study of the effect of surfactants on droplet deformation and coalescence,61,62 development of a technique to measure the viscosity of nano-liter fluid drops,63 the use of steady and transient 3-D drop investigations to accurately evaluate drop deformation theories,64 the deformation and break-up of polymeric drops,65 and the dynamics of vesicles in all types of flow.42,43 Most of the recent four-roll mill devices were observed to be characteristically miniaturized, which could preclude any simple “scaling” type arguments that could potentially serve as a basis for predicting the outcome of design changes in blenders or emulsifiers.51 In addition to all these somewhat tangible drop deformation applications, on a broader scale, the stagnation point flow generated by the four-roll mill has been recurrently used to extend and validate theories on perturbation methods for small deformations57,66–70 and the ellipsoidal framework that preserves the drop volume for large deformations.71–73
In retrospect, it is evident that the introduction of stagnation point flows in this field served as a turning point; it enabled researchers avoid the complexity of viscous drag while analyzing the effect of stirring on droplet dynamics. However, the four-roll mill device is on the bulky side, with dynamic components, and these limits its potential use for microfluidic applications. In as much as the opto-electronic automation integrated by Bentley and Leal's34 was key to ensuring the practicability of using these stagnation points for drop deformation and break up, it can be argued that the setup increased the overall complexity of the system, which further limits its potential use in microfluidics but transits its configuration to electro-mechanical systems. Overall, based on these advancements, it can be concluded that the stagnation point flow contributed a great deal in optimizing the synthesizing process of emulsions, but miniaturization would be key for its application in microfluidics, μTAS, microelectromechanical systems (MEMS), and nanoelectromechanical systems (NEMS).
2.2 Drop coalescence studies
By definition, coalescence is the process by which two or more objects (droplets or particles) combine to form a single spawn object. This process, akin to droplet break-up, affects the microscopic morphological development of a resulting emulsion or polymer blend, which eventually affects the final product's macroscopic properties.74 Although it has been established that drops collision do not necessarily lead to coalescence, collision is a necessary precursor for any coalescence process.75–77 In the event of coalescence, after collision, the thin film separating the two drops flatten-out, while the translational motion of the drops is impeded and the two drops become small enough for non-hydrodynamic attractive forces to cause rupture and then coalescence.38,78 Fig. 3c shows an experimentally captured time-lapse of this process.Coalescence plays an equally important role in liquid–liquid extraction79 and polymer blending process,80 as much as drop break up does. Studying this process in isolation has proven to be beneficial in engineering the final properties of the resulting blend. However, compared to drop break up, relatively less experimental investigations have been carried out on coalescence due to its more complicated nature; coalescence requires two drops to collide and remain together long enough for film drainage to occur.81 This process is extremely difficult to control as such, classically, the drop collision topic has been predominantly approached from a theoretical perspective,82–87 with Batchelor and Green's solution (in 1972) to its creeping flow problem being a pioneer.88 A few studies performed experiments to verify developed theories.89,90 However, most of these studies used Coquette flow, with collision established under the influence of simple shear, and/or electric fields.91,92 In the typically applied Couette apparatus, drops were placed in the suspending liquid using a needle probe so that on applying shear and/or electric fields, they assumed trajectories and collided relative to the equatorial planes.89,93 This required a tedious drop control mechanism in order to effect collision. To ease the drop manipulation process that precedes collision, and extend the range of flows to include pure shear and extensional flows, Treatheway et al.36 and Hu et al.62 considered using the four-roll mill to generate the bulk fluid motion. Treatheway et al. complimented previous drop collision and coalescence studies in shear flow and the buoyancy-driven flows by investigating this phenomenon in a four-roll mill generated extensional flow – manipulated by an active control scheme.36 Their approach included splitting parent silicon-based Newtonian drops and trapping two equal volume daughter drops at the stagnation point of a four-roll mill generated extensional flow of castol oil, while monitoring the trajectory and collision of the droplets. This work aided the validation of existing theories for estimating trajectory, collision, and observing the dynamics of interacting spherical drops. Similarly, Yang et al.37 used the “miniaturized” four-mill roll to study the drop coalescence phenomenon but found that the predictions of Chesters' theoretical formulation76 did not quantitatively agree with their experimental results. For collisions when the initial position offset between the drops are relatively small, the measured time for film drainage was found to be shorter, and the critical capillary numbers were smaller than the predictions of the model (see Fig. 3d). Also, for larger initial drop offsets, experimentally measured film drainage was delayed relative to predictions by theoretical models.
Coalescence of polymer drops has also been carried out using the four-roll mill. Ha et al.38 extended a previous study62 on copolymer drop coalescence; by varying the viscosity ratio and using fixed copolymer interface concentrations to ensure drop size independence. The “miniaturized” computer-controlled four-roll mill was also used to investigate the coalescence process for two equal-sized polybutadiene drops suspended in polydimethylsiloxane.39,94 While some studies focused on the head-on configuration,39 others considered both head-on and glancing configurations.94
In addition to providing a means of avoiding the effect of forces, stagnation point flows also brought an improved droplet control capability to the coalescing studies. Credit for this feature can be attributed to the automation efforts during droplet deformation studies. As such, early droplet deformation studies can be seen as a prerequisite the feats achieved in coalescing studies. This is the main reason that while droplet coalescing studies are technically more complicated than deformation and break-up studies, more efforts towards miniaturization were found in the coalescence literature – Borell et al.39 and Yoon et al.94 considered droplets of 10–100 μm. However, it must be noted that neither of these studies provided details about the exact size of their four-roll mills so very little can be said about the extent of miniaturization that can be achieved with the device for applications in the microscale.
2.3 Flow birefringence of polymer
Flow birefringence describes an anisotropic state of flow – a state where flow properties depend on the direction of propagation.95,96 Using birefringence measurements, the molecular weight distribution of a polymer blend can be calculated if the molecular weight and coil-stretch relaxation time are known.97,98 Investigations on this phenomenon have been predominantly performed using the Couette-type apparatus with the solution contained within the annular gap concentric cylinders.99 However, observed polymer birefringence in these flows only slightly deform the polymer chains with a uniform intensity between the inner and outer cylinder.40 This is in contrast to the observed marked localized birefringence when the extensional and compressional flows are used for polymer birefringence.100 This revelation combined with the potential of studying birefringence in a wide range of flow types motivated the use of a four-roll mill by Crowley et al. for polymer birefringence.40 In their study, birefringence of polyethylene oxide solutions (region where polymer molecules were significantly stretched) was observed to be localized at the area close to the outgoing asymptotic plane, and held at the stagnation point, as shown in Fig. 3e. More striking, localizations were observed with the four-roll mill and this was attributed to the use of extensional flows, which elongate molecules in such a way that only elements close to the “outgoing” asymptotic axis are exposed to the field for the required amount of polymer elongation time. Subsequently, the four-roll mill was used to orient and measure the deformation response of polymers to flow fields.101 The aim of this study was to understand and ultimately characterize flow-induced changes of molecules in polymer solutions, which could dictate the eventual property of a polymer blend.102 These studies have also been predominantly motivated by the wide range of flow types the device offers, as early studies in this line had focused on just shear flows.40Using the four-roll mill generated stagnation point flow; Fuller and Leal30,31 found that the normalized birefringence of polystyrene dissolved in polychlorinated biphenyl (dilute solution) approached a saturation value at high velocity gradients, in purely extensional flows. Birefringence saturation was found to be consistent with the state where the chains are nearly fully extended, independent of concentration and molecular weight, and in agreement with theoretical estimates of Tanner.103 Transient birefringence measurements in pure extensional flows revealed that birefringence went through a pronounced overshoot in time.31 More recently, transient extension of polymers was numerically simulated and the local strain at the stagnation point proved useful in interpreting birefringence data41 and used to experimentally investigate flow instabilities as a function of Weissenberg number.104
The improved control offered by the computerized four-roll mill served as the impetus for the successful application of microfluidic stagnation point flows for birefringence studies. The highlight for this technique is that the birefringence phenomenon led to a more telling saturation – that can be interpreted as full extensions of the polymer – when confined to the plane generated by the microfluidic stagnation point. In addition to its promise as a particle extension device, this technique facilitated localized polymer examination and evolved to a classical technique for inferring the degree of polymer extension,105 to become an alternative to light scattering technique that could imply deformations of only two to four times the equilibrium size.106 As opposed to the averaging procedure adapted by the optical technique, the isolated stagnation point increased the resolution to single polymer molecules, which eliminated polymer–polymer interactions and polymer-induced alterations of the flow field. Such integrations ultimately led to an improved blending of polymer solutions, and to the discovery of an interesting overshoot phenomenon that is still an open topic in the field.31
3. Cross-slot microfluidics
In microfluidics, the cross-slot generally refers to a device with multiple channels intersecting at the center of the configuration. These devices can be used to generate microfluidic stagnation point flows of all types by concurrently injecting and withdrawing fluids through the channels. In 1979, use of the cross slot (called elongation flow cell back then) as an experimental apparatus for generating stagnation point flows came into the light as an equivalent of Taylor's four-roll mill without rollers. It served as an alternative that offered the possibility of exploiting the fine flow control in the microscale,107,108 which is otherwise complicated feat with the four-roll mill.109The archetypal microfluidic cross-slot consisted of four channels arranged in resemblance of the four arms of a cross, with flows injected via two opposite channels and concurrently aspirated out via the other two channels. Imaging of the resulting flow was performed using microscopy techniques,110 however; X-ray techniques have been reported to provide higher spatial resolution.111,112 Fig. 4a shows a schematic of this device with injection carried out via channels in the compression axis, and aspiration via channels in the elongation axis. In this configuration, when all flow rates are equal, a purely extensional flow is created and the stagnation point is formed at the center.
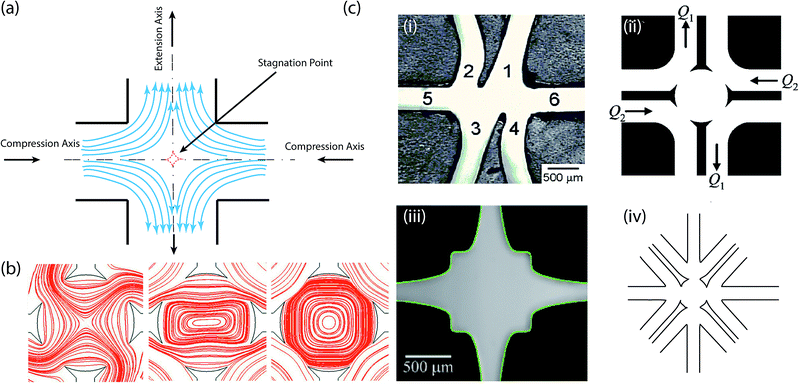 | ||
| Fig. 4 The microfluidic cross-slot device. (a) Prototypical design. (b) The application of the cross-slot microfluidic device to create stagnation point flows of all types; numerically calculated flow-type streamlines.114 Reprinted with permission. Copyright© 1976 John Wiley & Sons, Inc. (c) Geometric modification of the cross-slot microfluidic device. (i) Micrograph of the first microfluidic analog of the four-roll mill. Reprinted with permission. Copyright© AIP Publishing LLC. (ii) Schematic diagrams of a microfluidic four-roll mill devices that can generate all types of stagnation point flows shown in (b).114 Reprinted with permission. Copyright© AIP Publishing LLC. (iii) Micrograph of an optimized cross-slot geometry.116 Reprinted with permission. Copyright© 2012 American Physical Society. (iv) Schematic of a six channel cross-slot device. | ||
The use of this device can be traced back to when Scrivener et al. applied the stagnation point flow generated by the “cross flow” apparatus to investigate the dynamics of polymer molecules during birefringence.107 Although the original configuration proposed back then is still the most predominantly used today, various modifications have been made to optimize flow characteristics and extend the device's range of application. The following sections highlight key modifications of the cross-slot's configuration and trapping mechanism, report on its flow transition characteristics, and reviews its application in particle dynamics studies and DNA sequence detection.
3.1 Configurations
Over the years, several investigations have been carried out on either optimizing the typical cross-slot device or improving its range of application. In 2004, Phelan and Hudson sought a “microfluidic analog” of the four-roll mill and used a numerical approach to evaluate candidates of channel flows, which could generate the full range of linear flows.109 In their follow-up studies,108,113 they developed a nifty asymmetric configuration consisting of six intersecting channels (see Fig. 4c(i)). This configuration was derived by combining the pure stretching capability of the prototypical configuration, with rotational conformations introduced by two channels arms; offsetting the opposing arm of the four-arm configuration. However, the asymmetric nature means that pure rotational flows cannot be obtained. To overcome this, a microfluidic channel based device that keeps the stagnation point at the center, and the flow symmetric, was demonstrated (see Fig. 4c(ii)).114 This allows for generation of the full range of flow types; rotational, shear and extensional. The appropriate central cavity radius and orifice size for this device was later specified through spectral boundary element numerical simulations.115Haward et al.116 followed the recommendation of Alves' numerical optimization of the cross-slot flow geometry (see Fig. 4c(iii)),117 to facilitate an enhanced definition of the extension rate. Experiments showed that this optimized shape, provide an expansion of the inlet and outlet channels domains characterized by a nominally constant extension rate.116,118 Very recently, the configuration of the cross-slot evolved to a more complicated form, which constitutes six intersecting channels arranged in a symmetric manner (see Fig. 4c(iv)).9,119 These have been portrayed to be capable of producing an even wider range of flow patterns119 and multiple stagnation points.9
In order to minimize the fluid volumes used, the stagnation point flow generated by the cross-slot device has been combined with an oscillatory flow, to create an extensional flow oscillatory rheometer.120 Oscillation was achieved by using four micro-piezoelectric pumps situated at the end of each slot channel to provide the required repetitive flow profile. An additional advantage of this configuration lay in its clean and inert conditions that are ideal for biological samples; drawn from the enclosed cross-slot nature.121 Odell and coworker used the cross-slot configuration to measure extensional viscosity of polystyrene and hyaluronan polymer solutions.120 This application was later extended to the characterization of ultra-dilute polymer solutions, hyaluronic acid ubiquitous in the body (synovial fluid, vitreous body of eye),121 human saliva,122 closely mono-disperse atactic polystyrene,123 and for chaotic mixing.124,125 A pulsatile micro pump, based on a deflecting diaphragm, has also been recently designed and tested for the setup.126
Furthermore, the stagnation point formed by other crossed micro channels i.e. the “T” and “Y” geometries, have also been used to trap particles,127 break droplets,128 study adsorption kinetics,129 and visualize flow streamline for preferential real time blood plasma separation.130 More recently, parallel flow channels have been used to develop stagnation points in separating flows, to achieve high deformation rates and ease stagnation point control,131 and stagnation points from 3D cross slot devices have been modeled.132 Theoretical and experimental investigations on these types of flow can be found in ref. 133–137. This review is focused on isolated stagnation point flows – stagnations generated away from walls – exclusively.
In general, advancements in the physical configuration of the cross-slot have mostly focused on miniaturization and geometrical modifications. While miniaturization efforts have been motivated by microfluidic applications, studies have explored the potential of creating more stable and/or increased number of stagnation points by modifying the cross-slot's geometry and including opto-electronic systems. However, regardless of the modification implemented, the hydrodynamic implication has always been key; miniaturization facilitated microfluidic applications and geometrical changes had an implication of more complex flow structures.
3.2 Trapping and manipulation
Interest in trapping and manipulating micro-particles lies in their use for organizing complex structures out of micrometer-scale particles; or in other words, making order out of disorder. Such methods hold a great potential in developing complex aggregates, where micro-particles or cells of varying formulation, sizes, and shapes can be put together into new types of biological assemblies, possibly forming novel materials, in a bottom up bio-fabrication procedures.138–140 In doing so, a great deal of control can be exercised over the properties of assembled entity. The common route to achieving this is self-assembly,140–142 which could be driven by DNAs,143,144 particle wettability and shape,145 Fisher's lock and key principle,146,147 and electric field actuation.148,149 Other existing means for trapping and manipulating micro-particles include optical,150,151 dielectrophoresis,152,153 optoelectronics,154,155 acoustic,156,157 and magnetic tweezers.158,159 The drawbacks of these methods are that their complicated control mechanisms often rely on multi-physics interactions, which could interact with the particle to obscure properties. However, using pure hydrodynamic forces as traps, and potentially manipulators, for micro-particles has proved to be an attractive alternative for non-contact trapping and manipulation of single cells in suspensions.160 Compared to other methods, manipulating micro- or nano-particles in this way can make the process simpler, and broader in steering range. These enable new capabilities like placement of specific quantum dots to desired chips with nanoscale precision.161A wealth of fundamental studies have been carried out on demonstrating the operation and increasing the efficiency of purely hydrodynamic control of the stagnation generated by the cross-slot device, for the purpose of particle trapping, manipulation and assembly. In 2002, the stagnation point flow generated by a T-junction network, was used to study the deposition of bacteria (Marinobacter hydrocarbonoclasticus, Psychrobacter sp. and Halomonas pacifica, suspended in artificial seawater); in view of investigating the effect of deposition efficiency of different technologies.162 The study concluded that, in comparison to the parallel plate deposition technique, the stagnation point flow chamber has higher deposition rate and better reproducibility, but lower deposition efficiency. Such studies are relevant in examining the influence of marine coating properties on formation of biofilms on marine vessels,163,164 which is a serious problem in the shipping industry.165,166
Schroeder et al. featured cross-slot configuration, together with T-, V-, and Y-junctions channel flows, for stagnation point based particle trapping device.167 The system was described as a pressure controlled, particle confining tool using stagnation points generated in a channel flow, with a feedback control system – which used the instantaneous position of the trapped object to adjust the flow rates at each channel – in order to keep the particle confined for an indefinite length of time; without an optical trap, micropipette or other tethering device. They suggested applications of this stagnation point flow in biology, chemistry, physics, material science, and medical sciences.
Defining the microfluidic cross-slot as a “microfluidic four-roll mill”, Lee et al.114 used experiments and simulations to demonstrate how the device can be used to generate all types of flows; extensional, shear or rotational flows (see Fig. 4b). Their study suggested the application of the device in examining the dynamics of single cells and micro-drops for enhancing mixing efficiency.114 In separate studies, the device was also shown to be applicable in trapping and manipulating quantum dots168 and multiple particles simultaneously.169,170 Subsequently, the confinement of particles as small as 100 nm, with up to 1 μm of resolution, for more than 10 minutes was demonstrated.171,172 The achieved resolution and extended trapping period was enabled by their active feedback control, which was programmed to guide the particle back to the set point position of stagnation (see Fig. 5a–c). Although many previous studies had managed to trap the particle for an extended period of time, the absence of this type of feedback control – a system originally suggested by Bentley34 – meant that Brownian fluctuations would eventually cause the particle to escape. The control mechanism operated with an image acquisition device, a particle-tracking algorithm to determine the movement of the particle away from the set centroid position, and an active adjustment pneumatic valve for the adjustment of fluid flow based on the position of the particle.173 The application of this control system was only on the extensional direction, since the flow in the compressional direction is intrinsically stable.174 The feedback control algorithm adjusted a valve constriction based on a linear equation relating the particle's hydrodynamic forces to its distance from the stagnation point.175 To fully automate the system, calibration of the trap's response as a function of flow control valve characteristics and channel dimensions were also performed.175 A detailed description of the experimental setup for generating this feedback-controlled stagnation can be found in ref. 173.
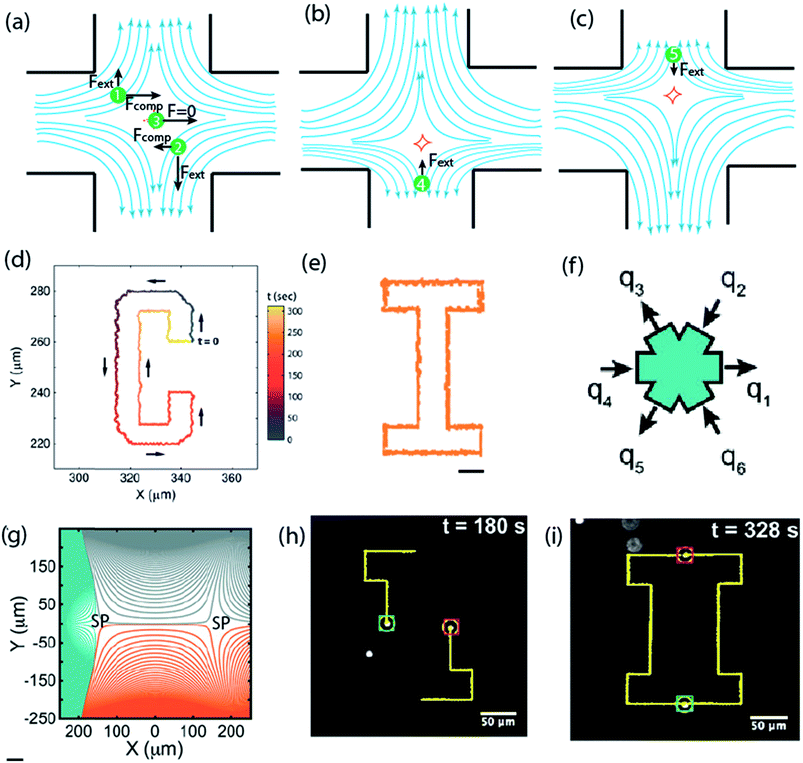 | ||
| Fig. 5 Microfluidic stagnation points for manipulation of single and multiple particles. (a) Schematics showing forces acting on particles at different positions within the vicinity stagnation point flow. In the compressional axis, the particle 1 and 2 experience an attractive force propelling them towards the stagnation point in the center, and an extension force pulling them away in the extensional axis. Particle 3 is positioned at the stagnation point and has a zero net force. (b & c) Use of feedback control system to steer particle back to the stagnation point by adjusting outlet flows.171,172 Reprinted with permission. Copyright© AIP Publishing LLC. (d) Sample trajectory of a single 2.2 μm diameter Nile red fluorescent polystyrene bead using the cross-slot microfluidic trap. Trajectory was set to spell the letter “C”. Micromanipulation starts at t = 0 and ends when the particle returns to the initial point at t = 300 s.176 Reprinted with permission. Copyright© 2013, American Chemical Society. (e) Trajectory set to draw the letter “I”. Scale bar is 10 μm.176 Reprinted with permission. Copyright© 2013, American Chemical Society. (f) Schematic of the six channel cross-slot with relative magnitude and direction of the flow rates for generating the streamline topologies in (g). (g) Numerically obtained streamlines showing the linked-arms topology, generated when all flow rates are identical. Two stagnation points are clearly visible (denoted as SP).9 Reprinted with permission. Copyright PNAS. (h and i) Snap shots demonstrating the manipulation of the paths of two 2.2 μm beads to trace the letter I. Yellow line showing the spatial history of both particles.9 Reprinted with permission. Copyright PNAS. | ||
The very fine degree to which the microfluidic stagnation point can be controlled and manipulated, with the aid of the feedback control system, was demonstrated by Tanyeri et al.176 As a proof-of-concept, the study used the microfluidic stagnation point to trap and manipulate 500 nm and 2.2 μm diameter particles in two-dimensions, with a positioning precision as small as 180 nm during confinement (see Fig. 5d and e).176 The spring constant of the flow-based particle-micromanipulation technique was shown to scale linearly with particle size and viscosity of the medium, which offers the possibility for facile trapping of small nanoparticles in free solutions.176 Characterization of the effect of strain rate on particle confinement and effective trap potential were further used to demonstrate the importance of strain rate on the trap performance and the minimum size of particle that can be trapped.176
Shenoy et al.174 investigated the performance of the cross-slot based stagnation trap using three different controllers – the proportional (P), proportional-integral (PI), and proportional-derivative (PD) controllers. Trap performance was quantified by examining the magnitude of particle fluctuation as functions of controller gain constant, system response time, and particle Peclet number. This revealed that the proportional and derivative controllers yield improvements in trap stability, while the integral controllers does not.
Advancements of the stagnation capability of the cross-slot setup to trap and manipulate multiple particles,9 and sequentially assemble particles,177 have also been reported. The device for multiple particle trapping constitutes a systematic charging and discharging of fluid from a six channel cross-slot, in such a way that two stagnation points are generated (see Fig. 5f and g).9 Typically, the controllers used are a combination of proportional-integral-differential (PID), but this study suggests that the “integral” component does not necessarily improve trap efficiency. Development of the multiple trapping capability was achieved using the model predictive control (MPC) algorithm for a more robust control strategy, with 5–7 times increase in trap stiffness compared to previous generation traps. Using these, simultaneous confinement and manipulation of two particles to switch center of mass positions and draw shapes were achieved. Fig. 5h and i shows transient photographs of devices operation in drawing the letter I with both particles trajectory paths. Similarly, a sequential assembly algorithm was demonstrated to be applicable in sequentially joining particles, trapped in a seven-slot channel generated microfluidic stagnation point, to arrange particles in the form of all of the English alphabets in 2-D. The study suggested that to achieve same in 3-D, eleven slots will be required.177
An unanswered question in these studies is the actual stabilization time of the particles at the stagnation point. As stabilization time and strain rate are expected to affect the overall scanning speed, they are key considerations for this tool's effectiveness for micro particle manipulation. Estimates suggest that the patterns of Fig. 5d and e were drawn in about 300 seconds, which seems long for a moderate throughput micro fluidic device and hence leaves some room for improvement. The size of particles that have been trapped suggest that the device can be used to trap even cells as small as the sperm cell but no indication has been made to the maximum particle size that can be accommodated.
3.3 Flow transitions
Flow birefringence has been observed for a range of multiple polymers using the cross-slot microfluidics, experimentally,178 and numerically.179 Attention to the phenomenon started when Arratia et al.180 reported two distinct transitions in an extensional cross-slot flow of flexible polyacrylamide solutions, at low Reynolds number (<10−2). The first transition led to a spatial break of symmetry and bi-stability (see Fig. 6), while the second produced broadband temporal fluctuations. Similar asymmetric positioning was also observed in T-junction microfluidics. However, it was not observed in semi rigid polymer solutions.181 Although no conclusion was made regarding the origin of this asymmetric arrangement, the study presented a theory on how the arrangements can be controlled by stretching polymer molecules near the hyperbolic point. Before then, such phenomena had never been observed in either experimental or numerical investigations. This could be attributed to the small range of Reynolds number (Re) mostly considered by experiments before then, and the symmetry approximations commonly adapted in numerical studies; where only one-quarter of the full-geometry is modeled.182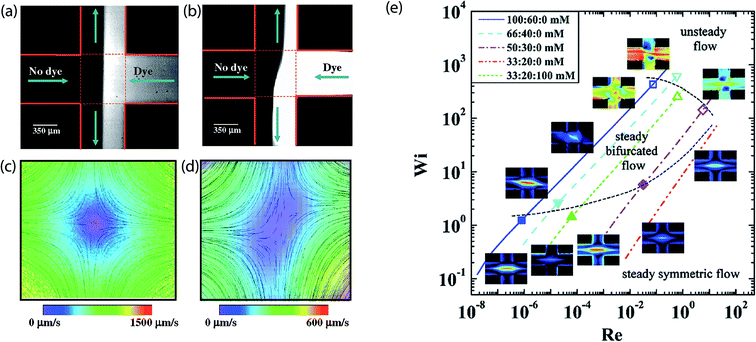 | ||
| Fig. 6 Studying flow instabilities using the microfluidic stagnation point flow of the cross-slot. (a) Dye advection pattern for a low Re cross-slot stagnation point flow. (b) Flexible polyacrylamide solution flow pattern deformed by instability. (c) Particle streak lines and velocity field magnitudes corresponding to (a). Stagnation point position (indicated by white box) is centralized. (d) Particle streak lines and velocity field magnitudes corresponding to (b) showing the symmetry-breaking instability.180 Stagnation point position (indicated by white box) skewed because of the instability. Reprinted with permission. Copyright© 2006, American Physical Society. (e) Stability diagram for cetylpyridinium chloride mixed with sodium salicylate and sodium chloride (CPyCl:NaSal:NaCl) solutions in the cross slot stagnation point flow. Solid symbols denote the beginning of pure elastic flow instabilities while the hollow symbols denote the beginning of inertia-elastic flow instabilities.184 Reprinted with permission. Copyright© 2012 American Physical Society. | ||
Haward and McKinley shed more light into the asymmetric and unstable transitions using elongation flows generated by their optimized cross-slot geometry.183 Using flow birefringence observations, their study characterized the cross-slot flows as functions of Weissenberg (Wi) and elasticity numbers 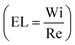 , by varying the type of solutions and flow rates passed through the device. In flows with EL > 1, asymmetric steady elastic flows were observed beyond a critical Weissenberg number (Wicrit), in correlation to previous findings.180 However, beyond a critical Re (EL < 1), rather than a single instability, a sequence of transient instabilities was observed. These instabilities were characterized by high frequency spatiotemporal oscillations of the birefringent strand.
, by varying the type of solutions and flow rates passed through the device. In flows with EL > 1, asymmetric steady elastic flows were observed beyond a critical Weissenberg number (Wicrit), in correlation to previous findings.180 However, beyond a critical Re (EL < 1), rather than a single instability, a sequence of transient instabilities was observed. These instabilities were characterized by high frequency spatiotemporal oscillations of the birefringent strand.
In recent microfluidic cross-slot based experiments, the other classes of solution that have exhibited these asymmetric and unstable transitions are high EL and low viscosity ratio wormlike micellar of poorly defined extensibility.184–186 In 2006, wormlike micelles187 were portrayed as a macromolecule suitable for single-chain dynamics in the cross-slot produced stagnation point flow.188,189 Initial applications of wormlike micelles in these experiments were limited to investigations on coil-stretch transition, the alignment kinetics, and macromolecular conformations.188 However, a transition of the observed birefringence to an asymmetric flow at higher Re, then unstable and time dependent flows at much higher Re, was soon reported by Pathak and Hudson.189 This is in accordance with Arratia et al.180 reports but the quantitative difference between saturation stress-optical coefficient and Wi for two different wormlike micelles – cetyltrimethylammonium bromide or cetylpyridinium chloride in aqueous sodium salicylate – could not be conclusively explained.
Haward et al.186 later performed cross-slot based experiments on similar solutions used by Pathak and Hudson189 but used a smaller cross-slot device and presented more detailed experimental results; obtained over a much broader range of Wi. Their study also utilized a deep cross-section cross-slot, so as to obviate the effect of shear along the channel walls. Both transitions – steady asymmetric and transient unstable – were also observed in this study, but the instabilities were suggested to be influenced by the micellar fluid shear localization within the micro channels and around the re-entrant corners of the cross-slot. This claim was substantiated by the formation of lip vortices along the walls of the inlet channels, reported by Dubash and coworkers.185 In a later study, Haward and McKinley184 extended the rheological properties of the examined micellar fluid – by varying the zero-shear viscosity over three orders of magnitude – and investigated the resulting changes in dynamical response. The extensional properties and critical conditions for the start of flow instabilities in the fluids were shown to be reliant on the fluid formulation. By plotting Wi as a function of Re for all considered solutions, their report presented a stability diagram outlining the steady symmetric, steady asymmetric and inertia-elastic flow regimes (see Fig. 6e), which covered a wider range of Wi and Re than that presented in their previous study.183
Arratia et al.180 findings also motivated full sized numerical models over a wide range of flow parameters and qualitatively revealed similar transitions190–192 using the modeled full cross-slot geometry. It was also showed numerically that introducing a small degree of curvature to the cross-slot corners has no influence upon the transitions.182
Although a general concession has not been reached on the origin of these transitions, based on findings mostly facilitated by the microfluidic stagnation point, it is widely accepted that they are complex phenomena, which are influenced by a combination of factors such as Wi, inertial effects, and rheological behavior of the micellar solutions.185 A more detailed explanation was offered by Haward and McKinley who attributed the phenomena to extensional stresses overcoming entropic elasticity as the velocity gradient at the stagnation point exceeds the reciprocal of the characteristic relaxation time; such that Wi exceeds unity.184 This can result in a significant extension and alignment of any deformable microstructural constituents of the fluid. Such stretching and orientation effects can result in significant increases in the fluid extensional viscosity and, when inertia is not significant, can give rise to purely elastic instabilities.184
3.4 Particle dynamics studies
Following the pioneering work of Scrivener et al. in 1979, the cross-slot generated extensional flow was used to demonstrate trapping and flow-induced fracture of mono-disperse atactic polystyrene (a-PS) chains in a controlled manner.107,193 One of the main highlights of the study is the accuracy at which these chains break at their center. This work was extended to explore the effect of chemical composition, chain length and force magnitude on the fracture mechanisms of the chains,194 and the use of the stretched macromolecule to examine molecular weight distribution, dimensions and draining characteristics chains.105 During this period (1970–1990), many extensional flow based particle dynamics studies were carried out and a review of some of their experimental results can be found in the literature.195 Simplified models of polymer strands in a cross flow were also used to predict birefringence behavior that portrayed good agreement with experiments.196,197Experimental use of the cross-slot generated stagnation point flow for particle dynamics studies resurfaced in the 1990's when it was used in studying single polymer dynamics and stretching.106,198 Perkins et al.106 used this setup to decouple the effects of strain rate and time on the conformation and extension of single polymer molecules. Amongst other heterogeneity in polymer dynamics, they observed that polymer chains with a dumbbell shape stretched more rapidly than folded ones. This led to deductions that the shapes of stretched macromolecules (e.g. dumbbell, folded, coiled, kinked) is highly dependent on the initial conformation (see Fig. 7), which has been corroborated by other studies.199,200 In Perkins's study, the polymers were introduced through the cross-slots, and hence, were exposed to velocity gradients prior to entrapment at the stagnation point.106 This methodology led to concerns relating to the thermal equilibrium state of the polymer before the inception of the elongation flow, which might have caused the observed heterogeneity. Smith et al.198 circumvented this by initiating the cross-slot based stagnation point flow with the polymer coils at rest in the observation region and by using a higher viscosity solvent. Although heterogeneities in polymer dynamics were still observed, their investigation led to a quantitative understanding of how the initial state of the polymer can lead to elongated appearances of different conformations, and these quantitatively agreed with Brownian dynamics simulations.201
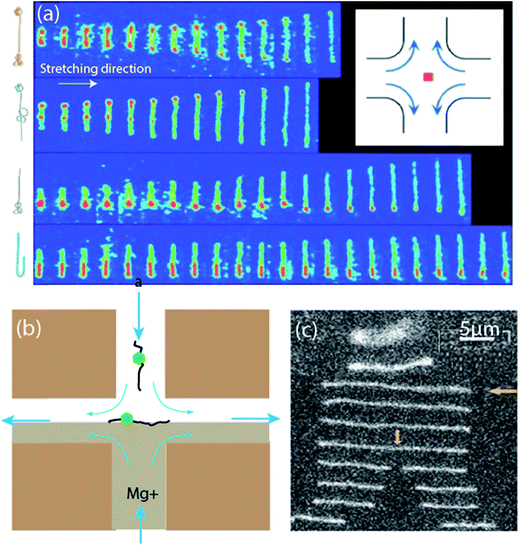 | ||
| Fig. 7 Cross-slot stagnation point flow as a DNA trapping stretching device. (a) DNA elongating in the stagnation point flow showing the effects of initial polymer conformation on the time-dependent extension of single DNA molecules. Top to bottom: dumbbell, kinked, half-dumbbell, and folded conformations (sketches of molecular configurations are included on the left). Time between images is 0.13 seconds. Inset: cross-slot device and the position of the stagnation point trap.106 Reprinted with permission. Copyright© 1997, The American Association for the Advancement of Science. (b) Schematic for single DNA sequence detection with stagnation point flow. Flow direction denoted by blue arrows. DNA–enzyme complexes flow via the top slot, while Mg2+ solution flows via the bottom slot. DNA–enzyme complex trapped at the stagnation point and elongated along the extensional axis.203 (c) Photographs of molecular configurations with non-uniform time intervals (smallest time interval, at cleavage, is 100 ms) to show the trapping, stretching and subsequent cleavage of dsDNA.203 Reprinted with permission. Copyright© 2010, Royal Society of Chemistry. | ||
By adapting the feedback control loop, the cross-slot based flow was used to decouple the effect of initial conformation, length, strain rate and Deborah number, on the extension dynamics of Escherichia coli (E. coli) DNA polymer chains.202 Results showed that the extended conformation of the polymer depends on the conformation dependent hydrodynamic forces and deformation. The control system provided long-term stability of the polymer's physical properties, which afforded long observation duration of the molecules.
Following these groundbreaking investigations, the cross-slot generated flow was also adapted for techniques in investigating cell deformability,204,205 polymersome dynamics,206 break up of CNT bundles,207 stretch-coil instabilities,208 solution dynamics,110,118,209 extensional viscosity,120 DNA stretching/compaction,210,211 and polymer rheology.123,212–216 Using this device, cell deformability measurements were achieved by harnessing cell concentrations by viscoelastic micro flows of polymer solution,204 CNT breakup was attained by simply increasing flow rates,207 drop deformation was examined as a function of confinement,209 and DNA compaction was triggered by introducing Na+ and polyethylene glycol (PEG) to the DNA molecules held at the stagnation point.210
Of the aforementioned applications, one particularly interesting use of the cross-slot generated stagnation is for the precise control of droplet coalescence,217 while generating multiple emulsions; a concept that hold a lot of promise in pharmaceutics.218 Wang et al. suggested that the simple cross-slot generated flow field is inadequate to accurately control the coalescence of multiple droplets; hence they adapted the geometry of Fig. 4c(iv) and developed numerical methodologies to investigate the rheology of multiple emulsions.217,219,220 In their work, they numerically demonstrated the use of cross-slot flow control techniques to precisely engineer the adhesion of single drops to form bigger drops – even to the point of dictating the angle of contact.217 By adjusting the extensional and compressional flow towards the stagnation point, they were able to achieve location specific consecutive coalescence of multiple droplets.
The extensional flow of the oscillating cross-slot device has also been recently used to quantitatively assess cell mechanical damage in an extensional field, which is relevant in designing practical bioreactors.221 The cells were deformed at the stagnation point of the cross-slot that mimic the extensional flow produced during the bubble bursting process. This process consists of film receding, film impact and upward/downward jet formations—cell-damaging mechanics inherent in conventional agitation based bioreactors used to homogenize culturing medium.222–224 Although, the bioreactors flow includes shear and extensional flow components,225 the extensional component has been demonstrated to have a greater effect on cell.224,226 Their experiments suggest that the critical extensional stress for Chinese hamster ovary (CHO) cells is 250 Pa, which is less than the numerically estimated stress induced by bubble bursting (632.8 Pa).221 This quantitatively indicates that extensional stresses in bioreactors can be critical to mechanical cell damage.
3.5 Target sequence detection
One of the earliest uses of the microfluidic cross-slot generated stagnation point flow in biomedicine was directed toward a single-molecule genotyping assay; for detecting DNA target sequences and marker position.227,228 To achieve this, tagged DNA molecules were trapped at the stagnation point, elongated by the extensional flow, and directly observed with a microscope. Previous methods of doing this involve immobilizing the DNAs on surfaces, and stretching them using surface chemistries favoring the adsorption of DNA as a fluid meniscus recedes.229 However, the stagnation point flow approach potentially offers a purely hydrodynamic technique for continuous on-chip genotype assay. This potential was demonstrated by using the cross-slot to view sequences in images of trapped DNA–beads hybrids and peaked intensities signifying the position of the beads.227 Comparing the accuracy of the microfluidic technique to that of stretching on slides shows that although the slide stretching is more accurate in detecting target sequences, the stagnation point flow technique results in a 50% reduction in the detection's standard deviation.In view of improving detection accuracy, Xu and Muller extended their earlier study by introducing enzyme pre-bound in the investigated dsDNA and then introducing Mg2+ required for dsDNA cleavage.203 Upon linearizing the DNA–enzyme complex at the stagnation point, cofactor Mg2+ is introduced and the binding location of the enzyme are determined by optical restriction mapping without surface immobilization of the DNAs (see Fig. 7b and c). The accuracy of this technique in sequence detection was found to be comparable to other single molecule techniques. In addition, the technique offers a means of simultaneously obtaining kinetic information for all DNA recognition sites in the same process.
While previous applications of the stagnation point have focused on trapping and translating the particle as a whole, particle stretching presents another functional feature of the microfluidic stagnation point flow concept. The capability of isolating the induced strain rates to that applied by the flow field – avoiding the contribution of wall shearing effects – allows for a fine control of the stretching rates. This again highlights the appeal of microfluidic stagnation point flows in this particular biological field and hence, its prospects for application in commercial integrated on-chip devices.
4. Open space microfluidics
Microfluidic systems that operate in the “open space” – without the need for the sealed channels and chambers commonly used in microfluidics – is an emerging class of fluid localization technique that isolates chemical reactions on biological samples without imposing significant “constraints”, like encapsulation, pre-processing steps, or the need for scaffolds.44 This is achieved by eliminating walls and channels in microfluidic devices. Stagnation points have also been produced using these open microfluidic setups, and these are covered in the following section.4.1 Opposed jets
Opposed jets, as the name implies, is a configuration of two oppositely directed fluid streams in an immersed surrounding solution. Depending on the intended application, the jets could be made to oppose via impinging, or via suction flows to produce either compressional or extensional flows, respectively.230,231 The concept was originally conceived as a premixed flame stabilization technique,232–234 due to the uniform strain rate inherent in the flow produced by the counter jets235,236 – which is normally not the case for a regular flame surface.237,238 According to Schaffer and Cambel,232 the stability of the flame so maintained, is ascribed to the existence of a small reaction zone around the stagnation point of the jet. The opposed jet setup was also adapted as an experimental technique for investigating the stability of diffusion flames, where the gaseous fuel and oxidant coaxial jets are opposed to produce a flame at their junction (stagnation plane).239–242 For a more detailed description of the early adaptations of opposed jets, one of the earliest review of the topic can be found in ref. 243. In this line of research, studies adapted the apparatus in studying non-equilibrium anomalies,244 chemical kinetics,245,246 numerical modeling approaches,247 and flame structures.248 Existence of a reaction zone at the stagnation point also serves as the stabilizing mechanism in diffusion flames;240 with the flame tilting to the oxidant side of the stagnation plane.240,249The flow generated by opposed jets have also been adapted in studying purely homogeneous kinetics of endothermic reactions;250 particularly in metal–organic chemical vapor deposition (MOCVD) of compound semiconductors.251,252 During the conventional MOCVD of semiconductors, growth of a thin solid film is achieved by passing a gas mixture over a heated substrate. This involves both homogeneous reactions in the gas phase near the heated substrate and surface reactions on the substrate.250,253 The use of opposed-jets based reactors for such studies stems from the need to decouple the effects of surface and gas-phase kinetics during MOCVD. In the opposed-jet setup, reactions can be confined near the stagnation point and away from hot surfaces by controlling the jet velocities.250 Furthermore, by adjusting flow rates, residence time of species and the location of the reaction zone can be adjusted, which allows for the detection of the onset of homogeneous thermal decomposition.250
Although the stagnation plane formed by opposed jets were originally only significant as the reference plane for rapid and effective mixing in fluid reactors,254 these flows have also been adapted for particle dynamics studies. Frank and co-workers adapted this apparatus for producing compressional and extensional flows (see Fig. 8a) for studying polythene birefringence in xylene solution, as a function of temperature.255 This concept was later highlighted as an extensional flow apparatus,105,256 for performing rheological changes,257 flow induced molecular scission,258 and coil-stretch transition.259,260 Subsequently, the Rheometrics RFX laboratory apparatus was produced using opposed nozzles through which liquid is sucked or ejected from a reservoir, as an elongation flow analyzer.261 The device was used to make extensional viscosity measurements as a function of strain rate262 and polymer solution.263
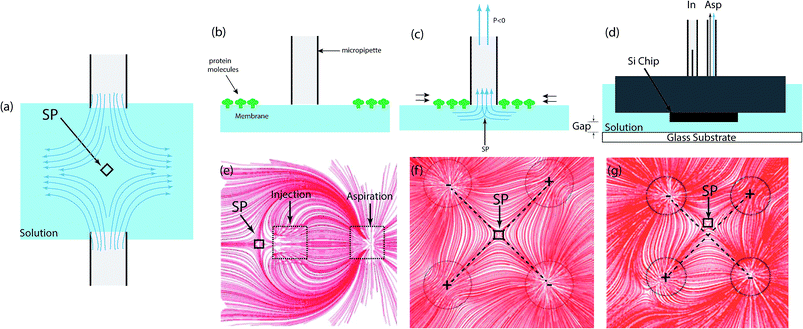 | ||
| Fig. 8 Microfluidic stagnation point flows in open microfluidics. (a) Schematic drawing of an opposed-jets apparatus in “push mode,” which generates a uniaxial compressional flow along the stagnation point axis. The jets can also be inverted into “sucking mode” in order to generate a biaxial extensional flow. (b) Pipette placed above the membrane.267 (c) Negative hydrostatic pressure results in fluid flow into the pipette. The subsequent fluid flow causes a stagnation point to form beneath the pipette and molecules to gather and trapped at the tip of the pipette.267 (d) Schematic representation of the two-aperture MFP. The MFP is set close to the glass substrate and the fluid is injected and fully aspirated from the capillary tubes, which makes the injected flow hydro-dynamically confined. (e) Numerically calculated streamlines of the two-aperture MFP flow showing the confinement area and stagnation point (SP). The stagnation position (R) is defined as the distance between the center of the MFP and the stagnation point.275 Reprinted with permission. Copyright© 2015, Rights Managed by Nature Publishing Group. (f) Numerical deduced streamlines of the microfluidic quadrupole. The stagnation point is at the center of the flow when the both flow rates ratio (aspiration flow/ injection flow) are identical. (g) Streamline of the microfluidic quadrupole demonstrating manipulation of the stagnation point's position. Varying flow rate ratio moves the stagnation point from the center in the XY plane. | ||
Advantages of the opposed-jet setup (see Fig. 8a) include, the ability to generate relatively large velocity gradients,264 and its applicability for a wide range of concentrations and fluids.264,265 However, these are overshadowed by the difficulty of obtaining high-resolution images of the flow field in the setup, and its requirement for relatively large fluid volumes.97 Furthermore, the device's measurement of extensional viscosity were labeled as “3 times greater than the real value” due to the effect of dynamic pressure, nozzle shear and liquid inertia.266
4.2 Microfluidic pipettes
Microfluidic pipettes are a unique technology that use hydrodynamically confined flows to carry out a variety of complex functions like mixing, multiplexing, or gradient generation. These devices are capable of handling and dispensing solutions in cellular and sub-cellular levels, and some of their advantageous features include easy positioning, and compatibility with standard cell cultures and laboratory methods.The use of these devices for microfluidic stagnation point flows is relatively sparse in the literature, but there are exemplar studies that highlight the simplicity of the setup that can be used for this application. A conical microfluidic pipette – in the form of a single conical tube – was demonstrated to be applicable as a trap for 5 nm large protein molecules (Streptavidin) bound to biotin receptors on a supported lipid bilayer, based on the stagnation point flow formed below the pipette's tip.267 In that study, this was achieved by positioning the pipette, of about 1 micrometer tip radius, above the lipid bilayer and applying a negative pressure difference to cause a net flow of fluid through the pipette and an accumulation of protein molecules around the tip of the pipette (see Fig. 8b and c). The method was presented as a means of experimentally obtaining protein dynamics information and quantifying the intermolecular forces between molecules bound to a membrane; as long as the membrane can be approached by a pipette.267
Ainla et al. also demonstrated the use of a similar principle to deposit vesicles adhered to a film, at the stagnation point of a three-aperture on-chip multifunctional micropipette.268,269 In this configuration, injection is through the middle aperture while aspiration through the two outer apertures. This causes the vesicles to be trapped beneath the aspiration aperture, and upon switching the middle aperture to high aspiration, the vesicles are drawn into the channel opening. Using this multifunctional pipette, a variety of complex microfluidic processing operations, such as mixing, multiplexing, writing, erasing, functionalizing on a substrate, or gradient generation at the single cell level, can be achieved at high resolution.270,271 Its use in multiple-compound delivery for pharmacological screening of intact adherent cells was demonstrated by applications in activating hTRPV1 receptors in single cells, and exposing specific cells to formaldehyde/dithiothreitol-containing solutions.270 It was also used to electroporate single-cells,272 and administer pharmacological active substances to selected areas on brain slices.273,274
4.3 Microfluidic probes
The microfluidic probe (MFP) is a multi-aperture, mobile and channel-less microfluidic system, which operates by concurrently injecting fluid and aspirating from a surrounding immersion liquid.275 Fig. 8d and e show representations of the setup and flow profile of the conventional two-aperture MFP. More details on the MFP's assembly, operation, and theoretical formulation of the MFP can be found in ref. 276 and 277. The configuration of the two-aperture MFP generates a stagnation point when the injected stream get pulled back and split equally by the hydrodynamically confined flow (HCF) forces that are generated by the aspiration flow rate, given the small confinement gap between the MFP and the bottom substrate (see Fig. 8e). Some applications of the two-aperture MFP include bio-patterning surfaces,278 delivery of reagents to reaction site,279 selective detachment and collection of a living single cell,278 and analyzing tissue samples.280,281 Applications of the three-aperture and four-aperture MFPs/micropipttes have also been reported for single cell analyses,271,282 local lysis of live adherent cells,283 surface processing and patterning,284–286 region-selective micro-treatment of cells,287 and studying cell interactions.288 In addition, the potential of the convective–diffusive concentration gradient289 generated by the MFP in studying neutrophils chemotaxis – phenomenon that describes the dynamic nature of the immune defense barrier against infections290–292 – has also been demonstrated.293,294The stagnation point flow generated by the four-aperture MFP is typically referred to as the microfluidic quadrupole (MQ).284,295–297 The flow field of the conventional MQ is reminiscence of the classical quadrupolar electrostatic field (see Fig. 8f), and is also very similar to that generated by the four-roll mill and the cross-slot. However, the absence of channels in the MFP means that there is no wall induced shear stress in the planar flow, which is an impeccable condition to study shear effect on cells and tissues in cases where shear stresses play an important role.295,298 A typical example of this is the transduction of applied shear stress stimulus by endothelial cells and neutrophils, into intracellular responses in order to regulate the vessel structure.299,300
Although no record of the explicit application of the MFP generated stagnation point was found, precise control of the location of the stagnation point has been demonstrated (see Fig. 8g),284 combining its maneuverability and open space nature, huge promise for the applications demonstrated with the four roll mill and the cross-slot stagnations is evident. However, for any practical application, based on the instability of the stagnation point demonstrated by earlier microfluidic stagnation devices, a similar automated feedback control system might have to be designed and implemented for the MFP.
5. Summary and perspectives
Over a century has passed since Prandtl formulated the boundary layer theory and described its significance in estimating drag and flow streamlines.4,5 Since then, the concept of fluidic stagnation has evolved from a theoretical concept in aerodynamics, to a useful tool for trapping and manipulating micro-particles. Numerous studies have focused on the effect of the stagnation region formed at fluid–solid interfaces on aerodynamics5,301 and heat transfer.302 In comparison to vast literature on the boundary layer stagnation, literature on the constructive use of isolated microfluidic stagnation point flows is limited.This review presented a summary on the generation techniques and application of microfluidic stagnation point flows. In general, to experimentally generate and examine microfluidic stagnation point flow, the following equipment are required: (1) flow generation (injection and suction) and control devices (injector, pressure controller or rolling mills); (2) a reservoir to store fluids; (3) a chip configuration of converging-diverging flow pairs and; (4) an optical microscope. Some setups also include a stage for precise translation of the stagnation point, and a feedback control system for improved stagnation stability. The microfluidic stagnation flow can then be generated by connecting one end of each reservoir to a flow generation device, connecting the other end to each channel of the converging–diverging flow chip, and applying appropriate flow rates in each channel. Upon mounting the chip on the stage of an optical microscope, the flow profiles and stagnation points can be visualized with the aid of fluorescence beads. Readers can refer to the literature for precise setups and methodologies for the individual techniques discussed.10,176,267,284 In terms of applications, the use of stagnation points for performing droplet characterization studies, trapping and manipulation of cells and polymers, and investigating flow instabilities were discussed. The devices that have been used for generating these flows all lend principles from the pioneering four-roll mill.10 Early applications of the four-roll mill were inclined towards investigations on the primary mechanisms governing droplet dynamics with an aim of engineering emulsions and polymers. Today, the cross-slot deduced stagnation point flows represent the most advanced applications of microfluidic stagnations; from trapping micro-objects, to studying flow instabilities and stretching DNAs. Table 1 summarizes the features and applications of each microfluidic stagnation point flow device.
| Device | Key applications | Key biological applications | Proven particle size | Section | Key references |
|---|---|---|---|---|---|
| Four-roll mill | Emulsion and polymer engineering | — | 800–2000 μm | 2 | 10, 26, 34, 39, and 56 |
| Cross slot microfluidics | Polymer science and single particle manipulation | DNA trapping and stretching | 100 nm to 2.2 μm | 3 | 9, 114, 171, 176, 203, 210, and 228 |
| Micropipettes | Single particle deposition and manipulation, localized bio-patterning | Protein molecules trapping; cell electroporation | 5 nm | 4.2 | 267, 268, 270, 272, 282, and 288 |
| Microfluidic probe | Single particle manipulation, micropatterning, and concentration gradient generation | Shear-stress studies on cells; protein patterning, and neutrophil chemotaxis studies | 20 μm | 4.3 | 275, 278, 280, 284, 285, and 295 |
The single most important feature of the microfluidic stagnation point flow lay in its ability to incubate the analysis in an environment in interaction with only one external field – hydrodynamics of the surrounding flow. As such, by manipulating this hydrodynamic field, precise stimulus can be applied on the sample with assurance that the observed effects can be directly correlated with the applied stimuli. In the early days of this concept, the naturally instable nature of the stagnation point presented a frustration that was immediately fixed by the introduction of a feedback control system. This development unleashed the full capability of the concept, and starting from its classic macroscopic forms, it has been a consequential tool for optimizing the parameters for synthesizing emulsions, polymer blending and birefringence. However, the bulky nature and dynamic-parts of the four roll mill presented an obvious drawback towards miniaturization. The cross-slot device, often termed the microfluidic four-roll mill was developed to avert this problem. Its simple design and straightforward fabrication technique propelled several applications that later led to the successful trapping and manipulation of nanoparticles, with a very fine degree of precision. This led to one of its first biology applications in trapping and stretching DNA for detecting target sequences. However, the cross-slot is associated with its own drawbacks – akin to most of classical “closed-channel” microfluidic devices – which is its reliance on channel flows with walls/boundaries that restricts its maneuverability and might induce shear stresses on the analysis region. Although still fledgling, the advent of open space microfluidics (i.e. opposed jets, micropipettes, & MFPs) and the MQ mitigated these issue, and presented immense promise for the future.
The development of microfluidic stagnation point has undoubtedly come a long way. The concept has shown some promise for single cell analysis – trapping of 100 nm particles171,172 with very minimal wall shear stress at the stagnation point have been demonstrated.284 Yet, biological applications are still very limited. This sparse application in biological research can be attributed to the relatively unstable nature of its stagnation point that require complicated feedback control mechanisms, and the potential cell damage that can occur when high flow rates in channel based microfluidic chips induce significant wall shear stresses at vicinity of the stagnation point.
The MFP and micropipettes recently entered the scene of generating microfluidic stagnation points however, explicit practical applications are lacking. Majority of studies stopped at demonstrating the existence of microfluidic stagnation points,284 while others did not even give the generated stagnation point any considerations.271,282 One might now expect the adjunct open space microfluidic and MQ concepts would lead the way for microfluidic stagnation points to become fully integrated as lab-on-a-tip devices for μTAS and new innovative biomedical applications. But to achieve this, future works must learn from the developmental phase of the concept – the absence of external fields, simple designs, and precise stagnation control are key features that cannot be compromised. While the open space microfluidic devices incubates the sample from external fields and have relatively simple designs, the feedback control mechanism adapted by previous devices might have to be significantly simplified before it can be integrated into a single miniaturized analytical tool.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Ayoola T. Brimmo acknowledges NYUAD Global PhD Fellowship, and the authors acknowledge financial support from New York University Abu Dhabi (NYUAD).References
- R. W. Fox, A. T. McDonald and P. J. Pritchard, Introduction to Fluid Mechanics, John Wiley & Sons, New York, 1985, vol. 7 Search PubMed
.
- G. A. Tokaty, A History and Philosophy of Fluid Mechanics, Courier Corporation, Mineola, New York, 1971 Search PubMed
.
- C. M. Ho and S. H. Chen, Unsteady Kutta Condition of a Plunging Airfoil, in Unsteady Turbulent Shear Flows, Springer, Berlin, 1981 Search PubMed
.
- J. D. Anderson, Ludwig Prandtl's Boundary Layer, Phys. Today, 2005, 58(12), 42–48 CrossRef
.
- H. Schlichting and K. Gersten, Boundary-Layer Theory, Springer-Verlag, Berlin Heidelberg, 2003, vol. 8 Search PubMed
.
- S. F. Hoerner, Fluid-Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance, Hoerner Fluid Dynamics, Midland Park, NJ, US, 1965 Search PubMed
.
- M. J. Lighthill, Contributions to the Theory of Heat Transfer through a Laminar Boundary Layer, Proc. R. Soc. London, Ser. A, 1950, 202(1070), 359–377, DOI:10.1098/rspa.1950.0106
.
- J. A. Fay and F. R. Riddell, Theory of Stagnation Point Heat Transfer in Dissociated Air, J. Aeronaut. Sci., 1958, 25(2), 73–85 Search PubMed
.
- A. Shenoy, C. V. Rao and C. M. Schroeder, Stokes Trap for Multiplexed Particle Manipulation and Assembly Using Fluidics, Proc. Natl. Acad. Sci. U. S. A., 2016, 201525162 Search PubMed
.
- G. I. Taylor, The Formation of Emulsions in Definable Fields of Flow, Proc. R. Soc. London, Ser. A, 1934, 146(858), 0501–0523, DOI:10.1098/rspa.1934.0169
.
- G. M. Whitesides, The Origins and the Future of Microfluidics, Nature, 2006, 442(7101), 368–373, DOI:10.1038/nature05058
.
- T. M. Squires and S. R. Quake, Microfluidics: Fluid Physics at the Nanoliter Scale, Rev. Mod. Phys., 2005, 77(3), 977–1026, DOI:10.1103/RevModPhys.77.977
.
- C. J. Pipe and G. H. McKinley, Microfluidic Rheometry, Mech. Res. Commun., 2009, 36(1), 110–120, DOI:10.1016/j.mechrescom.2008.08.009
.
- D. J. Beebe, G. A. Mensing and G. M. Walker, Physics and Applications of Microfluidics in Biology, Annu. Rev. Biomed. Eng., 2002, 4(1), 261–286, DOI:10.1146/annurev.bioeng.4.112601.125916
.
- H. A. Stone, A. D. Stroock and A. Ajdari, Engineering Flows in Small Devices: Microfluidics toward a Lab-on-a-Chip, Annu. Rev. Fluid Mech., 2004, 36, 381–411, DOI:10.1146/annurev.fluid.36.050802.122124
.
- P. Gravesen, J. Branebjerg and O. S. Jensen, Microfluidics-a Review, J. Micromech. Microeng., 1993, 3(4), 168 CrossRef CAS
.
- H. Andersson and A. VanDenBerg, Microfluidic Devices for Cellomics: A Review, Sens. Actuators, B, 2003, 92(3), 315–325 CrossRef CAS
.
- Y. Zhang and P. Ozdemir, Microfluidic DNA Amplification—a Review, Anal. Chim. Acta, 2009, 638(2), 115–125 CrossRef CAS PubMed
.
- P. Abgrall and A. M. Gue, Lab-on-Chip Technologies: Making a Microfluidic Network and Coupling It into a Complete Microsystem—a Review, J. Micromech. Microeng., 2007, 17(5), R15 CrossRef
.
- L. Gervais, N. De Rooij and E. Delamarche, Microfluidic Chips for Point-of-Care Immunodiagnostics, Adv. Mater., 2011, 23(24), H151–H176 CrossRef CAS PubMed
.
- S. Saleh-Lakha and J. T. Trevors, Perspective: Microfluidic Applications in Microbiology, J. Microbiol. Methods, 2010, 82(1), 108–111, DOI:10.1016/j.mimet.2010.03.022
.
- S. Haeberle and R. Zengerle, Microfluidic Platforms for Lab-on-a-Chip Applications, Lab Chip, 2007, 7(09), 1094–1110 RSC
.
- A. Mukherjee and C. M. Schroeder, Microfluidic Methods for Molecular Biology, in Microfluidic Methods in Single Cell Biology, Switzerland, 2016, pp. 19–54 Search PubMed
.
- J. Nilsson, M. Evander, B. Hammarstrom and T. Laurell, Review of Cell and Particle Trapping in Microfluidic Systems, Anal. Chim. Acta, 2009, 649(2), 141–157, DOI:10.1016/j.aca.2009.07.017
.
- R. R. Lagnado, N. Phanthien and L. G. Leal, The Stability of Two-Dimensional Linear Flows, Phys. Fluids, 1984, 27(5), 1094–1101, DOI:10.1063/1.864755
.
- R. R. Lagnado and L. G. Leal, Visualization of Three-Dimensional Flow in a Four-Roll Mill, Exp. Fluids, 1990, 9, 25–32 CrossRef CAS
.
- H. A. Barnes and J. M. Maia, Rheometry, in Rheology, Encyclopedia of Life Support Systems (EOLSS), 2010, pp. 331–362 Search PubMed
.
- C. W. Macosko, M. A. Ocansey and H. H. Winter, Steady Planar Extensions with Lubricated Dies, J. Non-Newtonian Fluid Mech., 1982, 11, 301–316 CrossRef CAS
.
- J. M. Dealy, Extensional Flow of Non-Newtonian Fluids—a Review, Polym. Eng. Sci., 1961, 11(6), 433–445 Search PubMed
.
- G. G. Fuller and L. G. Leal, Flow Birefringence of Dilute Polymer Solutions in Two-Dimensional Flows, Rheol. Acta, 1980, 19, 580–600 CrossRef CAS
.
- G. G. Fuller and L. G. Leal, Flow Birefringence of Concentrated Polymer Solutions in Two-Dimensional Flows, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 557–587 CrossRef CAS
.
- F. D. Rumscheidt and S. G. Mason, Suspensions Xii. Deformation and Burst of Fluid Drops in Shear and Hyperbolic Flow, J. Colloid Sci., 1961, 16(3), 238–261 CrossRef CAS
.
- H. P. Grace, Dispersion Phenomena in High Viscosity Immiscible Fluid Systems and Application of Static Mixers as Dispersion in Such Systems, Chem. Eng. Commun., 1982, 14, 225–277 CrossRef CAS
.
- B. J. Bentley and L. G. Leal, A Computer-Controlled Four-Roll Mill for Investigations of Particle and Drop Dynamics in Two-Dimensional Linear Shear Flows, J. Fluid Mech., 1986, 167, 219–240 CrossRef CAS
.
- B. J. Bentley and L. G. Leal, An Experimental Investigation of Drop Deformation and Breakup in Steady, Two-Dimensional Linear Flows, J. Fluid Mech., 1986, 167, 241–283 CrossRef CAS
.
- D. C. Tretheway, M. Muraoka and L. G. Leal, Experimental Trajectories of Two Drops in Planar Extensional Flow, Phys. Fluids, 1999, 11(5), 971–981, DOI:10.1063/1.869969
.
- H. Yang, C. C. Park, Y. T. Hu and L. G. Leal, The Coalescence of Two Equal-Sized Drops in a Two-Dimensional Linear Flow, Phys. Fluids, 2001, 13(5), 1087–1106, DOI:10.1063/1.1358873
.
- J. W. Ha, Y. Yoon and L. G. Leal, The Effect of Compatibilizer on the Coalescence of Two Drops in Flow, Phys. Fluids, 2003, 15(4), 849–867, DOI:10.1063/1.1555803
.
- M. Borrell, Y. Yoon and L. G. Leal, Experimental Analysis of the Coalescence Process Via Head-on Collisions in a Time Dependent Flow, Phys. Fluids, 2004, 16(11), 3945–3953 CrossRef CAS
.
- D. G. Crowley, F. C. Frank, M. R. Mackley and R. G. Stephenson, Localized Flow Birefringence of Polyethylene Oxide Solutions in a Four-Roll Mil, J. Polym. Sci., Polym. Phys. Ed., 1976, 14, 1111–1119 CrossRef CAS
.
- J. Feng and L. G. Leal, Transient Extension and Relaxation of a Dilute Polymer Solution in a Four-Roll Mill, J. Non-Newtonian Fluid Mech., 2000, 90(1), 117–123, DOI:10.1016/S0377-0257(99)00052-X
.
- J. Deschamps, V. Kantsler, E. Segre and V. Steinberg, Dynamics of a Vesicle in General Flow, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(28), 11444–11447, DOI:10.1073/pnas.0902657106
.
- M. Levant, J. Deschamps, E. Afik and V. Steinberg, Characteristic Spatial Scale of Vesicle Pair Interactions in a Plane Linear Flow, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(5 Pt 2), 056306, DOI:10.1103/PhysRevE.85.056306
.
- V. Narayanamurthy, S. Nagarajan, F. Samsuri and T. M. Sridhar, Microfluidic Hydrodynamic Trapping for Single Cell Analysis: Mechanisms, Methods and Applications., Anal. Methods, 2017, 9, 3751 RSC
.
- G. V. Kaigala, R. D. Lovchik and E. Delamarche, Microfluidics in the “Open Space” for Performing Localized Chemistry on Biological Interfaces, Angew. Chem., Int. Ed., 2012, 51(45) CrossRef CAS PubMed
.
- E. N. Horsford, Report on Vienna Bread, Government Printing Office, Washington, 1875 Search PubMed
.
- L. Rayleigh, On the Instability of Jets, Proc. Lond. Math. Soc., 1878, 1(1), 4–13 CrossRef
.
- J. W. Strutt and L. Rayleigh, On the Instability of Jets, Proc. Lond. Math. Soc., 1878, 10, 4 Search PubMed
.
- S. Tomotika, On the Instability of a Cylindrical Thread of a Viscous Liquid Surrounded by Another Viscous Fluid, Proc. R. Soc. London, Ser. A, 1935, 150(8790), 322–337 CrossRef
.
- J. O. Hinze, Fundamentals of the Hydrodynamic Mechanism of Splitting in Dispersion Processes, AIChE J., 1955, 1(3), 289–295, DOI:10.1002/aic.690010303
.
- J. W. Ha and L. G. Leal, An Experimental Study of Drop Deformation and Breakup in Extensional Flow at High Capillary Number, Phys. Fluids, 2001, 13(6), 1568–1576, DOI:10.1063/1.1358306
.
- J. M. Rallison, The Deformation of Small Viscous Drops and Bubbles in Shear Flows, Annu. Rev. Fluid Mech., 1984, 16(1), 45–66 CrossRef
.
- J. M. Rallison, Note on the Time-Dependent Deformation of a Viscous Drop Which Is Almost Spherical, J. Fluid Mech., 1980, 98, 625–633, DOI:10.1017/S0022112080000316
.
- H. A. Stone, Dynamics of Drop Deformation and Breakup in Viscous Fluids, Annu. Rev. Fluid Mech., 1994, 26(1), 65–102, DOI:10.1146/annurev.fluid.26.1.65
.
- S. Torza, R. G. Cox and S. G. Mason, Particle Motions in Sheared Suspensions Xxvii. Transient and Steady Deformation and Burst of Liquid Drops, J. Colloid Interface Sci., 1972, 38(2), 395–411 CrossRef CAS
.
- M. V. Berry and M. R. Mackley, The Six Roll Mill: Unfolding an Unstable Persistently Extensional Flow, Philos. Trans. R. Soc., A, 1977, 287(1337), 1–16 CrossRef
.
- D. L. Barthes-Biese and A. Acrivos, Deformation and Burst of a Liquid Droplet Freely Suspended in a Linear Shear Field, J. Fluid Mech., 1973, 61, 1–21 CrossRef
.
- E. J. Hinch and A. Acrivos, Steady Long Slender Droplets in Two-Dimensional Straining Motion, J. Fluid Mech., 1979, 91, 401–414 CrossRef
.
- J. M. Rallison, A Numerical Study of the Deformation and Burst of a Viscous Drop in General Shear Flows, J. Fluid Mech., 1981, 109, 465–482 CrossRef CAS
.
- H. A. Stone and L. G. Leal, The Influence of Initial Deformation on Drop Breakup in Subcritical Time-Dependent Flows at Low Reynolds Numbers., J. Fluid Mech., 1989, 206, 223–263 CrossRef CAS
.
- Y. Pawar and K. J. Stebe, Marangoni Effects on Drop Deformation in an Extensional Flow: The Role of Surfactant Physical Chemistry. I. Insoluble Surfactants, Phys. Fluids, 1996, 8(7), 1738–1751 CrossRef CAS
.
- Y. T. Hu, D. J. Pine and L. G. Leal, Drop Deformation, Breakup, and Coalescence with Compatibilizer, Phys. Fluids, 2000, 12(3), 484–489, DOI:10.1063/1.870254
.
- Y. T. Hua and A. Lips, Determination of Viscosity from Drop Deformation, J. Rheol., 2001, 45(6), 1453–1463 CrossRef
.
- Y. T. Hu and A. Lips, Transient and Steady State Three-Dimensional Drop Shapes and Dimensions under Planar Extensional Flow, J. Rheol., 2003, 47(2), 349–369, DOI:10.1122/1.1545078
.
- W. J. Milliken and L. G. Leal, Deformation and Breakup of Viscoelastic Drops in Planar Extensional Flows, J. Non-Newtonian Fluid Mech., 1991, 40(3), 355–379, DOI:10.1016/0377-0257(91)87018-S
.
- C. E. Chaffey, A Second-Order Theory for Shear Deformation of Drops, J. Colloid Interface Sci., 1967, 24(2), 258–269 CrossRef CAS
.
- R. G. Cox, The Deformation of a Drop in a General Time-Dependent Fluid Flow, J. Fluid Mech., 1969, 37(3), 601–623 CrossRef
.
- N. A. Frankel and A. Acrivos, The Constitutive Equation for a Dilute Emulsion, J. Fluid Mech., 1970, 44(01), 65–78 CrossRef
.
- S. Guido and F. Greco, Drop Shape under Slow Steady Shear Flow and During Relaxation. Experimental Results and Comparison with Theory, Rheol. Acta, 2001, 40(2), 176–184, DOI:10.1007/s003970000144
.
- J. J. Higdon, The Kinematics of the Four-Roll Mill, Phys. Fluids A, 1993, 5(1), 274–276 CrossRef CAS
.
- P. L. Maffettone and M. Minale, Equation of Change for Ellipsoidal Drops in Viscous Flow, J. Non-Newtonian Fluid Mech., 1998, 78(2–3), 227–241, DOI:10.1016/S0377-0257(98)00065-2
.
- E. D. Wetzel and C. L. Tucker, Droplet Deformation in Dispersions with Unequal Viscosities and Zero Interfacial Tension, J. Fluid Mech., 2001, 426, 199–228, DOI:10.1017/S0022112000002275
.
- Y. Y. Wu, A. Z. Zinchenko and R. H. Davis, Ellipsoidal Model for Deformable Drops and Application to Non-Newtonian Emulsion Flow, J. Non-Newtonian Fluid Mech., 2002, 102(2), 281–298, DOI:10.1016/S0377-0257(01)00183-5
.
- U. Sundararaj and C. W. Macosko, Drop Breakup and Coalescence in Polymer Blends: The Effects of Concentration and Compatibilization, Macromolecules, 1995, 28(8), 2647–2657 CrossRef CAS
.
- J. Qian and C. K. Law, Regimes of Coalescence and Separation in Droplet Collision, J. Fluid Mech., 1997, 331, 59–80, DOI:10.1017/S0022112096003722
.
- A. K. Chesters, The Modelling of Coalescence Processes in Fluid-Liquid Dispersions: A Review of Current Understanding, Chem. Eng. Res. Des., 1991, 68(A4), 259–270 Search PubMed
.
- P. R. Brazier-Smith, S. G. Jennings and J. Latham, The Interaction of Falling Water Drops: Coalescence, Proc. R. Soc. London, Ser. A, 1972, 326(1566), 393–408 CrossRef
.
- S. Guido and M. Simeone, Binary Collision of Drops in Simple Shear Fow by Computer-Assisted Video Optical Microscopy, J. Fluid Mech., 1998, 357, 1–20 CrossRef CAS
.
- T. Ban, F. Kawaizumi, S. Nii and K. Takahashi, Study of Drop Coalescence Behavior for Liquid–Liquid Extraction Operation, Chem. Eng. Sci., 2000, 55(22), 5385–5391 CrossRef CAS
.
- J. J. Elmendorp and A. K. Van der Vegt, A Study on Polymer Blending Microrheology: Part Iv. The Influence of Coalescence on Blend Morphology Origination, Polym. Eng. Sci., 1986, 26(19), 1332–1338 CAS
.
- V. E. Ziegler and B. A. Wolf, Bimodal Drop Size Distributions During the Early Stages of Shear Induced Coalescence, Polymer, 2005, 46(22), 9265–9273 CrossRef CAS
.
- H. Wang, A. Z. Zinchenko and R. H. Davis, The Collision Rate of Small Drops in Linear Flow Fields, J. Fluid Mech., 1994, 265, 161–188 CrossRef CAS
.
- M. Loewenberg and E. J. Hinch, Collision of Two Deformable Drops in Shear Flow, J. Fluid Mech., 1997, 338, 299–315, DOI:10.1017/S0022112097005016
.
- A. Z. Zinchenko, M. A. Rother and R. H. Davis, A Novel Boundary-Integral Algorithm for Viscous Interaction of Deformable Drops, Phys. Fluids, 1997, 9(6), 1493–1511, DOI:10.1063/1.869275
.
- D. J. Jeffrey and Y. Onishi, Calculation of the Resistance and Mobility Functions for Two Unequal Rigid Spheres in Low-Reynolds-Number Flow, J. Fluid Mech., 1984, 139, 261–290 CrossRef
.
- S. Haber, G. Hetsroni and A. Solan, On the Low Reynolds Number Motion of Two Droplets, Int. J. Multiphase Flow, 1973, 1(1), 57–71 CrossRef
.
- A. Z. Zinchenko, The Slow Asymmetric Motion of Two Drops in a Viscous Medium, J. Appl. Math. Mech., 1980, 44(13), 30–37 CrossRef
.
- G. K. Batchelor and J. T. Green, The Hydrodynamic Interaction of Two Small Freely-Moving Spheres in a Linear Flow Field, J. Fluid Mech., 1972, 56(2), 375–400 CrossRef
.
- P. A. Arp and S. G. Mason, The Kinetics of Flowing Dispersions: Ix. Doublets of Rigid Spheres (Experimental), J. Colloid Interface Sci., 1977, 61(1), 44–61 CrossRef CAS
.
- W. Bartok and S. G. Mason, Particle Motions in Sheared Suspensions: V. Rigid Rods and Collision Doublets of Spheres, J. Colloid Sci., 1957, 12(3), 243–262 CrossRef CAS
.
- P. M. Adler, Interaction of Unequal Spheres: III. Experimental, J. Colloid Interface Sci., 1981, 84(2), 489–496 CrossRef CAS
.
- P. A. Arp, R. T. Foister and S. G. Mason, Some Electrohydrodynamic Effects in Fluid Dispersions, Adv. Colloid Interface Sci., 1980, 12(4), 295–356 CrossRef
.
- C. L. Darabaner, J. K. Raasch and S. G. Mason, Particle Motions in Sheared Suspensions Xx: Circular Cylinders, Can. J. Chem. Eng., 1967, 45(1), 3–12 CrossRef CAS
.
- Y. Yoon, M. Borrell, C. C. Park and L. G. Leal, Viscosity Ratio Effects on the Coalescence of Two Equal-Sized Drops in a Two-Dimensional Linear Flow, J. Fluid Mech., 2005, 525, 355–379, DOI:10.1017/S0022112004002824
.
- W. Philippoff, Flow Birefringence and Stress, J. Appl. Phys., 1956, 27, 984 CrossRef CAS
.
- P. G. DeGennes, Coil-Stretch Transition of Dilute Flexible Polymers under Ultrahigh Velocity Gradients, J. Chem. Phys., 1974, 60, 5030 CrossRef CAS
.
- S. J. Haward, Microfluidic Extensional Rheometry Using Stagnation Point Flow, Biomicrofluidics, 2016, 10(4) DOI:10.1063/1.4945604
.
- S. J. Haward, Synovial Fluid Response to Extensional Flow: Effects of Dilution and Intermolecular Interactions, PLoS One, 2014, 9(3), e92867, DOI:10.1371/journal.pone.0092867
.
- R. Cerf and H. A. Scheraga, Flow Birefringence in Solutions of Macromolecules, Chem. Rev., 1952, 51(2), 185–261, DOI:10.1021/cr60159a001
.
- M. R. Mackley and A. Keller, Flow Induced Polymer Chain Extension and Its Relation to Fibrous Crystallization, Philos. Trans. R. Soc. London, Ser. A, 1975, 278(1276), 29–66 CrossRef CAS
.
- P. N. Dunlap and L. G. Leal, Dilute Polystyrene Solutions in Extensional Flows: Birefringence and Flow Modification, J. Non-Newtonian Fluid Mech., 1987, 23, 5–48 CrossRef CAS
.
- S. B. Kharchenko, J. F. Douglas, J. Obrzut, E. A. Grulke and K. B. Migler, Flow-Induced Properties of Nanotube-Filled Polymer Materials, Nat. Mater., 2004, 3(8), 564–568 CrossRef CAS PubMed
.
- R. I. A. Tanner, Test Particle Approach to Flow Classification for Viscoelastic Fluids, AIChE J., 1976, 22(5), 910–918 CrossRef CAS
.
- B. Liu, M. Shelley and J. Zhang, Oscillations of a Layer of Viscoelastic Fluid under Steady Forcing, J. Non-Newtonian Fluid Mech., 2012, 175, 38–43 CrossRef
.
- A. Keller and J. A. Odell, The Extensibility of Macromolecules in Solution; a New Focus for Macromolecular Science, Colloid Polym. Sci., 1985, 263(3), 181–201 CAS
.
- T. T. Perkins, D. E. Smith and S. Chu, Single Polymer Dynamics in an Elongational Flow, Science, 1997, 276(5321), 2016–2021 CrossRef CAS PubMed
.
- O. Scrivener, C. Berner, R. Cressely, R. Hocquart, R. Sellin and N. S. Vlachos, Dynamical Behaviour of Drag-Reducing Polymer Solutions, J. Non-Newtonian Fluid Mech., 1979, 5, 475–495 CrossRef CAS
.
- S. D. Hudson, F. R. Phelan Jr, M. D. Handler, J. T. Cabral, K. B. Migler and E. J. Amis, Microfluidic Analog of the Four-Roll Mill, Appl. Phys. Lett., 2004, 85(2), 335–337 CrossRef CAS
.
- F. R. Phelan and S. D. Hudson, Modeling of a Microfluidic Analog of the Four-Roll Mill for Materials Characterization, in ANTEC Conference Proceedings Society of Plastics Engineers, 2004, pp. 1054–1058 Search PubMed
.
- S. J. Haward, A. Jaishankar, M. S. N. Oliveira, M. A. Alves and G. H. McKinley, Extensional Flow of Hyaluronic Acid Solutions in an Optimized Microfluidic Cross-Slot Device, Biomicrofluidics, 2013, 7(4), 044108 CrossRef CAS PubMed
.
- J. Penfold, E. Staples, I. Tucker, P. Carroll, I. Clayton, J. S. Cowan, G. Lawton, S. Amin, A. Ferrante and N. Ruddock, Elongational Flow Induced Ordering in Surfactant Micelles and Mesophases, J. Phys. Chem. B, 2006, 110(2), 1073–1082, DOI:10.1021/jp051122m
.
- M. Kisilak, H. Anderson, N. S. Babcock, M. R. Stetzer, S. H. J. Idziak and E. B. Sirota, An X-Ray Extensional Flow Cell, Rev. Sci. Instrum., 2001, 72(11), 4305–4307, DOI:10.1063/1.1412259
.
- F. R. Phelan, S. D. Hudson and M. D. Handler, Fluid Dynamics Analysis of Channel Flow Geometries for Materials Characterization in Microfluidic Devices, Rheol. Acta, 2005, 45(1), 59–71 CrossRef CAS
.
- J. S. Lee, R. Dylla-Spears, N. P. Teclemariam and S. J. Muller, Microfluidic Four-Roll Mill for All Flow Types, Appl. Phys. Lett., 2007, 90(7), 074103, DOI:10.1063/1.2472528
.
- J. Wang, J. Han and D. Yu, Numerical Studies of Geometry Effects of a Two-Dimensional Microfluidic Four-Roll Mill on Droplet Elongation and Rotation, Eng. Anal. Bound. Elem., 2012, 36(10), 1453–1464 CrossRef
.
- S. J. Haward, M. S. Oliveira, M. A. Alves and G. H. McKinley, Optimized Cross-Slot Flow Geometry for Microfluidic Extensional Rheometry, Phys. Rev. Lett., 2012, 109(12), 128301, DOI:10.1103/PhysRevLett.109.128301
.
- M. A. Alves, Design of a Cross-Slot Flow Channel for Extensional Viscosity Measurements, Proceedings of the XVth International Congress on Rheology, ed. L. G. Leal, R. H. Colby and A. J. Giacomin, American Institute of Physics, Monterey, 2008 Search PubMed
.
- A. H. Motagamwala, A Microfluidic, Extensional Flow Device for Manipulating Soft Particles, 2013 Search PubMed
.
- J. Guan, J. Liu, X. D. Li, J. Tao and J. T. Wang, Stokes Flow in a Two-Dimensional Micro-Device Combined by a Cross-Slot and a Microfluidic Four-Roll Mill, Z. Angew. Math. Phys., 2015, 66(1), 149–169, DOI:10.1007/s00033-013-0396-z
.
- J. A. Odell and S. P. Carrington, Extensional Flow Oscillatory Rheometry, J. Non-Newtonian Fluid Mech., 2006, 137(1–3), 110–120, DOI:10.1016/j.jnnfm.2006.03.010
.
- S. J. Haward, V. Sharma and J. A. Odell, Extensional Opto-Rheometry with Biofluids and Ultra-Dilute Polymer Solutions, Soft Matter, 2011, 7(21), 9908–9921, 10.1039/c1sm05493g
.
- S. J. Haward, J. A. Odell, M. Berry and T. Ha, Extensional Rheology of Human Saliva, Rheol. Acta, 2011, 50(11), 869–879 CrossRef CAS
.
- S. J. Haward, J. A. Odell, Z. Li and X. F. Yuan, Extensional Rheology of Dilute Polymer Solutions in Oscillatory Cross-Slot Flow: The Transient Behaviour of Birefringent Strands, Rheol. Acta, 2010, 49(6), 633–645, DOI:10.1007/s00397-009-0420-6
.
- F. R. Phelan Jr, N. R. Hughes and J. A. Pathak, Chaotic Mixing in Microfluidic Devices Driven by Oscillatory Cross Flow, Phys. Fluids, 2008, 20(2), 023101 Search PubMed
.
- F. R. Phelan, P. Kutty and J. A. Pathak, An Electrokinetic Mixer Driven by Oscillatory Cross Flow, Microfluid. Nanofluid., 2008, 5(1), 101–118, DOI:10.1007/s10404-007-0231-y
.
- R. C. van der Burgt, P. D. Anderson, J. M. den Toonder and F. N. Van De Vosse, A Microscale Pulsatile Flow Device for Dynamic Cross-Slot Rheometry, Sens. Actuators, A, 2014, 220, 221–229 CrossRef CAS
.
- A. R. Wheeler, W. R. Throndset, R. J. Whelan, A. M. Leach, R. N. Zare, Y. H. Liao, K. Farrell, I. D. Manger and A. Daridon, Microfluidic Device for Single-Cell Analysis, Anal. Chem., 2003, 75(14), 3581–3586 CrossRef CAS PubMed
.
- D. R. Link, S. L. Anna, D. A. Weitz and H. A. Stone, Geometrically Mediated Breakup of Drops in Microfluidic Devices, Phys. Rev. Lett., 2004, 92(5), 054503, DOI:10.1103/PhysRevLett.92.054503
.
- J. C. Dijt, M. A. C. Stuart, J. E. Hofman and G. J. Fleer, Kinetics of Polymer Adsorption in Stagnation Point Flow, Colloids Surf., 1990, 51, 141–158, DOI:10.1016/0166-6622(90)80138-T
.
- S. Yang, A. Undar and J. D. Zahn, A Microfluidic Device for Continuous, Real Time Blood Plasma Separation, Lab Chip, 2006, 6(7), 871–880, 10.1039/b516401j
.
- G. Dockx, T. Verwijlen, W. Sempels, M. Nagel, P. Moldenaers, J. Hofkens and J. Vermant, Simple Microfluidic Stagnation Point Flow Geometries., Biomicrofluidics, 2016, 10(4), 043506 CrossRef PubMed
.
- A. Lanzaro, D. Corbett and X. F. Yuan, Non-Linear Dynamics of Semi-Dilute Paam Solutions in a Microfluidic 3d Cross-Slot Flow Geometry, J. Non-Newtonian Fluid Mech., 2017, 242, 57–65 CrossRef CAS
.
- M. G. Perera and K. Walters, Long-Range Memory Effects in Flows Involving Abrupt Changes in Geometry: Part I: Flows Associated with I-Shaped and T-Shaped Geometries, J. Non-Newtonian Fluid Mech., 1977, 2(1), 49–81 CrossRef
.
- T. Nishimura, K. Nakamura and A. Horikawa, Two-Dimensional Viscoelastic Flow of Polymer Solution at Channel Junction and Branch, J. Text. Mach. Soc. Jpn., 1987, 33(2), 37–45 Search PubMed
.
- T. Nishimura, K. Nakamura and A. Horikawa, Two-Dimensional Viscoelastic Flow of Polymer Solution at Channel Junction and Branch, J. Text. Mach. Soc. Jpn., 1985, 31(1), 1–6 Search PubMed
.
- D. M. Binding, K. Walters, J. Dheur and M. J. Crochet, Interfacial Effects in the Flow of Viscous and Elasticoviscous Liquids, Philos. Trans. R. Soc. London, Ser. A, 1987, 323(1573), 449–469 CrossRef
.
- B. Thomases, M. Shelley and J. L. Thiffeault, A Stokesian Viscoelastic Flow: Transition to Oscillations and Mixing, Phys. D, 2011, 240(20), 1602–1614 CrossRef
.
- H. A. Stone, Particle Assembly from Fluids, Physics, 2011, 4, 17 CrossRef
.
- B. A. Parviz, D. Ryan and G. M. Whitesides, Using Self-Assembly for the Fabrication of Nano-Scale Electronic and Photonic Devices, IEEE Trans. Adv. Packag., 2003, 26(3), 233–241, DOI:10.1109/Tadvp.2003.817971
.
- S. Zhang, Fabrication of Novel Biomaterials through Molecular Self-Assembly, Nat. Biotechnol., 2013, 21(10), 1171–1178 CrossRef PubMed
.
- G. M. Whitesides and B. Grzybowski, Self-Assembly at All Scales, Science, 2002, 295(5564), 2418–2421, DOI:10.1126/science.1070821
.
- G. M. Whitesides, J. P. Mathias and C. T. Seto, Molecular Self-Assembly and Nanochemistry: A Chemical Strategy for the Synthesis of Nanostructures (No. Tr-45), CA, MA, 1991 Search PubMed
.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-Based Method for Rationally Assembling Nanoparticles into Macroscopic Materials, Nature, 1996, 382(6592), 607–609 CrossRef CAS PubMed
.
- R. Häner, F. Samain and V. L. Malinovskii, DNA-Assisted Self-Assembly of Pyrene Foldamers, Chem.–Eur. J., 2009, 15(23), 5701–5708 CrossRef PubMed
.
- N. Bowden, A. Terfort, J. Carbeck and G. M. Whitesides, Self-Assembly of Mesoscale Objects into Ordered Two-Dimensional Arrays, Science, 1997, 276(5310), 233–235, DOI:10.1126/science.276.5310.233
.
- E. Fischer, Einfluss Der Configuration Auf Die Wirkung Der Enzyme, Ber. Dtsch. Chem. Ges., 1894, 27(3), 2985–2993 CrossRef CAS
.
- S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Lock and Key Colloids, Nature, 2010, 464(7288), 575–578, DOI:10.1038/nature08906
.
- O. Englander, D. Christensen, J. Kim, L. Lin and S. J. Morris, Electric-Field Assisted Growth and Self-Assembly of Intrinsic Silicon Nanowires, Nano Lett., 2005, 5(4), 705–708, DOI:10.1021/nl050109a
.
- A. Winkleman, B. D. Gates, L. S. McCarty and G. M. Whitesides, Directed Self-Assembly of Spherical Particles on Patterned Electrodes by an Applied Electric Field., Adv. Mater., 2005, 17(12), 1507–1511 CrossRef CAS
.
- A. Ashkin and J. M. Dziedzic, Optical Trapping and Manipulation of Viruses and Bacteria, Science, 1987, 235(4795), 1517–1520 CAS
.
- H. Zhang and K. K. Liu, Optical Tweezers for Single Cells., J. R. Soc., Interface, 2008, 5(24), 671–690 CrossRef CAS PubMed
.
- N. G. Green, H. Morgan and J. J. Milner, Manipulation and Trapping of Sub-Micron Bioparticles Using Dielectrophoresis, J. Biochem. Biophys. Methods, 1997, 35(2), 89–102, DOI:10.1016/S0165-022x(97)00033-X
.
- J. Voldman, R. A. Braff, M. Toner, M. L. Gray and M. A. Schmidt, Holding Forces of Single-Particle Dielectrophoretic Traps, Biophys. J., 2001, 80(1), 531–541, DOI:10.1016/S0006-3495(01)76035-3
.
- A. T. Ohta, P. Y. Chiou, T. H. Han, J. C. Liao, U. Bhardwaj, E. R. B. McCabe, F. Q. Yu, R. Sun and M. C. Wu, Dynamic Cell and Microparticle Control Via Optoelectronic Tweezers, J. Microelectromech. Syst., 2007, 16(3), 491–499, DOI:10.1109/Jmems.2007.896717
.
- M. C. Wu, Optoelectronic Tweezers, Nat. Photonics, 2011, 5(6), 322–324 CrossRef CAS
.
- J. Shi, D. Ahmed, X. Mao, S. C. Lin, A. Lawit and T. J. Huang, Acoustic Tweezers: Patterning Cells and Microparticles Using Standing Surface Acoustic Waves (Ssaw), Lab Chip, 2009, 9(20), 2890–2895 RSC
.
- C. R. Courtney, C. E. Demore, H. Wu, A. Grinenko, P. D. Wilcox, S. Cochran and B. W. Drinkwater, Independent Trapping and Manipulation of Microparticles Using Dexterous Acoustic Tweezers, Appl. Phys. Lett., 2014, 104(15), 154103 Search PubMed
.
- C. Haber and D. Wirtz, Magnetic Tweezers for DNA Micromanipulation, Rev. Sci. Instrum., 2000, 71(12), 4561–4570, DOI:
.
- K. C. Neuman and A. Nagy, Single-Molecule Force Spectroscopy: Optical Tweezers, Magnetic Tweezers and Atomic Force Microscopy, Nat. Methods, 2008, 5(6), 491 CrossRef CAS PubMed
.
- B. R. Lutz, J. Chen and D. T. Schwartz, Hydrodynamic Tweezers: 1. Noncontact Trapping of Single Cells Using Steady Streaming Microeddies, Anal. Chem., 2006, 78(15), 5429–5435 CrossRef CAS PubMed
.
- R. Probst, Z. Cummins, C. Ropp, E. Waks and B. Shapiro, Flow Control of Small Objects on Chip: Manipulating Live Cells, Quantum Dots, and Nanowires, IEEE Control Systems, 2012, 32(2), 26–53 CrossRef
.
- D. P. Bakker, H. J. Busscher and H. C. van der Mei, Bacterial Deposition in a Parallel Plate and a Stagnation Point Flow Chamber: Microbial Adhesion Mechanisms Depend on the Mass Transport Conditions, Microbiology, 2002, 148(2), 597–603, DOI:10.1099/00221287-148-2-597
.
- M. J. Dempsey, Colonisation of Antifouling Paints by Marine Bacteria, Bot. Mar., 1981, 24(4), 185–191 CAS
.
- J. Tsibouklis, M. Stone, A. A. Thorpe, P. Graham, V. Peters, R. Heerlien, J. R. Smith, K. L. Green and T. G. Nevell, Preventing Bacterial Adhesion onto Surfaces: The Low-Surface energy Approach, Biomaterials, 1999, 20(13), 1229–1235 CrossRef CAS PubMed
.
- K. E. Cooksey and B. Wigglesworth-Cooksey, Adhesion of Bacteria and Diatoms to Surfaces in the Sea: A Review, Aquat. Microb. Ecol., 1995, 9(1), 87–96 CrossRef
.
- B. Little, R. Ray, P. Jones-Meehan, C. Lee and F. Mansfeld, Spatial Relationships between Marine Bacteria and Localized Corrosion on Polymer Coated Steel, Biofouling, 1999, 13(4), 301–321 CrossRef CAS
.
- C. M. Schroeder, E. S. Shaqfeh, H. P. Babcock and S. Chu, System and Method for Confining an Object to a Region of Fluid Flow Having a Stagnation Point, US Pat. 7,013,739, US-Patent-Appl-SN-10/841,011, March 21, 2006
.
- C. Ropp, Z. Cummins, R. Probst, S. Qin, J. T. Fourkas, B. Shapiro and E. Waks, Positioning and Immobilization of Individual Quantum Dots with Nanoscale Precision, Nano Lett., 2010, 10(11), 4673–4679, DOI:10.1021/nl1029557
.
- M. Armani, S. Chaudhary, R. Probst and B. Shapiro, Using Feedback Control and Micro-Fluidics to Steer Individual Particles, in 18th IEEE International Conference on Micro Electro Mechanical Systems, IEEE, 2005, pp. 855–858 Search PubMed
.
- M. D. Armani, S. V. Chaudhary, R. Probst and B. Shapiro, Using Feedback Control of Microflows to Independently Steer Multiple Particles, J. Microelectromech. Syst., 2006, 15(4), 945–956, DOI:10.1109/Jmems.2006.878863
.
- M. Tanyeri, E. M. Johnson-Chavarria and C. M. Schroeder, Hydrodynamic Trap for Single Particles and Cells, Appl. Phys. Lett., 2010, 96(22), 224101 CrossRef PubMed
.
- M. Tanyeri, E. M. Johnson-Chavarria and C. M. Schroeder, Hydrodynamic Trap for Single Cells and Micro- and Nanoparticles, Biophys. J., 2011, 100(3), 623a CrossRef
.
- E. M. Johnson-Chavarria, M. Tanyeri and C. M. Schroeder, A Microfluidic-Based Hydrodynamic Trap for Single Particles, J. Visualized Exp., 2011, 47(47), e2517, DOI:10.3791/2517
.
- A. Shenoy, M. Tanyeri and C. M. Schroeder, Characterizing the Performance of the Hydrodynamic Trap Using a Control-Based Approach, Microfluid. Nanofluid., 2015, 18(5–6), 1055–1066, DOI:10.1007/s10404-014-1495-7
.
- M. Tanyeri, M. Ranka, N. Sittipolkul and C. M. Schroeder, A Microfluidic-Based Hydrodynamic Trap: Design and Implementation, Lab Chip, 2011, 11(10), 1786–1794, 10.1039/c0lc00709a
.
- M. Tanyeri and C. M. Schroeder, Manipulation and Confinement of Single Particles Using Fluid Flow, Nano Lett., 2013, 13(6), 2357–2364, DOI:10.1021/nl4008437
.
- T. M. Schneider, S. Mandre and M. P. Brenner, Algorithm for a Microfluidic Assembly Line, Phys. Rev. Lett., 2011, 106(9), 094503, DOI:10.1103/PhysRevLett.106.094503
.
- K. D. Coventry and M. R. Mackley, Cross-Slot Extensional Flow Birefringence Observations of Polymer Melts Using a Multi-Pass Rheometer, J. Rheol., 2008, 52(2), 401–415, DOI:10.1122/1.2836671
.
- D. Auhl, D. M. Hoyle, D. Hassell, T. D. Lord, O. G. Harlen, M. R. Mackley and T. C. B. McLeish, Cross-Slot Extensional Rheometry and the Steady-State Extensional Response of Long Chain Branched Polymer Melts, J. Rheol., 2011, 55(4), 875–900 CrossRef CAS
.
- P. E. Arratia, C. C. Thomas, J. Diorio and J. P. Gollub, Elastic Instabilities of Polymer Solutions in Cross-Channel Flow, Phys. Rev. Lett., 2006, 96(14), 144502, DOI:10.1103/PhysRevLett.96.144502
.
- J. Soulages, M. S. N. Oliveira, P. C. Sousa, M. A. Alves and G. H. McKinley, Investigating the Stability of Viscoelastic Stagnation Flows in T-Shaped Microchannels, J. Non-Newtonian Fluid Mech., 2009, 163(1–3), 9–24, DOI:10.1016/j.jnnfm.2009.06.002
.
- G. N. Rocha, R. J. Poole, M. A. Alves and P. J. Oliveira, On Extensibility Effects in the Cross-Slot Flow Bifurcation, J. Non-Newtonian Fluid Mech., 2009, 156(1–2), 58–69, DOI:10.1016/j.jnnfm.2008.06.008
.
- S. J. Haward and G. H. McKinley, Instabilities in Stagnation Point Flows of Polymer Solutions, Phys. Fluids, 2013, 25(8), 083104, DOI:10.1063/1.4818151
.
- S. J. Haward and G. H. McKinley, Stagnation Point Flow of Wormlike Micellar Solutions in a Microfluidic Cross-Slot Device: Effects of Surfactant Concentration and Ionic Environment, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(3), 031502 CrossRef PubMed
.
- N. Dubash, P. Cheung and A. Q. Shen, Elastic Instabilities in a Microfluidic Cross-Slot Flow of Wormlike Micellar Solution, Soft Matter, 2012, 8(21), 5847 RSC
.
- S. J. Haward, T. J. Ober, M. S. Oliveira, M. A. Alves and G. H. McKinley, Extensional Rheology and Elastic Instabilities of a Wormlike Micellar Solution in a Microfluidic Cross-Slot Device, Soft Matter, 2011, 8(2), 536–555 RSC
.
- C. A. Dreiss, Wormlike Micelles: Where Do We Stand? Recent Developments, Linear Rheology and Scattering Techniques, Soft Matter, 2007, 3, 956–970 RSC
.
- P. A. Stone, S. D. Hudson, P. Dalhaimer, D. E. Discher, E. J. Amis and K. B. Migler, Dynamics of Wormlike Micelles in Elongational Flows, Macromolecules, 2006, 39(20), 7144–7148, DOI:10.1021/ma0611016
.
- J. A. Pathak and S. D. Hudson, Rheo-Optics of Equilibrium Polymer Solutions: Wormlike Micelles in Elongational Flow in a Microfluidic Cross-Slot, Macromolecules, 2006, 39(25), 8782–8792, DOI:10.1021/ma061355r
.
- M. S. N. Oliveira, F. T. Pinho, R. J. Poole, P. J. Oliveira and M. A. Alves, Purely Elastic Flow Asymmetries in Flow-Focusing Devices, J. Non-Newtonian Fluid Mech., 2009, 160(1), 31–39, DOI:10.1016/j.jnnfm.2009.02.010
.
- A. M. Afonso, M. A. Alves and F. T. Pinho, Purely Elastic Instabilities in Three-Dimensional Cross-Slot Geometries, J. Non-Newtonian Fluid Mech., 2010, 165(13–14), 743–751, DOI:10.1016/j.jnnfm.2010.03.010
.
- B. Thomases and M. Shelley, Transition to Mixing and Oscillations in a Stokesian Viscoelastic Flow, Phys. Rev. Lett., 2009, 103(9), 094501 CrossRef PubMed
.
- J. A. Odell, A. Keller and M. J. Miles, A Method for Studying Flow Induced Polymer Degradation-Verification of Chain Halving, Polym. Commun., 1983, 24(1), 7–10 CAS
.
- J. A. Odell and A. Keller, Flow-Induced Chain Fracture of Isolated Linear Macromolecules in Solution, J. Polym. Sci., Part B: Polym. Phys., 1986, 24(9), 1889–1916 CrossRef CAS
.
- J. A. Odell, A. Keller and Y. Rabin, Flow induced Scission of Isolated Macromolecules, J. Chem. Phys., 1988, 88(6), 4022–4026 CrossRef CAS
.
- O. G. Harlen, E. J. Hinch and J. M. Rallison, Birefringent Pipes: The Steady Flow of a Dilute Polymer Solution near a Stagnation Point, J. Non-Newtonian Fluid Mech., 1992, 44, 229–265 CrossRef CAS
.
- O. G. Harlen, J. M. Rallison and M. D. Chilcott, High-Deborah-Number Flows of Dilute Polymer Solutions, J. Non-Newtonian Fluid Mech., 1990, 34(3), 319–349 CrossRef CAS
.
- D. E. Smith and S. Chu, Response of Flexible Polymers to a Sudden Elongational Flow, Science, 1998, 281(5381), 1335–1340 CrossRef CAS PubMed
.
- T. Pfohl, F. Mugele, R. Seemann and S. Herminghaus, Trends in Microfluidics with Complex Fluids, ChemPhysChem, 2003, 4(12), 1291–1298, DOI:10.1002/cphc.200300847
.
- D. J. Mai, C. Brockman and C. M. Schroeder, Microfluidic Systems for Single DNA Dynamics, Soft Matter, 2012, 8(41), 10560–10572, 10.1039/C2SM26036K
.
- R. G. Larson, H. Hu, D. E. Smith and S. Chu, Brownian Dynamics Simulations of a DNA Molecule in an Extensional Flow Field, J. Rheol., 1999, 43(2), 267–304, DOI:10.1122/1.550991
.
- C. M. Schroeder, H. P. Babcock, E. S. Shaqfeh and S. Chu, Observation of Polymer Conformation Hysteresis in Extensional Flow, Science, 2003, 301(5639), 1515–1519, DOI:10.1126/science.1086070
.
- W. Xu and S. J. Muller, Exploring Both Sequence Detection and Restriction Endonuclease Cleavage Kinetics by Recognition Site Via Single-Molecule Microfluidic Trapping, Lab Chip, 2011, 11(3), 435–442 RSC
.
- S. Cha, T. Shin, S. S. Lee, W. Shim, G. Lee, S. J. Lee, W. Shim and J. M. Kim, Cell Stretching Measurement Utilizing Viscoelastic Particle Focusing, Anal. Chem., 2012, 84(23), 10471–10477 CrossRef CAS PubMed
.
- N. Neve, S. S. Kohles, S. R. Winn and D. C. Tretheway, Manipulation of Suspended Single Cells by Microfluidics and Optical Tweezers, Cell. Mol. Bioeng., 2010, 3(3), 213–228, DOI:10.1007/s12195-010-0113-3
.
- S. Kumar, A. Shenoy and C. Schroeder, Observing Polymersome Dynamics in Controlled Microscale Flows, in APS Meeting Abstracts, 2015, p. 50013 Search PubMed
.
- P. R. Start, S. D. Hudson, E. K. Hobbie and K. B. Migler, Breakup of Carbon Nanotube Flocs in Microfluidic Traps, J. Colloid Interface Sci., 2006, 297(2), 631–636, DOI:10.1016/j.jcis.2005.11.044
.
- Y. N. Young and M. J. Shelley, Stretch-Coil Transition and Transport of Fibers in Cellular Flows, Phys. Rev. Lett., 2007, 99(5), 058303, DOI:10.1103/PhysRevLett.99.058303
.
- C. Ulloa, A. Ahumada and M. L. Cordero, The Effect of Confinement on the Deformation of Microfluidic Drops, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 033004 CrossRef PubMed
.
- W. Xu and S. J. Muller, Polymer-Monovalent Salt-Induced DNA Compaction Studied Via Single-Molecule Microfluidic Trapping, Lab Chip, 2012, 12(3), 647–651, 10.1039/c2lc20880f
.
- Y. Li, C. Brockman, D. Yates, G. McKenna, C. Schroeder, M. San Francisco, J. Kornfield and R. Anderson, Comparison of the Coil-Stretch Transition of Linear and Circular DNA in Planar Extensional Flow, in Abstracts of Papers of the American Chemical Society, American Chemical Society, 2014, p. 420 Search PubMed
.
- Y. Li, K. W. Hsiao, C. A. Brockman, D. Y. Yates, R. M. Robertson-Anderson, J. A. Kornfield, M. J. San Francisco, C. M. Schroeder and G. B. McKenna, When Ends Meet: Circular DNA Stretches Differently in Elongational Flows, Macromolecules, 2015, 48(16), 5997–6001 CrossRef CAS
.
- Y. Zhou and C. M. Schroeder, Single Polymer Dynamics under Large Amplitude Oscillatory Extensional (Laoe) Flow, in APS Meeting Abstracts, Chicago, 2016, p. 7 Search PubMed
.
- S. J. Haward, Buckling Instabilities in Dilute Polymer Solution Elastic Strands, Rheol. Acta, 2010, 49(11–12), 1219–1225, DOI:10.1007/s00397-010-0467-4
.
- V. Sharma, S. J. Haward, J. Serdy, B. Keshavarz, A. Soderlund, P. Threlfall-Holmes and G. H. McKinley, The Rheology of Aqueous Solutions of Ethyl Hydroxy-Ethyl Cellulose (Ehec) and Its Hydrophobically Modified Analogue (Hmehec): Extensional Flow Response in Capillary Break-up, Jetting (Rojer) and in a Cross-Slot Extensional Rheometer, Soft Matter, 2015, 11(16), 3251–3270, 10.1039/c4sm01661k
.
- S. J. Haward, J. A. Odell, Z. Li and X. F. Yuan, The Rheology of Polymer Solution Elastic Strands in Extensional Flow, Rheol. Acta, 2010, 49(7), 781–788 CrossRef CAS
.
- J. T. Wang, D. M. Yu, H. F. Jing and J. Tao, Hydrodynamic Control of Droplets Coalescence in Microfluidic Devices to Fabricate Two-Dimensional Anisotropic Particles through Boundary Element Method, Chem. Eng. Res. Des., 2014, 92(11), 2223–2230, DOI:10.1016/j.cherd.2014.02.026
.
- A. T. Florence and D. Whitehill, The Formulation and Stability of Multiple Emulsions, Int. J. Pharm., 1982, 11(4), 277–308, DOI:10.1016/0378-5173(82)90080-1
.
- J. Wang, J. Liu, J. Han and J. Guan, Effects of Complex Internal Structures on Rheology of Multiple Emulsions Particles in 2d from a Boundary Integral Method, Phys. Rev. Lett., 2013, 110(6), 066001, DOI:10.1103/PhysRevLett.110.066001
.
- J. T. Wang, J. X. Liu, J. J. Han and J. Guan, Rheology Investigation of the Globule of Multiple Emulsions with Complex Internal Structures through a Boundary Element Method, Chem. Eng. Sci., 2013, 96, 87–97, DOI:10.1016/j.ces.2013.02.065
.
- Y. B. Bae, H. K. Jang, T. H. Shin, G. Phukan, T. T. Tran, G. Lee, W. R. Hwang and J. M. Kim, Microfluidic Assessment of Mechanical Cell Damage by Extensional Stress., Lab Chip, 2016, 16(1), 96–103 RSC
.
- E. T. Papoutsakis, Fluid-Mechanical Damage of Animal Cells in Bioreactors, Trends Biotechnol., 1991, 9(1), 427–437 CrossRef CAS PubMed
.
- Y. Chisti, Animal-Cell Damage in Sparged Bioreactors, Trends Biotechnol., 2000, 18(10), 420–432 CrossRef CAS PubMed
.
- Y. Chisti, Hydrodynamic Damage to Animal Cells, Crit. Rev. Biotechnol., 2001, 21(2), 67–110, DOI:10.1080/20013891081692
.
- M. A. Garcia-Briones and J. J. Chalmers, Flow Parameters Associated with Hydrodynamic Cell Injury, Biotechnol. Bioeng., 1994, 44(9), 1089–1098 CrossRef CAS PubMed
.
- R. I. Tanner and R. R. Huilgol, On a Classification Scheme for Flow Fields, Rheol. Acta, 1975, 14(11), 959–962 CrossRef
.
- R. Dylla-Spears, L. L. Sohn and S. J. Muller, Use of Stagnation Point Flows for DNA Trapping, Manipulation, and Target Sequence Detection, in The XV International Congress On Rheology: The Society of Rheology 80th Annual Meeting, 2008, pp. 959–961 Search PubMed
.
- R. Dylla-Spears, J. E. Townsend, L. Jen-Jacobson, L. L. Sohn and S. J. Muller, Single-Molecule Sequence Detection Via Microfluidic Planar Extensional Flow at a Stagnation Point, Lab Chip, 2010, 10(12), 1543–1549, 10.1039/b926847b
.
- A. Castro and J. G. Williams, Single-Molecule Detection of Specific Nucleic Acid Sequences in Unamplified Genomic DNA, Anal. Chem., 1997, 69(19), 3915–3920 CrossRef CAS PubMed
.
- M. Champion and P. A. Libby, Reynolds Stress Description of Opposed and Impinging Turbulent Jets. Part I: Closely Spaced Opposed Jets, Phys. Fluids A, 1993, 5(1), 203–216 CrossRef CAS
.
- A. M. Dehkordi, Application of a Novel-Opposed-Jets Contacting Device in Liquid–Liquid Extraction, Chem. Eng. Process., 2002, 41(3), 251–258 CrossRef CAS
.
- A. Schaffer and A. B. Cambel, The Effect of an Opposing Jet on Flame Stability, Jet Propul., 1955, 25(6), 284–287 CrossRef CAS
.
- A. Schaffer and A. B. Cambel, Continued Investigations of the Opposing Jet Flameholder, Jet Propul., 1956, 26(7), 576–578 CrossRef
.
- S. S. Penner and F. Williams, Recent Studies on Flame Stabilization of Premixed Turbulent Gases, Appl. Mech. Rev., 1957, 10(6), 229–237 CAS
.
- G. Dixon-Lewis, Laminar Premixed Flame Extinction Limits. I Combined Effects of Stretch and Upstream Heat Loss in the Twin-Flame Unburnt-to-Unburnt Opposed Flow Configuration, in Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences London, The Royal Society, London, 1996, pp. 1857–1884 Search PubMed
.
- G. Dixon-Lewis, Laminar Premixed Flame Extinction Limits. II Combined Effects of Stretch and Radiative Loss in the Single Flame Unburnt-to-Burnt and the Twin-Flame Unburnt-to-Unburnt Opposed Flow Configurations, in Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences London, London, 2006, pp. 349–370 Search PubMed
.
- M. Matalon, On Flame Stretch, Combust. Sci. Technol., 1983, 31(3–4), 169–181 CrossRef CAS
.
- S. M. Candel and T. J. Poinsot, Flame Stretch and the Balance Equation for the Flame Area, Combust. Sci. Technol., 1990, 70(1–3), 1–15, DOI:10.1080/00102209008951608
.
- A. E. Potter and J. N. Butler, A Novel Combustion Measurement Based on the Extinguishment of Diffusion Flames, ARS J., 1959, 29(1), 54–56 CAS
.
- A. E. Potter, S. Heimel and J. N. Butler, in Apparent Flame Strength: A Measure of Maximum Reaction Rate in Diffusion Flames, Symposium on Combustion (International) Elsevier, 1961, pp. 1027–1034 Search PubMed
.
- V. K. Jain and H. S. Mukunda, On the Ignition and Extinction Problems in Forced Convection Systems, Int. J. Heat Mass Transfer, 1968, 11(3), 491–508 CrossRef
.
- K. Seshadri, C. Trevino and M. D. Smooke, Analysis of the Structure and Mechanisms of Extinction of a Counterflow Methanol-Air Diffusion Flame, Combust. Flame, 1989, 76(2), 111–132, DOI:10.1016/0010-2180(89)90061-8
.
- A. Tamir and A. Kitron, Applications of Impinging-Streams in Chemical Engineering Processes—Review, Chem. Eng. Commun., 1987, 50(1–6), 241–330 CrossRef CAS
.
- P. M. Chung, F. E. Fendell and J. F. Holt, Nonequilibrium Anomalies in the Development of Diffusion Flames, AIAA J., 1966, 4(6), 1020–1026 CrossRef CAS
.
- F. E. Fendell, Ignition and Extinction in Combustion of Initially Unmixed Reactants, J. Fluid Mech., 1965, 21(2), 281–303, DOI:10.1017/S0022112065000186
.
- S. A. Safvi and T. J. Mountziaris, Gas Phase Decomposition Kinetics of Movpe Precursors in a Counterflow Jet Reactor, in Chemical Perspectives of Microelectronic Materials III (Mat. Res. SOC. Symp. Proc.), ed. C. R. Abernathy, 1993 Search PubMed
.
- V. K. Jain and H. S. Mukunda, The Extinction Problem in an Opposed Jet Diffusion Flame with Competitive Reactions, Combust. Sci. Technol., 1969, 1(2), 105–117 CrossRef CAS
.
- A. Linan, The Asymptotic Structure of Counterflow Diffusion Flames for Large Activation Energies, Acta Astronaut., 1974, 1(7), 1007–1039 CrossRef
.
- D. B. Spalding, Theory of Mixing and Chemical Reaction in the Opposed-Jet Diffusion Flame, ARS J., 1961, 31(6), 763–771 CrossRef CAS
.
- S. A. Safvi and T. J. Mountziaris, A New Reactor Studies for Purely Homogeneous Kinetic of Endothermic Reactions, AIChE J., 1994, 40(9), 1535–1548 CrossRef CAS
.
- J. L. Zilko, Metallo-Organic Cvd Technology and Equipment, in Handbook of Thin-Film Deposition Processes and Techniques, ed. K. K. Shuegraf, Noyes Publications, Park Ridge, NJ, 1988, pp. 84–101 Search PubMed
.
- H. O. Pierson, Handbook of Chemical Vapor Deposition: Principles, Technology and Applications, 1999 Search PubMed
.
- P. Burgraaf, The Status of Mocvd Technology, Semiconductor International, 1993, pp. 80–83 Search PubMed
.
- Z. G. Sun, W. F. Li and H. F. Liu, Stagnation Point Offset of Two Opposed Jets, Ind. Eng. Chem. Res., 2010, 49(12), 5877–5883 CrossRef CAS
.
- F. C. Frank, A. Keller and M. R. Mackley, Polymer Chain Extension Produced by Impinging Jets and Its Effect on Polyethylene Solution, Polymer, 1971, 12(7), 467–473 CrossRef CAS
.
- M. R. Mackley, Flow Singularities, Polymer Chain Extension and Hydrodynamic Instabilities, J. Non-Newtonian Fluid Mech., 1978, 4(1), 111–136 CrossRef CAS
.
- A. J. Muller, J. A. Odell and A. Keller, Elongational Flow and Rheology of Monodisperse Polymers in Solution, J. Non-Newtonian Fluid Mech., 1988, 30(2–3), 99–118, DOI:10.1016/0377-0257(88)85018-3
.
- J. A. Odell, A. J. Muller, K. A. Narh and A. Keller, Degradation of Polymer Solutions in Extensional Flows, Macromolecules, 1990, 23(12), 3092–3103 CrossRef CAS
.
- S. P. Carrington, J. P. Tatham, J. A. Odell and A. E. Saez, Macromolecular Dynamics in Extensional Flows: 1. Birefringence and Viscometry, Polymer, 1997, 38(16), 4151–4164 CrossRef CAS
.
- S. P. Carrington, J. P. Tatham, J. A. Odell and A. E. Saez, Macromolecular Dynamics in Extensional Flows: 2. The Evolution of Molecular Strain, Polymer, 1997, 38(18), 4595–4607 CrossRef CAS
.
- R. K. Prud'homme and G. G. Warr, Elongational Flow of Solutions of Rodlike Micelles, Langmuir, 1994, 10(10), 3419–3426 CrossRef
.
- C. G. Hermansky and D. V. Boger, Opposing-Jet Viscometry of Fluids with Viscosity Approaching That of Water, J. Non-Newtonian Fluid Mech., 1995, 56(1), 1–14 CrossRef CAS
.
- S. L. Ng, R. P. Mun, D. V. Boger and D. F. James, Extensional Viscosity Measurements of Dilute Solutions of Various Polymers, J. Non-Newtonian Fluid Mech., 1996, 65(2–3), 291–298, DOI:10.1016/0377-0257(96)01463-2
.
- G. G. Fuller, C. A. Cathey, B. Hubbard and B. E. Zebrowski, Extensional Viscosity Measurements for Low-Viscosity Fluids, J. Rheol., 1987, 31(3), 235–249 CrossRef CAS
.
- C. A. Cathey and G. G. Fuller, Uniaxial and Biaxial Extensional Viscosity Measurements of Dilute and Semi-Dilute Solutions of Rigid Rod Polymers, J. Non-Newtonian Fluid Mech., 1988, 30(2–3), 303–316, DOI:10.1016/0377-0257(88)85030-4
.
- P. Dontula, M. Pasquali, L. E. Scriven and C. C. W. Macosko, Can Extensional Viscosity Be Measured with Opposed-Nozzle Devices?, Rheol. Acta, 1997, 36(4), 429–448 CrossRef CAS
.
- P. Jonsson, J. McColl, R. W. Clarke, V. P. Ostanin, B. Jonsson and D. Klenerman, Hydrodynamic Trapping of Molecules in Lipid Bilayers, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(26), 10328–10333, DOI:10.1073/pnas.1202858109
.
- A. Ainla, G. D. M. Jeffries, R. Brune, O. Orwar and A. Jesorka, A Multifunctional Pipette, Lab Chip, 2012, 12, 1255–1261 RSC
.
- A. Ainla, I. Gozen, B. Hakonen and A. Jesorka, Lab on a Biomembrane: Rapid Prototyping and Manipulation of 2d Fluidic Lipid Bilayer Circuits, Sci. Rep., 2013, 3, 2734, DOI:10.1038/srep03317
.
- A. Ainla, E. T. Jansson, N. Stepanyants, O. Orwar and A. Jesorka, A Microfluidic Pipette for Single-Cell Pharmacology, Anal. Chem., 2010, 82(11), 4529–4536, DOI:10.1021/ac100480f
.
- A. Ainla, E. T. Jansson, N. Stepanyants, O. Orwar and A. Jesorka, A Multi Purpose Microfluidic Pipette for Single Cell Analysis, in 14th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Groningen, Netherlands, 2010, pp. 932–934 Search PubMed
.
- A. Ainla, S. J. Xu, N. Sanchez, G. D. M. Jeffries and A. Jesorka, Single-Cell Electroporation Using a Multifunctional Pipette, Lab Chip, 2012, 12(22), 4605–4609, 10.1039/c2lc40563f
.
- A. Ahemaiti, A. Ainla, G. D. Jeffries, H. Wigström, O. Orwar, A. Jesorka and K. Jardemark, A Multifunctional Pipette for Localized Drug Administration to Brain Slices, J. Neurosci. Methods, 2013, 219(2), 292–296 CrossRef CAS PubMed
.
- A. Ahemaiti, H. Wigstrom, A. Ainla, G. D. M. Jeffries, O. Orwar, A. Jesorka and K. Jardemark, Spatial Characterization of a Multifunctional Pipette for Drug Delivery in Hippocampal Brain Slices, J. Neurosci. Methods, 2015, 241, 132–136, DOI:10.1016/j.jneumeth.2014.12.017
.
- M. Safavieh, M. A. Qasaimeh, A. Vakil, D. Juncker and T. Gervais, Two-Aperture Microfluidic Probes as Flow Dipole: Theory and Application, Sci. Rep., 2015, 5, 11943 CrossRef CAS PubMed
.
- C. M. Perrault, M. A. Qasaimeh and D. Juncker, The Microfluidic Probe: Operation and Use for Localized Surface Processing, J. Visualized Exp., 2009, 28, e1418, DOI:10.3791/1418
.
- T. Gervais, M. Safavieh, M. A. Qasaimeh and D. Juncker, Systematic Analysis of Microfluidic Probe Design and Operation, in 36th Annual International Conference of the IEEE in Engineering in Medicine and Biology Society (EMBC), 2014, pp. 1567–1570 Search PubMed
.
- D. Juncker, H. Schmid and E. Delamarche, Multipurpose Microfluidic Probe, Nat. Mater., 2005, 4(8), 622–628 CrossRef CAS PubMed
.
- N. Ostromohov, M. Bercovici and G. V. Kaigala, Delivery of Minimally Dispersed Liquid Interfaces for Sequential Surface Chemistry, Lab Chip, 2016, 15, 3015–3023 RSC
.
- R. D. Lovchik, G. V. Kaigala, M. Georgiadis and E. Delamarche, Micro-Immunohistochemistry Using a Microfluidic Probe, Lab Chip, 2012, 12(6), 1040–1043, 10.1039/c2lc21016a
.
- A. Queval, N. R. Ghattamaneni, C. M. Perrault, R. Gill, M. Mirzaei, R. A. McKinney and D. Juncker, Chamber and Microfluidic Probe for Microperfusion of Organotypic Brain Slices, Lab Chip, 2010, 10(3), 326–334, 10.1039/b916669f
.
- A. Sarkar, S. Kolitz, D. A. Lauffenburger and J. Han, Microfluidic Probe for Single-Cell Analysis in Adherent Tissue Culture, Nat. Commun., 2014, 5, 3421, DOI:10.1038/ncomms4421
.
- A. Kashyap, J. Autebert, E. Delamarche and G. V. Kaigala, Selective Local Lysis and Sampling of Live Cells for Nucleic Acid Analysis Using a Microfluidic Probe, Sci. Rep., 2016, 6, 29579 CrossRef CAS PubMed
.
- M. A. Qasaimeh, T. Gervais and D. Juncker, Microfluidic Quadrupole and Floating Concentration Gradient, Nat. Commun., 2011, 2, 464 CrossRef PubMed
.
- J. Autebert, A. Kashyap, R. D. Lovchik, E. Delamarche and G. V. Kaigala, Hierarchical Hydrodynamic Flow Confinement: Efficient Use and Retrieval of Chemicals for Microscale Chemistry on Surfaces, Langmuir, 2014, 30(12), 3640–3645, DOI:10.1021/la500875m
.
- J. Autebert, J. F. Cors, D. P. Taylor and G. V. Kaigala, Convection-Enhanced Biopatterning with Recirculation of Hydrodynamically Confined Nanoliter Volumes of Reagents, Anal. Chem., 2016, 88(6), 3235–3242 CrossRef CAS PubMed
.
- S. Mao, Y. Zhang, W. Zhang, H. Zeng, H. Nakajima, J. M. Lin and K. Uchiyama, Convection-Diffusion Layer in an “Open Space” for Local Surface Treatment and Microfabrication Using a Four-Aperture Micro Chemical Pen, ChemPhysChem, 2017, 18(17), 2357–2363 CrossRef CAS PubMed
.
- H. Shiku, T. Yamakawa, Y. Nashimoto, Y. Takahashi, Y.-s. Torisawa, T. Yasukawa, T. Ito-Sasaki, M. Yokoo, H. Abe, H. Kambara and T. Matsue, A Microfluidic Dual Capillary Probe to Collect Messenger Rna from Adherent Cells and Spheroids, Anal. Biochem., 2009, 385, 138–142 CrossRef CAS PubMed
.
- T. Kang, J. Han and K. S. Lee, Concentration Gradient Generator Using a Convective–Diffusive Balance, Lab Chip, 2008, 8(7), 1220–1222 RSC
.
- E. Kolaczkowska and P. Kubes, Neutrophil Recruitment and Function in Health and Inflammation, Nat. Rev. Immunol., 2003, 13(3), 159–175 CrossRef PubMed
.
- T. M. Keenan and A. Folch, Biomolecular Gradients in Cell Culture Systems, Lab Chip, 2008, 8(1), 34–57, 10.1039/b711887b
.
- D. Irimia, Microfluidic Technologies for Temporal Perturbations of Chemotaxis, Annu. Rev. Biomed. Eng., 15(12), 259–284 Search PubMed
.
- M. A. Qasaimeh, M. Astolfi, M. Pyzik, S. Vidal and D. Juncker, Neutrophil Dynamics During Migration in Microfluidic Concentration Gradients, in Proceeding of the 40th Annual Northeast Bioengineering Conference (NEBEC), Boston, USA, April 25–27, 2014, pp. 1–2 Search PubMed
.
- M. A. Qasaimeh, M. Astolfi, M. Pyzik, S. Vidal and D. Juncker, Neutrophils Migrate Longer Distances in Moving Microfluidic Concentration Gradients Compared to Static Ones, in The 17th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Freiburg, Germany, October 2013, pp. 2007–2009 Search PubMed
.
- M. A. Qasaimeh, S. G. Ricoult and D. Juncker, Microfluidic Probes for Use in Life Sciences and Medicine, Lab Chip, 2013, 13(1), 40–50, 10.1039/c2lc40898h
.
- M. A. Qasaimeh, R. Stefavieh and D. Juncker, The Generation of Biochemical Gradients in a Microfluidic Stagnant Zone, in Proceedings of MMB 2009, The fifth International Conference on Microtechnologies in Medicine and Biology, Quebec, QC, Canada, April 2009, pp. 62–63 Search PubMed
.
- A. T. Brimmo and M. A. Qasaimeh, Microfluidic Probes and Quadrupoles: A New Era of Open Microfluidics, IEEE Nanotechnol. Mag., 2017, 11(1), 20–31 CrossRef
.
- M. A. Qasaimeh, S. G. Ricoult and D. Juncker, Microfluidic probes to process surfaces, cells, and tissues, Selected Topics in Nanomedicine (Regenerative Medicine, Artificial Cells and Nanomedicine), World Science Publisher/Imperial College Press, 2013, ch. 11, pp. 257–280 Search PubMed
.
- M. Chachisvilis, Y. L. Zhang and J. A. Frangos, G Protein-Coupled Receptors Sense Fluid Shear Stress in Endothelial Cells, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(42), 15463–15468, DOI:10.1073/pnas.0607224103
.
- N. Li Jeon, H. Baskaran, S. K. W. Dertinger, G. M. Whitesides, L. Van De Water and M. Toner, Neutrophil Chemotaxis in Linear and Complex Gradients of Interleukin-8 Formed in a Microfabricated Device, Nat. Biotechnol., 2002, 20(8), 826–830 CrossRef PubMed
.
- J. A. Fay, Theory of Stagnation Point Heat Transfer in Dissociated Air, J. Aerosp. Sci., 1958, 25(2), 73–85 CrossRef
.
- G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge university press, 2000
.
| This journal is © The Royal Society of Chemistry 2017 |
