Large-scale comparison of machine learning methods for drug target prediction on ChEMBL

Abstract

Deep learning is currently the most successful machine learning technique in a wide range of application areas and has recently been applied successfully in drug discovery research to predict potential drug targets and to screen for active molecules. However, due to (1) the lack of large-scale studies, (2) the compound series bias that is characteristic of drug discovery datasets and (3) the hyperparameter selection bias that comes with the high number of potential deep learning architectures, it remains unclear whether deep learning can indeed outperform existing computational methods in drug discovery tasks. We therefore assessed the performance of several deep learning methods on a large-scale drug discovery dataset and compared the results with those of other machine learning and target prediction methods. To avoid potential biases from hyperparameter selection or compound series, we used a nested cluster-cross-validation strategy. We found (1) that deep learning methods significantly outperform all competing methods and (2) that the predictive performance of deep learning is in many cases comparable to that of tests performed in wet labs (i.e., in vitro assays).

---

Introduction

The drug development process typically involves a large number of biological experiments and tests, termed “assays”, that measure biological effects of chemical compounds. These effects include toxicity¹ and inhibition or activation of proteins or whole cellular processes, and determine failure or success of a chemical compound on its way to becoming a marketed drug.

Conducting these experiments is a time- and cost-intensive process. Usually, a cell line must be cultivated to obtain a single data point. For example, even the Tox21 project,² an unprecedented multi-million-dollar effort, could test only a few thousand compounds for as few as twelve toxic effects. Therefore, accurate computational target prediction methods are of great value in supporting and improving the drug discovery process.

Deep learning, a new computational technique that has made an impact in many research areas, has recently not only been applied very successfully to target prediction,^3,4 but also to certain other tasks in chemistry. Examples are the automatic generation of molecules,^5–9 chemical synthesis planning,¹⁰ drug synergy prediction¹¹ or modelling quantum interactions¹² and speeding quantum mechanical computations up,¹³ which might further help in the design of new efficient molecular organic light-emitting diodes.¹⁴ The main goal of this study was therefore to compare the performance of deep learning with that of other methods for drug target prediction.

Deep learning architectures seem well suited to target prediction because they both allow multitask learning^15–17 and automatically construct complex features.¹⁷ First, multitask learning has the advantage that it naturally allows for multi-label information and can therefore utilize relations between targets. Multitask learning allows hidden unit representations to be shared among prediction tasks. This is particularly important because for some targets very few measurements are available, and therefore single task prediction may fail to construct an effective representation. In contrast, deep learning can exploit representations learned across different tasks and can boost the performance on tasks with few training examples. Fig. 1 shows that many compounds were measured by multiple assays (left), and – based on this observation – that there are strongly correlated assays available (right). Second, deep networks provide hierarchical representations of a compound, where higher levels represent more complex properties.¹⁸ A hierarchy of features naturally emerges: single atoms are grouped together as functional groups and reactive centers, which in turn define pharmacophores. Such features are the state-of-the-art way in which chemists and drug designers think about the properties of each chemical compound.¹⁹

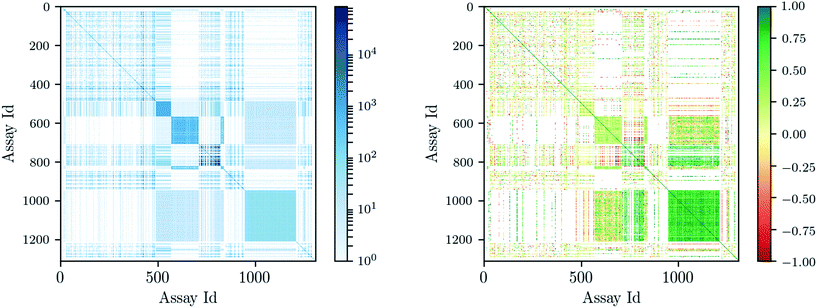Fig. 1 Assay correlation [left: number of compounds (log-scaled) measured on both assays, right: Pearson correlation on commonly measured compounds].

There are several pitfalls in comparing drug target prediction methods, which especially concern the selection of a comparison dataset, the compound series bias inherent in chemical datasets and hyperparameter selection.

First, many method comparison studies comprise only single or very few assays or targets,^3,20–22 whereas compound databases, such as ChEMBL,²³ contain many more assays. Therefore, these studies both restrict the conclusions of the method comparisons to a certain subset of assays and underestimate the multitask learning effect in spite of the large amount of data being available publicly. Some target prediction algorithms can exploit the information of similar assays to improve the predictive performance of a particular assay of interest. Such algorithms are referred to as multitask learning algorithms. Assays with few measurements in particular can benefit from information from similar assays. Aside from the underestimated predictive performance, other potential benefits of multitask settings are ignored: a multitask model is able to provide predictions for a large number of assays at once, which can help chemists and biologists to conceptualize how certain compounds might act at the cellular level. It is therefore highly desirable to include a large number of assays in a method comparison study to evaluate the benefits of multitask learning in terms of predictive performance and to provide more general, comparative statements on target prediction methods.

Second, most comparative studies suffer from the compound series bias²⁴ and hence overestimate the performance of certain methods. The compound series bias arises from the way chemical compounds are generated: chemists typically generate new chemical scaffolds rather than individual compounds, and derive new substances from these scaffolds by adding various functional groups. Target activity prediction for a compound from a new compound series is a more difficult task than target activity prediction for compounds, that are from a series, which is contained in the training set. Hence, if the estimated prediction performance suffers from the compound series bias, it is overoptimistic compared to the situation in which the prediction method is used in practice for the prediction of compounds from new compound series.

Third, performance estimates are biased by hyperparameter selection (hyperparameter selection bias). This is especially pronounced in deep learning because it allows many combinations of architectures, activation functions, learning rates, and regularization parameters. The bias may appear if label information from the test set influences the adjustment of hyperparameters for building predictive models. However, in practice no test set labels are available to adjust hyperparameters. In many cases the prediction performance estimation is therefore overoptimistic. Since different learning algorithms have different numbers of hyperparameters, and the hyperparameters also have different adjustment capabilities, different learning algorithms have different tendencies to overfit. Hence, a method comparison that is affected by the hyperparameter selection bias is typically unfair.

To avoid the first pitfall, we extracted a large benchmark dataset from the ChEMBL database that allows reliable assessment of the performance of machine learning methods for compound target prediction. The dataset contains about 500 000 compounds and more than 1000 assays. These assays correspond to a variety of target classes (e.g. enzymes, ion channels and receptors) and differ in size. In particular, the dataset has many assays that comprise only relatively few measurements (a hundred to several hundreds), but there are also several assays with a very large number of measured compounds (tens of thousands).

The second problem is solved by cluster-cross-validation⁴ (for details see section “Methods”). In conventional cross-validation, the set of data points is partitioned randomly into several folds. Processing iteratively, each fold serves once as a test set while the remaining folds form the training set. In each iteration, the training set is available to build a new predictive model, while the prediction performance of this model is estimated on the test set. Instead of randomly assigning data points to folds, cluster-cross-validation distributes whole clusters of compounds across folds. As a consequence, chemical compounds from the same cluster are either in the training set or in the test set. Specifically, cluster-cross-validation avoids that some of the data points that belong to a certain cluster fall into the training set while other data points from the same cluster fall into the test set. In a cluster-cross-validation benchmark, a machine learning method must therefore successfully predict the activity of compounds from new scaffolds in a very large number of cases. Cluster-cross-validation provides performance estimates of methods for the prediction of compounds that are based on new chemical scaffolds and thus takes into account the way chemical compounds are generated.

The third problem is tackled by applying a nested cross-validation scheme.^25,26 An outer loop measures the prediction performance of the algorithms, while an inner loop is used to adjust the hyperparameters of the individual methods such that the methods can choose their best settings for building predictive models in the outer loop. In total, we used three different folds in our nested cluster-cross-validation setting. In each iteration, the inner loop uses one of the three folds from our benchmark dataset for training and one fold for validating the hyperparameter combinations searched while keeping the last fold aside as a test fold for the outer loop. The outer loop uses both the training and the test fold of the inner loop for training a model. The hyperparameters in the outer loop are selected based on a prediction performance criterion from inner loop cross-validation. Thus, the performance estimates provided by nested cross-validation are not biased by hyperparameter selection.

Aside from carrying out an in silico prediction performance comparison study, we also carried out an experiment, that compares the accuracy of in silico predictions to the accuracy of in vitro measurements. Here we explicitly consider the case in which two assays are different but should measure the same biological effect of a compound. Since we could consider our in silico prediction method as a virtual assay, we tried to compare whether a virtual assay or a surrogate in vitro assay is more accurate at predicting the outcome of an assay of interest.

Results & discussion

We considered target prediction as a binary classification problem in creating a benchmark dataset. The task is to predict a binary assay outcome, that indicates whether a certain compound, for example, binds to a specific receptor, inhibits some pathway or induces toxic effects. More specifically, each ChEMBL assay is considered to be an individual classification problem, even if the considered assays share the same biomolecular target. Thus, we avoid aggregating measurements of incomparable types of assays²⁷ (e.g., binding assays, assays measuring antagonists, and assays measuring agonists cannot be compared, since an antagonist is negative in an agonist assay and vice versa). As the raw assay measurement signal is often a real number, and binary labels are not given, we developed a protocol for assigning binary labels to the assay measurements, thereby generating a large-scale benchmark dataset from ChEMBL. Details of this protocol are given in ESI Section S2.1.†

We compared the prediction performances of several deep learning architectures with a variety of methods, in particular with support vector machines²⁸ (SVMs) and K-nearest-neighbours (KNNs) as representatives of similarity-based classification methods and with random forests²⁹ (RFs) as a representative feature-based classification method. Furthermore, we included naive bayes (NB) and SEA^30–32 in the comparison, which we considered as representatives of target prediction methods that were constructed specifically for the purpose of drug discovery. More details on the individual methods are given in the “Methods” section and in ESI Section S3.†

For deep learning methods, we considered three main architectures of deep neural networks (DNNs): feed-forward neural networks (FNNs), convolutional neural networks³³ (CNNs), and recurrent neural networks (RNNs). FNNs take vectorial inputs and consist of several layers of (affine) linear maps followed by an activation or the final output function. CNNs are highly successful at image processing tasks.^34–37 They usually take a whole 2D image as an input and an important characteristic of this network type is that parameters are shared across neurons. CNNs consist of several convolution and pooling layers where the convolution layer outputs are typically computed by a parametrized kernel and the pooling layer outputs are computed by a simple aggregation function. We consider graph convolutional networks, that make use of neighbourhoods as they are defined by a molecular graph topology instead of a pixel neighbourhood as in 2D images. Explicitly, we looked at two implementations. One is referred to as GC^38,39 and the second one is referred to as Weave.⁴⁰ Both were available in the DeepChem^39,41 package. RNNs are successfully used in applications that have to process sequence data, such as natural language processing^42–44 or speech recognition.⁴⁵ In RNNs, network parameters are shared across the time steps of the sequences. As vanishing gradients^46,47 are a problem in learning these networks, memory was introduced, which led to the LSTM architecture.⁴⁸ Here we consider LSTM networks, that take SMILES⁴⁹ strings as an input. We refer to this architecture as SmilesLSTM.

For comparisons of target prediction methods, we used the area under the receiver operating characteristic curve⁵⁰ (abbreviated as ROC-AUC or since it is our default metric, if there is no ambiguity, as AUC) as a performance assessment criterion. AUC is a commonly used criterion for assessing computational target prediction methods.^2,51

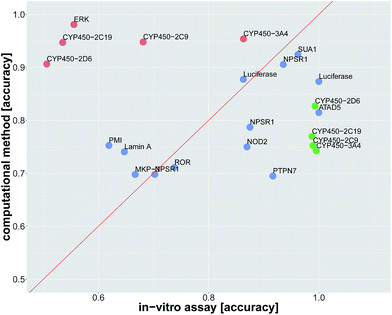
In order to compare in silico predictions to in vitro measurements, we identified assay pairs in ChEMBL, that measure the same biological effect. We considered the assay with fewer measured compounds as the ground truth and the assay with the higher number of measured compounds as surrogate assay. We then compared the in silico prediction accuracy against the in vitro prediction accuracy of the surrogate assay. Using stringent criteria and manual supervision, we found 22 such assay pairs (see Table 2, ESI Section S2.4.1, ESI Tables S14 and S15†).

Table 1 Performance comparison of target prediction methods. The table gives the means and standard deviations of assay-AUC values for the compared algorithms and feature categories or input types. Overall, FNNs (second column) performed best. They significantly (α = 0.01) outperformed all other considered methods. The methods GC and Weave work directly on graph representations of compounds and SmilesLSTM uses the SMILES representations of compounds

	FNN	SVM	RF	KNN	NB	SEA	GC	Weave	SmilesLSTM
StaticF	0.687 ± 0.131	0.668 ± 0.128	0.665 ± 0.125	0.624 ± 0.120
SemiF	0.743 ± 0.124	0.704 ± 0.128	0.701 ± 0.119	0.660 ± 0.119	0.630 ± 0.109
ECFP6	0.724 ± 0.125	0.715 ± 0.127	0.679 ± 0.128	0.669 ± 0.121	0.661 ± 0.119	0.593 ± 0.096
DFS8	0.707 ± 0.129	0.693 ± 0.128	0.689 ± 0.120	0.648 ± 0.120	0.637 ± 0.112
ECFP6 + ToxF	0.731 ± 0.126	0.722 ± 0.126	0.711 ± 0.131	0.675 ± 0.122	0.668 ± 0.118
Graph							0.692 ± 0.125	0.673 ± 0.127
SMILES									0.698 ± 0.130

---

Table 2 Performance comparison of deep learning and surrogate in vitro assays. The first and second columns list the ChEMBL-IDs of the assay to be predicted and the surrogate in vitro assay, that serves as the predictor, respectively. The third column shows the biomolecular target which the assays intended to measure. The fourth and fifth columns report respectively the accuracies of the surrogate in vitro assay and of the computational method together with their 90% confidence intervals. The last column gives the p-values of proportion tests for difference in accuracy. Significant results are indicated in bold

Assay	Surrogate assay	Target	Surrogate assay accuracy	Deep learning accuracy	p-value
CHEMBL1909134	CHEMBL1613777	CYP450-2C19	0.54 [0.4136, 0.653]	0.95 [0.9198, 0.9658]	1.95 × 10^−17
CHEMBL1909200	CHEMBL1614521	ERK	0.56 [0.4012, 0.7005]	0.98 [0.9615, 0.9912]	9.57 × 10^−17
CHEMBL1909136	CHEMBL1614110	CYP450-2D6	0.51 [0.3923, 0.6197]	0.91 [0.8734, 0.9319]	2.76 × 10^−15
CHEMBL1909135	CHEMBL1614027	CYP450-2C9	0.68 [0.5567, 0.7853]	0.95 [0.9213, 0.9664]	1.35 × 10^−9
CHEMBL1909138	CHEMBL1614108	CYP450-3A4	0.86 [0.8041, 0.9071]	0.95 [0.9278, 0.9713]	1.76 × 10^−4
CHEMBL1614310	CHEMBL1614544	Lamin A	0.65 [0.5797, 0.7092]	0.74 [0.657, 0.8105]	7.83 × 10^−2
CHEMBL1737863	CHEMBL1614255	PMI	0.62 [0.3869, 0.8105]	0.75 [0.6504, 0.8337]	2.77 × 10^−1
CHEMBL1614016	CHEMBL1794352	Luciferase	0.86 [0.8086, 0.9043]	0.88 [0.8108, 0.9238]	7.53 × 10^−1
CHEMBL1794393	CHEMBL1614512	MKP-3	0.67 [0.4469, 0.8357]	0.70 [0.5945, 0.7853]	8.07 × 10^−1
CHEMBL1614355	CHEMBL1614052	NPSR1	0.70 [0.5913, 0.7947]	0.70 [0.5549, 0.8126]	1.00 × 10^0
CHEMBL1614479	CHEMBL1614052	NPSR1	0.94 [0.835, 0.9791]	0.91 [0.7858, 0.9647]	7.31 × 10^−1
CHEMBL1614197	CHEMBL1614087	ROR	0.74 [0.6572, 0.8058]	0.71 [0.6045, 0.7994]	6.54 × 10^−1
CHEMBL1614539	CHEMBL1614052	NPSR1	0.88 [0.724, 0.9531]	0.79 [0.6393, 0.888]	3.95 × 10^−1
CHEMBL1738575	CHEMBL1614247	NOD2	0.87 [0.6533, 0.9657]	0.75 [0.6235, 0.8462]	3.78 × 10^−1
CHEMBL1737868	CHEMBL1738317	ATAD5	1.00 [0.6555, 1]	0.81 [0.7098, 0.8893]	2.05 × 10^−1
CHEMBL1613806	CHEMBL1613949	PTPN7	0.92 [0.5975, 0.9956]	0.69 [0.5598, 0.8046]	1.61 × 10^−1
CHEMBL1614105	CHEMBL1614290	SUA1	0.96 [0.9267, 0.9814]	0.92 [0.8715, 0.9575]	1.20 × 10^−1
CHEMBL1963940	CHEMBL1794352	Luciferase	1.00 [0.8076, 1]	0.87 [0.775, 0.9344]	1.15 × 10^−1
CHEMBL1741321	CHEMBL1614110	CYP450-2D6	0.99 [0.9889, 0.9956]	0.83 [0.8184, 0.8352]	5.80 × 10^−164
CHEMBL1741325	CHEMBL1614027	CYP450-2C9	0.99 [0.9839, 0.993]	0.75 [0.7428, 0.762]	1.82 × 10^−198
CHEMBL1741323	CHEMBL1613777	CYP450-2C19	0.99 [0.9822, 0.9911]	0.77 [0.7602, 0.7789]	1.20 × 10^−204
CHEMBL1741324	CHEMBL1613886	CYP450-3A4	1.00 [0.9925, 0.9971]	0.74 [0.7328, 0.7522]	<1.0 × 10^−250

---

The ChEMBL benchmark dataset which we created and used to compare various target prediction methods consists of 456 331 compounds. Chemical compounds are described by their molecular graphs. However, only graph convolutional networks can process graphs directly. For the other compared machine learning methods, we generated a sequence or a vectorial representation of the compounds. We generated the SMILES representation that serves as an input for LSTM. For methods that need numerical vectors, we computed a number of chemical descriptors by means of standard software.^52,53 We grouped different feature types together into four categories: static features, semisparse features, toxicophore features and dynamic features. Static features are typically those identified by experts as indicating particular molecular properties. Their number is typically fixed, while dynamic features are extracted on the fly from the chemical structure of a compound in a prespecified way. Typically, dynamic features exhibit sparse binary or count distributions, which means that only a small subset of compounds possess the feature. In contrast, static features typically exhibit continuous and/or less-sparse distributions. As with static features, the number of semisparse features is predefined, but the construction idea is similar to that of dynamic features. Toxicophore features describe a compound by the absence or presence of a set of predefined structural alerts, so-called toxicophores. More details on the description of chemical compounds and on which feature types form the individual feature categories, are given in ESI Section S2.2.† In the following, we consider extended connectivity fingerprint features⁵⁴ (ECFP) and depth first search features⁵⁵ (DFS) as an own dynamic feature category respectively and compared the prediction performances for the following feature categories or combinations of feature categories individually: common static features⁵² (StaticF), common semisparse features (SemiF) including MACCS descriptors,⁵⁶ ECFP features⁵⁴ with radius radius 3 (ECFP6), DFS features⁵⁵ with diameter 8 (DFS8) and a combination of ECFP6 and toxicophore features⁴ (ECFP6 + ToxF).

Large-scale comparison

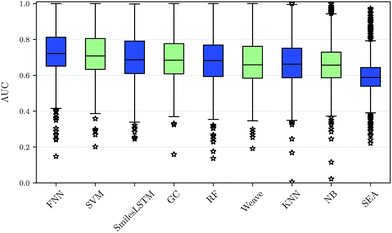
Using our nested cluster-cross-validation procedure, we obtained a performance estimate for each method, feature category and assay, which we denote as “assay-AUC” (mean of ROC-AUC values over the folds). This estimate is neither biased by compound series nor by the hyperparameter selection procedure. The means and the corresponding standard deviations over the assay-AUC values for the algorithms and feature categories described are shown in Table 1. The distribution of the assay-AUC values is additionally shown in Fig. 2 for ECFP6 features. In order to check whether a certain algorithm significantly outperformed another algorithm, we applied Wilcoxon signed rank tests between all pairs of algorithms. The p-values are given in ESI Table S9 (ESI Section S4.1†) for ECFP6 features as well as for the combination of ECFP6 and ToxF (ECFP6 + ToxF) features. In addition to these results, we provide the assay-AUC values of FNNs for each individual ChEMBL assay in ESI Table S11.† Furthermore, we provide the individual ROC-AUC values for each fold separately in ESI Table S12† and PR-AUC (area under the precision recall curve) values in ESI Table S13.†

Fig. 2 Performance comparison of drug target prediction methods. The assay-AUC values for various target prediction algorithms based on ECFP6 features, graphs and sequences are displayed as boxplot. Each compared method yields 1310 AUC values for each modelled assay. On average, deep feed-forward neural networks (FNN) perform best followed by support vector machines (SVM), sequence-based networks (SmilesLSTM), GC graph convolution networks (GC), random forests (RF), Weave graph convolution networks (Weave), k-nearest neighbour (KNN), naive bayes (NB) and SEA.

Note that, for the NB statistics, we could not run the method on the static features, as the method required binary features; for the other feature categories in NB we used a binarized version of the features, that mapped all count values above zero to one. Further, for SEA, we calculated only results for ECFP6 features. Given the low performance compared to other methods and the non-negligible computational demand, we skipped computation of the other feature categories.

We observed that FNNs significantly outperform (α = 0.01) the other tested methods for each feature category. Furthermore, FNNs are significantly better than graph convolutions (GC, Weave) or SmilesLSTM, for almost all feature categories except StaticF features. The second best method are SVMs. They are significantly better than graph convolution networks or SmilesLSTM, if ECFP6, ECFP6 + ToxF or SemiF features are used. Interestingly, the SmilesLSTM has a higher average AUC than the two graph-based approaches. Further, it can be observed that classical machine learning methods, such as SVMs or RFs, perform better than typical chemoinformatics methods. In general, ECFP6 + ToxF features work well for many algorithms, although the best performance was achieved by FNNs based on the feature category “SemiF”. Overall, FNNs exhibit the best performance across prediction tasks.

Machine learning models as virtual assays

Since we identified deep learning as the best method for compound target prediction, we checked whether FNNs can predict assay outcomes as accurately as another (surrogate) in vitro assay measuring the same target. The activity of both considered in vitro assays is defined by our protocol for creating the benchmark dataset, where we additionally used weakly active and weakly inactive compounds. The predicted activity is given by the computational model in the case of in silico assays and it is given by the measurements itself in the case of the surrogate in vitro assay. In that way, we can compare the performance of an in silico assay with that of an in vitro assay. Details of the comparison procedure are given in ESI Section S2.4.2.†

The average accuracy for predicting a selected assay by a surrogate in vitro assay measuring the same target was 0.81 ± 0.17, and the average accuracy by using DNN models for the prediction of the selected assay was 0.82 ± 0.10. For 13 of 22 assay pairs, there was no significant difference between the accuracy of the surrogate in vitro assay and that of the computational method (see Fig. 3 and Table 2). In 5 of 22 cases, the computational method outperformed the surrogate in vitro assay in terms of accuracy. In 4 of 22 assays, the surrogate in vitro assay was significantly better than deep learning. Overall, the predictive performance of deep learning for an assay with a certain target is on par with surrogate assays measuring the same target.

Fig. 3 Comparison of prediction accuracy for an in vitro assay. The dots represent the in vitro assays, that should be predicted. The prediction is either by a surrogate in vitro assay with the same target as the assay, which has to be predicted, or by an in silico deep learning virtual assay. The x-axis indicates the in vitro accuracy and the y-axis the FNN deep learning accuracy. Significantly better accuracies of one prediction method over the other one are indicated in green and red. Blue dots denote assays for which the difference in accuracy was not significant. Point labels give the biomolecular target.

Dataset size and prediction performance

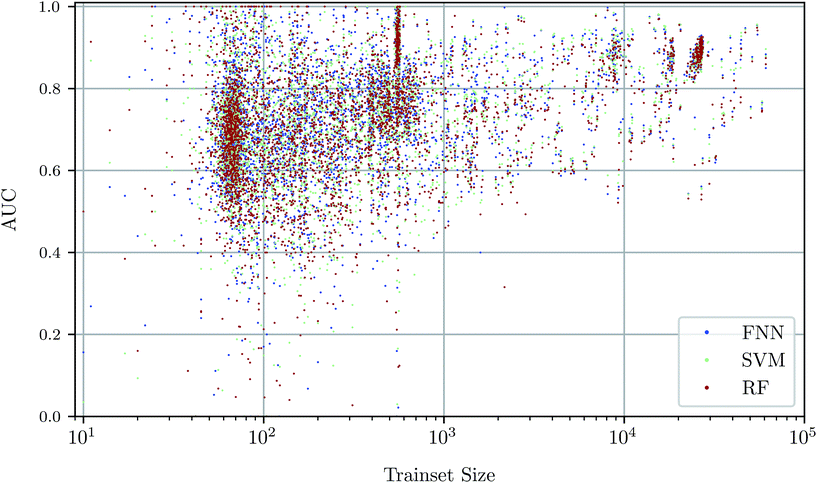
To investigate the relationship between dataset size and performance, we checked the correlation of the AUC values of the test set against size of the training set (see Fig. 4). It can be observed that larger training set sizes lead to better predictions in principle. However, even if only few samples are available, the AUC indicates that the performance is almost always better than random classification. ESI Fig. S4 in ESI Section S4.2† gives additional information on relationship between AUC value and test set size.

Fig. 4 Scatterplot of predictive performance (“AUC”, y-axis) and size of the training set (“trainset size”, x-axis). Colors indicate three different predictive methods, namely FNNs, SVMs, and RFs. The trend that assays with a large number of training data points lead to better predictive models is consistent between the three shown machine learning methods.

Prediction performance for different ChEMBL target classes and assay types

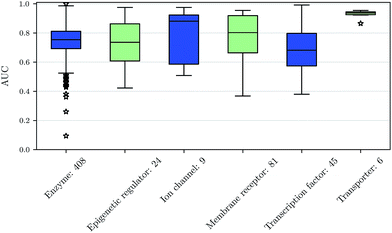
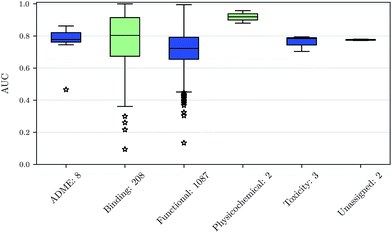
We also investigated whether there are performance differences between different types of assays. To this end, we considered on the one hand the main target classes of ChEMBL assigned to the assays and on the other hand the assay types themselves, to which an assay belongs. Fig. 5 shows a boxplot of the prediction performance for each main ChEMBL target class while Fig. 6 shows a boxplot for the different assay types. The exact number of assays on which the boxplots are based is given beside the class or type name. Note that Fig. 5 is based only on a certain number of assays (that have an annotation) and that assays may belong to more than one class. Fig. 5 shows, that the prediction performance over all classes is clearly better than random, which suggests that the scope for the usage of DNNs may be really broad and is not specific to certain well-known targets. Fig. 6 shows that deep learning works well for functional and binding assays.

Fig. 5 Boxplot of assay-AUC values for various assay classes when using a DNN on a combination of ECFP6 and ToxF features. The number after the name of the x-axis label gives the amount of assays in the respective class.

Fig. 6 Boxplot of assay-AUC values for various assay types when using a DNN on a combination of ECFP6 and ToxF features. The number after the name of the x-axis label gives the amount of assays for the respective type.

Methods

Cluster-cross-validation

Cluster-cross-validation⁴ can be considered an advancement of time-split cross-validation, which uses a temporal time split²⁴ to avoid that compounds of the same cluster are part of both the training set and the test set. Since previously used compound series could be continued after the selected time point, time-split cross-validation does, however, not guarantee that compounds of the same cluster are present either only in the training or only in the test set. Cluster-cross-validation, in contrast, identifies clusters of compounds in the database and distributes these to folds, to which cross-validation is then applied.

We identified clusters in ChEMBL by applying single-linkage clustering to all 1 456 020 compounds of the ChEMBL database. Single-linkage clustering is an agglomerative clustering method which is able to find a clustering with guaranteed minimum distances between any two clusters. This is an important property for cluster-cross-validation, as it avoids that a compound in the training set is closer than some minimum distance to a compound in the test set. We used the Jaccard distance on binarized ECFP4 features as a distance measure between any two compounds.

A critical parameter in the agglomerative clustering process is the threshold that determines the granularity of the clustering, that is, how many clusters of what sizes emerge. The exact procedure of how we obtained a value for this parameter and further details on clustering are given in ESI Section S2.3.†

We investigated the difference of the performance estimates based on cluster-cross-validation to that of random cross-validation. As the distribution of actives and inactives can be different for the folds of a target, we tried to keep the unbalancedness structure to a certain degree. We estimated the performance of FNNs with ECPF + ToxF features (see Table 3). The performance estimates are on average 0.02 (p-value of paired Wilcoxon signed rank test 2.8E-51) higher than the ones from cluster-cross-validation indicating that random cross-validation is more optimistic about the performance on future data than cluster-cross-validation.

Table 3 Comparison of performance estimates based on random cross-validation and cluster-cross-validation. The table provides the performances in terms of AUC averaged over the different targets for both random cross-validation and cluster-cross validation. The performance estimates obtained from random cross-validation are on average 0.02 higher, i.e., more optimistic, than the ones from cluster-cross-validation

Cluster-cross-validation	Fold 1:	0.722 ± 0.138	Fold 2:	0.729 ± 0.148	Fold 3:	0.743 ± 0.147
Random cross-validation	Fold I:	0.747 ± 0.145	Fold II:	0.760 ± 0.136	Fold III:	0.754 ± 0.142

---

Hyperparameter selection by nested cluster-cross-validation

In a nested cross-validation procedure,²⁵ various model hyperparameters are tested in an inner loop and the selected hyperparameters are then evaluated in an outer loop, which avoids the hyperparameter selection bias of the performance estimates. For each hyperparameter combination searched, we obtained assay-AUC values from the inner loop and summarized these inner loop assay-AUC values by computing their means. These mean AUC values were used as a criterion to select the best hyperparameter combination for the corresponding outer fold loop. Thus we obtain performance estimates that are unbiased by hyperparameter selection.

Benchmark dataset

The original ChEMBL database is relatively heterogeneous with respect to the assays and their outcomes. It is often unclear which measurement can be considered as active, inactive or unknown. Furthermore, the number of assays varies widely, and there may even be multiple measurement entries in the database. Therefore, we developed a protocol for extracting the benchmark dataset from the ChEMBL database. Details are given in ESI Section S2.1.†

Machine learning methods compared

Here we give a short overview of deep learning and the other compared methods. Further implementation details are given in ESI Section S3.†

Deep learning

We considered three types of deep learning methods. Concretely we looked at standard feed-forward DNNs (FNNs) with real-valued input neurons, graph-based neural networks, and sequence-based neural networks.

A common property, is, that these methods comprise neurons that are arranged hierarchically in layers. The first layer is usually considered as the input layer, where neurons are considered to represent the input features. The following hidden layers consist of hidden neurons with weighted connections to the neurons of the layer below. The activation pattern of these neurons can be considered as an abstract representation of the input, built from features below. The last (i.e., output) layer provides the predictions of the model. A formal description of DNNs is given in ESI Section S3.1.1.† While classical artificial neural networks consist of a small number of neurons, DNNs may comprise thousands of neurons in each layer.⁵⁷

Deep learning naturally enables multitask learning by incorporating multiple tasks into the learning process. This can support the construction of indicative abstract features that are shared across tasks. Especially for tasks with small or imbalanced training sets, multitask learning allows these tasks to borrow features from related tasks, thereby increasing the performance considerably. Fig. 7 emphasizes the fact that multitask learning may be of interest, since it shows that there are many compounds measured by more than one assay.

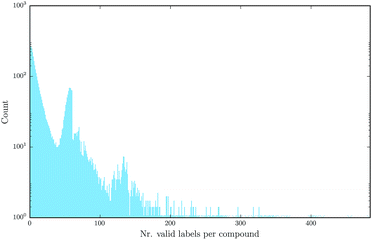Fig. 7 Number of different assay labels (log-scaled) per compound for the finally used benchmark dataset, numbers occurring only once are marked with a star.

For FNNs, the input features are usually properties of the compound structure, e.g., whether a substructure is present in the molecule. We used either a network architecture with rectified linear units^58,59 or a network architecture with scaled exponential linear units⁶⁰ in all hidden layers to avoid vanishing gradients, and logistic sigmoid units in the output layer to constrain values to the range between 0 and 1. The actually used network architecture was determined by hyperparameter selection. For regularization, we used dropout⁶¹ to avoid overfitting. More details, especially on the hyperparameter combinations searched, are given in ESI Section S3.1.2.†

The idea of graph-based neural networks is that these networks learn to extract promising features directly from the graph structure in a similar way as CNNs in image processing do this from raw pixel inputs. Usually, neurons have a hidden state and they represent an atom of the graph. Messages on the hidden states are exchanged between neighboring atoms in the graph and based on incoming messages, the hidden states are updated.⁶² An essential property of graph convolution ideas is that they introduce operations that are invariant to graph isomorphisms. There are several variations of graph convolutional neural networks, where e.g. also edges may have hidden states. Further details on the usage of graph convolutional networks and the hyperparameter combinations searched are given in ESI Section S3.1.3.†

RNNs work on sequences of input feature vectors that may even differ in their length. We used the LSTM architecture, which is based on LSTM memory cells, that were constructed to avoid vanishing gradients. In analogy to FNNs, it is possible to stack multiple layers of LSTM cells. We used an architecture in which we did not predict the assay outcomes, but also used structural properties of the input compound as auxiliary prediction tasks, which should help in training such a sequence-based network architecture. Further, as a compound may have multiple equivalent string representations, we used random representations of the compounds while training to avoid overfitting. Furthermore, dropout was used against overfitting (details on our used LSTM architecture can be found in ESI Section S3.1.4†).

Support vector machines (SVMs)

An SVM is a state-of-the art machine learning method that determines a classification function based on the concept of structural risk minimization. SVMs are widely used in chemoinformatics⁶³ and are among the top-performing methods across all research areas.⁶⁴ Typically, a positive semi-definite similarity measure between data points (i.e., a kernel) is required.

The choice of similarity measure is crucial to the performance of SVMs. In chemoinformatics, the Tanimoto kernel is a popular and performant similarity measure for chemical compounds. We used the Minmax kernel, an extension of the Tanimoto kernel, that can also be applied to real-valued features when analyzing compounds.⁴

A formal description of SVMs, implementation details and the formula of the Minmax kernel can be found in ESI Section S3.2.†

Random forests (RFs)

RF models have a long tradition in chemoinformatics tasks, for instance, in the prediction of assay outcomes.^65–67 RFs work well with different types of chemical descriptors, and their performance is relatively robust with respect to hyperparameter settings. ESI Section S3.3† lists the hyperparameter combinations searched.

K-nearest-neighbour (KNN)

KNN classification is one of the most fundamental classification algorithms in machine learning. KNN depends on a distance metric between data points in order to determine the K nearest neighbours of the data point to be classified. The predicted class label of a data point is then simply a majority vote of the neighbours. The distance function used for KNN and the hyperparameter combinations searched are described in ESI Section S3.4.†

Naive bayes (NB) statistics

Several approaches contrast active samples of a target with the whole (background) compound database, one⁶⁸ of which uses NB statistics to predict whether a compound is likely to become active. The approach computes Laplacian-adjusted probability estimates for the features, which yields individual feature weights that are finally summed to give the predictions. The commercial product “Pipeline Pilot” implements such an approach. A formal description of the application of NB statistics to target prediction along with further implementation details can be found in ESI Section S3.5.†

Similarity ensemble approach (SEA)

SEA is based on the idea that two targets are similar if the ligand sets of targets are similar to one another. The similarity of two ligand sets is computed by the sum of ligand pair similarities that exceed a predefined threshold. The ligand pair similarity is measured as a sum of Tanimoto similarities. To correct for size or chemical composition bias, a correction technique based on the similarity obtained from randomly drawn ligand sets is introduced. This leads to z-scores for similarities between the sets. It is argued that the z-scores conform to an extreme value distribution. Using this extreme value distribution, the probability that a compound is active on a certain target is calculated by assuming that one of the two ligand sets consists only of the compound to be predicted. Details on our reimplementation of SEA can be found in ESI Section S3.6.†

Conclusion

We compared the predictive performance of deep learning to a variety of other drug target prediction methods, avoiding the usual biases in comparison studies of compound target prediction methods. We observed, that FNNs outperform the other methods for drug target prediction. This observation is not specific to a particular feature encoding of the compounds, but generalizes across different types of molecular descriptors. Furthermore, we found that deep learning allows models with high predictive performance to be built for a wide variety of targets. This performance improves as the training dataset increases. We also showed that the performance of deep learning for predicting a certain target is comparable to – and often better than – that of surrogate in vitro assays. Large compound-assay databases, such as ChEMBL, offer sufficient amounts of data to construct highly accurate deep learning models. We envision that further performance improvements could be gained by using in-house databases held by pharmaceutical companies as high-quality, large-scale training sets.

Availability

Dataset and source code are available at: http://www.bioinf.jku.at/research/lsc/index.html.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by the research grants IWT135122 ChemBioBridge, IWT150865 Exaptation of the Flanders, Innovation and Entrepreneurship agency, by the European Union's Horizon 2020 Research and Innovation programme under Grant Agreement no. 671555 (ExCAPE) and by Zalando SE with Research Agreement 01/2016. We thank the NVIDIA Corporation for the GPU donations, Bayer AG with Research Agreement 09/2017, Merck KGaA, Audi JKU Deep Learning Center, Audi Electronic Venture GmbH, LIT grants LSTM4Drive and LIT-2017-3-YOU-003, and FWF grant P 28660-N31.

References

1. D. M. Molina, R. Jafari, M. Ignatushchenko, T. Seki, E. A. Larsson, C. Dan, L. Sreekumar, Y. Cao and P. Nordlund, Science, 2013, 341, 84–87.
2. R. Huang, M. Xia, D.-T. Nguyen, T. Zhao, S. Sakamuru, J. Zhao, S. A. Shahane, A. Rossoshek and A. Simeonov, Front. Environ. Sci. Eng., 2016, 3, 85.
3. J. Ma, R. P. Sheridan, A. Liaw, G. E. Dahl and V. Svetnik, J. Chem. Inf. Model., 2015, 55, 263–274.
4. A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, Front. Environ. Sci. Eng., 2016, 3, 80.
5. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 4, 268–276.
6. M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131.
7. M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 48.
8. X. Yang, J. Zhang, K. Yoshizoe, K. Terayama and K. Tsuda, Sci. Technol. Adv. Mater., 2017, 18, 972–976.
9. K. Preuer, P. Renz, T. Unterthiner, S. Hochreiter and G. Klambauer, arXiv preprint arXiv: 1803.09518, 2018.
10. M. H. Segler, M. Preuss and M. P. Waller, Nature, 2018, 555, 604.
11. K. Preuer, R. P. I. Lewis, S. Hochreiter, A. Bender, K. C. Bulusu and G. Klambauer, Bioinformatics, 2017, 34, 1538–1546.
12. K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Advances in Neural Information Processing Systems 30, 2017, pp. 991–1001.
13. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
14. R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al. , Nat. Mater., 2016, 15, 1120.
15. R. Caruana, Mach. Learn., 1997, 28, 41–75.
16. L. Deng, J. Li, J.-T. Huang, K. Yao, D. Yu, F. Seide, M. Seltzer, G. Zweig, X. He, J. Williams, Y. Gong and A. Acero, Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference, 2013, pp. 8604–8608.
17. Y. Bengio, A. Courville and P. Vincent, IEEE Trans. Pattern Anal. Mach. Intell., 2013, 35, 1798–1828.
18. Y. Bengio, Proceedings of the First International Conference on Statistical Language and Speech Processing, 2013, pp. 1–37.
19. J. Kazius, R. McGuire and R. Bursi, J. Med. Chem., 2005, 48, 312–320.
20. B. Ramsundar, S. Kearnes, P. Riley, D. Webster, D. Konerding and V. Pande, arXiv preprint arXiv: 1502.02072, 2015.
21. S. Kearnes, B. Goldman and V. Pande, arXiv preprint arXiv: 1606.08793, 2016.
22. A. Koutsoukas, K. J. Monaghan, X. Li and J. Huan, J. Cheminf., 2017, 9, 42.
23. A. P. Bento, A. Gaulton, A. Hersey, L. J. Bellis, J. Chambers, M. Davies, F. A. Krüger, Y. Light, L. Mak and S. McGlinchey, et al. , Nucleic Acids Res., 2014, 42, D1083–D1090.
24. R. P. Sheridan, J. Chem. Inf. Model., 2013, 53, 783–790.
25. D. Baumann and K. Baumann, J. Cheminf., 2014, 6, 1.
26. S. Hochreiter and K. Obermayer, Kernel Methods in Computational Biology, MIT Press, 2004, pp. 319–355.
27. T. Kalliokoski, C. Kramer, A. Vulpetti and P. Gedeck, PLoS One, 2013, 8, 1–12.
28. C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297.
29. L. Breiman, Mach. Learn., 2001, 45, 5–32.
30. M. J. Keiser, B. L. Roth, B. N. Armbruster, P. Ernsberger, J. J. Irwin and B. K. Shoichet, Nat. Biotechnol., 2007, 25, 197–206.
31. M. J. Keiser, V. Setola, J. J. Irwin, C. Laggner, A. I. Abbas, S. J. Hufeisen, N. H. Jensen, M. B. Kuijer, R. C. Matos, T. B. Tran, R. Whaley, R. A. Glennon, J. Hert, K. L. Thomas, D. D. Edwards, B. K. Shoichet and B. L. Roth, Nature, 2009, 462, 175–181.
32. M. J. Keiser and J. Hert, Chemogenomics, Humana Press, 2009, pp. 195–205.
33. Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, Proc. IEEE, 1998, 86, 2278–2324.
34. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg and L. Fei-Fei, Int. J. Comput. Vis., 2015, 115, 211–252.
35. A. Krizhevsky, I. Sutskever and G. E. Hinton, Advances in Neural Information Processing Systems 25, 2012, pp. 1097–1105.
36. K. Simonyan and A. Zisserman, arXiv preprint arXiv: 1409.1556, 2014.
37. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke and A. Rabinovich, The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 1–9.
38. D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Advances in Neural Information Processing Systems 28, 2015, pp. 2224–2232.
39. Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530.
40. S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput. Aided Mol. Des., 2016, 30, 595–608.
41. Democratizing Deep-Learning for Drug Discovery, Quantum Chemistry, Materials Science and Biology, https://github.com/deepchem/deepchem, 2016.
42. K. Cho, B. Van Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk and Y. Bengio, arXiv preprint arXiv: 1406.1078, 2014.
43. D. Bahdanau, K. Cho and Y. Bengio, arXiv preprint arXiv: 1409.0473, 2014.
44. I. Sutskever, O. Vinyals and Q. V. Le, Advances in Neural Information Processing Systems 27, 2014, pp. 3104–3112.
45. A. Graves and N. Jaitly, Proceedings of the 31st International Conference on Machine Learning, 2014, pp. II-1764–II-1772.
46. S. Hochreiter, MSc thesis, Institut für Informatik, Lehrstuhl Prof. Dr. Dr. h.c. Brauer, Technische Universität München, 1991.
47. S. Hochreiter, Y. Bengio, P. Frasconi and J. Schmidhuber, A Field Guide to Dynamical Recurrent Networks, IEEE, 2000, pp. 237–244.
48. S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780.
49. D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
50. J. A. Hanley and B. J. McNeil, Radiology, 1982, 143, 29–36.
51. G. E. Dahl, N. Jaitly and R. Salakhutdinov, arXiv preprint arXiv: 1406.1231, 2014.
52. D.-S. Cao, Q.-S. Xu, Q.-N. Hu and Y.-Z. Liang, Bioinformatics, 2013, 29, 1092–1094.
53. G. Hinselmann, L. Rosenbaum, A. Jahn, N. Fechner and A. Zell, J. Cheminf., 2011, 3, 1–14.
54. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
55. S. J. Swamidass, J. Chen, J. Bruand, P. Phung, L. Ralaivola and P. Baldi, Bioinformatics, 2005, 21, i359–i368.
56. J. L. Durant, B. A. Leland, D. R. Henry and J. G. Nourse, J. Chem. Inf. Comput. Sci., 2002, 42, 1273–1280.
57. D. C. Cireşan, U. Meier, L. M. Gambardella and J. Schmidhuber, Neural Networks: Tricks of the Trade, Springer, 2012, pp. 581–598.
58. V. Nair and G. E. Hinton, Proceedings of the 27th International Conference on Machine Learning, 2010, pp. 807–814.
59. X. Glorot, A. Bordes and Y. Bengio, AISTATS, 2011, pp. 315–323.
60. G. Klambauer, T. Unterthiner, A. Mayr and S. Hochreiter, Advances in Neural Information Processing Systems 30, 2017, pp. 972–981.
61. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958.
62. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, arXiv preprint arXiv: 1704.01212, 2017.
63. L. Rosenbaum, G. Hinselmann, A. Jahn and A. Zell, J. Cheminf., 2011, 3, 11.
64. M. Fernández-Delgado, E. Cernadas, S. Barro and D. Amorim, J. Mach. Learn. Res., 2014, 15, 3133–3181.
65. D. S. Palmer, N. M. O'Boyle, R. C. Glen and J. B. Mitchell, J. Chem. Inf. Model., 2007, 47, 150–158.
66. P. G. Polishchuk, E. N. Muratov, A. G. Artemenko, O. G. Kolumbin, N. N. Muratov and V. E. Kuz'min, J. Chem. Inf. Model., 2009, 49, 2481–2488.
67. S. Li, A. Fedorowicz, H. Singh and S. C. Soderholm, J. Chem. Inf. Model., 2005, 45, 952–964.
68. X. Xia, E. G. Maliski, P. Gallant and D. Rogers, J. Med. Chem., 2004, 47, 4463–4470.

---

Footnotes

† Electronic supplementary information (ESI) available: Overview, Data Collection and Clustering, Methods, Results, Appendix. See DOI: 10.1039/c8sc00148k

‡ These authors contributed equally to this work.

---