Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Resolution of minor size differences in a family of heteroleptic coordination cages by trapped ion mobility ESI-MS†
Kristina E.
Ebbert
,
Laura
Schneider
,
André
Platzek
,
Christoph
Drechsler
,
Bin
Chen
,
Robin
Rudolf
and
Guido H.
Clever
 *
*
Fakultät für Chemie und Chemische Biologie, TU Dortmund, Otto-Hahn Straße 6, 44227 Dortmund, Germany. E-mail: guido.clever@tu-dortmund.de
First published on 28th June 2019
Abstract
We report a complex system of heteroleptic coordination cages based on the combination of four bis-monodentate ligands whose backbones only slightly differ in shape and length. cis-[Pd2L2L′2] assemblies cleanly form after addition of PdII cations to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of two shape-complementary ligands, each. When three or even all four ligands are used in combination, the unambiguous discrimination of all individual species in the product mixture becomes difficult by conventional NMR spectroscopic and mass spectrometric methods. Due to steric constraints, the system is restricted to the formation of ten different coordination cages in total, two of which are isomeric. We show that high-resolution trapped ion mobility mass spectrometry (TIMS) allows the clear differentiation of all ten species. Observed size trends could be readily reproduced by the calculation of theoretical values for collisional cross sections (CCS) from geometry-optimized models.
1 mixture of two shape-complementary ligands, each. When three or even all four ligands are used in combination, the unambiguous discrimination of all individual species in the product mixture becomes difficult by conventional NMR spectroscopic and mass spectrometric methods. Due to steric constraints, the system is restricted to the formation of ten different coordination cages in total, two of which are isomeric. We show that high-resolution trapped ion mobility mass spectrometry (TIMS) allows the clear differentiation of all ten species. Observed size trends could be readily reproduced by the calculation of theoretical values for collisional cross sections (CCS) from geometry-optimized models.
Introduction
Metal-mediated self-assembly of organic building blocks into larger supramolecules has yielded a plethora of structures over the last decades.1 Amongst these, coordination cages take a special role due to their guest recognition capabilities and potential to serve as nanoscopic reaction containers.2 Most reported examples have usually been based on one type of organic ligand, each, thus reducing synthetic effort, avoiding the formation of complicated reaction mixtures and simplifying analytical characterization. While this approach has produced a large number of systems with unique structures and functions, for example lantern-shaped, tetrahedral, octahedral, cubic cages and large spheres,3 the restriction to a single ligand component puts a limit on the achievable architectural design and functionality. We and others have therefore recently begun to invest effort in the rational design of multi-ligand heteroleptic coordination cages that form selectively from more than one kind of ligand – mostly under thermodynamic control – without generating statistical mixtures.4 While some of our recently reported approaches make use of donor-site engineering to achieve the formation of heteroleptic assemblies,5 the method forming the basis for the herein reported findings makes use of the size and shape complementarity of pairs of bis-monodentate ligands to selectively form a series of cis-configured [Pd2L2L′2] cages with a bent appearance (Fig. 1).4a,6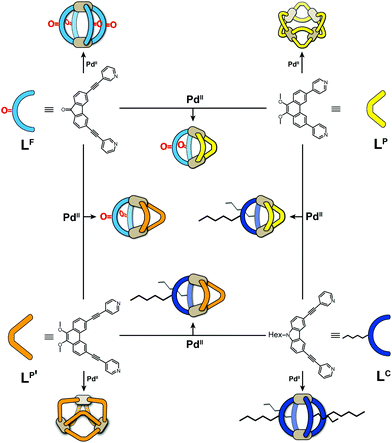 | ||
| Fig. 1 Schematic overview of bis-monodentate ligands LF, LP, LP′ and LC reacting with Pd(II) cations to form homoleptic cages or rings and – by pairwise combination – heteroleptic cages. | ||
2D NMR spectroscopic methods and single crystal diffraction are key methods for the structural characterization of pure samples of such heteroleptic species. However, these techniques show limitations when complex mixtures of species have to be examined. While diffusion ordered (DOSY) NMR spectroscopy is a powerful tool for the discrimination of individual components in a complex mixture, it becomes difficult to deliver unambiguous answers when larger objects show only small size differences and NMR signals of the separate species overlap heavily.7 Since increasing the complexity of supramolecular multi-component mixtures is common practice in the field of systems chemistry, powerful analytical techniques are required to keep track of such a system's composition. Chromatographic methods are often not suited for metallosupramolecular assemblies due to stability issues on the stationary phases. High resolution mass spectrometric analysis has developed into a powerful tool in supramolecular chemistry but cannot readily discriminate between isomeric/isobaric species (except for special cases allowing MSMS fragmentation pattern analysis).8 Furthermore, standard MS methods do not deliver information related to the spatial dimensions of the analytes.
Recently, ion mobility spectrometry (IMS), usually coupled with high-resolution mass spectrometry, is gradually turning into a popular addition to the structural analysis toolbox used in supramolecular chemistry,9 in particular since user-friendly instruments have become commercially available. Among the different techniques that have been developed to unravel the size and shape of a molecule in the gas phase, expressed by its electric potential-driven mobility through a collision gas, trapped ion mobility spectrometry (TIMS) has been identified as an attractive method owing to the high resolution that can be achieved even without having to use metre-long drift tubes.10 We have recently applied this method for the discrimination of photo switchable cage isomers and their host–guest complexes,11 the visualization of guest-induced expansion/contraction of helicene-based cages,12 and the analysis of G-quadruplex DNA folding states.13
Here, we show how ion mobility mass spectrometry can be used to clearly differentiate components in a mixture of up to ten different heteroleptic coordination cages, so close in size that DOSY NMR spectroscopy is not able to deliver an unambiguous differentiation (Fig. 1).
The herein described system is based on our recently developed approach of integrative self-sorting heteroleptic coordination cages from pairs of bis-monodentate ligands with wider and smaller donor angles, respectively.6 We chose to use two ligands with angles of 80° based on a fluorenone-, respectively carbazole-backbone (LF and LC) and two phenanthrene-based ligands (LP and LP′) which differ only in the length of their coordinating arms while both have donor angles of about 60°. While heteroleptic cage [Pd2LC2LP2] has been previously reported by us,6 all other systems described herein are new.
Results and discussion
All heteroleptic cages were found to form selectively by adding a stoichiometric amount of PdII cations to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
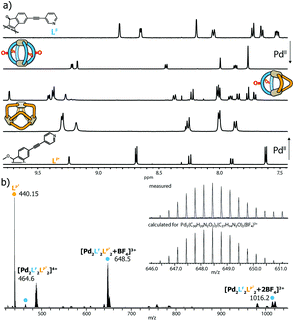
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of two matching banana-shaped ligands in DMSO or acetonitrile (details see ESI†). Representative for all examined systems, the standard analytical data for the characterization of the LF/LP′ system (i.e. showing the 1H NMR traces of homoleptic [Pd2LF4]4+, homoleptic [Pd3LP′6]6+ and heteroleptic [Pd2LF2LP′2]4+ plus the ESI mass spectrum of the latter one) is shown in Fig. 2.
1 mixture of two matching banana-shaped ligands in DMSO or acetonitrile (details see ESI†). Representative for all examined systems, the standard analytical data for the characterization of the LF/LP′ system (i.e. showing the 1H NMR traces of homoleptic [Pd2LF4]4+, homoleptic [Pd3LP′6]6+ and heteroleptic [Pd2LF2LP′2]4+ plus the ESI mass spectrum of the latter one) is shown in Fig. 2.
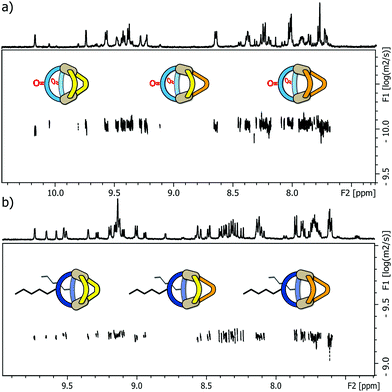
Next, we examined the behaviour of ternary systems: with ligands LP and LP′ only differing by the lengths of their coordinating arms, we first prepared a system consisting of two equivalents of LF one equivalent of LP and one equivalent of LP′ (besides the stoichiometric amount of PdII cations). ESI-MS analysis of the sample indicated the formation of three different species [Pd2LF2LPxLP′y] with x + y = 2; x = {0–2}; y = {0–2}. The same situation was observed when repeating the experiment with LC instead of LF, namely the formation of [Pd2LC2LPxLP′y] with x + y = 2; x = {0–2}; y = {0–2}. While this three-component mixture does not represent an entirely statistic outcome of all possible combinations of the three ligands (since LF or LC, respectively, are always contributing two ligands to the structure), it certainly posed a quite sophisticated analytical problem due to the structural similarity of the contained species. As a result, we observed very complex 1H NMR spectra for the ternary mixtures (see ESI†) in which unambiguous signal assignment was not only hampered by an extensive peak overlap between the three components, but also by an additional symmetry-related signal splitting in compounds [Pd2LF2LP1LP′1] and [Pd2LC2LP1LP′1], respectively. We tried to distinguish the three heteroleptic cages, each, using standard 1H DOSY NMR routines but also here, a reliable compound discrimination was thwarted by multiple signal overlaps and the substantial size similarity of the contained species. The recorded 1H DOSY NMR spectra of both mixtures are shown in Fig. 3.
The DOSY spectra show, that for these minor size differences a clear differentiation of the cages from each other is almost impossible, not to mention obtaining reliable values for the respective diffusion coefficients.
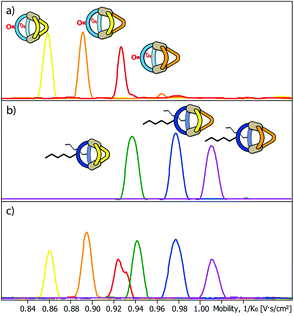
Next, we subjected the mixtures to a Trapped Ion Mobility Spectrometry (TIMS) analysis on a Bruker timsTOF instrument which was indeed found to be capable of clearly discriminating the different cage species by their spatial dimension in the gas phase. We first analysed the two mixtures [Pd2LF2LPxLP′y] and [Pd2LC2LPxLP′y] (x + y = 2; x = {0–2}; y = {0–2}) in separate measurements. In every measurement the [Pd2LF2LPxLP′y + BF4]3+ respectively [Pd2LC2LPxLP′y + BF4]3+ (Fig. 4a and b) species was chosen for the mobility comparison as it represented the most prominent peak in the ESI-MS spectrum (see ESI†). For both systems, the TIMS measurement delivered baseline separated signals for the contained species with average peak-to-peak separations of 0.024 V s cm−2 and average peak widths of 0.029 V s cm−2 (baseline) and 0.014 V s cm−2 (FWHM).
Being able to achieve a very clear differentiation within the two ternary systems, we decided to combine the two mixtures and tried to obtain separate ion mobility values for each of the six species from the resulting mixture (Fig. 4c). The measurement was performed right after combining the mixtures in order to avoid ligand shuffling between LF and LC, both sharing almost the same donor geometry. While the absolute peak positions were found show minor deviations when comparing the mobilograms of the ternary mixtures (Fig. 4a and b) with the six-cage mixture (Fig. 4c), all six species can be unambiguously discriminated and assigned to their molecular structures.
TIMS analysis shows that the species containing the fluorenone-based ligand LF have an overall lower ion mobility, and thus a smaller collisional cross section (CCS), serving as an isotropic measure for comparing cage dimensions,9 than the species with the carbazole-based ligand LC, even though they share a very similar backbone structure (all values refer to the results shown in Fig. 4a and b; details see ESI†). The effect can thus be ascribed to the hexyl-chains attached to the carbazole-backbone. The significant difference in ion mobility suggests, that the chains do not seem to completely fold back to the backbone in the gas phase but instead significantly contribute to the spatial extent of the [Pd2LC2LPxLP′y + BF4]3+ species. The same effect can also be seen when comparing the 1H DOSY NMR spectra of the two mixtures where the [Pd2LF2LPxLP′y] species have a larger diffusion coefficient than the [Pd2LC2LPxLP′y] species (x + y = 2; x = {0–2}; y = {0–2}) corresponding to an overall smaller hydrodynamic radius in comparison to the latter (Fig. 3). It should be noted, however, that care has to be taken when comparing the behaviour of the alkyl chains in the gas and solution phase, since London dispersion effects will dominate the interaction of the chains with the cage's core in the former case while chain-solvent interactions will be more decisive in the latter case.
Remarkably, ion mobility analysis – in tandem with mass spectrometry – allows the detection of quite small size differences. For example, compounds [Pd2LF2LP′2 + BF4]3+ and [Pd2LC2LP2 + BF4]3+ show only a small mobility difference (Fig. 4c). Nevertheless, ion mobility mass spectrometry allows their clear differentiation in the six-cage mixture for two reasons: (a) their different mass allows the superposition of mass-selected mobilograms even when both species are parts of the same sample and (b) the high resolution of the TIMS analyser yields a clear separation of the peak maxima. Interestingly, two mobilities can be assigned to the m/z value corresponding to [Pd2LF2LP′2 + BF4]3+ (clearly visible as double-peak in Fig. 4a and in the measurement of the clean heteroleptic cage depicted in the ESI†). As possible explanation we suggest the existence of two energetically locked cage conformations under the given gas-phase conditions. Arguing with a tentative trans-arrangement of the contained ligands, however, can be ruled out based on strain calculations comparing cis- and trans-isomers of [Pd2LC2LP2].6
Encouraged by these results, we prepared a sample by mixing one equivalent of every ligand (4 eq. in total) followed by the addition of two equivalents of PdII cations. Where we prevented LC- and LF-containing species from mixing in the previous experiment, we were now aiming for complete ligand shuffling. Due to the almost identical shape of LC and LF, we expected them to appear in the formed cages in a statistical manner. The distinct shape complementarity between L and L′, however, only allows for the formation of Pd2L2L′2 species in which L must be either LC or LF and L′ must be LP or LP′. This restriction was expected to lead to the formation of ten distinct coordination cages of which two are isomers, carrying all four ligands in a cis (LF next to LP) or trans (LF opposite to LP) arrangement. As it has been stated before, differentiation of most species can be made based on their mass alone. This, however, does not apply to the two isomers which do not only have the exact same mass but also a very similar shape and size. The mobilogram obtained from the TIMS measurement of the ten cage mixture is shown in Fig. 5.
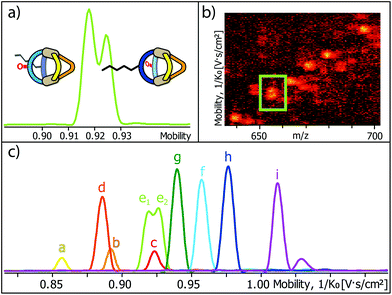 | ||
| Fig. 5 (a) High resolution TIMS mobilogram allowing the discrimination of cis-[Pd2LCLFLPLP′ + BF4]3+ and trans-[Pd2LCLFLPLP′ + BF4]3+; (b) partial heat map and (c) full mobilogram of the simultaneous ion mobility measurement of all ten coordination cages; assignments a–i correspond to cages shown in Fig. 6. | ||
The measurement shows that distinguishing all ten cages by high resolution trapped ion mobility is indeed possible, including the isomeric cis and trans-[Pd2LCLFLPLP′ + BF4]3+ species with an m/z value of 656.15 (Fig. 5a–c). It should be noted that these isomers only differ by 4.3 Å2 (0.8% with an achieved resolution of up to 160 1/K0) in their collisional cross sections.
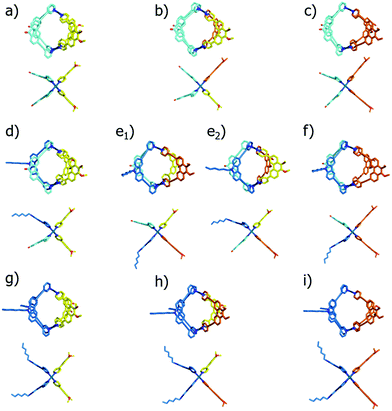
In order to illustrate and theoretically reproduce the structural differences between all examined cage derivatives, we prepared molecular models shown in Fig. 6 by geometry optimization on a semi-empiric (PM6) level of theory using the Spartan ‘14 software’.14 While the models show that the height of the cages (in direction of the Pd–Pd axis) remains almost the same, the average diameters differ significantly.
To further validate the results from the ion mobility measurements and to yield an assignment for the isomeric cage species to the corresponding mobilities, we chose two in silico approaches for calculating theoretical CCS (tCCS) values via the programs IMoS,15 using the ‘projected area method’ which averages the projected 2D area according to van der Waals radii, and a modified version of MOBCAL,16 using a ‘trajectory method’ which simulates the interaction of the analyte with the collision gas molecules. As the factor for compensating the neglect of momentum transfer and long-range potential interactions17 for the ‘projected area method’ a value ξ = 1.2 was chosen. In preparation for these calculations we used a new, efficient method for geometry optimization on a semi-empiric level, namely the GFN-xTB method developed by Grimme et al.18 As an alternative to MOBCAL and IMoS, another software based on the trajectory method, collidoscope,19 was used but found to perform worse to yield reasonable results and correct trends for this system (see ESI†). Table 1 compares the experimental with the theoretical values.
| Species | eCCS [Å2] | tCCSPA [Å2] | tCCSM [Å2] |
|---|---|---|---|
| a: [Pd2LF2LP2 + BF4]3+ | 526.3 ± 0.7 | 491.0 | 540.8 |
| b: [Pd2LF2LPLP′ + BF4]3+ | 547.9 ± 0.5 | 515.1 | 566.9 |
| c: [Pd2LF2LP′2 + BF4]3+ | 566.1 ± 1.3 | 543.7 | 600.4 |
| d: [Pd2LCLFLP2 + BF4]3+ | 543.8 ± 0.4 | 526.1 | 572.9 |
| e1: [Pd2LCLFLPLP′ + BF4]3+ | 562.9 ± 1.0 | 553.7 | 601.8 |
| e2: [Pd2LCLFLPLP′ + BF4]3+ | 567.2 ± 0.8 | 556.6 | 602.6 |
| f: [Pd2LCLFLP′2 + BF4]3+ | 587.2 ± 0.7 | 581.7 | 630.6 |
| g: [Pd2LC2LP2 + BF4]3+ | 575.2 ± 1.1 | 565.7 | 611.9 |
| h: [Pd2LC2LPLP′ + BF4]3+ | 598.2 ± 1.0 | 591.1 | 633.8 |
| i: [Pd2LC2LP′2 + BF4]3+ | 619.1 ± 1.2 | 616.7 | 664.8 |
Theoretical values derived from the ‘projected area method’ and the ‘trajectory method’ were both found to fit the experimentally observed values quite well (Table 1; Fig. 7). While MOBCAL shows an average overestimation of 33.2 Å2 (6%), IMoS gives a slight underestimation of 15.2 Å2 (2%). Most pleasingly, both calculation methods confirm the order in the assignment of the two isomers [Pd2LCLFLPLP′ + BF4]3+ to the observed peaks in the mobilogram, although these structures are extremely close in structure and size. We assume that remaining deviations between experimental and calculated values are in part caused by simplifying the analysis to single, geometry-optimized conformers. Consequently, our current efforts focus on systematic investigations of Boltzmann-weighted conformational distributions for structurally flexible species.
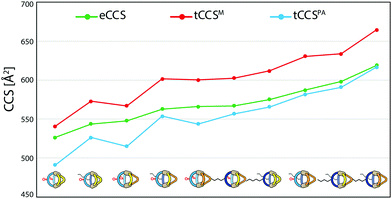 | ||
| Fig. 7 Graphical representation of the measured CCS values (eCCS, green) compared to the calculated CCS values using MOBCAL (tCCSM, red) and IMoS (tCCSPA, blue). | ||
Conclusions
With supramolecular self-assemblies becoming more and more complex over the past years, both in terms of individual structures as well as complex system composition, researchers in the field are in need of new powerful analytical methods. The herein introduced system consists of ten heteroleptic cages, two of them being isomers, very close in size, that standard DOSY NMR analytics could not resolve. Trapped ion mobility mass spectrometry (TIMS), however, proved to be a valuable tool for analysing such a complex system. We were not only able to differentiate the cage species from a mixture of three different heteroleptic cages but could furthermore show that discrimination is even possible from a six- and even ten-component system while the cages feature differences in their radii of less than 0.1 Å. Furthermore, the theoretical calculation of collisional cross sections allowed us to reproduce the experimentally found size trends and unambiguously assign the signals of two isomeric metallo-supramolecular assemblies, extremely close in structure and size.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (CL489/2-2, CL489/3-2 [SPP1807] and GRK2376 “Confinement-controlled Chemistry” – project number 331085229) and the European Research Council, ERC Consolidator grant 683083 (RAMSES) for financial support. We thank Dr Julian Holstein for help with the determination of theoretical CCS data. We thank Dr Witold Bloch for ligand LP, and Prof. Dr Wolf Hiller and team for support with NMR measurements.Notes and references
-
(a) B. H. Northrop, Y.-R. Zheng, K.-W. Chi and P. J. Stang, Acc. Chem. Res., 2009, 42, 1554 CrossRef CAS PubMed
; (b) R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810 CrossRef CAS PubMed
; (c) M. M. J. Smulders, I. A. Riddell, C. Browne and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728 RSC
.
- G. H. Clever and P. M. Punt, Acc. Chem. Res., 2017, 50, 2233 CrossRef CAS PubMed
.
-
(a) S. Saha, I. Regeni and G. H. Clever, Coord. Chem. Rev., 2018, 374, 1 CrossRef CAS
; (b) R. Custelcean, Chem. Soc. Rev., 2014, 43, 1813 RSC
; (c) L. R. Holloway, P. M. Bogie and R. J. Hooley, Dalton Trans., 2017, 46, 14719 RSC
.
-
(a) W. M. Bloch and G. H. Clever, Chem. Commun., 2017, 53, 8506 RSC
; (b) S. Mukherjee and P. S. Mukherjee, Chem. Commun., 2014, 50, 2239 RSC
; (c) S. Pullen and G. H. Clever, Acc. Chem. Res., 2018, 51, 3052 CrossRef CAS PubMed
; (d) D. Preston, J. E. Barnsley, K. C. Gordon and J. D. Crowley, J. Am. Chem. Soc., 2016, 138, 10578 CrossRef CAS PubMed
; (e) B. Mondal, K. Acharyya, P. Howlader and P. S. Mukherjee, J. Am. Chem. Soc., 2016, 138, 1709 CrossRef CAS PubMed
; (f) L. Zhang, Y.-J. Lin, Z.-H. Li and G.-X. Jin, J. Am. Chem. Soc., 2015, 137, 13670 CrossRef CAS PubMed
; (g) Q.-F. Sun, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2014, 53, 13510 CrossRef CAS PubMed
; (h) M. Yamanaka, Y. Yamada, Y. Sei, K. Yamaguchi and K. Kobayashi, J. Am. Chem. Soc., 2006, 128, 1531 CrossRef CAS PubMed
.
- R. Zhu, W. M. Bloch, J. J. Holstein, S. Mandal, L. V. Schäfer and G. H. Clever, Chem. – Eur. J., 2018, 24, 12976 CrossRef CAS PubMed
.
-
(a) W. M. Bloch, Y. Abe, J. J. Holstein, C. M. Wandtke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2016, 138, 13750 CrossRef CAS PubMed
; (b) W. M. Bloch, J. J. Holstein, W. Hiller and G. H. Clever, Angew. Chem., Int. Ed., 2017, 56, 8285 CrossRef CAS PubMed
; (c) S. Saha, B. Holzapfel, Y.-T. Chen, K. Terlinden, P. Lill, C. Gatsogiannis, H. Rehage and G. H. Clever, J. Am. Chem. Soc., 2018, 140, 17384 CrossRef CAS PubMed
.
-
(a) L. Avram and Y. Cohen, Chem. Soc. Rev., 2015, 44, 586 RSC
; (b) S. V. Kharlamov and S. K. Latypov, Russ. Chem. Rev., 2010, 79, 635 CrossRef CAS
; (c) A. Pastor and E. Martinez-Viviente, Coord. Chem. Rev., 2008, 252, 2314 CrossRef CAS
.
-
(a) C. A. Schalley, Mass Spectrom. Rev., 2001, 20, 253 CrossRef CAS PubMed
; (b) Analytical Methods in Supramolecular Chemistry, ed. C. A. Schalley, WILEY-VCH, Weinheim, Germany, 2007 Search PubMed
; (c) Z. Qi, T. Heinrich, S. Moorthy and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 515 RSC
.
-
(a) E. Kalenius, M. Groessl and K. Rissanen, Nat. Rev. Chem., 2019, 3, 4 CrossRef CAS
; (b) M. Wang, C. Wang, X.-Q. Hao, X. Li, T.-J. Vaughn, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, M.-P. Song, H.-B. Yang and X. Li, J. Am. Chem. Soc., 2014, 136, 10499 CrossRef CAS PubMed
; (c) C. A. Scarff, J. R. Snelling, M. M. Knust, C. L. Wilkins and J. H. Scrivens, J. Am. Chem. Soc., 2012, 134(22), 9193 CrossRef CAS PubMed
; (d) E. R. Brocker, S. E. Anderson, B. H. Northrop, P. J. Stang and M. T. Bowers, J. Am. Chem. Soc., 2010, 132(38), 13486 CrossRef CAS PubMed
; (e) Y.-T. Chan, X. Li, J. Yu, G. A. Carri, C. N. Moorefield, G. R. Newkome and C. Wesdemiotis, J. Am. Chem. Soc., 2011, 133(31), 11967 CrossRef CAS PubMed
; (f) J. Ujma, M. De Cecco, O. Chepelin, H. Levene, C. Moffat, S.-J. Pike, P.-J. Lusby and P.-E. Barran, Chem. Commun., 2012, 48, 4423 RSC
; (g) P. J. Robbins, A. J. Surman, J. Thiel, D.-L. Long and L. Cronin, Chem. Commun., 2013, 49, 1909 RSC
; (h) P. Bonakdarzadeh, F. Topic, E. Kalenius, S. Bhowmik, S. Sato, M. Groessl, R. Knochenmuss and K. Rissanen, Inorg. Chem., 2015, 54, 6055 CrossRef CAS PubMed
; (i) J. Thiel, D. Yang, M. H. Rosnes, X. Liu, C. Yvon, S. E. Kelly, Y.-F. Song, D.-L. Long and L. Cronin, Angew. Chem., Int. Ed., 2011, 50, 8871 CrossRef CAS PubMed
; (j) X. Li, Y.-T. Chan, M. Casiano-Maldonado, J. Yu, G. A. Carri, G. R. Newkome and C. Wesdemiotis, Anal. Chem., 2011, 83, 6667 CrossRef CAS PubMed
; (k) C. Lapthorn, F. Pullen and B. Z. Chowdhry, Mass Spectrom. Rev., 2013, 32, 43 CrossRef CAS PubMed
; (l) J. M. Ludlow, M. Tominaga, Y. Chujo, A. Schultz, X. Lu, T. Xie, K. Guo, C. N. Moorefield, C. Wesdemiotis and G. R. Newkome, Dalton Trans., 2014, 43, 9604 RSC
; (m) C. Wang, X.-Q. Hao, M. Wang, C. Guo, B. Xu, E. N. Tan, Y.-Y. Zhang, Y. Yu, Z.-Y. Li, H.-B. Yang, M.-P. Song and X. Li, Chem. Sci., 2014, 5, 1221 RSC
; (n) N. J. Rijs, T. Weiske, M. Schlangen and H. Schwarz, Anal. Chem., 2015, 87, 9769 CrossRef CAS PubMed
; (o) F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281 CrossRef CAS PubMed
; (p) F. J. Rizzuto, M. Kiefer and J. R. Nitschke, Chem. Sci., 2018, 9, 1925 RSC
; (q) K. Caprice, M. Pupier, A. Kruve, C. A. Schalley and F. B. L. Cougnon, Chem. Sci., 2018, 9, 1317 RSC
.
-
(a) J.-F. Greisch, J. Chmela, M. Harding, D. Wunderlich, B. Schäfer, M. Ruben, W. Klopper, D. Schooss and M. M. Kappes, Phys. Chem. Chem. Phys., 2017, 19, 6105 RSC
; (b) J.-F. Greisch, P. Weis, K. Brendle, M. M. Kappes, J. R. N. Haler, J. Far, E. De Pauw, C. Albers, S. Bay, T. Wurm, M. Rudolph, J. Schulmeister and A. S. K. Hashmi, Organometallics, 2018, 37, 1493 CrossRef CAS
.
- R. Li, J. J. Holstein, W. G. Hiller, J. Andréasson and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 2097 CrossRef CAS PubMed
.
- T. R. Schulte, J. J. Holstein and G. H. Clever, Angew. Chem., Int. Ed., 2019, 58, 5526 CrossRef PubMed
.
- P. M. Punt and G. H. Clever, Chem. Sci., 2019, 10, 2513 RSC
.
-
Spartan ‘14 Version 1.1.8, Wavefunction, Inc., Irvine, CA, 2014 Search PubMed
.
- C. Larriba and C. J. Hogan, J. Phys. Chem., 2013, 19, 3887 CrossRef PubMed
.
-
(a) M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082 CrossRef CAS
; (b) I. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Anal. Chem., 2012, 84, 1026 CrossRef CAS PubMed
.
- C. Larriba and C. J. Hogan, J. Comput. Phys., 2013, 251, 344 CrossRef CAS
.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989 CrossRef CAS PubMed
.
- S. A. Ewing, M. T. Donor, J. W. Wilson and J. S. Prell, J. Am. Soc. Mass. Spectrom., 2017, 28, 587 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9dt01814j |
| This journal is © The Royal Society of Chemistry 2019 |