Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolution of the reactive surface area of ferrihydrite: time, pH, and temperature dependency of growth by Ostwald ripening†
Tjisse
Hiemstra
 *,
Juan C.
Mendez
*,
Juan C.
Mendez
 and
Jiayu
Li
and
Jiayu
Li
Department of Soil Chemistry, Wageningen University, P.O. Box 47, 6700 AA Wageningen, The Netherlands. E-mail: tjisse.hiemstra@wur.nl; Tel: +31 317 48 2342
First published on 4th February 2019
Abstract
Surface area is a crucial property of metal oxides for scaling ion adsorption phenomena. For ferrihydrite (Fh), the value is uncertain. Moreover, it rapidly changes with time, pH, and temperature. In this study, the dynamic change of the reactive surface area has been probed with phosphate for ferrihydrite, produced by ultra-fast neutralization at 20 °C. The initial nanoparticles are very small (d ∼ 1.68 nm), have a remarkably large specific surface area (A ∼ 1100 m2 g−1), and contain on average only 45 Fe atoms. Our data reveal the rapid change of the surface area showing that the rate of growth decreases by nearly three orders of magnitude (R ∼ 0.01–10 μmol Fe m−2 h−1) within one week of ageing. The rate of growth is proportional to the square of the super saturation of the solution (Qso/Kso)2, which suggests a rate limitation by dual attachment of Fe to a surface site of growth. This process is significantly hindered by the presence of weakly bound organic molecules, particularly at low pH, implying for soils that natural organic matter may considerably contribute to the kinetic stability of the natural iron oxide fraction. Our data also show that the reaction pathways are very different in NaNO3 and NaCl solutions. The decrease of surface area in NaNO3, prepared in traditional batch experiments, can be described excellently with the above rate law implemented in our dynamic model. This model also covers the temperature dependency (4–120 °C) of Fh ageing using an activation energy of Ea = 68 ± 4 kJ mol−1. For traditionally prepared 2LFh, our model suggests that with solely dual Fe attachment, the growth of the primary particles is limited to d ∼ 3–4 nm (A ∼ 350–500 m2 g−1). Larger particles can be formed by oriented attachment of particles, particularly at a high temperature. Using forced hydrolysis at 75 °C, large particles (d ∼ 5.5 nm) can also be produced directly. According to our model, Ostwald ripening of such 6LFh particles will be limited due to their low solubility.
Environmental significanceIon adsorption data require scaling to the specific surface area. For ferrihydrite, this crucial property is continuously changing with time due to Ostwald ripening. This change has been traced as a function of pH and temperature covering the time scale of minutes to seven days using phosphate as probe ion. The collected data give insight into the mechanism and rate of growth, i.e. dual Fe attachment limited by the size dependent solubility of ferrihydrite. Implemented in a dynamic model, it discloses the ultra-small initial size of Fh particles and predicts the subsequent change of surface area and particle size. It allows a tunable synthesis of this nanomaterial and a suitable scaling of its ion adsorption properties, improving the development of thermodynamic ion adsorption databases. |
Introduction
Ferrihydrite (Fh) is a nanoparticle omnipresent in nature and used in environmental engineering. Its properties contribute to the fate of many elements in the geochemical cycle and environmental technology. Ferrihydrite nanoparticles are highly reactive and have a high ion adsorption capacity that is relevant for applications. For this reason, it is used and widely studied as model material to elucidate the adsorption of cations, anions, and organic matter.1–19 The surface area of ferrihydrite is an essential characteristic particularly from the perspective of surface complexation modelling. One reason is that ferrihydrite particles are usually charged. This charge is scaled to a surface area. It allows calculation of the variable electrostatic energy contribution that largely controls the variation in binding of ions to surfaces in relation to solution conditions.7,20–24 In addition, the supposed surface area determines the number of available adsorption sites at a given surface site density. Therefore, proper scaling is crucial for describing ion adsorption behavior of Fh.Ferrihydrite is easily synthesized in the lab.25 However, variations in protocols lead to different and not well-known surface areas.26,27 Moreover, the surface area of ferrihydrite will decrease with time because nanoparticles are thermodynamically unstable and will spontaneously grow. For ferrihydrite, the rate of change depends on controlling factors such as pH, adsorbed ions, and temperature.28
Relatively, little information is available about the evolution of the reactive surface area and particle size of Fh immediately after preparing the nanomaterial for use in for instance ion adsorption experiments. Formation of ferrihydrite starts with nucleation and it is followed by the binding of yet unreacted Fe(III), still present in the solution phase. The combination of nucleation and supplementary Fe adsorption results in a polydisperse suspension that initially contains ultra-small nanoparticles with a very high surface area, a high reactivity, and a high instability.
In a Fh suspension, the smallest particles will maintain a labile equilibrium between Fe in solution and the solid phase.29 Fh particles, larger than a critical size, will spontaneously grow at the expense of the smaller particles that dissolve. This will lead to an increase of the mean particle size. This process of simultaneous growth and dissolution was first described by Ostwald,30 and therefore, we will refer to this process of coarsening as Ostwald ripening (OR).
For relatively large Fh particles, the rate of growth by classical Ostwald ripening becomes very small, as will be demonstrated in the present study. Nevertheless, experimental data show that Fh particles can still increase significantly in size.31 This is due to growth by oriented particle attachment.32 As soon as the Fh particles become sufficiently large, patches of specific crystal faces may develop that allow oriented attachment (OA).33 Even larger particles may form by fusion as shown for ZnS.34 Self-assembly of primary Fh particles results in rod-shaped entities as shown with TEM by Murphy et al.35 and more recently, by Burleson and Penn.31 These units get a typical aspect ratio of 5 ± 1.31,35 The process of oriented particle attachment typically occurs for Fh particles with a size near ∼4 nm and larger.33 The rate of this particle–particle interaction is second-order-dependent on the suspension concentration of the primary nanoparticles and has a rate constant that depends on the pH and interface structure.36 The process is most evident during aging at high temperature (60–120 °C) and high pH (10–12).31
Ultimately, ferrihydrite transforms into more stable Fe (hydr)oxides. In the presence of dissolved Fe(II), the conversion is accelerated,37 forming lepidocrocite and goethite within hours. Otherwise, Fh may convert into goethite, hematite, or maghemite.38–41 This conversion occurs at a relatively large particle size29 and therefore, it has often been studied at hydrothermal conditions. To quantify the degree of transformation, the difference in rate of dissolution in an oxalate42–44 or ascorbate solution45 has been used to assess the amount of Fh left at transformation, or X-ray diffraction and/or EXAFS is used to estimate the amount of crystalline material formed.41,46,47
The initial size of primary Fh nanoparticles immediately formed after instantaneous hydrolysis of Fe(III) upon base addition is very small but not well known. It has been proposed that the initial formation of Fh is via the formation of ultra-small Fe13 nuclei48 with a Keggin structure having one central tetrahedral Fe. Similar clusters may form in ferritin when loaded with little Fe.2 Fe13 nuclei are stable at very acid conditions but they grow above pH ∼ 2 to ferrihydrite.48 This growth is driven by the adsorption of dissolved Fe-complexes such as dimers.49,50 Immediately after ultrafast synthesis of Fh at room temperature in a NaCl solution,51 the particles have a mean particle size of d ∼ 1.8 nm, a specific surface area of A ∼ 1000 m2 g−1, and contain nFe ∼ 60 Fe.2
With classical protocols for Fh synthesis, the specific surface area can be significantly smaller than with fast hydrolysis. Traditionally synthesized two-line ferrihydrite usually has a specific surface area in the range of just A ∼ 530–710 m2 g−1 when kept in the wet state.27 The corresponding mean particle size is between d ∼ 2.3–2.9 nm and the number of Fe per particle is nFe ∼ 140–325 Fe. When dried, the particles are irreversibly bound together in porous aggregates having a significantly lower reactive surface area.7,16,52–55
The above overview illustrates that the particle size and surface area of Fh ultimately used in laboratory experiments may largely differ from the nanoparticles initially formed. At storage, the surface area will further decrease. The present study is meant to quantify the rate of ageing of freshly prepared Fh. We will study the change in reactive surface area of Fh in NaNO3 for a time scale up to one week, covering a particle size range of d ∼ 1.7–3 nm. We like to reveal the factors that control the change in specific surface area. The challenge is to elucidate the underlying mechanism of growth of the primary Fh particles at Ostwald ripening in the early stage of growth. The ultimate goal is to develop a mechanistic model for describing the time-dependent change of particle size and surface area once the initial nanoparticles have been formed. With the collected insights, we also hope to disclose the size of the initial particles, immediately after formation.
There are several approaches to assess the reactive surface area of Fh. Traditionally the specific surface area of metal (hydr) oxides is determined by probing the surface with gas molecules (N2, Ar, and Kr). For oxides in general, it gives good results compared to other methods.56 The BET equation is used to derive the specific surface area from the collected gas adsorption data. This method cannot be applied to assess the specific surface area of Fh nanoparticles in the wet state. Use of transmission electron microscopy (TEM) can be seen as an alternative, but the approach is experimentally challenging as fresh Fh particles are very small, usually strongly aggregated, and have a particle size distribution.40,57–60 In case of ZnS nanoparticles, peak broadening at X-ray diffraction has been used34 to derive the mean particle size. The translation of size to specific surface area requires information about the particle shape,61 while particle porosity should be unimportant.
Davis and Leckie62 have suggested to use H+ as probe ion to assess the specific surface area of freshly-prepared Fh. In that approach, the pH-dependent proton adsorption is interpreted with surface complexation modeling. Basic assumptions are the value of the capacitance of the inner Stern layer and the value of the molar mass of the Fh. Both are strongly size-dependent2 but its variation can be consistently included, making the specific surface area the only adjustable parameter in a 1-pK approach.27 Applying this approach to H+ adsorption data from literature reveals a specific surface area ranging from 530–710 m2 g−1 for the various Fh preparations.27 The upper value corresponds to particles with a mean size of 2.3 nm, in agreement with TEM data for freshly prepared Fh without specific ageing.40
An alternative to H+ as probe ion is the use of PO4 ions.2 Use of the latter has the advantage that the adsorption of PO4 can be measured easily and accurately, since this anion has a high affinity for Fe. Comparison of the results found with proton titrations suggests good agreement27 and is further supported by yet unpublished data. In the approach, the CD and MUSIC model recently developed for Fh has been used2 and will also be applied in the present study.
In the present work, we will study the dynamic change of the reactive surface area of Fh kept in the wet state. We will start by producing Fh with high-speed neutralization of a Fe(III) nitrate solution with base, mixed in a flow chamber. For this material, the change of the specific surface area will be studied at a time scale between 0.1 hour and ∼7 days for pH values of 5–9, maintained by means of organic pH buffer solutions, similarly as used recently by Mao et al.51 In the second set of experiments, we will study the time and pH dependent ageing of traditionally produced Fh, and we will include in that study the temperature dependency (4–20 °C). The results will be compared to data for Oswald ripening of primary particles at high temperature (60–120 °C) collected with TEM.31 For the latter data, we will show that the observed growth of the primary particles can be described with the same model that we developed for our freshly prepared Fh.
Experimental
Fh was produced by neutralizing a Fe(III) nitrate solution with NaOH, which was subsequently aged. The experiments were done in the presence and absence of organic pH buffers. In the latter case, temperature dependency was studied too. At each reaction time and pH condition, the specific surface area was measured using phosphate as probe ion. The collected PO4 adsorption isotherms or edges were interpreted with the charge distribution (CD) and multiple site complexation (MUSIC) model of Hiemstra and Zhao,2 making the specific surface area the only adjustable parameter. From the value of the specific surface area, the mean particle size and number of Fe ions per particle were calculated.Ferrihydrite synthesis
For ageing, the suspensions produced were transferred into closed plastic bottles and shaken with a reciprocal shaker (180 strokes per minute). At a predefined reaction time between 0.1 hour and 7 days, the suspension was characterized with a PO4 adsorption experiment using 6 different initial PO4 concentrations, and the actual Fe concentration (∼45 mM) was measured using Inductively coupled plasma optical emission spectrometry (ICP-OES) after dissolving a sub sample in a final concentration of 0.1 M HNO3.
In some cases, the pH was slightly changed after re-suspending the particles in the final background electrolyte solution. In that case, the pH was re-adjusted to the target value by using either 0.01 M HNO3 or 0.01 M NaOH solution. These ferrihydrite suspensions were aged in a closed bottle at 20 °C for 4 hours since neutralization. Part of this stock suspension was subsequently kept at 20 °C while another part was stored at 4 °C to determine the temperature dependency of ageing. The surface area of both suspensions was measured with PO4 as probe ion covering the time span of 4–168 h since neutralization. The total Fe concentration of the suspensions (∼20 mM) was measured by ICP-OES in a matrix of 0.8 M H2SO4.
Phosphate adsorption experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 (pH 5), 1
99 (pH 5), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (pH 6), 1
9 (pH 6), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (pH 7), 3
1 (pH 7), 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (pH 8), and 7
7 (pH 8), and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (pH 9). Six different initial PO4 concentrations were used ranging from ∼2.3–4.5 mM at low pH, to ∼1.6–3.2 mM at high pH. In addition, two systems (pH 5 and 6) with a 10 fold higher initial PO4 concentration range were used to test the possible influence of the buffer on the PO4-adsorption, showing no evidence for this in agreement with the work of Mao et al.51 The background electrolyte solution contained ∼0.10 M NO3, 3.8 mM MES, and 3.8 mM MOPs. Equilibration was established by shaking for 16 hours at 180 strokes per minute. Equilibration for 1 hour (ref. 51) was found to be not enough. After measuring the pH and subsequent centrifugation (3750g for 20 min), the supernatant was filtered over a 0.45 μm filter, acidified with 1 M HNO3 and analyzed for P with ICP-OES.
3 (pH 9). Six different initial PO4 concentrations were used ranging from ∼2.3–4.5 mM at low pH, to ∼1.6–3.2 mM at high pH. In addition, two systems (pH 5 and 6) with a 10 fold higher initial PO4 concentration range were used to test the possible influence of the buffer on the PO4-adsorption, showing no evidence for this in agreement with the work of Mao et al.51 The background electrolyte solution contained ∼0.10 M NO3, 3.8 mM MES, and 3.8 mM MOPs. Equilibration was established by shaking for 16 hours at 180 strokes per minute. Equilibration for 1 hour (ref. 51) was found to be not enough. After measuring the pH and subsequent centrifugation (3750g for 20 min), the supernatant was filtered over a 0.45 μm filter, acidified with 1 M HNO3 and analyzed for P with ICP-OES.
Results and discussion
Primary adsorption data
The PO4 adsorption isotherms have been measured for Fh systems aged at pH 5.00, 6.00, 7.00, 8.00, and 9.00. The pH was stabilized during aging by a combination of organic pH buffers (∼0.02 M MES and ∼0.02 M MOPS). Ageing times were 0.1, 1.5, 6, 24, and 168 hours in all pH experiments except pH 7, where 24, 48, 72, and 144 hours were selected to measure the particle growth. For the systems at pH 5 and 6, the growth was also characterized by studying it with a 10-fold higher initial PO4 concentration (∼15–35 mM). Fig. 1 gives two examples of the decrease of the PO4 adsorption isotherm with ageing. The trend of decrease with time of ageing is very similar in both cases. For pH 5, the P/Fe ratios are much higher than for pH 8, but this is mainly due to less PO4 adsorption at higher pH values as follows from CD modeling. Initially, all particles are very small. The PO4 adsorption is roughly halved during 168 hours of ageing, suggesting a change of the surface area by a factor of about 2.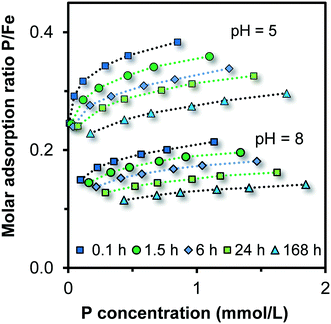 | ||
| Fig. 1 Time-dependent PO4 adsorption isotherms in ∼0.10 M NaNO3 measured at pH 5.38 ± 0.12 and 8.01 ± 0.21 buffered with 3.8 mM MES and 3.8 mM MOPS (symbols). The Fh was formed and aged at pH 5.00 and 8.00 (20 °C) in solution containing finally ∼0.10 M NaNO3, ∼19 mM MOPS, and ∼19 mM MES. The lines have been calculated with the CD model, taking for each individual data point the corresponding experimental pH and total concentrations of Na, NO3, PO4, MES, MOPS, and Fe. The molar masses of Fh were found iteratively with CD modelling from the fitted specific surface area A (eqn (1)). With time, it typically decreased from Mnano ∼ 107 to ∼94 g mol−1 Fe. | ||
CD MUSIC modelling
The adsorption measured in the various systems can be described with the CD model. Previously, the PO4 adsorption has been studied extensively2 and the resulting parameter set has been applied to describe the present data sets. In this approach, the reactive surface area is the only adjustable parameter and its value can be found by fitting the measured PO4 adsorption isotherms. However, for a proper interpretation, the molar PO4/Fe ratio needs to be translated into the PO4 adsorption per unit mass of Fh. This requires the value of the molar mass. The latter is not constant, but depends on the (yet unknown) specific surface area. The molar mass of the nanoparticle Mnano (g mol−1 Fe) is a function of the specific surface area A (m2 g−1) and the excess surface water density NH2O (12.6 10−6 mol m−2), as derived previously.29,63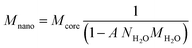 | (1) |
The reason for a variable molar mass is the presence of surface groups that lead to a change of the molar composition.
The molar composition of Fh can be given as FeO1.4(OH)0.2.nH2O in which n is the molar amount of chemisorbed water in excess to the bulk composition FeO1.4(OH)0.2. This excess amount of coordinated water (n) can be calculated from the difference in the molar mass of the nanoparticle (Mnano) and mineral core or bulk (Mcore), scaled to the molar mass of water MH2O, according to:
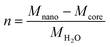 | (2) |
The molar mass Mnano (g mol−1) and surface area A (m2 g−1) are iteratively found in a cycle of CD modeling and recalculation of the PO4 adsorption per unit mass (mol kg−1) from the primary PO4/Fe ratio, and this is used to generate a new input for the fitting procedure. In this process, the values of the Stern layer capacitances are also continuously adapted to account for the surface curvature of the spherical particle with a diameter d calculated from the corresponding specific surface area A. In Fig. S2,† the influence of the surface curvature on the PO4 adsorption is shown.
The translation from A (m2 g−1) to d (m) requires the value of the mass density of the nanoparticle ρnano (g m−3), which is variable since the amount of coordinated water (n) adds more to the volume than to the mass of the particle. The relationship between the mass density and molar mass of a nanoparticle can be given as:
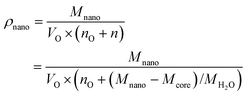 | (3) |
In the above approach, the primary PO4 adsorption data of Fh in the various systems have been used to derive the specific surface area. In a self-consistent manner, the effect of surface curvature is also included by translating the surface area to the corresponding spherical particle diameters d (m) according to:
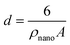 | (4) |
The corresponding number of Fe ions in the particle (nFe) follows from:
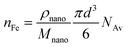 | (5) |
The above-described theoretical relation between chemical composition and particle size is shown for Fh in Fig. 2 (line) together with experimental data (blue spheres) of Michel et al.,40 as well as data derived by constructing Fh particles with Crystalmaker® (open squares) with a procedure described previously.33,64 Good agreement exits between model and data, which implicitly indicates the correct calculation of molar mass Mnano and mass density ρnano.
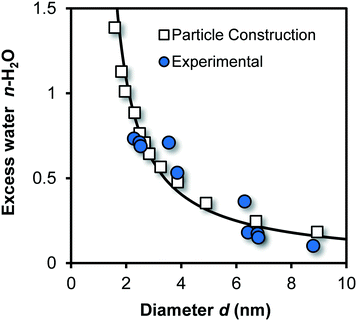 | ||
| Fig. 2 Excess water (n) of Fh (FeO1.6H0.2.nH2O) as a function of particle size. The blue spheres are data collected by Michel et al.40 for a series of Fh particles aged at high temperature. The mean diameter has been found with high-resolution transmission electron microscopy (HR-TEM). The white squares have been derived by constructing near-spherical Fh particles from which all Fe2 and Fe3 were removed that formed singly coordinated surface groups.33,64 The corresponding size was calculated based on the number of oxygen in the particle and the value for lattice volume expressed per oxygen VO (107 10−6 m3 mol−1). Using the principle of electro neutrality, the total number of H can be found for each particle from which one gets the excess number of protons by subtracting the number of structural H according to the composition FeO1.4(OH)0.2. It yields the corresponding amount of coordinated surface water. The model line is calculated applying eqn (1)–(4), showing good agreement with the data. | ||
At very low pH (<2), small angle X-ray scattering (SAXS) points to the formation of ultra-small nuclei.48 The reported Fe-dominated radius of ro = 0.41 nm translates to a particle size by incorporating an effective O diameter of about ∼0.20–0.25 nm, leading d ∼ 1.22–1.32 nm, in agreement with our equivalent spherical diameter of ∼1.25 nm calculated for Fe13. A neutral Fe13 cluster will have a chemical composition of Fe13O40H41. Compared to the bulk composition of Fh, the excess amount of coordinated water is nH2O = 2.9, which is extremely above any of the values for excess water of Fh particles, given in Fig. 2. It indicates that the Fh structure is significantly more condensed than any collection of aggregated Fe13 clusters. The core–shell structure suggested for the Fh48 is in line with the particle size dependency of the ferrimagnetic behavior of Fh as shown recently.33 Other SAXS data59,60 for characterizing Fh will be discussed later.
Particle evolution with time
In Fig. 3, the pH and time dependent evolution of Fh is given showing the specific surface area A, the mean particle diameter d, and the number of Fe per particle nFe (symbols), obtained by interpreting the primary PO4 adsorption data collected at the various pH values and times of ageing at 20 °C. At the logarithmic time scale, the measured specific surface area decreases almost linearly. After a few minutes of ageing, the particles are still very small. Depending on the pH, A = 1100–900 m2 g−1, d = 1.7–1.9 nm, and nFe = 50–80.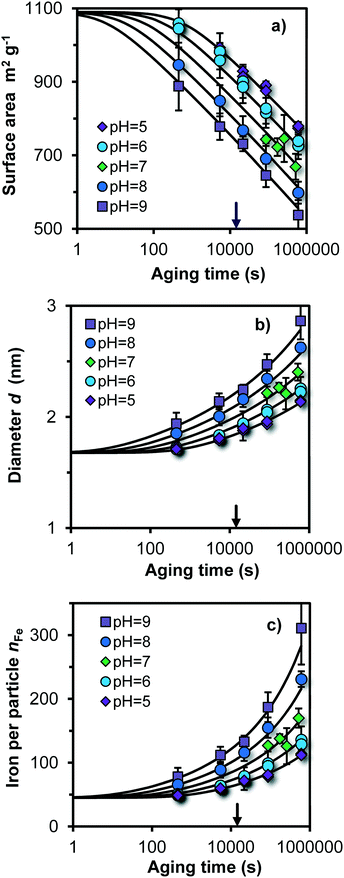 | ||
Fig. 3 a) Evolution of the specific surface area (A), b) mean particle diameter (d), and c) number of Fe per particle (nFe) as a function of the logarithm of the ageing time for Fh produced and aged at 20 °C in a solution with 0.2 M NaNO3, 19 mM MOPS, and 19 mM MES with pH values as indicated. The lines have been calculated with the dynamic simulation model presented and discussed using eqn (9) as rate law with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k0 = 4.80 (m−2 s−1) or log k0 = 4.80 (m−2 s−1) or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k0 = −9.58 (μmol m−2 s−1) and a = −0.5. The arrow at the x-axis indicates the ageing time of 4 hours that is often used in ion adsorption experiments with Fh. k0 = −9.58 (μmol m−2 s−1) and a = −0.5. The arrow at the x-axis indicates the ageing time of 4 hours that is often used in ion adsorption experiments with Fh. | ||
Rate of growth
To get insight into the process of growth during Ostwald ripening, the data require rescaling to reveal the rate of growth that allows deriving the underlying rate law.At particle growth, there is a flux of Fe towards the surface. This flux (mol h−1) can be expressed per unit surface area (mol m−2 h−1). To do this scaling, the data have been described with a mathematical trial function that can excellently depict the evolution of the particle size (d) with time of ageing (t). The equation used is d = at1/n + do in which the parameters a, do, and 1/n are derived by fitting. This can be done conveniently by plotting the diameter d against the time parameter (t1/n), evaluating linearity by searching for the best value of the exponent 1/n (Fig. S3†). The correlation coefficients obtained are very high (R2 ≥ 0.99), i.e. this linear relationship describes the time dependency very well.
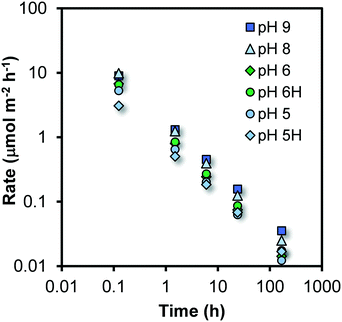
The parameterized trial functions can be used to calculate the rate of growth at the various times of ageing by taking the derivative (∂d/∂t) that also allows the calculation of the change of the number of Fe per particle (nFe) with time (∂nFe/∂t). By scaling to the corresponding surface area (m2) of the particle (A# = πd2), one derives the rate of growth R expressed as the number of Fe ions that become attached per unit surface area and time i.e. R = (∂nFe/∂t)/A# with the unit μmol m−2 h−1. At each reaction time, it represents the Fe-flux towards one unit of surface area. This rate of particle growth R is shown in Fig. 4 as a function of time for the various systems studied.
Rate limiting step
It is obvious from Fig. 4 that the rate of growth R is not constant. Initially, it is around 3–10 μmol m−2 h−1 but decreases dramatically by nearly three orders of magnitude during the course of the experiment. At the highest measured rates, the particles grow with less than one monolayer of Fe polyhedra per hour, as the Fe density of the Fh surfaces is 15–20 μmol m−2 (Fig. S4†). However, our dynamic model suggests significantly higher rates immediately after the formation of the initial, yet non-aged, particles (scale of seconds).As mentioned, the Fe-flux towards the surface becomes substantially less with time. Considering the process of growth as a chemical reaction of Fe in solution with specific reactive surface sites, the decrease of the rate of growth suggests that the solution concentration of Fe is considerably changing since the reactive site density can be seen as an intrinsic surface property of Fh.
At a given pH, the concentration of Fe in solution will be a function of the solubility product of Fh (Qso). The solubility of nanoparticles is enhanced relatively to the intrinsic solubility of the bulk material (Kso). In a suspension with a given particle size distribution, the solubility is determined by a labile equilibrium between Fe in solution and particles in the critical state having the highest Gibbs free energy.29 All particles larger than the critical ones will have a lower chemical potential, a higher stability, and consequently, a lower solubility. For this reason, the vast majority of particles will grow, which will be at the expense of the smallest particles that dissolve in an attempt to maintain the solution concentration. This is the driving force for Ostwald ripening. The rate-limiting step of growth is the binding of Fe to the surface because the rate of dissolution of the smallest particles is sufficiently high to maintain an equilibrium concentration in the solution.
The solubility of the critical nuclei of Fh with a surface area Acrit (m2 g−1) can be described with the Ostwald–Freundlich equation, according to:
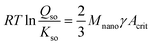 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kso = −40.6 ± 0.2 (ref. 29) in agreement with calculations of Pinney et al.65 Furthermore, Mnano is the molar mass (eqn (1)), R is the gas constant, and T is the absolute temperature. For Fh, the surface Gibbs free energy γ (J m−2) has recently been derived by Hiemstra29 interpreting a set of thermochemical data of Majzlan et al.66 and Snow et al.67 The value of the surface Gibbs free energy is exceptionally low (γ = 0.186 ± 0.01 J m−2) compared to the values for all other Fe (hydr)oxides.68 It indicates that the surface of Fh has a relatively high stability, which can be explained by the absence of unstable Fe2 and Fe3 polyhedra at the surface according to the surface depletion model.29 We assume that the value of γ is particle size independent, based on recent results obtained from silver nanoparticles.69
Kso = −40.6 ± 0.2 (ref. 29) in agreement with calculations of Pinney et al.65 Furthermore, Mnano is the molar mass (eqn (1)), R is the gas constant, and T is the absolute temperature. For Fh, the surface Gibbs free energy γ (J m−2) has recently been derived by Hiemstra29 interpreting a set of thermochemical data of Majzlan et al.66 and Snow et al.67 The value of the surface Gibbs free energy is exceptionally low (γ = 0.186 ± 0.01 J m−2) compared to the values for all other Fe (hydr)oxides.68 It indicates that the surface of Fh has a relatively high stability, which can be explained by the absence of unstable Fe2 and Fe3 polyhedra at the surface according to the surface depletion model.29 We assume that the value of γ is particle size independent, based on recent results obtained from silver nanoparticles.69
As follows from TEM data,40,58 freshly prepared Fh has a particle size distribution in which the mean and minimum particle sizes are linearly correlated.29 Introducing the ratio ϕ ≡ Acrit/Amean between the specific surface area of the measurable mean (Amean) and critical (Acrit) particle (m2 g−1), the Ostwald–Freundlich equation can be rewritten to:
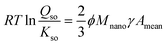 | (7) |
Eqn (7) shows that the super saturation of a solution relatively to the bulk material of infinite size (Qso/Kso) is related to the mean specific surface area of Fh material (Amean). This relation will be used in our derivation of the rate law of particle growth at Ostwald ripening. Analysis of the TEM data of Michel et al.40 reveals a factor ϕ = 3/2.29 The same conclusion follows from the data of Burrows et al.58 Introducing this information (ϕ = 3/2) in the above Ostwald–Freundlich equation (eqn (7)) leads to an equation without the factor 2/3 ϕ, known as the Ostwald equation.29
Rate law
As pointed out above, the process of growth can be considered as the attachment of dissolved Fe to reactive sites at the surface of Fh having a certain Fe-reactive site density Nr (mol m−2). Since the solubility of Fh can be related to the mean specific surface area A (eqn (7)), a relation between the rate of growth R and the ratio for super saturation Qso/Kso is expected. In Fig. 5, the growth rate R has been related to Qso/Kso by plotting both on a logarithmic scale. The data for pH 7 have been omitted in this part of the analysis, because the time scale of the measurement is too limited due to the absence of data for short ageing times.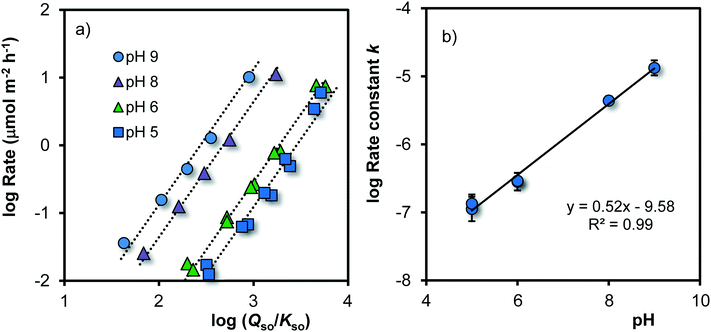 | ||
Fig. 5 a. Logarithm of the rate of growth R (μmol m−2 h−1) as a function of the logarithm of the super saturation of the solution (Qso/Kso) for Fh in 0.2 M NaNO3 buffered with 19 mM MES and 19 mM MOPS at the given pH values (T = 20 °C). The slopes of the calculated lines (s) have been set to s = 2. The intercept at log(Qso/Kso) = 0 equals the logarithm of the rate constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k), which is plotted in Fig. 5b against the pH, revealing the pH dependency of log k), which is plotted in Fig. 5b against the pH, revealing the pH dependency of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (eqn (8)) with k in μmol m−2 h−1. k (eqn (8)) with k in μmol m−2 h−1. | ||
Fig. 5a shows that the rate of growth varies with the super saturation of the solution (Qso/Kso). Initially, the super saturation is typically ∼1.000–10.000 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qso/Kso = 3–4). After a few minutes of ageing, the mean size is 1.8 ± 0.1 nm and the corresponding solubility is about log
Qso/Kso = 3–4). After a few minutes of ageing, the mean size is 1.8 ± 0.1 nm and the corresponding solubility is about log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qso ∼ −37.2 ± 0.3, which matches within the uncertainties with the solubility (log
Qso ∼ −37.2 ± 0.3, which matches within the uncertainties with the solubility (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qso ∼ −37.5 ± 0.1) at rapid titration of Fe(II)/Fe(III) solution with NaOH in NaClO4, back calculated to pH = PZC from the measured free [Fe3+] concentration.70
Qso ∼ −37.5 ± 0.1) at rapid titration of Fe(II)/Fe(III) solution with NaOH in NaClO4, back calculated to pH = PZC from the measured free [Fe3+] concentration.70
The data in Fig. 5a reveal a mean slope of s = 1.97 ± 0.18, which implies that within the uncertainty, the rate of growth R (μmol m−2 h−1) is proportional to the square of the super saturation (Qso/Kso). Therefore, the rate can be described with the conceptual equation:
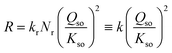 | (8) |
The observation of a quadratic relation between rate and solubility can be interpreted as rate limitation by a site binding reaction of two Fe with one site (S + 2 Fe → SFe2). The rate-limiting step is the simultaneous attachment of two Fe species forming together a stable surface complex. The value of 2 for the exponent of Qso/Kso expresses the chance that two Fe species occupy simultaneous a single site of growth, resulting in a stable complex. If only one monomeric Fe species is attached, it may be labile and desorb again in dynamic events, while the binding of two Fe ions, i.e. formation of an adsorbed Fe-dimer, may be irreversibly. Possibly, the formation of the adsorbed Fe-dimer is via the attachment of individual Fe-monomers since aqueous Fe-dimers are typically formed at high total Fe-concentrations present in systems with very acidic conditions (pH ∼ 2), as confirmed experimentally.49,50
In Fig. 5a, the intercept at the y-axis is equal to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k of eqn (8). That intercept is pH dependent. The pH dependency of log
k of eqn (8). That intercept is pH dependent. The pH dependency of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k can be revealed by plotting its value versus pH (Fig. 5b). To reduce the interrelation between the intercept value and the slope (s) of the lines in Fig. 5a, the latter has been fixed to s ≡ 2. Incorporating the obtained pH dependency of the rate constant, we can rewrite eqn (8) to:
k can be revealed by plotting its value versus pH (Fig. 5b). To reduce the interrelation between the intercept value and the slope (s) of the lines in Fig. 5a, the latter has been fixed to s ≡ 2. Incorporating the obtained pH dependency of the rate constant, we can rewrite eqn (8) to:
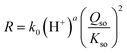 | (9) |
Dynamic modelling
The above-derived rate law for Ostwald ripening of primary Fh particles in a suspension can be applied in dynamic modeling by defining a flux of Fe towards the surface of an Fh nanoparticle of certain mean size (d) and surface area of A# = πd2. The Fe flux F (mol h−1) can be related to the rate of surface growth of the particle R (mol m−2 h−1), according to:| F = RA# | (10) |
At each (small) time step (Δt) in the modeling, the total number of Fe in the particle (nFe) has been calculated according to nFe = nFe(t=0) + Σ ΔnFe/Δt. Additionally, a corresponding set of related parameters was calculated, i.e. the molar mass Mnano (g mol−1), mass density ρnano (g m−3), diameter d (m), particle surface area A# (m2), and the specific surface area Amean = NAv/(nFeMnano) A# (m2 g−1). Combining the latter with the surface Gibbs free energy γ (J m−2) and molar mass Mnano (g mol−1) allows the calculation (eqn (7)) of the relative solubility Qso/Kso (ϕ = 3/2), which is subsequently applied in the rate equation (eqn (9)) to find ΔnFe/Δt before calculating the next time step.
In the modeling approach, the initial particle size at t = 0 is an adjustable parameter. Application of the model shows that we can describe the evolution of the size and specific surface area of the particles using a single value for the number of Fe present in the initial particle, independent of the pH. The data indicate that the non-aged particle (made at room temperature) has an equivalent spherical size of d ∼ 1.68 nm and a corresponding Fe content of nFe ∼ 45. One may construct such a representative particle by linking two Fe13 moieties and extend it with attaching additionally Fe polyhedra in accordance to the surface depletion model as given in Fig. S5.†
For different pH values, we find at the first sampling point (t = 0.1 h) a significant difference with the calculated initial size at t = 0. At pH = 9, nFe ∼ 80, while for pH = 5, nFe ∼ 50 for t = 0.1 h. The reason for this difference is the variation in the rate of growth. The model curves in Fig. 3c show that practically no difference exits in the calculated number of Fe per particle (nFe) at the typically time scale of about a second. This is also the time scale of physical mixing of the Fe(III) and base solution in the flow chamber. The differences in size observed at the first sampling point, a few minutes after the formation, are due to differences in rate of growth by Ostwald ripening, being relatively high at pH 9 and low at pH 5. We note that the data for the first sampling point at t = 0.1 h are potentially affected by the kinetics of the adsorption of PO4. However, one may expect that the added PO4 will promptly stop the ageing process when adsorbed, even though full equilibration2 may take more time.
Visual inspection of the process of formation in a flow chamber and connected tubing system shows a rapid change in color from pale-yellow to a yellow-brown upon mixing of the reactants. In the next seconds, the transparency changes and one starts to observe the formation of aggregated, reddish-brown Fe (hydr)oxide that contains micro-aggregates with a size of about 50 nm or larger.48,60,71 Formation of loose flocs (∼mm) in the tubing system is almost complete in less than 30 seconds. These observations illustrate the ultra-high speed of the formation reaction of Fh and the subsequent very fast physical process of aggregation and floc formation.
Ageing of transitionally synthesized Ferrihydrite
Above, we find that flash neutralization of Fe(III) in a pH-buffered solution leads to the synthesis of relatively small particles that reach a specific surface area of 750–950 m2 g−1 after ageing for 4 hours (Fig. 3a). These values are significantly higher than the typical values of 530–710 m2 g−1 found with the classical synthesis of 2LFh described in literature.27 This difference is an important motivation to extend our work by including Fh synthesized with the traditional approach of Fe(III) neutralization.To extend the lifetime of freshly prepared two-line Fh (2LFh), researchers have stored their suspensions at low temperature in a refrigerator. Therefore, we have also studied the ageing at 4 °C to derive the temperature dependency of the particle growth. Our results refer to a single 2LFh material made by neutralizing a 3.3 mM Fe(III) nitrate solution with a 0.02 M NaOH solution to a pH value of pH 6.0 or 8.2 and an initial ageing for 4 hours since neutralization. After sampling, the ageing was continued at temperatures of either 4 °C or 20 °C. The experimental results are shown in Fig. 6.
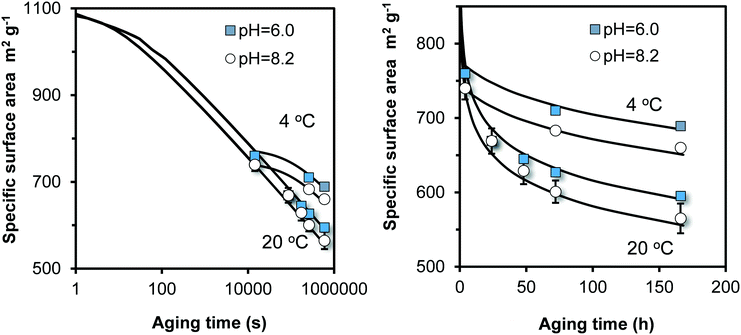 | ||
Fig. 6 Time dependency of the specific surface area (m2 g−1) for traditionally synthesized Fh, aged in 0.01 M NaNO3 in the absence organic pH buffers. After synthesis at pH 6.0 or 8.2, the Fh materials were aged for 4 hours since neutralization before a first sample was taken. The remaining suspensions were split and further aged at either 4 °C or 20 °C. The lines have been calculated with the model (eqn (8)), only adjusting the rate constant k. At 20 °C, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 9.25 (pH = 8.2) and 9.00 (pH = 6), and at 4 °C, log k = 9.25 (pH = 8.2) and 9.00 (pH = 6), and at 4 °C, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 8.35 (pH = 8.2) and 8.10 (pH = 6) with k in Fe per m2 per second. Subtracting a value of 14.22 from these log k = 8.35 (pH = 8.2) and 8.10 (pH = 6) with k in Fe per m2 per second. Subtracting a value of 14.22 from these log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values gives log k values gives log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k in the unit μmol m−2 s−1. k in the unit μmol m−2 s−1. | ||
Analysis of the data of particle growth at pH 8.2 along the same lines as presented above (Fig. 5) revealed that the rate dependency of the particle growth is basically the same as in the systems of Fig. 3, in the sense that the exponent for the dependency on the solubility is the same, i.e. R ∝ (Qso/Kso).2 It strongly suggests that the ageing process has the same rate-limiting step as found above, i.e. a dual attachment of Fe.
When the dynamic model was applied, we found that we can use the same value for the initial size of the non-aged primary Fh particles (nFe = 45) as in the experiments with the formation of Fh in the flow chamber in the presence of organic pH buffers. However, a somewhat higher value is also possible as our data only refer to a relatively long time of ageing (≥4 h), making the approach less sensitive to pinpointing the precise initial value at t = 0. This is illustrated in Fig. S6,† showing that an increase of the initial size hardly affects the particle size at a longer time of ageing (>day). The modeling of Fig. S6† also shows that it is difficult to grow Fh particles to sizes larger than ∼3–4 nm by the process of Ostwald ripening at room temperature and circumneutral pH values. However, additionally growth will occur by oriented attachment.31
Evolution of ferrihydrite according to TEM
The growth of Fh can also be studied by directly observing the change in particle size with TEM. This was done by Burleson and Penn31 studying the ageing of Fh for 20–2000 h as a function of temperature (60, 90, and 120 °C) and pH. The initial Fh sample was prepared by neutralizing a Fe(III) solution with NaHCO3, followed by dialysis at 4 °C during 5 days with a final pH of ∼ 3.5. The created particles have a mean diameter of 3.0 nm (black square in Fig. 7a), and will contain about 360 Fe.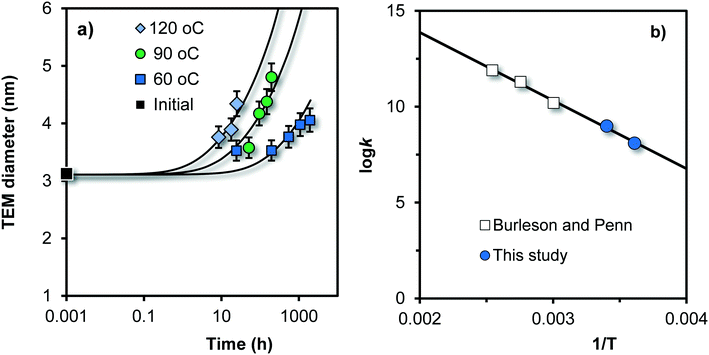 | ||
| Fig. 7 a) Time dependency of the mean size of primary particles in Fh suspensions, measured with TEM at pH = 6 by Burleson and Penn31 for different temperatures (symbols). The data only refer to the fraction of primary particles in the suspension, excluding the particles that formed by oriented particle attachment. The k value (eqn (8)) in Fig. 7b) is given in the unit Fe per m2 per second. The slope to the line is equivalent to an activation energy of Eact = 68 ± 4 kJ mol−1 (see text). | ||
The TEM data of Burleson and Penn31 show the simultaneous presence of relatively small primary particles as well as larger particles with another aspect ratio (∼5) that have formed by oriented attachment, particularly at pH ∼ 10–12. However, the data in Fig. 7a refer only to the growth of the fraction of primary particles. The other particles have been excluded and were evaluated differently by Burleson and Penn.31 With increase of temperature, the rate of growth of the primary particles increases. Despite the high temperature, the Ostwald ripening of these particles is still relatively slow. At 120 °C, the mean diameter increases with only ∼0.5–1.5 nm in one day.
Fh particles can also grow by oriented attachment.31 This typically occurs at high temperature, similarly as found for ZnS.34 Oriented attachment of Fh may occur once the particle size of Fh is large enough to develop preferred crystal faces. Ferrihydrite, hydrothermally aged at 175 °C,40 shows a rapid near-doubling of the mean particle size as soon as the particles reach a mean size of about 3.5–4 nm.33 Simultaneously, the magnetic saturation becomes less than expected for defect free Fh,33 which suggests imperfect attachments. Upon further hydrothermal ageing, the reduction of the magnetic saturation (i.e. defects) gradually disappears, signifying completion of the particle fusion. These particles are large enough (∼8 nm29) to transform into hematite.40
The TEM data (symbols) of Fig. 7a have been described with our kinetic model (lines) by only adjusting the rate constant k of eqn (8) while using the reported experimentally value (3 nm) as initial particle size. These rate constants have been given as open squares in Fig. 7b as a function of the inverse of the temperature (1/T). The k value is given in the unit m−2 s−1 but can be expressed in μmol m−2 h−1 using Avogadro's number and 1 h = 3600 s. The blue spheres in Fig. 7b refer to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values obtained from our data collected at the same pH (pH = 6) in 0.01 M NaNO3.
k values obtained from our data collected at the same pH (pH = 6) in 0.01 M NaNO3.
Temperature dependency
The temperature dependency of the rate constants k obtained by modeling (Fig. 7b) can be described with the classical Arrhenius equation:| k = Ae−Eact/RT | (11) |
Time dependency
Burleson and Penn31 have previously used the classical model of Lifshitz and Slyozov72 to evaluate the growth of the primary Fh particles. In that model, the rate of growth is limited by the diffusion of Fe between the free solution and particle surface. In the model, the Ostwald–Freundlich equation is linearized which is increasingly justified for systems with little supersaturation (Fig. S7†). For a polydisperse system, Lifshitz and Slyozov72 derived that the particle volume increases linearly with time (ΔVmean ∝ t). This increase is equivalent to a time-dependent change of the particle diameter according to Δd ∝ t1/3. However, our data do not show this time dependency. It can be shown that the growth of Fh is likely not limited by diffusion across the solid–solution interface (Fig. S8 and Table S1†). The process is much slower.For a polydisperse system, Wagner73 derived a time dependency of the mean size of Δd ∝ t1/2 if the growth is limited by a chemical reaction that is first order in concentration (c1). In case of a surface reaction that is second order with respect to the concentration (c2), the rate will be more time-dependent. Our data analysis and model suggest Δd ∝ t1/n with n = 3.9 ± 0.7 (Fig. S3†), i.e. approximately Δd ∝ t1/4. Remarkably, the theoretical growth of lens-shaped particles at the boundary between two matrices may exhibit the same time dependency,74 indicating that time dependency should be interpreted with care.34
Six-line Fh (6LFh) can be made by forced hydrolysis at 75 °C in about 10–12 minutes25 without base addition. It leads to particles with a size of ∼5.5 nm according to TEM57 and SAXS.59 If formed by prompt adsorption of Fe to Fe13 nuclei, about 7 ± 1 monolayers of Fe polyhedra are needed (Fig. S4†). This assumption implies less nucleation in the solution than at the formation of 2LFh by Fe(III) neutralization with base at room temperature. The 6LFh particles with d = 5.5 nm typically contain nFe ∼ 2600 Fe. Further growth by classical Ostwald ripening will be little at room temperature according to our model (Fig. S9†). This is due to the very low solubility of these particles and super saturation (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qso/Kso ∼ 0.6) of the solution. Indeed, no ageing occurs during storage for months at room temperature, according to SAXS.59 Apparently, oriented attachment or particle fusion does not play a significant role in that case.
Qso/Kso ∼ 0.6) of the solution. Indeed, no ageing occurs during storage for months at room temperature, according to SAXS.59 Apparently, oriented attachment or particle fusion does not play a significant role in that case.
pH dependency
The logarithms of the rate constants, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (eqn (8)), for Fh aged in the absence and presence of organic pH buffers are compared in Fig. 8. At low pH, the rate constants for growth are much lower in the presence of organic pH buffers (MES and MOPS), resulting in a larger pH-dependency. At low pH, the rates constants are strongly reduced compared to Fh systems without these organics. It suggests that at low pH the organic molecules are present at the surface, hindering the process of Fe adsorption. The interaction of these organic molecules with the surface will be relatively weak since these ions do not influence the adsorption of PO4 at the concentration scales studied.51 These organic molecules are negatively charged in the pH range studied (At 20 °C and I = 0.1 M, log
k (eqn (8)), for Fh aged in the absence and presence of organic pH buffers are compared in Fig. 8. At low pH, the rate constants for growth are much lower in the presence of organic pH buffers (MES and MOPS), resulting in a larger pH-dependency. At low pH, the rates constants are strongly reduced compared to Fh systems without these organics. It suggests that at low pH the organic molecules are present at the surface, hindering the process of Fe adsorption. The interaction of these organic molecules with the surface will be relatively weak since these ions do not influence the adsorption of PO4 at the concentration scales studied.51 These organic molecules are negatively charged in the pH range studied (At 20 °C and I = 0.1 M, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH = 6.16 for MES add log
KH = 6.16 for MES add log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH = 7.17 for MOPS) and may interact by electrostatic forces with the positively charged surface groups at a pH below the value of the PZC (∼8.2). At higher pH, the interaction will largely disappear leading to the same rates as in the pure Fh systems.
KH = 7.17 for MOPS) and may interact by electrostatic forces with the positively charged surface groups at a pH below the value of the PZC (∼8.2). At higher pH, the interaction will largely disappear leading to the same rates as in the pure Fh systems.
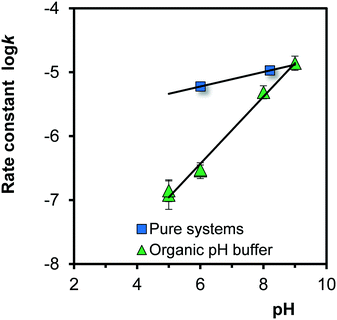 | ||
Fig. 8 pH dependency of the rate constant of growth of Fh at 20 °C (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k of eqn (8) with k in μmol m−2 h−1) in the absence (squares) and presence (triangles) of an organic pH buffer solution. In the latter case, the rate is strongly reduced at low pH, which can be explained by a weak interaction of the organic molecules with the surface. k of eqn (8) with k in μmol m−2 h−1) in the absence (squares) and presence (triangles) of an organic pH buffer solution. In the latter case, the rate is strongly reduced at low pH, which can be explained by a weak interaction of the organic molecules with the surface. | ||
Role of organic matter and anions
The above indicates that any disturbance of the Fe attachment by the presence of organic molecules may highly reduce the rate of growth and transformation. As organic matter is readily available in nature, it implies that Fh particles may have significantly lower rates of transformation in the natural environment. This will contribute to the nano-character of the natural iron oxide fraction of many top soils.75 The primary iron and aluminum (hydr)oxide particles remain ultra-small, and are embedded in and/or covered by organic matter, since for the soils a good correlation is found between the reactive oxide surface area and the organic matter content.75As oxyanions may also interfere in the formation of Fh,44 primary particles may remain small if these anions adsorb.2 For instance, the adsorption of Si reduces the coherent length of scattering of Fh.76 This explains the small size (2 nm) of siliceous Fh particles produced in drinking water facilities at aeration of groundwater with Fe(II).27 Interference of oxyanions may also explain the small size of 2LFh (pH = 8) prepared in the presence of As(OH)3.60 The characterization with SAXS suggested a size near 2 × (0.8 + 0.2) = ∼2 nm.60 Such particles will have a surface area of ∼850 m2 g−1. According to our model (Fig. 6), this would require ageing for ∼0.5 hours while the particles were aged for 24 h. The difference may be due to the adsorption of As(OH)3, suppressing the rate of ageing.
In literature,51 Fh has been prepared and aged in the presence of Cl as major anion. The measured growth is very different from the growth observed in systems with NO3 as major anion, as shown in Fig. 9 (squared colored symbols). Initially, the particles have nearly the same size in both systems. Shortly later, the time dependency of growth becomes very different. In NaNO3, the rate of growth on a volume basis decreases continuously, while in NaCl the volume or number of Fe per particle (nFe) increases linearly with time.2 This linearity is typical for a diffusion-controlled growth in systems with little super saturation, as derived by Lifshitz and Slyozov,72 resulting in ΔV ∝ t or nFe ∝ t.
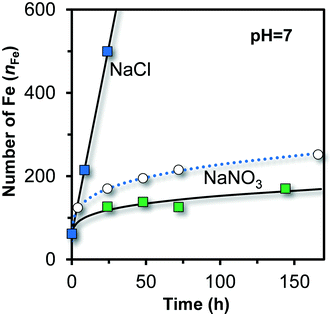 | ||
| Fig. 9 Ageing of ultra-fast synthesized Fe (hydr)oxide in 0.1 M NaCl (ref. 51) and 0.1 M NaNO3 (present study) at pH = 7 in the presence of organic pH buffers (squares). The reaction pathways start to deviate significantly after ∼4 hours of ageing. In NaCl, the number of Fe per particle (volume) increases linearly with time while it is non-linear in NaNO3. The open symbols and dotted line are for Fh aged in 0.01 M NaNO3 at pH 7 in the absence of organic pH buffers, derived by interpolation of the data collected at pH 6.0 and pH 8.2 (Fig. 6). | ||
The data in Fig. 9 illustrate that the reaction pathways followed in NaCl and NaNO3 are very different. In Cl systems, akaganéite (β-FeOOH·xHCl) may form as found by X-ray diffraction77 and with HRTEM.78 This mineral has internal sites occupied with Cl ions, giving rise to a Cl/Fe ratio of x ∼ 0.15–0.19.79,80 One may expect that such internal sites are still relatively unimportant in the initial particles from which akaganéite is formed because initially, most Fe is part of the surface and little is part of the bulk.
Conclusions
Fh is thermodynamically unstable and will ultimately transform into a more stable Fe (hydr)oxide. When initially formed, the particles are ultra-small and subject to Oswald ripening in which the smallest particles dissolve and the larger ones grow, resulting in a decrease of the reactive surface area. In the present study this pH, temperature, and time-dependent process has been probed using PO4. We show how the time-dependent change of the surface area can be translated into the rate of growth per unit surface area (μmol Fe m−2 h−1). In all calculations, we have accounted for the size dependency of molar mass and mass density that is the result of a variable contribution of coordinated surface water (n) in excess to the bulk composition (FeO1.4(OH)0.2·nH2O).The rate of growth R is highly time-dependent and decreases by nearly three orders of magnitude at ageing from a few minutes to one week. It varies between R ∼ 0.01–10 μmol m−2 h−1. These rates can be considered as low because particle growth of Fh by a monolayer of Fe polyhedra requires 15–20 μmol m2, i.e. hours or days are needed to grow a single monolayer at room temperature. Additionally, we showed that the rate of growth of Fh is too low to be limited by a diffusion flux across the solid–solution interface.
Our data only refer to primary particles (d = 1.7–2.9 nm) for which we show that the rate of growth is related to the solubility of Fh. The data analysis reveals that the rate of growth is proportional to the square of the super saturation of the solution, expressed in the ratio of the solubility product of the actual particle (Qso) and the virtual bulk (Kso). In our analysis, the size dependency of the solubility and super saturation is calculated using the surface Gibbs free energy of Fh (γ = 0.186 J m−2) that is implemented in the Ostwald–Freundlich equation accounting for the difference in surface area of the critical and mean particle (ϕ = 3/2). The squared proportionality of the super saturation in the rate law can be interpreted as a rate limitation by a chemical reaction with dual attachment of Fe to a single site of growth (S + 2 Fe → SFe2). The time dependency of the change of the diameter is close to Δd ∝ t1/4 for model and data.
The rate constant for the process of growth is pH dependent. The presence of organic pH buffers reduces the rate constant for Ostwald ripening at low pH by a factor 10 or more, but its effect disappears at high pH, which is explained by the variable interference of the organic molecules in the Fe attachment. Interference will be enhanced if Fh is covered by natural organic matter and consequently, organic matter contributes to the kinetic stability of Fh in soils.
Application of our dynamic model for particle growth discloses the initial size of non-aged Fh particles of d ∼ 1.68 nm and the corresponding specific surface area of A ∼ 1100 m2 g−1. These particles formed at room temperature contain on average ∼45 Fe. Dynamic modeling further shows that the growth of the primary particles by Ostwald ripening is usually limited to a size of ∼3.5–4 nm (A ∼ 350–500 m2 g−1). Additional growth will be by (oriented) particle attachment at the onset of the formation of crystal faces. This is typically observed at ageing in high temperature systems, particularly at high pH.
If 6LFh is produced with the classical method of forced hydrolysis at 75 °C, the initial particles are significantly larger (∼5.5 nm). According to our model, Ostwald ripening becomes little because these particles have a relatively low solubility.
Combining various data for growth of primary Fh particles at pH = 6, collected with TEM and PO4 probing, reveals an activation energy of Ea = 68 ± 4 kJ mol−1 for the growth by Ostwald ripening, which is lower than that for growth by oriented attachment.
The reaction pathway of Ostwald ripening in NaCl is very different from that in NaNO3. In NaCl, the particle volume increases linearly with time while in NaNO3, it is clearly non-linear. In NaCl, akaganéite may start to form according to evidence obtained by X-ray diffraction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We grateful acknowledge the modelling contributions of Imtiaz Mia. Part of this project has been funded by a grant provided of the University of Costa Rica (UCR) and by NanoNextNL (FES 5120756-02), both being gratefully acknowledged.References
- C. Tiberg, C. Sjostedt, I. Persson and J. P. Gustafsson, Geochim. Cosmochim. Acta, 2013, 120, 140–157 CrossRef CAS.
- T. Hiemstra and W. Zhao, Environ. Sci.: Nano, 2016, 3, 1265–1279 RSC.
- L. Tian, Z. Q. Shi, Y. Lu, A. C. Dohnalkova, Z. Lin and Z. Dang, Environ. Sci. Technol., 2017, 51, 10605–10614 CrossRef CAS PubMed.
- S. Meng, H. L. Wang, H. Liu, C. H. Yang, Y. Wei and D. L. Hou, Appl. Geochem., 2014, 45, 114–119 CrossRef CAS.
- J. Liu, R. L. Zhu, T. Y. Xu, Y. Xu, F. Ge, Y. F. Xi, J. X. Zhu and H. P. He, Chemosphere, 2016, 144, 1148–1155 CrossRef CAS PubMed.
- G. Pieczara and G. Rzepa, Environ. Eng. Manage. J., 2016, 15, 2095–2107 CrossRef CAS.
- D. A. Dzombak and F. M. M. Morel, Surface complexation modeling: Hydrous Ferric Oxide, John Wiley & Sons, New York, 1990, p. 393 Search PubMed.
- H. Fu, Y. Yang, R. Zhu, J. Liu, M. Usman, Q. Chen and H. He, J. Colloid Interface Sci., 2018, 530, 704–713 CrossRef CAS PubMed.
- T. D. Sowers, J. W. Stuckey and D. L. Sparks, Geochem. Trans., 2018, 19, 11 CrossRef PubMed.
- L. Tian, Y. Z. Liang, Y. Lu, L. F. Peng, P. X. Wu and Z. Q. Shi, Soil Sci. Soc. Am. J., 2018, 82, 96–105 CrossRef CAS.
- A.-C. Senn, R. Kaegi, S. J. Hug, J. G. Hering, S. Mangold and A. Voegelin, Geochim. Cosmochim. Acta, 2017, 202, 341–360 CrossRef CAS.
- C. P. Johnston and M. Chrysochoou, Environ. Sci. Technol., 2016, 50, 3589–3596 CrossRef CAS PubMed.
- A. Rossberg, K. U. Ulrich, S. Weiss, S. Tsushima, T. Hiemstra and A. C. Scheinost, Environ. Sci. Technol., 2009, 43, 1400–1406 CrossRef CAS PubMed.
- M. A. Larsson, I. Persson, C. Sjostedt and J. P. Gustafsson, Environ. Chem., 2017, 14, 141–150 CrossRef CAS.
- P. C. M. Francisco, T. Sato, T. Otake, T. Kasama, S. Suzuki, H. Shiwaku and T. Yaita, Environ. Sci. Technol., 2018, 52, 4817–4826 CrossRef CAS PubMed.
- X. Wang, J. D. Kubicki, J.-F. Boily, G. A. Waychunas, Y. Hu, X. Feng and M. Zhu, ACS Earth Space Chem., 2018, 2, 125–134 CrossRef CAS.
- P. J. Swedlund, H. Holtkamp, Y. Song and C. J. Daughney, Environ. Sci. Technol., 2014, 48, 2759–2765 CrossRef CAS PubMed.
- S. Zhang, P. N. Williams, C.-Y. Zhou, L. Q. Ma and J. Luo, Chemosphere, 2017, 184, 812–819 CrossRef CAS PubMed.
- X. M. Wang, Y. F. Hu, Y. D. Tang, P. Yang, X. H. Feng, W. Q. Xu and M. Q. Zhu, Environ. Sci.: Nano, 2017, 4, 2193–2204 RSC.
- W. Stumm, C. P. Huang and S. R. Jenkins, Croat. Chem. Acta, 1970, 42, 223–245 CAS.
- J. A. Davis, R. James and J. O. Leckie, J. Colloid Interface Sci., 1978, 63, 480–499 CrossRef CAS.
- M. Abbas, B. P. Rao, S. M. Naga, M. Takahashi and C. Kim, Ceram. Int., 2013, 39, 7605–7611 CrossRef CAS.
- D. E. Yates, S. Levine and T. W. Healy, J. Chem. Soc., Faraday Trans. 1, 1974, 70, 1807–1818 RSC.
- T. Hiemstra and W. H. Van Riemsdijk, J. Colloid Interface Sci., 1996, 179, 488–508 CrossRef CAS.
- U. Schwertmann and R. M. Cornell, Iron Oxides in the Laboratory, VCH Publishers, 1991, p. 137 Search PubMed.
- N. Bompoti, M. Chrysochoou and M. Machesky, Chem. Geol., 2017, 464, 34–45 CrossRef CAS.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2018, 238, 453–476 CrossRef CAS.
- R. M. Cornell and U. Schwertmann, The iron oxides: structures, properties, reactions, occurrence and uses, VCH, Weinheim, 1996 Search PubMed.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2015, 158, 179–198 CrossRef CAS.
- W. Ostwald, Z. Phys. Chem., 1897, 22, 289–330 CAS.
- D. J. Burleson and R. L. Penn, Langmuir, 2006, 22, 402–409 CrossRef CAS PubMed.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS PubMed.
- T. Hiemstra, Environ. Sci.: Nano, 2018, 5, 752–764 RSC.
- F. Huang, H. Z. Zhang and J. F. Banfield, Nano Lett., 2003, 3, 373–378 CrossRef CAS.
- P. J. Murphy, A. M. Posner and J. P. Quirk, J. Colloid Interface Sci., 1976, 56, 270–283 CrossRef CAS.
- N. D. Burrows, C. R. H. Hale and R. L. Penn, Cryst. Growth Des., 2013, 13, 3396–3403 CrossRef CAS.
- D. D. Boland, R. N. Collins, C. J. Miller, C. J. Glover and T. D. Waite, Environ. Sci. Technol., 2014, 48, 5477–5485 CrossRef CAS PubMed.
- Z. Jiang, Q. Liu, A. P. Roberts, V. Barrón, J. Torrent and Q. Zhang, Geology, 2018, 46, 987–990 CrossRef.
- L. Cao, Z.-X. Jiang, Y.-H. Du, X.-M. Yin, S.-B. Xi, W. Wen, A. P. Roberts, A. T. S. Wee, Y.-M. Xiong, Q.-S. Liu and X.-Y. Gao, Environ. Sci. Technol., 2017, 51, 2643–2651 CrossRef CAS PubMed.
- F. M. Michel, V. Barron, J. Torrent, M. P. Morales, C. J. Serna, J. F. Boily, Q. S. Liu, A. Ambrosini, A. C. Cismasu and G. E. Brown, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- S. Mitsunobu, C. Muramatsu, K. Watanabe and M. Sakata, Environ. Sci. Technol., 2013, 47, 9660–9667 CrossRef CAS PubMed.
- E. E. Roden and J. M. Zachara, Environ. Sci. Technol., 1996, 30, 1618–1628 CrossRef CAS.
- U. Schwertmann, H. Stanjek and H. H. Becher, Clay Miner., 2004, 39, 433–438 CrossRef CAS.
- N. Galvez, V. Barron and J. Torrent, Clays Clay Miner., 1999, 47, 304–311 CrossRef CAS.
- R. Raiswell, H. P. Vu, L. Brinza and L. G. Benning, Chem. Geol., 2010, 278, 70–79 CrossRef CAS.
- R. M. Bolanz, U. Blass, S. Ackermann, V. Ciobotaa, P. Rosch, N. Tarcea, J. Popp and J. Majzlan, Clays Clay Miner., 2013, 61, 11–25 CrossRef CAS.
- S. Das, M. J. Hendry and J. Essilfie-Dughan, Environ. Sci. Technol., 2011, 45, 268–275 CrossRef CAS PubMed.
- J. S. Weatherill, K. Morris, P. Bots, T. M. Stawski, A. Janssen, L. Abrahamsen, R. Blackham and S. Shaw, Environ. Sci. Technol., 2016, 50, 9333–9342 CrossRef CAS PubMed.
- R. N. Collins, K. M. Rosso, A. L. Rose, C. J. Glover and T. D. Waite, Geochim. Cosmochim. Acta, 2016, 177, 150–169 CrossRef CAS.
- M. Q. Zhu, C. Frandsen, A. F. Wallace, B. Legg, S. Khalid, H. Zhang, S. Morup, J. F. Banfield and G. A. Waychunas, Geochim. Cosmochim. Acta, 2016, 172, 247–264 CrossRef CAS.
- Y. P. Mao, A. N. Pham, Y. J. Xin and T. D. Waite, Sep. Purif. Technol., 2012, 91, 38–45 CrossRef CAS.
- J. Antelo, F. Arce and S. Fiol, Chem. Geol., 2015, 410, 53–62 CrossRef CAS.
- X. M. Wang, F. Liu, W. F. Tan, W. Li, X. H. Feng and D. L. Sparks, Soil Sci., 2013, 178, 1–11 CrossRef CAS.
- E. B. Cerkez, N. Bhandari, R. J. Reeder and D. R. Strongin, Environ. Sci. Technol., 2015, 49, 2858–2866 CrossRef CAS PubMed.
- J. Antelo, S. Fiol, C. Perez, S. Marino, F. Arce, D. Gondar and R. Lopez, J. Colloid Interface Sci., 2010, 347, 112–119 CrossRef CAS PubMed.
- H. J. Van den Hul and J. Lyklema, J. Am. Chem. Soc., 1968, 90, 3010–3015 CrossRef CAS.
- Y. Guyodo, S. K. Banerjee, R. L. Penn, D. Burleson, T. S. Berquo, T. Seda and P. Solheid, Phys. Earth Planet. Inter., 2006, 154, 222–233 CrossRef CAS.
- N. D. Burrows, C. R. H. Hale and R. L. Penn, Cryst. Growth Des., 2012, 12, 4787–4797 CrossRef CAS.
- L. Gentile, T. Wang, A. Tunlid, U. Olsson and P. Persson, J. Phys. Chem. A, 2018, 122, 7730–7738 CrossRef CAS PubMed.
- H. Guénet, M. Davranche, D. Vantelon, J. Gigault, S. Prévost, O. Taché, S. Jaksch, M. Pédrot, V. Dorcet, A. Boutier and J. Jestin, Environ. Sci.: Nano, 2017, 4, 938–954 RSC.
- R. L. Penn, J. J. Erbs and D. M. Gulliver, J. Cryst. Growth, 2006, 293, 1–4 CrossRef CAS.
- J. A. Davis and J. O. Leckie, J. Colloid Interface Sci., 1978, 67, 90–107 CrossRef CAS.
- T. Hiemstra and W. H. Van Riemsdijk, Geochim. Cosmochim. Acta, 2009, 73, 4423–4436 CrossRef CAS.
- T. Hiemstra, Geochim. Cosmochim. Acta, 2013, 10, 316–325 CrossRef.
- N. Pinney, J. D. Kubicki, D. S. Middlemiss, C. P. Grey and D. Morgan, Chem. Mater., 2009, 21, 5727–5742 CrossRef CAS.
- J. Majzlan, A. Navrotsky and U. Schwertmann, Geochim. Cosmochim. Acta, 2004, 68, 1049–1059 CrossRef CAS.
- C. L. Snow, K. I. Lilova, A. V. Radha, Q. Shi, S. Smith, A. Navrotsky, J. Boerio-Goates and B. F. Woodfield, J. Chem. Thermodyn., 2013, 58, 307–314 CrossRef CAS.
- A. Navrotsky, L. Mazeina and J. Majzlan, Science, 2008, 319, 1635–1638 CrossRef CAS PubMed.
- B. Molleman and T. Hiemstra, Phys. Chem. Chem. Phys., 2018, 20, 20575–20587 RSC.
- R. H. Byrne and Y. R. Luo, Geochim. Cosmochim. Acta, 2000, 64, 1873–1877 CrossRef CAS.
- F. Y. Li, L. Koopal and W. F. Tan, Sci. Rep., 2018, 8, 13 CrossRef PubMed.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- C. Wagner, Z. Elektrochem., 1961, 65, 581–591 CAS.
- M. V. Speight, Acta Metall., 1968, 16, 133–135 CrossRef CAS.
- T. Hiemstra, J. Antelo, R. Rahnemaie and W. H. van Riemsdijk, Geochim. Cosmochim. Acta, 2010, 74, 41–58 CrossRef CAS.
- A. C. Cismasu, F. M. Michel, A. P. Tcaciuc, T. Tyliszczak and G. E. Brown, C. R. Geosci., 2011, 343, 210–218 CrossRef CAS.
- G. Biedermann and J. T. Chow, Acta Chem. Scand., 1966, 20, 1376–1388 CrossRef CAS.
- B. A. Legg, M. Q. Zhu, H. Z. Zhang, G. Waychunas, B. Gilbert and J. F. Banfield, Cryst. Growth Des., 2016, 16, 5726–5737 CrossRef CAS.
- P. A. Kozin and J.-F. Boily, J. Phys. Chem. C, 2013, 117, 6409–6419 CrossRef CAS.
- M. Kersten, S. Karabacheva, N. Vlasova, R. Branscheid, K. Schurk and H. Stanjek, Colloids Surf., A, 2014, 448, 73–80 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Flow chamber design, deriving the rate of growth R from the collected data, size-dependency of Stern layer capacitances and adsorption, monolayer density of Fe, polyhedral representation of a non-aged initial Fh particle, influence of initial particle size on ageing, rate limitation by diffusion across the solid–water interface. Ageing of 6LFh. See DOI: 10.1039/c8en01198b |
| This journal is © The Royal Society of Chemistry 2019 |