Open Access Article
Open Access ArticleLiquid phase exfoliation of MoO2 nanosheets for lithium ion battery applications†
John B.
Boland
ab,
Andrew
Harvey
ab,
Ruiyuan
Tian
ab,
Damien
Hanlon
ab,
Victor
Vega-Mayoral
ab,
Beata
Szydlowska
 ab,
Aideen
Griffin
ab,
Tanja
Stimpel-Lindner
c,
Sonia
Jaskaniec
ad,
Valeria
Nicolosi
ad,
Georg
Duesberg
c and
Jonathan N.
Coleman
ab,
Aideen
Griffin
ab,
Tanja
Stimpel-Lindner
c,
Sonia
Jaskaniec
ad,
Valeria
Nicolosi
ad,
Georg
Duesberg
c and
Jonathan N.
Coleman
 *ab
*ab
aCRANN & AMBER Research Centers, Trinity College Dublin, Dublin 2, Ireland. E-mail: colemaj@tcd.ie
bSchool of Physics, Trinity College Dublin, Dublin 2, Ireland
cUniversität der Bundeswehr München, Werner-Heisenberg-Weg 39, München, D-85577 Neubiberg, Germany
dSchool of Chemistry, Trinity College Dublin, Dublin 2, Ireland
First published on 4th February 2019
Abstract
Molybdenum dioxide (MoO2) is a layered material which shows promise for a number of applications in the electrochemical energy storage arena. Mostly studied as a bulk layered material, MoO2 has not previously been exfoliated in large quantities. Here we demonstrate the liquid phase exfoliation of MoO2 in the solvent isopropanol, yielding reasonable amounts of good quality nanosheets. However, we found that, when dispersed in isopropanol under ambient conditions, MoO2 nanosheets are gradually oxidized to higher oxides such as MoO3 over a period of days. Conversely, if the nanosheets are processed into dried films immediately after exfoliation, and before oxidation has had a chance to progress, the nanosheets are relatively stable under ambient conditions, remaining unoxidised unless the films are heated. We also found that MoO2 nanosheets can be size selected by controlled centrifugation and show size-dependent optical properties. This allows us to propose spectroscopic metrics which allow concentration- and size-estimation from extinction spectra. Finally, we found that liquid-exfoliated MoO2 nanosheets could be used to produce lithium ion battery anodes with capacities of up to 1140 mA h g−1.
Introduction
Over the past decade, 2-dimensional (2D) materials have become a very important part of materials science research.1–4 While graphene is probably the most well-known 2D material, many more exist such as boron nitride (BN),5 transition metal dichalcogenides (TMDs, e.g. MoS2 and WS2etc),3 III–VI layered semiconductors such as GaS and InSe,6,7 and of course the layered oxides.8–10 These materials are exciting, not only because they display interesting properties, but also because of their potential for use in a range of applications. Here, their diversity is a strength: the many different types11 of 2D materials lead to a very broad palette of properties and potential uses. As a result, 2D materials have been demonstrated in applications as diverse as electronic devices,4 water filtration,12 drug delivery13 and battery electrodes.14–162D materials can be produced in a variety of ways including mechanical cleavage,17,18 chemical synthesis,19,20 growth,21 as well as various liquid exfoliation techniques,9,22–25 with each method having distinctive advantages and disadvantages. Of the liquid exfoliation techniques,11 liquid phase exfoliation (LPE)22,23 is particularly versatile. This method involves the production of 2D nanosheets by shearing or ultrasonicating layered crystals in appropriate stabilizing liquids.23,26,27 LPE can produce dispersions with nanosheet concentrations in the order of g L−1 which are quite stable against aggregation.28–30 It should be noted that this procedure mostly produces few-layer nanosheets,31 with monolayer contents which are low compared to those from other liquid exfoliation processes.24 Nevertheless, its simplicity, versatility and scalability26,32 has meant that LPE has been applied to a wide range of 2D materials including graphene,22,33,34 BN,5 TMDs,23,35 TMOs,36 LDHs,28,37 GaS,7 phosphorene38 and MXenes.39 The resultant dispersions can be processed into functional structures through spray casting,40 inkjet printing,41–43 gravure printing44 and freeze drying.45
Because so many layered materials exist46 and because LPE has been so successful at exfoliating a wide range of different layered crystals, an obvious strategy is to use this method to generate as many new 2D materials as possible. One candidate layered material is molybdenum dioxide (MoO2). Layered MoO2 is metallic, is relatively cheap to buy and has been shown to be promising in catalytic applications47,48 and as an anode material in Li ion storage batteries.49–52 Although MoO2 has been produced through synthesis,53–56 it has yet to be exfoliated by any liquid exfoliation procedure. Achieving liquid exfoliation of MoO2 would yield a number of advantages including a nanoscale morphology as well as significantly improved processability. In addition, for battery electrode applications, exfoliation of layered materials into nanosheets has been shown to significantly improve both capacity and stability in materials such as gallium sulfide57 and vanadium oxide.58 Thus, liquid phase exfoliation of MoO2 should yield advantages in battery applications and possibly other application areas. However, it goes without saying that little is known about the properties, processability or stability of liquid exfoliated MoO2.
Here we will show that MoO2 nanosheets can be produced by liquid phase exfoliation in a range of solvents. A combination of Raman and extinction spectroscopy shows that the resultant nanosheets are oxidized over a number of days to form higher oxides such as MoO3. However, if processed rapidly, these nanosheets can be used to prepare reasonably stable networks. We demonstrate their application potential by using such networks to fabricate high performance Li-ion battery anodes.
Results and discussion
Exfoliation and basic characterization
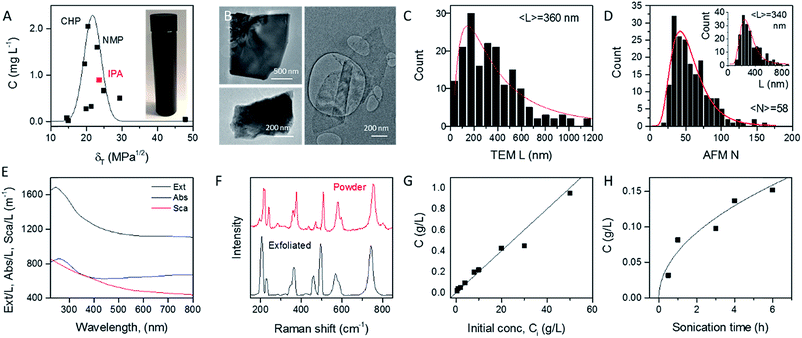
In order to identify appropriate solvents which can be used to produce MoO2 nanosheets, we applied established methods to exfoliate MoO2 powder in a range of solvents (see Experimental section). Briefly, 1600 mg of MoO2 powder was ultrasonicated in 80 mL of solvent for 6 hours at 750 W. This dispersion was then centrifuged twice to remove both very small nanosheets and unexfoliated powder to yield what we refer to as a standard sample (Fig. 1A, inset). Such standard samples would be expected to contain almost all nanosheets produced, yielding a relatively high mass, but also to be extremely polydisperse, containing a wide range of nanosheet sizes and thicknesses. Measurement of the dispersed concentration (Fig. 1A) showed a significant variation between 0.01 and 2 mg L−1. Plotting the dispersed concentration, C, versus the Hildebrand solubility parameter, δT,59 shows maximized MoO2 concentrations for solvents with δT ∼ 18–25 MPa1/2. Fitting the data to a Gaussian envelope function implies the solubility parameter of the nanosheets themselves to be ∼22 MPa1/2. This is similar to previously reported data for a range of 2D materials.7,36,60 We find the best solvents to be cyclohexyl-pyrrolidone (CHP) and N-methyl-pyrrolidone (NMP). However both of these solvents have very high boiling points which can make them difficult to work with. We note that isopropanol (IPA) yields a reasonably high nanosheet concentration (∼1 mg mL−1) coupled with a relative low boiling point. As such, we choose to work with IPA for the rest of this study. Dispersions produced in this way using IPA as a solvent are referred to as standard samples. Shown in Fig. 1B are selected TEM images of MoO2 nanosheets from an IPA standard sample. It can be seen from these images that MoO2 nanosheets produced by LPE tend to be a few hundred nanometers in size and display a range of thicknesses. To measure the nanosheet dimensions accurately, we performed both TEM and AFM characterization on the nanosheets obtained from the standard sample produced in IPA (see Experimental methods section: Production of MoO2 nanosheets). As shown in Fig. 1C and D (inset), both methods showed the nanosheet length (defined as the longest dimension) to range between ∼25 and 800 nm with means of 360 and 340 nm respectively. The AFM data can also be used to measure nanosheet thicknesses (expressed as layer number, N) with the resultant histogram shown in Fig. 1D. Representative images and step height analysis are shown in Fig. S4 of the ESI.† This graph shows the nanosheets produced in the standard sample to be on average relatively thick (〈N〉 = 58), and to display a very broad range of thicknesses, up to N > 100 monolayers. However, as we will show below, size selection can be used to extract fractions with much lower mean thicknesses.The optical extinction spectrum of a standard sample dispersion of MoO2 nanosheets in IPA is plotted in Fig. 1E. This curve displays a peak at low wavelength combined with a plateau at high wavelength with the latter feature expected for a metallic material. However, we note that in nanoparticle dispersions, the extinction spectrum is often not a good representation of optical absorption because of the presence of strong scattering effects.7,61 In general, the extinction (Ext) is the sum of absorption (Abs) and scattering (Sca) contributions, Ext(λ) = Abs(λ) + Sca(λ), which can be separated using an integrating sphere.61,62 The resulting absorbance and scattering spectra are shown in Fig. 1E. Importantly, the high wavelength plateau persists in the absorption spectrum, confirming the nanosheets to be metallic in nature.
To confirm the identity of the exfoliated material, we performed Raman spectroscopy on both starting and a vacuum-filtered film of exfoliated nanosheets (Fig. 1F). Both spectra were similar and showed a significant number of peaks (at 203, 228, 350, 362, 459, 495, 568, 587 and 742 cm−1), all of which were assigned to MoO2.63 No other compounds were observed in freshly prepared samples such as these.
As is generally the case,36 the concentration of liquid-exfoliated nanosheets depends on the exfoliation conditions. We have shown this by varying both the initial concentration of MoO2 powder (Fig. 1G) and the sonication time (Fig. 1H), and found the resultant nanosheet concentration to display linear and square-root scaling, respectively. Such behavior is as expected and has been observed in many studies on liquid exfoliation. In particular, the fact that  has been attributed to the effect of the diffusion of solvent molecules between the layers.64
has been attributed to the effect of the diffusion of solvent molecules between the layers.64
Stability of MoO2 nanosheets
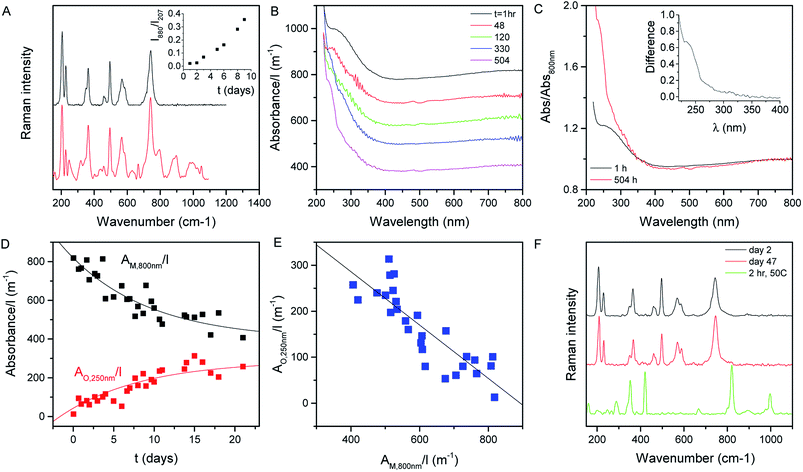
Shown in Fig. 2A (black curve) is the Raman spectrum of a newly prepared film of MoO2 nanosheets prepared from a fresh 1 day old dispersion. As discussed above, a range of lines can be seen in the range of ∼200 to ∼800 cm−1, all of which can be assigned to MoO2. However, this situation changes somewhat when the dispersion is allowed to stand under ambient conditions for a number of days before film preparation. As illustrated by the red curve, which shows the spectrum collected from a freshly-made film prepared from a 10 day old dispersion, aging results in the appearance of a number of new lines. This can be most clearly seen in the 800–1100 cm−1 spectral window, where a number of new features appear. These features can be assigned to higher oxides of molybdenum with the peaks at 796 and 896 cm−1, for example, associated with Mo4O11.65 Evidence of higher oxide formation can also be seen in XPS data (see the ESI†).The appearance of these new peaks is indicative of the oxidation of MoO2 to higher oxides such as Mo4O11 and MoO3.66 We can track the evolution of this process by measuring the Raman spectra of freshly prepared films made from dispersions which were left to stand under ambient conditions for various time periods. Fig. 2A (inset) shows the ratio of the intensity of the 880 cm−1 peak (representing Mo4O11) to that of the peak at 207 cm−1 (representing MoO2)67 plotted versus the time the dispersion was left to stand after exfoliation. This shows a well-defined increase, indicating a continuous oxidation process.
We can test this quantitatively by measuring the optical absorption spectra (i.e. with scattering removed) of MoO2 dispersions as a function of time after dispersion preparation (the dispersion was shaken before each measurement to remove any sedimentation effects). Subsets of such absorption spectra (normalized to cell length, l) are shown in Fig. 2B. From this data, it is clear that subtle shape changes occur over time. This can be seen more clearly by plotting the spectra collected after 1 and 504 h together in Fig. 2C, with both curves normalized to the absorbance at 800 nm. It is clear from this plot that the spectral shape is invariant with time in the range ∼350 to >800 nm. However, for λ < 350 nm, there is a clear increase in absorbance over time. This can be seen clearly by plotting the difference between these (normalized) spectra in the Fig. 2C inset.
We interpret this data as follows. MoO2 is expected to be metallic68 as evidenced by the plateau in absorbance at high wavelength.69 However, oxidation of MoO2 should result in the formation of structures such as MoO3 which is semiconducting.70 Thus we would expect the oxidation to result in the transfer of absorbance from the high wavelength region to the low wavelength region. This is exactly what is observed in Fig. 2B and C. We can analyze the time dependence of this process by plotting the cell-length-normalized absorbance at 800 nm, which we label AM,800 nm(t)/l (representing metallic MoO2), versus time in Fig. 2D. We see a clear exponential-like decay indicating that the concentration of MoO2 falls with time. If this is due to the oxidation of MoO2 to give semiconducting higher oxides, then this mass loss should be balanced by an increase in oxide concentration as evidenced by the relative absorbance increase at low wavelength. To quantify this we note that at t ∼ 0, the absorbance at 250 nm was 1.2× the absorbance at 800 nm. Assuming that this relationship is representative of MoO2, this means we can represent the absorbance due to the growing concentration of higher oxides as follows:
| AO,250 nm(t)/l = A250 nm(t)/l − 1.2AM,800 nm(t)/l | (1) |
This parameter is plotted versus time in Fig. 2D and shows a well-defined increase with time. We can analyze these data as follows.
We assume that there are two populations of Mo atoms, those incorporated into MoO2 (M) and those in higher oxides (O). We assume the total number of Mo atoms, n, is constant, allowing us to write:
| n = nM + nO | (2) |
For both MoO2 and higher oxides, we assume the absorbance per unit cell length scales with the total number of Mo atoms in each material type via a proportionality constant, σ, AM/l = σMnM and the same occurs for O such that
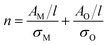 | (3) |
This allows us to write the absorbance associated with the oxide content as follows:
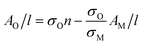 | (4) |
This predicts that the absorbance of the oxide component should scale linearly with that of the metallic MoO2, which we find to be true as shown in Fig. 2E for the AO,250 nm/l vs. AM,800 nm/l data. From the slope of this graph, we find the ratio σO,250 nm/σM,800 nm = 0.58.
Then, approximating the AM,800 nm/l data using an exponential decay as follows:
AM,800 nm/l = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−t/τ e−t/τ | (5) |
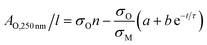 | (6) |
The last two equations have been used to fit the data in Fig. 2D, giving good fits in both cases with the same time constant of 243 h and yielding b = 423 m−1 and a = 396 m−1. These results show that the absorbance spectra are consistent with the idea that the metallic MoO2 converts to a semiconducting product over time. However the process is slow enough to allow exfoliation and processing to be carried out before any significant oxidation has occurred.
We attempted to confirm the oxidation of MoO2 to higher oxides over time using XRD (see the ESI, Fig. S7 and S8†). The bulk powder and freshly dispersed nanosheets displayed only the expected MoO2 lines. In addition to the MoO2 lines we saw very weak signals consistent with Mo4O11 and MoO3 in an aged sample which had been allowed to stand in IPA for ∼60 days. It is unclear why the higher oxides are only weakly observable using XRD. However, it may be that they actually contribute a smaller mass fraction than suggested by optical spectroscopy.
The data above imply that MoO2 is unstable against oxidation when suspended in IPA. However, this does not necessarily mean that MoO2 nanosheets are unstable when removed from the solvent. To test this, we prepared a fresh dispersion and rapidly filtered it through a porous membrane to form a film which was then dried and stored under ambient conditions. Shown in Fig. 2F are the Raman spectra of this film measured 2 days (black) and 47 days (red) after film formation. We find both spectra to be consistent with MoO2 with no evidence of higher oxide formation. However, when a freshly prepared film is heated to 50 °C for 2 h under ambient conditions, we find strong evidence of higher oxides (above 800 cm−1) as illustrated by the green spectrum. This indicates that air-stable MoO2 nanosheets can be produced once the exfoliation/preparation process is performed rapidly and the resultant structures are not exposed to high temperatures.
Size selection of molybdenum oxide nanosheets
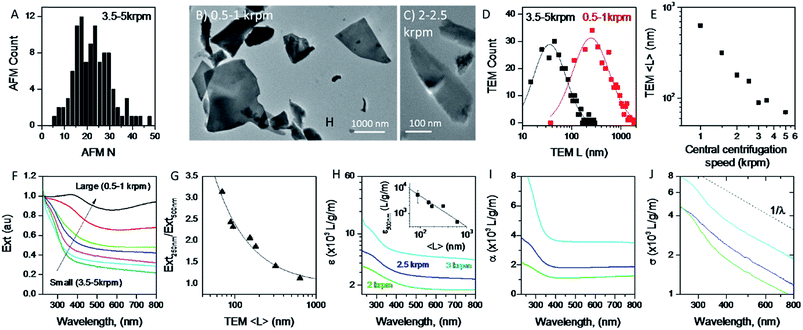
A great advantage of liquid phase exfoliation is that the nanosheets can be readily size selected and thus separated into fractions containing nanosheets of distinct length/thickness.7,28,31,38,61,71 This is of great importance as most applications require control of the lateral dimensions and thickness of nanosheets, e.g. small nanosheets for catalysis37,72 and large nanosheets for mechanical reinforcement.73 To achieve this, liquid cascade centrifugation31 was performed on the standard sample of MoO2. This method involves a number of sequential centrifugation steps, each using an increased centrifugation speed, to isolate nanosheets in different size ranges (see Experimental section).31 Here, we produced six distinctive sizes of nanosheets.Initially, AFM was performed on the smallest fraction to demonstrate the lower limit of the size distribution of the standard sample. To do this 0.1 mL of dispersion was deposited onto a silicon wafer placed on a hot plate to remove residual solvent. The histogram in Fig. 3A shows nanosheets considerably thinner than those shown in Fig. 1D with 〈N〉 = 25. We note that while this value is considerably smaller than that for the standard sample (Fig. 1D), these nanosheets are not particularly thin compared to results obtained for other 2D materials,31,61 suggesting MoO2 to be a relatively difficult material to exfoliate.
To ensure that the cascade was successful in creating a range of sizes, as well as to determine the average length of the nanosheets for each fraction, TEM was performed by pipetting a few drops of each dispersion onto carbon holey grids. As demonstrated in Fig. 3B and C, where the 0.5–1 krpm and 3.5–5 krpm samples are shown, the cascade resulted in well-exfoliated nanosheets ranging in size from microns to 10s of nanometers. Statistical analysis was also performed; shown in Fig. 3D are flake size distributions of the 0.5–1 krpm and 3.5–5 krpm fractions. Both show a log-normal distribution with the average shifted to much larger lengths for 0.5–1 krpm compared to the 3.5–5 krpm sample, as expected. To demonstrate the success of the centrifugation process a graph of mean nanosheet length, 〈L〉, (as measured by TEM) plotted vs. the central centrifugation speed is shown in Fig. 3E. This shows 〈L〉 to vary by over an order of magnitude over the range of speeds explored. Fig. S5 and S6, respectively, in the ESI† show histograms and representative TEM images for individual fractions.
It is now well-known that the optical properties of 2D materials are greatly affected by the dimensions of the nanosheets.31,61,74 The extinction (Ext), absorption (Abs) and scattering (Sca) spectra were measured for each fraction using a UV-vis spectrometer with an integrating sphere attachment.61 The extinction spectra normalised to 250 nm are shown in Fig. 3F (Abs and Sca spectra are shown in the ESI†). It can be seen clearly that there is large variation in spectral shape with nanosheet length. As mentioned previously the extinction spectra are made up of contributions from photons being both absorbed and scattered by the nanosheets.7,38 The resultant spectral shape change can be described quantitatively via the ratio of extinction values between the plateaus at long wavelengths and the peaks at short wavelengths. This disparity can be quantified as shown in Fig. 3G where the ratio between the extinction at 250 nm and 500 nm is plotted against 〈L〉 as calculated from TEM. Fitting this curve to an empirical equation yields an expression which relates 〈L〉 to the ratio mentioned above:
 | (7) |
It is also useful to characterise the extinction, absorption and scattering coefficient spectra for different nanosheet sizes. To achieve this, the concentration of each dispersion was determined through vacuum filtration and weighing (although some dispersions yielded a mass too low to be accurately weighed). The spectra were then converted to coefficient spectra using Ext = εCl, Abs = αCl, and Sca = σCl. Shown in Fig. 3H–J are the ε, α and σ spectra, respectively, for three fractions, 1–2 krpm, 2.5–3 krpm and 3–3.5 krpm. Despite the scattering contributions which increase for larger nanosheets (Fig. 3J), the extinction coefficient is greater for smaller nanosheets than for larger ones, which implies that a large contribution to the extinction spectra is due to absorption. This can be seen in Fig. 3I where the absorption spectra are similar in shape to the extinction spectra. Despite the material absorbing light across all wavelengths Fig. 3J still shows scattering coefficient spectra to display the typical power-law behaviour shown for other materials62 with a non-resonant region such as GaS7 and Ni(OH)2.28 The inset in Fig. 3H shows ε500 nm plotted against 〈L〉 which shows a well-defined trend which can be fitted with the empirical expression:
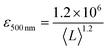 | (8) |
This equation can be used to estimate the extinction coefficient once the mean nanosheet length is known (e.g. from eqn (7)), returning a value in L g−1 m−1 when 〈L〉 is entered in nm.
Combining these equations with the fact that Ext500 nm = ε500 nmCl yields an expression for the MoO2 concentration:
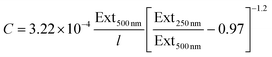 | (9) |
These relationships can be very useful as they can be used to determine the concentration of a nanosheet dispersion as well as the average length of nanosheets within the dispersion once the extinction spectrum is measured.
Applications of liquid-exfoliated MoO2 nanosheets in battery electrodes
A number of studies have demonstrated MoO2 to be a promising lithium storage material which has a theoretical capacity of 836 mA h per gram of MoO2 based on phase transitions and a conversion reaction.53,75,76 In the past, films of MoO2, which were synthesised in various ways, have been formed into lithium ion battery anodes with maximum capacities52,53,76,77 as high as ∼1200 mA h g−1, considerably beyond theoretical expectations. In addition, two papers75,78 report an “anomalous” capacity of up to 1800 mA h g−1 which has been explained via a Li-storage mechanism consisting of a Li-ion intercalation reaction and the formation of a metallic Li-rich phase between the Li-ion-intercalated MoO2 phases. It has been suggested that this mechanism strongly depends on the amount of accessible surface area present.75However, in all the reports that we have found, the MoO2 was prepared by chemical methods such as hydrothermal synthesis.77 Because of its simplicity and scalability, liquid phase exfoliation is an attractive alternative method for producing MoO2 for electrode applications. This method is advantageous in that it facilitates the addition of nano-conductors by solution mixing and allows simple, liquid-based film formation techniques. However, because liquid-exfoliated MoO2 nanosheets have never been tested for Li storage, their potential for use in this application area is unknown.
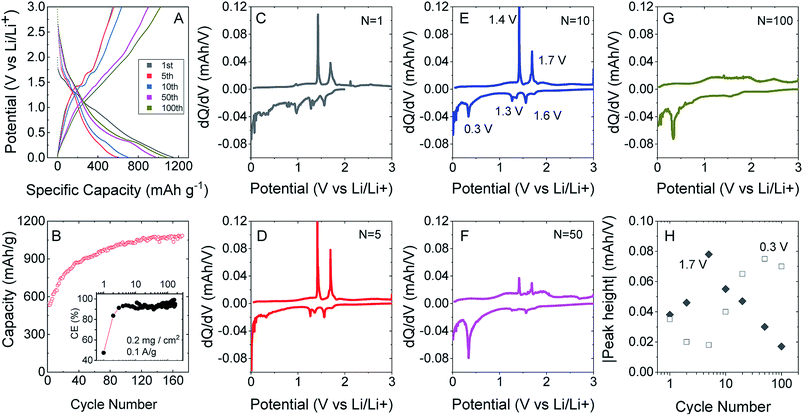
To test this, we produced lithium ion battery anodes based on liquid-exfoliated MoO2 nanosheets. To promote electrical conductivity as well as mechanical robustness,79 we added 20 wt% single wall nanotubes as both a conductive additive and mechanical binder. We studied basic electrochemical characterisation with galvanostatic charge–discharge curves and capacity versus cycle number data as shown in Fig. 4A and B. We found that MoO2-based electrodes (with a mass loading of 0.2 mg cm−2 MoO2) show good lithium storage capability. When measured at a specific current of 0.1 A g−1, the initial discharge and charge capacities were 1150 and 546 mA h g−1, respectively, yielding a 47.5% coulombic efficiency. The discharge and charge capacities were 635 and 531 mA h g−1, respectively, for the 2nd cycle (with 83.7% CE) with the irreversible capacity loss after the first cycle being due to the formation of a solid electrolyte interface.53,76,77 Interestingly, the discharge and charge capacities gradually increased to 1141 and 1085 mA h g−1 (with 95% CE) over 170 cycles. The coulombic efficiency is plotted versus cycle number in the inset of Fig. 4B. The low coulombic efficiency observed in the first cycle is typical of transition metal oxides,53,75–77,80 and is due to the formation of a solid electrolyte interface and electrolyte degradation.
After about 120 cycles, the capacitance values are comparable with those of the best non-anomalous MoO2 electrodes reported (up to 1200 mA h g−1).52,53,76,77 It is particularly interesting that the capacity increases steadily with cycling. This has been observed by a number of authors for MoO2 (ref. 52 and 76) and has been attributed to the increase in and activation of the surface area, which happens in discharge/charge and is caused by the separation of stacked layers during the process, improving the ability to store lithium ions and Li metal.75
We can understand the performance in more detail by studying differential capacity curves (dQ/dV) obtained by differentiating charge/discharge curves such as those shown in Fig. 4A. Both dQ/dV and cyclic voltammetry data have been reported and discussed in detail for MoO2.52,81,82 Shown in Fig. 4C–G are differential curves associated with cycles 1, 5, 10, 50 and 100. This evolution of the differential capacity with cycle number is closely aligned with previous reports,81 with the main features being oxidation peaks at 1.4 and 1.7 V and reduction peaks at 0.3, 1.3 and 1.6 V. The two sets of redox peaks at 1.3 V/1.4 V and 1.6 V/1.7 V are associated with the insertion of lithium into MoO2 to yield LiMoO2 and the accompanying monoclinic to orthorhombic to monoclinic phase transition.83 In addition, there is a sharp reduction peak at 0.3 V (accompanied by a broad oxidation peak at ∼0.5 V) associated with the conversion of LiMoO2 to Li2O (LiMoO2 + 3Li+ + 3e− → Mo + 4Li2O). While the insertion reaction has a theoretical capacity of 209 mA h g−1, the conversion reaction has a significantly larger theoretical capacity of 627 mA h g−1.81 In line with previous results,52,81,82 we find that the insertion peaks decrease with cycling while the conversion peak increases with cycling (Fig. 4H). It has previously been suggested that cycling opens up the layered crystal, increasing the active surface area and hence the capacity.75 This process may also be responsible for the simultaneous changes in insertion and conversion peaks. For example, a more open material with greater surface area may be more amenable to conversion.
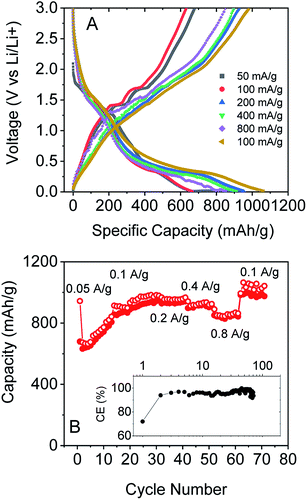
We also tested the rate performance of our electrodes as shown in Fig. 5A and B, although such data are complicated by the increase in capacity with cycle number shown in Fig. 4A and B. These electrodes exhibited an initial performance of 943 mA h g−1 for discharge and 679 mA h g−1 for charge at 0.05 A g−1. At 0.1 A g−1, the capacity is 673 mA h g−1 for discharge and 632 mA h g−1 for charge, with an increase to 978 and 950 mA h g−1 after 30 cycles. Furthermore, the composite electrode is capable of fast charge and discharge. When the specific currents were increased to 0.2, 0.4, and 0.8 A g−1, specific charge capacities of 928, 898, and 851 mA h g−1, respectively, are reversibly delivered. And when the current rate was 0.1 A g−1 again, the specific charge capacities could even reach 983 mA h g−1. Again, these results are comparable with those of the best reports of non-anomalous MoO2.52
All the battery data above indicate that our exfoliated MoO2 flakes with CNTs are capable of high specific capacity and excellent cyclability. We attribute the outstanding lithium storage performance of the MoO2/CNT nanocomposite to the following factors: (1) high surface area leads to a large lithium storage capacity. (2) The pathway for Li+ diffusion is significantly reduced on exfoliation compared to bulk MoO2, thus the rate capability is improved. (3) The CNT network not only provides good conductivity, but also maintains the stable structure of the electrode films upon cycling, and hence the excellent cycling stability observed is achievable.
Conclusions
In summary, we have demonstrated the production of MoO2 nanosheets via liquid phase exfoliation. However, it is clear that these nanosheets are somewhat unstable, being oxidised over a period of days when suspended in isopropanol under ambient conditions. Moreover, we found that if the nanosheets are processed into films quickly after exfoliation, the subsequent oxidation is dramatically slowed, unless the films are heated under ambient conditions. In addition, we have shown that MoO2 nanosheets can be size selected by controlled centrifugation. As with other 2D materials, we observe significant variations in optical properties with nanosheet size, allowing us to propose spectroscopic metrics which allow the estimation of concentration and mean nanosheet size from the extinction spectra. Finally, MoO2 dispersions tested for application in Li ion batteries show good storage capacity which is comparable with that of the best non-anomalous MoO2 electrodes.Experimental methods section
Material
Molybdenum dioxide powder (99%) was purchased from Sigma Aldrich and was used as received. When not in use, the MoO2 powder was stored in a glovebox in argon to prevent exposure to O2/H2O and subsequent oxidation.Production of MoO2 nanosheets
MoO2 powder was sonicated in a solvent using a horn probe sonic tip (VibraCell CVX, 750 W) at 60% amplitude in an aluminium cup with 80 mL isopropanol (IPA) at a MoO2 concentration of 20 mg mL−1. The dispersion was sonicated for 6 hours with a 6 s/2 s on/off pulse ratio and ice cooling was used to prevent boiling off of the solvent. Once sonicated the dispersion was centrifuged using a Hettich Mikro 220R centrifuge equipped with a fixed angle rotor (where RCF = 106.4 (krpm)2). The dispersion was centrifuged for one hour at 500 rpm (26.6g) to extract unexfoliated material and then at 5000 rpm (2660g) to remove extremely small nanosheets. The sediment from the 5000 rpm step was then redispersed using bath sonication. A sample produced in this way is referred to as a standard sample.A comparative experiment was carried out to identify the optimal solvent for exfoliating the material. Aliquots of each solvent (20 mL) were used to exfoliate MoO2 with an initial concentration of 5 mg mL−1 for 30 minutes using a tapered tip. The resulting dispersion was then centrifuged at 2500 rpm (665g) for 2.5 hours, and the sediment was discarded. Spectroscopic analysis of each dispersion using a UV Vis spectrophotometer allows the concentration of the dispersions to be measured and plotted as a function of the Hildebrand solubility parameter. List of solvents used: deionised water (δ = 47.5 MPa1/2), isopropanol (δ = 23.6 MPa1/2), acetone (δ = 19.9 MPa1/2), N-cyclohexyl-2-pyrrolidone (δ = 20.5 MPa1/2), N-methyl-2-pyrrolidone (δ = 23 MPa1/2), pentane (δ = 14.4 MPa1/2), dimethylformamide (δ = 24.9 MPa1/2), methanol (δ = 29.6 MPa1/2), hexane (δ = 14.9 MPa1/2), 2-isopropoxyethanol (δ = 21.4 MPa1/2), and 1-dodecyl-2-pyrrolidinone (δ = 18.8 MPa1/2). To determine the optimal sonication time a dispersion of MoO2 in IPA (80 mL) at an initial concentration of 20 mg mL−1 was prepared and sonicated. Aliquots were removed after fixed sonication times (0.5, 1, 3, 4, 6, 8, and 24 hours) and each was centrifuged between 500 and 5000 rpm. The concentration of each sample was obtained by absorption spectroscopy and plotted against sonication time.
Size selection
Dispersions of MoO2 in IPA were size selected using Liquid Cascade Centrifugation,31 a technique consisting of multiple centrifugation steps with incremental increases in rpm. After each centrifugation step the supernatant was decanted and was used for the subsequent centrifugation step. The sediment was redispersed and labelled as appropriate.Film preparation
The MoO2 dispersions mixed with SWCNTs84 were vacuum-filtered using porous cellulose filter membranes (MF-Millipore membrane, mixed cellulose esters, hydrophilic, 0.025 μm, 47 mm) to give thin films with 20 wt% SWCNTs. 0.1 mg mL−1 dispersions of SWCNTs were prepared by dispersing 10 mg of P3-SWCNT in 100 mL of IPA for one hour in a Fisherbrand Sonic Dismembrator (30 W, 40% amplitude). The mass loading of these films was controlled by the volume of dispersion filtered.The resulting films (diameter, 36 mm) were cut to the desired dimensions for electrochemical testing and then transferred to Cu foil using IPA to paste the film to the substrate. The cellulose filter membrane was removed by treatment with acetone vapour and subsequent acetone liquid baths. The mass loading of MoO2 is 0.5 mg cm−2 for rate capability measurements and 0.2 mg cm−2 for cycling performance measurements.
Characterisation
Optical characterisation was performed using a Perkin Elmer Lambda 1050 ultraviolet-visible spectrometer, equipped with an integrating sphere for measuring the absorption (the extinction with scattering effects removed) and a quartz cuvette with a path length of 4 mm.A Horiba Jobin-Yvon LabRAM HR800 was used to acquire the Raman spectra. 632 nm was chosen as the laser line. The laser power was set to 0.2 mW in order to avoid sample degradation. No heating or degradation effects were observed at this power. A 100× objective focused the beam to a ∼2 μm diameter spot, a diffraction grating of 600 grooves per mm was used, and a spectral resolution of ∼1.2 cm−1 was obtained.
For solid samples, measurements were performed at room temperature. Due to the low Raman cross section 1200 s was chosen as the acquisition time, and two spectra were averaged in order to obtain a single spectrum. Each map has an area of 20 μm × 20 μm and a step of 10 μm was used (25 measurements per map, 20 × 2 min per single spectrum, 16.6 hours per map).
In situ liquid sample measurement was impossible. As long integration times were needed, the solvent evaporated during measurement causing defocusing. Instead a few hundred μL were drop cast and 8 to 10 spectra from manually selected spots were averaged to obtain the final spectra. 1500 s was chosen as the measurement integration time and 3 spectra were averaged in each spot (10–12.5 h per sample).
AFM imaging was performed using a Veeco Nanoscope-IIIa from Digital Instruments. An E-head in tapping mode was used for all measurements. The MoO2 nanosheet dispersion in isopropanol (IPA) was further diluted with IPA at a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (old sample) and 1
5 (old sample) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 (fresh sample) and drop cast (10 μL) on preheated (140 °C) Si/SiO2 wafers (0.25 cm2) with an oxide layer of 300 nm. After deposition the wafers were rinsed with IPA and dried with compressed air prior to measurement. Typical image size used was 8 μm2 with 512 lines per image and scan rates of 0.6 Hz. The measured thickness was corrected and then converted to number of layers based on conducted step height analysis.
20 (fresh sample) and drop cast (10 μL) on preheated (140 °C) Si/SiO2 wafers (0.25 cm2) with an oxide layer of 300 nm. After deposition the wafers were rinsed with IPA and dried with compressed air prior to measurement. Typical image size used was 8 μm2 with 512 lines per image and scan rates of 0.6 Hz. The measured thickness was corrected and then converted to number of layers based on conducted step height analysis.
The nanosheets were imaged using a JEOL 2100 series Transmission Electron Microscope (TEM). Dispersions of MoO2 were prepared for imaging by drop casting on holey carbon TEM grids (Agar Scientific). During the drop casting process the grids were placed on filter paper to absorb excess solvent. After imaging, the lengths of nanosheets were recorded using ImageJ software and histograms of the flake size distribution were compiled. The longest dimension observed was designated as the flake length.
For X-ray photoelectron spectroscopy (XPS) measurements, a PHI VersaProbe III instrument equipped with a micro-focused, monochromatic Al Kα source (1486.6 eV) and a dual beam charge neutralization was used. Core level spectra were recorded with a spot size of 100 μm and a pass energy of 69 eV using PHI SmartSoft VersaProbe software, and processed with PHI MultiPak 9.8. Sputter depth profiling was conducted using 1 keV Ar+ ions. Binding energies were referenced to the adventitious carbon signal at 284.8 eV. After subtraction of a Shirley type background, the spectra were fitted with Gaussian–Lorentzian peak shapes.
Li-ion storage
For the electrochemical measurement, metallic lithium foil (diameter: 14 mm, MTI Corp.) was used as the negative electrodes. The electrolyte used was 1 M LiPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (volume ratio) mixture of ethylene carbonate (EC) and dimethyl carbonate (DMC). A Celgard 2320 was used as the separator. The cells were assembled in a glovebox filled with highly pure argon gas (O2 and H2O levels <1 ppm), and the electrochemical properties of the electrodes were measured within a voltage range of 3.0–0.01 V using constant current (CC) mode on an automatic battery tester (VMP 3, Bio-Logic). For rate capability measurement, cells were run at different current rates of 0.05 A g−1, 0.1 A g−1, 0.2 A g−1, 0.4 A g−1, and 0.8 A g−1, and then at 0.1 A g−1. There is only 1 cycle at 0.05 A g−1 for activation, followed by 30 cycles at 0.1 A g−1. Then there are 10 cycles for the next steps at different current rates. For cycling capability tests, the cells were tested at 0.1 A g−1.
1 (volume ratio) mixture of ethylene carbonate (EC) and dimethyl carbonate (DMC). A Celgard 2320 was used as the separator. The cells were assembled in a glovebox filled with highly pure argon gas (O2 and H2O levels <1 ppm), and the electrochemical properties of the electrodes were measured within a voltage range of 3.0–0.01 V using constant current (CC) mode on an automatic battery tester (VMP 3, Bio-Logic). For rate capability measurement, cells were run at different current rates of 0.05 A g−1, 0.1 A g−1, 0.2 A g−1, 0.4 A g−1, and 0.8 A g−1, and then at 0.1 A g−1. There is only 1 cycle at 0.05 A g−1 for activation, followed by 30 cycles at 0.1 A g−1. Then there are 10 cycles for the next steps at different current rates. For cycling capability tests, the cells were tested at 0.1 A g−1.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The research leading to these results has received funding from the European Union Seventh Framework Programme under grant agreement no. 604391 Graphene Flagship. We have also received support from the Science Foundation Ireland (SFI) funded center AMBER (SFI/12/RC/2278). In addition, JNC acknowledges the SFI (11/PI/1087) for financial support.References
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- M. Chhowalla, H. S. Shin, G. Eda, L. J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- C. Y. Zhi, Y. Bando, C. C. Tang, H. Kuwahara and D. Golberg, Adv. Mater., 2009, 21, 2889–2893 CrossRef CAS.
- W. Feng, J. B. Wu, X. L. Li, W. Zheng, X. Zhou, K. Xiao, W. W. Cao, B. Yang, J. C. Idrobo, L. Basile, W. Q. Tian, P. H. Tan and P. A. Hu, J. Mater. Chem. C, 2015, 3, 7022–7028 RSC.
- A. Harvey, C. Backes, Z. Gholamvand, D. Hanlon, D. McAteer, H. C. Nerl, E. McGuire, A. Seral-Ascaso, Q. M. Ramasse, N. McEvoy, S. Winters, N. C. Berner, D. McCloskey, J. F. Donegan, G. S. Duesberg, V. Nicolosi and J. N. Coleman, Chem. Mater., 2015, 27, 3483–3493 CrossRef CAS.
- K. Kalantar-zadeh, J. Z. Ou, T. Daeneke, A. Mitchell, T. Sasaki and M. S. Fuhrer, Appl. Mater. Today, 2016, 5, 73–89 CrossRef.
- M. Osada and T. Sasaki, J. Mater. Chem., 2009, 19, 2503–2511 RSC.
- S. Balendhran, S. Walia, H. Nili, J. Z. Ou, S. Zhuiykov, R. B. Kaner, S. Sriram, M. Bhaskaran and K. Kalantar-zadeh, Adv. Funct. Mater., 2013, 23, 3952–3970 CrossRef CAS.
- V. Nicolosi, M. Chhowalla, M. G. Kanatzidis, M. S. Strano and J. N. Coleman, Science, 2013, 340, 1226419 CrossRef.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- R. Tkacz, R. Oldenbourg, S. B. Mehta, M. Miansari, A. Verma and M. Majumder, Chem. Commun., 2014, 50, 6668–6671 RSC.
- A. E. D. Castillo, V. Pellegrini, H. Y. Sun, J. Buha, D. A. Dinh, E. Lago, A. Ansaldo, A. Capasso, L. Manna and F. Bonaccorso, Chem. Mater., 2018, 30, 506–516 CrossRef.
- C. Chen, X. Q. Xie, B. Anasori, A. Sarycheva, T. Makaryan, M. Q. Zhao, P. Urbankowski, L. Miao, J. J. Jiang and Y. Gogotsi, Angew. Chem., Int. Ed., 2018, 57, 1846–1850 CrossRef CAS PubMed.
- Y. Y. Wang, J. H. Zhou, J. H. Wu, F. J. Chen, P. R. Li, N. Han, W. J. Huang, Y. P. Liu, H. L. Ye, F. P. Zhao and Y. G. Li, J. Mater. Chem. A, 2017, 5, 25618–25624 RSC.
- R. F. Frindt, Phys. Rev., 1965, 140, A536–A539 CrossRef.
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- H. S. S. R. Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. N. R. Rao, Angew. Chem., Int. Ed., 2010, 49, 4059–4062 CrossRef CAS PubMed.
- M. O'Brien, K. Lee, R. Morrish, N. C. Berner, N. McEvoy, C. A. Wolden and G. S. Duesberg, Chem. Phys. Lett., 2014, 615, 6–10 CrossRef.
- C. Berger, Z. M. Song, T. B. Li, X. B. Li, A. Y. Ogbazghi, R. Feng, Z. T. Dai, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, J. Phys. Chem. B, 2004, 108, 19912–19916 CrossRef CAS.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Y. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS PubMed.
- J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H. Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- G. Eda, H. Yamaguchi, D. Voiry, T. Fujita, M. W. Chen and M. Chhowalla, Nano Lett., 2011, 11, 5111–5116 CrossRef CAS PubMed.
- C. Sole, N. E. Drewett, F. Liu, A. M. Abdelkader, I. A. Kinloch and L. J. Hardwick, J. Electroanal. Chem., 2015, 753, 35–41 CrossRef CAS.
- K. R. Paton, E. Varrla, C. Backes, R. J. Smith, U. Khan, A. O'Neill, C. Boland, M. Lotya, O. M. Istrate, P. King, T. Higgins, S. Barwich, P. May, P. Puczkarski, I. Ahmed, M. Moebius, H. Pettersson, E. Long, J. Coelho, S. E. O'Brien, E. K. McGuire, B. M. Sanchez, G. S. Duesberg, N. McEvoy, T. J. Pennycook, C. Downing, A. Crossley, V. Nicolosi and J. N. Coleman, Nat. Mater., 2014, 13, 624–630 CrossRef CAS PubMed.
- A. E. Del Rio Castillo, V. Pellegrini, A. Ansaldo, F. Ricciardella, H. Sun, L. Marasco, J. Buha, Z. Dang, L. Gagliani, E. Lago, N. Curreli, S. Gentiluomo, F. Palazon, M. Prato, R. Oropesa-Nuñez, P. S. Toth, E. Mantero, M. Crugliano, A. Gamucci, A. Tomadin, M. Polini and F. Bonaccorso, Mater. Horiz., 2018, 5, 890–904 RSC.
- A. Harvey, X. Y. He, I. J. Godwin, C. Backes, D. McAteer, N. C. Berner, N. McEvoy, A. Ferguson, A. Shmeliov, M. E. G. Lyons, V. Nicolosi, G. S. Duesberg, J. F. Donegan and J. N. Coleman, J. Mater. Chem. A, 2016, 4, 11046–11059 RSC.
- J. N. Coleman, Acc. Chem. Res., 2013, 46, 14–22 CrossRef CAS PubMed.
- U. Khan, H. Porwal, A. O'Neill, K. Nawaz, P. May and J. N. Coleman, Langmuir, 2011, 27, 9077–9082 CrossRef CAS PubMed.
- C. Backes, B. M. Szydlowska, A. Harvey, S. Yuan, V. Vega-Mayoral, B. R. Davies, P. L. Zhao, D. Hanlon, E. J. Santos, M. I. Katsnelson, W. J. Blau, C. Gadermaier and J. N. Coleman, ACS Nano, 2016, 10, 1589–1601 CrossRef CAS PubMed.
- M. Yi and Z. G. Shen, Carbon, 2014, 78, 622–626 CrossRef CAS.
- L. H. Liu, G. Zorn, D. G. Castner, R. Solanki, M. M. Lerner and M. D. Yan, J. Mater. Chem., 2010, 20, 5041–5046 RSC.
- W. C. Du, X. Q. Jiang and L. H. Zhu, J. Mater. Chem. A, 2013, 1, 10592–10606 RSC.
- G. S. Bang, K. W. Nam, J. Y. Kim, J. Shin, J. W. Choi and S. Y. Choi, ACS Appl. Mater. Interfaces, 2014, 6, 7084–7089 CrossRef CAS PubMed.
- D. Hanlon, C. Backes, T. M. Higgins, M. Hughes, A. O'Neill, P. King, N. McEvoy, G. S. Duesberg, B. M. Sanchez, H. Pettersson, V. Nicolosi and J. N. Coleman, Chem. Mater., 2014, 26, 1751–1763 CrossRef CAS.
- D. McAteer, I. J. Godwin, Z. Ling, A. Harvey, L. He, C. S. Boland, V. Vega-Mayoral, B. Szydlowska, A. A. Rovetta, C. Backes, J. B. Boland, X. Chen, M. E. G. Lyons and J. N. Coleman, Adv. Energy Mater., 2018, 8, 1702965 CrossRef.
- D. Hanlon, C. Backes, E. Doherty, C. S. Cucinotta, N. C. Berner, C. Boland, K. Lee, A. Harvey, P. Lynch, Z. Gholamvand, S. F. Zhang, K. P. Wang, G. Moynihan, A. Pokle, Q. M. Ramasse, N. McEvoy, W. J. Blau, J. Wang, G. Abellan, F. Hauke, A. Hirsch, S. Sanvito, D. D. O'Regan, G. S. Duesberg, V. Nicolosi and J. N. Coleman, Nat. Commun., 2015, 6, 8563 CrossRef CAS PubMed.
- M. Naguib, O. Mashtalir, J. Carle, M. Kurtoglu, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6(2), 1322–1331 CrossRef CAS PubMed.
- B. Mendoza-Sanchez, J. Coelho, A. Pokle and V. Nicolosi, Electrochim. Acta, 2015, 174, 696–705 CrossRef CAS.
- A. G. Kelly, D. Finn, A. Harvey, T. Hallam and J. N. Coleman, Appl. Phys. Lett., 2016, 109, 023107 CrossRef.
- A. G. Kelly, T. Hallam, C. Backes, A. Harvey, A. S. Esmaeily, I. Godwin, J. Coelho, V. Nicolosi, J. Lauth, A. Kulkarni, S. Kinge, L. D. A. Siebbeles, G. S. Duesberg and J. N. Coleman, Science, 2017, 356, 69–72 CrossRef CAS PubMed.
- F. Torrisi, T. Hasan, W. P. Wu, Z. P. Sun, A. Lombardo, T. S. Kulmala, G. W. Hsieh, S. J. Jung, F. Bonaccorso, P. J. Paul, D. P. Chu and A. C. Ferrari, ACS Nano, 2012, 6, 2992–3006 CrossRef CAS PubMed.
- E. B. Secor, S. Lim, H. Zhang, C. D. Frisbie, L. F. Francis and M. C. Hersam, Adv. Mater., 2014, 26, 4533–4538 CrossRef CAS PubMed.
- X. T. Zhang, Z. Y. Sui, B. Xu, S. F. Yue, Y. J. Luo, W. C. Zhan and B. Liu, J. Mater. Chem., 2011, 21, 6494–6497 RSC.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- Z. J. Chen, J. X. Cao, L. W. Yang, W. J. Yin and X. L. Wei, J. Phys. D: Appl. Phys., 2018, 51(26), 265106 CrossRef.
- C. Zhang, X. L. Zou, Z. G. Du, J. N. Gu, S. M. Li, B. Li and S. B. Yang, Small, 2018, 14, 1703960 CrossRef PubMed.
- A. Kim, E. Park, H. Lee and H. Kim, J. Alloys Compd., 2016, 681, 301–306 CrossRef CAS.
- Y. F. Shi, B. K. Guo, S. A. Corr, Q. H. Shi, Y. S. Hu, K. R. Heier, L. Q. Chen, R. Seshadri and G. D. Stucky, Nano Lett., 2009, 9, 4215–4220 CrossRef CAS PubMed.
- L. C. Yang, Q. S. Gao, Y. H. Zhang, Y. Tang and Y. P. Wu, Electrochem. Commun., 2008, 10, 118–122 CrossRef CAS.
- Z. W. Xu, H. L. Wang, Z. Li, A. Kohandehghan, J. Ding, J. Chen, K. Cui and D. Mitlin, J. Phys. Chem. C, 2014, 118, 18387–18396 CrossRef CAS.
- Y. M. Sun, X. L. Hu, W. Luo and Y. H. Huang, J. Mater. Chem., 2012, 22, 425–431 RSC.
- Q. Yang, Q. Liang, J. Liu, S. Q. Liang, S. S. Tang, P. J. Lu and Y. K. Lu, Mater. Lett., 2014, 127, 32–35 CrossRef CAS.
- H. X. Zhang, L. X. Zeng, X. M. Wu, L. F. Lian and M. D. Wei, J. Alloys Compd., 2013, 580, 358–362 CrossRef CAS.
- S. Balendhran, J. Z. Ou, M. Bhaskaran, S. Sriram, S. Ippolito, Z. Vasic, E. Kats, S. Bhargava, S. Zhuiykov and K. Kalantar-zadeh, Nanoscale, 2012, 4, 461–466 RSC.
- C. F. Zhang, S. H. Park, O. Ronan, A. Harvey, A. Seral-Ascaso, Z. F. Lin, N. McEvoy, C. S. Boland, N. C. Berner, G. S. Duesberg, P. Rozier, J. N. Coleman and V. Nicolosi, Small, 2017, 13(34), 1701677 CrossRef PubMed.
- C. F. Zhang, S. H. Park, S. E. O'Brien, A. Seral-Ascaso, M. Y. Liang, D. Hanlon, D. Krishnan, A. Crossley, N. McEvoy, J. N. Coleman and V. Nicolosi, Nano Energy, 2017, 39, 151–161 CrossRef CAS.
- J. M. Hughes, D. Aherne and J. N. Coleman, J. Appl. Polym. Sci., 2013, 127, 4483–4491 CrossRef CAS.
- G. Cunningham, M. Lotya, C. S. Cucinotta, S. Sanvito, S. D. Bergin, R. Menzel, M. S. P. Shaffer and J. N. Coleman, ACS Nano, 2012, 6, 3468–3480 CrossRef CAS PubMed.
- C. Backes, R. J. Smith, N. McEvoy, N. C. Berner, D. McCloskey, H. C. Nerl, A. O'Neill, P. J. King, T. Higgins, D. Hanlon, N. Scheuschner, J. Maultzsch, L. Houben, G. S. Duesberg, J. F. Donegan, V. Nicolosi and J. N. Coleman, Nat. Commun., 2014, 5, 4576 CrossRef CAS PubMed.
- A. Harvey, C. Backes, J. B. Boland, X. Y. He, A. Griffin, B. Szydlowska, C. Gabbett, J. F. Donegan and J. N. Coleman, Nat. Commun., 2018, 9, 4553 CrossRef PubMed.
- M. A. Camacho-Lopez, L. Escobar-Alarcon, M. Picquart, R. Arroyo, G. Cordoba and E. Haro-Poniatowski, Opt. Mater., 2011, 33, 480–484 CrossRef CAS.
- J. Texter, Angew. Chem., Int. Ed., 2015, 54, 10258–10262 CrossRef CAS PubMed.
- K. A. Olson and G. L. Schrader, Mater. Res. Soc. Symp. Proc., 1990, 187, 167–171 CrossRef CAS.
- G. Rodriguez-Gattorno, A. Martinez-Hernandez, L. O. Aleman-Vazquez and E. Torres-Garcia, Appl. Catal., A, 2007, 321, 117–124 CrossRef CAS.
- M. Dieterle and G. Mestl, Phys. Chem. Chem. Phys., 2002, 4, 822–826 RSC.
- Y. S. Jin and P. K. Shen, J. Mater. Chem. A, 2015, 3, 20080–20085 RSC.
- K. M. Hercule, Q. L. Wei, A. M. Khan, Y. L. Zhao, X. C. Tian and L. Q. Mai, Nano Lett., 2013, 13, 5685–5691 CrossRef CAS PubMed.
- E. Comini, L. Yubao, Y. Brando and G. Sberveglieri, Chem. Phys. Lett., 2005, 407, 368–371 CrossRef CAS.
- A. A. Green and M. C. Hersam, Nano Lett., 2009, 9, 4031–4036 CrossRef CAS PubMed.
- Z. Gholamvand, D. McAteer, A. Harvey, C. Backes and J. N. Coleman, Chem. Mater., 2016, 28, 2641–2651 CrossRef CAS.
- P. May, U. Khan, A. O'Neill and J. N. Coleman, J. Mater. Chem., 2012, 22, 1278–1282 RSC.
- C. Backes, K. R. Paton, D. Hanlon, S. Yuan, M. I. Katsnelson, J. Houston, R. J. Smith, D. McCloskey, J. F. Donegan and J. N. Coleman, Nanoscale, 2016, 8, 4311–4323 RSC.
- J. K. Shon, H. S. Lee, G. O. Park, J. Yoon, E. Park, G. S. Park, S. S. Kong, M. Jin, J. M. Choi, H. Chang, S. Doo, J. M. Kim, W. S. Yoon, C. Pak, H. Kim and G. D. Stucky, Nat. Commun., 2016, 7, 11049 CrossRef CAS PubMed.
- A. Bhaskar, M. Deepa and T. N. Rao, ACS Appl. Mater. Interfaces, 2013, 5, 2555–2566 CrossRef CAS PubMed.
- L. Zhou, H. B. Wu, Z. Y. Wang and X. W. Lou, ACS Appl. Mater. Interfaces, 2011, 3, 4853–4857 CrossRef CAS PubMed.
- C. Xia, Y. G. Zhou, D. B. Velusamy, A. A. Farah, P. Li, Q. Jiang, I. N. Odeh, Z. G. Wang, X. X. Zhang and H. N. Alshareef, Nano Lett., 2018, 18, 1506–1515 CrossRef CAS PubMed.
- Y. P. Liu, X. Y. He, D. Hanlon, A. Harvey, U. Khan, Y. G. Li and J. N. Coleman, ACS Nano, 2016, 10, 5980–5990 CrossRef CAS PubMed.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J. M. Tarascon, Nature, 2000, 407, 496–499 CrossRef CAS PubMed.
- H. Fu, Z. W. Xu, T. Wang, K. Li, X. T. Shen, J. Y. Li and J. F. Huang, J. Electrochem. Soc., 2018, 165, A439–A447 CrossRef CAS.
- Z. W. Xu, T. Wang, L. Kong, K. Yao, H. Fu, K. Li, L. Y. Cao, J. F. Huang and Q. L. Zhang, Part. Part. Syst. Charact., 2017, 34(3), 1600223 CrossRef.
- Y. M. Sun, X. L. Hu, W. Luo and Y. H. Huang, ACS Nano, 2011, 5, 7100–7107 CrossRef CAS PubMed.
- C. Gabbett, C. S. Boland, A. Harvey, V. Vega-Mayoral, R. J. Young and J. N. Coleman, Chem. Mater., 2018, 30, 5245–5255 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00241j |
| This journal is © The Royal Society of Chemistry 2019 |