Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mapping binary copolymer property space with neural networks†
Liam
Wilbraham
 a,
Reiner Sebastian
Sprick
a,
Reiner Sebastian
Sprick
 b,
Kim E.
Jelfs
b,
Kim E.
Jelfs
 c and
Martijn A.
Zwijnenburg
c and
Martijn A.
Zwijnenburg
 *a
*a
aDepartment of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: m.zwijnenburg@ucl.ac.uk
bDepartment of Chemistry and Materials Innovation Factory, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK
cDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, Wood Lane, London, W12 0BZ, UK
First published on 1st April 2019
Abstract
The extremely large number of unique polymer compositions that can be achieved through copolymerisation makes it an attractive strategy for tuning their optoelectronic properties. However, this same attribute also makes it challenging to explore the resulting property space and understand the range of properties that can be realised. In an effort to enable the rapid exploration of this space in the case of binary copolymers, we train a neural network using a tiered data generation strategy to accurately predict the optical and electronic properties of 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 binary copolymers that are, in principle, synthesizable from their dihalogen monomers via Yamamoto, or Suzuki–Miyaura and Stille coupling after one-step functionalisation. By extracting general features of this property space that would otherwise be obscured in smaller datasets, we identify simple models that effectively relate the properties of these copolymers to the homopolymers of their constituent monomers, and challenge common ideas behind copolymer design. We find that binary copolymerisation does not appear to allow access to regions of the optoelectronic property space that are not already sampled by the homopolymers, although it conceptually allows for more fine-grained property control. Using the large volume of data available, we test the hypothesis that copolymerisation of ‘donor’ and ‘acceptor’ monomers can result in copolymers with a lower optical gap than their related homopolymers. Overall, despite the prevalence of this concept in the literature, we observe that this phenomenon is relatively rare, and propose conditions that greatly enhance the likelihood of its experimental realisation. Finally, through a ‘topographical’ analysis of the co-polymer property space, we show how this large volume of data can be used to identify dominant monomers in specific regions of property space that may be amenable to a variety of applications, such as organic photovoltaics, light emitting diodes, and thermoelectrics.
000 binary copolymers that are, in principle, synthesizable from their dihalogen monomers via Yamamoto, or Suzuki–Miyaura and Stille coupling after one-step functionalisation. By extracting general features of this property space that would otherwise be obscured in smaller datasets, we identify simple models that effectively relate the properties of these copolymers to the homopolymers of their constituent monomers, and challenge common ideas behind copolymer design. We find that binary copolymerisation does not appear to allow access to regions of the optoelectronic property space that are not already sampled by the homopolymers, although it conceptually allows for more fine-grained property control. Using the large volume of data available, we test the hypothesis that copolymerisation of ‘donor’ and ‘acceptor’ monomers can result in copolymers with a lower optical gap than their related homopolymers. Overall, despite the prevalence of this concept in the literature, we observe that this phenomenon is relatively rare, and propose conditions that greatly enhance the likelihood of its experimental realisation. Finally, through a ‘topographical’ analysis of the co-polymer property space, we show how this large volume of data can be used to identify dominant monomers in specific regions of property space that may be amenable to a variety of applications, such as organic photovoltaics, light emitting diodes, and thermoelectrics.
Introduction
Conjugated polymers are a highly versatile class of organic materials that can be used in a wide variety of applications such as photovoltaics,1–5 light-emitting diodes,6,7 field-effect transistors,8 batteries,9 supercapacitors,10 thermoelectrics,11,12 and photocatalysts.13–18 All of these applications exploit a combination of the optoelectronic and/or redox properties of the polymers, the earth-abundance of their constituents, and the relatively facile tunability of polymer properties. Generally, property tuning of conjugated polymers is performed through copolymerisation; combining different building blocks to yield a repeating motif, which is replicated to form the polymer chain. The properties of the resulting copolymers arise from a combination of those of the building blocks, although the exact connection between the two or between the properties of the copolymer and the related homopolymers is not clear. Models that aim to explain this connection for the optoelectronic properties in terms of the donor and acceptor character of building blocks have been proposed in the literature, but these are generally qualitative in nature.19–21While an attractive attribute of polymer chemistry, the ability to both tune polymer properties through copolymerisation, and to explore their compositional space presents a dimensionality problem that arises from the large number of available monomers and is exaggerated with increasing copolymer complexity. To illustrate this numerically, consider a pool of 500 different monomers. Combining these monomers in all possible ways results in 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 binary copolymer compositions, increasing to over 250
250 binary copolymer compositions, increasing to over 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 when we consider that each repeat unit (if asymmetric) has two isomers. With more complex repeat units, i.e. three- and four-component copolymers,4,5 we arrive at billions of possible combinations. From a materials design standpoint, these astronomically large numbers make it impossible to explore the copolymer compositional space experimentally, even with high-throughput robotic synthesis and characterisation techniques, or computationally, particularly with more complex polymer repeat units, using standard approaches based around Density Functional Theory (DFT).
000 when we consider that each repeat unit (if asymmetric) has two isomers. With more complex repeat units, i.e. three- and four-component copolymers,4,5 we arrive at billions of possible combinations. From a materials design standpoint, these astronomically large numbers make it impossible to explore the copolymer compositional space experimentally, even with high-throughput robotic synthesis and characterisation techniques, or computationally, particularly with more complex polymer repeat units, using standard approaches based around Density Functional Theory (DFT).
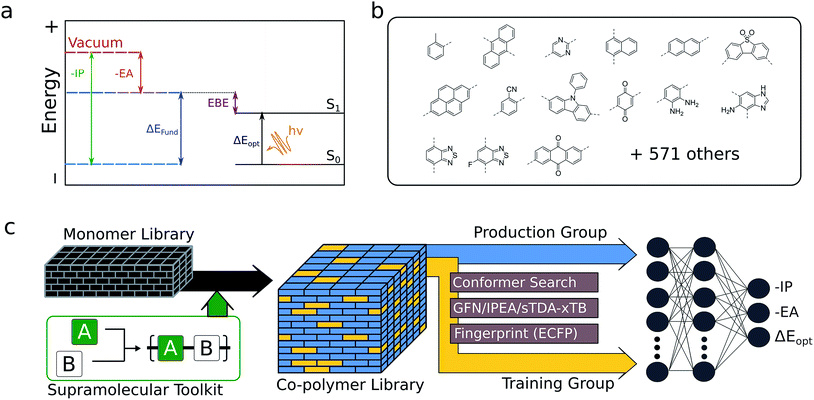
Naturally, we can overcome the copolymer dimensionality problem with a fast enough way of determining relevant properties for known copolymer compositions. A first step towards this was a move from DFT to semi-empirical methods, which allowed for the screening of short oligomers for high efficiency organic photovoltaic materials.22–24 In recent years, machine-learning techniques have emerged as a promising way of tackling analogous problems in other areas of organic and inorganic materials design,25–33 and conceptually could allow for the exploration of much larger compositional spaces, unlimited by polymer length. In this context, (supervised) machine learning involves ‘training’ a model with examples of molecules/materials for which the properties are known. Once trained, the model essentially acts as a function able to map molecular structure and/or composition to material properties. However, use of these techniques is often prohibited by the requirement for large amounts of clean, high quality, data with which to conduct training. We could obtain training data from electronic structure calculations, where, in the context of organic materials, DFT is the standard. However, DFT is simply too computationally intensive to use for large numbers of conjugated copolymers, where representative oligomer models can contain upwards of 150 atoms. Indeed, recent work34 on non-conjugated polymers using Gaussian Process Regressors trained using DFT data as input highlighted the challenge of exploring a wide chemical space with large numbers of possible compositions, as well as restrictions on the type of machine learning algorithms that are feasible, due to the limited size of the training data-set that is computationally affordable. Until recently, using semi-empirical methods, as discussed above, to generate this data could mean significantly reduced performance of a given machine learning model due to their lower accuracy with respect to DFT.35 However, we recently showed that optoelectronic properties calculated with xTB36–38 – a recently developed family of density functional tight binding methods – calibrated to a small, representative subset of (time-dependent-) DFT-derived results – provides highly accurate copolymer optoelectronic properties with computational cost reduced by at least three orders of magnitude relative to DFT.35 Further, we used the resulting high-throughput approach to demonstrate the weak dependence of the predicted properties on the exact polymer conformation.39 In turn, these two observations suggest that (i) xTB can be used to generate DFT-quality training data and (ii) 3D structural models of polymer chains may not be necessary for the prediction of optoelectronic properties (i.e. we can ignore conformation effects while focussing only on composition, see below), permitting the use of 2D molecular representations as descriptors.
Here we show how high-quality training data obtained via xTB, in combination with 2D molecular descriptors (in this case, Extended-Connectivity (Morgan) Fingerprints40), can be used to train a neural network model capable of the simultaneous, near-instant prediction of the key optoelectronic properties of copolymers with very high accuracy (RMSE < 0.12 eV). Using this model, we explore the binary copolymer property space spanned by a pool of 586 monomeric units that are compatible with Yamamoto, Suzuki–Miyaura or Stille coupling (see Fig. 1b for examples), generating around 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible unique copolymer structures. This library was compiled from commercially available aromatic dibromides and distannanes, as well as non-commercially available building blocks from the organic photovoltaics literature. With this large volume of data, we are able to identify general features of the property space of binary copolymers and their homopolymer counterparts, test the ideas behind common synthetic strategies used to yield low-optical-gap materials, and explore the extent to which polymer properties can be tuned through copolymerisation.
000 possible unique copolymer structures. This library was compiled from commercially available aromatic dibromides and distannanes, as well as non-commercially available building blocks from the organic photovoltaics literature. With this large volume of data, we are able to identify general features of the property space of binary copolymers and their homopolymer counterparts, test the ideas behind common synthetic strategies used to yield low-optical-gap materials, and explore the extent to which polymer properties can be tuned through copolymerisation.
Methodology
Properties of interest and polymer models
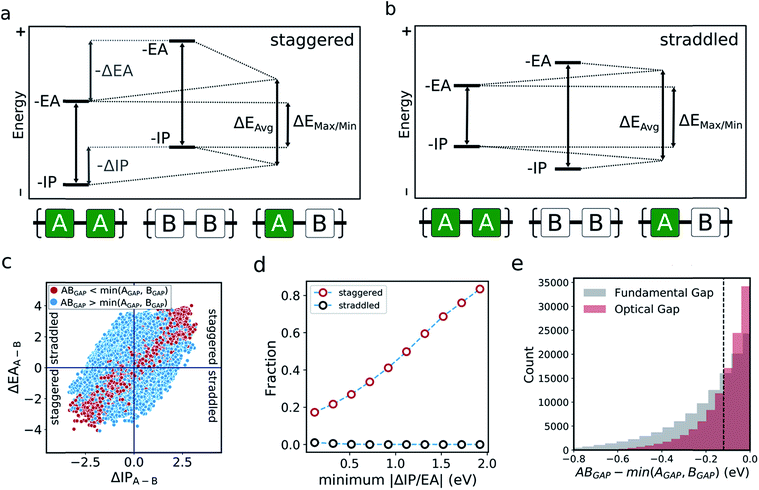
The optoelectronic properties of a conjugated polymer may be characterised by the key quantities41 outlined in Fig. 1a. These are the ionisation potential (IP), the energy required to remove an electron from the polymer; the electron affinity (EA), the energy released upon adding an electron to the polymer; and the optical gap, the minimum energy at which the polymer absorbs light to form an interacting electron–hole pair (exciton). Two additional quantities may be derived from these: the fundamental gap, the energy required to form a completely non-interacting electron–hole pair; and the exciton binding energy, a measure of the interaction energy between the excited electron and hole in the exciton (the difference between the optical and fundamental gaps). Note that, throughout the text, we generally focus on the negative of IP and EA, (−IP and −EA), which map directly onto the commonly used HOMO (−IP) and LUMO (−EA) concepts which are often used as approximations to these quantities. Additionally, we approximate the optical gap as the lowest energy excitation (S0 → S1) for all polymers.In line with previous work,18,42–45 we model polymer materials as long-chain oligomers, with the environment of an oligomer in the bulk polymer approximated in the xTB calculations by a dielectric continuum. In previous work we showed that such a model yields accurate −IP, −EA and optical gap values compared with experimental measurements derived from photoelectron spectroscopy44 and UV-vis absorption spectra.18,45
Training data generation
The generation of training data follows a tiered strategy, where a relatively small, diverse subset of copolymers is used to calibrate the accurate trends in properties given by a family of semi-empirical methods to the absolute values given by DFT. Within this family of semi-empirical, density functional tight-binding methods, GFN-xTB37 is used for structural optimisation of the neutral polymers. For −IP/−EA calculations, we use an extension of the parent GFN-xTB method, IPEA-xTB,38 a variant of GFN-xTB especially parameterised by Grimme and co-workers for the calculation of −IP and −EA values. For optical gaps, we employ the tight binding simplified Tamm–Dancoff approximation (sTDA)36 applied to orbitals and orbital eigenvalues obtained from xTB (sTDA-xTB),46 an approach capable of ultrafast computation of entire UV-vis absorption spectra. All GFN-xTB and IPEA-xTB calculations were performed using the xtb code,47 while the sTDA results were obtained using the stda code.48 All GFN-xTB and IPEA-xTB calculations, but not sTDA calculations, used the generalised Born surface area solvation model, with the default parameters for benzene distributed with the xtb code, so as to approximate the environment of a polymer chain in an amorphous polymeric solid. The xTB −IP, −EA and optical gap values are calibrated to those predicted by B3LYP49–52 using a linear model and our previously published parameters for the low dielectric permittivity case.35Structures for the xTB calculations are generated in a 3-step approach. Starting from a 2D simplified molecular-input line-entry system (SMILES)53 representation of each monomeric unit, linear polymer structures were generated using the Supramolecular Toolkit (stk),54,55 a Python library for the assembly, structure generation and property calculation of supramolecules, which takes base functionality from RDKit. stk allows for flexible copolymer formation from arbitrary monomer units, control over monomer sequence within repeat units, and the automatic generation of different structural isomers where asymmetric monomer units (e.g. 2,5 linked pyridine) are concerned. In all cases, we restrict repeat units to two monomer units and the polymer chains to 8 monomer units in total, a length that we have previously shown to provide approximately converged optoelectronic properties.44 Where asymmetric monomer units are concerned, we generate both possible ordered isomers. In a second step, a conformer search is performed using the stochastic Experimental-Torsion Distance Geometry with additional basic knowledge (ETKDG)56 method, where we typically generate 500 conformers per polymer. The resulting conformers undergo a subsequent optimisation and energy ranking procedure using the Merck Molecular Force Field (MMFF)57 as implemented in RDKit,58 where the lowest energy conformer according to MMFF is selected for the xTB calculations.
Neural network training and evaluation
Although all xTB calculations are performed on long-chain oligomer models, we use trimers to generate molecular descriptors in the form of fixed-dimensional bit vectors using Extended-Connectivity Fingerprints (ECPF). These bit vectors are obtained directly from the 2D SMILES representations of each trimer using RDKit. Using trimers instead of the entire oligomer chain to obtain molecular fingerprints dramatically reduces the computational effort required for fingerprinting, while preserving all of the sub-structural information of the polymer. The use of 2D SMILES rather than representations of the 3D structures of the polymers is supported by the weak dependence of the optoelectronic properties of the polymer on the conformational degrees of freedom,35,39 already alluded to in the introduction (see also Fig. S1†). Though we explored different bit lengths and fingerprint radii, it may be assumed that results were obtained using a 2048 bit and radius 2 fingerprint, unless otherwise stated. The neural network itself has two hidden layers of 128 neurons each, using rectified linear (ReLu)59 activation functions throughout. To avoid overfitting, the neural network is regularised using dropout.60 Each of the training hyper-parameters, the dropout fraction, as well as the neural network architecture, were obtained by 100 iterations of a random search across the hyper-parameter space (for details, see the ESI†). The network was trained to minimise the mean absolute error (MAE) of the predicted IP, EA and optical gap values using the Adam optimisation algorithm as implemented in Tensorflow.61 The model was evaluated using a simple 50% train-test split of ∼50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polymer structures for which the target properties are calculated. The fingerprinting, model construction, and model training can be reproduced using a freely-available, easy-to-use Python interface.62
000 polymer structures for which the target properties are calculated. The fingerprinting, model construction, and model training can be reproduced using a freely-available, easy-to-use Python interface.62
Results and discussion
Model generation and performance
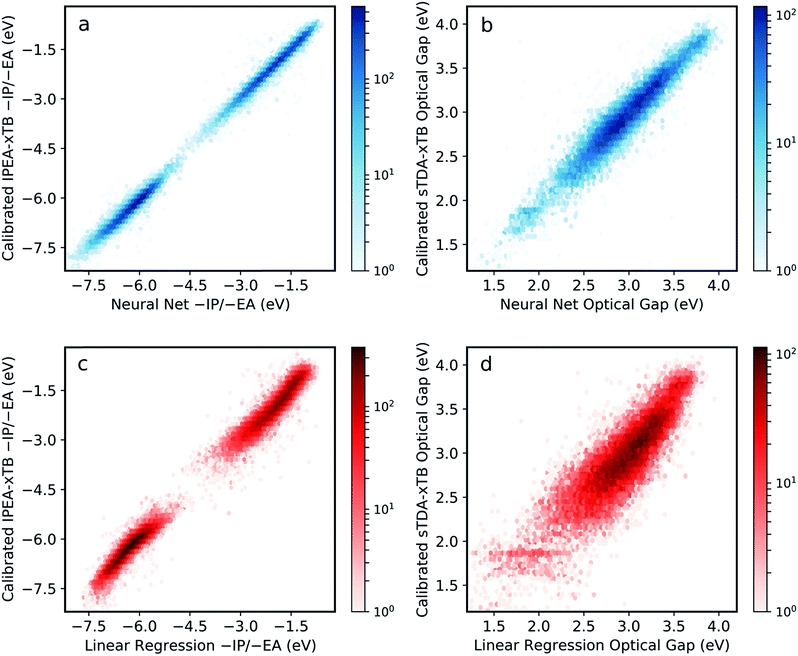
The final model was obtained via a ‘data enrichment’ process, whereby predictions made for all polymers by the initial model were projected onto 2D property spaces (e.g. −IP vs. −EA). Areas towards the edge of these property projections with a low density of points (i.e. shallow −IP, deep −EA and low optical gap) were identified. Monomer units, which were statistically over-represented in these regions, were combined exhaustively with each other and the properties of the resulting copolymers calculated. A fraction (50%, approximately 900 additional examples) of the resulting data is then applied in re-training the neural network model. Here, this procedure is only conducted once, but it is conceivable that it could be performed over many iterations to generate more robust models from more limited training data. Fig. S2† shows the effect of this data enrichment process. Generally, we see that points at the extrema of the property projection plots tend to be exaggerated (e.g. −EA values are under-estimated) prior to re-training.The resulting neural network model clearly performs very well across the entire range of properties and property values, with root mean square error (RMSE) of less than 0.12 eV when predicting −IP, −EA and optical gap simultaneously (Fig. 2a and b). This represents a significant improvement in performance over previous attempts for polymers,34 and a far larger compositional space by several orders of magnitude. Comparing to a linear regression model obtained with an identical ECFP bit length and radius (Fig. 2c and d), we see that the neural network outperforms the linear model significantly for all properties (the linear regression model yields an RMS error of 0.30 eV overall). This comparison demonstrates that the neural network model captures some degree of non-linearity when mapping molecular substructures to optoelectronic properties. For high-throughput screening purposes, the neural network model accuracy is perhaps even greater than required, with absolute values as well as relative ordering of polymer properties adequately recovered. Further, high-throughput workflows, which rely on a cost-efficient method to screen very large number of structures, generally involve a post-large-scale-screening stage, where a promising subset of systems are taken forward and treated at a more computationally intensive level of theory. In this case, however, it appears that this step could effectively be negated by the inherent model accuracy.
Fig. S3† shows model performance when predicting differences in optical gap between isomers using different fingerprint bit lengths and radii. While we observe improvements in this quantity at longer bit lengths and radii, no significant improvement of the overall model performance is observed and, indeed, increasing these parameters may be detrimental to model generality. On the other hand, effects of monomer isomerism (in the case of asymmetric monomer units) are far better (albeit still roughly) captured at longer radii. This is consistent with the idea that distinctions between repeat unit isomers can only be made effectively when considering larger molecular fragments. In the future, some form of feature engineering could potentially be used to account for monomer isomerism more explicitly.
Comparing the property space of homo and binary copolymers
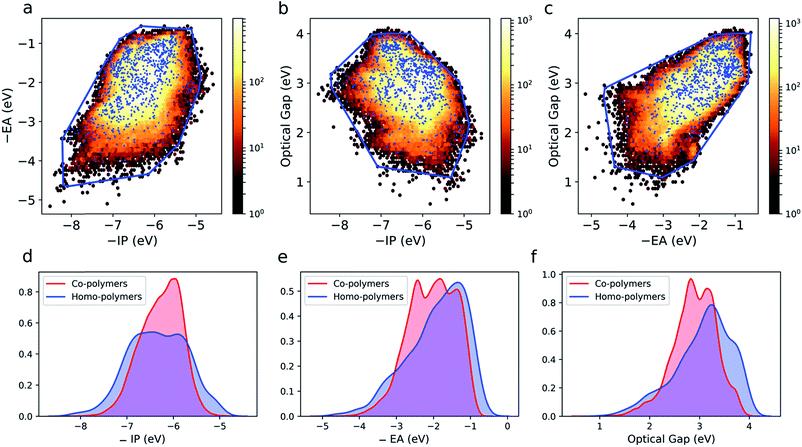
The large and varied data set at our disposal means that we can empirically probe the optoelectronic property space of binary copolymers and how it differs from that of homopolymers. The optoelectronic property space is a 3D space spanned by vectors corresponding to a polymer's −IP, −EA and optical gap values. The fundamental gap is by definition equal to the difference between −IP and −EA and hence not a free parameter. Fig. S4† shows an image of this property space, showing that all polymers lie in an almost 2D plane embedded in the 3D space. The quasi-two-dimensional nature of the optoelectronic property space finds its origin in the fact that (i) in the limit of zero exciton binding energy, the optical gap would equal the fundamental gap and (ii) the predicted exciton binding energies (∼0.5–2 eV), while large compared to classical inorganic semiconductors, are small relative to the fundamental gap (∼2–6 eV, see Fig. S5†).Fig. 3a–c shows projections of the 3D optoelectronic property space on 2D surfaces spanned by (i) −IP and −EA, (ii) −IP and optical gap, and (iii) −EA and optical gap, respectively, where we have drawn convex hulls enclosing all homopolymers in each case. Comparing these homopolymer convex hulls with the plotted points for the copolymers it appears that only a very small number – likely to be statistically insignificant for a dataset of this size – of copolymers lie outside of the property space spanned by homopolymers. The homopolymers also appear to sample the property space proportionally to the density of copolymers within a given subspace. This suggests that copolymerisation, at least in the case of ordered binary copolymers, does not allow access to additional regions of the optoelectronic property space not already sampled by the homopolymers. The density of points in the case of the copolymers is much larger though, conceptually allowing for more fine-grained property control. Further, we would like to emphasise that these observations may not hold for other properties (e.g. charge-transport properties) and more complex co-polymer repeat units (e.g. ternary and quaternary co-polymers). Finally, we note that, even if the vast majority of copolymers lie inside the homopolymer convex hulls, this does not necessarily mean that the properties of a specific copolymer lie in between those of the two corresponding homopolymers, as we will discuss later.
Fig. 3d–f shows kernel density estimates of the distributions of −IP, −EA and optical gap values for both the homo and copolymers. Here we see that the co-polymer property space spans a broad range of values, with significant numbers of materials present over a range of more than 4 eV for each property. It is clear that in all cases the copolymer distributions are more symmetrical than those of their homopolymer counterparts.
Correlations between copolymer properties
The 2D projections in Fig. 3a–c shows that there are weak correlations between the different properties. In the case of −IP and −EA, binary copolymers and homopolymers with deep −IP values are likely to also have deep −EA values and vice versa. In the case of the optical gap, binary copolymers and homopolymers with small(er) optical gaps are more likely to have shallower −IP values. Similarly, the same polymers are more likely to have deeper −EA values. It is unclear if these correlations are evidence of some deeper relationship or merely result from the fact that the fundamental gap values of the polymers span a range of around 4 eV. Regardless, as we study a large range of monomers, and therefore copolymers, it is apparent that certain property combinations might be difficult to achieve (e.g. copolymers that both have a shallow −EA value and a small optical gap; copolymers with a shallow −IP value and a large optical gap) due to the absence of copolymers in these regions of property space. As these regions are also not sampled by the homopolymers, this is simply the result of practically all binary copolymers lying within the homopolymer convex hull.Emergence of copolymer properties and the donor–acceptor model
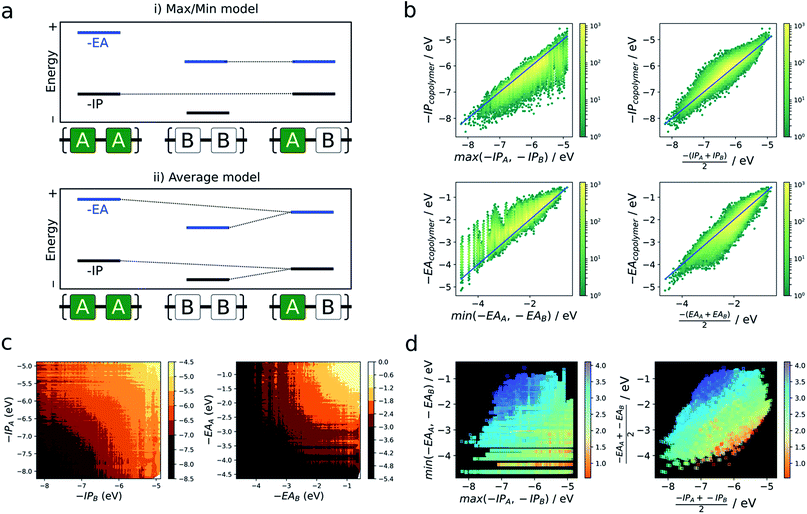
As briefly mentioned in the introduction, models that explain the copolymer optoelectronic properties in terms of the donor and acceptor properties of the monomeric building blocks have been proposed in the literature. In the same vein, we compare the optoelectronic properties of copolymers to their homopolymer counterparts formed from the same building blocks. The reason for comparing with homopolymers rather than monomers is two-fold. Firstly, we do not have direct access to the optoelectronic properties of the isolated building blocks via the neural network. Secondly, the direct comparison of optoelectronic monomer and copolymer properties is inherently fraught by the conflation of effects due to the electronic coupling between the different monomers and their polymerisation.In the absence of a clear first principles model for this relationship, we employ two simple empirical models which explore two different regimes (i) a “max/min” model in which the −IP and −EA of the copolymer are predicted by the least negative (shallowest) −IP value and the most negative (deepest) −EA value of the relevant homopolymer pair, and (ii) an “averaging” model in which the −IP and −EA values are approximated by the arithmetic mean of the −IP and −EA values of the homopolymer pair (Fig. 4a).
Fig. 4b shows the performance of these models in terms of the −IP and −EA value of the copolymers. We observe that the averaging model performs well in terms of predicting the −IP and −EA values of the copolymers, with an RMSE of 0.16 eV overall. The max/min model performs less well (RMSE = 0.38 eV), while appearing to estimate a lower (upper) boundary to the −EA (−IP) value of a copolymer, reflecting the convex hull analysis in Fig. 2a–c. Additionally, we observe that the average model shows the largest deviation for copolymers where the difference between the −IP (or −EA) values of the homopolymer pair is large (see Fig. S6†), with a general over- and under-estimation of −EA and −IP, respectively. This is also consistent with the qualitatively curved contour lines shown in Fig. 4c, where, when the difference between −IP/−EA homopolymer values is large, the more positive −IP/more negative −EA homopolymer skews the resulting copolymer property further from a perfect average value. Conversely, where the difference between homopolymer values is small, the resulting copolymer properties are closer to the simple average value. Finally, as can be seen in Fig. S8† use of the averaging model can also qualitatively reproduce the convex hull picture shown in Fig. 2a. Overall, expressing copolymer properties as a simple average of ‘parent’ homopolymers appears to be an effective model for most polymers.
In the literature, the case for copolymerisation is often based on the ‘donor–acceptor’ strategy,19,21 where combining monomers with ‘donor’ and ‘acceptor’ qualities allows one to obtain copolymers with small(er) optical gaps. Here, we can use the large volume of data at our disposal to explore this concept and how it relates to the two empirical models discussed above. Indeed, the predictions made by the neural network identify some co-polymers for which the optical gap is lower than that of the two corresponding homopolymers (Fig. 5c). Specifically, we observe that ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 out of ∼350
000 out of ∼350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 copolymers studied have an optical gap that is at least 0.12 eV (the overall RMSE of the neural network) lower than that of the homopolymers. As can be seen from Fig. 5c, such copolymers generally correspond to cases where the related homopolymers have significantly different −IP and/or −EA values, and almost exclusively for cases where the −IP and −EA values of the two homopolymers are staggered with respect to one another (Fig. 5a). Conversely, when the −IP and −EA values of one homopolymer straddle the other (Fig. 5b), no reduction in optical gap upon copolymerisation is predicted. Furthermore, the likelihood of reducing optical gap through copolymerisation appears to increase with the extent to which the −IP and −EA values are staggered (Fig. 5d), which we rationalise through the concomitant decreasing likelihood of this effect being countered by differences in the exciton binding energy between homo and copolymers. Overall, accounting for the overall RMSE of the neural network, we find that in our dataset ∼100
000 copolymers studied have an optical gap that is at least 0.12 eV (the overall RMSE of the neural network) lower than that of the homopolymers. As can be seen from Fig. 5c, such copolymers generally correspond to cases where the related homopolymers have significantly different −IP and/or −EA values, and almost exclusively for cases where the −IP and −EA values of the two homopolymers are staggered with respect to one another (Fig. 5a). Conversely, when the −IP and −EA values of one homopolymer straddle the other (Fig. 5b), no reduction in optical gap upon copolymerisation is predicted. Furthermore, the likelihood of reducing optical gap through copolymerisation appears to increase with the extent to which the −IP and −EA values are staggered (Fig. 5d), which we rationalise through the concomitant decreasing likelihood of this effect being countered by differences in the exciton binding energy between homo and copolymers. Overall, accounting for the overall RMSE of the neural network, we find that in our dataset ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 out of the ∼350
000 out of the ∼350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 copolymers are staggered by at least 0.12 eV, ∼17
000 copolymers are staggered by at least 0.12 eV, ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of which display an optical gap reduction of at least 0.12 eV. In contrast, the −IP and −EA values of the copolymers strictly lie in between those of the two corresponding homopolymers when accounting for the RMSE of the neural network model.
000 of which display an optical gap reduction of at least 0.12 eV. In contrast, the −IP and −EA values of the copolymers strictly lie in between those of the two corresponding homopolymers when accounting for the RMSE of the neural network model.
One can explain the above observations by noting that, while the averaging model predicts that the fundamental gap of copolymers always strictly lies in between that of both corresponding homopolymers, and while it is very successful for most copolymers considered, there are copolymers that deviate considerably from its predictions. Such copolymers, as discussed above, tend to correspond to cases where the difference between the −IP (and/or −EA) values of the homopolymer pair is large (see Fig. 4c and S5†). In these cases the fundamental gap tends towards that predicted by the max/min model. A combination of this with a staggered arrangement of the −IP and −EA values of the two homopolymers then gives rise to a fundamental gap that is smaller than either of the homopolymers (see ΔEmax/min in Fig. 5a). As can be seen from Fig. 1a, this explanation translates directly to the case of the optical gap, as long as the exciton binding energies in the co and homopolymers are not sufficiently different. As such, the requirement for a staggered arrangement maps on to the intuitive donor–acceptor picture used in the experimental literature, but stresses that these labels are only really meaningful when considering pairs of monomers and their properties relative to one another.
Overall, these observations and their explanation lend both context and understanding to the donor–acceptor strategy proposed in the literature. With knowledge of the optoelectronic properties of homopolymers alone, we can provide a simple heuristic to predict promising combinations of monomers, which are likely to result in low optical gap materials. Specifically, for optical gap reduction to likely occur, not only should the −IP and −EA values of the two corresponding homopolymers be significantly different, but they should also be staggered, along the lines of Fig. 5a. This is strongly illustrated by Fig. 5d, which shows that for staggered cases with large −IP and −EA differences optical gap reduction is highly likely, while for straddled cases the odds of optical gap reduction are effectively zero. The same observation would also suggest that a likely side effect of reducing the optical gap is that the −IP and −EA values of the resulting copolymers will lie closer to those predicted by the max/min model than its averaging counterpart. As a result, such copolymers will likely combine relatively shallow −IP and deep −EA values, reducing their potential applicability in domains such as photocatalysis, where the alignment of the polymer potentials relative to those of other materials or solution half-reactions is crucial.
Monomer topography of the property space
Aside from the general exploration of copolymer property space and the testing of models able to describe it, high-throughput calculations have the potential to guide synthetic efforts towards promising materials with properties amenable to certain applications. In the context of copolymers, this could mean either the identification of specific copolymer compositions or – perhaps more interestingly from synthetic accessibility and material morphology standpoints – monomers (i.e. dibromo compounds or diboronic acids/acid esters) – which target a particular region of property space. To illustrate this, we give examples of the most prevalent co-monomers in different regions of the property space (Fig. 6). From this analysis, we see the emergence of some common motifs found in, for example, the organic photovoltaics literature (namely, diketopyrrolopyrrole and benzothiadiazole), where smaller optical gaps are sought after to absorb more of the solar spectrum. Similarly, monomers that give rise to materials with deep −IP and not too deep −EA values, which are potentially attractive for water-splitting due to their large driving force for both proton reduction and water oxidation, contain electron-withdrawing substituents like –F and –NO2 (1,3-linked tetrafluorophenylene and 1,3-linked nitropyrazole). Additionally, these same monomers illustrate the idea that, due to the quasi-two-dimensional nature of the optoelectronic property space, choosing monomers that place −IP and −EA within a desired range also fixes the possible optical gap values to within the domain of possible exciton binding energy values. Finally, Fig. 6 also suggests that, for applications in which ohmic contacts between the polymer and an electrode are important, e.g. organic photovoltaics and organic light emitting diodes, to achieve barrierless charge injection or collection, the properties of the copolymer relative to an electrode can be anchored to a particular value range by copolymerisation with suitably chosen monomers.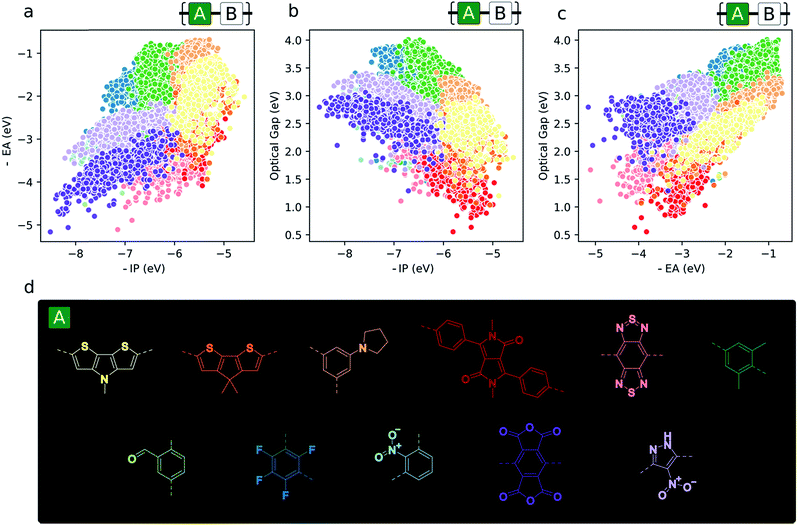 | ||
| Fig. 6 (a–c) 2D property spaces where the most prevalent monomer units within different regions are highlighted. (d) Colour key for monomer property sub-spaces shown in (a–c). | ||
Conclusions
We have demonstrated that machine learning techniques – neural networks – can be used to resolve the optoelectronic property landscape of conjugated organic copolymers with very diverse monomer compositions. The neural network training is facilitated by the availability of large amounts of accurate, low-noise data derived from a tiered strategy based on calibrated density functional tight binding calculations, which display an accuracy on par with density functional theory. The property space generated by the neural network allows for the data-driven testing of simple models that link the properties of the constituent monomers of a copolymer to the properties of the copolymer itself. We observe that copolymerisation to make binary copolymers does not appear to allow access to regions of the optoelectronic property space not already sampled by the homopolymers, while allowing for more fine-grained property control. The large dataset at our disposal also facilitates the testing of common synthetic strategies such as using ‘donor’ and ‘acceptor’ monomers to construct low-optical-gap materials. Generally, despite the prevalence of this concept in the literature, we observe that this phenomenon is relatively rare. We predict that for a copolymer to have a significantly smaller optical gap than its related homopolymers, the potentials of these should be substantially offset and arranged in a staggered fashion. From here, one can imagine an application-specific, optimal balance between absolute value of the homopolymer potentials themselves and the extent to which they are staggered relative to one another that achieves ideal copolymer light absorption and redox properties. Additionally, we demonstrate that high-throughput methods could be used to identify promising monomers which target specific regions of property space.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Enrico Berardo, Dr Hugo Bronstein, Prof. Andrew I. Cooper, Prof. Iain McCulloch, Dr Frank Otto, Prof. David Scanlon, Dr Bob Schroeder and Lukas Turcani for useful discussions. The UK Engineering and Physical Sciences Research Council (EPSRC) is kindly acknowledged for funding (EP/N004884/1). KEJ acknowledges the Royal Society for a University Research Fellowship and the ERC through grant agreement number 758370 (ERC-StG-PE5-CoMMaD) for funding.References
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Device Structure Consisted Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor–Acceptor Heterojunctions, Science, 1995, 270, 1789–1791 CrossRef CAS.
- J. J. M. Halls, C. A. Walsh, N. C. Greenham, E. A. Marseglia, R. H. Friend, S. C. Moratti and A. B. Holmes, Efficient Photodiodes from Interpenetrating Polymer Networks, Nature, 1995, 498–500 CrossRef CAS.
- A. Facchetti, Polymer Donor–Polymer Acceptor (All-Polymer) Solar Cells, Mater. Today, 2013, 16, 123–132 CrossRef CAS.
- K. A. Mazzio and C. K. Luscombe, The Future of Organic Photovoltaics, Chem. Soc. Rev., 2015, 44, 78–90 RSC.
- S. Holliday, Y. Li and C. K. Luscombe, Recent Advances in High Performance Donor–Acceptor Polymers for Organic Photovoltaics, Prog. Polym. Sci., 2017, 70, 34–51 CrossRef CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Light-Emitting Diodes Based on Conjugated Polymers, Nature, 1990, 347, 539–541 CrossRef CAS.
- L. Akcelrud, Electroluminescent Polymers, Prog. Polym. Sci., 2003, 28, 875–962 CrossRef CAS.
- H. Sirringhaus, Organic Field-Effect Transistors: The Path beyond Amorphous Silicon, Adv. Mater., 2014, 26, 1319–1335 CrossRef CAS PubMed.
- J. Xie, P. Gu and Q. Zhang, Nanostructured Conjugated Polymers: Toward High-Performance Organic Electrodes for Rechargeable Batteries, ACS Energy Lett., 2017, 2, 1985–1996 CrossRef CAS.
- Q. Meng, K. Cai, Y. Chen and L. Chen, Research Progress on Conducting Polymer Based Supercapacitor Electrode Materials, Nano Energy, 2017, 36, 268–285 CrossRef CAS.
- R. Kroon, D. A. Mengistie, D. Kiefer, J. Hynynen, J. D. Ryan, L. Yu and C. Müller, Thermoelectric Plastics: From Design to Synthesis, Processing and Structure-Property Relationships, Chem. Soc. Rev., 2016, 45, 6147–6164 RSC.
- L. M. Cowen, J. Atoyo, M. J. Carnie, D. Baran and B. C. Schroeder, Review—Organic Materials for Thermoelectric Energy Generation, ECS J. Solid State Sci. Technol., 2017, 6, N3080–N3088 CrossRef CAS.
- S. Yanagida, A. Kabumoto, K. Mizumoto, C. Pac and K. Yoshino, Poly(p-phenylene)-Catalysed Photoreduction of Water to Hydrogen, J. Chem. Soc., Chem. Commun., 1985, 474–475 RSC.
- T. Shibata, A. Kabumoto, T. Shiragami, O. Ishitani, C. Pac and S. Yanagida, Novel Visible-Light-Driven Photocatalyst. Poly(p-Phenylene)-Catalyzed Photoreductions of Water, Carbonyl Compounds, and Olefins, J. Phys. Chem., 1990, 94, 2068–2076 CrossRef CAS.
- C. Yang, B. C. Ma, L. Zhang, S. Lin, S. Ghasimi, K. Landfester, K. A. I. Zhang and X. Wang, Molecular Engineering of Conjugated Polybenzothiadiazoles for Enhanced Hydrogen Production by Photosynthesis, Angew. Chem., Int. Ed., 2016, 55, 9202–9206 CrossRef CAS PubMed.
- R. S. Sprick, B. Bonillo, R. Clowes, P. Guiglion, N. J. Brownbill, B. J. Slater, F. Blanc, M. A. Zwijnenburg, D. J. Adams and A. I. Cooper, Visible-Light-Driven Hydrogen Evolution Using Planarized Conjugated Polymer Photocatalysts, Angew. Chem., Int. Ed., 2016, 55, 1792–1796 CrossRef CAS PubMed.
- M. Sachs, R. S. Sprick, D. Pearce, S. J. Hillman, A. Monti, A. A. Y. Guilbert, N. J. Brownbill, S. Dimitrov, F. Blanc and M. A. Zwijnenburg, et al. Understanding Structure-Activity Relationships in Linear Polymer Photocatalysts for Hydrogen Evolution, Nat. Commun., 2018, 9, 4968 CrossRef PubMed.
- R. S. Sprick, C. M. Aitchison, E. Berardo, L. Turcani, L. Wilbraham, B. M. Alston, K. E. Jelfs, M. A. Zwijnenburg and A. I. Cooper, Maximising the Hydrogen Evolution Activity in Organic Photocatalysts by Co-Polymerisation, J. Mater. Chem. A, 2018, 6, 11994–12003 RSC.
- A. Ajayaghosh, Donor–Acceptor Type Low Band Gap Polymers: Polysquaraines and Related Systems, Chem. Soc. Rev., 2003, 32, 181–191 RSC.
- J. R. Reynolds, Spectral Engineering in π-Conjugated Polymers with Intramolecular Donor–Acceptor Interactions, Acc. Chem. Res., 2010, 43, 1396–1407 CrossRef PubMed.
- X. Guo, M. Baumgarten and K. Müllen, Designing π-Conjugated Polymers for Organic Electronics, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- N. M. Oboyle, C. M. Campbell and G. R. Hutchison, Computational Design and Selection of Optimal Organic Photovoltaic Materials, J. Phys. Chem. C, 2011, 115, 16200–16210 CrossRef CAS.
- I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, Efficient Computational Screening of Organic Polymer Photovoltaics, J. Phys. Chem. Lett., 2013, 4, 1613–1623 CrossRef CAS PubMed.
- I. Y. Kanal and G. R. Hutchison, Rapid Computational Optimization of Molecular Properties Using Genetic Algorithms: Searching Across Millions of Compounds for Organic Photovoltaic Materials, 2017, arXiv:1707.02949 Search PubMed.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Finding Natures Missing Ternary Oxide Compounds Using Machine Learning and Density Functional Theory, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Learning from the Harvard Clean Energy Project: The Use of Neural Networks to Accelerate Materials Discovery, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D. G. Ha and T. Wu, et al. Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach, Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- J. D. Evans and F. X. Coudert, Predicting the Mechanical Properties of Zeolite Frameworks by Machine Learning, Chem. Mater., 2017, 29, 7833–7839 CrossRef CAS.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9, 1064–1071 CrossRef CAS PubMed.
- P. B. Jørgensen, M. Mesta, S. Shil, J. M. García Lastra, K. W. Jacobsen, K. S. Thygesen and M. N. Schmidt, Machine Learning-Based Screening of Complex Molecules for Polymer Solar Cells, J. Chem. Phys., 2018, 148, 241735 CrossRef PubMed.
- L. Turcani and K. Jelfs, Machine Learning for Organic Cage Property Prediction, Chem. Mater., 2019, 31, 714–727 CrossRef CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine Learning for Molecular and Materials Science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, Polymer Genome: A Data-Powered Polymer Informatics Platform for Property Predictions, J. Phys. Chem. C, 2018, 122, 17575–17585 CrossRef CAS.
- L. Wilbraham, E. Berardo, L. Turcani, K. E. Jelfs and M. A. Zwijnenburg, A High-Throughput Screening Approach for the Optoelectronic Properties of Conjugated Polymers, J. Chem. Inf. Model., 2018, 28, 2450–2459 CrossRef PubMed.
- C. Bannwarth and S. Grimme, A Simplified Time-Dependent Density Functional Theory Approach for Electronic Ultraviolet and Circular Dichroism Spectra of Very Large Molecules, Comput. Theor. Chem., 2014, 1040–1041, 45–53 CrossRef CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- V. Ásgeirsson, C. A. Bauer and S. Grimme, Quantum Chemical Calculation of Electron Ionization Mass Spectra for General Organic and Inorganic Molecules, Chem. Sci., 2017, 8, 4879–4895 RSC.
- I. Heath-apostolopoulos, L. Wilbraham and M. A. Zwijnenburg, Computational High-Throughput Screening of Polymeric Photocatalysts: Exploring the Effect of Composition, Sequence Isomerism and Conformational Degrees of Freedom, Faraday Discuss., 2019 10.1039/c8fd00171.
- D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- J.-L. Bredas, Mind the Gap!, Mater. Horiz., 2014, 1, 17–19 RSC.
- P. Guiglion, E. Berardo, C. Butchosa, M. C. C. Wobbe and M. A. Zwijnenburg, Modelling Materials for Solar Fuel Synthesis by Artificial Photosynthesis; Predicting the Optical, Electronic and Redox Properties of Photocatalysts, J. Phys.: Condens. Matter, 2016, 28, 074001 CrossRef PubMed.
- P. Guiglion, C. Butchosa and M. A. Zwijnenburg, Polymer Photocatalysts for Water Splitting: Insights from Computational Modeling, Macromol. Chem. Phys., 2016, 217, 344–353 CrossRef CAS.
- P. Guiglion, A. Monti and M. A. Zwijnenburg, Validating a Density Functional Theory Approach for Predicting the Redox Potentials Associated with Charge Carriers and Excitons in Polymeric Photocatalysts, J. Phys. Chem. C, 2017, 121, 1498–1506 CrossRef CAS.
- R. S. Sprick, L. Wilbraham, Y. Bai, P. Guiglion, A. Monti, R. Clowes, A. I. Cooper and M. A. Zwijnenburg, Nitrogen Containing Linear Poly(Phenylene) Derivatives for Photo-Catalytic Hydrogen Evolution from Water, Chem. Mater., 2018, 30, 5733–5742 CrossRef CAS.
- S. Grimme and C. Bannwarth, Ultra-Fast Computation of Electronic Spectra for Large Systems by Tight-Binding Based Simplified Tamm-Dancoff Approximation (sTDA-sTB), J. Chem. Phys., 2016, 145, 054103 CrossRef PubMed.
- https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/xtb/xtb, accessed Dec 4, 2018.
- https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/stda/stda, accessed Dec 4, 2018.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- D. Weininger, SMILES, a Chemical Language and Information System: 1: Introduction to Methodology and Encoding Rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- L. Turcani, E. Berardo and K. E. Jelfs, Stk: A Python Toolkit for Supramolecular Assembly, J. Comput. Chem., 2018, 39, 1931–1942 CrossRef CAS PubMed.
- http://www.jelfs-group.org/software/, accessed Dec 4, 2018.
- S. Riniker and G. A. Landrum, Better Informed Distance Geometry: Using What We Know to Improve Conformation Generation, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- T. A. Halgren, Merck Molecular Force Field, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- RDKit: open source cheminformatics software, http://www.rdkit.org, accessed Dec 4, 2018.
- V. Nair and G. E. Hinton, Rectified Linear Units Improve Restricted Boltzmann Machines, Proc. 27th Int. Conf. Mach. Learn., ICML-10, 2010, pp. 807–814 Search PubMed.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. D. Salakhutdinov, A Simple Way to Prevent Neural Networks from Overfitting, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, R. Jozefowicz, Y. Jia, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, M. Schuster, R. Monga, S. Moore, D. Murray, C. Olah, J. Shlens, J. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-scale machine learning on heterogeneous systems, 2015, Software available from, https://tensorflow.org Search PubMed.
- L. Wilbraham, pychemlp, https://github.com/ZwijnenburgGroup/pychemlp, accessed Dec 4, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Training data (before and after calibration), co-polymer optoelectronic property space data and associated SMILES for all copolymer compositions, machine learning model and training parameters, Python module (pychemlp, ref. 61) for recreating fingerprints, model and data. Raw data can be accessed freely via a GitHub repository (https://github.com/ZwijnenburgGroup/2019-polymer-neural-network). See DOI: 10.1039/c8sc05710a |
| This journal is © The Royal Society of Chemistry 2019 |