Open Access Article
Open Access ArticleSubstrate inhibition by the blockage of product release and its control by tunnel engineering†
Piia
Kokkonen‡
a,
Andy
Beier‡
ab,
Stanislav
Mazurenko
a,
Jiri
Damborsky
 ab,
David
Bednar
ab,
David
Bednar
 *ab and
Zbynek
Prokop
*ab and
Zbynek
Prokop
 *ab
*ab
aLoschmidt Laboratories, Department of Experimental Biology and RECETOX, Faculty of Science, Masaryk University, Kamenice 5/A13, 625 00 Brno, Czech Republic. E-mail: 222755@mail.muni.cz; zbynek@chemi.muni.cz
bInternational Clinical Research Center, St. Anne's University Hospital Brno, Pekarska 53, 656 91 Brno, Czech Republic
First published on 11th January 2021
Abstract
Substrate inhibition is the most common deviation from Michaelis–Menten kinetics, occurring in approximately 25% of known enzymes. It is generally attributed to the formation of an unproductive enzyme–substrate complex after the simultaneous binding of two or more substrate molecules to the active site. Here, we show that a single point mutation (L177W) in the haloalkane dehalogenase LinB causes strong substrate inhibition. Surprisingly, a global kinetic analysis suggested that this inhibition is caused by binding of the substrate to the enzyme–product complex. Molecular dynamics simulations clarified the details of this unusual mechanism of substrate inhibition: Markov state models indicated that the substrate prevents the exit of the halide product by direct blockage and/or restricting conformational flexibility. The contributions of three residues forming the possible substrate inhibition site (W140A, F143L and I211L) to the observed inhibition were studied by mutagenesis. An unusual synergy giving rise to high catalytic efficiency and reduced substrate inhibition was observed between residues L177W and I211L, which are located in different access tunnels of the protein. These results show that substrate inhibition can be caused by substrate binding to the enzyme–product complex and can be controlled rationally by targeted amino acid substitutions in enzyme access tunnels.
Introduction
Substrate inhibition (SI) is a common phenomenon affecting about 25% of known enzymes.1–3 Instead of reaching a steady-state equilibrium at the maximum reaction speed, the excess substrate starts inhibiting the enzyme-catalyzed reaction. SI is often claimed to be an artefact caused by the use of artificially high substrate concentrations in enzymatic assays. However, multiple physiological phenomena are controlled by SI. Perhaps the most common example of SI comes from housekeeping metabolism, where high levels of ATP suppress glycolysis (and thus halt ATP production) by inhibiting phosphofructokinase.1,4 Other examples include the processes that maintain constant levels of neurotransmitters, rapidly terminate neural signals, maintain stable folate levels even under conditions of folate deprivation, and prevent de novo DNA methylation during cell replication.1The most commonly invoked model of SI is that proposed by Haldane, in which there are two substrate-binding sites, only one of which is catalytic.5 Binding of the substrate to the allosteric binding site in the empty enzyme or the enzyme–substrate complex forms an inhibitory complex in which the catalyzed reaction is either very slow or completely stalled. Most published studies on SI have supported this allosteric mechanism6–17 or not discussed mechanistic details at all.18–27
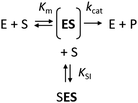
The kinetics of Haldane's traditional mechanism in which excess substrate binds to the enzyme–substrate complex is readily described using a minimal steady-state model (Scheme 1), where an enzyme E can bind one (ES) or two (SES) substrate molecules (S). The equilibrium is described by the Michaelis constant Km and the dissociation constant for the inhibitory complex KSI.
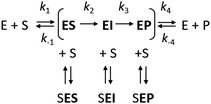
However, it is often noted that steady-state analysis provides only indirect information and cannot be considered to provide strong support for any particular complete reaction pathway28,29 because the steady-state parameters are complex functions of elementary steps along the kinetic pathway that are buried within these terms and cannot be individually resolved. These limitations can be avoided by examining the reaction pathway using transient-state kinetic methods that provide more detailed information on individual steps. Such methods can provide data on complete reaction pathways (Scheme 2), enabling investigation of other ways in which excess substrate may affect the reaction velocity. For example, excess substrate molecules may interact with enzyme forms other than the enzyme–substrate complex, such as the reaction intermediate (EI) or the enzyme–product complex (EP) to form the SEI, or SEP complexes, respectively. Transient kinetic experiments have been used in several studies to obtain detailed mechanistic insights into SI in multi-substrate reactions. The inhibitory effects of substrates in these cases were attributed to an accumulation of a catalytically incompetent assembly of the enzyme, cofactor, and substrate30 or, more interestingly, to the formation of a mismatched enzyme–substrate–product complex.31,32 While such mismatched formation of abortive complexes has been reported for multi-substrate and multi-product enzymes with multiple binding sites,33,34 no comparable mechanism of substrate inhibition has yet been described for single substrate enzymes, where the formation of an enzyme–substrate–product complex is considered less likely.
Here we present a study on SI in the enzyme–product complex of haloalkane dehalogenase LinB from Sphingobium japonicum UT26, which sheds further light on this unusual mechanism of SI. We initially studied the wild type enzyme and two variants with engineered access pathways. Disturbing the transport of ligands into and out of the active site by blocking the main tunnel with a bulky Trp residue (L177W) unexpectedly caused strong SI.35,36 To investigate this effect, a new variant (LinBW140A/F143L/L177W/I211L) bearing three further mutations was generated. These three mutations opened an auxiliary access tunnel to the active site, modified the dynamics of the main tunnel, and restored the level of SI to that observed in the wild type. Here, we delve deeper into the mechanisms of the SI in these LinB variants using molecular dynamics simulations and steady-state and transient kinetics experiments. We also characterize three new LinB variants (W140A/L177W, F143L/L177W, and L177W/I211L) to determine how SI is affected by the individual mutations in the quadruple mutant. In addition to revealing an unusual mechanism of SI, this is the first study to combine molecular dynamics simulations with Markov state models (MSM) to investigate enzyme inhibition mechanisms.
Materials and methods
Computational methods
The systems were solvated in a cubical water box of TIP3P water molecules so that all atoms were at least 10 Å from the surface of the box using the ember build module of HTMD with the Amber FF14SB force field for the protein.42 Cl− and Na+ ions were added to neutralize the protein's charge and establish a final salt concentration of 0.1 M. The charges of all ions were scaled by a factor of 0.7 in the parameter file to counter the missing polarization effect of the force field.43 Without this scaling step, the bromide ion left the active site during the equilibration steps or at the start of the first epoch of the simulations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ns, 23
000 ns, 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ns and 24
900 ns and 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 ns for WT, L177W, and W140A/F143L/L177W/I211L, respectively, and 25
450 ns for WT, L177W, and W140A/F143L/L177W/I211L, respectively, and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ns for W140A/L177W, L177W/I211L, and F143L/L177W.
000 ns for W140A/L177W, L177W/I211L, and F143L/L177W.
Because of the small number of available observations, our permutation analysis was reinforced by performing random Monte Carlo simulations. We generated a probability matrix and kinetic constants of the same sizes as in our analysis that were drawn randomly and independently from a uniform distribution 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times. The PLS analysis was repeated for each drawing to calculate R2 and Q2 values, including the selection of the 3 most important descriptors (out of 12) in the models based on their VIP values and repeated the PLS.
000 times. The PLS analysis was repeated for each drawing to calculate R2 and Q2 values, including the selection of the 3 most important descriptors (out of 12) in the models based on their VIP values and repeated the PLS.
Experimental methods
Chemicals and growth media
1,2-Dibromoethane (DBE) and LB medium were purchased from Sigma-Aldrich Co. (St. Louis, MO, USA). IPTG was purchased from Duchefa Biochemie B.V. (Haarlem, The Netherlands). All chemicals used in this study were of analytical grade.Strains
Escherichia coli Dh5α cells were obtained from Invitrogen and Escherichia coli BL21 (DE3) from New England Biolabs.Site-directed mutagenesis
The gene encoding LinB (from Sphingobium japonicum UT26) on the pET21b vector (Invitrogen) was used as a template to synthesize the LinB mutants. Primers were designed using the one-click web server (http://tucksengwong.staff.shef.ac.uk/OneClick/index) and then modified to be suitable for the synthesis of megaprimers (ESI,† Table S5). A standard pET vector primer was used as a reverse primer for megaprimer generation.Site-directed mutagenesis was performed using a megaprimer mutagenesis protocol. First, a PCR to generate the megaprimers was performed. The PCR program started with 30 s at 98 °C, followed by 30 cycles of denaturation (98 °C, 10 s), annealing (55 °C, 20 s), and extension (72 °C, 30 s). Finally, the temperature was held at 72 °C for 120 s. The reaction mix (50 μL) contained 10x Phusion buffer (5 μL), a mixture of deoxynucleoside triphosphates (1 μL, 0.25 mM each), Phusion DNA polymerase (0.5 μL), plasmid DNA (1 μL), and the forward and reverse primers (2 μL, 0.2 μM each). After analysis by agarose gel electrophoresis, the megaprimers were used for the mutagenesis. The PCR program was almost identical to that for the first PCR, except that the extension and final extension steps were extended to 150 s and 480 s, respectively. The reaction mix (25 μL) contained 10x Phusion buffer (2.5 μL), a mixture of deoxynucleoside triphosphates (0.5 μL, 0.25 mM each), Phusion DNA polymerase (0.25 μL), plasmid DNA (0.5 μL), and the appropriate megaprimer (1 μL). The reaction mixtures were then subjected to DpnI digestion (2 μL DpnI and 3 μL CutSmart buffer/reaction mix, 37 °C for 2 h then 65 °C for 20 min) to remove the template DNA. Chemo-competent E. coli Dh5α cells were then transformed with 10 μL of the reaction solution for DNA strand repair and plasmid amplification. After plasmid isolation with the “InnuPREP Plasmid Mini Kit” (Analytik Jena), the success of the mutagenesis was confirmed by sequencing (performed by Eurofins MWG GmbH).
Cultivation and expression in E. coli BL21 (DE3)
The generated plasmids were used to transform chemo-competent E. coli BL21 (DE3) cells. Obtained colonies were used to prepare precultures by inoculating 10 mL LB medium (with 100 μg mL−1 ampicillin) followed by incubation at 37 °C and 180 rpm overnight. To express each variant, 2 L LB medium supplemented with 100 μg mL−1 ampicillin was inoculated with 5 mL of the appropriate preculture (1/200). The flasks were incubated at 37 °C and 180 rpm until OD600 0.6–0.8 was reached, then at 20 °C for 30 min. β-D-1-thiogalactopyranoside (IPTG, 0.2 mM) was added for induction, followed by incubation at 20 °C at 180 rpm overnight. The cultures were harvested by centrifugation at 4500×g, 4 °C for 15 min and the cell pellets were frozen at −80 °C until further use.Protein purification
The cell pellets were suspended in 50 mL equilibration buffer (20 mM phosphate buffer pH 7.5 containing 0.5 M NaCl and 10 mM imidazole) and disrupted by sonication with a Hielscher UP200S ultrasonic processor (Hielscher, Germany) four times for four minutes each. Disrupted cells were centrifuged at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×g and 4 °C for 1 h (Laborzentrifugen, Germany). The crude extract was collected, filtered, and loaded onto a Ni-NTA Superflow Cartridge (Qiagen, Germany) in equilibration buffer. Unbound and weakly bound proteins were washed out using increasing imidazole concentrations. The target enzyme was then eluted with purification buffer containing 300 mM imidazole. The eluted protein was dialyzed three times overnight against 50 mM phosphate buffer (pH 7.5). The purity of the protein was checked by SDS-polyacrylamide gel electrophoresis (SDS-PAGE). 15% polyacrylamide gels were stained with Instant Blue (Fluka, Switzerland). Protein concentrations were determined using a NanoDrop spectrophotometer (Sigma-Aldrich, USA). The enzymes were lyophilized using a vacuum pump system for long-term storage.
000×g and 4 °C for 1 h (Laborzentrifugen, Germany). The crude extract was collected, filtered, and loaded onto a Ni-NTA Superflow Cartridge (Qiagen, Germany) in equilibration buffer. Unbound and weakly bound proteins were washed out using increasing imidazole concentrations. The target enzyme was then eluted with purification buffer containing 300 mM imidazole. The eluted protein was dialyzed three times overnight against 50 mM phosphate buffer (pH 7.5). The purity of the protein was checked by SDS-polyacrylamide gel electrophoresis (SDS-PAGE). 15% polyacrylamide gels were stained with Instant Blue (Fluka, Switzerland). Protein concentrations were determined using a NanoDrop spectrophotometer (Sigma-Aldrich, USA). The enzymes were lyophilized using a vacuum pump system for long-term storage.
Circular dichroism (CD) spectroscopy
CD spectra were recorded at 20 °C using a Chirascan spectropolarimeter (Applied Photophysics, United Kingdom). Data were collected from 190 to 260 nm at 100 nm min−1 with a 1 s response time and 1 nm bandwidth using a 0.1 cm quartz cuvette. Each spectrum shown is an average of five individual scans and was corrected for the buffer's absorbance. Collected CD data were expressed in terms of the mean residue ellipticity (ΘMRE) using eqn (1), where Θobs is the observed ellipticity in degrees, Mw is the protein's molecular weight, n is the number of residues, l is the cell path length, c is the protein concentration (0.2 mg ml−1), and factor 100 originates from the conversion of the molecular weight to mg dmol−1 (ESI,† Fig. S10).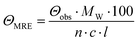 | (1) |
Thermal denaturation
Thermal unfolding was followed by monitoring the ellipticity at 224 nm over the temperature range of 20 to 94 °C, with a resolution of 0.1 °C, at a heating rate of 1 °C min−1. Recorded thermal denaturation curves were roughly normalized to represent signal changes between approximately 1 and 0, and were fitted to sigmoidal curves using Origin 6.1 (OriginLab Corporation, USA). The melting temperatures (Tm) were evaluated as the midpoints of the normalized thermal transitions (ESI,† Table S6).Specific activity measurements
Dehalogenation activity was assayed using the colorimetric method of Iwasaki et al.53 Halide ion release was analysed spectrophotometrically at 460 nm using an Eon microplate reader (BioTek, USA) after reaction with mercuric thiocyanate and ferric ammonium sulfate. The reactions were performed at 37 °C in 25 ml Reacti flasks sealed with Mininert valves. The reaction mixtures consisted of 10 ml of 100 mM glycine buffer (pH 8.6) and 10 μl of the substrate DBE. Reactions were initiated by adding enzymes to final concentrations of 0.0047 (L177W), 0.0029 (W140A/L177W), 0.0014 (F143L/L177W), 0.0073 (L177W/I211L), or 0.0005 mg ml−1 (W140A/F143L/L177W/I211L). The reactions were monitored by withdrawing 1 ml samples from the reaction mixture after 0, 5, 10, 15, 20 and 30 min. These samples were immediately mixed with 0.1 ml of 35% nitric acid to stop the reaction. Dehalogenation activity was quantified as the rate of product formation over time. Each activity was measured in three independent replicates (ESI,† Table S7).Steady-state kinetic measurements
The steady-state kinetics of DBE conversion by LinB variants were measured at 37 °C using a VP-ITC isothermal titration microcalorimeter (MicroCal, Piscataway, NJ, USA).54 The microcalorimeter's reaction vessel was filled with 1.4 mL of enzyme solution at a concentration of 0.001–0.12 mg mL−1 (100 mM glycine buffer, pH 8.6). The substrate solution was prepared in the same buffer by adding DBE to a final concentration of 12–18 mM. The substrate concentration was verified by gas chromatography (Finnigen, USA). The enzyme was titrated at 150 s intervals in the reaction vessel with increasing amounts of the substrate while maintaining pseudo-first-order conditions. Each injection increased the substrate concentration, thereby increasing the rate of the catalyzed reaction (and the heat generated) until the enzyme became saturated. In total, 28 injections were performed during the titration. The reaction rates reached after each injection (in units of thermal power) were converted into enzyme turnover values using the apparent molar enthalpy (ΔHapp), as shown in eqn (2), where [P] is the molar concentration of product generated and Q is the enzyme-generated thermal power.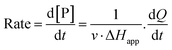 | (2) |
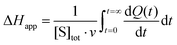 | (3) |
Apparent molar enthalpy (ΔHapp) was determined using eqn (3), where [S] is the molar concentration of DBE converted by LinB in a separate experiment where the reaction was allowed to proceed to completion. The calculated enzyme turnover plotted against the actual concentration of the substrate after each injection was then fitted by nonlinear regression to kinetic models using Origin 8.0 (OriginLab, Northampton, MA, USA).
Global data analysis
The steady-state and transient kinetic data were fit globally using Global Kinetic Explorer (KinTek Corporation). Rate equations were numerically integrated by using the Bulirsch–Stoer algorithm with an adaptive step size to search for a set of kinetic parameters derived from the input model that minimized the χ2 value. Nonlinear regression to fit the data was performed using the Levenberg–Marquardt method.55 To account for variations in the data, enzyme and substrate concentrations were slightly adjusted by treating them as parameters during the fitting procedure with enforced boundaries at ±5%. Residuals were normalized by the Sigma value for each data point. The standard error (SE) was calculated from the covariance matrix when performing nonlinear regression. The standard error estimates in the fitted parameters were propagated to obtain estimates of the error in the calculated values, the equilibrium dissociation constant of the substrate-inhibited complex (KSI), the specificity constant (kcat/Km), and the degree of substrate inhibition (KSI/Km).Results
Kinetic models and global data analysis
The modification of the export pathways of the haloalkane dehalogenase LinB presented in our previous study showed that a single mutation blocking the main access tunnel (L177W) could induce strong SI, which was subsequently removed by modifying the auxiliary tunnel (W140A/F143L/L177W/I211L) altering the dynamics of the main tunnel (Fig. 1).35,36 To provide a deeper understanding of the mechanism of this inhibitory effect, we performed in a first step a systematic global kinetic analysis. We simultaneously fitted the steady-state and transient kinetic data by numerically integrating the rate equations derived from the minimal kinetic pathway of the HLD-catalyzed reaction (Scheme 2). Even for the simple kinetic pathway including one reaction intermediate, the excess substrate could inhibit the catalytic cycle in three ways: by interacting with the enzyme–substrate complex, the alkyl–enzyme intermediate, or the enzyme–product complex (ESI,† Schemes S2–S4). To identify the model that fits best the kinetic observations, we analyzed all three possible scenarios, examined the error in the fitted parameters and evaluated the goodness of fit visually and computationally. The normalized standard deviation χ2 and goodness of fit estimate (χ2/DoF, degrees of freedom) suggested that the model where the substrate binds to the enzyme–product complex is more likely than the other two. Detailed inspection of the fit quality showed that although the steady-state data agreed reasonably well with the simulations for all three models, there were significant discrepancies between the experimental and simulated values for both transient kinetic datasets, which were obtained by performing stopped-flow multiple turnover fluorescence and rapid-quench burst experiments. In particular, the rates and amplitudes derived from the rapid quench burst data strongly supported one mechanism for the substrate inhibition of LinB by DBE and excluded others. Specifically, the only model consistent with the rates and amplitudes observed in all phases was that where the substrate binds to the enzyme–product complex (ESI,† Fig. S1 and Table S1).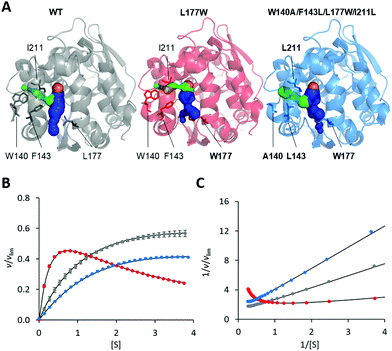 | ||
| Fig. 1 Overview of LinB variants with engineered access tunnels. (A) The crystal structures PDB ID 1MJ5 (WT, grey), 4WDR (L177W, red) and 4WDQ (W140A/F143L/L177W/I211L, blue). The mutated residues are shown in stick form, with a bold label where mutated, and the location of the catalytic site is indicated by an orange sphere representing the co-crystallized chloride ion. The main tunnel is shown in blue. It is divided into two smaller tunnels in L177W and W140A/F143L/L177W/I211L by the introduced L177W mutation. The target of the W140A/F143L/L177W/I211L mutations, the p3 tunnel, is shown in green. (B) Steady-state relative initial velocity (v/vlim) as a function of substrate concentration [S], and (C) the Lineweaver–Burk double-reciprocal plot for the WT (grey), L177W (red) and W140A/F143L/L177W/I211L (blue) enzymes. Kinetic data were acquired in three independent replicate experiments; error bars represent the upper and lower bounds of 95% confidence intervals. | ||
The estimates of the equilibrium dissociation constant of the substrate-inhibited complex KSI also differed strongly between the models. The estimate for the model involving inhibitory binding of the substrate to the enzyme–product complex (KSI = 1.21 ± 0.01 mM) agreed reasonably well with experiment, whereas the estimates for the other two models were in the sub-micromolar range. A detailed description of the global data analysis and the statistical results is provided in the ESI,† (Section S1).
Molecular dynamics simulations and Markov state models
Because the kinetic model suggested that the observed SI was due to the formation of an enzyme–product–substrate complex (Fig. 2), the starting structures for the molecular dynamics simulations consisted of systems with the two products (BRE and Br−) bound and DBE in the vicinity of the enzyme in the solvent. Also, to clarify the impact of the individual mutations differentiating L177W from W140A/F143L/L177W/I211L, the corresponding double-point mutants were simulated (W140A/L177W, F143L/L177W and L177W/I211L). Each system was simulated using AceMD for ∼25 μs using the distances of the three ligands to the catalytic site as the metric for adaptive sampling. Around 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshots were obtained for each system and used to create MSMs with eight Markov states using the binary contact map for the protein's Cα atoms and the atoms of the ligands as the metric (Table 1). The implied time-scale plots, Chapman–Kolmogorov test results, and figures depicting the states are presented in the ESI,† (Section SII).
000 snapshots were obtained for each system and used to create MSMs with eight Markov states using the binary contact map for the protein's Cα atoms and the atoms of the ligands as the metric (Table 1). The implied time-scale plots, Chapman–Kolmogorov test results, and figures depicting the states are presented in the ESI,† (Section SII).
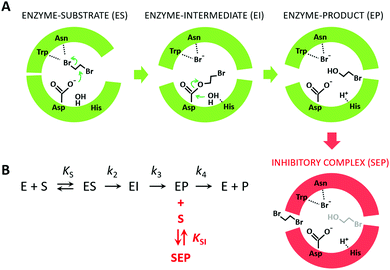 | ||
Fig. 2 The mechanism of substrate inhibition. (A) Scheme of the catalytic mechanism of haloalkane dehalogenases (HLDs), the active states in green and proposed SI state in red. The reaction mechanism of HLDs adapted from Verschueren et al. 1993![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 is a two-step process that occurs inside the enzyme active site. A nucleophilic attack on a carbon atom is initiated by Asp, forming an ester intermediate that is then hydrolyzed by a nucleophilic attack of a water molecule activated by the basic His. Trp and Asn are halide-stabilizing residues. (B) The minimal kinetic model for the catalytic cycle of HLDs (black). S represents a substrate, P a product, E an enzyme, ES a non-covalent enzyme–substrate complex, EI a covalently bound alkyl–enzyme intermediate, and EP an enzyme–product complex. KS is the equilibrium dissociation constant for the ES complex (KS = k-1/k1), k2 is the rate constant for carbon–halogen bond cleavage (SN2), k3 is the rate constant for hydrolysis of the alkyl–enzyme intermediate via nucleophilic addition (AdN), and k4 is the rate constant for product release. The mechanism of substrate inhibition (in red) is based on a global kinetic data analysis. KSI is the equilibrium dissociation constant for the inhibitory enzyme–substrate–product complex (SEP). 56 is a two-step process that occurs inside the enzyme active site. A nucleophilic attack on a carbon atom is initiated by Asp, forming an ester intermediate that is then hydrolyzed by a nucleophilic attack of a water molecule activated by the basic His. Trp and Asn are halide-stabilizing residues. (B) The minimal kinetic model for the catalytic cycle of HLDs (black). S represents a substrate, P a product, E an enzyme, ES a non-covalent enzyme–substrate complex, EI a covalently bound alkyl–enzyme intermediate, and EP an enzyme–product complex. KS is the equilibrium dissociation constant for the ES complex (KS = k-1/k1), k2 is the rate constant for carbon–halogen bond cleavage (SN2), k3 is the rate constant for hydrolysis of the alkyl–enzyme intermediate via nucleophilic addition (AdN), and k4 is the rate constant for product release. The mechanism of substrate inhibition (in red) is based on a global kinetic data analysis. KSI is the equilibrium dissociation constant for the inhibitory enzyme–substrate–product complex (SEP). | ||
| State | WT | L177W | W140A/L177W | F143L/L177W | L177W/I211L | W140A/F143/L177W/I211L |
|---|---|---|---|---|---|---|
| a Consists of two states with different binding orientations having probabilities of 17% and 14%. b Consists of two states with different binding orientations having probabilities of 28% and 5%. c Consists of three states with different binding orientations having probabilities of 39%, 5% and 2%. | ||||||
| All unbound | 20 | 6.1 | 17 | 13 | 37 | 24 |
| All bound | 0.2 | 2.2 | 0.2 | 0.02 | 0.04 | 0.4 |
| Active state | ||||||
| DBE bound | 30 | 22 | 50 | 48 | 22 | |
| Possible SI states | ||||||
| DBE on surface + Br− bound | 31 | |||||
| DBE + Br− bound | 31a | 10 | 0.1 | 0.6 | ||
| Other states | ||||||
| BRE + Br− bound + DBE on surface | 3.9 | 1.2 | 6.8 | |||
| DBE on surface | 1.8 | |||||
| BRE + Br− bound | 16 | 0.2 | ||||
| DBE + BRE bound | 35b | 27 | 15 | 6 | 46c | |
| BRE bound + DBE on surface | 11 | 5.6 | ||||
| BRE bound | 4.1 | 22 | 5.1 | |||
| Br− bound | 24 | 0.4 | 0.7 | 2.6 | ||
The starting state (BRE + Br− bound) was identified in all systems other than the WT. This is consistent with the experimental finding that the rate-limiting step of the WT-catalyzed reaction is the release of BRE rather than Br− release.35 The WT enzyme also had the greatest number of BRE bound states, further supporting this conclusion.
States with all of the ligands bound or unbound were found for all systems. It is rare (<3%) for any system to have all three ligands bound, and it is relatively common for all systems to have all ligands unbound, perhaps except for L177W (6.1%). With the same exception, the systems were frequently observed in states that could be considered “ready for the next catalytic cycle”, i.e. active states in which the only DBE was bound. This state was not observed at all for L177W. The failure to observe the substrate-bound state could be due to the relatively short simulation time or the fact that L177W is one of the least catalytically proficient enzymes studied here.
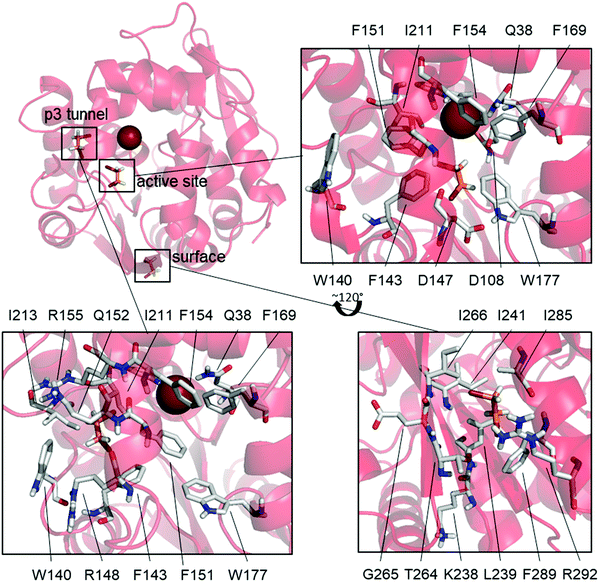
L177W was also the only studied enzyme variant for which states having both DBE and Br− bound simultaneously were observed, supporting our hypothesized SI mechanism. This variant has a common state with Br− bound and DBE bound to the surface (31%), as well as two states where DBE is bound inside the active site (14%) or the p3 tunnel (17%) (Fig. 3).
The high frequency of the state with DBE bound on the surface and Br− also bound (31%) suggests that DBE could cause the observed SI via an allosteric mechanism, but there are no modifications to this part of the enzyme that would explain the diminished SI in W140A/F143L/L177W/I211L. Additionally, binding at the same surface site is observed as an uncommon state of W140A/F143L/L177W/I211L (6.8%) and the WT (BRE bound + DBE on the surface, 11%) even though Br− is not bound in these cases. These results suggest that DBE sometimes binds to this part of the enzyme surface but that such binding does not cause SI because it is also observed in the WT and W140A/F143L/L177W/I211L, both of which exhibit only weak SI. Mutagenesis studies targeting this surface binding site could clarify its effects on the catalytic properties of LinB variants.
The mutations differentiating L177W from W140A/F143L/L177W/I211L are clustered around the p3 tunnel region, which, interestingly, is a binding site for DBE in one L177W state (DBE + Br− bound, 17%, Fig. 3). This region of L177W should be identical to that in the WT, which does not exhibit strong SI. By looking at the individual Markov states (ESI,† Table S4 and Fig. S4–S9), we can see that both DBE and BRE can bind to this binding site in the WT, but such binding is rare (<6%). The Br− bound states may occur frequently in L177W because the L177W mutation hinders the exit of reaction products; the binding of DBE in this site could further hinder the exit of Br−. Fig. 3 shows that the binding of DBE to the p3 tunnel forces F151 to face the active site, creating yet another a steric barrier to the exit of Br−. In the third possible SI state, DBE binds to the active site (Fig. 3) and interacts with the mutated L177W. Since DBE occupies the active site, it sterically blocks the exit of Br− and affects the interactions of water molecules involved in releasing Br− from the halide-stabilizing residues.
We next examined possible SI states in variants that combine L177W with individual mutations from the W140A/F143L/L177W/I211L quadruple mutant. In F143L/L177W and L177W/I211L, the states responsible for SI (DBE bound at the active site or p3 tunnel) are very rarely observed (<1% probability). W140A/L177W, on the other hand, often adopts a state with DBE and Br− bound (10%). In this state, DBE interacts with both binding sites observed for L177W, i.e. the active site and the p3 tunnel region (Fig. 3), suggesting a possible enhancement of the SI effect. Additionally, the most common states of F143L/L177W and L177W/I211L resemble those of the catalytically efficient WT enzyme and W140A/F143L/L177W/I211L, and are thus expected to have greater catalytic activity than W140A/L177W.
Based on the MSM results, the following predictions can be made for L177W/I211L, W140A/L177W and F143L/L177W: (i) L177W/I211L and F143L/L177W should display weaker SI than L177W, (ii) W140A/L177W should display the strongest SI of the three double-point variants, and (iii) F143L/L177W and L177W/I211L should be more effective than W140A/L177W in the transport of ligands and thus also in catalysis.
Mutagenesis of p3 tunnel residues
To test the MSM-based predictions against experiment and to dissect the importance of individual p3 tunnel mutations in W140A/F143L/L177W/I211L, we constructed and characterized three additional LinB double-point variants: W140A/L177W, F143L/L177W, and L177W/I211L (ESI,† Section SIII). The equilibrium dissociation constants (KSI) estimated for these variants using steady-state kinetic data showed (Table 2) that compared to L177W, the substrate affinity of the inhibitory complex precursor was reduced in F143L/L177W and L177W/I211L but significantly enhanced in W140A/L177W. These findings agree well with the simulations, which predicted that W140A/L177W would show the strongest SI effect among the tested double-point variants.| Variant | K m (mM) | k cat (s−1) | K SI (mM) | k cat/Km (mM−1 s−1) | K SI/Km |
|---|---|---|---|---|---|
| a Steady-state kinetic constants adopted from Brezovsky et al. 2016.36 b Steady-state kinetic constants adopted from Kokkonen et al. 2019.35 | |||||
| WTa | 1.7 ± 0.2 | 12 ± 4 | 12.4 ± 0.3 | 7 ± 2 | 7.3 ± 0.9 |
| L177Wa | 0.42 ± 0.1 | 3.1 ± 0.1 | 1.34 ± 0.03 | 7 ± 2 | 3.2 ± 0.8 |
| W140A/F143L/L177W/I211La | 2.35 ± 0.03 | 57 ± 3 | 7.3 ± 0.1 | 24 ± 1 | 3.1 ± 0.1 |
| W140A/L177W | 4.5 ± 0.9 | 7 ± 1 | 0.39 ± 0.06 | 1.6 ± 0.4 | 0.09 ± 0.02 |
| F143L/L177W | 2.1 ± 0.1 | 16 ± 1 | 2.06 ± 0.01 | 7.6 ± 0.6 | 0.98 ± 0.05 |
| L177W/I211L | 0.12 ± 0.01 | 2.33 ± 0.04 | 1.9 ± 0.4 | 19 ± 2 | 16 ± 4 |
| I211L | 0.76 ± 0.04 | 8.3 ± 0,2 | 4.6 ± 0.1 | 11 ± 1 | 6.1 ± 0.3 |
| F143L | 1.56 ± 0.05 | 2.1 ± 0.1 | 1.8 ± 0.2 | 1.3 ± 0.1 | 1.2 ± 0.1 |
| W140A/F143L/I211Lb | 3.9 ± 1.7 | 3.8 ± 0.1 | 23 ± 3 | 1.0 ± 0.4 | 6 ± 3 |
The kinetic data also agree well with the computational predictions of the catalytic efficiency: F143L/L177W and L177W/I211L were expected to frequently exist in the active state (the probabilities of DBE bound-states were 50% and 48% for F143L/L177W and L177W/I211L, respectively) and accordingly had a significantly higher specificity constant kcat/Km than W140A/L177W, for which the frequency of the active DBE-bound state was rather low (22%). The overall impact of substrate inhibition depends on the relative magnitude of the Michaelis constant Km and KSI. The estimated KSI/Km ratios (Table 2) are consistent with strong SI in W140A/L177W (KSI/Km = 0.09 ± 0.02) and also indicate significant attenuation of inhibition in L177W/I211L (KSI/Km= 16 ± 4), even compared to the WT (KSI/Km = 7.3 ± 0.9). Moreover, L177W/I211L had the highest specificity constant of any tested variant (kcat/Km = 19 ± 2 mM−1 s−1), suggesting that the I211L substitution contributes greatly to the unusual efficiency of W140A/F143L/L177W/I211L (kcat/Km = 24 ± 2 mM−1 s−1).
We also constructed the single-point p3 tunnel variants W140A, F143L and I211L to test their possible synergistic effects with L177W. Only two of these variants, F143L and I211L, were successfully expressed and purified for kinetic analysis. Relative to the WT, F143L exhibited reduced catalytic efficiency and weaker SI. I211L showed a similar kinetic impact of SI (KSI/Km = 6.1 ± 0.3) and partially improved the catalytic efficiency (kcat/Km = 11 ± 1 mM−1 s−1), but none of these parameters reached the level obtained for L177W/I211L. These results show that the presence of Trp at the position 177 has important effects on the catalytic performance of W140A/F143L/L177W/I211L (kcat/Km = 24 ± 1 mM−1 s−1) and L177W/I211L (kcat/Km = 19 ± 2 mM−1 s−1). A similar effect was observed for the back mutation at position 177 leading to W140A/F143L/I211L with kcat/Km = 1.0 ± 0.4 mM−1 s−1. Moreover, the systematic mutagenesis showed an interesting synergism between L177W and I211L, which significantly suppressed the SI (KSI/Km = 16 ± 4), although these mutations had a rather opposite effect when introduced separately (KSI/Km = 3.2 ± 0.8 and 6.1 ± 0.3 for L177W and I211L, respectively).
Multivariate data analysis
A partial least squares (PLS) analysis was performed to test how well the theoretical assumptions and models of the molecular dynamics simulations reproduced the macroscopic experimental data (ESI,† Section SIV). The PLS analysis yielded a statistically significant model correlating the probabilities of the Markov states calculated based on the molecular dynamics simulations and the logarithm of the experimentally determined ratio of the substrate inhibition constant and the Michaelis–Menten constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KSI/Km). A model based on two principal components had a significant coefficient of determination (R2 = 0.84) and a cross-validation coefficient of Q2 = 0.68. The small difference between R2 and Q2 confirms that the model is not over-fitted. Significant variables contributing to the explanation of the experimental KSI/Km values were BRE_bound, BRE_bound + DBE_surface, BR_bound and All_unbound. A permutation test using 300 rounds of permutation of the y-components significantly reduced both R2 and Q2 because the correlation between the permutated and original data weakened, implying that the obtained values are not due to pure chance (ESI,† Fig. S13). Because of the small number of observations, Monte Carlo simulations were performed to test the validity of the permutation analysis. Ten thousand data sets of the same size as in our analysis were generated by drawing randomly and independently from a uniform distribution. These data sets were then subjected to the same PLS analysis protocol and their R2 and Q2 values were computed. In addition, the PLS was repeated for each dataset using only the 3 variables with the best VIP values of the 12 available. While there were several instances in which the R2 coefficient for random datasets exceeded that for the real data, the small p-values for the coefficient Q2 (ESI,† Fig. S14) indicate that the observed Q2 of 0.68 would be unlikely to be observed by chance even given the small sample size. We thus conclude that our theoretical models based on the molecular dynamic simulations reproduced the experimental kinetic observations well.
KSI/Km). A model based on two principal components had a significant coefficient of determination (R2 = 0.84) and a cross-validation coefficient of Q2 = 0.68. The small difference between R2 and Q2 confirms that the model is not over-fitted. Significant variables contributing to the explanation of the experimental KSI/Km values were BRE_bound, BRE_bound + DBE_surface, BR_bound and All_unbound. A permutation test using 300 rounds of permutation of the y-components significantly reduced both R2 and Q2 because the correlation between the permutated and original data weakened, implying that the obtained values are not due to pure chance (ESI,† Fig. S13). Because of the small number of observations, Monte Carlo simulations were performed to test the validity of the permutation analysis. Ten thousand data sets of the same size as in our analysis were generated by drawing randomly and independently from a uniform distribution. These data sets were then subjected to the same PLS analysis protocol and their R2 and Q2 values were computed. In addition, the PLS was repeated for each dataset using only the 3 variables with the best VIP values of the 12 available. While there were several instances in which the R2 coefficient for random datasets exceeded that for the real data, the small p-values for the coefficient Q2 (ESI,† Fig. S14) indicate that the observed Q2 of 0.68 would be unlikely to be observed by chance even given the small sample size. We thus conclude that our theoretical models based on the molecular dynamic simulations reproduced the experimental kinetic observations well.
Discussion
Substituting the L177 position of LinB with a bulky residue (L177W) introduced a strong SI effect into the enzyme's catalytic cycle. This mutation reduces the size of the access tunnel and catalytic site, making it implausible that the SI was due to the formation of an unproductive complex resulting from an increase in the number of substrate molecules bound simultaneously at the catalytic site. Thus, as expected, the kinetic simulations produced unrealistic values when trying to fit the data to comply with this classical theory. No allosteric binding sites were found on LinB that might explain the observed SI, although we did observe a possible substrate-binding site at the surface (Fig. 3). However, non-specific binding of DBE to this region was observed in almost all studied LinB variants.The global kinetic analysis was used to systematically test three possible models of SI. In addition to Haldane's traditional mechanism including an enzyme complex with two substrate molecules, the binding of the substrate to an alkyl–enzyme intermediate and the enzyme–product complex were evaluated kinetically. The simultaneous analysis of steady-state and transient kinetic data using numerical integration made it possible to distinguish between the expected models and suggested that the observed SI is due to the formation of an unproductive enzyme–product–substrate complex. In particular, the transient-state burst analysis strongly supported this inhibition mechanism. Clear discrimination between the different inhibition models was achieved upon comparing the experimentally observed and numerically simulated amplitudes for the bursts of the halide and alcohol products, which corresponded to the fractions of the alkyl–enzyme intermediate and enzyme–product-complex available during the catalytic cycle. The only model consistent with the rates and amplitudes observed in all of the kinetic experiments was that in which the substrate binds to the enzyme–product complex, leading to an unproductive form. Since halide release is a slow rate-limiting step,36,57 the enzyme-bromide complex accumulates strongly during the conversion of DBE catalyzed by L177W. This makes the enzyme–product complex the main target for potential inhibition.
Mechanistically, SI in L177W may occur because DBE binds to the catalytic site and presents a steric barrier to the exit of Br−. The binding of DBE to the p3 tunnel could not induce SI via direct steric blockage because in this case, DBE would only block a rarely-used auxiliary tunnel.36 However, the binding of DBE to this position forces F151 to face the catalytic site, creating a steric blockage similar to that formed when DBE binds to the catalytic site. The W177 residue in the L177W variant forms a parallel displaced π-stacking interaction with F151, stabilizing the blocking conformation. This conformation of F151 is also stabilized via T-shaped π stacking with F143, which may partly explain the loss of SI in the F143L/L177W variant.
The other possible mechanism of SI by DBE is based on locking the W177 residue of L177W into the closed conformation. We have previously shown that L177W undergoes slow conformational changes between open and closed states and that it is difficult for Br− to exit from the closed conformation.35 W140A/F143L/L177W/I211L displays similar conformational dynamics but over shorter time scales. When DBE is bound to the p3 tunnel or the active site, it forms favorable lipophilic interactions with the surrounding residues, reducing the likelihood that the protein will go from the closed to the open state.
The mutations at the p3 tunnel (W140A/F143L/I211L) widened the tunnel and reduced the number of possible lipophilic interactions, thereby reducing the site's affinity for DBE. This can be seen in the Markov states of L177W-containing double-point variants: only W140A/L177W has a relatively common SI state like L177W. The experimental results confirmed that the double-point mutants generally had weaker SI than L177W. Additionally, the experimental data showed that the W140A mutation causes structural instability, possibly because too many hydrophobic contacts are lost in the region responsible for the conformational dynamics of L177W and W140A/F143L/L177W/I211L (for a more detailed discussion, see our previous manuscript35). Additionally, systematic mutagenesis of p3 tunnel residues revealed an unusual synergy between L177W and I211L, which are key residues providing high catalytic efficiency and reduced substrate inhibition. The essential role of L177W was previously tested by back-mutation of W140A/F143L/L177W/I211L in the position 177.36 The W140A/F143L/I211L variant completely lacked the high catalytic efficiency of W140A/F143L/L177W/I211L. Similarly, the efficiency of L177W/I211L was not replicated by either the L177W or the I211L substitutions individually. Interestingly, the synergistic substitutions L177W and I211L are located in two different access tunnels in remote parts of the protein.
Conclusions
We have shown that SI can be caused by a substrate molecule blocking the exit of the product from the enzyme–product complex. This mechanism is not typically considered for single substrate reactions. Additionally, we have shown that single amino acid substitutions in enzyme access tunnels can introduce or weaken SI. This effect should therefore be taken into account during enzyme engineering studies. Experimental analysis including studies on transient kinetics can identify the specific stages of the catalytic cycle affected by SI. This information can be then used to conduct molecular dynamics simulations with MSMs to clarify the SI mechanism at the molecular level. Once a mechanism is established, rational protein engineering targeting the relevant states can be undertaken to reduce the probability of undesirable SI. This strategy should be generally applicable to many other enzyme systems with available structural information.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank the RECETOX research infrastructure (the Czech Ministry of Education, Youth and Sports: LM2018121) and Teaming project: CETOCOEN EXCELLENCE Teaming 2 project supported by Horizon2020 (857560) and the Czech Ministry of Education, Youth and Sports (02.1.01/0.0/0.0/18_046/0015975). Computational resources were supplied by the project “e-Infrastruktura CZ” (e-INFRA LM2018140) provided within the program Projects of Large Research, Development and Innovations Infrastructures. PK, SM, and AB are supported by the Operational Programme Research, Development and Education – Projects “MSCAfellow@MUNI” CZ.02.2.69/0.0/0.0/17_050/0008496 and CZ.02.2.69/0.0/0.0/19_074/0012727, respectively.References
- M. C. Reed, A. Lieb and H. F. Nijhout, BioEssays, 2010, 32, 422–429 CrossRef CAS
.
- B. Wu, Drug Metab. Rev., 2011, 43, 440–456 CrossRef CAS
.
- M. Yoshino and K. Murakami, SpringerPlus, 2015, 4, 292 CrossRef
.
- A. W. Fenton and G. D. Reinhart, Biochemistry, 2003, 42, 12676–12681 CrossRef CAS
.
-
J. B. S. Haldane, Reprint by MIT, Cambridge, 1965, p. 84 Search PubMed
.
- Y. Lin, P. Lu, C. Tang, Q. Mei, G. Sandig, A. D. Rodrigues, T. H. Rushmore and M. Shou, Drug Metab. Dispos., 2001, 29, 368–374 CAS
.
- C. Chen, J. C. Joo, G. Brown, E. Stolnikova, A. S. Halavaty, A. Savchenko, W. F. Anderson and A. F. Yakunin, Appl. Environ. Microbiol., 2014, 80, 3992–4002 CrossRef
.
- K. D. Tidemand, G. H. Peters, P. Harris, E. Stensgaard and H. E. M. Christensen, Biochemistry, 2017, 56, 6155–6164 CrossRef CAS
.
- J. R. Warner, L. S. Behlen and S. D. Copley, Biochemistry, 2008, 47, 3258–3265 CrossRef CAS
.
- E. H. Jang, S. A. Park, Y. M. Chi and K. S. Lee, Biochem. Biophys. Res. Commun., 2015, 461, 487–493 CrossRef CAS
.
- G. W. Heberlig, M. Wirz, M. Wang and C. N. Boddy, Org. Lett., 2014, 16, 5858–5861 CrossRef CAS
.
- P. Kallio, P. Patrikainen, G. A. Belogurov, P. Mäntsälä, K. Yang, J. Niemi and M. Metsä-Ketelä, Biochemistry, 2013, 52, 4507–4516 CrossRef CAS
.
- A. E. Leroux, J. R. Haanstra, B. M. Bakker and R. L. Krauth-Siegel, J. Biol. Chem., 2013, 288, 23751–23764 CrossRef CAS
.
- T. Liu, Q. Wu, L. Liu and Q. Yang, Process Biochem., 2013, 48, 103–108 CrossRef CAS
.
- A. Tramonti, C. Nardella, M. L. di Salvo, A. Barile, F. Cutruzzolà and R. Contestabile, Biochemistry, 2018, 57, 6984–6996 CrossRef CAS
.
- P. Mehrabi, C. Di Pietrantonio, T. H. Kim, A. Sljoka, K. Taverner, C. Ing, N. Kruglyak, R. Pomès, E. F. Pai and R. S. Prosser, J. Am. Chem. Soc., 2019, 141, 11540–11556 CrossRef CAS
.
- I. L. Mainprize, J. D. Bean, C. Bouwman, M. S. Kimber and C. Whitfield, J. Biol. Chem., 2013, 288, 23064–23074 CrossRef CAS
.
- R. A. G. Reis, F. Salvi, I. Williams and G. Gadda, Biochemistry, 2019, 58, 2594–2607 CrossRef
.
- F. B. H. Rehm, M. A. Jackson, E. D. Geyter, K. Yap, E. K. Gilding, T. Durek and D. J. Craik, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7831–7836 CrossRef CAS
.
- I. N. Kiburu and N. LaRonde-LeBlanc, PLoS One, 2012, 7, e37371 CrossRef CAS
.
- L. Jin, K. Yang, K. Yao, S. Zhang, H. Tao, S.-T. Lee, Z. Liu and R. Peng, ACS Nano, 2012, 6, 4864–4875 CrossRef CAS
.
- H. Jahić, C. F. Liu, J. Thresher, S. Livchak, H. Wang and D. E. Ehmann, Biochem. Pharmacol., 2012, 84, 654–660 CrossRef
.
- W. Fang, T. Du, O. G. Raimi, R. Hurtado-Guerrero, M. D. Urbaniak, A. F. M. Ibrahim, M. A. J. Ferguson, C. Jin and D. M. F. van Aalten, Mol. Microbiol., 2013, 89, 479–493 CrossRef CAS
.
- J. Wang, J. Zhu, C. Min and S. Wu, BMC Biotechnol., 2014, 14, 40 CrossRef
.
- Y.-L. Tao, D.-H. Yang, Y.-T. Zhang, Y. Zhang, Z.-Q. Wang, Y.-S. Wang, S.-Q. Cai and S.-L. Liu, Appl. Microbiol. Biotechnol., 2014, 98, 2519–2531 CrossRef CAS
.
- J. J. Sánchez-Romero and L. F. Olguin, Biochem. Biophys. Rep., 2015, 3, 161–168 Search PubMed
.
- S. Reich, D. Guilligay and S. Cusack, Nucleic Acids Res., 2017, 45, 3353–3368 CAS
.
-
K. A. Johnson, in Wiley Encyclopedia of Chemical Biology, American Cancer Society, 2008, pp. 1–8 Search PubMed
.
-
K. A. Johnson, in The Enzymes, ed. D. S. Sigman, Academic Press, 1992, vol. 20, pp. 1–61 Search PubMed
.
- H. Hu, C. Luo and Y. G. Zheng, J. Biol. Chem., 2016, 291, 26722–26738 CrossRef CAS
.
- M. T. Kamlay and J. D. Shore, Arch. Biochem. Biophys., 1983, 222, 59–66 CrossRef CAS
.
- Y. Wei, P. Kuzmič, R. Yu, G. Modi and L. Hedstrom, Biochemistry, 2016, 55, 5279–5288 CrossRef CAS
.
- H. J. Fromm and D. R. Nelson, J. Biol. Chem., 1962, 237, 215–220 CrossRef CAS
.
- D. B. Northrop and W. W. Cleland, J. Biol. Chem., 1974, 249, 2928–2931 CrossRef CAS
.
- P. Kokkonen, J. Sykora, Z. Prokop, A. Ghose, D. Bednar, M. Amaro, K. Beerens, S. Bidmanova, M. Slanska, J. Brezovsky, J. Damborsky and M. Hof, J. Am. Chem. Soc., 2018, 140, 17999–18008 CrossRef CAS
.
- J. Brezovsky, P. Babkova, O. Degtjarik, A. Fortova, A. Gora, I. Iermak, P. Rezacova, P. Dvorak, I. K. Smatanova, Z. Prokop, R. Chaloupkova and J. Damborsky, ACS Catal., 2016, 6, 7597–7610 CrossRef CAS
.
- P. W. Rose, C. Bi, W. F. Bluhm, C. H. Christie, D. Dimitropoulos, S. Dutta, R. K. Green, D. S. Goodsell, A. Prlic, M. Quesada, G. B. Quinn, A. G. Ramos, J. D. Westbrook, J. Young, C. Zardecki, H. M. Berman and P. E. Bourne, Nucleic Acids Res., 2013, 41, D475–D482 CrossRef CAS
.
- J. J. Gehret, L. Gu, T. W. Geders, W. C. Brown, L. Gerwick, W. H. Gerwick, D. H. Sherman and J. L. Smith, Protein Sci., 2012, 21, 239–248 CrossRef CAS
.
- A. J. Oakley, M. Klvana, M. Otyepka, Y. Nagata, M. C. J. Wilce and J. Damborský, Biochemistry, 2004, 43, 870–878 CrossRef CAS
.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS
.
- The PyMOL Molecular Graphics System, Version 1.7.4 Schrödinger, LLC.
- S. Doerr, M. J. Harvey, F. Noé and G. De Fabritiis, J. Chem. Theory Comput., 2016, 12, 1845–1852 CrossRef CAS
.
- I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626 RSC
.
- M. J. Harvey and G. De Fabritiis, J. Chem. Theory Comput., 2009, 5, 2371–2377 CrossRef CAS
.
- M. J. Harvey, G. Giupponi and G. D. Fabritiis, J. Chem. Theory Comput., 2009, 5, 1632–1639 CrossRef CAS
.
- K. A. Feenstra, B. Hess and H. J. C. Berendsen, J. Comput. Chem., 1999, 20, 786–798 CrossRef CAS
.
- C. W. Hopkins, S. Le Grand, R. C. Walker and A. E. Roitberg, J. Chem. Theory Comput., 2015, 11, 1864–1874 CrossRef CAS
.
- Y. Naritomi and S. Fuchigami, J. Chem. Phys., 2011, 134, 065101 CrossRef
.
- A. Höskuldsson, J. Chemom., 1988, 2, 211–228 CrossRef
.
-
S. Wold, E. Johansson and M. Cocchi, in 3D QSAR in Drug Design. Theory, Methods, and Applications, ESCOM Science Publisher, Leiden, 1993, pp. 523–550 Search PubMed
.
- S. Wold and W. J. Dunn, J. Chem. Inf. Comput. Sci., 1983, 23, 6–13 CrossRef CAS
.
- S. Wold, Quant. Struct.-Act. Relat., 1991, 10, 191–193 CrossRef CAS
.
- I. Iwasaki, S. Utsumi and T. Ozawa, Bull. Chem. Soc. Jpn., 1952, 25, 226 CrossRef CAS
.
- M. J. Todd and J. Gomez, Anal. Biochem., 2001, 296, 179–187 CrossRef CAS
.
- K. A. Johnson, Z. B. Simpson and T. Blom, Anal. Biochem., 2009, 387, 20–29 CrossRef CAS
.
- K. H. G. Verschueren, F. Seljée, H. J. Rozeboom, K. H. Kalk and B. W. Dijkstra, Nature, 1993, 363, 693–698 CrossRef CAS
.
- L. Biedermannová, Z. Prokop, A. Gora, E. Chovancová, M. Kovács, J. Damborsky and R. C. Wade, J. Biol. Chem., 2012, 287, 29062–29074 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cb00171f |
| ‡ P. K. and A. B. contributed equally |
| This journal is © The Royal Society of Chemistry 2021 |