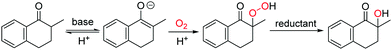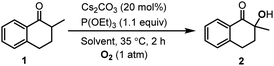Aerobic α-hydroxylation of 2-Me-1-tetralone in 1-alkyl-3-methylimidazolium ionic liquids

Abstract

The aerobic α-hydroxylation of 2-Me-1-tetralone was investigated in imidazol-based ionic liquids (ILs), where reactions in 1-alkyl-3-methylimidazolium tetrafluoroborates were found to generate considerable products. By correlating the conversion at 2 h with viscosity, relative permittivity and the E_T(30) value of ILs, we found that the local polarity in ILs represented by the E_T(30) value or the chemical shift of α-proton at the substrate was the critical factor influencing the reaction rate. Furthermore, two-dimensional nuclear Overhauser effect spectroscopy (2D NOESY) was used to characterize the distribution of 2-Me-1-tetralone in ILs. As a result, the mesoscopic structures in ILs were recommended to have crucial influences on the distribution of the substrate in ILs, and the caused local polarity could affect the activation of 2-Me-1-tetralone. These findings revealed the solvent effects of ILs with different structures on the α-hydroxylation of 2-Me-1-tetralone, and may encourage the explorations of more types of aerobic oxidations in ILs.

---

Introduction

Aerobic oxidation is an important field in industry and chemical science, where the greenest and most abundant dioxygen is used as the oxidant, producing diverse compounds with functional groups.^1,2 In this kind of reactions, solvent effects generally influence the outcome of oxidized products significantly.³ In place of conventional molecular solvents, the application of ionic liquids (ILs) in aerobic oxidations has many advantages, such as their low vapor pressure, low explosion risk, and high stability under oxidative and heated conditions.^4–6 However, because the aerobic oxidations are gas–liquid phase reactions, the high viscosity of ILs could limit the mass transport velocity,⁵ and the solubility of dioxygen was found quite low in ILs.⁷ Therefore, only a few studies reported more efficient aerobic oxidations in ILs than in molecular solvents.^5,6,8 For example, the oxidation of benzylic alcohols has been efficiently carried out in imidazole-based ILs,^9,10 selectively producing aldehydes or ketones. Moreover, the highly selective aerobic oxidation of sulfides to sulfoxides has also been developed in [C₁₂mim]NO₃.¹¹

For reactions in molecular solvents, solvent polarity has been found to significantly affect the reactivity, even giving rise to totally different products in different solvents.³ The polarity of molecular solvents can be similarly represented by relative permittivity as well as various empirical parameters,^3,12 including reaction rate constant, the E_T(30) value, and the hyperfine coupling constant of nitrogen (A_N). Unlike molecular solvents, the polarity of ionic liquids (ILs) is much more complicated, because the different empirical parameters of ILs usually lead to quite different polarity order.^5,13–15 The previous work in our laboratory has modified the classical Onsager reaction field to relate the spectral parameters, the E_T(30) value and A_N, with the relative permittivity of polar molecular solvents and ILs.^16,17 The volume of the reaction field was redefined toward different types of solvents, where the radius of the reaction field for ILs was much smaller than that for molecular solvents, indicating that the local polarity truly affects the electronic structure and reactivity of solutes in ILs. Moreover, the heterogeneous mesoscopic structures have been revealed in ILs with small- and wide-angle X-ray scattering, Raman spectroscopy, mass spectrometry, and molecular dynamics, where there are polar and nonpolar domains.^18–23 The local polarity of ILs may be caused by their stable mesoscopic structures,²⁴ and the distribution of reactants in ILs should be also heterogeneous.²² We previously addressed the restricting effect of solvent aggregations on the selectivity of aerobic oxidation of 2,3,6-trimethylphenol in 3-hexanol,²⁵ so the mesoscopic structures in ILs may also affect the aerobic oxidations.

In this work, the aerobic α-hydroxylation of ketones was selected to explore the efficiency of ILs as a solvent, and to investigate the influencing factors of ILs on the aerobic oxidations. As an important reaction in organic chemistry, the aerobic α-hydroxylation of carbonyl compounds has been efficiently realized in polar solvents like DMSO, catalyzed by strong bases, such as Cs₂O₃, NaOH and KO^tBu.^26–30 Recently, we reported a guanidine catalyzed α-hydroxylation of ketones,³¹ and uncovered the crucial role of double hydrogen bonds. Talking about the mechanism (Fig. 1), the α-proton at ketone was abstracted by the base, then dioxygen reacts with the carbanion to form a peroxide intermediate, which is reduced by the phosphine reductant, and generate the hydroxylated product.³⁰ Due to the ionic reaction route of this reaction, we anticipate that the aerobic α-hydroxylation could be achieved in ILs.

Fig. 1 Reported mechanism for the base-catalyzed aerobic α-hydroxylation of ketones.

Herein, we investigated the aerobic α-hydroxylation of 2-Me-1-tetralone in various 1-alkyl-3-methylimidazolium ILs, catalyzed by Cs₂CO₃. To make out the solvent effects, we correlated the conversion at 2 h with different properties of ILs, and found the essential role of local polarity for reaction rate. Moreover, by means of one- and two-dimensional proton nuclear magnetic resonance (1D and 2D ¹H NMR), as well as theoretical calculations, we suggested the essential role of ILs’ mesoscopic structure and local polarity during the activation of 2-Me-1-tetralone.

Results and discussion

Reaction developments

The hydroxylation of ketones has been realized in molecular solvents, where the highly polar solvent, DMSO, was commonly used to gain high yields. In this work, we developed the method for the hydroxylation of ketones in 1-alkyl-3-methylimidazolium ILs, and the cyclic ketone, 2-methyl-1-tetralone (1), was chosen as the model substrate. Liang et al. have reported that Cs₂CO₃ was an efficient catalyst for the hydroxylation of ketones with 2.0 equiv. P(OEt)₃ as the reductant.²⁶ Therefore, we explored the Cs₂CO₃ catalyzed hydroxylation of 1 in 1-ethyl-3-methylimidazolium tetrafluoroborate ([Emim]BF₄), with P(OEt)₃ as the reductant (Table 1).

Table 1 Effect of different parameters on the aerobic hydroxylation of 1^a

Entry	Cs2CO3	P(OEt)3	Solvent	Conv. [%]	Sel. [%]
a Reaction conditions: 1 (0.5 mmol), Cs2CO3 (0.1–0.5 mmol), P(OEt)3 (0.25–1.0 mmol), solvent (2 mL); the reaction was performed at room temperature under 1 atm dioxygen, and was determined with GC after extraction. The selectivity was calculated by dividing the yield with conversion. b In this reaction, 0.2 mL water was added, and the reaction was performed for 30 h.
1	20 mol%	1.1 equiv.	[Emim]BF4	90.7	83.3
2	50 mol%	1.1 equiv.	[Emim]BF4	97.3	88.7
3	1 equiv.	1.1 equiv.	[Emim]BF4	99.6	84.0
4	50 mol%	0.5 equiv.	[Emim]BF4	81.5	73.6
5	50 mol%	2.0 equiv.	[Emim]BF4	99.4	84.6
6	50 mol%	1.1 equiv.	[Emim]BF4	98.4	86.1
7^b	50 mol%	1.1 equiv.	[Emim]BF4	27.6	30.3
8	50 mol%	1.1 equiv.	[Bmim]BF4	99.4	93.6
9	50 mol%	1.1 equiv.	[Bmim]PF6	98.0	82.5

---

The reaction in [Emim]BF₄ was fast enough to be terminated within 3 h. The conversion and selectivity were determined using gas chromatography (GC). Increasing the usage of Cs₂CO₃ from 20 to 100 mol%, we found that the selectivity was not sensitive to the catalyst loading. However, the selectivity decreased with the decrease of the reductant, P(OEt)₃. In order to exclude the influence of possibly contained water in [Emim]BF₄,⁵ we added 0.2 mL water into the reaction, then the reaction rate and the selectivity were both reduced significantly (Table 1, entry 7). The results in [Emim]BF₄ encouraged us to investigate this reaction in other ILs. In place of [Emim]BF₄, the reactions in 1-butyl-3-methylimidazolium tetrafluoroborate ([Bmim]BF₄) and 1-butyl-3-methylimidazolium hexafluorophosphate ([Bmim]PF₆) also generate 2 in a considerable yield (Table 1, entries 8 and 9). Following this, in order to have a deep insight on reactions in ILs, we studied the solvent effect.

Solvent effects in aerobic hydroxylation

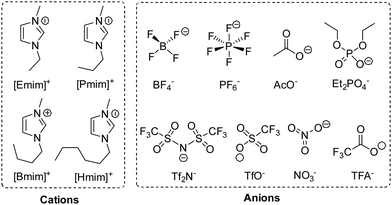
To investigate the effect of a solvent, we performed this reaction in various 1-alkyl-3-methylimidazolium ILs, whose structures and abbreviations are given in Fig. 2. To exclude the influence of solubility, a 20 mol% catalyst was used, and the reaction was performed at 35 °C. The solvent effect was studied via comparing reaction rate, which was represented by the conversion of 1 at 2 h. Moreover, to make sure the intrinsic reaction rate was determined rather than the rate of diffusion, the stirring rate and the rotor size were both increased to obtain an unincremented reaction rate. After extraction, the conversion and selectivity were obtained in use of GC.

Fig. 2 Structure and abbreviation of the cations and anions of ILS used in this work.

As shown in Table 2, the reactions in different 1-alkyl-3-methylimidazolium ILs showed quite different rates, with apparent differences in conversion at 2 h, and the higher conversion was also along with a higher selectivity for 2. Having the same cation, for example, the oxidations in [Emim]TFA, [Emim]AcO and [Emim]Et₂PO₄ were much slower than that in [Emim]BF₄ (entries 5–7 vs. entry 1). Moreover, with the same BF₄⁻ anion, the increasing length of the carbon chain at imidazolium cations leads to decreasing reaction rate (entries 1–4). Being aware of the different reaction rate, we investigated the solvent effects causing different reactivities in different ILs.

Table 2 The effect of solvents on the aerobic hydroxylation of 1 in ILs^a

Entry	Ionic liquid	Label	δα–H (ppm)	Conv. [%]	Sel. [%]
a Reaction conditions: 1 (0.5 mmol), Cs2CO3 (0.1 mmol), P(OEt)3 (0.55 mmol), solvent (2 mL); the reaction was performed at 35 °C under 1 atm dioxygen. The selectivity was calculated by dividing the yield with conversion.
1	[Emim]BF4	EB	2.347	87.4	75.2
2	[Pmim]BF4	PB	2.387	71.4	70.3
3	[Bmim]BF4	BB	2.428	80.4	70.2
4	[Hmim]BF4	HB	2.474	40.2	56.2
5	[Emim]TFA	EAF	2.486	10.3	Trace
6	[Emim]AcO	EA	2.592	14.2	13.8
7	[Emim]Et2PO4	EPO	2.601	8.3	Trace
8	[Pmim]Tf2N	PN	2.533	17.6	1.0
9	[Bmim]Tf2N	BN	2.540	14.7	3.2
10	[Bmim]TfO	BSO	2.521	12.7	8.9
11	[Bmim]PF6	BP	2.423	52.1	77.9
12	[Bmim]NO3	BNO	2.617	11.2	1.1

---

Factors causing solvent effects

To learn the reason for different reactivities in different ILs, we tried to relate the conversion of 1 at 2 h with the properties of ILs. Because this reaction is a gas–liquid phase reaction, the viscosity of the solvent may influence the diffusion process of dioxygen in liquid phase. Though we have increased stirring rate and rotor size to exclude the influence of diffusion, in this case, we correlated the conversion of 1 at 2 h with the viscosity of ILs obtained from references (Fig. 3a).^32,33 As expected, very poor relationship was observed, indicating that viscosity is not an important factor to affect this reaction.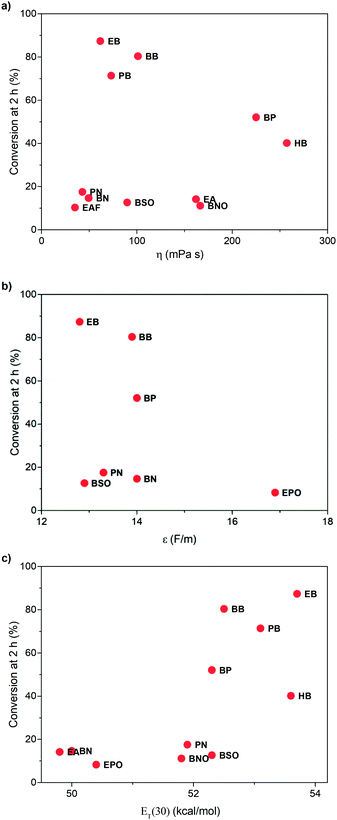

Fig. 3 Relationship between the conversion of 1 at 2 h and the viscosity (a), relative permittivity (b), and the E_T(30) value (c) of ILs.

Afterwards, we evaluated the relative permittivity, which is generally used to represent the polarity of molecular solvents. It has been revealed that the aerobic hydroxylation of ketone went through an ionic mechanism, involving anion intermediates.³⁰ Thus, the high polar solvent should benefit the hydroxylation. We used the relative permittivity data from the work by Huang et al.,³⁴ detected by the frequency-dependent dielectric dispersion curve. As illustrated in Fig. 3b, the conversion of 1 at 2 h in ILs was poorly correlated with the relative permittivity data.

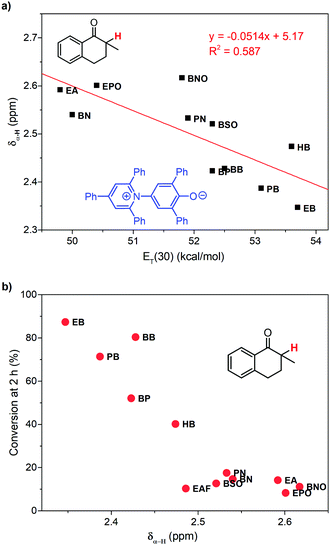
Our previous work has revealed that relative permittivity is not a good indicator of the polarity of ILs.¹⁷ Instead, the E_T(30) value is widely used to represent the polarity of ILs, which is the molar electronic transition energy of the longest-wavelength intramolecular CT absorption band of betaine dye no. 30.³⁵ Reichardt et al. have obtained E_T(30) values of abundant ILs.³⁶ Using these data, we found the E_T(30) value a better parameter to correlate with the reaction rate (Fig. 3c), and higher E_T(30) values were associated with faster conversion of 1. The E_T(30) values in 1-alkyl-3-methylimidazolium ILs were higher than those in molecular solvents, and this may give rise to their excellent performance as the solvent for aerobic hydroxylation. Next, we focused on how the E_T(30) value presented polarity affects the selectivity as well as the reaction rate.

Mesoscopic structure of ILs and its effect on the reaction

The reactivity of hydroxylation in ILs may be mainly influenced by the mesoscopic structure of solvents. The relative permittivities of 1-alkyl-3-methylimidazolium ILs are much lower than that of DMSO (46.7), but their E_T(30) values are larger. The existence of the mesoscopic structure in ILs should be a possible interpretation. Nanostructural organization has been observed in 1-alkyl-3-methylimidazolium ILs by Lopes and Pádua using molecular simulation,^18,20 in which the ILs are constructed with charged domains and nonpolar domains. Consequently, different types of solutes should distribute in different domains in ILs, and the polarity perceived by the solutes should be a local property other than a global property. As an indicator of local polarity of ILs, the E_T(30) value was calculated according to the visible absorption of negatively solvatochromic pyridinium N-phenolate betaine dyes.³⁵ Because of the ionic mechanism, it was reasonable that the reaction rate was more relevant with E_T(30) values, rather than the relative permittivities, which represented the global polarity.

Considering the effect of local polarity on the reaction, we correlated the chemical shift of α-proton at 1 (δ_α-H) with the E_T(30) value in 1-alkyl-3-methylimidazolium ILs (Fig. 4a), and a negative correlation was revealed. Therefore, the carbonyl group of ketones and the hydroxyl anion of betaine dye no. 30 should reflect the same local polarity in ILs, which possibly is of the charged domain. As to the negative relationship, the more polar local surroundings should result in more electron density, transferring from the benzyl part of 1 to the carbonyl part, leading to the upfield peak shift of the α-proton. As a result, the conversion of 1 at 2 h was in good correlation with the δ_α-H (Fig. 4b), which should be a better indicator of the local polarity perceived by the reactive site of 1 in ILs. Thus, the higher local polarity around the substrate leads to the faster conversion of 1 to the ionic intermediate.

Fig. 4 (a) Correlated chemical shift of the α-proton in 1 with the E_T(30) value in 1-alkyl-3-methylimidazolium ILs. (b) The relationship between the conversion of 1 at 2 h and the chemical shift of the α-proton in 1.

We suggested above that the carbonyl group distributed close to the imidazole cation in ILs. As an evidence, the chemical shift of the α-proton at 1 was found well related with that of the methyl group proton at imidazole cations (Fig. 5a). Distributing in the same region, the methyl group in the imidazole cation has the similar response to the local polarity as the α-proton at 1. Further ¹H NMR characterization was also conducted to confirm the neighboring carbonyl group and the imidazole cation. As two protons are spatially close, the two-dimensional nuclear Overhauser effect spectroscopy (2D NOESY) could detect the dipolar cross-relaxation. Therefore, we investigated the NOESY spectrum of the solution of 1 in [Emim]BF₄ (Fig. 5b), and the clear correlation between the methyl protons in 1 (H_b) and the N-methyl protons in [Emim] (H_a) was observed. Consequently, the spatially neighbouring unit between the carbonyl group at 1 and the imidazole cation was confirmed.

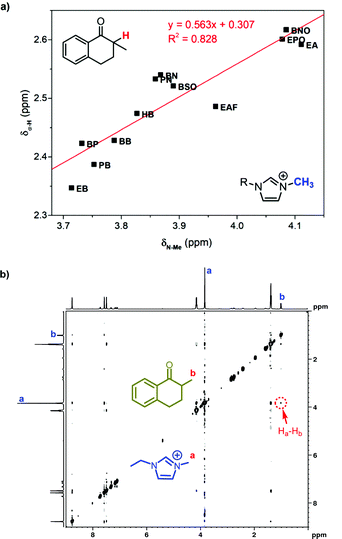Fig. 5 (a) Correlated chemical shift of the α-proton in 1 with that of the methyl group in 1-alkyl-3-methylimidazolium ILs. (b) The H,H-NOESY spectrum of 1 mol L⁻¹1 in [Emim]BF₄.

Effect of local polarity on the activation of 1

According to the discussions above, the oxidation of 1 in ILs with higher local polarity was fastened. The local polarity was caused by the special mesoscopic structures in ILs, and the dissolved 1 should distribute at the polar regions, where the local polarity could be much larger than the global polarity represented by relative permittivity. The activation of 1 by proton abstraction mainly determined the reaction rate. Therefore, we proposed that higher local polarity should benefit the proton abstraction from 1 to generate the carbanion intermediate, leading to faster conversion of 1.

As a support of our proposal, the Gibbs free energy change for proton abstraction of 1 was calculated using the Onsager model^37–39 to simplistically evaluate the effect of local polarity. The dielectric constant was set from 10 to 60, and the solute radius was obtained by a volume calculation. The calculated differences of Gibbs free energy change are shown in Fig. 6. The proton abstraction was obviously preferred at a larger dielectric constant, due to the smaller Gibbs free energy change.

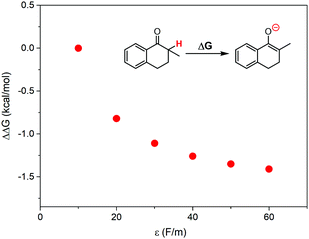Fig. 6 Calculated differences of Gibbs free energy change for proton abstraction of 1 at various dielectric constants, where the Onsager model was used as the solvent reaction field.

Conclusions

In summary, we uncovered a gas–liquid phase reaction, the aerobic hydroxylation of 2-methyl-1-tetralone (1) in 1-alkyl-3-methylimidazolium ILs, where the considerable yield of a hydroxylated product was obtained. While correlating the conversion of 1 at 2 h with the properties of ILs, we revealed that the local polarity represented by the E_T(30) value or δ_α-H of 1 was a critical factor to affect the reactivity, rather than the viscosity or the relative permittivity. To explain the effect of local polarity, the mesoscopic structure of ILs was introduced to restrict the distribution of 1, whose carbonyl group was suggested to neighbor the imidazole cations by ¹H NMR and NOESY spectra.

This work revealed that imidazole-based ILs were efficient solvents for aerobic reactions, while gas–liquid phase reactions were generally considered hardly executable in ILs with high viscosity. With these findings, more applications of ILs for aerobic oxidations are predictable. Moreover, the mesoscopic structure of ILs was found crucial for the reaction rate, shedding light on the quite different performance of ILs with different structures.

Methodology

General methods

Unless otherwise stated, all reagents were purchased from commercial sources without further treatment. GC-MS spectra were recorded on a Shimadzu GC/MS-QP2010 system (Shimadzu, Germany). Gas chromatography with a flame ionization detector (GC-FID) was carried out on GC-2014 (Shimadzu, Japan). ¹H NMR, ¹³C NMR and NOESY spectra were recorded on Bruker AVANCE III 500.

Procedures for aerobic α-hydroxylation

To a 25 mL Schlenk tube equipped the magnetic bar, Cs₂CO₃ (33 mg, 0.1 mmol), 1 (80 mg, 0.5 mmol) and P(OEt)₃ (93 mg, 0.55mmol) were added in succession, and solvents (2.0 mL) at last. After mixing and vacuation, the suspension was charged with 1 atm O₂ and linked to a 20 mL injector filled with O₂. And then the suspension was stirred at 35 °C. After the reaction, the solution was quenched with 10 mL water and diluted with ethyl acetate (4 mL). Then 1.0 mL ethyl acetate solution of phenylbenzene was added as an inner standard. Washed by saturated brine (20 mL), the solution was extracted with ethyl acetate (10 mL × 3). Then the organic phase was characterized with GC-FID or GC-MS.

NMR characterizations

The solution of 0.5 mmol 1 with 2.0 mL solvent was stirred in room temperature for 1 hour, then 0.3 mL solution was put into a 5 mm NMR tube. Following this, a sealed 3 mm NMR tube charged with CDCl₃ was put in the 5 mm NMR tube, and the ¹H NMR spectrum was obtained at room temperature. For NOESY detection, 1 mmol 1 was mixed with 2.0 mL [Emim]BF₄.

Theoretical methods

DFT calculations were carried out using Gaussian 09 D.01.⁴⁰ The geometries were fully optimized using the B3LYP^41,42/6-31+G(d,p)^43–46 method. At the same level, the volumes were calculated, and frequency analyses were performed to confirm the minimum structure. The Onsager model^37–39 was applied to calculate the solvent effct, and the dielectric constant was set from 10 to 60.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Fundamental Research Funds for the Central Universities, and the National Natural Science Foundation of China (No. 22073081).

Notes and references

1. H. Sterckx, B. Morel and B. U. W. Maes, Angew. Chem., Int. Ed., 2019, 58, 7946–7970.
2. A. Gavriilidis, A. Constantinou, K. Hellgardt, K. K. M. Hii, G. J. Hutchings, G. L. Brett, S. Kuhn and S. P. Marsden, React. Chem. Eng., 2016, 1, 595–612.
3. C. Reichardt and T. Welton, Solvents and solvent effects in organic chemistry, John Wiley & Sons, 2011.
4. J. Muzart, Adv. Synth. Catal., 2006, 348, 275–295.
5. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
6. C. Dai, J. Zhang, C. Huang and Z. Lei, Chem. Rev., 2017, 117, 6929–6983.
7. J. L. Anthony, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2002, 106, 7315–7320.
8. W. Guan, C. Wang, X. Yun, X. Hu, Y. Wang and H. Li, Catal. Commun., 2008, 9, 1979–1981.
9. N. Jiang and A. J. Ragauskas, J. Org. Chem., 2007, 72, 7030–7033.
10. Y. Oda, K. Hirano, T. Satoh, S. Kuwabata and M. Miura, Tetrahedron Lett., 2011, 52, 5392–5394.
11. Y.-L. Hu, D. Fang and R. Xing, RSC Adv., 2014, 4, 51140–51145.
12. A. R. Katritzky, D. C. Fara, H. Yang, K. Tämm, T. Tamm and M. Karelson, Chem. Rev., 2004, 104, 175–198.
13. X. Wang, K. Chen, J. Yao and H. Li, Sci. China: Chem., 2016, 59, 517–525.
14. O. Zech, J. Hunger, J. R. Sangoro, C. Iacob, F. Kremer, W. Kunz and R. Buchner, Phys. Chem. Chem. Phys., 2010, 12, 14341–14350.
15. A. Pandey, R. Rai, M. Pal and S. Pandey, Phys. Chem. Chem. Phys., 2014, 16, 1559–1568.
16. X. Wang, R. Dao, J. Yao, D. Peng and H. Li, ChemPhysChem, 2017, 18, 763–771.
17. X. Wang, S. Zhang, J. Yao and H. Li, Ind. Eng. Chem. Res., 2019, 58, 7352–7361.
18. J. N. A. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335.
19. K. Iwata, H. Okajima, S. Saha and H.-O. Hamaguchi, Acc. Chem. Res., 2007, 40, 1174–1181.
20. A. S. Pensado, M. F. Costa Gomes, J. N. Canongia Lopes, P. Malfreyt and A. A. Padua, Phys. Chem. Chem. Phys., 2011, 13, 13518–13526.
21. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
22. Y. L. Wang, B. Li, S. Sarman, F. Mocci, Z. Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877.
23. F. Endres and Phys Chem, Chem. Phys., 2010, 12, 1648.
24. K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929.
25. Y. Wang, G. Wang, J. Yao and H. Li, ACS Catal., 2019, 9, 6588–6595.
26. Y. F. Liang and N. Jiao, Angew. Chem., Int. Ed., 2014, 53, 548–552.
27. S.-B. D. Sim, M. Wang and Y. Zhao, ACS Catal., 2015, 5, 3609–3612.
28. A. S. Tsang, A. Kapat and F. Schoenebeck, J. Am. Chem. Soc., 2016, 138, 518–526.
29. M. B. Chaudhari, Y. Sutar, S. Malpathak, A. Hazra and B. Gnanaprakasam, Org. Lett., 2017, 19, 3628–3631.
30. Y. F. Liang and N. Jiao, Acc. Chem. Res., 2017, 50, 1640–1653.
31. Y. Wang, R. Lu, J. Yao and H. Li, Angew. Chem., Int. Ed., 2021 DOI:10.1002/anie.202014478.
32. K. Tochigi and H. Yamamoto, J. Phys. Chem. C, 2007, 111, 15989–15994.
33. H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459.
34. M.-M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, J. Chem. Eng. Data, 2011, 56, 1494–1499.
35. V. G. Machado, R. I. Stock and C. Reichardt, Chem. Rev., 2014, 114, 10429–10475.
36. C. Reichardt, Green Chem., 2005, 7, 339–351.
37. L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493.
38. M. W. Wong, M. J. Frisch and K. B. Wiberg, J. Am. Chem. Soc., 1991, 113, 4776–4782.
39. M. W. Wong, K. B. Wiberg and M. Frisch, J. Chem. Phys., 1991, 95, 8991–8998.
40. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013.
41. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
42. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
43. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
44. W. J. Hehre, J. Chem. Phys., 1972, 56, 2257.
45. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
46. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265.

---

Footnotes

† Electronic supplementary information (ESI) available: Characterization spectra, property data, and Cartesian coordinates. See DOI: 10.1039/d0cp06047j

‡ These authors contributed equally to this work.

---