Selection rule for Raman spectra of two-dimensional materials using circularly-polarized vortex light
Received
19th May 2021
, Accepted 13th July 2021
First published on 14th July 2021
Abstract
Conservation of spin and orbital angular momenta of circularly-polarized vortex light is discussed for Raman spectra of two-dimensional materials. We first show the selection rule for optical absorption of two-dimensional materials as a function of the spin and orbital angular momentum of incident vortex light. In the case of two-dimensional materials, the Raman tensor for the incident vortex light does not change the symmetry of the phonon mode. Furthermore, the Raman active modes are classified by either “helicity-changing” or “helicity-conserved” Raman modes, in which the scattered photon of circularly polarized light either changes or does not change the helicity of the light, respectively. We show tables of selection rules for the Raman active modes of two-dimensional materials with 2, 3, 4, and 6 rotational symmetry for vortex light.
1 Introduction
Vortex light is an electro-magnetic wave (EM) with an orbital angular momentum. Vortex light has received a lot of attention due to its potential applications in areas such as quantum information protocols and optical communications.1,2 In 1966, Kogelnik and Li derived the Laguerre–Gaussian mode of the vortex light by solving the paraxial Helmholtz equation in which the amplitude of the EM changes slowly compared with the wavelength as the wave propagates.3 The amplitude of the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) th Laguerre-Gaussian mode has an azimuthal phase shift term, exp(i
th Laguerre-Gaussian mode has an azimuthal phase shift term, exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ), where φ is the azimuthal angle in the cylindrical coordinate and the integer
φ), where φ is the azimuthal angle in the cylindrical coordinate and the integer ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is called the topological charge. The corresponding vortex light has an orbital angular momentum
is called the topological charge. The corresponding vortex light has an orbital angular momentum ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ħ.4 In this paper, we discuss the conservation law of angular momentum in the Raman scattering of two-dimensional (2D) materials.
ħ.4 In this paper, we discuss the conservation law of angular momentum in the Raman scattering of two-dimensional (2D) materials.
For vortex light, we have another freedom of spin-angular-momentum ±ħ depending on the left-handed (+ħ) or right-handed (−ħ) circularly polarized light, or the helicity of the photon (±1), which was observed experimentally by Beth in 1936.5 Since the spin and orbital angular momenta are related to the amplitude and the phase of EM, respectively, the spin and orbital angular momenta of light are independent of each other. In previous work, we have shown the conservation law of spin-angular-momentum of circularly polarized light in the Raman spectroscopy for 2D materials that have rotational symmetry.6 We have shown that the inelastically scattered light either changes or conserves the helicity of the incident photon, which depends on the Raman-active phonon mode and the rotational symmetry of 2D materials. The prediction of the helicity-changing Raman mode is consistent with the analysis of the Raman tensor and the Raman measurement using circularly polarized light for graphene (6-fold),7 TaP or LaAlSi (4-fold),8,9 transition-metal dichalcogenides (TMDs) (3-fold),10 and ReS2 (2-fold)11 2D materials. In this paper, we consider the angular momentum of the vortex light for discussing the selection rule for Raman active modes of 2D materials. Although we do not evaluate the Raman intensity, we discuss the selection rule for Raman spectra by using the incident vortex light.
Raman spectroscopy has been frequently used as a non-contact characterization technique for low-dimensional materials such as carbon nanotubes and 2D materials under ambient conditions, that is, room temperature and atmospheric pressure.12,13 Chen et al. observed Raman spectra of 2D MoS2 by using circularly-polarized light.10 They showed that the scattered light by the in-plane E′-symmetry phonon changes the helicity of the incident circularly-polarized light as is known as helicity-changing Raman spectra, while the scattered light by the out-of-plane 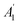 -symmetry phonon does not change the helicity (helicity-conserved Raman spectra). Occurrence of the helicity-changing Raman spectra is simply understood by the Raman tensor for a given phonon mode using the Jones vector of circularly-polarized light.6
-symmetry phonon does not change the helicity (helicity-conserved Raman spectra). Occurrence of the helicity-changing Raman spectra is simply understood by the Raman tensor for a given phonon mode using the Jones vector of circularly-polarized light.6
Tatsumi et al. have discussed the helicity-changing Raman spectra using the conservation law of angular momentum in the Raman scattering process.6 They have predicted several helicity-changing Raman active modes of 2D materials with 2, 3, 4, or 6 fold rotational symmetry around the axis perpendicular to the 2D material, which is consistent with the calculated resonant-Raman spectra14 and the experiments.7,10 In the first-order Raman process, we have three Raman sub-processes (see Fig. 1): (1) optical absorption of an incident photon, (2) a phonon emission by the photo-excited electron, and (3) a photon emission as the inelastic-scattered light. Each sub-process is given by the matrix elements of electron–photon (1, 3) and electron–phonon (2) interactions. When a 2D material has an N-fold rotational symmetry and when the ν-th phonon has an Nν-fold rotational symmetry, the electron–photon and electron–phonon matrix elements have the optical selection rules by the N-fold and Nν-fold rotational symmetry, respectively, whose products give the conservation law of angular momentum of the materials.6 This concept can be extended to the angular momentum of the vortex light, which is the motivation of the present paper.
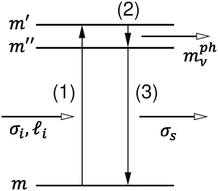 |
| | Fig. 1 Illustration of the Raman process. The first-order Raman process for emitting a phonon consists of (1) optical absorption from the m to m′ electronic state by electron–photon interaction, (2) the photo-excited electron emits a phonon by the electron–phonon interaction with transition from the m′ to m′′ state, and (3) the photo-excited electron recombines with a hole by emitting the scattered photon by the electron–phonon interaction with transition from the m′′ to m state.12,18 | |
Ishii et al.15 discussed the optical selection rule for optical absorption of the vortex light for monolayer MoS2 with a 3-fold rotational symmetry, in which they showed that the orbital angular momentum gives the valley-dependent selection rule at the K and K′ points in the hexagonal Brillouin zone. Li et al.16 discussed the Raman scattering of 3D cubic material using the vortex light in which they assumed that orbital angular momentum is not coupled with the materials but that the Raman tensor changed the form as a function of the orbital angular momentum which results in the appearance of a new Raman-active mode as a function of orbital angular momentum in the case of 3D materials. Here we explain that the shape of the Raman tensor does not change for vortex light in the case of 2D materials.
The organization of the paper is as follows. In Section 2, we discuss how to obtain the conservation of angular momentum. In Section 3, we show the selection rules of electron–photon and electron–phonon matrix elements in the Raman scattering. In Section 4, we calculate the conservation law in Raman scattering for two-dimensional materials with 2, 3, 4, and 6 rotational symmetry. In Section 5, the main results of the conservation law are tabulated, followed by discussion and summary.
2 Conservation law of angular momentum
Here, we consider a 2D material that has N-fold rotational symmetry around the z axis perpendicular to the material in the xy plane. Hereafter, we consider the case where the incident and scattered light propagates in the directions of −z and +z, respectively. Let us define the rotation operator around the z axis with an angle α = 2π/N as follows:| | 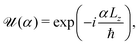 | (1) |
where Lz ≡ −iħ∂/∂φ is the z component of the angular momentum operator in a cylindrical coordinate. Since the Hamiltonian ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) is commutable with
is commutable with ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), [
(α), [![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ,
, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)] = 0, any wavefunction of
(α)] = 0, any wavefunction of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , |m〉, is also an eigenfunction of
, |m〉, is also an eigenfunction of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), that is,
(α), that is, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = C|m〉. Using the facts that {
(α)|m〉 = C|m〉. Using the facts that {![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)}N is a 2π rotation and that CN = 1, the eigenvalues of
(α)}N is a 2π rotation and that CN = 1, the eigenvalues of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) are expressed by,
(α) are expressed by,| | ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = exp(−imα)|m〉, (m = 0, 1, 2, …, N − 1) (α)|m〉 = exp(−imα)|m〉, (m = 0, 1, 2, …, N − 1) | (2) |
When we consider the cylindrical coordinate, the eigenfunction of Lz is given by exp(imφ) whose eigenvalue is mħ. When we multiply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) by exp(imφ), we get
(α) by exp(imφ), we get| | 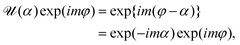 | (3) |
which means that exp(imφ) is an eigenfunction of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for the eigenvalue of exp(−imα). Thus it is reasonable for us to call mħ a pseudo angular momentum though the definition is valid only for a discrete rotational angle.
(α) for the eigenvalue of exp(−imα). Thus it is reasonable for us to call mħ a pseudo angular momentum though the definition is valid only for a discrete rotational angle.
Let us consider how to rotate a matrix element, 〈m′|![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |m〉 by
|m〉 by ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for an interaction operator
(α) for an interaction operator 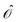 which has an N′-fold rotational symmetry. In general, the value of N′ is smaller than N. However, if
which has an N′-fold rotational symmetry. In general, the value of N′ is smaller than N. However, if ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) does not depend on φ, N′ becomes infinite. In this case, we can select as N′ = N. When we operate
does not depend on φ, N′ becomes infinite. In this case, we can select as N′ = N. When we operate ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) on
(α) on ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) , the variable φ in
, the variable φ in ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is changed to φ + α. If the
is changed to φ + α. If the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) has a φ dependence as exp(imOφ), we obtain
has a φ dependence as exp(imOφ), we obtain
| | ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ + α) = exp(−imOα) (φ + α) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ), (φ), | (4) |
where an integer
mO is taken from
mO = 0, 1, …,
N′ − 1 which satisfies
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
φ + 2π) =
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
φ).
When we apply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) to
(α) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ), we get
(φ), we get
| | ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) (α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ) = (φ) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ + α) (φ + α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (φ) = exp(−imOα) (φ) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ) (φ)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), (α), | (5) |
from which we obtain the unitary transformation of
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
φ) as follows
| | ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) (α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) = exp(−imOα) −1(α) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) . . | (6) |
Using
eqn (2) and (6), when we rotate the matrix element, 〈
m′|
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
|
m〉, we get
| | 〈m′|![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) −1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) (α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) −1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = exp{i(−m + m′ − mO)α}〈m′| (α)|m〉 = exp{i(−m + m′ − mO)α}〈m′|![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |m〉. |m〉. | (7) |
It is noted that
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
generally has a lower symmetry than
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
and that
α in
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
(
α) should be selected for the
N′-fold rotational symmetry. Here we assume that
N′ is a divisor of
N. If the matrix elements of
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
have an
N′-fold rotational symmetry, the exp
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i
i(
m −
m′ +
mO)
α should be unity, in which
m and
m′ (or
mO) are integers from 0 to
N′ − 1. Otherwise, by integration of the matrix elements over the
φ from 0 to 2π, the integration would give zero. From this fact, we get the conservation law of angular momentum as follows
where
p is any integer.
Eqn (8) is understood by the conservation law of angular momentum for the operator
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
.
In the next section we consider the selection rule for electron–photon and electron–phonon matrix elements using eqn (8).
3 Selection rule of the matrix element
3.1 Electron–photon matrix element
The electron–photon matrix element ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt is given by time-dependent perturbation theory as follows17
opt is given by time-dependent perturbation theory as follows17| | 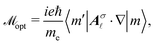 | (9) |
where me is the mass of an electron and Aσ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the vector potential of the light. For the Laguerre–Gaussian mode of the vortex light, the vector potential in the cylindrical coordinate is given by15
is the vector potential of the light. For the Laguerre–Gaussian mode of the vortex light, the vector potential in the cylindrical coordinate is given by15| | 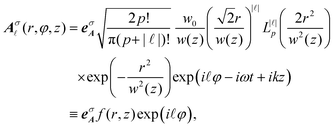 | (10) |
where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , p, z, r, L|
, p, z, r, L|![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |p, w0, and w(z) denote, respectively, orbital angular momentum, the radial index, propagation direction (z) and radial direction (r) in the cylindrical coordinate, the Laguerre polynomial function, the beam waist and the beam width function. eσA is the unit vector for the amplitude of light, which is known as the Jones vector,
|p, w0, and w(z) denote, respectively, orbital angular momentum, the radial index, propagation direction (z) and radial direction (r) in the cylindrical coordinate, the Laguerre polynomial function, the beam waist and the beam width function. eσA is the unit vector for the amplitude of light, which is known as the Jones vector,| | 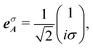 | (11) |
where σ = +1 and σ = −1 denote the spin-angular momentum of the light, and correspond to the left-handed and right-handed circularly polarized light (LCP and RCP), respectively. The function f(r, z) in eqn (10) is defined as the remaining part of Aσ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) except for the factors of eσA and exp(i
except for the factors of eσA and exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ). We will use the fact that the f(r, z) does not contain φ.
φ). We will use the fact that the f(r, z) does not contain φ.
The optical transition is allowed when ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt ≠ 0, while the transition is forbidden when
opt ≠ 0, while the transition is forbidden when ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt = 0. When we multiply
opt = 0. When we multiply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α)
−1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) in eqn (9), we obtain the following expression, by putting eqn (10) into eqn (9).
(α) in eqn (9), we obtain the following expression, by putting eqn (10) into eqn (9).
| | 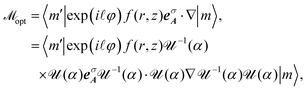 | (12) |
where ∇ corresponds to
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
in
eqn (7). Since
f(
r,
z) does not contain
φ, and since
eσA is commutable
6 with
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
(
α), that is,
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
(
α)
eσA![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1
−1(
α) =
eσA, the left-most
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1
−1(
α) in
eqn (12) applies to the product of the functions, 〈
m′|exp(
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ
φ) from the right as follows
| | 〈m′|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ) φ)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) = exp{i(m′ − −1(α) = exp{i(m′ − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )α}〈m′| )α}〈m′|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ). φ). | (13) |
In
eqn (13), we use
eqn (3) for exp(
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ
φ) as follows,
| | ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) (α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ) = exp(−i φ) = exp(−i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α) α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ). φ). | (14) |
For the inner product of
eσA·{
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
(
α)∇
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1
−1(
α)}, we get as follows,
6| | 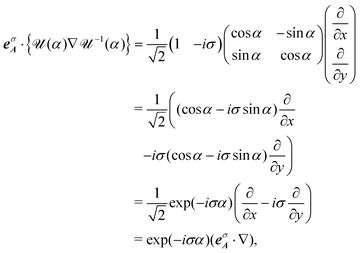 | (15) |
where we use the relation that exp(−
iσα) = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α
α −
iσ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α
α, for
σ = ±1.
Using eqn (10), (12), (13) and (15), eqn (12) becomes
| | ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt = exp{i(m′ − m − σ − opt = exp{i(m′ − m − σ − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )α}〈m′|Aσ )α}〈m′|Aσ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ·∇|m〉. ·∇|m〉. | (16) |
Since
eqn (9) and (12) are identical, we get the following selection rule for the vortex light from
eqn (16)| | m′ − m − σ − ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = Np, = Np, | (17) |
where
p is any integer. In particular, if
eqn (17) does not satisfy,
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt
opt should be zero. It is important to note that both
σ and
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
can be either a positive or negative integer. Although we have the expression of −
σ −
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
, we have any combination of
σ and
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
with a positive or negative integer.
3.2 Electron–phonon matrix element
The electron–phonon matrix element ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep is given by
ep is given by| | ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep = 〈m′′|Aν·∇V|m′〉, ep = 〈m′′|Aν·∇V|m′〉, | (18) |
where Aν and ∇V denote, respectively, the amplitude of the ν-th phonon mode and deformation potential. Tatsumi et al. give the selection rule for ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep,6 which is common for the Raman spectra for non-vortex light as follows.
ep,6 which is common for the Raman spectra for non-vortex light as follows.| | | m′′ − m′ = −mphν + Nνp2, | (19) |
where p2 is any integer, mphν is an angular momentum of the ν-th phonon, and Nν is an integer for the Nν-th rotational symmetry for the ν-th phonon. For example, in a TMD which has a three-fold rotational symmetry and thus N = 3, Tatsumi et al. gave Nν = N = 3 or Nν = 1 for the  and the E′ Raman active modes, respectively.6
and the E′ Raman active modes, respectively.6
It is important to comment on the treatment of the Nν. A phonon eigen-mode at the Γ point in the Brillouin zone belongs to the irreducible representation of the point group of the unit cell. For the Raman active modes, the phonon oscillation behaves as a quadratic function for the irreducible representation such as x2 − y2 or xy from which we can make the Raman tensor. The linear combination of these functions can be an eigenfunction of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for N (not Nν) rotational symmetry. For example, the E′ mode (x2 − y2, xy) of TMD, which was given by Nν = 1 and mphν = 0,6 can be expressed by Nν = N = 3 and mphν = ±2. In fact, when we multiply
(α) for N (not Nν) rotational symmetry. For example, the E′ mode (x2 − y2, xy) of TMD, which was given by Nν = 1 and mphν = 0,6 can be expressed by Nν = N = 3 and mphν = ±2. In fact, when we multiply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) with α = 2π/3 by (x2 − y2 ± i2xy), we get
(α) with α = 2π/3 by (x2 − y2 ± i2xy), we get
| | 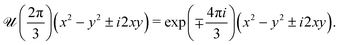 | (20) |
Eqn (20) means that the phonon amplitude for the
E′ mode is expressed by the linear combination of eigenstate of
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
(
α) with
mphν = ±2. Since we have several possible
mphν for one phonon mode, we need to consider
eqn (19) for each value of
mphν.
We think that the new expression of mphν is reasonable for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i ≠ 0, though both expressions give almost the same results for
i ≠ 0, though both expressions give almost the same results for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0. In order to avoid any confusion between the notations by Tatsumi et al. and those in the present paper, we keep using eqn (19) but hereafter we set Nν = N and we use the new value of mphν.
i = 0. In order to avoid any confusion between the notations by Tatsumi et al. and those in the present paper, we keep using eqn (19) but hereafter we set Nν = N and we use the new value of mphν.
3.3 Raman process
In Fig. 1, we illustrate the first-order Raman process for emitting a phonon which consists of (1) optical absorption from the m to m′ electronic states by the electron–photon interaction, (2) the photo-excited electron emits a phonon by the electron–phonon interaction with transition from the m′ to m′′ state, and (3) the photo-excited electron recombines with a hole by emitting the scattered photon by the electro–phonon interaction with transition from the m′′ to m state.12,18 For (1) and (2), the optical selection rules of eqn (17) and (19) are applied, respectively, to get the selection rule for each sub-process.
For the absorption sub-process (1), we get the conservation rule from eqn (17)
| | m′ − m = σi + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i + Np1, (p1 = 0, ±1, ±2,…), i + Np1, (p1 = 0, ±1, ±2,…), | (21) |
where
σi and
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i denote the spin and orbital quantum numbers of the incident light, respectively. For the phonon emission sub-process (2), we get the conservation rule from
eqn (19)| | | m′′ − m′ = −mphν + Nνp2, (p2 = 0, ±1, ±2,…). | (22) |
For the optical transition to the bottom of the conduction band, since the
m′′ state is a virtual state that is given by a linear combination of excited states in perturbation theory, we usually approximate as
m′′ =
m′. However, it is noted that we can take many possible values of
m′′ in
eqn (22) in the selection rule, since the intermediate state for
m′′ is a virtual state. For the scattered photon emission sub-process (3), the matrix element is the complex conjugate of that for absorption. Then, we get the conservation rule without
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
from
eqn (17) as follows
| | | m − m′′ = −σs + Np3, (p3 = 0, ±1, ±2,…), | (23) |
where
σs denotes the spin quantum numbers of the scattered light. Here, we assume that the scattered light does not have orbital angular momentum. The assumption is reasonable since the generation of the angular momentum in vortex light does not come from the dipole transition of electron but from some optical techniques such as spiral phase plate
19etc. By adding each side of
eqn (21)–(23), we get the conservation rule for the Raman process as follows;
| | σs − σi − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −mphν + Nνp, (p = 0, ±1, ±2,…) i = −mphν + Nνp, (p = 0, ±1, ±2,…) | (24) |
where we adopt
Nν =
N as discussed in Section 3.2. Since
eqn (24) does not contain
m,
m′ and
m′′, the final result does not depend on the quantum number of the wavefunction. This does not mean that the optical selection rule for Raman scattering does not contain the information of wavefunction. When one of the three matrix elements in the Raman process becomes zero by
eqn (21)–(23), the Raman-scattering amplitude becomes zero. Thus, we need to consider each optical selection rule for the Raman process. When we put
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = 0, the conservation rule should correspond to the case of non-vortex light that we obtained in previous work except for
eqn (22).
6
4 Examples of MoS2 and graphene
Let us show examples of the selection rule for the Raman active modes of 2D materials with N = 2, 3, 4, 6 rotational symmetry. First, we discuss the transition-metal dichalcogenides, MoS2 (N = 3) since the effect of rotational symmetry works not only for the Raman tensor but also the selection rule for optical absorption.
4.1 Valley polarization effect in MoS2 with ![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif) i ≠ 0 (N = 3)
i ≠ 0 (N = 3)
The monolayer, MoS2, has a three-fold rotational symmetry (N = 3). It is known that the valley polarization effect for optical absorption occurs for circularly polarized light, in which the optical absorption occurs for LCP (RCP) light at the K (K′) point in the hexagonal Brillouin zone.20–27 We note here that the label of either K or K′ points in the hexagonal Brillouin zone can be determined by the valley polarization effect in which we define the K (K′) point by optical absorption of the LCP (RCP) light. The valley polarization corresponds to the case in eqn (21)| | m′ − m = (σi + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i) + 3p1 (p1 = 0, ±1, ±2,…), i) + 3p1 (p1 = 0, ±1, ±2,…), | (25) |
in which the value of m (m′) is the eigenvalues of the 3-fold rotational symmetry for the valence (conduction) band that depends on the K or K′ valleys. It is noted that the values of m (m′) give an opposite sign between K and K′ valleys because of time-reversal symmetry.
In Fig. 2, we show the valence and conduction bands near the K and K′ points that are split into the spin-up (red) and spin-down (blue) sub-bands by spin–orbit interactions. At the K and K′ points, the valence band consists of the dx2–y2 + 2iτdxy orbital of a Mo atom in which τ is the valley index (τ = +1 for the K point and τ = −1 for the K′ point).28 The corresponding m value is 2τ. The conduction band consists of dz2 with m = 0 at both the K and K′ points. It is noted that the phase factor, exp(ik·R), of the Bloch wavefunction at k = K(K′) point does not change the shape by operating C3 (α = 2π/3) rotation to R, that is, exp(ik·(C3R)) = exp(ik·R). Only the atomic orbitals at each R are rotated 2π/3 around C3R by the C3 rotation.
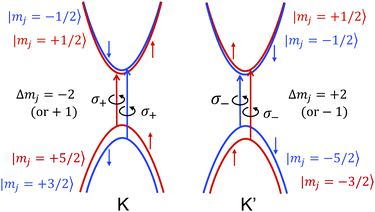 |
| | Fig. 2 The valley polarization appears in MoS2 in which the optical absorption selectively occurs for the left-handed (or right-handed) circularly polarized light (LCP σ+, or RCP σ−) at the K (or K′) point in the hexagonal Brillouin zone. At the K (τ = +1) and K′ (τ = −1) points, the valence band consists of the dx2–y2 + 2iτdxy orbitals of Mo whose m values are +2 and −2, respectively. The conduction band consists of dz2 with m = 0 at both the K and K′ points. Furthermore, the valence band and conduction band are split into two spin-dependent subbands with mj values by spin–orbit interactions. Optical dipole transition occurs between the same spin subbands with Δmj = ∓2 which is equivalent to Δmj = ±1 in the 3-fold rotational symmetry with a non-zero p1 value in eqn (25). | |
The half-integer values of mj for each subband in Fig. 2 are given by summing m and ±1/2 (for up (+) and down (−) spin) by spin–orbit interactions. The dipole optical transition occurs from the valence band to the conduction band with keeping the spin direction unchanged, which gives Δmj = −2(2) for the K(K′) points. Since Δmj = −2(2) is equivalent to Δmj = 1(−1) in the 3-fold rotational symmetry by adopting non-zero p1 in eqn (25), the left-hand side of eqn (25) can be written as follows:
| | 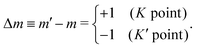 | (26) |
In
Table 1, we show either
K or
K′ point at which the optical absorption occurs by showing the possible
p1 values in
eqn (25). The data in
Table 1 are consistent with the results shown in
Table 1 by Ishii
et al. though they did not show the derivation of the results.
15 When we consider a non-vortex light (
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = 0),
p1 = 0 satisfies
eqn (25) as Δ
m =
σi, which is the origin of the valley polarization effect. When
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = −1 and
σi = 1 (LCP),
eqn (25) is not satisfied for any
p1 for Δ
m = −1 (the
K′ point). On the other hand, for Δ
m = 1 (the
K point),
p1 = 1 satisfies
eqn (25) when
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = −1 and
σi = −1. This means that only RCP with
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = −1 is absorbed at the
K point (not the
K′ point) and that there is no optical absorption for LCP with
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = −1. Similarly, when
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = +1, only LCP is absorbed at the
K′ point and there is no optical absorption for RCP.
Table 1 Selection rule of optical absorption of MoS2 for vortex light. K and K′ denote that the absorption occurs at the K and K′ points for LCP or RCP. Corresponding values of p1 in eqn (25) are also listed. The symbol “—” denotes optically forbidden
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i i |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
| LCP (σi = + 1) |
K
|
K′ |
— |
K
|
K′ |
— |
K
|
|
p
1
|
1 |
0 |
— |
0 |
−1 |
— |
−1 |
| RCP (σi = −1) |
K′ |
— |
K
|
K′ |
— |
K
|
K′ |
|
p
1
|
1 |
— |
1 |
0 |
— |
0 |
−1 |
Thus, the optical absorption always occurs for any ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i as shown in Table 1, which makes it difficult to observe the optical absorption at one valley for
i as shown in Table 1, which makes it difficult to observe the optical absorption at one valley for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p ± 1 (p is an integer). Since the conduction band is split by spin–orbit interactions, the lowest conduction band is spin-polarized whose direction is opposite for the K and K′ points. Thus, if we can measure the spin of photo-excited carrier excited by the light with the excitation energy at the energy gap (or A exciton), we can observe whether the optical absorption occurs at the K and K′ points for a given
i = 3p ± 1 (p is an integer). Since the conduction band is split by spin–orbit interactions, the lowest conduction band is spin-polarized whose direction is opposite for the K and K′ points. Thus, if we can measure the spin of photo-excited carrier excited by the light with the excitation energy at the energy gap (or A exciton), we can observe whether the optical absorption occurs at the K and K′ points for a given ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i.
i.
4.2 Raman selection rule of MoS2
From eqn (24), let us obtain the selection rule for Raman spectra. In MoS2, there are two Raman-active modes, that is, the out-of-plane chalcogen (OC) mode and the in-plane metal and chalcogen (IMC) mode which belong to A1g and E2g irreducible representation of D3h, respectively. As is discussed in Section 3.2, we adopt Nν = N for both the OC and IMC modes. The value of mphν for the OC mode is 0 while mphν of the IMC mode is ±2.
When we discuss the Raman selection rule of the resonant Raman spectra by vortex light for 2D materials, we can use the following three rules: (1) conservation of angular momentum (eqn (24)), (2) optical absorption selection rule (eqn (21)) and (3) either helicity-conserved (σi = σs) or helicity-changing (σi = −σs) Raman mode. The reason why we can use rule (3) even for the vortex light is that the symmetry of the Raman tensor does not change even though we consider the function of r = (x2 + y2)1/2 in the vector potential A, eqn (10). Here we consider the geometry of the incident (scattered) light in the direction of −z (+z), any function of r is invariant for a rotation around the z axis and thus the symmetry for the function of r belongs the A1g symmetry. Thus, any product of (1) phonon wavefunction in an irreducible representation and (2) the function of r in the A1g irreducible representation does not change the symmetry of the phonon wavefunction. As a result, the fact of either helicity-conserved (σi = σs) or helicity-changing (σi = −σs) Raman mode does not change even for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i ≠ 0. In the case of 3D material, on the other hand, since the cylindrical variable r = (x2 + y2)1/2 does not belong to A1g that usually belongs to r = (x2 + y2 + z2)1/2 in 3D, the shape of Raman tensor depends on
i ≠ 0. In the case of 3D material, on the other hand, since the cylindrical variable r = (x2 + y2)1/2 does not belong to A1g that usually belongs to r = (x2 + y2 + z2)1/2 in 3D, the shape of Raman tensor depends on ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which was discussed by Li et al.16
, which was discussed by Li et al.16
In the case of Raman spectra by non-vortex light, Chen et al. observed that the IMC mode (x2 − y2, xy, mphIMC = ±2) is the helicity-changing Raman mode (Δσ ≡ σi − σs = ±2) while the OC mode (x2 + y2, mphOC = 0) is helicity-conserved Raman mode (Δσ = 0), which is consistent in the case of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0 and the above values of Nν and mphν in eqn (24).6
i = 0 and the above values of Nν and mphν in eqn (24).6
In Table 2, we list the selection rule of 2D MoS2 for Raman spectra of the OC and IMC modes using LCP or RCP light. For a given ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, σi is the possible incident LCP (σi = 1) or RCP (σi = −1) light that give Raman scattering. When we put the values of Nν = 3, σs = σi and mphOC = 0 for the OC mode in eqn (23), we get −
i, σi is the possible incident LCP (σi = 1) or RCP (σi = −1) light that give Raman scattering. When we put the values of Nν = 3, σs = σi and mphOC = 0 for the OC mode in eqn (23), we get −![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p. Thus, the Raman signal for OC can be observed only for
i = 3p. Thus, the Raman signal for OC can be observed only for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p. When we put the values of Nν = 3, σs = −σi and mphIMC = ±2 for the IMC mode in eqn (23), we get −2σi −
i = 3p. When we put the values of Nν = 3, σs = −σi and mphIMC = ±2 for the IMC mode in eqn (23), we get −2σi − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = ±2 + 3p. For
i = ±2 + 3p. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 1, since σi = 1, we do not have a solution for p. Similarly, for
i = 1, since σi = 1, we do not have a solution for p. Similarly, for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1, since σi = −1, we do not have a solution for p, either. Thus, we expect that the Raman signal might appear only when
i = −1, since σi = −1, we do not have a solution for p, either. Thus, we expect that the Raman signal might appear only when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is a multiple of 3 as listed in Table 2.
i is a multiple of 3 as listed in Table 2.
Table 2 Raman selection rule of 2D MoS2 for vortex light. For a given ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, σi is the possible incident LCP (σi = 1) and RCP (σi = 1) where optical absorption occurs. For each σi = 1 or −1, σs becomes either helicity-conserved or helicity-changing scattered circularly polarized light for the OC and IMC phonon modes, respectively. We expect that Raman signal might appear only when
i, σi is the possible incident LCP (σi = 1) and RCP (σi = 1) where optical absorption occurs. For each σi = 1 or −1, σs becomes either helicity-conserved or helicity-changing scattered circularly polarized light for the OC and IMC phonon modes, respectively. We expect that Raman signal might appear only when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is a multiple of 3
i is a multiple of 3
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i i |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
|
σ
i
|
±1 |
+1 |
−1 |
±1 |
+1 |
−1 |
±1 |
|
σ
s(OC) |
±1 |
— |
— |
±1 |
— |
— |
±1 |
|
σ
s(IMC) |
∓1 |
— |
— |
∓1 |
— |
— |
∓1 |
4.3 Raman selection rule for graphene (N = 6)
In the case of graphene (N = 6), the first-order Raman mode is the G band with E2g symmetry (x2 − y2, xy, mphG = ±2) of the D6h point group.6 The helicity-resolved Raman intensity of the G band is calculated14 and is observed experimentally7 as the helicity-changing Raman mode σi = −σs for non-vortex, incident light. In the case of graphene, since there is no energy gap at the K (K′) point, we cannot use the selection rule of optical absorption at the high-symmetry K (K′) points. Furthermore, since the optical transition from the π to π* bands occurs for the atomic dipole moment of the 2pz orbitals between the nearest-neighbor carbon atoms,29 we cannot obtain the value of Δm for the optical absorption at a general k. Thus, we generally expect optical absorption for any ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i.
i.
When we put in eqn (24)σs − σi = ±2 and mphG = ±2, we get,
| | ±2 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = ±2 + 6p i = ±2 + 6p | (27) |
In the case of
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = 0, we have a solution
p = 0 in
eqn (27). When
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i is an odd number, we do not have a solution of
p in
eqn (27) and thus we do not expect a Raman signal of the G band for odd numbers of
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i. For
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = 2, if
σs −
σi = −2, we have a solution of
p = −1 and
mphG = + 2 in
eqn (27), which correspond to the helicity changing Raman scattering from LCP to RCP. For
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i = −2, if
σs −
σi = +2, we have a solution of
p = +1 and
mphG = −2 in
eqn (27), which correspond to the helicity changing Raman scattering from RCP to LCP.
In Table 3, we show the possible σi for observing the G band Raman spectra. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When
i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light.
i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light.
Table 3 Raman selection rule of graphene for vortex light. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When
i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light. For odd numbers of
i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light. For odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, although we expect optical absorption, we do not expect G band Raman signal
i, although we expect optical absorption, we do not expect G band Raman signal
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i i |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
|
σ
i
|
+1 |
— |
−1 |
— |
±1 |
— |
+1 |
— |
−1 |
|
σ
s(G) |
−1 |
— |
+1 |
— |
∓1 |
— |
−1 |
— |
+1 |
4.4 Raman selection rule for 2D black phosphorus (N = 2)
2D black phosphorus has a rotational symmetry with N = 2.30,31 The observed Raman active modes are two Ag (x2 or y2) and one B1g (xy).32 Although there are no published experimental results for helicity-dependent Raman spectra for black phosphorus, we used the theoretical result by Tatsumi et al.6 in which both the Ag and B1g with N = 2 and Nν = 2 show the helicity-changing Raman spectra for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0, which is consistent with the shape of the Raman tensor. It is noted here that the Raman tensor for Ag (x2) consists of both helicity-changing and helicity-conserved Raman spectra since the Raman tensor for x2 can be expressed by the sum of x2 − y2 and x2 + y2, respectively. On the other hand, the Raman tensor for B1g (xy) has only the helicity-changing Raman spectra. As we discussed in the case of graphene, we get mphν = 0 for both the Ag (x2 or y2) and B1g (xy) modes for Nν = N = 2.
i = 0, which is consistent with the shape of the Raman tensor. It is noted here that the Raman tensor for Ag (x2) consists of both helicity-changing and helicity-conserved Raman spectra since the Raman tensor for x2 can be expressed by the sum of x2 − y2 and x2 + y2, respectively. On the other hand, the Raman tensor for B1g (xy) has only the helicity-changing Raman spectra. As we discussed in the case of graphene, we get mphν = 0 for both the Ag (x2 or y2) and B1g (xy) modes for Nν = N = 2.
The symmetry of the wavefunction of black phosphorus, which consists of the P 3pz orbitals, at the top of the valence band at the Γ point in the Brillouin zone is Γ2+ (B1g, xy) irreducible representation of D2h, while that the bottom of the conduction band belongs to Γ4− (B3u, x).33 Since the product of B1g × B3u is B2u, (x2y), the dipole transition occurs by linear polarization in the direction of y, (B2u) at the Γ point in the Brillouin zone. Furthermore, since the linear polarization of y is given by subtracting LCP (x + iy) from RCP (x − iy), the optical transition is allowed for both LCP and RCP light. Thus, we assumed that m′ − m = ±1 for σi = ±1 which satisfies eqn (21) with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0. In Table 4 we show σs for the Ag or B2g modes. When
i = 0. In Table 4 we show σs for the Ag or B2g modes. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an odd number, optical absorption for σi = ±1 does not occur. When
i is an odd number, optical absorption for σi = ±1 does not occur. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an even number, the helicity changing Raman spectra is observed for both the LCP and RCP light. The results in Table 4 are similar to those of Table 3 except for σs(Ag) that consists of both LCP and RCP.
i is an even number, the helicity changing Raman spectra is observed for both the LCP and RCP light. The results in Table 4 are similar to those of Table 3 except for σs(Ag) that consists of both LCP and RCP.
Table 4 Raman selection rule of 2D black phosphorus for vortex light. Here we consider helicity-conserved Ag and helicity-changing B2g modes. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an odd number, optical absorption for σi = ±1 does not occur. When
i is an odd number, optical absorption for σi = ±1 does not occur. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an even number, the helicity changing Raman spectra are observed for both LCP (σi = +1) and RCP (σi = −1). The label of (+1, −1) denotes that the both helicity-changing and helicity-conserved Raman spectra are observed
i is an even number, the helicity changing Raman spectra are observed for both LCP (σi = +1) and RCP (σi = −1). The label of (+1, −1) denotes that the both helicity-changing and helicity-conserved Raman spectra are observed
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i i |
−2 |
−1 |
0 |
1 |
2 |
|
σ
i
|
±1 |
— |
±1 |
— |
±1 |
|
σ
s(B2g) |
∓1 |
— |
∓1 |
— |
∓1 |
|
σ
s(Ag) |
(+1, −1) |
— |
(+1, −1) |
— |
(+1, −1) |
4.5 Raman selection rule for TaP or LaAlSi (N = 4)
Finally, let us discuss 2D materials with four-fold rotational symmetry (D4h, N = 4). Although some Weyl semi-metals such as TaP8 or LaAlSi9 show four-fold rotational symmetry, 2D materials of TaP or LaAlSi have not been obtained yet. The optical absorption of TaP and LaAlSi occurs at the Weyl nodes whose position is not at a high-symmetry point in the Brillouin zone. Thus, we do not expect the selection rule for optical absorption. For the D4h symmetry, B1g (x2 − y2) and B2g (xy) modes 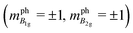 are helicity-changing Raman modes while A1g (x2 + y2,
are helicity-changing Raman modes while A1g (x2 + y2, 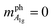 ) is the helicity-conserved Raman mode, which are quadratic functions of x and y for Nν = N = 4. In order to satisfy eqn (22) for the B1g (B2g) or A1g modes, m′′ − m′ has a component of m′′ − m′ = ±1 or m′′ − m′ = 0 for mph = ±1 or 0, respectively. Such a situation is possible in the case that the m′′ state is a virtual state that is expressed by a linear combination of the excited states.
) is the helicity-conserved Raman mode, which are quadratic functions of x and y for Nν = N = 4. In order to satisfy eqn (22) for the B1g (B2g) or A1g modes, m′′ − m′ has a component of m′′ − m′ = ±1 or m′′ − m′ = 0 for mph = ±1 or 0, respectively. Such a situation is possible in the case that the m′′ state is a virtual state that is expressed by a linear combination of the excited states.
In Table 5, we list σs for the A1g, B1g, and B2g modes for a given incident circularly polarized light (σi) which satisfies eqn (24). As shown in Table 5, helicity-conserved A1g Raman spectra can be observed for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of
i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i. It is important to note that the B1g or B2g Raman spectra by non-vortex light (
i. It is important to note that the B1g or B2g Raman spectra by non-vortex light (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0) are experimentally observed for 3D TaP8 or 3D LaAlSi9 which are comparable with the A1g Raman spectra. It is not consistent with the results for B1g or B2g with
i = 0) are experimentally observed for 3D TaP8 or 3D LaAlSi9 which are comparable with the A1g Raman spectra. It is not consistent with the results for B1g or B2g with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0 in Table 5. The reason for this inconsistency may come from the fact that the electron wavefunctions of the initial, intermediate and scattered states are not eigen function of D4h since the optical transition occurs at the not-high-symmetry k point. Thus, several values of m are possible for the original wavefunction. Thus, we could not use the present result for 2D TaP or 2D LaAlSi Wyle semimetals.
i = 0 in Table 5. The reason for this inconsistency may come from the fact that the electron wavefunctions of the initial, intermediate and scattered states are not eigen function of D4h since the optical transition occurs at the not-high-symmetry k point. Thus, several values of m are possible for the original wavefunction. Thus, we could not use the present result for 2D TaP or 2D LaAlSi Wyle semimetals.
Table 5 Selection rule for Raman spectra of N = 4 2D materials for vortex light. Here we consider the A1g and B1g (or B2g) modes for σs which are, respectively, helicity-conserved and helicity-changing modes. Helicity-conserved A1g Raman spectra can be observed for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of
i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i i |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
4 |
|
σ
i
|
±1 |
±1 |
— |
±1 |
±1 |
±1 |
— |
±1 |
±1 |
|
σ
s(A1g) |
±1 |
— |
— |
— |
±1 |
— |
— |
— |
±1 |
|
σ
s(B1g) |
— |
∓1 |
— |
∓1 |
— |
∓1 |
— |
∓1 |
— |
|
σ
s(B2g) |
— |
∓1 |
— |
∓1 |
— |
∓1 |
— |
∓1 |
— |
5 Discussion and summary
In this paper, we have shown the selection rule for Raman spectra by using circularly-polarized vortex light for 2D materials with N-fold (N = 2, 3, 4, and 6) rotational symmetry which is listed in Tables 2–5. In Table 6, we list the possible orbital angular momentum ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in the N fold rotational symmetry for given spin angular momentum of (1) incident light σi to have an optical absorption, (2) scattered light σs for helicity-conserved Raman mode (A) and helicity-exchanging Raman modes (E, B). When we compare the possible
in the N fold rotational symmetry for given spin angular momentum of (1) incident light σi to have an optical absorption, (2) scattered light σs for helicity-conserved Raman mode (A) and helicity-exchanging Raman modes (E, B). When we compare the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σi, the possible
values for σi, the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values depend on the sign of σi for N = 3 and 6, while not for N = 2 and 4. Possible
values depend on the sign of σi for N = 3 and 6, while not for N = 2 and 4. Possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σs are the same as those for σi for N = 2 and 6, while not for N = 3 and 4. Possible
values for σs are the same as those for σi for N = 2 and 6, while not for N = 3 and 4. Possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σs are the same as Np for N = 2 and 3 while not for N = 4 and 6. Thus for all four cases of N, the possible
values for σs are the same as Np for N = 2 and 3 while not for N = 4 and 6. Thus for all four cases of N, the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values have a behaviour independent of one another.
values have a behaviour independent of one another.
Table 6 In the N rotational symmetry, possible values of orbital angular momentum of vector light ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are listed for spin angular momentum σ for the incident light that gives optical absorption σi, and for Raman scattered light σs with helicity-conserved phonon modes (A, σs = σi) and helicity-changing modes (E and B, σs = −σi). p is an integer
are listed for spin angular momentum σ for the incident light that gives optical absorption σi, and for Raman scattered light σs with helicity-conserved phonon modes (A, σs = σi) and helicity-changing modes (E and B, σs = −σi). p is an integer
|
N
|
σ
i
|
σ
s
|
σ
s
|
| A |
E, B |
A1g for N = 2 shows both the helicity-conserving and helicity-changing modes.
Only σi = 1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p + 1 and only σi = −1 is possible for = 3p + 1 and only σi = −1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p − 1. σi = ±1 is possible for = 3p − 1. σi = ±1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p.
Only σi = 1 is possible for = 3p.
Only σi = 1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p + 2 and only σi = −1 is possible for = 6p + 2 and only σi = −1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p − 2. σi = ±1 is possible for = 6p − 2. σi = ±1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p.
In graphene, there is no A mode. = 6p.
In graphene, there is no A mode.
|
| 2 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p = 2p |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2pa = 2pa |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p = 2p |
| 3 |
Any ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b b |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p = 3p |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p = 3p |
| 4 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≠ 4p + 2 ≠ 4p + 2 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 4p = 4p |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p − 1 = 2p − 1 |
| 6 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2pc = 2pc |
Noned |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p = 2p |
In order to get the results shown in the tables and the conservation rule of eqn (24), we need the following conditions: (1) the wavefunction of the initial, intermediate and final states should be an eigenfunction of N-fold rotation, (2) the electronic wavefunction is sufficiently delocalized in the 2D materials compared with the wavelength of light, and (3) the Raman tensor does not change shape in the presence of vortex light, which we will discuss below.
In the case of MoS2, since the wavefunctions at the K and K′ valley are eigenfunctions of Lz, valley polarization occurs, which gives non-trivial selection rules for vortex light as shown in Table 2. For most cases of 2D materials, however, since the optical absorption occurs at not high-symmetry k points such as the case of graphene or TaP, we do not expect the selection rule for the optical absorption matrix element. As a result, the selection rule of eqn (24) does not work perfectly. Nevertheless, in the case of graphene, since the optical absorption occurs near the K and K′ points, the selection rule should be observed partially. It would be interesting to find 2D semiconductor materials whose optical absorption occurs at the high-symmetry k points. When we see the character tables of the point group, since the basis functions for C3h and C6 are expressed by either (x + iy)p or (x − iy)p, (p = 0, 1, 2) which are eigenfunctions of Lz, the optical selection rule for the vortex light would be interesting for such 2D materials.
When we obtain the selection rule of the optical absorption matrix element in eqn (21), we do not use the dipole approximation. In the dipole approximation, we take the vector potential out of the matrix element by assuming that the vector potential changes very slowly compared with the spatial change of the wavefunction. In this case, the effect of the factor exp(−i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α) of the vortex light would not appear in eqn (21). Since the typical diameter of vortex light is in the order of the wavelength, we require condition (2) as shown above. It is important to note that the present selection rule cannot be used for a molecule since the molecular wavefunction is localized in the molecule.
α) of the vortex light would not appear in eqn (21). Since the typical diameter of vortex light is in the order of the wavelength, we require condition (2) as shown above. It is important to note that the present selection rule cannot be used for a molecule since the molecular wavefunction is localized in the molecule.
In the case of 2D materials, since 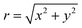 in the vector potential (eqn (10)) does not change by rotation around the z axis, the symmetry of the Raman tensor for vector light does not change even when we consider the vector potential for the vortex light as we discuss in Section 3.2. The shape of the Raman tensor will not change even for multi-layer 2D materials as long as the thickness is much smaller than the wavelength of the light. In this case, the phonon eigenmodes can be separated into either the in-plane of out-of-plane mode.
in the vector potential (eqn (10)) does not change by rotation around the z axis, the symmetry of the Raman tensor for vector light does not change even when we consider the vector potential for the vortex light as we discuss in Section 3.2. The shape of the Raman tensor will not change even for multi-layer 2D materials as long as the thickness is much smaller than the wavelength of the light. In this case, the phonon eigenmodes can be separated into either the in-plane of out-of-plane mode.
We hope that the selection rule will be observed experimentally for 2D materials which satisfy the above conditions.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
R. S. and M. S. U. acknowledge JSPS KAKENHI No. JP18H01810 and Center for Science and Innovations in Spintronics (CSIS) Tohoku University. N. T. H. acknowledges JSPS KAKENHI (Grant No. JP20K15178) and the financial support from the Frontier Research Institute for Interdisciplinary Sciences, Tohoku University. S. W. acknowledges the National Natural Science Foundation of China (Grant No. 11704165), the China Scholarship Council (Grant No. 201908320001) and the Natural Science Foundation of Jiangsu Province (Grant No. SBK2021020263).
Notes and references
- M.-T. Gabriel, J. P. Torres and L. Torner, Nat. Phys., 2007, 3, 305 Search PubMed
 .
.
- W. Zhang, Q. Qi, J. Zhou and L. Chen, Phys. Rev. Lett., 2014, 112, 153601 CrossRef
 .
.
- H. Kogelnik and T. Li, Proc. IEEE, 1966, 54, 1312 Search PubMed
 .
.
- K. Toyoda, F. Takahashi, S. Takizawa, Y. Tokizane, K. Miyamoto, R. Morita and T. Omatsu, Phys. Rev. Lett., 2013, 110, 143603 CrossRef PubMed
 .
.
- R. A. Beth, Phys. Rev., 1936, 50, 115 CrossRef
 .
.
- Y. Tatsumi, T. Kaneko and R. Saito, Phys. Rev. B, 2018, 97, 195444 CrossRef CAS
 .
.
- S. G. Drapcho, J. Kim, X. Hong, C. Jin, S. Shi, S. Tongay, J. Wu and F. Wang, Phys. Rev. B, 2017, 95, 165417 CrossRef
 .
.
- K. Zhang, X. Pang, T. Wang, F. Han, S.-L. Shang, N. T. Hung, A. R. T. Nugraha, Z.-K. Liu, M. Li, R. Saito and S. Huang, Phys. Rev. B, 2020, 101, 014308 CrossRef CAS
 .
.
- K. Zhang, T. Wang, X. Pang, F. Han, S.-L. Shang, N. T. Hung, Z.-K. Liu, M. Li, R. Saito and S. Huang, Phys. Rev. B, 2020, 102, 235162 CrossRef CAS
 .
.
- S.-Y. Chen, C. ZHeng, M. S. Fuhrer and J. Yan, Nano Lett., 2015, 15, 2526 CrossRef CAS
 .
.
- S. Zhang, N. Mao, N. Zhang, J. Wu, L. Tong and J. Zhang, ACS Nano, 2017, 11, 10366 CrossRef CAS PubMed
 .
.
- R. Saito, M. Hofmann, G. Dresselhaus, A. Jorio and M. S. Dresselhaus, Adv. Phys., 2011, 60, 413 CrossRef CAS
 .
.
-
A. Jorio, M. S. Dresselhaus, R. Saito and G. Dresselhaus, Raman Spectroscopy in Graphene Related Systems, Wiley-VCH Verlag GmbH & Co KGaA, WeinHeim, Germany, 2010, p. 368 Search PubMed
 .
.
- Y. Tatsumi and R. Saito, Phys. Rev. B, 2018, 97, 115407 CrossRef CAS
 .
.
- S. Ishii, N. Yokoshi and H. Ishihara, J. Phys.: Conf. Ser., 2019, 1220, 012056 CrossRef CAS
 .
.
- J. Li, J. J. Tu and J. L. Birman, J. Phys. Chem. Solids, 2015, 77, 117 CrossRef CAS
 .
.
- A. Grüneis, R. Saito, G. G. Samsonidze, T. Kimura, M. A. Pimenta, A. Jorio, A. G. S. Filho, G. Dresselhaus and M. S. Dresselhaus, J. Phys. Chem. Solid, 2003, 67, 165402 Search PubMed
 .
.
- R. Saito, Y. Tatsumi, S. Huang, X. Ling and M. S. Dresselhaus, J. Phys.: Condens. Matter, 2016, 28, 353002 CrossRef CAS
 .
.
- M. Beijersbergen, R. Coerwinkel, M. Kristensen and J. Woerdman, Opt. Commun., 1994, 112, 321 CrossRef CAS
 .
.
- K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494 CrossRef CAS PubMed
 .
.
- H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490 CrossRef CAS PubMed
 .
.
- T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887 CrossRef PubMed
 .
.
- A. M. Jones, H. Yu, N. J. Ghimire, S. Wu, G. Aivazian, J. S. Ross, B. Zhao, J. Yan, D. G. Mandrus, D. Xiao, W. Yao and X. Xu, Nat. Nanotechnol., 2013, 8, 634 CrossRef CAS PubMed
 .
.
- R. Suzuki, M. Sakano, Y. J. Zhang, R. Akashi, D. Morikawa, A. Harasawa, K. Yaji, K. Kuroda, K. Miyamoto, T. Okuda, K. Ishizaka, R. Arita and Y. Iwasa, Nat. Nanotechnol., 2014, 9, 611 CrossRef CAS
 .
.
- S. Wu, J. S. Ross, G.-B. Liu, G. Aivazian, A. Jones, Z. Fei, W. Zhu, D. Xiao, W. Yao, D. Cobden and X. Xu, Nat. Phys., 2013, 9, 149 Search PubMed
 .
.
- K. Ghalamkari, Y. Tatsumi and R. Saito, J. Phys. Soc. Jpn., 2018, 87, 024710 CrossRef
 .
.
- H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490 CrossRef CAS PubMed
 .
.
- D. Xiao, G.-B. L. nad Wanxiang Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef
 .
.
- A. Grüneis, R. Saito, G. G. Samsonidze, T. Kimura, M. A. Pimenta, A. Jorio, A. G. S. Filho, G. Dresselhaus and M. S. Dresselhaus, J. Phys. Chem. Solid, 2003, 67, 165402 Search PubMed
 .
.
- X. Ling, S. Huang, E. H. Hasdeo, L. Liang, W. M. Parkin, Y. Tatsumi, A. R. T. Nugraha, A. A. Puretzky, P. M. Das, B. G. Sumpter, D. B. Geohegan, J. Kong, R. Saito, M. Drndic, V. Meunier and M. S. Dresselhaus, Nano Lett., 2016, 16, 2260 CrossRef CAS PubMed
 .
.
- N. Mao, S. Zhang, J. Wu, H. Tian, J. Wu, H. Xu, H. Peng, L. Tong and J. Zhang, Nano Res., 2018, 11, 3154 CrossRef CAS
 .
.
- F. Xia, H. Wang and Y. Jia, Nat. Commun., 2014, 5, 4458 CrossRef CAS PubMed
 .
.
- Y. Takao and A. Morita, Phys. B, 1981, 105, 93 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Muhammad Shoufie
Ukhtary
*a,
Muhammad Shoufie
Ukhtary
 ab,
Sake
Wang
ab,
Sake
Wang
 a and
Nguyen Tuan
Hung
a and
Nguyen Tuan
Hung
 c
c
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) th Laguerre-Gaussian mode has an azimuthal phase shift term, exp(i
th Laguerre-Gaussian mode has an azimuthal phase shift term, exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ), where φ is the azimuthal angle in the cylindrical coordinate and the integer
φ), where φ is the azimuthal angle in the cylindrical coordinate and the integer ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is called the topological charge. The corresponding vortex light has an orbital angular momentum
is called the topological charge. The corresponding vortex light has an orbital angular momentum ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ħ.4 In this paper, we discuss the conservation law of angular momentum in the Raman scattering of two-dimensional (2D) materials.
ħ.4 In this paper, we discuss the conservation law of angular momentum in the Raman scattering of two-dimensional (2D) materials.
 -symmetry phonon does not change the helicity (helicity-conserved Raman spectra). Occurrence of the helicity-changing Raman spectra is simply understood by the Raman tensor for a given phonon mode using the Jones vector of circularly-polarized light.6
-symmetry phonon does not change the helicity (helicity-conserved Raman spectra). Occurrence of the helicity-changing Raman spectra is simply understood by the Raman tensor for a given phonon mode using the Jones vector of circularly-polarized light.6
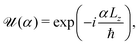
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) is commutable with
is commutable with ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), [
(α), [![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ,
, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)] = 0, any wavefunction of
(α)] = 0, any wavefunction of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , |m〉, is also an eigenfunction of
, |m〉, is also an eigenfunction of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), that is,
(α), that is, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = C|m〉. Using the facts that {
(α)|m〉 = C|m〉. Using the facts that {![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)}N is a 2π rotation and that CN = 1, the eigenvalues of
(α)}N is a 2π rotation and that CN = 1, the eigenvalues of ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) are expressed by,
(α) are expressed by,![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = exp(−imα)|m〉, (m = 0, 1, 2, …, N − 1)
(α)|m〉 = exp(−imα)|m〉, (m = 0, 1, 2, …, N − 1)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) by exp(imφ), we get
(α) by exp(imφ), we get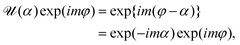
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for the eigenvalue of exp(−imα). Thus it is reasonable for us to call mħ a pseudo angular momentum though the definition is valid only for a discrete rotational angle.
(α) for the eigenvalue of exp(−imα). Thus it is reasonable for us to call mħ a pseudo angular momentum though the definition is valid only for a discrete rotational angle.
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |m〉 by
|m〉 by ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for an interaction operator
(α) for an interaction operator 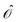 which has an N′-fold rotational symmetry. In general, the value of N′ is smaller than N. However, if
which has an N′-fold rotational symmetry. In general, the value of N′ is smaller than N. However, if ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) does not depend on φ, N′ becomes infinite. In this case, we can select as N′ = N. When we operate
does not depend on φ, N′ becomes infinite. In this case, we can select as N′ = N. When we operate ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) on
(α) on ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) , the variable φ in
, the variable φ in ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is changed to φ + α. If the
is changed to φ + α. If the ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) has a φ dependence as exp(imOφ), we obtain
has a φ dependence as exp(imOφ), we obtain![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ + α) = exp(−imOα)
(φ + α) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ),
(φ),![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ + 2π) =
(φ + 2π) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ).
(φ).
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) to
(α) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ), we get
(φ), we get![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)
(α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ) =
(φ) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ + α)
(φ + α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (φ) = exp(−imOα)
(φ) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ)
(φ)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α),
(α),![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (φ) as follows
(φ) as follows![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)
(α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) = exp(−imOα)
−1(α) = exp(−imOα)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) .
.![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |m〉, we get
|m〉, we get![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α)
−1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)
(α)![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α)
−1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)|m〉 = exp{i(−m + m′ − mO)α}〈m′|
(α)|m〉 = exp{i(−m + m′ − mO)α}〈m′|![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |m〉.
|m〉.![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) generally has a lower symmetry than
generally has a lower symmetry than ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) and that α in
and that α in ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) should be selected for the N′-fold rotational symmetry. Here we assume that N′ is a divisor of N. If the matrix elements of
(α) should be selected for the N′-fold rotational symmetry. Here we assume that N′ is a divisor of N. If the matrix elements of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) have an N′-fold rotational symmetry, the exp
have an N′-fold rotational symmetry, the exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i(m − m′ + mO)α should be unity, in which m and m′ (or mO) are integers from 0 to N′ − 1. Otherwise, by integration of the matrix elements over the φ from 0 to 2π, the integration would give zero. From this fact, we get the conservation law of angular momentum as follows
i(m − m′ + mO)α should be unity, in which m and m′ (or mO) are integers from 0 to N′ − 1. Otherwise, by integration of the matrix elements over the φ from 0 to 2π, the integration would give zero. From this fact, we get the conservation law of angular momentum as follows![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) .
.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt is given by time-dependent perturbation theory as follows17
opt is given by time-dependent perturbation theory as follows17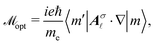
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the vector potential of the light. For the Laguerre–Gaussian mode of the vortex light, the vector potential in the cylindrical coordinate is given by15
is the vector potential of the light. For the Laguerre–Gaussian mode of the vortex light, the vector potential in the cylindrical coordinate is given by15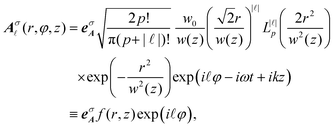
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , p, z, r, L|
, p, z, r, L|![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |p, w0, and w(z) denote, respectively, orbital angular momentum, the radial index, propagation direction (z) and radial direction (r) in the cylindrical coordinate, the Laguerre polynomial function, the beam waist and the beam width function. eσA is the unit vector for the amplitude of light, which is known as the Jones vector,
|p, w0, and w(z) denote, respectively, orbital angular momentum, the radial index, propagation direction (z) and radial direction (r) in the cylindrical coordinate, the Laguerre polynomial function, the beam waist and the beam width function. eσA is the unit vector for the amplitude of light, which is known as the Jones vector,
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) except for the factors of eσA and exp(i
except for the factors of eσA and exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ). We will use the fact that the f(r, z) does not contain φ.
φ). We will use the fact that the f(r, z) does not contain φ.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt ≠ 0, while the transition is forbidden when
opt ≠ 0, while the transition is forbidden when ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt = 0. When we multiply
opt = 0. When we multiply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α)
−1(α)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) in eqn (9), we obtain the following expression, by putting eqn (10) into eqn (9).
(α) in eqn (9), we obtain the following expression, by putting eqn (10) into eqn (9).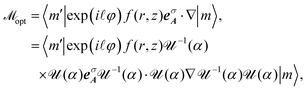
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) in eqn (7). Since f(r, z) does not contain φ, and since eσA is commutable6 with
in eqn (7). Since f(r, z) does not contain φ, and since eσA is commutable6 with ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α), that is,
(α), that is, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)eσA
(α)eσA![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) = eσA, the left-most
−1(α) = eσA, the left-most ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) in eqn (12) applies to the product of the functions, 〈m′|exp(i
−1(α) in eqn (12) applies to the product of the functions, 〈m′|exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ) from the right as follows
φ) from the right as follows![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i
exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ)
φ)![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α) = exp{i(m′ −
−1(α) = exp{i(m′ − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )α}〈m′|
)α}〈m′|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i
exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ).
φ).![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ) as follows,
φ) as follows,![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)
(α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i
exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ) = exp(−i
φ) = exp(−i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α)
α)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i
exp(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) φ).
φ).![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α)∇
(α)∇![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) −1(α)}, we get as follows,6
−1(α)}, we get as follows,6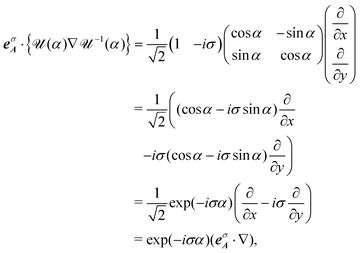
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α − iσ
α − iσ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, for σ = ±1.
α, for σ = ±1.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt = exp{i(m′ − m − σ −
opt = exp{i(m′ − m − σ − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )α}〈m′|Aσ
)α}〈m′|Aσ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ·∇|m〉.
·∇|m〉.![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = Np,
= Np,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) opt should be zero. It is important to note that both σ and
opt should be zero. It is important to note that both σ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) can be either a positive or negative integer. Although we have the expression of −σ −
can be either a positive or negative integer. Although we have the expression of −σ − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , we have any combination of σ and
, we have any combination of σ and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) with a positive or negative integer.
with a positive or negative integer.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep is given by
ep is given by![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep = 〈m′′|Aν·∇V|m′〉,
ep = 〈m′′|Aν·∇V|m′〉,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ep,6 which is common for the Raman spectra for non-vortex light as follows.
ep,6 which is common for the Raman spectra for non-vortex light as follows. and the E′ Raman active modes, respectively.6
and the E′ Raman active modes, respectively.6
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) for N (not Nν) rotational symmetry. For example, the E′ mode (x2 − y2, xy) of TMD, which was given by Nν = 1 and mphν = 0,6 can be expressed by Nν = N = 3 and mphν = ±2. In fact, when we multiply
(α) for N (not Nν) rotational symmetry. For example, the E′ mode (x2 − y2, xy) of TMD, which was given by Nν = 1 and mphν = 0,6 can be expressed by Nν = N = 3 and mphν = ±2. In fact, when we multiply ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) with α = 2π/3 by (x2 − y2 ± i2xy), we get
(α) with α = 2π/3 by (x2 − y2 ± i2xy), we get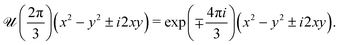
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (α) with mphν = ±2. Since we have several possible mphν for one phonon mode, we need to consider eqn (19) for each value of mphν.
(α) with mphν = ±2. Since we have several possible mphν for one phonon mode, we need to consider eqn (19) for each value of mphν.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i ≠ 0, though both expressions give almost the same results for
i ≠ 0, though both expressions give almost the same results for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0. In order to avoid any confusion between the notations by Tatsumi et al. and those in the present paper, we keep using eqn (19) but hereafter we set Nν = N and we use the new value of mphν.
i = 0. In order to avoid any confusion between the notations by Tatsumi et al. and those in the present paper, we keep using eqn (19) but hereafter we set Nν = N and we use the new value of mphν.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i + Np1, (p1 = 0, ±1, ±2,…),
i + Np1, (p1 = 0, ±1, ±2,…),![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i denote the spin and orbital quantum numbers of the incident light, respectively. For the phonon emission sub-process (2), we get the conservation rule from eqn (19)
i denote the spin and orbital quantum numbers of the incident light, respectively. For the phonon emission sub-process (2), we get the conservation rule from eqn (19)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from eqn (17) as follows
from eqn (17) as follows![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −mphν + Nνp, (p = 0, ±1, ±2,…)
i = −mphν + Nνp, (p = 0, ±1, ±2,…)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0, the conservation rule should correspond to the case of non-vortex light that we obtained in previous work except for eqn (22).6
i = 0, the conservation rule should correspond to the case of non-vortex light that we obtained in previous work except for eqn (22).6
![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif) i ≠ 0 (N = 3)
i ≠ 0 (N = 3)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i) + 3p1 (p1 = 0, ±1, ±2,…),
i) + 3p1 (p1 = 0, ±1, ±2,…),
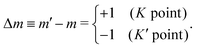
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0), p1 = 0 satisfies eqn (25) as Δm = σi, which is the origin of the valley polarization effect. When
i = 0), p1 = 0 satisfies eqn (25) as Δm = σi, which is the origin of the valley polarization effect. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1 and σi = 1 (LCP), eqn (25) is not satisfied for any p1 for Δm = −1 (the K′ point). On the other hand, for Δm = 1 (the K point), p1 = 1 satisfies eqn (25) when
i = −1 and σi = 1 (LCP), eqn (25) is not satisfied for any p1 for Δm = −1 (the K′ point). On the other hand, for Δm = 1 (the K point), p1 = 1 satisfies eqn (25) when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1 and σi = −1. This means that only RCP with
i = −1 and σi = −1. This means that only RCP with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1 is absorbed at the K point (not the K′ point) and that there is no optical absorption for LCP with
i = −1 is absorbed at the K point (not the K′ point) and that there is no optical absorption for LCP with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1. Similarly, when
i = −1. Similarly, when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = +1, only LCP is absorbed at the K′ point and there is no optical absorption for RCP.
i = +1, only LCP is absorbed at the K′ point and there is no optical absorption for RCP.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i as shown in Table 1, which makes it difficult to observe the optical absorption at one valley for
i as shown in Table 1, which makes it difficult to observe the optical absorption at one valley for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p ± 1 (p is an integer). Since the conduction band is split by spin–orbit interactions, the lowest conduction band is spin-polarized whose direction is opposite for the K and K′ points. Thus, if we can measure the spin of photo-excited carrier excited by the light with the excitation energy at the energy gap (or A exciton), we can observe whether the optical absorption occurs at the K and K′ points for a given
i = 3p ± 1 (p is an integer). Since the conduction band is split by spin–orbit interactions, the lowest conduction band is spin-polarized whose direction is opposite for the K and K′ points. Thus, if we can measure the spin of photo-excited carrier excited by the light with the excitation energy at the energy gap (or A exciton), we can observe whether the optical absorption occurs at the K and K′ points for a given ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i.
i.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i ≠ 0. In the case of 3D material, on the other hand, since the cylindrical variable r = (x2 + y2)1/2 does not belong to A1g that usually belongs to r = (x2 + y2 + z2)1/2 in 3D, the shape of Raman tensor depends on
i ≠ 0. In the case of 3D material, on the other hand, since the cylindrical variable r = (x2 + y2)1/2 does not belong to A1g that usually belongs to r = (x2 + y2 + z2)1/2 in 3D, the shape of Raman tensor depends on ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which was discussed by Li et al.16
, which was discussed by Li et al.16![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0 and the above values of Nν and mphν in eqn (24).6
i = 0 and the above values of Nν and mphν in eqn (24).6![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, σi is the possible incident LCP (σi = 1) or RCP (σi = −1) light that give Raman scattering. When we put the values of Nν = 3, σs = σi and mphOC = 0 for the OC mode in eqn (23), we get −
i, σi is the possible incident LCP (σi = 1) or RCP (σi = −1) light that give Raman scattering. When we put the values of Nν = 3, σs = σi and mphOC = 0 for the OC mode in eqn (23), we get −![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p. Thus, the Raman signal for OC can be observed only for
i = 3p. Thus, the Raman signal for OC can be observed only for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 3p. When we put the values of Nν = 3, σs = −σi and mphIMC = ±2 for the IMC mode in eqn (23), we get −2σi −
i = 3p. When we put the values of Nν = 3, σs = −σi and mphIMC = ±2 for the IMC mode in eqn (23), we get −2σi − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = ±2 + 3p. For
i = ±2 + 3p. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 1, since σi = 1, we do not have a solution for p. Similarly, for
i = 1, since σi = 1, we do not have a solution for p. Similarly, for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −1, since σi = −1, we do not have a solution for p, either. Thus, we expect that the Raman signal might appear only when
i = −1, since σi = −1, we do not have a solution for p, either. Thus, we expect that the Raman signal might appear only when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is a multiple of 3 as listed in Table 2.
i is a multiple of 3 as listed in Table 2.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, σi is the possible incident LCP (σi = 1) and RCP (σi = 1) where optical absorption occurs. For each σi = 1 or −1, σs becomes either helicity-conserved or helicity-changing scattered circularly polarized light for the OC and IMC phonon modes, respectively. We expect that Raman signal might appear only when
i, σi is the possible incident LCP (σi = 1) and RCP (σi = 1) where optical absorption occurs. For each σi = 1 or −1, σs becomes either helicity-conserved or helicity-changing scattered circularly polarized light for the OC and IMC phonon modes, respectively. We expect that Raman signal might appear only when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is a multiple of 3
i is a multiple of 3
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i.
i.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = ±2 + 6p
i = ±2 + 6p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0, we have a solution p = 0 in eqn (27). When
i = 0, we have a solution p = 0 in eqn (27). When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an odd number, we do not have a solution of p in eqn (27) and thus we do not expect a Raman signal of the G band for odd numbers of
i is an odd number, we do not have a solution of p in eqn (27) and thus we do not expect a Raman signal of the G band for odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i. For
i. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 2, if σs − σi = −2, we have a solution of p = −1 and mphG = + 2 in eqn (27), which correspond to the helicity changing Raman scattering from LCP to RCP. For
i = 2, if σs − σi = −2, we have a solution of p = −1 and mphG = + 2 in eqn (27), which correspond to the helicity changing Raman scattering from LCP to RCP. For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = −2, if σs − σi = +2, we have a solution of p = +1 and mphG = −2 in eqn (27), which correspond to the helicity changing Raman scattering from RCP to LCP.
i = −2, if σs − σi = +2, we have a solution of p = +1 and mphG = −2 in eqn (27), which correspond to the helicity changing Raman scattering from RCP to LCP.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When
i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light.
i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When
i = 6p, we get Raman spectra of the G band for both the LCP and RCP incident light. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light. For odd numbers of
i = 6p + 2 (or 6p − 2), we get Raman spectra of the G band for LCP (RCP) incident light. For odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i, although we expect optical absorption, we do not expect G band Raman signal
i, although we expect optical absorption, we do not expect G band Raman signal
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0, which is consistent with the shape of the Raman tensor. It is noted here that the Raman tensor for Ag (x2) consists of both helicity-changing and helicity-conserved Raman spectra since the Raman tensor for x2 can be expressed by the sum of x2 − y2 and x2 + y2, respectively. On the other hand, the Raman tensor for B1g (xy) has only the helicity-changing Raman spectra. As we discussed in the case of graphene, we get mphν = 0 for both the Ag (x2 or y2) and B1g (xy) modes for Nν = N = 2.
i = 0, which is consistent with the shape of the Raman tensor. It is noted here that the Raman tensor for Ag (x2) consists of both helicity-changing and helicity-conserved Raman spectra since the Raman tensor for x2 can be expressed by the sum of x2 − y2 and x2 + y2, respectively. On the other hand, the Raman tensor for B1g (xy) has only the helicity-changing Raman spectra. As we discussed in the case of graphene, we get mphν = 0 for both the Ag (x2 or y2) and B1g (xy) modes for Nν = N = 2.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0. In Table 4 we show σs for the Ag or B2g modes. When
i = 0. In Table 4 we show σs for the Ag or B2g modes. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an odd number, optical absorption for σi = ±1 does not occur. When
i is an odd number, optical absorption for σi = ±1 does not occur. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an even number, the helicity changing Raman spectra is observed for both the LCP and RCP light. The results in Table 4 are similar to those of Table 3 except for σs(Ag) that consists of both LCP and RCP.
i is an even number, the helicity changing Raman spectra is observed for both the LCP and RCP light. The results in Table 4 are similar to those of Table 3 except for σs(Ag) that consists of both LCP and RCP.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an odd number, optical absorption for σi = ±1 does not occur. When
i is an odd number, optical absorption for σi = ±1 does not occur. When ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is an even number, the helicity changing Raman spectra are observed for both LCP (σi = +1) and RCP (σi = −1). The label of (+1, −1) denotes that the both helicity-changing and helicity-conserved Raman spectra are observed
i is an even number, the helicity changing Raman spectra are observed for both LCP (σi = +1) and RCP (σi = −1). The label of (+1, −1) denotes that the both helicity-changing and helicity-conserved Raman spectra are observed
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i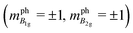 are helicity-changing Raman modes while A1g (x2 + y2,
are helicity-changing Raman modes while A1g (x2 + y2,  ) is the helicity-conserved Raman mode, which are quadratic functions of x and y for Nν = N = 4. In order to satisfy eqn (22) for the B1g (B2g) or A1g modes, m′′ − m′ has a component of m′′ − m′ = ±1 or m′′ − m′ = 0 for mph = ±1 or 0, respectively. Such a situation is possible in the case that the m′′ state is a virtual state that is expressed by a linear combination of the excited states.
) is the helicity-conserved Raman mode, which are quadratic functions of x and y for Nν = N = 4. In order to satisfy eqn (22) for the B1g (B2g) or A1g modes, m′′ − m′ has a component of m′′ − m′ = ±1 or m′′ − m′ = 0 for mph = ±1 or 0, respectively. Such a situation is possible in the case that the m′′ state is a virtual state that is expressed by a linear combination of the excited states.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of
i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i. It is important to note that the B1g or B2g Raman spectra by non-vortex light (
i. It is important to note that the B1g or B2g Raman spectra by non-vortex light (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0) are experimentally observed for 3D TaP8 or 3D LaAlSi9 which are comparable with the A1g Raman spectra. It is not consistent with the results for B1g or B2g with
i = 0) are experimentally observed for 3D TaP8 or 3D LaAlSi9 which are comparable with the A1g Raman spectra. It is not consistent with the results for B1g or B2g with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 0 in Table 5. The reason for this inconsistency may come from the fact that the electron wavefunctions of the initial, intermediate and scattered states are not eigen function of D4h since the optical transition occurs at the not-high-symmetry k point. Thus, several values of m are possible for the original wavefunction. Thus, we could not use the present result for 2D TaP or 2D LaAlSi Wyle semimetals.
i = 0 in Table 5. The reason for this inconsistency may come from the fact that the electron wavefunctions of the initial, intermediate and scattered states are not eigen function of D4h since the optical transition occurs at the not-high-symmetry k point. Thus, several values of m are possible for the original wavefunction. Thus, we could not use the present result for 2D TaP or 2D LaAlSi Wyle semimetals.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of
i = 4p, while helicity-changing B1g or B2g Raman spectra can be observed for odd numbers of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i
i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in the N fold rotational symmetry for given spin angular momentum of (1) incident light σi to have an optical absorption, (2) scattered light σs for helicity-conserved Raman mode (A) and helicity-exchanging Raman modes (E, B). When we compare the possible
in the N fold rotational symmetry for given spin angular momentum of (1) incident light σi to have an optical absorption, (2) scattered light σs for helicity-conserved Raman mode (A) and helicity-exchanging Raman modes (E, B). When we compare the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σi, the possible
values for σi, the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values depend on the sign of σi for N = 3 and 6, while not for N = 2 and 4. Possible
values depend on the sign of σi for N = 3 and 6, while not for N = 2 and 4. Possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σs are the same as those for σi for N = 2 and 6, while not for N = 3 and 4. Possible
values for σs are the same as those for σi for N = 2 and 6, while not for N = 3 and 4. Possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values for σs are the same as Np for N = 2 and 3 while not for N = 4 and 6. Thus for all four cases of N, the possible
values for σs are the same as Np for N = 2 and 3 while not for N = 4 and 6. Thus for all four cases of N, the possible ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values have a behaviour independent of one another.
values have a behaviour independent of one another.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are listed for spin angular momentum σ for the incident light that gives optical absorption σi, and for Raman scattered light σs with helicity-conserved phonon modes (A, σs = σi) and helicity-changing modes (E and B, σs = −σi). p is an integer
are listed for spin angular momentum σ for the incident light that gives optical absorption σi, and for Raman scattered light σs with helicity-conserved phonon modes (A, σs = σi) and helicity-changing modes (E and B, σs = −σi). p is an integer
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p + 1 and only σi = −1 is possible for
= 3p + 1 and only σi = −1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p − 1. σi = ±1 is possible for
= 3p − 1. σi = ±1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p.
c Only σi = 1 is possible for
= 3p.
c Only σi = 1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p + 2 and only σi = −1 is possible for
= 6p + 2 and only σi = −1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p − 2. σi = ±1 is possible for
= 6p − 2. σi = ±1 is possible for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 6p.
d In graphene, there is no A mode.
= 6p.
d In graphene, there is no A mode.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p
= 2p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2pa
= 2pa![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p
= 2p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) b
b![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p
= 3p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3p
= 3p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≠ 4p + 2
≠ 4p + 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 4p
= 4p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p − 1
= 2p − 1![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2pc
= 2pc![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2p
= 2p![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α) of the vortex light would not appear in eqn (21). Since the typical diameter of vortex light is in the order of the wavelength, we require condition (2) as shown above. It is important to note that the present selection rule cannot be used for a molecule since the molecular wavefunction is localized in the molecule.
α) of the vortex light would not appear in eqn (21). Since the typical diameter of vortex light is in the order of the wavelength, we require condition (2) as shown above. It is important to note that the present selection rule cannot be used for a molecule since the molecular wavefunction is localized in the molecule. in the vector potential (eqn (10)) does not change by rotation around the z axis, the symmetry of the Raman tensor for vector light does not change even when we consider the vector potential for the vortex light as we discuss in Section 3.2. The shape of the Raman tensor will not change even for multi-layer 2D materials as long as the thickness is much smaller than the wavelength of the light. In this case, the phonon eigenmodes can be separated into either the in-plane of out-of-plane mode.
in the vector potential (eqn (10)) does not change by rotation around the z axis, the symmetry of the Raman tensor for vector light does not change even when we consider the vector potential for the vortex light as we discuss in Section 3.2. The shape of the Raman tensor will not change even for multi-layer 2D materials as long as the thickness is much smaller than the wavelength of the light. In this case, the phonon eigenmodes can be separated into either the in-plane of out-of-plane mode..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
