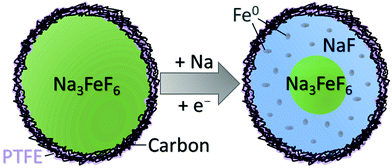
Probing reaction processes and reversibility in Earth-abundant Na₃FeF₆ for Na-ion batteries

Abstract

Sodium (Na)-ion batteries are the most explored ‘beyond-Li’ battery systems, yet their energy densities are still largely limited by the positive electrode material. Na₃FeF₆ is a promising Earth-abundant containing electrode and operates through a conversion-type charge–discharge reaction associated with a high theoretical capacity (336 mA h g⁻¹). In practice, however, only a third of this capacity is achieved during electrochemical cycling. In this study, we demonstrate a new rapid and environmentally-friendly assisted-microwave method for the preparation of Na₃FeF₆. A comprehensive understanding of charge–discharge processes and of the reactivity of the cycled electrode samples is achieved using a combination of electrochemical tests, synchrotron X-ray diffraction, ⁵⁷Fe Mössbauer spectroscopy, X-ray photoelectron spectroscopy, magnetometry, and ²³Na/¹⁹F solid-state nuclear magnetic resonance (NMR) complemented with first principles calculations of NMR properties. We find that the primary performance limitation of the Na₃FeF₆ electrode is the sluggish kinetics of the conversion reaction, while the methods employed for materials synthesis and electrode preparation do not have a significant impact on the conversion efficiency and reversibility. Our work confirms that Na₃FeF₆ undergoes conversion into NaF and Fe_(s) nanoparticles. The latter are found to be prone to oxidation prior to ex situ measurements, thus necessitating a robust analysis of the stable phases (here, NaF) formed upon conversion.

---

Introduction

Lithium (Li)-ion batteries (LIBs) have enabled the successful electrification of numerous devices ranging from laptops to electric vehicles to large-scale energy storage systems. However, with the continually increasing demand for these batteries, the sustainability, security, and economics of their comprising materials must be considered. Significant progress has been made towards utilizing more abundant transition metals in the cathode, rather than expensive cobalt, as well as increasing the energy density of LIBs.¹ However, an alternate solution entails transitioning to entirely non-lithium-based battery technologies. Sodium (Na)-ion batteries (NIBs) are the most explored beyond-Li battery systems. Due to the chemical similarity of sodium to lithium,² initial work on Na-ion electrodes has focused on Li-ion electrode analogues, namely layered sodium transition metal oxides and polyanion systems. However, transition metal oxides and polyanionic systems exhibit low theoretical energy densities (520 W h kg^−1 3 and 475 W h kg⁻¹,⁴ respectively). Therefore, new Na-ion electrode materials with high energy densities are needed. Several promising alternatives have been reported including conversion-type SnS nanospheres⁵ and insertion-type disordered rocksalts^6,7 and weberites.^8,9 However, there has been no conclusive Earth-abundant, energy dense, and inexpensive electrode material found for NIBs prompting further investigation.

Fluoride-based conversion-type NIB electrodes may reach energy densities up to 1400 W h kg⁻¹ on account of multi-electron redox processes¹⁰ and thus present a promising direction for NIB electrodes. Yet, conversion reactions lead to a redistribution of all species in the electrode material, as recently shown by Grey and coauthors for Li_xFe_yF₃.¹¹ Thus, these materials generally require a greater driving force (overpotential) and cause more irreversible behavior than intercalation reactions. Further, conversion-type electrodes are often more kinetically-limited than intercalation-type electrodes, leading to sluggish redox reaction kinetics that are exacerbated by the insulating fluoride compounds. As a result, significant discrepancies are observed between theoretically-computed thermodynamic pathways and the experimentally-observed kinetically-limited phenomena, making it difficult to identify conversion reaction mechanisms.^12,13 Furthermore, the structural changes that occur on cycling often result in the formation of amorphous and metastable phases that are difficult to capture via diffraction and ex situ methods. For these reasons, the majority of fluoride-based conversion electrodes for NIBs do not have well-established reaction pathways.¹⁰ In turn, a poor understanding of reaction mechanisms makes it difficult to distinguish between intrinsic limitations imposed by the conversion reaction, and practical losses due to the starting particle morphology and electrode preparation. Thus, to understand the reaction mechanisms and limitations of current conversion materials in NIBs, and to enable the rational design of next-generation systems combining high capacity and long cycle life, local structure probes are warranted.

Na₃FeF₆ is a particularly attractive candidate electrode material for NIBs, as it is exclusively composed of Earth-abundant species. This compound was first explored as a conversion-type NIB electrode by Shakoor et al. and displayed a first discharge capacity of 125 mA h g⁻¹ with very low reversibility.¹⁴ Two follow-up studies used solution-phase syntheses and obtained more stable cycling with initial reversible capacities of 140 mA h g⁻¹ and ≈64% capacity retention after 400 cycles.^15,16 These studies have focused on electrochemical characterization of Na₃FeF₆, with the only additional characterization reported being ex situ X-ray diffraction (XRD) by Shakoor et al.¹⁴ The ex situ XRD data collected on cycled electrode samples were used as evidence that NaF and Fe formed on discharge, and the following conversion reaction was proposed:

Na₃FeF₆ + 3Na ⇄ 6NaF + Fe.

However, the NaF and Fe peaks in the ex situ XRD are nearly indistinguishable from the baseline and incommensurate with the reported capacity, which suggests an incomplete understanding of the conversion mechanism at play. Thus, a closer investigation of the reaction process and limitations of Na₃FeF₆ is warranted.

In the present work, we revisit Na₃FeF₆ and aim for a complete understanding of key performance limitations to inform the design of next-generation NIB conversion electrodes. Here, Na₃FeF₆ is prepared through a similar mechanochemical method as Shakoor et al.,¹⁴ as well as a new assisted-microwave synthesis method. The latter is a rapid, environmentally-friendly, all solid-state synthesis method allowing for the facile preparation of inorganic materials,¹⁷ and this work demonstrates its promise for the preparation of battery electrode materials. Inspired by the need to test NIB materials in practical electrode setups and determine the intrinsic charge storage capacity of the conversion material in composite electrodes, we investigate the dependence of the electrochemical reversibility of Na₃FeF₆ on the electrode loading density and separate the capacity contributions associated with Na₃FeF₆ and with the conductive carbon matrix. We answer the question of why this material cannot reach its full conversion capacity based on Shakoor et al.'s proposed mechanism¹⁴ through an in-depth characterization of the long- and short-range chemical changes occurring on cycling. For this, we employ a suite of tools sensitive to both amorphous and crystalline phases, including synchrotron X-ray diffraction (SXRD), ²³Na/¹⁹F solid-state nuclear magnetic resonance (NMR) complemented with first principles calculations of NMR parameters, ⁵⁷Fe Mössbauer spectroscopy, magnetometry, and X-ray photoelectron spectroscopy (XPS). Our results indicate that the primary performance bottleneck of Na₃FeF₆ is the kinetic limitations of the conversion process due to the formation of insulating NaF domains that are also poorly Na⁺ conducting on discharge, leading to a low discharge capacity and rapid capacity decay on subsequent cycles. Interestingly, the impact of the electrode film thickness on the capacity and its retention is minimal, indicating that the kinetic limitations are already present at the (≤100 nm) particle scale. We also find that ex situ characterization of the electrode samples is complicated by the spontaneous oxidation of metastable Fe conversion phases during cell disassembly and sample handling (even in an inert environment), and develop a novel and robust analytical framework based on local structure probes and galvanostatic cycling to determine the true underlying conversion processes.

Results & discussion

Characterization of as-synthesized Na₃FeF₆

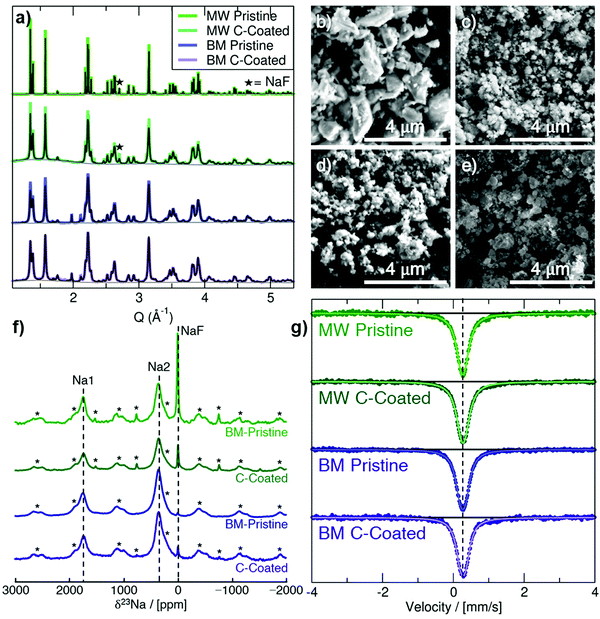
Na₃FeF₆ forms a distorted ordered double perovskite structure, more clearly written as (Na2)₂(Na1)FeF₆, with space group P2₁. This structure (Fig. S1, ESI†) is characterized by tilted corner-sharing (Na1)F₆ and FeF₆ octahedra, with the two remaining Na atoms filling the Na2 sites between the octahedral chains. Synchrotron XRD (SXRD) patterns collected on pristine and C-coated Na₃FeF₆ samples prepared via mechanochemical/ball-mill (BM) and microwave (MW) synthesis are shown in Fig. 1a along with their Rietveld refinements. A small NaF precursor impurity phase is seen at Q = 2.71 Å⁻¹ for the MW samples and a ZrO₂ impurity is seen at Q = 1.98 and 2.12 Å⁻¹ for the BM samples from the jars used for the milling. As summarized in Table S1 (ESI†), the Na₃FeF₆ lattice parameters for the as-synthesized materials show little variation between samples and are in good agreement with previously reported structures. The peak broadening observed for the BM and C-coated samples obtained by ball-milling with a conductive carbon additive is attributed to the formation of ≤100 nm particles upon high-energy milling, as shown in the scanning electron microscopy (SEM) images in Fig. 1b–e. This procedure may also result in strained particles and an overall decrease in crystallinity, which could also contribute to peak broadening. The greater size of the particle agglomerates in the C-coated materials (Fig. 1c and e) indicates successful formation of a C nanocomposite.¹⁸

Fig. 1 Structural characterization of as-prepared Na₃FeF₆ materials. (a) SXRD pattern and Rietveld refinement (black) for each sample. (b–e) SEM images obtained of MW pristine (b), MW C-coated (c), BM pristine (d), and BM C-coated (e) samples. (f) ²³Na spin echo NMR spectra collected on the as-prepared materials. Each spectrum is scaled according to the number of moles of material in the rotor and the number of scans collected during the experiment. Spinning sidebands are indicated by an asterisk (*). (g) Zero-field, 298 K ⁵⁷Fe Mössbauer spectra obtained on the as-prepared materials. The dashed line corresponds to an isomer shift (δ) of 0.27 mm s⁻¹ typical of an Fe³⁺ ion in an octahedral environment.

²³Na and ¹⁹F solid-state NMR experiments were conducted to obtain further insights into the local structure of Na₃FeF₆. The presence of open-shell Fe³⁺ species in these compounds results in strong paramagnetic interactions between unpaired electron spins nominally present in the Fe 3d orbitals and ²³Na/¹⁹F nuclear spins. These strong interactions result in significant NMR line broadening and large chemical shifts, complicating the attribution of spectral features to specific local environments in the material. Here, the assignment of the complex NMR spectra is assisted by first principles hybrid density functional theory (DFT)/Hartree Fock (HF) calculations of paramagnetic ²³Na and ¹⁹F NMR parameters using the CRYSTAL17 code on the optimized Na₃FeF₆ structure (details of the analysis in the ESI†). The isotropic chemical shift (δ_iso) of ²³Na and ¹⁹F nuclei in Na₃FeF₆ is dominated by the paramagnetic (Fermi contact) shift resulting from delocalization of unpaired electron spin density from the Fe 3d orbitals to the ²³Na/¹⁹F s orbitals. For an I = 3/2 quadrupolar nucleus such as ²³Na, the interaction between the nuclear quadrupole moment and the electric field gradient (EFG) present at the nucleus leads to a further broadening of the spectrum and to a shift of the ²³Na resonant frequency due to second-order effects (denoted δ_Q). The observed chemical shift (δ_obs) is then the sum of the isotropic Fermi contact shift and of the second-order quadrupolar shift: δ_obs = δ_iso + δ_Q. In contrast, ¹⁹F is a spin-1/2 nucleus with no quadrupole moment and so δ_obs = δ_iso.

²³Na NMR characterization of the as-synthesized and C-coated materials is shown in Fig. 1f. There are three main signals in the ²³Na NMR spectra: a diamagnetic signal at 0 ppm assigned to NaF and two paramagnetic signals near 350 ppm and 1750 ppm. The 350 and 1750 ppm signals observed experimentally are consistent with the computed NMR shifts for Na2 and Na1 sites in the Na₃FeF₆ structure, respectively, as summarized in Table 1. We note that two calculations were performed using two different hybrid DFT/HF exchange–correlation functionals (H20 and H35) as it has been shown that paramagnetic NMR shifts computed using the H20 and H35 functionals provide approximate upper and lower bounds to the observed shift, respectively. This is confirmed here with, e.g., the 350 ppm experimental shift lying in between the 120 ppm (H35) and 457 ppm (H20) values computed for Na2. By fitting the spectra in Fig. 1f to extract the relative integrated intensity of each ²³Na resonance, scaled by the transverse relaxation time (T₂′) to account for signal loss over the course of the experiment, we can deduce the population of NaF, Na1 and Na2 environments in the sample. We find that <1% of the integrated ²³Na signal intensity corresponds to NaF for the two BM samples, whereas about 7% (±3%) of the integrated ²³Na signal intensity corresponds to NaF for the two MW samples. In all spectra, the ratio of Na2 : Na1 present is 2 (±0.2) : 1, consistent with the multiplicity of Na1 and Na2 sites in the Na₃FeF₆ = (Na2)₂(Na1)FeF₆ crystal structure.

Table 1 First principles ²³Na paramagnetic NMR parameters computed on Na₃FeF₆ using the B3LYP hybrid functional with 20% (H20) and 35% (H35) Hartree–Fock exchange, respectively, as implemented in the CRYSTAL17 code. The predicted NMR properties were computed on ferromagnetically-aligned cells and subsequently scaled using a magnetic scaling factor Φ = 0.0328 to compare with the room temperature (paramagnetic) ²³Na solid-state NMR data obtained at an external magnetic field of B₀ = 7.05 T. δ_iso is the isotropic Fermi contact shift, δ_Q the second-order quadrupolar shift, and δ_obs = δ_iso + δ_Q the observed chemical shift

Environment	Parameter	OPT H20	OPT H35
Na1 (x1)	δ iso/ppm	2564	1923
	δ Q/ppm	−20	−20
	δ obs/ppm	2544	1903
Na2 (x2)	δ iso/ppm	484	148
	δ Q/ppm	−27	−28
	δ obs/ppm	457	120

---

The only signal observed in ¹⁹F NMR data shown in in Fig. S2a (ESI†) is the NaF impurity phase at −224 ppm. In agreement with the SXRD and ²³Na NMR data, this impurity does not appear for the BM samples and decreases for the MW samples after C-coating. No paramagnetic ¹⁹F NMR signal attributable to the Na₃FeF₆ phase is observed in the spectra. While this result may be surprising at first, it can easily be explained by the fact that NMR resonances associated with ¹⁹F nuclei directly bonded to paramagnetic species (here, Fe³⁺) are too broad and too short lived to be observed, as we recently showed in related electrode compounds.¹⁹

⁵⁷Fe Mössbauer spectra are shown in Fig. 1g for the as-synthesized materials. All Mössbauer spectra exhibit a singlet with an isomer shift (δ) of about 0.27 mm s⁻¹ and a small quadrupole splitting (ΔE_Q) of 0.1 to 0.15 mm s⁻¹ (exact values shown in Table S4, ESI†). This signal can be assigned to octahedrally-coordinated Fe³⁺ (O_h-Fe³⁺) surrounded by six F⁻ anions,²⁰ in good agreement with the Na₃FeF₆ crystal structure. The slightly larger quadrupole splitting in the BM samples is likely due to an increased amount of structural disorder, as expected from high-energy milling.

The magnetic susceptibility data collected on the pristine BM and MW Na₃FeF₆ powders are shown in Fig. S2b (ESI†). The susceptibility χ of the BM sample exhibits Curie–Weiss-like behavior, i.e., 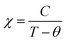, where C is the Curie constant, T is the temperature, and θ is the Weiss constant. A fit of the susceptibility data obtained between 150 and 350 K yields C = 4.211 emu K mol⁻¹ Oe⁻¹ and θ = −10 K. The value of C correlates with an effective magnetic moment (μ_eff) of 5.85 μ_B per Fe atom, indicating the presence of high-spin Fe³⁺ (theoretical spin-only magnetic moment μ^theo_SO(Fe³⁺) = 5.92 μ_B), which is consistent with the ⁵⁷Fe Mössbauer results. The small and negative θ = −10 K obtained for BM-Na₃FeF₆ is consistent with the previously reported value of θ = −12 K²¹ and suggests that this material is weakly antiferromagnetic. In contrast to BM-Na₃FeF₆, attempts to fit the susceptibility of MW-Na₃FeF₆ with the Curie–Weiss equation resulted in nonphysical properties. We suspect that this sample contains a small amount of an amorphous, unreacted FeF₃ phase compensating for the NaF impurity phase observed via NMR. This impurity is impossible to distinguish from the major Na₃FeF₆ phase via⁵⁷Fe Mössbauer spectroscopy, as both compounds have similar local Fe³⁺ environments and therefore similar resonances.

In summary, we have demonstrated that high-energy ball-milling and assisted-microwave synthesis are two possible preparation routes for Na₃FeF₆. While BM-Na₃FeF₆ is almost completely phase pure (with less than 1% of the total Na molar content in NaF domains), MW-Na₃FeF₆ has a moderate amount of NaF and FeF₃ impurities detected by ²³Na/¹⁹F NMR and magnetometry, respectively. Thus, despite being a fast and environmentally-friendly synthesis method,¹⁷ the assisted-microwave synthesis protocol used here is unable to produce as high purity of a material as mechanochemical synthesis.

Electrochemical properties

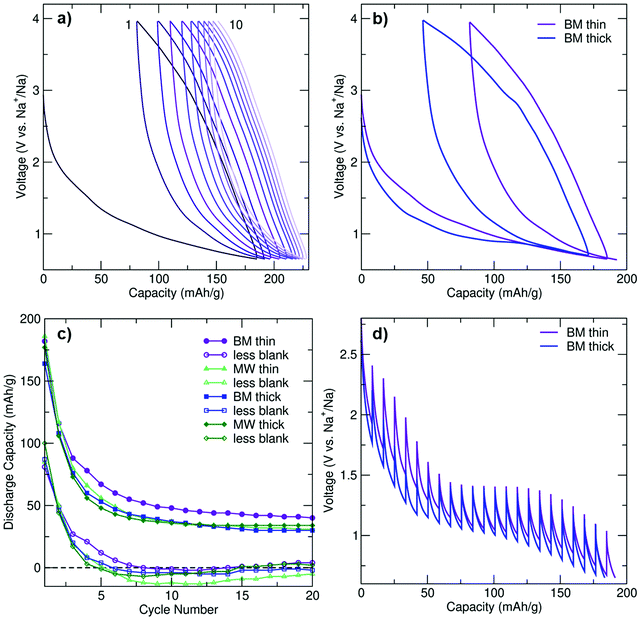
To determine the role of the electrode loading density on performance, the electrochemical properties of thin and thick (3 and 12 mg cm⁻² loading density, respectively) electrode films composed of BM and MW C-coated Na₃FeF₆ were investigated using galvanostatic cycling at a rate of C/20 (full (dis)charge in 20 hours) between 0.65 and 4 V vs. Na⁺/Na. Negligible capacity (<14 mA h g⁻¹) was observed when the cells were charged first (Fig. S3a, ESI†), indicating that a very small amount of Na (if any) can be extracted from the pristine structure. A rate of C/20 was used throughout as faster rates resulted in decreased capacities and reversibility (Fig. S3a, ESI†). Hence, all of the data shown in Fig. 2 and Fig. S3b–d (ESI†) were obtained on cells discharged first at a rate of C/20. As shown in Fig. S3b (ESI†), particle size reduction and C coating is required to achieve appreciable electrochemical activity from the intrinsically insulating Na₃FeF₆ phase.

Fig. 2 Electrochemical characterization of Na₃FeF₆. (a) First ten cycles for BM-Na₃FeF₆ thin cells (C/20 rate). (b) First two charge and discharge cycles for BM-Na₃FeF₆ thin and thick cells (C/20 rate). (c) Discharge capacity retention for Na₃FeF₆ cells (filled symbols) and for Na₃FeF₆ cells with the corresponding blank cell capacity subtracted (unfilled symbols). Three cells were averaged for each point. (d) GITT test (C/20 rate) for the first discharge cycle of BM thin and thick cells.

Galvanostatic electrochemical profiles are shown in Fig. 2a and b for the BM thin and BM thick electrodes, and Fig. S3c (ESI†) for the MW thin and MW thick electrodes. All cells exhibit first discharge capacities between 160 and 190 mA h g⁻¹, with significant capacity fade (>36%) on second discharge. The discharge capacity retention of BM and MW thin and thick electrodes over the first 20 cycles is shown in Fig. 2c. For each electrode type, the total capacity and the actual Na₃FeF₆ active material capacity obtained after subtracting the capacity of a thin or thick blank cell (as appropriate) are depicted. The blank cells (NaF in place of Na₃FeF₆) provide an estimate of the capacity due to the presence of a significant amount of conductive carbon additive in the composite Na₃FeF₆ electrodes (32 wt%). Galvanostatic cycling (Fig. S3d, ESI†) of these blank cells results in sloping electrochemical profiles with an average potential of 1.3 V and an initial reversible capacity of 75 and 100 mA h g⁻¹ for the thick and thin blank cells, respectively, that gradually decays on subsequent cycles. Thus, a significant fraction of the capacity observed for the Na₃FeF₆ electrodes arises from Na intercalation into the C matrix rather than the conversion process, as shown in Fig. 2c, with more Na intercalation into C expected for the thin electrodes. MW Na₃FeF₆ electrodes feature higher initial discharge capacities, but also faster capacity fade compared to their BM counterparts, likely due to the presence of an electrochemically active FeF₃ impurity.^22,23 Notably, the BM thin cell exhibits less capacity fade and a higher average potential (1.2 V vs. 1.1 V) compared to all other electrode formulations, and a more sloping discharge profile compared to that of the BM thick cell, as supported by the dQ/dV comparison shown in Fig. S3f (ESI†). Hence, for the high purity BM Na₃FeF₆ electrodes, thinner electrode films appear to enhance the reversibility of the charge–discharge reactions.

To investigate the origin of this loading density-dependent performance, galvanostatic intermittent titration technique (GITT) tests were conducted on BM-Na₃FeF₆ thin and thick electrodes, as shown in Fig. 2d. Following a 30 minute C/20 current pulse, the voltage was allowed to equilibrate for 4 hours to obtain an estimate of the equilibrium voltage and overpotential. A clear equilibrium voltage plateau is observed at 1.4 V for both electrodes in the GITT tests. In contrast, this plateau is only clearly visible in the galvanostatic voltage profile of the thick electrode cell and at a lower voltage of 0.95 V (see Fig. 2b), presumably due to the significant polarization upon galvanostatic discharge at a rate of C/20.

The evolution of the polarization or overpotential during the first discharge process as obtained from the GITT tests is plotted in Fig. S3e (ESI†). For the thick electrode, the overpotential initially decreases from 0.55 V at 10 mA h g⁻¹ to 0.3 V at 50 mA h g⁻¹. For the thin electrode, a similar albeit delayed decrease in the overpotential is observed from 30 mA h g⁻¹ to 60 mA h g⁻¹. We attribute this electrochemical region (≤50–60 mA h g⁻¹ of capacity) to Na intercalation into the C matrix and explain the decrease in overpotential to gradually more facile Na insertion upon discharge. The delay in the overpotential decrease in the case of the BM thin electrode may be due to side reactions and/or greater Na intercalation into C during the initial stages of discharge (at high voltage), which is consistent with the higher average potential observed for the thin BM electrode (Fig. 2b). Furthermore, greater Na intercalation into the C matrix of the thin BM electrode is consistent with its more sloping voltage profile and the absence of a clear electrochemical plateau in its galvanostatic profile.

The 1.4 V equilibrium voltage plateau region (50–60 to 150 mA h g⁻¹ of capacity) of the GITT curves in Fig. 2d is assigned to bulk Na₃FeF₆ conversion, and the steady increase in the overpotential up to 0.45 V for both electrodes is attributed to a kinetically-hindered conversion process and the build-up of insulating NaF domains that are also poorly Na⁺ conducting, as will be discussed later. Perhaps unsurprisingly, the 0.45 V overpotential value matches the voltage difference between the 0.95 V electrochemical plateau observed during galvanostatic cycling for the thick BM electrode and the 1.4 V equilibrium voltage obtained from GITT tests, indicating that kinetic limitations are important when cycling at a rate of C/20. The thin BM electrode results suggest that, at low electrode loading densities, Na intercalation into the C matrix is kinetically-preferred over Na₃FeF₆ conversion over the plateau region. Indeed, Na intercalation into C is more prevalent when the cell is discharged at C/20 without resting periods, resulting in a sloping galvanostatic profile and no voltage plateau (Fig. 2b). Yet, when the cell is allowed to rest at regular intervals (GITT results), or for thicker electrode films, differences in the rate of Na intercalation and Na₃FeF₆ conversion are reduced and a clear electrochemical plateau is observed (Fig. 2d).

In summary, the electrochemical performance is improved in the higher purity BM electrodes although the rapidly prepared MW electrodes perform comparably. While electrodes prepared with a lower loading density (e.g., BM thin) result in greater Na intercalation into the carbon matrix at practical C rates, leading to more sloping profiles and a greater average potential, the electrode loading density does not seem to affect the Na₃FeF₆ conversion mechanism nor its efficiency. The capacity fades quickly for all cells likely due to the significant kinetic limitations and irreversibility of the conversion process. Our comparison of the electrochemical activity of the C-coated Na₃FeF₆ cells with blank cells is particularly informative in this regard (Fig. 2c), as it clearly shows some electrochemical activity from the Na₃FeF₆ active material for the first 5 cycles, but past cycle 5 most of the capacity is attributable to Na intercalation into carbon. Thus, we conclude that Na₃FeF₆ suffers from severe charge–discharge irreversibility and is only electrochemically-active for about 5 cycles.

Characterization of conversion processes

To elucidate the reaction processes and causes of charge–discharge irreversibility for the Na₃FeF₆ conversion-type electrode, we carried out an in-depth characterization of ex situ electrode samples collected over the first 10 cycles, through a combination of solid-state NMR, SXRD, XPS, magnetometry and ⁵⁷Fe Mössbauer measurements.

High resolution ex situ SXRD was performed on several MW thick Na₃FeF₆ electrodes at various states of charge to identify the crystalline phases forming on (dis)charge as shown in Fig. S4 (ESI†). All patterns can be successfully fitted with contributions from Na₃FeF₆ (P2₁) and NaF (Fm3̄m) phases. The amount of NaF increases on discharge and decreases on charge, consistent with a conversion process. Moreover, low intensity reflections at Q ≈ 1.3, 1.9, 2.1, 2.4, 3.1, and 3.8 Å⁻¹ indicate the formation of a small amount of (a) crystalline phase(s) on discharge that is only partially reversible on subsequent charge. Yet, none of our attempts to match these reflections to any of the known Na-, Fe-, O- or F-containing phases in the International Crystal Structure Database (ICSD) database were successful (full list of attempted phases in Table S5, ESI†). The unidentifiable crystalline phase(s) appear(s) to only account for a small fraction of the sample and could potentially arise from side-reactions (e.g., electrolyte decomposition). A broad baseline is noticeable in all but the pristine sample due to its significantly higher signal intensity. This baseline is predominantly attributed to the Kapton capillary used to hold the sample, although contributions from amorphous phase(s) formed during the conversion process cannot be excluded for patterns collected on ex situ cycled sample. Notably, we could not detect any crystalline α-Fe in our ex situ samples, in contrast to Shakoor et al.'s findings.¹⁴ Yet, in this previous study, the claimed Fe reflections are extremely difficult to discern from the noise in the ex situ patterns. Overall, our results exemplify the limited utility of long-range diffraction techniques to monitor conversion processes, and warrant the implementation of more local and quantitative probes to gain insights into nano-sized and disordered/amorphous phases during cycling. Specifically, our ex situ SXRD results indicate the conversion of Na₃FeF₆ to NaF on discharge, yet are unable to identify any Fe-containing crystalline phase and cannot rule out the possibility of forming amorphous Fe nanoparticles, as has been reported in related conversion electrodes.^24,25

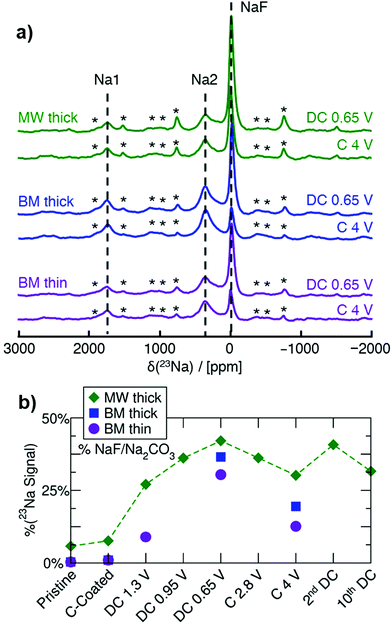
Ex situ ²³Na NMR is key in understanding the conversion behavior of Na₃FeF₆, as it enables us to identify and quantify both crystalline and amorphous Na-containing phases formed on (dis)charge. MW thick, BM thick and BM thin electrodes are examined here to investigate the impact of synthesis and electrode loading density on the degree of conversion during cycling. ²³Na spin echo spectra collected on ex situ samples stopped at the end of the initial discharge to 0.65 V, and upon subsequent charge to 4 V, for the three electrode types, are shown in Fig. 3. A more in-depth NMR analysis of a series of ex situ thick MW electrodes is shown in Fig. S5 (ESI†). The three main resonances at ≈0 ppm (NaF), 1750 ppm (Na1), and 350 ppm (Na2), present in the spectra collected on the as-synthesized materials (Fig. 1f) are also observed in the ex situ spectra, albeit with varying relative intensities as expected from the conversion process. Notably, no new ²³Na NMR signal appears on cycling. The evolution of the amount of diamagnetic Na-containing phase during cycling is obtained from the fitted ²³Na signal intensity at ≈0 ppm and shown in Fig. 3b, with the remainder of the ²³Na NMR signal intensity attributed to Na₃FeF₆. Although most of the diamagnetic ²³Na signal can be attributed to NaF present in the pristine MW sample or formed on discharge, we cannot rule out a small contribution to the 0 ppm signal intensity from Na₂CO₃ formed upon decomposition of the carbonate electrolyte and reaction with Na during cycling. Overall, the NaF signal increases on discharge and decreases on charge, with at least 50% of the total ²³Na signal intensity arising from the Na₃FeF₆ phase even at the bottom of discharge. Thus, Na₃FeF₆ conversion is incomplete on discharge and only partially reversible on subsequent charge.

Fig. 3 ²³Na NMR of ex situ Na₃FeF₆. (a) ²³Na spin echo NMR spectra of ex situ Na₃FeF₆ with each spectra scaled according to number of moles of material in the rotor and the number of scans used in the experiment. Spinning sidebands are indicated by an asterisk (*). (b) Percent of the ²³Na signal (±5%) after accounting for signal relaxation over the course of the NMR measurement (T₂′ losses) corresponding to diamagnetic NaF at various states of charge.

Complementary ex situ¹⁹F NMR experiments were performed to gain further insights into NaF formation during cycling. The ¹⁹F NMR spectra are shown in Fig. S6 (ESI†) and exhibit three main signals: the NaF resonance at −224 ppm, the PTFE binder resonance at −122 ppm, and a resonance at −74.5 ppm indicating adsorption of electrolyte salt (e.g. PF₆⁻) at the surface of the particles.²⁶ Overall, the relative intensity of the NaF signal, as shown in Fig. S6d (ESI†), follows the same trend as that already discussed for NaF through ²³Na NMR, confirming that Na₂CO₃ contributes minimally to the diamagnetic (≈0 ppm) resonance in the ²³Na NMR data.

After adjusting for the presence of NaF in the as-synthesized materials (see Table S6, ESI†), ²³Na and ¹⁹F NMR results indicate that high purity BM Na₃FeF₆ electrodes result in a higher degree of reconversion of NaF on charge (24 mol%) compared to MW Na₃FeF₆ (14 mol%), and therefore a higher degree of reversibility. Consistent with the electrochemical results presented earlier, the thinner BM electrode exhibits a low amount of conversion to NaF when discharged to 1.3 V (14 mol%) whereas the thicker MW electrode shows much more conversion (40 mol%), indicating that a larger amount of the observed electrochemical capacity in the thin electrodes is attributable to the carbon additive rather than Na₃FeF₆ conversion. Thus, the higher reversibility of the thinner electrode is partially attributed to Na⁺ intercalation into carbon^27,28 and/or capacitive storage at the surface of particles,^29,30 as these processes are fairly reversible.

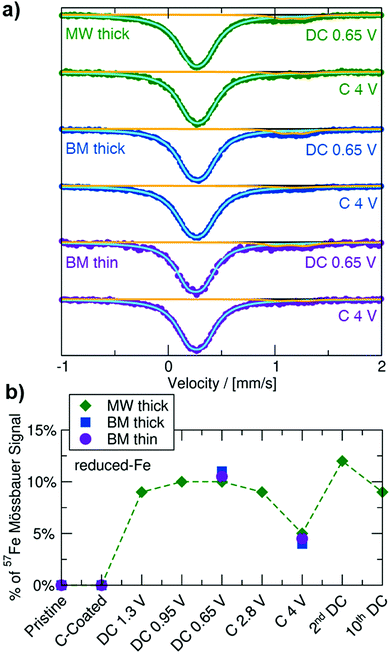
To monitor changes to the Fe redox state and local coordination environment on cycling, and to facilitate the identification of (a) new Fe-containing phase(s) formed during electrochemical cycling, ⁵⁷Fe Mössbauer experiments were performed on ex situ MW thick, BM thick and BM thin electrode samples collected at the end of the initial discharge to 0.65 V, and upon subsequent charge to 4 V, with results shown in Fig. 4 and values summarized in Table S4 (ESI†). All ex situ spectra exhibit a main (≥88%) resonance with similar δ and ΔE_Q values as the O_h-Fe³⁺ signal observed for the pristine Na₃FeF₆ powders. A minority (≤12%) doublet signal at δ ≈ 1.16 mm s⁻¹ with ΔE_Q ≈ 0.2 mm s⁻¹ is present in the spectra obtained on discharge and is attributed to a “reduced-Fe” species. Additional characterization of samples discharged to 0.65 V via XPS and magnetometry (details in Note S2, ESI†) suggests the presence of an amorphous Fe²⁺-containing phase that may also contain Fe³⁺ species. The evolution of the total ⁵⁷Fe Mössbauer signal throughout (dis)charge, as seen in Fig. 4b, shows minimal change in this “reduced-Fe” signal. Clearly, the absence of a significant change to the main ⁵⁷Fe Mössbauer resonance upon cycling cannot simply be interpreted as a lack of electrochemical conversion, as ²³Na NMR indicated significant Na₃FeF₆ conversion to NaF upon cycling. Instead, part of the main O_h-Fe³⁺ signal may come from relaxation^24,31 and/or oxidation^32,33 of the newly formed metastable conversion products to (a) O_h-Fe³⁺ containing phase(s) upon removal from the cell for ex situ characterization, complicating the analysis of the Fe redox behavior by ex situ⁵⁷Fe Mössbauer spectroscopy, XPS, and magnetometry.

Fig. 4 ⁵⁷Fe Mössbauer of ex situ Na₃FeF₆. (a) ⁵⁷Fe Mössbauer spectra of ex situ Na₃FeF₆ fit with two doublets for O_h-Fe³⁺ and reduced-Fe. (b) Change in the amount of ⁵⁷Fe signal (±2%) corresponding to the O_h-Fe³⁺ and reduced-Fe species at different states of charge.

Na₃FeF₆ conversion process and key insights into performance limitations

The reactive nature of the Fe-containing discharged products prevents the exploration of the electrochemical conversion mechanism using ex situ Fe probes, such as Mössbauer, XPS and magnetometry. Thus, the way to obtain insights into the conversion mechanism is to carry out real-time operando measurements or focus on ex situ experiments capable of identifying and quantifying stable conversion products (here, NaF). We employ the latter strategy here, and recall that ²³Na NMR is uniquely suited to quantitatively characterize all crystalline and amorphous Na-containing phases appearing upon (dis)charge. The only signals observed via²³Na NMR (Fig. 3) are NaF and Na₃FeF₆. Thus, NaF is the only Na-containing phase formed on discharge. Regarding Fe-containing phase(s) formed upon conversion, we consider two possible processes:

Mechanism A: Na₃FeF₆ + 3Na ⇄ 6NaF + Fe

and

Mechanism B: Na₃FeF₆ + Na ⇄ 4NaF + FeF₂.

To distinguish between these two reaction pathways, ²³Na NMR can be used to compute the expected capacity based on mechanisms A and B (with theoretical capacities of 337 and 112 mA h g⁻¹, respectively) and on the observed mol% of NaF formed at various states of charge (SOCs), and compare the expected capacities to the observed capacity at these SOCs. We note here that the observed capacity is the actual Na₃FeF₆ active material capacity obtained after subtracting the capacity of the blank cell. Table S6 (ESI†) shows the details of this analysis at various SOCs for MW thick, BM thick, and BM thin electrodes. Clearly, the observed capacity at the end of discharge is much larger than what would be expected for mechanism B, whereas the expected capacity for mechanism A is in much better agreement with what is observed experimentally, albeit still moderately lower. The good agreement between the expected capacity based on mechanism A and the observed capacity leads us to conclude that Na₃FeF₆ + 3Na ⇄ 6NaF + Fe is the likely reaction pathway. The small discrepancies between the expected and observed capacities in this scenario can be explained by the intrinsic limitations of our fits of the NMR data (the mol% of NaF phase in the samples extracted from the fits is accurate to ±5%), and how we have estimated the capacity solely attributable to Na₃FeF₆ conversion by subtracting out the blank cell capacity. Additionally, the presence of a small amount of electrochemically active FeF₃ in the MW Na₃FeF₆ electrode, which is unobservable in ²³Na/¹⁹F NMR, also likely contributes additional experimental capacity that we have not accounted for in our calculations. Overall, our analysis suggests the incomplete conversion of Na₃FeF₆ (no more than 60%) to NaF and Fe on discharge through mechanism A. As these Fe nanoparticles are likely less than a few nanometers in diameter,³⁴ they are metastable and oxidize upon ex situ analysis, even upon minimal exposure to ambient air (electrodes opened and samples handled in an inert atmosphere at all times). Additionally, ⁵⁷Fe Mössbauer analysis of a chemically reduced BM Na₃FeF₆ powder sample (Fig. S8, ESI†) shows a clear Fe⁰ singlet at δ = 0 mm s⁻¹, confirming that Fe⁰ does in fact form on chemical reduction, with a small reduced-Fe signal similar to our previous Mössbauer results (Fig. 4) also observed. We hypothesize that this Fe⁰ phase is still present in the chemically reduced ex situ Mössbauer spectra as these Fe particles are much larger than those obtained electrochemically and thus spontaneous Fe oxidation only occurs around the exterior of the particles.

The present work demonstrates that Na₃FeF₆ undergoes a conversion reaction to NaF and Fe on discharge, with the reverse transformation occurring on subsequent charge. While this process should provide a high capacity of 337 mA h g⁻¹, the electrochemical performance is limited by incomplete and poorly reversible phase transformations during cycling. Despite all particles in the C-coated starting materials being ≤100 nm in size, the sluggish conversion kinetics are exacerbated by the formation of NaF domains on the exterior of the Na₃FeF₆ particles. A schematic of the expected conversion process throughout a Na₃FeF₆ electrode particle is shown in Fig. 5. The exterior of the particles is expected to undergo conversion through mechanism A, but the interior of the particles is unable to convert on the time-scale of the electrochemical experiments as this process hinges on both Na diffusion and electron tunneling through the poorly Na⁺ conducting and insulating NaF. Indeed, NaF is a wide bandgap insulator, with a reported bandgap of 11.5 eV,^35,36 as well as a very poor Na⁺ conductor, with large predicted Na⁺ migration barriers (>1 eV) at room temperature,³⁷ indicating that both transport processes are exceedingly kinetically limited.

Fig. 5 Na₃FeF₆ conversion mechanism schematic. Schematic diagram of conversion of Na₃FeF₆ particle from Na₃FeF₆ (green) in a PTFE (yellow) and carbon (black) electrode composite to a shell of NaF (blue) with interspersed Fe (silver) nanoparticles with an unreacted core of Na₃FeF₆.

In an effort to facilitate more facile Na⁺ and electron transport, we have attempted to further decrease the Na₃FeF₆ particle size through an additional ball-milling step with a mixture of grinding ball sizes. SEM images of the resultant particles are shown in Fig. S9a (ESI†) where the particles are now reduced to about 60 nm. The first charge–discharge cycle for this extended ball-milling compared to the BM thin electrodes is shown in Fig. S9b (ESI†) with the capacity fade in Fig. S9c (ESI†). While the initial discharge capacity is not improved with these decreased particles, the reversibility is increased, albeit, still quickly fading with little to no capacity attributed to Na₃FeF₆ past cycle 15. Cycling this sample at faster rates (Fig. S9d, ESI†) results in comparable discharge capacities observed for C/20 and C/10 rates but with faster capacity fade observed for the higher rates. Thus, despite further reducing the particle sizes, Na₃FeF₆ is still intrinsically plagued by poor transport properties.

As the dominant kinetic limitation for Na₃FeF₆ prepared in this study is charge transport (Na⁺ ions and electrons) into the interior of the particles, rather than through the bulk of the electrode film, the film thickness does not affect the kinetics nor the reversibility of the Na₃FeF₆ conversion process. In fact, lower loading densities lead to more facile Na intercalation into the carbon additive rather than more conversion of the Na₃FeF₆ material. These results suggest that the energy density of Na₃FeF₆ and other fluoride-type Na-based conversion electrodes may be further increased through the preparation of thick electrodes utilizing nanosized particles of the active material embedded into a carbon matrix (e.g. carbon nanotubes), to further enhance the electronic conductivity of the composite. Ultimately, both the electronic conductivity and the Na⁺ diffusion properties of the discharged products are key considerations for the design of higher rate and reversible conversion electrodes, and sulfide- and oxide-type conversion electrodes may compare more favorably than fluoride-based compounds.

Conclusion

For the first time, Na₃FeF₆ was prepared through a rapid and sustainable assisted-MW preparation method. Electrochemical testing revealed that several distinct electrochemical processes occur in Na₃FeF₆ composite electrodes. Notably, carbon additives in the electrode film account for a large fraction of the observed capacity in this and other conversion-type fluoride electrodes, and thus should be accounted for in future studies of this class of materials. We identified that Na₃FeF₆ converts to NaF and Fe on discharge, as previously proposed. While this mechanism should yield a high theoretical capacity, conversion is incomplete and only moderately reversible due to sluggish conversion reaction kinetics that are exacerbated by the formation of insulating NaF domains with poor Na⁺ diffusion properties on the exterior of the Na₃FeF₆ particles. Further, we found that ex situ characterization data on the metastable Fe-containing phases formed on discharge are challenging to interpret due to spontaneous oxidation processes occurring during cell disassembly and/or sample handling, even in an inert environment. We devised a simple ex situ analytical method that relies on the quantification of stable conversion products using local structure probes (here, NaF characterized through ²³Na NMR) and a comparison with the observed capacity, to determine the conversion mechanism at play. This novel analytical framework holds promise for the study of a wide range of conversion processes that are often plagued by severe relaxation and oxidation processes during ex situ characterization. Ultimately, in situ and operando studies are better suited for the elucidation of conversion type processes and should be employed in the future for a more in-depth understanding of the thermodynamics and kinetics of conversion processes.

Experimental

Materials synthesis

Na₃FeF₆ was prepared via both microwave-assisted and mechanochemical methods using stoichiometric ratios of NaF (Strem, 99.99%) and FeF₃ (Sigma, 99.5%). For the microwave-assisted synthesis method, 300 mg of a ground stoichiometric mixture of the precursors was pressed into 6 mm pellets, placed inside BN crucibles, and sealed in vitreous silica ampules under 0.25 atm of Ar. The ampules were placed in a carbon-filled crucible and heated in a 1200 W domestic microwave oven (Panasonic, model NN-SN651WAZ) at 30% power (360 W) for 6 min. For the mechanochemical synthesis method, 1 g of a ground stoichiometric mixture of the precursors was placed in a 50 mL ZrO₂ ball-milling jar along with five 10 mm ZrO₂ balls and ten 5 mm ZrO₂ balls and sealed inside an Ar glovebox. The material was then ball-milled at 500 rpm for 24 h.

Electrochemical characterization

For all samples the Na₃FeF₆ active material was ball-milled for 24 h at 300 rpm with five 10 mm ZrO₂ balls with 34 wt% carbon (0.5 g in total) to form an electronically conductive carbon nanocomposite.¹⁸ This nanocomposite was then hand-ground with polytetrafluoroethylene (PTFE) for 15 minutes and made into electrodes with a 63 : 32 : 5 weight ratio of Na₃FeF₆ : C Super P : PTFE. The thick electrodes were prepared by pressing the electrode material into a thin 10 mm diameter pellet whereas for the thin electrodes the electrode material was hand-rolled into a film and punched into 6 mm disks. Their loading densities were 12 mg cm⁻² and 3 mg cm⁻², respectively. Blank cells were prepared in an analogous manner but now replacing the Na₃FeF₆ with NaF. All electrochemical testing occurred in Swagelok-type cells with an excess of 1 M NaPF₆ (≥99% Strem Chemicals) in EC : DMC (1 : 1 w/w, ≥99% Sigma-Aldrich) electrolyte with <25 ppm water content, a Na metal (Sigma-Aldrich) counter-electrode, and a glass fiber separator (Whatman GF/D).

Chemical reduction of the BM Na₃FeF₆ material was achieved by stirring a suspension of BM Na₃FeF₆ (25.0 mg, 0.1046 mmol) in anhydrous THF (2 mL) followed by the addition of Na metal (14.4 mg, 0.6281 mmol) and naphthalene (80.5 mg, 0.6281 mmol). The resulting green mixture was stirred at room temperature under an inert nitrogen atmosphere for three days, where the green coloration of the sodium naphthalenide had faded. The volatile components were then removed in vacuo, and the crude solid residue was analyzed spectroscopically.

Structural characterization

X-Ray diffraction. High-resolution synchrotron powder diffraction patterns were collected on Beamline 11-BM at the Advanced Photon Source (APS), Argonne National Laboratory using an average wavelength of 0.457897 Å. Room temperature data were collected between 2θ of 0.5° and 50°. Resulting patterns were refined using the Rietveld method in GSAS-II.³⁸

Solid-state nuclear magnetic resonance. ²³Na and ¹⁹F ssNMR data were collected on the Na₃FeF₆ pristine and ex situ samples using a Bruker Avance 300 MHz (7.05 T) super wide-bore NMR spectrometer with Larmor frequencies of 79.48 MHz and 282.40 MHz, respectively, at room temperature. The data were obtained at 60 kHz magic-angle spinning (MAS) using a 1.3 mm double-resonance HX probe. ²³Na and ¹⁹F NMR data were referenced against 1 M aqueous solutions of sodium chloride (NaCl, δ(²³Na) = 0 ppm) and sodium fluoride (NaF, δ(¹⁹F) = −118 ppm) and these samples were also used for pulse calibration. Lineshape analysis was carried out within the Bruker Topspin software using the SOLA lineshape simulation package. ²³Na spin echo spectra were acquired on all samples using a 90° radiofrequency (RF) pulse of 0.38 μs and a 180° RF pulse of 0.76 μs at 200 W. A recycle delay between 10 ms and 2 s was used with the exact value optimized for each sample to ensure the full ²³Na signal was fully relaxed between pulses. ²³Na pj-MATPASS (projected Magic-Angle Turning Phase-Adjusted Sideband Separation)³⁹ isotropic spectra were also acquired on the pristine samples using a 90° RF pulse of 0.38 μs at 200 W, with a recycle delay of 500 ms. Transverse (T₂′) relaxation times were obtained for each Na environment from an exponential fit of the decay of the signal intensity for each site as the echo delay was increased in an NMR spin echo pulse sequence, using an in-house MATLAB code written by Prof. Andrew Pell. ¹⁹F spin echo spectra were acquired on all samples using a 90° RF pulse of 4.9 μs and a 180° RF pulse of 9.8 μs at 200 W. A recycle delay between 500 ms and 2 s was used where the exact value was optimized for each sample to ensure the ¹⁹F NaF signal was fully relaxed between pulses. Further details on the analysis of the NMR results are provided in the ESI.†

Mössbauer spectroscopy. ⁵⁷Fe Mössbauer spectroscopy was performed using a SEECo Model W304 resonant gamma-ray spectrometer (activity = 100 mCi ± 10%, ⁵⁷Co/Rh source manufactured by Ritverc) equipped with a Janis Research Model SVT-400 cryostat system. The source linewidth was <0.12 mm s⁻¹ for the innermost lines of a 25 micron α-Fe foil standard. Isomer shifts were referenced to α-Fe foil at room temperature. All ⁵⁷Fe Mössbauer samples contained 10–20 mg of electrode material prepared inside an Ar filled glovebox. The sample was loaded into a plastic holder, coated with oil, capped, and then measured under a positive flow of N₂ at 298 K. The data were fit using MossA, a program developed by Clemens Prescher at the University of Bayreuth.⁴⁰

Magnetometry. Magnetic susceptibility measurements of pristine and ex situ samples of Na₃FeF₆ were measured with a Quantum Design Magnetic Property Measurement System 3 (MPMS) superconducting quantum interference device (SQUID) magnetometer. Samples of about 2 mg of Na₃FeF₆ were packed into a polypropylene holder in an Ar glovebox, snapped into a brass rod, and wrapped with a single layer of Kapton tape. Zero field-cooled (ZFC) and field-cooled (FC) susceptibility was measured on warming from 2 to 350 K in an applied field of 2000 Oe. Magnetic hysteresis curves were obtained at 2 K in the range of −7 T to 7 T.

X-Ray photoelectron spectroscopy. X-Ray photoelectron spectroscopy was performed on select pristine and ex situ samples. The samples were loaded onto an air-free sample holder in an Ar-filled glovebox. The powder was spread onto double-sided scotch tape attached to a stainless steel sample holder. A lid with an O-ring seal was secured onto the sample holder to transfer the samples into the XPS chamber. Once under vacuum, the lid was removed such that the samples were never exposed to air. The samples were measured using a Thermo Fisher Escalab Xi+ XPS equipped with a monochromated Al anode (E = 1486.7 eV). Survey scans were collected at 100 eV pass energy with 50 ms of dwell time; two scans were averaged. High resolution scans were collected for Fe from the pristine active material sample of Na₃FeF₆ at 20 eV pass energy with 100 ms of dwell time; five scans were averaged. Anticipating lower resolution from the discharged and charged ex situ Na₃FeF₆ samples, which were ground with carbon and polymeric binder for cycling, the Fe high resolutions scans were collected at a 20 eV pass energy with 100 ms of dwell time, and ten scans were averaged. Fits were executed using CasaXPS with Tougaard backgrounds and 60% Gaussian and 40% Lorentzian peak shapes. The spectra for the pristine Na₃FeF₆ was referenced to the adventitious carbon C 1s peak at 284.8 eV. The spectra for the ex situ samples were referenced to the C 1s peak of graphite at 284.4 eV.⁴¹

Calculation of NMR parameters

Spin-unrestricted hybrid density functional theory (DFT)/Hartree Fock (HF) calculations were performed using the CRYSTAL17 all-electron linear combination of atomic orbital code^42,43 to determine ²³Na and ¹⁹F NMR parameters in Na₃FeF₆. Two spin-polarized exchange–correlation functionals based upon the B3LYP form,^44–47 and with Fock exchange weights of F₀ = 20% (B3LYP or H20) and 35% (H35) were chosen for their good performance for the electronic structure and band gaps of transition metal compounds (B3LYP or H20),^48,49 and for their accurate description of the magnetic properties of related compounds (H35).^50–52 Besides, previous studies have shown that the hyperfine shifts calculated with the H20 and the H35 functionals on similar compounds are in good agreement with experiment.^53,54

All-electron atom-centered basis sets comprising fixed contractions of Gaussian primitive functions were employed throughout. Two types of basis sets were used: a smaller basis set (BS-I) was employed for structural optimizations, and a larger basis set (BS-II) was used for computing ²³Na and ¹⁹F NMR parameters which require an accurate description of the occupation of core-like electronic states. For BS-I, individual atomic sets are of the form (15s7p)/[1s3sp] for Na, (20s12p5d)/[1s4sp2d] for Fe, and (10s6p1d)/[4s3p1d] for F the values in parentheses denote the number of Gaussian primitives and the values in square brackets the contraction scheme. All BS-I sets were obtained from the CRYSTAL online repository and were unmodified from their previous use in a broad range of compounds.⁴² For BS-II, modified IGLO-III and (10s6p2d)/[6s5p2d] sets were adopted for F, a flexible and extended TZDP-derived (11s7p)/[7s3p] set was used for Na, and an Ahlrichs DZP-derived⁵⁵ (13s9p5d)/[7s5p3d] was adopted for Fe.

NMR parameters were computed on the fully optimized (atomic positions and cell parameters) Na₃FeF₆ structure (P2₁).⁵⁶ All first principles structural optimizations were carried out in the ferromagnetic (FM) state, after removal of all symmetry constraints (within the P1 space group) and using the H20 and H35 hybrid functionals. A 160 atom 2 × 2 × 2 supercell was used throughout. Structural optimizations were pursued using the quasi-Newton algorithm with RMS convergence tolerances of 10⁻⁷, 0.0003, and 0.0012 a.u. for total energy, root-mean-square (rms) force, and rms displacement, respectively. Tolerances for maximum force and displacement components were set to 1.5 times the respective rms values. Sufficient convergence in total energies and spin densities was obtained by application of integral series truncation thresholds of 10⁻⁷, 10⁻⁷, 10⁻⁷, 10⁻⁷, and 10⁻¹⁴ for Coulomb overlap and penetration, exchange overlap, and g- and n-series exchange penetration, respectively, as defined in the CRYSTAL17 documentation.⁴² The final total energies and spin and charge distributions were obtained in the absence of any spin and eigenvalue constraints. NMR parameters were obtained on ferromagnetically aligned supercells, and on supercells in which one Fe spin was flipped, using BS-II sets and a method identical to that described in Middlemiss et al.'s work.⁵⁴ Anisotropic Monkhorst–Pack reciprocal space meshes⁵⁷ with shrinking factors 6 9 3 were used for both H20 and H35 calculations. The lattice parameters for the Na₃FeF₆ structures relaxed using the H20 and H35 functionals are compared to the experimental (EXP) unit cell parameters⁵⁶ in Table S4 (ESI†).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work made use of the shared facilities of the UC Santa Barbara MRSEC (DMR 1720256), a member of the Materials Research Facilities Network (http://www.mrfn.org) and the computational facilities administered by the Center for Scientific Computing at the CNSI and MRL (an NSF MRSEC; CNS 1725797, DMR 1720256). E. E. Foley, R. C. Vincent, and E. Gonzalez-Correa were supported by the NSF Graduate Research Fellowship Program under Grant No. DGE 1650114. Synchrotron diffraction data was collected at beamlines 11-BM at the Advanced Photon Source, Argonne National Laboratory, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We gratefully acknowledge Howie Nguyen and Dr Ram Seshadri for the helpful discussions regarding magnetic measurements.

References

1. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: present and future, Mater. Today, 2015, 18, 252–264.
2. K. Kubota and S. Komaba, Review-Practical Issues and Future Perspective for Na-Ion Batteries, J. Electrochem. Soc., 2015, 162, A2538–A2550.
3. M. Keller, D. Buchholz and S. Passerini, Layered Na-Ion Cathodes with Outstanding Performance Resulting from the Synergetic Effect of Mixed P- and O-Type Phases, Adv. Energy Mater., 2016, 6, 1501555.
4. M. Bianchini, F. Fauth, N. Brisset, F. Weill, E. Suard, C. Masquelier and L. Croguennec, Comprehensive investigation of the Na3V2(PO4)2F3-NaV2(PO4)2F3 system by operando high resolution synchrotron X-ray diffraction, Chem. Mater., 2015, 27, 3009–3020.
5. Y. Wang, Y. Zhang, J. Shi, A. Pan, F. Jiang, S. Liang and G. Cao, S-doped porous carbon confined SnS nanospheres with enhanced electrochemical performance for sodium-ion batteries, J. Mater. Chem. A, 2018, 6, 18286–18292.
6. K. Sato, M. Nakayama, A. M. Glushenkov, T. Mukai, Y. Hashimoto, K. Yamanaka, M. Yoshimura, T. Ohta and N. Yabuuchi, Na-Excess Cation-Disordered Rocksalt Oxide: Na1.3Nb0.3Mn0.4O2, Chem. Mater., 2017, 29, 5043–5047.
7. T. Sato, K. Sato, W. Zhao, Y. Kajiya and N. Yabuuchi, Metastable and nanosize cation-disordered rocksalt-type oxides: revisit of stoichiometric LiMnO2 and NaMnO2, J. Mater. Chem. A, 2018, 6, 13943–13951.
8. H. Park, Y. Lee, M.-K. Cho, J. Kang, W. Ko, Y. H. Jung, T.-Y. Jeon, J. Hong, H. Kim, S.-T. Myung and J. Kim, Na2Fe2F7: a fluoride-based cathode for high power and long life Na-ion batteries, Energy Environ. Sci., 2021, 14, 1469–1479.
9. H. Euchner, O. Clemens and M. A. Reddy, Unlocking the potential of weberite-type metal fluorides in electrochemical energy storage, npj Comput. Mater., 2019, 5, 31.
10. M. A. Reddy and M. Fichtner, Advanced Fluoride-Based Materials for Energy Conversion, Elsevier Inc., 2015, pp. 51–76.
11. X. Hua, A. S. Eggeman, E. Castillo-Martínez, R. Robert, H. S. Geddes, Z. Lu, C. J. Pickard, W. Meng, K. M. Wiaderek, N. Pereira, G. G. Amatucci, P. A. Midgley, K. W. Chapman, U. Steiner, A. L. Goodwin and C. P. Grey, Revisiting metal fluorides as lithium-ion battery cathodes, Nat. Mater., 2021, 20, 841–850.
12. R. E. Doe, K. A. Persson, Y. S. Meng and G. Ceder, First-principles investigation of the Li-Fe-F phase diagram and equilibrium and nonequilibrium conversion reactions of iron fluorides with lithium, Chem. Mater., 2008, 20, 5274–5283.
13. V. L. Chevrier, G. Hautier, S. P. Ong, R. E. Doe and G. Ceder, First-principles study of iron oxyfluorides and lithiation of FeOF, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 94118.
14. R. A. Shakoor, S. Y. Lim, H. Kim, K. W. Nam, J. K. Kang, K. Kang and J. W. Choi, Mechanochemical synthesis and electrochemical behavior of Na3FeF6 in sodium and lithium batteries, Solid State Ionics, 2012, 218, 35–40.
15. H. Guo, W. Liu, M. Qin, J. Tang, J. Cheng and Y. Ling, Room-temperature liquid-phase synthesis of Na3FeF6 and its lithium/sodium storage properties, Mater. Res. Express, 2019, 6, 085507.
16. W. Liu, W. Wang, M. Qin and B. Shen, Successive synthesis and electrochemical properties of Na3FeF6 and NaFeF3/C cathode materials for lithium-ion and sodium-ion batteries, Ceram. Int., 2020, 46, 11436–11440.
17. E. E. Levin, J. H. Grebenkemper, T. M. Pollock and R. Seshadri, Protocols for High Temperature Assisted-Microwave Preparation of Inorganic Compounds, Chem. Mater., 2019, 31, 7151–7159.
18. F. Badway, N. Pereira, F. Cosandey and G. G. Amatucci, Carbon-Metal Fluoride Nanocomposites: Structure and Electrochemistry of FeF3:C, J. Electrochem. Soc., 2003, 150, A1209.
19. R. J. Clément, D. Kitchaev and J. Lee, and Gerbrand Ceder, Short-Range Order and Unusual Modes of Nickel Redox in a Fluorine-Substituted Disordered Rocksalt Oxide Lithium-Ion Cathode, Chem. Mater., 2018, 30, 6945–6956.
20. P. Gütlich, Fifty years of Mössbauer spectroscopy in solid state research - Remarkable achievements, future perspectives, Z. Anorg. Allg. Chem., 2012, 638, 15–43.
21. A. Tressaud, J. Portier, S. Shearer-Turrell, J. L. Dupin and P. Hagenmuller, Les hexafluoferrites M3FeF6 (M = Li, Na, K, Rb, Cs, Ag, Tl, NH4): Etude radiocristallographique, spectroscopique et magnetique, J. Inorg. Nucl. Chem., 1970, 32, 2179–2186.
22. H. Arai, S. Okada, Y. Sakurai and J. I. Yamaki, Cathode performance and voltage estimation of metal trihalides, J. Power Sources, 1997, 68, 716–719.
23. C. P. Guntlin, Z. Tanja, V. Kostiantyn Kravchyk, W. Michael, M. I. Bodnarchuk and M. V. Kovalenko, Nanocrystalline FeF3 and MF2 (M = Fe, Co, and Mn) from metal trifluoroacetates and their Li(Na)-ion storage properties, J. Mater. Chem. A, 2017, 5, 7383–7393.
24. G. Gershinsky, E. Bar, L. Monconduit and D. Zitoun, Operando electron magnetic measurements of Li-ion batteries, Energy Environ. Sci., 2014, 7, 2012–2016.
25. K. M. Wiaderek, O. J. Borkiewicz, E. Castillo-Martínez, R. Robert, N. Pereira, G. G. Amatucci, C. P. Grey, P. J. Chupas and K. W. Chapman, Comprehensive insights into the structural and chemical changes in mixed-anion FeOF electrodes by using operando pdf and NMR spectroscopy, J. Am. Chem. Soc., 2013, 135, 4070–4078.
26. N. Dupre, M. Cuisinier and D. Guyomard, Electrode/Electrolyte Interface Studies in Lithium Batteries Using NMR, Interface Mag., 2011, 20, 61–67.
27. K. A. See, M. A. Lumley, G. D. Stucky, C. P. Grey and R. Seshadri, Reversible Capacity of Conductive Carbon Additives at Low Potentials: Caveats for Testing Alternative Anode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2017, 164, 327–333.
28. J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Mechanistic insights into sodium storage in hard carbon anodes using local structure probes, Chem. Commun., 2016, 52, 12430–12433.
29. J. Nava-Avendaño, M. E. Arroyo-De Dompablo, C. Frontera, J. A. Ayllón and M. R. Palacín, Study of sodium manganese fluorides as positive electrodes for Na-ion batteries, Solid State Ionics, 2015, 278, 106–113.
30. N. Dimov, A. Nishimura, K. Chihara, A. Kitajou, I. D. Gocheva and S. Okada, Transition metal NaMF3 compounds as model systems for studying the feasibility of ternary Li-M-F and Na-M-F single phases as cathodes for lithium-ion and sodium-ion batteries, Electrochim. Acta, 2013, 110, 214–220.
31. K. E. Johnston, M. T. Sougrati, L. Stievano, A. Darwiche, N. Dupré, C. P. Grey and L. Monconduit, Effects of Relaxation on Conversion Negative Electrode Materials for Li-Ion Batteries: A Study of TiSnSb Using 119Sn Mössbauer and 7Li MAS NMR Spectroscopies, Chem. Mater., 2016, 28, 4032–4041.
32. K. Haneda, X. Z. Zhou, A. H. Morrish and R. J. Pollard, Mössbauer study of ultrafine FeF2 particles, Hyperfine Interact., 1990, 54, 551–556.
33. S. Ramasamy, J. Jiang, H. Gleiter, R. Birringer and U. Gonser, Investigation of nanocrystalline FeF2 by Mössbauer spectroscopy, Solid State Commun., 1990, 74, 851–855.
34. K. He, Y. Zhou, P. Gao, L. Wang, N. Pereira, G. G. Amatucci, K. W. Nam, X. Q. Yang, Y. Zhu, F. Wang and D. Su, Sodiation via heterogeneous disproportionation in FeF2 electrodes for sodium-ion batteries, ACS Nano, 2014, 8, 7251–7259.
35. F. C. Brown, C. Gähwiller, H. Fujita, A. B. Kunz, W. Scheifley and N. Carrera, Extreme-ultraviolet spectra of ionic crystals, Phys. Rev. B: Solid State, 1970, 2, 2126–2138.
36. G. Roy, G. Singh and T. E. Gallon, The electron energy loss spectra of some alkali halides in the band gap region, Surf. Sci., 1985, 152–153, 1042–1050.
37. H. Yildirim, A. Kinaci, M. K. Y. Chan and J. P. Greeley, First-Principles Analysis of Defect Thermodynamics and Ion Transport in Inorganic SEI Compounds: LiF and NaF, ACS Appl. Mater. Interfaces, 2015, 7, 18985–18996.
38. B. H. Toby and R. B. Von, Dreele, GSAS-II: The genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549.
39. I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, Isotropic High Field NMR Spectra of Li-Ion Battery Materials with Anisotropy > 1 MHz, J. Am. Chem. Soc., 2012, 134, 1898–1901.
40. C. Prescher, C. McCammon and L. Dubrovinsky, MossA: A program for analyzing energy-domain Mössbauer spectra from conventional and synchrotron sources, J. Appl. Crystallogr., 2012, 45, 329–331.
41. P. M. T. M. Van Attekum and G. K. Wertheim, Excitonic effects in core-hole screening, Phys. Rev. Lett., 1979, 43, 1896–1898.
42. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunel, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat and S. Casassa, CRYSTAL17 User's Manual, 2018.
43. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
44. A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
45. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211.
47. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, 1994, vol. 98.
48. F. Corà, M. Alfredsson, G. Mallia, D. S. Middlemiss, W. C. Mackrodt, R. Dovesi and R. Orlando, Structure and Bonding, Springer, Berlin, Heidelberg, 2012, vol. 113, pp. 171–232.
49. J. Muscat, A. Wander and N. M. Harrison, On the prediction of band gaps from hybrid functional theory, Chem. Phys. Lett., 2001, 342, 397–401.
50. X. Feng and N. M. Harrison, Magnetic coupling constants from a hybrid density functional with 35% Hartree-Fock exchange, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 092402.
51. D. S. Middlemiss, L. M. Lawton and C. C. Wilson, A solid-state hybrid density functional theory study of Prussian blue analogues and related chlorides at pressure, J. Phys.: Condens. Matter, 2008, 20, 335231.
52. I. de, P. R. Moreira, F. Illas and R. L. Martin, Effect of Fock exchange on the electronic structure and magnetic coupling in NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1551021.
53. J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, Linking local environments and hyperfine shifts: A combined experimental and theoretical 31P and 7Li solid-state NMR study of paramagnetic Fe(III) phosphates, J. Am. Chem. Soc., 2010, 132, 16825–16840.
54. D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Density functional theory-based bond pathway decompositions of hyperfine shifts: Equipping solid-state NMR to characterize atomic environments in paramagnetic materials, Chem. Mater., 2013, 25, 1723–1734.
55. A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
56. E. N. Matvienko, O. V. Yakubovich, M. A. Simonov, A. N. Ivashchenko, O. K. Mel’nikov and N. V. Belov, The crystal structure of the synthetic Fe-cryolite Na3FeF6, Dokl. Akad. Nauk SSSR, 1981, 257, 105–108.
57. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02763h

‡ Present address: School of Chemistry, University of St-Andrews, North Haugh, St-Andrews, KY16 9ST, UK.

---