On the fate of high-resolution electron energy loss spectroscopy (HREELS), a versatile probe to detect surface excitations: will the Phoenix rise again?
Antonio
Politano
 ab
ab
aDepartment of Physical and Chemical Sciences, University of L’Aquila, via Vetoio, 67100 L’Aquila, Abruzzo, Italy. E-mail: antonio.politano@univaq.it
bCNR-IMM Istituto per la Microelettronica e Microsistemi, VIII strada 5, I-95121 Catania, Italy
First published on 26th October 2021
Abstract
From its advent, high-resolution electron energy loss spectroscopy (HREELS) has emerged as one of the most versatile tools in surface science. In the last few decades, HREELS was widely used for the fundamental study of (i) chemical reactions at the surfaces of model catalysts (mostly single crystals), (ii) lattice dynamics (phonons), (iii) surface plasmons and (iv) magnons. However, HREELS has experienced a continuous decay of the number of daily users worldwide so far, due to several factors. However, the rise of Dirac materials (graphene, topological insulators, Dirac semimetals) offers new perspectives for HREELS, due to its unique features enabling ultrasensitive detection of (i) chemical modifications at their surfaces, (ii) Kohn anomalies arising from electron–phonon coupling and (iii) novel plasmonic excitations associated to Dirac-cone fermions, as well as their eventual mutual interplay with other plasmon resonances related to topologically trivial electronic states. By selected case-study examples, here we show that HREELS can uniquely probe these phenomena in Dirac materials, thus validating its outstanding relevance and its irreplaceability in contemporary solid-state physics, thus paving the way for a renewed interest. In addition, recent technological upgrades enable the combination of HREELS as an add-on to photoemission apparatuses for parallel readout of energy and momentum of surface excitations. Open issues for theoretical modelling of HREELS related to the dependence on primary electron beam energy and scattering geometry are also critically presented.
Introduction
Inelastic scattering of low-energy (<200 eV) electrons at surfaces represents one of the most sensitive tools to investigate surface excitations.1–7 The lack of penetration by probing slow electrons endows HREELS with an extreme sensitivity to surface excitations, which can be quite dissimilar compared to their bulk counterparts, especially for the case of collective electronic excitations.More than 50 years ago Propst and Piper reported for the first time the evidence of electron energy losses induced by the excitation of vibrational modes on a W(100) surface,8 paving the way for the rise of HREELS. Specifically, the design of spectrometers with nominal energy resolution of 0.5 meV (4 cm−1) by Harald Ibach in 1990s expanded the range of applications of probing slow electrons,2 determining the large-scale diffusion of HREELS spectrometers, whose success was determined by their compactness and easy integration with standard surface-science chambers.
In HREELS, probing electrons are reflected from a conductive single-crystal surface and scattered electrons are analyzed as a function of the loss energy. Usually, primary electron beam energies used in HREELS are below 6 eV. Such low energies are optimal for the obtainment of energy resolution in the meV range, enabling the investigation of surface vibrations, as well as plasmons.
Historically, the main aim of HREELS was to probe vibrations of chemisorbed species at single-crystal surfaces of metal catalysts to unveil surface chemical reactions ruling catalysis. HREELS was a valid ally in investigations on heterogeneous catalysis (see as examples papers by Nobel Prize winner Gerhard Ertl, in collaboration with Karl Jacobi9–18), also thanks to its possibility to identify adsorption sites of reactants19 (including sub-surface sites20,21).
Owing to the competitive energy resolution, HREELS became a suitable alternative to inelastic helium atom scattering (HAS)22–24 to probe the dispersion relation of phonons. While HAS is more powerful for acoustical phonons,25,26 HREELS is particularly suitable for semiconductors. Starting from 1997, i.e., seven years before the isolation of graphene,27 HREELS was used by Karl-Heinz Rieder in Germany28–37 and, moreover, Chuei Oshima and Takashi Aizawa in Japan38–42 to investigate the dispersion relation of phonons of “monolayer graphite”. These investigations already clarified the key features of graphene/metal interfaces, such as the strong hybridization of π states of graphene with Ni d bands, removed by the intercalation of atoms.
Furthermore, HREELS gave a huge contribution in the measurement of dispersion relations of plasmons of free-electron (alkali metals,43 magnesium44 and aluminum45) and d-electron metals (silver46–49 and gold50,51) and, successively, acoustic surface plasmons in Be(0001),52 Cu(111)53 and Au(111)54,55 and dynamic interfacial polarons for monolayer FeSe/SrTiO3.56 Especially, the capability to probe momentum-resolved excitations spectra evidenced differences in the dispersion relation, whose detection is hindered for optical techniques.
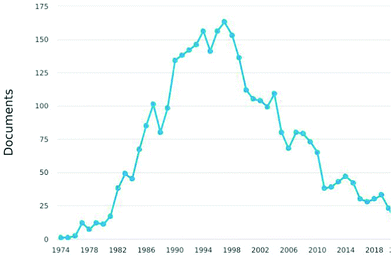
However, progressively users of HREELS have decreased after 2000 up to a surprisingly low number of groups worldwide, with most apparatuses abandoned or rarely working, as evident from statistics on published papers (Fig. 1). The reasons are related to the general decline of traditional surface science. For the specific case of HREELS, the reasons are (i) the complex preparation of surfaces of single crystals, (ii) the need of a deep surface-science expertise of users for experiments and data analysis, (iii) the lack of spatial resolution in conflict with research on nanostructures, (iv) high costs of experimental apparatuses working in ultrahigh vacuum only, and (v) prolonged acquisition times especially for plasmons and phonons.
Although statistics suggest the unfortunate decay of an historical technique for surface science, several issues suggest the possible renaissance of HREELS as a Phoenix from its ashes. Actually, the advent of nanostructures and nanomaterials (nanowires, nanotubes, exfoliated flakes of two-dimensional materials) was detrimental for HREELS, due to the lack of spatial resolution to probe nanomaterials. However, currently many groups working on nanomaterials are moving their interest towards topological materials,57 wherein topological surface states, existing only on highly ordered surfaces of bulk single crystals, play a pivotal role in electronic transport58–60 and catalysis.61–63
In this context, HREELS can provide a notable contribution to research in contemporary condensed matter physics and physical chemistry, as we will illustrate with case-study examples of recent applications of HREELS to study Dirac materials, demonstrating its irreplaceability and its crucial role to unveil physical and chemical processes at surfaces, complementary to state-of-the-art operando techniques for studying catalysis.64–71
Chemical reactions at the surface of Dirac materials
Graphene, the forefather of two-dimensional materials, has been long reputed as an inert material.72 Such an assumption is due to the use of Raman spectroscopy, characterized by a probing depth in the 300–650 nm range. The application of HREELS has changed this common picture with unambiguous data in ref. 73. Explicitly, the vibrational spectrum of water-exposed graphene probed by HREELS is dominated by intense bending and stretching C–H vibrations at 180 and 360 meV (Fig. 2b), associated to the vibration of carbon atoms against H fragments coming from water decomposition (Fig. 2a), as demonstrated by the expected shift of vibrational features upon D2O dosage. While high-resolution synchrotron-based X-ray photoelectron spectroscopy (XPS) at the highest surface sensitivity for C-1s (photon energy of 400 eV) only detects the effective decoupling of graphene from Ni substrate, due to intercalated water-derived fragments, HREELS can depict the microscopic mechanisms ruling water-derived graphene hydrogenation. As a matter of fact, the absence of O–H stretching at 450 meV in Fig. 2b indicates that OH fragments are intercalated below graphene. Thus, H atoms are adsorbed on the interior side of the graphene overlayer, while OH atoms form chemical bonds with the Ni substrate (Fig. 2a). While XPS do not clarify if water is totally decomposed or not, HREELS can ensure the absence of molecular water, whose vibrational spectrum is dominated by the typical modes of ice (see ref. 74 for a review), as evidenced in vibrational spectra taken at T = 100 K, with a desorption temperature of 140 K (Fig. 2c).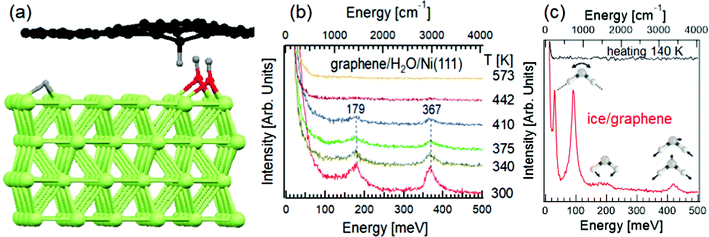 | ||
| Fig. 2 (a) Representation of water intercalation underneath graphene/Ni(111). The H atoms, coming from water decomposition, form bonds with graphene, inducing a buckling of the sheet. OH groups are buried underneath graphene and they are undetectable for HREELS. (b) HREELS spectra for water-dosed graphene/Ni(111) at room temperature. The evolution of spectra upon heating at different temperatures is shown. Adapted from ref. 73. (c) Vibrational spectrum of ice on graphene at T = 100 K (red curve) with the representation of librations, scissoring and stretching (both symmetric and asymmetric) modes. The black curve illustrates the vibrational spectrum of ice/graphene after heating at T = 140 K. Adapted from ref. 73. | ||
By means of a time-resolved HREELS spectra, one can follow the desorption of H fragments through the gradual quenching of C–H vibrational features, which disappear for the complete desorption at T = 450 K. Correspondingly, thermal programmed desorption (TPD) experiments indicated the recombination of H atoms into H2 desorbing from the graphene surface.
Accordingly, the evolution of the complex system depicted in Fig. 2 can be unveiled through HREELS, with conclusions fully validated by other surface-science techniques, which however are ineffective for providing a picture on the physicochemical processes owing to their missing surface sensitivity.
Another possible frontier for HREELS applications is related to the chemical reactivity of topological materials.
Specifically, the type-II Dirac semimetal PtTe2 was shown to display high chemical stability in its defect-free surface, while chemical instability and spontaneous oxidation in surface TeO2 phases are revealed in defective samples.75 In Fig. 3, HREELS spectra taken after having exposed (i) defects-free, (ii) defective and (iii) and C-doped surfaces of PtTe2 to H2O and O2 are reported.75 It is evident that the defect-free surface is chemically inert at room temperature (Fig. 3a) and surface oxide phases emerge only upon oxidation at 600 K, as indicated by the occurrence of libration and stretching vibrations of surface TeO275 at 61 and 94 meV, respectively. It is evident that the defects-free surface is chemically inert at room temperature and surface oxide phases emerge only upon oxidation at 600 K, as indicated by the occurrence of libration and stretching vibrations of surface TeO275 at 61 and 94 meV, respectively.
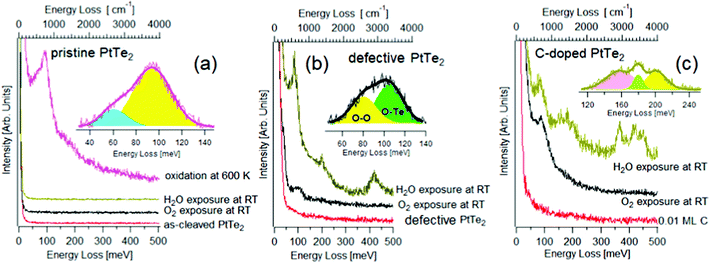 | ||
| Fig. 3 (a) HREELS spectra for pristine PtTe2 and for the same surface exposed to 103 L of O2 and H2O at room temperature. Contrariwise, upon oxidation at 600 K the vibrational spectrum assumes features related to surface oxidation. (b) HREELS spectra for PtTe2 modified with the implantation of Te vacancies through ion bombardment. The attained defective PtTe2 surface was then exposed to 103 L of O2 and H2O at room temperature. (c) HREELS spectra for C-doped PtTe2 and the same surface modified by the exposure of 103 L of O2 and H2O at room temperature. Adapted from ref. 75. | ||
The surface chemical reactivity is radically modified in defective samples, in which the O–Te stretching vibration at ∼100 meV is evident in the vibrational spectrum of oxygen-dosed defective PtTe2 surfaces (Fig. 3b). Definitely, Te vacancies represent the only active sites allowing oxygen adsorption at room temperature, though the saturation coverage is just 0.01 ML. Concerning water, the use of vibrational spectroscopy clarifies that water adsorbs molecularly at Te vacancies of the defective PtTe2 surface, as evidenced by the presence of characteristic vibrational peaks of H2O74 and by the lack of the O–H stretching vibration of isolated –OH groups at 450 meV, an undisputable fingerprint of the presence of isolated OH groups coming from water decomposition.74 Water molecules desorb upon annealing at 350 K, as indicated by the vanishing of H2O-related vibrational features.
The presence of surface carbon doping, with interstitial carbon atom occupying Te vacancies, activates water splitting at room temperature, as suggested by the O–H shoulder at 450 meV and C–OH vibration at 155 meV76 in the vibrational spectrum (Fig. 3c). Water decomposition is also confirmed by the emergence of both C-H bending and stretching vibrations at 179 and 366 meV, respectively. The theoretical model confirmed that the energy cost for water decomposition over substitutional carbon defects is negative (−60 kJ mol−1).
New frontiers for phonon dispersion by HREELS: Kohn anomalies and elasticity
Kohn anomalies are kinks in the phonon dispersion originated by sudden modifications in the screening of atomic vibrations by gapless electrons.77 Kohn anomalies are connected to the electron–phonon coupling and the shape of the Fermi surface. Accordingly, they allow the investigation of the interplay between electronic band structure and lattice dynamics. Based on Raman spectroscopy experiments by Andrea Ferrari and coworkers, two Kohn anomalies were recognized in graphite,78 namely, for the E2g mode at Γ and the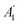 at K, which also are present in graphene.79,80
at K, which also are present in graphene.79,80
By means of HREELS, a new Kohn anomaly was identified in graphene/metal interfaces.6 Definitely, the presence of a substrate induces a significant coupling of ZO phonons in graphene with Dirac-cone states, which results into an intense Kohn anomaly at q = 2kF.
As well known, the phonon spectrum in graphene displays six phonon branches.25,81Fig. 4a display intensity maps for the various phonons probed by HREELS intensity, with four phonon branches (ZA, ZO, LA, and LO) can be distinctly detected (Fig. 4b). The remaining two phonon branches (TO and TA) are quenched owing to a selection rule impeding the emission of odd phonons under reflections by the scattering plane.82 The dispersion relation of LO (Fig. 4c) and ZO (Fig. 4d and e) modes around Γ exhibit a clear cusp at the same momentum q ∼ 0.13 Å−1, i.e. q = 2kF. Note that the deviation from the high symmetry point is due to the doping of the graphene/Pt(111) interface.
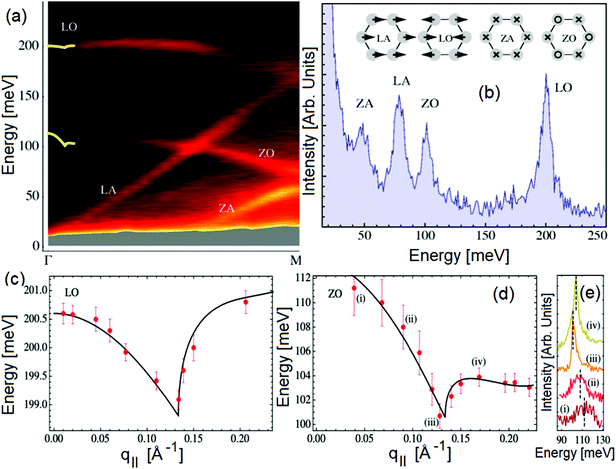 | ||
Fig. 4 (a) Map of HREELS intensity for phonons in graphene/Pt(111). Experiments were carried out with an impinging energy of 20 eV, to maximize cross-section for phonon excitations. (b) Typical phonon spectrum. (c) LO and (d) ZO dispersion relation at small momenta. (e) Spectra related to points denoted with (i)–(iv) in panel (d). Adapted from ref. 6. Note that the parallel momentum transfer q‖ is related to kinematic conditions through 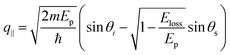 ,84 where Eloss is the loss energy. ,84 where Eloss is the loss energy. | ||
HREELS can be also adopted to evaluate the elastic properties of adsorbed layers, as demonstrated in ref. 83. Specifically, by extracting from phonon dispersion the transverse and longitudinal sound speed, the average Young's modulus and Poisson's ratio in graphite and in graphene grown on Ru(0001), Pt(111), Ir(111), and BC3/NbB2(0001) were evaluated to be 342 N m−1 and 0.19, respectively. On the other hand, Young's modulus and the Poisson's ratio, in the only case of graphene/Ni(111), were found to be 310 N m−1 and 0.36, owing to the stretching of C–C bonds existing in its commensurate overlayer.
Plasmonic excitations of topological materials
Plasmons—quantized collective oscillations of electrons observed in conventional metals and semiconductors—have several possible applications in sensing,85 photonics,86 nanomedicine87 and desalination.88 Plasmons are also present in novel topological phases of matter, as topological insulators7,89–91 and Dirac semimetals.5,92,93 The collective excitation of Dirac-cone electrons, namely the Dirac plasmon, displays many advantages over conventional ones, such as a higher propagation velocity and frequency tunability.Here, we discuss two case-study examples for HREELS applications to study plasmons in PtTe2 (a topological Dirac semimetal) and Bi2Se3 (a topological insulator).
HREELS experiments on PtTe2 (Fig. 5) revealed the presence of bulk-derived plasmonic excitations (“3D Dirac plasmons”), showing features directly connected to the anisotropic tilted cones distinctive of a type-II Dirac semimetal. In consideration of its bulk nature, the 3D Dirac plasmon is also robust against surface modifications, with consequent advantages for engineering plasmon-based applications. Moreover, plasmons could be excited at an energy of only 0.5 eV, corresponding to a wavelength of about 2.4 μm. Accordingly, this discovery has boosted the rise of optoelectronic applications in which plasmons are controlled with near-infrared light.92
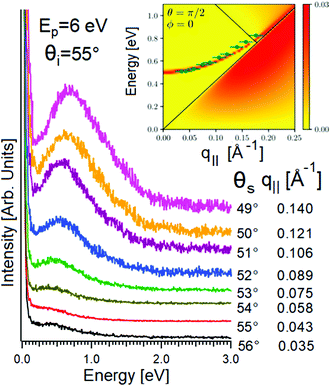
However, HREELS can be used also to investigate the interplay of different plasmonic excitations, as for Bi2Se3.7 At small momenta, the HREELS spectrum of Bi2Se3 is dominated by a feature at 104 meV (Fig. 6b), attributed to a surface plasmon considering the behavior of its cross-section as a function of the primary energy and scattering geometry (Fig. 6a). Nevertheless, at larger momenta (∼0.04 Å−1), an extra feature, recognized as the Dirac plasmon, emerges (Fig. 6c). Momentum-resolved HREELS spectra indicate the interplay between the surface and the Dirac plasmons of Bi2Se3 (Fig. 6d). Theory can reproduce experimental findings, considering the coincidence of three-dimensional doping electrons and two-dimensional Dirac fermions.(Fig. 6e).
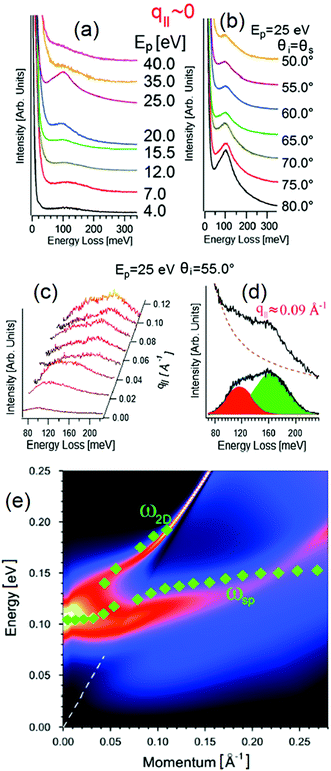 | ||
| Fig. 6 Dependence on (a) primary electron beam energy (taken in specular direction with the incidence angle of 55°) and (b) scattering geometry of the HREELS spectrum in Bi2Se3. (c) Momentum-resolved HREELS spectra; (d) fit procedure showing the presence of two well-distinct plasmonic excitations; (e) dispersion relation of the Dirac and surface plasmon. Adapted from ref. 73. | ||
Magnons
Wave packets of spin waves afford the exceptional ability to carry a quantum bit, the spin, without the transport of charge or mass. In such a framework, high-momentum/high-energy spin waves deserve a particular attention, since they allow spin confinement at the nanoscale. Nevertheless, several basic issues should be addressed yet. An important hurdle for a detailed comprehension of the main features of spin waves is that standard investigation tools do not cover properly the momentum-energy window, feasible with HREELS with a modified spectrometer presented in ref. 94 by Harald Ibach and coworkers.Despite the small cross section for electron/solid exchange scattering, it is now possible to detect spin waves in ultra-thin ferromagnetic films with an energy resolution of 3–4 meV.95,96
Fig. 7 displays HREELS spectra with spin wave excitations for a cobalt and nickel–cobalt film deposited on a copper crystal. The spin wave spectra exhibit features corresponding to diverse eigenmodes of the film.
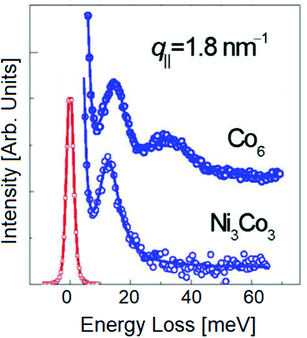 | ||
| Fig. 7 HREELS spectra with magnon excitations for Co6 and Ni3Co3 films grown on Cu(100), with correction to account the Bose occupation number. Adapted from ref. 95. | ||
New technological capabilities
Recently, a new HREELS source enabling parallel readout of energy and momentum has been introduced,97 allowing the integration of HREELS in modern hemispherical electron energy analyzers. In particular, this system is designed as an add-on device to typical photoemission chambers. Accordingly, the same apparatus could measure XPS and angle-resolved photoemission spectroscopy (ARPES), together with vibrational spectroscopy and phonon dispersion measurements. Using the 2D detector system of the analyzer enables considerable parallelization and decreases the acquisition time by orders of magnitude compared to the traditional approach.Conventional HREELS apparatuses have a single channel energy analyzer, providing angular resolution by a mechanical rotation. However, spanning a Brillouin zone to complete a dispersion relation could be time consuming. As an example, experiments for phonon dispersions, due to the weak signal, can last even more than one month. Similar to the introduction of energy and angular resolved detectors for ARPES in 1994, this latest development in HREELS represents a breakthrough to parallel energy and angular detection. Notably, a full phonon dispersion of a Cu(111) surface was acquired in seven minutes with an energy resolution of 4 meV.97
It is worth mentioning that the astonishing recent upgrades of EELS acquired with transmission electron microscopy (EELS-TEM) have enabled the acquisition of optical phonons of graphene with atomic resolution,98 although the energy resolution is ∼30 meV, i.e. still far from HREELS standards.
An open issue: the dependence of the loss function on kinematic conditions
Theoretical reproduction of HREELS spectra still does not cover successfully the effects of the change of the impinging energy and scattering geometry. However, HREELS spectra can show drastic changes by changing the primary electron beam energy and the scattering angle. Here, we show the case-study example of Ag thin films (Fig. 8). Beyond the surface plasmon of Ag at 3.9 eV, it is evident that a broad feature at 8 eV only can be observed in HREELS spectra acquired under nearly grazing incidence in a narrow range of primary electron beam energy from 40 to 43 eV (Fig. 8a). On the contrary, this mode (attributed to a multipole plasmon, according to predictions in ref. 99) is absent far from grazing incidence (Fig. 8b). One can infer that multipole plasmon can be excited merely upon stringent kinematical conditions. It was suggested that Ag multipole plasmon can be excited uniquely by electron reflection around the jellium edge.100–102 In these experimental conditions, interference effects between the incident and the reflected beam produce non-monotonous behavior of the intensity of the surface plasmon as a function of the impinging energy.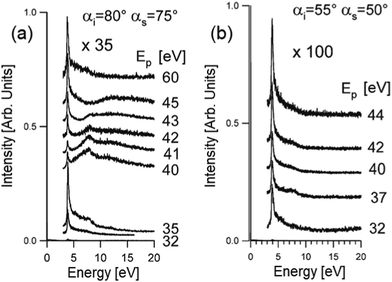 | ||
| Fig. 8 HREELS spectra of Ag/Ni(111) measured in off-specular geometry as a function of the impinging energy for two different conditions (a) αi = 80°, αs = 75°; (b) αi = 55°, αs = 50°. Adapted from ref. 101. | ||
Conclusions
HREELS had a relevant role in the rise of surface science, thanks to its versatility for studies regarding surface chemical reactions, phonons, plasmons, and magnons. The change of interest of the scientific community has caused an unequivocal decline, at least in the number of daily users. This trend is common to the whole surface science discipline, due to the severe hurdles represented by structure and pressure gaps, which complicate the comparison between experiments in ultrahigh vacuum on model single crystals with real disordered systems at near-ambient pressure. The lack of spatial resolution has also implied a difficulty for HREELS to provide contributions on exfoliated flakes of two-dimensional materials.Nevertheless, the advent of topological materials can determine a renaissance for HREELS, due to its unique features enabling to reveal surface excitations with remarkable versatility.
Definitely, HREELS is sharing the challenge, currently faced by surface science, to keep an appointment in modern research on physical chemistry, solid-state physics and materials science. Actually, three evident opportunities could put again HREELS at the vanguard: (i) to use HREELS to unveil physicochemical phenomena at surfaces of materials with high relevance for the scientific community; (ii) to embrace experimental procedures and methods typical of surface science to prevent wrong interpretation of data regarding novel materials, associated to an insufficient control of surface processes; and (iii) to use HREELS to characterize in-situ grown innovative interfaces and heterostructures displaying exotic phenomena, with broad potential interest.
Conflicts of interest
There are no conflicts to declare.References
-
H. Ibach and D. L. Mills, Electron Energy Loss Spectroscopy and Surface Vibrations, Academic Press, San Francisco, 1982 Search PubMed
.
- H. Ibach, J. Electron Spectrosc. Relat. Phenom., 1993, 64–65, 819–823 CrossRef CAS
.
- H. Ibach, M. Balden and S. Lehwald, J. Chem. Soc., Faraday Trans., 1996, 92, 4771–4774 RSC
.
- H. Ibach, M. Balden, D. Bruchmann and S. Lehwald, Surf. Sci., 1992, 270, 94–102 CrossRef
.
- A. Politano, G. Chiarello, B. Ghosh, K. Sadhukhan, C.-N. Kuo, C. S. Lue, V. Pellegrini and A. Agarwal, Phys. Rev. Lett., 2018, 121, 086804 CrossRef CAS
.
- A. Politano, F. de Juan, G. Chiarello and H. A. Fertig, Phys. Rev. Lett., 2015, 115, 075504 CrossRef
.
- A. Politano, V. M. Silkin, I. A. Nechaev, M. S. Vitiello, L. Viti, Z. S. Aliev, M. B. Babanly, G. Chiarello, P. M. Echenique and E. V. Chulkov, Phys. Rev. Lett., 2015, 115, 216802 CrossRef CAS
.
- F. M. Propst and T. C. Piper, J. Vacuum Sci. Technol., 1967, 4, 53–56 CrossRef CAS
.
- C. Y. Fan, J. Wang, K. Jacobi and G. Ertl, J. Chem. Phys., 2001, 114, 10058–10062 CrossRef CAS
.
- J. Wang, C. Y. Fan, K. Jacobi and G. Ertl, Surf. Sci., 2001, 481, 113–118 CrossRef CAS
.
- J. Wang, C. Y. Fan, K. Jacobi and G. Ertl, J. Phys. Chem. B, 2002, 106, 3422–3427 CrossRef CAS
.
- S. H. Kim, U. A. Paulus, Y. Wang, J. Wintterlin, K. Jacobi and G. Ertl, J. Chem. Phys., 2003, 119, 9729–9736 CrossRef CAS
.
- U. A. Paulus, Y. Wang, K. Jacobi and G. Ertl, Surf. Sci., 2003, 547, 349–354 CrossRef CAS
.
- Y. Wang, K. Jacobi and G. Ertl, J. Phys. Chem. B, 2003, 107, 13918–13924 CrossRef CAS
.
- U. A. Paulus, Y. Wang, H. P. Bonzel, K. Jacobi and G. Ertl, Surf. Sci., 2004, 566, 989–994 CrossRef
.
- U. A. Paulus, Y. Wang, S. H. Kim, P. Geng, J. Wintterlin, K. Jacobi and G. Ertl, J. Chem. Phys., 2004, 121, 11301–11308 CrossRef CAS
.
- U. A. Paulus, Y. Wang, H. P. Bonzel, K. Jacobi and G. Ertl, J. Phys. Chem. B, 2005, 109, 2139–2148 CrossRef CAS PubMed
.
- K. Jacobi, Y. Wang and G. Ertl, J. Phys. Chem. B, 2006, 110, 6115–6122 CrossRef CAS PubMed
.
- A. Politano and G. Chiarello, J. Phys. Chem. C, 2011, 115, 13541–13553 CrossRef CAS
.
- D. Farías, P. Schilbe, M. Patting and K. H. Rieder, J. Chem. Phys., 1999, 110, 559–569 CrossRef
.
- D. Farias, M. Patting and K. Rieder, Phys. Status Solidi A, 1997, 159, 255–262 CrossRef CAS
.
- A. L. Glebov, J. P. Toennies, S. Vollmer and G. Benedek, Europhys. Lett., 1999, 46, 369–375 CrossRef CAS
.
- G. Benedek, J. Ellis, N. S. Luo, A. Reichmuth, P. Ruggerone and J. P. Toennies, Phys. Rev. B, 1993, 48, 4917–4920 CrossRef CAS PubMed
.
- G. Benedek, J. P. Toennies and G. Zhang, Phys. Rev. Lett., 1992, 68, 2644–2647 CrossRef CAS
.
- A. Al Taleb and D. Farías, J. Phys.: Condens. Matter, 2016, 28, 103005 CrossRef
.
- A. Al Taleb, G. Anemone, D. Farías and R. Miranda, Carbon, 2016, 99, 416–422 CrossRef CAS
.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS
.
- S. Siebentritt, R. Pues, K. H. Rieder and A. M. Shikin, Phys. Rev. B, 1997, 55, 7927–7934 CrossRef CAS
.
- A. M. Shikin, D. Farías and K. H. Rieder, Europhys. Lett., 1998, 44, 44–49 CrossRef CAS
.
- S. Siebentritt, R. Pues, K. H. Rieder and A. M. Shikin, Surf. Rev. Lett., 1998, 5, 427–431 CrossRef CAS
.
- D. Farías, A. M. Shikin, K. H. Rieder and Y. S. Dedkov, J. Phys.: Condens. Matter, 1999, 11, 8453–8458 CrossRef
.
- A. M. Shikin, D. Farías, V. K. Adamchuk and K. H. Rieder, Surf. Sci., 1999, 424, 155–167 CrossRef CAS
.
- D. Farías, K. H. Rieder, A. M. Shikin, V. K. Adamchuk, T. Tanaka and C. Oshima, Surf. Sci., 2000, 454, 437–441 CrossRef
.
- A. M. Shikin, V. K. Adamchuk, S. Siebentritt, K. H. Rieder, S. L. Molodtsov and C. Laubschat, Phys. Rev. B, 2000, 61, 7752–7759 CrossRef CAS
.
- A. M. Shikin, G. V. Prudnikova, V. K. Adamchuk, F. Moresco and K. H. Rieder, Phys. Rev. B, 2000, 62, 13202–13208 CrossRef CAS
.
- W. H. Soe, A. M. Shikin, F. Moresco, V. K. Adamchuk and K. H. Rieder, Phys. Rev. B, 2001, 64, 235404 CrossRef
.
- W. H. Soe, K. H. Rieder, A. M. Shikin, V. Mozhaiskii, A. Varykhalov and O. Rader, Phys. Rev. B, 2004, 70, 115421 CrossRef
.
- T. Aizawa, R. Souda, Y. Ishizawa, H. Hirano, T. Yamada, K.-I. Tanaka and C. Oshima, Surf. Sci., 1990, 237, 194–202 CrossRef CAS
.
- T. Aizawa, R. Souda, S. Otani, Y. Ishizawa and C. Oshima, Phys. Rev. B, 1990, 42, 11469 CrossRef CAS
.
- T. Aizawa, R. Souda, S. Otani, Y. Ishizawa and C. Oshima, Phys. Rev. Lett., 1990, 64, 768–771 CrossRef CAS
.
- T. Aizawa, Y. Hwang, W. Hayami, R. Souda, S. Otani and Y. Ishizawa, Surf. Sci., 1992, 260, 311–318 CrossRef CAS
.
- Y. Hwang, T. Aizawa, W. Hayami, S. Otani, Y. Ishizawa and S.-J. Park, Surf. Sci., 1992, 271, 299–307 CrossRef CAS
.
- K.-D. Tsuei, E. W. Plummer and P. J. Feibelman, Phys. Rev. Lett., 1989, 63, 2256–2259 CrossRef CAS PubMed
.
- P. T. Sprunger, G. M. Watson and E. W. Plummer, Surf. Sci., 1992, 269–270, 551–555 CrossRef CAS
.
- Y. H. Yu, Z. Tang, Y. Jiang, K. H. Wu and E. G. Wang, Surf. Sci., 2006, 600, 4966–4971 CrossRef CAS
.
- F. Moresco, M. Rocca, T. Hildebrandt and M. Henzler, Phys. Rev. Lett., 1999, 83, 2238–2241 CrossRef CAS
.
- M. Rocca, M. Lazzarino and U. Valbusa, Phys. Rev. Lett., 1991, 67, 3197 CrossRef CAS PubMed
.
- M. Rocca, M. Lazzarino and U. Valbusa, Phys. Rev. Lett., 1992, 69, 2122–2125 CrossRef CAS PubMed
.
- M. Rocca and U. Valbusa, Phys. Rev. Lett., 1990, 64, 2398–2401 CrossRef CAS PubMed
.
- S. J. Park and R. E. Palmer, Phys. Rev. Lett., 2009, 102, 216805 CrossRef PubMed
.
- A. Politano, V. Formoso and G. Chiarello, Plasmonics, 2008, 3, 165–170 CrossRef CAS
.
- B. Diaconescu, K. Pohl, L. Vattuone, L. Savio, P. Hofmann, V. M. Silkin, J. M. Pitarke, E. V. Chulkov, P. M. Echenique, D. Farías and M. Rocca, Nature, 2007, 448, 57–59 CrossRef CAS PubMed
.
- K. Pohl, B. Diaconescu, G. Vercelli, L. Vattuone, V. M. Silkin, E. V. Chulkov, P. M. Echenique and M. Rocca, Europhys. Lett., 2010, 90, 57006 CrossRef
.
- L. Vattuone, M. Smerieri, T. Langer, C. Tegenkamp, H. Pfnür, V. M. Silkin, E. V. Chulkov, P. M. Echenique and M. Rocca, Phys. Rev. Lett., 2013, 110, 127405 CrossRef CAS PubMed
.
- S. J. Park and R. E. Palmer, Phys. Rev. Lett., 2010, 105, 016801 CrossRef
.
- S. Zhang, T. Wei, J. Guan, Q. Zhu, W. Qin, W. Wang, J. Zhang, E. Plummer, X. Zhu and Z. Zhang, Phys. Rev. Lett., 2019, 122, 066802 CrossRef CAS
.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045–3067 CrossRef CAS
.
- E. Wang, H. Ding, A. V. Fedorov, W. Yao, Z. Li, Y.-F. Lv, K. Zhao, L.-G. Zhang, Z. Xu, J. Schneeloch, R. Zhong, S.-H. Ji, L. Wang, K. He, X. Ma, G. Gu, H. Yao, Q.-K. Xue, X. Chen and S. Zhou, Nat. Phys., 2013, 9, 621–625 Search PubMed
.
- P. Roushan, J. Seo, C. V. Parker, Y. S. Hor, D. Hsieh, D. Qian, A. Richardella, M. Z. Hasan, R. J. Cava and A. Yazdani, Nature, 2009, 460, 1106–1109 CrossRef CAS PubMed
.
- M. S. Bahramy, O. J. Clark, B. J. Yang, J. Feng, L. Bawden, J. M. Riley, I. Marković, F. Mazzola, V. Sunko, D. Biswas, S. P. Cooil, M. Jorge, J. W. Wells, M. Leandersson, T. Balasubramanian, J. Fujii, I. Vobornik, J. E. Rault, T. K. Kim, M. Hoesch, K. Okawa, M. Asakawa, T. Sasagawa, T. Eknapakul, W. Meevasana and P. D. C. King, Nat. Mater., 2018, 17, 21–28 CrossRef CAS
.
- G. Li and C. Felser, Appl. Phys. Lett., 2020, 116, 070501 CrossRef CAS
.
- Q. Qu, B. Liu, J. Liang, H. Li, J. Wang, D. Pan and I. K. Sou, ACS Catal., 2020, 10, 2656–2666 CrossRef CAS
.
- Q. Yang, G. Li, K. Manna, F. Fan, C. Felser and Y. Sun, Adv. Mater., 2020, 32, 1908518 CrossRef CAS
.
- S. Porsgaard, L. R. Merte, L. K. Ono, F. Behafarid, J. Matos, S. Helveg, M. Salmeron, B. Roldan Cuenya and F. Besenbacher, ACS Nano, 2012, 6, 10743–10749 CrossRef CAS
.
- J.-J. Velasco-Velez, R. V. Mom, L.-E. Sandoval-Diaz, L. J. Falling, C.-H. Chuang, D. Gao, T. E. Jones, Q. Zhu, R. Arrigo, B. Roldan Cuenya, A. Knop-Gericke, T. Lunkenbein and R. Schlögl, ACS Energy Lett., 2020, 5, 2106–2111 CrossRef CAS
.
- Y. Fujimori, W. E. Kaden, M. A. Brown, B. Roldan Cuenya, M. Sterrer and H.-J. Freund, J. Phys. Chem. C, 2014, 118, 17717–17723 CrossRef CAS
.
- M. Amati, V. Bonanni, L. Braglia, F. Genuzio, L. Gregoratti, M. Kiskinova, A. Kolmakov, A. Locatelli, E. Magnano, A. A. Matruglio, T. O. Menteş, S. Nappini, P. Torelli and P. Zeller, J. Electron Spectrosc. Relat. Phenom., 2019, 146902 CrossRef
.
- S. Nappini, A. Matruglio, D. Naumenko, S. Dal Zilio, F. Bondino, M. Lazzarino and E. Magnano, Nanoscale, 2017, 9, 4456–4466 RSC
.
- M. Favaro, J. Yang, S. Nappini, E. Magnano, F. M. Toma, E. J. Crumlin, J. Yano and I. D. Sharp, J. Am. Chem. Soc., 2017, 139, 8960–8970 CrossRef CAS
.
- L. Braglia, F. Tavani, S. Mauri, R. Edla, D. Krizmancic, A. Tofoni, V. Colombo, P. D’Angelo and P. Torelli, J. Phys. Chem. Lett., 2021, 12, 9182–9187 CrossRef CAS
.
- L. Braglia, F. Tavani, S. Mauri, R. Edla, D. Krizmancic, A. Tofoni, V. Colombo, P. D’Angelo and P. Torelli, J. Phys. Chem. Lett., 2021, 12, 9182–9187 CrossRef CAS
.
- J. S. Qi, J. Y. Huang, J. Feng, D. N. Shi and J. Li, ACS Nano, 2011, 5, 3475–3482 CrossRef CAS PubMed
.
- A. Politano, M. Cattelan, D. W. Boukhvalov, D. Campi, A. Cupolillo, S. Agnoli, N. G. Apostol, P. Lacovig, S. Lizzit, D. Farías, G. Chiarello, G. Granozzi and R. Larciprete, ACS Nano, 2016, 10, 4543–4549 CrossRef CAS
.
- M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308 CrossRef CAS
.
- F. Pietrucci, S. Caravati and M. Bernasconi, Phys. Rev. B, 2008, 78, 064203 CrossRef
.
- C.-Y. Wu, W. J. Wolf, Y. Levartovsky, H. A. Bechtel, M. C. Martin, F. D. Toste and E. Gross, Nature, 2017, 541, 511–515 CrossRef CAS
.
- P. Aynajian, T. Keller, L. Boeri, S. M. Shapiro, K. Habicht and B. Keimer, Science, 2008, 319, 1509–1512 CrossRef CAS
.
- S. Piscanec, M. Lazzeri, F. Mauri, A. C. Ferrari and J. Robertson, Phys. Rev. Lett., 2004, 93, 185503 CrossRef CAS
.
- W. K. Tse, B. Y. K. Hu and S. Das Sarma, Phys. Rev. Lett., 2008, 101, 066401 CrossRef
.
- F. de Juan and H. A. Fertig, Solid State Commun., 2012, 152, 1460–1468 CrossRef CAS
.
- A. Politano, Crit. Rev. Solid State Mater. Sci., 2017, 42, 99–128 CrossRef CAS
.
- F. de Juan, A. Politano, G. Chiarello and H. A. Fertig, Carbon, 2015, 85, 225–232 CrossRef CAS
.
- A. Politano and G. Chiarello, Nano Res., 2015, 8, 1847–1856 CrossRef CAS
.
- M. Rocca, Surf. Sci. Rep., 1995, 22, 1–71 CrossRef CAS
.
- M. E. Stewart, C. R. Anderton, L. B. Thompson, J. Maria, S. K. Gray, J. A. Rogers and R. G. Nuzzo, Chem. Rev., 2008, 108, 494–521 CrossRef CAS PubMed
.
- E. Ozbay, Science, 2006, 311, 189–193 CrossRef CAS PubMed
.
- M. R. Ali, H. R. Ali, C. R. Rankin and M. A. El-Sayed, Biomaterials, 2016, 102, 1–8 CrossRef CAS
.
- A. Politano, G. Di Profio, E. Fontananova, V. Sanna, A. Cupolillo and E. Curcio, Desalination, 2019, 451, 192–199 CrossRef CAS
.
- N. Talebi, C. Ozsoy-Keskinbora, H. M. Benia, K. Kern, C. T. Koch and P. A. van Aken, ACS Nano, 2016, 10, 6988–6994 CrossRef CAS PubMed
.
- J.-Y. Ou, J.-K. So, G. Adamo, A. Sulaev, L. Wang and N. I. Zheludev, Nat. Commun., 2014, 5, 5139 CrossRef CAS
.
- P. Di Pietro, M. Ortolani, O. Limaj, A. Di Gaspare, V. Giliberti, F. Giorgianni, M. Brahlek, N. Bansal, N. Koirala, S. Oh, P. Calvani and S. Lupi, Nat. Nanotechnol., 2013, 8, 556–560 CrossRef CAS
.
- X. Hu, K. P. Wong, L. Zeng, X. Guo, T. Liu, L. Zhang, Q. Chen, X. Zhang, Y. Zhu and K. H. Fung, ACS Nano, 2020, 14, 6276–6284 CrossRef CAS PubMed
.
- D. E. Kharzeev, R. D. Pisarski and H.-U. Yee, Phys. Rev. Lett., 2015, 115, 236402 CrossRef
.
- H. Ibach, D. Bruchmann, R. Vollmer, M. Etzkorn, P. S. A. Kumar and J. Kirschner, Rev. Sci. Instrum., 2003, 74, 4089–4095 CrossRef CAS
.
- H. Ibach and C. Schneider, Phys. Rev. B, 2018, 98, 014413 CrossRef CAS
.
- H. Ibach and C. Schneider, Phys. Rev. B, 2019, 99, 184406 CrossRef CAS
.
- H. Ibach, F. C. Bocquet, J. Sforzini, S. Soubatch and F. S. Tautz, Rev. Sci. Instrum., 2017, 88, 033903 CrossRef
.
- R. Senga, K. Suenaga, P. Barone, S. Morishita, F. Mauri and T. Pichler, Nature, 2019, 573, 247–250 CrossRef CAS PubMed
.
- A. Liebsch, Phys. Rev. B, 1998, 57, 3803–3806 CrossRef CAS
.
- A. Politano, V. Formoso and G. Chiarello, J. Phys.: Condens. Matter, 2013, 25, 305001 CrossRef CAS PubMed
.
- A. Politano, V. Formoso and G. Chiarello, Plasmonics, 2013, 8, 1683–1690 CrossRef CAS
.
- A. Politano, V. Formoso and G. Chiarello, Superlattices Microstruct., 2009, 46, 166–170 CrossRef CAS
.
| This journal is © the Owner Societies 2021 |