Optimum in ligand density for conductivity in polymer electrolytes†
Nicole S.
Schauser
 abc,
Peter M.
Richardson
abc,
Peter M.
Richardson
 bc,
Andrei
Nikolaev
bc,
Andrei
Nikolaev
 cd,
Piper
Cooke
bd,
Gabrielle A.
Kliegle
bd,
Ethan M.
Susca
b,
Keith
Johnson
cd,
Piper
Cooke
bd,
Gabrielle A.
Kliegle
bd,
Ethan M.
Susca
b,
Keith
Johnson
 ab,
Hengbin
Wang
ab,
Hengbin
Wang
 c,
Javier
Read de Alaniz
d,
Raphaële
Clément
c,
Javier
Read de Alaniz
d,
Raphaële
Clément
 *abc and
Rachel A.
Segalman
*abc and
Rachel A.
Segalman
 *abce
*abce
aMaterials Department, University of California, Santa Barbara, California 93106, USA. E-mail: rclement@ucsb.edu; segalman@ucsb.edu
bMaterials Research Laboratory, University of California, Santa Barbara, California 93106, USA
cMitsubishi Chemical Center for Advanced Materials, University of California, Santa Barbara, California 93106, USA
dDepartment of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106, USA
eDepartment of Chemical Engineering, University of California, Santa Barbara, California 93106, USA
First published on 28th September 2021
Abstract
Current design rules for ion conducting polymers suggest that fast segmental dynamics and high solvation site density are important for high performance. In a family of imidazole side chain grafted siloxane polymer electrolytes containing LiTFSI, we conclude that while the presence of imidazole solvation sites promotes solubilization of Li+ containing salts, it is not necessary to substitute every monomer in the polymer design. Rather, optimization of Li+ conductivity relies on a balance between imidazole presence and the ability of the chains to rearrange locally to facilitate transport. Lowering the imidazole content in the ethane-imidazole series leads to a 10-fold increase in conductivity, while conductivity decreases for the phenyl-imidazole series due to differences in steric bulk. Normalizing conductivity by Tg reveals a threshold ligand density above which increased solvation sites do not improve conductivity, but below which the conduction gradually decreases. NMR spectroscopy shows the high temperature Li+ transport number increases slightly with increasing grafting density, from around 0.17 to 0.24. NMR T1ρ relaxation reveals that the Li+ ions are present in two environments with distinct dynamics within the polymer, matching X-ray scattering and PFG results which suggest ion aggregation exists in these polymers. These results emphasize the importance of local re-arrangements in facilitating ion transport at low solvation site density, confirming the role of dynamic percolation, and suggest that an optimum ligand density exists for improved charge transport.
Design, System, ApplicationLithium ion transport in salt-based polymer electrolytes necessitates a balance between salt dissolution and ionic mobility. Salts dissolve into a polymer matrix through solvation interactions with ligand species; however these ion-ligand interactions subsequently hinder ion motion. In this work we synthesize a library of polymers with varying ligand side chain concentrations, identifying the role of both ligand density and spacer identity on the polymer structure, dynamics, and ion transport. Our molecular design approach reveals an optimum intermediate ligand density which enables an order of magnitude increase in total ionic conductivity with negligible change in lithium transport number. These systems emphasize the importance of dynamic percolation in enabling lithium transport, and provide a roadmap towards optimizing ionic conductivity performance for rubbery lithium-ion electrolytes for energy storage applications. |
Introduction
Ion-conducting polymers have been proposed as safe, mechanically robust and electrochemically stable alternatives to organic liquid electrolytes for energy storage devices.1,2 Critically, while polymers have many advantages over their liquid counterparts, they continue to suffer from low ionic conductivity.3 Polymers form a relatively translationally-immobile matrix compared to liquids, requiring design rules emphasizing labile ion-solvation interactions.4–6To dissolve and conduct ions, polymers must contain solvating groups which interact favorably with ions to promote their dissociation, without immobilizing the ions within the polymer framework. The competition between effective salt dissolution and labile ion–polymer interactions results in necessary tradeoffs in electrolyte design and performance. For example, both intermediate polymer polarity7 and salt concentration8–10 seem to provide maximum conductivity performance due to the complex interplay between ion-polymer interactions, segmental dynamics, and ion mobility. Most polymer electrolytes contain at least two mobile ions, the cation and anion, which both contribute to the total conductivity. Salt dissolution is generally achieved by coordination with the cationic species. For cation motion, these same coordination sites must be dynamic and allow the ion to hop through the matrix by breaking and reforming coordination bonds on a reasonable timescale. Anions typically interact less strongly with the polymer, but still rely on free volume or local polymer re-arrangement, which is in turn generally coupled to cation-polymer interactions since these interactions dynamically cross-link the polymer matrix and result in increases in polymer glass transition temperature (Tg). While energy storage applications require cation transport, most electrolytes exhibit higher anion than cation mobility, underscoring a current challenge for these materials.11 Polymer design thus requires the incorporation of functional solvation groups which provide strong yet dynamic interactions between the polymer and ions to enable higher cation mobility.
One class of materials with labile ion-polymer interactions is metal–ligand coordination polymers,12 which we have previously shown to dissolve and conduct a range of metal salts relevant for energy storage.5,8 This family of polymers offers advantages in tunability through the wide range of possible combinations of polymer backbone13 and ligand choices which enables optimization of additional unexplored features for improving performance.
One promising route towards improving ionic conductivity is to increase the segmental mobility of the electrolyte. This can be achieved through the choice of a polymer matrix with inherently low Tg. The lowest Tg polymers generally do not contain the necessary solvation sites for dissolving ions, requiring the introduction of tethered species for ion solvation. One effective way to introduce such solvating groups is by adding side-chains to a low Tg polymer backbone. This has been successfully demonstrated for siloxane,14,15 phosphazene,16 acrylate17–20 and aliphatic13 backbones. However, the attachment of side-chains to a low Tg polymer backbone generally increases the Tg of the electrolyte.15,21,22 Thus, there is a trade-off between the inclusion of the necessary solvation sites for ion conduction and keeping a low Tg. Ideally, a minimal concentration of solvation sites would be added to a low Tg polymer backbone to achieve ion dissolution and conduction without increasing the Tg to a detrimental level.
For energy storage applications, maximizing the Li+ contribution to the total conductivity is important, and is quantified by the transport number (t+). Typically, a large Li+t+ reduces the concentration polarization during battery operation, yielding higher power densities.23 However, the determination of the transport number is challenging for polymer electrolytes systems.24 Several electrochemical techniques exist for extracting transport number values, although all come with drawbacks. Chronoamperometry, for instance, becomes inaccurate in systems with high interfacial impedance or ion pairing, and for polymeric systems which require large cell polarizations.25–27 More rigorous methods for the determination of transport numbers stem from thermodynamic considerations, but are limited by experimental complexity and propensity for propagation error, and are influenced by the solid electrolyte interphase that typically forms between the polymer and Li metal foil.11,28 Here, we use 7Li and 19F pulsed-field gradient nuclear magnetic resonance (PFG-NMR) to determine the diffusion coefficients of the ions of interest, Li+ and TFSI−.29 PFG-NMR typically measures the diffusion coefficient over a length-scale of a few micrometers, which means that the diffusion coefficient is therefore an average diffusion coefficient weighted by the time spent in the various mobile and immobile environments in the polymer.
In this work, we show that an intermediate ligand density optimizes total ionic conductivity and Li+t+ for a series of sidechain grafted polymer electrolytes. A library of polymers was synthesized from a poly(vinyl methyl siloxane) backbone functionalized with varying ratios of imidazole ligands and ‘inert’ (non-solvating) side chains, chosen to remove residual vinyl reactive groups and to test for the role of steric bulk on the electrolyte properties (Fig. 1). It is shown that replacing the imidazole ligands with small ethane side chains enables a reduction in the polymer Tg of over 80 °C, and a concomitant 10-fold conductivity increase. Interestingly, the use of phenyl side chains likewise results in dramatic decreases in Tg of about 60 °C, yet leads to a decrease in the conductivity performance of the polymer electrolyte. After normalization of the conductivity data by the corresponding values of Tg, both polymers show a decrease in conductivity at low grafting density, though the conductivity of the ethane-imidazole series is insensitive to imidazole grafting density at grafting percentages above 30% imidazole. These results are examined based on approximations of molar volume of imidazole and salt concentration, which suggests that reducing the imidazole molar concentration below a certain threshold leads to reduced conductivity performance. Importantly, there is not a strict threshold of imidazole concentration which results in zero ionic conductivity, suggesting that static percolation theories do not hold, and solvation site re-arrangement recovers some performance for even extremely low imidazole contents. The Li+ transport behavior of the ethane-imidazole series was also studied using PFG-NMR and relaxometry. The Li+t+ decreases from 0.27 to 0.17 as the imidazole content is reduced to 30% of side chains. Thus, a maximum in cation conductivity exists, emphasizing the need to consider t+ for ligand density optimization.
Experimental
Polymer synthesis
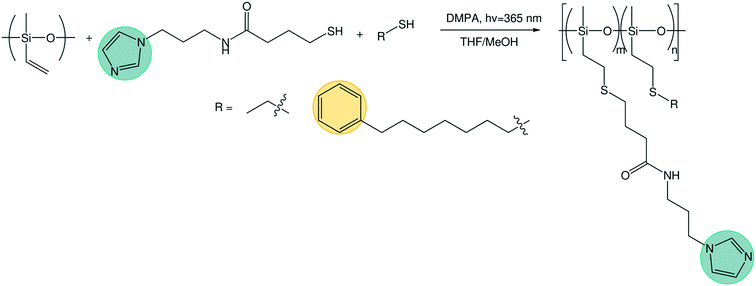
Two batches of poly(vinyl methyl siloxane) (PVMS) were synthesized by anionic polymerization using standard Schlenk line techniques. For the first, 200 mL of uninhibited and dry THF was further purified by distillation over n-butyl lithium and dried by the addition of 260 μL of sec-butyl lithium at 0 °C, after which the solution was allowed to warm to room temperature. The monomer, 1,3,5-trivinyl-1,3,5-trimethyl-cyclotrisiloxane (Gelest), was degassed by four freeze–pump–thaw cycles and used without additional purification. 260 μL of sec-butyl lithium was added to THF at 0 °C as initiator, followed by the addition of 15.5 mL of degassed monomer. The reaction was allowed to proceed for 10 min at 0 °C before termination with degassed methanol. The solution was concentrated and precipitated in methanol three times. The second batch followed a similar synthesis procedure, but with 50 mL of THF dried with the addition of 400 μL sec-butyl lithium. 8.5 mL degassed monomer was initiated with 75 μL n-butyl lithium. The reaction was allowed to proceed for 3 h at 0 °C before termination with degassed methanol. The polymer was purified through three precipitations in water, a 2 day dialysis in THF, and filtering through a PTFE plug. Size exclusion chromatography (SEC) was performed on a Waters Alliance HPLC instrument using a refractive index detector and Agilent PLgel 5 μm MiniMIX-D column at 35 °C with THF as the eluent. Dispersity index (Đ) was determined against polystyrene calibration standards (Agilent Technologies). The PVMS molecular weight was estimated from SEC using polystyrene standards.Phenyl thiol (Ph-SH) synthesis
To an oven dried round bottom flask equipped with a magnetic stir bar was added NaSH (1.1 equiv.) followed by a 0.35 M solution of (7-bromoheptyl)-benzene in degassed absolute DMF at 0 °C. This solution was stirred for one hour at ambient temperature under dinitrogen atmosphere. Upon completion, the reaction was diluted with DCM and extracted with brine 4×, dried with Na2SO4 and concentrated in vacuo. The 7-phenylheptane-1-thiol was isolated in 93% yield and used for the next step without further purification. The 1HNMR data matched that of the previously reported structure.30Polymer functionalization
N-(2-(1H-Imidazol-1-yl)propyl)-4-mercaptobutanamide (Im-SH) was synthesized as previously reported by Sanoja et al.8 Ethane thiol was purchased from Sigma Aldrich and used as-received. The PVMS polymer was dissolved in THF and added to a round bottom flask containing 2,2-dimethoxy-2-phenylacetophenone (0.2 mol% with respect to vinyl functional handle). An appropriate mass of Im-SH was dissolved in methanol and added to the flask to vary the imidazole grafting density. For the ethane-imidazole series, an appropriate amount of ethane thiol was added volumetrically using a syringe. For the phenyl-imidazole series, the Ph-SH was dissolved in THF and added into the flask. The total thiol to vinyl ratio was kept constant at 1.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The final methanol/THF solvent ratio was adjusted to be 20/80 to maintain solubility during all reactions. The reaction was degassed with nitrogen for 30 min, after which the reaction was allowed to proceed under UV (365 nm) light for 2 h. The polymers were purified either by precipitation in acetonitrile, methanol or water, or through dialysis in methanol/THF (50/50) solutions (SnakeSkin dialysis tubing with a 3.5 kDa MW cutoff, and solvent exchange every 12 h for a total of 5 to 7 times). The polymers were then dried in vacuo at 55 °C in the presence of phosphorous pentoxide and immediately transferred to a nitrogen glove box. The imidazole content of the resulting polymers was analyzed using NMR (DMSO-d6 or CDCl3, see Fig. S1–S8†).
1. The final methanol/THF solvent ratio was adjusted to be 20/80 to maintain solubility during all reactions. The reaction was degassed with nitrogen for 30 min, after which the reaction was allowed to proceed under UV (365 nm) light for 2 h. The polymers were purified either by precipitation in acetonitrile, methanol or water, or through dialysis in methanol/THF (50/50) solutions (SnakeSkin dialysis tubing with a 3.5 kDa MW cutoff, and solvent exchange every 12 h for a total of 5 to 7 times). The polymers were then dried in vacuo at 55 °C in the presence of phosphorous pentoxide and immediately transferred to a nitrogen glove box. The imidazole content of the resulting polymers was analyzed using NMR (DMSO-d6 or CDCl3, see Fig. S1–S8†).
Salt addition
Polymers were weighed into 7 mL vials and dissolved in anhydrous methanol or anhydrous THF (for low imidazole content polymers) inside a nitrogen glove box. Stock solutions of lithium bis(trifluoromethylsulfonyl)imide (LiTFSI, Alfa Aesar) ranging from 0.1 M to 1 M were prepared using anhydrous methanol. Appropriate volumes of LiTFSI stock solution were added to each polymer vial to achieve nominal molar ratios of Li+ to imidazole of 0.1, or Li+ to monomer of 0.1 or 0.05 (see Table 1 for concentrations used for each polymer). The sample vials were sealed, removed from the glovebox and frozen in LN2 before being opened and quickly transferred to a vacuum oven and dried in vacuo (1 × 10−3 Torr) at room temperature overnight, and then at 60 °C for 24 h. The samples were then transferred to a high vacuum oven (3 × 10−8 Torr) at 60 °C for 24 h to ensure complete removal of solvent. Finally, the samples were transferred into a nitrogen glove box for storage and measurement.| Name | % imidazole (NMR) | Polymer molar mass (g mol−1) | mmol imidazole per gram polymer | Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) monomer monomer |
Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) imidazole imidazole |
Salt concentration (mmol cm−3) | Salt wt% |
|---|---|---|---|---|---|---|---|
| PVMS–Phc | 0% | 294 | 0 | 0.1 | N/A | 0.340 | 8.9 |
| PVMS–Phc-Im 14 | 14% | 296.72 | 0.472 | 0.1 | 0.714 | 0.337 | 8.82 |
| PVMS–Phc-Im 40 | 40% | 301.76 | 1.326 | 0.1 | 0.25 | 0.331 | 8.69 |
| PVMS–Phc-Im 72 | 72% | 307.97 | 2.338 | 0.1 | 0.139 | 0.325 | 8.53 |
| PVMS–Et | 0% | 148 | 0 | 0.1 | N/A | 0.676 | 16.25 |
| PVMS–Et-Im 7 | 7% | 159.58 | 0.439 | 0.1 | 1.429 | 0.627 | 15.25 |
| 7% | 159.58 | 0.439 | 0.05 | 0.714 | 0.313 | 8.25 | |
| 7% | 159.58 | 0.439 | 0.007 | 0.1 | 0.044 | 1.24 | |
| PVMS–Et-Im 20 | 20% | 181.08 | 1.104 | 0.1 | 0.5 | 0.552 | 13.68 |
| PVMS–Et-Im 29 | 29% | 195.97 | 1.48 | 0.1 | 0.345 | 0.510 | 12.78 |
| PVMS–Et-Im 33 | 33% | 202.58 | 1.629 | 0.1 | 0.303 | 0.494 | 12.41 |
| 33% | 202.58 | 1.629 | 0.033 | 0.1 | 0.163 | 4.47 | |
| PVMS–Et-Im 49 | 49% | 229.05 | 2.139 | 0.1 | 0.204 | 0.437 | 11.14 |
| 49% | 229.05 | 2.139 | 0.049 | 0.1 | 0.214 | 5.79 | |
| PVMS–Et-Im 71 | 71% | 265.43 | 2.675 | 0.1 | 0.141 | 0.377 | 9.76 |
| 71% | 265.43 | 2.675 | 0.071 | 0.1 | 0.267 | 7.13 | |
| PVMS–Im | 100% | 313.4 | 3.191 | 0.1 | 0.1 | 0.319 | 8.39 |
Ionic conductivity measurement
Total ionic conductivity was measured as a function of temperature on samples sandwiched between parallel ITO blocking electrodes using electrochemical impedance spectroscopy (EIS). The ITO-coated glass electrodes (Thin Film Devices) were cleaned by sonication for 5 min each in detergent, DI water, acetone and isopropyl alcohol, followed by a 5 min UV/ozone treatment (Jelight Company Inc., Model 18). The electrode thicknesses were measured using a micrometer, after which a double-sided Kapton tape spacer with a 1/8′′ hole was added to one electrode. Polymer samples were loaded into the hole in the Kapton spacer in a nitrogen filled glove box. Samples were heated to about 30 °C above their Tg before being sealed with a second ITO electrode. All samples were then heated to 110 °C and pressed in a hand press. The final stack thickness was measured using a micrometer, and the sample thickness was determined by subtracting the electrode thicknesses. EIS was measured with a Biologic SP-200 potentiostat using a sinusoidal 100 mV signal from 1 MHz to 1 Hz at temperatures ranging from 30 °C to 110 °C. The data was converted into dielectric storage and loss, and the ionic conductivities determined from the real component of conductivity at the maximum in tan (δ).31 Three samples were measured for most compositions, with errors reported as standard deviations from the mean. For PVMS–Et-Im 7 Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Im = 0.1, only two samples were measured, while for PVMS–Phc, PVMS–Phc-Im 14, PVMS–Phc-Im 40 and PVMS–Et only one sample was measured.
Im = 0.1, only two samples were measured, while for PVMS–Phc, PVMS–Phc-Im 14, PVMS–Phc-Im 40 and PVMS–Et only one sample was measured.
Thermal characterization
Aluminum DSC pans were loaded with polymer samples in a nitrogen filled glove box and briefly exposed to air during sealing of the pans. The glass transition temperature (Tg) of each sample was measured using a Perkin Elmer DSC 8000 or TA Instruments Q2000 DSC on second heating at 20 °C min−1 at the midpoint of the step transition.X-ray scattering
X-ray scattering was performed as a function of temperature at the National Synchrotron Light Source II (NSLS-II, beamline 11-BM, Brookhaven National Laboratory) with an X-ray energy of 13.5 keV. Samples were packed into metal washers in a nitrogen glove box and covered on both sides with Kapton tape to prevent moisture uptake during measurement. Samples were equilibrated for 15 min at each temperature before collecting exposures. Data processing, including detector distance calibration using a silver behenate standard, reduction of 2D raw SAXS images into 1D intensity versus q curves and corrections for empty cell scattering were performed using the SciAnalysis software.32NMR
All 7Li and 19F solid-state NMR experiments were performed on a 300 MHz (7.05 T) SWB Bruker NMR spectrometer, using either a 4 mm double resonance (HX) magic angle spinning (MAS) probe or a Diff50 diffusion probe fitted with either a 10 mm 19F or 7Li coil. The polymer samples were packed inside an argon filled glovebox into 4 mm MAS rotors, then either used directly inside the 4 mm MAS probe or placed inside a 5 mm NMR tube equipped with a valve which kept an inert atmosphere around the sample. In both instances the sample was then temperature controlled by a flow of N2 gas at a rate of 800 L h−1 which ensured an inert atmosphere throughout the experiments. The temperature for each probe was calibrated using dry methanol and dry ethylene glycol at sub-ambient and elevated temperatures, respectively.The power level used for the 7Li on the Diff50 probe was either 100 W or 200 W with a 90° pulse duration of 16 μs (15.6 kHz) or 11 μs (22.7 kHz) respectively. The power level used for the 7Li on the 4 mm MAS probe was 76 W with a 90° pulse duration of around 3.3 μs (75.8 kHz). The power level used for the 19F insert on the Diff50 probe was 50 W with a 90° pulse duration of around 11 μs (22 kHz). For all measurements, a recycle delay of around 5T1 was applied before each scan when signal averaging, to allow full relaxation. The 7Li chemical shift was calibrated using a 1 M LiCl aqueous solution (single peak at 0 ppm) while the 19F chemical shift was referenced against aneat PF6 sample exhibiting a doublet centered around 71.7 ppm.
The T1ρ experiments were measured by applying a spin-locking pulse during evolution of the spins following an initial 90° excitation pulse. The spin-locking frequency chosen here was 10 kHz for all samples. The PFG-NMR experiments used a diffusion sequence which includes a stimulated echo to protect the signal from T2 relaxation, which is typically very short in these polymer systems. The diffusion was measured using a variable magnetic field gradient strength sequence, where the maximum gradient available was 2800 G cm−1. The selection of gradient strength, along with the gradient duration (δ) and diffusion time (Δ) were chosen for each measurement to ensure an appropriate window on the decay curve was acquired. The value of δ and diffusion time Δ never exceeded 10 ms and 100 ms respectively and were kept as low as possible while using the strongest gradient strength possible in order to achieve the greatest possible signal to noise.
To determine the Li+t+ for these polymer systems, diffusion constants can be measured for the Li+ (DLi+) and TFSI− (DTFS−) ions using 7Li and 19F NMR, respectively. The transport number is then defined as the proportion of the conductivity which arises from the Li+ ions only. If the relative concentration of anions and cations are equal, then the transport number can be determined as follows:
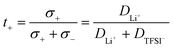 | (1) |
The use of NMR to determine Li+ transport numbers allow the direct detection of the self-diffusion of both ionic species independently in a single measurement. While electrochemical methods for Li+ transport determination (combing concentration cells and impedance spectroscopy, with galvanostatic polarization experiments)33–36 have the advantage that the experiments mimic the battery electrolyte conditions, these methods only provide an estimation of the transport properties and depend on multiple critical assumptions (such as the need for semi-infinite dilution). We therefore chose the NMR route, which is not subject to artefacts such as the formation of double layer capacitances overwhelming the resulting spectra.35 PFG-NMR is limited, however, by the difficulty in measuring slowly diffusing entities due to short NMR relaxation times, which is why we have coupled these measurements with the T1ρ measurements described above.
The transport numbers, along with the diffusion coefficients, for three different imidazole grafting density polymer samples ranging from 29% up to fully grafted (100%) with ethane side chain units have been measured. These data were collected at 72.7 °C and 81.4 °C only as the conductivity levels for these polymers are relatively low, resulting in NMR spin–spin (T2) relaxation times too short for diffusion measurements at ambient temperatures.
Typically, diffusion measurements do not give insight into the number of environments present and instead provide information that is averaged over all environments. Spin–spin relaxation time (T2) measurements can distinguish between multiple environments by fitting multiple exponents to the data. However, for the solid polymer systems of interest to this study, the T2 values are too short to be measured with accuracy. T1ρ measurements are analogous to T2 measurements, in that they are sensitive to multiple environments, with the additional benefit that the timescales are controllable through the choice of spin-lock frequency. Specifically, the T1ρ experiment measures the T1 relaxation time in the xy plane using a low power spin-lock pulse applied during the duration of the evolution period of the sequence. Here, a spin-locking frequency of 10 kHz (0.1 ms) was used for all samples, to establish whether multiple environments are present.
Results and discussion
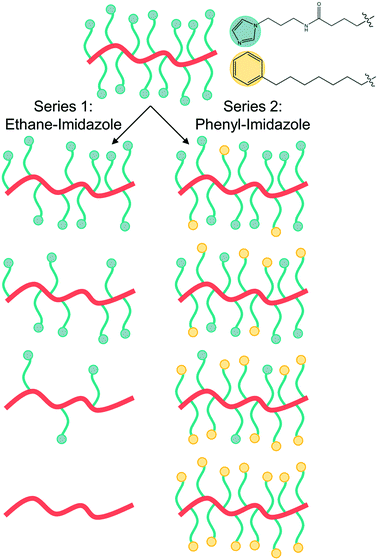
The two polymer series were designed to identify the role of the concentration of solvation sites (imidazole ligands)5 on both segmental dynamics and ion conduction (Fig. 1). Imidazole ligands are attached to a poly(vinyl methyl siloxane) backbone using thiol-ene click chemistry (Scheme 1). The remaining active vinyl functional groups are reacted with either ethane-thiol or phenyl-thiol. Ethane thiol was chosen as a small inert side chain unit to remove the residual vinyl functional groups and eliminate the possibility of unwanted reactions or cross-linking occurring in these polymers during processing or characterization. The phenyl-thiol side chains were chosen to maintain similar steric bulk to the imidazole ligand, while still removing the active coordination sites from the polymer. LiTFSI salt was then added to the polymer series at a few concentrations. The first concentration kept the molar ratio of Li+ to monomer repeat unit constant at 0.1. For the phenyl-imidazole system, this roughly also keeps the weight percent of salt constant (Table 1), while for the ethane-imidazole series, the weight percent changes due to the significant difference in molar mass between ethane-thiol and imidazole-thiol. The second salt concentration, explored only for the ethane-imidazole series, kept the molar ratio of Li+ to imidazole constant. This series tests the hypothesis that the salt dissociation is governed by the imidazole content. The total salt concentration added to the polymer varied more dramatically throughout the grafting density series for constant Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) imidazole (Table 1).
imidazole (Table 1).
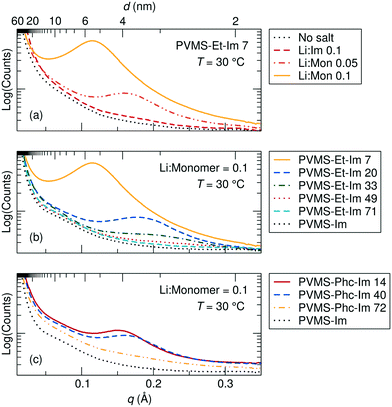
Structural changes with imidazole grafting density and salt concentration were probed using X-ray scattering, and revealed the presence of ion aggregation which increases with both salt concentration and decreasing imidazole content for both the ethane and phenyl side chain series (Fig. 2).
As salt concentration is increased in the PVMS–Et-Im 7 polymer, the aggregate peak grows in intensity and shifts to larger length scales, suggesting increased spacing between aggregated domains (Fig. 2a). A very low salt concentration does not result in ion aggregation in this polymer. The increase in peak intensity follows from the increase in ion concentration (see Table 1), and indicates that a larger number of ions aggregate as the concentration is increased. The increase in spacing between aggregates is less intuitive, as one might expect the aggregates to become larger and more numerous, which would lead to smaller inter-aggregate spacings. However, it is likely that the aggregates formed in these side-chain grafted imidazole systems are stringy or even percolated.13 In that case, higher salt concentrations may be elongating aggregate domains in such a way to increase the spacing between the closest distance between neighboring aggregates, or between parts of an individual aggregate. Interestingly, salt addition does not change the intermediate structure probed in the WAXS regime.
Increasing imidazole content for the ethane-imidazole polymer series at a constant Li+ to monomer ratio of 0.1 results in a smaller aggregation peak intensity and a shift in the correlation distance to smaller length scales (Fig. 2b). The reduction in peak intensity is likely a result of two factors. First, the higher imidazole grafting percentages result in a lower overall salt concentration, due to the increase in polymer volume from the imidazole side chain compared to the ethane side chain (see Table 1). Second, as the imidazole content increases the dielectric constant of the polymer matrix is expected to increase, which results in larger Debye screening lengths and therefore less ion aggregation. The shift in peak position to smaller length scales with increasing imidazole content might result from the decreased spacing between imidazoles. Since the salt interacts most strongly with the imidazole ligands in the polymer,5 it likely segregates to regions of higher imidazole density, resulting in ion aggregate clusters that are spaced closer together as imidazole content increases.
A similar trend of decreasing aggregate correlation distance with increasing imidazole content at a constant Li+ to monomer ratio of 0.1 exists for the imidazole-phenyl series (Fig. 2c). Compared to the ethane-imidazole polymer series, the aggregation scattering peak for the phenyl-imidazole is less intense, and is shifted to smaller length scales for a similar imidazole grafting percentage. The additional steric bulk of the phenyl group results in a lower density of imidazole functional groups for the phenyl-imidazole series at the same grafting percentage relative to the ethane-imidazole series (Table 1), which could be a contributing factor to the intensity of the peaks. The smaller aggregate peak distance in the phenyl system might be a result of the extra bulk of the phenyl side chains, which more effectively prevents ion-imidazole clusters from forming and results in aggregate clusters spaced farther apart instead.
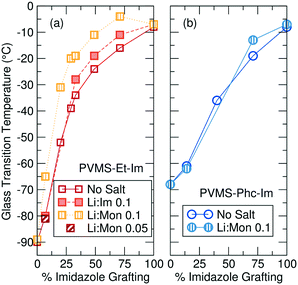
In addition to affecting polymer structure and propensity for ion aggregation, a lower grafting density of imidazole ligands results in significant decrease of the polymer Tg, as seen in Fig. 3. Before the addition of LiTFSI salt, the ethane-imidazole polymer series Tg ranges from −8 °C for fully imidazole-functionalized to −90 °C for fully ethane-functionalized (Fig. 3a). The Tg decrease for the phenyl-imidazole series is slightly smaller, with a drop to −68 °C for a fully phenyl-functionalized polymer (Fig. 3b). Expected Tg values for copolymers can be estimated using the Fox equation,37 but consistently underestimate the measured Tg for both series (Fig. S23 and S24†). The changing concentration of hydrogen-bonding amide functionality is likely playing a large role and at least partially accounts for this discrepancy.38 It is also possible that microphase separation or clustering of the polar imidazole side-chains away from the non-polar side chains (as suggested by the X-ray scattering profiles for the ethane-imidazole polymer series, see Fig. S10†) could be driving additional Tg increases for the copolymer series.
The significant decrease in Tg with lower imidazole content for both the ethane- and phenyl-imidazole series suggests that two effects contribute to the polymer Tg. First, the removal of the imidazole side chain eliminates both the polar imidazole group and the amide functional group, which is expected to participate in hydrogen bonding and dynamic cross-linking of the polymer. Elimination of hydrogen bonding and polar groups results in a −60 °C drop in Tg as measured for the phenyl-imidazole series. The ethane-imidazole series further eliminates the steric bulk of the phenyl unit, replacing it with a small ethane cap instead. The smaller side chain reduces steric crowding of the polymer backbone, and results in a further −20 °C drop of the polymer Tg.
Tuning the grafting density of solvating side chains can provide the desired Tg control, but also influences the density of solvation sites and extent of ion aggregation within the polymer. A recent computational study on ether-based electrolytes suggested that the connectivity of solvation sites within an electrolyte can play a critical role in conductivity performance.39,40 It is therefore expected that as the grafting density of solvation sites decreases, the efficacy of ion transport through the electrolyte decreases as well, resulting in reduced conductivity performance. Unfortunately, predicting the distribution of solvation sites within a polymer electrolyte can be challenging; experimental methods such as X-ray scattering may observe correlation peaks suggesting some amount of aggregation, but cannot determine the shape of any aggregate features.41 Furthermore, uniformly distributed coordination sites would not show any features in X-ray scattering at all, but may have significantly different connectivity. Computational tools can aid in this understanding by providing information about aggregate morphology and connectivity.13,41,42
Total ionic conductivity
While the ethane- and phenyl-imidazole series show similar Tg behavior, they differ markedly in their conductivity trend with changing grafting density at a constant temperature of 30 °C, likely due to the difference in steric bulk of the phenyl versus ethane side chain which might affect solvation site distribution and connectivity. The ethane-imidazole polymer series undergoes a steady increase of about an order of magnitude in ionic conductivity as the imidazole grafting density is reduced from 100% to around 30% (Fig. 4a). This conductivity increase reaches a plateau at imidazole contents less than 30%, until all the imidazole is removed from the polymer, which results in a significant drop in conductivity due to the poor solvation and conduction properties of the siloxane backbone and thioether functional group. Interestingly, for the phenyl-imidazole series, the conductivity peaks at a relatively high grafting density of 72%, and subsequently decreases with lower imidazole content (Fig. 4b). The maximum conductivity increase is also only approximately a factor of 2. The non-monotonic evolution of the conductivity with grafting density differs from the continually decreasing Tg trend. This result highlights that Tg is not the only important factor in controlling ionic conductivity. Instead, the difference in steric bulk of the phenyl group in comparison to the ethane side chain might be playing a role in determining the conductivity performance.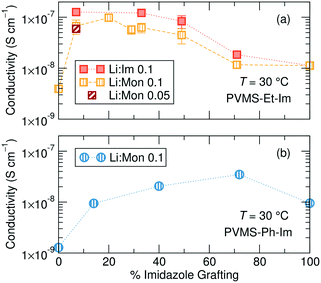 | ||
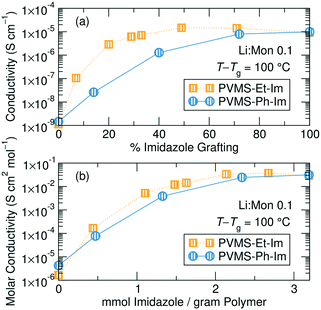
| Fig. 4 Total ionic conductivity for the (a) ethane-imidazole and (b) phenyl-imidazole series as a function of the percentage of monomers containing an imidazole sidechain. | ||
Analyzing conductivity at a constant temperature relative to Tg reveals a threshold grafting density above which extra imidazole is unimportant for the conductivity mechanism. Fig. 5a shows conductivity as a function of imidazole grafting percentage for both series at T − Tg = 100, which was chosen because this temperature was accessible for conductivity measurements for all the samples within both series. Fig. S28† shows the conductivity normalizations for concentrations not shown here, Table S2† provides the actual measurement temperatures for each sample and Fig. S29† shows Tg/T normalization. Eliminating the contribution due to changing Tg within each series isolates the role of inert side chain concentration and identity on conductivity performance. This representation shows a significantly different picture to the un-normalized conductivity data shown in Fig. 4.
The ethane-imidazole exhibits a plateau in ionic conductivity at imidazole grafting densities above ∼30%, suggesting that at these imidazole concentrations the conductivity is unaffected by a change in the imidazole content. This is an important design rule, as it indicates that increasing the concentration of solvating groups does not always result in improved ion transport. The phenyl-imidazole series, on the other hand, shows a continuous decline in conductivity with lower imidazole content, though the initial decrease in imidazole content to 72% only has minimal effect.
Below a grafting density threshold, which differs between the two series, the conductivity begins to decline more steeply, but also does not immediately reduce to zero. While it is tempting to discuss this decline in terms of a percolation threshold, static percolation theory does not hold in polymer electrolytes significantly above their Tg.43–45 In these polymers, electrolyte conductivity is measured well above the polymer Tg, suggesting significant segmental motion occurs, and solvation site rearrangement likely plays an important role in determining conductivity performance at lower grafting densities.
Instead, these results can be understood in terms of dynamic percolation theory, which suggests ion conductivity depends on both the rate of solvation site re-arrangement and the rate of ion ‘hopping’, or motion, between solvation sites. Of particular relevance is the timescale for solvation site re-arrangement relative to the timescale for ion motion. The importance of the timescale for solvation site re-arrangement was suggested by Druger, Nitzan and Ratner through the development of a dynamic percolation theory.45–48 This theory has two key timescales – the rate of ion hopping that would be present in a static matrix, and the rate of solvation site re-arrangement. In a system where ion hopping is much faster than solvation site re-arrangement, we recover the static percolation limit, which suggests there is a critical density of solvation sites required to enable ion conduction. However, in the limit where the solvation site re-arrangement is much faster than ion hopping, this percolation threshold disappears entirely, and ion conduction is predicted even for electrolytes with dilute solvation sites. Most electrolyte systems fall intermediate to these two limits, suggesting that both the rate of ion hopping, dictated by ion-solvation site dynamics, and the rate of solvation site re-arrangement, dictated by segmental dynamics, are important for ion transport.39 Indeed, this explains why Tg is an important lever for increasing conductivity, but that there is still a spread of conductivity performance between systems that have essentially the same Tg but different chemistries.49
The Tg-normalized conductivity representation eliminates differences in solvation site re-arrangement between the polymer electrolytes, enabling understanding of the impact of imidazole content on ion motion. Fig. 5a shows that ion conduction rates are invariant at high imidazole contents, especially for the ethane-imidazole series, but drop steadily below a threshold imidazole density. High imidazole contents likely form a percolated network of solvation sites,13 resulting in constant solvation site connectivity and thus invariant ion motion between solvation sites. When the ligand concentration drops below a threshold, the distribution and connectivity of solvation sites changes with imidazole content, resulting in decreasing Tg-normalized ionic conductivity. The role of solvation site distribution on ion motion was previously discussed in Webb et al.39 Note, this Tg-normalized conductivity representation eliminates differences in solvation site re-arrangement, but does not eliminate the importance of such re-arrangement, as the conductivities here are 100 degrees above Tg. This is why the conductivity declines but does not reduce to zero after the threshold imidazole content. The polymers free of imidazole show 1–2 orders of magnitude lower conductivity compared to those with imidazole; the conductivity in these systems is likely due to residual solvation ability of the thio-ether functional groups.50,51 This emphasizes the need for additional solvation sites, such as the imidazole ligands, to improve salt dissolution and subsequent ion motion.
The difference in grafting percentage below which a conductivity drop is seen in the two series likely results from the significantly different steric bulk, or volume, of the ethane versus the phenyl side chains used in this study (Fig. 5b). It is possible to convert the imidazole grafting percentage into a mass-normalized imidazole concentration by calculating the mmol of imidazole per gram of each polymer. If the densities of the polymers within the series does not appreciably change, then this mmol imidazole per gram polymer should translate directly into a volumetric concentration (mmol cm−3) of imidazole. This normalization scheme is shown in Fig. S30.† To better compare the two series, the conductivity is also normalized into an approximate molar conductivity. This requires assuming full salt dissociation and a constant polymer density (here taken as 1 g cm−3) for all polymers – see ESI† (page S19) for details. This form of normalization is commonly applied to both liquid and polymer electrolytes to aid in comparability between studies.52–55Fig. 5b shows the scaled conductivity behavior for the ethane- and phenyl-imidazole series with a Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) monomer ratio of 0.1. This approximate normalization scheme provides much stronger agreement between the two series in terms of the threshold imidazole content that results in a drop in conductivity performance.
monomer ratio of 0.1. This approximate normalization scheme provides much stronger agreement between the two series in terms of the threshold imidazole content that results in a drop in conductivity performance.
Pulsed-field gradient diffusion NMR
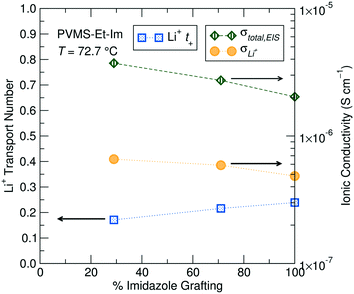
Unlike the total (cation + anion) conductivity, which decreases with increasing imidazole content at a fixed temperature, the Li+ transport number increases with increasing grafting density when measured at 72.7 °C, suggesting lithium mobility is preferentially enhanced over the TFSI− at higher imidazole densities (Table 2). This could be due to shorter distances between imidazole sites, potentially reducing the energy barrier for lithium hopping. For the 29% and 71% imidazole grafted samples the transport number was observed to increase with temperature. It is likely that at higher temperature the energy required for Li+ binding/unbinding to the imidazole (and amide) is more easily overcome (due to thermal fluctuations), and therefore speeds up the Li+ conduction process, leading to faster Li+ conduction while TFSI− conduction is relatively unchanged. Conversely, the 100% grafted sample is constant over the limited temperature range accessible for these systems. The diffusion and transport number values for all samples measured are displayed in Table 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) monomer ratio of LiTFSI, and measured at 72.7 °C and 81.4 °C
monomer ratio of LiTFSI, and measured at 72.7 °C and 81.4 °C
| Grafting | Diffusion (× 10−13 m2 s−1) | t + | Ionic conductivity (× 10−6 Scm−1) | |||||
|---|---|---|---|---|---|---|---|---|
| Density (%) | D 7Li | D 19F | (%) | σ + | σ − | σ total,PFG | σ total,EIS | |
| 72.7 °C | 29 | 0.62 | 2.87 | 17.7 | 1.02 | 4.74 | 5.76 | 3.72 |
| 71 | 0.53 | 1.91 | 21.6 | 0.64 | 2.33 | 2.97 | 2.73 | |
| 100 | 1.03 | 3.29 | 23.9 | 1.06 | 3.04 | 4.46 | 2.03 | |
| 81.4 °C | 29 | 1.11 | 4.88 | 18.6 | 1.79 | 7.86 | 9.65 | 6.63 |
| 71 | 1.14 | 3.59 | 24.1 | 1.36 | 4.27 | 5.63 | 5.24 | |
| 100 | 1.92 | 6.19 | 23.7 | 1.93 | 6.24 | 8.17 | 5.38 | |
Calculating an ideal expected ionic conductivity from PFG diffusion measurements (see eqn (S3) in ESI†) consistently overestimates the conductivity compared to the total ionic conductivity measured by impedance spectroscopy (EIS), suggesting that not all ions in the system contribute to the conductivity. One possible explanation for the over-estimation of the calculated conductivity is incomplete salt dissociation, which would result in neutral ion pairs or larger neutral aggregates that do not contribute to the overall conductivity but contribute to Li self-diffusion. While SAXS does not indicate significant ion aggregation at this salt concentration for the 71% and 100% imidazole grafting density, this does not preclude the existence of ion pairing or small-scale aggregates not detectable in X-ray scattering.
The transport number can be multiplied by the total EIS-measured ionic conductivity to provide the Li-ion conductivity in these electrolytes, and is plotted for the three grafting densities in Fig. 6. The adjustment of the total conductivity by t+ provides a better comparison of expected device performance, where only the Li+ contribution to the conductivity will enable steady-state operation. The lower grafting densities still show better performance due to a lower Tg compared to higher grafting densities, though the gap between the different grafting densities is reduced somewhat due to the lower Li+t+.
PFG-NMR can only provide dynamics information at elevated temperatures due to limitations imposed by short T2 relaxation times, thus NMR line-shape analysis and relaxometry were employed to compare local and longer-range dynamics, respectively, of the Li+ and TFSI− ions at lower temperatures not accessible by PFG-NMR.
NMR line-shape analysis
NMR line-shape analysis reveals that local Li+ and TFSI− ion mobility is most impeded at intermediate grafting density at ambient temperatures (Fig. 7). The NMR line width is inversely proportional to the local mobility of a species, but can only be compared across samples if the local environments of the species are also similar. Here, the local environments are likely reasonably similar between the PVMS–Et-Im polymers with 29%, 71% and 100% imidazole grafting, enabling a qualitative comparison. 7Li NMR measurements show evidence of two different Li+ sites through the existence of a broad and a narrow component contributing to overall peak shape (discussed in more detail below). The following discussion focuses on the narrower (more mobile) component, as the second, broader component in the 7Li NMR data can unfortunately not be fitted with accuracy. At ambient temperatures, the 29% imidazole grafted polymer has a significantly narrower line-shape than the 71% imidazole grafted polymer, which implies that Li+ ions are more locally mobile in the former compared to the latter polymer at room temperature. Interestingly, this local mobility increases again for the 100% grafted system, implying that both low and high grafting densities can enable rapid local ionic motion. Analogous to the 7Li data, the width of the 19F peaks converge at higher temperatures for all of the samples suggesting similar dynamics, although differences between samples are clearly observed at ambient temperatures. At temperatures above 47 °C (320 K), the order from fastest to slowest dynamics based on the width measurements are the 100%, 29% and 71% grafted samples, which is consistent with the diffusion values. However, below this temperature, the fastest moving ions are in the 29% grafted polymer.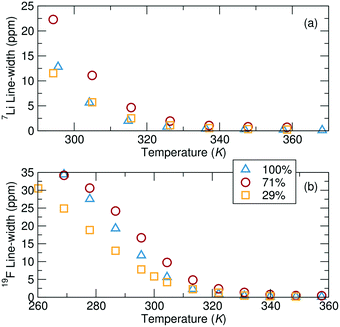 | ||
Fig. 7 (a) 7Li NMR and (b) 19F NMR peak width, as a function of temperature. All samples consist of a 0.1 Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) monomer ratio of LiTFSI added to the polymer. monomer ratio of LiTFSI added to the polymer. | ||
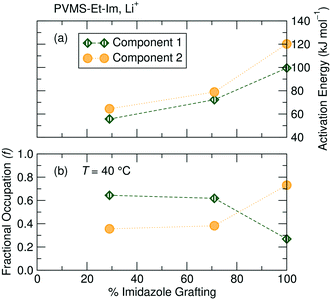
To predict the evolution of transport numbers with temperature, a comparison of activation energies extracted from Arrhenius fits of temperature-dependent line width measurements can be employed. For instance, the narrower 7Li component yield activation energies of 61.8 kJ mol−1, 54.2 kJ mol−1 and 68.2 kJ mol−1 for the 29%, 71% and 100% grafted polymers, respectively. Higher activation energy for the 100% imidazole grafted polymer suggests more constrained local mobility, likely due to the significantly higher Tg of that polymer. The activation energies derived from Fig. 7b for the TFSI− are 58.1 kJ mol−1, 62.9 kJ mol−1 and 80.6 kJ mol−1 for the 29%, 71% and 100% imidazole grafted samples, respectively. Since the activation energies for each ion for the 29% grafted sample are comparable, there is likely little change in the transport number with temperature. Conversely, these line width activation data indicate that the Li+ transport number for the 71% and 100% grafted samples will decrease slightly at ambient temperature. Interestingly, the line-shape activation energies of the TFSI− ion increases with increased grafting density. This suggests that as the grafting density is increased the local motion of the TFSI− ions slows down. Conversely, the Li+ ion activation energies go through a minimum at 71% grafting density. Since the TFSI− ions are not expected to directly interact with the polymer, one might expect the grafting density effect to only be one of local free volume/structure. On the other hand, Li+ ions interact with the polymer and these results suggest that there is an optimum for fast Li+ binding dynamics at 71% grafting density. This is likely due to more local freedom from fewer tethered side-chains, but enough grafting to allow efficient lithium association/dissociation from the polymer.
The line width activation energies obtained are close to those determined from the diffusion measurements (ESI† page S22), suggesting that ion diffusion is taking place at a similar rate at the local (nm) scale and at intermediate length scales (microns or more). Therefore, these simple peak width measurements seem to be a reasonable indicator of the diffusion behavior and thus transport properties at lower temperatures in polymer samples, where sluggish dynamics do not allow for diffusion to be directly measured via PFG-NMR.
NMR Relaxometry
NMR relaxometry (T1ρ) measurements reveal the presence of multiple 7Li (and 19F, below ambient temperature) environments, regardless of the imidazole grafting density. T1ρ can be used to probe much longer-range dynamics (on the order of 10 μs to 1 ms, depending on the spin-locking frequency used) compared with T1 and T2 and thus, in some instances is comparable to the timescale of the self-diffusion measurements (ms). T1ρ has the added benefit of providing site-specific information on the dynamics of the ionic species of interest.Here, 7Li T1ρ measurements reveal the presence of two Li+ environments within the polymer sample. It is difficult to ascertain the exact origins of these two 7Li components solely from NMR, though comparisons can be made based on mobility and fractional occupation of the two components as a function of grafting density. Arrhenius fits of the temperature-dependent relaxation rate R1ρ = 1/T1ρ (Fig. 8a, see ESI† eqn (S6)) for the 29%, 71% and 100% imidazole-grafted polymer samples reveal that Li+ ions giving rise to component 1 have a lower activation energy and are therefore more mobile than those associated with component 2. As shown in Fig. 8b, component 1 shows a higher fractional occupation than component 2 over the entire temperature range probed for the lower grafting density samples, while a lower occupation of component 1 is observed for the 100% grafted polymer.
One possible assignment of the two Li+ components is that they correspond to Li+ ions bound to the imidazole (less mobile) and Li+ ions in the unbound state (more mobile, possibly ‘free' in solution). Another possibility is that the multiple components correspond to Li+ ions bound to varying numbers of imidazole moieties, which would affect their mobility. We note that it is unlikely that the second environment is related to binding to the amide group present on the polymer side-chain, as two environments have also been observed in similar polymer systems which do not contain the amide functionality.38 We therefore conclude that the signal from immobile Li+ bound to the amide is likely too broad to be observed.
A comparison of the evolution of the population of the two Li+ environments across the three polymers reveals that component 1 becomes more populated and more mobile as the grafting density decreases (Fig. 8b). An increasing fraction of the more mobile component with lower imidazole content lends credence to the hypothesis that the two Li environments correspond to Li+ ions bound to varying numbers of imidazole moieties.
The lower activation energies for the 29% sample compared to higher grafting densities suggests that the Li+ mobility increases with decreasing imidazole content. This supports the results from conductivity measurements, which also show a higher conductivity for lower grafting density samples compared with higher grafting density at the same absolute temperature.
Even though the T1ρ relaxometry measurements indicate two Li+ environments, the 7Li PFG NMR results yield a single diffusion constant for 7Li. The PFG-NMR diffusion measurements carried out in this work are sensitive to Li+ ion motion over a 50–100 ms time period, which presumably results from multiple Li+ binding–unbinding events (based on the conductivity values) to a varying number of imidazole moieties. Hence, the measured Li diffusion coefficient is expected to be an average for the two Li+ populations determined by T1ρ relaxometry. This average diffusion coefficient allows for accurate evaluation of Li+ transport numbers (Fig. 6), while relaxometry data provide extra information on the links between chemical environment and ion dynamics that cannot be probed by PFG-NMR.
Interestingly, the trend in Li+ mobility extracted from the room temperature T1ρ measurements is in contrast to that observed from PFG-NMR Li+ diffusion measurements at elevated temperatures, where the Li+ is more mobile in the higher grafting density sample. This emphasizes the importance of performing mobility measurements (T1ρ and PFG-NMR) over the entire range of relevant temperatures. This study further demonstrates that T1ρ measurements are particularly insightful for the determination of the total number of environments available to each diffusing ion, and for the assessment of the dynamics of individual components. These insights are not readily available using any other technique, suggesting that T1ρ measurements coupled with PFG-NMR yield unique information on the ion dynamics of polymer systems and can be used to predict dynamics at lower temperatures, where diffusion measurements cannot easily be carried out.
Conclusions
Tuning the ligand grafting density of an imidazole side-chain siloxane polymer electrolyte doped with LiTFSI enables dramatic tunability over polymer glass transition temperature and total ionic conductivity. The choice of an inert side chain, either ethane thiol or phenyl thiol, has a significant impact on the ionic conductivity behavior, with the less bulky ethane side chain enabling an order of magnitude improvement in total ionic conductivity. The Tg-normalized conductivity is shown to be constant at high imidazole grafting density, and decreases below a threshold imidazole content that can be correlated with an approximate volume fraction of imidazole. PFG-NMR enables the measurement of Li+ transport numbers, which decrease slightly with decreasing imidazole content, likely due to poorer connectivity between neighboring coordination sites. These measurements also suggest ion pairing or incomplete salt dissociation. Relaxation NMR measurements indicate the existence of at least two ion environments, and prove useful for estimating t+ at lower temperatures not accessible to PFG-NMR. This system presents further opportunities for tuning polymer electrolyte conductivity performance by reducing, rather than increasing, the total ligand content to a value that optimizes polymer Tg, ionic conductivity, and Li+t+.Author contributions
N. S. S., P. M. R., R. C. and R. A. S. conceived of the experimental plan. N. S. S. and P. M. R. led the data curation and formal analysis. G. A. K. and P. C. helped with data collection and analysis. A. N., E. M. S., and K. J. helped with polymer synthesis. A. N. and J. R. A. conceived of the small molecule phenyl-thiol synthesis. H. W. and J. R. A. supervised and helped with project administration. N. S. S. and P. M. R. wrote the original draft. All authors contributed to reviewing and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Materials Research Science and Engineering Centers (MRSEC) Program of the National Science Foundation (NSF) under Award No. NSF DMR 1720256 (IRG-2). The NMR results reported here made use of the shared facilities of the UCSB MRSEC (NSF DMR #1720256), a member of the Materials Research Facilities Network (http://www.mfn.org). N. S. S. gratefully acknowledges the Fannie and John Hertz Foundation and the NSF Graduate Research Fellowship Program under Grant 1650114 for support. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.References
- M. A. Ratner and D. F. Shriver, Ion Transport in Solvent-Free Polymers, Chem. Rev., 1988, 88, 109–124 CrossRef CAS
.
- D. T. Hallinan and N. P. Balsara, Polymer Electrolytes, Annu. Rev. Mater. Res., 2013, 43, 503–525 CrossRef CAS
.
- J. B. Goodenough and Y. Kim, Challenges for Rechargeable Li Batteries, Chem. Mater., 2010, 22, 587–603 CrossRef CAS
.
- O. Borodin and G. D. Smith, Li+ Transport Mechanism in Oligo(Ethylene Oxide)s Compared to Carbonates, J. Solution Chem., 2007, 36, 803–813 CrossRef CAS
.
- N. S. Schauser, G. E. Sanoja, J. M. Bartels, S. K. Jain, J. G. Hu, S. Han, L. M. Walker, M. E. Helgeson, R. Seshadri and R. A. Segalman, Decoupling Bulk Mechanics and Mono- and Multivalent Ion Transport in Polymers Based on Metal-Ligand Coordination, Chem. Mater., 2018, 30, 5759–5769 CrossRef CAS
.
- D. Diddens, A. Heuer and O. Borodin, Understanding the Lithium Transport within a Rouse-Based Model for a PEO/LiTFSI Polymer Electrolyte, Macromolecules, 2010, 43, 2028–2036 CrossRef CAS
.
- B. K. Wheatle, N. A. Lynd and V. Ganesan, Effect of Polymer Polarity on Ion Transport: A Competition between Ion Aggregation and Polymer Segmental Dynamics, ACS Macro Lett., 2018, 7, 1149–1154 CrossRef CAS
.
- G. E. Sanoja, N. S. Schauser, J. M. Bartels, C. M. Evans, M. E. Helgeson, R. Seshadri and R. A. Segalman, Ion Transport in Dynamic Polymer Networks Based on Metal-Ligand Coordination: Effect of Cross-Linker Concentration, Macromolecules, 2018, 51, 2017–2026 CrossRef CAS
.
- A. Panday, S. Mullin, E. D. Gomez, N. Wanakule, V. L. Chen, A. Hexemer, J. Pople and N. P. Balsara, Effect of Molecular Weight and Salt Concentration on Conductivity of Block Copolymer Electrolytes, Macromolecules, 2009, 42, 4632–4637 CrossRef CAS
.
- S. Lascaud, M. Perrier, A. Vallke, S. Besner, J. Prud'homme and M. Armand, Phase Diagrams and Conductivity Behavior of Poly(ethylene oxide)-Molten Salt Rubbery Electrolytes, Macromolecules, 1994, 27, 7469–7477 CrossRef CAS
.
- D. M. Pesko, K. Timachova, R. Bhattacharya, M. C. Smith, I. Villaluenga, J. Newman and N. P. Balsara, Negative Transference Numbers in Poly(ethylene oxide)-Based Electrolytes, J. Electrochem. Soc., 2017, 164, E3569–E3575 CrossRef CAS
.
- J.-C. Lai, X.-Y. Jia, D.-P. Wang, Y.-B. Deng, P. Zheng, C.-H. Li, J.-L. Zuo and Z. Bao, Thermodynamically stable whilst kinetically labile coordination bonds lead to strong and tough self-healing polymers, Nat. Commun., 2019, 10, 1164 CrossRef PubMed
.
- N. S. Schauser, D. J. Grzetic, T. Tabassum, G. A. Kliegle, M. L. Le, E. M. Susca, S. Antoine, T. J. Keller, K. T. Delaney, S. Han, R. Seshadri, G. H. Fredrickson and R. A. Segalman, The Role of Backbone Polarity on Aggregation and Conduction of Ions in Polymer Electrolytes, J. Am. Chem. Soc., 2020, 142, 7055–7065 CrossRef CAS PubMed
.
- R. Hooper, L. J. Lyons, M. K. Mapes, D. Schumacher, D. A. Moline and R. West, Highly Conductive Siloxane Polymers, Macromolecules, 2001, 34, 931–936 CrossRef CAS
.
- J. C. Persson and P. Jannasch, Intrinsically Proton-Conducting Benzimidazole Units Tethered to Polysiloxanes, Macromolecules, 2005, 38, 3283–3289 CrossRef CAS
.
- K. M. Abraham and M. Alamgir, Dimensionally Stable MEEP-Based Polymer Electrolytes and Solid-State Lithium Batteries, Chem. Mater., 1991, 3, 339–348 CrossRef CAS
.
- N. Kobayashi, M. Uchiyama, K. Shigehara and E. Tsuchida, Ionically High Conductive Solid Electrolytes Composed of Graft Copolymer-Lithium Salt Hybrids, J. Phys. Chem., 1985, 89, 987–991 CrossRef CAS
.
- M. Morita, T. Fukumasa, M. Motoda, H. Tsutsumi, Y. Matsuda, T. Takahashi and H. Ashitaka, Polarization Behavior of Lithium Electrode in Solid Electrolytes Consisting of a Poly(Ethylene Oxide)-Grafted Polymer, J. Electrochem. Soc., 1990, 137, 3401 CrossRef CAS
.
- P. E. Trapa, Y.-Y. Won, S. C. Mui, E. A. Olivetti, B. Huang, D. R. Sadoway, A. M. Mayes and S. Dallek, Rubbery Graft Copolymer Electrolytes for Solid-State, Thin-Film Lithium Batteries, J. Electrochem. Soc., 2005, 152, A1–A5 CrossRef CAS
.
- M. Bergman, A. Bergfelt, B. Sun, T. Bowden, D. Brandell and P. Johansson, Graft Copolymer Electrolytes for High Temperature Li-Battery Applications, Using Poly(methyl methacrylate) Grafted Poly(ethylene glycol)methyl ether methacrylate and Lithium Bis(trifluoromethanesulfonimide), Electrochim. Acta, 2015, 175, 96–103 CrossRef CAS
.
- C. Karlsson and P. Jannasch, Highly Conductive Nonstoichiometric Protic Poly(ionic liquid) Electrolytes, ACS Appl. Energy Mater., 2019, 2, 6841–6850 CrossRef CAS
.
- S. Granados-Focil, R. C. Woudenberg, O. Yavuzcetin, M. T. Tuominen and E. B. Coughlin, Water-Free Proton-Conducting Polysiloxanes: A Study on the Effect of Heterocycle Structure, Macromolecules, 2007, 40, 8708–8713 CrossRef CAS
.
- M. Doyle, T. F. Fuller and J. Newman, The Importance of the Lithium Ion Transference Number in Lithium/Polymer Cells, Electrochim. Acta, 1994, 39, 2073–2081 CrossRef CAS
.
- N. S. Schauser, R. Seshadri and R. A. Segalman, Multivalent Ion Conduction in Solid Polymer Systems, Mol. Syst. Des. Eng., 2019, 4, 263–279 RSC
.
- P. G. Bruce and C. A. Vincent, Steady State Current Flow in Solid Binary Electrolyte Cells, J. Electroanal. Chem. Interfacial Electrochem., 1987, 225, 1–17 CrossRef CAS
.
- P. G. Bruce and C. A. Vincent, Effect of Ion Association on Transport in Polymer Electrolytes, Faraday Discuss. Chem. Soc., 1989, 88, 43–54 RSC
.
- N. P. Balsara and J. Newman, Relationship between Steady-State Current in Symmetric Cells and Transference Number of Electrolytes Comprising Univalent and Multivalent Ions, J. Electrochem. Soc., 2015, 162, A2720–A2722 CrossRef CAS
.
- Y. Ma, M. Doyle, T. F. Fuller, M. M. Doeff, L. C. De Jonghe and J. Newman, The Measurement of a Complete Set of Transport Properties for a Concentrated Solid Polymer Electrolyte Solution, J. Electrochem. Soc., 1995, 142, 1859–1868 CrossRef CAS
.
- S. Arumugam, J. Shi, D. P. Tunstall and C. A. Vincent, Cation and Anion Diffusion Coefficients in a Solid Polymer Electrolyte Measured by Pulsed-Field-Gradient Nuclear Magnetic Resonance, J. Phys.: Condens. Matter, 1993, 5, 153–160 CrossRef CAS
.
- S. Schoenauer, A. Buergy, J. Kreissl and P. Schieberle, Structure/Odor Activity Studies on Aromatic Mercaptans and Their Cyclohexane Analogues Synthesized by Changing the Structural Motifs of Naturally Occurring Phenyl Alkanethiols, J. Agric. Food Chem., 2019, 67, 2598–2606 CrossRef CAS PubMed
.
-
J. Runt and J. J. Fitzgerald, Dielectric Spectroscopy of Polymeric Materials: Fundamentals and Applications, American Chemical Society, 1997 Search PubMed
.
-
SciAnalysis, 2019, https://github.com/CFN-softbio/SciAnalysis Search PubMed
.
- Y. Ma, M. Doyle, T. F. Fuller, M. M. Doeff, L. C. De Jonghe and J. Newman, The measurement of a complete set of transport properties for a concentrated solid polymer electrolyte solution, J. Electrochem. Soc., 1995, 142, 1859 CrossRef CAS
.
- A. Nyman, M. Behm and G. Lindbergh, Electrochemical characterisation and modelling of the mass transport phenomena in LiPF6–EC–EMC electrolyte, Electrochim. Acta, 2008, 53, 6356–6365 CrossRef CAS
.
- H. Hafezi and J. Newman, Verification and analysis of transference number measurements by the galvanostatic polarization method, J. Electrochem. Soc., 2000, 147, 3036 CrossRef CAS
.
- L. Edman, M. M. Doeff, A. Ferry, J. Kerr and L. C. De Jonghe, Transport properties of the solid polymer electrolyte system P (EO) n LiTFSI, J. Phys. Chem. B, 2000, 104, 3476–3480 CrossRef CAS
.
- T. G. Fox and S. Loshaek, Influence of Molecular Weight and Degree of Crosslinking on the Specific Volume and Glass Temperature of Polymers, J. Polym. Sci., 1955, 15, 371–390 CrossRef CAS
.
- N. S. Schauser, A. Nikolaev, P. Richardson, K. Johnson, E. Susca, H. Wang, R. Seshadri, R. Clément, J. R. de Alaniz and R. A. Segalman, The Glass Transition Temperature and Ion Binding Determine Conductivity and Lithium-Ion Transport in Polymer Electrolytes, ACS Macro Lett., 2021, 10, 104–109 CrossRef CAS
.
- M. A. Webb, B. M. Savoie, Z.-G. Wang and T. F. Miller III, Chemically Specific Dynamic Bond Percolation Model for Ion Transport in Polymer Electrolytes, Macromolecules, 2015, 48, 7346–7358 CrossRef CAS
.
- D. M. Pesko, Y. Jung, A. L. Hasan, M. A. Webb, G. W. Coates, T. F. Miller III and N. P. Balsara, Effect of Monomer Structure on Ionic Conductivity in a Systematic Set of Polyester Electrolytes, Solid State Ionics, 2016, 289, 118–124 CrossRef CAS
.
- C. F. Buitrago, D. S. Bolintineanu, M. E. Seitz, K. L. Opper, K. B. Wagener, M. J. Stevens, A. L. Frischknecht and K. I. Winey, Direct Comparisons of X-ray Scattering and Atomistic Molecular Dynamics Simulations for Precise Acid Copolymers and Ionomers, Macromolecules, 2015, 48, 1210–1220 CrossRef CAS
.
- L. M. Hall, M. J. Stevens and A. L. Frischknecht, Effect of Polymer Architecture and Ionic Aggregation on the Scattering Peak in Model Ionomers, Phys. Rev. Lett., 2011, 106, 127801 CrossRef PubMed
.
- A. L. Frischknecht, B. A. Paren, L. R. Middleton, J. P. Koski, J. D. Tarver, M. Tyagi, C. L. Soles and K. I. Winey, Chain and Ion Dynamics in Precise Polyethylene Ionomers, Macromolecules, 2019, 52, 7939–7950 CrossRef CAS
.
- H. Scher and R. Zallen, Critical Density in Percolation Processes, J. Chem. Phys., 1970, 53, 3759–3761 CrossRef CAS
.
- S. D. Druger, A. Nitzan and M. A. Ratner, Dynamic Bond Percolation Theory: A Microscopic Model for Diffusion in Dynamically Disordered Systems, I. Definition and One-Dimensional Case, J. Chem. Phys., 1983, 79, 3133–3142 CrossRef CAS
.
- S. D. Druger, M. A. Ratner and A. Nitzan, Polymeric Solid Electrolytes: Dynamic Bond Percolation and Free Volume Models for Diffusion, Solid State Ionics, 1983, 9, 1115–1120 CrossRef
.
- S. D. Druger, M. A. Ratner and A. Nitzan, Generalized Hopping Model for Frequency-Dependent Transport in a Dynamically Disordered Medium, with Applications to Polymer Solid Electrolytes, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3939–3947 CrossRef CAS PubMed
.
- A. Nitzan and M. A. Ratner, Conduction in Polymers: Dynamic Disorder Transport, J. Phys. Chem., 1994, 98, 1765–1775 CrossRef CAS
.
- J. Mindemark, M. J. Lacey, T. Bowden and D. Brandell, Beyond PEO–Alternative Host Materials for Li+-Conducting Solid Polymer Electrolytes, Prog. Polym. Sci., 2018, 81, 114–143 CrossRef CAS
.
- P. Johansson, First principles modelling of amorphous polymer electrolytes: Li+–PEO, Li+–PEI, and Li+–PES complexes, Polymer, 2001, 42, 4367–4373 CrossRef CAS
.
- J. M. Sarapas and G. N. Tew, Poly (ether–thioethers) by Thiol–Ene Click and Their Oxidized Analogues as Lithium Polymer Electrolytes, Macromolecules, 2016, 49, 1154–1162 CrossRef CAS
.
- Y. Wang, F. Fan, A. L. Agapov, X. Yu, K. Hong, J. Mays and A. P. Sokolov, Design of Superionic Polymers - New Insights from Walden Plot Analysis, Solid State Ionics, 2014, 262, 782–784 CrossRef CAS
.
- E. W. Stacy, C. P. Gainaru, M. Gobet, Z. Wojnarowska, V. Bocharova, S. G. Greenbaum and A. P. Sokolov, Fundamental Limitations of Ionic Conductivity in Polymerized Ionic Liquids, Macromolecules, 2018, 51, 8637–8645 CrossRef CAS
.
- D. Bresser, S. Lyonnard, C. Iojoiu, L. Picard and S. Passerini, Decoupling Segmental Relaxation and Ionic Conductivity for Lithium-Ion Polymer Electrolytes, Mol. Syst. Des. Eng., 2019, 4, 779–792 RSC
.
- C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, Polymerized Ionic Liquids: Correlation of Ionic Conductivity with Nanoscale Morphology and Counterion Volume, ACS Macro Lett., 2017, 6, 941–946 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization including SEC traces, NMR integrations, DSC traces, conductivity as a function of temperature, NMR results. See DOI: 10.1039/d1me00089f |
| This journal is © The Royal Society of Chemistry 2021 |