Tetrazine molecules as an efficient electronic diversion channel in 2D organic–inorganic perovskites

Abstract

Taking advantage of an innovative design concept for layered halide perovskites with active chromophores acting as organic spacers, we present here the synthesis of two novel two-dimensional (2D) hybrid organic–inorganic halide perovskites incorporating for the first time 100% of a photoactive tetrazine derivative as the organic component. Namely, the use of a heterocyclic ring containing a nitrogen proportion imparts a unique electronic structure to the organic component, with the lowest energy optical absorption in the blue region. The present compound, a tetrazine, presents several resonances between the organic and inorganic components, both in terms of single particle electronic levels and exciton states, providing the ideal playground to discuss charge and energy transfer mechanisms at the organic/inorganic interface. Photophysical studies along with hybrid time-dependent DFT simulations demonstrate partial energy transfer and rationalise the suppressed emission from the perovskite frame in terms of different energy-transfer diversion channels, potentially involving both singlet and triplet states of the organic spacer. Periodic DFT simulations also support the feasibility of electron transfer from the conduction band of the inorganic component to the LUMO of the spacer as a potential quenching mechanism, suggesting the coexistence and competition of charge and energy transfer mechanisms in these heterostructures. Our work proves the feasibility of inserting photoactive small rings in a 2D perovskite structure, meanwhile providing a robust frame to rationalize the electronic interactions between the semiconducting inorganic layer and organic chromophores, with the prospects of optimizing the organic moiety according to the envisaged application.

---

New concepts

Layered metal halide perovskites are natural quantum-well semiconductors, where frontier electrons and holes are often confined on atomically thin inorganic sheets, spaced by insulating organic moieties. At the same time, the inclusion of optically active chromophores as an organic spacer represents an effective strategy to further tune the optoelectronic properties of these systems, opening the way for several charge and energy transfer phenomena at the inorganic/organic interface, like exciton separation or organic-mediated charge transport, potentially useful for optoelectronic applications. Still, thorough understanding of these processes has to be achieved, in order to fully exploit them in real devices. Here, we provide a detailed picture of the charge and energy transfer processes taking place in newly synthesized layered chloride and mixed chloride/bromide lead perovskites, incorporating a tetrazine-based chromophore as an organic spacer with a strong oxidizing character. Various resonances highlighted by optical characterization and hybrid DFT simulations at the level of monoelectronic and exciton states allowed us to discuss several decay channels for the photogenerated carriers, responsible for the observed perovskite emission quenching. This study provides then a robust foundation to discuss charge and energy transfer processes in layered halide perovskites, in the presence of active organic chromophores.

Introduction

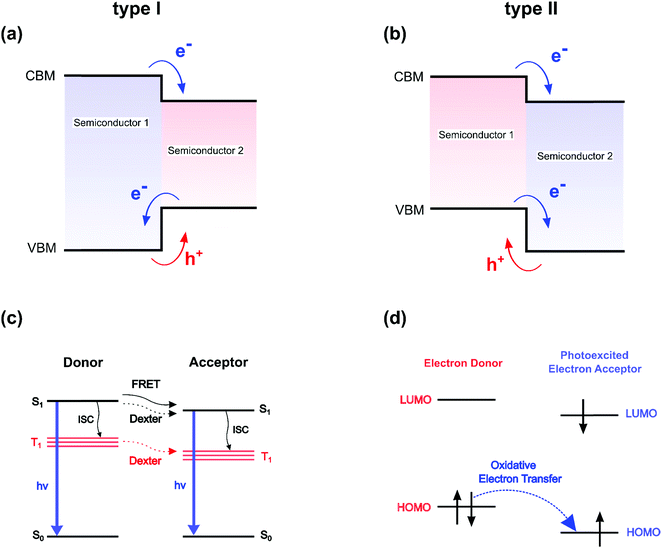
During the last 30 years, two-dimensional (2D) organic–inorganic hybrid semiconductors have attracted substantial attention owing to their remarkable properties and broad application potential in optoelectronic devices such as solar cells,^1–3 lasers,⁴ LEDs,^5,6 photodetectors^7–9 and devices working with cavity-polariton quasi-particles.^10–13 These self-assembled compounds naturally form well-ordered multi-layered microcrystals, simply using standard synthetic techniques like spin-coating.^14,15 Moreover, successful production of large size, thin quasi-2D crystals via crystallization in a confined space was recently demonstrated.^7,8,16 These synthetic approaches work under ambient conditions of temperature and pressure and are therefore less expensive and restrictive, compared to traditional deposition techniques for inorganic semiconductors and heterostructures, such as MBE (Molecular Beam Epitaxy), MOCVD (Metal–Organic Chemical Vapor Deposition) and PECVD (Plasma-Enhanced Chemical Vapor Deposition).

2D organic–inorganic perovskites are characterized by a usual chemical formula (R-NH₃)₂MX₄, where (R-NH₃⁺) is a bulky organic cation, M is a divalent metal (such as Sn²⁺ or more commonly Pb²⁺) and X is a halide anion (Cl⁻, Br⁻ or I⁻). To date, most of the studies on 2D perovskites have utilized aliphatic or mono aromatic compounds such as butylammonium or phenylethylammonium which are characterized by large optical band gaps (5–6 eV). It is now known that many of these 2D perovskites form type I multiple quantum well (QW)-like structures¹⁷ in which the organic spacers act as an insulating barrier while the inorganic haloplumbate layers act as QWs for both electrons and holes. The classical concept of type I semiconductor QW (Fig. 1a) must be however handled with great care, because several fundamental differences exist between 2D perovskites and classical QW. These include the lack of suitable definition of a transverse effective mass for the barrier, the strong influence of carrier dispersion non-parabolicity in the well and the absence of common Bloch states for the well and the barrier.¹⁸ In classical semiconductor heterostructures, this schematic representation is usually associated with a free carrier picture, where a pair of electrons and holes can flow from one region to the other almost independently. In such a case the overlap of wavefunctions between the two semiconductors plays a major role in the transport of particles. The weakness of the excitonic interaction modifies only slightly the free carrier picture, and an indirect exciton may for example appear at the interface between two materials for type II QW (Fig. 1b). On the other hand, the free carrier picture breaks down in 0D semiconductor quantum dots owing to charge localization effects and enhanced quantum confinement. In that case, multiexcitons and charged excitonic states provide a more suitable representation of the crystal optoelectronic properties. For 2D perovskites, additionally to the quantum confinement in the quantum wells, the large difference between the dielectric constants of the inorganic haloplumbate layers and the organic layers leads to a dielectric confinement,^19,20 which sizeably enhances the electron–hole pair interaction and results in exciton binding energies in the typical alkylammonium-based 2D organic–inorganic perovskites up to 500 meV.²⁰ As a consequence, these self-assembled films exhibit bright and narrow photoluminescence at room temperature, which makes them ideal candidates for light-emitting applications.^21,22 Conceptually although highly localized within the stacking axis, these 2D excitonic states can be considered as Wannier-like delocalized excitations developed on the basis of monoelectronic states²⁰ and free to travel along the inorganic layer.²³ They are therefore prone to carrier deconfinement (Fig. 1b) and vertical localization.

Fig. 1 Standard energy and charge transfer mechanisms. (a and b) Classical semiconductor picture. Diagram of band alignments for type I and type II classical semiconductor heterostructures. VBM represents the Valence Band Maximum and CBM the Conduction Band Minimum. (c and d) Donor–acceptor picture. Jablonski energy diagram (c) that illustrates various energy transfer mechanisms in donor–acceptor pairs. S₀, S₁ are the molecular ground and excited spin singlet states, while T₁ are the spin triplets for the molecular excited states. ISC is the intramolecular intersystem crossing. Molecular orbital diagram (d) showing an oxidative electron transfer between an electron donor and a photoexcited electron acceptor. HOMO and LUMO are the highest occupied molecular orbital and lowest unoccupied molecular orbitals, respectively.

On the opposite side of the barricade, donor–acceptor molecular pairs are interacting systems dominated by localized Frenkel pair states. The Förster resonance energy transfer (FRET) from a donor to an acceptor (Fig. 1c) is a perfect example of a non-radiative excitation transfer, not relying on a monoelectronic state picture (Fig. 1a and b). The transfer or optical matching between two optically allowed transitions depends on the overlap integral of the acceptor absorption spectrum with the donor emission spectrum and the mutual transition dipole orientation, and classically exhibits a long-range ∼1/d⁶ dependence on the distance d between the donor and the acceptor. Let's also mention that the energy matching between the two optically allowed transitions, and the resulting resonance effect, are usually attributed to two singlet excited spin states (S₁ on Fig. 1c). The Dexter non-radiative mechanism allows transferring excitations between two optically forbidden states, carrying null transition dipoles, as in the case of spin-forbidden triplet states T₁ on Fig. 1c or dipole-forbidden singlet S₁ states (Fig. 1c). This short-range interaction requires overlap between the wavefunctions, which in that sense makes this mechanism closer than FRET to the classical semiconductor processes depicted in Fig. 1a and b. Era and coworkers deduced that the observed exponential variation of the energy transfer from the perovskite lattice to naphthalene was more compatible with a Dexter mechanism than FRET.²⁴ Still, it is worth mentioning that the classification of energy transfer processes in lead halide perovskites as singlet–singlet or triplet–triplet is conceptually challenging, as exciton states in these systems are not pure spin-states (either singlet or triplet) but have mixed character, resulting from sizable spin–orbit coupling interaction.^25,26 Apart from the optical resonance effect, the overlap between wavefunctions at the heart of the Dexter process led several authors to the empirical conclusion that beside energy matching, band alignments between the well and the barrier in a hybrid perovskite structure will also play an important role.²⁷

From that perspective, 2D hybrid halide perovskites featuring a type II organic/inorganic interface, i.e. one frontier orbital HOMO/LUMO of the organic spacer lies in the energy gap between the CBM and VBM of the perovskite frame, have been seldom reported.^28–33 In that case, the band alignment is expected to enhance charge separation at the interface, and subsequently improve out-of-plane conductivity, as well as the photovoltaic performances.^29,33 Suitable band alignment may be crucial for optimizing the perovskite material for a given application. Energy matching and band alignment engineering between the organic/inorganic parts can either be carried out by tuning the halide composition,^34,35 by modifying the number of haloplumbate layers,³⁶ or by adjusting the HOMO/LUMO gap and/or levels of the organic spacer, or in other words, incorporating optically active molecules in the perovskite structure. Indeed, instead of playing a simple passive barrier role, the organic part is flexible enough in the interstitial dimension (z-axis perpendicular to the perovskite planes), and therefore can be used to engineer the optoelectronic properties to these materials. Depending on the optical matching, defined for hybrid perovskites as the spectral overlap between the perovskite and organic absorber optical transitions, along with the electronic level alignment (type I/II, see Fig. 1a and b) at the interface, charge and/or energy transfers can be induced between the inorganic and organic moieties.

From the chemistry viewpoint, previous research focused on polyaromatic organic cations with reduced band gap such as polythiophene,^30,33,37,38 naphthalene derivatives,^39,40 anthryl,⁴¹ pyrene^29,35,42,43 and perylene²⁹ derivatives. One of the first trials was performed by Era et al. who prepared bromide-based perovskites containing a naphthalene luminophore.⁴⁴ It was later on shown, that these compounds feature extremely efficient (>99%) perovskite-to-luminophore energy transfers.²⁴ Another pioneering attempt to introduce a potent organic absorber was performed by Mitzi et al. who succeeded in preparing iodide-based perovskites featuring quaterthiophenes as the organic part.³⁷ They observed in that case mutual quenching between the optical properties of both partners,⁴⁵ which was recently associated with a type II interface.³¹ Recent studies also showed that molecular engineering may quench the perovskite exciton luminescence and lead to efficient formation of mobile free charge carriers allowing a better extraction of charge carriers from the perovskite material, as demonstrated in quasi-2D cesium lead bromide colloidal nanoplatelets, consisting of four layers of lead bromide octahedra (CsPbBr₃ NPLs, n = 4) with a reduced (∼80 meV) exciton binding energy.⁴⁶ A recent attempt by some of us was made to introduce a linear naphthalimide inside the organic part of a monolayered perovskite, in order to induce luminophore-to-perovskite energy transfer.⁴⁷ A perfect optical matching in the case of a bromide perovskite was obtained, leading to about a four-fold enhancement of the perovskite emission. However, only a limited amount of luminophore (10%) could be introduced while retaining the perovskite structure, probably because of the lattice mismatch between the lead octahedra and the ammonium salt containing the organic luminophore.

On the other hand, luminophores belonging to the tetrazine (Tz) family have been developed over the last 15 years by some of us, and demonstrated their efficiency as good organic emitters, associated with a very small size and molecular weight, allowing for example unexpected applications like fingerprint revelation.⁴⁸ Tz derivatives possess quite unique optical and electronic features as regards to others luminophores used as active barriers in 2D perovskites. Most notably, these systems exhibit low energy optical transition in the blue region, which in acenes- and thiophenes-derivatives is usually obtained via the fusion of 3–5 rings. Such low energy transition for a small-size organic molecule is due to its peculiar electronic structure, as the partial substitution of carbon with nitrogen atoms turns the character of the frontier orbitals from π–π*, common to benzene-derivatives, to n–π*, with corresponding narrowing of the HOMO–LUMO band gap.⁴⁹ A higher energy π–π* transition is also found in these compounds, in the near-UV range. Tetrazine derivatives also show significant fluorescence, with record quantum emission efficiency (ca. 40%) and lifetime (160 ns),⁵⁰ along with a strong oxidizing character both in the ground and excited states. In particular, Tz is known to undergo oxidative electron transfer in the presence of an electron donor, a process that consists in the oxidation of a nearby molecular species by the photoexcited tetrazine moiety, see Fig. 1d. In light of its intriguing light-emitting properties along with its reduced molecular size, Tz represents the ideal organic dye for incorporation in the lead halide frame, to probe charge and energy transfer processes in hybrid layered perovskite materials. Altogether, the use of nitrogen containing heterocycles as spacers in layered perovskite structures represents a novel strategy for the incorporation of optically active organic components in these systems, at least, compared to the dominant paradigm of extending the π-conjugation of the molecular spacer.³⁰ In this work, we synthesise two novel layered perovskites containing tetrazines as the sole organic spacer and report thorough optical characterization via optical spectroscopy, with theoretical support from Density Functional Theory (DFT). We focused more specifically on the competition between several deactivation channels possibly leading to luminescence quenching of the perovskite frame, with the aim to better rationalize the possible charge and/or energy transfer mechanisms at the interface between the two components.

Design of tetrazine-based hybrid layered perovskites

Chemical synthesis of a tetrazine precursor with an ammonium function

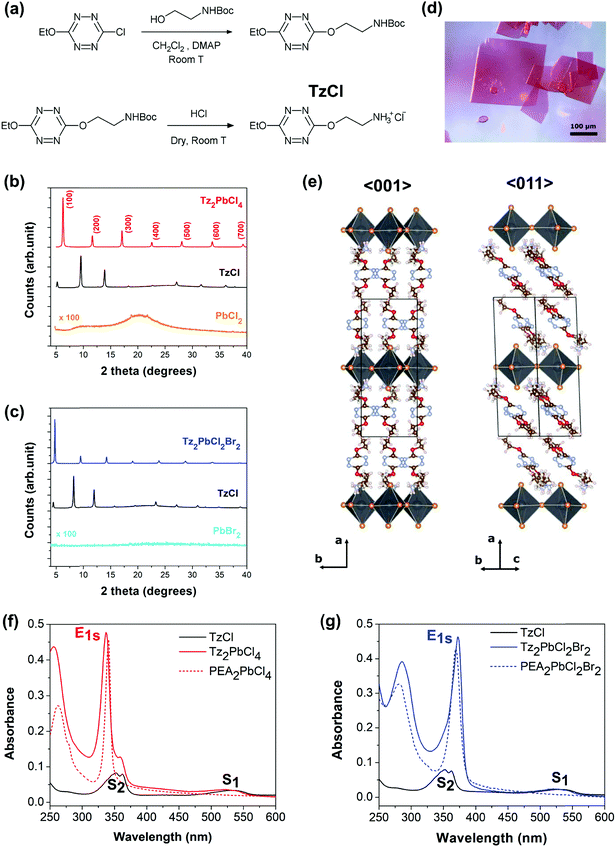
The design of a tetrazine featuring an ammonium end, linked by a spacer is not a trivial task. First, free amines are not stable in the presence of the Tz ring (because of nucleophilic attack) therefore the Tz-amine has to be produced with the amine protected, and with protection allowing the direct conversion into ammonium. Second, previous research has shown that a spacer length between one and three methylene units between the main organic moiety (in our case the Tz ring, in most cases a benzene ring) was mandatory to obtain a 2-dimensional perovskite structure with corner-sharing PbX₆ octahedra.^15,51 Finally, we opted for a Boc (tert-butoxycarbonyl) protecting group that can be cleaved directly to the ammonium salt of the corresponding halide by dry acid. The following synthetic Scheme 1 (see Fig. 2a) was therefore followed. Although the dialkoxy tetrazines are less emissive than the chloroalkoxy ones,⁵⁰ the liability of a possible chlorine substituent was too high and a more stable ethoxy substituent was preferred.

Fig. 2 Tetrazine-based hybrid layered perovskites. (a) Formation of 2-(6-ethoxy-1,2,4,5-tetrazin-3-yl)oxyethylammonium chloride (TzCl), (b) X-ray diffraction pattern of Tz₂PbCl₄ thin films compared to TzCl and PbCl₂ precursors, (c) X-ray diffraction pattern of Tz₂PbBr₂Cl₂ thin films compared to TzCl and PbBr₂ precursors, (d) single crystals of Tz₂PbCl₄ grown by the anti-solvent crystallization method, (e) structural model for Tz₂PbCl₄ from XRD single crystal measurement, projected along the 〈001〉 and 〈011〉 directions. Absorbance of (f) chloride perovskite and (g) mixed chloride–bromide perovskite spin-coated layers with Tz (solid line) or PEA (dash line) as the organic moiety.

Unfortunately, only the chloride salt of the tetrazinammonium could be produced, because of the impossibility to obtain hydrobromic acid dry enough, resulting in salt degradation during the formation reaction. This chloride salt, 2-(6-ethoxy-1,2,4,5-tetrazin-3-yl)oxyethylammonium chloride, will be designed by TzCl in the following. This situation limited the relative incorporation of any other ion than chloride into the final perovskite to 50%, as this must be introduced via the lead halide precursor. Since iodide is easily photo-oxidized by the tetrazine ring, the choice was limited to chloride and bromide. Two perovskites were finally investigated, the pure chloride based one Tz₂PbCl₄ and the mixed bromide–chloride one Tz₂PbCl₂Br₂. They were prepared from the precursors according to the following chemical reactions:

2TzCl + PbCl₂ → Tz₂PbCl₄

2TzCl + PbBr₂ → Tz₂PbCl₂Br₂

Structural characterization of the tetrazine-based perovskite thin-films and single crystals

The first characterization of the new Tz-based perovskites aimed at checking that their crystal structures are different from the ones of organic Tz, and any generic lead halide salt. Thin films with good crystallinity were produced for that purpose by spin-coating (see the ESI† for details). Fig. 2b and c show respectively the X-ray diffraction diagrams of both the pure chloride perovskite thin films, and the mixed chloride/bromide one, compared with those of the corresponding precursors. It can be clearly seen that a new phase has been obtained, different from the reagents. Next, single crystals of Tz₂PbCl₄ were grown by an anti-solvent crystallization method (see ref. 16) to gain a better insight into the crystalline lattice.

Additional XRD measurements performed on single crystals of Tz₂PbCl₄ definitely demonstrate that this compound crystallizes in the form of a monolayered lead halide perovskite (R-NH₃)₂MX₄, with an inorganic layer thickness consisting of just one PbCl₄ octahedron (see the ESI† for details). The resolved structure is monoclinic and belongs to the P2₁/c space group, with lattice parameters a, b and c, equal to 19.05 Å, 7.75 Å and 8.29 Å, respectively and a β angle of 93.02° (Fig. 2e and Fig. SX1, ESI†). The atomic positions associated with the ammonium bridge are affected by conformational disorder, with two accessible molecular conformations, as shown in Fig. SX1 (ESI†), but with the spacer clearly exhibiting a well-oriented molecular stacking. The newly introduced Tz organic spacer features similar herringbone packing as found in phenylethylammonium lead chloride.⁵² The long molecular axis does not lie orthogonal to the inorganic plane, as often occurs for short spacers, but is tilted with respect to it by 46 degrees, comparable to the 47 degrees found for the phenylethylammonium spacer (see Fig. SX2, ESI†). The centre of mass distances between nearest neighbour π-conjugate rings correspond to 5.0 Å and 6.4 Å but with the molecules shifted with respect to each other, both along their molecular axis and along the b-axis of the lattice, in a non-optimal configuration for π–π interactions. A very short distance of 3.5 Å is found instead between the centre of the π-conjugated ring of the spacer and the closest apical chlorine (see Fig. SX3, ESI†), which is compatible with energy transfer processes, or with a modification of the electronic structure allowing the separation and transfer of charge carriers. For the sake of comparison, a distance of 4.05 Å was found by Dou and co-workers for a lead-iodide lattice incorporating thiophene derivatives, for which charge transfer from the inorganic lattice to the spacer has been reported (see Fig. SX3, ESI†). Thanks to the single crystal data, Tz₂PbCl₄ thin film diffraction peaks shown in Fig. 2b (red curve) can be indexed, thus revealing the (h 0 0) family of planes that corresponds to the inorganic haloplumbate layers (see Fig. SX4, ESI†). This shows that Tz₂PbCl₄ thin-films grow with a preferential in-plane direction with respect to the inorganic layers, which is a typical behaviour observed in 2D hybrid perovskites.

Unfortunately, single crystals of Tz₂PbCl₂Br₂ could not be obtained, and the 2D hybrid perovskite-like diffraction pattern shown in Fig. 2c was not indexed. However, the similarities between both perovskites’ diffraction diagrams and further optical absorption studies allow us to reasonably infer that this compound also presents a (R-NH₃)₂MX₄ layered perovskite structure.

Study of the optical matching in tetrazine-based perovskite thin-films

We have performed steady state UV-vis absorption characterization of both new Tz-based perovskite thin films. Furthermore, in order to clearly rationalise the effect of the introduction of Tz as an organic spacer, we also performed comparable measurements on TzCl salts and on analogous 2D layered phenylethylammonium (PEA) lead chloride perovskites PEA₂PbCl₄ and PEA₂PbCl₂Br₂. For these systems in fact it is well-established that the organic component does not play a direct role in the optical response.¹⁷Fig. 2f and g show the comparison between the spectra of the perovskites and the TzCl ammonium salt. The optical response of TzCl consists in two broad signatures at 540 nm and at 365 nm, whose energetics nicely correspond respectively to the S₁ and S₂ excitonic resonances reported for the Tz molecule.^50,53,54 By contrast, the optical response of layered 2D hybrid perovskites of reference is imposed by the inorganic lattice and consists in a sharp absorption signal, named E_1s, falling at 340 nm and 375 nm, for PEA₂PbCl₄ and PEA₂PbCl₂Br₂, respectively. This feature is associated with the 1s component of the Wannier exciton series for the inorganic sheet, characterised by a binding energy of a few hundreds of meV, followed by band-to-band direct transitions taking place at higher energy.

Interestingly, our newly synthesised Tz-based hybrid perovskites show absorption signals resulting from the superimposition of both Tz salt and inorganic PbX₄ lattice optical responses. Indeed, both Tz-based perovskites show an intense excitonic peak at ∼335 nm and ∼375 nm for the chloride and mixed halide compound, respectively. The existence of this sharp excitonic peak is additional proof that a perovskite structure has been synthesised. Additionally, the Tz S₁ and S₂ excitonic resonances, at ∼540 nm and ∼365 nm respectively, are superimposed on the lead-halide layer absorption. These results demonstrate that the Tz moiety has been successfully included in the lattice as an organic spacer. Contrary to the case of PEA-based perovskites, where the PEA plays little role close to the band gap, Tz is actively involved in the optical response of the hybrid perovskite materials. The optical properties of our newly reported compounds are summarized in Table SX1 (ESI†). Notably, both in the case of Tz₂PbCl₄ and Tz₂PbCl₂Br₂, there is sizable spectral overlap between the S₂ state of the organic spacer and the E_1s state of the inorganic frame, which is a crucial requirement for energy transfer to take place. Halide composition clearly influences the detailed S₂/E_s1 alignment, with S₂ being more stable by ca. 0.3 eV than the E_1s interaction, for the pure chlorine compound, while the reverse order is found for the mixed one. As this order determines the energetic gain/barrier associated with the energy transfer process, halide substitution may be sought as a strategy to tune/detune this mechanism, although partial substitution of chlorine with bromine, as pursued here, was not sufficient to completely switch off this non-radiative mechanism.⁴⁶

Electronic diversion channels in tetrazine-based hybrid layered perovskites

Quenching of the perovskite excitonic emission in tetrazine-based perovskite thin-films

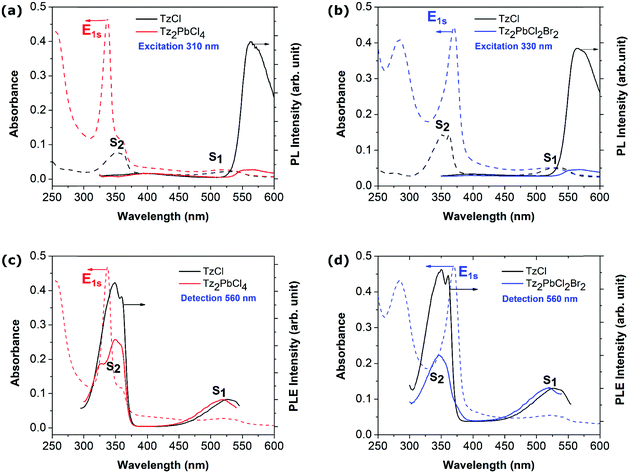
Beyond the picture of a composite system that emerges from the previous part and the observation of the active participation of the organic component to the optical response of the hybrid perovskite material, additional optical measurements were carried out. We first performed photoluminescence (PL) measurements for both Tz₂PbCl₄ and Tz₂PbCl₂Br₂ perovskite thin films (Fig. 3a and b). For Tz₂PbCl₄, the excitation was carefully tuned to the absorption spectrum of the lead-halide layer (dashed line in Fig. 3) away from the maximum of the Tz S₂ absorption feature, thereby minimizing the absorption of the Tz molecule with respect to the one of the inorganic frame (Fig. 2f). Generally, layered perovskites such as PEA-based perovskites are characterized by efficient emission from the Wannier exciton E_1s, with reduced FWHM (Full Width at Half Maximum) and Stokes shift at room temperature (see the ESI,† Fig. SX5-a). PEA₂PbCl₄ exhibits also a bright white light emission (see the ESI,† Fig. SX5-b), which is commonly observed in several chloride-based 2D perovskites.⁵⁵ In the case of Tz₂PbCl₄, instead, the emission from the inorganic component is completely suppressed, in spite of its direct photoexcitation at 310 nm. By contrast, a signal around 575 nm is clearly visible in Fig. 3, which matches well the emission from the TzCl salt and is therefore associated with the emission from the lowest lying S₁ state of Tz, with a measured Stokes shift of ∼80 meV (see black curve in Fig. 3a). Similar results are found in the case of the mixed halide perovskite Tz₂PbCl₂Br₂. Here, the exciting light follows the red-shift of the Wannier resonance induced by the partial substitution of chlorine with bromine. The 330 nm excitation slightly overlaps the vibronic progression of the S₂ signal from Tz, but the absorption is still dominated by the inorganic component. Also, in this case, we do not observe emission corresponding to the E_1s exciton of the perovskite, while we found again emission from the S₁ state of Tz (see black curve in Fig. 3b). We therefore conclude that the incorporated tetrazine spacer does play an active role in the de-excitation mechanisms of the exciton generated within the inorganic PbX₄ frame, hence directly calling for charge and/or energy transfer processes, as illustrated in Fig. 1a and b and in Fig. 1c, respectively, taking place at the organic/inorganic interface.

Fig. 3 Experimental observation of the energy transfer diversion channel. (top) Photoluminescence (PL, solid line) and absorbance (dash line) spectra of (a) Tz₂PbCl₄ and (b) Tz₂PbCl₂Br₂ are quantitatively compared to TzCl spin-coated layers containing the same amount of Tz molecules. (bottom) Photoluminescence excitation (PLE, solid line) and absorbance (dash line) spectra of (c) Tz₂PbCl₄ and (d) Tz₂PbCl₂Br₂ are quantitatively compared to TzCl spin-coated layers containing the same amount of Tz molecules.

It is important to stress here that the concentration of the precursors was chosen such that the Tz-based perovskites and TzCl thin films present the same optical density at the wavelength of S₁, that is to say that the quantity of Tz molecules are the same in the TzCl and Tz-based perovskite layers. This allows direct comparison of the PL intensities between Tz-based perovskites and the TzCl salt. The S₁ emission from the Tz molecule in the Tz-based perovskites appears one order of magnitude smaller than in TzCl films (Fig. 3a and b). This observation could tentatively be attributed to the different packing of the Tz moieties in the perovskite in comparison with the TzCl salt. In fact, a decrease of the luminescence efficiency has been already observed in ref. 50 from TzCl in solution and TzCl in the solid phase, and attributed to the increase of non-radiative losses associated with lattice vibrations in the condensed phase. The quantitative decrease of the S₁ emission from TzCl to Tz₂PbCl₄ thin films could then be attributed to the different organizations of the Tz molecules in these two compounds as shown by the XRD experiments. Besides, we note that considering the standard redox potential of the different species (see discussion in the ESI†), it is very unlikely that the partial quenching of the luminescence of the tetrazine moiety is due to oxidative electron transfer (Fig. 1d). In addition, if such a process were to occur, we would observe fast degradation, not only of the perovskite, but also already of the generic tetrazine-ammonium TzCl salt, accompanied by halogen formation, under UV light (the intermediately produced tetrazine anion-radical being efficiently restored by oxygen, a catalytic oxidation would take place).⁵⁶ This is not the case, with the tetrazine contained in the perovskite matrix appearing even a little more stable than the generic TzCl salt (see the ESI,† Fig. SX6).

Optical characterization of the excitation transfer

Photoluminescence excitation (PLE) spectroscopy has been performed on the Tz-based perovskites and TzCl thin layers, to highlight a potential energy transfer mechanism between the two components of the composite (Fig. 3c and d). In these experiments, the emission intensity of the Tz is recorded as a function of the excitation wavelength. In the PLE spectra of both Tz-based perovskites and TzCl, the Tz S₂ resonance is clearly observed, confirming the efficiency of the internal conversion from S₂ to S₁ inside the Tz molecule. In the Tz₂PbCl₄ perovskite, an excitation resonance is observed when tuned with the wavelength of the Wannier exciton of the lead-halide part. This is clear evidence of an energy transfer from the perovskite Wannier exciton to the Tz molecule through its S₂ state, followed by the efficient internal conversion from S₂ to S₁. However, the PLE spectrum of Tz₂PbCl₄ does not superimpose on the absorption of Tz₂PbCl₄. In particular, the respective weights of the S₂ and E_1S resonances are reversed while comparing absorption and PLE spectra. In other words, the S₁ emission is much more efficient when the excitation is tuned directly with the Tz S₂ resonance in comparison to the situation where the energy transfer takes place. This suggests that the energy transfer from the Wannier resonance of the inorganic frame to the S₂ state of Tz is likely not the only process but also competes with other non-radiative mechanisms. Energy transfer is further confirmed by the PLE spectrum of Tz₂PbCl₂Br₂, which only shows a small shoulder located at about 375 nm on the low energy side of the S₂ peak, and corresponding to the red-shifted perovskite Wannier exciton. In addition to energy transfer, charge transfer/ionization of the lead halide exciton could account for another non-radiative channels contributing to the quenching of the inorganic emission of these new perovskites.

Singlet and triplet excited states of tetrazine: exciton transfer as a diversion channel for quenched emission

The quasi resonance between an exciton state of the organic spacer (in the present case, the S₂ state of Tz) and the Wannier exciton E_1s of the inorganic PbX₄ (X = Cl, Cl_0.5Br_0.5) frame represents a very special case, seldom reported in the literature and whose photophysics has still to be clarified.⁴¹ In this frame, energy resonance between the inorganic PbX₄ component and the exciton states of Tz can be at the basis of the emission quenching observed in our compounds. In fact, within a purely exciton description, this resonance can potentially drive to efficient transfer of the exciton E_1s, formed upon light absorption on the inorganic component, to the S₂ exciton of Tz, via FRET and/or Dexter mechanisms (Fig. 1c). Here, we calculate the singlet and triplet excited states in Tz by performing Time Dependent-Density Functional Theory (TD-DFT). Calculations are carried out here using the PBE0 exchange–correlation functional, which provided accurate results for a non-functionalised Tz molecule with a D_2h point group symmetry (a detailed description of the computational approach is reported in the ESI†).⁵⁷ Results from TD-DFT are shown in Fig. 4a, with computed singlet and triplet excitation energies nicely matching those from accurate wavefunction based methods (Equation Of Motion Coupled Cluster EOM-CC and Complete-Active-Space 2nd order Perturbation Theory, CAS-PT2)^58,59 at least for the two/three lowest singlet/triplet excited states. Some sizable difference is found for the energy of the second triplet excited state T₂ but we verified this as being due to the oxygen-bridges in our Tz derivative, compared to the non-functionalised tetrazine molecule (see the ESI,† Fig. SX7). The diversion channel via transfer from E_1s excitons to singlet S₂ is depicted in Fig. 4b.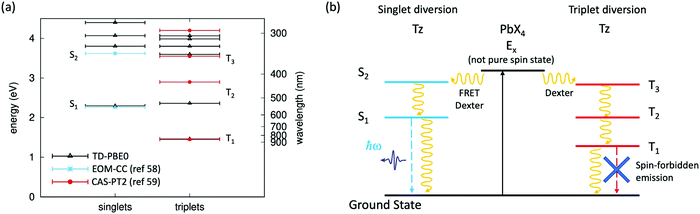

Fig. 4 Singlet and triplet exciton states in tetrazine and related exciton diversion channels for the hybrid halide perovskite. (a) Singlet and triplet excited state energies computed with TD-DFT for the Tz molecule, compared with previous estimates for non-functionalised tetrazine, from wavefunction-based approaches (Equation Of Motion Coupled Cluster EOM-CC,⁵⁸ and Complete-Active-Space 2nd order Perturbation Theory, CAS-PT2);⁵⁹ (b) diversion channels for the radiative emission from the exciton E_1s of the inorganic PbX₄ frame, involving exciton transfer (via FRET and/or Dexter mechanisms) either to the S₂ singlet or the T₃ triplet excited state of Tz. Continuous and dashed lines represent light absorption and radiative recombination, respectively, while curved lines represent excitation transfer (FRET/Dexter) and non-radiative recombination mechanisms.

Moreover, we have seen in Fig. 3a and b that the emission of the Tz molecules is one order of magnitude lower in the perovskite, as compared to the TzCl salt. As mentioned earlier this observation could be related to the enhancement of the non-radiative exciton relaxation, as a result of the different packing of the Tz molecules in the salt and in the perovskite frame. However, another possibility is related to an efficient exciton transfer from the inorganic E_1s exciton to a triplet excited state of Tz, via a Dexter transfer mechanism.^24,60 The latter is traditionally associated with the quenching of the emission due to the spin–forbidden radiative relaxation from the molecular excited triplet to the singlet ground state. This is justified by the non-pure spin character of the excited state E_1s of the perovskite (as induced by large spin–orbit coupling²⁵) which makes possible both singlet–singlet and triplet–triplet transfer mechanisms. Most notably, this exciton transfer requires the existence of a triplet excited state in Tz with energetics close to E_1s. Here, our calculations show that a triplet state T₃ exists, with energy close to the E_1s state of the perovskite PbX₄ frame, hence potentially supporting the transfer from E_1s to the triplet excited state manifold of Tz as a potential mechanism of the emission decrease of the organic molecules in the perovskite structure. The diversion channel via transfer from E_1s to the triplet T₃ state of Tz is also schematized in Fig. 4b.

HOMO/VBM and LUMO/CBM alignment at the inorganic–organic interface: charge injection as a diversion channel for quenched emission

A completely different perspective in the opto-electronic behaviour of these tetrazine containing halide-perovskites comes when passing from a description involving exciton excited states, as from Fig. 1c and 4b, to a single particle description involving the electronic states of Tz and of the PbX₄ frame, as from Fig. 1a and b.³⁰ The reduced exciton transition energy of Tz compared to the reference PEA molecule is in fact accompanied by a reduced single particle HOMO/LUMO band gap (Highest Occupied/Lowest Unoccupied Molecular Orbitals) which can therefore approach the energetics of the VBM/CBM (Valence Band Maximum/Conduction Band Minimum) states of the PbX₄ frame, hence potentially driving to the formation of a type II electronic heterointerface (see Fig. 1b). This in turn may allow for the spontaneous ionization of the exciton E_1s and consequent charge injection of the electron/hole from the inorganic frame to the Tz molecule. Aiming to address this point, we performed periodic Density Functional Theory (DFT) simulations on model crystal structures of the Tz₂PbCl₄ and Tz₂PbBr₂Cl₂ perovskites (detailed description of the computational approach is reported in the ESI†). The lack of crystalline models for the mixed halide perovskite, namely cell parameters and the relative distribution of Cl/Br atoms in the inorganic layer, represents a serious issue for the accurate prediction of the electronic structures of these systems. To overcome this limitation, we constructed different guess models for mixed halide structures, starting from the reference structure of Tz₂PbCl₄, in Fig. 2e. In particular, we considered the three different situations in Fig. 5a, with bromine atoms occupying only apical positions in the PbX₄ frame, only equatorial positions and randomly distributed between equatorial and apical positions, these systems being referred to as Br-ap, Br-eq and Br-rand, respectively. In addition, the pure chloride (Cl) and bromide systems (Br) were taken as references. We then proceeded to optimise both the atomic positions and cell parameters at zero Kelvin temperature for all the models, accounting for organic–organic dispersive interactions via the van-der-Waals Density Functional vdw-DF2 approach, developed by Langreth and co-authors.⁶¹ The cell parameters computed for the pure chloride compound are in acceptable agreement with the experiment (see Table SX2, ESI†), although slightly underestimated. More interestingly, the monoclinic cell is maintained during optimisation, clearly indicating that this represents an equilibrium crystalline structure, for the adopted DFT approach.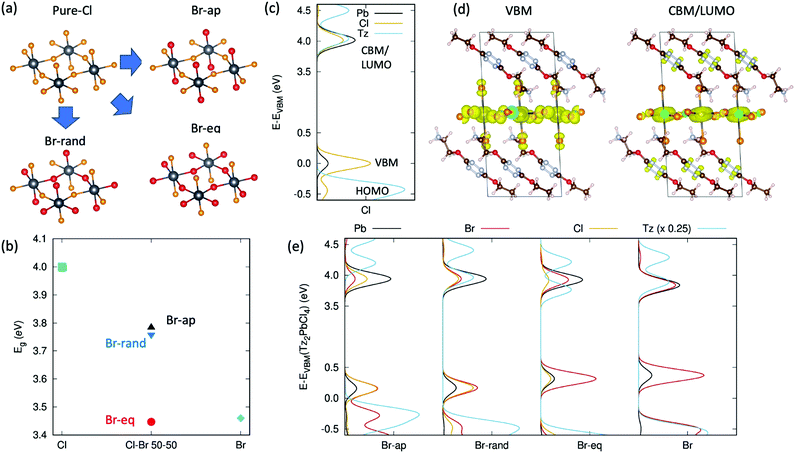

Fig. 5 DFT simulations of the electron energy level alignment at the organic/inorganic interface. (a) Derivation of the models for mixed chloride/bromide perovskites (bromine in the apical position, Br-ap, in the equatorial position, Br-eq, or randomly distributed, Br-rand) from the pure chloride model in Fig. 2e. The color-scale is: black = lead, orange = chlorine, red = bromine; (b) DFT band gap variation for the different models and composition of Tz-based halide perovskites; (c) projected Density of State computed for the pure chloride Tz₂PbCl₄ compound. The positions of the frontier orbitals of the organic and inorganic components are indicated, for clarity; (d) density isosurfaces corresponding to the valence band maximum and conduction band minimum/LUMO level (VBM, CBM/LUMO); (e) projected Density of State of the various mixed halides Tz₂PbCl₂Br₂ and pure halide Tz₂PbBr₄.

We then simulated the single particle electronic structure of these crystalline models, with specific interest in the alignment between VBM/HOMO and CBM/LUMO levels. It is worth mentioning in this respect that the quantitative estimates of single particle energetics for lead-based halide perovskites is a challenging task, as it requires the inclusion of both relativistic, spin–orbit coupling effects²⁵ and the accurate treatment of exchange correlation interaction. The latter is accounted for in the literature either via many-body approaches based on the GW approximation⁶² or via the use of hybrid DFT functionals.^26,63 We followed here this second approach, by adopting the PBE0 hybrid exchange–correlation functional⁶⁴ with the exact exchange contribution increased to 30%, as this was shown to provide accurate estimates of the electronic band gap of layered lead–iodide perovskites.²⁶ The band gaps computed for pure and mixed chloride–bromide systems are reported in Fig. 5b.

For the pure chloride compound, our approach predicts a band gap of ∼4.0 eV, which nicely parallels the exciton resonance from UV-vis measurements in Fig. 2f at 3.68 V, assuming additional exciton binding energy of ∼300 meV.²⁰ For mixed halide perovskites, the resulting band gap depends on the distribution of chlorine/bromine atoms in apical/equatorial distribution, as expected both from physical intuition and symmetry arguments.²³ Namely, with bromine in an equatorial position (Br-eq), the band gap is very close to that of the pure bromine case, consistent with the fact that the electronic dispersion in the inorganic plane is associated with the electronic interaction between lead and the atoms in an equatorial position. Actually, in-deep symmetry analyses of the layered perovskite structure reveal that apical halides still take part to the valence band edge and can therefore affect the band gap of the system.⁶⁵ This fact can explain the unexpected result for the band gap computed for the Br-ap model, in Fig. 5d. In spite of having all equatorial atoms corresponding to chlorides, this system presents in fact an intermediate band gap between pure bromide and chloride phases. In this sense, symmetry analysis justifies the trend in the band gaps depicted in Fig. 5b either in terms of indirect perturbation, due to not only different dielectric environments or structural distortions, but also as direct perturbation on the atomic hybridization pattern, as induced to the apical bromides.⁶⁵ Finally, random distribution of the halides in apical/equatorial positions (Br-rand) results in an intermediate band gap, compared with the pure case, consistent with the monotonic dependence of the band gap on the bromide/iodide ratio reported in the literature.²³ Most notably, the 250 meV band gap closing compared to pure chloride nicely parallels the 300 meV reduction of the exciton E_1s resonance from Fig. 2f and g, suggesting that the halides are randomly distributed in the apical/equatorial position, in real samples. This conclusion is further supported by our DFT total energy estimates, which suggest that Br-rand and Br-eq are almost iso-energetic at zero Kelvin, while Br-ap is less stable by ∼50 meV per chemical unit. In other words, there is no energy gain going from bromines randomly distributed in apical/equatorial positions to all bromines located in the equatorial position, with hence the former configuration favoured for entropic reasons.

VBM/HOMO and CBM/LUMO alignment is first evaluated for the pure chloride model, considering the atomic projected Density of States (pDOS) in Fig. 5c. The VBM and CBM of the PbCl₄ frame nicely correspond to 3p_Cl–6s_Pb and 3s_Cl–6p_Pb orbitals, respectively, as widely reported in the literature.^26,28,66 The HOMO level of Tz lies 0.4 eV below the VBM of the inorganic lattice, making the hole injection process from the PbCl₄ frame to the Tz molecule thermodynamically non-spontaneous. In the energy region of the CBM/LUMO orbitals, instead, both the organic and inorganic components similarly contribute to the electronic states, hence complicating the rigorous assignment of the CBM and LUMO levels (magnification of the pDOS in the CBM/LUMO region is reported in the ESI,† Fig. SX8). To clarify such an assignment, we therefore analysed the surface isodensities associated with the wavefunction of the last occupied and first unoccupied state, shown in Fig. 5d. These results clearly indicate that the highest energy occupied electronic level is a pure state of the inorganic PbCl₄ lattice, consistent with the pDOS in Fig. 5c. In contrast, the first unoccupied state cannot be assigned solely to the inorganic/organic component, as it delocalises over both the Pb-atoms and on the π-conjugated system of Tz. This result is likely strongly influenced by the close energy resonance of the inorganic CBM and organic LUMO levels and should therefore be considered with care, in light of the possible perturbations to the organic/inorganic level alignment. In particular, thermally induced atomic vibrations (phonons) are expected to alter the energetics of these states. On the other hand, the electronic configuration reported in Fig. 5d opens the prospect for potential ionization of the exciton E_1s photogenerated on the PbCl₄ site and subsequent charge transfer of the electron into the organic Tz spacer.

Similar analysis of the VBM/HOMO–CBM/LUMO alignment is performed in Fig. 5e for all the mixed halide models. Notice that the pDOS of all the mixed chlorides/bromides and of the pure bromide compound have been aligned with respect to the 5d_3/2 Pb states of the chloride compound (see the ESI,† Fig. SX9), so as to provide a common energy reference for all the models. The band gap closing from Tz₂PbCl₄ to Tz₂PbCl₂Br₂, and finally to pure Tz₂PbBr₄ is mainly associated with a destabilization of the valence band, as shown in Fig. 5e, consistent with the fact that the valence is mainly composed by the outer p-shell of the halide. As a result, the VBM/HOMO energy mismatch increases from Tz₂PbCl₄ to Tz₂PbCl₂Br₂, therefore enhancing the energy barrier for the hole injection process from the inorganic to the organic Tz molecule. In contrast, the CBM/LUMO levels of the Br-rand and pure Br models remain very close in energy, hence resulting in null (or small) energy barrier for the electron transfer from the PbX₄ frame to the Tz dye. For the Br-rand model, unoccupied electronic states lie very close in energy (within 40 meV) and result in similar mixing of states from the organic/inorganic components as found for the pure chloride compound in Fig. 5d. In the pure Tz₂PbBr₄ model, the states are slightly more spaced (ca. 60 meV) hence reducing the mixing between inorganic and organic electronic states, which is however still visible (see the ESI,† Fig. SX12). For the Br-eq model, instead, the energy spacing among non-occupied states of ca. 165 meV results in clear separation of the organic and inorganic states, with a more stable LUMO, compared to the CBM, still allowing for spontaneous electron injection from the PbX₄ frame into Tz. Only in the case of Br-ap, we found the LUMO to be less stable and well separated from the CBM (ca. 250 meV), in a final alignment that therefore does not allow for the spontaneous injection of the electron. This model however was found to be significantly less stable than the others, hence representing a less reliable model for the investigation of the electronic interface between the PbX₄ lattice and the organic Tz spacer.

Conclusions

We have demonstrated the possibility to prepare a 2D perovskite, homothetic to the widely studied phenylethylammonium halide perovskite, containing a 100% theoretical content of a photoactive organic moiety, a tetrazine. A new design concept is therefore demonstrated, which exploits the small n–π* electronic band gap of high nitrogen content heterocyclic aromatics, instead of increasing the size of the conjugated backbone. The optical properties of the resulting materials correspond to the combination of those of the composing inorganic PbX₄ frame and the organic tetrazine spacer, and feature a resonance between the exciton state of the former and the second excited state of the latter. Photoluminescence and photoluminescence excitation measurements evidence the suppression of light emission from the PbX₄ sheet, following the incorporation of the tetrazine, and indicate partial energy transfer from the inorganic lattice to the organic chromophore. In this frame, different decay quenching mechanisms are discussed. With respect to energy-transfer mechanisms, two potential pathways may occur, either via the second singlet state of the tetrazine (S₂) or via its third triplet state (T₃). In fact, one should bear in mind that the concepts of singlet–singlet and triplet–triplet energy transfer should be taken with great care in these hybrid compounds, since the excitons of the inorganic PbX₄ lattice do not possess pure spin-character, in light of the strong spin–orbit-coupling associated with the heavy lead atoms. Concerning charge transfer mechanisms, accurate hybrid DFT simulations evidence type II energy level alignment for the conduction band/LUMO states, consistent with electron transfer from the PbX₄ lattice to the spacer. Unfortunately, our efforts to disentangle these two classes of mechanisms via a halide mixing strategy were not successful. On one hand, in fact, the red-shift of the exciton absorption, associated with halide mixing, ∼100 meV below the second excited state of the tetrazine did not coincide with full suppression of the energy transfer mechanism. On the other hand, DFT simulations indicate that the band gap closure resulting from halide mixing mainly involves the valence band/HOMO energy offset, while keeping the conduction band/LUMO resonance comparably less affected, a fact that does not allow an electron transfer mechanism to be ruled out, with absolute confidence. Still, other strategies can be devised, to clarify the reciprocal role of charge and energy transfer mechanisms in these and other organic/inorganic heterointerfaces. Improvement of the synthetic approach may open the way for full incorporation of tetrazines in the lead–iodide lattice. The corresponding band gap closing is expected to lead to organic/inorganic electronic heterointerfaces with more common type I heterojunctions, meanwhile leaving open potential energy transfer channels, from the excitonic resonance of the perovskite to the S₁ or T₂ states of the tetrazine. Alternatively, we might expect some chemical modifications of molecular units to tune the relative importance of singlet or triplet diversion channels. Dipolar tuning, for instance (as proposed in ref. 67) is a relatively unexplored approach that would still allow tuning from a type II to a type I electronic heterostructure.

Finally, while the tetrazines were chosen for their perfect steric hindrance matching with the phenyl ring, they are not the only photoactive small rings to possibly adapt and insert into a 2D perovskite structure. Several polyaza aromatic heterocycles are eligible (and among them especially a-triazines) to this characteristic (see Fig. 6), the only mandatory condition being the possibility to bear an aminoethyl chain collinear with the aromatic ring, with in addition some flexibility linked to the possible introduction of small substituents (e.g. halogens) on the phenyl ring to tune the orbital levels. Suitable molecular engineering could lead to e.g. total quenching or enhancement of the luminescence of the two parts, depending on the target application. The recent work of H. Karunadasa et al. also showed that partial insertion of reduced pyrazinium heterocycles in expanded 3D perovskite analogues offers a new route for chemical doping of the semiconductor.⁶⁸ Building a 2D perovskite with a full load of active organic moieties, tuned with the perovskite emission, is therefore an emerging field allowing hope in the building of new and better performing materials in this family.

Fig. 6 Molecular design. Possible aromatic heterocyclic luminophore candidates for functionalization of the organic moiety in 2D perovskite.

Experimental methods

Synthesis of the ammonium salts

All chemicals were purchased from commercial providers (Sigma–Aldrich, VWR). A scheme of TzCl synthesis is depicted in Fig. 2a. ¹H and ¹³C nuclear magnetic resonance (NMR) measurements were recorded using a JEOL ECS 400 NMR Spectrometer. Details of the synthesis, NMR and mass spectroscopy data are given in the ESI.† PEACl was synthesized from phenylethylamine and hydrochloric acid.⁴⁷ Briefly, to a solution at 2 °C of phenylethylamine (10 mL, 80 mmol) (99%, Sigma–Aldrich) in 200 mL of diethyl ether, 2 equivalents of HCl (13,3 mL, 160 mmol) (37%w in water) were dropped carefully. The precipitate was filtrated, recrystallized in a mixture of diethyl ether/ethanol and then dried under vacuum. All the powders were stored in a desiccator prior to use.

Tz₂PbCl₄ single crystal growth and XRD measurements

Single crystals were grown using an anti-solvent crystallization method.¹⁶ 0.5 M solution of Tz₂PbCl₄ was prepared by dissolving TzCl and PbCl₂ (99,999%, Aldrich) with 2 : 1 molar ratio in anhydrous DMF. The solution was sonicated for 2 hours until complete dissolution of the precursors. The vial containing the solution was then placed in a bigger vessel filled with 1,2-dichloroethane. After 1 week of anti-solvent diffusion, square-like pink crystals were recovered using a pipette and immediately dipped in paratone oil.

Perovskite thin film deposition

Tz₂PbCl₄, PEA₂PbCl₄, Tz₂PbCl₂Br₂ and PEA₂PbCl₂Br₂ 0.1 M precursor solutions were prepared by dissolving the corresponding ammonium salts and lead chloride (respectively lead bromide) with a 2 : 1 molar ratio in anhydrous DMF. The solutions were sonicated for 2 hours until complete dissolution of the precursors. Anhydrous DMF (99.8%, Sigma–Aldrich) was purchased in a septum-sealed bottle and stored in a nitrogen filled box prior to use. All the depositions were performed in air. Quartz substrates were cleaned by sonicating in subsequent baths of acetone, ethanol and 10%w KOH solution in ethanol, then rinsed with water and dried in a N₂ flow. The perovskite materials were then deposited by spin-coating the precursor solutions at 2000 rpm for 15 seconds. The perovskite layers were formed after annealing at 80 °C for 2 minutes. Tetrazine ammonium salt reference layers were obtained by dissolving TzCl in anhydrous DMF. In order to obtain the same optical density at the maximum of the tetrazine S₁ band, the molar concentration of the TzCl solution was 0.2 M. The TzCl solution was then deposited on quartz by spin-coating at 2000 rpm for 15 seconds, followed by a short annealing at 80 °C for 1 minute.

Thin film characterization

Powder XRD patterns of chloride-based films (Fig. 2b) were acquired using a Brücker D9000 powder diffractometer with a cobalt Kα radiation source. Powder XRD patterns of mixed chloride–bromide and bromide-based films (Fig. 2c) were acquired using a Siemens D5000 powder diffractometer with a copper Kα radiation source. UV/Vis absorption spectra were obtained from a PerkinElmer Lambda 950 spectrophotometer. PL and PLE spectra were collected using a HORIBA Fluorolog equipped with a xenon lamp as an excitation source. PL spectra shown in the ESI,† Fig. SX5 were collected using a Princeton Instrument Spectrapro 2500i spectrometer coupled with a Roper Scientific Pixis: 100B CCD. In that case, films were excited using a He–Cd Laser at 325 nm.

Author contributions

P. A. and E. D. conceived the idea and designed the experiments. J. E. proposed the analysis framework and underlying concept. C. K. and C. Q. designed the theoretical work. J. E., C. K. and C. Q. provided insights into the mechanism with support from D. G. and F. L. C. Q. performed the DFT calculations and analysed the data with support from J. E. and C. K. P. A., F. L., J. E. and C. Q. co-wrote the manuscript. P. A. developed the chemistry for the synthesis of tetrazines and perovskites. F. L. synthesized the tetrazines and the perovskites under the supervision of P. A. and G. T. A. and performed X-ray diffraction and optical spectroscopy measurements of the spin-coated films under the supervision of D. G., J. S. L. and E. D. J. M. performed the X-diffraction measurements on single crystal and solved the crystallographic structure. All authors contributed to this work, to the discussions and read the manuscript and agree to its contents.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has received funding from the European Union's Horizon 2020 programme, through an FET Open research and innovation action under Grant Agreement No. 687008. The information and views set out in this Manuscript are those of the authors and do not necessarily reflect the official opinion of the European Union. Neither the European Union institutions and bodies nor any person acting on their behalf may be held responsible for the use which may be made of the information contained herein. This work has also been supported by Agence Nationale de la Recherche, projects ANR-18-CE24-0016 (EMIPERO) and ANR-18-CE05-0026 (MORELESS). J. E. and J. S. L. acknowledge the financial support from the Institut Universitaire de France. Computational investigations were conducted thanks to HPC resources provided by [TGCC/CINES/IDRIS] under the allocation 2020-A0010907682 made by GENCI.

References

1. D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 7843–7850.
2. I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235.
3. H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, Nature, 2016, 536, 312–316.
4. W. K. Chong, K. Thirumal, D. Giovanni, T. W. Goh, X. Liu, N. Mathews, S. Mhaisalkar and T. C. Sum, Phys. Chem. Chem. Phys., 2016, 18, 14701–14708.
5. D. Liang, Y. Peng, Y. Fu, M. J. Shearer, J. Zhang, J. Zhai, Y. Zhang, R. J. Hamers, T. L. Andrew and S. Jin, ACS Nano, 2016, 10, 6897–6904.
6. N. Wang, L. Cheng, R. Ge, S. Zhang, Y. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang, Y. Wei, Q. Guo, Y. Ke, M. Yu, Y. Jin, Y. Liu, Q. Ding, D. Di, L. Yang, G. Xing, H. Tian, C. Jin, F. Gao, R. H. Friend, J. Wang and W. Huang, Nat. Photonics, 2016, 10, 699–704.
7. Y. Liu, Y. Zhang, Z. Yang, H. Ye, J. Feng, Z. Xu, X. Zhang, R. Munir, J. Liu, P. Zuo, Q. Li, M. Hu, L. Meng, K. Wang, D. M. Smilgies, G. Zhao, H. Xu, Z. Yang, A. Amassian, J. Li, K. Zhao and S. F. Liu, Nat. Commun., 2018, 9, 5302.
8. Y. Liu, H. Ye, Y. Zhang, K. Zhao, Z. Yang, Y. Yuan, H. Wu, G. Zhao, Z. Yang, J. Tang, Z. Xu and S. (Frank) Liu, Matter, 2019, 1, 465–480.
9. W. Peng, J. Yin, K.-T. Ho, O. Ouellette, M. De Bastiani, B. Murali, O. El Tall, C. Shen, X. Miao, J. Pan, E. Alarousu, J.-H. He, B. S. Ooi, O. F. Mohammed, E. Sargent and O. M. Bakr, Nano Lett., 2017, 17, 4759–4767.
10. A. Brehier, R. Parashkov, J. S. Lauret and E. Deleporte, Appl. Phys. Lett., 2006, 89, 171110.
11. T. Fujita, Y. Sato, T. Kuitani and T. Ishihara, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12428–12434.
12. Z. Han, H.-S. Nguyen, F. Boitier, Y. Wei, K. Abdel-Baki, J.-S. Lauret, J. Bloch, S. Bouchoule and E. Deleporte, Opt. Lett., 2012, 37, 5061–5063.
13. G. Lanty, J. S. Lauret, E. Deleporte, S. Bouchoule and X. Lafosse, Appl. Phys. Lett., 2008, 93, 081101.
14. D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12.
15. S. Zhang, G. Lanty, J.-S. Lauret, E. Deleporte, P. Audebert and L. Galmiche, Acta Mater., 2009, 57, 3301–3309.
16. F. Lédée, G. Trippé-Allard, H. Diab, P. Audebert, D. Garrot, J.-S. Lauret and E. Deleporte, CrystEngComm, 2017, 19, 2598–2602.
17. J. Leveillee, C. Katan, L. Zhou, A. D. Mohite, J. Even, S. Tretiak, A. Schleife and A. J. Neukirch, Phys. Rev. Mater., 2018, 2, 105406.
18. J. Even, L. Pedesseau and C. Katan, ChemPhysChem, 2014, 15, 3733–3741.
19. T. Ishihara, J. Takahashi and T. Goto, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11099–11107.
20. J.-C. Blancon, A. V. Stier, H. Tsai, W. Nie, C. C. Stoumpos, B. Traoré, L. Pedesseau, M. Kepenekian, F. Katsutani, G. T. Noe, J. Kono, S. Tretiak, S. A. Crooker, C. Katan, M. G. Kanatzidis, J. J. Crochet, J. Even and A. D. Mohite, Nat. Commun., 2018, 9, 2254.
21. K. Gauthron, J.-S. Lauret, L. Doyennette, G. Lanty, A. A. Choueiry, S. J. Zhang, A. Brehier, L. Largeau, O. Mauguin, J. Bloch and E. Deleporte, Opt. Express, 2010, 18, 5912–5919.
22. X. Hong, T. Ishihara and A. V. Nurmikko, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 6961–6964.
23. G. Lanty, K. Jemli, Y. Wei, J. Leymarie, J. Even, J.-S. Lauret and E. Deleporte, J. Phys. Chem. Lett., 2014, 5, 3958–3963.
24. K. Ema, M. Inomata, Y. Kato, H. Kunugita and M. Era, Phys. Rev. Lett., 2008, 100, 257401.
25. J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005.
26. C. Quarti, N. Marchal and D. Beljonne, J. Phys. Chem. Lett., 2018, 9, 3416–3424.
27. J. Leveillee, C. Katan, J. Even, D. Ghosh, W. Nie, A. D. Mohite, S. Tretiak, A. Schleife and A. J. Neukirch, Nano Lett., 2019, 19, 8732–8740.
28. C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192.
29. J. V. Passarelli, D. J. Fairfield, N. A. Sather, M. P. Hendricks, H. Sai, C. L. Stern and S. I. Stupp, J. Am. Chem. Soc., 2018, 140, 7313–7323.
30. Y. Gao, E. Shi, S. Deng, S. B. Shiring, J. M. Snaider, C. Liang, B. Yuan, R. Song, S. M. Janke, A. Liebman-Peláez, P. Yoo, M. Zeller, B. W. Boudouris, P. Liao, C. Zhu, V. Blum, Y. Yu, B. M. Savoie, L. Huang and L. Dou, Nat. Chem., 2019, 11, 1151–1157.
31. C. Liu, W. Huhn, K.-Z. Du, A. Vazquez-Mayagoitia, D. Dirkes, W. You, Y. Kanai, D. B. Mitzi and V. Blum, Phys. Rev. Lett., 2018, 121, 146401.
32. W. A. Dunlap-Shohl, E. T. Barraza, A. Barrette, S. Dovletgeldi, G. Findik, D. J. Dirkes, C. Liu, M. K. Jana, V. Blum, W. You, K. Gundogdu, A. D. Stiff-Roberts and D. B. Mitzi, Mater. Horiz., 2019, 6, 1707–1716.
33. S. Deng, J. M. Snaider, Y. Gao, E. Shi, L. Jin, R. D. Schaller, L. Dou and L. Huang, J. Chem. Phys., 2020, 152, 044711.
34. N. Kawano, M. Koshimizu and K. Asai, J. Phys. Chem. C, 2012, 116, 22992–22995.
35. M. Braun, W. Tuffentsammer, H. Wachtel and H. C. Wolf, Chem. Phys. Lett., 1999, 307, 373–378.
36. G. C. Papavassiliou, G. A. Mousdis, G. Pagona, N. Karousis and M.-S. Vidali, J. Lumin., 2014, 149, 287–291.
37. D. B. Mitzi, K. Chondroudis and C. R. Kagan, Inorg. Chem., 1999, 38, 6246–6256.
38. W. T. M. Van Gompel, R. Herckens, P.-H. Denis, M. Mertens, M. C. Gélvez-Rueda, K. Van Hecke, B. Ruttens, J. D’Haen, F. C. Grozema, L. Lutsen and D. Vanderzande, J. Mater. Chem. C, 2020, 8, 7181–7188.
39. K. Morimoto and K. Matsuishi, J. Phys.: Conf. Ser., 2010, 215, 012044.
40. A. H. Proppe, M.-H. Tremblay, Y. Zhang, Z. Yang, R. Quintero-Bermudez, S. O. Kelley, S. Barlow, S. R. Marder and E. H. Sargent, J. Phys. Chem. C, 2020, 124, 24379–24390.
41. M. Braun, W. Tuffentsammer, H. Wachtel and H. C. Wolf, Chem. Phys. Lett., 1999, 303, 157–164.
42. W. T. M. V. Gompel, R. Herckens, K. V. Hecke, B. Ruttens, J. D’Haen, L. Lutsen and D. Vanderzande, Chem. Commun., 2019, 55, 2481–2484.
43. N. Marchal, W. Van Gompel, M. C. Gélvez-Rueda, K. Vandewal, K. Van Hecke, H.-G. Boyen, B. Conings, R. Herckens, S. Maheshwari, L. Lutsen, C. Quarti, F. C. Grozema, D. Vanderzande and D. Beljonne, Chem. Mater., 2019, 31, 6880–6888.
44. M. Era, K. Maeda and T. Tsutsui, Chem. Phys. Lett., 1998, 296, 417–420.
45. K. Chondroudis and D. B. Mitzi, Chem. Mater., 1999, 11, 3028–3030.
46. M. C. Gélvez-Rueda, M. B. Fridriksson, R. K. Dubey, W. F. Jager, W. van der Stam and F. C. Grozema, Nat. Commun., 2020, 11, 1901.
47. K. Jemli, P. Audebert, L. Galmiche, G. Trippé-Allard, D. Garrot, J.-S. Lauret and E. Deleporte, ACS Appl. Mater. Interfaces, 2015, 7, 21763–21769.
48. F. Miomandre and P. Audebert, J. Photochem. Photobiol., C, 2020, 44, 100372.
49. G. Clavier and P. Audebert, Chem. Rev., 2010, 110, 3299–3314.
50. P. Audebert, F. Miomandre, G. Clavier, M.-C. Vernières, S. Badré and R. Méallet-Renault, Chem. – Eur. J., 2005, 11, 5667–5673.
51. M. E. Kamminga, H.-H. Fang, M. R. Filip, F. Giustino, J. Baas, G. R. Blake, M. A. Loi and T. T. M. Palstra, Chem. Mater., 2016, 28, 4554–4562.
52. D. B. Mitzi, J. Solid State Chem., 1999, 145, 694–704.
53. C. Quinton, V. Alain-Rizzo, C. Dumas-Verdes, G. Clavier and P. Audebert, RSC Adv., 2015, 5, 49728–49738.
54. J. Waluk, J. Spanget-Larsen and E. W. Thulstrup, Chem. Phys., 1995, 200, 201–213.
55. D. Cortecchia, J. Yin, A. Petrozza and C. Soci, J. Mater. Chem. C, 2019, 7, 4956–4969.
56. T. Le, T. Courant, J. Merad, C. Allain, P. Audebert and G. Masson, J. Org. Chem., 2019, 84, 16139–16146.
57. C. Adamo and V. Barone, Chem. Phys. Lett., 2000, 330, 152–160.
58. M. Nooijen, J. Phys. Chem. A, 2000, 104, 4553–4561.
59. M. Rubio and B. O. Roos, Mol. Phys., 1999, 96, 603–615.
60. S. Yang, D. Wu, W. Gong, Q. Huang, H. Zhen, Q. Ling and Z. Lin, Chem. Sci., 2018, 9, 8975–8981.
61. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101.
62. G. Giorgi, K. Yamashita and M. Palummo, J. Phys. Chem. Lett., 2018, 9, 5891–5896.
63. D. Cortecchia, S. Neutzner, A. R. Srimath Kandada, E. Mosconi, D. Meggiolaro, F. De Angelis, C. Soci and A. Petrozza, J. Am. Chem. Soc., 2017, 139, 39–42.
64. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
65. C. Quarti, C. Katan and J. Even, JPhys Mater., 2020, 3, 042001.
66. T. Umebayashi, K. Asai, T. Kondo and A. Nakao, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155405.
67. I. García-Benito, C. Quarti, V. I. E. Queloz, Y. J. Hofstetter, D. Becker-Koch, P. Caprioglio, D. Neher, S. Orlandi, M. Cavazzini, G. Pozzi, J. Even, M. K. Nazeeruddin, Y. Vaynzof and G. Grancini, Front. Chem., 2020, 7, 946.
68. D. Umeyama, L. Leppert, B. A. Connor, M. A. Manumpil, J. B. Neaton and H. I. Karunadasa, Angew. Chem., Int. Ed., 2020, 59, 19087–19094,  DOI:10.1002/anie.202005012.

---

Footnote

† Electronic supplementary information (ESI) available: Details on the synthesis and XRD characterization (cif file deposited at the CCDC with reference 2038924); photoluminescence for pristine PEA₂PbCl₄ perovskite; detailed optical properties of the newly synthesized compounds; details on oxidative electron transfer; details on the computational parameters for periodic DFT and molecular TD-DFT calculations; detailed analysis of the atomic projected Density of States from DFT and related isosurfaces of frontier electronic levels. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0mh01904f

---