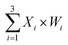Development of a neuron model based on DNAzyme regulation

Abstract

Neural networks based on DNA molecular circuits play an important role in molecular information processing and artificial intelligence systems. In fact, some DNA molecular systems can become dynamic units with the assistance of DNAzymes. The complex DNA circuits can spontaneously induce corresponding feedback behaviors when their inputs changed. However, most of the reported DNA neural networks have been implemented by the toehold-mediated strand displacement (TMSD) method. Therefore, it was important to develop a method to build a neural network utilizing the TMSD mechanism and adding a mechanism to account for modulation by DNAzymes. In this study, we designed a model of a DNA neuron controlled by DNAzymes. We proposed an approach based on the DNAzyme modulation of neuronal function, combing two reaction mechanisms: DNAzyme digestion and TMSD. Using the DNAzyme adjustment, each component simulating the characteristics of neurons was constructed. By altering the input and weight of the neuron model, we verified the correctness of the computational function of the neurons. Furthermore, in order to verify the application potential of the neurons in specific functions, a voting machine was successfully implemented. The proposed neuron model regulated by DNAzymes was simple to construct and possesses strong scalability, having great potential for use in the construction of large neural networks.

---

1 Introduction

Thanks to the rapid development of DNA nanotechnology, DNA molecules have become reliable programming materials due to their great parallel computing power, excellent data storage capacity, and predictable base pairing.^1,2 DNA-based logic gates have been used as the elementary building components of computing systems, each of which implements a Boolean function. These blocks were combined to realize the transformation process from abstract information to concrete data. Thus far, DNA has been widely used to construct logic circuits,^3–5 cascading networks,^6–9 molecular machines,^10,11 and biochemical reaction networks.^12,13 In particular, building on the richness of DNA computing^14,15 and logic circuits,¹⁶ DNA-based nanotechnology provides a new way of developing emerging neural networks. As a type of information processing technology, DNA neural networks¹⁷ play a crucial role in artificial intelligence systems, processing input signals efficiently and accurately. Signal processing is performed through various DNA molecular circuits, such as signal amplification and transmission.^18–20 However, in DNA-based neural networks,¹⁷ the main implementation method of realizing DNA molecular circuits is toehold-mediated strand displacement (TMSD). This method is simple and fast in identifying the link between adjacent logic modules. In practice, the method can be combined with others to improve the efficiency of molecular devices so as to achieve more complex molecular calculation operations. For instance, some DNA molecular systems can become dynamic units with autonomous behaviors under DNAzyme assistance.^21–23 Therefore, the introduction of DNAzyme-assisted mechanisms provides a new direction for the structural execution of neurons.

Actually, DNAzymes are a type of DNA molecule capable of catalyzing various types of biochemical reactions.²⁴ As a tool enzyme, DNAzymes can perform a gene knockout at the cellular level; that is, it can recognize specific sequences of certain viruses to inactivate them, which provides a powerful technical aid for biosensors.^25,26 Additionally, DNAzymes have been widely used in the construction of molecular machines, due to their high cutting efficiency and catalytic capability such as DNA walkers for intelligent molecular machines^27,28 and programmable target-initiated DNA motors.²⁹ DNAzymes have the advantage of specific recognition and fast reaction speed which have been proven to be suitable for the execution of DNA molecular circuits, such as feedback circuits,^30,31 majority voting logic circuits,³² and multiple cascade logic circuits.^33,34 The activity of DNAzymes is affected by many factors and can be adjusted in several ways, such as pH control^35,36 and metal ions triggers.^37,38 Generally speaking, DNAzymes show their activity only within a certain pH range. When the pH level is too high or too low, the binding arm of DNAzyme may be in a closed state, which is not conducive to binding with substrate.^39–41 In addition, pH may also affect the stability of the DNAzyme and change the conformation of the catalytic core. On the other hand, some metal ions can enable DNAzymes to form a stable catalytic core to maximize cutting efficiency. For example, some DNAzymes can form a more stable catalytic domain under the action of divalent cations,^42–44 and increase the interaction force between the binding arms of the DNAzyme and the substrate. Based on the ion dependence of DNAzymes, a DNA molecular intelligent platform for targeted drug delivery^45,46 and a sensor for detecting heavy metal ions^47,48 have been constructed. In this research, the reaction conditions play an important role in controlling the activity of DNAzymes.

Interestingly, the activity of DNAzyme can also be controlled by adding an external strand to form a secondary structure.⁴⁹ For example, DNAzyme activity was temporarily inactivated by introducing an inhibition strand to close part of the catalytic core of the DNAzyme, and the cleavage activity was restored under the action of a trigger signal. DNAzymes play a double role of signal generation and transmission. Allosteric regulation of DNAzymes through secondary structures not only ensures the integrity of the totality of DNA sequences, but also reduces the impacts of factors like pH and metal ions on other reactants in the system. This ultimately improves the stability of the molecular system to a certain extent. In a typical DNAzyme-based reaction,⁵⁰ a DNAzyme can specifically catalyze the hydrolysis of a phosphodiester linkage at the marker site, and the separations of the cleaved substrates are typically used as a signal to trigger downstream reactions.⁵¹ Therefore, the advantages of DNAzymes provide an efficient platform to introduce to the neuron model.

Herein, we propose a strategy based on DNAzyme activity to adjust the operation of neurons, combing two reaction mechanisms: DNAzyme digestion and TMSD. The strategy was applied to E6-type DNAzyme.^24,52 The Mg²⁺-dependent and allosterically regulated E6-type DNAzyme can cut DNA substrate containing ribonucleobase (TrAGG) at a high rate. In the initial state, the neurons could not work properly because the inhibitor strand impeded the activity of DNAzymes. First, the input signal of the neuron hybridized with the inhibitor in the weight by the exposed toehold region, thereby releasing the catalytic core of the DNAzyme. Then, DNAzyme digestion activity was activated and the neurons started to perform calculation functions. In our design, DNAzymes and strand displacement take part in the reactions jointly, thus realizing the control of neurons by DNAzyme. In addition, the introduction of DNAzymes simplified the normalization process and improved the stability of the system. We verified the logical function of each component step by step. On this basis, these components were strung together to verify the correctness of the model calculation function and to structure a voting machine. This molecular platform can make a reasonable, autonomous judgment after the addition of input signals. The results were confirmed via native polyacrylamide gel electrophoresis (PAGE) and fluorescence detection. This neuron model was simple to build, with rapid response and high stability. It has a great potential to construct large neural networks, which may have more applications in intelligent computing.

2 Results and discussion

2.1. DNA neuron details

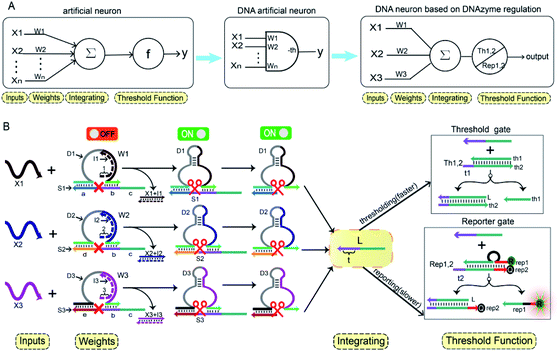
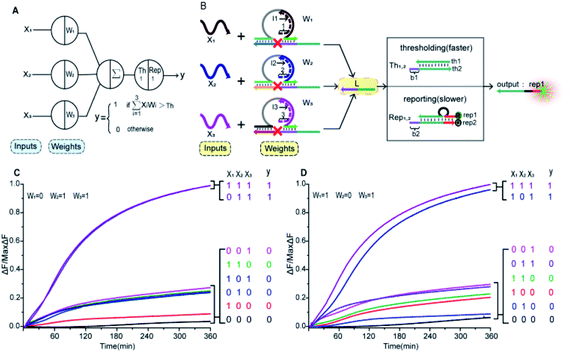
In Fig. 1A, the left panel is a diagram of an artificial neuron in an electronic computer. As an information processing unit accepting multiple input signals from other neurons and having singular output, an artificial neuron can have any number of inputs (X₁, X₂, …, X_n ∈ {0,1}), with weights (W₁, W₂, …, W_n) indicating the connection strength of each input signal. The neuron is activated to produce an output signal when the weighted sum of all inputs exceeds a threshold. The basic characteristics of artificial neuronal behavior in DNA molecular systems include analog inputs and weights, analog summation, analog thresholding and output. We used DNA molecular circuits to build a neuron based on DNAzyme regulation (Fig. 1A, right panel). The specific DNA molecule realization is shown in Fig. 1B. Here, we used the relative concentration of each reactant in the system to express its value. The input signal of the DNA neuron consisted of three different DNA strands: X₁, X₂ and X₃. W₁, W₂ and W₃ represent the weight of each input signal connection. The weight of neuron was composed of three parts: an E6-type DNAzyme, an inhibitor and a marked cleavage site substrate strand. The upstream product strand L was outputted as a normalized product, followed by quantitative threshold processing. The Th_1,2 in the threshold gate is composed of the base strand th2 and the top complementary strand th1. After the threshold process was completed, the Rep_1,2 in the reporter gate consisting of a base strand rep2 and a top strand rep1, released the output signal. The top strand rep1 was labeled at the 5′-end with ROX fluorophore and the base strand rep2 was labeled at the 3′-end with BHQ2 quencher.

Fig. 1 (A) Abstract diagram of the artificial neuron. (B) Illustration of the DNA neuron.

To imitate the input and weight of the neuron, each input was multiplied by the corresponding weight, which was calculated as X_i × W_i (the value of “i” in the text is 1, 2, 3). When the value of W_i is “0” the output must be “0”; when the value of W_i is “1” the calculated output value is equal to the input value. Here, we added excess W_i to the solution to ensure the validity of the results. The input signal hybridized with the inhibitor strand in the W_i to form a double-stranded complex, which has a blunt end and thus can remain stable. The DNAzyme obtained completed the catalytic core to restore the ability of DNAzyme digestion. Subsequently, the summation of the neuron was calculated as ∑X_i × W_i. DNAzyme can cut the substrate strand with specific marker after its reactivated. After the DNAzyme digestion process is completed, the binding ability of the DNAzyme binding arm to substrates is weakened, and strand L is released as a normalized product. In order to ensure the performance of threshold processing, the base length of t1 in Th_1,2 is greater than that of t2 in the Rep_1,2. Because t1 is exposed to the more complementary sticky end, the normalized product L preferentially reacts with Th_1,2. The amount of upstream product L consumed depends on the amount of Th_1,2, the remaining L is read by the Rep_1,2 after the upstream product is consumed. The strand L binds to the Rep_1,2 base strand rep2, releases the top strand rep1, separates the ROX and BHQ2, and results in an increasing fluorescent signal. The output value of the neuron is inferred from the fluorescent signal reaching the maximum completion level.

2.2. Design of neuron weight unit

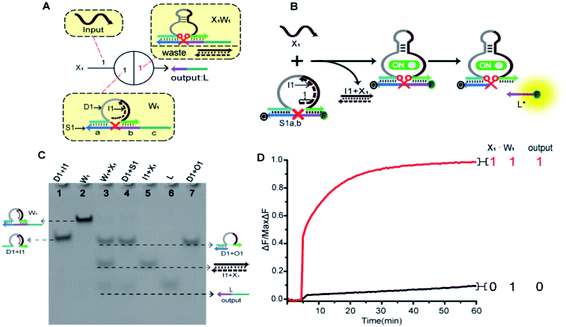
In order to fully realize the function of an artificial neuron in the experimental work, we introduced DNA gate architecture that modifies DNAzyme activity via triggering signals to implement the input and weight of neurons. As shown in Fig. 2A, the abstract diagram for the weight unit 1 (W₁) motif provides a concise representation of a full DNA implementation. The input signal X₁ was a single strand; the W₁ was composed of three parts: DNAzyme 1 (D1), inhibitor 1 (I1) and a marked cleavage site substrate strand 1 (S1). In the model, we used the initial relative concentrations to indicate the weight values. The reaction is depicted in Fig. 2B. The cutting activity of D1 was inhibited because the catalytic core of D1 hybridizes with the I1, while the substrate S1_a,b could not be cut. The reaction could only be triggered after the addition of input signal X₁, which first hybridized with I1 through the exposed toehold domain (7n in domain 1) so that D1 had a complete catalytic core to restore the specific digestion ability. Then, S1_a,b was cleaved into O1 and L*. Here, strand S1_a,b was designed to have a ribonucleotide cleavage site (TrAGG) in the middle region, with the 5′-end fluorescently labelled (FAM) and the 3′-end labelled with quencher (BHQ1). Finally, the cleaved short segment L* was released serving as the output signal, and the long segment O1 hybridized with D1, resulting in a significant fluorescence increase.

Fig. 2 (A) Abstract diagram of the weight unit 1 motif and its DNA implementation. The black numbers indicate the initial relative concentration. Red number indicates relative product concentrations, and different colours indicate distinct DNA sequences. S1a is the left (3′-end) recognition domain of substrate strand 1 (S1), while S1b is the right (5′-end) recognition domain of S1. (B) Illustration of the weight unit 1. The substrate strand sequence is S1_a,b, 5′-end fluorophore FAM and 3′-end quencher BHQ1 for fluorescent signal determination. (C) Native PAGE analysis of the weight unit 1. The strands and complex involved were labelled above the lane number. Lane 1, complex (D1 + I1) consists of DNAzyme 1 (D1) and inhibitor 1 (I1); lane 2, weight unit 1 (W₁) consists of D1, I1 and S1; lane 3, products of W₁ triggered by input X₁; lane 4, products of D1 digestion; lane 5, complex (I1 + X₁); lane 6, output strand L; lane 7, complex (D1 + O1). (D) Time-dependent fluorescence changes according to different inputs. The standard concentration was 1× = 0.2 μM, [X₁] and [W₁] was 1 : 1. The red curve reflects the reaction with the addition of X₁ and the black curve is the case with no input.

Here, the logical function of W₁ was verified by native PAGE gel electrophoresis. As shown in Fig. 2C, lane 2 indicated that the initial W₁ was present and stable in a single gel band. Lane 3, in the presence of input signal X₁, the W₁ band disappeared to produce three new bands (D1 + O1), (I1 + X₁) and L. Lane 5 indicated the location of the complex (I1 + X₁); lane 6 indicated the location of the output signal strand L; and lane 7 indicated the location of the other product (D1 + O1). The band (I1 + X₁) signifies the input signal X₁ hybridized with I1. Band (D1 + O1) and L were generated because the input signal promoted the digestion of D1, cutting S1 to release the output signal strand L. These results prove the correctness of the neuron weight unit 1. In addition, the remaining weight units were verified in ESI Fig. S1 and S2.†

A fluorescence assay was also conducted to monitor the W₁ in real time. The red curve indicated that the input signal X₁ was added, and a significant fluorescence increase can be observed. On the contrary, no remarkable increase of fluorescent signal could be observed in the black curve without the addition of input strand X₁. The results demonstrate the successful performance of W₁.

2.3. Integration gate

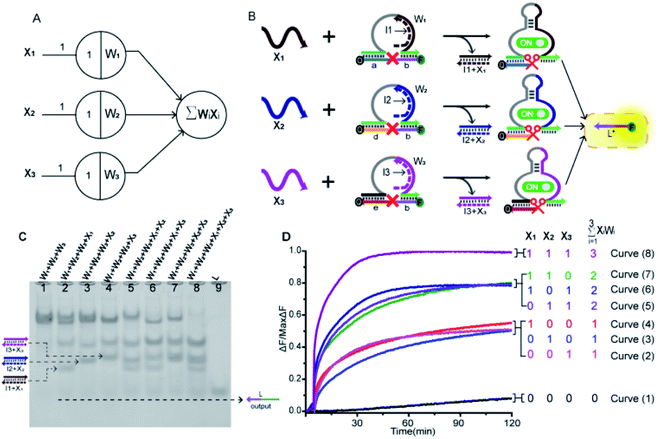
In order to prove the application potential of the weight unit in the construction of neuron models, we built a three-input integration gate as shown in Fig. 3A to implement the summation function of neurons. As shown in Fig. 3B, X₁, X₂ and X₃ were used as input signals to trigger the digestion reaction of the DNAzyme in the weight unit. Then, the catalytic core of the DNAzyme was liberated and the substrate strand was cut. The sum of all of the weighted inputs was calculated to get the normalized output strand L*. With the reaction was irreversible, the output of each weight unit continued to be released until the input signal was exhausted. Here, we used the relative concentration for each value and the normalized output product was dependent on the input signal value. The normalized product was inferred from the fluorescent signal with the highest intensity. We used gel electrophoresis experiments and fluorescence tests to verify this function.

Fig. 3 (A) Abstract diagram of the three-input integration gate motif and its DNA implementation. The black numbers indicate the initial relative concentration. (B) Illustration of the integration gate. The inputs signal consisted of three parts: X₁, X₂ and X₃; the weights consisted of three parts: W₁, W₂ and W₃. All substrate strands (S1_a,b, S2_d,b, S3_e,b) were labelled with fluorophore FAM at 5′-end and quencher BHQ1 at 3′-end for fluorescent signal determination; L* was the normalized output. (C) Native PAGE analysis of the integration gate. The strands and complex involved were labelled above the lane number. Lane 1, weight unit mixture (W₁ + W₂ + W₃); lane 2, X₁ was added to the weight unit mixture; lane 3, X₂ was added to the weight unit mixture; lane 4, X₃ was added to the weight unit mixture; lane 5, X₁ and X₂ were added to the weight unit mixture; lane 6, X₁ and X₃ were added to the weight unit mixture; lane 7, X₂ and X₃ were added to the weight unit mixture; lane 8, all signals were added to the weight unit mixture; lane 9, normalized product strand L. (D) Normalized fluorescence of the integration gate. The standard concentration was 1× = 0.2 μM, [W₁] : [W₂] : [W₃] : [X₁] : [X₂] : [X₃] = 1 : 1 : 1 : 1 : 1 : 1. The sum value was inferred from the fluorescent signal. Curve (1) had no input signals added; Curves (2)–(4) had only one input signal added; Curves (5)–(7) had two kinds of input signals added; Curve (8) had all input signals added.

By adding different inputs, we validated the function of the three-input integration gate. As shown in Fig. 3C, from lane 1 to lane 4, the added input signals were 0, X₁, X₂, X₃; lane 5 to lane 7, the added input signals were X₁ + X₂, X₁ + X₃, X₂ + X₃; lane 8, the added input signal were X₁ + X₂ + X₃. Lane 9 indicated the location of the normalized product strand L. A new single gel band strand L had appeared in lane 2 to lane 8. In particular, the most obvious observation is in lane 8, the weight unit mixture (W₁ + W₂ + W₃) band disappeared and the band strand L was the darkest color. This was because three weight units were triggered, making the DNAzyme exert its ability to cut the substrate strand. And produce more normalized product. More details can be observed in the ESI S3,† the disappearance of gel band W₁, W₂, and W₃ also proved the correctness of the summation function.

Next, we used fluorescence determination of the three-input integration gate for more detailed analysis and the sum value was inferred from the fluorescent signal. The initial state were weight unit mixture (W₁ + W₂ + W₃), and the fluorescence changes were observed by adding input signals. As shown in Fig. 3D, we divided all the reactions into four categories: (I) no input was added; (II) only one input signal was added; (III) two kinds of signals were added arbitrarily; (IV) all of the input signals were added. In the absence of input signals, Curve (1) had almost no increase in fluorescent signals that could be observed. Curve (2) to Curve (4), the added input signals were X₃, X₂, X₁. In the case of adding a signal, the fluorescent started to rise and roughly rising to the same level. Curve (5) to Curve (7), the added input signals were X₂ + X₃, X₁ + X₃, X₁ + X₂. It was shown that when any two signals were inputted, the fluorescence intensity increases more significantly and also rose to the same level. In Curve (8), all of the signals were added and the fluorescence intensity reached its maximum. This indicated that as the input signal increases, more normalized products were obtained.

2.4. Thresholding gate

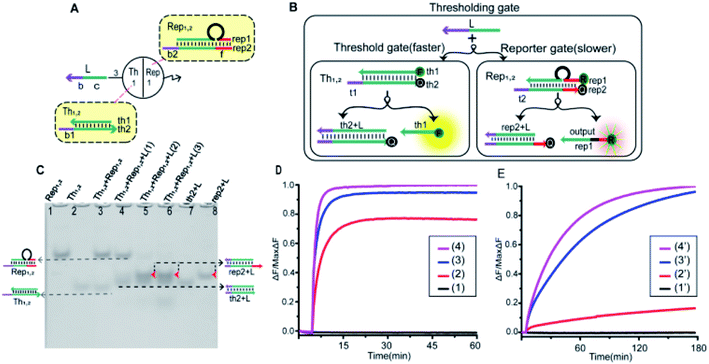
To implement the thresholding and output of artificial neurons, we constructed the thresholding gate as shown in Fig. 4A. The thresholding gate consists of threshold gate and reporter gate. The Th_1,2 in the threshold gate was a double-stranded complex composed of the bottom base strand th2 and the top complementary strand th1. In order to read the output signal, a “Reporter gate” was used. The Rep_1,2 in the reporter gate was composed of the base strand rep2 and the top bubble-like complementary strand rep1. The Th_1,2 and the Rep_1,2 have similar toehold regions. In order to ensure the processing performance of the Th_1,2, through experimental exploration, the toehold b1 of the threshold gate had six bases, and the toehold b2 of the reporter gate had four bases (more details were in the ESI S6†). As shown in Fig. 4B, due to the threshold gate exposing more toehold, the input signal strand L reacted first with the Th_1,2. If the signal strand L exceeded a threshold, the reporter gate reaction was initiated. The redundant strand L hybridized with rep2 through the toehold region of the reporter gate and the output signal rep1 was substituted. In order to better reflect the processing performance of the thresholding gate, the quencher BHQ1 was used at the 3′-end of the base strand th2, and the fluorophore FAM was used at the 5′-end of the complementary strand th1 of the threshold gate; the reporter gate used the fluorophore ROX and quencher BHQ2, the strand rep2 3′-end marked quencher BHQ2, strand rep1 5′-end marked fluorophore ROX. Trajectories for corresponding inputs are shown with matching colors. The step-by-step verification and combination optimization of threshold gate and reporter gate were in ESI S4 and S5.†

Fig. 4 (A) Abstract diagram of the thresholding gate motif and its DNA implementation. The black numbers indicate the initial relative concentration. (B) Illustration of the thresholding gate. In the Th_1,2, the top strand th1 was labeled with the fluorophore FAM at the 5′-end, and the bottom base strand th2 was labeled with the quencher BHQ1 at the 3′-end for fluorescent signal determination; in the Rep_1,2, the top strand rep1 was labeled with the fluorophore ROX at the 5′-end, and the bottom base strand rep2 was labeled with quencher BHQ2 at the 3′-end for fluorescent signal measurement. (C) Native PAGE analysis of the thresholding gate. The strands and complex involved were labeled above the lane number. The molality of [Th_1,2] and [Rep_1,2] was 1 : 1. Input signals with different concentration gradients were added to verify the threshold effect. Lane 1, the Rep_1,2 (rep1 + rep2) in the reporter gate; lane 2, the Th_1,2 (th1 + th2) in the threshold gate; lane 3, [Th_1,2] and [Rep_1,2] mixture; lane 4, to add 1 time input signal strand L; lane 5, to add 2 times input signal strand L; lane 6, to add 3 times input signal strand L; lane 7, the product of threshold gate (th2 + L); lane 8, the product of reporter gate (rep2 + L). (D) The fluorescence of the threshold gate. The standard concentration was 1× = 0.2 μM. Curve (1) no input signal was added; Curves (2)–(4) indicate that 1, 2 and 3 times input signal strand L were added in turn. (E) The fluorescence of the reporter gate. The standard concentration was 1× = 0.2 μM. Curve (1′) no input signal was added; Curves (2′)–(4′) indicate that 1, 2 and 3 times the input signal strand L were added in turn. (D) and (E) were detected in the same solution.

As shown in Fig. 4C, the performance of threshold processing was verified by PAGE gel. In the case that the molality of the [Th_1,2] and the [Rep_1,2] was 1 : 1, we added input signals with different concentration gradients to verify the threshold effect. Lane 1 was the location of the Rep_1,2 in the reporter gate, lane 2 was the location of the Th_1,2 in the threshold gate, lane 7 was the location of the threshold gate output signal (th2 + L), and lane 8 was the location of the reporter gate product (rep2 + L). From lanes 3–6, the 0, 1, 2 and 3 times of input signal strand L were added. When no input was added, no new gel band was observed in lane 3. Lane 4, when adding 1 time of input signal strand L, the band Th_1,2 disappeared to produce a new band (th2 + L). When more than 2 times the input signal strand L was added, the Th_1,2 and Rep_1,2 all disappeared to produce two new bands (th2 + L) and (rep2 + L) (lane 5 and lane 6). This indicated that the input signal strand L reacted first with the threshold gate, and when the strand L exceeded the threshold, the reporter gate started to work.

Equal proportions of [Th_1,2] and [Rep_1,2] were added to the solution. By adding different concentrations of the input signals, we observed their fluorescence changes. In order to observe the fluorescence changes more intuitively, the fluorescence results of thresholding gate were shown separately in Fig. 4D (threshold gate) and Fig. 4E (reporter gate). Curve (n) and Curve (n′) (n = 1, 2, 3, 4) were added with 0, 1, 2 and 3 times input signal strand L, respectively. Curve (1) and Curve (1′) fluorescent signal did not raise when no input was added. When 1 time of input signal strand L was added, Curve (2) rose rapidly and tended to be stable. Curve (2′) did not change significantly at that time because the signal strand L first reacted with the threshold gate. When more than 2 times of the input signal strand L was added, Curves (3) and (4) rose at a faster rate and tended to be stable. At that point, the strand L exceeded the maximum capacity of threshold, and the fluorescent of Curves (3′) and (4′) also started to rise significantly. The results of fluorescence testing also show that the threshold function was correct.

2.5. An artificial DNA neuron model

To prove the reliability and scalability of the neuron components, we cascaded the above modules together to construct a three-input linear threshold gate as shown in Fig. 5A. By calculating the analog value of a three-input linear threshold function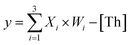 to test the correctness of a calculated function of the neuron. The first layer in DNA neuron each input was multiplied by the corresponding weight; the second layer calculated the sum of all weighted inputs; the third layer implemented the corresponding threshold for output; and the final layer of reporter gate read the output signal. The molecular implementation process is shown in Fig. 5B. The input signals X₁, X₂ and X₃ were three different single strands of DNA. Three parallel weights, W₁, W₂ and W₃ were used to receive input signals. The input signal hybridized with the inhibitor in the corresponding weight unit after the addition of input signals. With the liberation of the catalytic core, the DNAzyme restored its hydrolysis ability, cut the substrate with ribonucleotide cleavage site, and the cleaved long segment L was released serving as normalized product output. Then, the normalized output was used as the input signal of the next level was precedence response the threshold gate reaction for quantitative consumption. When the normalized product exceeded the maximum capacity of the threshold gate, the reporter gate released the output signal.

Fig. 5 (A) Demonstration of a 3-input 1-output linear threshold gate. The black numbers indicate the initial relative concentration. Each input value was represented by a relative concentration. The sum of the 3-input is calculated as . (B) Abstract diagram of DNA neuron. (C) Fluorescence detection with W₁ = 0, W₂ = 1 and W₃ = 1. (D) Fluorescence detection with W₁ = 1, W₂ = 0 and W₃ = 1. In (C) and (D), the standard concentration was 1× = 0.2 μM. Input strands X₁, X₂ and X₃ were then added with relative concentrations of 0× or 1×.

The output values were inferred by fluorescence signals normalized to the maximum completion level. To clean up variations due to leaky reactions and signal decay, we used the relative concentration for each value. If the function output was “0” the fluorescence “OFF” signal would be between 0 and 0.3, and if the function output was “1” the fluorescence “ON” signal would be between 0.8 and 1. We tuned weights to show that the same set of DNA molecules can implement different linear threshold functions. When weights W₁ = 0, W₂ = 1 and W₃ = 1, the output results were shown in Fig. 4C. When weights W₁ = 1, W₂ = 0 and W₃ = 1, the output results were shown in Fig. 4D. Both weight conditions achieved the correct ON or OFF state with the eight complete sets of inputs. Other cases were in ESI Fig. S7 and S8.†

2.6. Voting machine

In particular, when the weights of neuron W₁ = W₂ = W₃ = 1, they could be applied to voting machines. We constructed as shown in Fig. 6A a voting apparatus. The three input signals of the neuron were equivalent to the vote of the elector. With our regulation, if the vote was “yes” then the corresponding input signal was “1”, if “no” the corresponding input signal was “0”. Only when two or more votes agreed the result was valid. All of the voting information is shown in Fig. 6B.

Fig. 6 (A) Abstract diagram of the DNA voting machine. (B) Voting information form. (C) Native PAGE analysis of the voting circuit. The strands and complex involved were labeled above the lane number. The voting system consisted of [W₁], [W₂], [W₃], [Th_1,2], [Rep_1,2], and their proportion of 1 : 1 : 1 : 1 : 1. Different inputs were added to validate the voting result. Lane 1, the Rep_1,2 (rep1 + rep2); lane 2, the components required for voting system were Th_1,2 + Rep_1,2 + W₁ + W₂ + W₃; lane 3, the signal X₁ was added to the voting system; lane 4, the signal X₂ was added to the voting system; lane 5, the signal X₃ was added to the voting system; lane 6, the signal X₁ and X₂ were added to the voting system; lane 7, the signal X₁ and X₃ were added to the voting system; lane 8, the signal X₂ and X₃ were added to the voting system; lane 9, all input signals X₁, X₂ and X₃ were added to the voting system; lane 10, the product of the reporter gate (rep2 + L). (D) Fluorescence of the voting device circuit. Each case was marked below the bar chart. The fluorescence “OFF” signal was set at 0.3 to determine the positive and negative output signals. Fluorescence modification was shown in Fig. 5B.

As shown in Fig. 6C, the performance of the voting machine was first confirmed by native PAGE gel electrophoresis. Lane 1 was the Rep_1,2 in the reporter gate. Lane 2 was the reactant (Th_1,2 + Rep_1,2 + W₁ + W₂ + W₃) required by the voting system. Lane 10 was the location of the reported product (rep2 + L). The input signals X₁, X₂ and X₃ were added to lanes 3, 4 and 5, respectively. When only one vote “agreed” the result was deemed invalid, so the gel band Rep_1,2 still existed in lanes 3–5. The input signals X₁ + X₂, X₁ + X₃ and X₂ + X₃ were added to lanes 6, 7 and 8, respectively, and lane 9 contained all of the input signals. In these lanes, the gel band Rep_1,2 disappeared, and a new band (rep2 + L) was generated, indicating that the voting device was correctly performing its function. More details were in the ESI S9.†

To visually reflect the results of the voting machine, fluorescent signals were used to detect the system. As shown in Fig. 5D, when none agree or only one agrees, the fluorescent value remains below 0.3 in the “OFF” signal area. However, when two or more agree, the output signal increases to a high level (above 0.8). This suggests that the DNA neuron worked very well as expected.

3 Experimental

3.1. Materials of DNA strands

DNA strands were obtained from Sangon Biotech Co., Ltd. (Shanghai, China). Unmodified DNA strands were purified by polyacrylamide gel electrophoresis (PAGE), and modified DNA strands with RNA bases and fluorophore were purified by high-performance liquid chromatography (HPLC). The Nucleic Acid Package (NUPACK) was used to simulate the DNA sequence (ESI S10†). The sequence of the DNA strand is listed in ESI Table S1.† All of the DNA strands were dissolved in ultrapure water (MiaoKang water treatment technology, MU5100DUVFR, Shanghai) as stock solution and quantified using a Nanodrop 2000 spectrophotometer (Thermo Fisher Scientific Inc., USA), with absorption intensities measured at λ = 260 nm. All other chemicals were of analytical grade and were used without further purification.

3.2. Preparation of neuron components

Weight units were formed by annealing twice. First, to inhibit DNAzyme activity, the mixture of the inhibitor DNA strands and E6-type DNAzymes were annealed in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA 2Na and 12.5 mM Mg(OAc)₂, pH 8.0) at the same molarity, heated at 95 °C for 4 min, 65 °C for 30 min, 50 °C for 30 min, 37 °C for 30 min, 22 °C for 30 min, and preserved at 20 °C; and then the substrates were added into the annealed mixture and incubated at constant temperature 20 °C for 4 hours. The threshold and reporter units were mixed with the corresponding single strands at equal molar concentrations in 1× TAE/Mg²⁺ buffer solution, heated at 95 °C for 4 min, 65 °C for 30 min, 50 °C for 30 min, 37 °C for 30 min, 22 °C for 30 min, and preserved at 4 °C.

3.3. Native polyacrylamide gel electrophoresis

Each sample (30 μL, 0.5 μM) was mixed with a 60% glycerol solution (5 μL), and the components of the neuron were verified by electrophoresis on 12% natural polyacrylamide gel in 1× TAE/Mg²⁺ buffer. The gel was run under a constant voltage of 90 V over a period of 2 hours at 4 °C.

3.4. Fluorescent biosensing assays

Fluorescence experiments were implemented using real-time PCR (Bio-Rad, C1000) equipped with a 96-well fluorescent plate reader. Fluorescence measurements for all components were performed in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA 2Na and 12.5 mM Mg(OAc)₂, pH 8.0) solution with a reaction volume of 50 μL, reaction temperature of 25 °C, and a final reactant concentration of 0.2 μM. The FAM fluorescent signal was detected at 492 nm excitation and 518 nm emission, while the ROX fluorescent signal was detected at 586 nm excitation and 606 nm emission. The fluorescence sampling interval was set at 30 seconds. The normalized fluorescence intensity was calculated by subtracting the baseline intensity at each time point, and then the fluorescence increment at each time point was divided by the maximum fluorescence increment to obtain the final value. All fluorescence experiments were repeated three times to ensure repeatability.

4 Conclusions

In summary, we introduced a neuron model based on DNAzyme regulation. DNAzyme specific cutting realized the corresponding relationship between input signal (X_i) and weight (W_i) in the neuron model. In this model, a strategy is used to initiate the activity of DNAzymes via trigger signals. The key method was to block part of the catalytic core of the DNAzyme through the secondary structure to inhibit its activity. The input signal and the inhibitor strand caused strand displacement by exposed toehold domain so that the DNAzyme restored its hydrolytic ability to cut substrates. The cleaved substrate was outputted as a normalized product to realize the normalization process. This process not only simplifies the normalization function of neurons, but also provides a new mode for processing inputted information. In addition, we also applied DNA molecular implementations of other components of artificial neurons, including the construction of weight units and thresholding gate. On this basis, a complete neuron was constructed by cascading the components together, and the value of a linear threshold function was calculated from it. The computing power of the model was verified.

In addition, E6-type DNAzyme has good stability and enzyme activity, has been proven to be suitable for molecular logic operations, raising the possibility of “artificial intelligence” in biological experiments. We envision that this approach can be combined with other methods (restriction enzyme, DNA origami) to provide more ideas for molecular logic operations and DNA neural networks. The experimental results show that this strategy is versatile in building molecular logic circuits. We envision that, this method can be extended to other variable construct types of DNAzymes and other DNA computing systems. By modifying the DNAzyme allosteric regulatory domain of the weight unit, multiple input DNA neurons can be constructed based on this model. Compared with traditional DNA neurons, the neuron model presented in this work is simple to construct and easy to extend. And the successful application of the DNA voting circuit of this model can prove its potential in DNA computing. It is possible to establish a connection between input signals and certain diseases, so that the “smart” DNA system can make rational judgments independently. With the continuous progress in experimental technology, this model will be useful in providing new ideas for research in computer science, biomedicine and artificial intelligence systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Key R&D Program of China (No. 2018YFC0910500), the National Natural Science Foundation of China (No. 61425002, 61751203, 61772100, 61972266, 61802040, 61672121), the Natural Science Foundation of Liaoning Province (No. 20180551241, 2019-ZD-0567), the High-level Talent Innovation Support Program of Dalian City (No. 2017RQ060, 2018RQ75).

Notes and references

1. E. Stulz, G. Clever, M. Shionoya and C. Mao, Chem. Soc. Rev., 2011, 40, 5633–5635.
2. C. Xing, Z. Chen, J. Dai, J. Zhou, L. Wang, K.-L. Zhang, X. Yin, C. Lu and H. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 6336–6342.
3. T. Song, A. Eshra, S. Shah, H. Bui, D. Fu, M. Yang, R. Mokhtar and J. Reif, Nat. Nanotechnol., 2019, 14, 1075–1081.
4. J. Yang, R. Wu, Y. Li, Z. Wang, L. Pan, Q. Zhang, Z. Lu and C. Zhang, Nucleic Acids Res., 2018, 46, 8532–8541.
5. H. Cho, S. B. Mitta, Y. Song, J. Son, S. Park, T. H. Ha and S. H. Park, ACS Nano, 2018, 12, 4369–4377.
6. T. Fu, Y. Lyu, H. Liu, R. Peng, X. Zhang, M. Ye and W. Tan, Trends Biochem. Sci., 2018, 43, 547–560.
7. C. Zhang, J. Yang, S. Jiang, Y. Liu and H. Yan, Nano Lett., 2016, 16, 736–741.
8. G. Chatterjee, N. Dalchau, R. A. Muscat, A. Phillips and G. Seelig, Nat. Nanotechnol., 2017, 12, 920.
9. K. Morihiro, N. Ankenbruck, B. Lukasak and A. Deiters, J. Am. Chem. Soc., 2017, 139, 13909–13915.
10. R. Peng, X. Zheng, Y. Lyu, L. Xu, X. Zhang, G. Ke, Q. Liu, C. You, S. Huan and W. Tan, J. Am. Chem. Soc., 2018, 140, 9793–9796.
11. X. Zhang, Q. Zhang, Y. Liu, B. Wang and S. Zhou, Comput. Struct. Biotechnol. J., 2020, 18, 2107–2116.
12. X. Ma, X. Chen, Y. Tang, R. Yan and P. Miao, ACS Appl. Mater. Interfaces, 2019, 11, 41157–41164.
13. S. B. Ebrahimi, D. Samanta and C. A. Mirkin, J. Am. Chem. Soc., 2020, 142, 11343–11356.
14. B. Cao, X. Li, X. Zhang, B. Wang, Q. Zhang and X. Wei, IEEE/ACM Trans. Comput. Biol. Bioinf. DOI:10.1109/TCBB.2020.3011582.
15. B. Cao, X. Zhang, J. Wu, B. Wang, Q. Zhang and X. Wei, IEEE Trans. NanoBioscience DOI:10.1109/TNB.2021.3056351.
16. Z. Tian, P. Peng, H. Wang, J. Zheng, L. Shi and T. Li, Anal. Chem., 2020, 92, 10357–10364.
17. L. Qian, E. Winfree and J. Bruck, Nature, 2011, 475, 368–372.
18. F. Xia, X. Zuo, R. Yang, R. J. White, Y. Xiao, D. Kang, X. Gong, A. A. Lubin, A. Vallée-Bélisle and J. D. Yuen, J. Am. Chem. Soc., 2010, 132, 8557–8559.
19. P. Miao, T. Zhang, J. Xu and Y. Tang, Anal. Chem., 2018, 90, 11154–11160.
20. S. Zhou, P. He and N. Kasabov, Entropy, 2020, 22, 1091.
21. L. Wang, H. Zhou, B. Liu, C. Zhao, J. Fan, W. Wang and C. Tong, Anal. Chem., 2017, 89, 11014–11020.
22. F. Li, H. Chen, J. Pan, T.-G. Cha, I. L. Medintz and J. H. Choi, Chem. Commun., 2016, 52, 8369–8372.
23. W. P. Klein, R. P. Thomsen, K. B. Turner, S. A. Walper, J. Vranish, J. Kjems, M. G. Ancona and I. L. Medintz, ACS Nano, 2019, 13, 13677–13689.
24. R. R. Breaker and G. F. Joyce, Chem. Biol., 1995, 2, 655–660.
25. R. J. Lake, Z. Yang, J. Zhang and Y. Lu, Acc. Chem. Res., 2019, 52, 3275–3286.
26. P. Song, D. Ye, X. Zuo, J. Li, J. Wang, H. Liu, M. T. Hwang, J. Chao, S. Su and L. Wang, Nano Lett., 2017, 17, 5193–5198.
27. C. Li, H. Li, J. Ge and G. Jie, Chem. Commun., 2019, 55, 3919–3922.
28. C. Liu, Y. Hu, Q. Pan, J. Yi, J. Zhang, M. He, M. He, T. Chen and X. Chu, Biosens. Bioelectron., 2019, 136, 31–37.
29. Y. Yang, Y. He, Z. Deng, J. Li, X. Li, J. Huang and S. Zhong, ACS Appl. Bio Mater., 2020, 3, 6310–6318.
30. C. Briat, C. Zechner and M. Khammash, ACS Synth. Biol., 2016, 5, 1108–1116.
31. R. Deng, H. Yang, Y. Dong, Z. Zhao, X. Xia, Y. Li and J. Li, ACS Sens., 2018, 3, 2660–2666.
32. J. Zhu, L. Zhang, S. Dong and E. Wang, ACS Nano, 2013, 7, 10211–10217.
33. S. Lilienthal, M. Klein, R. Orbach, I. Willner, F. Remacle and R. D. Levine, Chem. Sci., 2017, 8, 2161–2168.
34. Y. V. Gerasimova and D. M. Kolpashchikov, Angew. Chem., 2016, 128, 10400–10403.
35. A. Idili, A. Vallée-Bélisle and F. Ricci, J. Am. Chem. Soc., 2014, 136, 5836–5839.
36. A. Amodio, A. F. Adedeji, M. Castronovo, E. Franco and F. Ricci, J. Am. Chem. Soc., 2016, 138, 12735–12738.
37. L. Freage, A. Trifonov, R. Tel-Vered, E. Golub, F. Wang, J. S. McCaskill and I. Willner, Chem. Sci., 2015, 6, 3544–3549.
38. X.-H. Zhao, L.-Z. Zhang, S.-Y. Zhao, X.-H. Cui, L. Gong, R. Zhao, B.-F. Yu and J. Xie, Analyst, 2019, 144, 1982–1987.
39. J. Elbaz, F. Wang, F. Remacle and I. Willner, Nano Lett., 2012, 12, 6049–6054.
40. M.-R. Cui, X.-L. Li, J.-J. Xu and H.-Y. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 13005–13012.
41. C. Yang, X. Yin, S.-Y. Huan, L. Chen, X.-X. Hu, M.-Y. Xiong, K. Chen and X.-B. Zhang, Anal. Chem., 2018, 90, 3118–3123.
42. X. Shi, H.-M. Meng, X. Geng, L. Qu and Z. Li, ACS Sens., 2020, 5, 3150–3157.
43. J. Chen, A. Zuehlke, B. Deng, H. Peng, X. Hou and H. Zhang, Anal. Chem., 2017, 89, 12888–12895.
44. W. Zhou, Q. Chen, P.-J. J. Huang, J. Ding and J. Liu, Anal. Chem., 2015, 87, 4001–4007.
45. J. Wang, H. Wang, H. Wang, S. He, R. Li, Z. Deng, X. Liu and F. Wang, ACS Nano, 2019, 13, 5852–5863.
46. Z.-M. He, P.-H. Zhang, X. Li, J.-R. Zhang and J.-J. Zhu, Sci. Rep., 2016, 6, 1–10.
47. X.-H. Zhao, R.-M. Kong, X.-B. Zhang, H.-M. Meng, W.-N. Liu, W. Tan, G.-L. Shen and R.-Q. Yu, Anal. Chem., 2011, 83, 5062–5066.
48. J. Chen, J. Pan and S. Chen, Chem. Commun., 2017, 53, 10224–10227.
49. X. Zheng, J. Yang, C. Zhou, C. Zhang, Q. Zhang and X. Wei, Nucleic Acids Res., 2019, 47, 1097–1109.
50. L. Gong, Z. Zhao, Y.-F. Lv, S.-Y. Huan, T. Fu, X.-B. Zhang, G.-L. Shen and R.-Q. Yu, Chem. Commun., 2015, 51, 979–995.
51. B. Peeters, D. Daems, T. Van der Donck, F. Delport and J. Lammertyn, ACS Appl. Mater. Interfaces, 2019, 11, 6759–6768.
52. J. Elbaz, O. Lioubashevski, F. Wang, F. Remacle, R. D. Levine and I. Willner, Nat. Nanotechnol., 2010, 5, 417–422.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10515e

---