NMR-based metabolomics with enhanced sensitivity

Abstract

NMR-based metabolomics, which emerged along with mass spectrometry techniques, is the preferred method for studying metabolites in medical research and food industries. However, NMR techniques suffer from inherently low sensitivity, regardless of their superior reproducibility. To overcome this, we made two beneficial modifications: we detuned the probe to reach a position called “Spin Noise Tuning Optimum” (SNTO), and we replaced the conventional cylindrical 5 mm NMR tube with an electric field component-optimized shaped tube. We found that concerted use of both modifications can increase the sensitivity (signal to noise ratio per unit volume) and detection of metabolites and decrease the measurement time by order of magnitude. In this study, we demonstrate and discuss the achieved signal enhancement of metabolites on model non-human (bovine serum, amino acid standard mixture) and human urine samples.

---

Introduction

Metabolites are the end products of biochemical processes in biological systems. Since any physiological change is an interplay of multiple biochemical processes, the identification and tracking of a particular set of metabolites can often help to monitor and understand the details of the associated physiological changes. Metabolomics has emerged as a useful tool to identify specific biomarkers for the diagnosis and monitoring of specific diseases. There has been a progressive increase in in-depth metabolic studies for biomarkers specific to many human diseases such as neurological¹ and cardiovascular disease,^2–4 cancer,⁵ and in-born errors of metabolism (IEM) diseases.⁶

NMR-based metabolomics relies mainly on one-dimensional ¹H NMR spectroscopy. The significant limitations of 1D NMR include inherently modest sensitivity and substantial signal overlap.^7,8 A computational approach⁹ and, more recently, multidimensional NMR have been proposed to enhance the resolution. However, multidimensional NMR requires a higher acquisition time.¹⁰ Therefore, a subset of two-dimensional heteronuclear and homonuclear experiments^11,12 are occasionally used for characterization in the field of metabolomics. Efforts to increase the sensitivity of NMR include hardware development. For instance, for NMR instruments operating with a high static magnetic field up to 1.2 GHz, their cryogenically cooled probe heads have been designed to minimize thermal noise.¹³ Experimental part modifications, like l-opt technique,^14,15 selective optimized flip angle short transient (SOFAST) technique,¹⁶ ASAP-HMQC (acceleration by sharing adjacent polarization heteronuclear multiple quantum correlation spectroscopy),¹⁷ BEST techniques (band-selective excitation short-transient),¹⁷ and ALSOFAST-HMQC (alternate implementation of SOFAST HSQC)¹⁸ have also been developed for rapid data acquisition.

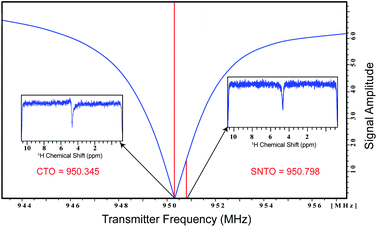
Here we propose and implement a non-invasive, general, and easy-to-use approach to enhance the signal in NMR-based metabolomics. The first modification is the implementation of Spin Noise Tuning Optimum (SNTO), which utilizes the concept of spin noise that was first predicted by Bloch in 1946.¹⁹ Spin noise corresponds to intrinsic non-coherent magnetization that originates from the spins of the sample due to random fluctuation. This phenomenon is an interplay of multiple parameters such as resonance offset, offset from the radiofrequency (RF) circuit's tuning center frequency, circuit resistance, sample temperature and probe temperature ratio, radiation damping, etc.^20–27 Since spin-noise arises from intrinsic magnetization during collection, no RF pulses are applied. The shape of the spin noise power signal shows absorptive and dispersive components from the otherwise flat baseline, which represents the thermal noise level. An absorptive or bump profile represents more than thermal noise, while a dip or absorptive signal represents less than a thermal noise situation. It has been experimentally observed that this line shape has tuning dependence. Usually, the symmetrical dip is found at a considerable offset from the conventional tuning optimum, and this position of less noise is the SNTO, which represents the optimized receiving condition for the signal.²⁷ The SNTO position must be determined for each probe separately as SNTO depends mostly on the particular probe circuit tuning characteristics and the electronic component properties and depends firmly on good shimming. For room temperature probes, the NMR noise signals may appear too weak to be observed. Thus, the solvent signal is usually chosen to determine the SNTO position.

There is practically no sample dependence for the SNTO position (below 40 kHz) for a particular probe.²⁸ For a sample with paramagnetic substances, a broadening of the noise signal is also observed. The sample's ionic strengths can have a detrimental effect on the probe quality factor, probe tuning, matching, and pulse length. As a result, at a high salt concentration (200 mM and above), sensitivity decreases significantly, especially for cryogenically cooled probes.²⁹ For triple channel inverse detection (TCI) and triple resonance direct observation (TXO) probes, above 50–100 mM, the signal height reduces by 25–33%.

Additionally, the pulse length also increases significantly (by 50% or more).²⁹ Previous studies have shown that when using a glucose sample, or even a protein sample, signal enhancement at the spin-noise tuning optimum decreases with increasing salt concentration. For a one-dimensional experiment, using glucose anomer peaks with no salt in the sample, an SNR gain of about 7–22% is observed at SNTO optimization.²⁸ This varies over different experiments, depending on the types and dimensions. However, for the same sample with 200 mM NaCl, there is hardly any effect on the signal-to-noise ratio (SNR) upon moving from conventional tuning optimum (CTO) to SNTO.²² To the best of our knowledge, this detuning effect of SNTO has not been utilized for metabolomics studies so far. However, many metabolomics samples, such as urine containing high salt concentrations, are routinely used for high throughput studies. We wanted a solution where both salty and non-salty samples can have more sensitivity, and to this end, we incorporated a second modification.

Signal enhancement can be achieved both from the instrument setup (SNTO) and NMR sample preparation. Thus, we attempted to achieve signal enhancement by focusing on these two variables and changing to a shaped tube. This shaped tube is constructed in such a way that magnetic susceptibility matches the sample cavity, which is rectangular, and the sample detection zone remains in the axial direction, which provides tolerance to sensitivity loss in the sample space.³⁰ Additionally, the temperature rise due to the RF pulse heating is much lower because of this shape. This effect is most beneficial for samples with high salt concentration because, in such cases, the RF pulses tend to be longer and generate heat. Compared to the regular 5 mm sample volume, the sample content is almost three times less than the detection volume, which leads to a narrow pulse width, which is also beneficial for less concentrated samples. The implementation of both these modifications is straightforward, which is essential for large-scale high-throughput studies that involve multiple samples running in different batches. Since the SNTO position is independent of the samples and mostly specific to probe circuit designs, detecting for each scenario is not necessary. To be more precise, for certain kinds of examples, the SNTO position can be detected once using the involved solvent signal and can be applied uniformly after that. Another significant advantage is that these modifications are cost-effective because the amount of instrument time saved is enormous. Previous methodology advancements can easily be implemented further, and all experiments can benefit from this altered tuning position using the shaped tube. We have demonstrated these modifications on both non-salty real metabolomics samples, such as bovine serum albumin and media, and salty samples such as human urine, on different spectrometers with ¹H RFs of 950 MHz and 800 MHz spectrometers with a 5 mm high-resolution triple resonance cryoprobe, also equipped with an internal z-gradient coil for shimming. For all cases, we observe at least an order of magnitude increase in the SNR per unit volume, which proves the robustness of the approach. Hence, this approach is general, easy, and cost-effective, which will be attractive to the metabolomics community.

Results and discussion

The simultaneous combination of this new instrument setup and sample tube selection allowed us to achieve significant signal enhancement (on average >3 times SNR per unit volume), which corresponds to an order of magnitude decrease in measurement time. We changed the tuning optimum from CTO to SNTO, which was the best position for the excitation of RF pulses. We found the symmetrical dip corresponding to SNTO at 950.79 MHz, which is about 450 kHz away from the CTO (Fig. 1). At the CTO (950.35 MHz), the noise profile had some dispersive component (Fig. 1). In the newly developed cryoprobe (2018 after) manufactured by Bruker, care was taken to lower the gap between CTO and SNTO because SNTO is the best receiving condition for the probe. Hence, in this kind of probe, the SNTO effect will be less than older probes. For example, for a comparatively older 800 MHz Bruker Avance cryoprobe, the gap between the CTO and SNTO was 600 kHz. Although the SNTO position does not differ significantly between different solvents and samples (±40 kHz), SNTO is recommended for salty samples like human urine. Once we moved to a shaped tube, we determined the SNTO once again on the sample. We observed that for the same 800 MHz Bruker Avance cryoprobe, the SNTO position was almost 450 kHz away from CTO in the shaped tube, whereas in a 5 mm tube, the SNTO position was 600 kHz. The possible reason for this change in the SNTO position in the case of highly salty samples is that, upon changing from a 5 mm tube to the shaped tube, the sample volume decreases by more than 3-fold. Furthermore, the relative degradation in the probe circuit's quality factor is much less³⁰ in the shaped tube, which affects the spin noise signal.

Fig. 1 Representation of the wobble curve. The conventional tuning optimum (CTO) and spin noise tuning optimum (SNTO) position are noted. The spin noise profile at CTO and SNTO are presented in the inset.

The presence of high concentrations of salt also abolishes the sensitivity gain at SNTO, as reported in the previous studies.²⁸ Some of the most common physiological biofluid samples contain considerable concentrations of salt or salt substitutes, such as human urine that contains more than 250 mM urea alone, which is routinely analyzed in the field of metabolomics. This decrease of sensitivity is even present for cryogenically cooled probes due to ionic conductivity and dielectric losses at high magnetic field strengths. This has been a long-standing problem that severely limits NMR sensitivity for salty samples; however, recent developments in sample tube design have helped to compensate for these sensitivity losses. The sensitivity loss is directly proportional to RF power dissipation and heat generation. Upon placing a cylindrical tube in a cryogenically cooled probe, the magnitude of RF power dissipation increases with increasing distance from the center of the tube in a perpendicular direction to the B1 field, which results in the highest power dissipation at the regions nearest the edges. This RF relationship thus prompted us to use a cylindrical tube with a smaller diameter or a rectangular tube, which reduces the heating effect significantly. Here, we have chosen a simple rectangular-shaped tube instead of a Shigemi or slot tube because it shows the highest sensitivity and also restricts sensitivity loss for salty samples. Moreover, using a shaped tube also requires less sample volume (1/3 of the conventional 5 mm tube volume). We observed sensitivity gain in most cases with less volume. Considering the volume effect, we found more than a 3-fold increase in the sensitivity per the number of spins (measured as SNR per unit volume), which corresponds to an order of magnitude quicker experimental time for the same number of spins, thus verifying the exceptional benefits for scarce samples with limited availability.

We first recorded the 1D spectra for proton employing excitation sculpting for solvent suppression. Fig. 2 shows two 1D proton NMR spectra of bovine serum (A) and media (B) used for culturing human embryos in in vitro fertilization (IVF),³¹ respectively. We performed a similar measurement for human urine. The data were processed identically, and we chose five distinct peaks as representative cases for the calculation of the SNR for the two different conditions: the first condition being the SNR at CTO in a conventional 5 mm tube and the second being at the SNTO position in a shaped tube. The results are given in Table S3a–c† for bovine serum, media, and urine, respectively.

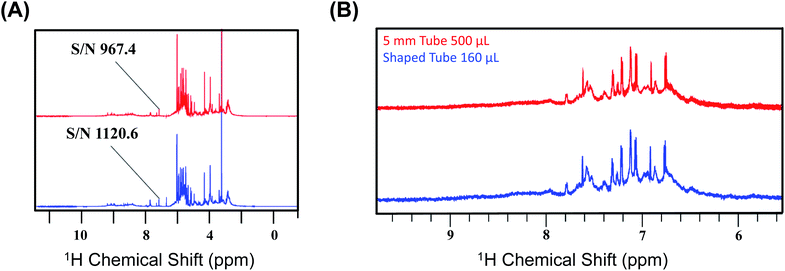Fig. 2 (A) Representation of the 1D NMR proton spectra of bovine serum albumin at CTO with a 5 mm tube (red) and at SNTO with a shaped tube (blue). The peak at 5.25 ppm is highlighted as the signal to noise ratio (SNR), calculated for both the cases using this peak. The noise region was kept at 11–12 ppm during the calculation of SNR. (B) Representation of the two 1D NMR proton spectra of media used for culturing human embryos in in vitro fertilization (IVF) recorded on 800 MHz spectrometers (Bruker Avance) with a cryoprobe. The top profile represents the spectra which was recorded at CTO with a 5 mm tube (red), and the bottom spectra were recorded at SNTO with a shaped tube (blue). The peaks that are considered for the SNR calculation are given in Table S3b.†

We calculated the average SNR gain for the altered tuning position in the shaped tube compared to the conventional 5 mm tube at CTO. The results presented in Table S3a–c† and plotted in Fig. 3A show that, in all cases, there is a significant gain in sensitivity per unit volume. The sensitivity enhancement ranges from 3.26 to 3.78 times more SNR per unit volume. An increase of 3.16 represents a decrease in measurement time by order of magnitude for the same number of spins. Thus, we achieved enough gain to justify this combination for setting up the experiments.

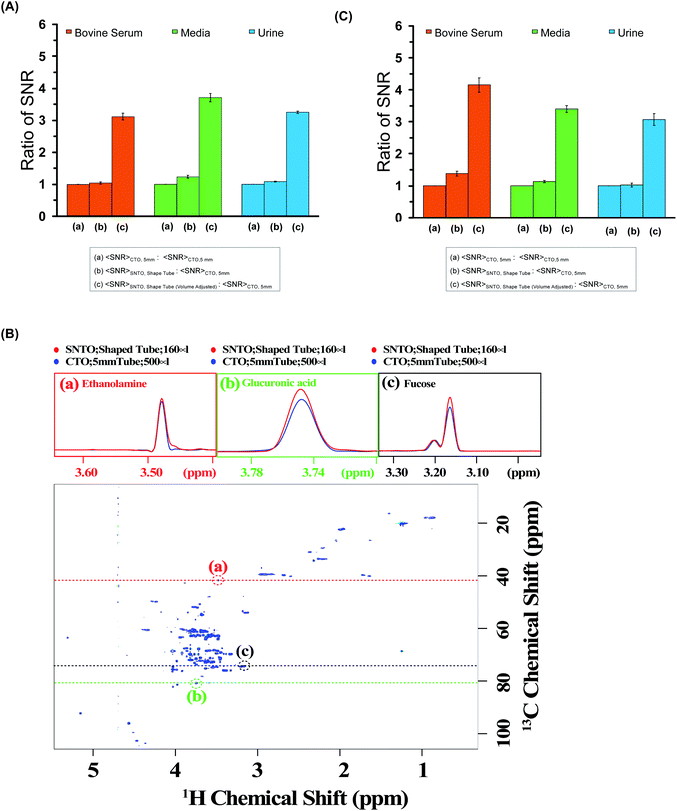Fig. 3 (A) The ratios of average SNR gain in different situations for bovine serum (red), media (green), and urine (blue) for the 1D experiment. The average SNR is calculated for five distinct peaks for each case, and all the values are reported in Table S3a–c† for bovine serum, media, and urine, respectively. There are three bars for each sample. The first one represents average SNR (CTO, 5 mm)/average SNR (CTO, 5 mm); the second one represents average SNR (SNTO, shaped tube)/average SNR (CTO, 5 mm); and the last one represents average SNR (SNTO, shaped tube) with volume adjustment/average SNR (CTO, 5 mm). The volume adjustment is performed by multiplying by three the number of spins in the shaped tube, which is 1/3 of the number of spins present in a 5 mm tube. Error bars represent standard error of the mean (SEM). (B) represents the 2D [¹H,¹³C] HSQC (Heteronuclear Single Quantum Correlation) spectra of bovine serum albumin at SNTO with a shaped tube. The same data was acquired with a 5 mm tube at CTO also to compare sensitivity. Along the peaks highlighted in the red, green, and black circles, a trace along the proton axis is taken, represented as the black dashed line. The overlay of the traces is shown in the above panels. The red represents the trace for SNTO for the shaped tube case, while the blue represents the case for a 5 mm tube at the CTO situation. (C) The ratios of average SNR gain in different situations for bovine serum (red), and urine (blue) Media (green) is presented for the 2D [¹H,¹³C] HSQC experiment. The average SNR is calculated for distinct peaks for each case, and all the values are reported in Tables S4–S6† for bovine serum, urine, and media, respectively. There are three bars for each sample. The first one represents average SNR (CTO, 5 mm)/average SNR (CTO, 5 mm); the second one represents average SNR (SNTO, shape tube)/average SNR (CTO, 5 mm); and the last one represents average SNR (SNTO, shape tube) with volume adjustment/average SNR (CTO, 5 mm). Error bars represent standard error of the mean (SEM).

2D hetero-nuclear experiments can take considerably longer than 1D proton NMR experiments, and thus, ways to reduce the experimental time are sought. We also examined the effect on 2D heteronuclear [¹H,¹³C] HSQC, which has a significant application in protein chemistry and small molecule chemistry, and metabolomics.^32–35 2D [¹H,¹³C] HSQC has the unique advantage of serving as a molecular fingerprint because spectral dispersion in carbon is greater than the proton dimension, which can resolve the peak overlap in the indirect dimension. The main disadvantage of heteronuclear experiments is that the measurement time required for this kind of experiment is typically longer due to the low natural abundance of ¹³C. In this work, we recorded the conventional 2D [¹H,¹³C] HSQC spectra of all three samples while implementing the same experimental setup modifications as those used in the 1D experiments. We also maintain (I) the CTO in a conventional 5 mm tube and (II) the SNTO position in a shaped tube. Fig. 3B shows the HSQC spectra of bovine serum at the SNTO position in the shaped tube. To compare sensitivity, we also acquired the same data with a 5 mm tube at CTO. The bovine serum data was recorded using a 950 MHz Bruker Avance NEO operating with a TCI inverse-detected cryoprobe following conventional linear sampling. The same experiment was carried out for the media sample and urine sample at 800 MHz spectrometers. Fig. S1 and S2† represent the HSQC spectra of the media sample and urine, respectively. Here we have additionally implemented non-uniform sampling and recorded 50% points to decrease the experimental time. Because we are proposing a new way of setting up the experiment, we can, in principle, combine all the previous modifications from the pulse programming side with the newly proposed methods. To demonstrate, we used non-uniform sampling because NUS has been implemented with heteronuclear multidimensional NMR and has been explored in the field of metabolomics.^36,37

For a visual representation, we chose three isolated peaks (highlighted by the red, green, and black circles in Fig. 3B) and compared the trace along the proton axis for both situations. Fig. 3B clearly shows that the modified strategy with SNTO with the shaped tube (highlighted in red) has better SNR than the 5 mm tube at the CTO situation (highlighted in blue). Subsequently, for each sample, we processed the data acquired in both conditions identically and calculated SNR for the observed peaks in the 2D [¹H,¹³C] HSQC spectra for each situation. The isolated peak positions that were considered for calculation of the SNR are detailed in Tables S3–S5† for bovine serum, urine, and media, respectively. In all cases, we considered the full dynamic range of peaks of different intensities and reported the average sensitivity. There are some variations in the increase because of the dynamic range and relaxation effect. Fig. 3C shows the average gain in the SNTO position in the shaped tube over the conventional setting of the CTO position in the 5 mm tube, considering the volume effect. As shown in Fig. 3C and Tables S4–S6,† for the multidimensional heteronuclear experiments, in all cases, we also observe a significant gain in sensitivity per unit volume, which is between 3.33- to 3.63-fold gain in sensitivity. This implies a decrease in measurement time by more than an order of magnitude for the same number of spins, which becomes even more profound for hetero-nuclear multidimensional experiments. Enhanced sensitivity can be easily used for higher resolution because more data points can be recorded in the indirect dimension. This is important because moving to a larger magnetic field demands that a higher number of points be recorded to implement the improvement in resolution in the indirect dimension. This can now be achieved with fewer scans to ensure the same measurement time. This new way of setting up the experiment is extremely general and does not make any changes to the pulse program front. These modifications ensure the best-receiving conditions for the signal with the least possible sample heating. Hence, in principle, this method can serve as the new benchmark, and all the previous modifications from the pulse programming side can easily be combined.³⁸ We showed that a combination of NUS with SOFAST could reduce the acquisition time without compromising the sensitivity.³² All these advanced methods can be easily implemented. Continued studies to realize the full potential of this new setting are underway to expand heteronuclear multidimensional NMR in the realm of high-throughput studies.

Experimental

Preparation of samples

We have chosen three different examples for demonstration. The first sample is media, which contains a mixture of amino acids similar to that of the medium used for culturing human embryos in in vitro fertilization (IVF) (Table S1†). Initially, the individual components of the mixture were prepared as a 10 mM stock solution for each component in 100% ²H₂O. From this stock, each metabolite was mixed accordingly. The volume used for the 5 mm tube was 500 μL and 160 μL for the shaped tube. We also used fetal bovine serum (FBS) that was purchased from corning (product no. 35-010-CV). Urine samples were taken in compliance with the ethical guidelines of the Indian Institute of Science (IISc) from a healthy donor. 1% sodium azide was added to both the serum and urine samples, and 10% D₂O was used for locking.

NMR experiments

All NMR data were acquired at 298 K using Bruker Avance NEO NMR spectrometers. We carried out the tests on two different spectrometers operating at a resonance frequency of 800 MHz and 950 MHz. Both spectrometers were equipped with TCI cryogenic probes (the first two channels were cooled for the 950 MHz Triple channel H/C/N cryoprobe). The spin noise spectra were recorded on a standard sample of uniformly 15N,13C labeled ubiquitin in phosphate buffer (pH 6.5). The noise spectra of water were also collected. All noise spectra were recorded at 298 K without RF excitation pulses and relaxation delays. Only 30 were kept and stored due to hardwire limitations. Noise data were collected in a pseudo-two-dimensional mode where each noise data block was stored separately. The spectral width of 12 ppm and an acquisition time of 90 ms per data block was used. 2048 data blocks were collected to achieve good sensitivity. The data processing was carried out using the Bruker software Top Spin 4.7. First Fourier transformation along the direct dimension was performed in the magnitude mode using the command xf2. Subsequently, individual noise data blocks were added to produce a single spin noise spectrum (command f2sum). Because the line-shape of the spin noise spectrum depends on the type of probe tuning that is adopted, the same sample was kept for determining the SNTO individually for each probe in 800 and 950 MHz. For the 800 MHz NMR spectrometer, the SNTO position was 583 kHz away, whereas, for 950 MHz, the SNTO position was 453 kHz from the conventional tuning optimum (CTO). Fig. 1 shows the line shape at the SNTO at 950 MHz. This symmetrical pure absorptive dip signature in spin noise spectra represents less than a thermal noise situation. In contrast, the spin noise spectrum at CTO represents a mixed absorptive and dispersive component. Carbon was decoupled with the GARP decoupling sequence with the 11 W power level. One-dimensional proton NMR spectra were recorded with water suppression using exciting sculpting and 2D heteronuclear 2D [¹H,¹³C] HSQC at both CTO and SNTO for each sample in each tube to compare the sensitivity gain. Non-uniform sampling in 800 MHz for HSQC was also implemented. The acquisition parameter for the experiments in each sample is provided in Table S2 of ESI.†

Conclusion

The proposed approach based on setting the NMR experiment and selecting the proper NMR tube can decrease the measurement time of salty samples by more than an order of magnitude for the same number of spins. Additionally, this approach is straightforward to implement on every instrument without modifications of the pulse programs. Our modifications focus on the receiving condition for the probe with the least possible sample heating, which promises robustness and excellent reproducibility.

Conflicts of interest

The authors declare that they have no conflict of interest. Informed consent was obtained from all subjects prior to sample collection. All experiments were performed in accordance with the Guidelines provided by Institutional Ethics Committee, and appropriate approval was obtained before initiation of the study at the Indian Institute of Science (IISc). The experiments done at King Abdullah University of Science and Technology (KAUST) were also performed according to the institutional ethics committee's guidelines and with proper approval.

Acknowledgements

The authors would like to thank the Imaging and Characterization Core Lab at the King Abdullah University of Science and Technology (KAUST) for access to the NMR facilities. KC acknowledges the NMR facilities of NMR Research Centre, Indian Institute of Science, and DST, India. This publication is based on work supported by KAUST Smart Health Initiative grants (SHI REI 4447) (LJ and MJ) and through baseline-funds (LJ and MJ).

Notes and references

1. F. Kork, J. Holthues, R. Hellweg, V. Jankowski, M. Tepel, R. Ohring, I. Heuser, J. Bierbrauer, O. Peters, P. Schlattmann, W. Zidek and J. Jankowski, Curr. Alzheimer Res., 2009, 6, 519–524.
2. J. T. Brindle, H. Antti, E. Holmes, G. Tranter, J. K. Nicholson, H. W. Bethell, S. Clarke, P. M. Schofield, E. McKilligin, D. E. Mosedale and D. J. Grainger, Nat. Med., 2002, 8, 1439–1444.
3. A. H. Emwas, E. Saccenti, X. Gao, R. T. McKay, V. Dos Santos, R. Roy and D. S. Wishart, Metabolomics, 2018, 14, 31.
4. A.-H. M. Emwas, R. M. Salek, J. L. Griffin and J. Merzaban, Metabolomics, 2013, 9, 1048–1072.
5. J. P. Gu, C. H. Huang, X. M. Hu, J. M. Xia, W. Shao and D. H. Lin, Cancer Sci., 2020, 111, 3195–3209.
6. Y. López-Hernández, J. J. Oropeza-Valdez, J. O. Blanco-Sandate, A. S. Herrera-Van Oostdam, J. Zheng, A. Chi Guo, V. Lima-Rogel, R. Rajabzadeh, M. Salgado-Bustamante, J. Adrian-Lopez, C. G. Castillo, E. Robles Arguelles, J. Monárrez-Espino, R. Mandal and D. S. Wishart, Metabolites, 2020, 10.
7. A. A. Zaki, M. Hagar, R. B. Alnoman, M. Jaremko, A.-H. Emwas and H. A. Ahmed, Crystals, 2020, 10, 1044.
8. A. H. Emwas, R. Roy, R. T. McKay, D. Ryan, L. Brennan, L. Tenori, C. Luchinat, X. Gao, A. C. Zeri, G. A. Gowda, D. Raftery, C. Steinbeck, R. M. Salek and D. S. Wishart, J. Proteome Res., 2016, 15, 360–373.
9. A. M. Weljie, J. Newton, P. Mercier, E. Carlson and C. M. Slupsky, Anal. Chem., 2006, 78, 4430–4442.
10. A. H. Emwas, C. Luchinat, P. Turano, L. Tenori, R. Roy, R. M. Salek, D. Ryan, J. S. Merzaban, R. Kaddurah-Daouk, A. C. Zeri, G. A. Nagana Gowda, D. Raftery, Y. Wang, L. Brennan and D. S. Wishart, Metabolomics, 2015, 11, 872–894.
11. K. Bingol, L. Bruschweiler-Li, D. W. Li and R. Bruschweiler, Anal. Chem., 2014, 86, 5494–5501.
12. S. Ghosh, A. Sengupta and K. Chandra, Amino Acids, 2015, 47, 2229–2236.
13. H. Kovacs, D. Moskau and M. Spraul, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 46, 131–155.
14. H. S. Atreya and T. Szyperski, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9642–9647.
15. K. Pervushin, B. Vogeli and A. Eletsky, J. Am. Chem. Soc., 2002, 124, 12898–12902.
16. P. Schanda, E. Kupce and B. Brutscher, J. Biomol. NMR, 2005, 33, 199–211.
17. P. Schanda, H. Van Melckebeke and B. Brutscher, J. Am. Chem. Soc., 2006, 128, 9042–9043.
18. D. Schulze-Stinninghausen, J. Becker, M. R. M. Koos and B. Luy, J. Magn. Reson., 2017, 281, 151–161.
19. F. Bloch, Phys. Rev., 1946, 70, 460–474.
20. D. Adilakshmi, K. Chandra and K. V. Ramanathan, ChemPhysChem, 2019, 20, 456–462.
21. K. Chandra, J. Indian Inst. Sci., 2014, 94, 517–526.
22. K. Chandra, J. Schlagnitweit, C. Wohlschlager, A. Jerschow and N. Muller, J. Phys. Chem. Lett., 2013, 4, 3853–3856.
23. C. L. Degen, M. Poggio, H. J. Mamin, C. T. Rettner and D. Rugar, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1313–1317.
24. S. J. Ginthor, K. Chandra, M. Bechmann, V. V. Rodin and N. Muller, ChemPhysChem, 2018, 19, 907–912.
25. M. A. McCoy and R. R. Ernst, Chem. Phys. Lett., 1989, 159, 587–593.
26. N. Muller and A. Jerschow, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6790–6792.
27. M. Nausner, J. Schlagnitweit, V. Smrecki, X. Yang, A. Jerschow and N. Muller, J. Magn. Reson., 2009, 198, 73–79.
28. M. Nausner, M. Goger, E. Bendet-Taicher, J. Schlagnitweit, A. Jerschow and N. Muller, J. Biomol. NMR, 2010, 48, 157–167.
29. M. W. Voehler, G. Collier, J. K. Young, M. P. Stone and M. W. Germann, J. Magn. Reson., 2006, 183, 102–109.
30. M. Takeda, K. Hallenga, M. Shigezane, M. Waelchli, F. Löhr, J. L. Markley and M. Kainosho, J. Magn. Reson., 2011, 209, 167–173.
31. F. D'Souza, S. M. Pudakalakatti, S. Uppangala, S. Honguntikar, S. R. Salian, G. Kalthur, R. Pasricha, D. Appajigowda, H. S. Atreya and S. K. Adiga, Sci. Rep., 2016, 6, 37291.
32. S. Ghosh, A. Sengupta and K. Chandra, Anal. Bioanal. Chem., 2017, 409, 6731–6738.
33. T. Man, M. B. Tessem, T. F. Bathen, H. Bertilsson, A. Angelsen, M. Hedenstrm and T. Andreassen, BMC Bioinf., 2014, 15.
34. P. K. Mandal and A. Majumdar, Concepts Magn. Reson., Part A, 2004, 20, 1–23.
35. A.-H. Emwas, M. Alghrably, S. Al-Harthi, B. Gabriel Poulson, K. Szczepski, K. Chandra and M. Jaremko, Nucl. Magn. Reson., 2019, 1–24.
36. A. L. Guennec, P. Giraudeau and S. Caldarelli, Anal. Chem., 2014, 86, 5946–5954.
37. A. H. Emwas, R. Roy, R. T. McKay, L. Tenori, E. Saccenti, G. A. N. Gowda, D. Raftery, F. Alahmari, L. Jaremko, M. Jaremko and D. S. Wishart, Metabolites, 2019, 9, 1–24.
38. A. H. Emwas, K. Szczepski, B. G. Poulson, K. Chandra, R. T. McKay, M. Dhahri, F. Alahmari, L. Jaremko, J. I. Lachowicz and M. Jaremko, Molecules, 2020, 25, 4597.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra01103k

---