Open Access Article
Open Access ArticleIs there a photochemical Hammond postulate?†‡
Christian G.
Bochet
 * and
Freya M.
Harvey
* and
Freya M.
Harvey

Department of Chemistry, University of Fribourg, Chemin du Musée 9, CH-1700 Fribourg, Switzerland. E-mail: christian.bochet@unifr.ch
First published on 11th November 2020
Abstract
The Hammond postulate is a useful tool for approximating the energy and the structure of transition states. It was designed for use in ground state reactions, and has been applied successfully on many occasions. On the other hand, its usefulness for photochemical reactions is more questionable, as different energy surfaces are involved. So far, no systematic studies on the validity of the Hammond postulate for photochemical reactions are available. The present work aims at filling this gap by providing a simple, unbiased series of test reactions based on the stereospecificity of isotopically labelled substrates.
Introduction
The molecular world, unlike the macroscopic world, can only be accurately described by quantum mechanics, and is dominated by quantum mechanical effects. The natural properties and behaviour of molecules are difficult to imagine, and they are impossible to predict without resorting to approximations. One such approximation is the Born–Oppenheimer approximation (BOA).1 The BOA states that the movement of the nuclei in a molecule can be treated separately from the movement of the electrons, because the electrons are much lighter than the nuclei. When the nuclei move, the electrons can adapt their positions to the new molecular geometry immediately. The BOA has a fundamental consequence: it allows the concept of a potential energy surface and separate electronic states to exist.2 Many aspects of physical chemistry rely on the concept of an energy surface, including the Hammond postulate (HP) and the Kinetic Isotope Effect (KIE). The BOA is at the heart of how chemists imagine and understand chemical reactivity. However, when movement of the nuclei is significant, vibrational and electronic coupling (vibronic coupling) is no longer negligible and the BOA breaks down.3 This breakdown of the BOA is especially prevalent in photochemical reactions, namely, at excited state transition states (ESTS) and at conical intersections (CI).4 For ESTSs at higher energy levels, states are denser and mixing is much more likely. If another energy level is nearby, nonadiabatic transition can occur.5 At a CI, the system is “unsure” about which energy surface governs its motion. As it passes from one surface to another, the forces acting on the nuclei change suddenly, and cannot be described using the BOA.6 These instances of breakdown of the BOA mean that there are currently no guiding principles like the HP in photochemistry to help predict the location and geometry of transition states.While best known as the Hammond postulate, Jack Leffler proposed a similar idea two years before Hammond's paper was published.7 To give credit to both scientists, we will refer to the Hammond–Leffler postulate (HLP) throughout this text.
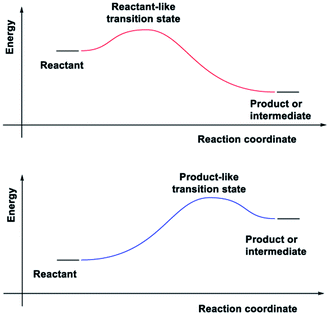
In adiabatic ground-state reactions, the HLP is the tool of choice for estimating the structure of transition states (TS).8 The postulate states that: if the TS is close in energy to the reactant along a given reaction coordinate, it will be similar in structure to the reactant; and likewise, if the TS is close in energy to the product, it will be similar in structure to the product (Fig. 1).
Due to the HLP's reliance on the concept of an energy surface and the Born–Oppenheimer approximation, its applicability for ESTSs or CIs has not yet been studied. The HLP's roots in classical transition state theory, which is strictly adiabatic,9 could also explain the reluctance to apply it to photochemical reactions.
Kinetic Isotope Effects (KIE) are another vital tool in physical chemistry for understanding reaction mechanisms.10 Like the HLP, the KIE relies on the concept of a potential energy surface and the Born–Oppenheimer approximation. Additionally, it shares a link with the Hammond postulate: when a transition state is early or late, the hydrogen or deuterium atom is still partially bound to the starting material or product (the transition state is said to be asymmetrical).11 In these cases, the difference between the ZPE of the starting material or product and the transition state is not very large, which gives a small KIE (Fig. 2(a and b)). For a transition state where the H or D atom is equally shared between the reactant and the product (a symmetrical transition state), the KIE is at its largest (Fig. 2(c)).12 Therefore, it is reasonable to suggest that the KIE can, in some cases, provide complementary information to the HLP for estimating the geometry of a transition state. KIEs are often measured for photochemical reactions; the abundance of examples in the literature leaves no question as to the efficacy of KIEs for understanding excited-state chemistry.
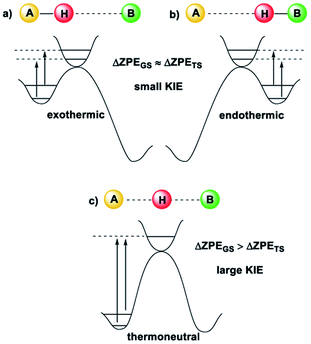 | ||
| Fig. 2 The size of the KIE can be an indicator of the position of the transition state12 (image reproduced from ref. 11). (a) For an early TS, the difference in ZPE between the TS and A is small, and a small KIE is obtained. (b) For a late TS, the difference in ZPE between the TS and B is small, and a small KIE is obtained. (c) For a symmetrical TS, where the H or D atom is fully dissociated, the KIE is largest. | ||
In previous experimental work on the photolysis of o-nitrobenzyl derivatives,13 our group observed that the Bell–Evans–Polanyi principle14 was followed, and the position of the CI also varied with the substituents. We became interested in the validity of the HLP for photochemical reactions, and whether it could be general, for ESTSs or CIs or both.
Results and discussion
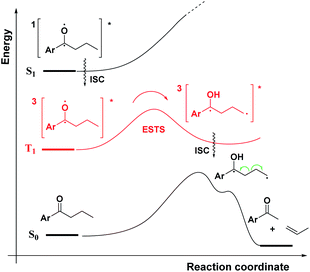
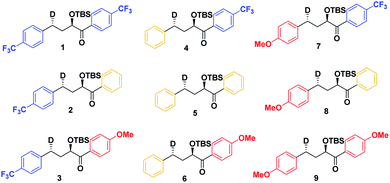
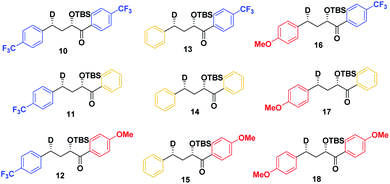
As a first step in studying the applicability of the HLP to photochemical reactions, we decided to investigate the ESTS of a Norrish–Yang Type II (NYII) reaction of an aryl alkyl ketone (Fig. 3). Upon absorption of a photon, the molecule reaches the S1 excited state, then undergoes efficient intersystem crossing (ISC) onto the triplet energy surface.15 At this stage, γ-hydrogen abstraction occurs to give a triplet 1,4-biradical via a six-membered-ring ESTS. After the γ-hydrogen abstraction, ISC onto S0 takes place to give the products. In this reaction, the ESTS is a true transition state as defined by transition state theory:16 it is a saddle point which separates reactants from products, it is a bottle-neck that can impact the reaction rate, it is linked to a chemical change, and it leads to a single product.To study the triplet ESTS, we defined a series of deuterated substrates 1–9 able to undergo a NYII reaction (Fig. 4).
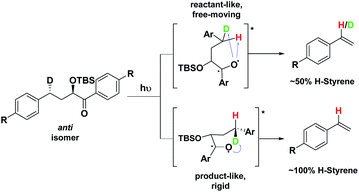
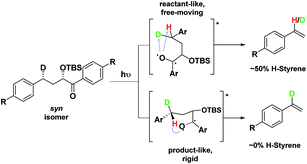
Depending on the geometry at the transition state, abstraction of either H or D will occur to give styrene containing a specific percentage of hydrogen and deuterium. The bulky aryl groups and the OTBS group anti to the deuterium atom will be positioned equatorially in a putative chair-like ESTS, which forces a single conformation in the six-membered ring at the H/D abstraction step. We imagined that the reactant before the abstraction would be more free-moving, and the product 1,4-biradical would be rigid and structured: before the reaction, the 1,2-biradical would have relaxed into a spectroscopic minimum, likely in a low-energy, open-chain linear conformation. After the reaction, the geometry of the 1,4-biradical is such that it can cyclize to the cyclobutanol or fragment to the styrene. Both of these products are formed if the orbitals are aligned favourably, as is the case in a rigid, folded geometry.17 This brings us to the Hammond postulate for a reactant-like or product-like ESTS (Scheme 1):
• If the ESTS is early, reactant-like and free-moving (more of an open-chain structure), both H and D will be available for abstraction. The ratio of H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene in the product mixture will be closer to 50
D-styrene in the product mixture will be closer to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 in such a case.
50 in such a case.
• If the ESTS is late and more product-like, it will be structured and rigid. There will be a clear preference for the abstraction of D, to give close to 100% H-styrene.
The quantity of deuterated styrene in the mixture should be measurable by integrating the α-styrene signal in the 1H-NMR spectrum and comparing it to a β-styrene signal. Thus, the integral of the α-styrene proton will give us information about the geometry of the molecule at the ESTS. For these anti substrates 1–9, we expect to see between 50% (reactant-like) and 100% (product-like) H-styrene, depending on the geometry at the transition state.
Given that an isotope is involved, we must also consider the possibility of an isotope effect. A strong isotope effect would mean that the deuterium atom is difficult to abstract, even if it is positioned favourably for the reaction. This would alter the percentage of H-styrene we expect to observe. For example: we have stated above that for a product-like ESTS, we expect the deuterium to be abstracted preferentially, to obtain close to 100% H-styrene. However, if the isotope effect is very strong, deuterium abstraction will be difficult, and some H abstraction may occur to give a ratio closer to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H
50 H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene. It would be hard to tell this result apart from the case of a reactant-like ESTS with a small isotope effect, which should also give closer to 50
D-styrene. It would be hard to tell this result apart from the case of a reactant-like ESTS with a small isotope effect, which should also give closer to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H
50 H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene (as mentioned above).
D-styrene (as mentioned above).
Therefore, we decided to also study the NY-II reaction of the syn diastereoisomers 10–18 (Fig. 5). This will give us a different set of results and allow us to separate the isotope effect from the geometry of the ESTS. For the syn diastereoisomers, we expect to see between 0–50% of H-styrene if the KIE is weak (Scheme 2). By comparing the results of both diastereoisomers, we should be able to tell which scenario is operating in the excited state.
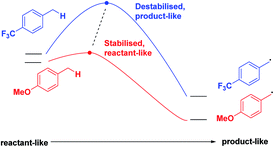
Finally, we expect that varying the electron density on the aromatic rings will shift the ESTS along the reaction coordinate and alter the percentage of H-styrene in the product mixture. We chose p-CF3 as an electron-withdrawing group, and p-OMe as an electron-donating group. p-CF3 destabilizes the radical (this is because benzylic C–H bonds are better donors than the radical centre, so the product is less stabilized by π → σ* C–F hyperconjugation than the reactant), and will give a later ESTS. p-OMe stabilizes the radical, and gives an earlier ESTS (Fig. 6).18 If the HLP is valid in the excited state, we should see a trend which follows these electronic effects.
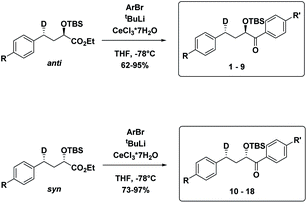
The substrates 1–18 were synthesized according to Scheme 3. The starting esters have been prepared previously.19 Aryl cerium reagents allowed for successful addition of the aryl group to the ester without epimerization of the α-carbon carrying the OTBS group, and the substrates were obtained in good yields.
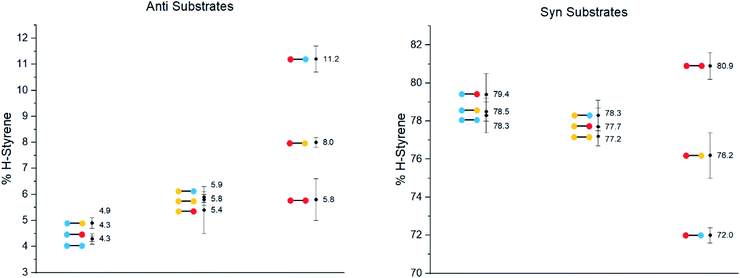
The substrates were photolyzed in CD3CN at λ = 340 nm and T = 25 °C. 1H-NMR of the crude reaction mixtures was measured. The styrenes were then isolated by column chromatography, because side-products which formed during the reaction sometimes covered the 1H-NMR signal of the α-styrene proton. The chromatography should not significantly alter the H/D ratio. The isolation of pure styrene was complicated by its rapid polymerization, but so long as the styrene was never concentrated to dryness, polymerization was minimal (see ESI‡ for details). The percentages of H-styrene were measured by integration of the α proton of the purified styrene. Three to six separate reactions were done for each substrate, so that at least three styrene 1H-NMR spectra from three different reactions could be obtained for integration. The results are summarized in Fig. 7. The substrates were colour-coded for clarity (red = electron-rich, yellow = electron-neutral, and blue = electron-poor).
The following observations can be made from these results:
(1) The kinetic isotope effect (KIE) is small, because the anti and syn values are almost “mirror images” of one another. Substituting a hydrogen atom for a deuterium atom does not change the reaction outcome significantly.
(2) The styrene percentage is the opposite to what was expected. The anti isomers were predicted to give high percentages of H-styrene (50–100%), and the syn isomers were predicted to give low percentages (0–50%).
(3) The percentages of H-styrene are close to 0% for the anti substrate and close to 100% for the syn substrate: there is a clear preference for abstraction of H for the anti substrate, or D for the syn substrate. This means that the transition state is quite structured and not free-moving. If the transition state were free-moving, the result would be closer to 50%.
(4) There is a clear trend for both anti and syn substrates: with growing electron density at the γ-position where H or D abstraction takes place, the percentage of H-styrene moves towards 50%. In other words, the ESTS becomes more free-moving with growing electron density, and there is less preference for either H or D abstraction. However, the percentage remains close to 100% or 0% in all cases, suggesting an overall rigid transition state. The electron density on the ketone side of the molecule has a smaller influence on the resulting styrene percentage.
The second observation—that the percentage is the opposite to what was expected—indicates that our predicted chair-like transition state was incorrect (in a previous publication, we have proven that the anti and syn configurations of the substrates are correctly assigned).19 We found two likely explanations as to why the structure may be different in the ESTS.
Our first hypothesis was that the aryl groups, instead of being positioned equatorially, are bound together axially by a π-stacking interaction. This way, for the anti isomer, H is abstracted rather than D, and for the syn isomer, D is abstracted rather than H. π-stacking interactions are a well-documented occurrence in photochemistry; they are particularly useful for bringing alkenes into close proximity for [2 + 2] photocycloadditions.20 To test this hypothesis, we performed the reaction in toluene-d8 instead of CD3CN. We theorized that if π-stacking is important at the ESTS, the toluene molecules may π-stack with the aromatic rings on the substrate to some degree, and alter the H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene ratio in the product mixture. However, we obtained exactly the same styrene percentages in toluene-d8 and CD3CN.
D-styrene ratio in the product mixture. However, we obtained exactly the same styrene percentages in toluene-d8 and CD3CN.
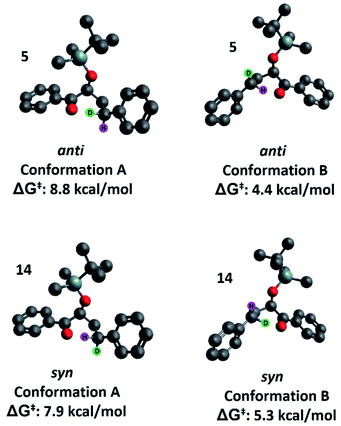
Our second hypothesis was that a homoanomeric effect21 is present at the ESTS. The homoanomeric effect, like the anomeric effect seen in sugars,22 results from a stabilizing interaction between the lone pair of the ring oxygen and the β-C–O bond, mediated by the radical itself. This effect has been observed in pyranosyl radicals (also known as a quasi-homoanomeric effect), where it forces a boat conformation rather than a chair conformation in a hexacyclic radical.23 To verify this hypothesis, we turned to computational methods using density functional theory (DFT) as implemented in Gaussian 09. NYII reactions have been studied before with DFT by Phillips and co-workers; we used the same methodology to study the present NYII reaction.24 At the B3LYP/6-31G* level of theory, we calculated both possible triplet ESTS conformations, A and B (Fig. 8).
Conformation A corresponds to the transition state with the OTBS group positioned equatorially, as we had initially predicted. This was calculated for both diastereoisomers 5 and 14. For 5, conformation A corresponds to the rigid ESTS scenario shown in Scheme 1 and leads to D abstraction (which does not match the experimentally observed result). For 14, conformation A corresponds to the rigid ESTS scenario shown in Scheme 2 and leads to H abstraction (which does not match the experimentally observed result).
Conformation B corresponds to the transition state with the OTBS group positioned axially due to a homoanomeric effect in the transition state. If this is the case, it could explain the experimentally observed percentages of H-styrene. Conformation B was calculated for both diastereoisomers 5 and 14 (it is important to note here that conformation A and B are not competing reaction outcomes; rather, they are two different scenarios). For both 5 and 14, conformation B—which results in the experimentally observed styrene ratios—has a lower activation energy ΔG‡ than conformation A (Fig. 8). This indicates that conformation B is the most likely transition state structure. In the resulting calculated structures, the chair geometry is not present; instead, the structure is boat-like, and the OTBS group is positioned to minimize steric hindrance with the aromatic rings. The aromatic rings are oriented perpendicular to the benzylic radical SOMO, presumably to stabilize the radical by overlapping of the π orbitals. Due to the orientation of the rings and the homoanomeric effect which forces a boat conformation, conformation B is the least hindered compared to conformation A. This explains the experimentally observed H-styrene percentages. The reaction with the corrected transition state structure is depicted in Scheme 4: for anti substrates 1–9, a free-moving transition state gives close to 50% H-styrene, and a structured transition state gives close to 0% H-styrene. For syn substrates 10–18, a free-moving transition state gives close to 50% H-styrene, and a structured transition state gives close to 100% H-styrene.
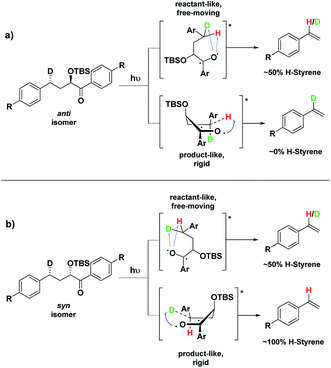 | ||
| Scheme 4 Boat-like ESTS (conformation B): (a) photolysis of the anti isomer gives between 0–50% H-styrene. (b) Photolysis of the syn isomer gives between 50–100% H-styrene. | ||
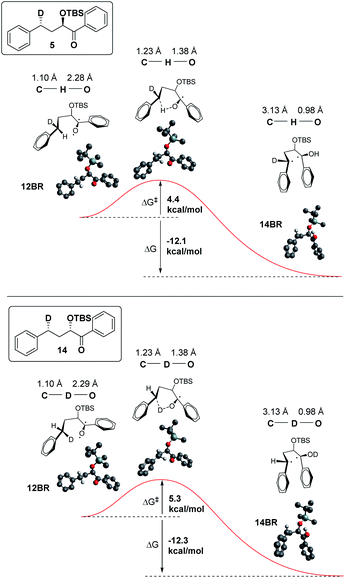
In addition, we have calculated the energies of the starting triplet 1,2-biradical (12BR) and the product 1,4 biradical (14BR), which show an exothermic reaction with a TS close in energy to the reactant (Fig. 9).
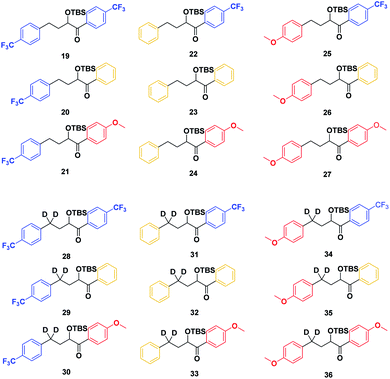
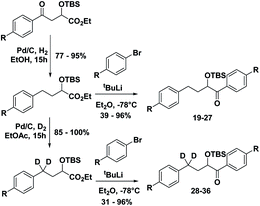
With the ESTS structure clarified, we moved on to the kinetic isotope effect. To measure the KIE, we synthesized a series of fully deuterated and non-deuterated substrates, 19–36 (Fig. 10).
Starting from known benzylic ketones,19 the ketone could be hydrogenolyzed over Pd/C, and the benzylic position was fully deuterated using D2 gas over Pd/C (Scheme 5). Then, addition of aryl lithium onto the ester gave substrates 19–36.
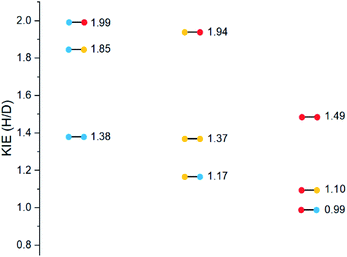
Substrates 19–36 were photolyzed for 5 minutes in CD3CN with cyclohexane as a standard, and 1H-NMR was measured to determine the quantity of styrene which had formed. Small KIEs were obtained, with kH/kD ranging from 1 (no effect) to 2 (Fig. 11).
A similar trend to substrates 1–18 is visible for the KIEs of substrates 19–36. With growing electron density on the left-hand side of the molecule, the radical is stabilized, and the ESTS becomes more reactant-like and free-moving. This gives us a more asymmetric transition state structure, which experiences less of a kinetic isotope effect.
Overall, we can determine that both the reactant 1,2-biradical and the product 1,4-biradical on the triplet energy surface are quite rigid, but as expected, the reactant 1,2-biradical is a little more free-moving. The transition state is early and reactant-like in all cases. With growing electron density at the γ-position where H or D abstraction takes place, the radical is stabilized, ΔG‡ is lowered, and the ESTS is earlier on the reaction coordinate. This more free-moving, earlier ESTS gives a ratio of H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene closer to 50
D-styrene closer to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. These results are in accord with the KIE measurements: the KIE is small in all cases, indicating a rigid, asymmetric transition state. With growing electron density at the γ-position, the KIE shrinks. This is because the ESTS is even earlier along the reaction coordinate, and it is even more asymmetric, giving an even smaller KIE.
50. These results are in accord with the KIE measurements: the KIE is small in all cases, indicating a rigid, asymmetric transition state. With growing electron density at the γ-position, the KIE shrinks. This is because the ESTS is even earlier along the reaction coordinate, and it is even more asymmetric, giving an even smaller KIE.
Conclusion
To probe whether the Hammond postulate could be extended to the excited state, we have synthesized a series of deuterated substrates, 1–18, which can undergo a NY-II reaction upon exposure to UV light. The first step of the reaction is H- or D-abstraction at the γ-position on the triplet energy surface. The deuterium atom at the benzylic position is anti or syn to a bulky OTBS group, which forces a single conformation at the ESTS. Styrene is produced during the reaction, and its level of deuteration is indicative of the geometry at the ESTS on the triplet energy surface. We observed a trend towards a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio of H
50 ratio of H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene with growing electron density at the γ-position. Electron-rich substituents at the γ-position stabilize the radical, lowering the ESTS and moving it closer to the reactant along the reaction coordinate. The reactant 1,2-biradical is more free-moving than the rigid product 1,4-biradical, which means that it has less preference for either H or D abstraction. This explains the trend towards a 50
D-styrene with growing electron density at the γ-position. Electron-rich substituents at the γ-position stabilize the radical, lowering the ESTS and moving it closer to the reactant along the reaction coordinate. The reactant 1,2-biradical is more free-moving than the rigid product 1,4-biradical, which means that it has less preference for either H or D abstraction. This explains the trend towards a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 H
50 H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D-styrene ratio with growing electron density at the γ-position. DFT calculations shed light on the conformation of the ESTS: unexpectedly, the OTBS is axial rather than equatorial.
D-styrene ratio with growing electron density at the γ-position. DFT calculations shed light on the conformation of the ESTS: unexpectedly, the OTBS is axial rather than equatorial.
The trend is in accord with the KIEs: we have prepared and photolyzed a series of fully deuterated and non-deuterated substrates 19–36, and the amount of styrene formed after 5 minutes was measured. The KIEs are generally small, indicating an early ESTS. With growing electron density at the γ-position, we observe smaller KIEs, because the ESTS is earlier and more asymmetric. Overall, the same trend is observed as for substrates 1–18.
Approximations like the BOA are essential for understanding, calculating, and predicting various aspects of chemistry. The BOA is so ubiquitous that it is at the heart of how chemists think about chemical reactivity. However, it is known to break down for photochemical ESTSs and CIs, because at these points, the movement of the nuclei is significant and vibronic coupling is no longer negligible. Many of the guiding principles of physical organic chemistry, such as the Hammond–Leffler postulate, rely on the BOA and the concept of an energy surface. This has limited their use in photochemical reactions. While we must tread carefully when applying old approximations to new systems, the HLP has proven its worth for estimating the transition states of photochemical reactions. Given this work and previous results in our laboratories, we feel that the HLP can be extended to the excited state. Along with the KIE, the HLP is a pertinent tool for studying excited state transition states of photochemical reactions.
Future work on the applicability of the Hammond postulate to conical intersections will be published in due course.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of the Swiss National Science Foundation is gratefully acknowledged.References
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457 CrossRef.
- E. Lewars, Computational Chemistry. Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer, London, 2nd edn, 2011 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Ann. Rev. Phys. Chem., 2004, 55, 127 CrossRef CAS.
- T. C. Allison, S. L. Mielke, D. W. Schwenke and D. G. Truhlar, J. Chem. Soc. Faraday Trans., 1997, 93, 825 RSC.
- (a) Z. H. Top and M. Baer, Chem. Phys., 1975, 10, 95 CrossRef CAS; (b) P. W. Kash, G. C. G. Waschewsky, R. E. Morss, L. J. Butler and M. M. Francl, J. Chem. Phys., 1994, 100, 3463 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Sausalito, California, 2010 Search PubMed.
- J. E. Leffler, Science, 1953, 117, 340 CrossRef CAS.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334 CrossRef CAS.
- E. Wigner, Trans. Faraday Soc., 1938, 34, 29 RSC.
- J. Bigeleisen, J. Chem. Phys., 1949, 17, 675 CrossRef CAS.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Sausalito, California, 2006 Search PubMed.
- (a) F. H. Westheimer, Chem. Rev., 1961, 61, 265 CrossRef CAS; (b) J. E. Dixon and T. C. Bruice, J. Am. Chem. Soc., 1970, 92, 905 CrossRef CAS.
- (a) T. Šolomek, S. Mercier, T. Bally and C. G. Bochet, Photochem. Photobiol. Sci., 2012, 11, 548 RSC; (b) T. Šolomek, C. G. Bochet and T. Bally, Chemistry, 2014, 20, 8062 CrossRef.
- (a) R. P. Bell, Proc. R. Soc. Lond. A, 1936, 154, 414 CrossRef; (b) M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11 RSC.
- G. Dormán, H. Nakamura, A. Pulsipher and G. D. Prestwich, Chem. Rev., 2016, 116, 15284 CrossRef.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- A. G. Griesbeck and H. Heckroth, J. Am. Chem. Soc., 2002, 124, 396 CrossRef CAS.
- (a) A. M. Arafat, S. K. Mathew, S. O. Akintobi and A. A. Zavitsas, Helv. Chim. Acta, 2006, 89, 2226 CrossRef CAS; (b) A. S. Menon, T. Bally and L. Radom, J. Phys. Chem. A, 2012, 116, 10203 CrossRef CAS; (c) R. D. Gilliom and J. R. Howles, Can. J. Chem., 1968, 46, 2752 CrossRef CAS.
- F. M. Harvey and C. G. Bochet, J. Org. Chem., 2020, 85, 7611 CrossRef CAS.
- V. Ramamurthy and K. S. Schanze, Organic Photochemistry, CRC Press, Florida, 1997, vol. 1 Search PubMed.
- I. V. Alabugin, M. Manoharan and T. A. Zeidan, J. Am. Chem. Soc., 2003, 125, 14014 CrossRef CAS.
- E. Juaristi and G. Cuevas, Tetrahedron, 1992, 48, 5019 CrossRef CAS.
- H.-G. Korth, R. Sustmann, B. Giese, B. Rückert and K. S. Gröninger, Chem. Ber., 1990, 123, 1891 CrossRef CAS.
- H.-Y. He, W.-H. Fang and D. L. Phillips, J. Phys. Chem. A, 2004, 108, 5386 CrossRef CAS.
Footnotes |
| † The authors dedicate this paper to Professor Thomas Bally (1948–2019). |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04370b |
| This journal is © The Royal Society of Chemistry 2021 |