A ground-state-dominated magnetic field effect on the luminescence of stable organic radicals

Abstract

Organic radicals are an emerging class of luminophores possessing multiplet spin states and potentially showing spin-luminescence correlated properties. We investigated the mechanism of recently reported magnetic field sensitivity in the emission of a photostable luminescent radical, (3,5-dichloro-4-pyridyl)bis(2,4,6-trichlorophenyl)methyl radical (PyBTM) doped into host αH-PyBTM molecular crystals. The magnetic field (0–14 T), temperature (4.2–20 K), and the doping concentration (0.1, 4, 10, and 22 wt%) dependence on the time-resolved emission were examined by measuring emission decays of the monomer and excimer. Quantum mechanical simulations on the decay curves disclosed the role of the magnetic field; it dominantly affects the spin sublevel population of radical dimers in the ground states. This situation is distinctly different from that in conventional closed-shell luminophores, where the magnetic field modulates their excited-state spin multiplicity. Namely, the spin degree of freedom of ground-state open-shell molecules is a new key for achieving magnetic-field-controlled molecular photofunctions.

---

Introduction

Controlling chemical reactions or materials properties with an external magnetic field has attracted much attention both as an area of theoretical interest and for its potential applications.^1–4 In molecular luminescence, magnetic field effects (MFEs) have been realized by modulating kinetics among energetically comparable states with different spin multiplicities in the excited states via intersystem crossing (ISC) of radical pairs (RPs)^3,4 and triplet–triplet annihilation.^5–8 These processes are explained by mechanisms originating from Δg, hyperfine coupling, and relaxation. In contrast, MFEs in the ground state are not expected for conventional ground-state closed-shell molecules because there is no degree of freedom in spin multiplicity.

Monoradicals possessing one unpaired electron are attracting increasing interest as a new class of luminescent materials.^9–19 Their emission characteristics are unique to their doublet spin states, such as the absence of the heavy atom effect and high electron–photon conversion efficiency in organic light-emitting diodes.^9–16 We have reported the magnetic-field-sensitive luminescence properties of (3,5-dichloro-4-pyridyl)bis(2,4,6-trichlorophenyl)methyl radicals (PyBTM) doped into host αH-PyBTM crystals (Fig. 1).¹⁸ The luminescence behaviors of 10 wt%-doped crystals, in which PyBTM molecules were aggregated, were modulated strongly by an external magnetic field. This was the first clear example of the magnetic-field-sensitive luminescence properties of organic radicals; thus, understanding the MFE mechanism would contribute hugely to exploring the magnetic-field-sensitive photofunctionalities of radicals. However, the mechanism has not been fully established, because the effects of the magnetic field on the emission properties have remained unclarified in magnetic fields over 3 T, where an efficient MFE was observed.

Fig. 1 Molecular structures of PyBTM and αH-PyBTM.

In this study, we determined the mechanism and key factors of the MFE for PyBTM-doped crystals. Previously, excited-state dynamics has been investigated by optically detected magnetic resonance (ODMR) and time-resolved emission spectroscopy combined with quantum mechanical simulations,¹⁹ in which the magnetic field accessed for the investigations was limited to the X-band region (ca. 326 mT). Here, the photophysical properties in magnetic fields from 0 to 14.5 T, covering the entire region where an appreciable MFE was observed, were firstly investigated by time-resolved luminescence measurements. These measurements enabled us to construct a complete picture of the luminescence dynamics, which had not been able to be accessed by previous studies. The magnetic field and temperature dependences of the emission spectra and decay profiles were measured for αH-PyBTM crystals doped with various concentrations of the PyBTM radical. Quantum simulations based on these measurements revealed that the magnetic-field-sensitive spin sublevel population of aggregated radicals in the ground states was the main factor governing the MFE.

Results and discussion

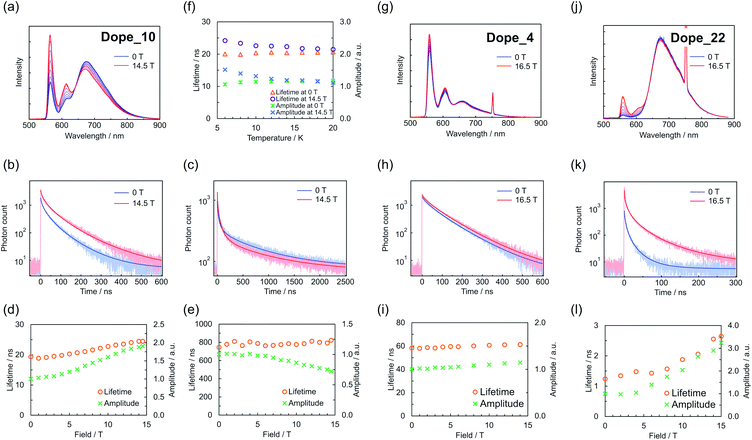
PyBTM-doped αH-PyBTM crystals (Dope_R, where R is the concentration (wt%) of PyBTM in the crystal) were prepared and characterized using our previous method.¹⁸ The luminescence decay curves of Dope_10 were investigated in detail to elucidate the effect of the magnetic field on the excited-state characteristics. Dope_10 exhibited magnetic-field-sensitive monomer and excimer PyBTM emissions, with maximum emission wavelengths of 563 and 674 nm, respectively (Fig. 2a). Decays were monitored at both maximum emission wavelengths with external magnetic fields from 0 to 14.5 T (Fig. 2b and c). Each decay curve was fitted with a stretched exponential function (eqn (1)) to visualize the changes in decay curves.^20,21

I(t) = I₀ exp{−(t/τ)^β} (1)

where τ is the lifetime and β is the stretch factor, a dimensionless parameter with a range of 0 < β ≤ 1. Stretched exponential functions can be used when distributions of decay times or rate constants are expected, such as in rigid solutions,²² polymers,²³ and energy transfer in assemblies of fluorophores.²⁴Fig. 2d summarizes the magnetic field dependences of the lifetimes and amplitudes for monomer emissions at 563 nm. The lifetimes at 4.2 K increased from 19 ns at 0 T to 24 ns at 14.5 T. The amplitude also increased with the magnetic field and reached about 1.9 times the initial amplitude at 14.5 T. The decays at 674 nm were fitted with two stretched exponential functions; one of which is for the corresponding monomer emission, because the monomer and excimer emissions were expected to overlap.¹⁹Fig. 2e shows the magnetic field dependences of the lifetimes and amplitudes for the components corresponding to the excimer emission. The amplitude decreased while the lifetime seemed unchanged as the magnetic field increased. The magnetic field insensitivity of the lifetime indicated that the radiative transition from the excimer excited state to the ground state was the rate-determining process.

Fig. 2 (a–e) Emission spectra of Dope_10 at 4.2 K under magnetic fields of 0–14.5 T (a), emission decays and corresponding fits at 4.2 K under magnetic fields of 0 and 14.5 T at 563 nm (b) and 674 nm (c), and magnetic field dependences of lifetimes and amplitudes at 4.2 K at 563 nm (d; β = 0.59) and 674 nm (e; β = 0.88). (f) Temperature dependences of lifetimes and amplitudes at 563 nm under magnetic fields of 0 and 14.5 T (β = 0.59). (g–i) Emission spectra of Dope_4 at 4.2 K under magnetic fields of 0–16.5 T (g), emission decays and corresponding fits at 4.2 K under magnetic fields of 0 and 16.5 T (h), and magnetic field dependences of lifetimes and amplitudes at 4.2 K (i) (β = 0.78). (j–l) Equivalent results as in (g–i) for Dope_22 (β = 0.41). Peaks at 750 nm are due to the excitation laser light (λ_ex = 375 nm).

Similar emission decay behavior was also observed in Dope_4 (Fig. 2g–i) and Dope_22 (Fig. 2j–l), with lower and higher radical concentrations than Dope_10. In contrast, Dope_0.1, which exhibited only a monomer-centered emission, showed no changes in the luminescence intensity or lifetime (Fig. S4†). These results indicated that the MFE mechanism and species of aggregated PyBTM were the same in all the Dope_R crystals.

The thermal effect counteracted the MFE in the emission spectra of Dope_10.¹⁸Fig. 2f shows the temperature dependence of emission decay for the monomer emission of Dope_10 at 0 and 14.5 T. The differences in the amplitude and lifetime between these cases (i.e., the MFE) at 4.2 K reduced as the temperature increased and were negligible at 20 K. These results indicate that thermally activated processes are involved in the mechanism of the MFE with its activation energy below k_BT with T = 20 K.

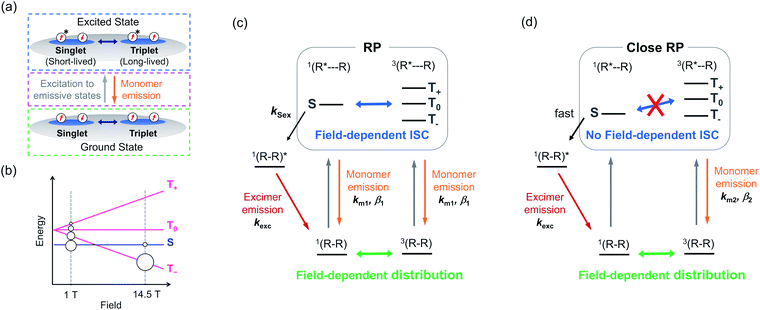
The emission lifetime measurements allowed us to construct a scheme for the MFE based on the following four results (Fig. 3a): the monomer emission amplitude increased with the magnetic field (Fig. 2d, i and l), the MFE was decreased by thermal energy (Fig. 2f), the monomer emission decay did not show a slow increase, and the photon counts had the largest values just after photoexcitation (Fig. 2b, h and k), and the monomer emission lifetime increased with the magnetic field (Fig. 2d, i and l).

Fig. 3 (a) Scheme based on lifetime measurements, showing the changes in spin sublevel populations in the ground state (green dashed box), direct excitations to emissive states (magenta dashed box), and two excited states with different lifetimes (blue dashed box). (b) Population distribution as a function of the applied magnetic field. (c and d) Proposed species responsible for the MFE. k_m1, k_m2, and k_exc are the totals of radiative and nonradiative transition rates for the monomer emission of RP, that of close RP, and the excimer emission, respectively.

The increase in the monomer emission amplitude with the magnetic field suggests that the spin sublevel population of a PyBTM dimer in the ground state is associated with the MFE (Fig. 3a, green dashed box).²⁵ The spin states of the dimer radicals (i.e., the population between the S, T₊, T₀, and T₋ states) are modulated by the magnetic field (via Zeeman splitting) and heat (via the Boltzmann distribution). In the absence of a magnetic field, the population of the S state is the largest, whereas the population of the T₋ state increases with the magnetic field and becomes dominant because the exchange interactions (J) between the radicals in Dope_R are antiferromagnetic (Fig. 3b).¹⁹ This ground-state associated MFE is consistent with the decrease in the MFE with thermal energy; increasing the temperature at 14.5 T increases the population in the S state and decreases the population in the T₋ state, and thus counteracts the MFE. The highest photon count occurring just after photoexcitation suggests that the radical dimers are first excited to emissive states (Fig. 3a, magenta dashed box), because the photon count reflects the populations in the emissive excited states. Furthermore, the increase in the monomer emission lifetime with the magnetic field suggests the existence of two excited states with different lifetimes. Considering that the populations of triplet ground states are increased by increasing the magnetic field, the triplet excited states have longer lifetimes than the singlet excited states (Fig. 3a, blue dashed box).

Based on this discussion, we proposed the following MFE scheme for Dope_R (Fig. 3c). This scheme has two factors sensitive to the magnetic field: the distribution among the singlet (S) and triplet (T₋, T₀, and T₊) ground states (ground-state MFE) and the ISC between singlet (S) and triplet (T₀) RP states by the Δg mechanism (excited-state MFE). (R–R) is a PyBTM dimer in the ground state with singlet or triplet spin multiplicity. Irradiation with 370 nm light photoexcites radical R in (R–R) to form an RP state, (R*⋯R). The coupling between R* and R in (R*⋯R) is so weak that it can behave as monomer PyBTM and show luminescence with transition rate k_m1 (k = 1/τ in eqn (1)) and stretch factor β₁.²⁰¹(R⋯R)* can generate the singlet excimer state, ¹(R–R)*, with rate constant k_Sex. We also assumed that a close RP,^26–29 (R*⋯R), is formed, where field-sensitive ISC does not happen due to the energy gap between the S and the T₀ states resulting from non-negligible exchange interactions (Fig. 3d). Although the ³(R–R) state shows a monomer emission in the excited state with transition rate k_m2 and stretch factor β₂, the ¹(R–R) state is assumed to form the excimer immediately after photoexcitation because of strong intramolecular interactions. As the population of the ³(R–R) state increased with the applied magnetic field, the populations in the emissive states responsible for monomer emission increased, which is consistent with the increase in monomer emission amplitudes with the magnetic field.

A quantum mechanical simulation was performed based on the scheme in Fig. 3c and d.³⁰Fig. 4a and b show that the magnetic field dependences of the monomer emission intensities and decays were well reproduced by the simulation, although the excimer emission intensity changes were overestimated (Fig. S11†). This overestimation indicated that more aggregated species, which are negligibly sensitive to the magnetic field, contributed to the excimer emission.

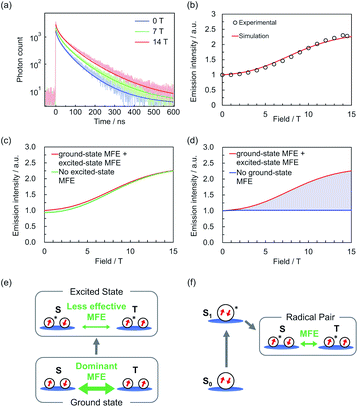Fig. 4 (a) Simulated and experimental monomer emission decays at 0, 7, and 14 T.³¹ (b) Simulated and experimental magnetic field dependences of monomer emission intensities. (c and d) Simulated monomer emission intensities without considering the MFE on (c) the ground states and (d) the excited states (for details of the simulations, see the ESI†). (e and f) Scheme of MFEs on (e) radicals (this system) and (f) conventional ground-state closed-shell molecules.

The trends of temperature dependence of the emission decay (Fig. S8 and S9†) and a steady-state ODMR signal (Fig. S12†) were also reproduced. Fig. 4c and d show the simulated monomer emission intensities without considering the excited-state or ground-state MFE, and the shaded areas show the contribution of each MFE. Although the excited-state MFE slightly increased the emission intensity in the low-field region, the ground-state MFE greatly increased the intensity in the high-field region. These results suggest that the ground-state MFE is critical to magnetoluminescence in this system (Fig. 4e); this is distinct from conventional ground-state closed-shell systems, in which only excited state MFEs occur (Fig. 4f).

Conclusions

In this study, the mechanism of the MFE on the luminescence of PyBTM-doped αH-PyBTM crystals was revealed by luminescence lifetime measurements under a magnetic field and the dependences of lifetime on the doping concentration and temperature. In-depth investigations in the magnetic field region of 0–14.5 T, covering the entire region where a substantial MFE was observed, enabled us to construct MFE schemes unique to organic radicals. The simulated luminescence decay curves based on the MFE schemes agreed well with experimental data. The results suggested that the MFE in this system was dominated by magnetic-field-sensitive spin sublevel populations in the ground states. These characteristics arise from the degree of freedom in the ground-state spin multiplicities of aggregated radicals, and have not been observed in conventional ground-state closed-shell molecules to the best of our knowledge. Considering the excellent designability of the spin–spin interactions in ground states compared with those in excited states, these findings will contribute to the molecular design of magnetoluminescent materials based on organic radicals to achieve magnetic-field-sensitive photofunctions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The present study was supported by JST CREST Grant Number JPMJCR15F2 and JSPS KAKENHI Grant Numbers JP20H02759, JP17H04870, JP19H05460, JP26220801, JP16H04136, and JP20H02715. T. K. is grateful to the Iketani Science and Technology Foundation and Kato Foundation for Promotion of Science for financial support. Shu. K. acknowledges MERIT (Material Education program for the future leaders in Research, Industry, and Technology) in the MEXT Leading Graduate School Doctoral Program. This work was performed at the High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University (Project No. 17H0018 and 16H0067).

Notes and references

1. H. Mouritsen, Nature, 2018, 558, 50–59.
2. M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen, V. Dau, F. Petroff, P. Eitenne, G. Creuzet, A. Friederich and J. Chazelas, Phys. Rev. Lett., 1988, 61, 2472–2475.
3. U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147.
4. H. Hayashi, Introduction to Dynamic Spin Chemistry: Magnetic Field Effects on Chemical and Biochemical Reactions, World Scientific, Singapore, 2004.
5. R. C. Johnson and R. E. Merrifield, Phys. Rev. B, 1970, 1, 896–902.
6. R. E. Merrifield, J. Chem. Phys., 1968, 48, 4318–4319.
7. T. Mani and S. A. Vinogradov, J. Phys. Chem. Lett., 2013, 4, 2799–2804.
8. L. R. Faulkner and A. J. Bard, J. Am. Chem. Soc., 1969, 91, 6495–6497.
9. X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Nature, 2018, 563, 536–540.
10. H. Guo, Q. Peng, X. K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J. L. Brédas and F. Li, Nat. Mater., 2019, 18, 977–984.
11. Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095.
12. A. Obolda, X. Ai, M. Zhang and F. Li, ACS Appl. Mater. Interfaces, 2016, 8, 35472–35478.
13. Y. Beldjoudi, M. Nascimento, Y. J. Cho, H. Yu, H. Aziz, D. Tonouchi, K. Eguchi, M. M. Matsushita, K. Awaga, I. O. Osorio-roman, C. P. Constantinides and J. M. Rawson, J. Am. Chem. Soc., 2018, 140, 6260–6270.
14. Y. Hattori, T. Kusamoto and H. Nishihara, Angew. Chem., Int. Ed., 2014, 53, 11845–11848.
15. Y. Hattori, T. Kusamoto and H. Nishihara, Angew. Chem., Int. Ed., 2015, 54, 3731–3734.
16. Y. Hattori, S. Kimura, T. Kusamoto, H. Maeda and H. Nishihara, Chem. Commun., 2018, 54, 615–618.
17. P. Mayorga Burrezo, V. G. Jiménez, D. Blasi, I. Ratera, A. G. Campaña and J. Veciana, Angew. Chem., Int. Ed., 2019, 58, 16428–16434.
18. S. Kimura, T. Kusamoto, S. Kimura, K. Kato, Y. Teki and H. Nishihara, Angew. Chem., Int. Ed., 2018, 57, 12711–12715.
19. K. Kato, S. Kimura, T. Kusamoto, H. Nishihara and Y. Teki, Angew. Chem., Int. Ed., 2019, 58, 2606–2611.
20. M. N. Berberan-Santos, E. N. Bodunov and B. Valeur, Chem. Phys., 2005, 315, 171–182.
21. D. Blasi, D. M. Nikolaidou, F. Terenziani, I. Ratera and J. Veciana, Phys. Chem. Chem. Phys., 2017, 19, 9313–9319.
22. V. Ptatschek, B. Schreder, K. Herz, U. Hilbert, W. Ossau, G. Schottner, O. Raha, T. Bischof, G. Lermann, A. Materny, W. Kiefer, G. Bacher, A. Forchel, D. Su, M. Giersig, G. Mu and L. Spanhel, J. Phys. Chem. B, 1997, 101, 8898–8906.
23. A. L. Wong, J. M. Harris and D. B. Marshall, Can. J. Phys., 1990, 68, 1027–1034.
24. R. Métivier, I. Leray, J.-P. Lefévre, M. Roy-Auberger, N. Zanier-Szydlowski and B. Valeur, Phys. Chem. Chem. Phys., 2003, 5, 758–766.
25. The amplitude should be independent of the magnetic field-sensitive kinetics in the excited states (i.e., field-dependent ISC) and thus be determined by the ground state.
26. Y. Zhang, G. P. Berman and S. Kais, Int. J. Quantum Chem., 2015, 115, 1327–1341.
27. M. Murakami, K. Maeda and T. Arai, J. Phys. Chem. A, 2005, 109, 5793–5800.
28. S. Stob, J. Kemmink and R. Kaptein, J. Am. Chem. Soc., 1989, 111, 7036–7042.
29. L. M. Antill and J. R. Woodward, J. Phys. Chem. Lett., 2018, 9, 2691–2696.
30. Details of the simulation are described in the ESI.†.
31. Parameters used in the simulations are as follows: k_m1 = 3.24 × 10⁷ s⁻¹, k_m2 = 3.51 × 10⁷ s⁻¹, β₁ = β₂ = 0.63, k_Sex = 1.71 × 10⁷ s⁻¹, J/k_B = −4.8 K, and the ratio of (population) × (radiative transition rate) for (RP species)/(close RP species) = 0.7. For details, see Table S1 in the ESI.†.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and simulation details and supplementary figures. See DOI: 10.1039/d0sc05965j

---