DeepFrag: a deep convolutional neural network for fragment-based lead optimization

Abstract

Machine learning has been increasingly applied to the field of computer-aided drug discovery in recent years, leading to notable advances in binding-affinity prediction, virtual screening, and QSAR. Surprisingly, it is less often applied to lead optimization, the process of identifying chemical fragments that might be added to a known ligand to improve its binding affinity. We here describe a deep convolutional neural network that predicts appropriate fragments given the structure of a receptor/ligand complex. In an independent benchmark of known ligands with missing (deleted) fragments, our DeepFrag model selected the known (correct) fragment from a set over 6500 about 58% of the time. Even when the known/correct fragment was not selected, the top fragment was often chemically similar and may well represent a valid substitution. We release our trained DeepFrag model and associated software under the terms of the Apache License, Version 2.0.

---

1 Introduction

Drug discovery is benefiting from an upsurge in machine-learning approaches for tasks such as binding-affinity prediction,^1–3 virtual screening,^4–7 and quantitative structure–activity relationship (QSAR).⁸ Massive molecular datasets have enabled data-driven models that outperform handcrafted algorithms in nearly all applications. As these powerful new approaches come of age, they are increasingly used to augment the drug-discovery pipeline and reduce the time and cost of developing new pharmaceuticals.

While classification and regression models for drug discovery have been studied extensively, the problem of molecular generation remains challenging. In the field of computer vision, generative models such as recurrent neural networks (RNNs) and generative adversarial networks (GANs) have had great success in performing tasks such as realistic image synthesis⁹ and style transfer.¹⁰ Naturally one wonders if this same technology can be applied to molecular synthesis. Several recent works in generative molecular modeling have demonstrated that it is possible to generate libraries of 2D SMILES-string representations with desired properties¹¹ as well as 3D ligand pharmacophore-type maps from a given receptor pocket.¹²

However, the field still faces some challenges. First, it is difficult to enforce the generation of valid molecular structures. Models that produce SMILES strings may contain grammatical errors, and 3D molecular shapes tend to be blurry and lacking in detail. Second, the inner workings of generative models are difficult to interpret. Failure cases are hard to diagnose both during training and inference (i.e., prospective prediction). Finally, while it is clear how to evaluate a regression model (e.g., by calculating L2 loss), it is not entirely clear how to quantitatively evaluate a generative model. The current best practice is to demonstrate “enrichment” for some metric such as QED compared to a random baseline.¹³

In this paper, we address some of these limitations by restructuring the question of molecular generation as a type of classification problem. Specifically, we propose a new “fragment reconstruction” task where we take a ligand/receptor complex, remove a portion of the ligand, and ask the question “what molecular fragment should go here?” To successfully answer this question, a machine-learning model must consider the surrounding receptor pocket and the intact portion of the ligand. This task is immediately applicable to lead optimization, which seeks to improve the binding of a known ligand by swapping and/or adding molecular fragments. It also represents an important step towards fully de novo drug design.

We here demonstrate that a 3D convolutional network trained on experimentally derived crystal-structure data can select a missing fragment with roughly 58% accuracy from a set of more than 6500 fragments. Even when the network does not predict the correct answer, the top predictions are often chemically similar and may well represent plausible substitutions. We release our trained model and associated software under the terms of the Apache License, Version 2.0. A copy can be obtained free of charge from http://durrantlab.com/deepfragmodel, where interested users can also find a link to a Google Colaboratory Notebook¹⁴ for testing.

2 Results and discussion

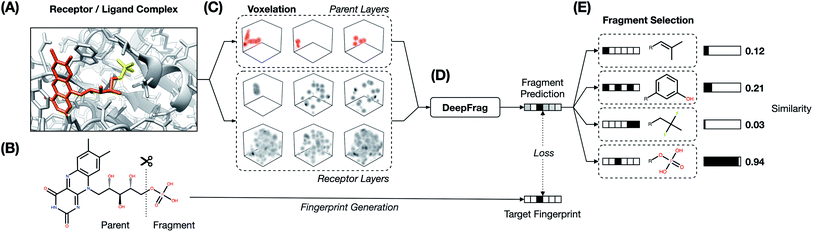
The fragment-reconstruction task we here introduce aims to complete a partial, receptor-bound ligand (“parent”) by adding a new molecular fragment such that the combined molecule is highly complementary to the given receptor. For the purpose of this work, a fragment is a terminal ligand substructure with a mass less than 150 Da (Fig. 1A). The cutoff choice of 150 Da is relatively arbitrary; this value allows for a large variety of fragment types without including overly complex structures. The fragment may be an explicit functional group with known behavior such as a hydroxyl or phenyl group, but this is not a requirement.

Fig. 1 DeepFrag workflow. (A) Receptor/ligand complex. Example “parent” and “fragment” portions of the ligand are highlighted in orange and yellow, respectively. (B) The ligand is cut along a single bond to separate the parent and fragment. (C) Atoms from the receptor and parent are converted to 3D voxel grids (density channels). (D) Density channels are concatenated and fed to the DeepFrag model, which predicts a fragment fingerprint. (E) The fingerprint is compared against a fingerprint library (label set) to generate predictions.

The intuition behind this task is that fragment selection is a function of the local receptor environment and the existing ligand scaffold (parent). Therefore, it should be possible to learn a model that predicts appropriate fragments given the structure of a receptor/parent complex. We here introduce just such a model and show that it can be used to implicitly rank a set of candidate complementary fragments. We expect such a model to be useful for lead optimization (e.g., to generate congeneric series of small-molecule ligands with improved binding affinities). The same model could be used indirectly as a way to evaluate the importance of each group in an existing ligand by removing and re-predicting existing fragments.

2.1 Generating and representing molecular data

2.1.1 A dataset of (receptor/parent, fragment) examples. Ideally, we would like to train a model to predict the single, optimal fragment for any receptor/parent pair. But given that there are roughly 10⁶⁰ drug-like molecules,¹⁵ identifying optimal fragments for training is impracticable. We instead trained on datasets derived from the Binding MOAD¹⁶ database (Table 1), which currently includes experimentally derived structural data for 38 702 receptor/ligand complexes.

Table 1 Fragment dataset details. Receptors: number of unique receptor targets per split. Ligands: number of unique ligands per split (determined by SMILES comparison). Unique fragments: number of unique molecular fragments per split. Examples: total number of (receptor/parent, fragment) examples

	TRAIN	VAL	TEST	ALL
Receptors	22 968	7641	8093	38 702
Ligands	10 284	3677	4101	18 062
Unique fragments	4654	2070	2328	6522
Examples	185 198	55 221	68 270	308 689

---

We make the assumption that because each ligand in the dataset is known to bind the corresponding target, its structure must be to some extent optimized relative to a random molecule. It follows that each ligand fragment (i.e., substructure) is also at least somewhat optimized—especially those fragments that interact directly with the receptor. We therefore trained a model to reconstruct correct fragments from known active ligands, as a surrogate for training on optimal fragments (Fig. 1A and B).

2.1.2 Voxelizing receptor/parent complexes. We represented the input receptor/parent complexes as 3D grids (tensors, Fig. 1C) similar to those described elsewhere.^4,5,17 Each grid point corresponds to a cubic region of 3D space (a voxel), analogous to a pixel in the 2D-image context. We chose a grid representation because the 3D local context is certainly critical for fragment binding. Converting molecular structures to voxel grids also allowed us to easily translate machine-learning techniques from other fields (e.g., computer vision). To learn a rotation-invariant model and prevent overfitting, each grid was randomly rotated each time it was used (i.e., once per training epoch).

2.1.3 Converting fragments to fingerprints. We represented the fragments (DeepFrag output) as continuous molecular fingerprints rather than 3D grids. We converted the known fragments in our dataset to fingerprints using the RDKFingerprint algorithm (Fig. 1D).^18,19 Each fingerprint is a vector (i.e., a simple list of numbers) that serves as a numerical description of the fragment's topology, or structure. These fingerprint outputs distinguish DeepFrag from other methods that perform more typical categorical classification tasks, where the output is instead a vector containing class scores or normalized class probabilities. In this typical formalization, classes must be fixed at training time (i.e., the model has no capacity to predict unseen classes), and any prior knowledge about class relationships is effectively stripped, precluding the training of a more generalizable model. Instead of predicting from a limited number of possible fragments (classes), we predict a continuous representation of an RDKFingerprint describing the desired output fingerprint. Substituting numerical values (between zero and one) for the binary bits of a traditional fingerprint allows for “fuzzy” matching to a greater variety of chemotypes.

2.2 The DeepFrag model

We systematically considered many combinations of machine-learning and grid-generation parameters (hyperparameters) to find a combination well suited to our fragment-prediction task (see ESI†). To evaluate each parameter combination, we trained a corresponding model using a set of (receptor/parent, fragment) examples set aside specifically for training (the TRAIN set, roughly 60% of the data; see Table 1 and Subsection 4.1.3). We then evaluated how well the trained model performed when applied to a distinct validation set, comprised of examples set aside for identifying acceptable hyperparameters (the VAL set, roughly 20% of the data; Table 1).

After identifying a reasonable set of machine-learning and grid-generation parameters, we trained the final model, which we call “DeepFrag”. We again trained using the examples of the TRAIN set, but this time we trained until full convergence (i.e., until we no longer saw substantial improvements in the accuracy of the VAL-set predictions; about five days on a TITAN-X GPU).

Although all grids were randomly rotated once per epoch (training step) to encourage rotation-invariant training, the model was still not perfectly robust to rotation. That is, otherwise identical grids with different rotations generated slightly different prediction fingerprints, and some rotations even generated poor predictions. We found that averaging the fingerprint predictions of multiple randomly rotated grids improved accuracy by “smoothing out” any rotation dependence of the DeepFrag model (see ESI†).

As a final evaluation, we applied our fully trained DeepFrag model to a distinct testing set comprised of examples set aside specifically for evaluating the final model (the TEST set, roughly 20% of the data; see Table 1 and Subsection 4.1.3). For each TEST-set example, we randomly rotated the associated receptor/parent voxel grid 32 times and used DeepFrag to predict 32 fragment fingerprints. In all cases, we averaged the 32 fingerprints to produce one fragment fingerprint per receptor/parent pair.

This averaged fingerprint output is not easily human interpretable, so as a final step we selected fragments with similar fingerprints from a look-up library of known fragments, which we call a “label set” (Fig. 1E). This fragment-selection task is entirely independent of the training and testing used to generate the model itself and so can be seen as a post-processing step.

To assess accuracy on the TEST set, we constructed the LBL-ALL label set, which includes the correct fragment fingerprints from the TEST set as well as the other fingerprints seen during training, from the TRAIN and VAL sets. By comparing the DeepFrag output fingerprint to those fingerprints in the label set, one can identify the k fragments that are most similar. TOP-k accuracy is simply the frequency with which the correct fragment is among those k fragments. We found that the correct fragment and the single most similar LBL-ALL fragment were the same 57.77% of the time (i.e., the TOP-1 accuracy of the final DeepFrag model was 57.77%; Table 2).

Table 2 The TOP-k % accuracy, for k ∈ {1, 8, 64}, of the final model (DeepFrag with full rotation augmentation; N = 32) evaluated on the withheld TEST set (68 270 examples), using the LBL-ALL label set. For reference, we also report the accuracy using the LBL-TEST set. The expected accuracy of an equivalent random model is given in parenthesis

	TOP-1	TOP-8	TOP-64
TEST/LBL-ALL (6522)	57.77 (0.02)	66.16 (0.12)	72.26 (0.98)
TEST/LBL-TEST (2328)	57.80 (0.04)	66.67 (0.34)	74.28 (2.75)

---

2.3 Fragment selection: label-set size and composition

A large label set such as the LBL-ALL set (6522 fragment fingerprints) is advantageous in that it gives the model the freedom to select from a wider range of fragments. On the other hand, smaller sets may also have their advantages. For example, allowing DeepFrag to choose from a smaller label set could conceivably improve accuracy. Using smaller sets comprised of easily synthesizeable fragments may also be critical when chemical synthesizeability is a concern. Even a few dozen fragments can cover a wide range of potential biochemical interactions.

In some circumstances, generating smaller label sets composed only of fragments with druglike chemical properties may also be beneficial. For example, in creating the LBL-ALL label set, we considered all TRAIN-, VAL-, and TEST-set fragments, regardless of their chemical properties. Some crystallographic ligands in our original dataset are not particularly druglike, so occasionally DeepFrag recommends a fragment that is not suitable for drug discovery (e.g., *OOOH, derived from crystal structure 1U21;²⁰ see Fig. 2). We opted to retain these fragments based on the assumption that an expert end user will be able to select those that are most promising for further evaluation. Furthermore, even fragments that are not druglike might serve to inspire a trained medicinal chemist in search of optimization strategies. But researchers generating alternative label sets may wish to further filter by chemical properties so that only druglike fragments can be selected.

Fig. 2 Example predictions using the final model. Examples are drawn from the (unseen) TEST set, and fragments are selected from the LBL-ALL label set (6522 choices) each predicted fingerprint is the average of 32 predictions obtained by randomly rotating the corresponding input voxel grid. Left: the ground-truth (correct) fragments. Right: the top eight predicted fragments, labeled with the cosine similarity (1 – cosine distance) to the respective averaged prediction fingerprint.

Given that some users may wish to use smaller label sets, we specifically evaluated the impact of label-set size on accuracy. We applied DeepFrag to all the (receptor/parent, fragment) examples in the TEST set (68 270 examples) and recalculated TOP-k accuracy using a much smaller label set comprised of only the fragment fingerprints present in our TEST set (LBL-TEST, 2328 fingerprints, Table 1). Remarkably, the correct label was the closest roughly 58% of the time (Table 2), regardless of the label set used. Increasing the size of the label space by nearly threefold (LBL-TEST → LBL-ALL) thus bears little cost on accuracy. In other words, model predictions are fairly precise; despite “cluttering” the label space with many more incorrect fragments, top predictions from the smaller space are generally also top predictions in the larger space.

By default, DeepFrag uses a label set that includes the fragment fingerprints “seen” during training (i.e., the 5564 fingerprints in the TRAIN and VAL sets), which we call the LBL-SEEN label set. The LBL-ALL and LBL-TEST label sets described above are useful for evaluating DeepFrag accuracy on the TEST set because they include the correct TEST-set fragments. But the LBL-SEEN set is more appropriate for standard use (when a specific correct fragment need not be known beforehand) because it excludes TEST-only fragments, which are artifacts of data-set selection and do not contribute to the training of the model.

2.4 Parent and receptor information both improve accuracy

DeepFrag considers the atoms of both the parent ligand and protein receptor when predicting potential fragments. Several factors informed our decision to train using both these atom sets. We trained using the parent-atom information because we reasoned that it would be critical for selecting appropriately sized fragments (i.e., ideal fragments should be able to fit within the available space between the parent and receptor). Including parent atoms may also allow DeepFrag to deduce fragment orientation (i.e., the general direction towards which the selected fragments must extend). Finally, information about the parent atoms may allow DeepFrag to learn some limited rules of chemical synthesizability. For example, if the user-specified connection point falls at the location of a parent oxygen atom, fragments that connect through carbon atoms are more appropriate than those that connect through nitrogen atoms because oxygen–carbon bonds are more common than oxygen–nitrogen bonds.

Our decision to include receptor atoms was similarly motivated. We expect that DeepFrag leverages this information to select appropriately sized fragments. The receptor atoms also provide DeepFrag with the information needed to select fragments that can participate in complementary interactions (e.g., fragments with hydrogen-bond acceptors are best if the adjacent receptor atoms form a hydrogen-bond donor).

To test the relative importance of parent and receptor atoms, we trained two additional machine-learning models using either the parent-atom information or the receptor-atom information, but not both. In Table 3 we report the accuracy of these two model variants on the withheld TEST set when selecting fragments from the LBL-TEST label set. The final (parent + receptor) DeepFrag model performed substantially better than the models trained on the parent or receptor information alone (Table 3). Somewhat surprisingly, the model trained on the parent-atom information alone outperformed the model trained on the receptor-atom information (Table 3). It may be that the model learned implicit “ligand-like molecule” priors. For example, asking the model to predict a fragment on an aromatic ring will likely yield a fragment such as a single fluorine atom or a nitro group. These types of predictions match intuitions of what a “drug-like” molecule might look like. Additionally, while the “parent” model retains information about the specific placement of the target fragment, the “receptor” model simply sees a receptor pocket with no orientation or placement information. It is surprising that the receptor model performs as well as it does, given these limitations.

Table 3 Impact of parent vs. receptor information. In all cases, the TOP-k accuracy (%) was calculated using the LBL-TEST label set (2328 fragments). We here used DeepFrag without rotation augmentation (i.e., N = 1, see Table S5). The architectures of the parent- and receptor-only models are identical except for the number of input layers

Model	TOP-1	TOP-8	TOP-64
Random baseline	0.04	0.34	2.75
Parent and receptor	57.74	65.36	72.16
Parent only	47.85	56.70	66.34
Receptor only	38.39	46.61	58.46

---

2.5 Examples demonstrating effectiveness

2.5.1 DeepFrag generalizability. We were encouraged to see evidence that our model can generalize beyond the correct fragments used for training. The true optimal fragment for a given protein/parent pair is unlikely to ever be in any chosen label set. Generalizability ensures that the model can nevertheless predict chemically similar fragments that are well suited for a given binding-pocket region. Synthesizing and testing congeneric series of distinct compounds that each incorporate a different top-scoring fragment may enable the rapid discovery of optimized ligands with improved binding affinities.

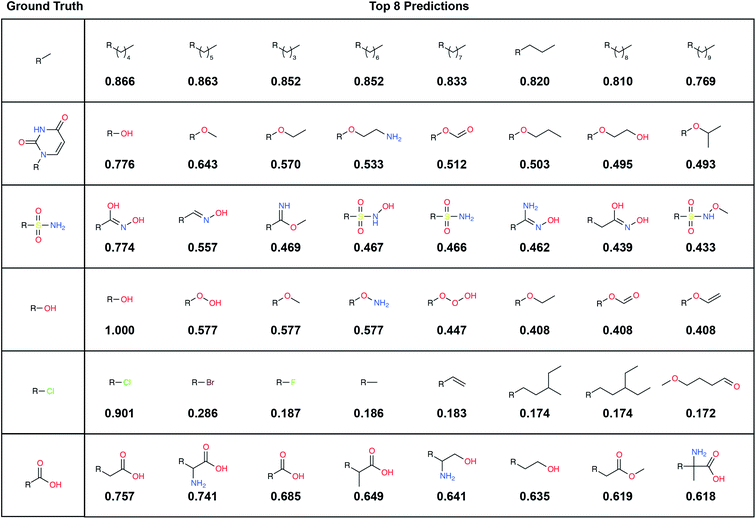
To illustrate, we randomly selected six TEST-set (protein/parent, fragment) examples and identified the eight LBL-ALL fragment fingerprints that were most similar to each DeepFrag-predicted fingerprint (Fig. 2). The correct fragment was selected first in two of the six cases, and among the top five in another two cases. But it is telling that the other top-ranked fragments are often very plausible substitutes. Interestingly, the single-atom halogen fragments (*Cl, *Br, and *F) share no common fingerprint bits, yet the model learned to group them together. This result suggests that our model may be more predictive than even the TOP-k metric would suggest. It is entirely possible that in some cases where DeepFrag does not select the correct fragment, the selected fragment may in fact be superior.

2.5.2 Human and DeepFrag intuition are complementary. To provide a simple comparison of human and DeepFrag “intuition,” we next considered H. sapiens peptidyl-prolyl cis–trans isomerase NIMA-interacting 1 (HsPin1p), a cancer drug target,²¹ bound to a phenyl-imidazole ligand (IC₅₀ = 8 μM, PDB 2XP9,²²Fig. 3). Importantly, neither HsPin1p nor the ligand were included in the DeepFrag TRAIN or VAL sets.

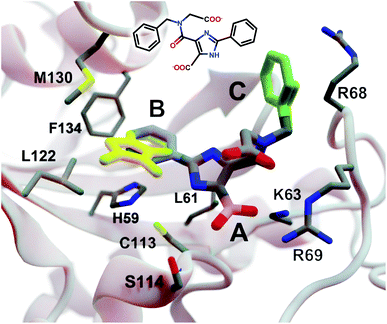Fig. 3 A crystal structure of HsPin1p bound to a phenyl-imidazole ligand (PDB 2XP9 (ref. 22)). The crystallographic ligand is also shown in 2D representation (overlaid). A, B, and C indicate a carboxyl (pink) and two phenyl (blue and green) fragments that we reassessed with DeepFrag. The DeepFrag-suggested bicyclic and ethyl replacements for phenyl B and phenyl C, respectively, are shown in yellow. Fragments were positioned using RDKit¹⁹ (see ESI†). Figure rendered using BlendMol.²³

Intuitively, carboxylate A (Fig. 3, highlighted in pink) seems well optimized, per the crystal structure. It forms electrostatic interactions with R69 and K63, and hydrogen bonds with C113 and S114. We removed this carboxylate group and used DeepFrag to predict replacement moieties from among those in the default LBL-SEEN set. The top predicted fragment was the correct carboxylate group. Interestingly, the second- and third-place fragments were chemically similar: *CO and *CC(=O)O.

Phenyl B (Fig. 3, highlighted in blue) also appears to be well optimized. It binds near multiple hydrophobic residues (L122, F134, M130, and L61) and forms π–π interactions with H59. We repeated the same DeepFrag analysis multiple times, this time removing phenyl B. Multiple runs are useful in some cases because DeepFrag is not strictly deterministic; it randomly rotates the default 32 grids it uses for output-fingerprint averaging, so different DeepFrag runs can in some cases predict different outputs. While some of our DeepFrag runs targeting phenyl B did identify a phenyl group as the correct fragment, we focus on a run in which the top predicted fragment was the bicyclic moiety *c1ccnc2c1C(=O)N(C)C2 (Fig. 3, in yellow). This fragment may preserve the π–π interactions with H59 while enhancing hydrophobic interactions with M130 and L122 (Fig. 3), illustrating how DeepFrag can serve as a useful tool for lead optimization.

To provide further evidence that the bicyclic substitution is reasonable, we positioned it relative to the parent molecule using RDKit. We then used the docking program smina²⁴ to (1) optimize the geometry (i.e., pose) of the composite (fragment + parent) compound within the binding pocket and (2) map that pose to a score that ideally correlates with binding affinity (see ESI† for important details). Computer docking is a useful tool for first-pass assessment, but, as is the case with all docking scoring functions, the correlation between smina scores and experimentally measured binding affinities is far from perfect. That is, if one compound has a slightly better score than another, one cannot confidently conclude that it has a better binding affinity. On the other hand, if a compound has a far better docking score, an actual difference in affinity is more likely.

Given that the original HsPin1p ligand is itself the product of experimental lead optimization,²² it is noteworthy that the DeepFrag bicyclic modification did not substantially impact the smina score. The docking scores of the DeepFrag compound and original crystallographic ligand were −7.13 and −7.17 kcal mol⁻¹, respectively. This suggests that the DeepFrag substitution is reasonable (i.e., it fits well within the protein binding pocket and so does not substantially impact the docking score).

As negative controls, we similarly generated three additional molecules by substituting phenyl B with random fragments. These fragments were selected by sampling the same distribution as the training data (i.e., TRAIN + VAL); that is, small fragments such as *O and *C, which occur more frequently, had a better chance of being selected than larger rare fragments. The three randomly generated compounds had an average smina score of −5.55 ± 0.26 (stdev) kcal mol⁻¹. Given that the crystallographic ligand is already the product of careful experimental optimization, it is not surprising that random moiety replacements would worsen the docking score. That the score of the DeepFrag compound resembles that of the crystallographic ligand—and not the randomly generated negative controls—provides additional evidence that DeepFrag has successfully identified an effective fragment in this case.

Finally, human intuition suggests that phenyl C (Fig. 3, highlighted in green) is not well optimized. Aside from possible hydrophobic interactions with a portion of the R68 side chain, there are no other specific interactions with HsPin1p. This phenyl group also appears to be more solvent exposed than is phenyl B. When we applied DeepFrag, it in fact did not suggest aromatic groups at this position. The top predicted fragments were methyl and ethyl groups. Interestingly, the methyl compound maintains the potential hydrophobic interactions with the R68 side chain (Fig. 3, in yellow). Its smina score was comparable to that of the original ligand (−6.30 vs. −7.17 kcal mol⁻¹; see ESI†). The average score of three similar compounds generated using randomly sampled moiety substitutions was worse than that of the original and DeepFrag-optimized ligands (−5.85 ± 0.04 kcal mol⁻¹), again suggesting that DeepFrag selected an effective fragment.

This analysis suggests that DeepFrag has learned much of the same chemical–biology intuition typical of experts in the field.

2.5.3 Predicting diverse interaction types. To evaluate whether the DeepFrag model can account for a wide range of interaction types (e.g., electrostatic, hydrophobic, halogen, hydrogen-bond, and aromatic interactions), we selected three additional protein/ligand complexes for testing. These complexes were well suited for our purposes because (1) the associated PDBs were among those in the TEST set, not the TRAIN or VAL sets; (2) the associated ligands had diverse low-weight fragments of the type commonly considered during lead optimization; and (3) visual inspection confirmed that those fragments formed specific interactions with their respective protein receptors.
2.5.3.1 Myeloid cell leukemia 1 (Mcl-1). We first applied DeepFrag to the cancer-implicated protein myeloid cell leukemia 1 (Mcl-1) bound to a low-nanomolar inhibitor designated “10d” (K_d = 24 nM; Fig. 4A; PDB 6QZ8 (ref. 25)). As a demonstration of DeepFrag's ability to optimize for electrostatic interactions, we removed the ligand carboxylate group, which forms a strong electrostatic interaction with R263, and used DeepFrag to predict appropriate replacement fragments from among those in the default LBL-SEEN set. The top predicted fragment was in fact a carboxylate group, and the second- and third-ranked fragments were chemically similar: *C(=O)OC and *C(=O)OO.

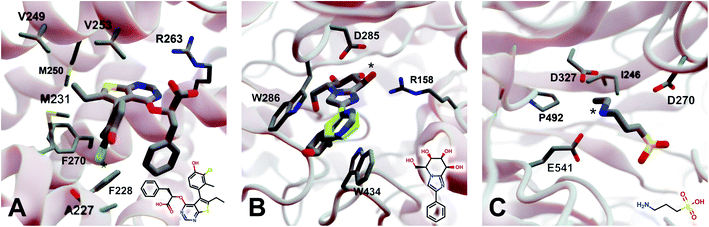Fig. 4 Crystal structures used to explore DeepFrag's ability to predict a broad range of molecular interactions. Two-dimensional depictions of the corresponding crystallographic ligands are overlaid in the lower right-hand corners. (A) Protein myeloid cell leukemia1 (Mcl-1) (PDB 6QZ8 (ref. 25)). A key ligand chlorine atom is marked with an asterisk. (B) Family GH3 β-D-glucan glucohydrolase from barley (PDB 1X38 (ref. 26)). A key ligand hydroxyl group is marked with an asterisk, and an original phenyl group is shown in yellow. (C) NanB Sialidase from S. pneumoniae (PDB 4FOW (ref. 27)). A key ligand primary amine, which DeepFrag replaced with an ethylamine, is marked with an asterisk. Fragments were positioned using RDKit¹⁹ (see ESI†). Figure rendered using BlendMol.²³

To demonstrate DeepFrag's ability to optimize for hydrophobic interactions, we separately removed a terminal methyl and ethyl group from the ligand. Both appear to be well optimized. The methyl group forms hydrophobic contacts with F270, F228, and M231; and the ethyl group forms hydrophobic contacts with F270, V253, V249, M250, and M231. In both cases, DeepFrag identified the correct fragment as the top-ranked candidate and also suggested other chemically plausible hydrophobic fragments.

We also removed the ligand chlorine atom, which is predicted to form a halogen bond with the A227 backbone carbonyl oxygen atom (Fig. 4A, marked with an asterisk). The top-ranked replacement fragments were methyl, methyl alcohol, and ethyl groups. Although methyl halide fragments did rank well (e.g., methyl floride, methyl chloride, methyl bromide, and methyl iodide ranked 8th, 12th, 13th, and 15th, respectively), it is reasonable that DeepFrag preferred a small, hydrophobic fragment (methyl) at this location because surrounding amino acids (F228, A227, and M231) are also hydrophobic. Indeed, swapping the chlorine for a methyl group slightly improved the smina score over the original ligand (−8.03 vs. −7.92 kcal mol⁻¹). Encouragingly, the average score of three similar compounds generated via random moiety substitutions was again worse than that of both the original and DeepFrag-optimized ligands (−7.51 ± 0.65 kcal mol⁻¹).

2.5.3.2 Family GH3 β-D-glucan glucohydrolase (barley). We next applied DeepFrag to family GH3 β-D-glucan glucohydrolase from barley, bound to the low-nanomolar inhibitor gluco-phenylimidazole (1.7 nM; Fig. 4B; PDB 1X38 (ref. 26)). To show how DeepFrag can optimize for hydrogen-bond interactions, we first removed the hydroxyl group at position 8 (Fig. 4B, marked with an asterisk), which participates in hydrogen bonds with R158 and D285. The top-ranked replacement fragment was in fact a hydroxyl group, and other top-scoring fragments were chemically similar (e.g., *OC and *COO).

To test DeepFrag's ability to optimize for aromatic stacking interactions, we next removed the ligand phenyl group (Fig. 4B, in yellow), which participates in π–π stacking interactions with W286 and W434. Phenyl groups are larger than those tested above, making it less likely that DeepFrag will select the exact, correct fragment. But DeepFrag does often produce reasonable alternatives in these cases, showing that it has learned a certain degree of chemical intuition. The top replacement fragments were in fact all aromatic. The best fragment, *c1ncnc2c1C(C)CC2(O), has a bicyclic structure that may enable more extensive contacts with W286 (Fig. 4B). Interestingly, the fragment also overlaps with a crystallographic glycerol molecule (not shown), suggesting the expanded ligand may now occupy a new but “druggable” subpocket. The bicyclic addition also had a smina-score estimate of binding affinity comparable to that of the original ligand (−10.10 vs. −10.72 kcal mol⁻¹), suggesting the substitution is sensible given the known crystallographic pose. The average score of three similar compounds generated using moiety substitutions sampled randomly from the training data was substantially worse than that of both the original and DeepFrag-optimized ligands (−8.00 ± 0.15 kcal mol⁻¹), lending further credence to the DeepFrag fragment selection.

2.5.3.3 NanB sialidase (Streptococcus pneumoniae). Finally, we applied DeepFrag to NanB Sialidase from S. pneumoniae bound to 3-ammoniopropane-1-sulfonate (Fig. 4C; PDB 4FOW (ref. 27)). The primary amine of the ligand (marked with an asterisk) is likely positively charged because it is positioned among three negatively charged amino acids (E541, D327, and D270). To further illustrate how DeepFrag can account for electrostatic interactions, we removed the amino group and used DeepFrag to replace it. Though the correct amino group was among the top-ranked fragments (8th), the top fragment was in fact ethylamine (*NCC). The secondary amine can still form electrostatic interactions, but the expanded ethyl group may form additional hydrophobic interactions with I246 and P492, possibly explaining why DeepFrag preferred the larger fragment at this position. The ethyl addition also slightly improved the smina-score estimate of binding affinity over that of the original ligand (−4.94 vs. −4.86 kcal mol⁻¹).

In this case, the average score of three similar negative-control compounds (−4.99 ± 0.41 kcal mol⁻¹) was comparable to the scores of the crystallographic and DeepFrag ligands. We note that the crystallographic ligand (3-aminopropane-1-sulfonic acid) is a notably weak inhibitor (25.7% inhibition at 500 μM, and no inhibition at 100 μM) that had not previously been subject to extensive experimental lead optimization.²⁷ While docking-score and/or DeepFrag inaccuracies cannot be ruled out, the affinity of the (unoptimized) crystallographic ligand may in fact be comparable to the affinities of the chemically similar compounds with random substitutions.

2.6 DeepFrag optimization by moiety addition

Thus far we have shown that DeepFrag can identify effective moiety replacements. While moiety swapping is a useful lead-optimization strategy, optimization often involves the addition of new moieties rather than the replacement of existing ones. To demonstrate the utility of our approach in this additional context, we turned to a recently published crystallographic screen targeting the SARS-CoV-2 main protease (M^Pro).²⁸ This screen identified multiple non-covalent ligands that bind in the protease active site. We used DeepFrag to recommend 24 moieties from the default LBL-SEEN set that might replace the various hydrogen atoms of 13 crystallographic ligands. We then used RDKit¹⁹ and smina²⁴ to position the resulting molecules within the M^Pro active site and to predict binding affinities (see ESI† for details).

The smina scores of the 24 DeepFrag-optimized compounds were on average 0.16 kcal mol⁻¹ better than those of the corresponding original ligands, suggesting the added moieties are sensible given the known crystallographic binding poses of the parents. When only the best-scoring DeepFrag-optimized compound associated with each crystallographic ligand was considered (13 compounds), the average improvement was 0.38 kcal mol⁻¹.

The DeepFrag modification that ranked first in terms of smina-score improvement is shown in Fig. 5A. This example shows how a DeepFrag addition can notably improve receptor/ligand shape complementarity. Adding a fused bicyclic moiety to the known Z1619978933 ligand (PDB 5RGH (ref. 28)) improved the smina score by 0.85 kcal mol⁻¹ (from −4.46 to −5.31 kcal mol⁻¹). Fig. 5B illustrates the third-ranked DeepFrag optimization in terms of score improvement, chosen because it provides a good illustration of an optimization that enables a novel interaction with the protein receptor. The addition of a single hydroxyl group to compound Z1367324110 (PDB 5R81 (ref. 28)) improved the score by 0.73 kcal mol⁻¹ (from −6.09 to −6.82 kcal mol⁻¹; see ESI† for details).

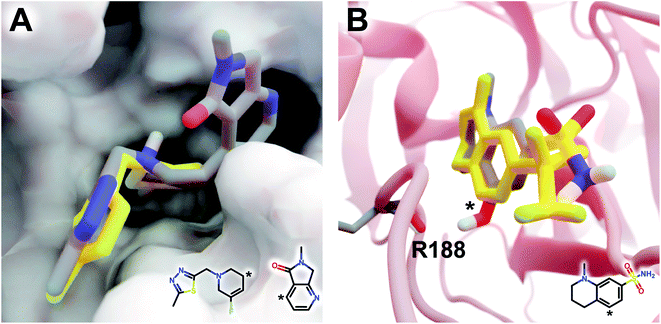Fig. 5 Optimized compounds derived from crystallographic ligands known to bind SARS-CoV-2 (M^Pro).²⁸ In both cases, the original ligand is shown in yellow sticks (crystallographic pose), and the DeepFrag-optimized compound is colored by element (positioned using RDKit¹⁹ and smina;²⁴ see ESI†). (A) In one case (compound Z1619978933; PDB 5RGH (ref. 28)), DeepFrag suggested a fused bicyclic addition that may extend into a distinct subpocket, enhancing shape complementarity with the protein receptor (shown in surface representation). The crystallographic fragment and DeepFrag-suggested moiety (2D) are overlaid, with connection points marked with asterisks. (B) In another case (compound Z1367324110; PDB 5R81 (ref. 28)), DeepFrag suggested a hydroxyl addition (marked with an asterisk) that may form a hydrogen bond with R188. The hydroxyl hydrogen atom was manually rotated to illustrate the bond, given that smina does not position hydrogen atoms. A 2D representation of the original crystallographic fragment is overlaid, with the location of the added hydroxyl marked with an asterisk. Figure rendered using BlendMol.²³

Encouragingly, in each of these cases the average score of three similar compounds generated by adding randomly sampled fragments (negative controls; −4.97 ± 0.42 kcal mol⁻¹ and −6.66 ± 0.03 kcal mol⁻¹, respectively) was worse than that of the corresponding DeepFrag-optimized compound. These negative controls were generated via moiety additions (not substitutions) to unoptimized, presumably low-affinity fragments identified in a crystallographic screen,²⁸ so it is only somewhat surprising that they have better scores (on average) than the original crystallographic fragments.

2.7 Comparison with other approaches

Recently, machine-learning techniques have been applied to many tasks in computer-aided drug discovery. Specifically, the use of 3D-voxel descriptors in conjunction with convolutional neural networks is now commonplace, in part because the use of voxel-grid descriptors allows researchers to re-purpose machine-learning techniques from computer vision. But voxelation approaches do have their limitations. For example, molecular structures have no canonical orientation, so effectively training a machine-learning model on these descriptors requires “tricks” such as rotation augmentation in order to learn rotation invariance. In contrast, graph-based machine-learning models such as PotentialNet⁸ have rotation and translation invariance “built-in” and could therefore represent an effective alternative. We pursued a voxelation-based approach because it has been successfully applied to related tasks such as binding-affinity prediction,^1–3 virtual screening,^4–7 and QSAR,⁸ but graph-based methods are promising alternatives.

DeepFrag is also unique among programs for generative modeling. Several authors have repurposed generative architectures used in computer vision for use in drug design (e.g., generative adversarial networks, GANs; variational autoencoders, VAEs). For example, Skalic et al. developed a generative adversarial model derived from BicycleGan²⁹ that can create 3D pharmacophoric maps from a receptor target. A subsequent step generates SMILES strings using a recurrent “captioning network”.¹¹ Several other authors have created models that generate molecular analogues independently of a target receptor using a continuous, learned latent space,^30,31 generative recurrent networks,³² or deep reinforcement learning.³³ While promising, these approaches are difficult to evaluate quantitatively, making it challenging to decide when to use them in a production pipeline. In contrast, DeepFrag is unique in that it (1) formulates small-molecule lead optimization as a classification problem rather than a generative modeling problem and (2) predicts a fragment fingerprint given a 3D-voxel grid representation of a ligand/protein complex. To the best of our knowledge, ours is the first system to perform data-driven lead optimization in this way.

Others have applied more traditional approaches to fragment-based lead optimization that do not leverage machine learning.^34,35 For example, a recent publication by Shan et al.³⁴ proposed FragRep, a program that also aims to guide local fragment optimization in the context of a binding pocket. Whereas FragRep uses hand-crafted rules to identify suitable fragments, DeepFrag infers these rules from a large dataset of examples. Additionally, generating a prediction in DeepFrag takes roughly 0.3 seconds on a GPU, compared to 60–120 seconds for FragRep. On the other hand, FragRep is advantageous in that it can also generate predictions for internal scaffold fragments (i.e., non-terminal fragments).

3 Conclusions

Lead optimization is a critical early step in the drug-discovery process. DeepFrag, a free machine-learning program aimed at guiding this important process, will thus be a useful tool for the computational-biology community. Though not a substitute for a trained medicinal chemist, DeepFrag is highly effective for hypothesis generation. It provides fragment suggestions that trained chemists and biologists can then evaluate, synthesize, and experimentally test.

Although DeepFrag accuracy is impressive, the approach has several notable limitations. Two of these limitations stem from our use of crystallographic data for training. First, crystallographic artifacts (e.g., due to crystallographic packing³⁶) occasionally produce ligand/receptor conformations that differ from the physiological conformations that are most useful for drug discovery. Second, even when a crystallographic conformation is physiologically relevant, it represents only a single conformation. In reality, binding pockets are often highly dynamic, sampling multiple druggable conformations. And ligand/fragment binding can influence those dynamics via conformational-selection and induced-fit mechanisms.³⁷

Our approach also assumes that adding a fragment does not substantially impact the binding geometry of the initial parent portion of the ligand, an assumption that underlies many lead-optimization approaches. A common goal of moiety swapping or fragment addition is to improve binding affinity by enabling additional interactions with the receptor. When a chemical modification does not change how the remainder of the ligand interacts with the protein, structure-based rational design is possible because improvements to affinity can be largely isolated to the modified fragment itself. For example, the bovine trypsin inhibitor N-cyclooctylglycyl-N-(4-carbamimidoylbenzyl)-L-prolinamide has a K_d of 276 nM.³⁸ When its cyclooctyl moiety is replaced with a cyclohexyl moiety, the K_d improves to 239 nM. Crystal structures of both ligands bound to trypsin reveal that the binding geometries of their common (parent) substructures are nearly superimposable (PDBs 2ZQ2 and 3LJO, respectively³⁸), so the improvement in affinity can be largely attributed to the cyclooctyl-to-cyclohexyl modification.

In contrast, if a molecular modification forces the rest of the molecule to shift substantially within the binding site, it is more difficult to attribute changes in affinity to the modification alone. Rational design is complicated in these scenarios because ligand–receptor interactions distant from the fragment may be disrupted in unpredictable ways, and new unexpected interactions may form. For example, the endothiapepsin inhibitor N-ethyl-2-({N-[2-(1H-indol-3-yl)ethyl]glycyl}amino)-4-phenylthiophene-3-carboxamide has a K_i of 4.0 μM.³⁹ In contrast, the very similar compound N-benzyl-2-[(N-benzyl-beta-alanyl)amino]-4-phenylthiophene-3-carboxamide, which can be derived from the first by swapping a methyl for a phenyl group and a tryptamine for a benzyl(methyl)amine, has a K_i of 545 nM. Crystal structures reveal that the binding geometries of these two ligands are entirely different, despite their chemical similarities (PDBs 4L6B and 4LAP, respectively³⁹). In those rare cases where small chemical modifications fundamentally alter the binding modes of entire ligands, DeepFrag will also likely fail.

These limitations aside, we expect DeepFrag to be useful in many applications. To encourage broad adoption, we release the DeepFrag model and software under the permissive Apache License, Version 2.0 (http://durrantlab.com/deepfragmodel). The git repository also includes a link to a Google Colaboratory Notebook¹⁴ for testing.

4 Materials and methods

4.1 Training datasets: receptor/ligand complexes

Our goal was to train a supervised model to complete a 3D structure of a receptor-bound partial ligand (“parent”) with a molecular fragment, such that the resulting composite molecule (parent + fragment) is highly complementary to the receptor. To this end, we constructed a library of (receptor/parent, fragment) examples, where each fragment is a well-suited choice for the corresponding receptor/parent complex. We assembled this library from the Binding MOAD dataset,¹⁶ which includes experimentally derived structure data for 38 702 receptor/ligand complexes (Fig. 1A).

4.1.1 Data pre-processing. The crystal structures contained water molecules as well as crystallographic additives (e.g., buffers, salts). The Binding MOAD specifically catalogues which ligands are biologically relevant. We used these annotations to strip irrelevant artifacts before generating fragments. Additionally, some complexes contain several bound ligands per receptor. In these cases, we isolated each ligand as a separate receptor/ligand complex.

4.1.2 Ligand fragmentation. For each receptor/ligand complex, we generated multiple (receptor/parent, fragment) training examples by iterating over all ligand single bonds and performing a cut (Fig. 1B). We retained the resulting example if it satisfied the following criteria:

• The cut split the ligand into two disconnected pieces (e.g., cutting a ring was not permitted)

• The smaller piece contained at least one heavy atom.

• The smaller piece had a molecular weight < 150 Da.

• The connection point between the parent and fragment was within 4 Å of a receptor atom.

When these conditions were met, we labeled the smaller and larger pieces of the ligand the fragment and parent, respectively. All fragments were standardized using MolVS transformation rules.⁴⁰ Specifically, for each fragment, we neutralized the charge and generated a canonical tautomer. By constraining our dataset to only fragments located near the receptor surface, we ensured that they were likely to form interaction(s) with their respective receptors. There were ultimately 308 689 (receptor/parent, fragment) examples that met these criteria.

4.1.3 Data splits. The examples were partitioned into three sets (TRAIN, VAL, and TEST), in the approximate ratio 60/20/20. We trained models on the TRAIN set and used the VAL set to monitor performance, tune hyperparameters, and prevent over-fitting. We report final results on the withheld TEST set.

Some protein targets are repeated in the Binding MOAD. To ensure our model generalized to unseen receptors, we created a three-way “vertical split” so that homologous targets were not shared between the TRAIN, VAL, or TEST sets. The Binding MOAD provides 90% similarity families that we used to determine if two targets were homologous.

Similarly, many ligands bind to multiple targets, and some metabolites such as ATP occur very frequently. To prevent the model from simply memorizing common ligands, we further ensured that ligands (in addition to receptors) were not shared between the TRAIN, VAL, and TEST sets. We examined the previous “vertical split” dataset and identified ligands shared across multiple splits by comparing canonical SMILES strings. Each shared ligand was then randomly assigned to one of the sets, and examples from the other set(s) were discarded.

4.2 Receptor/parent complexes as voxel grids

We converted the structures of each receptor/parent example into a 3D voxel grid (Fig. 1C). To generate each grid, we placed a virtual box in the receptor pocket, centered on the fragment/parent connection point (i.e., the location of the parent atom from which the fragment should branch). A technical description of the approach can be found in the ESI.†

4.2.1 Data-handling optimizations. We used two optimizations to accelerate data handling. First, to load the receptor/parent data faster, we stripped all irrelevant information from the source PDB files and saved only atomic coordinates and atom types to a packed HDF5 file. During training, we loaded this entire dataset into memory for rapid access, thereby drastically decreasing training startup time.

Second, to convert this data to a voxel grid, we developed a GPU-accelerated grid-generation routine using Numba, a high-performance Python just-in-time compiler.⁴¹ As others have noted,⁴² a GPU-accelerated approach reduces grid-generation wall-time substantially (more than 10× in our case). We therefore opted to generate all grids on the fly each time they were needed (i.e., once per epoch), without ever saving them to the disk or storing them long-term in memory. As part of the grid-generation process, we randomly rotated each example. The model was thus trained on differently rotated grids every epoch, a form of data augmentation aimed at encouraging rotation-invariant learning.

4.3 Representing fragments as fingerprint vectors

We converted the fragments of the TRAIN, VAL, and TEST sets to fingerprint vectors by applying the RDKFingerprint algorithm¹⁸ provided by the RDKit library.¹⁹ RDKFingerprint is an implementation of a daylight-like topological fingerprint, which enumerates subpaths in a molecule and computes hashes. Each hash seeds a pseudo-random number generator, which is used to randomly set bits in the fingerprint bitstring. Molecules with matching subpaths share common bits. Specifically, we allowed the subpath enumeration to consider all paths of size ≤10 to differentiate between larger fragments (e.g., alkanes). We folded the final bitstring to a size of 2048. The generated fingerprints contained only 0's or 1's, but we allowed our model to predict continuous vectors with each element in the range (0, 1) (enforced with a sigmoid activation layer).

4.4 DeepFrag model

4.4.1 Architecture. We used a deep 3D convolutional neural network to predict fragment RDKFingerprints from voxel-grid representations of receptor/parent complexes (Fig. 1D). The model consists of several repeated blocks of 3D convolution layers followed by a global average pooling layer and several fully connected layers. Each convolution block starts with a batch normalization layer and ends with a 3D max pooling layer (except the last block). In the fully connected section, we use dropout layers to prevent overfitting. All intermediate activations are ReLU except for the last layer, which uses a sigmoid activation to map values into the range (0, 1). The final “optimized” model architecture is shown in Fig. S2.†

4.4.2 Training details. Models were implemented in PyTorch.⁴³ We used the Adam optimizer⁴⁴ with the default momentum schedule. For each epoch, we randomly sampled batches from the TRAIN set and computed predicted fingerprints after applying random grid rotations. 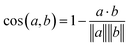The loss was computed as the average cosine distance between the predicted fragment fingerprints and the fingerprints of the corresponding correct (known) fragments for each batch (eqn (1)).

Eqn (1) Cosine distance between fingerprint vectors a and b. A distance of 0 represents parallel vectors. A distance of 1 represents orthogonal vectors.

To monitor training, we randomly sampled a subset of the VAL set after each epoch and computed an average validation loss using the same loss function. We only saved new model checkpoints when the validation loss reached a new global minimum. Training continued until we observed convergence. To accelerate training, we trained models using either NVIDIA Titan X or NVIDIA GTX1080 GPUs.

4.5 Label sets, fragment selection, and TOP-k accuracy

The model itself predicts a fingerprint in RDKFingerprint space, not a human-interpretable fragment representation. To map an output fingerprint to specific fragments, we compute the cosine distance (eqn (1)) between the predicted fingerprint and each fingerprint in a large library of RDKFingerprints corresponding to known fragments (Fig. 1E), which we call a “label set”. Using these distances we can rank fragments by similarity to the predicted fingerprint and identify the “closest match”. The label set is not necessarily the same set of fingerprints used to train, validate, or test the model. Rather, it is the set of all fragments from which the model can ultimately choose.

If the label set contains fragments known to be correct (i.e., if it includes the fragments of the VAL and/or TEST sets), it is possible to quantitatively evaluate a model's accuracy. We consider TOP-k accuracy, for k ∈ {1, 8, 64}. For example, TOP-8 accuracy represents the probability of finding the correct fragment in the set of the top eight predicted fragments.

4.6 Final model: training to convergence

Once we settled on a set of effective hyperparameters (see ESI†), we trained an “optimal” model, which we call DeepFrag. We trained the final model to convergence (5 days on a GPU) and evaluated its TOP-k accuracy on the withheld TEST set, using as a label set the fragment fingerprints of the TRAIN, VAL, and TEST sets. Training to convergence required substantial computer resources. But using DeepFrag to prospectively evaluate a single receptor/parent complex (i.e., at inference time) requires only a few grid-generation steps that can easily run on a CPU.

Using the fully converged model, we also explored the effect of test-time augmentation on model accuracy. We evaluated the effect of sampling multiple random rotations per example and averaging the predicted fingerprints to generate a multi-rotation, ensemble prediction. See the ESI† for full details.

Author contributions

H. G., D. R. K., and J. D. D. designed the study, discussed the results, and contributed to writing the manuscript. H. G. designed and trained the machine-learning model. H. G. and J. D. D. performed the tests to demonstrate effectiveness. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Matthew Ragoza, Tomohide Masuda, and Dale Erikson for useful discussions. We also thank the University of Pittsburgh's Center for Research Computing for providing helpful computer resources. This work was supported by the National Institute of General Medical Sciences of the National Institutes of Health [R01GM132353 to J. D. D. and R01GM108340 to D. R. K]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Notes and references

1. J. Gomes, B. Ramsundar, E. N. Feinberg and V. S. Pande, 2017, arXiv:1703.10603.
2. M. M. Stepniewska-Dziubinska, P. Zielenkiewicz and P. Siedlecki, Bioinformatics, 2018, 34, 3666–3674.
3. J. Jiménez-Luna, L. Pérez-Benito, G. Martínez-Rosell, S. Sciabola, R. Torella, G. Tresadern and G. De Fabritiis, Chem. Sci., 2019, 10, 10911–10918.
4. I. Wallach, M. Dzamba and A. Heifets, 2015, arXiv:1510.02855.
5. M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2017, 57, 942–957.
6. J. Cruz Pereira, E. Rauí Caffarena and C. Nogueira dos Santos, J. Chem. Inf. Model., 2016, 56, 2495–2506.
7. J. Lim, S. Ryu, K. Park, Y. J. Choe, J. Ham and W. Y. Kim, J. Chem. Inf. Model., 2019, 59, 3981–3988.
8. E. N. Feinberg, D. Sur, Z. Wu, B. E. Husic, H. Mai, Y. Li, S. Sun, J. Yang, B. Ramsundar and V. S. Pande, ACS Cent. Sci., 2018, 4, 1520–1530.
9. T. Karras, S. Laine and T. Aila, 2018, arXiv:1812.04948.
10. L. A. Gatys, A. S. Ecker and M. Bethge, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, 2016, pp. 2414–2423.
11. M. Skalic, D. Sabbadin, B. Sattarov, S. Sciabola, G. D. Fabritiis, M. Skalic, D. Sabbadin, B. Sattarov and S. Sciabola, Mol. Pharm., 2019, 4282–4291.
12. M. Skalic, A. Varela-Rial, J. Jiménez, G. Martínez-Rosell and G. De Fabritiis, Bioinformatics, 2019, 35, 243–250.
13. N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inf. Model., 2019, 59, 1096–1108.
14. E. Bisong, in Google Colaboratory, Apress, Berkeley, CA, 2019, pp. 59–64.
15. C. M. Dobson, Chemical space and biology, 2004.
16. L. Hu, M. L. Benson, R. D. Smith, M. G. Lerner and H. A. Carlson, Proteins, 2005, 60, 333–340.
17. J. Jiménez, S. Doerr, G. Martínez-Rosell, A. S. Rose and G. De Fabritiis, Bioinformatics, 2017, 33, 3036–3042.
18. G. Landrum, The RDKit 2020.09.1 documentation, 2020, http://rdkit.org/docs/source/rdkit.Chem.rdmolops.html.
19. G. Landrum, RDKit: open-source cheminformatics, http://www.rdkit.org/.
20. R. L. Wiseman, S. M. Johnson, M. S. Kelker, T. Foss, I. A. Wilson and J. W. Kelly, J. Am. Chem. Soc., 2005, 127, 5540–5551.
21. Y. Nakatsu, T. Yamamotoya, K. Ueda, H. Ono, M.-K. Inoue, Y. Matsunaga, A. Kushiyama, H. Sakoda, M. Fujishiro, A. Matsubara and T. Asano, Cancer Lett., 2020, 470, 106–114.
22. A. Potter, V. Oldfield, C. Nunns, C. Fromont, S. Ray, C. J. Northfield, C. J. Bryant, S. F. Scrace, D. Robinson and N. Matossova, et al. , Bioorg. Med. Chem. Lett., 2010, 20, 6483–6488.
23. J. D. Durrant, Bioinformatics, 2018, 35, 2323–2325.
24. D. R. Koes, M. P. Baumgartner and C. J. Camacho, J. Chem. Inf. Model., 2013, 53, 1893–1904.
25. Z. Szlávik, L. Ondi, M. Csékei, A. Paczal, Z. B. Szabó, G. Radics, J. Murray, J. Davidson, I. Chen, B. Davis, R. E. Hubbard, C. Pedder, P. Dokurno, A. Surgenor, J. Smith, A. Robertson, G. LeToumelin-Braizat, N. Cauquil, M. Zarka, D. Demarles, F. Perron-Sierra, A. Claperon, F. Colland, O. Geneste and A. Kotschy, J. Med. Chem., 2019, 62, 6913–6924.
26. M. Hrmova, V. A. Streltsov, B. J. Smith, A. Vasella, J. N. Varghese and G. B. Fincher, Biochemistry, 2005, 44, 16529–16539.
27. P. Brear, J. Telford, G. L. Taylor and N. J. Westwood, ChemBioChem, 2012, 13, 2374–2383.
28. A. Douangamath, D. Fearon, P. Gehrtz, T. Krojer, P. Lukacik, C. D. Owen, E. Resnick, C. Strain-Damerell, A. Aimon, P. Ábrányi-Balogh, J. Brandão-Neto, A. Carbery, G. Davison, A. Dias, T. D. Downes, L. Dunnett, M. Fairhead, J. D. Firth, S. P. Jones, A. Keeley, G. M. Keserü, H. F. Klein, M. P. Martin, M. E. M. Noble, P. O'Brien, A. Powell, R. N. Reddi, R. Skyner, M. Snee, M. J. Waring, C. Wild, N. London, F. von Delft and M. A. Walsh, Nat. Commun., 2020, 11, 5047.
29. J. Y. Zhu, R. Zhang, D. Pathak, T. Darrell, A. A. Efros, O. Wang and E. Shechtman, Advances in Neural Information Processing Systems, 2017, pp. 466–477.
30. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276.
31. M. Ragoza, T. Masuda and D. R. Koes, 2020, arXiv:2010.08687.
32. A. Gupta, A. T. Müller, B. J. Huisman, J. A. Fuchs, P. Schneider and G. Schneider, Mol. Inf., 2018, 37, 1700111.
33. Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Sci. Rep., 2019, 9, 1–10.
34. J. Shan, X. Pan, X. Wang, X. Xiao and C. Ji, J. Chem. Inf. Model., 2020, 60, 5900–5906.
35. J. O. Spiegel and J. D. Durrant, J. Cheminf., 2020, 12, 1–16.
36. K. Elez, A. M. J. J. Bonvin and A. Vangone, BMC Bioinf., 2018, 19, 438.
37. J. D. Durrant and J. A. McCammon, BMC Biol., 2011, 9, 71–79.
38. T. Brandt, N. Holzmann, L. Muley, M. Khayat, C. Wegscheid-Gerlach, B. Baum, A. Heine, D. Hangauer and G. Klebe, J. Mol. Biol., 2011, 405, 1170–1187.
39. M. Kuhnert, H. Köster, R. Bartholomäus, A. Y. Park, A. Shahim, A. Heine, H. Steuber, G. Klebe and W. E. Diederich, Angew. Chem., Int. Ed. Engl., 2015, 54, 2849–2853.
40. M. Swain, MolVS: Molecule Validation and Standardization, 2018, https://github.com/mcs07/MolVS.
41. S. K. Lam, A. Pitrou and S. Seibert, Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC – LLVM15, 2015, pp. 1–6.
42. J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2020, 60, 1079–1084.
43. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2019, vol. 32, pp. 8024–8035.
44. D. P. Kingma and J. Ba, Adam: a method for stochastic optimization, 2017.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc00163a

---