Stretching [8]cycloparaphenylene with encapsulated potassium cations: structural and theoretical insights into core perturbation upon four-fold reduction and complexation

Abstract

The consequences of four-electron addition to [8]cycloparaphenylene ([8]CPP, 1) have been evaluated crystallographically, revealing a significant core deformation. The structural analysis exposes an elliptical distortion observed upon electron transfer, with the deformation parameter (D.P.) increased by 28% in comparison with neutral [8]CPP. The C–C bond length alteration pattern also indicates a quinoidal structural rearrangement upon four-fold reduction. The large internal cavity of [8]CPP⁴⁻ allows the encapsulation of two {K⁺(THF)₂} cationic moieties with two additional cations bound externally in the solid-state structure of [{K⁺(THF)₂}₄([8]CPP⁴⁻)]. The experimental structural data have been used as a benchmark for the comprehensive theoretical description of the geometric changes and electronic properties of the highly-charged [8]CPP⁴⁻ nanohoop in comparison with its neutral parent. While neutral [8]CPP and the [8]CPP²⁻ anion clearly show aromatic behavior of all six-membered rings, subsequent addition of two more electrons completely reverses their aromatic character to afford the highly-antiaromatic [8]CPP⁴⁻ anion, as evidenced by structural, topological, and magnetic descriptors. The disentanglement of electron transfer from metal binding effects allowed their contributions to the overall core perturbation of the negatively-charged [8]CPP to be revealed. Consequently, the internal coordination of potassium cations is identified as the main driving force for drastic elliptic distortion of the macrocyclic framework upon reduction.

---

Introduction

Curved, bent, and contorted polycyclic aromatic hydrocarbons (PAHs) attract significant attention due to their unique structures, chemical reactivity, and molecular strain, providing new opportunities in design of optoelectronic materials and novel supramolecular architectures.^1–5 Non-planar PAHs can also serve as multi-electron acceptors and have the capacity to supercharge,^6–10 which has been realized in high-performance batteries and ultracapacitors.^11–15 Recent advances in organic synthesis have provided access to new classes of non-planar PAHs with different carbon framework topologies and very interesting properties.^16–21 Among those, cycloparaphenylenes representing the shortest fragments of armchair carbon nanotubes (CNTs) have emerged on the scene as unique non-planar macrocyclic PAHs with radially oriented p orbitals.^16,17 Back in 1934, their structures have been conceptualized by Parekh and Guha,²² followed by Vögtle's pioneering synthetic efforts 60 years later.²³ The first [n]CPPs were successfully synthesized by Jasti and Bertozzi in 2008.²⁴ Following their seminal work, the selective syntheses of numerous [n]CPPs (n = 5–36) have been accomplished by various groups.^25–41 The recent focus has been concentrated at the preparation of large CPP-based nanocarbons with different topological frameworks^42–49 and studies of their structure-related properties, including size-dependent optoelectronic properties, host abilities and supramolecular behaviour.^50–55

Notably, the HOMO–LUMO gaps of CPPs become narrow with decreasing size, which contrasts most other non-planar PAHs that show narrowing of the HOMO–LUMO gaps upon increasing the number of aromatic rings.^56,57 Thus, the redox chemistry of [n]CPPs should be of special interest for a variety of applications, including new organic electroconductive or energy storage materials.^54,57–59 However, these investigations have been mainly limited to oxidation of several [n]CPPs reported by the Yamago group.^57,60 While various spectroscopic and computational tools have been used for investigation of the oxidized cationic species,^{53,56,57,59,60} multi-electron reduction properties of CPPs remained largely unexplored.⁶¹ The first crystal structure of the only highly-reduced [8]CPP tetraanion was reported back in 2013,⁶² revealing multi-electron accepting abilities of [n]CPPs. More recently, a series of the doubly-reduced [n]CPPs (n = 6, 8, 10, and 12) has been successfully characterized by single crystal X-ray diffraction,^63,64 illustrating their macrocyclic core changes upon two-electron acquisition and unique size-dependent host abilities for encapsulation of various guests.

Herein, we report the synthesis and X-ray crystallographic study of a new highly-reduced product of [8]CPP (C₄₈H₃₂, 1) that was crystallized from the reaction of 1 with K metal in THF without additional secondary ligands as [{K⁺(THF)₂}₄(1^4–)]. This has allowed in-depth theoretical analysis of structural and electronic consequences of four-fold electron transfer to the [8]CPP nanohoop. Importantly, decoupling of consequences of electron transfer from metal binding effects and separation of internal vs. external coordination has been carefully executed using computational tools.

Results and discussion

Four-fold reduction of [8]CPP: crystal structure and supramolecular packing

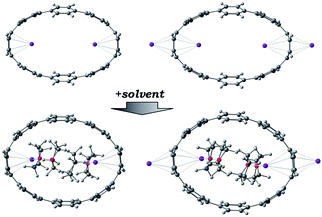
The chemical reduction of [8]CPP (1) with excess K metal in THF afforded black plate-shaped crystals grown in situ in moderate yield (Scheme 1). The air- and moisture sensitive crystals were suitable for direct X-ray diffraction analysis but exhibited very low solubility in common organic solvents, thus limiting their solution characterization. The reduction process can be followed by UV-vis spectroscopy (Fig. S2†), as the reaction proceeds through several distinctive steps accompanied by characteristic color changes: a pale-brown solution turns to purple (associated with the doubly-reduced state) and then transforms to a final black-blue color (associated with the title product). The absorbance maximum corresponding to the π–π* transition in the UV-vis spectrum of 1⁴⁻/4K⁺ (THF) is observed at λ_max = 431 nm (Fig. S3†). A significant bathochromic shift is seen upon reduction compared to neutral [8]CPP (λ_max = 340 nm),⁶⁵ illustrating substantial alteration of the electronic structure of 1⁴⁻vs. neutral 1⁰.

Scheme 1 Chemical reduction of [8]CPP (1).

The X-ray diffraction analysis of the above crystals confirmed the formation of a new complex with four potassium cations, [{K⁺(THF)₂}₄(1^4–)] (2). In the crystal structure, two crystallographically equivalent K⁺ ions (Fig. S4†) are filling the internal cavity of the [8]CPP⁴⁻ nanohoop, while the other two are coordinated to the core exterior (Fig. 1). Specifically, the internal K⁺ ions are bound to the opposite six-membered rings of 1^4– in a η⁶-fashion, with the corresponding K⋯C distances ranging over 2.977(11)–3.341(10) Å. Additionally, these ions show K⋯C contacts to the neighboring six-membered rings with the distances of 3.086(10)–3.122(12) Å. The coordination environment of each K⁺ ion is completed by two THF molecules (K⋯O_THF, 2.634(19) and 2.693(9) Å), fully filling the internal void of [8]CPP⁴⁻.

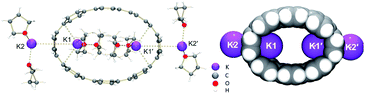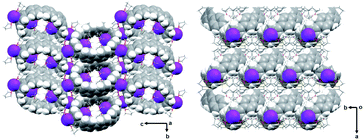
Fig. 1 Crystal structure of [{K⁺(THF)₂}₄(1^4–)] (2) (ball-and-stick model) and metal coordination (space-filling model).

Two remaining K⁺ ions are η⁶-coordinated to the same six-membered rings from the outside of the 1^4– core with the K⋯C distances spanning over 3.114(10)–3.402(10) Å. Similarly, each K⁺ ion has two coordinated THF molecules (K⋯O_THF, 2.687(8) and 2.699(9) Å), with all K⋯C and K⋯O distances being comparable to those previously reported.^{8,62,63,66,67}

In the solid-state structure of 2, additional K⋯C contacts (3.102(11)–3.309(11) Å) are found between the external K⁺ ions and the exterior π-surface of the adjacent 1^4– anions (Fig. 2). These intermolecular cation-π interactions result in the formation of a 2D supramolecular layered structure (Fig. 3). Notably, this solid-state arrangement differs from the zigzag 1D polymeric chains observed in [{K⁺(18-crown-6)(THF)}{K⁺(18-crown-6)}{K⁺₂(THF)₂(1^4–)}].⁶² In the latter, the encapsulation of external K⁺ ions with 18-crown-6 ether prevented multiple additional intermolecular contacts and reinforced the 1D chain propagation through the interior K⁺ ion interactions with the adjacent 1⁴⁻ anions. The two crystallographically confirmed examples of 1^4– existing in different coordination environments provide a unique pair for direct structural comparison with their neutral parent. These two crystal structures not only allow the comparative evaluation of core deformation upon four-electron acquisition but could reveal the influence of subtle differences in metal binding and crystal packing.

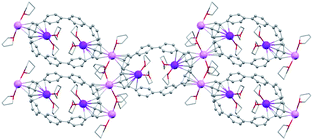Fig. 2 Additional K⋯C contacts between external K⁺ ions and four neighboring molecules in 2 (mixed model; H-atoms are removed and external K ions are shown in pink).

Fig. 3 Solid-state packing of 2, mixed models.

Structural deformation and host–guest properties of [8]CPP^4–

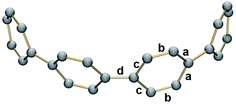
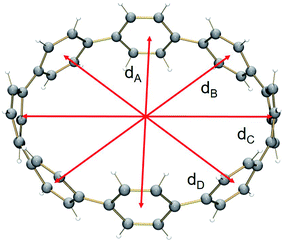
In 2, significant deformation of the [8]CPP⁴⁻ core is observed compared to the neutral parent which is clearly reflected by the change of C–C bond length distances (Table 1). In 1^4–, the average bridging C–C bond distance is significantly shortened from 1.486(2) Å in [8]CPP²⁶ to 1.442(15) Å (Δ = 0.044 Å). In contrast, the average C–C bond distances at a and c are elongated upon four-fold reduction by up to 0.03 Å. These changes are generally similar to those observed previously.⁶²

Table 1 Key C–C bond distances (Å)^a of [8]CPP in its neutral and reduced forms, along with a labeling scheme

	1	1 ^2−	1 ^4−	1 ^4–
a The values for bond distances are all averaged. b Ref. 26. c Ref. 64. d Ref. 62.
a	1.401(2)	1.422(3)	1.429(9)	1.431(15)
b	1.383(2)	1.366(4)	1.365(9)	1.373(15)
c	1.400(2)	1.419(3)	1.427(9)	1.430(15)
d	1.486(2)	1.443(4)	1.437(9)	1.442(15)

---

The structural deformation of 1 upon reduction can be revealed by comparison of inner diameters and angles between the plane of six-membered rings and the macrocycle central axis of the reduced forms vs. neutral parent. Upon two-electron addition to 1, the deformation parameter (D.P. = d_max/d_min) is increased from 1.09 to 1.19 in 1^2–, and this value is significantly increased to 1.40–1.45 in the tetrareduced form, 1^4– (Table 2). This notable change indicates that the nanohoop core is gradually compressed along the d_A direction by ca. 9% and 30% upon two- and four-electron charging, respectively. This is accompanied by an elongation along the opposite d_C direction, changing the round shape of 1 to pronounced elliptical in 1^4–.

Table 2 Inner diameters (Å) of [8]CPP in its neutral and reduced forms, along with a labeling scheme

	1	1 ^2−	1 ^4−	1 ^4–
a Ref. 26. b Ref. 64. c Ref. 62. d DP = dmax/dmin.
d A	10.364	9.958	8.868	9.138
d B	10.376	10.678	10.917	10.712
d C	11.281	11.856	12.866	12.748
d D	11.351	10.098	10.337	10.757
DP^d	1.09	1.19	1.45	1.40

---

Compared with the neutral parent, the average angle between the plane of six-membered rings and the macrocycle central axis is decreased by 10.7° in the highly-reduced 1^4– state (Table 3 and Fig. S9†). This structural change is consistent with the coplanarization of the phenyl rings expected for the increased quinoidal character of the negatively-charged [8]CPP anions. The observed ring re-orientation also increases an internal open space of the four-fold reduced nanohoop, thus enhancing its host-guest binding ability.

Table 3 Selected angles (°) of [8]CPP in its neutral and reduced forms, along with a labeling scheme

	1	1 ^2−	1 ^4−	1 ^4–
a Ref. 26. b Ref. 64. c Ref. 62.
a A/L	25.4	5.9	14.9	5.2
a B/L	19.9	5.0	6.3	4.3
a C/L	7.0	1.3	4.7	1.3
a D/L	8.5	6.6	6.0	7.3

---

In the doubly-reduced 1^2–, the internal space is increased to 608 ų compared to 493 ų in 1 (Table 4), allowing the accommodation of two halves of large {K⁺(18-crown-6)} moieties.⁶⁴ In 2, the internal void volume of 1^4– of 548 ų is sufficient for entrapment of two {K⁺(THF)₂} cations (Fig. 4a). An inclusion of the {K⁺₂(THF)₂} cationic guest facilitated by high negative charge of the [8]CPP⁴⁻ host has been seen previously (Fig. 4b).⁶² Importantly, a clear elliptical distortion of the nanohoop core has been detected for 1^4– in both crystallographically characterized complexes. To untie the effect of electron transfer from metal binding influence, we turned to a comprehensive computational investigation.

Table 4 Internal volumes (ų) in the neutral and reduced forms of [8]CPP

	1	1 ^2−	1 ^4−	1 ^4–
a Ref. 26. b Ref. 64. c Ref. 62. d V void ≈ 4/3 × π × (dmin/2 × cos amin)^2 × (dmax/2 × cos amax). e V moiety ≈ N × 20. N is the number of non-hydrogen atoms in the moiety.
Void space^d	493	608	492	548
Moiety	—	1/2{K^+(18-crown-6)} × 2	{K^+(THF)2} & {K^+}	{K^+(THF)2} × 2
Moiety volume^e	—	380	240	440
Host–guest formula	—	1/2{K^+(18-crown-6)}2 ⊂ 1^2–	{K^+2(THF)2} ⊂ 1^4–	{K^+(THF)2}2 ⊂ 1^4–

---

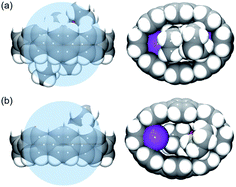Fig. 4 Comparison of host–guest interactions of 1^4– nanohoop in 2 (a) vs. that in ref. 62 (b), side and face views, space-filling models. The internal space is shown as the blue sphere.

Theoretical study: the effect of electron transfer

We performed a systematic theoretical investigation of the consequences of adding up to four electrons to the [8]CPP (1) framework focusing on geometric changes and electronic characteristics (see the ESI† for more details). In contrast to the crystallographic study, the computational investigation provides a powerful tool to separate the impact of electron acquisition from alkali metal binding effects. The geometries of the resulting products stemming from two and four electron addition to 1, along with selected geometric parameters, are presented in Fig. 5.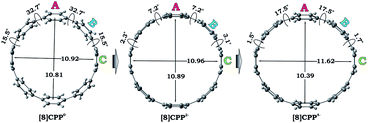

Fig. 5 Optimized geometries along with selected geometrical parameters for 1⁰, 1²⁻, and 1⁴⁻ (PBE0/cc-pVTZ).

Interestingly, addition of two electrons to [8]CPP leads to a simultaneous increase of both geometrical parameters d_A and d_C by 0.04 Å and 0.08 Å, respectively (Fig. 5 center), thus leaving the shape of the macrocycle essentially unchanged. In contrast, further reduction of [8]CPP to the tetrareduced state results in an elliptical distortion of the [8]CPP⁴⁻ core with a notable elongation of the d_C parameter to 11.62 Å (Δ = 0.70 Å) and contraction of the d_A distance down to 10.39 Å (Δ = 0.42 Å) (Fig. 5 right). These shape distortions are accompanied by significant changes in mutual orientation of rings A, B, and C as the function of the reduction state (Fig. 5). Specifically, the dihedral angle between rings A and B undergoes dramatic decrease from 32.7° to 7.2° upon acquisition of two electrons by [8]CPP. The same trend persists for the neighboring six-membered rings. However, addition of two more electrons results in restoring of the angle between rings A and B to 17.5°, whereas the angle between rings B and C shows further decrease down to 1.5°.

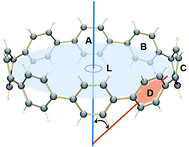
The observed trends are in agreement with the conclusion that two-fold reduction of [8]CPP leads to the electronic structure transformation from the benzenoid type to the quinoidal one.⁶⁸ This structural rearrangement is supported by distribution of carbon–carbon bond lengths in [8]CPP⁰ and [8]CPP²⁻ (distances b and d are shortened, whereas a and c become elongated upon reduction) as well as by the corresponding bond orders (Fig. 6). However, the highly-reduced [8]CPP⁴⁻ anion was found to exhibit a substantially different behavior. While the ring A clearly shows some restoration of the benzenoid character, the ring C can be best described as of a quinoidal type, with that character being even more pronounced compared with [8]CPP²⁻. Interestingly, the ring B represents an intermediate case where both benzenoid and quinoidal characteristics are mixed. It can be illustrated by the bond length and bond order distribution (Fig. 6). Thus, addition of four electrons to the [8]CPP core results in the formation of a unique hybrid macrocyclic π-system, which combines properties and elements of electronic structure of both quinoid and benzenoid types.

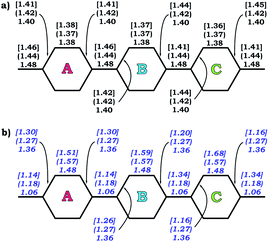Fig. 6 Selected C–C bond lengths (a) and bond orders (b) calculated for rings A, B, and C (PBE0/cc-pVTZ) in 1⁰, 1²⁻ (round brackets), and 1⁴⁻ [square brackets].

The observed trends prompted us to look into details of the electronic structure of [8]CPP and to analyze changes upon its sequential reduction. First of all, it should be mentioned that both doubly- and tetrareduced states have a closed-shell singlet ground state. However, whereas for [8]CPP²⁻ the singlet is well-energetically isolated from the corresponding triplet state by ∼8 kcal mol⁻¹, in the case of [8]CPP⁴⁻, the singlet-triplet gap is relatively small (∼2 kcal mol⁻¹). The 3D distribution of negative charge in the form of molecular electrostatic potentials (Fig. 7 top) immediately revealed another unique feature of this macrocyclic system. While in neutral [8]CPP both positive and negative charges are equally distributed between the external and internal surfaces, the anions show notable localization of negative charge in their internal part, which is especially pronounced in the highly-reduced [8]CPP⁴⁻ macrocycle. Such unusual behavior of [8]CPP upon reduction was further confirmed by 2D cross-section maps (Fig. 7 bottom), which show distribution of MEP (molecular electrostatic potential) in the plane of the macrocycle (see the ESI† for details). These 2D maps provide evidence that the endo-surface is substantially more negatively charged than the exo-surface in the doubly- and tetrareduced anions. This finding is in sharp contrast with open geodesic polyaromatic hydrocarbons such as bowl-shaped corannulene and sumanene, in which the corresponding anions show localization of negative charge on the convex surface.^69–71

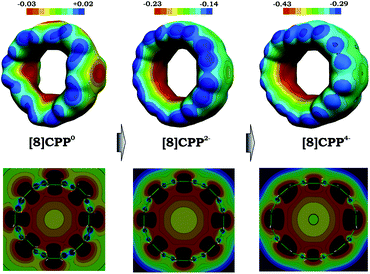Fig. 7 3D maps (top) and 2D cross-section (bottom) of the molecular electrostatic potential (MEP) for 1⁰, 1²⁻, and 1⁴⁻ (PBE0/cc-pVTZ).

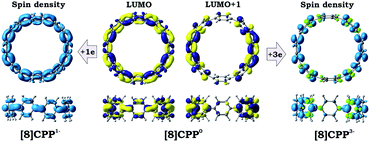
Transformation of the electronic structure of [8]CPP core from benzenoid to a quinoidal one upon electron acquisition can be rationalized by considering the lowest unoccupied molecular orbitals (LUMOs) of the neutral parent (Fig. 8 center). In order to further shed light on where extra electrons are localized, we investigated the reduced species with odd number of electrons, namely [8]CPP¹⁻ and [8]CPP³⁻, and analyzed their spin density distribution (Fig. 8 left and right, respectively). Together with the nature and topology of LUMO and LUMO+1 for [8]CPP, these data provide a complete picture of the electronic structure and its transformation upon stepwise reduction.

Fig. 8 LUMO and LUMO+1 of neutral [8]CPP (isosurface 0.035 a.u.; central) and spin density distribution (isosurface 0.03 a.u.) in the paramagnetic [8]CPP¹⁻ (left) and [8]CPP³⁻ (right) anions (both in their doublet state), respectively (PBE0/cc-pVTZ).

The nature of the LUMO clearly indicates possible formation of carbon–carbon double bonds at the connecting sites between the six-membered rings in the target system. Thus, occupation of this orbital by one or two electrons should lead to stabilization of the quinoidal resonance electronic structure with shortened c and d bonds and increased bond orders for these sites. Indeed, this is observed in the case of [8]CPP upon one and two electrons transfer. This conclusion is further supported by spin density distribution, which shows strong localization of the unpaired electron between the six-membered rings with a clear topology of the π-bond (Fig. 8). It is also worth mentioning that all d bonds equally participate in delocalization of the spin density in [8]CPP¹⁻ (Fig. 8 left). In contrast, LUMO+1 exhibits significant localization on the ring C with substantial participation of the ring B, whereas the ring A remains almost unaffected. These results are in excellent correlation with the spin density distribution in [8]CPP³⁻ (Fig. 8 right). Topologies of both spin density and LUMO+1 orbital evidence that addition of the third and fourth electrons should result in accumulation of the electron density on the bonds d and b of the ring C. As a result, the latter site is expected to show even more pronounced quinoidal character, which is in full agreement with the observed trends in the calculated bond lengths and bond orders (Fig. 6).

Significant changes in the electronic stricture of [8]CPP upon reduction are further confirmed by Anisotropic Induced Current Density (ACID) function (Fig. 9). Importantly, the ACID function represents mainly anisotropies of interatomic current and thus the electron delocalization. While neutral [8]CPP can be described as a sequence of six-membered rings connected by single C–C bonds, the [8]CPP²⁻ anion clearly shows a distinct charge delocalization over the d bond. This is especially notable when π-contribution to the ACID isosurface is considered (Fig. 10). For [8]CPP⁴⁻, such delocalization becomes even more pronounced, reaching its maximum for the ring C. This observation is also supported by numerical parameters such as structure-based HOMA (Table 5). However, subsequent plotting of current density vectors onto the ACID surface reveals a striking difference in aromatic behavior of six-membered rings, as the function of the reduction state of [8]CPP. In the neutral and doubly-reduced forms of [8]CPP, all six-membered rings exhibit diatropic ring currents attributed to aromatic behavior, whereas the highly-reduced [8]CPP⁴⁻ anion shows the paratropic current indicative of its anti-aromatic character.

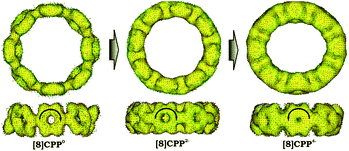Fig. 9 Full ACID isosurfaces for 1⁰, 1²⁻, and 1⁴⁻ (PBE0/cc-pVTZ). Current density vectors are plotted onto the ACID isosurface to indicate dia- and paratropic ring currents.

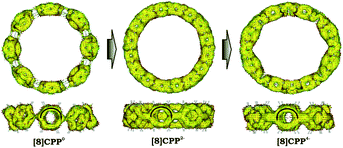Fig. 10 π-Contribution to the ACID isosurface for 1⁰, 1²⁻, and 1⁴⁻ (PBE0/cc-pVTZ). Current density vectors are plotted onto the ACID isosurface to indicate dia- and paratropic ring currents.

Table 5 Aromaticity descriptors^a calculated for [8]CPP in different reduction states

System	Ring	HOMA	NICS(0)	AIM^b		Fuzzy atomic space^c
				PDI	FLU	PDI	FLU
a Reference of C–C in HOMA is 1.388 Å and a = 257.7; NICSs are calculated at the PBE0/cc-pVTZ level (in ppm); the reference delocalization index of C–C in Bader's FLU is 1.3921e from benzene optimized at the PBE0/cc-pVTZ level, and in Becke's FLU, is 1.4637e. b Atomic overlap matrix is based on the basin integral in AIM. c Atomic overlap matrix is based on the fuzzy atom space integral over Becke atomic space.
[8]CPP^0	A	0.978	−6.88	0.089	0.002	0.090	0.004
	B	0.981	−7.45	0.090	0.002	0.091	0.004
	C	0.978	−6.89	0.089	0.002	0.090	0.004
[8]CPP^2−	A	0.846	−8.81	0.064	0.009	0.068	0.011
	B	0.845	−8.96	0.065	0.009	0.068	0.011
	C	0.849	−8.77	0.065	0.009	0.068	0.011
[8]CPP^4−	A	0.894	11.63	0.075	0.005	0.078	0.007
	B	0.672	17.88	0.054	0.014	0.059	0.017
	C	0.389	22.47	0.039	0.025	0.045	0.027
C6H6		1.000	−8.21	0.105	0.000	0.106	0.000

---

Subsequent investigation of magnetic nucleus independent chemical shifts (NICS) unambiguously confirmed the above conclusions. The calculated NICS(0) values (Table 5) for all rings in neutral [8]CPP (−6.88 to −7.45 ppm) clearly illustrate their aromatic character. Addition of two electrons further increases their aromaticity reaching its maximum of up to −9 ppm. At the same time, charging [8]CPP with four electrons completely reverses the aromaticity of the six-membered rings. The computed values of NICS(0) become highly positive ranging from +11.63 ppm for the ring A to its highest value of +22.47 for the ring C, illustrating their distinct anti-aromatic character.

The effect of alkali metal binding on the [8]CPP⁴⁻ core

For the next step, the influence of alkali metal coordination on the [8]CPP core has been carefully investigated. Four different models were considered, namely, two anionic systems, [{K⁺}₂([8]CPP⁴⁻)] and [{K⁺(THF)₂}₂([8]CPP⁴⁻)], and two neutral complexes, [(K⁺)₂{K⁺}₂([8]CPP⁴⁻)] and [(K⁺)₂{K⁺(THF)₂}₂([8]CPP⁴⁻)] (Fig. 11). Graphical comparison of the [8]CPP⁴⁻ core with and without alkali metals (Fig. 12) clearly shows that interaction of K⁺ ions with the selected nanohoop leads to its significant elliptic core distortion. It is worth noting that the energetics of such distortion was evaluated to be +10.78 kcal mol⁻¹, as compared with the unperturbed [8]CPP⁴⁻ macrocycle. At the same time, coordination by two potassium cations significantly stabilizes the closed-shell singlet ground state, increasing the singlet-triplet gap up to ∼15 kcal mol⁻¹.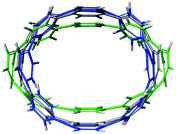

Fig. 11 Complexation of [8]CPP⁴⁻ with potassium counterions considered in this study.

Fig. 12 Depiction of the [8]CPP⁴⁻ core with alkali metal counterions (model [{K⁺}₂([8]CPP⁴⁻)], green) and without (gray) overlapped with a skeleton of neutral [8]CPP⁰ macrocycle (blue).

As expected, the first two potassium cations occupy the most negatively charged part of [8]CPP⁴⁻ host, namely its internal cavity, in full agreement with the topology of its HOMO. Coordination of two metal ions within the interior space leads to a dramatic decrease of the d_A parameter from 10.39 Å in the “naked” [8]CPP⁴⁻ host to 8.33 Å. Interestingly, addition of two more K⁺ ions to the exterior surface of [8]CPP⁴⁻ in accordance with crystallographic data (Fig. 11 top) does not result in any notable change of the core ellipticity (d_A = 8.12 Å). At the same time, inclusion of four coordinated THF molecules (Fig. 11 bottom) into consideration led to the closest resemblance with the experimentally observed parameters (d_A = 9.41 Å vs. 9.14 Å in 2). Moreover, subsequent addition of two external K⁺ cations again resulted in negligible changes in the macrocycle geometry. This comparison clearly supports the importance of inclusion of coordinated solvents into the computational model in order to achieve a high accuracy in reproducing the experimental geometric parameters. It also shows that the nature and size of internally encapsulated guests dominates over the effect of external alkali metal binding in these systems.

The influence of mechanical bending and metal coordination on the electronic structure of [8]CPP⁴⁻

Dramatic distortion of the [8]CPP geometry upon addition of four electrons and coordination by potassium cations prompted us to closely look into changes in the electronic structure and aromaticity. The influence of the mechanical bending and metal coordination were separated and individual contributions were evaluated. For these purposes, one additional model (noK-[8]CPP⁴⁻) was prepared by using the geometry of the [8]CPP⁴⁻ host from the [{K⁺}₂([8]CPP⁴⁻)] adduct, in which potassium cations were removed. No further geometry optimizations or modifications were performed. Such model allowed us to independently study the influence of the mechanical bending of the highly-charged cycloparaphenylene on its electronic structure. Analysis of 3D charge distribution accompanied by a 2D cross-section of the MEP for the noK-[8]CPP⁴⁻ model clearly revealed a substantially larger accumulation of the negative charge on rings C (Fig. 13) when compared with uncomplexed [8]CPP⁴⁻ species (Fig. 7). Subsequent investigation of frontier molecular orbitals showed that the elliptical distortion of the macrocycle leads to a significant increase of the HOMO–LUMO gap from 1.06 eV to 1.44 eV (Fig. 14). Subsequent addition of two K⁺ ions to the system further enlarges this gap, reaching its maximum of 1.64 eV in the [{K⁺}₂([8]CPP⁴⁻)] product. These findings provide a solid explanation for the aforementioned stabilization of the closed-shell singlet ground state (by increasing singlet-triplet states separation) in the complex with potassium cations. It is also worth emphasizing that analysis of the bonding between alkali metal cations and [8]CPP-ligand in the [{K⁺}₂([8]CPP⁴⁻)] complex shows the lack of any notable covalent contribution, leaving the bond purely ionic or electrostatic in nature. The low Wiberg bond orders (>0.01) for all K⋯C contacts, insignificant magnitude of the condensed Wiberg indexes for K-centers (∼0.15), large NBO atomic charge (q(K) = +0.93), and estimation of the donor–acceptor interactions in term of the second-order perturbation theory in NBO basis calculated to be <1 kcal mol⁻¹, all clearly confirm this conclusion. Thus, the internal potassium cations can be described as “electrostatic squeezers” for the highly charged [8]CPP⁴⁻ nanohoop.

Fig. 13 3D (left) and 2D cross-section (right) of the MEP for the noK-[8]CPP⁴⁻ model (PBE0/cc-pVTZ).

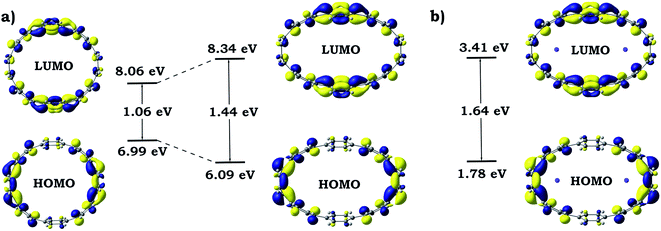Fig. 14 Schematic MO diagram along with energies for isolated and elliptically distorted [8]CPP⁴⁻ systems (a) and for adduct with potassium cations [{K⁺}₂([8]CPP⁴⁻)] (b).

Next, we turned to analysis of changes in aromaticity caused by both oval distortion and metal coordination (Table 6). The calculation results immediately revealed a dramatic impact of the mechanical bending on aromaticity of different rings in the [8]CPP skeleton. Such geometrical distortion led to an unprecedented decrease of anti-aromatic behavior of all rings A, B, and C, by more than 10 ppm. Subsequent coordination of metal cations resulted in further decrease of the paratropic character of rings. This is especially pronounced in the case of the ring A, which became even slightly aromatic (showing diatropic current) with calculated NICS value of −2.20 ppm.

Table 6 Aromaticity descriptors calculated for noK-[8]CPP⁴⁻ and [{K⁺}₂([8]CPP⁴⁻)]

System/Model	Ring	HOMA	NICS	AIM		Fuzzy atomic space
				PDI	FLU	PDI	FLU
noK-[8]CPP^4−	A	0.939	0.42	0.077	0.004	0.08	0.006
	B	0.749	4.58	0.058	0.012	0.063	0.014
	C	0.185	9.10	0.037	0.032	0.044	0.033
[{K^+}2([8]CPP^4−)]	A	0.939	−2.20	0.080	0.004	0.082	0.006
	B	0.749	2.16	0.060	0.011	0.062	0.016
	C	0.185	6.21	0.036	0.032	0.039	0.036

---

Overall, the highly-reduced tetra-anionic form of [8]CPP exhibits an unprecedented flexibility of its electronic structure and aromaticity in particular as a function of mechanical distortion and metal coordination.

Conclusions

In summary, the X-ray crystallographic characterization of the highly-reduced tetraanion of [8]CPP crystallized with four THF-solvated potassium counterions revealed a significant elliptical distortion of the macrocyclic core accompanied by notable C–C bond and angle perturbation in comparison with the neutral parent. Subsequent comprehensive theoretical analysis allowed us to shed light on structural and electronic changes observed upon two and four electron reduction of [8]CPP. Addition of two electrons causes the transformation of the electronic structure of [8]CPP²⁻ from benzenoid to a quinoidal type. However, subsequent transfer of two additional electrons leads to a striking change of the geometric and electronic structure of the highly-reduced [8]CPP⁴⁻ anion. In contrast to the uniform changes observed in [8]CPP²⁻, the four-fold reduction results in drastic differentiation of the six-membered rings. The geometric parameters and the calculated Wiberg bond orders of [8]CPP⁴⁻ (Fig. 6) both clearly show a hybrid nature of the π-system, with a mixture of the benzenoid and quinoidal type of rings. Notably, this electronic perturbation and ring inequality in [8]CPP⁴⁻ is also reflected in their aromaticity. While neutral [8]CPP and [8]CPP²⁻ dianion clearly show aromatic behavior of all six-membered rings, subsequent addition of two more electrons completely reverses their aromatic character to afford the highly-antiaromatic [8]CPP⁴⁻ tetraanion, as indicated by structural, topological, and magnetic descriptors (Table 5). Consistently, the NICS parameters calculated for [8]CPP⁴⁻ vary broadly from to +22.47 ppm to +11.63, while these parameters fall into a very narrow range from −8.77 to −8.96 ppm in [8]CPP²⁻.

Interestingly, in contrast to the bowl-shaped polyanions,^6,10,72 the negative charge of [8]CPP⁴⁻ is accumulated inside the belt, creating a unique internal trap for cationic quest entrapment. Furthermore, symmetrically delocalized charge distribution in [8]CPP²⁻ becomes severely perturbed in the case of [8]CPP⁴⁻, where the negative charge is localized at the opposite sides of the elliptic core in accordance with topology of LUMO+1 (Fig. 8). Consequent investigation of metal complexation reveals that exactly these specific sites of the [8]CPP⁴⁻ host are occupied by K⁺ ions in a full agreement with experimental data. Direct comparison of the neutral parent, bare [8]CPP⁴⁻ anion, and its [{K⁺}₂([8]CPP⁴⁻)] complex, identified the internal coordination of potassium cations as the main driving force for a dramatic elliptic distortion of the macrocyclic skeleton upon reduction (Fig. 13). An importance of inclusion of coordinated solvent molecules into the calculated model in order to achieve high accuracy in reproducing experimental crystallographic parameters is also demonstrated. Altogether, these findings unambiguously demonstrate high structural and electronic flexibility of the [8]CPP system, expanding our understanding of complex behavior of the highly-charged nanosized macrocycles.

Author contributions

A. Yu. R. conceived and carried out DFT calculations, provided computational data analysis and wrote the corresponding manuscript sections; Z. Z. synthesized the title reduced product, completed its detailed structural description, contributed to the draft preparation; S. L. carried out theoretical calculations; Z. W. performed the X-ray data collection and refinement; T. S. synthesized the [8]CPP sample; R. J. contributed to the discussion and presentation of results; M. A. P. conceived and supervised this work, drafted the manuscript with the support and contribution from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support of this work from the National Science Foundation (CHE-2003411 and CHE-1800586) is gratefully acknowledged by M. A. P. R. J. was supported by the National Science Foundation (CHE-1800586) and T. A. S. acknowledges the German Research Council (DFG, SCHA 2061/1-1) for a postdoctoral fellowship.

Notes and references

1. M. A. Petrukhina and L. T. Scott, Fragments of Fullerenes and Carbon Nanotubes: Designed Synthesis, Unusual Reactions, and Coordination Chemistry, Wiley, Hoboken, New Jersey, 2012.
2. M. Ball, Y. Zhong, Y. Wu, C. Schenck, F. Ng, M. Steigerwald, S. Xiao and C. Nuckolls, Acc. Chem. Res., 2015, 48, 267–276.
3. M. Rickhaus, M. Mayor and M. Juríček, Chem. Soc. Rev., 2017, 46, 1643–1660.
4. S. H. Pun and Q. Miao, Acc. Chem. Res., 2018, 51, 1630–1642.
5. I. V. Alabugin and E. Gonzalez-Rodriguez, Acc. Chem. Res., 2018, 51, 1206–1219.
6. A. V. Zabula, A. S. Filatov, S. N. Spisak, A. Y. Rogachev and M. A. Petrukhina, Science, 2011, 333, 1008–1011.
7. A. V. Zabula, S. N. Spisak, A. S. Filatov and M. A. Petrukhina, Organometallics, 2012, 31, 5541–5545.
8. A. V. Zabula, S. N. Spisak, A. S. Filatov, V. M. Grigoryants and M. A. Petrukhina, Chem.–Eur. J., 2012, 18, 6476–6484.
9. A. V. Zabula, S. N. Spisak, A. S. Filatov, A. Y. Rogachev, R. Clérac and M. A. Petrukhina, Chem. Sci., 2016, 7, 1954–1961.
10. A. V. Zabula, S. N. Spisak, A. S. Filatov, A. Y. Rogachev and M. A. Petrukhina, Acc. Chem. Res., 2018, 51, 1541–1549.
11. G. Sandi, R. Gerald, L. Scanlon, R. Klingler and J. Rathke, J. New Mater. Electrochem. Syst., 2000, 3, 13–19.
12. R. E. Gerald, C. S. Johnson, J. W. Rathke, R. J. Klingler, G. Sandí and L. G. Scanlon, J. Power Sources, 2000, 89, 237–243.
13. D. Odkhuu, D. Jung, H. Lee, S. S. Han, S.-H. Choi, R. Ruoff and N. Park, Carbon, 2014, 66, 39–47.
14. S. Sato, A. Unemoto, T. Ikeda, S.-i. Orimo and H. Isobe, Small, 2016, 12, 3381–3387.
15. J. Park, S. H. Joo, Y.-J. Kim, J. H. Park, S. K. Kwak, S. Ahn and S. J. Kang, Adv. Funct. Mater., 2019, 29, 1902888.
16. H. Omachi, Y. Segawa and K. Itami, Acc. Chem. Res., 2012, 45, 1378–1389.
17. M. R. Golder and R. Jasti, Acc. Chem. Res., 2015, 48, 557–566.
18. Y. Segawa, H. Ito and K. Itami, Nat. Rev. Mater., 2016, 1, 15002.
19. X. Lu and J. Wu, Chem, 2017, 2, 619–620.
20. Y. Segawa, D. R. Levine and K. Itami, Acc. Chem. Res., 2019, 52, 2760–2767.
21. P. Liu, J. R. Williams and J. J. Cha, Nat. Rev. Mater., 2019, 4, 479–496.
22. V. C. Parekh and P. C. Guha, J. Indian Chem. Soc., 1934, 11, 95–100.
23. R. Friederich, M. Nieger and F. Vögtle, Chem. Ber., 1993, 126, 1723–1732.
24. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647.
25. T. J. Sisto, M. R. Golder, E. S. Hirst and R. Jasti, J. Am. Chem. Soc., 2011, 133, 15800–15802.
26. J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021.
27. J. Xia and R. Jasti, Angew. Chem., Int. Ed., 2012, 51, 2474–2476.
28. P. J. Evans, E. R. Darzi and R. Jasti, Nat. Chem., 2014, 6, 404–408.
29. E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410.
30. Y. Segawa, S. Miyamoto, H. Omachi, S. Matsuura, P. Šenel, T. Sasamori, N. Tokitoh and K. Itami, Angew. Chem., Int. Ed., 2011, 50, 3244–3248.
31. H. Omachi, T. Nakayama, E. Takahashi, Y. Segawa and K. Itami, Nat. Chem., 2013, 5, 572–576.
32. F. Sibbel, K. Matsui, Y. Segawa, A. Studer and K. Itami, Chem. Commun., 2014, 50, 954–956.
33. Y. Segawa, T. Kuwabara, K. Matsui, S. Kawai and K. Itami, Tetrahedron, 2015, 71, 4500–4503.
34. E. Kayahara, Y. Sakamoto, T. Suzuki and S. Yamago, Org. Lett., 2012, 14, 3284–3287.
35. E. Kayahara, T. Iwamoto, T. Suzuki and S. Yamago, Chem. Lett., 2013, 42, 621–623.
36. E. Kayahara, V. K. Patel and S. Yamago, J. Am. Chem. Soc., 2014, 136, 2284–2287.
37. S. Yamago, E. Kayahara, V. Patel, J. Xia and R. Jasti, Synlett, 2015, 26, 1615–1619.
38. E. Kayahara, L. Sun, H. Onishi, K. Suzuki, T. Fukushima, A. Sawada, H. Kaji and S. Yamago, J. Am. Chem. Soc., 2017, 139, 18480–18483.
39. E. Kayahara, Y. Cheng and S. Yamago, Chem. Lett., 2018, 47, 1108–1111.
40. T. Kawanishi, K. Ishida, E. Kayahara and S. Yamago, J. Org. Chem., 2020, 85, 2082–2091.
41. W. Zhang, A. Abdulkarim, F. E. Golling, H. J. Räder and K. Müllen, Angew. Chem., Int. Ed., 2017, 56, 2645–2648.
42. K. Matsui, Y. Segawa and K. Itami, Org. Lett., 2012, 14, 1888–1891.
43. A. Yagi, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2012, 134, 2962–2965.
44. Y. Ishii, S. Matsuura, Y. Segawa and K. Itami, Org. Lett., 2014, 16, 2174–2176.
45. K. Matsui, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2014, 136, 16452–16458.
46. J. M. Van Raden, S. Louie, L. N. Zakharov and R. Jasti, J. Am. Chem. Soc., 2017, 139, 2936–2939.
47. Q. Huang, G. Zhuang, H. Jia, M. Qian, S. Cui, S. Yang and P. Du, Angew. Chem., Int. Ed., 2019, 58, 6244–6249.
48. Q. Huang, G. Zhuang, M. Zhang, J. Wang, S. Wang, Y. Wu, S. Yang and P. Du, J. Am. Chem. Soc., 2019, 141, 18938–18943.
49. Y. Segawa, M. Kuwayama, Y. Hijikata, M. Fushimi, T. Nishihara, J. Pirillo, J. Shirasaki, N. Kubota and K. Itami, Science, 2019, 365, 272–276.
50. T. Nishihara, Y. Segawa, K. Itami and Y. Kanemitsu, Chem. Sci., 2014, 5, 2293–2296.
51. N. Kubota, Y. Segawa and K. Itami, J. Am. Chem. Soc., 2015, 137, 1356–1361.
52. E. Kayahara, V. K. Patel, A. Mercier, E. P. Kündig and S. Yamago, Angew. Chem., Int. Ed., 2016, 55, 302–306.
53. M. P. Alvarez, M. C. Ruiz Delgado, M. Taravillo, V. G. Baonza, J. T. Lopez Navarrete, P. Evans, R. Jasti, S. Yamago, M. Kertesz and J. Casado, Chem. Sci., 2016, 7, 3494–3499.
54. N. Ozaki, H. Sakamoto, T. Nishihara, T. Fujimori, Y. Hijikata, R. Kimura, S. Irle and K. Itami, Angew. Chem., Int. Ed., 2017, 56, 11196–11202.
55. Y. Xu, R. Kaur, B. Wang, M. B. Minameyer, S. Gsänger, B. Meyer, T. Drewello, D. M. Guldi and M. von Delius, J. Am. Chem. Soc., 2018, 140, 13413–13420.
56. M. Fujitsuka, S. Tojo, T. Iwamoto, E. Kayahara, S. Yamago and T. Majima, J. Phys. Chem. A, 2015, 119, 4136–4141.
57. E. Kayahara, T. Kouyama, T. Kato and S. Yamago, J. Am. Chem. Soc., 2016, 138, 338–344.
58. D. Wu, W. Cheng, X. Ban and J. Xia, Asian J. Org. Chem., 2018, 7, 2161–2181.
59. Y. Masumoto, N. Toriumi, A. Muranaka, E. Kayahara, S. Yamago and M. Uchiyama, J. Phys. Chem. A, 2018, 122, 5162–5167.
60. N. Toriumi, A. Muranaka, E. Kayahara, S. Yamago and M. Uchiyama, J. Am. Chem. Soc., 2015, 137, 82–85.
61. M. Fujitsuka, S. Tojo, T. Iwamoto, E. Kayahara, S. Yamago and T. Majima, J. Phys. Chem. Lett., 2014, 5, 2302–2305.
62. A. V. Zabula, A. S. Filatov, J. Xia, R. Jasti and M. A. Petrukhina, Angew. Chem., Int. Ed., 2013, 52, 5033–5036.
63. S. N. Spisak, Z. Wei, E. Darzi, R. Jasti and M. A. Petrukhina, Chem. Commun., 2018, 54, 7818–7821.
64. Z. Zhou, Z. Wei, T. A. Schaub, R. Jasti and M. A. Petrukhina, Chem. Sci., 2020, 11, 9305–9401.
65. S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759.
66. Z. Zhou, X.-Y. Wang, Z. Wei, K. Müllen and M. A. Petrukhina, Angew. Chem., Int. Ed., 2019, 58, 14969–14973.
67. Z. Zhou, R. K. Kawade, Z. Wei, F. Kuriakose, Ö. Üngör, M. Jo, M. Shatruk, R. Gershoni-Poranne, M. A. Petrukhina and I. V. Alabugin, Angew. Chem., Int. Ed., 2020, 59, 1256–1262.
68. S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304.
69. A. Y. Rogachev, A. S. Filatov, A. V. Zabula and M. A. Petrukhina, Phys. Chem. Chem. Phys., 2012, 14, 3554–3567.
70. C. Dubceac, A. S. Filatov, A. V. Zabula, A. Y. Rogachev and M. A. Petrukhina, Chem.–Eur. J., 2015, 21, 14268–14279.
71. J. Li, G. da Silva Ramos and A. Y. Rogachev, J. Comput. Chem., 2016, 37, 2266–2278.
72. S. N. Spisak, Z. Wei, N. J. O'Neil, A. Y. Rogachev, T. Amaya, T. Hirao and M. A. Petrukhina, J. Am. Chem. Soc., 2015, 137, 9768–9771.

---

Footnote

† Electronic supplementary information (ESI) available: Details of preparation and X-ray diffraction study. CCDC 2058175. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc00713k

---