The dynamic face of lipid membranes
Sudipta
Gupta
 ab and
Rana
Ashkar
ab and
Rana
Ashkar
 *ab
*ab
aDepartment of Physics, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: ashkar@vt.edu
bCenter for Soft Matter and Biological Physics, Virginia Tech, Blacksburg, VA 24061, USA
First published on 8th July 2021
Abstract
Cell membranes – primarily composed of lipids, sterols, and proteins – form a dynamic interface between living cells and their environment. They act as a mechanical barrier around the cell while selectively facilitating material transport, signal transduction, and various other functions necessary for the cell viability. The complex functionality of cell membranes and the hierarchical motions and responses they exhibit demand a thorough understanding of the origin of different membrane dynamics and how they are influenced by molecular additives and environmental cues. These dynamic modes include single-molecule diffusion, thermal fluctuations, and large-scale membrane deformations, to name a few. This review highlights advances in investigating structure-driven dynamics associated with model cell membranes, with a particular focus on insights gained from neutron scattering and spectroscopy experiments. We discuss the uniqueness of neutron contrast variation and its remarkable potential in probing selective membrane structure and dynamics on spatial and temporal scales over which key biological functions occur. We also present a summary of current and future opportunities in synergistic combinations of neutron scattering with molecular dynamics (MD) simulations to gain further understanding of the molecular mechanisms underlying complex membrane functions.
1. Introduction
Cell membranes are two-dimensional biostructures that are central to life.1 They define the boundaries of cells and thus they act as the interaction front between the cell and its environment and as the first layer of cellular defense against invasion by foreign particles, including toxins and viruses.2 Cell membranes also play a key role in vital cellular processes, including molecular transport, cellular signaling, and the regulation of protein functions.3–8Primordial membranes, thought to be the first structures formed in protocells, have most likely emerged from the self-assembly of simple prebiotic surfactants stabilized by amino acids, the building blocks of proteins.9 The assembly of biogenic lipids and amphiphiles into membranes is driven by their amphiphilic properties and their sparse solubility (10−10 to 10−6 moles per liter) in water, causing them to form rather extended aggregates or membranous structures that facilitate the compartmentalization of cellular components.10 However, with the evolution of cellular structures and multicellular organisms, cell membranes developed complex lipid compositions commensurate with the functions of the cells that they envelope.11 This rich chemical and structural diversity of lipid components within cell membranes often results in heterogeneous mixtures, particularly over the nanoscopic length scales of small lipid clusters and membrane proteins.12 This view of the cell membrane as a laterally compartmentalized assembly of lipids and proteins, constantly undergoing reorganization, is the central concept of the lipid raft hypothesis13,14 and similar “membrane nanodomain” models.15 Within such models, the dynamics of lipid domains, including their formation, growth, and fluctuations, serve as a regulatory mechanism for complex membrane functions.16–18 Another consequence of lipid diversity within cell membranes is the asymmetric distribution of lipids across the inner and outer membrane leaflets – the two monolayers constituting the bilayer structure of the membrane.19 Lipid asymmetry is thought to be tightly linked to membrane functions and the selective recruitment of proteins to the cytoplasmic and exoplasmic leaflets.18,20
To interrogate the intricate properties of plasma membranes, under controlled compositions and environmental settings, biophysical studies over the last few decades have focused on biomimetic lipid bilayers as a proxy to cell membranes. Liposomes, one of classic model systems used, were first introduced by Banghman and coworkers in the 1980s,21 but their applications have since extended to artificial cells, drug delivery vehicles, and chemical microreactors.22–25 Modern liposomes are typically prepared from phospholipids, sometimes in presence of cholesterol26,27 or other amphiphilic compounds28,29 to improve the bilayer stability, permeability, or other properties. On the other hand, liposomes consisting of few lipid components, or lipids mixed with membrane proteins, have been regularly used to study key membrane processes on molecular and collective levels, including lipid domain formation30–34 and ion channel gating.35–37 From a physical point of view, model membranes can provide direct insights into how universal physical properties regulate membrane behavior and functions, allowing their exploitation in advanced therapeutic and biotechnological applications, such as targeted drug delivery38 and biosensing applications.39
While various experimental approaches have been used in the structural and dynamical characterization of lipid membranes, elastic and spectroscopic studies primarily utilizing neutrons or X-rays have proven extremely valuable in directly accessing molecular and nanoscale membrane properties.40,41 For example, joint refinement of small-angle X-ray and neutron scattering data made it possible to determine explicit membrane structures, including membrane thickness, molecular packing, and lipid conformations.41–46 These studies leverage on the high resolution (sub-nm) of X-rays and neutrons and their innate ability to sense different moieties within membranes, with X-rays primarily detecting high electron density moieties (e.g. phosphate subgroup) and neutrons detecting variations in the hydrogen vs. deuterium content. Notably, the unique ability of neutrons to differentiate between hydrogen's two stable isotopes has proven to be a powerful tool in advancing the general understanding of functional membrane features on the nanoscale, including lipid nanodomains and leaflet asymmetry.47–50
The unique isotope sensitivity of neutrons has also put neutron spectroscopy methods in a leading role in directly accessing and understanding select dynamic processes in lipid membranes, offering complementary capabilities to existing characterization methods. This is particularly important as membrane dynamics encompass motions that span multiple spatial and temporal scales.51 A schematic representation of the dynamic processes accessed by neutron spectroscopy methods over different length and time scales is illustrated in Fig. 1. On short length (∼sub-nm) and time (∼ps) scales, molecular and sub-molecular motions are dominant, e.g. vibrational, conformational, and rotational dynamics. Whereas, at larger length (∼10–100 nm) and time (∼1–100 ns) scales collective membrane dynamics, in the form of bending and thickness fluctuations, become prominent. Other membrane motions, such as lipid exchange and lipid flip-flop across the two membrane leaflets, occur at much larger time scales,52–54 and are not shown in Fig. 1.
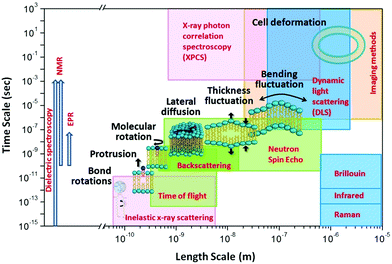 | ||
| Fig. 1 Schematic diagram of lipid membrane dynamics accessible by neutron spectroscopic techniques over different length and time scales (reproduced with permission from Qian et al., Langmuir, 36, 15189–15211.63 Copyright 2020 American Chemical Society). | ||
In comparison, other techniques (shown in Fig. 1) provide access to membrane dynamics over different spatial and temporal scales. This includes dynamic light scattering (DLS) for probing translational diffusion of lipid vesicles,55–57 fluorescence correlation spectroscopy (FCS) for probing localized lipid motions,58 and X-ray photon correlation spectroscopy (XPCS) for probing slow membrane undulations.59 Another notable technique is solid-state 2H NMR spectroscopy which utilizes nuclear-spin-relaxations of deuterium moieties along the lipid hydrocarbon chains to measure both static line-shapes and relaxation spectra, enabling concomitant studies of membrane structure and dynamics.60–62 More methods will be discussed throughout the review.
2. Elastic neutron scattering: a unique tool for probing nanoscopic membrane structures
Since membrane dynamics are tightly dependent on probed structures, we first introduce elastic neutron scattering capabilities in resolving structural membrane properties. This is critical in studies where selective deuteration is applied to enhance or suppress specific membrane features. In such studies, the validation of the applied neutron contrast scheme is necessary for the faithful association of the measured dynamics with the corresponding membrane structure. Below we describe how isotope labeling can be used to effectively modify the neutron contrast of membranes, and how different contrast schemes have been applied to determine membrane structures on molecular and nanoscopic scales.2.1. Isotope sensitivity
Neutrons interact with atomic nuclei, and their scattering cross-sections depend on the nuclear structure of the scattering object. Therefore, neutrons interacting with different isotopes of the same element have different scattering cross-sections, usually expressed in terms of a material quantity known as the neutron scattering length density (NSLD). The NSLD is akin to the optical index of refraction, and the possibility of tuning the NSLD by isotope labeling offers unique capabilities in contrast matching or contrast variation studies.64 This capability is particularly powerful in biological materials which are inherently rich in hydrogen.65 Note that the neutron scattering lengths of protium and deuterium isotopes of hydrogen are bH = −3.741 fm and bD = 6.671 fm, respectively. Therefore substituting H for D results in significant differences in the corresponding NSLD given by: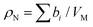 , where VM is the molecular volume, and
, where VM is the molecular volume, and 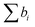 is the sum over all the scattering lengths of constituent nuclei. Since the scattering length can be positive or negative, as shown above for H and D, this can accordingly result in dramatically distinct NSLD values for isotopically labelled compounds, e.g. ρN(D2O) = 6.4 × 10−6 Å−2 whereas ρN(H2O) = −0.5 × 10−6 Å−2. Importantly, the neutron scattering cross section, dΣ/dΩ, or the measured scattering intensity, is directly proportional to the contrast, ΔρN, between different moieties within the sample, i.e. dΣ/dΩ ∝ ΔρN2.
is the sum over all the scattering lengths of constituent nuclei. Since the scattering length can be positive or negative, as shown above for H and D, this can accordingly result in dramatically distinct NSLD values for isotopically labelled compounds, e.g. ρN(D2O) = 6.4 × 10−6 Å−2 whereas ρN(H2O) = −0.5 × 10−6 Å−2. Importantly, the neutron scattering cross section, dΣ/dΩ, or the measured scattering intensity, is directly proportional to the contrast, ΔρN, between different moieties within the sample, i.e. dΣ/dΩ ∝ ΔρN2.
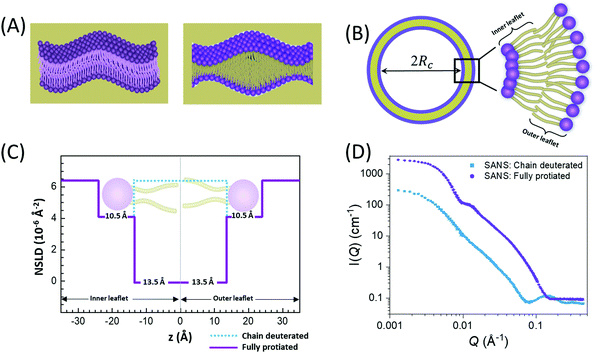
In membranes, deuterium replacement of protiated moieties can be effectively used to highlight specific membrane features or mask others by respectively amplifying their ρN relative to the medium they reside in or by setting the contrast, ΔρN, to zero. For example, to selectively visualize the lipid headgroup region of lipid membranes, bilayers are prepared with perdeuterated lipid analogues in which the hydrogen atoms of the lipid chains are replaced by deuterium, resulting in a scenario where the chain region of the membrane is contrast-matched to the deuterated buffer (see Fig. 2).27,66–68 Here, we note that deuterium labeling is different than probe labeling required in other experimental techniques such as fluorescence light microscopy69 or electron spin resonance,70 where the bulky nature of the used probes can interfere with the measured structural and dynamical properties. In contrast, substituting H for D in membranes does not alter the physiochemical properties for the most part, but substantially changes the contrast.
2.2. Liposomal structures: small-angle neutron scattering
Small-angle neutron scattering (SANS) has been routinely used for nanoscale structural characterization of liposomal samples. SANS is an elastic scattering technique which utilizes a pinhole geometry and large sample-to-detector distances to resolve the angular dependence of neutron scattering from the sample. The resultant signal is detected in the form of scattering intensity as a function of the scattering angle, θ.71 In scattering, it is common to express the scattering angle in terms of the momentum transfer, Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)/λ, where λ is the neutron wavelength. Note that Q is a reciprocal quantity which is inversely proportional to the probed length scales. In SANS measurements, the accessible length scales range of ∼1–100 nm, making SANS well-suited for studying liposomal membrane structures, including membrane thickness and packing density.72 To refine the structural parameters obtained from SANS, small-angle X-ray scattering (SAXS) is commonly applied in tandem with SANS, providing an additional scattering contrast based on electron density distribution within the membrane.
sin(θ/2)/λ, where λ is the neutron wavelength. Note that Q is a reciprocal quantity which is inversely proportional to the probed length scales. In SANS measurements, the accessible length scales range of ∼1–100 nm, making SANS well-suited for studying liposomal membrane structures, including membrane thickness and packing density.72 To refine the structural parameters obtained from SANS, small-angle X-ray scattering (SAXS) is commonly applied in tandem with SANS, providing an additional scattering contrast based on electron density distribution within the membrane.
An example of combined SAXS and SANS data modeling of liposomes is shown in Fig. 3. The figure shows slab models of the electron density (ED) and the neutron scattering length density (NSLD) profiles, as well as scattering density profile (SDP) models which capture more details of intramembrane structures.42 Notice that due to the charged nature of the phosphate moiety in the lipid headgroup region of the membrane, the ED of the corresponding slabs is much higher than that of the hydrophobic tail region and the aqueous solvent. This results in a distinct ED profile which yields pronounced features in the SAXS signal (Fig. 3) and enables reliable data fitting.
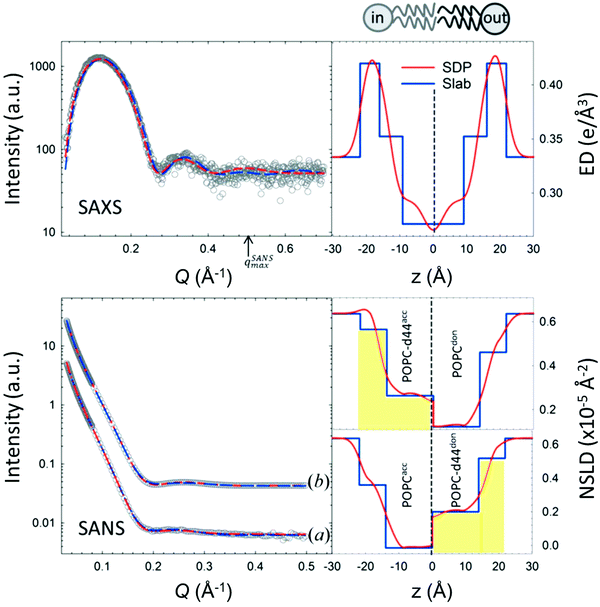 | ||
| Fig. 3 SAXS and SANS data on asymmetric POPC liposomes, prepared with protiated and (partially) deuterated leaflets, along with the corresponding electron density (ED) and neutron scattering length density (NSLD) profiles. The panels to the right show two types of models commonly used in fitting SAXS and SANS data: slab models which divide the membrane into shells, or slabs, with constant ED or NSLD, and scattering density profile (SDP) models which depict more realistic gradual variations in ED and NSLD. Notice that the NSLD profile of the asymmetric membranes reflects the deuteration scheme of the inner/outer leaflet of the isotopically asymmetric membrane, whereas the ED profile shows no differences with selective leaflet deuteration. It is also worth noting that the NSLD of the protiated leaflet matches that shown in Fig. 2. This figure is adapted from Eicher et al., J. Appl. Crystallogr., 50, 419–429. Wiley 2017.42 | ||
In comparison, SANS signals on protiated liposomes in deuterated buffer, lack these features partly due to the NSLD profile of protiated membranes (see Fig. 2C) and partly due to the high incoherent background from the hydrogen content in the sample. This conceals the signal from the membrane (i.e. oscillation at high Q in Fig. 2D) and makes it difficult to determine the membrane structure with high certainty. To circumvent these limitations, it is common to use chain-deuterated lipid analogues as shown in Fig. 2. This yields a significant NSLD difference between the head and chain regions, along with a lower incoherent background (Fig. 2D), allowing for more accurate fitting of the obtained SANS signals. Notably, slab models are readily available for fitting SANS/SAXS data on lipid membranes and have been successfully used to extract liposomal structures of various compositions under different solution conditions,8,27,73,74 including studies of the loading efficiency in drug delivery liposomes.75
In addition to slab models, scattering models using volume probability distributions of lipid subgroups yield molecularly-detailed scattering density profiles, allowing the extraction of finer membrane structures, such as the area per lipid, hydrocarbon chain thickness, and phosphate-to-phosphate thickness.40,76 An example of such models (i.e. SDP) is shown in Fig. 3. These models have been validated against MD simulations46,77 and have since been used in numerous studies of lipid bilayer structures as a function of lipid unsaturation,45 cholesterol content,27,44 and drug inclusion.78 Here we note that other models with atomic details of the ED and SLD profiles provide an even higher internal resolution than the SDP model.79 It is also worth noting that developments of self-consistent slab models, with some input on molecular compositions and volumes, has been shown to yield consistent results with SDP models.27,80
To date, the most intriguing and distinctive application of SANS on liposomal membranes is in studies of nanoscale lipid domains and leaflet asymmetry – two hallmarks of functional cell membranes.40,50,81,82 The potential use of SANS in measuring lipid phase-separation was recognized in the early 1980 by Knoll, Sackmann, and coworkers. In these pioneering studies, a series of contrast variation experiments on binary membranes, using protiated and deuterated lipids, successfully detected lipid phase separation into nanodomains.83,84 Later, Pencer et al. used coarse-grained models of heterogeneous membranes and demonstrated the efficacy of contrast variation SANS experiments in characterizing the dimensions and spatial correlations of the formed domains.85 More recently, Heberle et al. used a similar approach, in conjunction with Monte Carlo simulations, to measure the size of raft-like liquid-ordered (Lo) nanodomains in a liquid-disordered (Ld) matrix as a function of membrane composition, by changing the ratio of monounsaturated to di-monounsaturated lipids (Fig. 4).48 They predicted that the line tension originating from the hydrophobic thickness mismatch between the domains and the lipid matrix would strongly influence the size of the formed nanodomains. Indeed, their SANS findings demonstrated experimentally that thickness mismatch is an important structural (and compositional) property which underlies domain size and stability in model cell membranes. Here we note that while studies of lipid nanodomains have been uniquely enabled by SANS and selective lipid deuteration, current advances in high resolution microscopy have been pushing the boundaries in nanoscopic characterization of lipid membranes. Of note are two recent studies using cryogenic transmission electron microscopy (cryo-TEM) which reported direct imaging of nanodomains in model domain-forming membranes,86,87 demonstrating new capabilities in direct visualization of nanoscale membrane structures.
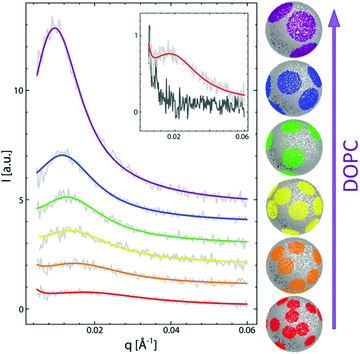 | ||
| Fig. 4 Monte Carlo fits to SANS data on domain-forming DSPC/DOPC/POPC/Chol membranes. The data and calculations show that the increase in di-monounsaturated DOPC lipids relative to monounsaturated POPC lipids results in an increase in domain size and a concomitant increase in the thickness difference between the domains and the lipid matrix. Figure is adapted with permission from Heberle et al., J. Am. Chem. Soc., 135, 6853–6859.48 Copyright 2013 American Chemical Society. | ||
Another feature of lipid membranes which is uniquely accessed by SANS is compositional asymmetry across the two membrane leaflets. To interrogate this phenomenon, recent SANS experiments have utilized selectively deuterated lipid components to inspect the mechanisms influencing leaflet asymmetry. Marquardt et al. used cyclodextrin to prepare asymmetric vesicles by exchanging lipids from the outer leaflet of deuterated vesicles to protiated vesicles.88 SANS measurements of the thickness and area per lipid revealed reduced lipid packing density in the outer membrane leaflet compared to symmetric vesicles,50 suggesting fluidization of the outer leaflet by the more disordered inner leaflet through interleaflet coupling. They also showed that the incorporation of peptides and gramicidin channels strongly influenced membrane homogenization and flip-flop kinetics – to be discussed later.89,90 In another study, Liu et al. prepared asymmetric vesicles through lipid exchange between free-standing vesicles and membranes supported on silica nanoparticles.54 Their SANS studies showed that the lipid flip-flop rate across the two leaflets is similar to that in asymmetric vesicles prepared using cyclodextrin. These studies, and the protocols they generated for the preparation of asymmetric liposomal membranes, open new possibilities for interrogating functional-like membrane features and understanding how cells utilize compositional variations to impart function.
2.3. Layered structures: reflectometry and grazing-incidence scattering
Although liposomal membranes are widely utilized in addressing outstanding questions in membrane biophysics, other queries related to structural investigations of monolayers and their relation to multilayer properties are difficult to address in liposomal membranes. Instead, other membrane systems, in the form of floating or supported monolayers/bilayers, are typically used. Supported lipid layers are mechanically stable and can be used to investigate the electric, mechanical, or diffusive properties in lipid membranes.91 In such systems, neutron and X-ray reflectometry have been widely applied to study – with sub nm resolution – structures normal to the membrane surface.92,93 In this type of experiments, the scattering geometry is defined by a sheet-like configuration of the incident beam, with tight collimation along the incident direction (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i in Fig. 5) and relaxed collimation within the plane of incidence (i.e. normal to the page in Fig. 5). As a result, the reflectivity is detected as a function of the momentum transfer, Qz, as shown in Fig. 5. By orienting the membrane normal along Qz, reflectometry measurements provide sub-nm characterization of the membrane structures along the z-direction (Fig. 5).
i in Fig. 5) and relaxed collimation within the plane of incidence (i.e. normal to the page in Fig. 5). As a result, the reflectivity is detected as a function of the momentum transfer, Qz, as shown in Fig. 5. By orienting the membrane normal along Qz, reflectometry measurements provide sub-nm characterization of the membrane structures along the z-direction (Fig. 5).
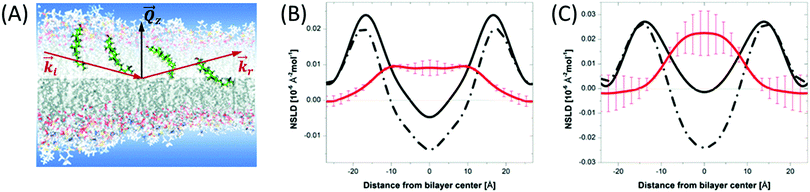 | ||
Fig. 5 (A) Schematic diagram of the location of cholesterol in lipid membranes of different hydrocarbon thickness. The incident and reflected beams are represented by wavevectors ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) i and i and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) r, respectively, and the momentum transfer is indicated by r, respectively, and the momentum transfer is indicated by ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) z. (B) and (C) NSLD profiles for bilayers of DMPC and DAPC with 10 mol% cholesterol. The solid and dashed lines represent the NSLD profiles of membranes with perdeuterated and protiated cholesterol, respectively. The red NSLD difference corresponding to the distribution of perdeuterated cholesterol in the membrane. Figure adapted from ref. 94 with permission from The Royal Society of Chemistry. z. (B) and (C) NSLD profiles for bilayers of DMPC and DAPC with 10 mol% cholesterol. The solid and dashed lines represent the NSLD profiles of membranes with perdeuterated and protiated cholesterol, respectively. The red NSLD difference corresponding to the distribution of perdeuterated cholesterol in the membrane. Figure adapted from ref. 94 with permission from The Royal Society of Chemistry. | ||
When combined with selective deuterium labeling, neutron reflectometry can be effectively used to investigate the relative distribution of individual components within lipid assemblies, including the location of cholesterol in membranes of different thicknesses94 (Fig. 5) and lipid redistribution by flip-flop in asymmetric supported bilayers.95 Neutron reflectometry has also been utilized in determining the insertion profiles of proteins within lipid bilayers or monolayers96–98 and in understanding ion transport across polymer-cushioned membranes.99 We note that in reflectometry experiments, the membrane structures are modeled in terms of the average in-plane NSLD profiles along the membrane normal.100–102 These measurements yield the thickness and NSLD of structurally and compositionally distinct layers within the membrane system. For example, early neutron reflectometry studies of DPPC and surfactants in a mixed monolayer demonstrated the effect of surfactant inclusion on the packing and distribution of each of the membrane components under normal and high pressure conditions.103
But despite the superb resolution of specular reflectometry techniques in the direction normal to the reflecting surface (here assumed to be in the z-direction and normal to the membrane), the sheet-like configuration of the incident beam results in very poor lateral, or in-plane, resolution (i.e. in the xy-plane in Fig. 5). However, combining specular reflectivity and grazing incidence (GI) scattering can provide additional details of lateral structural features within the membrane. For example, neutron reflectivity (NR) and GISANS have been synergistically used to demonstrate that beta blocker drugs, like propranolol, promote the formation of highly curved and disordered surfaces resulting in the formation of lamellar powders in phosphatidylcholine lipid membranes.104 In the same study, further induction of pain relief drugs, like benzocaine, was found to stimulate a crystal-like packing as well as crystal-like defects in the arrangement of hydrophobic chains of the PC lipids.104 More recent GISANS and NR studies showed that Ibuprofen, a common pain reliever, induces the formation of hexagonal and tetragonal lattices in phospholipid membranes, which could be attributed to cytotoxicity in living cells.105 These examples and others demonstrate the efficacy of neutron reflectometry and grazing incidence scattering in investigating possible structural modifications of lipid bilayers by drugs and small-molecule additives, which is of utmost importance in the design of new drugs and membrane-focused therapeutic agents.
3. Neutron spectroscopy: a unique tool for probing molecular and collective membrane dynamics
The realization that cell membranes are constantly undergoing structural and organizational changes has prompted the use of lipid membranes as a proxy to plasma cell membranes to explore the dynamics underlying complex membrane functions. Many of these functions require collective membrane responses in the form of molecular rearrangements and nanoscale fluctuations over length and time scales that are intermediate between individual molecular motions and continuum elastic membrane deformations. Hence, a full understanding of membrane functions requires knowledge of how collective membrane dynamics and molecular motions are regulated by membrane composition, molecular additives, protein inclusion, and environmental conditions. Indeed, evidence from NMR studies confirm that both molecular fluctuations and collective membrane dynamics depend on the bilayer physical chemistry.106 So, it is essential to directly measure the corresponding membrane dynamics – not only to verify existing models, but also to extend our knowledge beyond the capabilities of current theory or simulations and to develop next generation membrane-based materials. The challenge is that collective dynamics manifest on spatial and temporal scales that stifle conventional experimental methods. This has resulted in a significant gap in the understanding of membrane behavior on collective scales and consequently of relevant membrane properties and biological functions.To address this information gap, neutron spin echo (NSE) spectroscopy has proven to be particularly valuable in directly accessing collective membrane dynamics over broad length and time scales simultaneously.51,56 Importantly, NSE accesses length scales in the range of 1–100 s Å and timescales in the range of 1–100 s ns,107,108 concomitant with key coherent collective dynamic modes in membranes, namely bending undulations and thickness fluctuations (a.k.a. breathing mode).51,109 These capabilities enabled by NSE complement other neutron spectroscopy methods enabling quasi-elastic neutron scattering (QENS) observations, including neutron backscattering spectroscopy (NBS) accessing incoherent dynamics, e.g. lateral lipid diffusion on ps timescales in membranes containing drug molecules or antimicrobial peptides,110–112 and inelastic neutron scattering accessing nondispersive (optical) modes in gel and fluid phases in lipid membranes.113 Other neutron spectroscopy techniques like time-of-flight spectroscopy (TOF),114 and triple-axis spectrometers (TAS)115 have also been employed to understand different dynamic modes which are directly relevant to biological functions, including protein–protein interactions, undulatory motions, and diffusive dynamics.
NSE spectroscopy is a spin-coding technique which measures the energy exchange of neutrons during a scattering event through changes in the neutron spin or polarization state. The Larmor precession of the spin around a magnetic field serves as a timer for each neutron and enables the detection of tiny velocity changes (Δv/v < 10−5) due to sample scattering. This allows energy resolution as high as Δħω = 0.7 neV and enables access to timescales as high as 1 μs.116 However, it is important to note that the timescales in NSE measurements are inherently restricted by the probed length scales. This is a consequence of the wavelength dependence of both Q and the accessible Fourier times.117 Therefore, measurements at higher Q (i.e. shorter length scales) have a lower upper limit of accessible timescales.
NSE measures dynamics in the form of decays of the normalized dynamic structure factor or intermediate scattering function S(Q, t)/S(Q, 0) in terms of the Fourier time t at a given Q. Here we note that the intermediate scattering function, S(Q, t), measured by NSE is the Fourier transform of the scattering function, S(Q, ω), discussed later in Section 4.3. This uniquely positions NSE among other neutron spectroscopy methods in its ability to directly measure the time dependence of sample dynamics. In contrast, other neutron spectroscopy methods measure the scattering function, S(Q, ω) and detect the measured dynamics as energy broadening around the elastic line, to be discussed later in Section 4.3.
The unique aspect of NSE and other spectroscopy methods measuring QENS is that they directly access thermal energy scales (kBT ∼ 25 meV) commensurate with thermal fluctuations and diffusive relaxation modes in lipid membranes and protein-membrane complexes.118 These techniques are also probe-free approaches that do not interfere with or influence the intrinsic dynamics of lipid molecules. In the sections below, we discuss the various applications of neutron spectroscopy approaches in the dynamic characterization of membranes and the major insights that they have provided into membrane properties.
4. Collective dynamics
4.1. Membrane undulations
The stability and shape of membranes, how they interact with proteins and with foreign particles, such as drug molecules, nanoparticles, or polymers, depends on membrane undulations. These undulations, also referred to as height-height correlations, are governed by membrane elastic properties, primarily the bending rigidity modulus, κ. Early NSE measurements provided the first experimental proof that membrane bending undulations follow the elastic sheet model.119 As predicted by Zilman and Granek (ZG),120 signatures of such undulatory motions manifest in relaxation spectra with stretched exponential decays given by:120SZG(Q, t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(ΓZGt)2/3] exp[−(ΓZGt)2/3] | (1) |
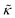 . In this notation,
. In this notation, 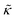 is related to the bilayer curvature modulus, κ, by
is related to the bilayer curvature modulus, κ, by 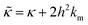 ,121 where km is the monolayer area compressibility and h is the height of the neutral surface from the bilayer midplane. Considering the neutral surface to be at the interface between the hydrophilic head group and the hydrophobic chain, the ZG relaxations rates for bending fluctuations can be expressed as:55,67,121–126
,121 where km is the monolayer area compressibility and h is the height of the neutral surface from the bilayer midplane. Considering the neutral surface to be at the interface between the hydrophilic head group and the hydrophobic chain, the ZG relaxations rates for bending fluctuations can be expressed as:55,67,121–126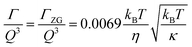 | (2) |
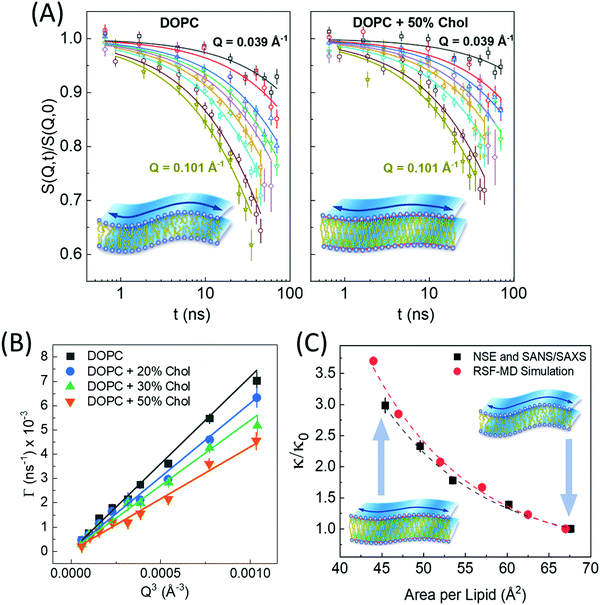 | ||
| Fig. 6 (A) Intermediate scattering functions, S(Q,t)/S(Q,0), of DOPC liposomal membranes with different 0 and 50 mol% cholesterol, along with stretched exponential fits (solid lines) given by eqn (1). The suppressed decays in DOPC-cholesterol membranes (right) indicates slowdown in the measured dynamics. (B) The Q-dependence of the decay rates Γ(Q) follow the classical Q3 behavior of bending undulations. Fits of the decay rates to eqn (2) yield the bending rigidity moduli, κ, shown in (C). The plots of κ vs. area per lipid indicate structural dependence of membrane mechanics on molecular packing obtained from SANS/SAXS studies. The results are confirmed by real-space fluctuation (RSF) analysis of atomistic molecular dynamics (MD) simulations. Figure is reproduced from Chakraborty et al., Proc. Nat. Acad. Sci. U. S. A. 2020.27 | ||
Similar observations were reported in another recent study by Chakraborty et al. on cholesterol-containing di-monounsaturated DOPC lipid membranes.27 Contrary to previous experiments reporting a null stiffening effect of cholesterol on DOPC membranes, they showed that, on the nanoscale, the increase in molecular packing with increasing cholesterol mole fraction results in a commensurate increase in the bending rigidity modulus measured by NSE (Fig. 6C). These results were validated by solid-state deuterium (2H) NMR relaxometry and MD simulations.27 Notably, NSE accesses similar length and time scales as solid-state 2H NMR spectroscopy60–62 and MD simulations.130 Thus, the agreement in the obtained values and trends in κ is a promising observation but it also points to possible scale dependence of observed membrane mechanics.
We note that several other measurement techniques have been used to determine the bending rigidity of lipid membranes, including studies by Klösgen et al. who used cryo-TEM to observe the evolution of vesicle morphologies and indirectly assess the membrane mechanical properties.131 Other techniques utilize direct visualization or manipulation of membrane shape fluctuations to extract the membrane elastic properties. For example, flickering spectroscopy uses image processing to analyze thermally induced shape fluctuations of giant vesicles,132,133 whereas micropipette aspiration methods uses vesicle stretching and applied tension to calculate the membrane area compressibility and bending rigidity.134,135 Other approaches including phase contrast microscopy136 and electrodeformation132 have also been effectively used to examine membrane mechanics. In addition to vesicle studies, diffuse X-ray137 and neutron138 scattering methods on stacked lipid membranes treat diffuse scattering signals as signatures of membrane undulations and use corresponding theoretical models to measure κ. However, unified values of membrane bending rigidity by different methods130 are still a topic of active discussion.
Besides fundamental biophysical studies of structure-driven dynamics in lipid membranes, NSE has also been utilized in understanding the effect of the chemical membrane environment on dynamical and mechanical membrane properties. For example, De Mel et al. used NSE measurements to show that common salt, i.e. sodium chloride (NaCl), increases the bending rigidity of DOPC membranes.73 Their results are in agreement with structural observations by SANS and SAXS indicating an increase in bilayer thickness caused by dehydration effects with increasing ion concentrations. The conclusions from this study concur with a previous NSE study in which the change in solution pH towards acidic conditions resulted in a decrease in the hydration of the lipid head groups and a corresponding increase in membrane rigidity.139
Other NSE studies have focused on the effect of molecular additives on membrane elasticity. For example, Hoffmann et al. showed that the uptake of hydrophobic silica nanoparticles in the tail-region of phospholipid membranes results in a substantial reduction in the membrane bending rigidity, indicating nanoparticle-induced membrane softening.55 In contrast, the interaction of membranes with end-phosphorylated polyethylene glycol (PEG) copolymers, which adsorb weakly to the membrane surface, was found to cause membrane stiffening in DMPC liposomal membranes.140 The obtained results are contrary to conclusions from another NSE study by De Mel et al. where the introduction of membrane-inserting n-alkyl-PEO polymer in liposomal DOPC suspensions caused a decrease in membrane rigidity.74 These studies are starting to illustrate the importance of the mode of interaction between membranes and extracellular macromolecules which resemble the biological polymers abundant in cell environments.
In recent years, NSE has found wide use in drug delivery and pharmaceutical applications, providing crucial information about liposomal stability in the presence of membrane-incorporated drugs or changes in membrane mechanics under disease conditions. For example, NSE studies on antimicrobial peptides, like melittin, showed that melittin induces pore formation and causes a decrease in membrane rigidity,28 potentially elucidating the mechanism by which melittin impacts host cells. Similarly, nonsteroidal anti-inflammatory drugs, like aspirin, were reported to cause up to 33% reduction in bending rigidity.110 These observations are in agreement with the structural effects of common nonsteroidal anti-inflammatory drugs which cause a decrease in bilayer thickness and head group hydration in phospholipid membranes, consequently resulting in reduced membrane rigidity.139 Similar results were reported on aescin, a drug successfully used in treating diseases like chronic venus insufficiency (CVI), hemorrhoids and peripheral oedemic formation. Measurements by SAXS and NSE showed that the H-bond formation between the OH group of aescin and the negatively-charged phosphate groups of phospholipids causes a reduction in membrane rigidity in the gel rippled phase, whereas, the incorporation of the large triterpene backbone of aescin in the bilayer causes an increase in rigidity in the liquid-disordered phase.29
Among the most impactful and unique applications of NSE are studies that utilize judicious isotope labeling to probe selective membrane dynamics not accessible with other experimental approaches. For example, Nickels et al.141 used selectively deuterated lipids and cholesterol to probe the mechanical properties of raft-like lipid domains in quaternary lipid mixtures with well-defined domain sizes (see Fig. 4).32,48 Using different deuteration schemes they were able to isolate the scattering signals from the domains and the matrix, showing that, beside thickness mismatch, the domains and matrix also exhibit different bending rigidities. In a later study, they used bioengineering to control the deuteration profile of the cell membrane of B. subtilis, a Gram-negative bacterium.47 Using SANS, they were able to confirm, for the first time, the existence of nanoscopic lipid domains in live cell membranes. While this study did not look into the mechanical or dynamical properties of the domains, it has paved the way for future neutron spectroscopy studies of membrane dynamics in vivo.
In another remarkable NSE study, Rickeard et al. utilized selective deuteration of a single leaflet in asymmetric liposomal membranes to show that asymmetric bilayers exhibit a higher stiffness than either of their leaflets.49 This led to the conclusion that membrane mechanics are more complex than the simple sum of the properties of their individual leaflets, and that these properties could be influenced by leaflet coupling and internal membrane dissipation.
While the examples highlighted above do not constitute a comprehensive list of NSE studies on lipid membranes, they illustrate the plethora of biological and biophysical phenomena that can be uniquely addressed by NSE.
4.2. Membrane thickness fluctuations
The concept of breathing mode or thickness fluctuations in lipid membranes was theoretically introduced in the early 1980s.142–145 Shortly after, this dynamic mode was associated with vital membrane processes including pore formation146,147 and passive membrane permeation.148 However, the first direct experimental observation of membrane thickness fluctuations was made on oil-swollen surfactant membranes using NSE and isotope labeling.149 Later NSE experiments on phospholipid membranes validated the existence of thickness fluctuations in lipid membranes.68 The experiments utilized selectively deuterated lipids such that the lipid chain region of the membrane was contrast-matched to the D2O medium, amplifying the signal from fluctuations in the head-to-head distance, i.e. membrane thickness (Fig. 2A, right).68In this type of measurements, the thickness fluctuations signal manifests as excess dynamics relative to the bending fluctuation signal and appears at Q values that correspond to the membrane thickness (Fig. 7A). The initial theoretical description of NSE thickness fluctuation signals was formulated in terms of the physical fluctuation parameters, namely the amplitude and relaxation time given by ξ−1 and τTF, respectively. The Lorentzian function used for data fitting assumed the following expression67,68,150
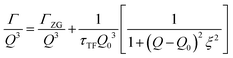 | (3) |
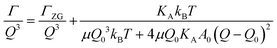 | (4) |
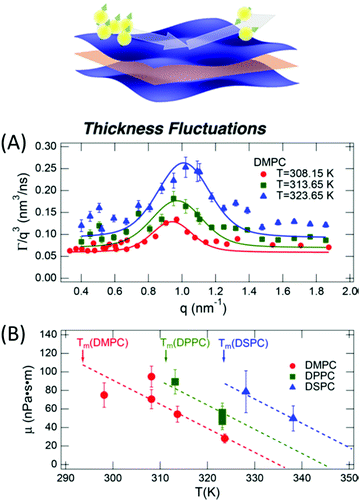 | ||
| Fig. 7 (A) Thickness fluctuations signals measured by NSE on chain deuterated DMPC membranes at different temperatures beyond the membrane phase transition. The signal manifest as a Lorentz distribution of Γ/Q3vs. Q. (B) Fits of the NSE thickness fluctuation signals on DMPC, DPPC, and DSPC following eqn (4) enable estimates of the membrane viscosity. When plotted as a function of temperature, the membrane viscosity shows similar scaling behavior commensurate with changes in temperature-induced changes in the area per lipid (not shown here). Figure is adapted with permission from Nagao et al., J. Phys. Chem. Lett., 8, 19, 4679–4684.67 Copyright 2017 American Chemical Society. | ||
Recently, NSE thickness fluctuation measurements were also conducted on unsaturated DOPC membranes, enabled by the synthesis of a chain-deuterated variant of DOPC.27 Importantly, the viscosity of the DOPC membranes obtained from NSE measurements closely matched viscosity results from tracer diffusion experiments with asymmetric membrane-linked particles.152 When perdeuterated cholesterol, obtained from genetically modified bacteria, was added to DOPC membranes, NSE measurements showed an increase in the membrane viscosity, as expected with increased cholesterol-induced lipid packing. This points toward a scenario where local lipid organization could serve as a mechanism for regulating local membrane viscosity and emergent membrane functions. More importantly, these studies are starting to bridge the gap between diffusive molecular motions governed by membrane viscosity and collective membrane dynamics in the form of thickness fluctuations, thus enabling insights into membrane viscoelastic properties and how they manifest over different scales.
In a similar vein, Gupta et al. used NSE to simultaneously investigate molecular and collective dynamics in lipid membranes. They adopted a model independent approach to calculate the mean squared displacement (MSD) from NSE relaxation spectra of different lipid membranes.56,153 The power-law dependences of the MSDs showed a crossover between ZG membrane undulations and fast lipid tail motions around t ∼ 3 ns, highlighting the hierarchical nature of lipid membranes and the overlap in their different dynamic modes.
4.3. In-plane dynamics and internal motions
Lipid lateral motions are central to the ability of the membrane to organize into rafts, to facilitate the functions of membrane proteins, and to regulate the diffusion of signaling molecules. These motions may include self-diffusion of single lipids or lipid clusters, or collective coordinated lateral dynamics. Importantly, these motions tend to overlap with other membrane dynamics. For instance, lateral motions (∼ns time scales) overlap with internal lipid vibrations (∼ps time scales) as well as collective membrane undulations (∼100 ns time scales). The timescales and energies associated with these motions make them an excellent target for neutron spectroscopy studies. Here we note that some of the neutron backscattering spectrometers (NBS) performing QENS can operate with the highest elastic energy resolution, full width at half maximum (FWHM) of 3.5 μeV for 0.2 < Q < 2.0 Å−1 (BASIS at SNS, USA),154 0.93 μeV for 0.6 < Q < 1.6 Å−1 (HFBS at NIST, USA),155 0.75 μeV for 0.1 < Q < 1.8 Å−1 (IN16B at ILL, France),156 8 μeV for 0.2 < Q < 4.9 Å−1 (IN13 at ILL, France),157 1.4 μeV for 0.08 < Q < 1.98 Å−1 (DNA at J-PARC, Japan).158 Therefore, NBS spectrometers can access membrane dynamics from ns to sub-ps time scales over a range of ∼1–60 Å in length scales, which is ideally suited for characterizing sub-molecular and molecular motions of lipids within model and cell membranes.Indeed, using neutron backscattering spectroscopy, Busch et al. were able, for the first time, to access the fast-localized motion of DMPC lipid molecules and they observed that the entire lipid molecules along with its neighbors undergoes flow-like localized diffusive motions.159 As mentioned earlier, in this type of measurements, the measured dynamics manifest as a broadening of the energy spectrum (as shown in Fig. 8A). Assuming that lateral and internal motions are independent of each other one can model the energy dependent dynamic structure factor as:110,111
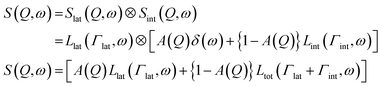 | (5) |
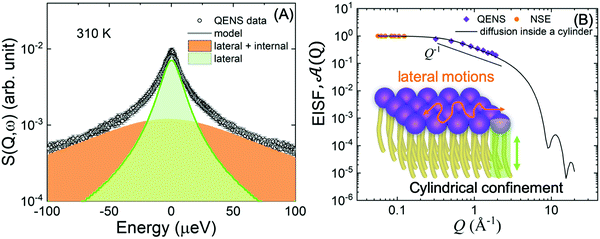 | ||
Fig. 8 (A) Illustration of QENS data fitting using two Lorentzian models described in eqn (5), depicting lateral motions and internal motions of the lipids along with the background. Data adapted from ref. 110. (B) The Q-dependence of the EISF and weighting parameter, ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (Q), compared with a model for a particle confined in a cylinder. Data for figures (A) and (B) are adapted with permission from Sharma et al., J. Phys. Chem. Lett., 7, 2394-2401.111 (Copyright 2016 American Chemical Society) and from Gupta et al., J. Phys. Chem. B, 123, 5667–5669.162 (Copyright 2019 American Chemical Society.) (Q), compared with a model for a particle confined in a cylinder. Data for figures (A) and (B) are adapted with permission from Sharma et al., J. Phys. Chem. Lett., 7, 2394-2401.111 (Copyright 2016 American Chemical Society) and from Gupta et al., J. Phys. Chem. B, 123, 5667–5669.162 (Copyright 2019 American Chemical Society.) | ||
An example of this is shown in Fig. 8A for DMPC membranes at 310 K.111 The quasi-elastic contributions from the lateral and internal motions of the lipids are depicted along with a schematic illustration for easy visualization. From the Q2-dependence of Γlat one can calculate the lateral diffusion coefficient, Dlat. For DMPC membranes, Dlat was found to range from 0.67 to 1.62 Å2 ns−1,51,160 in agreement with results from other techniques, such as pulsed field gradient (PFG) NMR, fluorescence recovery after photobleaching (FRAP), and resonance energy transfer (RET).153,160,161 However, as shown in a recent review by Gupta et al., it is not uncommon to observe discrepancies in diffusion coefficients reported by different methods, since different diffusive regimes are generally associated with different observation length and time scales.51 A comparison of the relaxation spectra between NSE and QENS data has further demonstrated the nature of tail confinement to a cylindrical volume.153Fig. 8B shows the elastic incoherent structure factor (EISF) from QENS, compared with the relative weighting parameter ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (Q) representing the elastic fraction of lipid tail motions from NSE. These results demonstrate the importance of lateral and internal motions, accessed through QENS observations in backscattering spectroscopy, and their effect on lipid tail motions studied by NSE.
(Q) representing the elastic fraction of lipid tail motions from NSE. These results demonstrate the importance of lateral and internal motions, accessed through QENS observations in backscattering spectroscopy, and their effect on lipid tail motions studied by NSE.
The importance of QENS measurements of sub-diffusion and lateral lipid diffusion were exemplified by all atom MD simulation in the work of Rheinstädter and co-workers.163,164 They predicted strong influence of sub-diffusive lipid dynamics on the self-intermediate scattering function and the incoherent dynamic structure factor measured in neutron-scattering experiments. In another study, they reported that the molecular mechanism for lipid motion in a single supported bilayer membrane is continuous diffusion, rather than the flow-like ballistic motion found in the stacked membrane systems.165 More recently, a similar approach was used to study diffusive dynamics in domain-forming lipid membranes with varying temperature.166 The results showed that formed domains function as buffers of diffusive membrane properties, such that high melting lipids increasingly partition to the fluid phase with increasing temperature thus keeping the diffusion coefficient relatively invariable. Note that such measurements are usually performed on lipid stacks oriented parallel to the momentum transfer ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) (i.e. along the z-direction in Fig. 5A). In this case, the measured signal is sensitive to motions along
(i.e. along the z-direction in Fig. 5A). In this case, the measured signal is sensitive to motions along ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) thus enabling studies of in-plane diffusive dynamics.
thus enabling studies of in-plane diffusive dynamics.
Lipid motions in pico- to nanosecond range are also crucial to nanoscopic transport mechanisms in living cells, e.g. these motions could influence the G protein coupled signal transduction cascades where two proteins have to come into contact.167 Thus, QENS studies offer remarkable capabilities in interrogating fast molecular motions and how they relate to biological functions and other membrane properties. These motions are also critical in therapeutic developments. For instance, how drug molecules influence membrane dynamics on a molecular level is central to assessing the drug efficacy or damaging effects. Indeed, QENS studies have already been utilized in evaluating the effect of some drugs on the diffusive dynamics of the lipid membranes they target, showing coefficients that are commensurate with changes to the lipid packing and the membrane rigidity.110,111 These results are reassuring. They assert the conclusions that, despite the complexity of lipid membrane dynamics, common themes are starting to emerge in their structure–property relations.
Recently, QENS was successfully utilized to observe the difference in sub-ns relaxation dynamics of the head groups in single phospholipids in presence of tryptophan amino acid causing a stiffening effect in phospholipid-anchored biomolecules.168 The study demonstrated that the molecular stress and viscoelastic properties of transient lipid rafts can be modulated by using tryptophan. Given that QENS studies bridge dynamical process with corresponding atomic and molecular length scale, they are well positioned for direct validation of force fields used in MD simulations.114 Indeed, different relaxation modes have been validated by combining QENS and MD simulations,169 offering a powerful synergistic approach to gain insight into the molecular interactions governing the structure and dynamics of plasma membranes.
4.4. Exchange kinetics and flip-flop motions
Lipid flip-flop motion is another important feature of cell membrane that is associated with key biological functions including intracellular trafficking, membrane permeability, and programmed cell death.170,171 This mode refers to transverse lipid translocation between the two membrane leaflets. Lipid flip-flop disrupts membrane asymmetry and compositional difference between leaflets in living cells. For example, phospholipid scramblase is associated with increased binding and phagocytosis of human erythrocyte cells by macrophages.172 Thus, interrogating lipid flip-flop motions is crucial to understanding the biophysical processes responsible for the cell viability. These motions are most commonly measured by electron paramagnetic resonance (EPR),173 fluorescence spectroscopy,174 and sum frequency vibrational spectroscopy.175In comparison, approaches based on neutron scattering and selective isotope replacement present a relatively non-invasive means to probe these motions. Indeed, time-resolved SANS (TR-SANS) was first demonstrated by Nakano et al. to determine lipid kinetics described by the rates of trans-bilayer and inter-bilayer exchange in DMPC forming large unilamellar vesicles (LUV).176 They used a strategic contrast-matching scheme where equimolar amounts of deuterated (d) LUVs and protiated (h) LUVs were mixed in 50 vol% of D2O. Lipid exchange between the deuterated and protiated LUVs, as well as flip-flop within individual liposomes, resulted in a reduction of the contrast of LUVs against the solvent, which was detected as a decrease in the scattering intensity over time. They reported the half-life of lipid exchanges and flip-flop motions to be 151 min and 513 min, respectively, and also determined the corresponding rate constants.176 In a later work, the same group showed that the length and saturation of the acyl chain of the lipids used (DMPC, POPC, and POPA) influenced the measured rates. They also found that the inclusion of cholesterol can inhibit the flip-flop motions in DMPC vesicles.177
In recent studies, TR-SANS was successfully employed in understanding the effect of methanol content on flip-flop kinetics using DMPC liposomes with asymmetric isotope labeling.178 Measurements showed that increasing the methanol content in the membrane sped up the flip-flop kinetics and resulted in faster scrambling of the membrane, detected as a homogenization of the NSLDs of the two membrane leaflets which were initially contrasted. On the other hand, Nguyen et al. used TR-SANS to inspect the effects of peptide association on the membrane homogenization by flip-flop.89 They found that external peptide addition resulted in faster flip-flop kinetics and accelerated lipid scrambling across the two leaflets, as opposed to peptide pre-incorporation within the membrane (Fig. 9). In a recent study by Wah et al., TR-SANS studies were performed to compare the inter-membrane transport rates of DMPC on flat solid supports and curved free-standing membranes.53 They reported faster flipping rates for supported layers compared to free-standing membranes, but with similar inter-membrane exchange rates. In another study, they used TR-SANS to validate a novel approach of generating asymmetric phospholipid vesicles through lipid exchange between selectively-labeled liposomes and lipid membrane coatings on silica nanoparticles.54
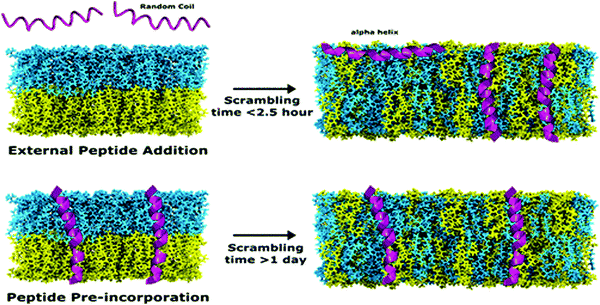 | ||
| Fig. 9 Illustration of the scrambling of asymmetric lipid membranes by flip-flop, as measured by SANS. The study shows that flip-flop kinetics depend on the type of peptides incorporated within the membrane. Figure is adapted with permission from Nguyen et al., Langmuir, 35, 11735–11744.89 Copyright 2019 American Chemical Society. | ||
5. Synergistic approaches: molecular dynamics simulations
A unique feature of neutron scattering and spectroscopy methods in probing membrane structure and dynamics is the length and time scales that they access, which overlap with the scales of molecular dynamics (MD) simulations. Indeed, this powerful combination of experiments and computations has provided significant insights into the molecular mechanisms underlying various structural and dynamic membrane properties, using a consistent feedback loop between experiments and simulations. For instance, the high-resolution measurements of structural membrane parameters, e.g. hydrophobic thickness and area per lipid, by SANS and SAXS has been crucial to the refinement of simulation force fields.179–181 Conversely, using simulations to understand and interpret experimental scattering data has resulted in a better understanding of the molecular behavior of lipid membranes.For instance, recent simulations by Doktorova et al. provided a mechanistic analysis for experimentally-observed changes in flip-flop rates in POPC membranes containing gramicidin.90 They found that accelerated lipid flip-flop is likely driven by the deformation of the membrane by gramicidin. In another study, they used a real-space fluctuation analysis to determine the bending rigidity and area compressibility of common lipid membranes.182 Importantly, their approach provided a plausible explanation for observed discrepancies in the dependence of the membrane bending rigidity, κ, on the area compressibility modulus, KA, in saturated and unsaturated lipid membranes containing cholesterol. Saturated membranes follow the polymer brush model: KA = 24κ/(2Dc)2, where 2Dc is the hydrocarbon chain thickness, also equivalent to mechanical thickness.183 However, this relation fails for unsaturated membranes. Fortunately, the simulations showed that redefining the membrane mechanical thickness in unsaturated lipid membranes, to account for the incompressible double-bond region, rectified the expected polymer brush dependence. These simulations were recently used in DOPC-cholesterol membranes and showed excellent agreement with experimental NSE data of membrane bending fluctuations (Fig. 6C),27 shedding light on the importance of time and length scales over which membrane bending dynamics are measured.
Beside detailed information obtainable from all-atom MD simulations, the development of coarse-grained models has facilitated numerous studies of collective membrane structures and dynamics.184,185 In a recent study, Dorrell et al. used a coarse-grained MD simulation to calculate the SANS spectra on domain-forming lipid membranes.186 They found that, even in the absence of selective isotope labeling or lateral contrast, the presence of lipid domains results in a distinct SANS signal, compared to laterally homogeneous membranes. In another study by Carrillo et al., ultra-coarse-grained modeling of lipid membranes enabled the simulation of an entire lipid vesicle and the calculation of SANS and NSE signals from liposomal suspensions.187 Their simulations showed the same structural and dynamical features observed in neutron scattering experiments. Specifically, the calculated dynamic structure factor yielded the same Lorentz-type NSE signals observed experimentally, confirming that the measured signals are indeed a signature of membrane thickness fluctuations (Fig. 10). A similar ultra-coarse-grained approach was recently applied to large-scale simulations of domain-forming membranes with modulated topography, indicating the dependence of domain growth and localization on the imposed membrane curvature.188 These simulations form a foundation for neutron reflectometry and QENS measurements of lateral membrane organization and in-plane dynamics in a biologically relevant model system where changes in membrane curvature can be used as a mechanical cue to induce organizational and functional changes in the membrane.
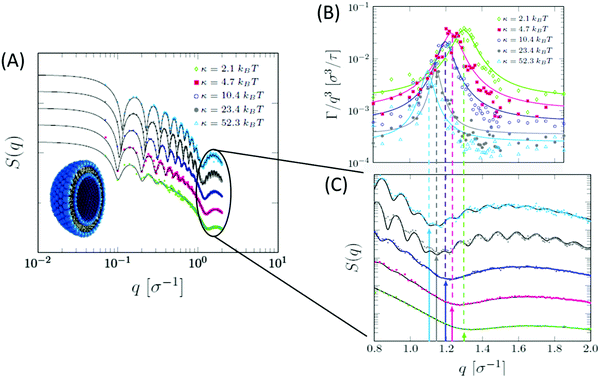 | ||
| Fig. 10 Ultra-coarse-grained MD simulations of liposomes with different membrane rigidities. (A) Structurally, stiffer membranes yielded lower Q values of the dip position in the static structure factor, indicating membrane thickening, as expected. (B) The dynamic structure factor showed the same excess dynamics observed in NSE experiments on tail-contrast-matched liposomes. The observed Lorentz-type signal coincided with the Q values corresponding to the membrane thickness in the static structure factor (C). Data adapted in permission from Carrillo et al., J. Chem. Theory and Comput., 13, 916–925.187 Copyright 2017 American Chemical Society. | ||
These examples illustrate the scientific advances enabled by synergistic developments and applications of scattering methods and computer simulations on lipid membranes. With increasing computing power and advancing scattering techniques, it is more possible than ever to understand the intricate and complex properties of membranes on unexplored scales and under more realistic conditions.
6. Conclusions and outlook
This review summarizes the application of state-of-the art neutron scattering and spectroscopy approaches in investigating molecular and nanoscale structures and dynamics of lipid membranes. The conclusions afforded by recent neutron scattering experiments point to dominant structure-dynamic relationships underlying membrane functions. This type of studies is important not only in understanding the fundamental biophysical properties of lipid and cell membranes, but also in establishing design rules for use in technological and therapeutic membrane applications. This requires knowledge of how the inclusion of drug molecules, sterols, and other molecular additives affect the membrane structural and dynamical response. In addition, the inherently interfacial nature of cell membranes makes them susceptible to environmental changes. Therefore, the ability to simulate physiochemical environments in neutron scattering measurements, while simultaneously probing changes in key membrane features, presents a feat in our biophysical and biological understanding of complex membrane functions.The review also highlights the importance of neutron contrast manipulation in selectively accessing structural hallmarks of functional membranes and their dynamic signatures. While the majority of isotope-labeling in neutron experiments has been done on model lipid membranes, conclusions from these studies have enriched our understanding of analogous functional features in plasma cell membranes. Nonetheless, with advances in bioengineering and selective deuterium labeling of lipidomic components within live cell membranes, it is reasonable to assume that neutron scattering methods can be a game changer in investigating nanoscopic membrane properties, in real time and under real biological conditions.
These possibilities will be further enabled by synergistic combinations of neutron scattering and MD simulations, whereby unexplored molecular mechanisms in membranes can be predicted and validated. This synergistic combination of two powerful techniques has resulted in significant advances in explaining molecular and collective membrane phenomena and relating them to emergent functional membrane properties. The extrapolation of this approach to more complex membrane systems will provide new and unique insights into the complex functions of membranes, their response to environmental changes, and their potential use in advanced technologies.
In summary, neutron scattering techniques are uniquely positioned to play a key role in current and future studies of molecular and nanoscale membrane properties, structurally and dynamically. When combined with MD simulations, these techniques have the potential to reshape our understanding of cell membranes and their continuous structural remodeling, allowing a view of membranes “in action”.
Abbreviations
| DMPC | 1,2-dimyristoyl-sn-glycero-3-phosphocholine |
| DPPC | 1,2-distearoyl-sn-glycero-3-phosphocholine |
| DSPC | 1,2-dipalmitoyl-sn-glycero-phosphocholine |
| DOPC | 1,2-dioleoyl-sn-glycero-phosphocholine |
| POPC | 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine |
| DAPC | diarachidonyl phosphatidyl-choline |
| POPA | 1-palmitoyl-2-oleoylphosphatidic acid |
| NSLD | neutron scattering length density |
| ED | electron density |
| SLD | scattering length density |
| SANS | small-angle neutron scattering |
| SAXS | small-angle X-ray scattering |
| NSE | neutron spin echo |
| QENS | quasi-elastic neutron scattering |
| EISF | elastic incoherent structure factor |
| EPR | electron paramagnetic resonance |
| TR-SANS | time-resolved SANS |
| NR | neutron reflectivity |
| GISANS | grazing incidence SANS |
| NMR | nuclear magnetic resonance |
| MD | molecular dynamics |
Conflicts of interest
There are no conflicts to declare.References
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef CAS PubMed
.
-
T. Auth, S. Dasgupta and G. Gompper, in Physics of Biological Membranes, ed. P. Bassereau and P. Sens, Springer International Publishing, Cham, 2018, pp. 471–498 DOI:10.1007/978-3-030-00630-3_17
.
- E. M. Storck, C. Ozbalci and U. S. Eggert, Annu. Rev. Biochem., 2018, 87, 839–869 CrossRef CAS PubMed
.
- J. S. Bonifacino and B. S. Glick, Cell, 2004, 116, 153–166 CrossRef CAS PubMed
.
- S. V. Verstraeten, G. G. Mackenzie and P. I. Oteiza, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1739–1749 CrossRef CAS PubMed
.
- B. P. Head, H. H. Patel and P. A. Insel, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 532–545 CrossRef CAS PubMed
.
-
N. J. Yang and M. J. Hinner, in Site-Specific Protein Labeling: Methods and Protocols, ed. A. Gautier and M. J. Hinner, Springer New York, New York, NY, 2015, pp. 29–53 DOI:10.1007/978-1-4939-2272-7_3
.
- O. S. Andersen and R. E. Koeppe, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 107–130 CrossRef CAS PubMed
.
- C. E. Cornell, R. A. Black, M. Xue, H. E. Litz, A. Ramsay, M. Gordon, A. Mileant, Z. R. Cohen, J. A. Williams, K. K. Lee, G. P. Drobny and S. L. Keller, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17239–17244 CrossRef CAS PubMed
.
-
G. Cevc, T. M. Allen and S. L. Neidleman, Phospholipids handbook, Marcel Dekker, New York, 1993 Search PubMed
.
- T. Harayama and H. Riezman, Nat. Rev. Mol. Cell Biol., 2018, 19, 281 CrossRef CAS PubMed
.
- E. Lyman, C.-L. Hsieh and C. Eggeling, Biophys. J., 2018, 115, 595–604 CrossRef CAS PubMed
.
- D. Lingwood and K. Simons, Science, 2010, 327, 46–50 CrossRef CAS PubMed
.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef CAS PubMed
.
- S. M. Lu and G. D. Fairn, Crit. Rev. Biochem. Mol. Biol., 2018, 53, 192–207 CrossRef CAS PubMed
.
- K. Simons and D. Toomre, Nat. Rev. Mol. Cell Biol., 2000, 1, 31 CrossRef CAS PubMed
.
- L. Rajendran and K. Simons, J. Cell Sci., 2005, 118, 1099–1102 CrossRef CAS PubMed
.
- I. Levental, K. R. Levental and F. A. Heberle, Trends Cell Biol., 2020, 30, 341–353 CrossRef CAS PubMed
.
- M. Doktorova, J. L. Symons and I. Levental, Nat. Chem. Biol., 2020, 16, 1321–1330 CrossRef CAS PubMed
.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed
.
-
A. D. Banghman, Liposomes: From Physical Studies to Therapeutic Applications, Elsevier/North-Holland, Amsterdam, 1981 Search PubMed
.
- Y. Elani, R. V. Law and O. Ces, Nat. Commun., 2014, 5, 5305 CrossRef CAS PubMed
.
- C. G. Siontorou, G.-P. Nikoleli, D. P. Nikolelis and S. K. Karapetis, Membranes, 2017, 7, 38 CrossRef PubMed
.
- A. Pohorille and D. Deamer, Trends Biotechnol., 2002, 20, 123–128 CrossRef CAS PubMed
.
- C. Xu, S. Hu and X. Chen, Mater. Today, 2016, 19, 516–532 CrossRef CAS PubMed
.
- H. P. Duwe, J. Kaes and E. Sackmann, J. Phys., 1990, 51, 945–961 CrossRef CAS
.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L. R. Stingaciu, R. F. Standaert, F. N. Barrera, J. Katsaras, G. Khelashvili, M. F. Brown and R. Ashkar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 CrossRef CAS PubMed
.
- J. H. Lee, S. M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101 CrossRef PubMed
.
- R. Sreij, C. Dargel, P. Geisler, Y. Hertle, A. Radulescu, S. Pasini, J. Perez, L. H. Moleiro and T. Hellweg, Phys. Chem. Chem. Phys., 2018, 20, 9070–9083 RSC
.
- S. L. Goh, J. J. Amazon and G. W. Feigenson, Biophys. J., 2013, 104, 853–862 CrossRef CAS PubMed
.
- J. Zhao, J. Wu, F. A. Heberle, T. T. Mills, P. Klawitter, G. Huang, G. Costanza and G. W. Feigenson, Biochim. Biophys. Acta, 2007, 1768, 2764–2776 CrossRef CAS PubMed
.
- T. M. Konyakhina, J. Wu, J. D. Mastroianni, F. A. Heberle and G. W. Feigenson, Biochim. Biophys. Acta, 2013, 1828, 2204–2214 CrossRef CAS PubMed
.
- S. L. Veatch, O. Soubias, S. L. Keller and K. Gawrisch, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17650–17655 CrossRef CAS PubMed
.
- S. L. Veatch and S. L. Keller, Phys. Rev. Lett., 2002, 89, 268101 CrossRef PubMed
.
- J. A. Lundbæk, S. A. Collingwood, H. I. Ingólfsson, R. Kapoor and O. S. Andersen, J. R. Soc., Interface, 2010, 7, 373–395 CrossRef PubMed
.
- T. Wacker, J. J. Garcia-Celma, P. Lewe and S. L. A. Andrade, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9995–10000 CrossRef CAS PubMed
.
- S. Aimon, J. Manzi, D. Schmidt, J. A. Poveda Larrosa, P. Bassereau and G. E. S. Toombes, PLoS One, 2011, 6, e25529 CrossRef CAS PubMed
.
- V. P. Torchilin, Nat. Rev. Drug Discovery, 2005, 4, 145–160 CrossRef CAS
.
- G.-P. Nikoleli, C. G. Siontorou, M.-T. Nikolelis, S. Bratakou and D. K. Bendos, Appl. Sci., 2019, 9(9), 1745–1765 CrossRef CAS
.
- F. A. Heberle, J. Pan, R. F. Standaert, P. Drazba, N. Kučerka and J. Katsaras, Eur. Biophys. J., 2012, 41, 875–890 CrossRef CAS PubMed
.
- N. Kučerka, F. A. Heberle, J. Pan and J. Katsaras, Membranes, 2015, 5, 454–472 CrossRef PubMed
.
- B. Eicher, F. A. Heberle, D. Marquardt, G. N. Rechberger, J. Katsaras and G. Pabst, J. Appl. Crystallogr., 2017, 50, 419–429 CrossRef CAS PubMed
.
- N. Kucerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef CAS PubMed
.
- N. Kučerka, J. Pencer, M. P. Nieh and J. Katsaras, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 247–254 CrossRef PubMed
.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef PubMed
.
- N. Kučerka, J. Gallová, D. Uhríková, P. Balgavý, M. Bulacu, S.-J. Marrink and J. Katsaras, Biophys. J., 2009, 97, 1926–1932 CrossRef PubMed
.
- J. D. Nickels, S. Chatterjee, C. B. Stanley, S. Qian, X. Cheng, D. A. A. Myles, R. F. Standaert, J. G. Elkins and J. Katsaras, PLoS Biol., 2017, 15, e2002214 CrossRef PubMed
.
- F. A. Heberle, R. S. Petruzielo, J. Pan, P. Drazba, N. Kučerka, R. F. Standaert, G. W. Feigenson and J. Katsaras, J. Am. Chem. Soc., 2013, 135, 6853–6859 CrossRef CAS PubMed
.
- B. W. Rickeard, M. H. L. Nguyen, M. DiPasquale, C. G. Yip, H. Baker, F. A. Heberle, X. Zuo, E. G. Kelley, M. Nagao and D. Marquardt, Nanoscale, 2020, 12, 1438–1447 RSC
.
- F. A. Heberle, D. Marquardt, M. Doktorova, B. Geier, R. F. Standaert, P. Heftberger, B. Kollmitzer, J. D. Nickels, R. A. Dick, G. W. Feigenson, J. Katsaras, E. London and G. Pabst, Langmuir, 2016, 32, 5195–5200 CrossRef CAS PubMed
.
- S. Gupta, J. U. De Mel and G. J. Schneider, Curr. Opin. Colloid Interface Sci., 2019, 42, 121–136 CrossRef CAS
.
-
A. K. Menon and A. Herrmann, in Encyclopedia of Biophysics, ed. G. C. K. Roberts, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 1261–1264 Search PubMed
.
- B. Wah, J. M. Breidigan, J. Adams, P. Horbal, S. Garg, L. Porcar and U. Perez-Salas, Langmuir, 2017, 33, 3384–3394 CrossRef CAS PubMed
.
- Y. Liu, E. G. Kelley, K. C. Batchu, L. Porcar and U. Perez-Salas, Langmuir, 2020, 36, 8865–8873 CrossRef CAS
.
- I. Hoffmann, R. Michel, M. Sharp, O. Holderer, M. S. Appavou, F. Polzer, B. Farago and M. Gradzielski, Nanoscale, 2014, 6, 6945–6952 RSC
.
- S. Gupta, J. U. De Mel, R. M. Perera, P. Zolnierczuk, M. Bleuel, A. Faraone and G. J. Schneider, J. Phys. Chem. Lett., 2018, 9, 2956–2960 CrossRef CAS PubMed
.
- S. Gupta, M. Camargo, J. Stellbrink, J. Allgaier, A. Radulescu, P. Lindner, E. Zaccarelli, C. N. Likos and D. Richter, Nanoscale, 2015, 7, 13924–13934 RSC
.
- Y. Wu, M. Stefl, A. Olzynska, M. Hof, G. Yahioglu, P. Yip, D. R. Casey, O. Ces, J. Humpolickova and M. K. Kuimova, Phys. Chem. Chem. Phys., 2013, 15, 14986–14993 RSC
.
- I. Sikharulidze, I. P. Dolbnya, A. Fera, A. Madsen, B. I. Ostrovskii and W. H. de Jeu, Phys. Rev. Lett., 2002, 88, 115503 CrossRef PubMed
.
- M. F. Brown, J. Chem. Phys., 1982, 77, 1576–1599 CrossRef CAS
.
- T. R. Molugu, S. Lee and M. F. Brown, Chem. Rev., 2017, 117, 12087–12132 CrossRef CAS PubMed
.
- H. I. Petrache, S. W. Dodd and M. F. Brown, Biophys. J., 2000, 79, 3172–3192 CrossRef CAS PubMed
.
- S. Qian, V. K. Sharma and L. A. Clifton, Langmuir, 2020, 36, 15189–15211 CrossRef CAS PubMed
.
- R. Ashkar, J. Appl. Phys., 2020, 127, 151101 CrossRef CAS
.
- R. Ashkar, H. Z. Bilheux, H. Bordallo, R. Briber, D. J. E. Callaway, X. Cheng, X.-Q. Chu, J. E. Curtis, M. Dadmun, P. Fenimore, D. Fushman, F. Gabel, K. Gupta, F. Herberle, F. Heinrich, L. Hong, J. Katsaras, Z. Kelman, E. Kharlampieva, G. R. Kneller, A. Kovalevsky, S. Krueger, P. Langan, R. Lieberman, Y. Liu, M. Losche, E. Lyman, Y. Mao, J. Marino, C. Mattos, F. Meilleur, P. Moody, J. D. Nickels, W. B. O'Dell, H. O'Neill, U. Perez-Salas, J. Peters, L. Petridis, A. P. Sokolov, C. Stanley, N. Wagner, M. Weinrich, K. Weiss, T. Wymore, Y. Zhang and J. C. Smith, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 1129–1168 CrossRef CAS PubMed
.
- R. Ashkar, M. Nagao, P. D. Butler, A. C. Woodka, M. K. Sen and T. Koga, Biophys. J., 2015, 109, 106–112 CrossRef CAS PubMed
.
- M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler, J. Phys. Chem. Lett., 2017, 4679–4684, DOI:10.1021/acs.jpclett.7b01830
.
- A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao, Phys. Rev. Lett., 2012, 109, 058102 CrossRef PubMed
.
- J. S. Allhusen and J. C. Conboy, Acc. Chem. Res., 2017, 50, 58–65 CrossRef CAS PubMed
.
- U. Essmann and M. L. Berkowitz, Biophys. J., 1999, 76, 2081–2089 CrossRef CAS PubMed
.
- C. J. Glinka, J. G. Barker, B. Hammouda, S. Krueger, J. J. Moyer and W. J. Orts, J. Appl. Crystallogr., 1998, 31, 430–445 CrossRef CAS
.
- P. Balgavý, M. Dubničková, N. Kučerka, M. A. Kiselev, S. P. Yaradaikin and D. Uhríková, Biochim. Biophys. Acta, Biomembr., 2001, 1512, 40–52 CrossRef
.
- J. U. De Mel, S. Gupta, R. M. Perera, L. T. Ngo, P. Zolnierczuk, M. Bleuel, S. V. Pingali and G. J. Schneider, Langmuir, 2020, 36, 9356–9367 CrossRef CAS PubMed
.
- J. U. De Mel, S. Gupta, L. Willner, J. Allgaier, L. R. Stingaciu, M. Bleuel and G. J. Schneider, Langmuir, 2021, 37, 2362–2375 CrossRef CAS PubMed
.
- S. Ristori, J. Oberdisse, I. Grillo, A. Donati and O. Spalla, Biophys. J., 2005, 88, 535–547 CrossRef CAS PubMed
.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef PubMed
.
- A. R. Braun and J. N. Sachs, J. Chem. Theory Comput., 2014, 10, 4160–4168 CrossRef CAS PubMed
.
- E. Drolle, N. Kučerka, M. I. Hoopes, Y. Choi, J. Katsaras, M. Karttunen and Z. Leonenko, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 2247–2254 CrossRef CAS PubMed
.
- J. C. Fogarty, M. Arjunwadkar, S. A. Pandit and J. Pan, Biochim. Biophys. Acta, Biomembr., 2015, 1848, 662–672 CrossRef CAS PubMed
.
- L. Tan, J. G. Elkins, B. H. Davison, E. G. Kelley and J. Nickels, J. Appl. Crystallogr., 2021, 54, 363–370 CrossRef CAS
.
- J. J. Kinnun, D. Bolmatov, M. O. Lavrentovich and J. Katsaras, Chem. Phys. Lipids, 2020, 232, 104976 CrossRef CAS PubMed
.
- F. A. Heberle and G. Pabst, Biophys. Rev., 2017, 9, 353–373 CrossRef CAS PubMed
.
- W. Knoll, K. Ibel and E. Sackmann, Biochemistry, 1981, 20, 6379–6383 CrossRef CAS PubMed
.
- W. Knoll, G. Schmidt, E. Sackmann and K. Ibel, J. Chem. Phys., 1983, 79, 3439–3442 CrossRef CAS
.
- J. Pencer, T. Mills, V. Anghel, S. Krueger, R. M. Epand and J. Katsaras, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 18, 447–458 CrossRef CAS PubMed
.
- F. A. Heberle, M. Doktorova, H. L. Scott, A. D. Skinkle, M. N. Waxham and I. Levental, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19943–19952 CrossRef CAS PubMed
.
- C. E. Cornell, A. Mileant, N. Thakkar, K. K. Lee and S. L. Keller, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19713–19719 CrossRef CAS PubMed
.
- M. Doktorova, F. A. Heberle, B. Eicher, R. F. Standaert, J. Katsaras, E. London, G. Pabst and D. Marquardt, Nat. Protoc., 2018, 13, 2086–2101 CrossRef CAS PubMed
.
- M. H. L. Nguyen, M. DiPasquale, B. W. Rickeard, M. Doktorova, F. A. Heberle, H. L. Scott, F. N. Barrera, G. Taylor, C. P. Collier, C. B. Stanley, J. Katsaras and D. Marquardt, Langmuir, 2019, 35, 11735–11744 CrossRef CAS PubMed
.
- M. Doktorova, F. A. Heberle, D. Marquardt, R. Rusinova, R. L. Sanford, T. A. Peyear, J. Katsaras, G. W. Feigenson, H. Weinstein and O. S. Andersen, Biophys. J., 2019, 116, 860–873 CrossRef CAS PubMed
.
-
J. Katsaras and T. Gutberlet, Lipid Bilayers: Structure and Interactions, Springer-Verlag, Berlin, Heidelberg, 2001 Search PubMed
.
- J. Majewski, T. L. Kuhl, J. Y. Wong and G. S. Smith, Rev. Mol. Biotechnol., 2000, 74, 207–231 CrossRef CAS PubMed
.
- J. Y. Wong, J. Majewski, M. Seitz, C. K. Park, J. N. Israelachvili and G. S. Smith, Biophys. J., 1999, 77, 1445–1457 CrossRef CAS PubMed
.
- D. Marquardt, F. A. Heberle, D. V. Greathouse, R. E. Koeppe, R. F. Standaert, B. J. Van Oosten, T. A. Harroun, J. J. Kinnun, J. A. Williams, S. R. Wassall and J. Katsaras, Soft Matter, 2016, 12, 9417–9428 RSC
.
- Y. Gerelli, L. Porcar and G. Fragneto, Langmuir, 2012, 28, 15922–15928 CrossRef CAS PubMed
.
- D. P. Hoogerheide, S. Y. Noskov, D. Jacobs, L. Bergdoll, V. Silin, D. L. Worcester, J. Abramson, H. Nanda, T. K. Rostovtseva and S. M. Bezrukov, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E3622–E3631 CrossRef CAS PubMed
.
- H. Nanda, S. A. K. Datta, F. Heinrich, M. Lösche, A. Rein, S. Krueger and J. E. Curtis, Biophys. J., 2010, 99, 2516–2524 CrossRef CAS PubMed
.
- B. Akgun, S. Satija, H. Nanda, G. F. Pirrone, X. Shi, J. R. Engen and M. S. Kent, Structure, 2013, 21, 1822–1833 CrossRef CAS PubMed
.
- R. J. El-khouri, D. A. Bricarello, E. B. Watkins, C. Y. Kim, C. E. Miller, T. E. Patten, A. N. Parikh and T. L. Kuhl, Nano Lett., 2011, 11, 2169–2172 CrossRef CAS PubMed
.
- D. Vaknin, K. Kjaer, J. Als-Nielsen and M. Lösche, Biophys. J., 1991, 59, 1325–1332 CrossRef CAS PubMed
.
- S. J. Johnson, T. M. Bayerl, D. C. McDermott, G. W. Adam, A. R. Rennie, R. K. Thomas and E. Sackmann, Biophys. J., 1991, 59, 289–294 CrossRef CAS PubMed
.
- J. Pan, F. A. Heberle, J. R. Carmichael, J. F. Ankner and J. Katsaras, J. Appl. Crystallogr., 2012, 45, 1219–1227 CrossRef CAS
.
- J. R. Lu, Z. X. Li, R. K. Thomas, B. P. Binks, D. Crichton, P. D. I. Fletcher, J. R. McNab and J. Penfold, J. Phys. Chem. B, 1998, 102, 5785–5793 CrossRef CAS
.
- G. Mangiapia, M. Gvaramia, L. Kuhrts, J. Teixeira, A. Koutsioubas, O. Soltwedel and H. Frielinghaus, Phys. Chem. Chem. Phys., 2017, 19, 32057–32071 RSC
.
- S. Jaksch, F. Lipfert, A. Koutsioubas, S. Mattauch, O. Holderer, O. Ivanova, H. Frielinghaus, S. Hertrich, S. F. Fischer and B. Nickel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022716 CrossRef PubMed
.
- M. F. Brown, A. A. Ribeiro and G. D. Williams, Proc. Natl. Acad. Sci. U. S. A., 1983, 80, 4325–4329 CrossRef CAS PubMed
.
- M. Monkenbusch, R. Schatzler and D. Richter, Nucl. Instrum. Methods Phys. Res., Sect. A, 1997, 399, 301–323 CrossRef CAS
.
- M. Ohl, M. Monkenbusch, N. Arend, T. Kozielewski, G. Vehres, C. Tiemann, M. Butzek, H. Soltner, U. Giesen, R. Achten, H. Stelzer, B. Lindenau, A. Budwig, H. Kleines, M. Drochner, P. Kaemmerling, M. Wagener, R. Möller, E. B. Iverson, M. Sharp and D. Richter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 696, 85–99 CrossRef CAS
.
- M. C. Rheinstadter, W. Haussler and T. Salditt, Phys. Rev. Lett., 2006, 97, 048103 CrossRef PubMed
.
- V. K. Sharma, E. Mamontov, M. Ohl and M. Tyagi, Phys. Chem. Chem. Phys., 2017, 19, 2514–2524 RSC
.
- V. K. Sharma, E. Mamontov, M. Tyagi, S. Qian, D. K. Rai and V. S. Urban, J. Phys. Chem. Lett., 2016, 7, 2394–2401 CrossRef CAS PubMed
.
- M. C. Rheinstadter, T. Seydel, F. Demmel and T. Salditt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061908 CrossRef PubMed
.
- M. C. Rheinstadter, C. Ollinger, G. Fragneto, F. Demmel and T. Salditt, Phys. Rev. Lett., 2004, 93, 108107 CrossRef CAS PubMed
.
- L. Lautner, K. Pluhackova, N. K. H. Barth, T. Seydel, W. Lohstroh, R. A. Bockmann and T. Unruh, Chem. Phys. Lipids, 2017, 206, 28–42 CrossRef CAS PubMed
.
- M. C. Rheinstadter, K. Schmalzl, K. Wood and D. Strauch, Phys. Rev. Lett., 2009, 103, 128104 CrossRef PubMed
.
- B. Farago, P. Falus, I. Hoffmann, M. Gradzielski, F. Thomas and C. Gomez, Neutron News, 2015, 26, 15–17 CrossRef
.
- T. Kumarage, J. Nguyen and R. Ashkar, JoVE, 2021, e62396, DOI:10.3791/62396
.
- M. Ferrand, A. J. Dianoux, W. Petry and G. Zaccaï, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 9668–9672 CrossRef CAS PubMed
.
- L. N. Yamada, H. Seto, T. Takeda, M. Nagao, Y. Kawabata and K. Inoue, J. Phys. Soc. Jpn., 2005, 74, 2853–2859 CrossRef
.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS PubMed
.
- M. C. Watson and F. L. Brown, Biophys. J., 2010, 98, L9–L11 CrossRef CAS PubMed
.
- R. P. Rand and N. L. Fuller, Biophys. J., 1994, 66, 2127–2138 CrossRef CAS PubMed
.
- R. H. Templer, B. J. Khoo and J. M. Seddon, Langmuir, 1998, 14, 7427–7434 CrossRef CAS
.
- M. Winterhalter and W. Helfrich, J. Phys. Chem., 1992, 96, 327–330 CrossRef CAS
.
- F. Campelo, C. Arnarez, S. J. Marrink and M. M. Kozlov, Adv. Colloid Interface Sci., 2014, 208, 25–33 CrossRef CAS PubMed
.
- B. Kollmitzer, P. Heftberger, M. Rappolt and G. Pabst, Soft Matter, 2013, 9, 10877–10884 RSC
.
- L. R. Arriaga, I. Lopez-Montero, G. Orts-Gil, B. Farago, T. Hellweg and F. Monroy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031908 CrossRef PubMed
.
- M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler, J. Phys. Chem. Lett., 2017, 8, 4679–4684 CrossRef CAS PubMed
.
- E. G. Kelley, P. D. Butler, R. Ashkar, R. Bradbury and M. Nagao, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 23365–23373 CrossRef CAS PubMed
.
- M. Doktorova, D. Harries and G. Khelashvili, Phys. Chem. Chem. Phys., 2017, 19, 16806–16818 RSC
.
- B. Klösgen and W. Helfrich, Biophys. J., 1997, 73, 3016–3029 CrossRef
.
- G. Niggemann, M. Kummrow and W. Helfrich, J. Phys. II, 1995, 5, 413–425 CrossRef CAS
.
- D. Drabik, G. Chodaczek, S. Kraszewski and M. Langner, Langmuir, 2020, 36, 3826–3835 CrossRef CAS PubMed
.
- J. Henriksen, A. C. Rowat, E. Brief, Y. W. Hsueh, J. L. Thewalt, M. J. Zuckermann and J. H. Ipsen, Biophys. J., 2006, 90, 1639–1649 CrossRef CAS PubMed
.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097 CrossRef CAS PubMed
.
- P. Méléard, C. Gerbeaud, T. Pott, L. Fernandez-Puente, I. Bivas, M. D. Mitov, J. Dufourcq and P. Bothorel, Biophys. J., 1997, 72, 2616–2629 CrossRef
.
- J. Pan, S. Tristram-Nagle and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021931 CrossRef PubMed
.
- T. Salditt, C. Münster, U. Mennicke, C. Ollinger and G. Fragneto, Langmuir, 2003, 19, 7703–7711 CrossRef CAS
.
- M. B. Boggara, A. Faraone and R. Krishnamoorti, J. Phys. Chem. B, 2010, 114, 8061–8066 CrossRef CAS PubMed
.
- J. Yu, J. Mao, M. Nagao, W. Bu, B. Lin, K. Hong, Z. Jiang, Y. Liu, S. Qian, M. Tirrell and W. Chen, Soft Matter, 2020, 16, 983–989 RSC
.
- J. D. Nickels, X. Cheng, B. Mostofian, C. Stanley, B. Lindner, F. A. Heberle, S. Perticaroli, M. Feygenson, T. Egami, R. F. Standaert, J. C. Smith, D. A. A. Myles, M. Ohl and J. Katsaras, J. Am. Chem. Soc., 2015, 137, 15772–15780 CrossRef CAS PubMed
.
- D. Bach and I. R. Miller, Biophys. J., 1980, 29, 183–187 CrossRef CAS PubMed
.
- S. B. Hladky and D. W. Gruen, Biophys. J., 1982, 38, 251–258 CrossRef CAS
.
- I. R. Miller, Biophys. J., 1984, 45, 643–644 CrossRef CAS
.
- J. N. Israelachvili and H. Wennerstroem, J. Phys. Chem., 1992, 96, 520–531 CrossRef CAS
.
- L. Movileanu, D. Popescu, S. Ion and A. I. Popescu, Bull. Math. Biol., 2006, 68, 1231–1255 CrossRef CAS PubMed
.
- W. F. Bennett, N. Sapay and D. P. Tieleman, Biophys. J., 2014, 106, 210–219 CrossRef CAS PubMed
.
- M. Orsia and J. W. Essex, Soft Matter, 2010, 6, 3797–3808 RSC
.
- M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031606 CrossRef PubMed
.
- M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031606 CrossRef PubMed
.
- R. J. Bingham, S. W. Smye and P. D. Olmsted, EPL, 2015, 111, 18004 CrossRef
.
- T. T. Hormel, S. Q. Kurihara, M. K. Brennan, M. C. Wozniak and R. Parthasarathy, Phys. Rev. Lett., 2014, 112, 188101 CrossRef PubMed
.
- S. Gupta and G. J. Schneider, Soft Matter, 2020, 16, 3245–3256 RSC
.
- E. Mamontov and K. W. Herwig, Rev. Sci. Instrum., 2011, 82, 085109 CrossRef CAS
.
- A. Meyer, R. M. Dimeo, P. M. Gehring and D. A. Neumann, Rev. Sci. Instrum., 2003, 74, 2759–2777 CrossRef CAS
.
- M. Appel, B. Frick and A. Magerl, Sci. Rep., 2018, 8, 13580 CrossRef
.
- N. Francesca, J. Peters, D. Russo, S. Barbieri, C. Chiapponi, A. Cupane, A. Deriu, M. T. Di Bari, E. Farhi, Y. Gerelli, P. Mariani, A. Paciaroni, C. Rivasseau, G. Schirò and F. Sonvico, Neutron News, 2008, 19, 14–18 CrossRef
.
- R. Kajimoto, T. Yokoo, M. Nakamura, Y. Kawakita, M. Matsuura, H. Endo, H. Seto, S. Itoh, K. Nakajima and S. Ohira-Kawamura, Phys. B: Condens. Matter, 2019, 562, 148–154 CrossRef CAS
.
- S. Busch, C. Smuda, L. C. Pardo and T. Unruh, J. Am. Chem. Soc., 2010, 132, 3232–3233 CrossRef CAS PubMed
.
- M. E. Johnson, D. A. Berk, D. Blankschtein, D. E. Golan, R. K. Jain and R. S. Langer, Biophys. J., 1996, 71, 2656–2668 CrossRef CAS PubMed
.
- T. Kawaguchi, R. Kita, N. Shinyashiki, S. Yagihara and M. Fukuzaki, Trans. Mater. Res. Soc. Jpn., 2016, 41, 359–362 CrossRef CAS
.
- S. Gupta, J. U. De Mel and G. J. Schneider, J. Phys. Chem. B, 2019, 123, 5667–5669 CrossRef CAS PubMed
.
- E. Flenner, J. Das, M. C. Rheinstadter and I. Kosztin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011907 CrossRef PubMed
.
- C. L. Armstrong, M. Trapp, J. Peters, T. Seydel and M. C. Rheinstädter, Soft Matter, 2011, 7, 8358–8362 RSC
.
- C. L. Armstrong, M. D. Kaye, M. Zamponi, E. Mamontov, M. Tyagi, T. Jenkins and M. C. Rheinstädter, Soft Matter, 2010, 6, 5864–5867 RSC
.
- J. D. Nickels, M. D. Smith, R. J. Alsop, S. Himbert, A. Yahya, D. Cordner, P. Zolnierczuk, C. B. Stanley, J. Katsaras, X. Cheng and M. C. Rheinstädter, J. Phys. Chem. B, 2019, 123(9), 2050–2056 CrossRef CAS PubMed
.
- M. I. Simon, M. P. Strathmann and N. Gautam, Science, 1991, 252, 802–808 CrossRef CAS PubMed
.
- D. Bolmatov, D. Soloviov, M. Zhernenkov, D. Zav'yalov, E. Mamontov, A. Suvorov, Y. Q. Cai and J. Katsaras, Langmuir, 2020, 36, 4887–4896 CrossRef CAS PubMed
.
- H. Morhenn, S. Busch, H. Meyer, D. Richter, W. Petry and T. Unruh, Phys. Rev. Lett., 2013, 111, 173003 CrossRef
.
- F. X. Contreras, L. Sánchez-Magraner, A. Alonso and F. M. Goñi, FEBS Lett., 2010, 584, 1779–1786 CrossRef CAS
.
- A. A. Gurtovenko and I. Vattulainen, J. Phys. Chem. B, 2007, 111, 13554–13559 CrossRef CAS
.
- L. McEvoy, P. Williamson and R. A. Schlegel, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 3311–3315 CrossRef CAS PubMed
.
- H. M. McConnell and R. D. Kornberg, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS PubMed
.
- E. Pantaler, D. Kamp and C. W. M. Haest, Biochim. Biophys. Acta, Biomembr., 2000, 1509, 397–408 CrossRef CAS
.
- J. Liu and J. C. Conboy, Biophys. J., 2005, 89, 2522–2532 CrossRef CAS PubMed
.
- M. Nakano, M. Fukuda, T. Kudo, H. Endo and T. Handa, Phys. Rev. Lett., 2007, 98, 238101 CrossRef PubMed
.
- M. Nakano, M. Fukuda, T. Kudo, N. Matsuzaki, T. Azuma, K. Sekine, H. Endo and T. Handa, J. Phys. Chem. B, 2009, 113, 6745–6748 CrossRef CAS PubMed
.
- M. H. L. Nguyen, M. DiPasquale, B. W. Rickeard, C. B. Stanley, E. G. Kelley and D. Marquardt, Biophys. J., 2019, 116, 755–759 CrossRef CAS PubMed
.
- N. Kučerka, B. W. Holland, C. G. Gray, B. Tomberli and J. Katsaras, J. Phys. Chem. B, 2012, 116, 232–239 CrossRef PubMed
.
- M. Doktorova, N. Kučerka, J. J. Kinnun, J. Pan, D. Marquardt, H. L. Scott, R. M. Venable, R. W. Pastor, S. R. Wassall, J. Katsaras and F. A. Heberle, J. Phys. Chem. B, 2020, 124, 5186–5200 CrossRef CAS PubMed
.
- A. R. Braun, J. N. Sachs and J. F. Nagle, J. Phys. Chem. B, 2013, 117, 5065–5072 CrossRef CAS PubMed
.
- M. Doktorova, M. V. LeVine, G. Khelashvili and H. Weinstein, Biophys. J., 2019, 116, 487–502 CrossRef CAS PubMed
.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS
.
- M. W. Dorrell, F. A. Heberle, J. Katsaras, L. Maibaum, E. Lyman and A. J. Sodt, J. Chem. Theory Comput., 2020, 16, 5287–5300 CrossRef CAS PubMed
.
- J.-M. Y. Carrillo, J. Katsaras, B. G. Sumpter and R. Ashkar, J. Chem. Theory Comput., 2017, 13, 916–925 CrossRef CAS PubMed
.
- W. Li, J. M. Y. Carrillo, J. Katsaras, B. G. Sumpter, R. Ashkar and R. Kumar, Soft Matter, 2019, 15, 6642–6649 RSC
.
| This journal is © The Royal Society of Chemistry 2021 |